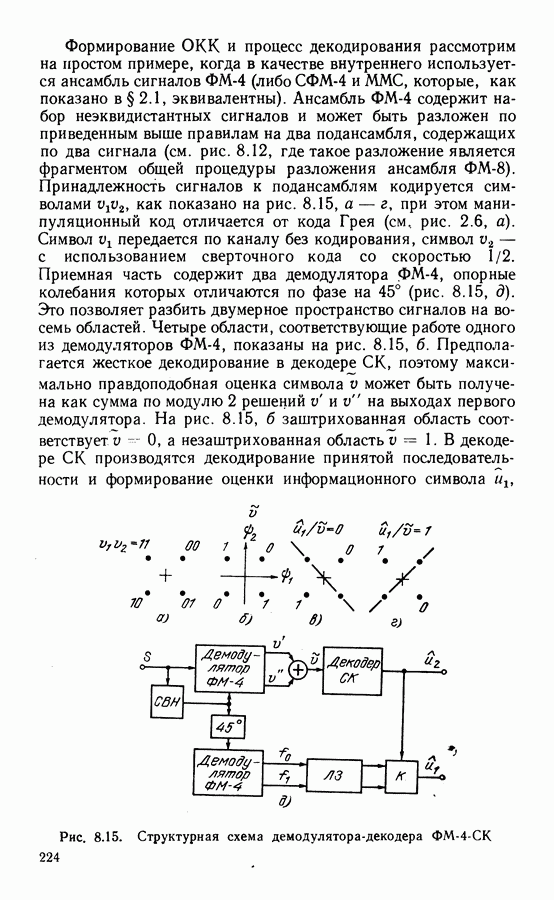
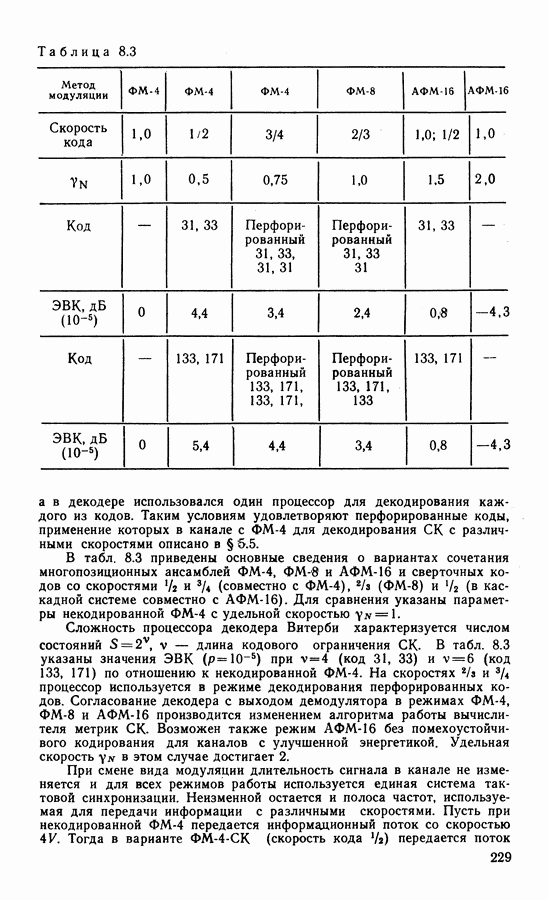
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 8. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ И КОДИРОВАНИЯ В ЦССС
8.1. МОДУЛЯЦИЯ С НЕПРЕРЫВНОЙ ФАЗОЙ
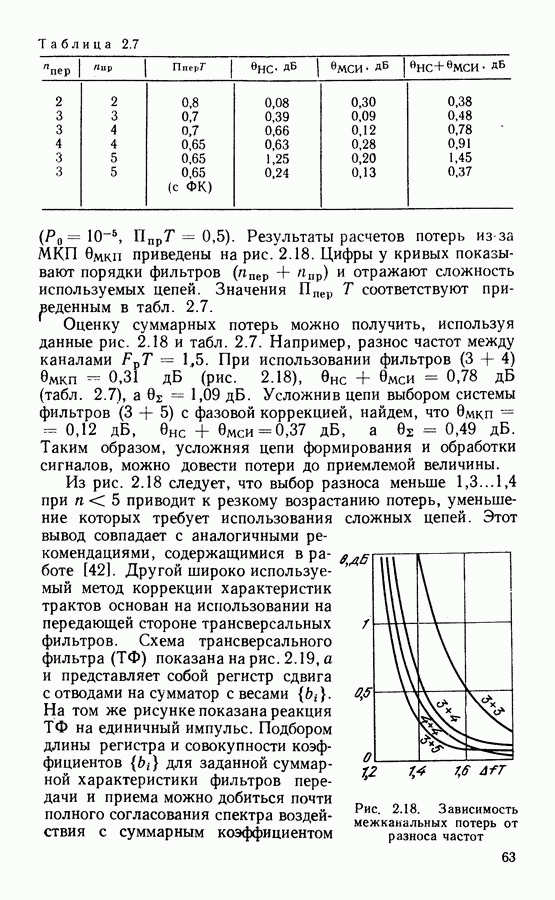
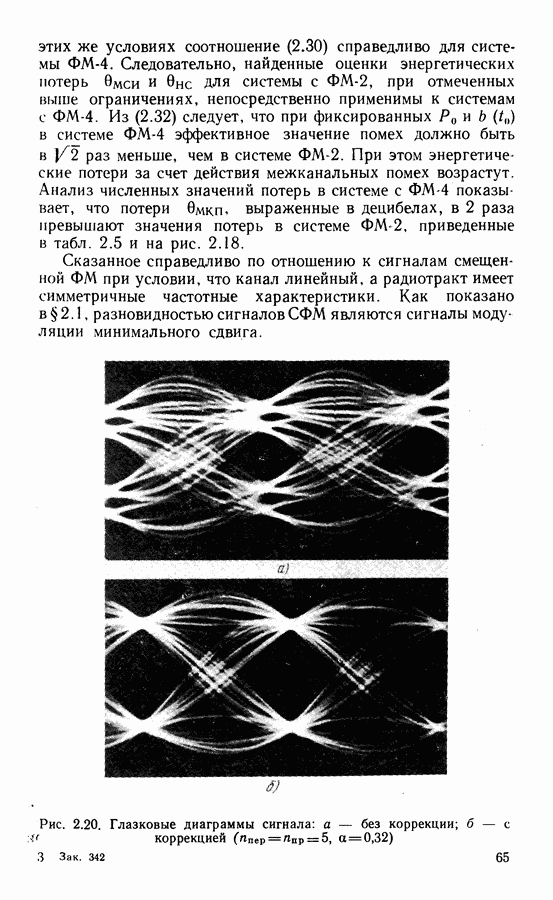
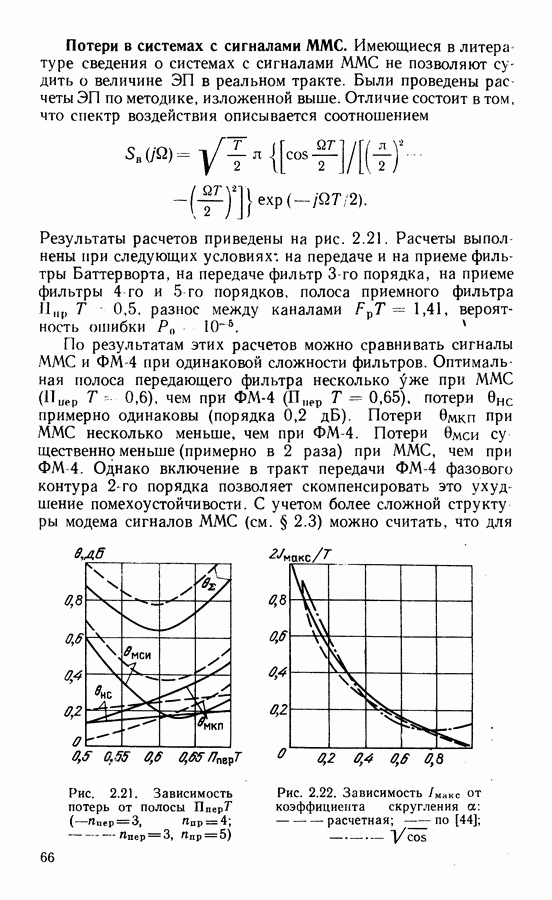
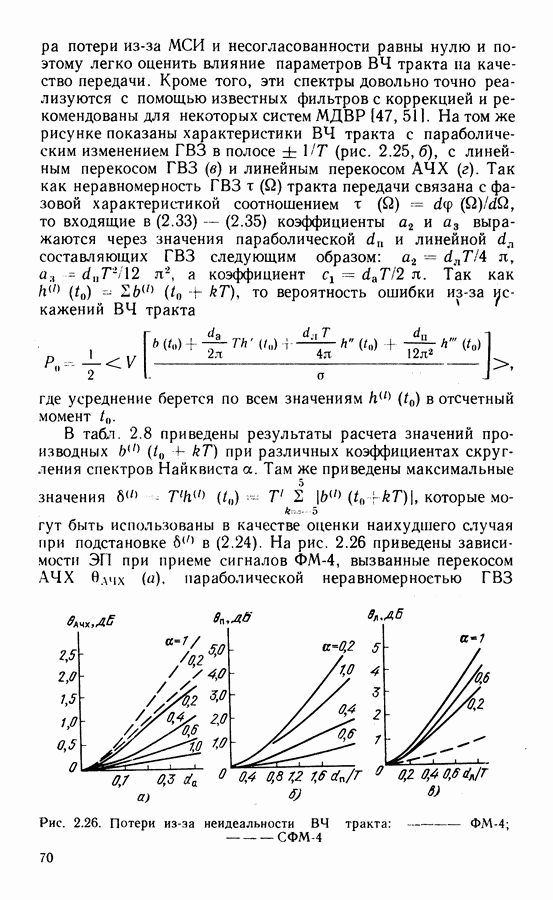
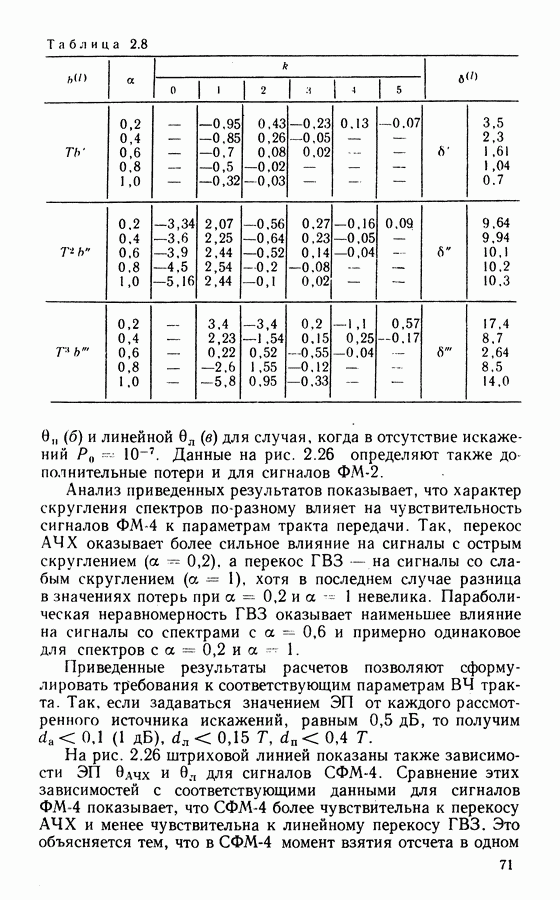
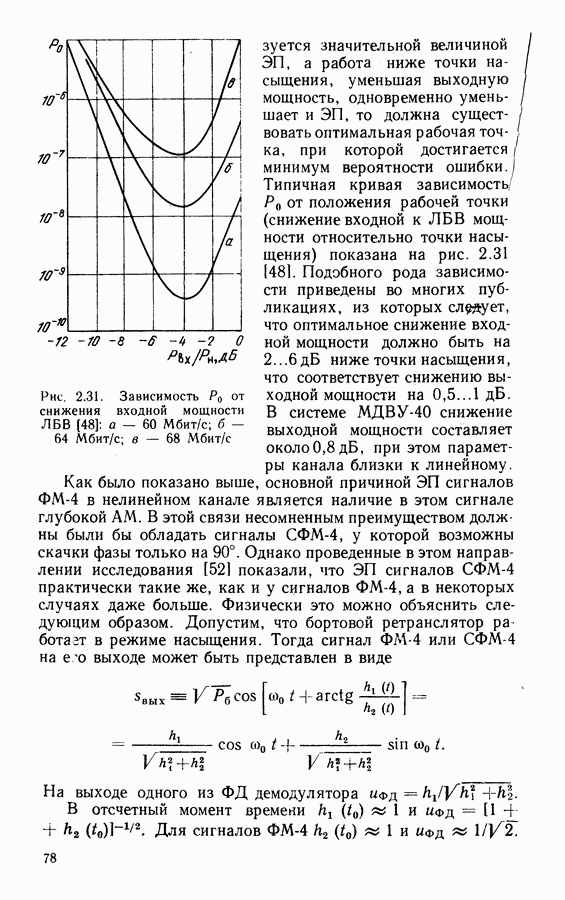
Как отмечалось в гл. 2, в современных ССС широко применяют сигналы ФМ-4, обеспечивающие предельную частотную эффективность 2 бит/с Гц, высокую энергетическую эффективность при простой реализации модема. С учетом межсимвольных и межканальных помех удельная скорость снижается до 1,5 ... 1,9 бит/с Гц. Уменьшение потерь частотной эффективности возможно при переходе к сигналам с постоянной огибающей и компактным спектром. Этим требованиям удовлетворяют фазомодулированные сигналы с непрерывной фазой (НФ).
В общем случае дискретный сигнал с постоянной огибающей и НФ

где  последовательность М-ичных информационных символов (М — четное);
последовательность М-ичных информационных символов (М — четное);  длительность символа. Передаваемая информация заключена в фазе
длительность символа. Передаваемая информация заключена в фазе

Здесь  частотный импульс, отражающий форму изменения частоты сигнала при действии единичного информационного символа
частотный импульс, отражающий форму изменения частоты сигнала при действии единичного информационного символа  индекс модуляции
индекс модуляции 
Выражения (8.1), (8.2) определяют один из способов формирования сигналов НФ с использованием частотного модулятора ЧМ (рис. 8.1). Каждый входной информационный символ  умножается на функцию
умножается на функцию  Поступающие последовательно во времени сигналы
Поступающие последовательно во времени сигналы  умножаются на постоянный коэффициент
умножаются на постоянный коэффициент  и подаются на вход ЧМ с центральной частотой
и подаются на вход ЧМ с центральной частотой 
Длительность частотного импульса полагается равной  При
При  модулирующие импульсы не перекрываются (модуляция полным откликом). При
модулирующие импульсы не перекрываются (модуляция полным откликом). При  имеет место модуляция частичным откликом.
имеет место модуляция частичным откликом.
Изменения фазы сигнала можно определить формой фазового импульса

В этом случае

Формирование сигнала с НФ возможно также с применением фазового модулятора. При этом в соответствии с выражениями (8.3), (8.4) необходимо учитывать накопление текущих значений фазы на предыдущих интервалах  Параметры
Параметры  а также форма импульса
а также форма импульса  либо
либо  полностью определяют вид сигнала.
полностью определяют вид сигнала.
В простейшем случае частотный импульс имеет форму прямоугольника

Тогда фазовый импульс

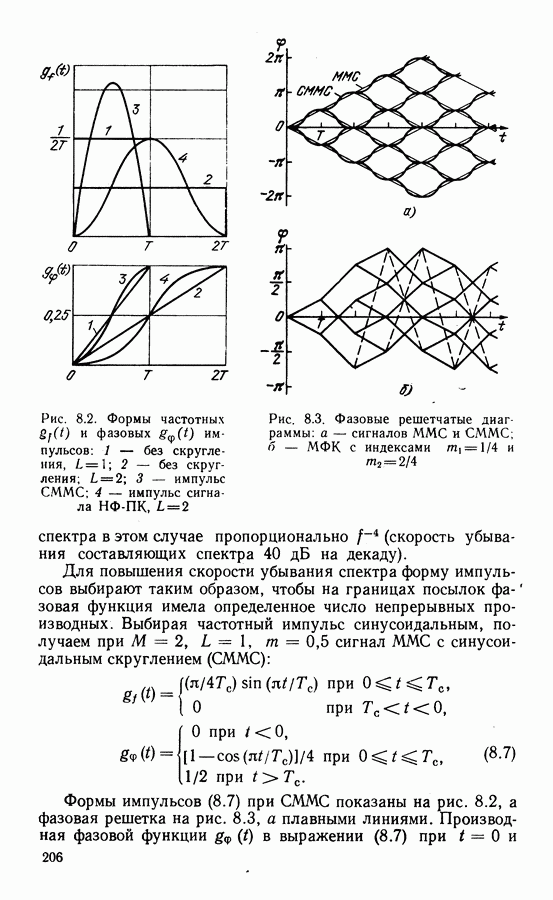
Формы  для
для  показаны на рис. 8.2. При
показаны на рис. 8.2. При  частотный и фазовый импульсы (8.5), (8.6) определяют сигнал модуляции минимального частотного сдвига ММС, подробно рассмотренный в § 2.1
частотный и фазовый импульсы (8.5), (8.6) определяют сигнал модуляции минимального частотного сдвига ММС, подробно рассмотренный в § 2.1  .
.
Зависимость текущей фазы сигнала с импульсами вида (8.5), (8.6) от времени имеет вид ломаной линии, составленной из отрезков длительностью, кратной  На рис. 8.3, а показано множество фазовых траекторий сигнала ММС в виде фазовой решетки. Приращение фазы
На рис. 8.3, а показано множество фазовых траекторий сигнала ММС в виде фазовой решетки. Приращение фазы  на интервале
на интервале  соответствует поступлению на вход модулятора символа
соответствует поступлению на вход модулятора символа 
1, а приращение  поступлению символа
поступлению символа  Фаза сигнала с фазовым импульсом
Фаза сигнала с фазовым импульсом  без скругления вида (8.6) не имеет непрерывных произвольных
без скругления вида (8.6) не имеет непрерывных произвольных  Как отмечалось в § 2.2, убывание
Как отмечалось в § 2.2, убывание

Рис. 8.1. Структурная схема модулятора сигналов с НФ

Рис. 8.2. Формы частотных  и фазовых
и фазовых  импульсов: 1 — без скругления,
импульсов: 1 — без скругления,  без скругления;
без скругления;  импульс СММС; 4 - импульс сигнала
импульс СММС; 4 - импульс сигнала 

Рис. 8.3. Фазовые решетчатые диаграммы: а — сигналов ММС и СММС; б - МФК с индексами 
спектра в этом случае пропорционально  (скорость убывания составляющих спектра
(скорость убывания составляющих спектра  на декаду).
на декаду).
Для повышения скорости убывания спектра форму импульсов выбирают таким образом, чтобы на границах посылок  зовая функция имела определенное число непрерывных производных. Выбирая частотный импульс синусоидальным, получаем при
зовая функция имела определенное число непрерывных производных. Выбирая частотный импульс синусоидальным, получаем при  сигнал ММС с синусоидальным скруглением
сигнал ММС с синусоидальным скруглением 

Формы импульсов (8.7) при СММС показаны на рис. 8.2, а фазовая решетка на рис. 8.3, а плавными линиями. Производная фазовой функции  в выражении (8.7) при
в выражении (8.7) при  и
и
 равна нулю. Следовательно,
равна нулю. Следовательно,  и спектр сигнала СММС убывает как
и спектр сигнала СММС убывает как  на декаду).
на декаду).
Для сглаживания модулирующих импульсов широко используется функция поднятого косинуса. В общем случае частотный и фазовый импульсы сигнала с непрерывной фазой и скруглением по закону поднятого косинуса имеют вид

Форма импульсов для  показана на рис. 8.2. Для функций вида (8.8) параметр
показана на рис. 8.2. Для функций вида (8.8) параметр  и спектр сигнала убывает в этом случае как
и спектр сигнала убывает в этом случае как  (
( на декаду). Возможны и другие формы функций
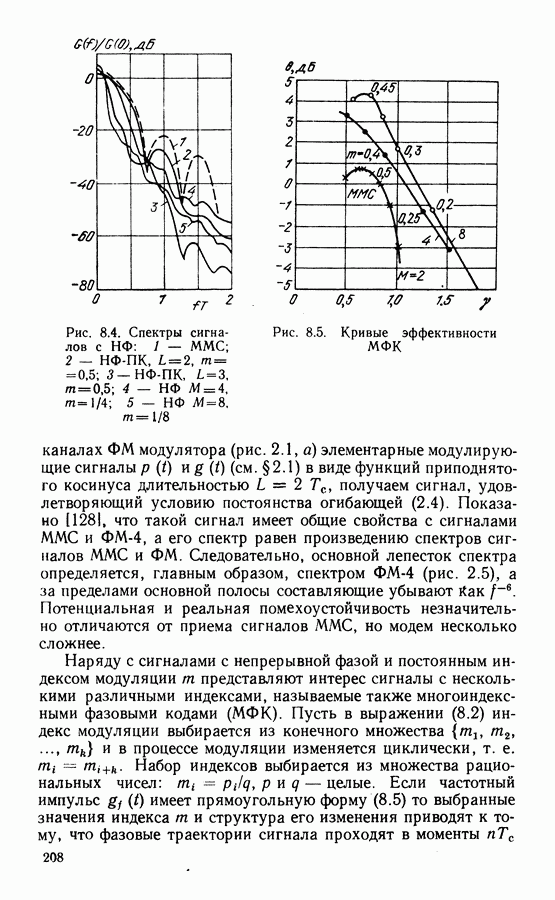
на декаду). Возможны и другие формы функций  обеспечивающих быстрое убывание спектра. На рис. 8.4 показаны результаты расчетов спектра некоторых сигналов с НФ и различными формами частотных и фазовых импульсов [126, 1271. Сравнение ведется со спектром сигнала ММС. Анализ показывает, что при СММС основной лепесток спектра несколько шире, чем у ММС, но последующие составляющие спектра убывают значительно быстрее. Переход к сигналам с частичным откликом
обеспечивающих быстрое убывание спектра. На рис. 8.4 показаны результаты расчетов спектра некоторых сигналов с НФ и различными формами частотных и фазовых импульсов [126, 1271. Сравнение ведется со спектром сигнала ММС. Анализ показывает, что при СММС основной лепесток спектра несколько шире, чем у ММС, но последующие составляющие спектра убывают значительно быстрее. Переход к сигналам с частичным откликом  приводит к значительному сужению основного лепестка спектра и быстрому убыванию составляющих с ростом частоты. Переход от двоичных к
приводит к значительному сужению основного лепестка спектра и быстрому убыванию составляющих с ростом частоты. Переход от двоичных к  -позиционным методам модуляции также обеспечивает сужение спектра.
-позиционным методам модуляции также обеспечивает сужение спектра.
Условие непрерывности фазы сигнала устанавливает между символами определенную фазовую связь. Полный учет такой связи возможен, например, при декодировании сигналов с НФ по решетчатой диаграмме на достаточно протяженном интервале с использованием алгоритма Витерби (аналогично декодированию сверточных кодов, описанному в § 4.5). Вместе с тем для ряда случаев глубина прослеживания по решетке может быть небольшой. Так, потенциальная помехоустойчивость приема сигналов ММС при обработке на интервале  совпадает, как отмечалось в § 1.3, с помехоустойчивостью сигналов ФМ-4. Прием на интервале
совпадает, как отмечалось в § 1.3, с помехоустойчивостью сигналов ФМ-4. Прием на интервале  понижает величину
понижает величину  примерно на
примерно на  а дальнейшее увеличение интервала к существенному выигрышу не приводит.
а дальнейшее увеличение интервала к существенному выигрышу не приводит.
Введение корреляции между символами при модуляции с частичным откликом  позволяет уменьшить ширину спектра сигнала и соответственно снизить требования к характеристикам канала. Используя, к примеру, в квадратурных
позволяет уменьшить ширину спектра сигнала и соответственно снизить требования к характеристикам канала. Используя, к примеру, в квадратурных

Рис. 8.4. Спектры сигналов с 

Рис. 8.5. Кривые эффективности МФК
каналах ФМ модулятора (рис. 2.1, а) элементарные модулирующие сигналы  (см. §2.1) в виде функций приподнятого косинуса длительностью
(см. §2.1) в виде функций приподнятого косинуса длительностью  получаем сигнал, удовлетворяющий условию постоянства огибающей (2.4). Показано [1281, что такой сигнал имеет общие свойства с сигналами ММС и ФМ-4, а его спектр равен произведению спектров сигналов ММС и ФМ. Следовательно, основной лепесток спектра определяется, главным образом, спектром ФМ-4 (рис. 2.5), а за пределами основной полосы составляющие убывают Как
получаем сигнал, удовлетворяющий условию постоянства огибающей (2.4). Показано [1281, что такой сигнал имеет общие свойства с сигналами ММС и ФМ-4, а его спектр равен произведению спектров сигналов ММС и ФМ. Следовательно, основной лепесток спектра определяется, главным образом, спектром ФМ-4 (рис. 2.5), а за пределами основной полосы составляющие убывают Как  Потенциальная и реальная помехоустойчивость незначительно отличаются от приема сигналов ММС, но модем несколько сложнее.
Потенциальная и реальная помехоустойчивость незначительно отличаются от приема сигналов ММС, но модем несколько сложнее.
Наряду с сигналами с непрерывной фазой и постоянным индексом модуляции  представляют интерес сигналы с несколькими различными индексами, называемые также многоиндексными фазовыми кодами (МФК). Пусть в выражении (8.2) индекс модуляции выбирается из конечного множества
представляют интерес сигналы с несколькими различными индексами, называемые также многоиндексными фазовыми кодами (МФК). Пусть в выражении (8.2) индекс модуляции выбирается из конечного множества  и в процессе модуляции изменяется циклически, т. е.
и в процессе модуляции изменяется циклически, т. е.  Набор индексов выбирается из множества рациональных чисел:
Набор индексов выбирается из множества рациональных чисел:  целые. Если частотный импульс
целые. Если частотный импульс  имеет прямоугольную форму (8.5) то выбранные значения индекса
имеет прямоугольную форму (8.5) то выбранные значения индекса  и структура его изменения приводят к тому, что фазовые траектории сигнала проходят в моменты
и структура его изменения приводят к тому, что фазовые траектории сигнала проходят в моменты 
через дискретные значения фаз, кратные  и тем самым образуют периодическую решетчатую диаграмму. На рис. 8.3, б показана диаграмма ИФК с параметрами
и тем самым образуют периодическую решетчатую диаграмму. На рис. 8.3, б показана диаграмма ИФК с параметрами 
Как и для сверточных кодов, потенциальная помехоустойчивость приема МФК зависит от свободного расстояния  определяемого как минимальное расстояние между двумя различными путями, проходящими через один и тот же узел решетчатой диаграммы. Тогда вероятность ошибки на узел при приеме МФК по алгоритму Витерби может быть определена по формуле (4.22). Оценка свободного расстояния позволяет определить асимптотический выигрыш подобно тому, как это сделано для кодов в § 4.6. Результаты расчетов АЭВК по данным работы [1291 для сигналов
определяемого как минимальное расстояние между двумя различными путями, проходящими через один и тот же узел решетчатой диаграммы. Тогда вероятность ошибки на узел при приеме МФК по алгоритму Витерби может быть определена по формуле (4.22). Оценка свободного расстояния позволяет определить асимптотический выигрыш подобно тому, как это сделано для кодов в § 4.6. Результаты расчетов АЭВК по данным работы [1291 для сигналов  различными индексами модуляции
различными индексами модуляции  и числом позиций
и числом позиций  и 8 показаны на рис. 8.5. Удельная скорость у определялась с учетом полосы частот, в которой сосредоточено 99 % мощности сигнала. Кривые при фиксированном М носят обменный характер: с увеличением индекса
и 8 показаны на рис. 8.5. Удельная скорость у определялась с учетом полосы частот, в которой сосредоточено 99 % мощности сигнала. Кривые при фиксированном М носят обменный характер: с увеличением индекса  растет выигрыш 0, но снижается удельная скорость у. Переход к
растет выигрыш 0, но снижается удельная скорость у. Переход к  и 8 позволяет увеличить либо у в
и 8 позволяет увеличить либо у в  раз, либо 0 на
раз, либо 0 на  Использование МФК только с двумя индексами модуляции
Использование МФК только с двумя индексами модуляции  позволяет получить АЭВК около 3 дБ.
позволяет получить АЭВК около 3 дБ.
Таким образом, сигналы с постоянной огибающей и непрерывной фазой характеризуются более компактным спектром. Введение фазовой связи между символами повышает помехоустойчивость приема. Однако это улучшение характеристик эффективности рассмотренных выше методов модуляции приводит к усложнению устройств формирования и обработки сигналов на приеме. В модуляторе наряду с линейными фильтрующими цепями для формирования сложных форм частотных и фазовых импульсов могут использоваться и нелинейные цепи. В демодуляторе для получения помехоустойчивости, близкой к потенциальной, необходимо применение оптимальных алгоритмов (корреляционный прием с учетом формы сигналов, алгоритм Витерби и др.).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ I. ОСНОВЫ ПОСТРОЕНИЯ ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМ СВЯЗИ
- ГЛАВА 1. СПУТНИКОВЫЕ СИСТЕМЫ С МНОГОСТАНЦИОННЫМ ДОСТУПОМ
- 1.2. ПРЕОБРАЗОВАНИЕ АНАЛОГОВЫХ СИГНАЛОВ В ЦИФРОВУЮ ФОРМУ
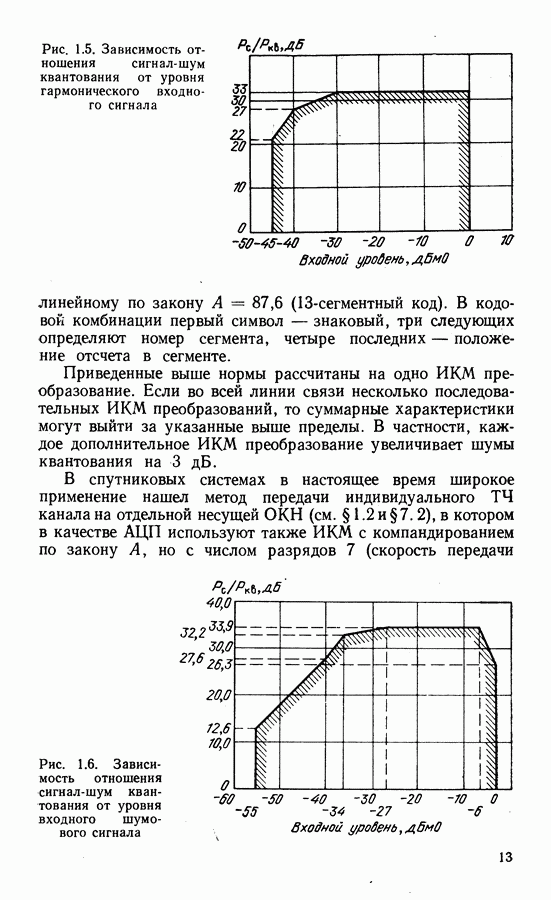
- Адаптивная ИКМ.
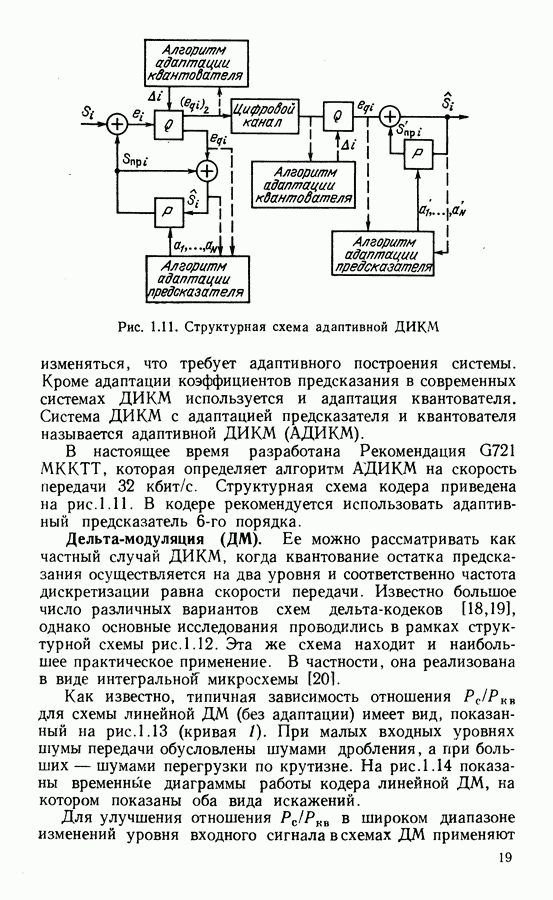
- Дифференциальная ИКМ (ДИКМ).
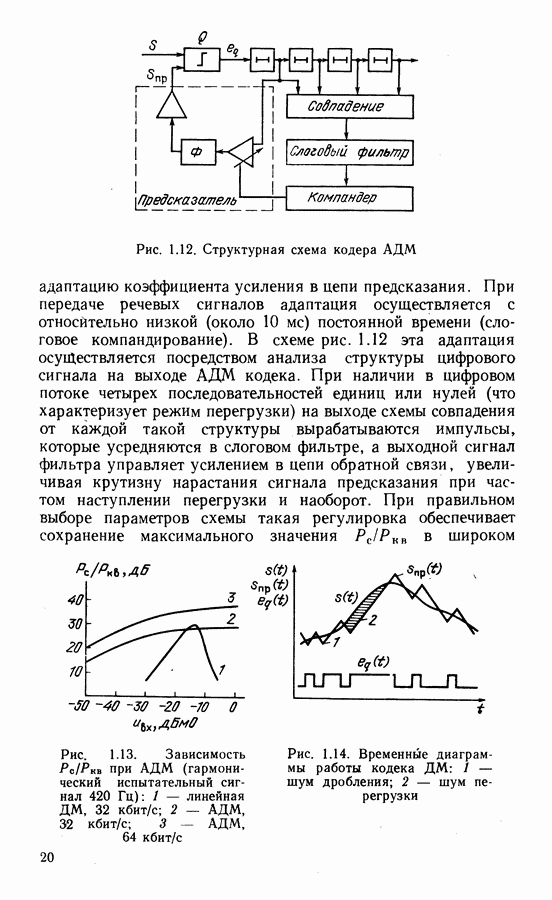
- Дельта-модуляция (ДМ).
- Преобразование сигналов телевидения, многоканальной телефонии и вещания в цифровую форму.
- 1.3. СТАТИСТИЧЕСКОЕ УПЛОТНЕНИЕ В ЦССС
- 1.4. МНОГОСТАНЦИОННЫЙ ДОСТУП В ЦССС
- Многостанционный доступ с временным разделением каналов (МДВР).
- Многостанционный доступ с разделением сигналов по форме (МДФР).
- Многостанционный доступ со случайным доступом (МДСД).
- 1.5. НОРМИРОВАНИЕ ПАРАМЕТРОВ ЦССС
- РАЗДЕЛ II. МОДУЛЯЦИЯ
- ГЛАВА 2. МЕТОДЫ МОДУЛЯЦИИ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.2. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СИГНАЛОВ
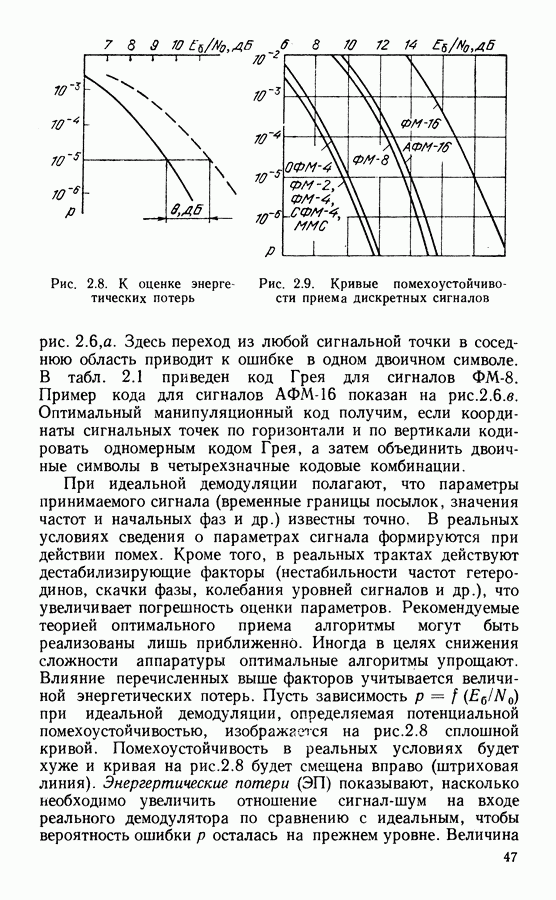
- 2.3. СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИГНАЛОВ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
- 2.4. СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ
- 2.5. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДЧР
- Результаты расчетов потерь в системе с ФМ-2 и стандартными фильтрами.
- Использование выравнивателей в тракте передачи.
- Анализ зависимости потерь от разноса между каналами.
- Энергетические потери в системе с ФМ-4.
- Потери в системах с сигналами ММС.
- 2.6. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДВР
- ГЛАВА 3. МОДЕМЫ
- 3.1. СТРУКТУРА МОДЕМА
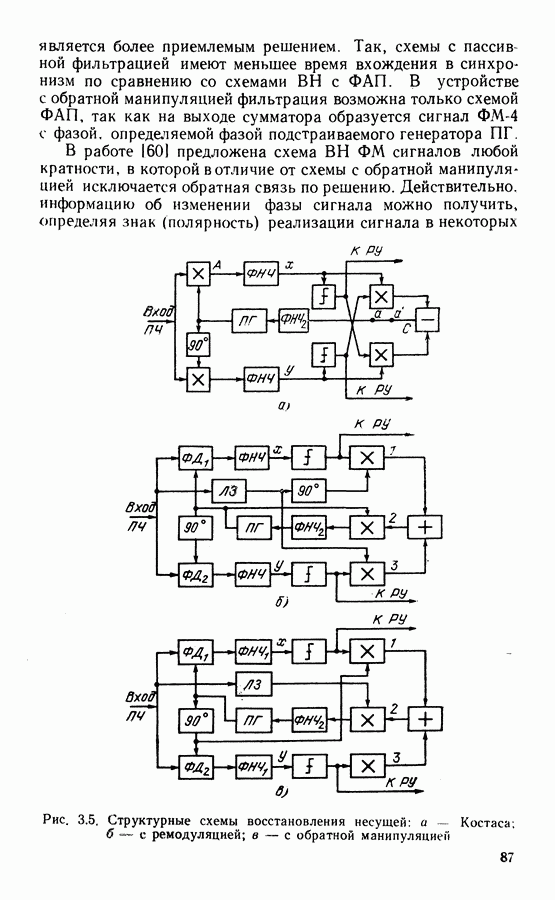
- 3.2. СИСТЕМЫ ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ
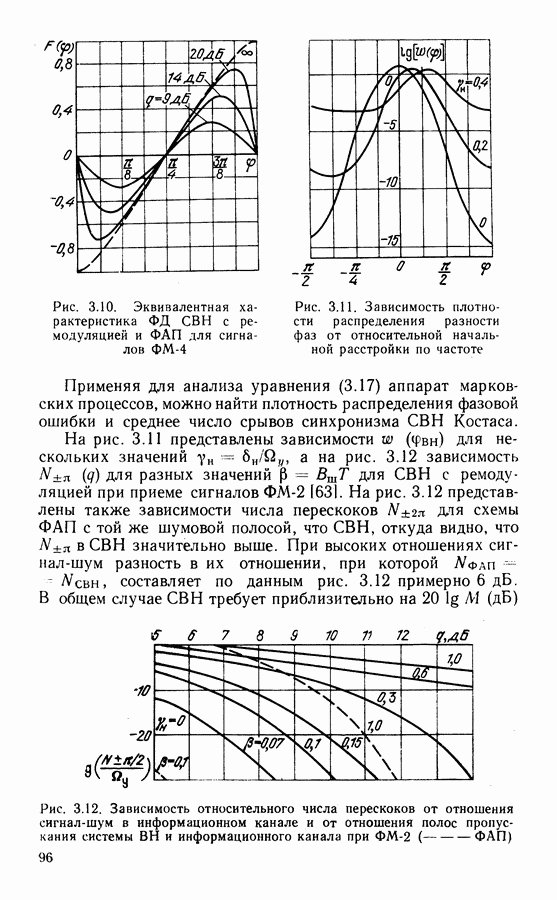
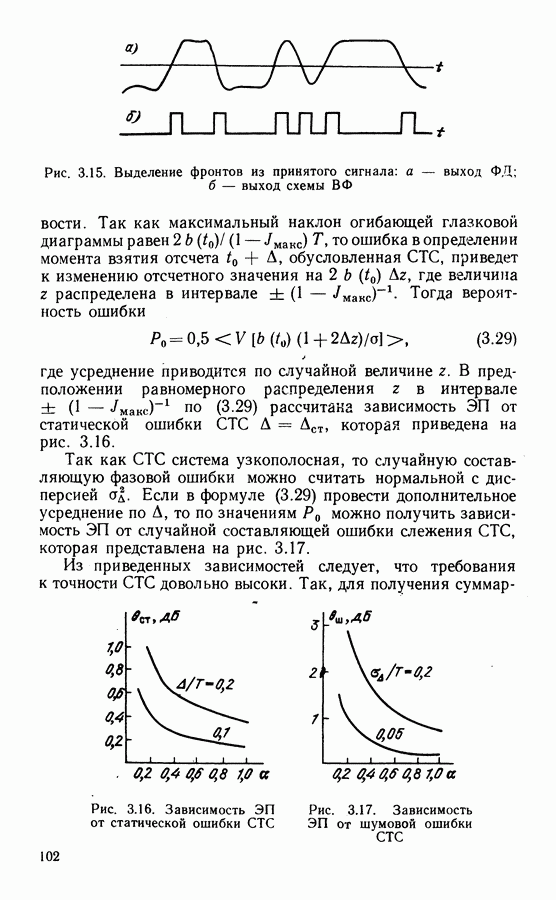
- Требования к точности работы системы ВН.
- Анализ точности систем ВН.
- Переходные процессы.
- 3.3. ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 3.4. ОТНОСИТЕЛЬНОЕ КОДИРОВАНИЕ
- 3.5. ПРИМЕРЫ РЕАЛИЗАЦИИ МОДЕМОВ В ЦССС
- РАЗДЕЛ III. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
- 4.2. АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ КОДОВ
- 4.3. БЛОКОВЫЕ КОДЫ И АЛГОРИТМЫ ИХ ДЕКОДИРОВАНИЯ
- 4.4. СТРУКТУРА И ХАРАКТЕРИСТИКИ СВЕРТОЧНЫХ КОДОВ
- 4.5. АЛГОРИТМЫ ДЕКОДИРОВАНИЯ СК
- 4.6. ПОМЕХОУСТОЙЧИВОСТЬ И ЭФФЕКТИВНОСТЬ СИСТЕМ С КОДИРОВАНИЕМ
- ГЛАВА 5. КОДЕКИ
- 5.1. СОГЛАСОВАНИЕ МОДЕМА И КОДЕКА
- 5.2. ДЕКОДЕРЫ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ СК
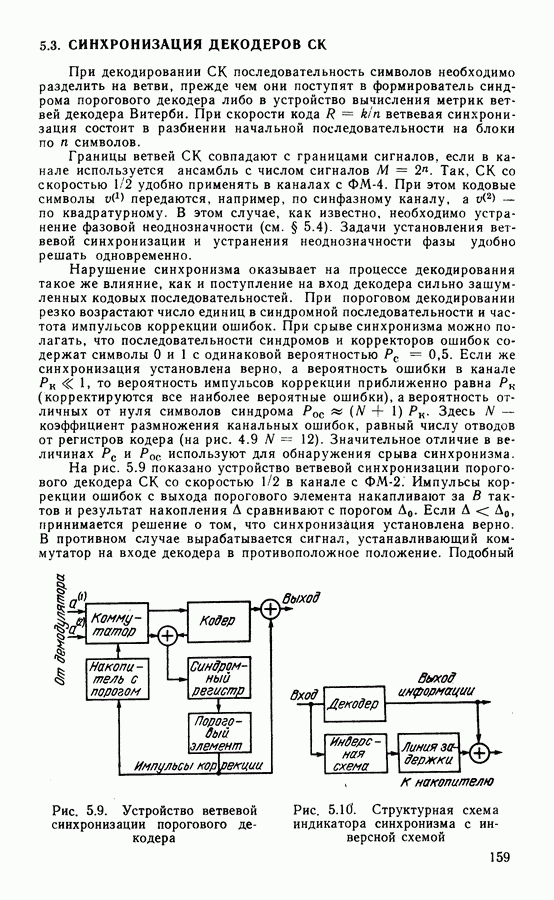
- 5.3. СИНХРОНИЗАЦИЯ ДЕКОДЕРОВ СК
- 5.4. КОДИРОВАНИЕ В КАНАЛАХ С НЕОДНОЗНАЧНОСТЬЮ
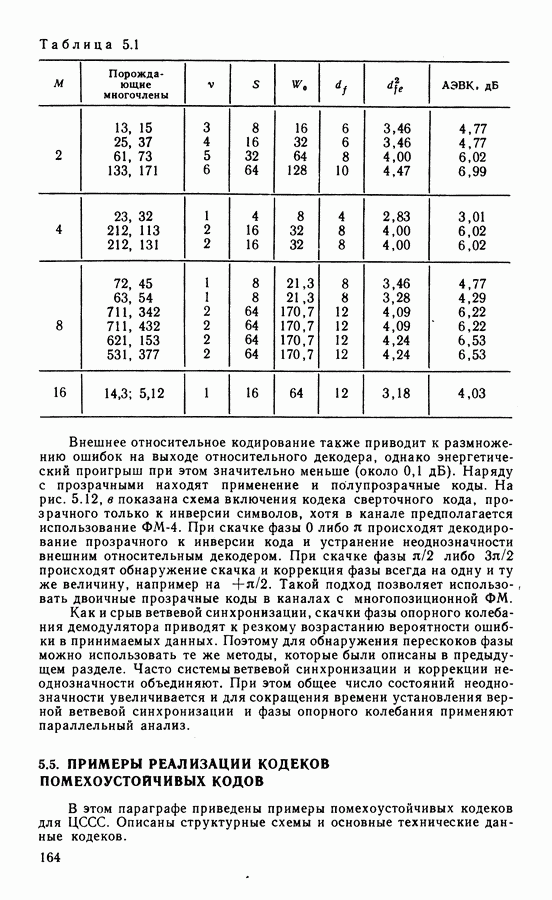
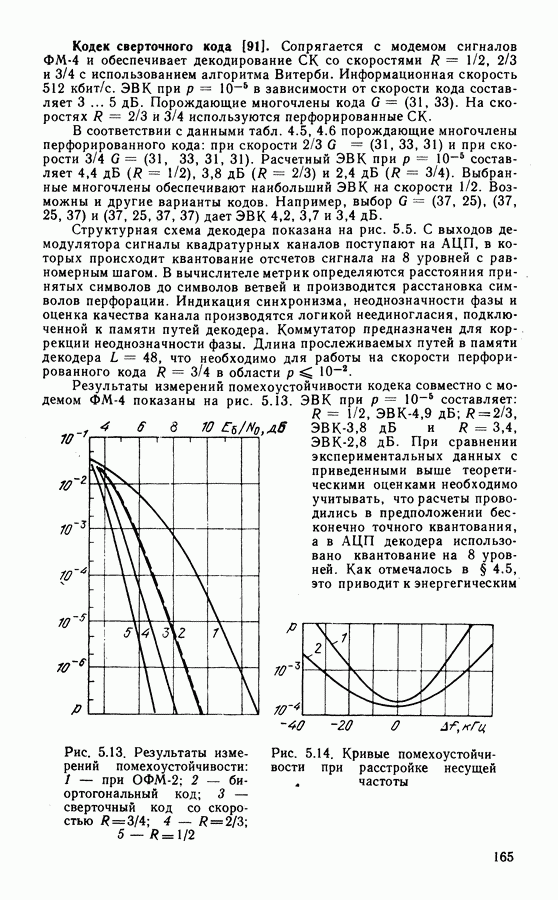
- 5.5. ПРИМЕРЫ РЕАЛИЗАЦИИ КОДЕКОВ ПОМЕХОУСТОЙЧИВЫХ КОДОВ
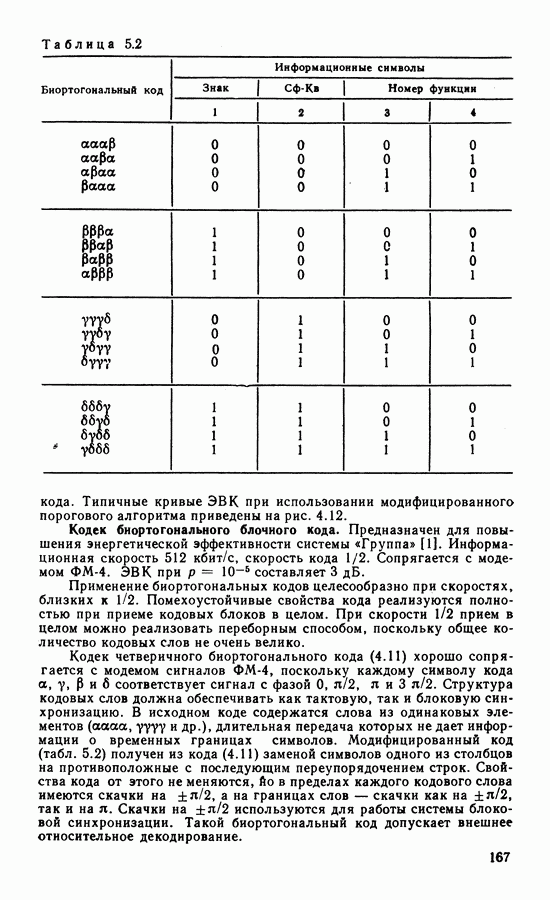
- Кодек биортогонального блочного кода.
- 5.6. РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
- РАЗДЕЛ IV. ЦИФРОВЫЕ СИСТЕМЫ СПУТНИКОВОЙ СВЯЗИ
- ГЛАВА 6. ВЗАИМНЫЕ ПОМЕХИ В ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМАХ
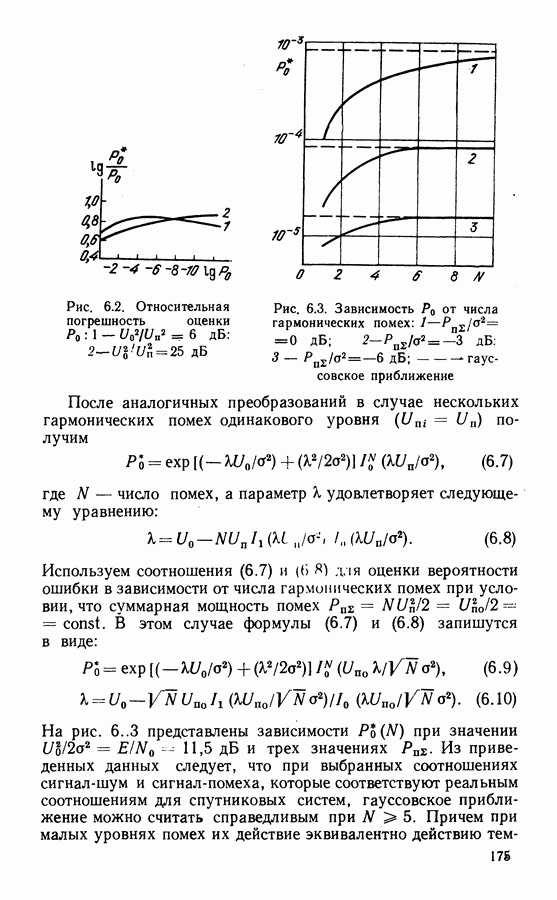
- 6.2. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ГАРМОНИЧЕСКИХ ПОМЕХ НА ДЕМОДУЛЯТОР ФМ СИГНАЛОВ
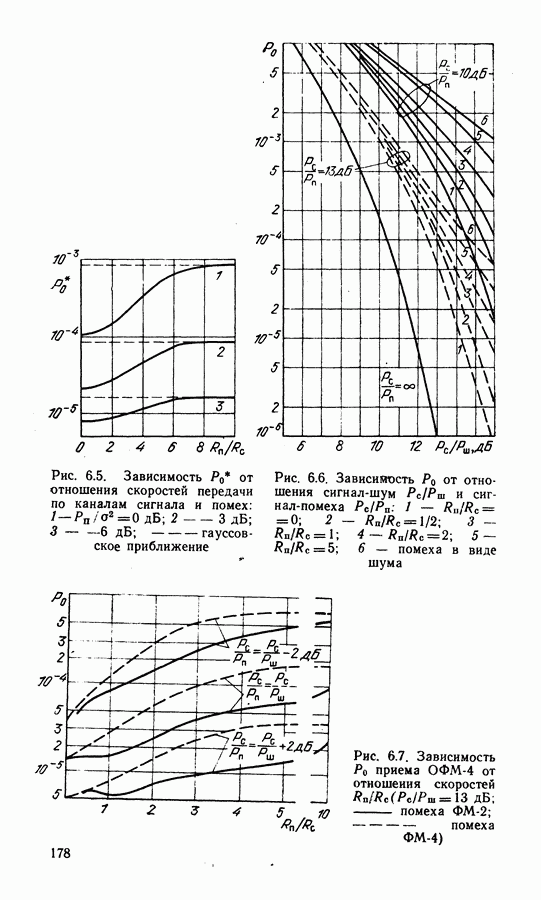
- 6.3. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ФМ ПОМЕХ
- 6.4. АНАЛИЗ МЕШАЮЩЕГО ДЕЙСТВИЯ ЧМ—ТВ СИГНАЛА С ДИСПЕРСИЕЙ
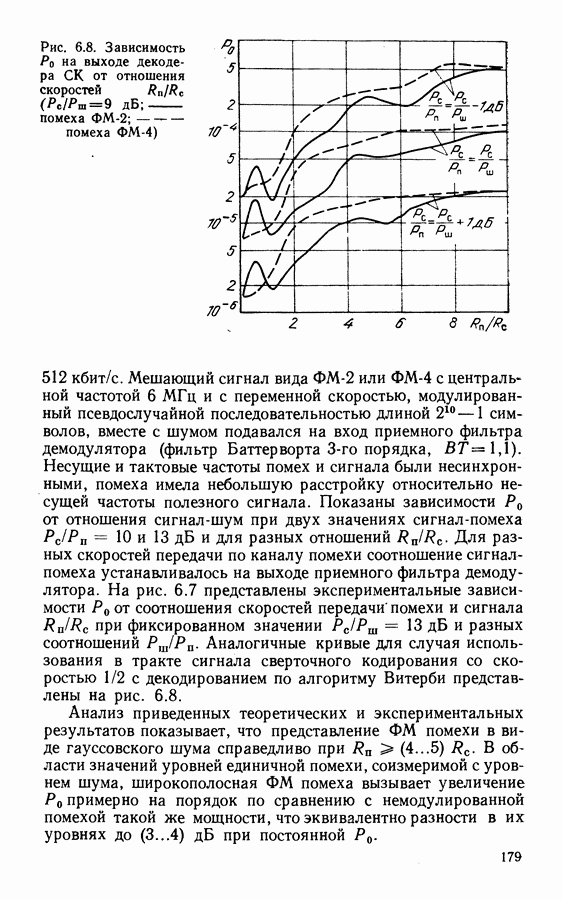
- 6.5. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ СИГНАЛОВ ЧУ-ЧМ
- ГЛАВА 7. СИСТЕМЫ С МДВР И МДЧР
- 7.1. ОЦЕНКА ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ РАЗЛИЧНЫХ МЕТОДОВ ПЕРЕДАЧИ В ЦССС С МДЧР
- 7.2. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДЧР
- 7.3. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДВР
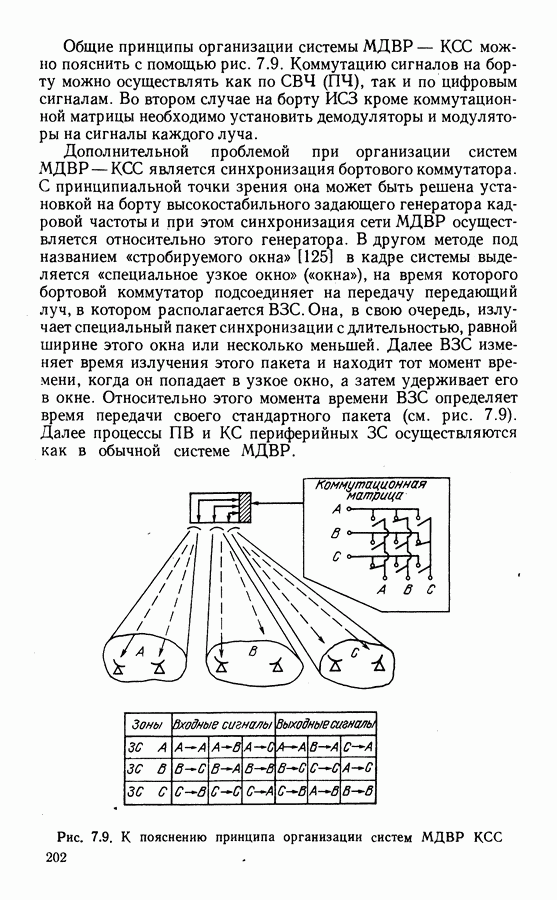
- Синхронизация систем МДВР.
- Организация кадра систем МДВР.
- Система МДВУ-40.
- ЦСС с ДВР ТДМА-120-(«Интелсат»/«Евросат»).
- МДВР с коммутацией сигналов на спутнике (КСС).
- Сопряжение систем МДВР с цифровыми наземными линиями.
- ГЛАВА 8. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ И КОДИРОВАНИЯ В ЦССС
- 8.2. СОГЛАСОВАНИЕ СИСТЕМ МОДУЛЯЦИИ И КОДИРОВАНИЯ
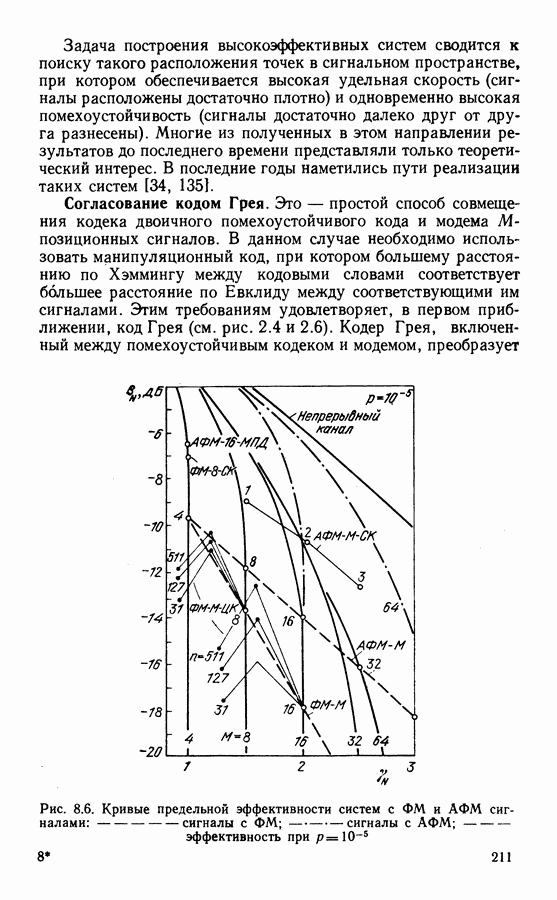
- Согласование кодом Грея.
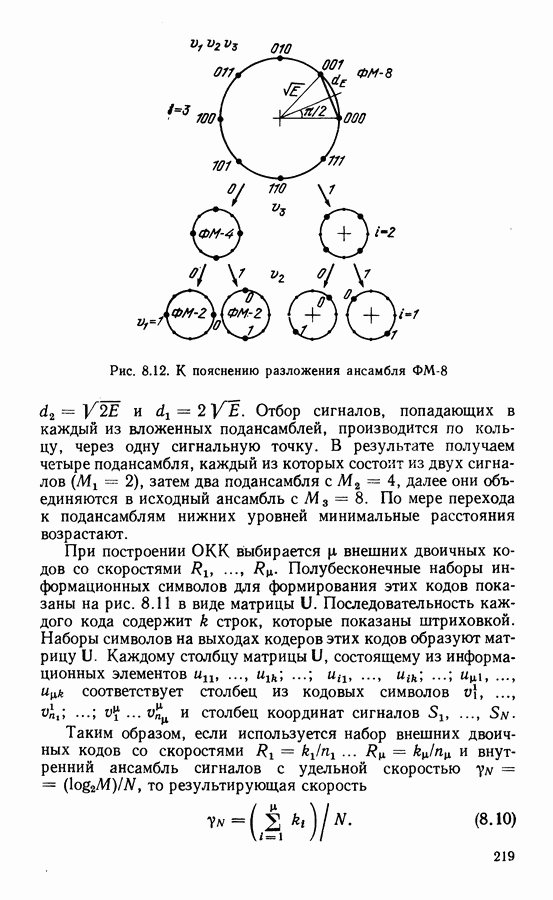
- Кодирование с разбиением ансамбля на подклассы.
- Применение недвоичных кодов.
- 8.3. СВЕРТОЧНОЕ КОДИРОВАНИЕ В КАНАЛЕ С МНОГОПОЗИЦИОННОИ ФМ
- 8.4. ОБОБЩЕННОЕ КАСКАДНОЕ КОДИРОВАНИЕ
- 8.5. ПРИМЕРЫ РЕАЛИЗАЦИИ ЭФФЕКТИВНЫХ КОДЕМОВ
- СПИСОК ЛИТЕРАТУРЫ