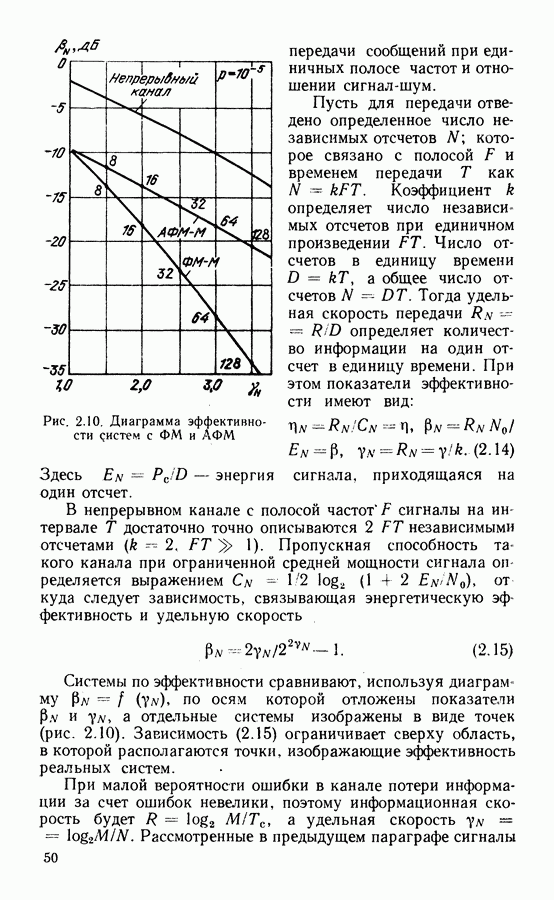
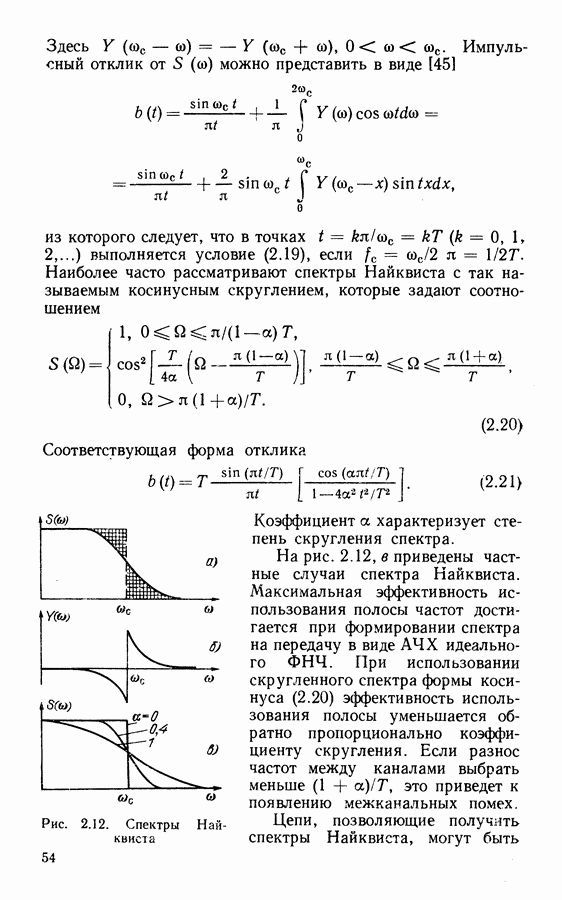
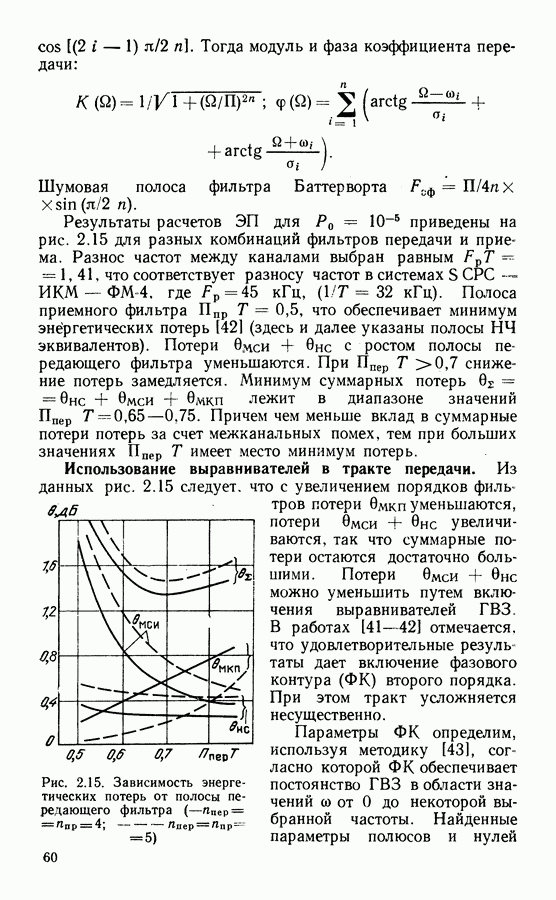
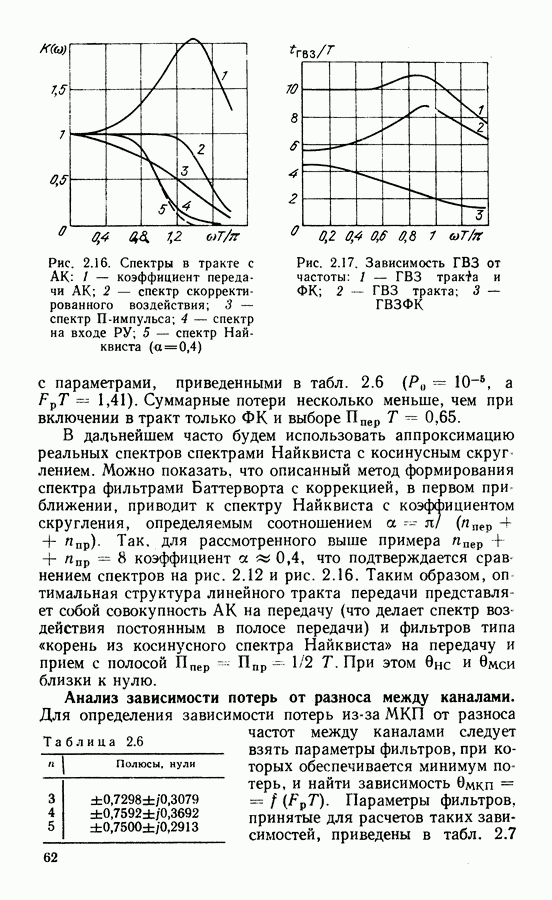
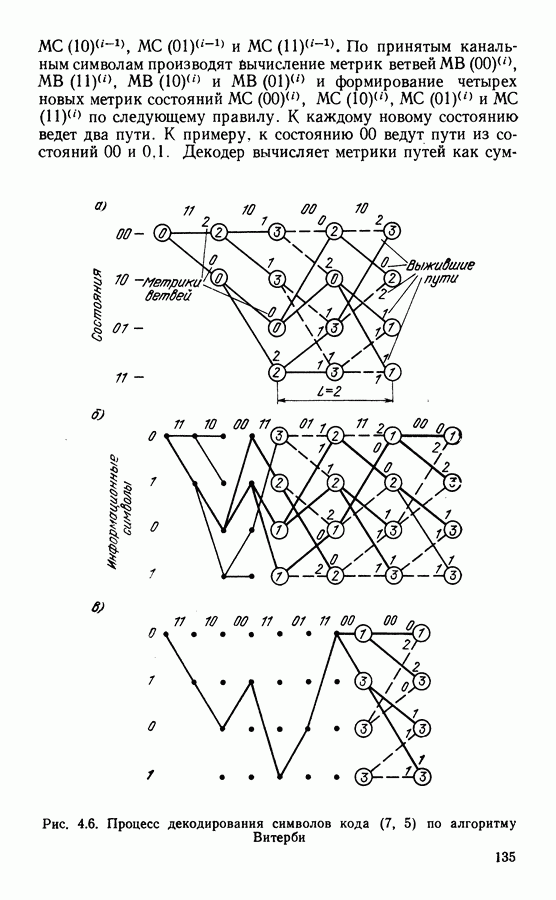
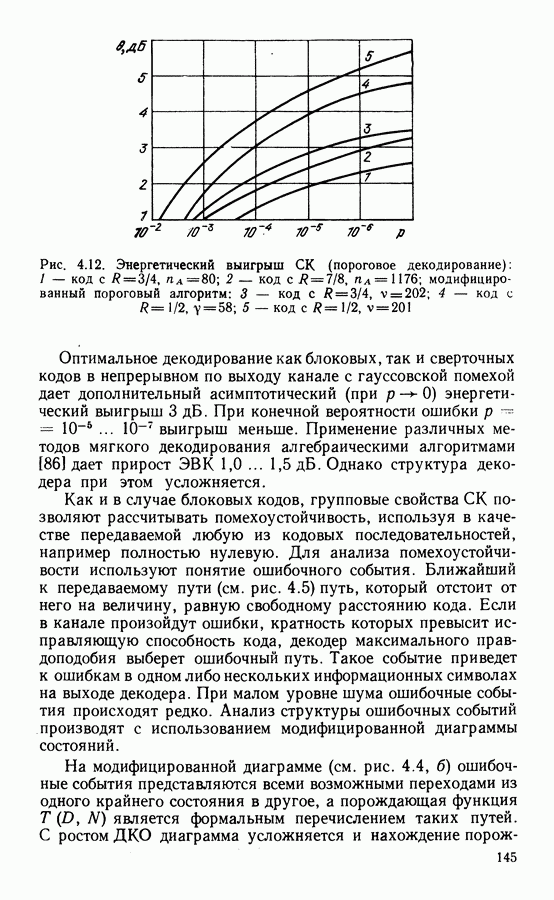
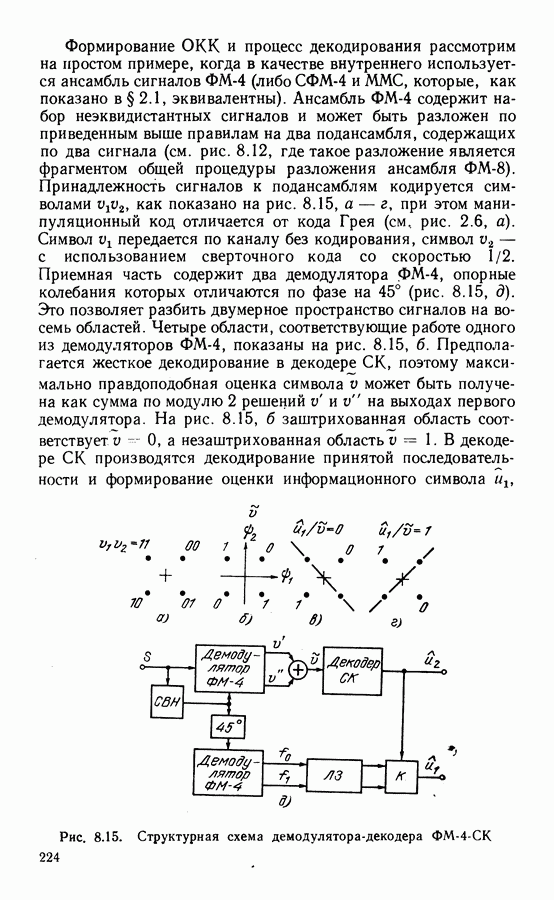
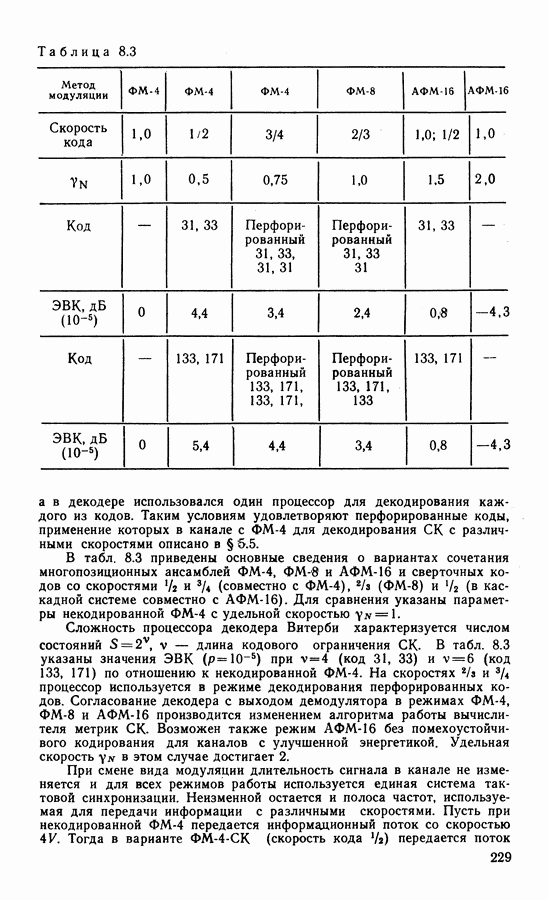
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
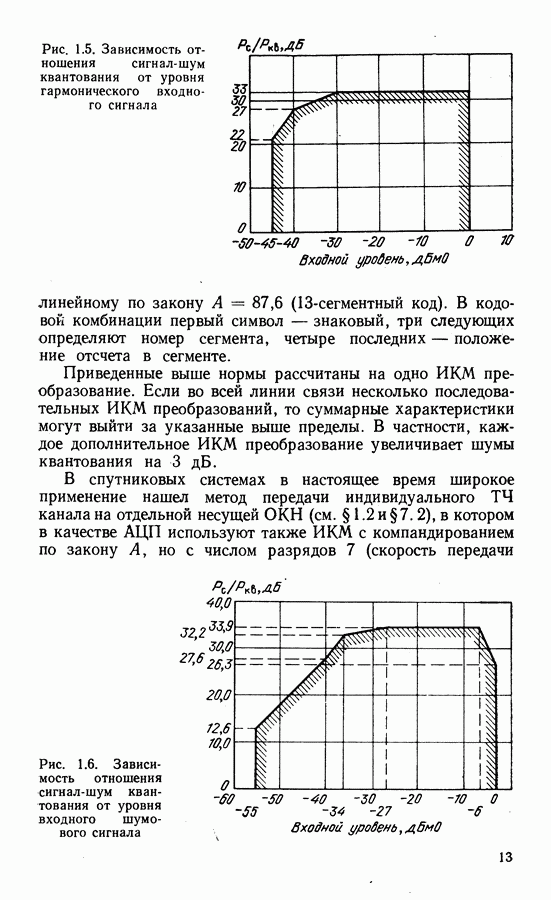
Анализ точности систем ВН.
Рассмотрим сначала схему ВН с учетверением (см. рис. 3.8). При возведении в четвертую степень суммы сигнала  и шума
и шума  получим
получим 
Ограничимся сначала случаем немодулированной несущей и малого шума, тогда  Для сигнала
Для сигнала  и шума в виде суммы двух ортогональных компонент
и шума в виде суммы двух ортогональных компонент  после некоторых преобразований получим выражение для четвертой гармоники учетверителя
после некоторых преобразований получим выражение для четвертой гармоники учетверителя

Здесь шум  имеет те же статистические характеристики, что и входной шум
имеет те же статистические характеристики, что и входной шум  но со спектром, перенесенным на частоту
но со спектром, перенесенным на частоту  Если в качестве фильтра используют схему ФАП (рис. 3.8, в), то уравнение для разности фаз имеет вид [61]
Если в качестве фильтра используют схему ФАП (рис. 3.8, в), то уравнение для разности фаз имеет вид [61]

Здесь  расстройка входной частоты ФМ сигнала
расстройка входной частоты ФМ сигнала  относительно номинальной частоты
относительно номинальной частоты  полоса удержания.
полоса удержания.
Рассмотрим сначала линеаризованное уравнение, положив в выражении 

Так как опорное колебание получается делением частоты  на четыре, то
на четыре, то  и, следовательно,
и, следовательно,  Это уравнение совпадает с линейным уравнением обычной ФАП, из которого следует, что
Это уравнение совпадает с линейным уравнением обычной ФАП, из которого следует, что

где  шумовая полоса ФАП, определяемая известным соотношением
шумовая полоса ФАП, определяемая известным соотношением

В частности, для случая использования в схеме ФАП пропор ционально-интегрирующего фильтра

Если в качестве фильтра в схеме ВН с учетверением используют ПФ в виде одиночного резонансного контура с полосой  , то
, то

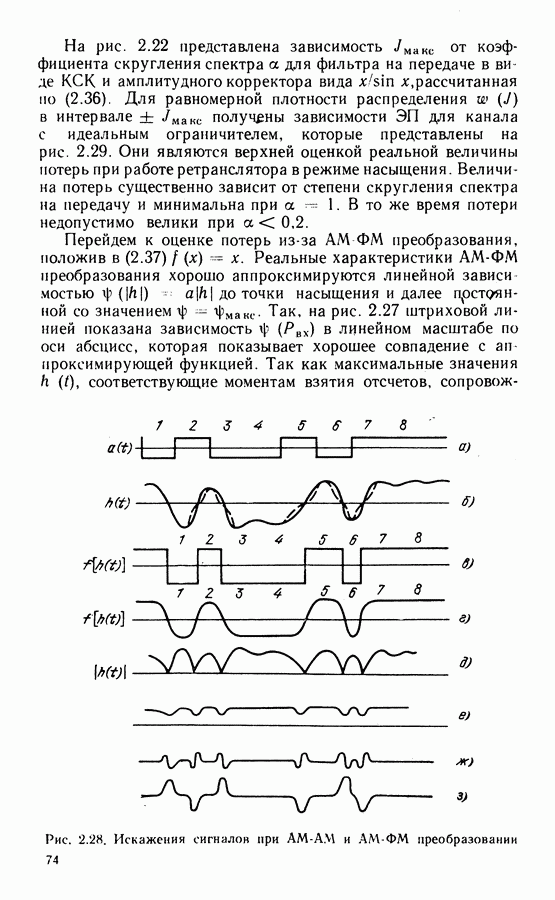
Определим плотность вероятности фазовой ошибки  и среднее число срывов синхронизации. Если в уравнении (3.5) перейти к фазе
и среднее число срывов синхронизации. Если в уравнении (3.5) перейти к фазе  то получим уравнение для фазовой ошибки в следующем виде:
то получим уравнение для фазовой ошибки в следующем виде:

Рассмотрим сначала бесфильтровую схему  Тогда
Тогда

Точки устойчивого равновесия уравнения (3.8) имеют период  поэтому срыв синхронизации (перескок фазы) соответствует переходу фазы из одного стационарного состояния
поэтому срыв синхронизации (перескок фазы) соответствует переходу фазы из одного стационарного состояния  в другое
в другое  что и является причиной неоднозначности фазы СВН (в данном случае 4-го порядка). При приеме сигналов с числом фаз М точки устойчивого равновесия любой СВН будут располагаться через
что и является причиной неоднозначности фазы СВН (в данном случае 4-го порядка). При приеме сигналов с числом фаз М точки устойчивого равновесия любой СВН будут располагаться через  вызывая неоднозначность фазы порядка М.
вызывая неоднозначность фазы порядка М.
Применяя для нахождения  и среднего числа перескоков фазы
и среднего числа перескоков фазы  аппарат теории марковских процессов 139], можно получить следующие выражения:
аппарат теории марковских процессов 139], можно получить следующие выражения:

При высоком соотношении сигнал-шум 

Здесь  дисперсия фазовой ошибки в линейном приближении.
дисперсия фазовой ошибки в линейном приближении.
Эти выражения можно получить также из (3.5) с учетом того, что спектральная плотность шума  равна
равна 
Для сигналов ФМ-М формулы (3.9), (3.10), очевидно, останутся без изменений, а входящая в них величина

Сопоставим полученные результаты с соответствующими  мулами для обычной ФАП, фильтрующей сигнал
мулами для обычной ФАП, фильтрующей сигнал  на фоне шума со спектральной плотностью
на фоне шума со спектральной плотностью  . В этом случае [39]:
. В этом случае [39]:

Здесь  дисперсия фазовой ошибки в линейном приближении, При малых шумах
дисперсия фазовой ошибки в линейном приближении, При малых шумах

Сравнивая выражения (3.9), (3.10) с формулами (3.12), (3.13), можно видеть, что в линейном приближении их характеристики одинаковы. Однако по величине среднего числа срывов синхронизма сравниваемые системы существенно различаются. Так, из (3.10), (3.11), (3.13) следует, что

т. е. число срывов синхронизма в СВН существенно больше, чем у схемы ФАП с той же шумовой полосой. Это можно объяснить сокращением интервала между точками устойчивого равновесия схемы ВН в М раз по сравнению с обычной ФАП.
Если в СВН используется для фильтрации полосовой фильтр, то среднее число перескоков фазы 

где  радиус инерции шума на выходе фильтра:
радиус инерции шума на выходе фильтра:  коэффициент корреляции шума на выходе
коэффициент корреляции шума на выходе  шумовая полоса. Сравнение (3.14) с аналогичными зависимостями для СВН ФАП, при одинаковой шумовой полосе, показывает, что число перескоков
шумовая полоса. Сравнение (3.14) с аналогичными зависимостями для СВН ФАП, при одинаковой шумовой полосе, показывает, что число перескоков  в СВН-ФАП несколько меньше. Точную оценку можно найти в [62].
в СВН-ФАП несколько меньше. Точную оценку можно найти в [62].
Учет продуктов умножения типа  увеличивает спектральную плотность шума на входе фильтра
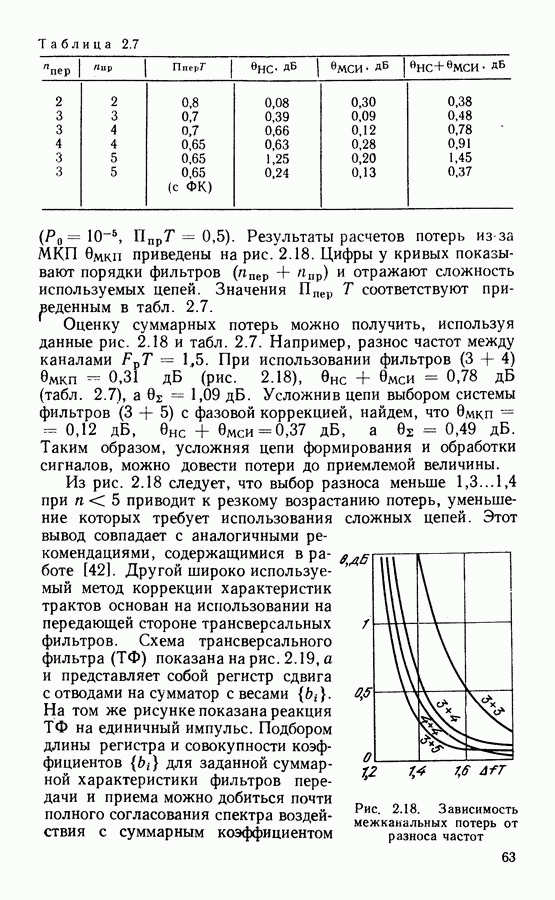
увеличивает спектральную плотность шума на входе фильтра
СВН и соответственно, величину  Это увеличение характеризуется коэффициентом
Это увеличение характеризуется коэффициентом

где  - отношение сигнал-шум на входе учетверителя.
- отношение сигнал-шум на входе учетверителя.
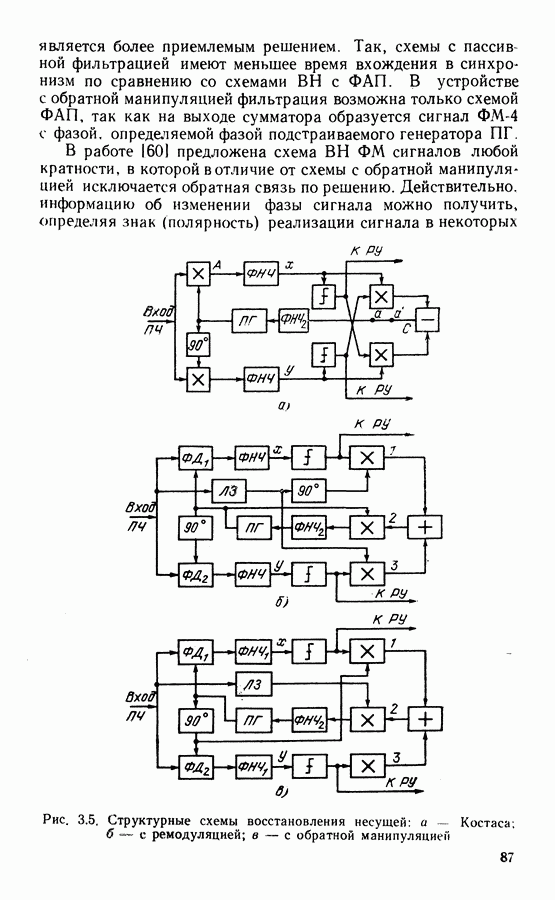
Обратимся к рассмотрению схемы Костаса. Если обозна чить напряжение на выходах  (см. рис. 3.5, а) соответст венно через х и у, то управляющее напряжение на выходе сумматора равно
(см. рис. 3.5, а) соответст венно через х и у, то управляющее напряжение на выходе сумматора равно  При приеме немодулирован ной несущей и шума
При приеме немодулирован ной несущей и шума

где  независимые гауссовские процессы со спектральной плотностью
независимые гауссовские процессы со спектральной плотностью 
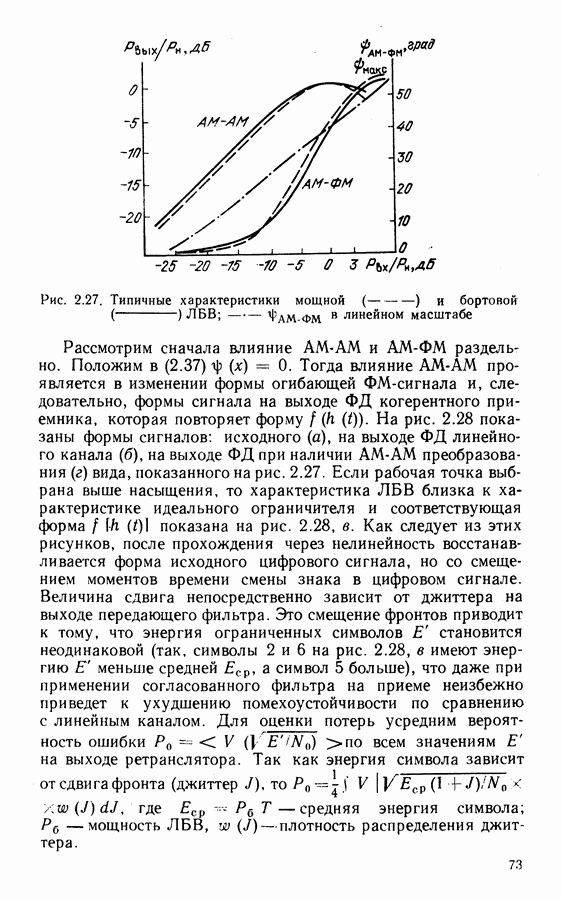
С учетом выражения (3.15) уравнение такой системы  можно представить в виде
можно представить в виде

Заменяя в  их условными средними значениями и обозначая
их условными средними значениями и обозначая

получаем уравнение схемы  в следующем виде [631:
в следующем виде [631:

Здесь

эквивалентная характеристика  отношение сигнал шум
отношение сигнал шум  на входе СВН.
на входе СВН.
Функция  имеет период
имеет период  и ее вид для нескольких значений
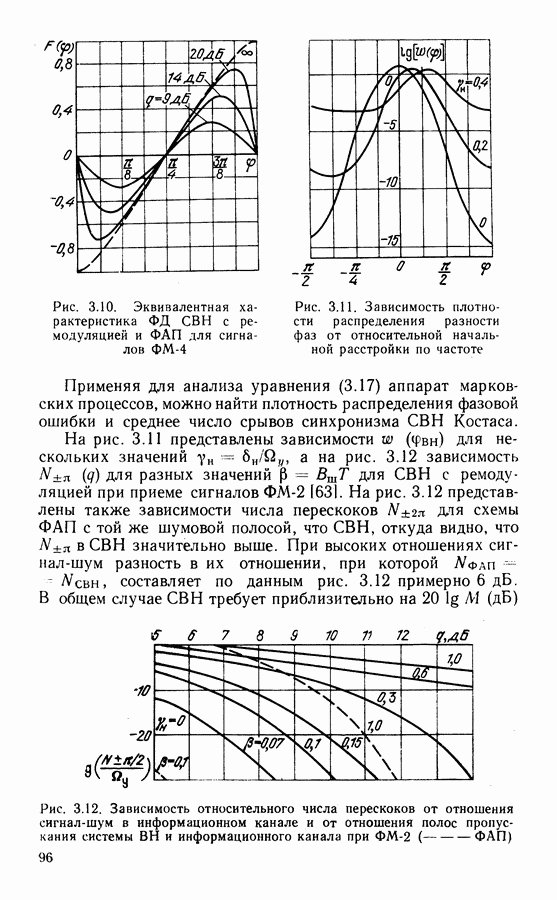
и ее вид для нескольких значений  на входе СФН дан на рис. 3.10. Как видно из этого рисунка, эквивалентная характеристика ФД в СВН Костаса зависит от отношения сигнал-шум и при отношении, примерно равном 10 дБ. ее можно считать практически синусоидальной вида
на входе СФН дан на рис. 3.10. Как видно из этого рисунка, эквивалентная характеристика ФД в СВН Костаса зависит от отношения сигнал-шум и при отношении, примерно равном 10 дБ. ее можно считать практически синусоидальной вида  Если подставить это выражение для
Если подставить это выражение для  в (3.17), то получим дифференциальное уравнение СВН Костаса в виде, аналогичном уравнению СВН с умноже нием
в (3.17), то получим дифференциальное уравнение СВН Костаса в виде, аналогичном уравнению СВН с умноже нием  . Следовательно, все основные характеристики этих двух схем при отношении сигнал-шум менее 10 дБ идентичны.
. Следовательно, все основные характеристики этих двух схем при отношении сигнал-шум менее 10 дБ идентичны.

Рис.  Эквивалентная характеристика ФД СВН с ремодуляцией и ФАП для сигналов ФМ-4
Эквивалентная характеристика ФД СВН с ремодуляцией и ФАП для сигналов ФМ-4

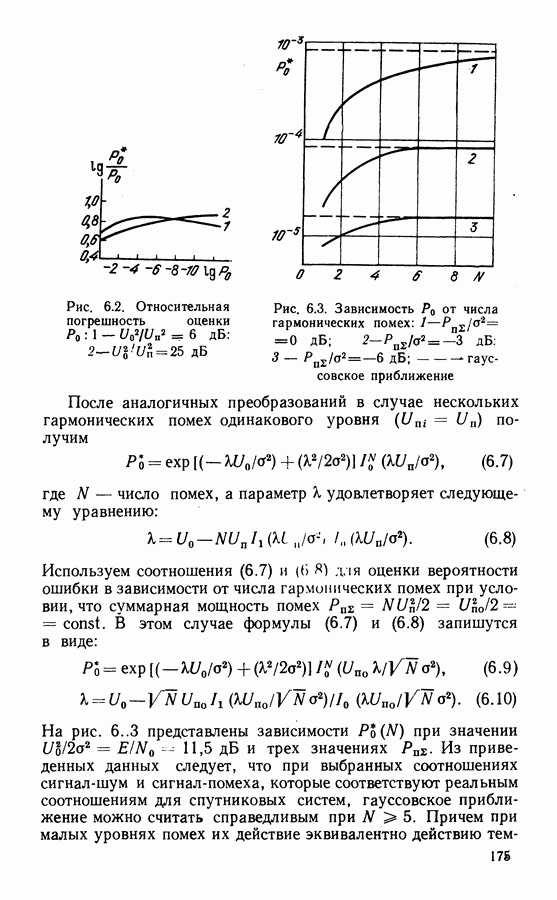
Рис. 3.11. Зависимость плотности распределения разности фаз от относительной начальной расстройки по частоте
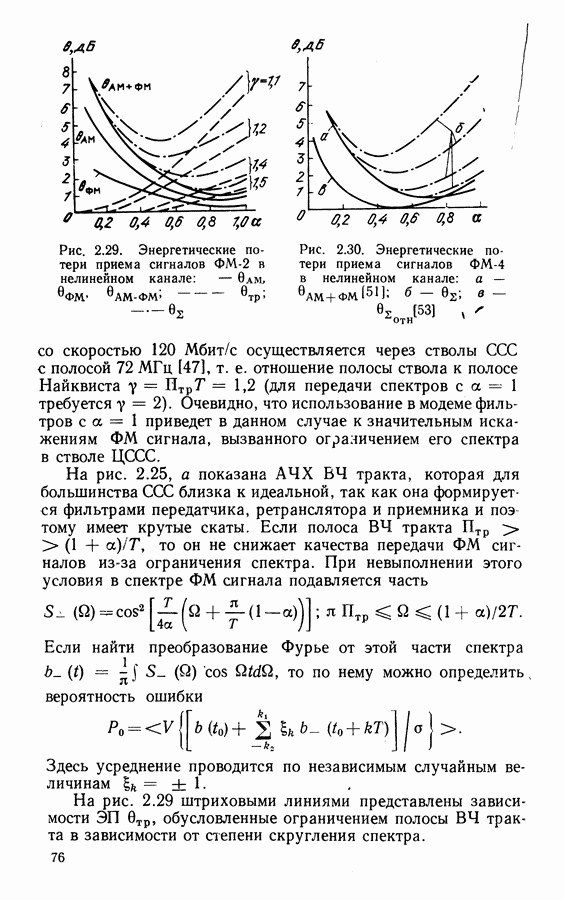
Применяя для анализа уравнения (3.17) аппарат марковских процессов, можно найти плотность распределения фазовой ошибки и среднее число срывов синхронизма СВН Костаса.
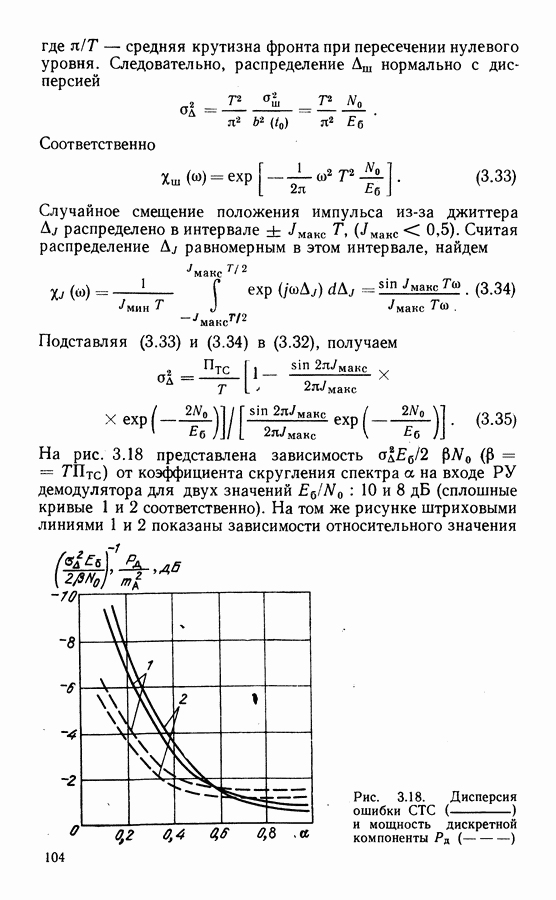
На рис. 3.11 представлены зависимости  для нескольких значений
для нескольких значений  на рис. 3.12 зависимость
на рис. 3.12 зависимость  для разных значений
для разных значений  для СВН с ремодуляцией при приеме сигналов ФМ-2 [631. На рис. 3.12 представлены также зависимости числа перескоков
для СВН с ремодуляцией при приеме сигналов ФМ-2 [631. На рис. 3.12 представлены также зависимости числа перескоков  для схемы ФАП с той же шумовой полосой, что
для схемы ФАП с той же шумовой полосой, что  откуда видно, что
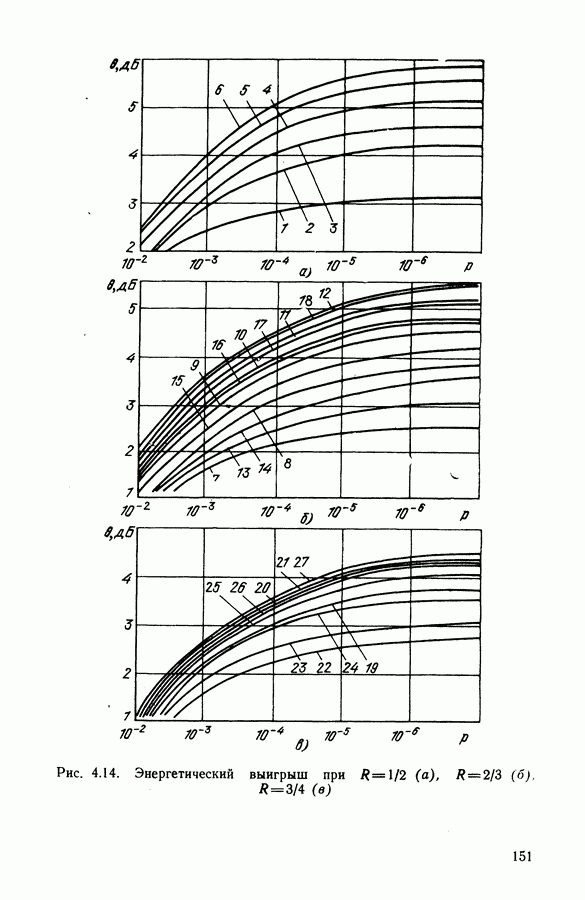
откуда видно, что  в СВН значительно выше. При высоких отношениях сигнал-шум разность в их отношении, при которой
в СВН значительно выше. При высоких отношениях сигнал-шум разность в их отношении, при которой  составляет по данным рис. 3.12 примерно 6 дБ. В общем случае СВН требует приблизительно на
составляет по данным рис. 3.12 примерно 6 дБ. В общем случае СВН требует приблизительно на 

Рис. 3.12. Зависимость относительного числа перескоков от отношения сигнал-шум в информационном канале и от отношения полос пропускания системы  и информационного канала при
и информационного канала при 
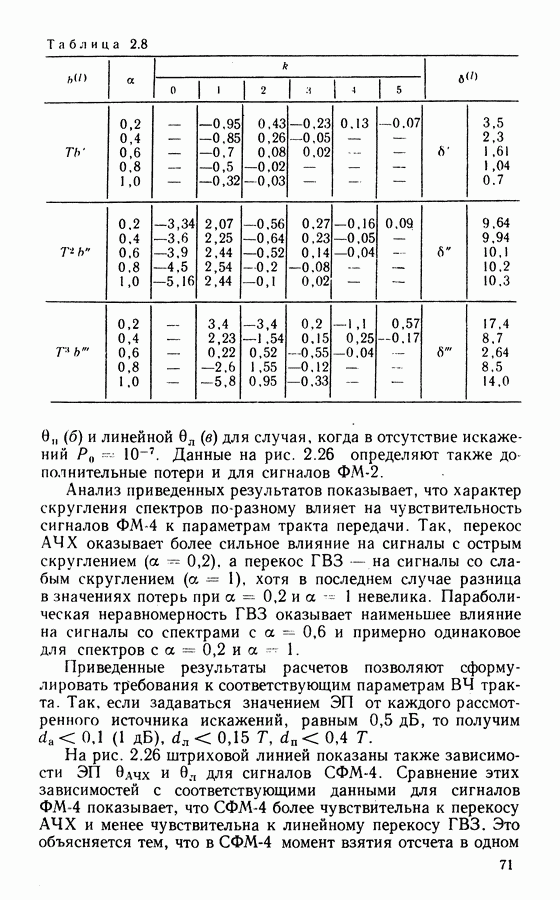
Таблица 3.1

более высокого отношения сигнал-шум для получения одинакового с ФАП числа срывов синхронизма.
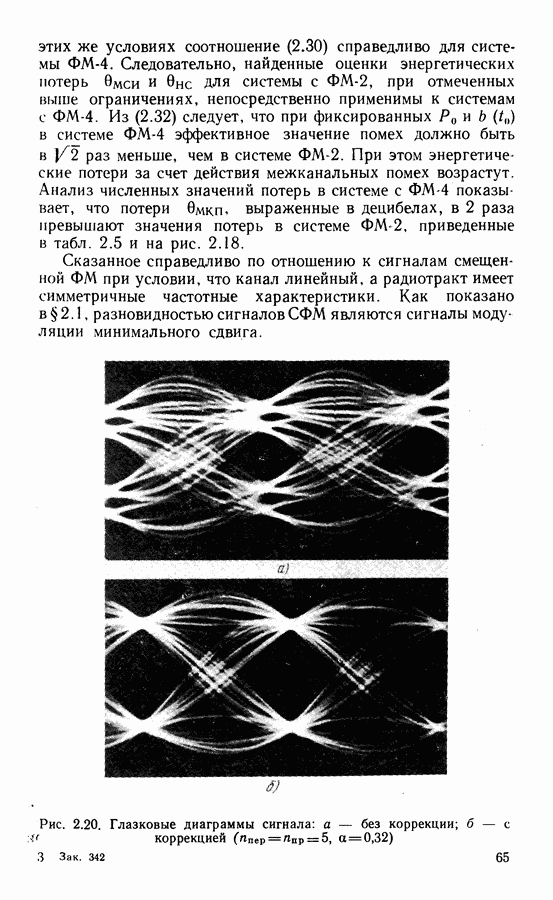
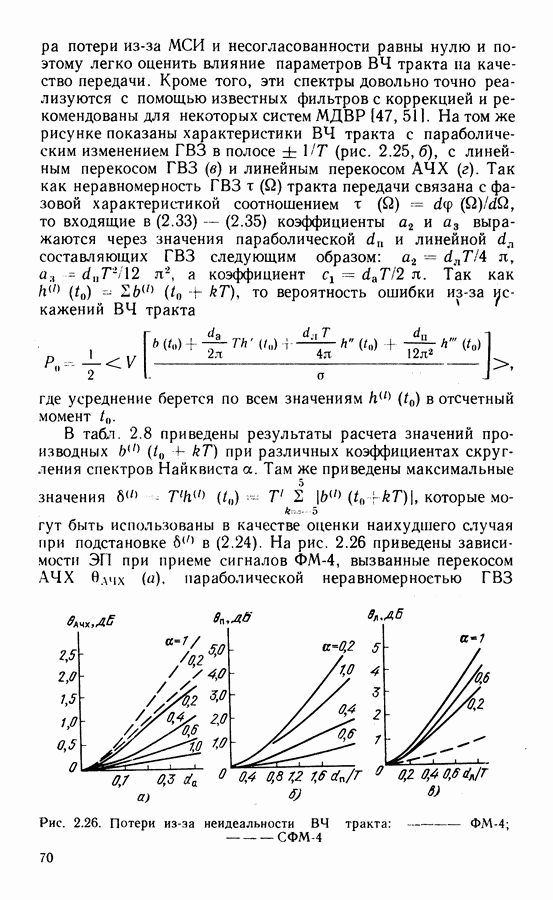
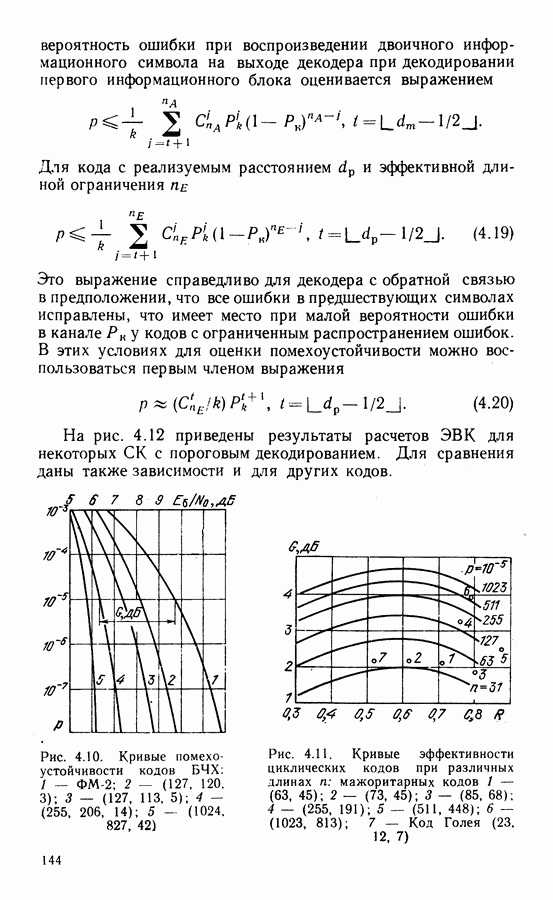
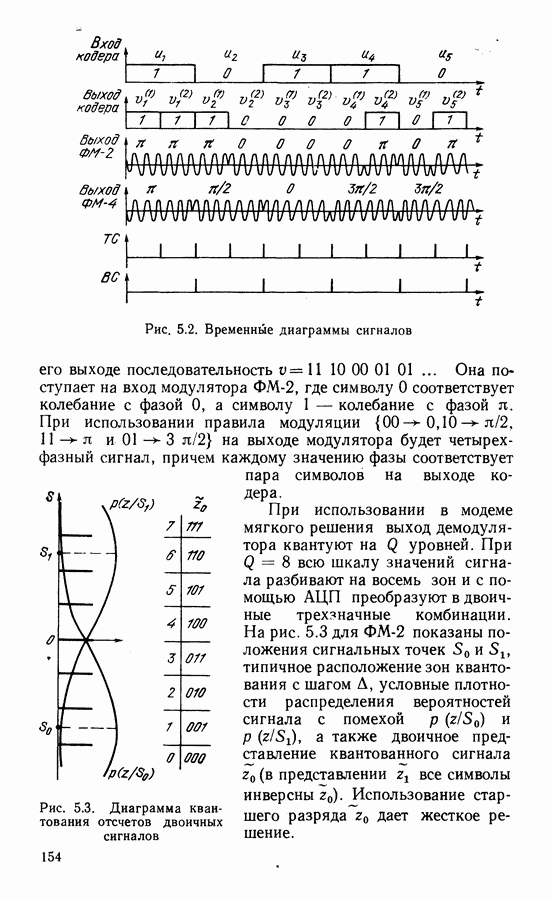
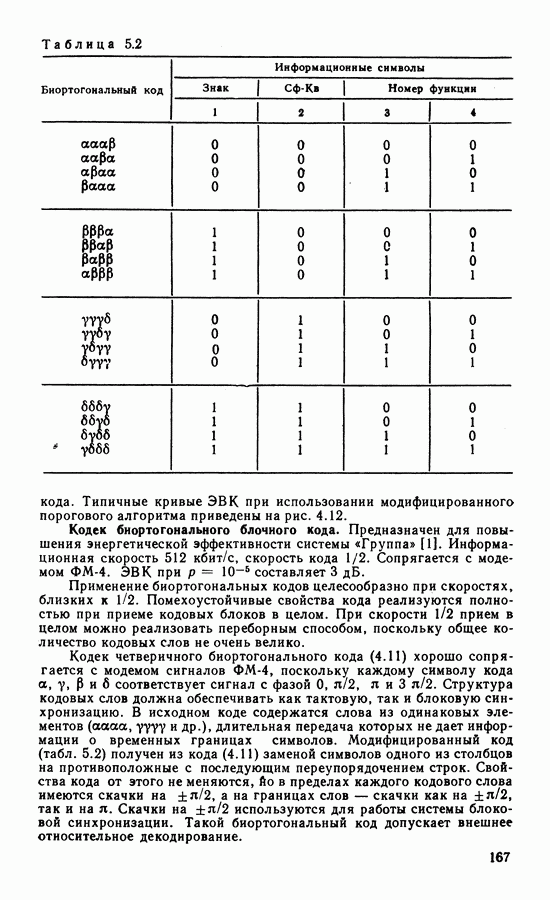
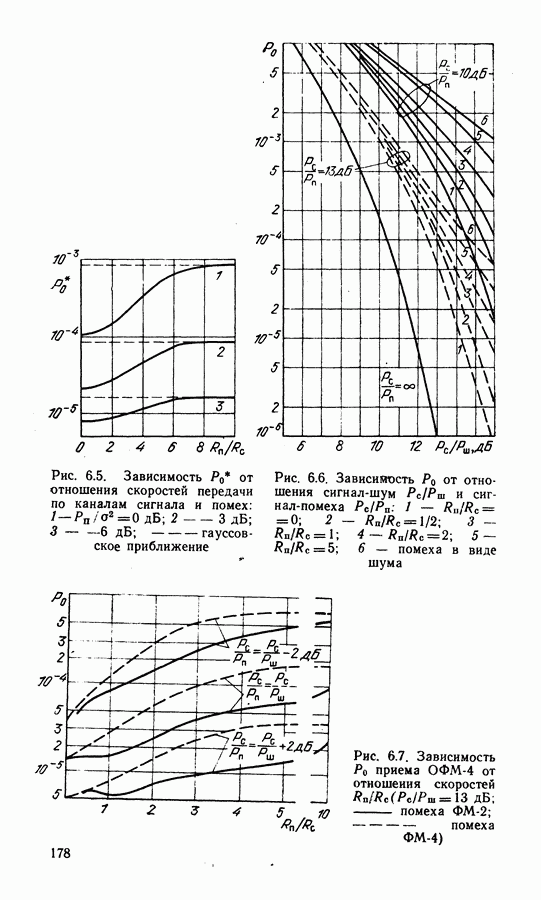
Выше рассмотрены характеристики СВН без учета манипуляции. При прохождении модулированного сигнала через тракт с ограниченной полосой изменения фазы сигнала происходят непрерывно и, следовательно, операции снятия манипуляции в СВН неточны. При этом, с одной стороны, уменьшается уровень восстановленной несущей в СВН, с другой, появляется случайная составляющая фазовой ошибки, обусловленная случайным характером манипуляции (манипуляционная помеха) [64]. Степень уменьшения уровня восстановленной несущей, определенная на основе спектрального анализа сигнала на выходе схем с возведением сигнала в степень и ремодуляцией в предположении, что при фильтрации огибающая сигнала приобретает трапецеидальную форму, представлена в табл. 3.1.
Фазовая ошибка, обусловленная манипуляционной помехой, незначительна для сигналов ФМ-2 и практически соизмерима с шумовой при  для сигналов ФМ-4 [64].
для сигналов ФМ-4 [64].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ I. ОСНОВЫ ПОСТРОЕНИЯ ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМ СВЯЗИ
- ГЛАВА 1. СПУТНИКОВЫЕ СИСТЕМЫ С МНОГОСТАНЦИОННЫМ ДОСТУПОМ
- 1.2. ПРЕОБРАЗОВАНИЕ АНАЛОГОВЫХ СИГНАЛОВ В ЦИФРОВУЮ ФОРМУ
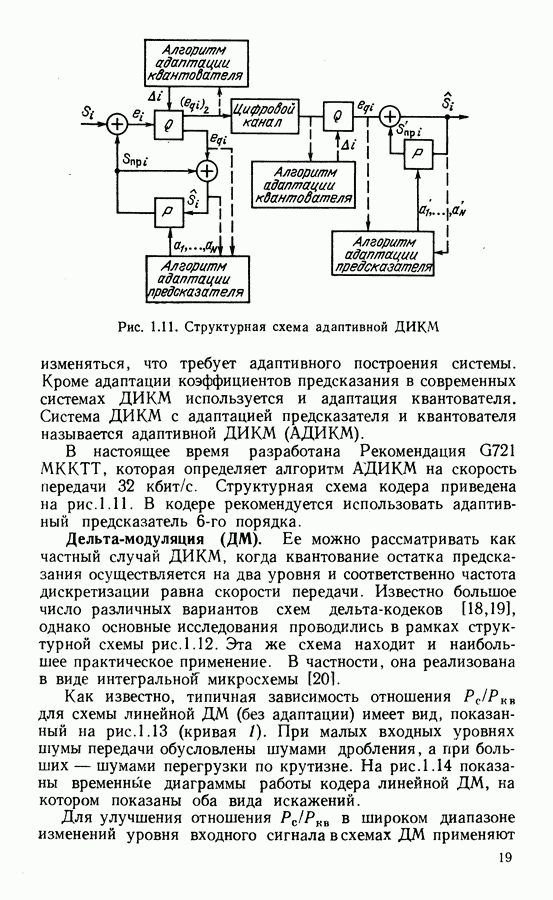
- Адаптивная ИКМ.
- Дифференциальная ИКМ (ДИКМ).
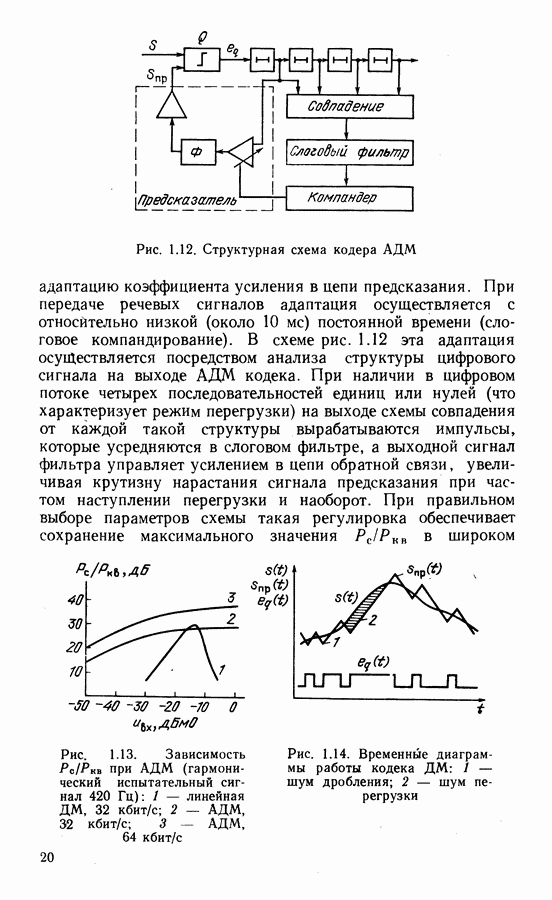
- Дельта-модуляция (ДМ).
- Преобразование сигналов телевидения, многоканальной телефонии и вещания в цифровую форму.
- 1.3. СТАТИСТИЧЕСКОЕ УПЛОТНЕНИЕ В ЦССС
- 1.4. МНОГОСТАНЦИОННЫЙ ДОСТУП В ЦССС
- Многостанционный доступ с временным разделением каналов (МДВР).
- Многостанционный доступ с разделением сигналов по форме (МДФР).
- Многостанционный доступ со случайным доступом (МДСД).
- 1.5. НОРМИРОВАНИЕ ПАРАМЕТРОВ ЦССС
- РАЗДЕЛ II. МОДУЛЯЦИЯ
- ГЛАВА 2. МЕТОДЫ МОДУЛЯЦИИ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.2. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СИГНАЛОВ
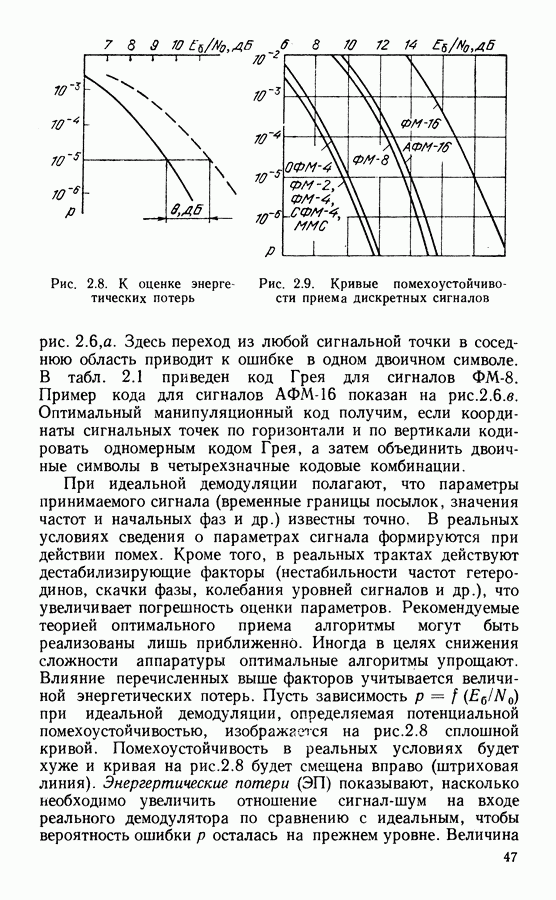
- 2.3. СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИГНАЛОВ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
- 2.4. СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ
- 2.5. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДЧР
- Результаты расчетов потерь в системе с ФМ-2 и стандартными фильтрами.
- Использование выравнивателей в тракте передачи.
- Анализ зависимости потерь от разноса между каналами.
- Энергетические потери в системе с ФМ-4.
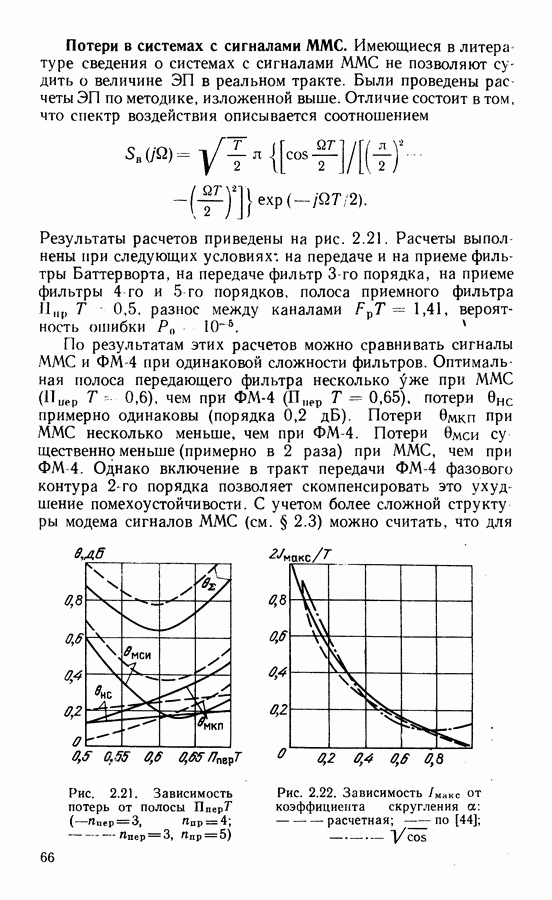
- Потери в системах с сигналами ММС.
- 2.6. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДВР
- ГЛАВА 3. МОДЕМЫ
- 3.1. СТРУКТУРА МОДЕМА
- 3.2. СИСТЕМЫ ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ
- Требования к точности работы системы ВН.
- Анализ точности систем ВН.
- Переходные процессы.
- 3.3. ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 3.4. ОТНОСИТЕЛЬНОЕ КОДИРОВАНИЕ
- 3.5. ПРИМЕРЫ РЕАЛИЗАЦИИ МОДЕМОВ В ЦССС
- РАЗДЕЛ III. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
- 4.2. АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ КОДОВ
- 4.3. БЛОКОВЫЕ КОДЫ И АЛГОРИТМЫ ИХ ДЕКОДИРОВАНИЯ
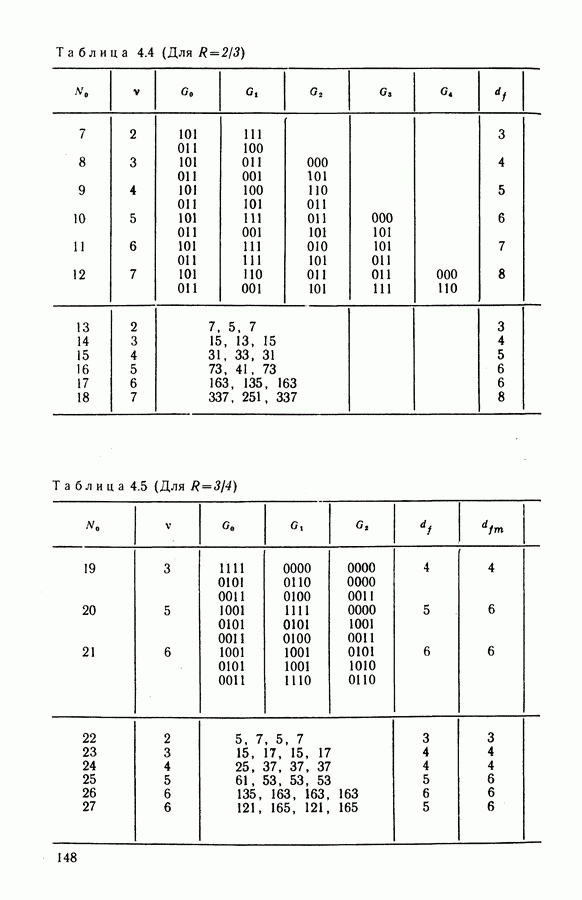
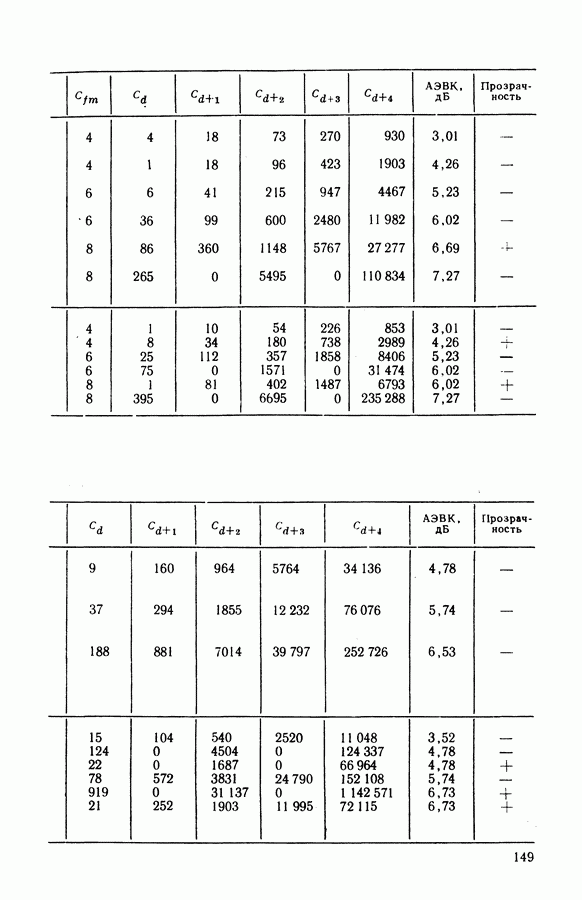
- 4.4. СТРУКТУРА И ХАРАКТЕРИСТИКИ СВЕРТОЧНЫХ КОДОВ
- 4.5. АЛГОРИТМЫ ДЕКОДИРОВАНИЯ СК
- 4.6. ПОМЕХОУСТОЙЧИВОСТЬ И ЭФФЕКТИВНОСТЬ СИСТЕМ С КОДИРОВАНИЕМ
- ГЛАВА 5. КОДЕКИ
- 5.1. СОГЛАСОВАНИЕ МОДЕМА И КОДЕКА
- 5.2. ДЕКОДЕРЫ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ СК
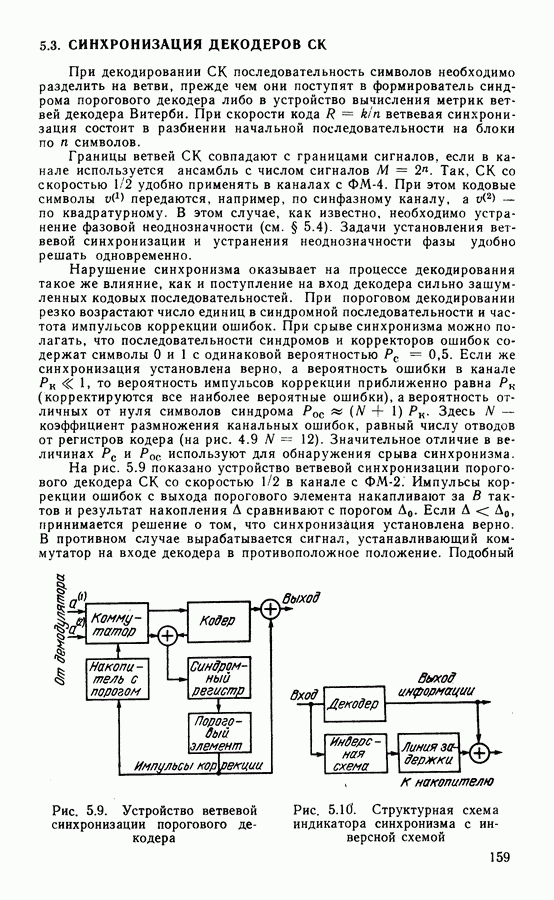
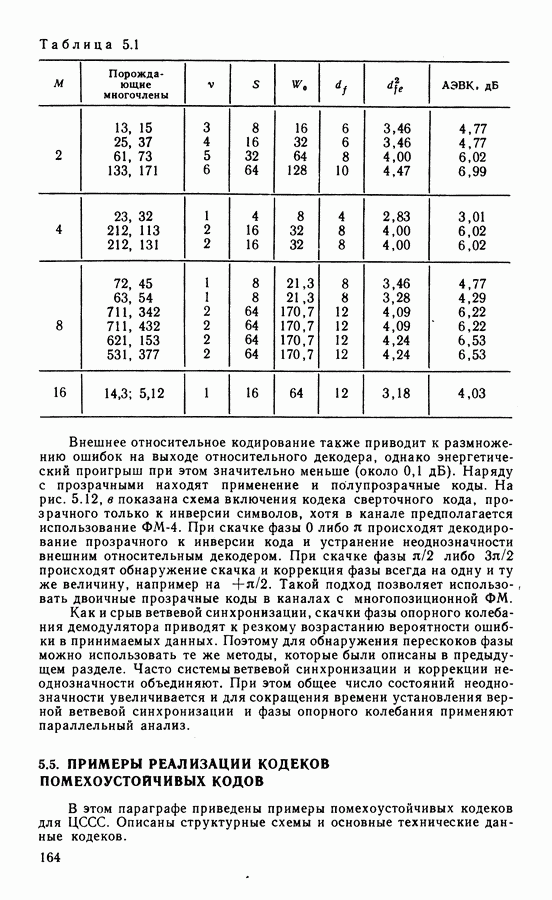
- 5.3. СИНХРОНИЗАЦИЯ ДЕКОДЕРОВ СК
- 5.4. КОДИРОВАНИЕ В КАНАЛАХ С НЕОДНОЗНАЧНОСТЬЮ
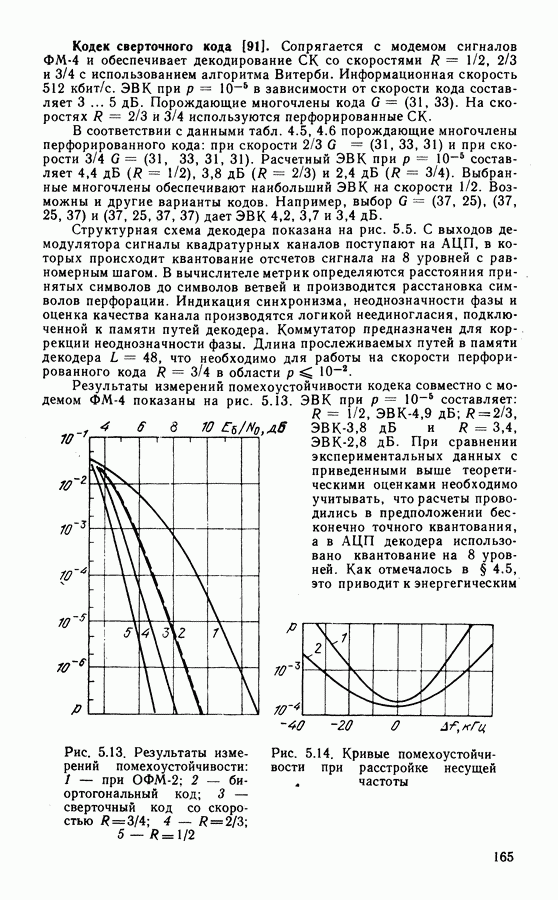
- 5.5. ПРИМЕРЫ РЕАЛИЗАЦИИ КОДЕКОВ ПОМЕХОУСТОЙЧИВЫХ КОДОВ
- Кодек биортогонального блочного кода.
- 5.6. РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
- РАЗДЕЛ IV. ЦИФРОВЫЕ СИСТЕМЫ СПУТНИКОВОЙ СВЯЗИ
- ГЛАВА 6. ВЗАИМНЫЕ ПОМЕХИ В ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМАХ
- 6.2. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ГАРМОНИЧЕСКИХ ПОМЕХ НА ДЕМОДУЛЯТОР ФМ СИГНАЛОВ
- 6.3. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ФМ ПОМЕХ
- 6.4. АНАЛИЗ МЕШАЮЩЕГО ДЕЙСТВИЯ ЧМ—ТВ СИГНАЛА С ДИСПЕРСИЕЙ
- 6.5. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ СИГНАЛОВ ЧУ-ЧМ
- ГЛАВА 7. СИСТЕМЫ С МДВР И МДЧР
- 7.1. ОЦЕНКА ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ РАЗЛИЧНЫХ МЕТОДОВ ПЕРЕДАЧИ В ЦССС С МДЧР
- 7.2. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДЧР
- 7.3. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДВР
- Синхронизация систем МДВР.
- Организация кадра систем МДВР.
- Система МДВУ-40.
- ЦСС с ДВР ТДМА-120-(«Интелсат»/«Евросат»).
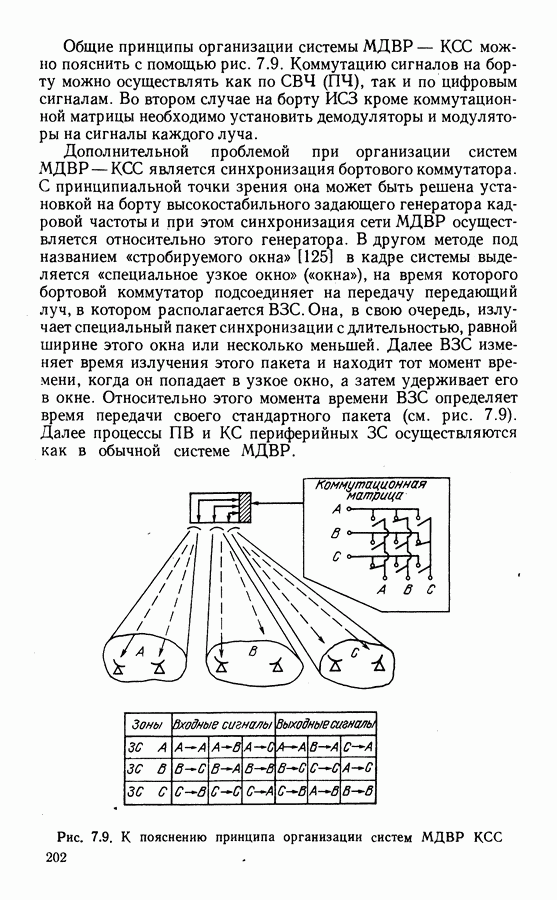
- МДВР с коммутацией сигналов на спутнике (КСС).
- Сопряжение систем МДВР с цифровыми наземными линиями.
- ГЛАВА 8. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ И КОДИРОВАНИЯ В ЦССС
- 8.2. СОГЛАСОВАНИЕ СИСТЕМ МОДУЛЯЦИИ И КОДИРОВАНИЯ
- Согласование кодом Грея.
- Кодирование с разбиением ансамбля на подклассы.
- Применение недвоичных кодов.
- 8.3. СВЕРТОЧНОЕ КОДИРОВАНИЕ В КАНАЛЕ С МНОГОПОЗИЦИОННОИ ФМ
- 8.4. ОБОБЩЕННОЕ КАСКАДНОЕ КОДИРОВАНИЕ
- 8.5. ПРИМЕРЫ РЕАЛИЗАЦИИ ЭФФЕКТИВНЫХ КОДЕМОВ
- СПИСОК ЛИТЕРАТУРЫ