| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.3. ТАКТОВАЯ СИНХРОНИЗАЦИЯ
Система тактовой синхронизации  предназначена для выделения колебаний тактовой частоты, период которой определяет границы посылок передаваемых дискретных сигналов. Относительно этих границ выбирают момент взятия отсчета в
предназначена для выделения колебаний тактовой частоты, период которой определяет границы посылок передаваемых дискретных сигналов. Относительно этих границ выбирают момент взятия отсчета в  демодулятора.
демодулятора.
В спектре случайного цифрового сигнала, как правило, не содержится компонента с тактовой частотой, поэтому ее приходится формировать из принятого сигнала путем некоторого нелинейного преобразования. Известны оптимальные структуры СТС [58], однако из-за сложности и ряда упрощающих предпосылок при их синтезе они не нашли применения.
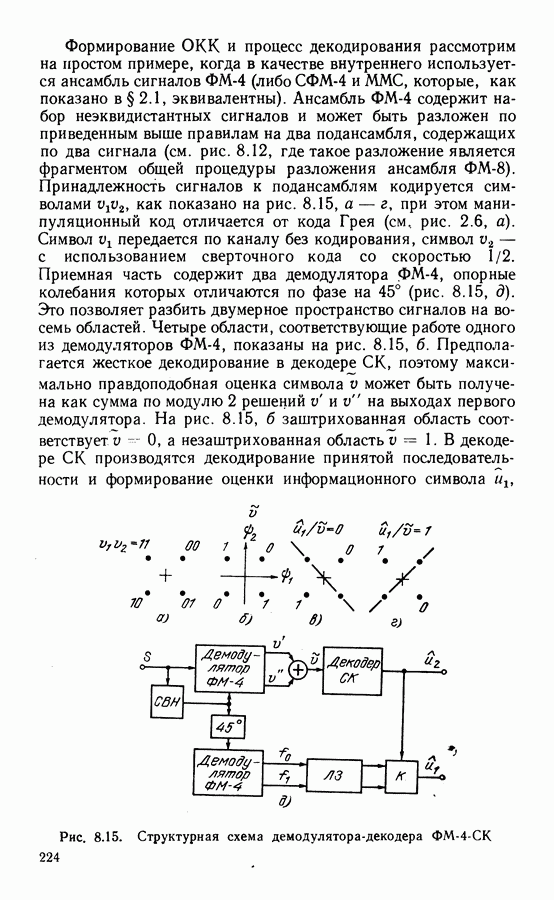
На практике часто используют структуру, схема которой представлена на рис. 3.14, а, где ВФ - схема выделения фронтов, Ф — фильтр [31. Имеется большое многообразие схем ВФ, на особенностях которых не будем останавливаться. Большинство схем  формируют импульсы от каждого перехода принятого цифрового сигнала через нуль, как это показано на рис. 3.15. Схемы фильтрации в СТС могут быть как пассивными на полосовых фильтрах, так и активными на основе ФАП. Системы ФАП СТС, в свою очередь, могут быть аналоговыми, цифровыми и цифро-аналоговыми.
формируют импульсы от каждого перехода принятого цифрового сигнала через нуль, как это показано на рис. 3.15. Схемы фильтрации в СТС могут быть как пассивными на полосовых фильтрах, так и активными на основе ФАП. Системы ФАП СТС, в свою очередь, могут быть аналоговыми, цифровыми и цифро-аналоговыми.
Требования к точности СТС.
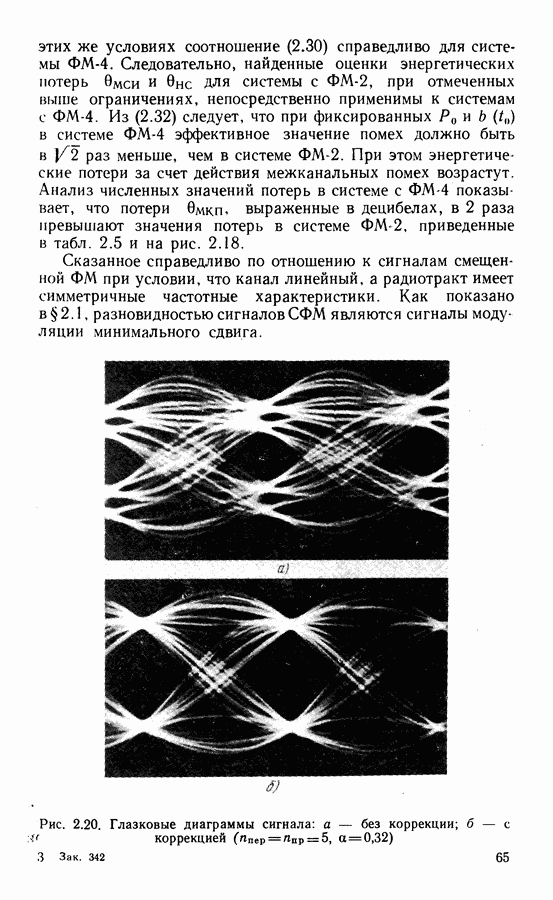
Оптимальный момент взятия отсчета  соответствует моменту времени, где имеется узел глазковой диаграммы (см. рис. 2.23). Любое отклонение от оптимального значения приводит к ухудшению помехоустойчивости.
соответствует моменту времени, где имеется узел глазковой диаграммы (см. рис. 2.23). Любое отклонение от оптимального значения приводит к ухудшению помехоустойчивости.

Рис. 3.14. Структурная схема СТС (а), ФВ с перемножением и полу-тактовым сдвигом (б)

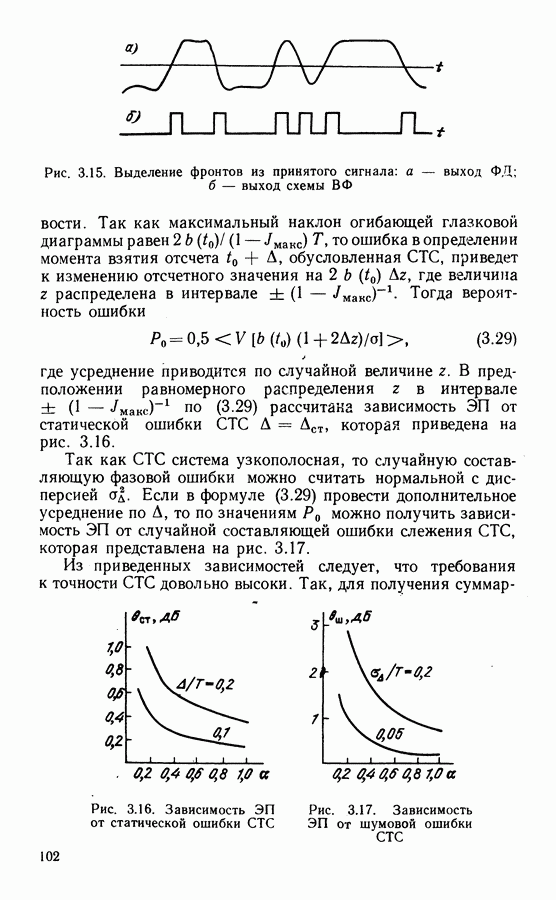
Рис. 3.15. Выделение фронтов из принятого сигнала: а — выход ФД; б - выход схемы ВФ
Так как максимальный наклон огибающей глазковой диаграммы равен  то ошибка в определении момента взятия отсчета
то ошибка в определении момента взятия отсчета  обусловленная СТС, приведет к изменению отсчетного значения на
обусловленная СТС, приведет к изменению отсчетного значения на  где величина
где величина  распределена в интервале
распределена в интервале  Тогда вероятность ошибки
Тогда вероятность ошибки

где усреднение приводится по случайной величине  . В предположении равномерного распределения
. В предположении равномерного распределения  в интервале
в интервале  по (3.29) рассчитана зависимость ЭП от статической ошибки
по (3.29) рассчитана зависимость ЭП от статической ошибки  которая приведена на рис. 3.16.
которая приведена на рис. 3.16.
Так как СТС система узкополосная, то случайную составляющую фазовой ошибки можно считать нормальной с дисперсией  Если в формуле (3.29) провести дополнительное усреднение по А, то по значениям
Если в формуле (3.29) провести дополнительное усреднение по А, то по значениям  можно получить зависимость ЭП от случайной составляющей ошибки слежения СТС, которая представлена на рис. 3.17.
можно получить зависимость ЭП от случайной составляющей ошибки слежения СТС, которая представлена на рис. 3.17.
Из приведенных зависимостей следует, что требования к точности СТС довольно высоки. Так, для получения суммарных

Рис. 3.16. Зависимость ЭП от статической ошибки СТС

Рис. 3.17. Зависимость ЭП от шумовой ошибки СТС
потерь  при спектре на входе
при спектре на входе  требуется
требуется  Соответственно для
Соответственно для  требуется
требуется  Отметим, что
Отметим, что  обусловленные СТС, резко возрастают при
обусловленные СТС, резко возрастают при 
Как и в случае  важным параметром СТС является перескок фазы на выходе
важным параметром СТС является перескок фазы на выходе  что эквивалентно появлению лишнего или пропуску одного тактового импульса. При таком событии кроме пакета ошибок длительностью порядка постоянной времени СТС нарушается работа различного рода цифровых распределителей, счетчиков, экспандеров, что также приводит к длинным блокам ошибок. Поэтому требования на вероятность перескока фазы (проскальзывания цикла) в СТС должны быть не хуже
что эквивалентно появлению лишнего или пропуску одного тактового импульса. При таком событии кроме пакета ошибок длительностью порядка постоянной времени СТС нарушается работа различного рода цифровых распределителей, счетчиков, экспандеров, что также приводит к длинным блокам ошибок. Поэтому требования на вероятность перескока фазы (проскальзывания цикла) в СТС должны быть не хуже 
Анализ помехоустойчивости СТС дадим для схемы  которая показана на рис. 3.14, а. Рассмотрим энергетический спектр импульсного процесса на выходе
которая показана на рис. 3.14, а. Рассмотрим энергетический спектр импульсного процесса на выходе  который характеризуется, во-первых, равновероятным наличием и отсутствием импульса в тактовые моменты времени
который характеризуется, во-первых, равновероятным наличием и отсутствием импульса в тактовые моменты времени  Так как наличие или отсутствие импульса на несовпадающих тактовых точках является независимым событием, то
Так как наличие или отсутствие импульса на несовпадающих тактовых точках является независимым событием, то  где
где  амплитуда импульса. Во-вторых, моменты пересечения нуля в принятом сигнале отличаются от точек
амплитуда импульса. Во-вторых, моменты пересечения нуля в принятом сигнале отличаются от точек  из-за воздействия шума в канале и из-за джиттера. Будем считать, что как шумовое смещение, так и джиттер на соседних тактовых интервалах независимы. Введем характеристические функции распределения шумового смещения
из-за воздействия шума в канале и из-за джиттера. Будем считать, что как шумовое смещение, так и джиттер на соседних тактовых интервалах независимы. Введем характеристические функции распределения шумового смещения  и джиттера
и джиттера  Тогда энергетический спектр на выходе
Тогда энергетический спектр на выходе  имеет дискретную часть [73]
имеет дискретную часть [73]

и непрерывную

где  коэффициент, зависящий от длительности импульса.
коэффициент, зависящий от длительности импульса.
В формуле (3.31) составляющая  относится к амплитудным флуктуациям, а
относится к амплитудным флуктуациям, а  к фазовым. Дисперсия фазовой ошибки на выходе узкополосного фильтра СТС с шумовой полосой
к фазовым. Дисперсия фазовой ошибки на выходе узкополосного фильтра СТС с шумовой полосой  и центральной частотой
и центральной частотой 

Определим входящие в (3.30) и (3.31) функции  При высоком отношении сигнал-шум шумовое смещение фронта
При высоком отношении сигнал-шум шумовое смещение фронта

где  средняя крутизна фронта при пересечении нулевого уровня. Следовательно, распределение
средняя крутизна фронта при пересечении нулевого уровня. Следовательно, распределение  нормально с дисперсией
нормально с дисперсией

Соответственно

Случайное смещение положения импульса из-за джиттера  распределено в интервале
распределено в интервале  . Считая распределение
. Считая распределение  равномерным в этом интервале, найдем
равномерным в этом интервале, найдем

Подставляя (3.33) и (3.34) в (3.32), получаем

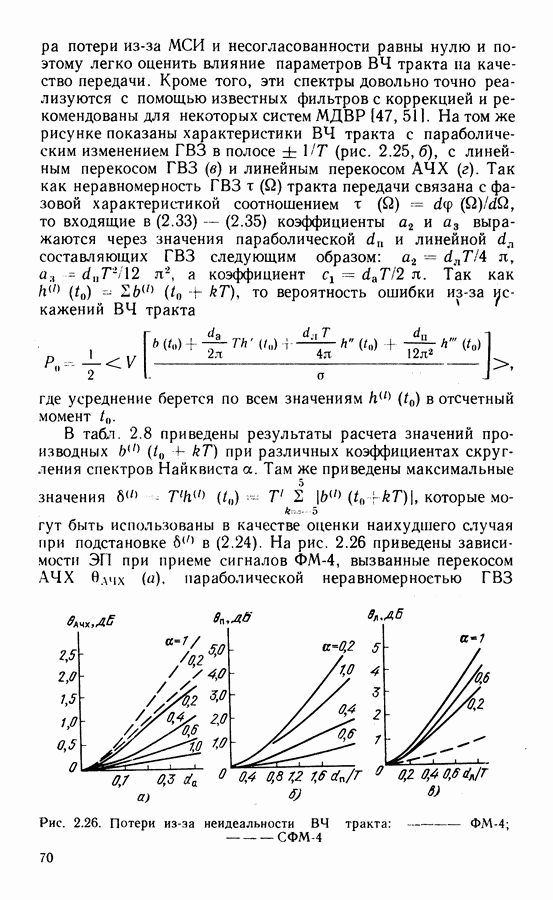
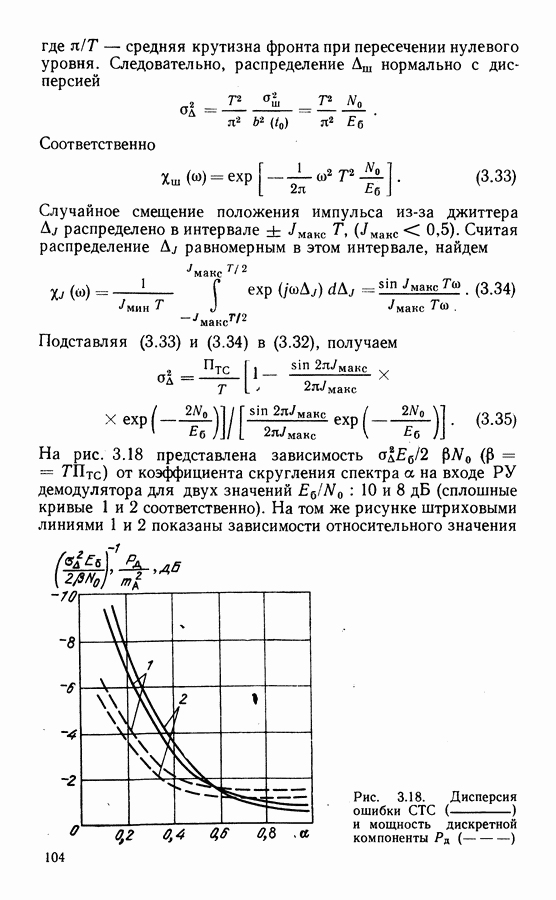
На рис. 3.18 представлена зависимость  от коэффициента скругления спектра а на входе
от коэффициента скругления спектра а на входе  демодулятора для двух значений
демодулятора для двух значений  (сплошные кривые 1 и 2 соответственно). На том же рисунке штриховыми линиями 1 и 2 показаны зависимости относительного значения
(сплошные кривые 1 и 2 соответственно). На том же рисунке штриховыми линиями 1 и 2 показаны зависимости относительного значения

Рис. 3.18. Дисперсия ошибки СТС  и мощность дискретной компоненты
и мощность дискретной компоненты 
 характеризующие уменьшение средней мощности колебания тактовой частоты на выходе схемы
характеризующие уменьшение средней мощности колебания тактовой частоты на выходе схемы  Формула (3.35) определяет предельную помехоустойчивость рассматриваемой СТС, и из нее и данных рис. 3.18 следует, что помехоустойчивость СТС в существенной мере зависит от степени скругления спектра, которая определяет колебания фронтов принимаемого дискретного сигнала. В частности, при
Формула (3.35) определяет предельную помехоустойчивость рассматриваемой СТС, и из нее и данных рис. 3.18 следует, что помехоустойчивость СТС в существенной мере зависит от степени скругления спектра, которая определяет колебания фронтов принимаемого дискретного сигнала. В частности, при  из (3.35) следует, что
из (3.35) следует, что  т. е. выделение тактовой частоты невозможно.
т. е. выделение тактовой частоты невозможно.
Сформулированные выше требования к точности СТС и данные формулы (3.35) и рис. 3.18 позволяют определить требования к узкополосности фильтра  Так, для получения
Так, для получения  при
при  соотношение
соотношение  должно быть не более 0,005, поэтому шумовая полоса СТС должна быть примерно в 200 раз меньше полосы Найквиста.
должно быть не более 0,005, поэтому шумовая полоса СТС должна быть примерно в 200 раз меньше полосы Найквиста.
Среднее число перескоков фазы в СТС можно рассчитать, если в СТС использована схема ВФ, показанная на рис. 3.14, б. Схема содержит перемножитель прямого и задержанного на половину бита ФМ сигнала. На выходе от каждого перехода ФМ-сигнала образуется импульс длительностью  . Шум в этой схеме добавляется аддитивно, что и позволяет для расчета среднего числа срывов синхронизма использовать известные результаты [70]. Не останавливаясь на них подробно, отметим, что при узкополосной СТС среднее число срывов синхронизации СТС можно рассчитать по формуле
. Шум в этой схеме добавляется аддитивно, что и позволяет для расчета среднего числа срывов синхронизма использовать известные результаты [70]. Не останавливаясь на них подробно, отметим, что при узкополосной СТС среднее число срывов синхронизации СТС можно рассчитать по формуле

где  определяется из формулы (3.30) или по кривым рис. 3.18.
определяется из формулы (3.30) или по кривым рис. 3.18.
Если не выполняется условие  , то следует учитывать амплитудную модуляцию колебания тактовой частоты на выходе фильтра. Плотности распределения амплитуды в зависимости от
, то следует учитывать амплитудную модуляцию колебания тактовой частоты на выходе фильтра. Плотности распределения амплитуды в зависимости от  даны в работе [70].
даны в работе [70].
Переходные процессы.
В отличие от СВН системы ТС в ЦССС работают при значительно меньших нестабильностях частоты, поэтому практически время вхождения в синхронизм определяется временем установления по фазе. Кроме того, в системах ФАП с импульсным  легко исключаются движения к стационарному состоянию, начинающиеся из начальных состояний фазы, равных
легко исключаются движения к стационарному состоянию, начинающиеся из начальных состояний фазы, равных  [66]. Следует отметить, что и в этих условиях для систем, работающих в пакетном режиме, меньшее время установления синхронизации обеспечивают СТС с пассивной фильтрацией, это послужило причиной их применения в демодуляторах систем МДВР [71].
[66]. Следует отметить, что и в этих условиях для систем, работающих в пакетном режиме, меньшее время установления синхронизации обеспечивают СТС с пассивной фильтрацией, это послужило причиной их применения в демодуляторах систем МДВР [71].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ I. ОСНОВЫ ПОСТРОЕНИЯ ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМ СВЯЗИ
- ГЛАВА 1. СПУТНИКОВЫЕ СИСТЕМЫ С МНОГОСТАНЦИОННЫМ ДОСТУПОМ
- 1.2. ПРЕОБРАЗОВАНИЕ АНАЛОГОВЫХ СИГНАЛОВ В ЦИФРОВУЮ ФОРМУ
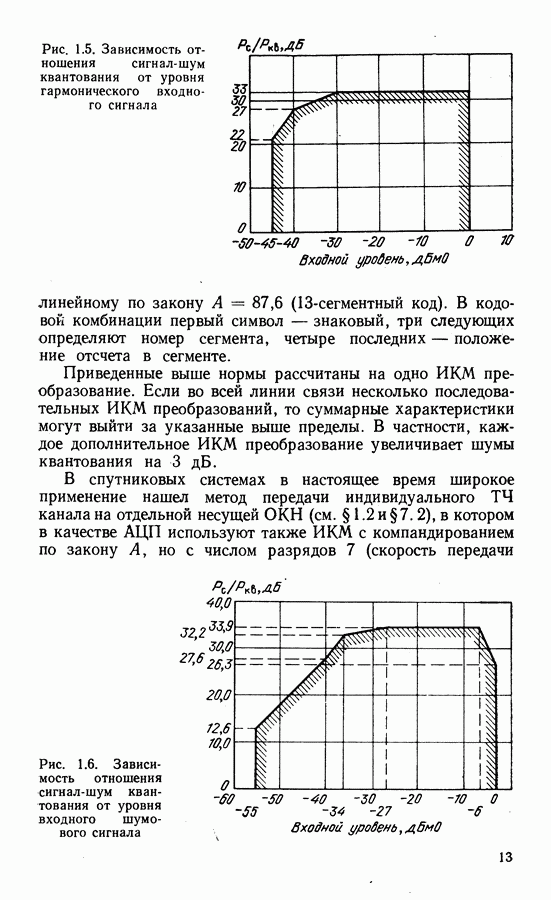
- Адаптивная ИКМ.
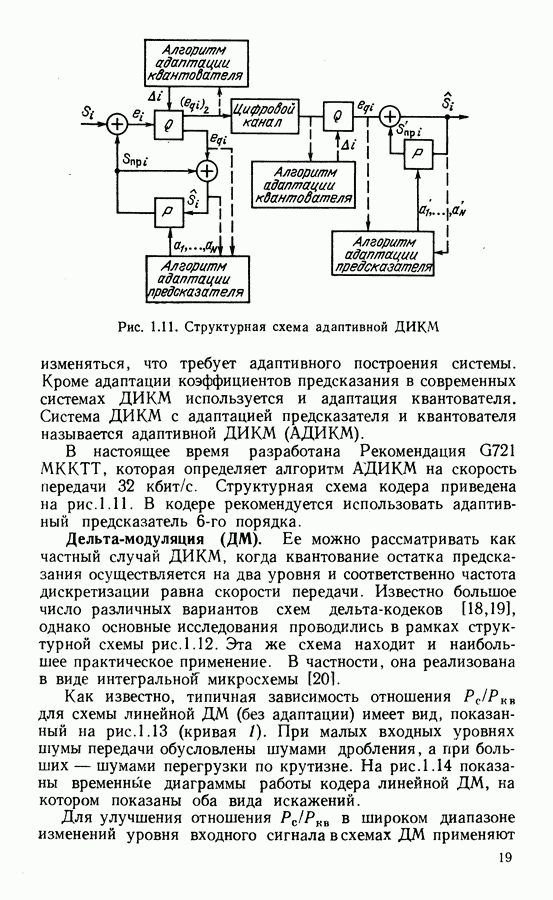
- Дифференциальная ИКМ (ДИКМ).
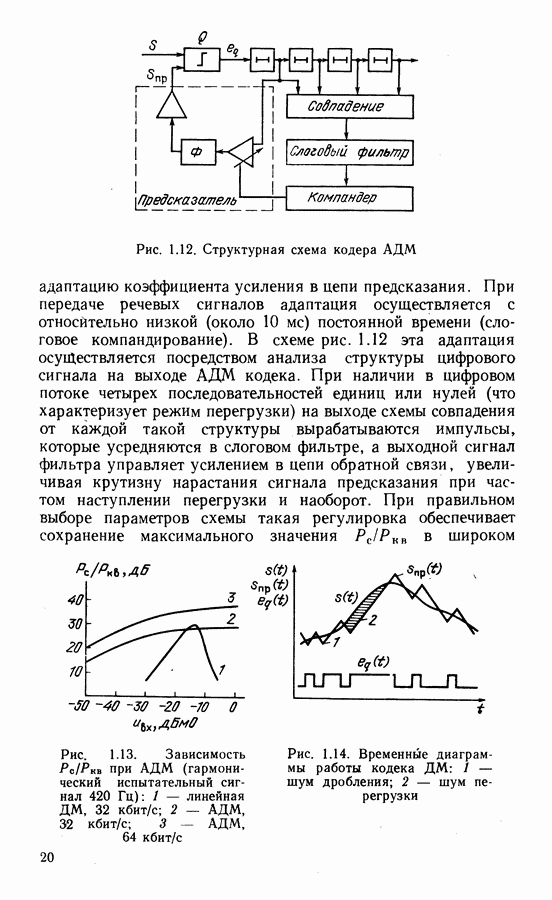
- Дельта-модуляция (ДМ).
- Преобразование сигналов телевидения, многоканальной телефонии и вещания в цифровую форму.
- 1.3. СТАТИСТИЧЕСКОЕ УПЛОТНЕНИЕ В ЦССС
- 1.4. МНОГОСТАНЦИОННЫЙ ДОСТУП В ЦССС
- Многостанционный доступ с временным разделением каналов (МДВР).
- Многостанционный доступ с разделением сигналов по форме (МДФР).
- Многостанционный доступ со случайным доступом (МДСД).
- 1.5. НОРМИРОВАНИЕ ПАРАМЕТРОВ ЦССС
- РАЗДЕЛ II. МОДУЛЯЦИЯ
- ГЛАВА 2. МЕТОДЫ МОДУЛЯЦИИ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.2. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СИГНАЛОВ
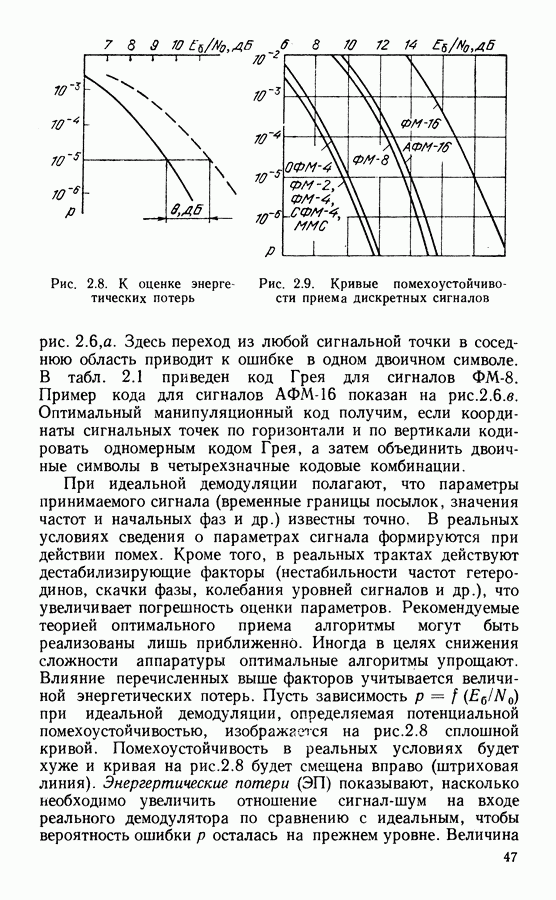
- 2.3. СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИГНАЛОВ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
- 2.4. СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ
- 2.5. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДЧР
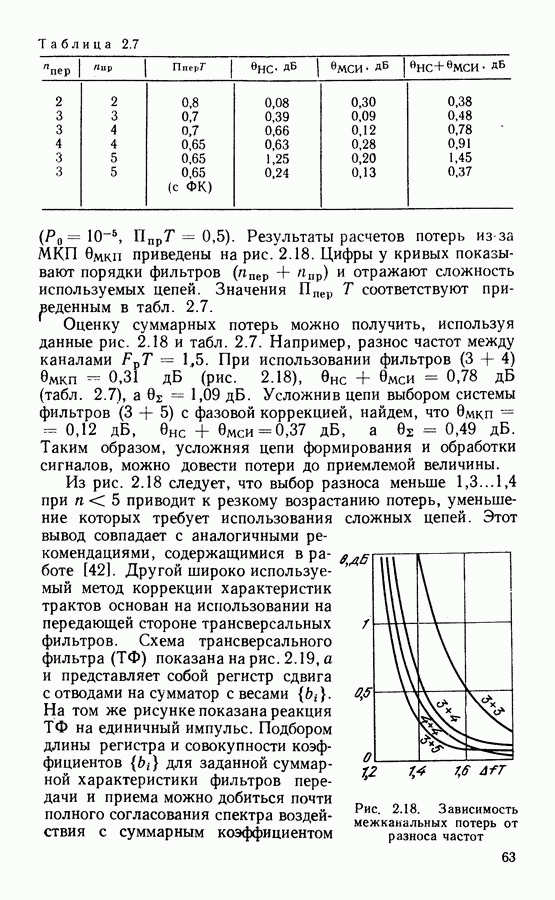
- Результаты расчетов потерь в системе с ФМ-2 и стандартными фильтрами.
- Использование выравнивателей в тракте передачи.
- Анализ зависимости потерь от разноса между каналами.
- Энергетические потери в системе с ФМ-4.
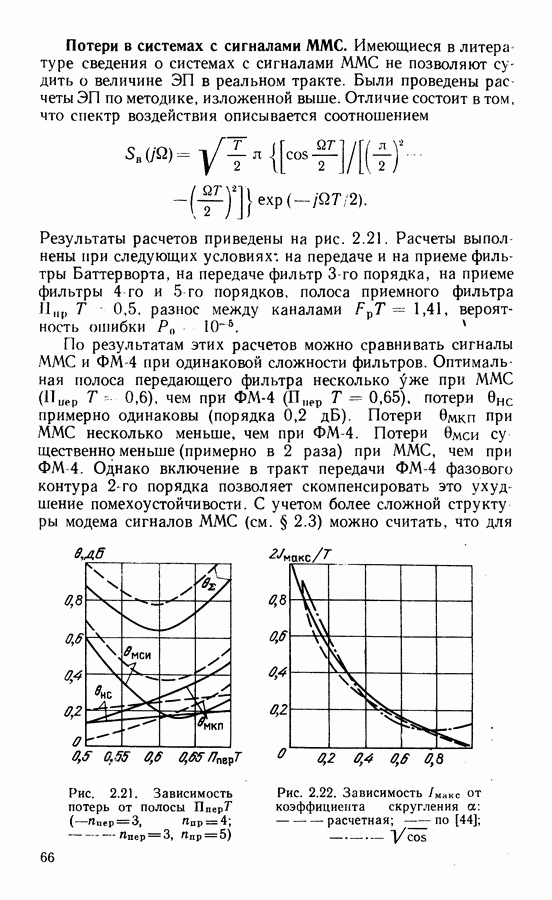
- Потери в системах с сигналами ММС.
- 2.6. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДВР
- ГЛАВА 3. МОДЕМЫ
- 3.1. СТРУКТУРА МОДЕМА
- 3.2. СИСТЕМЫ ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ
- Требования к точности работы системы ВН.
- Анализ точности систем ВН.
- Переходные процессы.
- 3.3. ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 3.4. ОТНОСИТЕЛЬНОЕ КОДИРОВАНИЕ
- 3.5. ПРИМЕРЫ РЕАЛИЗАЦИИ МОДЕМОВ В ЦССС
- РАЗДЕЛ III. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
- 4.2. АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ КОДОВ
- 4.3. БЛОКОВЫЕ КОДЫ И АЛГОРИТМЫ ИХ ДЕКОДИРОВАНИЯ
- 4.4. СТРУКТУРА И ХАРАКТЕРИСТИКИ СВЕРТОЧНЫХ КОДОВ
- 4.5. АЛГОРИТМЫ ДЕКОДИРОВАНИЯ СК
- 4.6. ПОМЕХОУСТОЙЧИВОСТЬ И ЭФФЕКТИВНОСТЬ СИСТЕМ С КОДИРОВАНИЕМ
- ГЛАВА 5. КОДЕКИ
- 5.1. СОГЛАСОВАНИЕ МОДЕМА И КОДЕКА
- 5.2. ДЕКОДЕРЫ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ СК
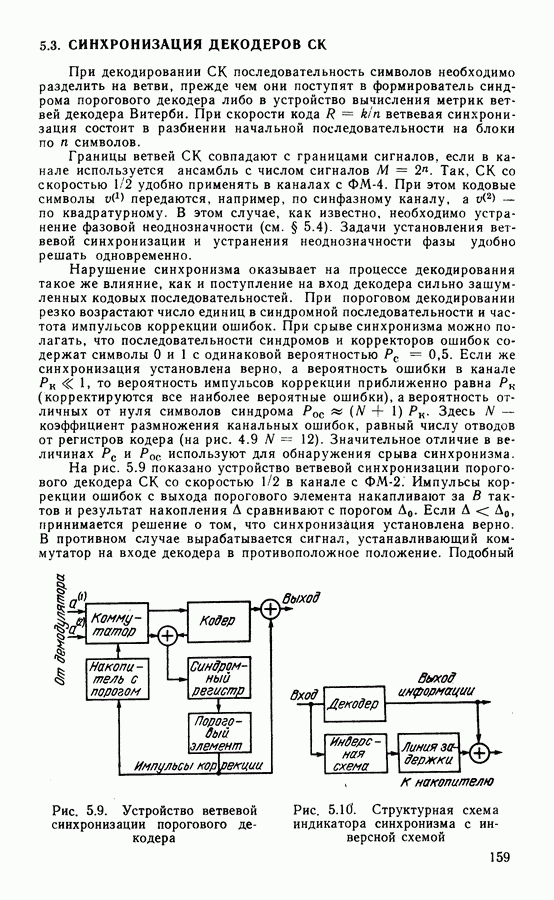
- 5.3. СИНХРОНИЗАЦИЯ ДЕКОДЕРОВ СК
- 5.4. КОДИРОВАНИЕ В КАНАЛАХ С НЕОДНОЗНАЧНОСТЬЮ
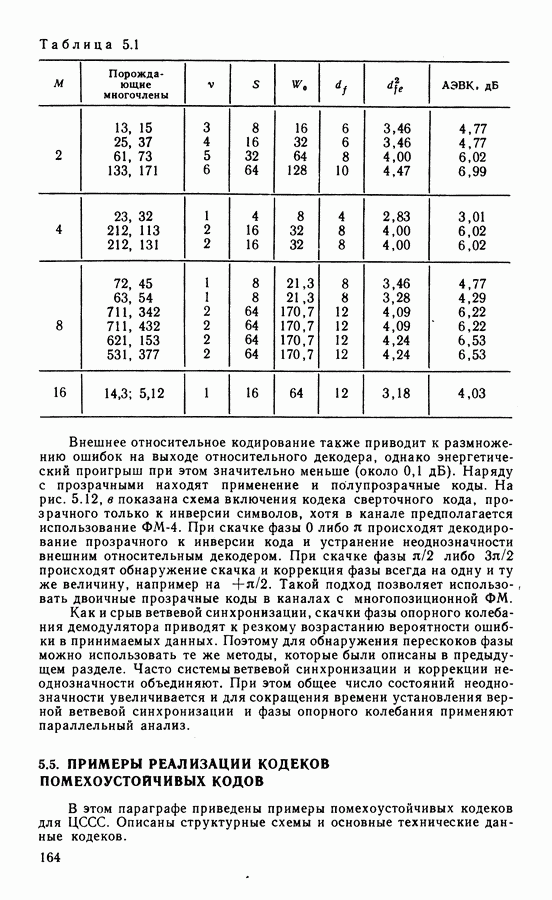
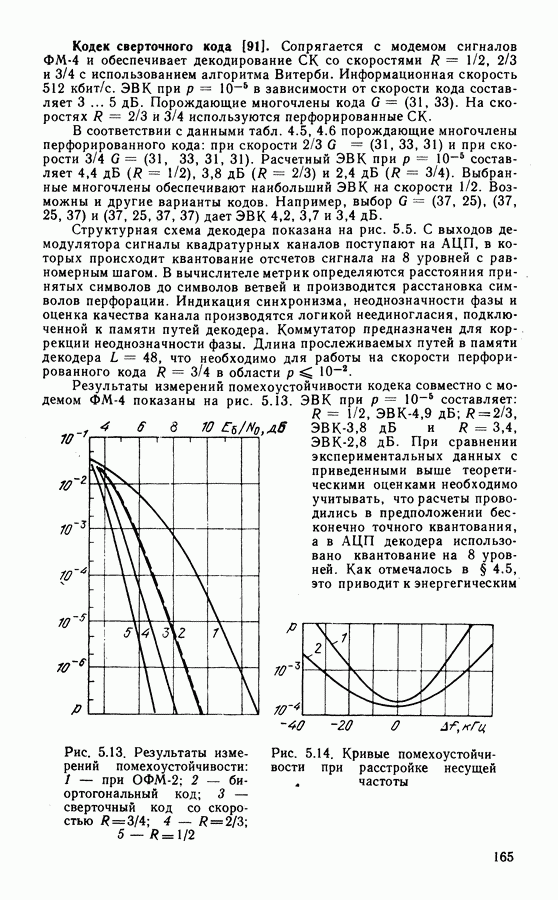
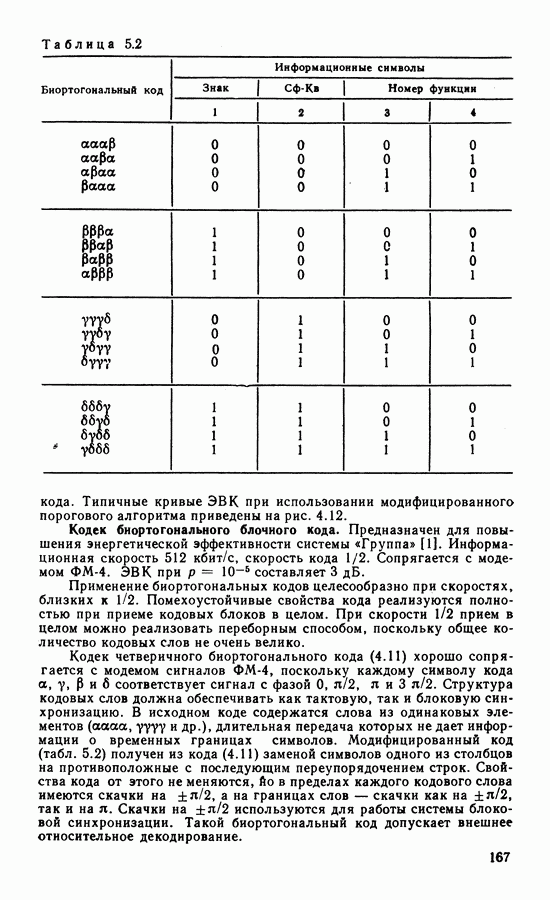
- 5.5. ПРИМЕРЫ РЕАЛИЗАЦИИ КОДЕКОВ ПОМЕХОУСТОЙЧИВЫХ КОДОВ
- Кодек биортогонального блочного кода.
- 5.6. РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
- РАЗДЕЛ IV. ЦИФРОВЫЕ СИСТЕМЫ СПУТНИКОВОЙ СВЯЗИ
- ГЛАВА 6. ВЗАИМНЫЕ ПОМЕХИ В ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМАХ
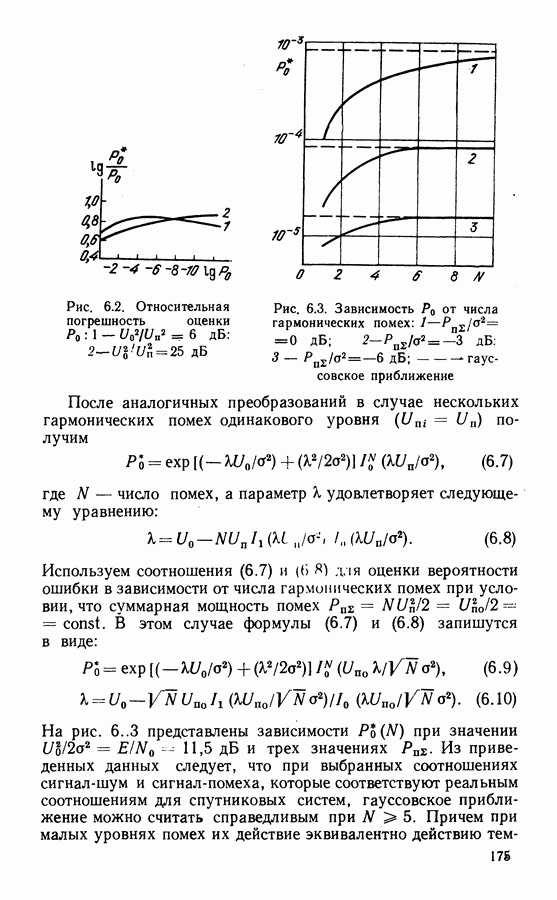
- 6.2. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ГАРМОНИЧЕСКИХ ПОМЕХ НА ДЕМОДУЛЯТОР ФМ СИГНАЛОВ
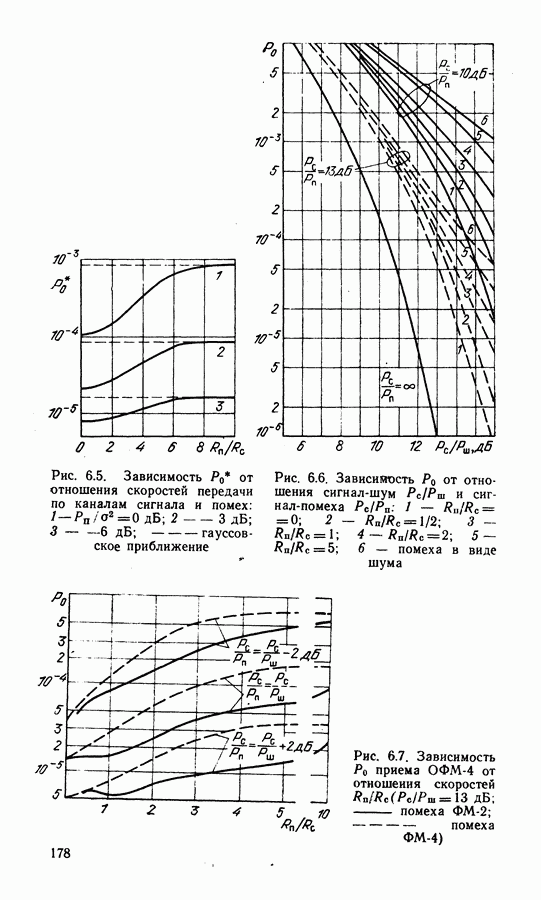
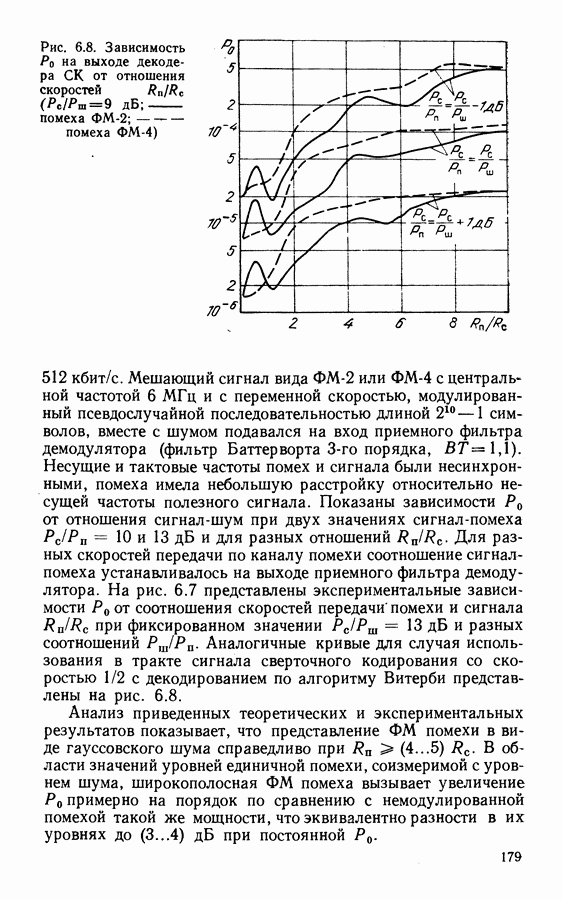
- 6.3. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ФМ ПОМЕХ
- 6.4. АНАЛИЗ МЕШАЮЩЕГО ДЕЙСТВИЯ ЧМ—ТВ СИГНАЛА С ДИСПЕРСИЕЙ
- 6.5. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ СИГНАЛОВ ЧУ-ЧМ
- ГЛАВА 7. СИСТЕМЫ С МДВР И МДЧР
- 7.1. ОЦЕНКА ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ РАЗЛИЧНЫХ МЕТОДОВ ПЕРЕДАЧИ В ЦССС С МДЧР
- 7.2. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДЧР
- 7.3. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДВР
- Синхронизация систем МДВР.
- Организация кадра систем МДВР.
- Система МДВУ-40.
- ЦСС с ДВР ТДМА-120-(«Интелсат»/«Евросат»).
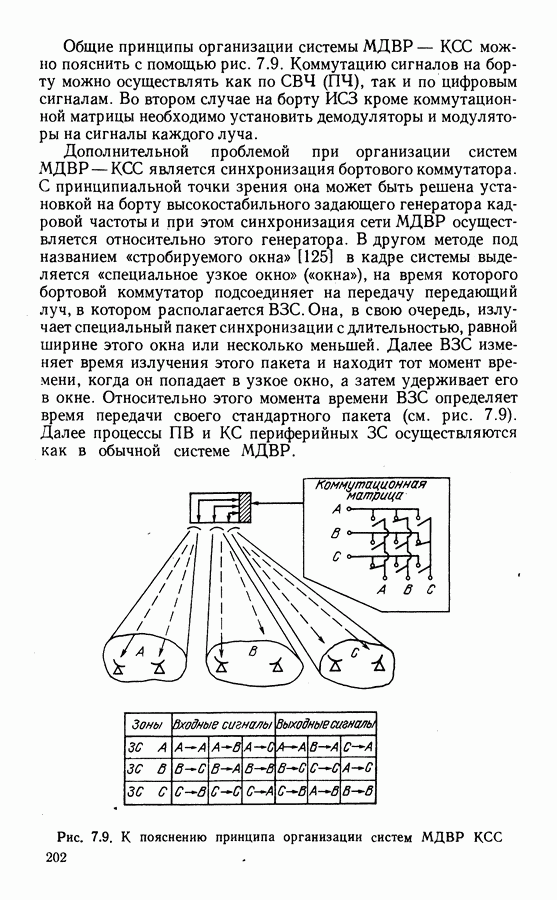
- МДВР с коммутацией сигналов на спутнике (КСС).
- Сопряжение систем МДВР с цифровыми наземными линиями.
- ГЛАВА 8. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ И КОДИРОВАНИЯ В ЦССС
- 8.2. СОГЛАСОВАНИЕ СИСТЕМ МОДУЛЯЦИИ И КОДИРОВАНИЯ
- Согласование кодом Грея.
- Кодирование с разбиением ансамбля на подклассы.
- Применение недвоичных кодов.
- 8.3. СВЕРТОЧНОЕ КОДИРОВАНИЕ В КАНАЛЕ С МНОГОПОЗИЦИОННОИ ФМ
- 8.4. ОБОБЩЕННОЕ КАСКАДНОЕ КОДИРОВАНИЕ
- 8.5. ПРИМЕРЫ РЕАЛИЗАЦИИ ЭФФЕКТИВНЫХ КОДЕМОВ
- СПИСОК ЛИТЕРАТУРЫ