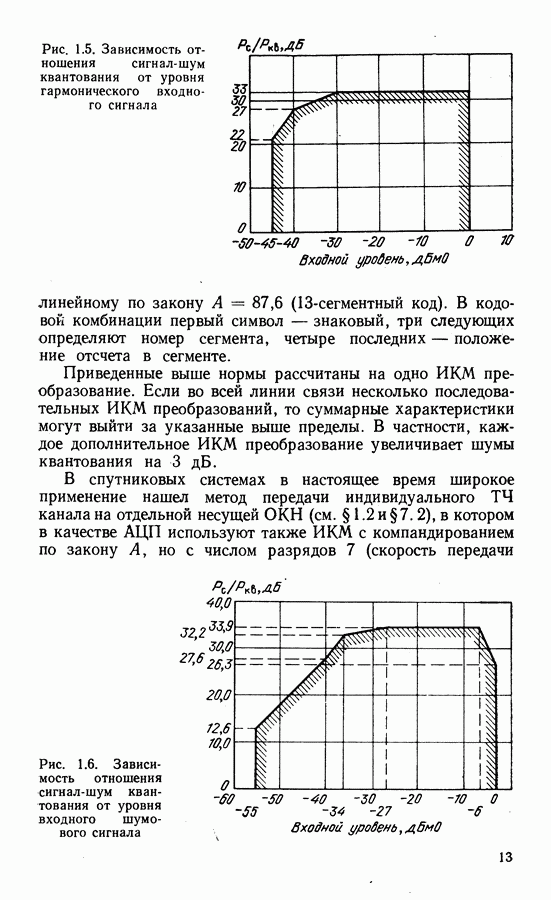
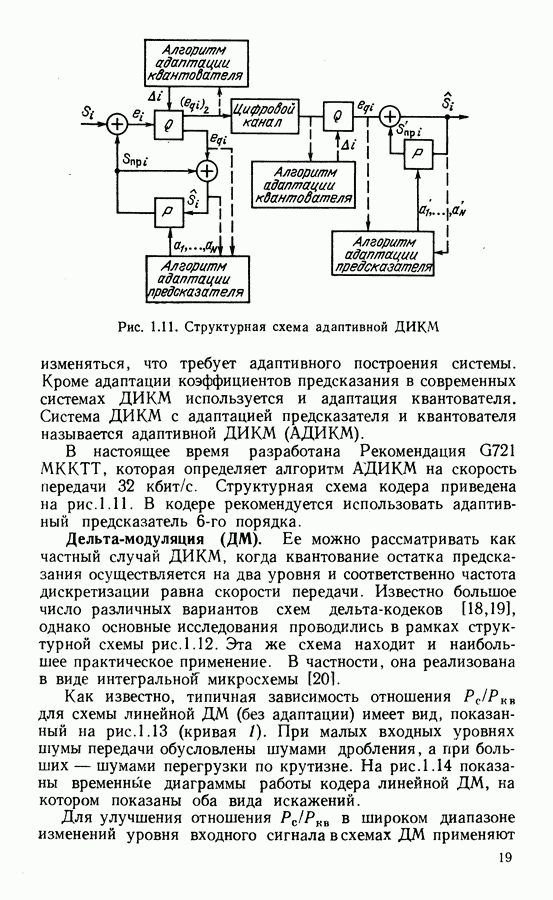
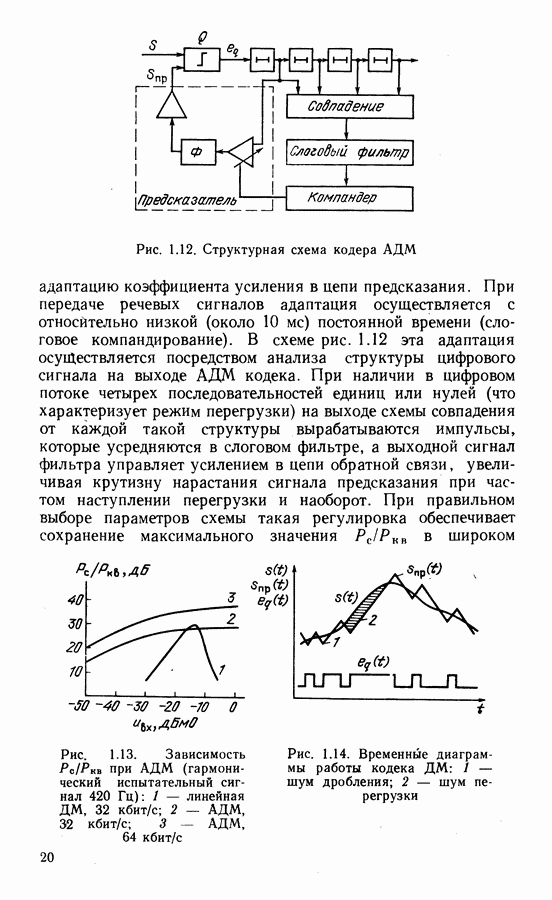
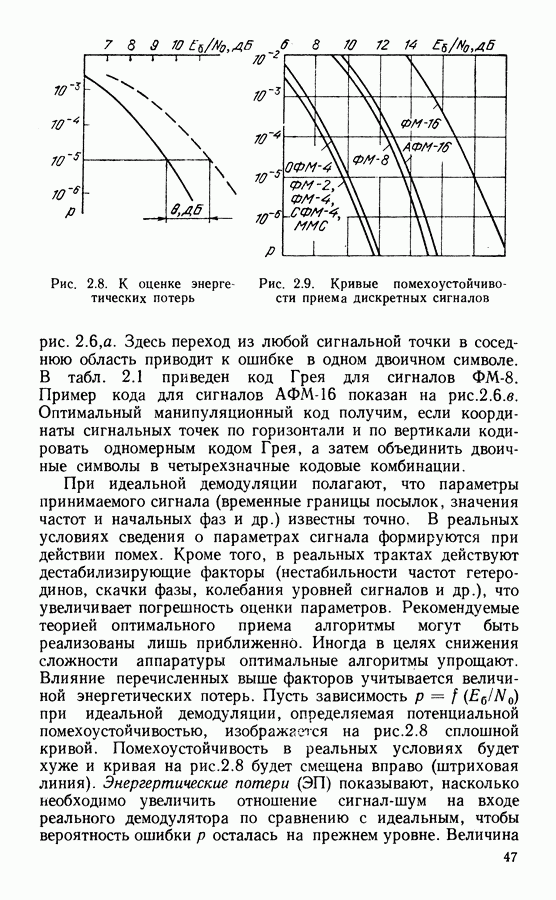
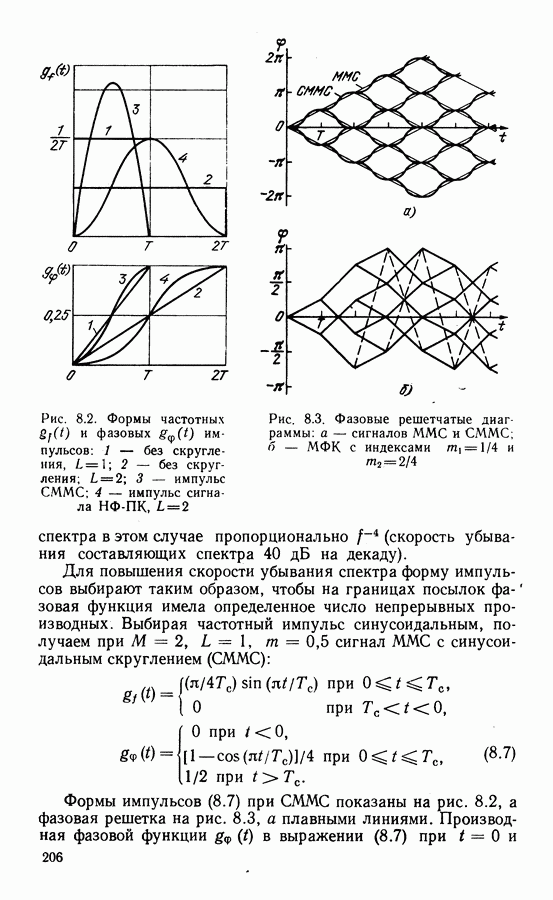
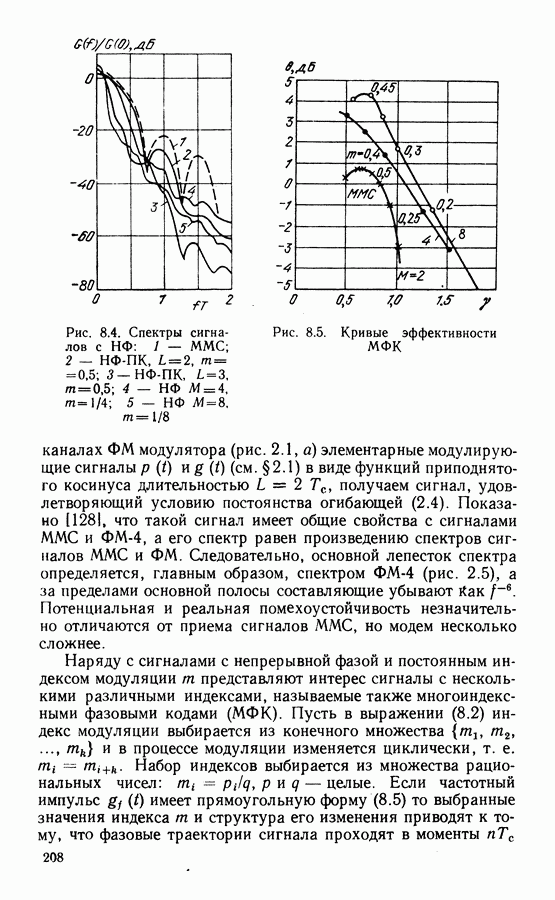
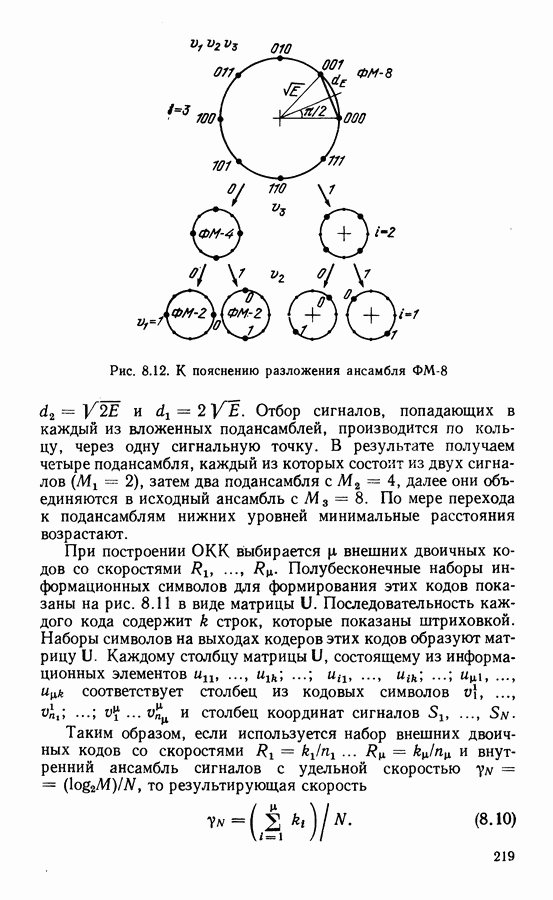
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
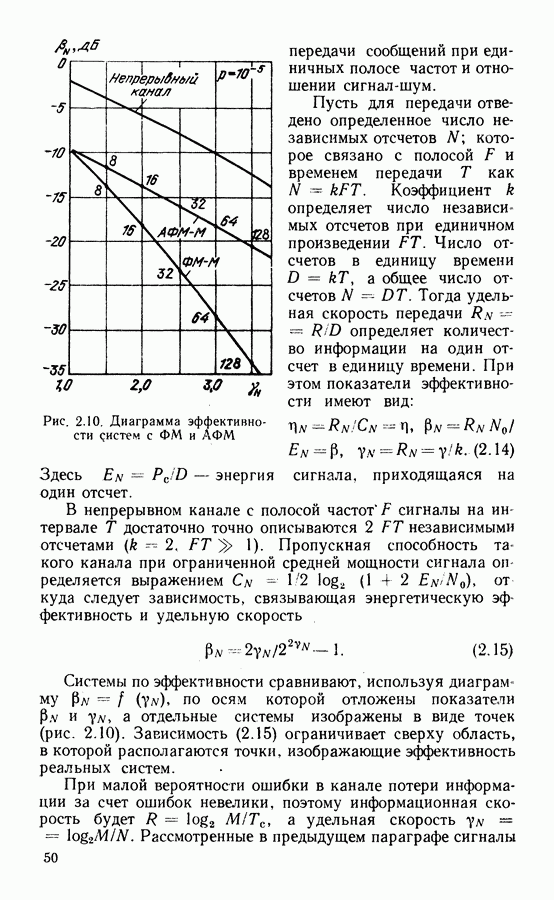
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.2. СИСТЕМЫ ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ
Как уже отмечалось, в спектре сигналов, используемых в ЦССС, не содержится остатка несущей, поэтому когерентное колебание выделяют из принимаемого сигнала посредством некоторого нелинейного преобразования и последующей фильтрацией. Ряд методов восстановления несущей ВН рассмотрены в монографиях [57, 58]. Современное состояние теории и техники систем ВН можно найти в обзоре [59].
Наиболее общим подходом, позволяющим синтезировать устройство ВН из принимаемого ФМ сигнала, является использование критерия максимального правдоподобия. Восстановление несущего колебания можно рассматривать как задачу оптимального оценивания фазы сигнала, пораженного помехой (на интервале длительности символа 

Здесь  белый гауссовский шум с односторонней спектральной плотностью
белый гауссовский шум с односторонней спектральной плотностью  Фаза сигнала
Фаза сигнала  в процессе модуляции принимает равновероятно одно из возможных значений
в процессе модуляции принимает равновероятно одно из возможных значений  начальная фаза, подлежащая оценке.
начальная фаза, подлежащая оценке.
Максимально правдоподобная оценка формируется с учетом возможных гипотез о посылаемых образцах сигнала  При оценке начальной фазы
При оценке начальной фазы  выбирают такое ее значение, которое доставляет максимум условной плотности вероятности
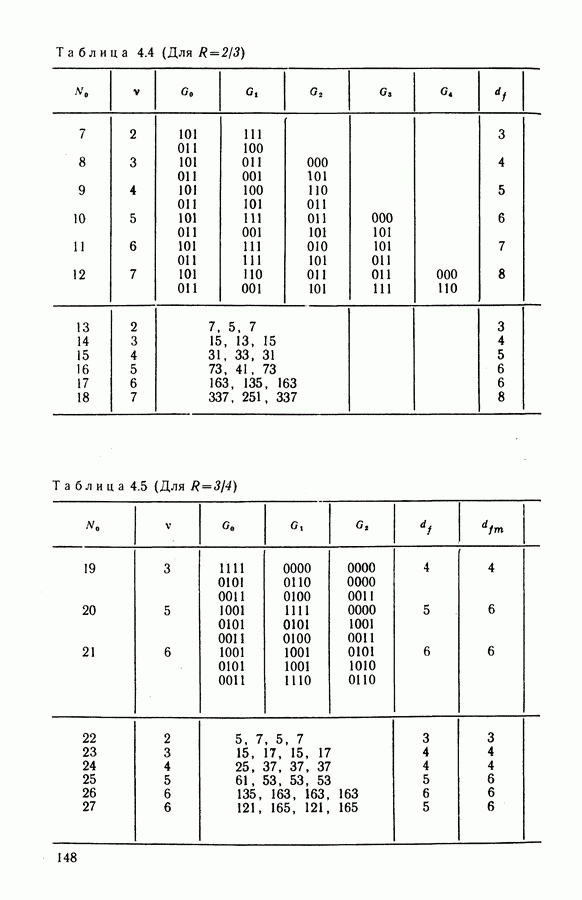
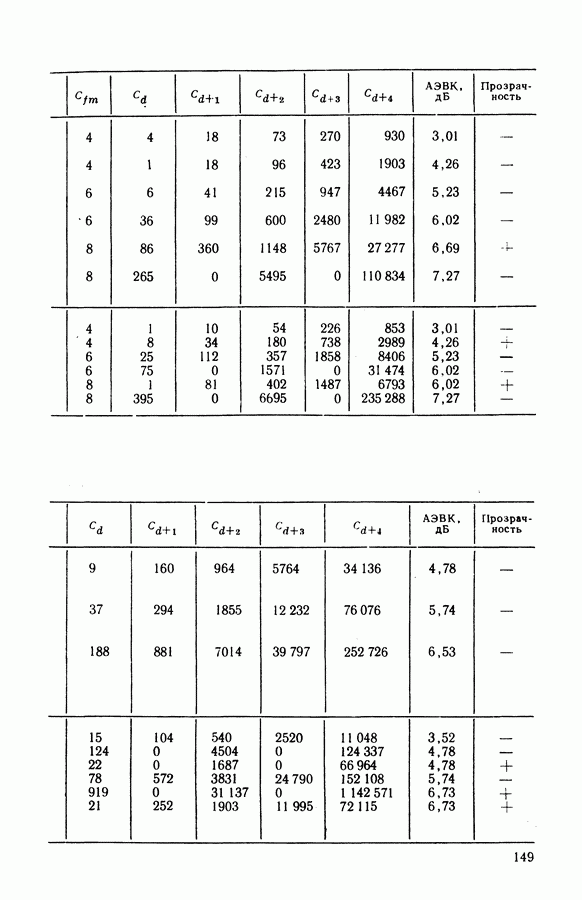
выбирают такое ее значение, которое доставляет максимум условной плотности вероятности  Поскольку начальная фаза
Поскольку начальная фаза  принимает равновероятно все возможные значения в интервале
принимает равновероятно все возможные значения в интервале  а плотность
а плотность  не зависит от
не зависит от  максимуму условной плотности
максимуму условной плотности  соответствует максимум апостериорного распределения
соответствует максимум апостериорного распределения  . С учетом всех возможных гипотез посылки сигнала с фазами
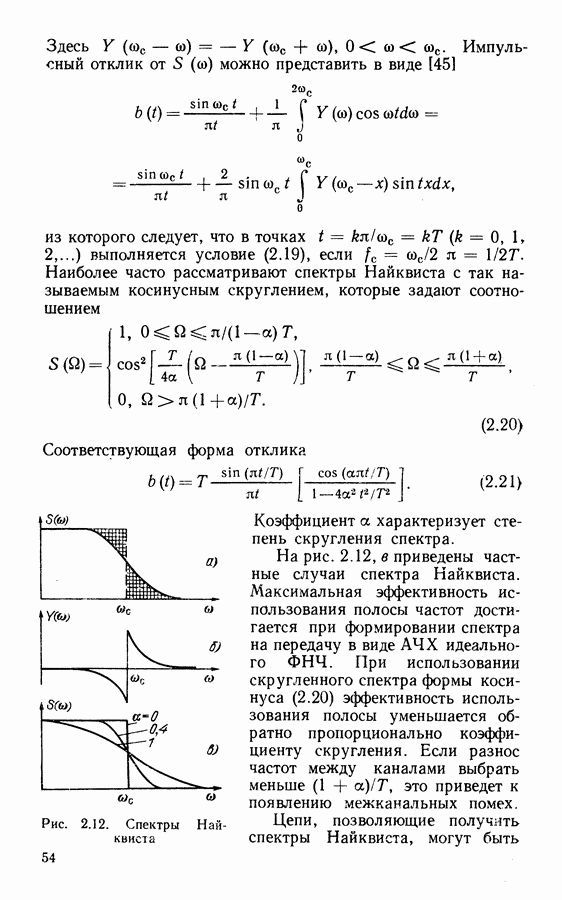
. С учетом всех возможных гипотез посылки сигнала с фазами  можно записать, что
можно записать, что  а условное распределение при фиксированной фазе
а условное распределение при фиксированной фазе 

Здесь

— выходы когерентных согласованных фильтров с квадратурными опорными колебаниями. Максимально правдоподобная оценка величины  является решением уравнения
является решением уравнения  которое обращает выражение (3.1) в максимум.
которое обращает выражение (3.1) в максимум.
Для сигналов ФМ-4 с учетом того, что фаза  принимает четыре возможных значения
принимает четыре возможных значения  выражение (3.1) приобретает вид
выражение (3.1) приобретает вид  а уравнение для отыскания оценки
а уравнение для отыскания оценки 

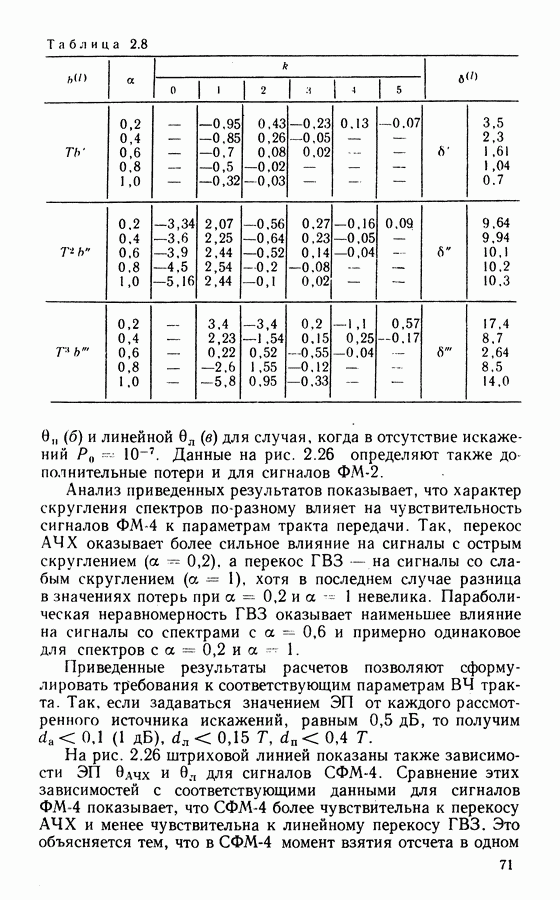
Поскольку оптимальная оценка а (0) и  [см. (3.2)] обычно заменяется фильтрацией,
[см. (3.2)] обычно заменяется фильтрацией,  при
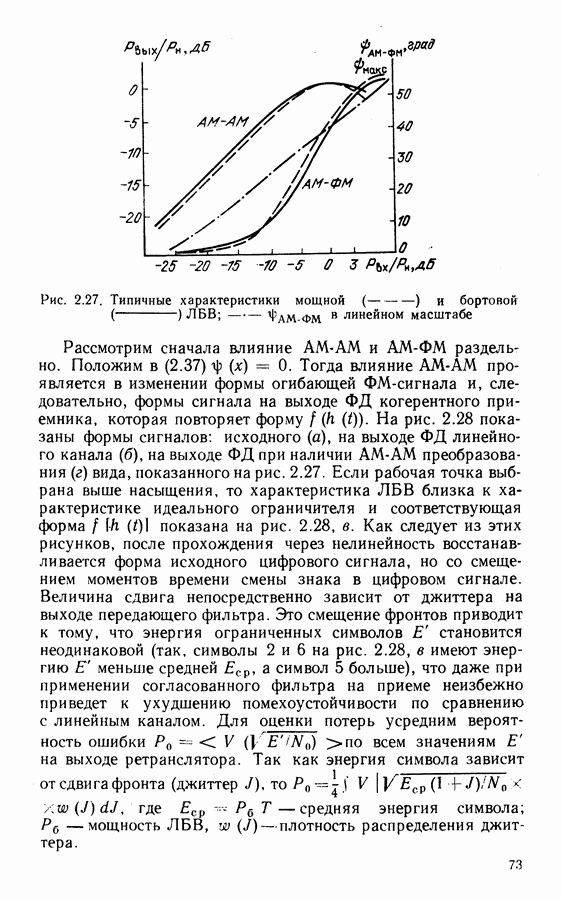
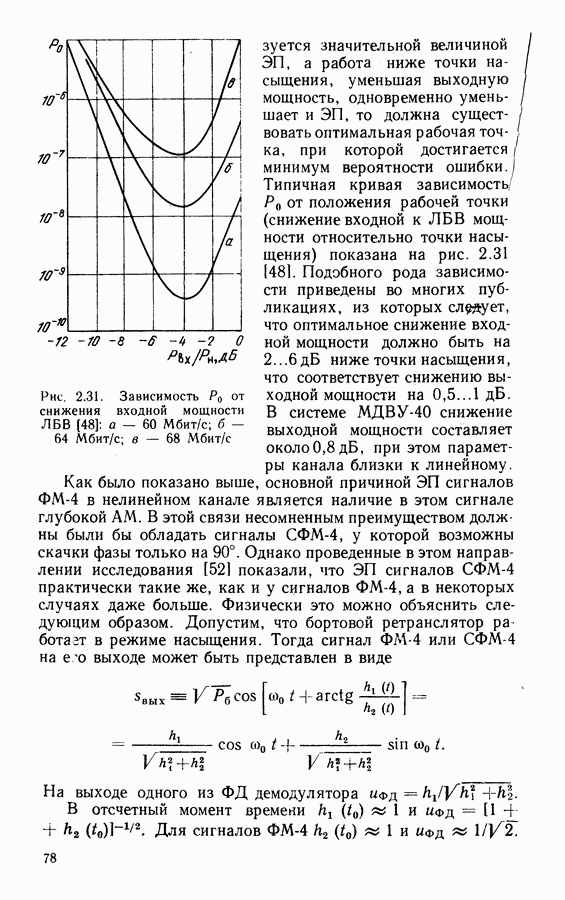
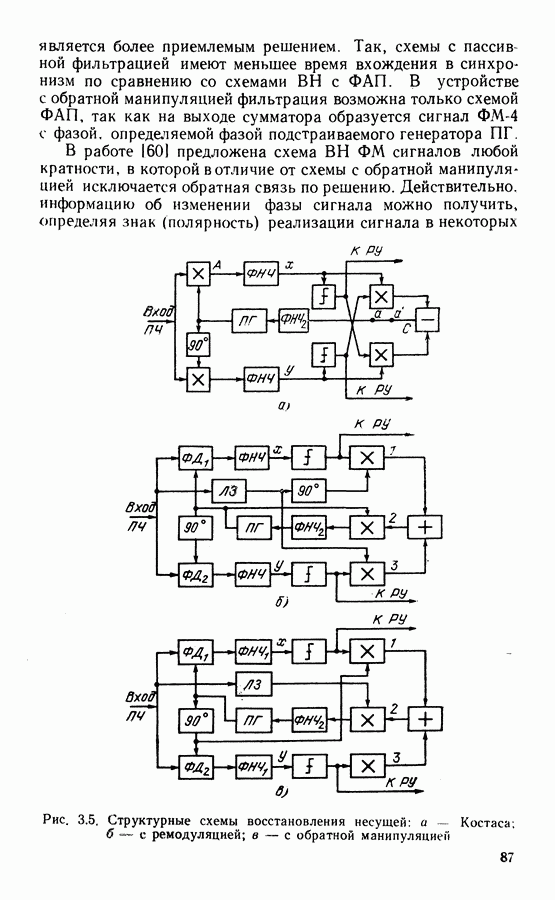
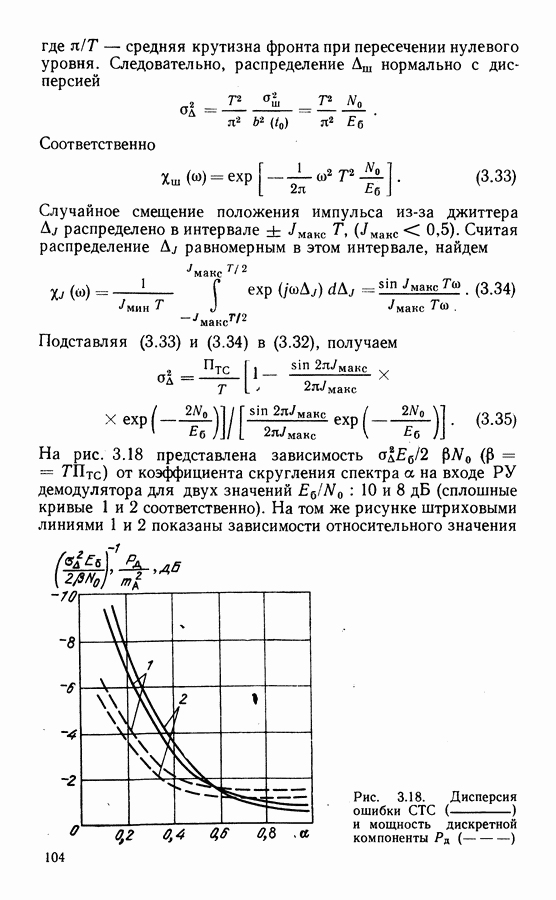
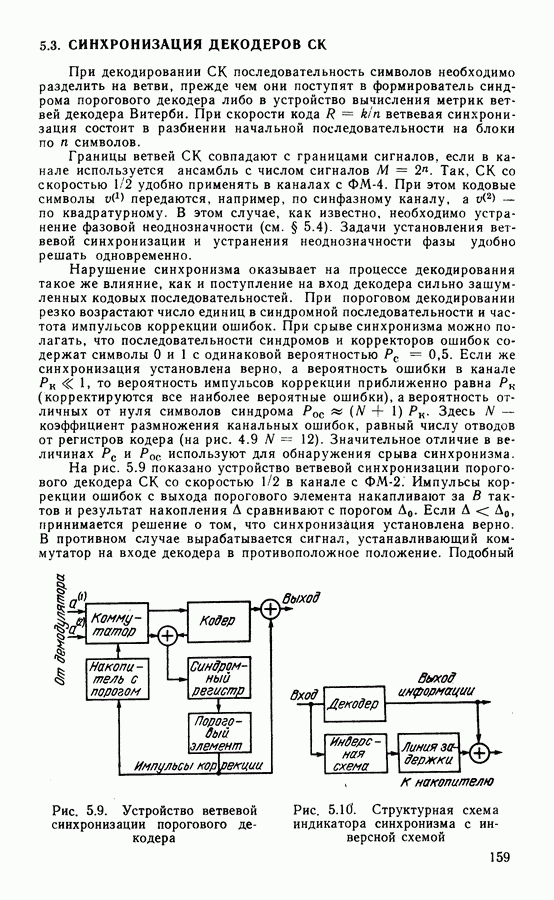
при  (что соответствует высокому отношению сигнал-шум), схема квазиоптимальной системы ВН будет иметь вид, показанный на рис. 3.5, а. Она представляет собой хорошо известную схему Костаса.
(что соответствует высокому отношению сигнал-шум), схема квазиоптимальной системы ВН будет иметь вид, показанный на рис. 3.5, а. Она представляет собой хорошо известную схему Костаса.
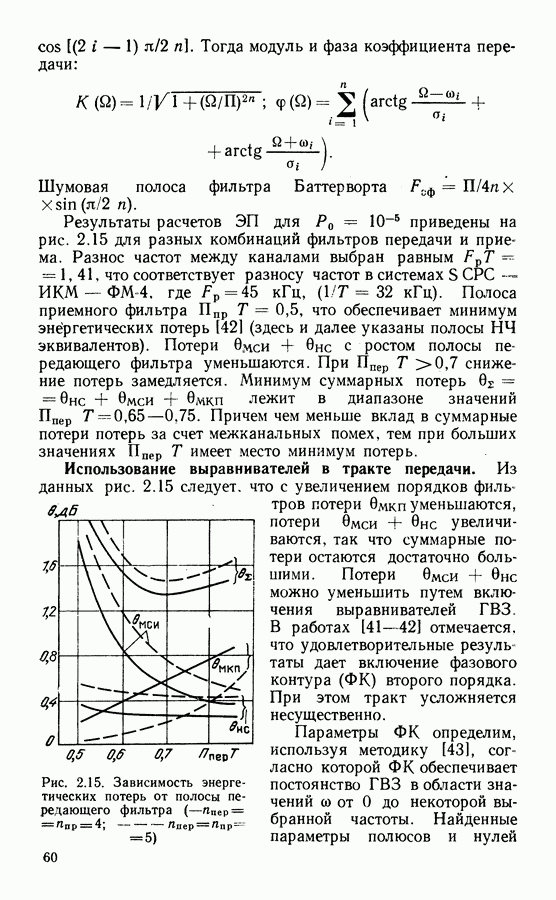
Другими вариантами схем ВН, имеющих такие же характеристики, что и схема Костаса [57], являются схема со снятием манипуляции (с ремодуляцией) (рис. 3.5, б) и схема с обратной манипуляцией (рис. 3.5, в), которые отличаются порядком включения перемножителей 1, 2 и 3. Линия задержки  в этих схемах компенсирует задержку сигналов в ФНЧ. Если основная фильтрация в демодуляторе осуществляется полосовым фильтром, что ФНЧ после перемножителей не включается и тогда необходимость в
в этих схемах компенсирует задержку сигналов в ФНЧ. Если основная фильтрация в демодуляторе осуществляется полосовым фильтром, что ФНЧ после перемножителей не включается и тогда необходимость в  отпадает.
отпадает.
В схеме с ремодуляцией на выходе сумматора образуется немодулированная несущая с фазой, равной фазе входного сигнала, что позволяет использовать для ее фильтрации не только систему ФАП, как это показано на рис. 3.5, б, но и обычные узкополосные полосовые фильтры, что в ряде случаев
является более приемлемым решением. Так, схемы с пассивной фильтрацией имеют меньшее время вхождения в синхронизм по сравнению со схемами ВН с ФАП. В устройстве с обратной манипуляцией фильтрация возможна только схемой ФАП, так как на выходе сумматора образуется сигнал ФМ-4 с фазой, определяемой фазой подстраиваемого генератора ПГ.
В работе 160] предложена схема ВН ФМ сигналов любой кратности, в которой в отличие от схемы с обратной манипуляцией исключается обратная связь по решению. Действительно, информацию об изменении фазы сигнала можно получить, определяя знак (полярность) реализации сигнала в некоторых

Рис. 3.5, Структурные схемы восстановления несущей: а — Костаса; б - с ремодуляцией; в — с обратной манипуляцией

Рис. 3.6. Структурная схема  по принципу обратной манипуляции
по принципу обратной манипуляции
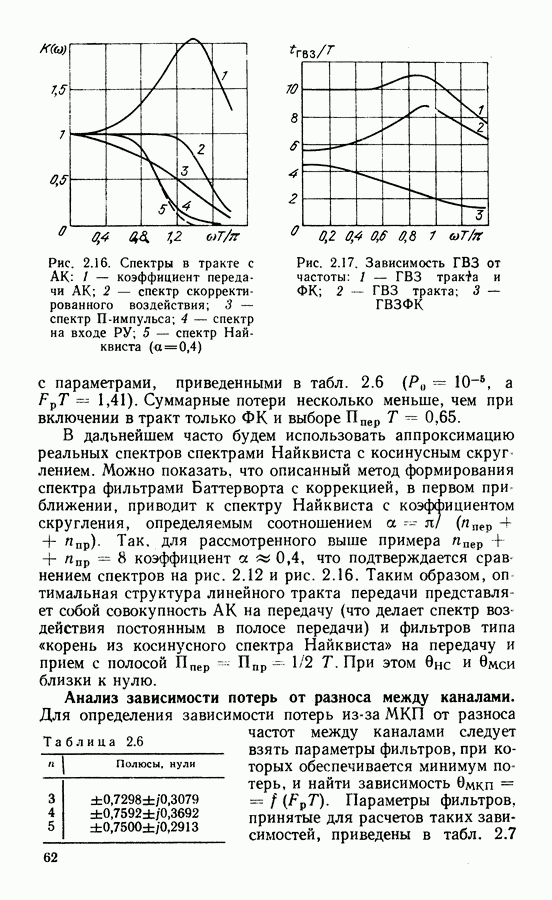
точках периода его ВЧ заполнения. Минимальное число таких точек на периоде соответствует числу фаз в ФМ сигнале. Структурная схема  в которой использован этот метод, представлена на рис. 3.6. На тактовый вход тактируемого
в которой использован этот метод, представлена на рис. 3.6. На тактовый вход тактируемого  -триггера подаются импульсы с частотой в М раз больше частоты ФМ сигнала
-триггера подаются импульсы с частотой в М раз больше частоты ФМ сигнала  На сигнальный вход триггера подается ограниченный по амплитуде ФМ сигнал. Врееннйе диаграмм мы, поясняющие работу схемы, показаны на рис. 3.7. В моменты тактирования, определяемые последовательностью импульсов с частотой
На сигнальный вход триггера подается ограниченный по амплитуде ФМ сигнал. Врееннйе диаграмм мы, поясняющие работу схемы, показаны на рис. 3.7. В моменты тактирования, определяемые последовательностью импульсов с частотой  (рис. 3.7, а),
(рис. 3.7, а),  -триггер фиксирует и запоминает знак реализации входного сигнала через каждые 90° (здесь
-триггер фиксирует и запоминает знак реализации входного сигнала через каждые 90° (здесь  режиме синхронизма на входе
режиме синхронизма на входе  -триггера образуется колебание с частотой входного сигнала, фаза которого изменяется в тактовые моменты времени на величину, кратную
-триггера образуется колебание с частотой входного сигнала, фаза которого изменяется в тактовые моменты времени на величину, кратную  Эти изменения определяются изменениями фазы входного сигнала, который показан на рис. 3.7, б. Здесь фаза сигнала изменяется на 90° в течение интервала времени
Эти изменения определяются изменениями фазы входного сигнала, который показан на рис. 3.7, б. Здесь фаза сигнала изменяется на 90° в течение интервала времени  Случай немодулированной несущей представлен на рис. 3.7, б, в штриховыми линиями.
Случай немодулированной несущей представлен на рис. 3.7, б, в штриховыми линиями.
Таким образом, на выходе  -триггера получают копию входного ФМ сигнала, фаза которого задается фазой ПГ схемы ФАП, что делает эту схему эквивалентной схеме с обратной манипуляцией. На выходе ФД образуется сигнал фазовой ошибки, который управляет работой ПГ в схеме ФАП. Коге рентные колебания с нужными фазами получают делением частоты ПГ в М раз. Структура схемы не меняется с
-триггера получают копию входного ФМ сигнала, фаза которого задается фазой ПГ схемы ФАП, что делает эту схему эквивалентной схеме с обратной манипуляцией. На выходе ФД образуется сигнал фазовой ошибки, который управляет работой ПГ в схеме ФАП. Коге рентные колебания с нужными фазами получают делением частоты ПГ в М раз. Структура схемы не меняется с

Рис. 3.7. Временные диаграммы в схеме рис. 3.6

Рис. 3.8. Структурные схемы ВН с умножением частоты
изменением кратности манипуляции входного сигнала, что позволяет использовать ее для синхронизации демодулятора ФМ сигналов с переменной кратностью.
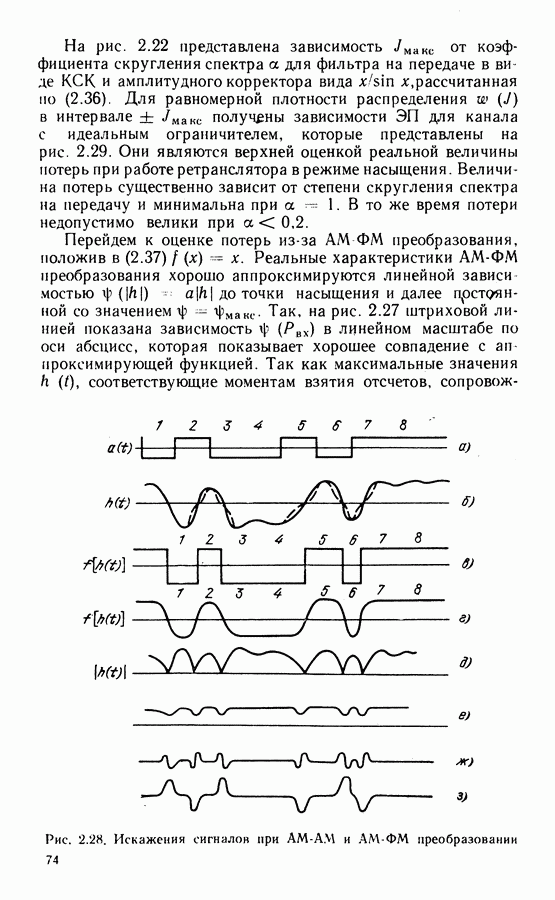
Некоторые из используемых на практике способов ВН основаны на нелинейном преобразовании ФМ сигнала. Таким является метод умножения частоты, который может быть реализован путем возведения принимаемого сигнала в  . Структурные схемы такого типа устройств для сигнала ФМ-4 показаны на рис. 3.8. При возведении сигнала в четвертую степень
. Структурные схемы такого типа устройств для сигнала ФМ-4 показаны на рис. 3.8. При возведении сигнала в четвертую степень  можно выделить четвертую гармонику
можно выделить четвертую гармонику  При этом фазовый сдвиг
При этом фазовый сдвиг  при любом из возможных значений
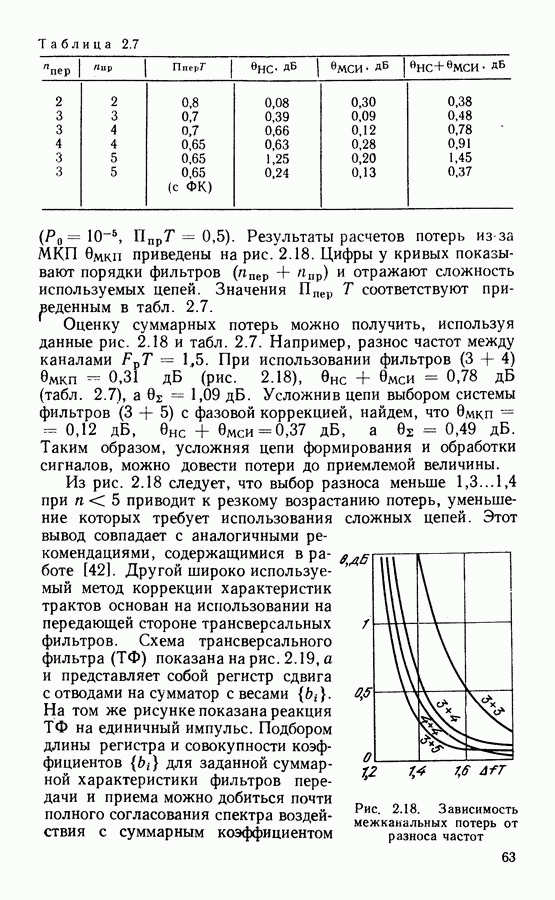
при любом из возможных значений  кратен
кратен  . В результате учетверения частоты модуляция несущей информационным сигналом устраняется и в спектре появляется дискретная составляющая с частотой, в 4 раза большей номинальной частоты
. В результате учетверения частоты модуляция несущей информационным сигналом устраняется и в спектре появляется дискретная составляющая с частотой, в 4 раза большей номинальной частоты  Ее выделяют по лосовым фильтром
Ее выделяют по лосовым фильтром  (рис. 3.8, а). Для получения исход ной частоты выход
(рис. 3.8, а). Для получения исход ной частоты выход  подан на делитель частоты на четыре.
подан на делитель частоты на четыре.
Кроме полосового фильтра для выделения несущей после умножения ФМ сигнала используют также схемы ФАП. При этом ПГ работает либо на частоте несущей  либо на учетверенной частоте
либо на учетверенной частоте  (рис. 3.8, б, в). В последнем случае необходимо предусмотреть деление частоты
(рис. 3.8, б, в). В последнем случае необходимо предусмотреть деление частоты  на четыре для получения выходного колебания. В некоторых случаях такой
на четыре для получения выходного колебания. В некоторых случаях такой  риант схемы предпочтительней, так как в процессе деления частоты на четыре легче реализовать фазорасщепитель, на выходах которого имеются сдвинутые по фазе на
риант схемы предпочтительней, так как в процессе деления частоты на четыре легче реализовать фазорасщепитель, на выходах которого имеются сдвинутые по фазе на  колебания с частотой
колебания с частотой 
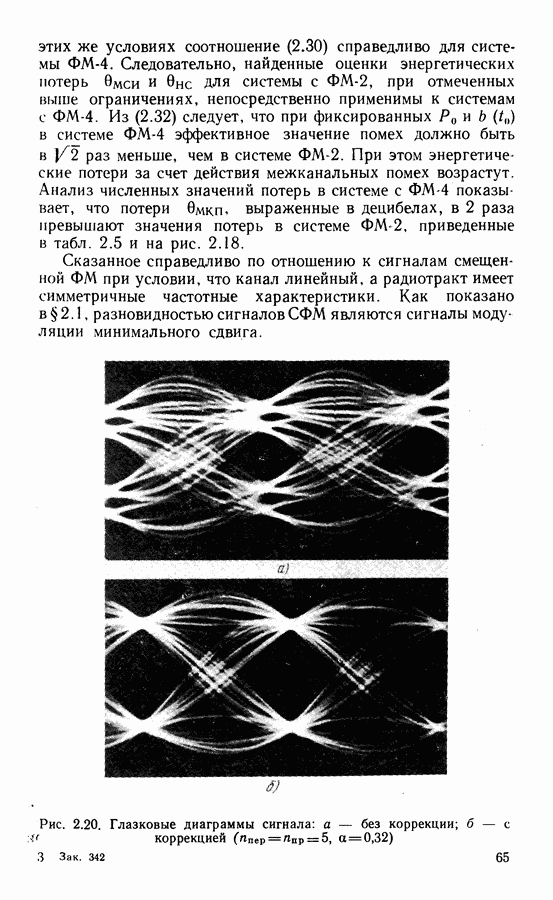
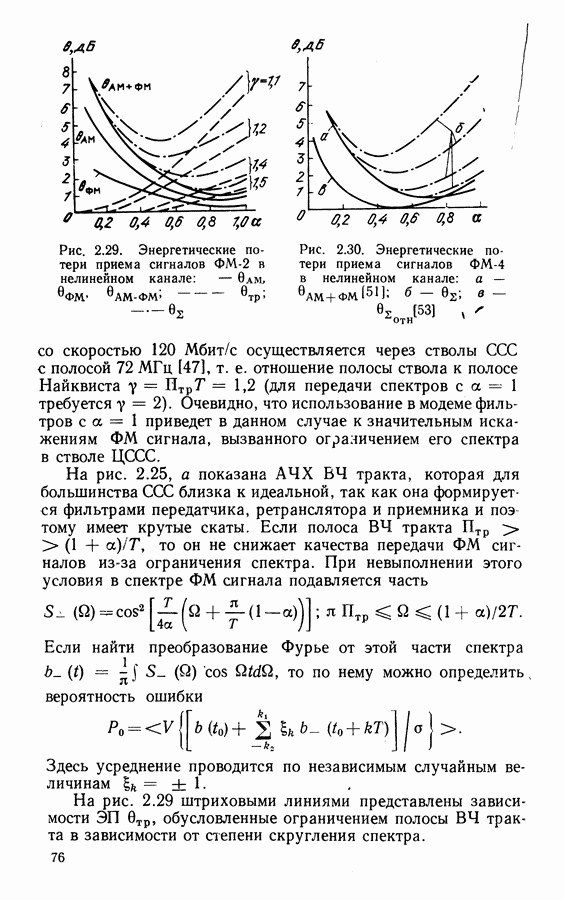
Рассмотрим способы восстановления когерентного колебания при приеме сигналов ММС. Можно показать, что при индексе модуляции  в спектре сигнала на частоте
в спектре сигнала на частоте

Рис. 3.9. Структурная схема  для сигналов ММС
для сигналов ММС
несущей отсутствуют дискретные составляющие, как и при ФМ. Вместе с тем при модуляции с индексом  на частотах
на частотах  соответствующих передаче информационных символов 0 и 1, появляются дискретные составляющие. Таким образом, удвоение частоты сигнала ММС позволяет выделить частоты
соответствующих передаче информационных символов 0 и 1, появляются дискретные составляющие. Таким образом, удвоение частоты сигнала ММС позволяет выделить частоты  где
где  центральная частота сигнала
центральная частота сигнала  длительность двоичного символа. Устройство восстановления опорных колебаний, необходимых для демодуляции сигнала ММС, показано на рис. 3.9. После фильтрации частот
длительность двоичного символа. Устройство восстановления опорных колебаний, необходимых для демодуляции сигнала ММС, показано на рис. 3.9. После фильтрации частот  и
и  системами ФАПЧ и по следующего деления на 2 получают ил
системами ФАПЧ и по следующего деления на 2 получают ил  Опорные колебания, необходимые для демодуляции, образуются путем их сложения и вычитания, т. е.
Опорные колебания, необходимые для демодуляции, образуются путем их сложения и вычитания, т. е.

Кроме того, в результате перемножения получаем

Второе слагаемое представляет собой колебание с тактовой частотой  что может быть использовано для его выделения. Следует отметить, что в этой схеме, как и в рассмотренных выше устройствах ВН сигнала ФМ-4, имеет место неоднозначность фазы четвертого порядка. Это обусловлено наличием двух независимых делителей частоты на два.
что может быть использовано для его выделения. Следует отметить, что в этой схеме, как и в рассмотренных выше устройствах ВН сигнала ФМ-4, имеет место неоднозначность фазы четвертого порядка. Это обусловлено наличием двух независимых делителей частоты на два.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ I. ОСНОВЫ ПОСТРОЕНИЯ ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМ СВЯЗИ
- ГЛАВА 1. СПУТНИКОВЫЕ СИСТЕМЫ С МНОГОСТАНЦИОННЫМ ДОСТУПОМ
- 1.2. ПРЕОБРАЗОВАНИЕ АНАЛОГОВЫХ СИГНАЛОВ В ЦИФРОВУЮ ФОРМУ
- Адаптивная ИКМ.
- Дифференциальная ИКМ (ДИКМ).
- Дельта-модуляция (ДМ).
- Преобразование сигналов телевидения, многоканальной телефонии и вещания в цифровую форму.
- 1.3. СТАТИСТИЧЕСКОЕ УПЛОТНЕНИЕ В ЦССС
- 1.4. МНОГОСТАНЦИОННЫЙ ДОСТУП В ЦССС
- Многостанционный доступ с временным разделением каналов (МДВР).
- Многостанционный доступ с разделением сигналов по форме (МДФР).
- Многостанционный доступ со случайным доступом (МДСД).
- 1.5. НОРМИРОВАНИЕ ПАРАМЕТРОВ ЦССС
- РАЗДЕЛ II. МОДУЛЯЦИЯ
- ГЛАВА 2. МЕТОДЫ МОДУЛЯЦИИ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.2. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.3. СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИГНАЛОВ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
- 2.4. СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ
- 2.5. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДЧР
- Результаты расчетов потерь в системе с ФМ-2 и стандартными фильтрами.
- Использование выравнивателей в тракте передачи.
- Анализ зависимости потерь от разноса между каналами.
- Энергетические потери в системе с ФМ-4.
- Потери в системах с сигналами ММС.
- 2.6. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДВР
- ГЛАВА 3. МОДЕМЫ
- 3.1. СТРУКТУРА МОДЕМА
- 3.2. СИСТЕМЫ ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ
- Требования к точности работы системы ВН.
- Анализ точности систем ВН.
- Переходные процессы.
- 3.3. ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 3.4. ОТНОСИТЕЛЬНОЕ КОДИРОВАНИЕ
- 3.5. ПРИМЕРЫ РЕАЛИЗАЦИИ МОДЕМОВ В ЦССС
- РАЗДЕЛ III. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
- 4.2. АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ КОДОВ
- 4.3. БЛОКОВЫЕ КОДЫ И АЛГОРИТМЫ ИХ ДЕКОДИРОВАНИЯ
- 4.4. СТРУКТУРА И ХАРАКТЕРИСТИКИ СВЕРТОЧНЫХ КОДОВ
- 4.5. АЛГОРИТМЫ ДЕКОДИРОВАНИЯ СК
- 4.6. ПОМЕХОУСТОЙЧИВОСТЬ И ЭФФЕКТИВНОСТЬ СИСТЕМ С КОДИРОВАНИЕМ
- ГЛАВА 5. КОДЕКИ
- 5.1. СОГЛАСОВАНИЕ МОДЕМА И КОДЕКА
- 5.2. ДЕКОДЕРЫ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ СК
- 5.3. СИНХРОНИЗАЦИЯ ДЕКОДЕРОВ СК
- 5.4. КОДИРОВАНИЕ В КАНАЛАХ С НЕОДНОЗНАЧНОСТЬЮ
- 5.5. ПРИМЕРЫ РЕАЛИЗАЦИИ КОДЕКОВ ПОМЕХОУСТОЙЧИВЫХ КОДОВ
- Кодек биортогонального блочного кода.
- 5.6. РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
- РАЗДЕЛ IV. ЦИФРОВЫЕ СИСТЕМЫ СПУТНИКОВОЙ СВЯЗИ
- ГЛАВА 6. ВЗАИМНЫЕ ПОМЕХИ В ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМАХ
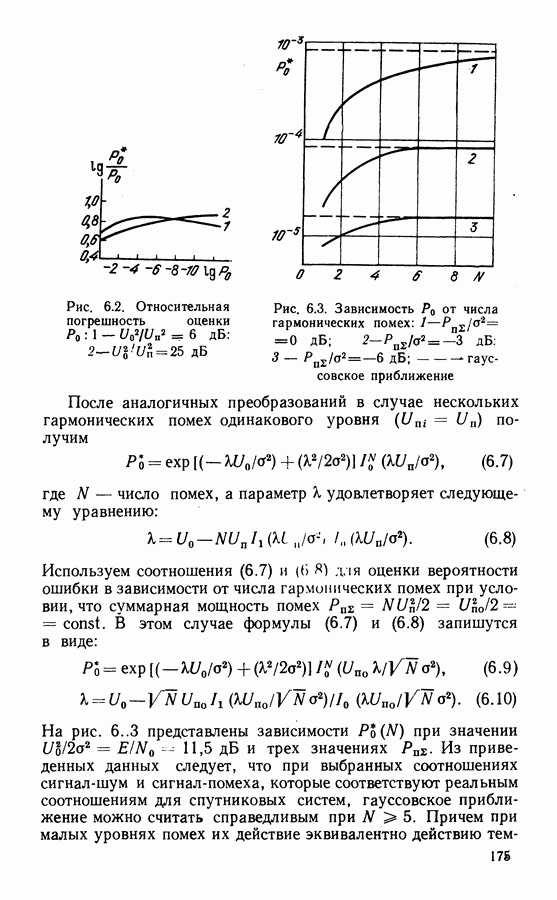
- 6.2. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ГАРМОНИЧЕСКИХ ПОМЕХ НА ДЕМОДУЛЯТОР ФМ СИГНАЛОВ
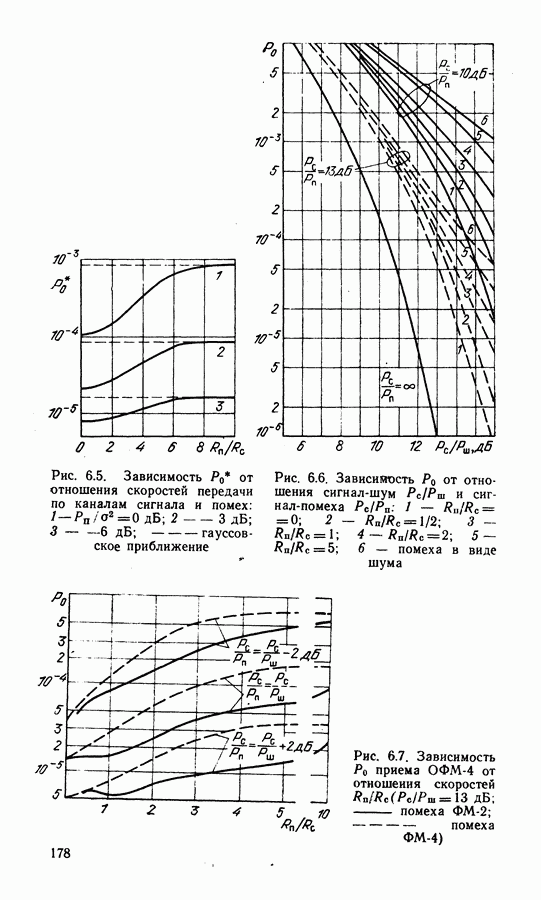
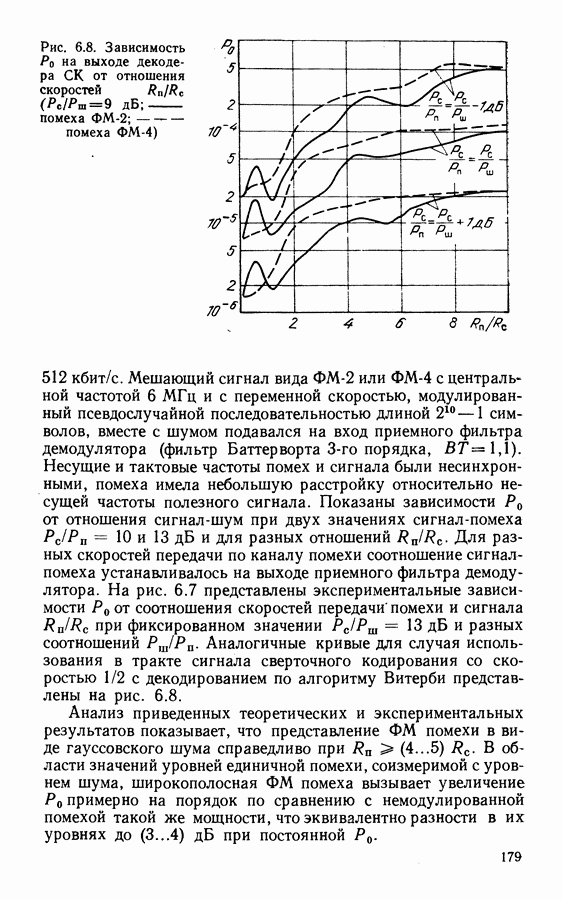
- 6.3. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ФМ ПОМЕХ
- 6.4. АНАЛИЗ МЕШАЮЩЕГО ДЕЙСТВИЯ ЧМ—ТВ СИГНАЛА С ДИСПЕРСИЕЙ
- 6.5. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ СИГНАЛОВ ЧУ-ЧМ
- ГЛАВА 7. СИСТЕМЫ С МДВР И МДЧР
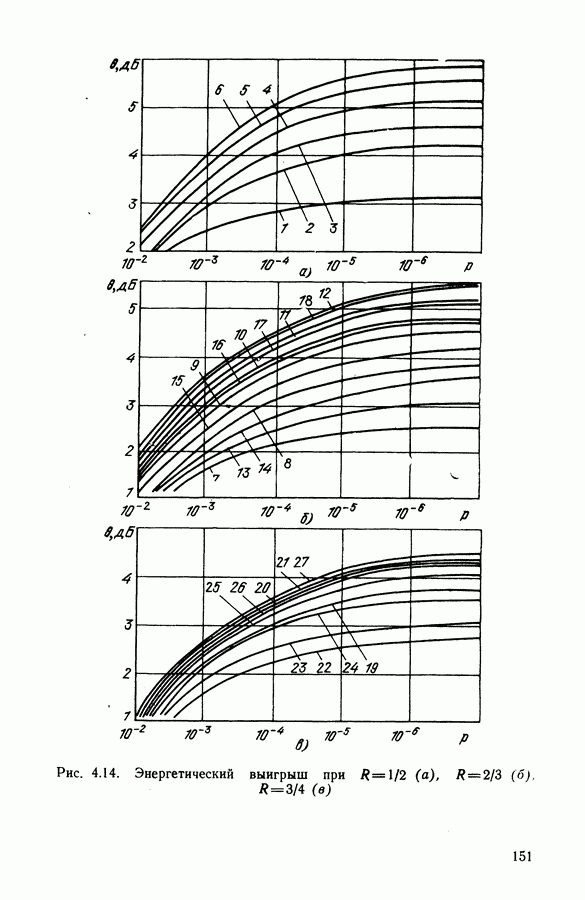
- 7.1. ОЦЕНКА ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ РАЗЛИЧНЫХ МЕТОДОВ ПЕРЕДАЧИ В ЦССС С МДЧР
- 7.2. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДЧР
- 7.3. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДВР
- Синхронизация систем МДВР.
- Организация кадра систем МДВР.
- Система МДВУ-40.
- ЦСС с ДВР ТДМА-120-(«Интелсат»/«Евросат»).
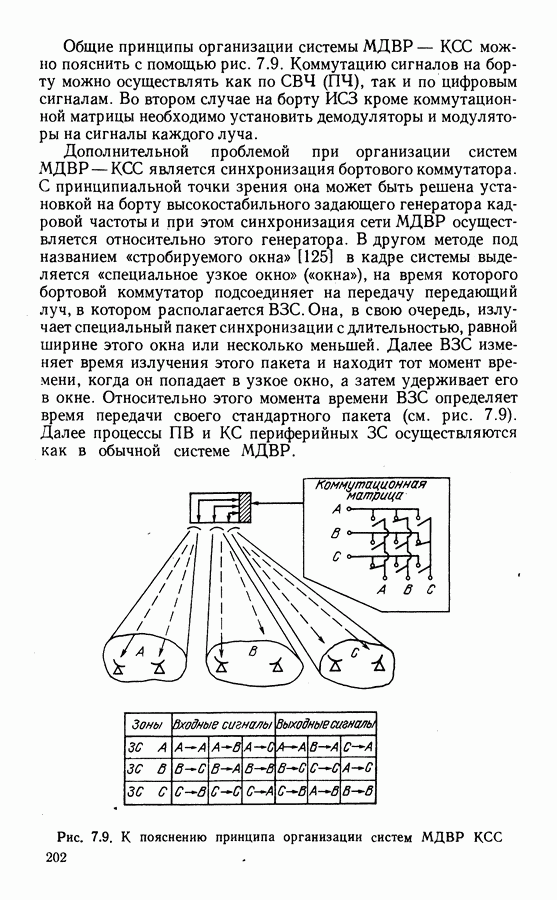
- МДВР с коммутацией сигналов на спутнике (КСС).
- Сопряжение систем МДВР с цифровыми наземными линиями.
- ГЛАВА 8. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ И КОДИРОВАНИЯ В ЦССС
- 8.2. СОГЛАСОВАНИЕ СИСТЕМ МОДУЛЯЦИИ И КОДИРОВАНИЯ
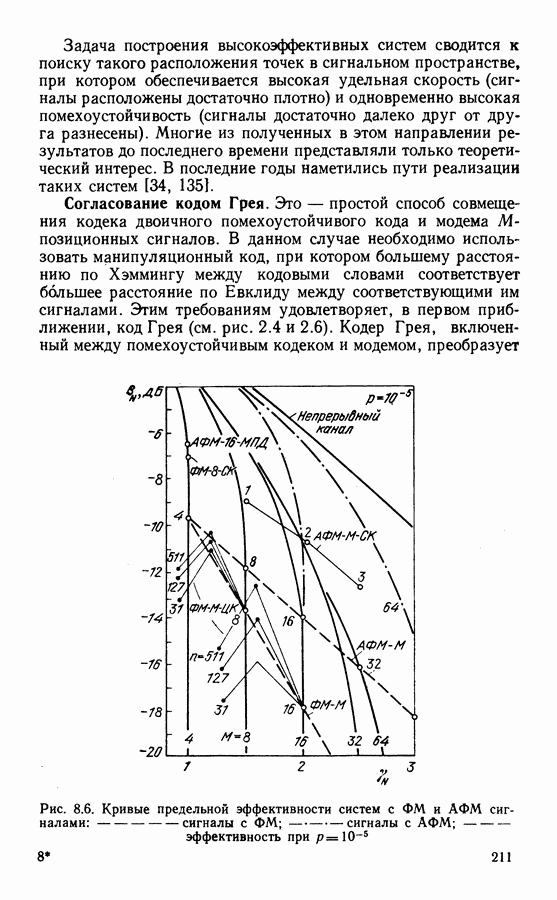
- Согласование кодом Грея.
- Кодирование с разбиением ансамбля на подклассы.
- Применение недвоичных кодов.
- 8.3. СВЕРТОЧНОЕ КОДИРОВАНИЕ В КАНАЛЕ С МНОГОПОЗИЦИОННОИ ФМ
- 8.4. ОБОБЩЕННОЕ КАСКАДНОЕ КОДИРОВАНИЕ
- 8.5. ПРИМЕРЫ РЕАЛИЗАЦИИ ЭФФЕКТИВНЫХ КОДЕМОВ
- СПИСОК ЛИТЕРАТУРЫ