| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
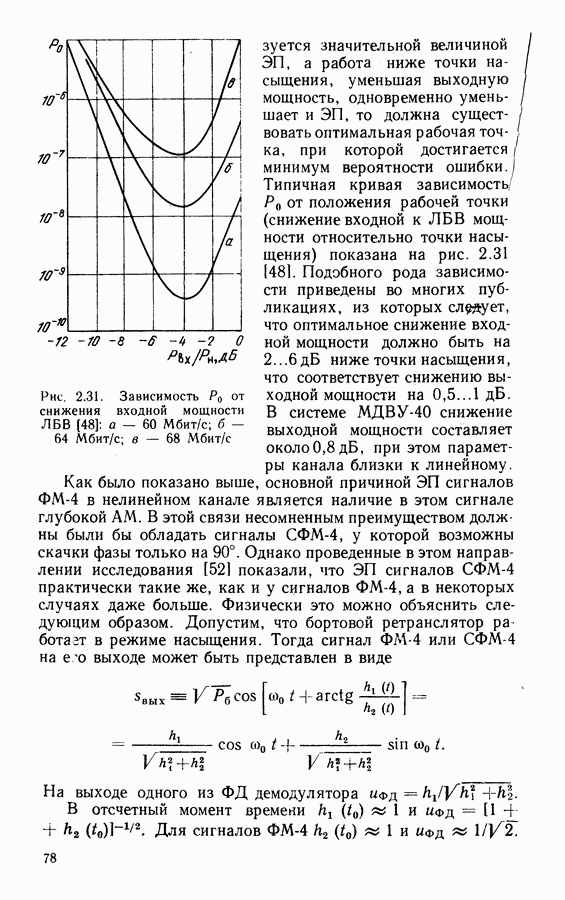
6.3. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ФМ ПОМЕХ
Пусть на входе ФМ демодулятора действует ФМ помеха. Скорость передачи по каналу сигнала обозначим через  а по каналу помехи
а по каналу помехи  Напряжение на выходе
Напряжение на выходе  демодулятора запишем в виде, аналогичном
демодулятора запишем в виде, аналогичном  где
где  закон манипуляции по каналу помехи. Допустим, что в демодуляторе используется интегральный прием. Тогда в отсчетные моменты времени напряжение на выходе интегратора
закон манипуляции по каналу помехи. Допустим, что в демодуляторе используется интегральный прием. Тогда в отсчетные моменты времени напряжение на выходе интегратора

Полагаем, что взаимная расстройка центральных частот сигнала и помехи невелика, так что случайную фазу  можно считать постоянной на интервале интегрирования. Допустим также, что соотношение скоростей по каналу помехи и сигнала
можно считать постоянной на интервале интегрирования. Допустим также, что соотношение скоростей по каналу помехи и сигнала  так что на интервале интегрирования Т всегда разместится полностью
так что на интервале интегрирования Т всегда разместится полностью  символов помехи (рис. 6.4). Тогда формулу (6.11) можно представить в виде
символов помехи (рис. 6.4). Тогда формулу (6.11) можно представить в виде

где  результат интегрирования единичного символа помехи;
результат интегрирования единичного символа помехи;  случайная величина
случайная величина  равномерно
равномерно

Рис. 6.4. К пояснению процесса интегрирования помехи
распределена на интервале  ли
ли  значение шума в конце интегрирования с дисперсией
значение шума в конце интегрирования с дисперсией 
Для оценки вероятности ошибки на выходе демодулятора воспользуемся методом Чернова

Проведя в (6.13) с учетом (6.12) сначала усреднение по случайным независимым величинам  и нормальному шуму
и нормальному шуму  получаем
получаем

Для усреднения по случайной фазе  и случайной величине
и случайной величине  в (6.14) надо степени и произведения гиперболического косинуса представить в виде суммы гиперболических функций с соответствующими аргументами. Эти преобразования просты, но довольно громоздки. Поэтому здесь приведем окончательные формулы для случая, когда
в (6.14) надо степени и произведения гиперболического косинуса представить в виде суммы гиперболических функций с соответствующими аргументами. Эти преобразования просты, но довольно громоздки. Поэтому здесь приведем окончательные формулы для случая, когда  (т. е. тактовые частоты сигнала и помехи кратны). Тогда из (6.14) при четном
(т. е. тактовые частоты сигнала и помехи кратны). Тогда из (6.14) при четном  получим
получим 

Здесь, как и ранее, параметр X выбирается из условия минимума правой части (6.15).
Как и в предыдущем параграфе, определим условия, при которых действие ФМ помехи можно считать эквивалентным действию теплового шума с мощностью, равной мощности ФМ помехи, попадающей в полосу ФМ демодулятора. Для соблюдения этого условия необходимо в (6.15) положить  где
где  амплитуда немодулированной ФМ помехи. При этом спектральная плотность ФМ помехи на центральной частоте будет оставаться постоянной при разных скоростях передачи.
амплитуда немодулированной ФМ помехи. При этом спектральная плотность ФМ помехи на центральной частоте будет оставаться постоянной при разных скоростях передачи.
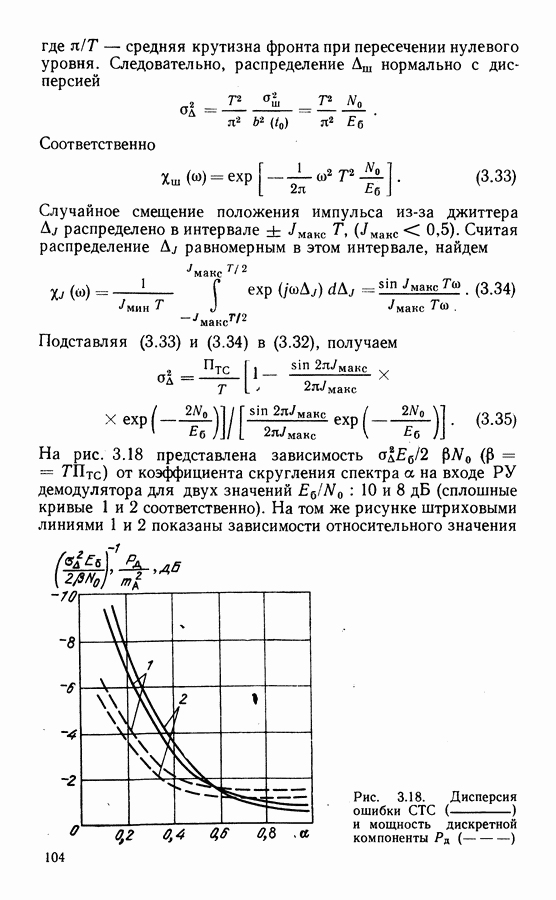
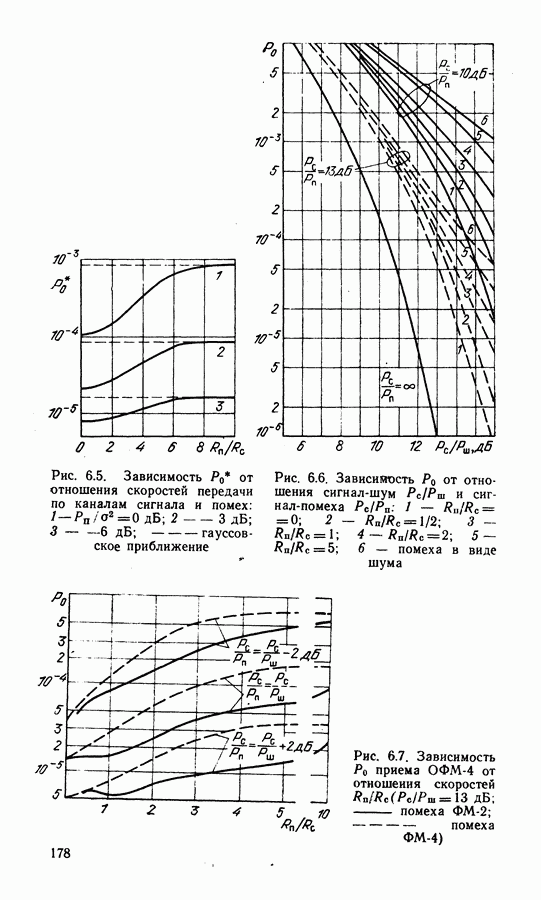
На рис. 6.5 представлены зависимости  для случая
для случая  (при этом
(при этом  в отсутствие помех) и трех значений
в отсутствие помех) и трех значений  На рис. 6.6 представлены результаты экспериментальных измерений ошибки на выходе демодулятора сигналов ОФМ-4 со скоростью
На рис. 6.6 представлены результаты экспериментальных измерений ошибки на выходе демодулятора сигналов ОФМ-4 со скоростью

(кликните для просмотра скана)

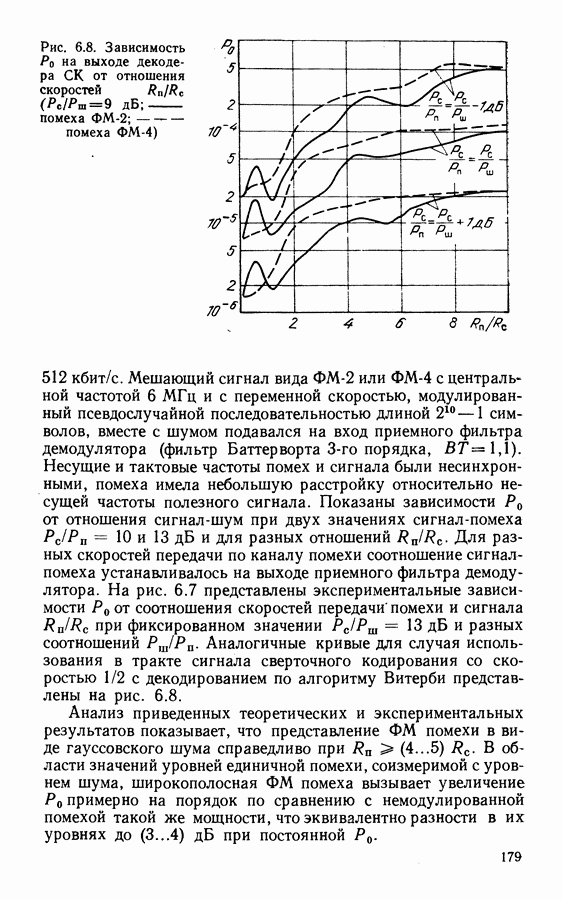
Рис. 6.8. Зависимость  на выходе декодера СК от отношения скоростей
на выходе декодера СК от отношения скоростей  помеха
помеха  помеха ФМ-4)
помеха ФМ-4)
512 кбит/с. Мешающий сигнал вида  или ФМ-4 с центральной частотой
или ФМ-4 с центральной частотой  и с переменной скоростью, модулированный псевдослучайной последовательностью длиной
и с переменной скоростью, модулированный псевдослучайной последовательностью длиной  символов, вместе с шумом подавался на вход приемного фильтра демодулятора (фильтр Баттерворта
символов, вместе с шумом подавался на вход приемного фильтра демодулятора (фильтр Баттерворта  порядка,
порядка,  Несущие и тактовые частоты помех и сигнала были несинхронными, помеха имела небольшую расстройку относительно несущей частоты полезного сигнала. Показаны зависимости
Несущие и тактовые частоты помех и сигнала были несинхронными, помеха имела небольшую расстройку относительно несущей частоты полезного сигнала. Показаны зависимости  от отношения сигнал-шум при двух значениях сигнал-помеха
от отношения сигнал-шум при двух значениях сигнал-помеха  и
и  и для разных отношений
и для разных отношений  Для разных скоростей передачи по каналу помехи соотношение сигнал-помеха устанавливалось на выходе приемного фильтра демодулятора. На рис. 6.7 представлены экспериментальные зависимости
Для разных скоростей передачи по каналу помехи соотношение сигнал-помеха устанавливалось на выходе приемного фильтра демодулятора. На рис. 6.7 представлены экспериментальные зависимости  от соотношения скоростей передачипомехи и сигнала
от соотношения скоростей передачипомехи и сигнала  фиксированном значении
фиксированном значении  и разных соотношений
и разных соотношений  Аналогичные кривые для случая использования в тракте сигнала сверточного кодирования со скоростью 1/2 с декодированием по алгоритму Витерби представлены на рис. 6.8.
Аналогичные кривые для случая использования в тракте сигнала сверточного кодирования со скоростью 1/2 с декодированием по алгоритму Витерби представлены на рис. 6.8.
Анализ приведенных теоретических и экспериментальных результатов показывает, что представление ФМ помехи в виде гауссовского шума справедливо при  . В области значений уровней единичной помехи, соизмеримой с уровнем шума, широкополосная ФМ помеха вызывает увеличение
. В области значений уровней единичной помехи, соизмеримой с уровнем шума, широкополосная ФМ помеха вызывает увеличение  примерно на порядок по сравнению с немодулированной помехой такой же мощности, что эквивалентно разности в их уровнях до
примерно на порядок по сравнению с немодулированной помехой такой же мощности, что эквивалентно разности в их уровнях до  при постоянной
при постоянной 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ I. ОСНОВЫ ПОСТРОЕНИЯ ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМ СВЯЗИ
- ГЛАВА 1. СПУТНИКОВЫЕ СИСТЕМЫ С МНОГОСТАНЦИОННЫМ ДОСТУПОМ
- 1.2. ПРЕОБРАЗОВАНИЕ АНАЛОГОВЫХ СИГНАЛОВ В ЦИФРОВУЮ ФОРМУ
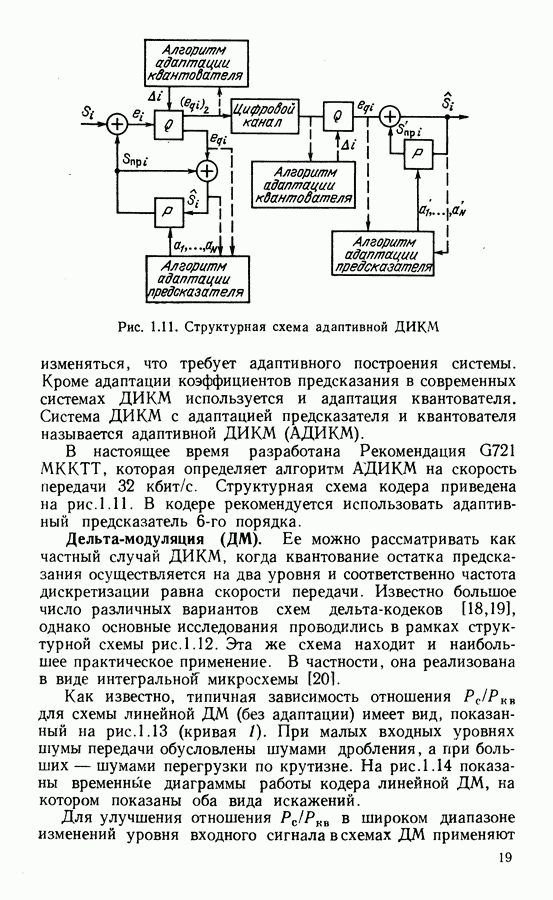
- Адаптивная ИКМ.
- Дифференциальная ИКМ (ДИКМ).
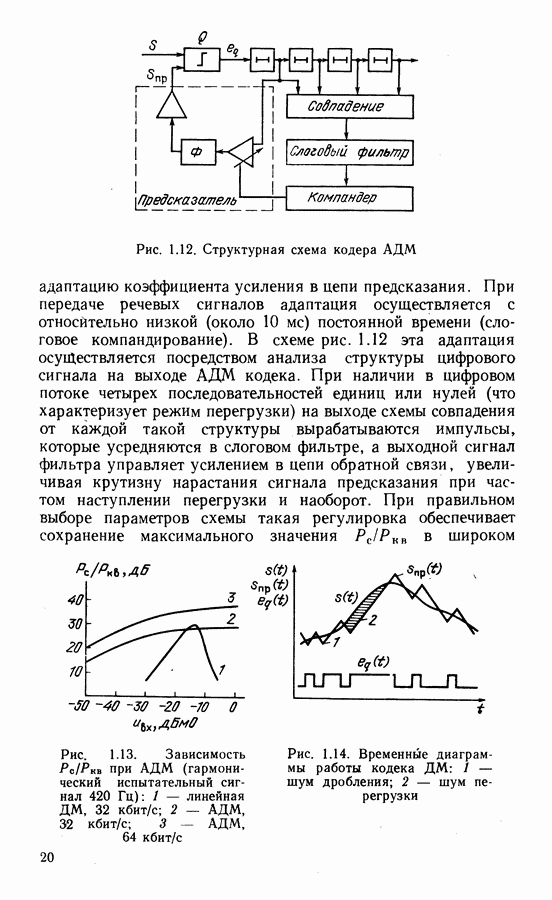
- Дельта-модуляция (ДМ).
- Преобразование сигналов телевидения, многоканальной телефонии и вещания в цифровую форму.
- 1.3. СТАТИСТИЧЕСКОЕ УПЛОТНЕНИЕ В ЦССС
- 1.4. МНОГОСТАНЦИОННЫЙ ДОСТУП В ЦССС
- Многостанционный доступ с временным разделением каналов (МДВР).
- Многостанционный доступ с разделением сигналов по форме (МДФР).
- Многостанционный доступ со случайным доступом (МДСД).
- 1.5. НОРМИРОВАНИЕ ПАРАМЕТРОВ ЦССС
- РАЗДЕЛ II. МОДУЛЯЦИЯ
- ГЛАВА 2. МЕТОДЫ МОДУЛЯЦИИ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.2. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.3. СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИГНАЛОВ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
- 2.4. СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ
- 2.5. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДЧР
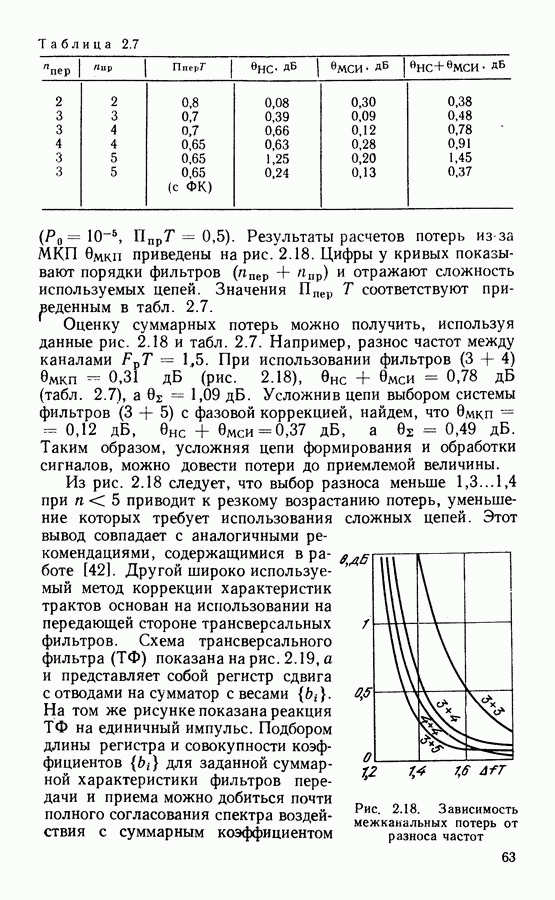
- Результаты расчетов потерь в системе с ФМ-2 и стандартными фильтрами.
- Использование выравнивателей в тракте передачи.
- Анализ зависимости потерь от разноса между каналами.
- Энергетические потери в системе с ФМ-4.
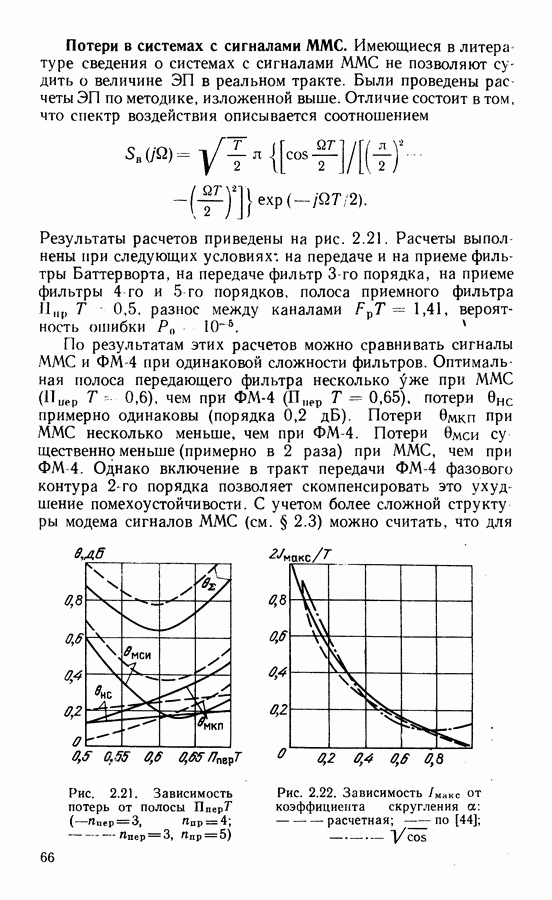
- Потери в системах с сигналами ММС.
- 2.6. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДВР
- ГЛАВА 3. МОДЕМЫ
- 3.1. СТРУКТУРА МОДЕМА
- 3.2. СИСТЕМЫ ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ
- Требования к точности работы системы ВН.
- Анализ точности систем ВН.
- Переходные процессы.
- 3.3. ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 3.4. ОТНОСИТЕЛЬНОЕ КОДИРОВАНИЕ
- 3.5. ПРИМЕРЫ РЕАЛИЗАЦИИ МОДЕМОВ В ЦССС
- РАЗДЕЛ III. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
- 4.2. АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ КОДОВ
- 4.3. БЛОКОВЫЕ КОДЫ И АЛГОРИТМЫ ИХ ДЕКОДИРОВАНИЯ
- 4.4. СТРУКТУРА И ХАРАКТЕРИСТИКИ СВЕРТОЧНЫХ КОДОВ
- 4.5. АЛГОРИТМЫ ДЕКОДИРОВАНИЯ СК
- 4.6. ПОМЕХОУСТОЙЧИВОСТЬ И ЭФФЕКТИВНОСТЬ СИСТЕМ С КОДИРОВАНИЕМ
- ГЛАВА 5. КОДЕКИ
- 5.1. СОГЛАСОВАНИЕ МОДЕМА И КОДЕКА
- 5.2. ДЕКОДЕРЫ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ СК
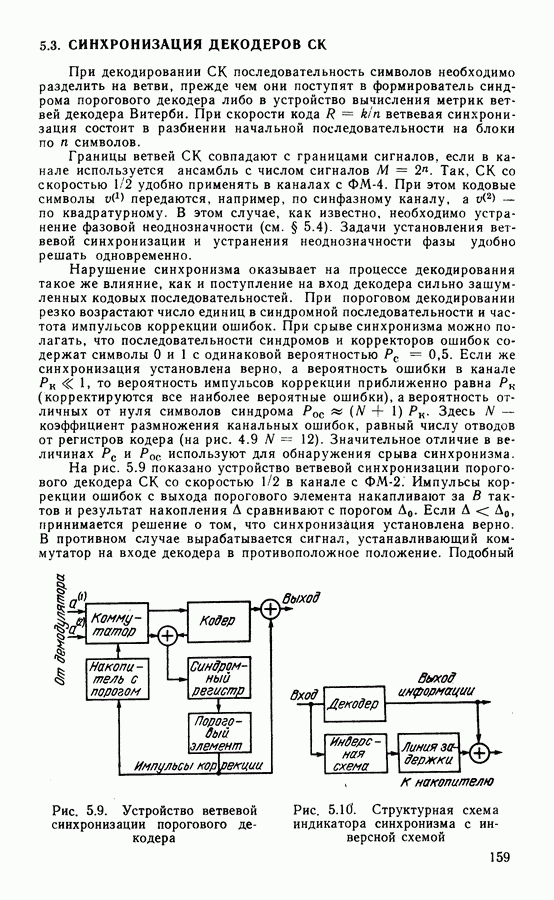
- 5.3. СИНХРОНИЗАЦИЯ ДЕКОДЕРОВ СК
- 5.4. КОДИРОВАНИЕ В КАНАЛАХ С НЕОДНОЗНАЧНОСТЬЮ
- 5.5. ПРИМЕРЫ РЕАЛИЗАЦИИ КОДЕКОВ ПОМЕХОУСТОЙЧИВЫХ КОДОВ
- Кодек биортогонального блочного кода.
- 5.6. РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
- РАЗДЕЛ IV. ЦИФРОВЫЕ СИСТЕМЫ СПУТНИКОВОЙ СВЯЗИ
- ГЛАВА 6. ВЗАИМНЫЕ ПОМЕХИ В ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМАХ
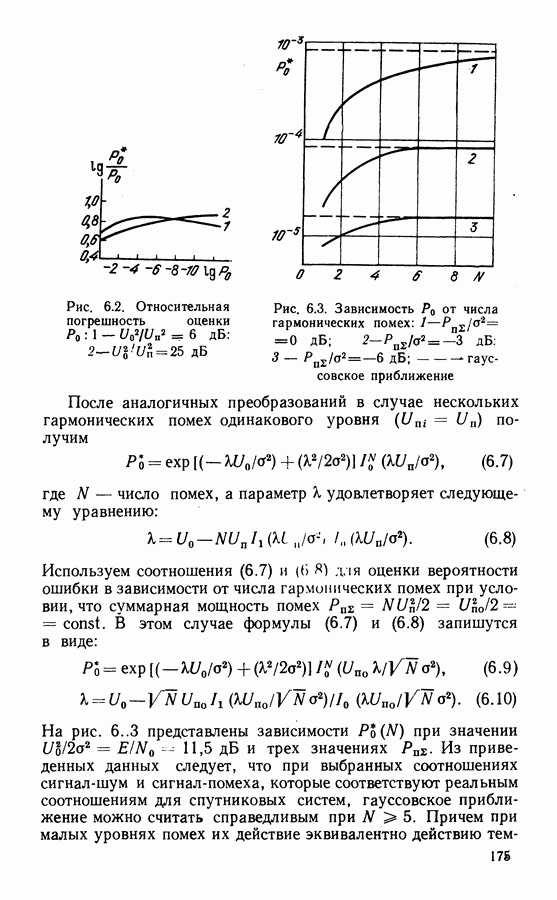
- 6.2. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ГАРМОНИЧЕСКИХ ПОМЕХ НА ДЕМОДУЛЯТОР ФМ СИГНАЛОВ
- 6.3. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ФМ ПОМЕХ
- 6.4. АНАЛИЗ МЕШАЮЩЕГО ДЕЙСТВИЯ ЧМ—ТВ СИГНАЛА С ДИСПЕРСИЕЙ
- 6.5. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ СИГНАЛОВ ЧУ-ЧМ
- ГЛАВА 7. СИСТЕМЫ С МДВР И МДЧР
- 7.1. ОЦЕНКА ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ РАЗЛИЧНЫХ МЕТОДОВ ПЕРЕДАЧИ В ЦССС С МДЧР
- 7.2. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДЧР
- 7.3. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДВР
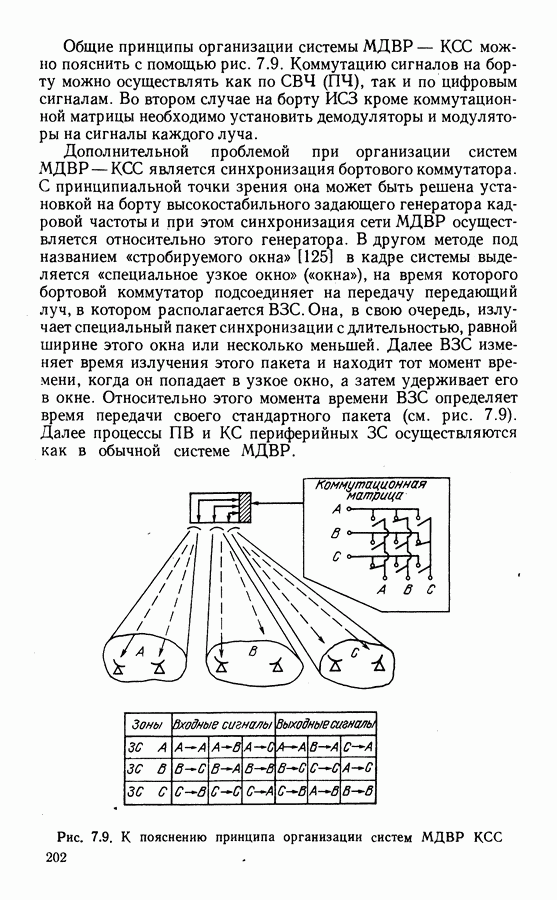
- Синхронизация систем МДВР.
- Организация кадра систем МДВР.
- Система МДВУ-40.
- ЦСС с ДВР ТДМА-120-(«Интелсат»/«Евросат»).
- МДВР с коммутацией сигналов на спутнике (КСС).
- Сопряжение систем МДВР с цифровыми наземными линиями.
- ГЛАВА 8. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ И КОДИРОВАНИЯ В ЦССС
- 8.2. СОГЛАСОВАНИЕ СИСТЕМ МОДУЛЯЦИИ И КОДИРОВАНИЯ
- Согласование кодом Грея.
- Кодирование с разбиением ансамбля на подклассы.
- Применение недвоичных кодов.
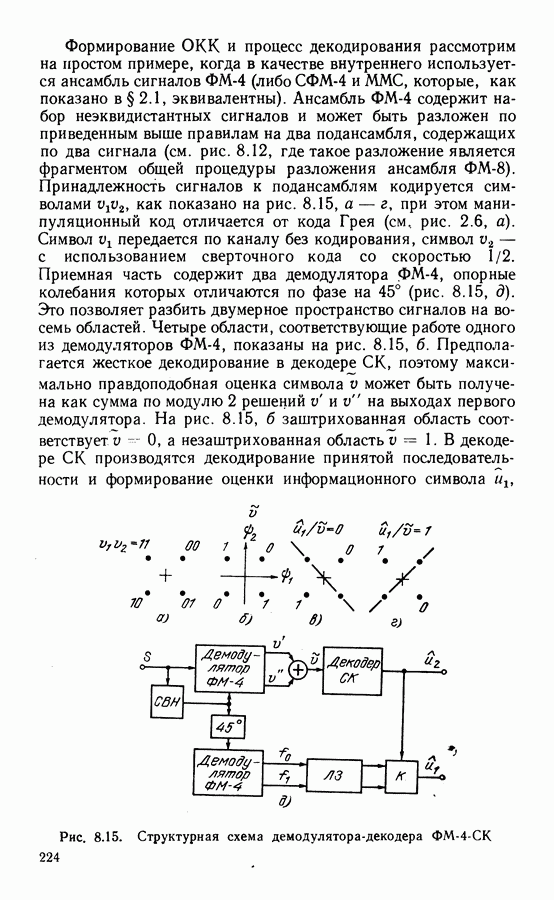
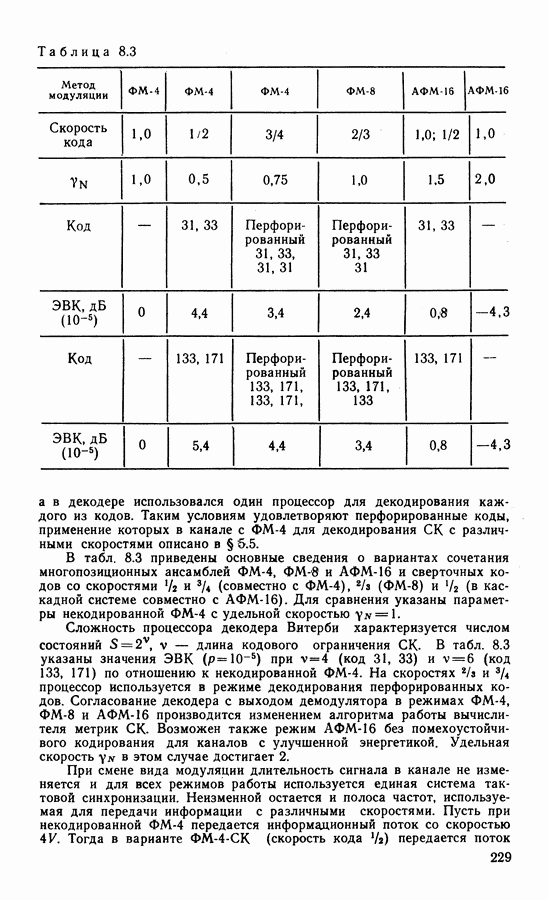
- 8.3. СВЕРТОЧНОЕ КОДИРОВАНИЕ В КАНАЛЕ С МНОГОПОЗИЦИОННОИ ФМ
- 8.4. ОБОБЩЕННОЕ КАСКАДНОЕ КОДИРОВАНИЕ
- 8.5. ПРИМЕРЫ РЕАЛИЗАЦИИ ЭФФЕКТИВНЫХ КОДЕМОВ
- СПИСОК ЛИТЕРАТУРЫ