| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
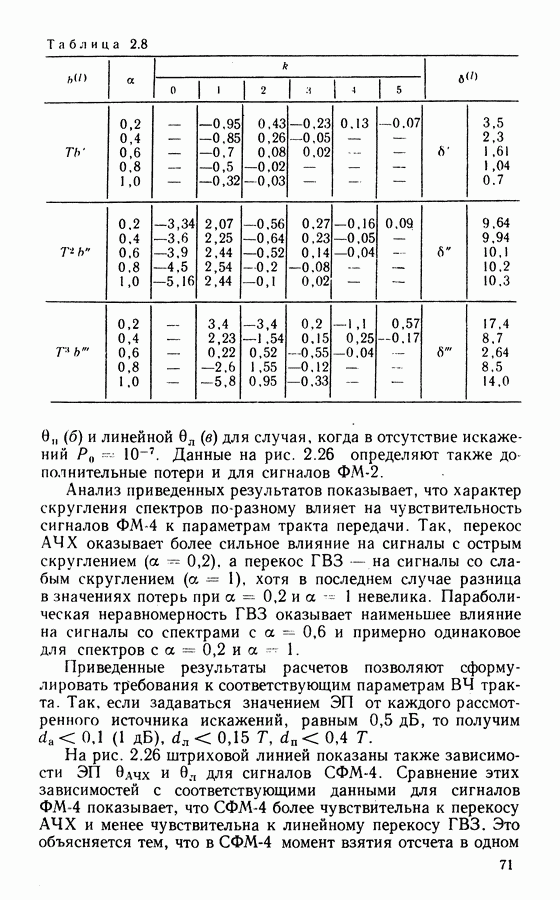
4.6. ПОМЕХОУСТОЙЧИВОСТЬ И ЭФФЕКТИВНОСТЬ СИСТЕМ С КОДИРОВАНИЕМ
Рассмотрим помехоустойчивость декодирования блоковых кодов с жестким решением на выходе демодулятора. В канале без памяти ошибки в последовательно передаваемых кодовых символах происходят независимо с вероятностью  Вероятность того, что будет ошибка кратности
Вероятность того, что будет ошибка кратности  на длине блока
на длине блока  Если при декодировании исправляются все ошибки кратности
Если при декодировании исправляются все ошибки кратности  и менее, то вероятность получения блока с неисправленными ошибками
и менее, то вероятность получения блока с неисправленными ошибками  Для определения вероятности ошибки в каждом информационном символе полагаем, что если в канале происходит
Для определения вероятности ошибки в каждом информационном символе полагаем, что если в канале происходит  и более ошибок, то из-за ошибочного декодирования на выходе декодера будет еще
и более ошибок, то из-за ошибочного декодирования на выходе декодера будет еще  ошибок. Эти ошибки возникают случайно и
ошибок. Эти ошибки возникают случайно и
в равной степени искажают как информационные, так и проверочные символы. Поэтому среднее значение вероятности ошибки в двоичном символе.

При малой вероятности ошибки в канале можно ограничиться первым членом ряда, при этом

Для каналов с фазовой модуляцией вероятность ошибки в канале определяется выражением, аналогичным формуле (2.13), в котором учтена скорость используемого кода 
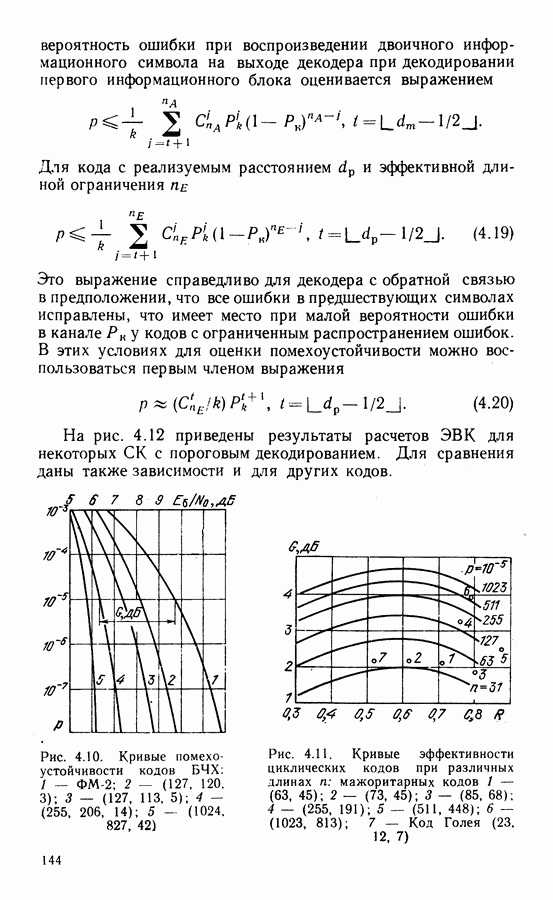
На рис. 4.10 приведены результаты расчетов вероятности ошибки декодирования циклических кодов. Показана также зависимость вероятности ошибки без кодирования в канале с ФМ-2, что позволяет определить энергетический выигрыш при применении кодирования  как разность значений
как разность значений  необходимых для получения заданной вероятности ошибки
необходимых для получения заданной вероятности ошибки  с учетом кодирования и без него. Для кода (255, 206, 14) величина ЭВК при
с учетом кодирования и без него. Для кода (255, 206, 14) величина ЭВК при  составляет
составляет 
Выбор параметров кодов удобно производить, используя диаграмму эффективности, показанную на рис. 4.11. Здесь по вертикали отложены значения ЭВК в зависимости от скорости кода  для различных длин циклических кодов. Видно, что при постоянной длине кода
для различных длин циклических кодов. Видно, что при постоянной длине кода  существует оптимальное значение скорости, при которой ЭВК имеет максимальное значение. Оптимум наступает при
существует оптимальное значение скорости, при которой ЭВК имеет максимальное значение. Оптимум наступает при  . С увеличением длины кода
. С увеличением длины кода  величина ЭВК также возрастает.
величина ЭВК также возрастает.
При равных длинах блока корректирующая способность мажоритарно декодируемых кодов несколько хуже, чем кодов БЧХ. Это подтверждается данными, приведенными на рис. 4.11, где точками показаны результаты расчетов эффективности таких кодов. Однако в среднем проигрыш невелик и не превышает  что подтверждает целесообразность применения кодов с мажоритарным декодированием. Здесь же показана эффективность кода Голея ((23, 12, 7), точка 7). Эти данные иллюстрируют свойства совершенного кода Голея, ЭВК которого при длине блока
что подтверждает целесообразность применения кодов с мажоритарным декодированием. Здесь же показана эффективность кода Голея ((23, 12, 7), точка 7). Эти данные иллюстрируют свойства совершенного кода Голея, ЭВК которого при длине блока  превышает ЭВК кода БЧХ с длиной блока
превышает ЭВК кода БЧХ с длиной блока 
При пороговом декодировании СК методика расчета вероятности ошибки аналогична изложенной выше. Если не учитывать влияния распространения ошибок при декодировании, то
вероятность ошибки при воспроизведении двоичного информационного символа на выходе декодера при декодировании первого информационного блока оценивается выражением

Для кода с реализуемым расстоянием  и эффективной длиной ограничения
и эффективной длиной ограничения 

Это выражение справедливо для декодера с обратной связью в предположении, что все ошибки в предшествующих символах исправлены, что имеет место при малой вероятности ошибки в канале  у кодов с ограниченным распространением ошибок. В этих условиях для оценки помехоустойчивости можно воспользоваться первым членом выражения
у кодов с ограниченным распространением ошибок. В этих условиях для оценки помехоустойчивости можно воспользоваться первым членом выражения

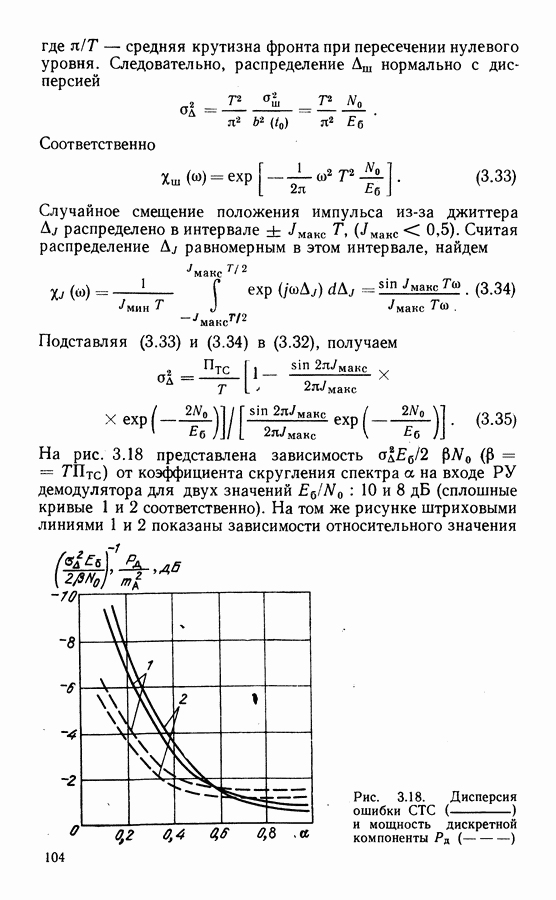
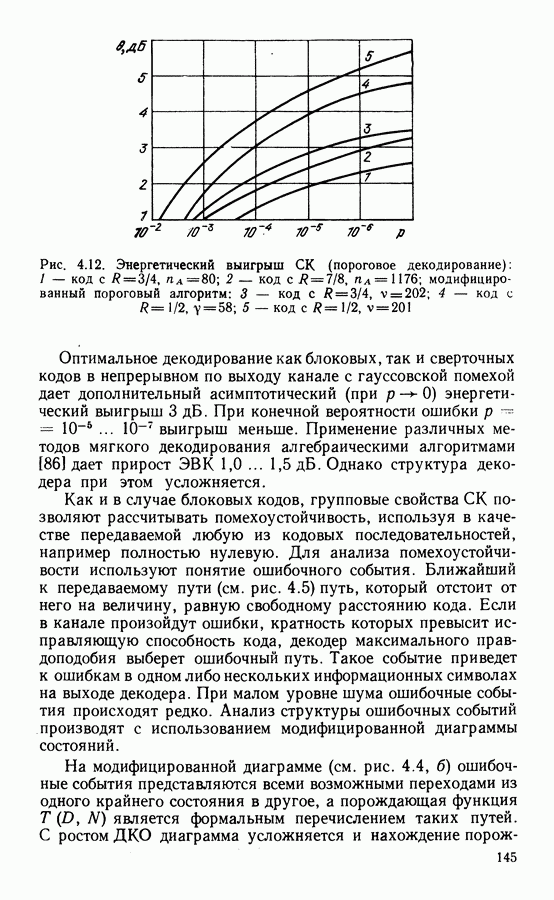
На рис. 4.12 приведены результаты расчетов ЭВК для некоторых СК с пороговым декодированием. Для сравнения даны также зависимости и для других кодов.

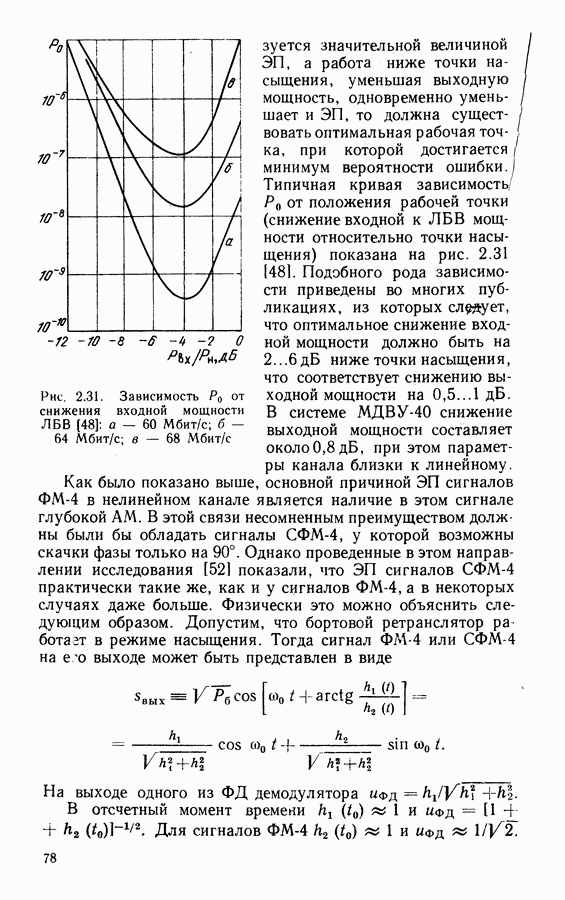
Рис. 4.10. Кривые помехоустойчивости кодов БЧХ: 1 - ФМ-2; 2 - (127, 120, 3); 3 - (127, ИЗ, 5); 4 -(255, 206, 14); 5 - (1024, 827, 42)

Рис. 4.11. Кривые эффективности циклических кодов при различных длинах  мажоритарных кодов
мажоритарных кодов  Код Голея (23, 12, 7)
Код Голея (23, 12, 7)

Рис. 4.12. Энергетический выигрыш СК (пороговое декодирование): 1 — код с  код с
код с  модифицированный пороговый алгоритм: 3 — код
модифицированный пороговый алгоритм: 3 — код 
Оптимальное декодирование как блоковых, так и сверточных кодов в непрерывном по выходу канале с гауссовской помехой дает дополнительный асимптотический (при  энергетический выигрыш
энергетический выигрыш  При конечной вероятности ошибки
При конечной вероятности ошибки  выигрыш меньше. Применение различных методов мягкого декодирования алгебраическими алгоритмами [86] дает прирост
выигрыш меньше. Применение различных методов мягкого декодирования алгебраическими алгоритмами [86] дает прирост  Однако структура декодера при этом усложняется.
Однако структура декодера при этом усложняется.
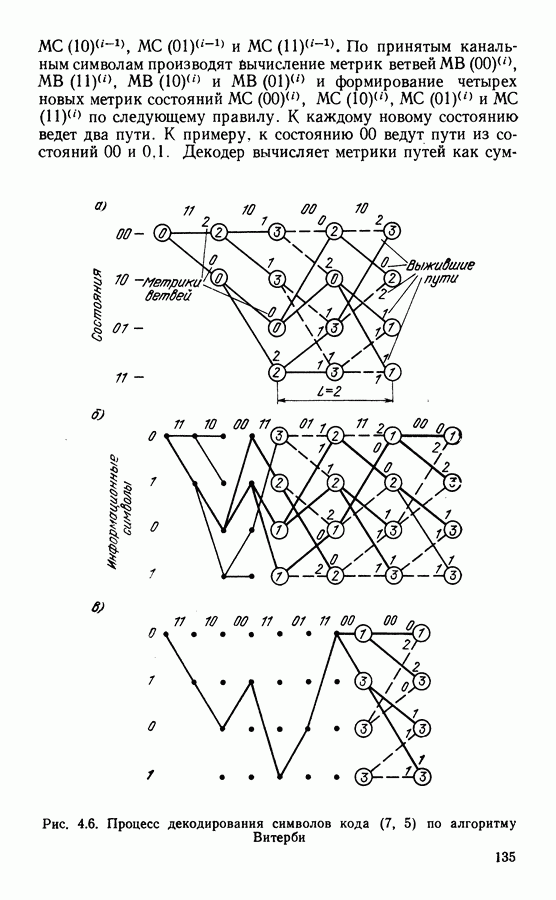
Как и в случае блоковых кодов, групповые свойства СК позволяют рассчитывать помехоустойчивость, используя в качестве передаваемой любую из кодовых последовательностей, например полностью нулевую. Для анализа помехоустойчивости используют понятие ошибочного события. Ближайший к передаваемому пути (см. рис. 4.5) путь, который отстоит от него на величину, равную свободному расстоянию кода. Если в канале произойдут ошибки, кратность которых превысит исправляющую способность кода, декодер максимального правдоподобия выберет ошибочный путь. Такое событие приведет к ошибкам в одном либо нескольких информационных символах на выходе декодера. При малом уровне шума ошибочные события происходят редко. Анализ структуры ошибочных событий производят с использованием модифицированной диаграммы состояний.
На модифицированной диаграмме (см. рис. 4.4, б) ошибочные события представляются всеми возможными переходами из одного крайнего состояния в другое, а порождающая функция  является формальным перечислением таких путей. С ростом
является формальным перечислением таких путей. С ростом  диаграмма усложняется и нахождение
диаграмма усложняется и нахождение
порождающей функции выполняют на ЭВМ [931. Производная порождающей функции по  при
при 

Набор коэффициентов  при
при  называется спектром весов
называется спектром весов  Он показывает суммарное количество ошибок на выходе декодера максимального правдоподобия, когда вместо передаваемого пути по решетчатой диаграмме выбираются ошибочные пути, отстоящие от него на величину
Он показывает суммарное количество ошибок на выходе декодера максимального правдоподобия, когда вместо передаваемого пути по решетчатой диаграмме выбираются ошибочные пути, отстоящие от него на величину  Например, производная функции
Например, производная функции  показывает, что имеется один ошибочный путь веса
показывает, что имеется один ошибочный путь веса  выбор которого приводит к одной ошибке в информационной последовательности на выходе декодера. Имеются также ошибочные пути веса
выбор которого приводит к одной ошибке в информационной последовательности на выходе декодера. Имеются также ошибочные пути веса  выбор которых дает четыре ошибки на выходе, пути веса
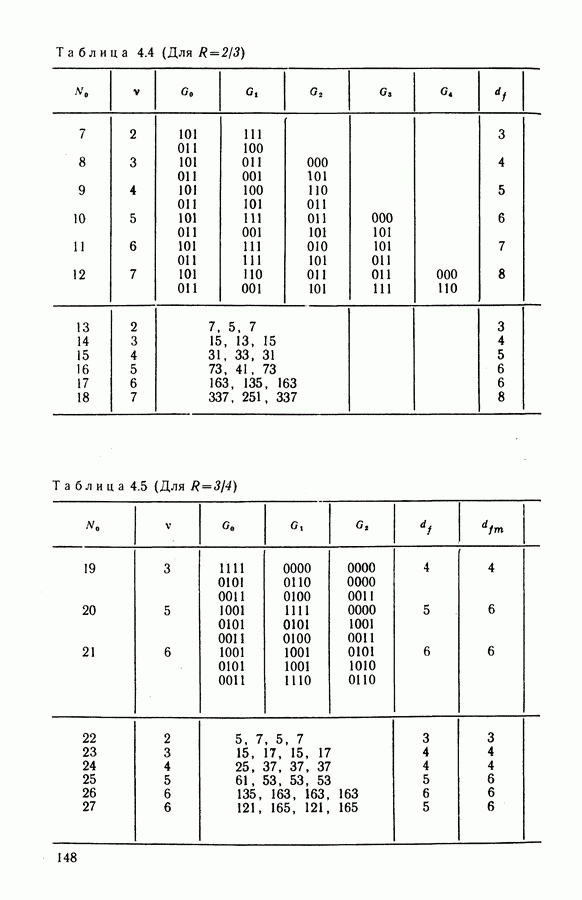
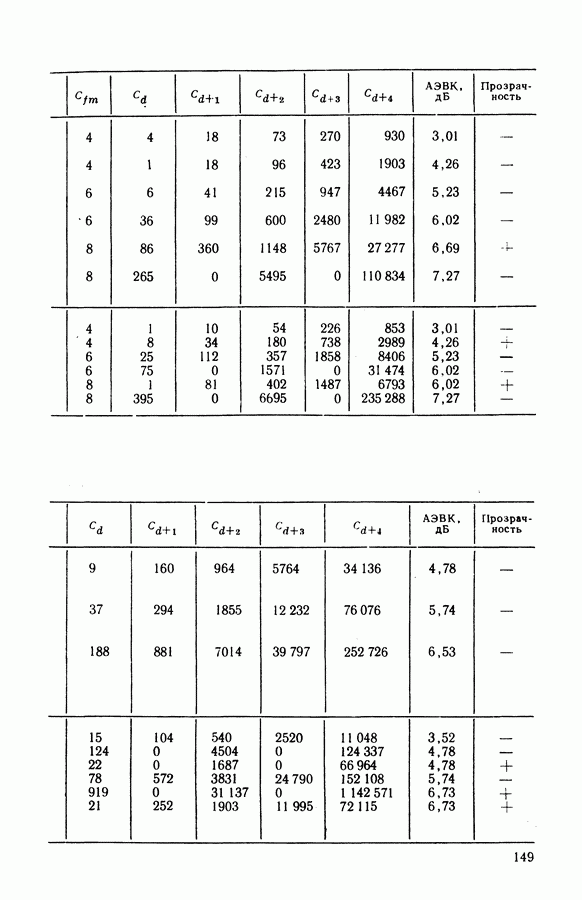
выбор которых дает четыре ошибки на выходе, пути веса  и т. д. В табл. 4.3 — 4.5 приведены основные характеристики и спектры весов коротких сверточных кодов с различными скоростями [34, 83, 89, 91, 93]. Коды заданы порождающими многочленами в восьмеричной форме записи либо базисными порождающими матрицами
и т. д. В табл. 4.3 — 4.5 приведены основные характеристики и спектры весов коротких сверточных кодов с различными скоростями [34, 83, 89, 91, 93]. Коды заданы порождающими многочленами в восьмеричной форме записи либо базисными порождающими матрицами  . Указаны первые пять членов спектра, свободное расстояние
. Указаны первые пять членов спектра, свободное расстояние  и его верхняя граница
и его верхняя граница  Из множества известных кодов отобраны лучшие, обладающие максимальным свободным расстоянием
Из множества известных кодов отобраны лучшие, обладающие максимальным свободным расстоянием  а при одинаковых расстояниях — наименьшим значением соответствующих коэффициентов спектра. Такой критерий отбора кодов наиболее распространен, а применение других, более сложных критериев [90] затруднено и дает улучшение по ЭВК не более
а при одинаковых расстояниях — наименьшим значением соответствующих коэффициентов спектра. Такой критерий отбора кодов наиболее распространен, а применение других, более сложных критериев [90] затруднено и дает улучшение по ЭВК не более 
Вероятность ошибки вычисляют в предположении, что ошибочные события происходят редко. Тогда при этом можно воспользоваться аддитивной границей. Вероятность ошибки при выборе пути по решетчатой диаграмме оценивают сверху суммой
Таблица 4.3 (Для R = 1/2)

вероятностей ошибочных событий  При декодировании с мягким решением расстояние между различными путями вычисляют в метрике Евклида. Если двоичные кодовые последовательности отличаются в
При декодировании с мягким решением расстояние между различными путями вычисляют в метрике Евклида. Если двоичные кодовые последовательности отличаются в  символах, а в канале используется ФМ-2, то расстояние между путями, соответствующими этим последовательностям, равно
символах, а в канале используется ФМ-2, то расстояние между путями, соответствующими этим последовательностям, равно  Учитывая, что энергия каждого кодового символа
Учитывая, что энергия каждого кодового символа  расстояние определим как
расстояние определим как  Суммарная дисперсия отсчетов помех, действующих на
Суммарная дисперсия отсчетов помех, действующих на  кодовых символов,
кодовых символов,  Ошибка в выборе пути произойдет, когда помеха превысит половину расстояния
Ошибка в выборе пути произойдет, когда помеха превысит половину расстояния  т. е.
т. е.

Таким образом, расчет вероятности ошибочного воспроизведения двоичного символа на выходе декодера сводится к вычислению спектра весов в соответствии с выражением (4.21), расчету вероятности ошибочного выбора пути по формуле (4.22) и последующему вычислению по фюрмуле

Такая методика достаточно точна при 
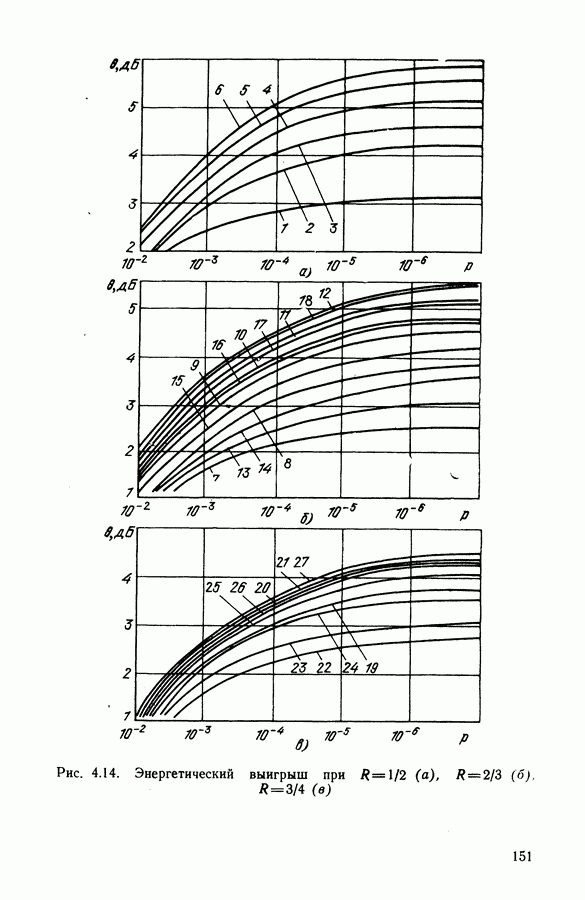
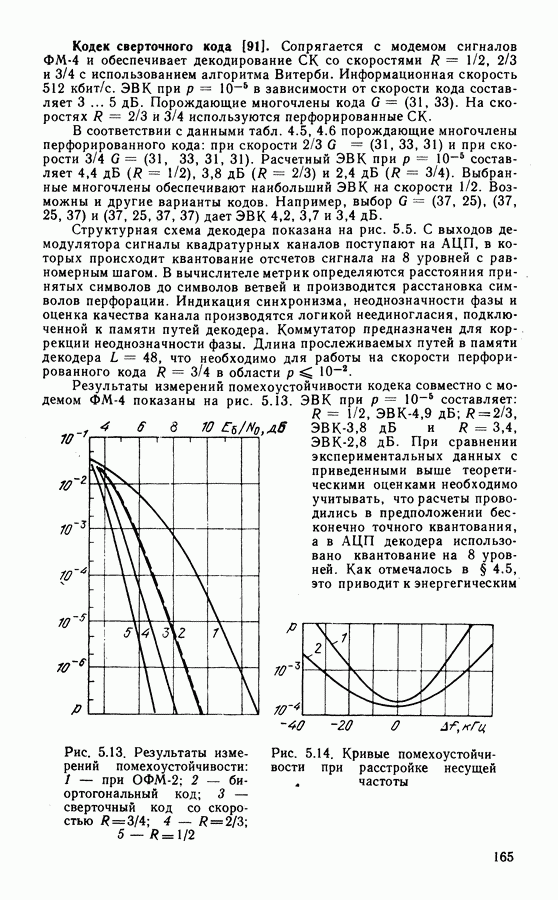
На рис. 4.13 показаны результаты расчетов вероятности ошибки для кодов со скоростью 1/2 и перфорированных кодов со скоростями 2/3 и 3/4. По кривым можно определить ЭВК. Например, при использовании кода (133, 171) выигрыш составляет  На рис. 4.14 приведены результаты расчетов ЭВК при различных вероятностях ошибки
На рис. 4.14 приведены результаты расчетов ЭВК при различных вероятностях ошибки  для кодов со скоростями
для кодов со скоростями  Номера кривых соответствуют номерам кодов, приведенных в табл. 4.3 — 4.5. Асимптотический энергетический выигрыш от кодирования
Номера кривых соответствуют номерам кодов, приведенных в табл. 4.3 — 4.5. Асимптотический энергетический выигрыш от кодирования  можно установить, сравнивая аргументы для функции
можно установить, сравнивая аргументы для функции  в выражениях для вероятности ошибки (4.22) и (2.13), определяющих помехоустойчивость систем с кодированием и без него. Полагая в формуле
в выражениях для вероятности ошибки (4.22) и (2.13), определяющих помехоустойчивость систем с кодированием и без него. Полагая в формуле  получаем АЭВК
получаем АЭВК

Величина АЭВК показывает изменение минимального расстояния при введении кодирования, характеризует ЭВК при  и является верхней границей реального ЭВК (при
и является верхней границей реального ЭВК (при  .
.
Анализ кривых рис. 4.14 показывает, что применение коротких СК, декодируемых по алгоритму Витерби с мягким решением, позволяет получить  Переход к жесткому решению снижает ЭВК примерно на 2 дБ. Квантование выхода
Переход к жесткому решению снижает ЭВК примерно на 2 дБ. Квантование выхода
(см. скан)
(см. скан)
демодулятора на четыре уровня снижает ЭВК на  а квантование на восемь уровней — на
а квантование на восемь уровней — на  Обычно ограничиваются квантованием на восемь уровней, используя практически полностью возможности мягкого решения.
Обычно ограничиваются квантованием на восемь уровней, используя практически полностью возможности мягкого решения.
Перфорированные коды по эффективности незначительно уступают оптимальным кодам. В среднем этот проигрыш не превышает  Приведенные данные позволяют оценить возможности построения кодеков на скорости 1/2, 2/3 и 3/4 (либо с другими вариантами скоростей), когда для работы на различных скоростях используют один набор порождающих многочленов. В § 5.5. рассмотрен пример построения такого кодека.
Приведенные данные позволяют оценить возможности построения кодеков на скорости 1/2, 2/3 и 3/4 (либо с другими вариантами скоростей), когда для работы на различных скоростях используют один набор порождающих многочленов. В § 5.5. рассмотрен пример построения такого кодека.
Важным параметром является длина памяти декодера. Результаты вычислений вероятности ошибки при декодировании СК с различными скоростями и их перфорированных вариантов приведены в работе [91]. С ростом длины памяти  вероятность ошибки
вероятность ошибки  убывает, стремясь к некоторому стационарному
убывает, стремясь к некоторому стационарному

Рис. 4.13. Кривые помехоустойчивости декодирования СК

(кликните для просмотра скана)

Рис. 4.15. Длина памяти декодера при различных скоростях кода
уровню, соответствующему декодированию с бесконечной памятью. Величина  при которой дальнейшее увеличение памяти не снижает вероятность ошибки, определяет номинальную длину памяти декодера. Она зависит от скорости кода, длины кодового ограничения и отношения сигнал-шум. На рис. 4.15 приведены зависимости длины памяти
при которой дальнейшее увеличение памяти не снижает вероятность ошибки, определяет номинальную длину памяти декодера. Она зависит от скорости кода, длины кодового ограничения и отношения сигнал-шум. На рис. 4.15 приведены зависимости длины памяти  от
от  для скоростей 1/2, 2/3 и 3/4, необходимой для декодирования кодов при вероятности ошибки на выходе декодера
для скоростей 1/2, 2/3 и 3/4, необходимой для декодирования кодов при вероятности ошибки на выходе декодера  Переход к скорости 3/4 требует увеличения длины памяти примерно вдвое по сравнению со скоростью 1/2.
Переход к скорости 3/4 требует увеличения длины памяти примерно вдвое по сравнению со скоростью 1/2.
Анализ показывает [341, что сверточные коды дают значительное повышение ЭВК при скорости кода  а при скорости
а при скорости  обмен ЭВК на снижение скорости значительно меньший. Эффективность биортогональных кодов монотонно возрастает при уменьшении скорости кода R [34]. Поскольку прием в целом комбинаций такого кода реализуется переборными методами [85], практическое использование длинных кодов затруднительно. Ограничиваются обычно скоростью
обмен ЭВК на снижение скорости значительно меньший. Эффективность биортогональных кодов монотонно возрастает при уменьшении скорости кода R [34]. Поскольку прием в целом комбинаций такого кода реализуется переборными методами [85], практическое использование длинных кодов затруднительно. Ограничиваются обычно скоростью  при этом число комбинаций
при этом число комбинаций  а ЭВК будет порядка
а ЭВК будет порядка 
Остановимся кратко на анализе эффективности каскадных кодов. Основы построения каскадных кодов изложены в работе [82], а оценка эффективности ряда каскадных кодов — в [34]. При каскадном кодировании предусмотрено несколько ступеней кодирования. Внутренний код работает в канале с сильным шумом. Здесь целесообразно применение алгоритмов максимального правдоподобия с мягким решением. Внешняя ступень находится в более легких условиях, и здесь часто используют алгебраические методы декодирования. При блоковом кодировании внутренний кодек вместе с исходным каналом образуют новый канал с  -ичными символами на входе и выходе
-ичными символами на входе и выходе  либо эквивалентный ему двоичный канал с пакетами ошибок. Во внешней ступени используют часто коды Рида — Соломона либо двоичные коды, исправляющие пакеты ошибок.
либо эквивалентный ему двоичный канал с пакетами ошибок. Во внешней ступени используют часто коды Рида — Соломона либо двоичные коды, исправляющие пакеты ошибок.
Одним из вариантов каскадного кодирования является система, в которой на внутренней ступени используются биортогональные коды с приемом в целом, а на внешней ступени — коды Рида — Соломона. Основание кода  равно объему кодовых комбинаций внутреннего биортогонального кода М. Результаты расчетов эффективности такого каскадного кода приведены в работе [34]. При
равно объему кодовых комбинаций внутреннего биортогонального кода М. Результаты расчетов эффективности такого каскадного кода приведены в работе [34]. При  результирующий ЭВК достигает
результирующий ЭВК достигает  и соизмерим с выигрышем при сверточном кодировании с декодированием по алгоритму Витерби.
и соизмерим с выигрышем при сверточном кодировании с декодированием по алгоритму Витерби.
Преимущества каскадных систем такого типа начинают сказываться при скорости  где величина ЭВК превосходит
где величина ЭВК превосходит 
Высокая эффективность сверточных кодов при скоростях  определяет их использование в качестве внутренних и каскадных системах. Приведем типичные примеры [34]: а) внутренний код — сверточный,
определяет их использование в качестве внутренних и каскадных системах. Приведем типичные примеры [34]: а) внутренний код — сверточный,  алгоритм Витерби, внешний код
алгоритм Витерби, внешний код  скорость каскадного кода
скорость каскадного кода  внутренний код — сверточный,
внутренний код — сверточный,  алгоритм Витерби, внешний код — циклический (67, 45) с перемежителем, скорость каскадного кода
алгоритм Витерби, внешний код — циклический (67, 45) с перемежителем, скорость каскадного кода 
Перспективным направлением повышения эффективности систем с кодированием является применение обобщенных каскадных кодов [82]. Наращивание числа каскадов и усложнение структуры кода на каждой из ступеней кодирования приводит к возрастанию  который, как показывает анализ, может достигать при скорости
который, как показывает анализ, может достигать при скорости  примерно
примерно 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ I. ОСНОВЫ ПОСТРОЕНИЯ ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМ СВЯЗИ
- ГЛАВА 1. СПУТНИКОВЫЕ СИСТЕМЫ С МНОГОСТАНЦИОННЫМ ДОСТУПОМ
- 1.2. ПРЕОБРАЗОВАНИЕ АНАЛОГОВЫХ СИГНАЛОВ В ЦИФРОВУЮ ФОРМУ
- Адаптивная ИКМ.
- Дифференциальная ИКМ (ДИКМ).
- Дельта-модуляция (ДМ).
- Преобразование сигналов телевидения, многоканальной телефонии и вещания в цифровую форму.
- 1.3. СТАТИСТИЧЕСКОЕ УПЛОТНЕНИЕ В ЦССС
- 1.4. МНОГОСТАНЦИОННЫЙ ДОСТУП В ЦССС
- Многостанционный доступ с временным разделением каналов (МДВР).
- Многостанционный доступ с разделением сигналов по форме (МДФР).
- Многостанционный доступ со случайным доступом (МДСД).
- 1.5. НОРМИРОВАНИЕ ПАРАМЕТРОВ ЦССС
- РАЗДЕЛ II. МОДУЛЯЦИЯ
- ГЛАВА 2. МЕТОДЫ МОДУЛЯЦИИ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СИГНАЛОВ
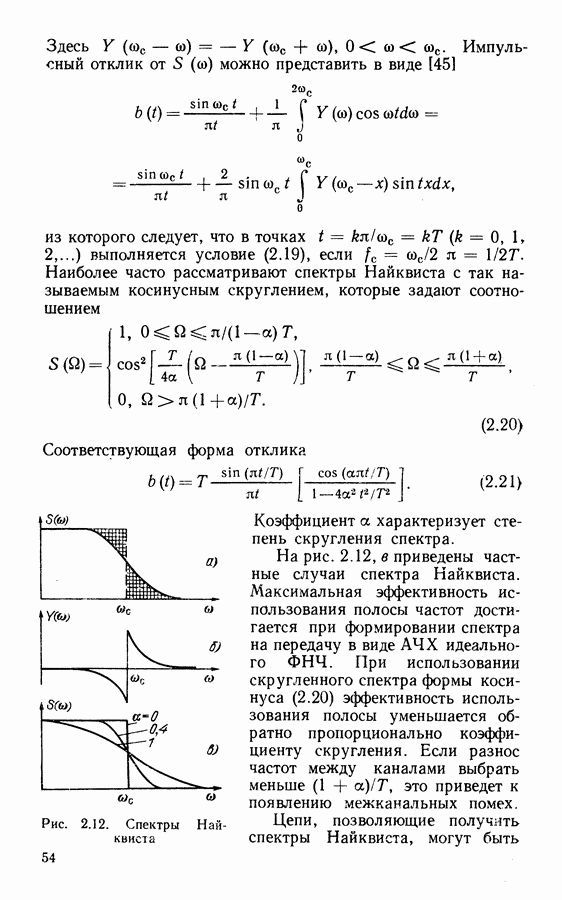
- 2.2. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.3. СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИГНАЛОВ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
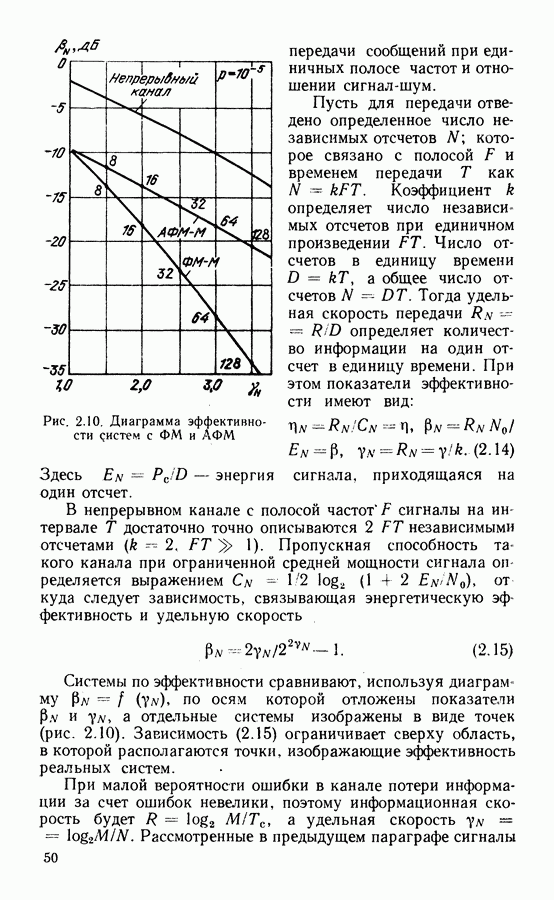
- 2.4. СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ
- 2.5. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДЧР
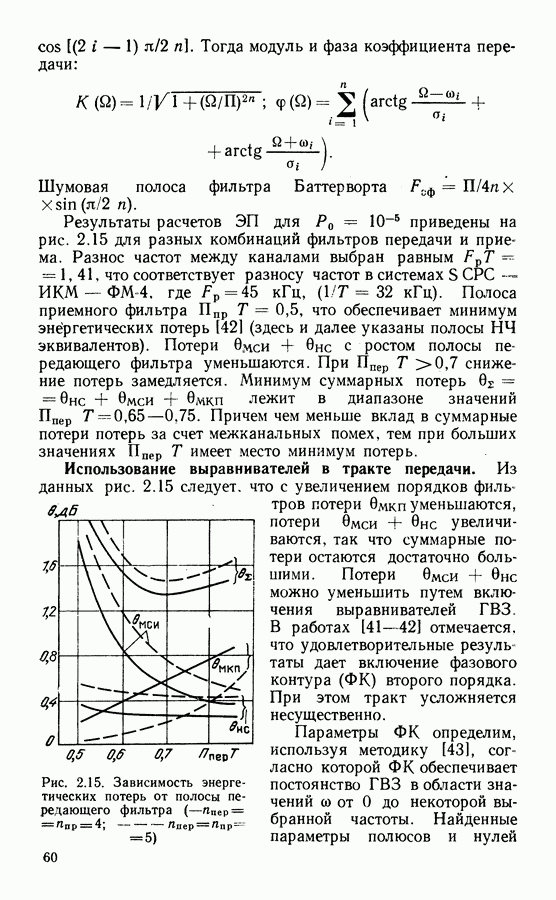
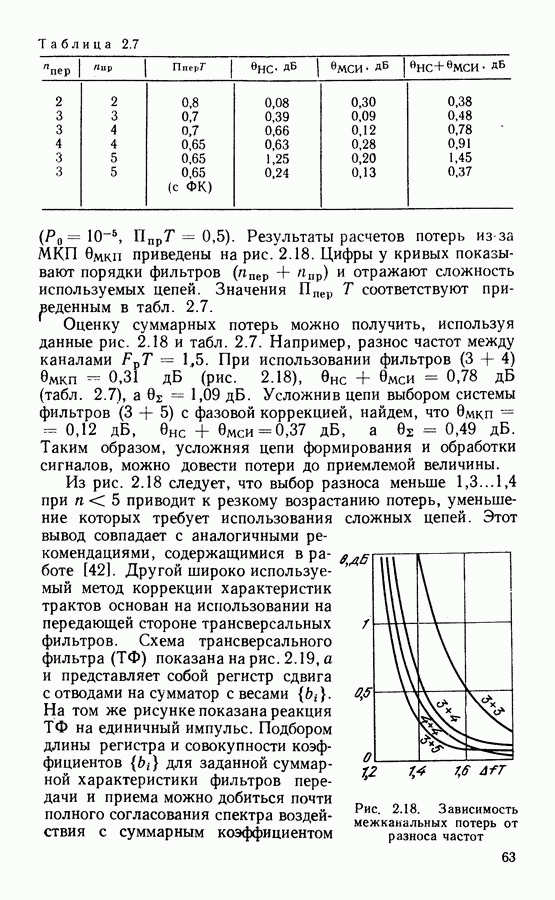
- Результаты расчетов потерь в системе с ФМ-2 и стандартными фильтрами.
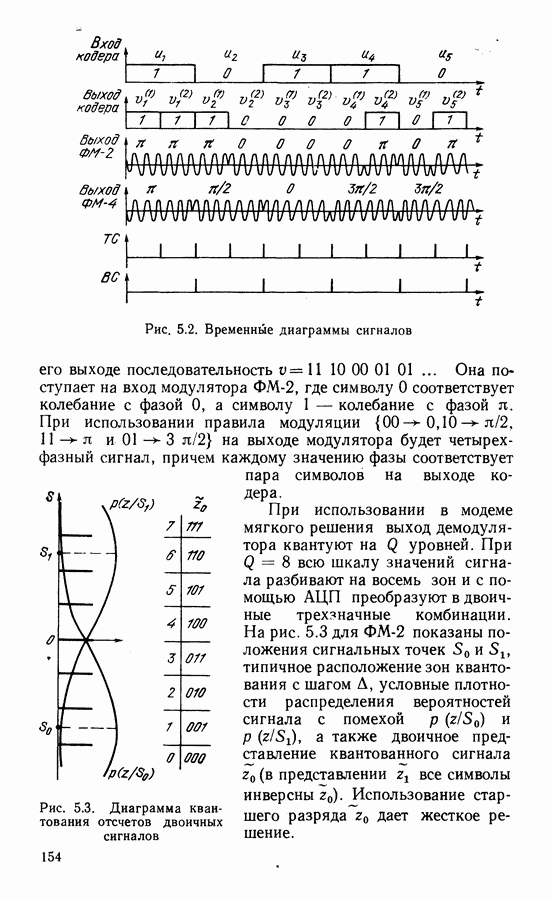
- Использование выравнивателей в тракте передачи.
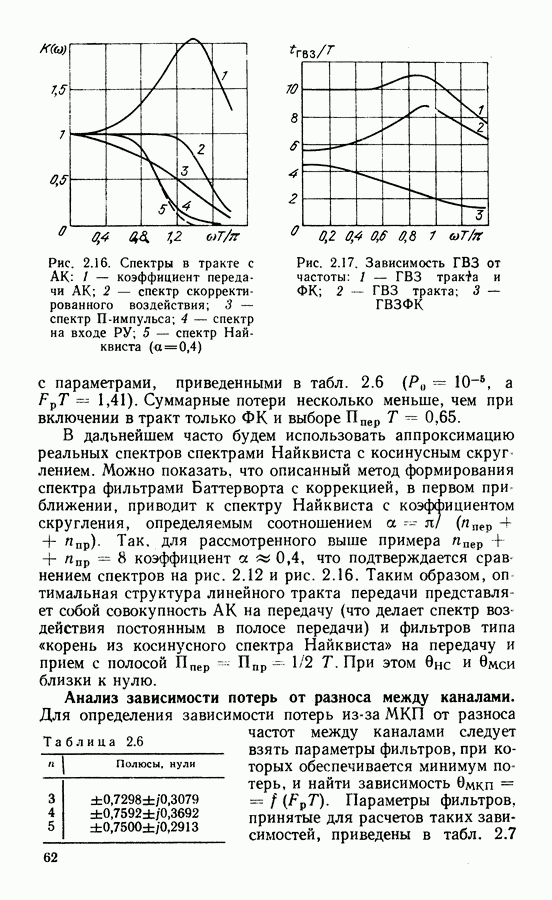
- Анализ зависимости потерь от разноса между каналами.
- Энергетические потери в системе с ФМ-4.
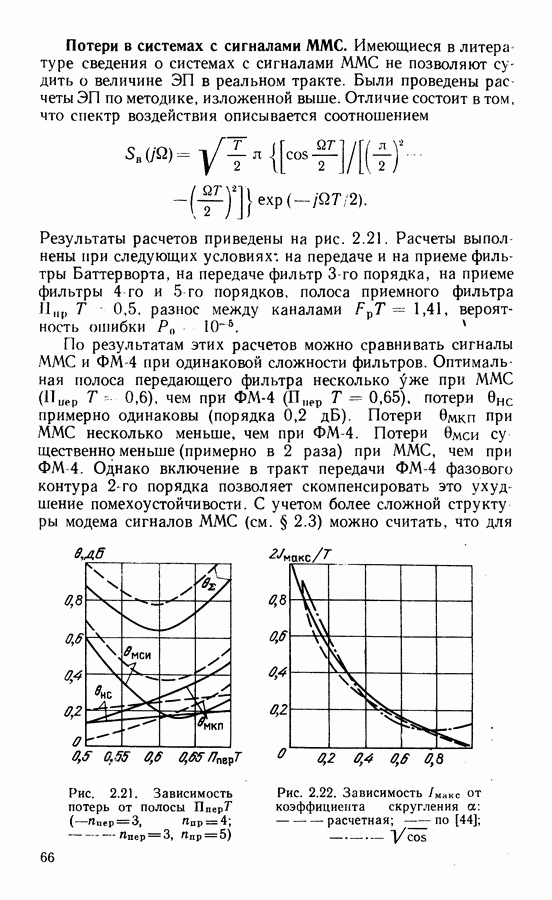
- Потери в системах с сигналами ММС.
- 2.6. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДВР
- ГЛАВА 3. МОДЕМЫ
- 3.1. СТРУКТУРА МОДЕМА
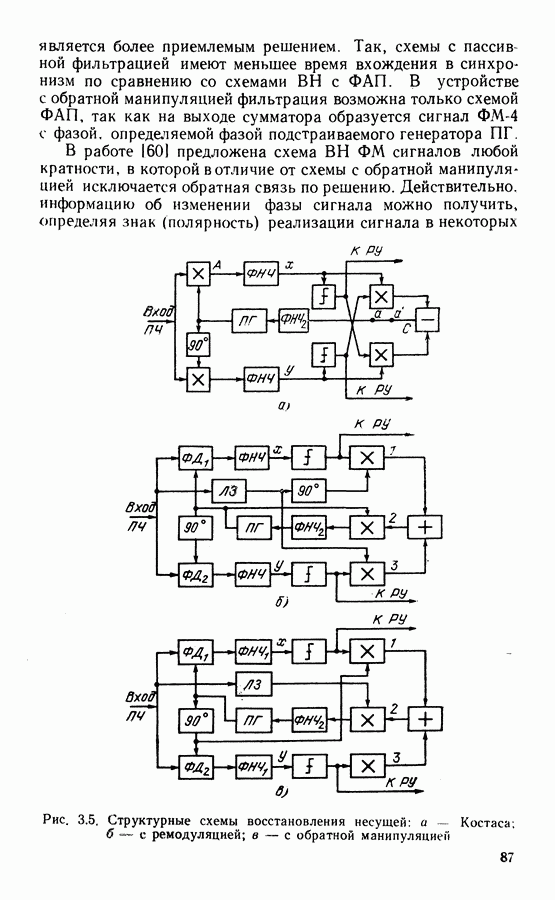
- 3.2. СИСТЕМЫ ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ
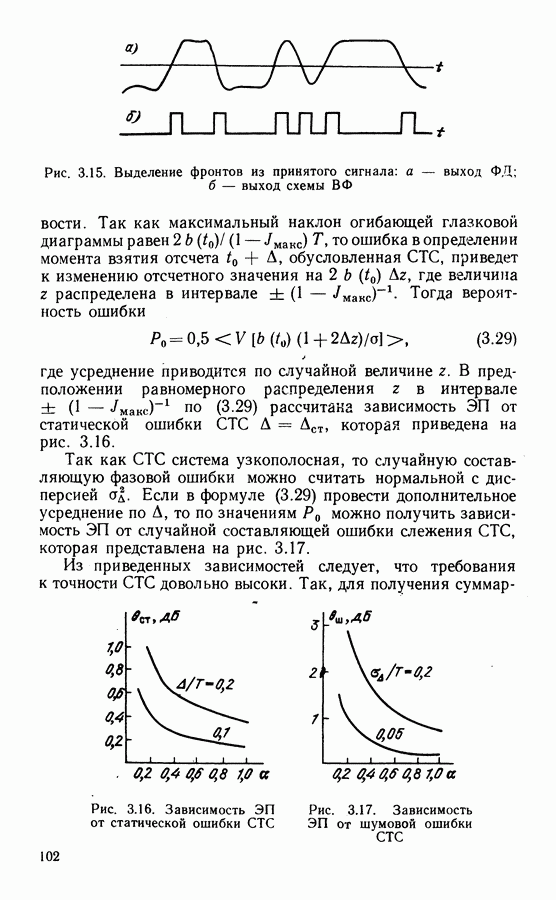
- Требования к точности работы системы ВН.
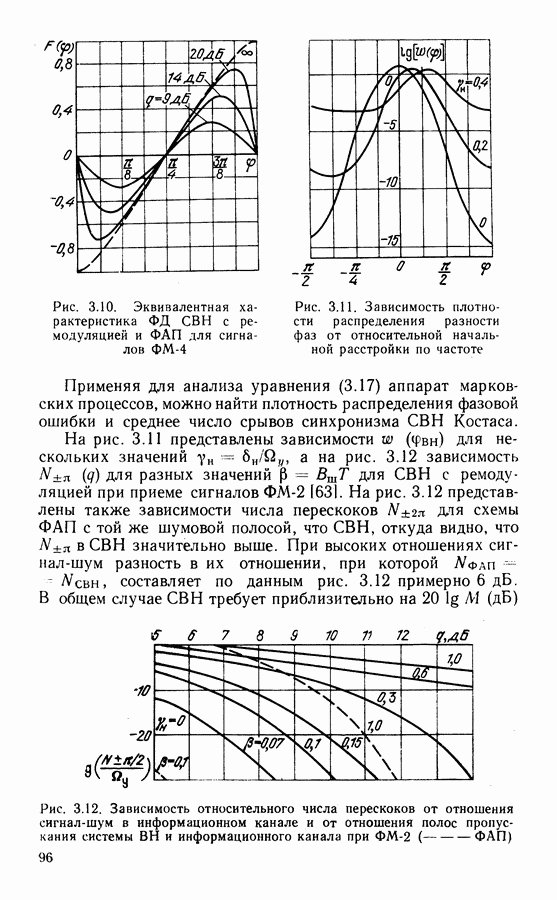
- Анализ точности систем ВН.
- Переходные процессы.
- 3.3. ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 3.4. ОТНОСИТЕЛЬНОЕ КОДИРОВАНИЕ
- 3.5. ПРИМЕРЫ РЕАЛИЗАЦИИ МОДЕМОВ В ЦССС
- РАЗДЕЛ III. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
- 4.2. АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ КОДОВ
- 4.3. БЛОКОВЫЕ КОДЫ И АЛГОРИТМЫ ИХ ДЕКОДИРОВАНИЯ
- 4.4. СТРУКТУРА И ХАРАКТЕРИСТИКИ СВЕРТОЧНЫХ КОДОВ
- 4.5. АЛГОРИТМЫ ДЕКОДИРОВАНИЯ СК
- 4.6. ПОМЕХОУСТОЙЧИВОСТЬ И ЭФФЕКТИВНОСТЬ СИСТЕМ С КОДИРОВАНИЕМ
- ГЛАВА 5. КОДЕКИ
- 5.1. СОГЛАСОВАНИЕ МОДЕМА И КОДЕКА
- 5.2. ДЕКОДЕРЫ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ СК
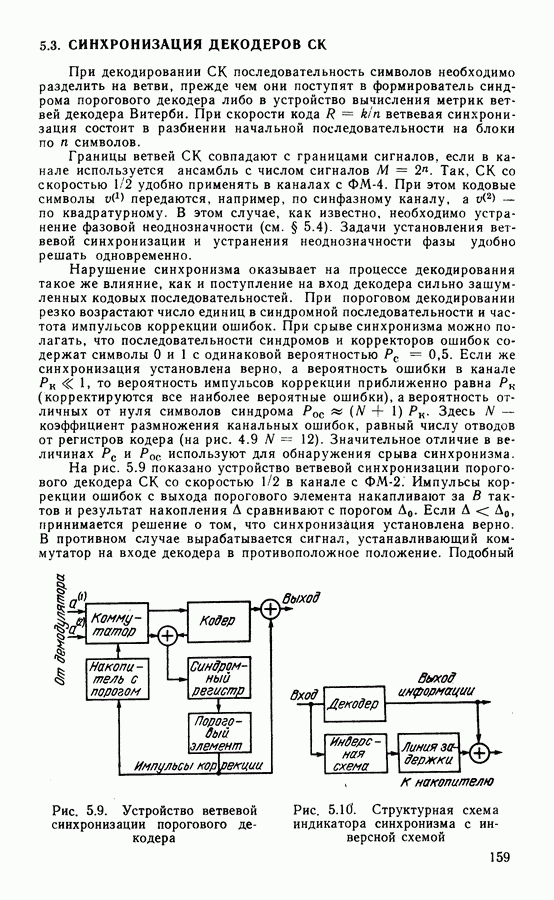
- 5.3. СИНХРОНИЗАЦИЯ ДЕКОДЕРОВ СК
- 5.4. КОДИРОВАНИЕ В КАНАЛАХ С НЕОДНОЗНАЧНОСТЬЮ
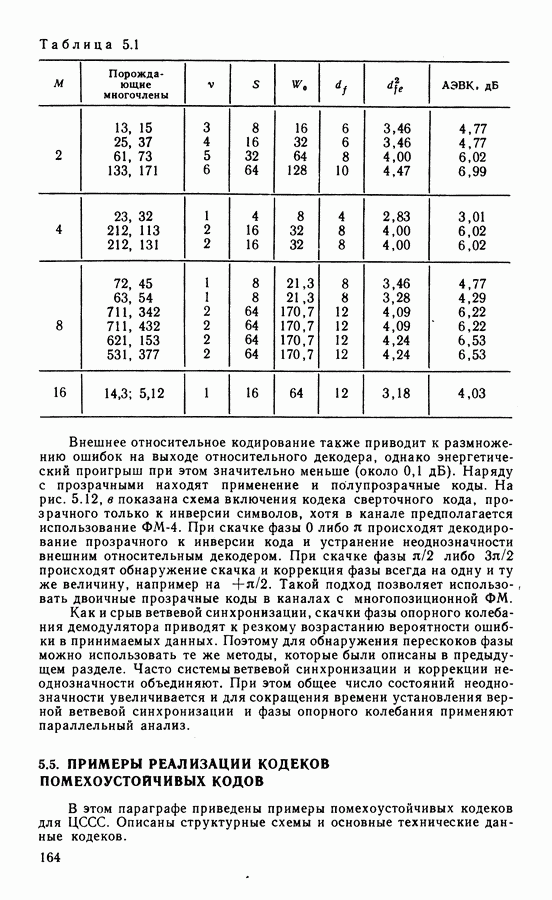
- 5.5. ПРИМЕРЫ РЕАЛИЗАЦИИ КОДЕКОВ ПОМЕХОУСТОЙЧИВЫХ КОДОВ
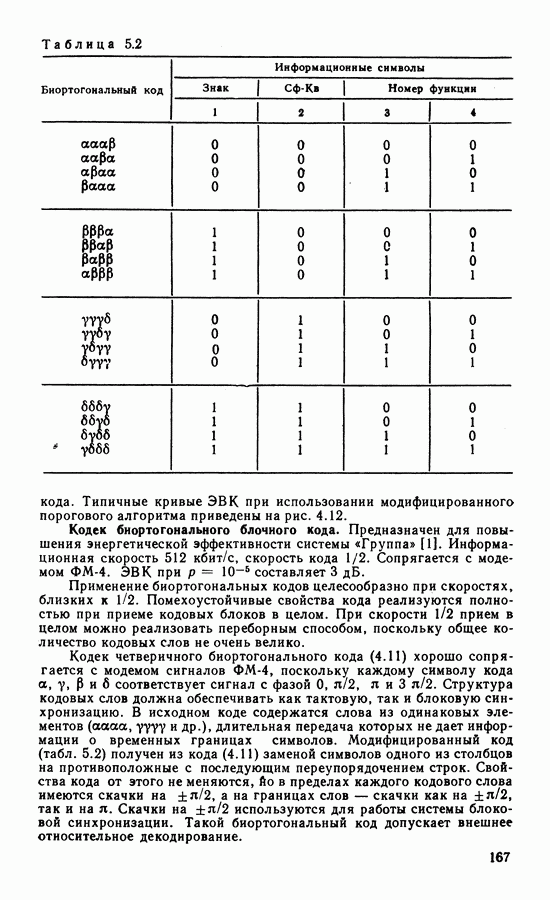
- Кодек биортогонального блочного кода.
- 5.6. РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
- РАЗДЕЛ IV. ЦИФРОВЫЕ СИСТЕМЫ СПУТНИКОВОЙ СВЯЗИ
- ГЛАВА 6. ВЗАИМНЫЕ ПОМЕХИ В ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМАХ
- 6.2. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ГАРМОНИЧЕСКИХ ПОМЕХ НА ДЕМОДУЛЯТОР ФМ СИГНАЛОВ
- 6.3. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ФМ ПОМЕХ
- 6.4. АНАЛИЗ МЕШАЮЩЕГО ДЕЙСТВИЯ ЧМ—ТВ СИГНАЛА С ДИСПЕРСИЕЙ
- 6.5. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ СИГНАЛОВ ЧУ-ЧМ
- ГЛАВА 7. СИСТЕМЫ С МДВР И МДЧР
- 7.1. ОЦЕНКА ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ РАЗЛИЧНЫХ МЕТОДОВ ПЕРЕДАЧИ В ЦССС С МДЧР
- 7.2. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДЧР
- 7.3. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДВР
- Синхронизация систем МДВР.
- Организация кадра систем МДВР.
- Система МДВУ-40.
- ЦСС с ДВР ТДМА-120-(«Интелсат»/«Евросат»).
- МДВР с коммутацией сигналов на спутнике (КСС).
- Сопряжение систем МДВР с цифровыми наземными линиями.
- ГЛАВА 8. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ И КОДИРОВАНИЯ В ЦССС
- 8.2. СОГЛАСОВАНИЕ СИСТЕМ МОДУЛЯЦИИ И КОДИРОВАНИЯ
- Согласование кодом Грея.
- Кодирование с разбиением ансамбля на подклассы.
- Применение недвоичных кодов.
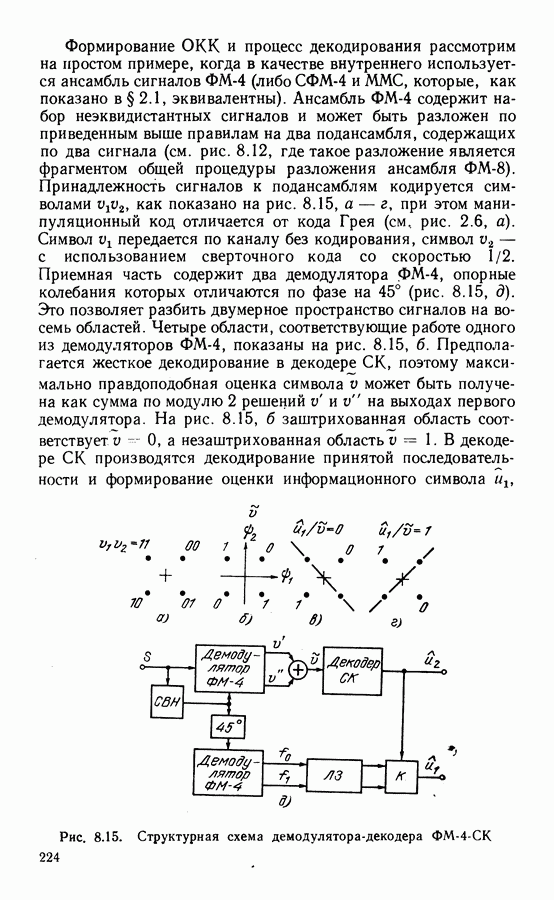
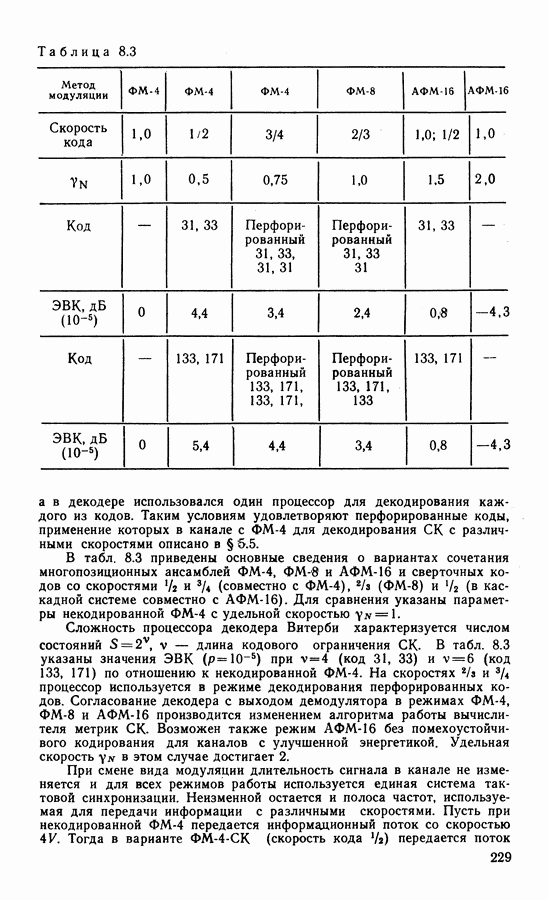
- 8.3. СВЕРТОЧНОЕ КОДИРОВАНИЕ В КАНАЛЕ С МНОГОПОЗИЦИОННОИ ФМ
- 8.4. ОБОБЩЕННОЕ КАСКАДНОЕ КОДИРОВАНИЕ
- 8.5. ПРИМЕРЫ РЕАЛИЗАЦИИ ЭФФЕКТИВНЫХ КОДЕМОВ
- СПИСОК ЛИТЕРАТУРЫ