| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.2. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ГАРМОНИЧЕСКИХ ПОМЕХ НА ДЕМОДУЛЯТОР ФМ СИГНАЛОВ
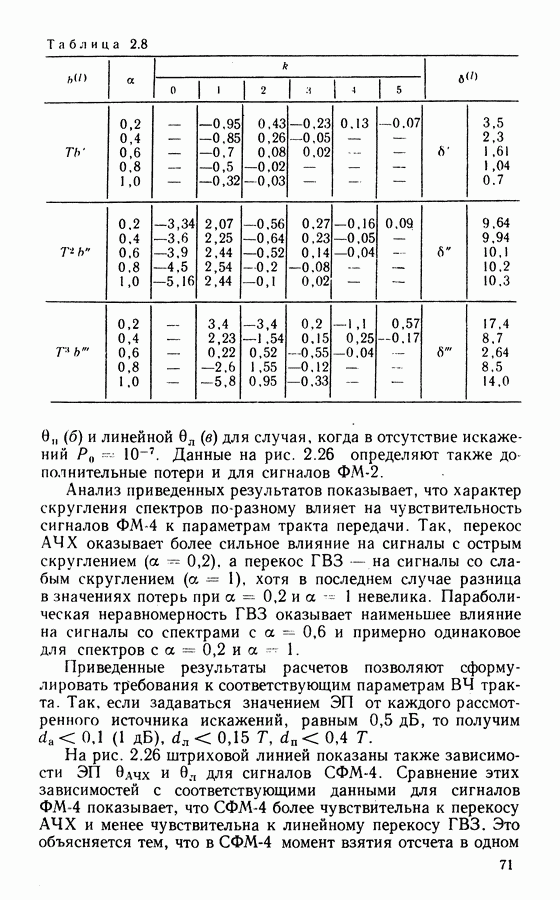
Рассмотрим сначала помехоустойчивость демодуляторов сигналов ФМ-2 при действии на входе шума и гармонической помехи. Переход к ФМ произвольной кратности будет рассмотрен далее. Гармонической помехой можно считать также мешающий ФМ или ЧМ сигнал со спектром более узким, чем спектр полезного ФМ сигнала.
Если на входе демодулятора действует ФМ сигнал  , шум
, шум  и гармоническая помеха
и гармоническая помеха  частота и случайная фаза помехи), то напряжение на выходе когерентного
частота и случайная фаза помехи), то напряжение на выходе когерентного  можно представить в виде
можно представить в виде

где случайная фаза  равномерно распределена в интервале
равномерно распределена в интервале  Откуда вероятность ошибки на выходе демодулятора
Откуда вероятность ошибки на выходе демодулятора

Здесь  дисперсия шума,
дисперсия шума,  а усреднение ведется по случайной фазе
а усреднение ведется по случайной фазе 
Аналогично, если на входе демодулятора действует несколько гармонических помех со случайными фазами, то

Здесь усреднение проводится по всем случайным фазам 
Расчеты по формулам (6.2), (6.3) выполнены в [101]. Соответствующие зависимости  можно найти в работе [100].
можно найти в работе [100].
Дадим аналитическую оценку  методом Чернова, поскольку в формулах (6.2) и (6.3) необходимо численное интегрирование. Согласно данному методу вероятность ошибки при действии одной гармонической помехи (6.1) оценивается сверху
методом Чернова, поскольку в формулах (6.2) и (6.3) необходимо численное интегрирование. Согласно данному методу вероятность ошибки при действии одной гармонической помехи (6.1) оценивается сверху  как
как

где параметр выбирают по минимуму правой части (6.4). Проведя в (6.4) усреднение по случайной фазе  и по нормальному шуму
и по нормальному шуму  получаем
получаем

Параметр X необходимо выбрать таким образом, чтобы правая часть (6.5) была минимальна. Дифференцируя (6.5) по X и приравнивая результат к нулю, для оптимального значения X получаем следующее трансцендентное уравнение:

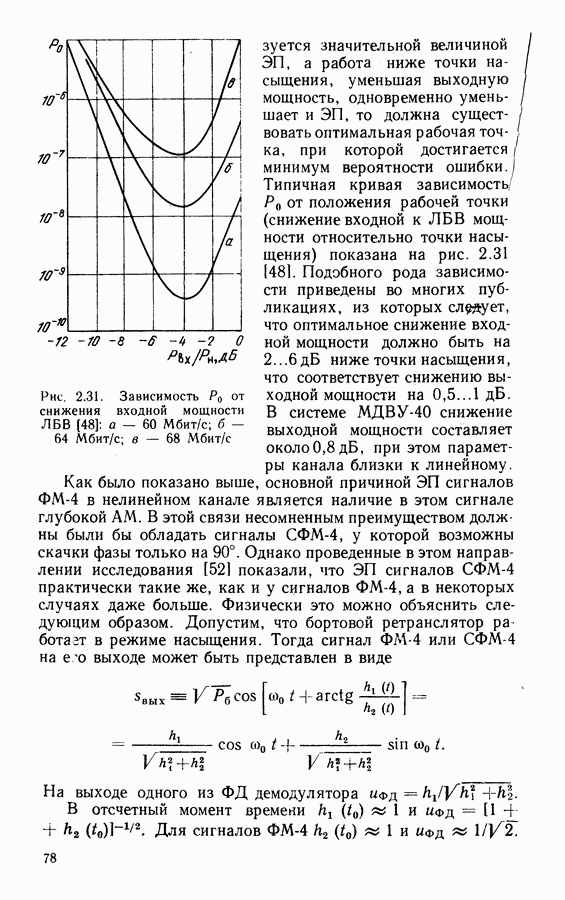
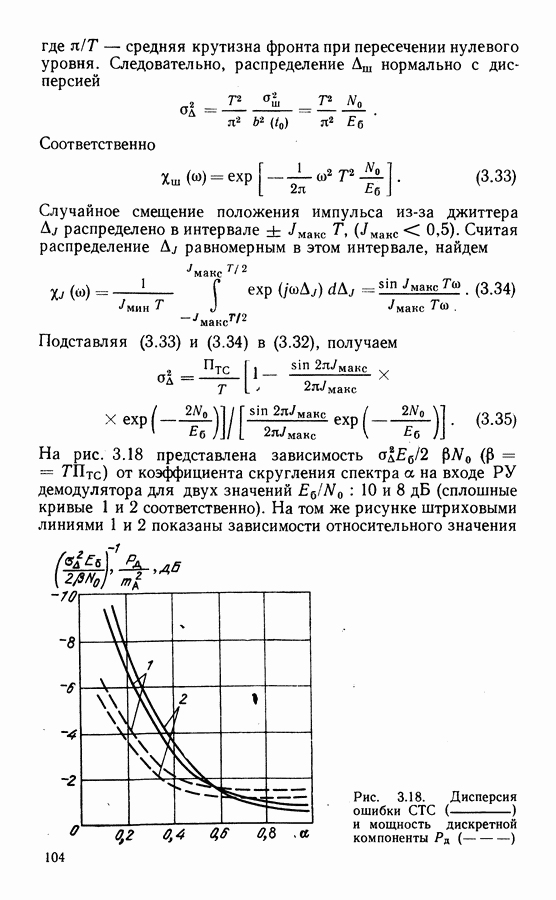
На рис. 6.1 представлены расчеты по формулам (6.5) и (6.6), а также приведены точные зависимости, полученные численным интегрированием по (6.2). На рис. 6.2 дана погрешность оценки в зависимости от вероятности ошибки. Кроме того, что используемое приближение вполне приемлемо, отметим также, что в большом диапазоне  эта погрешность практически постоянная. Поэтому оценку в виде
эта погрешность практически постоянная. Поэтому оценку в виде  хорошо аппроксимирует зависимость вероятности ошибки.
хорошо аппроксимирует зависимость вероятности ошибки.

Рис. 6.1. Зависимость  при одной гармонической помехе:
при одной гармонической помехе:  точная
точная  оценка сверху
оценка сверху

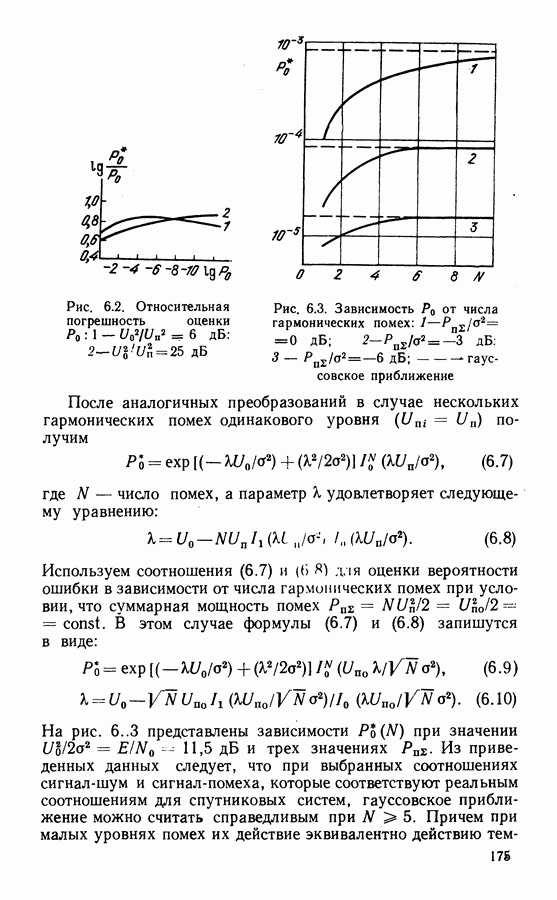
Рис. 6.2. Относительная погрешность оценки 

Рис. 6.3. Зависимость  от числа гармонических помех:
от числа гармонических помех:  гауссовское приближение
гауссовское приближение
После аналогичных преобразований в случае нескольких гармонических помех одинакового уровня  получим
получим

где  число помех, а параметр
число помех, а параметр  удовлетворяет следующему уравнению:
удовлетворяет следующему уравнению:

Используем соотношения (6.7) и (6 Я) для оценки вероятности ошибки в зависимости от числа гармонических помех при условии, что суммарная мощность помех  . В этом случае формулы (6.7) и (6.8) запишутся в виде:
. В этом случае формулы (6.7) и (6.8) запишутся в виде:

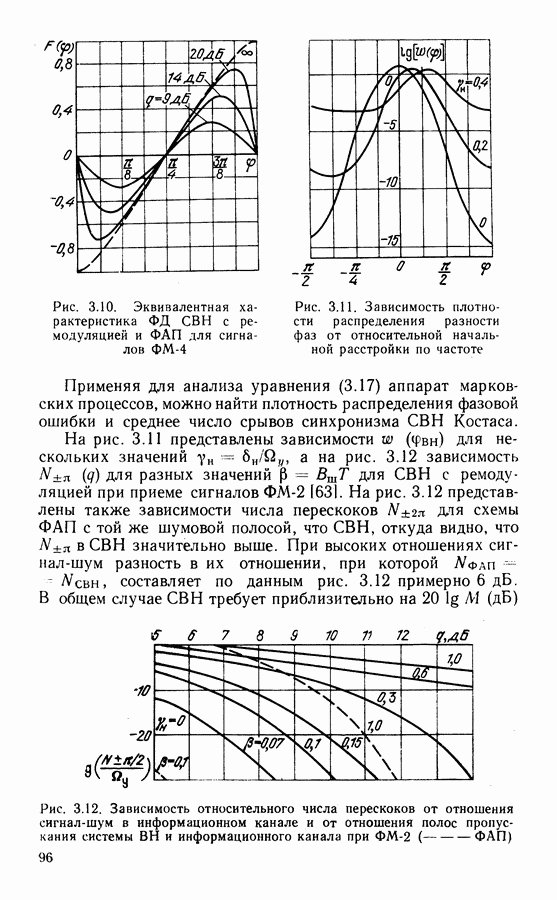
На рис. 6.3 представлены зависимости  при значении
при значении  и трех значениях
и трех значениях  Из приведенных данных следует, что при выбранных соотношениях сигнал-шум и сигнал-помеха, которые соответствуют реальным соотношениям для спутниковых систем, гауссовское приближение можно считать справедливым при
Из приведенных данных следует, что при выбранных соотношениях сигнал-шум и сигнал-помеха, которые соответствуют реальным соотношениям для спутниковых систем, гауссовское приближение можно считать справедливым при  Причем при малых уровнях помех их действие эквивалентно действию
Причем при малых уровнях помех их действие эквивалентно действию
темлового шума при меньшем числе помех. Отметим, что приведенные значения оценки  при выбранных параметрах
при выбранных параметрах  примерно в 5 раз больше
примерно в 5 раз больше  а характер же зависимостей сохраняется.
а характер же зависимостей сохраняется.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ I. ОСНОВЫ ПОСТРОЕНИЯ ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМ СВЯЗИ
- ГЛАВА 1. СПУТНИКОВЫЕ СИСТЕМЫ С МНОГОСТАНЦИОННЫМ ДОСТУПОМ
- 1.2. ПРЕОБРАЗОВАНИЕ АНАЛОГОВЫХ СИГНАЛОВ В ЦИФРОВУЮ ФОРМУ
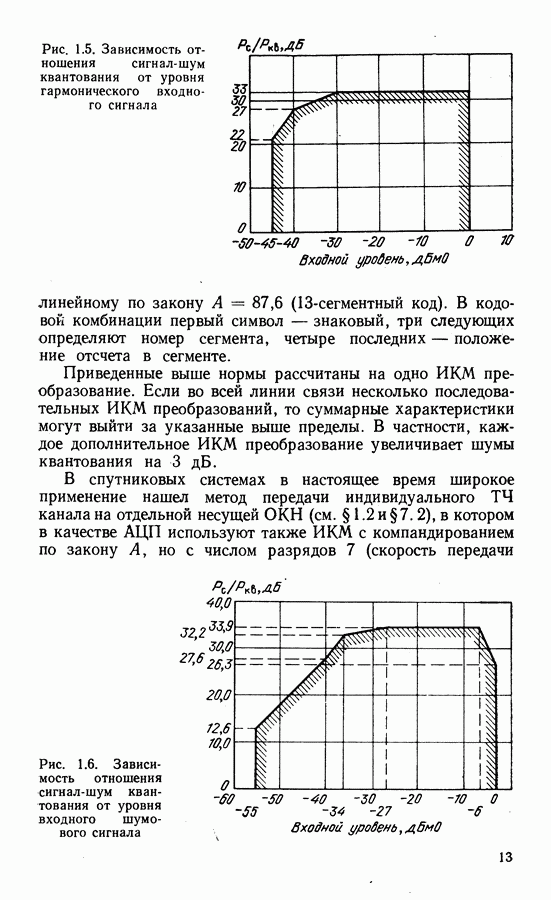
- Адаптивная ИКМ.
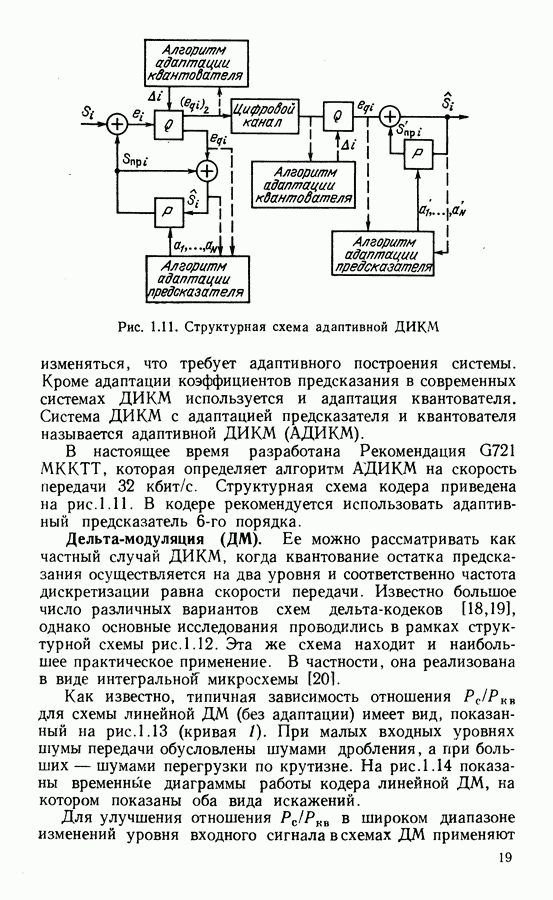
- Дифференциальная ИКМ (ДИКМ).
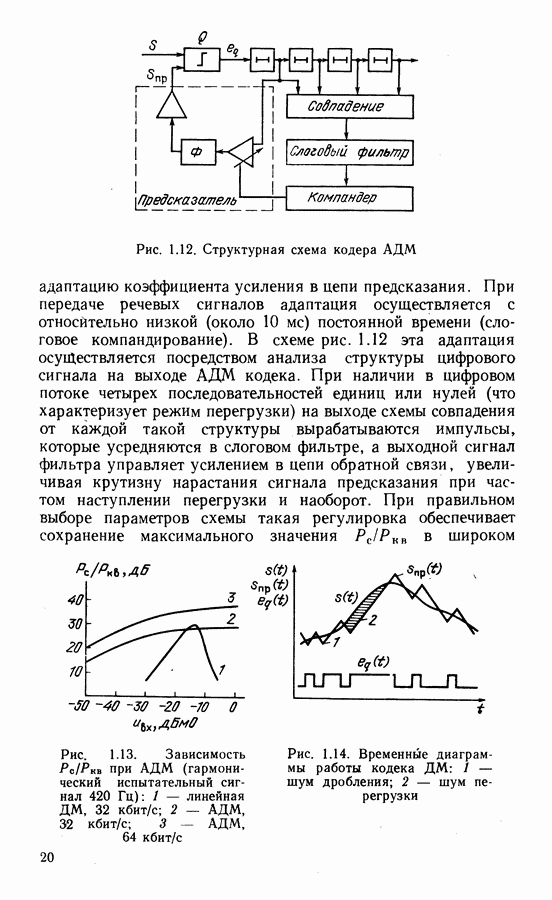
- Дельта-модуляция (ДМ).
- Преобразование сигналов телевидения, многоканальной телефонии и вещания в цифровую форму.
- 1.3. СТАТИСТИЧЕСКОЕ УПЛОТНЕНИЕ В ЦССС
- 1.4. МНОГОСТАНЦИОННЫЙ ДОСТУП В ЦССС
- Многостанционный доступ с временным разделением каналов (МДВР).
- Многостанционный доступ с разделением сигналов по форме (МДФР).
- Многостанционный доступ со случайным доступом (МДСД).
- 1.5. НОРМИРОВАНИЕ ПАРАМЕТРОВ ЦССС
- РАЗДЕЛ II. МОДУЛЯЦИЯ
- ГЛАВА 2. МЕТОДЫ МОДУЛЯЦИИ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.2. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СИГНАЛОВ
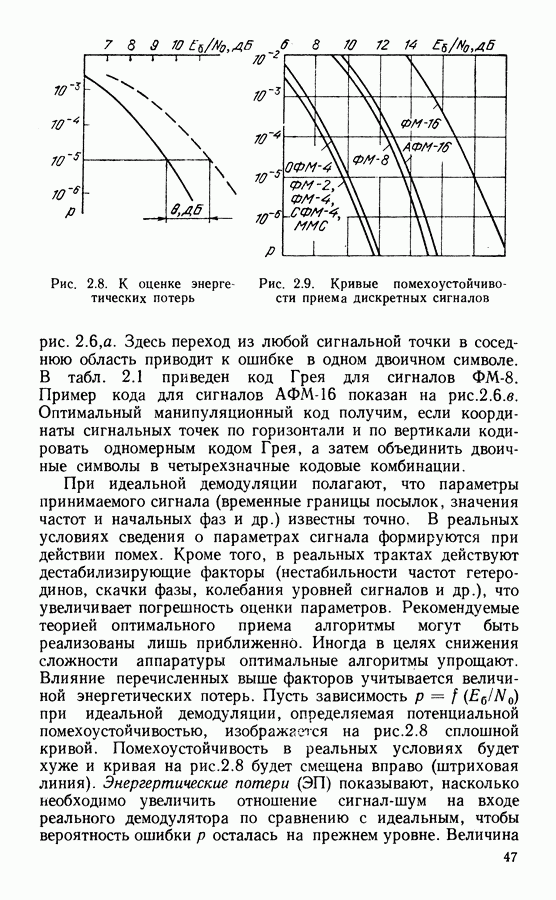
- 2.3. СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИГНАЛОВ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
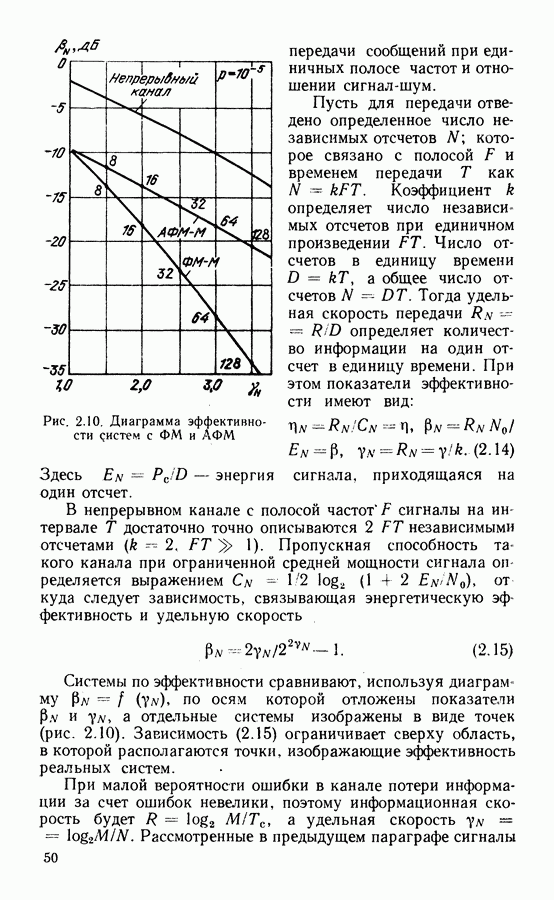
- 2.4. СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ
- 2.5. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДЧР
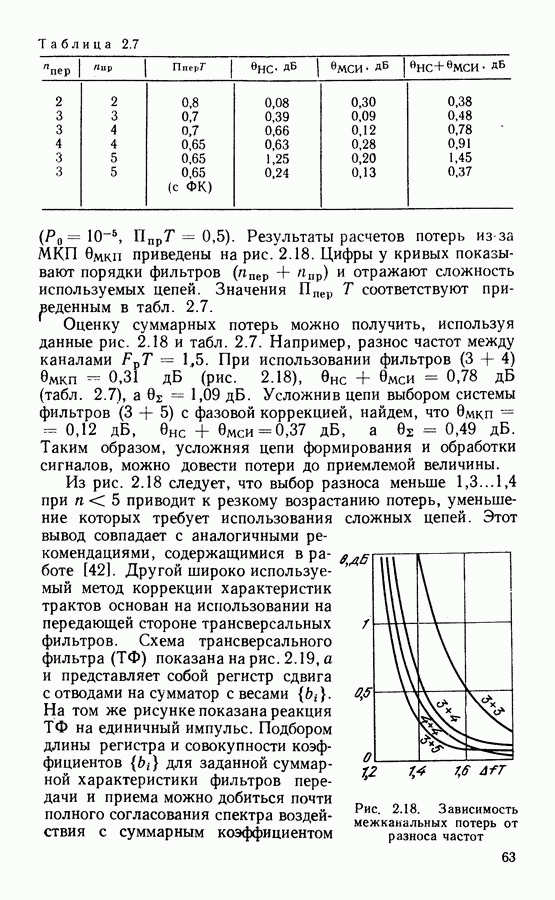
- Результаты расчетов потерь в системе с ФМ-2 и стандартными фильтрами.
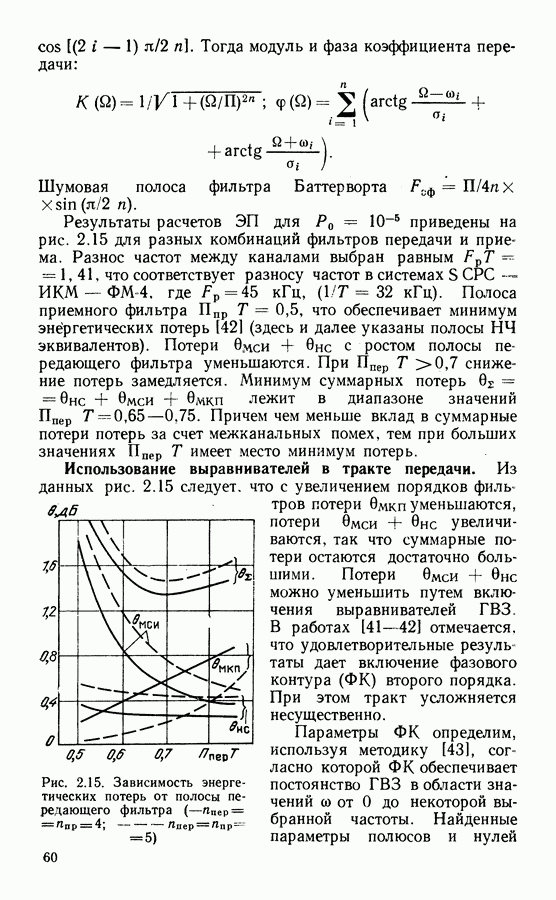
- Использование выравнивателей в тракте передачи.
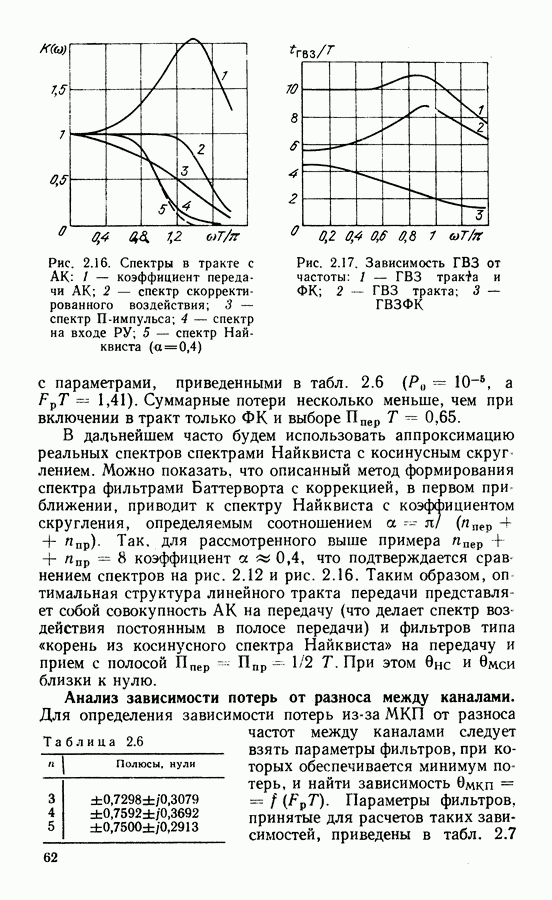
- Анализ зависимости потерь от разноса между каналами.
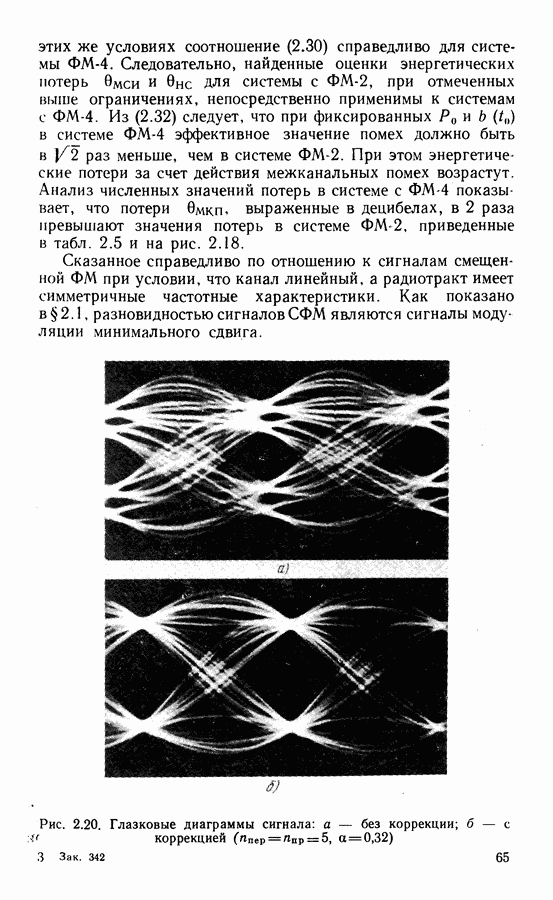
- Энергетические потери в системе с ФМ-4.
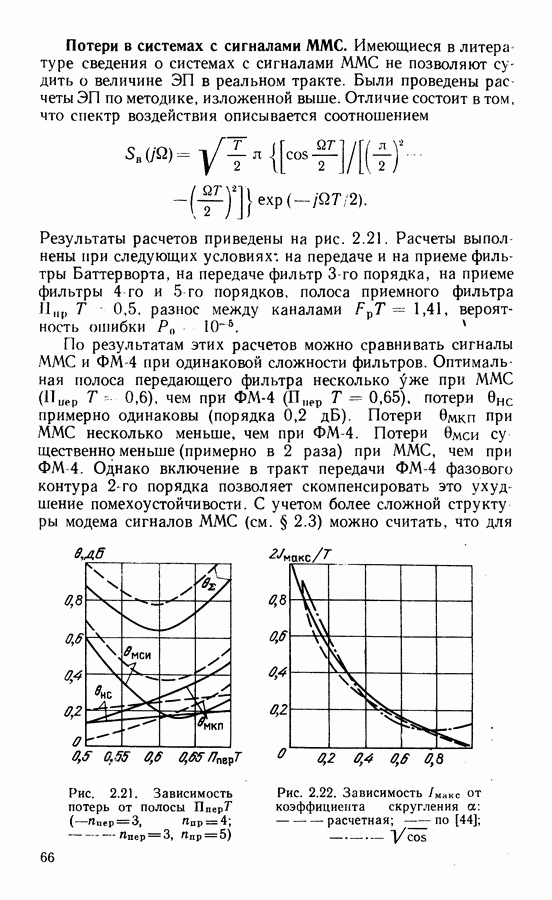
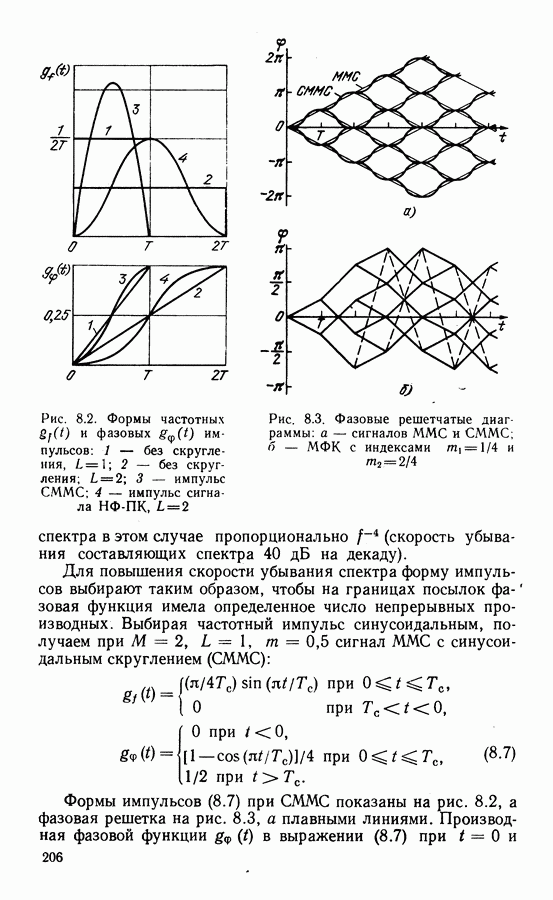
- Потери в системах с сигналами ММС.
- 2.6. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДВР
- ГЛАВА 3. МОДЕМЫ
- 3.1. СТРУКТУРА МОДЕМА
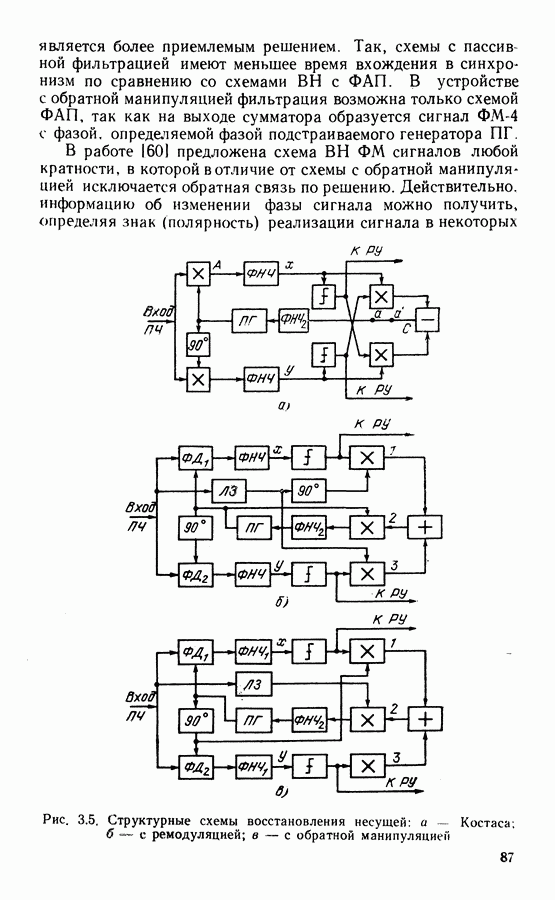
- 3.2. СИСТЕМЫ ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ
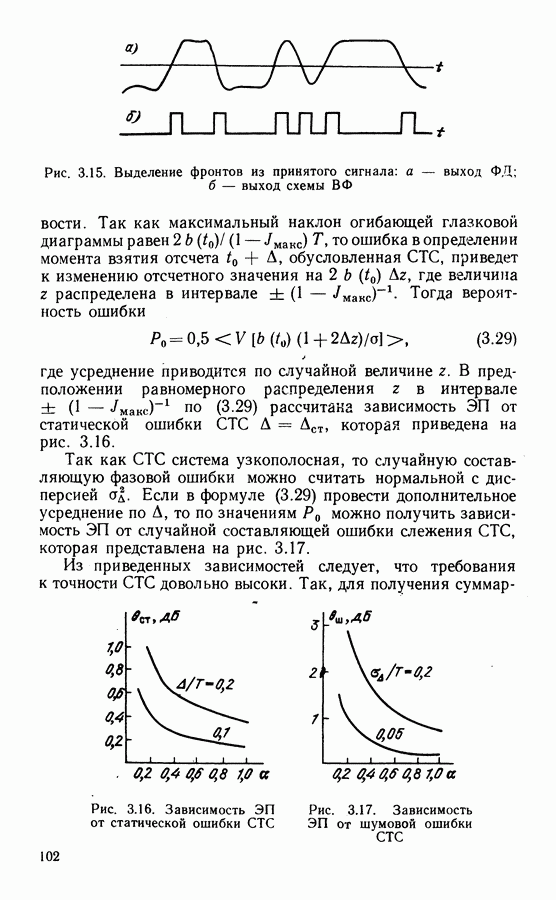
- Требования к точности работы системы ВН.
- Анализ точности систем ВН.
- Переходные процессы.
- 3.3. ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 3.4. ОТНОСИТЕЛЬНОЕ КОДИРОВАНИЕ
- 3.5. ПРИМЕРЫ РЕАЛИЗАЦИИ МОДЕМОВ В ЦССС
- РАЗДЕЛ III. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
- 4.2. АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ КОДОВ
- 4.3. БЛОКОВЫЕ КОДЫ И АЛГОРИТМЫ ИХ ДЕКОДИРОВАНИЯ
- 4.4. СТРУКТУРА И ХАРАКТЕРИСТИКИ СВЕРТОЧНЫХ КОДОВ
- 4.5. АЛГОРИТМЫ ДЕКОДИРОВАНИЯ СК
- 4.6. ПОМЕХОУСТОЙЧИВОСТЬ И ЭФФЕКТИВНОСТЬ СИСТЕМ С КОДИРОВАНИЕМ
- ГЛАВА 5. КОДЕКИ
- 5.1. СОГЛАСОВАНИЕ МОДЕМА И КОДЕКА
- 5.2. ДЕКОДЕРЫ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ СК
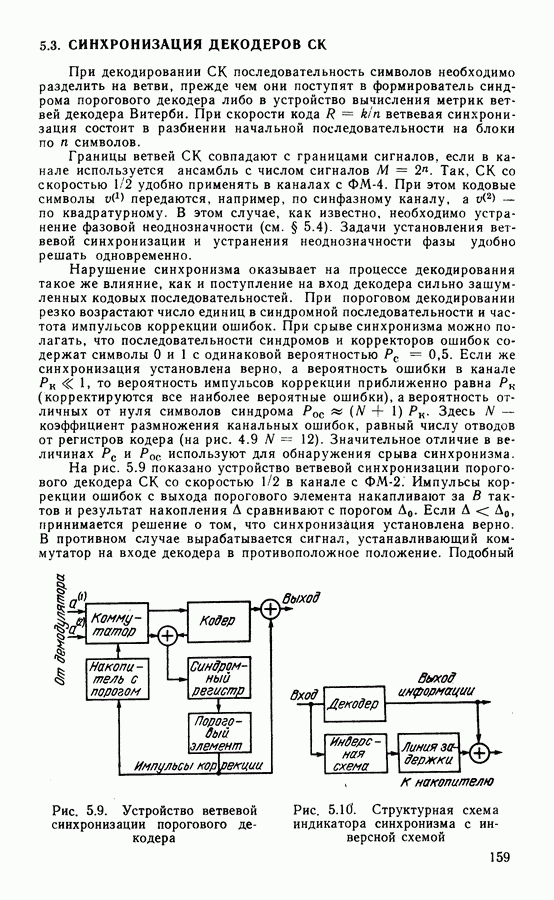
- 5.3. СИНХРОНИЗАЦИЯ ДЕКОДЕРОВ СК
- 5.4. КОДИРОВАНИЕ В КАНАЛАХ С НЕОДНОЗНАЧНОСТЬЮ
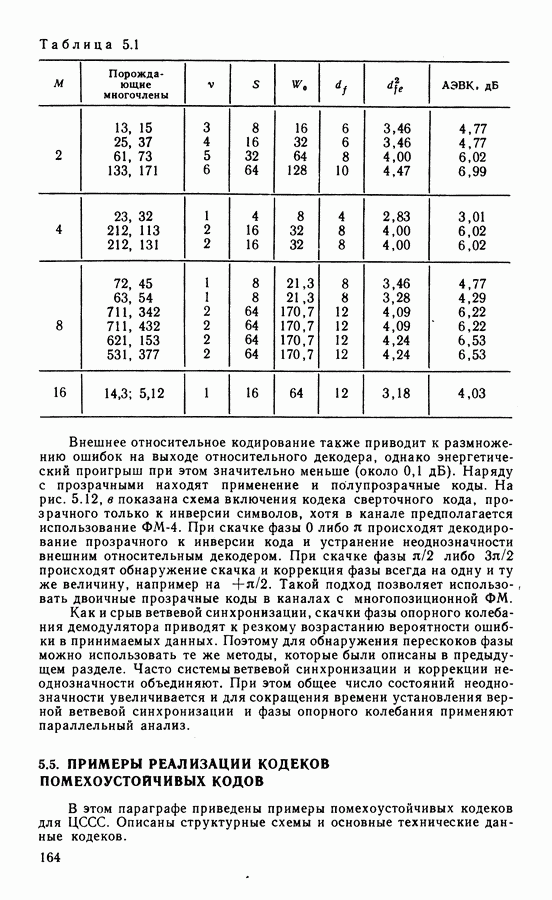
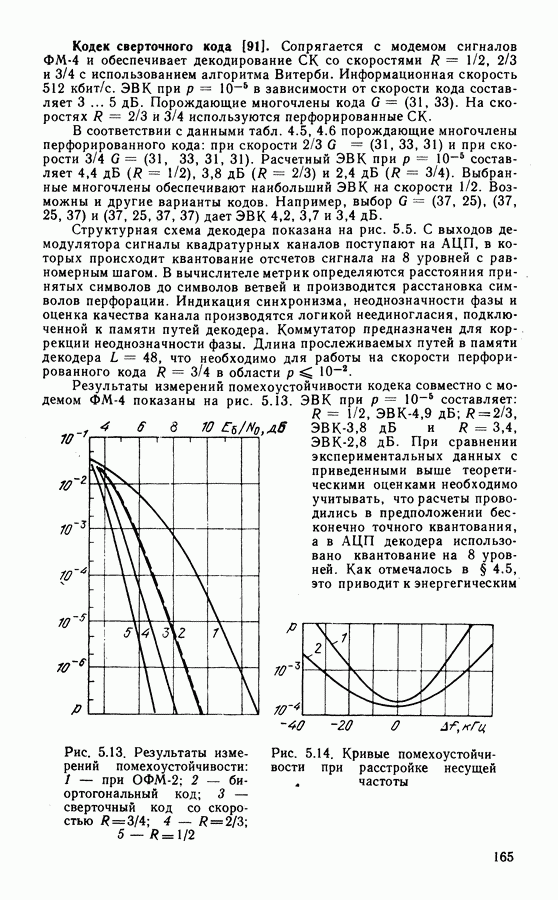
- 5.5. ПРИМЕРЫ РЕАЛИЗАЦИИ КОДЕКОВ ПОМЕХОУСТОЙЧИВЫХ КОДОВ
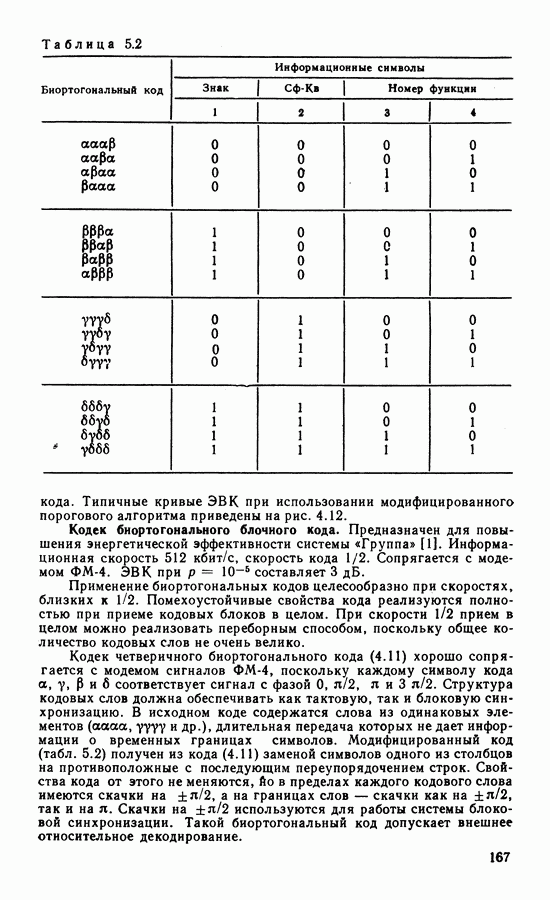
- Кодек биортогонального блочного кода.
- 5.6. РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
- РАЗДЕЛ IV. ЦИФРОВЫЕ СИСТЕМЫ СПУТНИКОВОЙ СВЯЗИ
- ГЛАВА 6. ВЗАИМНЫЕ ПОМЕХИ В ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМАХ
- 6.2. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ГАРМОНИЧЕСКИХ ПОМЕХ НА ДЕМОДУЛЯТОР ФМ СИГНАЛОВ
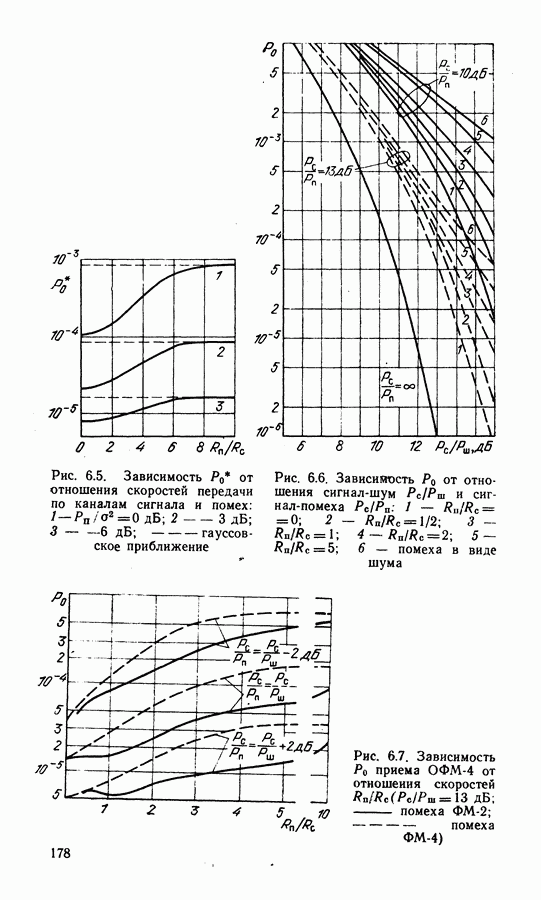
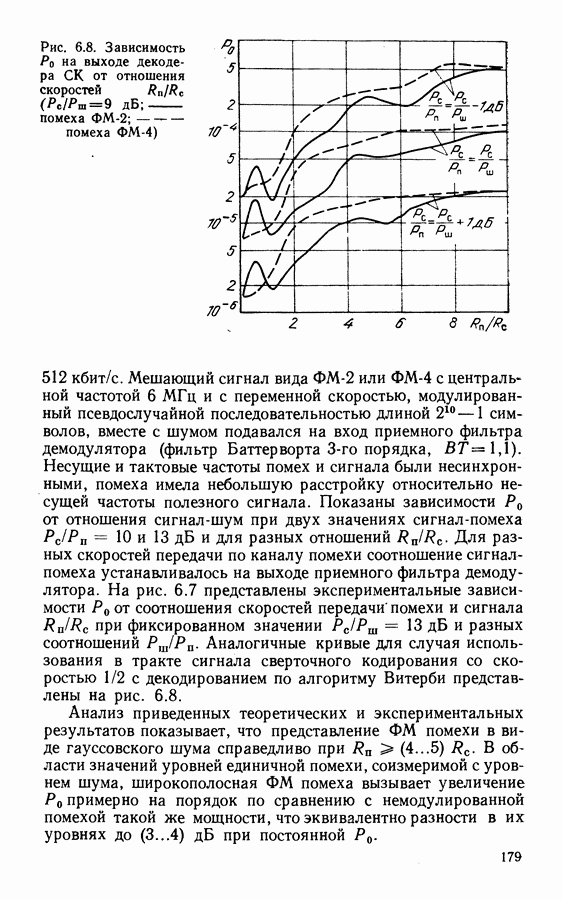
- 6.3. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ФМ ПОМЕХ
- 6.4. АНАЛИЗ МЕШАЮЩЕГО ДЕЙСТВИЯ ЧМ—ТВ СИГНАЛА С ДИСПЕРСИЕЙ
- 6.5. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ СИГНАЛОВ ЧУ-ЧМ
- ГЛАВА 7. СИСТЕМЫ С МДВР И МДЧР
- 7.1. ОЦЕНКА ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ РАЗЛИЧНЫХ МЕТОДОВ ПЕРЕДАЧИ В ЦССС С МДЧР
- 7.2. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДЧР
- 7.3. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДВР
- Синхронизация систем МДВР.
- Организация кадра систем МДВР.
- Система МДВУ-40.
- ЦСС с ДВР ТДМА-120-(«Интелсат»/«Евросат»).
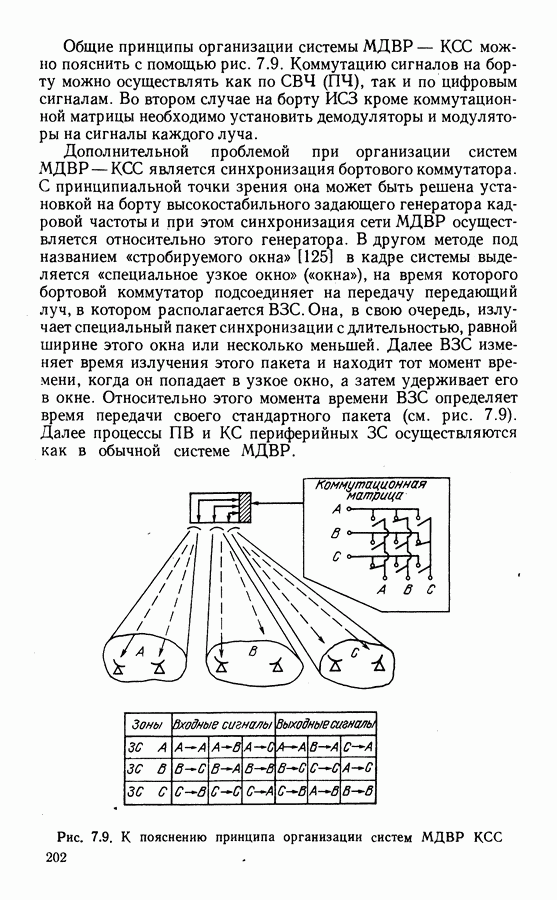
- МДВР с коммутацией сигналов на спутнике (КСС).
- Сопряжение систем МДВР с цифровыми наземными линиями.
- ГЛАВА 8. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ И КОДИРОВАНИЯ В ЦССС
- 8.2. СОГЛАСОВАНИЕ СИСТЕМ МОДУЛЯЦИИ И КОДИРОВАНИЯ
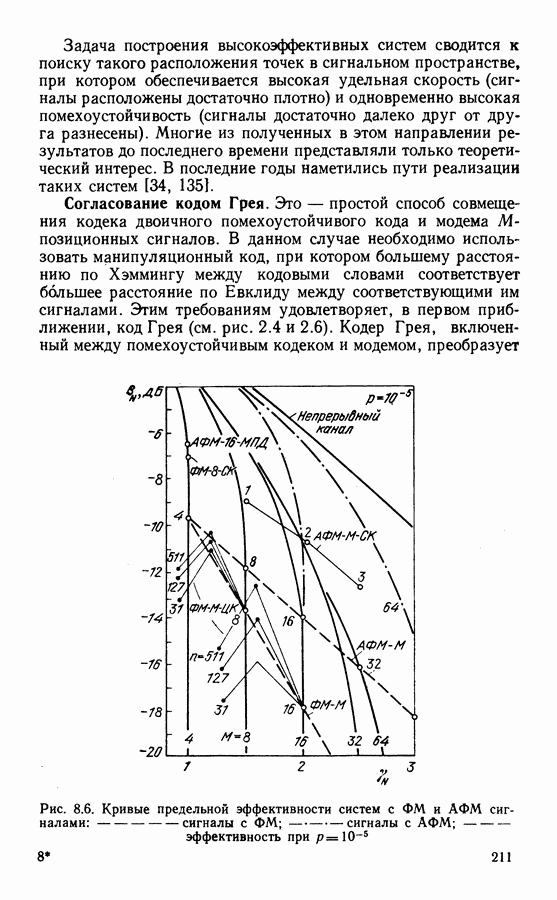
- Согласование кодом Грея.
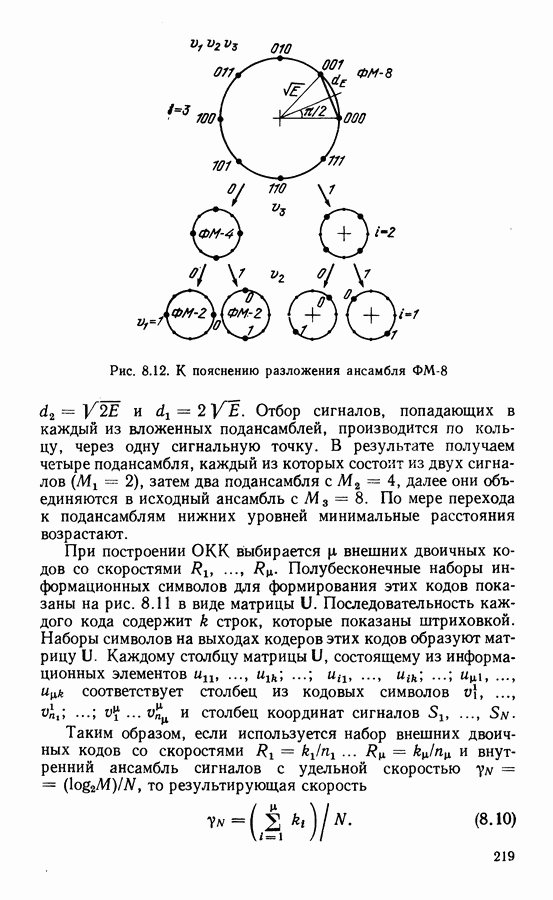
- Кодирование с разбиением ансамбля на подклассы.
- Применение недвоичных кодов.
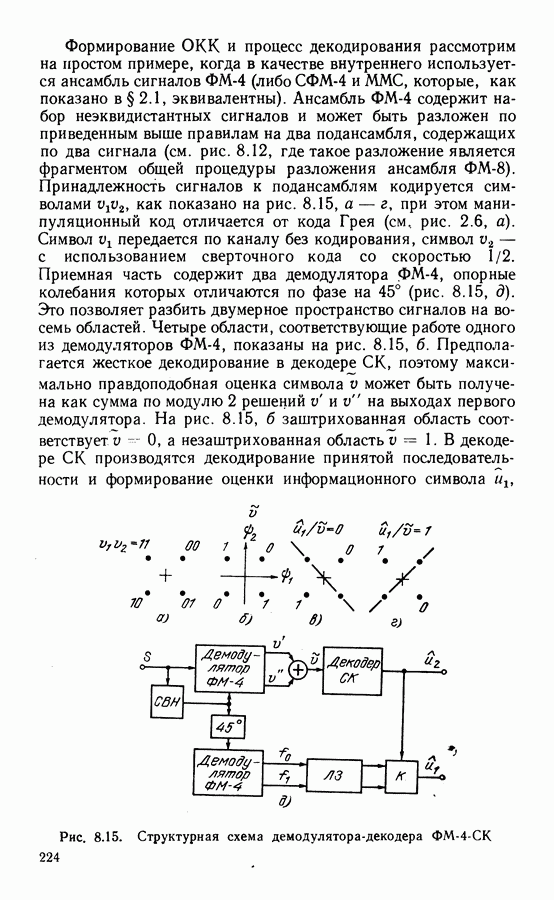
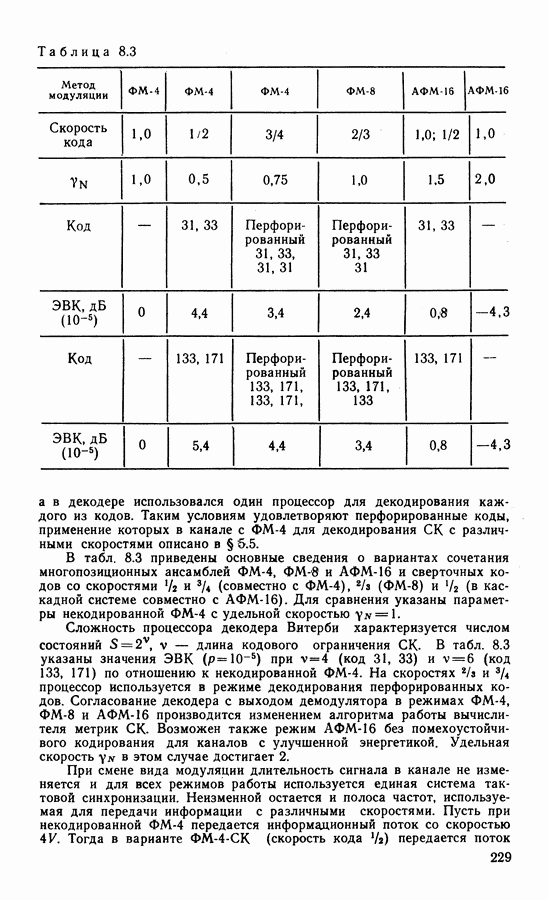
- 8.3. СВЕРТОЧНОЕ КОДИРОВАНИЕ В КАНАЛЕ С МНОГОПОЗИЦИОННОИ ФМ
- 8.4. ОБОБЩЕННОЕ КАСКАДНОЕ КОДИРОВАНИЕ
- 8.5. ПРИМЕРЫ РЕАЛИЗАЦИИ ЭФФЕКТИВНЫХ КОДЕМОВ
- СПИСОК ЛИТЕРАТУРЫ