| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.2.5. Модели каналов связи и их математическое описание
Точное математическое описание любого реального канала связи обычно весьма сложное. Вместо этого используют упрощенные математические модели, которые позволяют выявить важнейшие закономерности реального канала.
Рассмотрим наиболее простые и широко используемые связи модели каналов.
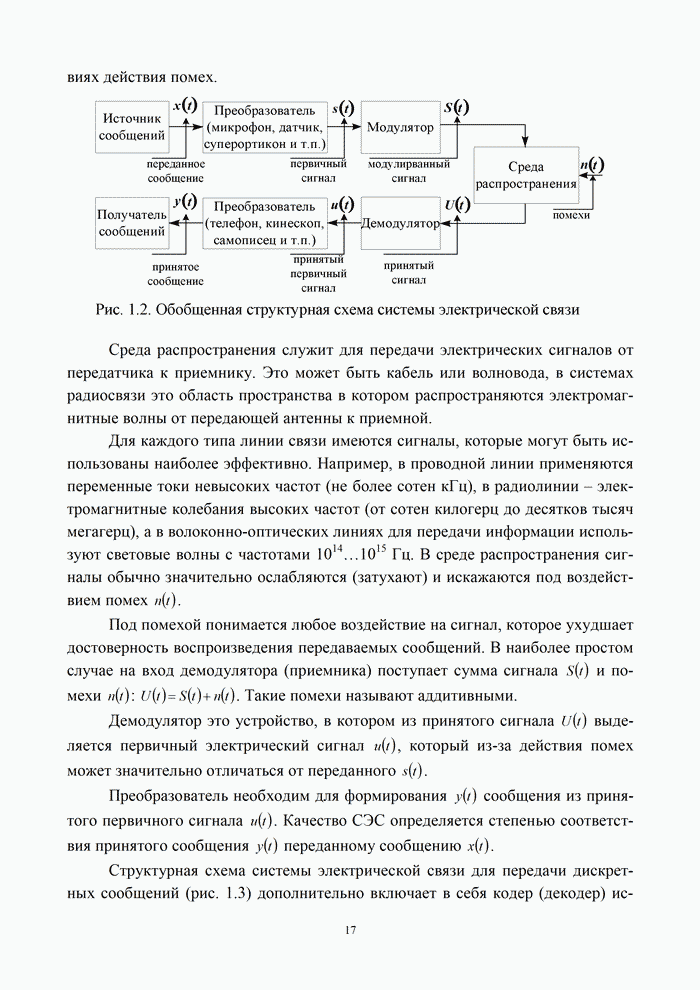
Непрерывные каналы. Идеальный канал без
помех вносит искажения, связанные с изменением амплитуды и
временного положения сигнала и представляет собой линейную цепь с
постоянной передаточной функцией, обычно сосредоточенной в ограниченной полосе
частот. Допустимы любые входные сигналы, спектр которых лежит в определенной
полосе частот ![]() ,
имеющие ограниченную среднюю мощность
,
имеющие ограниченную среднюю мощность ![]() [6, 32]. Эта
модель используется для описания каналов малой протяженности с закрытым
распространением сигналов (кабель, провод, волновод, световод
и т. д.).
[6, 32]. Эта
модель используется для описания каналов малой протяженности с закрытым
распространением сигналов (кабель, провод, волновод, световод
и т. д.).
Канал с гауссовским белым шумом представляет
собой идеальный канал, в котором на сигнал ![]() накладывается помеха:
накладывается помеха:
|
|
(1.4) |
Коэффициент передачи ![]() и запаздывание
и запаздывание ![]() считаются постоянными
и известными в точке приема;
считаются постоянными
и известными в точке приема; ![]() – аддитивная помеха. Такая модель,
например, соответствует радиоканалам, с приемо-передающими
антеннами работающими и находящимися в пределах прямой видимости.
– аддитивная помеха. Такая модель,
например, соответствует радиоканалам, с приемо-передающими
антеннами работающими и находящимися в пределах прямой видимости.
Гауссовский канал с неопределенной фазой сигнала
Эта модель отличается от предыдущей модели
тем, что в ней запаздывание является случайной величиной. Для узкополосных
сигналов выражение (1.4) при постоянном ![]() и случайных
и случайных ![]() можно представить в виде [6, 32]:
можно представить в виде [6, 32]:
|
|
(1.5) |
где ![]() – преобразование
Гильберта от сигнала
– преобразование
Гильберта от сигнала ![]() ;
;
![]() – случайная фаза.
– случайная фаза.
Распределение вероятностей ![]() предполагается
заданным, чаще всего равномерным на интервале от
предполагается
заданным, чаще всего равномерным на интервале от ![]() до
до ![]() . Эта модель удовлетворительно описывает
те же каналы, что и предыдущая, если фаза сигнала в них флуктуирует. Флуктуации
фазы обычно вызываются небольшими изменениями протяженности канала, свойств
среды, в которой проходит сигнал, а также фазовой нестабильностью опорных
генераторов.
. Эта модель удовлетворительно описывает
те же каналы, что и предыдущая, если фаза сигнала в них флуктуирует. Флуктуации
фазы обычно вызываются небольшими изменениями протяженности канала, свойств
среды, в которой проходит сигнал, а также фазовой нестабильностью опорных
генераторов.
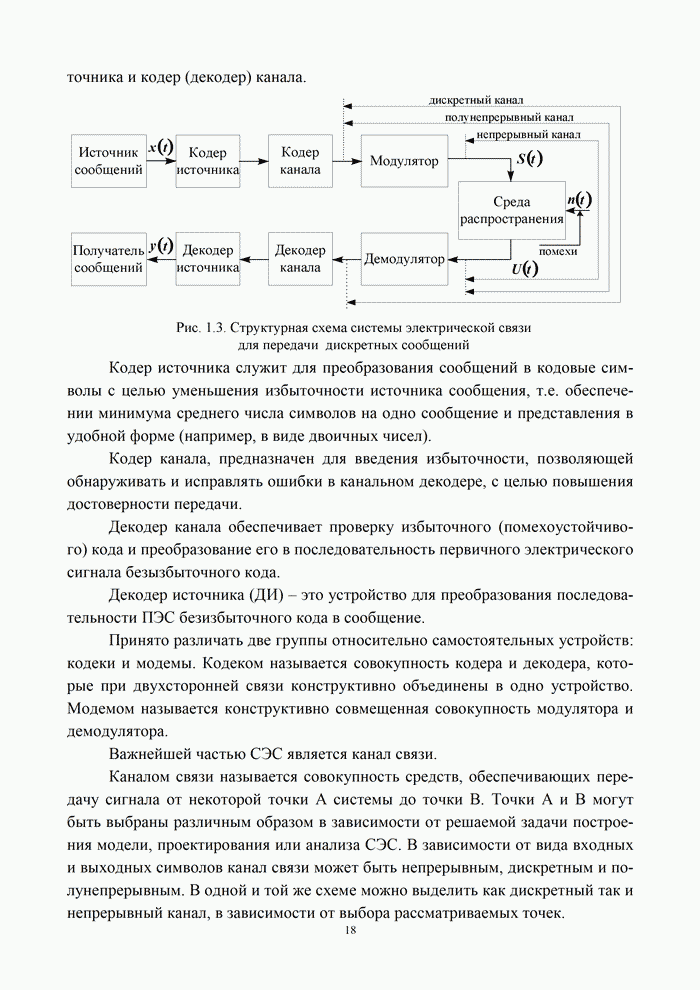
Дискретно-непрерывные каналы. Дискретно-непрерывный
канал имеет дискретный вход и непрерывный выход. Примером такого канала
является канал, образованный совокупностью технических средств между выходом
кодера канала и входом демодулятора (см. рис. 1.3). Для его описания необходимо
знать алфавит входных символов ![]() ,
, ![]() , вероятности
появления символов алфавита
, вероятности
появления символов алфавита ![]() , полосу
пропускания непрерывного
канала
, полосу
пропускания непрерывного
канала ![]() , входящего
в рассматриваемый канал и плотности распределения вероятностей (ПРВ)
, входящего
в рассматриваемый канал и плотности распределения вероятностей (ПРВ) ![]() появления сигнала
появления сигнала ![]() на выходе канала при условии, что передавался символ
на выходе канала при условии, что передавался символ ![]() .
.
Зная вероятности ![]() и ПРВ
и ПРВ ![]() по формуле Байеса можно найти апостериорные вероятности передачи символа
по формуле Байеса можно найти апостериорные вероятности передачи символа
![]() :
:
|
|
|
Решение
о переданном символе ![]() обычно
принимается из условия максимума
обычно
принимается из условия максимума ![]() .
.
Дискретные каналы. Примером
дискретного канала без памяти может служить m-ичный канал. Канал передачи
полностью описывается если заданы [20, 21] алфавит
источника ![]() ,
,
![]() , вероятности
появления символов алфавита
, вероятности
появления символов алфавита ![]() , скорость передачи символов
, скорость передачи символов ![]() , алфавит
получателя
, алфавит
получателя ![]() ,
,
![]() и значения переходных
вероятностей
и значения переходных
вероятностей ![]() появления символа
появления символа ![]() при
условии передачи символа
при
условии передачи символа ![]() .
.
Первые две характеристики определяются
свойствами источника сообщений, скорость ![]() – полосой пропускания непрерывного
канала, входящего в состав дискретного. Объем алфавита выходных символов зависит
от алгоритма работы решающей схемы; переходные вероятности
– полосой пропускания непрерывного
канала, входящего в состав дискретного. Объем алфавита выходных символов зависит
от алгоритма работы решающей схемы; переходные вероятности ![]() находятся на основе анализа
характеристик непрерывного канала.
находятся на основе анализа
характеристик непрерывного канала.
Стационарным называется дискретный канал, в
котором переходные вероятности ![]() не
зависят от времени.
не
зависят от времени.
Дискретный канал называется каналом без памяти, если переходные вероятности
![]() не
зависят от того, какие символы передавались и принимались ранее.
не
зависят от того, какие символы передавались и принимались ранее.
В качестве примера рассмотрим двоичный канал
(рис. 1.5). В этом случае
рассмотрим двоичный канал
(рис. 1.5). В этом случае ![]() , т.е. на входе канала алфавит источника и
алфавит получателя состоит из двух символов «0» и «1».
, т.е. на входе канала алфавит источника и
алфавит получателя состоит из двух символов «0» и «1».
Стационарный двоичный канал
называется симметричным, если алфавиты на входе и выходе совпадают. Каждый
переданный кодовый символ может быть принят ошибочно с фиксированной
вероятностью ![]() и
правильно с вероятностью
и
правильно с вероятностью ![]() .
.
Необходимо отметить, что в общем случае в
дискретном канале объемы алфавитов входных и выходных символов могут
не совпадать. Примером может быть канал со стиранием (рис.
1.6). Алфавит на его выходе содержит один добавочный символ по
сравнению с алфавитом на входе. Этот добавочный символ
(символ стирания «![]() »)
появляется на выходе канала тогда, когда анализируемый сигнал не
удается отождествить ни с одним из передаваемых символов. Стирание символов
при применении соответствующего помехоустойчивого кода позволяет повысить
помехоустойчивость.
»)
появляется на выходе канала тогда, когда анализируемый сигнал не
удается отождествить ни с одним из передаваемых символов. Стирание символов
при применении соответствующего помехоустойчивого кода позволяет повысить
помехоустойчивость.
 Большинство реальных каналов имеют «память», которая проявляется
в том, что вероятность ошибки в очередном символе зависит от того,
какие символы передавались до него и как они были приняты. Первый факт
обусловлен межсимвольными искажениями, являющимися результатом рассеяния
сигнала в канале, а второй – изменением отношения сигнал-шум в канале
или характера помех.
Большинство реальных каналов имеют «память», которая проявляется
в том, что вероятность ошибки в очередном символе зависит от того,
какие символы передавались до него и как они были приняты. Первый факт
обусловлен межсимвольными искажениями, являющимися результатом рассеяния
сигнала в канале, а второй – изменением отношения сигнал-шум в канале
или характера помех.
В постоянном симметричном канале без памяти
условная вероятность ошибочного приема (![]() )-го, символа если
)-го, символа если ![]() -й символ принят ошибочно, равна
безусловной вероятности ошибки. В канале с памятью она может быть больше или
меньше этой величины.
-й символ принят ошибочно, равна
безусловной вероятности ошибки. В канале с памятью она может быть больше или
меньше этой величины.
Наиболее простой моделью двоичного канала с памятью является марковская модель, которая задается матрицей переходных вероятностей:
|
|
|
где ![]() – условная вероятность
принять (
– условная вероятность
принять (![]() )-й
символ ошибочно, если
)-й
символ ошибочно, если ![]() -й принят правильно;
-й принят правильно; ![]() – условная вероятность принять
(
– условная вероятность принять
(![]() )-й символ
правильно, если
)-й символ
правильно, если ![]() -й
принят правильно;
-й
принят правильно; ![]() –
условная вероятность принять (
–
условная вероятность принять (![]() )-й символ ошибочно, если
)-й символ ошибочно, если ![]() -й принят ошибочно;
-й принят ошибочно; ![]() – условная вероятность
принять (
– условная вероятность
принять (![]() )-й
символ правильно, если
)-й
символ правильно, если ![]() -й принят ошибочно.
-й принят ошибочно.
Безусловная (средняя) вероятность ошибки в рассматриваемом канале должна удовлетворять уравнению:
![]() или
или
![]() .
.
Данная модель имеет достоинство – простоту
использования, не всегда адекватно воспроизводит свойства реальных каналов. Большую
точность позволяет получить модель Гильберта для дискретного канала с памятью. В
такой модели канал может находиться в двух состояниях ![]() и
и ![]() . В состоянии
. В состоянии ![]() ошибок не происходит; в
состоянии
ошибок не происходит; в
состоянии ![]() ошибки
возникают независимо с вероятностью
ошибки
возникают независимо с вероятностью ![]() . Также считаются известными вероятности перехода
. Также считаются известными вероятности перехода
![]() из состояния
из состояния
![]() в
в ![]() и вероятности перехода
и вероятности перехода
![]() из состояния
из состояния
![]() в состояние
в состояние ![]() . В этом случае простую
марковскую цепь образует не последовательность ошибок, а последовательность переходов:
. В этом случае простую
марковскую цепь образует не последовательность ошибок, а последовательность переходов:
 .
.
При этом достаточно легко выразить безусловные
вероятности нахождения канала в состояниях ![]() и
и ![]() :
:
 ,
,  .
.
Безусловная вероятность ошибки в этом случае может быть определена по формуле:
 .
.
Наиболее часто при использовании модели
Гильберта для двоичного канала полагают ![]() , т.е. состояние
, т.е. состояние ![]() рассматривается
как полный обрыв связи. Это согласуется с
представлением о канале, в котором действуют
коммутационные помехи.
рассматривается
как полный обрыв связи. Это согласуется с
представлением о канале, в котором действуют
коммутационные помехи.
Возможен другой подход к построению
математических моделей каналов, при котором вся предыстория до некоторого
фиксированного момента времени ![]() заменяется заданием некоторого начального
состояния цепи. Зная характеристики цепи, начальное состояние и сигнал,
действующий только на промежутке от
заменяется заданием некоторого начального
состояния цепи. Зная характеристики цепи, начальное состояние и сигнал,
действующий только на промежутке от ![]() до
до ![]() , можно определить сигнал на выходе и
новое состояние цепи в любой момент времени
, можно определить сигнал на выходе и
новое состояние цепи в любой момент времени ![]() .
.
Состоянием цепи называется минимальное множество
величин, в которое входит ![]() элементов, однозначно определяющих
поведение цепи в момент времени
элементов, однозначно определяющих
поведение цепи в момент времени ![]() . Элементы этого множества называют переменными
состояния, которые обычно рассматривают как составляющие компоненты
. Элементы этого множества называют переменными
состояния, которые обычно рассматривают как составляющие компоненты ![]() -мерного вектора. Для любой
цепи можно записать два уравнения, позволяющих по состоянию в момент
-мерного вектора. Для любой
цепи можно записать два уравнения, позволяющих по состоянию в момент ![]() и сигналу,
поступающему на вход, найти выходной сигнал и состояние в момент
и сигналу,
поступающему на вход, найти выходной сигнал и состояние в момент ![]() . Эти матричные уравнения
называют уравнением состояния и уравнением наблюдения.
. Эти матричные уравнения
называют уравнением состояния и уравнением наблюдения.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Список сокращений
- Основные обозначения
- ВВЕДЕНИЕ
- Глава 1. Сообщения, сигналы и помехи, их математические модели
- 1.1. Основные понятия и определения
- 1.1.1. Сообщение, сигнал, модуляция
- 1.1.2. Основные параметры сигналов
- 1.2. Системы связи. Каналы связи
- 1.2.1. Структура канала электросвязи
- 1.2.2. Линия и сеть связи
- 1.2.3. Помехи и искажения в канале
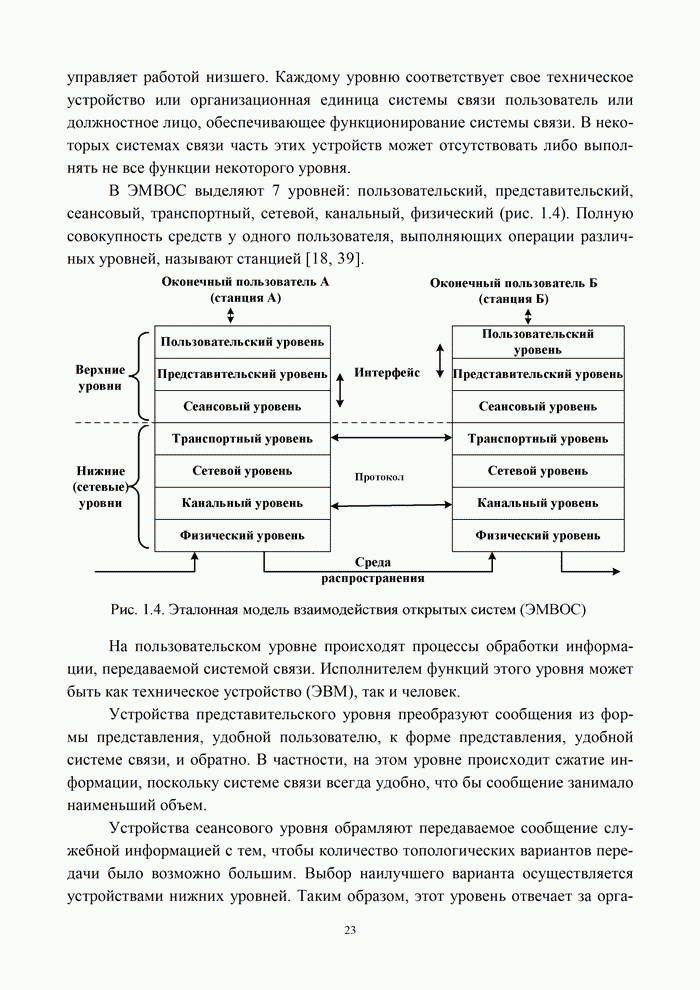
- 1.2.4. Эталонная модель взаимодействия открытых систем
- 1.2.5. Модели каналов связи и их математическое описание
- 1.3. Способы описания сигналов и помех
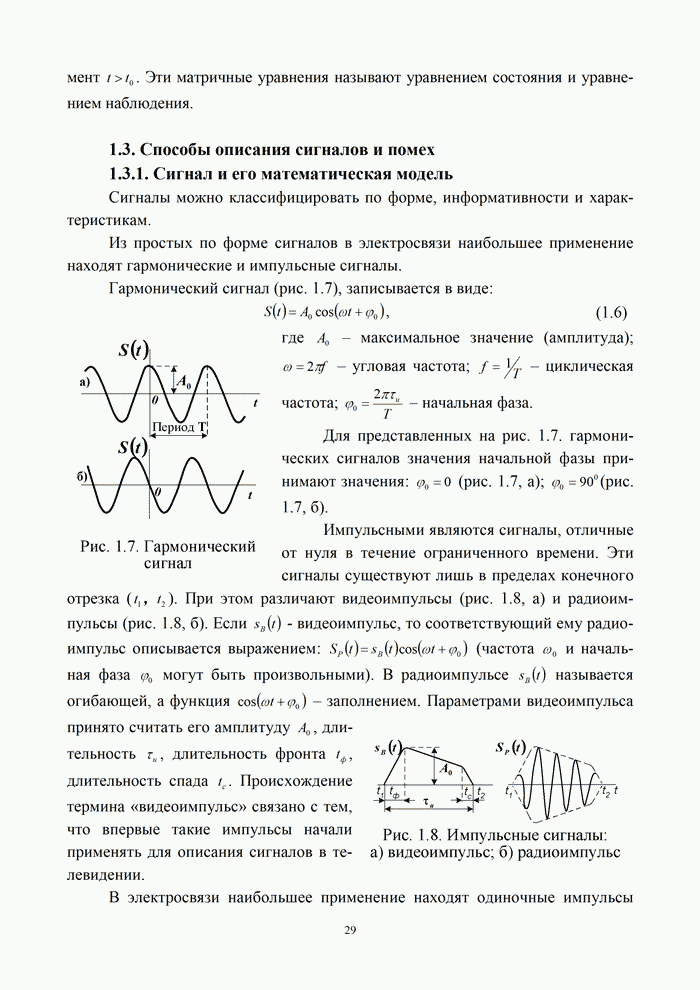
- 1.3.1. Сигнал и его математическая модель
- 1.3.2. Энергетические характеристики детерминированного сигнала
- 1.4.2. Представление сигналов и помех рядом Фурье
- 1.4.3. Применение преобразования Фурье для непериодических сигналов
- 1.5. Теорема Котельникова
- 1.6. Пространство сигналов
- 1.6.1. Линейное пространство
- 1.6.2. Представление сигнала в многомерном пространстве
- 1.7. Сигналы как случайные процессы
- 1.7.1. Характеристики случайного процесса
- 1.7.2. Флуктуационный шум
- 1.8. Комплексное представление сигналов и помех
- 1.8.1. Понятие аналитического сигнала
- 1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- Контрольные вопросы
- Глава 2. Методы формирования и преобразования сигналов
- 2.1. Модуляция сигналов
- 2.1.1. Амплитудная модуляция гармонической несущей
- 2.1.2. Балансная и однополосная модуляция гармонической несущей
- 2.2. Методы угловой модуляции
- 2.2.1. Принципы частотной и фазовой (угловой) модуляции
- 2.2.2. Спектр сигналов угловой модуляции
- 2.3. Формирование и детектирование модулированных сигналов
- 2.3.1. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
- 2.3.2. Формирование и детектирование сигналов угловой модуляции
- 2.4. Манипуляция сигналов
- 2.4.1. Временные и спектральные характеристики амплитудно-манипулированных сигналов
- 2.4.2. Временные и спектральные характеристики частотно-манипулированных сигналов
- 2.4.3. Фазовая (относительно-фазовая) манипуляция сигналов
- 2.5. Системы связи с многопозиционной относительной фазовой манипуляцией
- 2.5.1. Принцип формирования сигнала с многократной относительной фазовой манипуляцией
- 2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
- 2.5.3. Принцип частотной модуляции с непрерывной фазой
- Контрольные вопросы
- Глава 3. Помехоустойчивость приема дискретных сообщений
- 3.1. Критерии качества и правила приема дискретных сообщений
- 3.1.1. Понятие о помехоустойчивости систем электрической связи
- 3.1.2. Задача оптимального приема
- 3.1.3. Вычисление вероятностей ошибок
- 3.2. Оптимальная демодуляция при когерентном приеме сигналов
- 3.2.1. Оптимальные алгоритмы приема при полностью известных сигналах
- 3.2.2. Реализация алгоритмов оптимального когерентного приема
- 3.3. Помехоустойчивость приема сигналов с известными параметрами
- 3.4. Прием сигналов с неопределенной фазой
- 3.4.1. Оптимальный некогерентный прием дискретных сигналов
- 3.4.2. Помехоустойчивость оптимального некогерентного приема
- 3.5. Подоптимальные методы приема
- 3.5.1. Причины применения неоптимальных методов приема
- 3.5.2. Квазиоптимальные методы приема
- Контрольные вопросы
- Глава 4. Теория передачи информации
- 4.1. Информационные характеристики источника сообщений
- 4.1.1. Количественное определение информации
- 4.1.2. Энтропия и производительность дискретного источника сообщений
- 4.2. Пропускная способность дискретного канала
- 4.2.1. Количество информации переданной по дискретному каналу
- 4.2.2. Пропускная способность дискретного канала
- 4.2.3. Пропускная способность симметричного дискретного канала без памяти
- 4.3. Методы сжатия дискретных сообщений
- 4.3.1. Условия существования оптимального неравномерного кода
- 4.3.2. Прямая и обратная теоремы кодирования источника неравномерными кодами
- 4.3.3. Показатели эффективности сжатия
- 4.3.4. Кодирование источника дискретных сообщений методом Шеннона-Фано
- 4.3.5. Кодирование источника дискретных сообщений методом Хаффмена
- 4.4. Пропускная способность непрерывного канала
- 4.4.1. Постановка задачи передачи дискретных сообщений в непрерывном канале
- 4.4.2. Количество информации, переданной по непрерывному каналу
- 4.4.3. Пропускная способность непрерывного канала
- Контрольные вопросы
- Глава 5. Теория кодирования сообщений
- 5.1. Помехоустойчивое кодирование: блочные и непрерывные коды
- 5.1.1. Постановка задачи помехоустойчивого кодирования
- 5.1.2. Классификация кодов
- 5.1.3. Основные характеристики и свойства блочных кодов
- 5.2. Эффективность помехоустойчивого кодирования
- 5.2.1. Эффективность кода в режиме исправления ошибок
- 5.2.2. Эффективность кода в режиме обнаружения ошибок
- 5.2.3. Эффективность помехоустойчивых кодов
- 5.3. Математические основы теории помехоустойчивого кодирования
- 5.3.1. Краткие сведения из теории чисел
- 5.3.2. Группы
- 5.3.3. Кольца и поля
- 5.3.4. Векторное пространство
- 5.3.5. Конечные поля
- 5.4. Линейные блочные коды
- 5.4.1. Система передачи дискретных сообщений
- 5.4.2. Параметры линейного кода
- 5.4.3. Полиномиальные циклические коды
- 5.4.4. Циклические коды и корни полиномов
- 5.4.5. Спектральное описание циклических кодов
- 5.4.6. Простейшие блочные линейные коды
- 5.5. Коды Боуза-Чоудхури-Хоквингема
- 5.5.1. Методы задания кодов БЧХ
- 5.5.2. Принципы декодирования кодов БЧХ
- 5.5.3. Методы реализации этапов декодирования кодов БЧХ
- 5.6. Коды Рида-Соломона
- 5.6.1. Основные определения
- 5.6.2. Обнаружение и исправление пакетов ошибок
- 5.7. Коды Рида-Маллера
- 5.7.1. Задание и декодирование кодов Рида-Маллера
- 5.7.2. Симплексные коды и m-последовательности
- 5.7.3. Связь между блочными кодами
- 5.8. Сверточные коды
- 5.8.1. Основные параметры
- 5.8.2. Способы задания сверточного кода
- 5.8.3. Алгоритм декодирования Витерби
- 5.9. Помехоустойчивость систем передачи дискретных сообщений
- 5.9.1. Две процедуры приема сигналов
- 5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
- 5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
- Контрольные вопросы
- Глава 6. Сигналы с импульсной модуляцией
- 6.1. Методы импульсной модуляции
- 6.1.1. Импульсные методы передачи непрерывных сигналов
- 6.1.2. Спектральные характеристики импульсных методов модуляции
- 6.2. Помехоустойчивость непрерывных каналов связи с импульсной модуляцией
- 6.2.1. Помехоустойчивость систем передачи с импульсными методами модуляции
- 6.3. Цифровые методы передачи непрерывных сообщений
- 6.3.1. Передача сигналов с импульсно-кодовой модуляцией
- 6.3.2. Передача сигналов с дельта модуляцией
- 6.3.3. Квантование сигналов в системах с ИКМ и ДМ
- Контрольные вопросы
- Глава 7. Методы приема сигналов в сложных условиях
- 7.1. Прием сигналов в каналах с замираниями
- 7.1.1. Сущность замираний и их классификация
- 7.1.2. Принципы разнесенного приема сигналов
- 7.2. Методы борьбы с замираниями сигналов
- 7.2.1. Методы борьбы с замираниями в аналоговых системах связи
- 7.2.2. Методы борьбы с замираниями в цифровых системах связи
- 7.3. Методы борьбы с межсимвольной интерференцией
- 7.3.1. Причины возникновения и сущность межсимвольной интерференции
- 7.3.2. Обработка сигналов в каналах с межсимвольной интерференцией
- 7.3.3. Помехоустойчивость в каналах с межсимвольной интерференцией
- 7.4. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
- 7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
- 7.4.2. Борьба с сосредоточенными и импульсными помехами
- 7.5. Компенсация помех и искажений в канале
- 7.5.1. Принцип работы радиолинии с ФМ ПСС (ФМ ШПС)
- 7.5.2. Помехоустойчивость радиолинии с ФМ ПСС
- 7.5.3. Принципы работы радиолиний с ППРЧ
- 7.5.4. Помехоустойчивость радиолиний с ППРЧ
- Контрольные вопросы
- Глава 8. Многоканальная связь и распределение информации
- 8.1. Методы распределения ресурса общего канала
- 8.1.1. Классификация систем передачи информации, использующих единый ресурс
- 8.1.2. Постановка задачи объединения и разделения сигналов
- 8.1.3. Энергетическая и спектральная цена уплотнения
- 8.2. Частотное разделение каналов
- 8.2.1. Принцип частотного объединения и разделения каналов
- 8.2.2. Групповой сигнал, его структура и характеристики
- 8.3. Временное разделение каналов
- 8.3.1. Принцип временного разделения каналов
- 8.3.2. Характеристики группового сигнала систем с ВРК
- 8.4. Разделение сигналов по форме
- Контрольные вопросы
- Глава 9. Эффективность систем связи
- 9.1. Оценка эффективности систем связи
- 9.1.1. Подходы к оценке эффективности
- 9.1.2. Критерии эффективности
- 9.1.3. Эффективность аналоговых и цифровых систем
- 9.2. Выбор сигналов и помехоустойчивых кодов
- 9.2.1. Многопозиционные сигналы
- 9.2.2. Корректирующие коды
- 9.3. Оптимизация систем связи
- 9.3.1. Согласование методов модуляции и кодирования
- 9.3.2. Классификация сигнально – кодовых конструкций
- 9.4. Характеристики основных типов СКК
- 9.4.1. Согласование канала кодом Грея
- 9.4.2. Согласование на основе разбиения ансамбля на вложенные подансамбли
- 9.5. Алгоритмы цифровой обработки сигналов
- 9.5.1. Дискретные сигналы и их спектры
- 9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
- Контрольные вопросы
- Глава 10. Теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах
- 10.1. Классификация криптографических систем
- 10.1.2. Классификация криптографических систем защиты информации
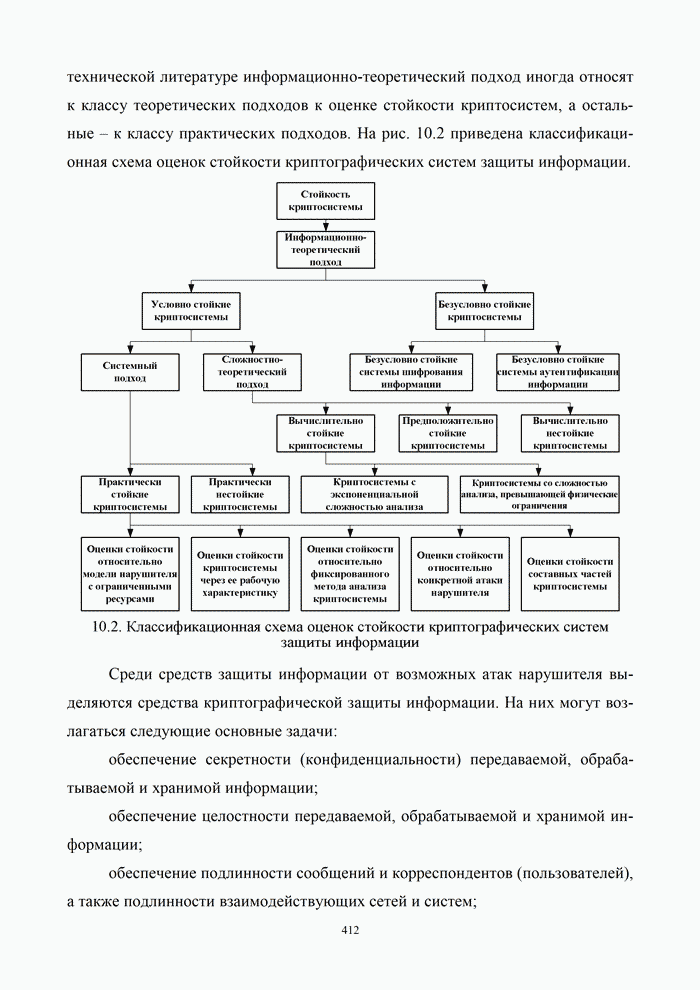
- 10.1.3. Оценка стойкости криптосистем
- 10.2. Функции, используемые в криптографических системах
- 10.2.1. Общее описание функций, используемых в криптографических системах
- 10.2.2. Однонаправленные функции
- 10.2.3. Криптографические хэш-функции
- 10.3. Модели криптографических систем
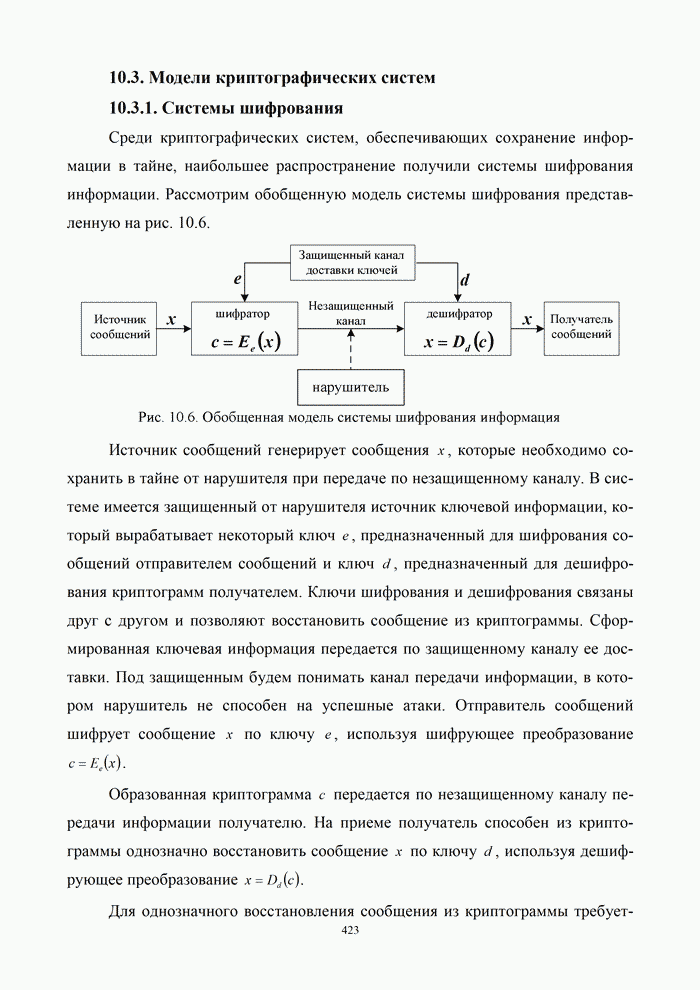
- 10.3.1. Системы шифрования
- 10.3.2. Традиционные симметричные криптосистемы
- 10.4. Алгоритмы криптографической защиты
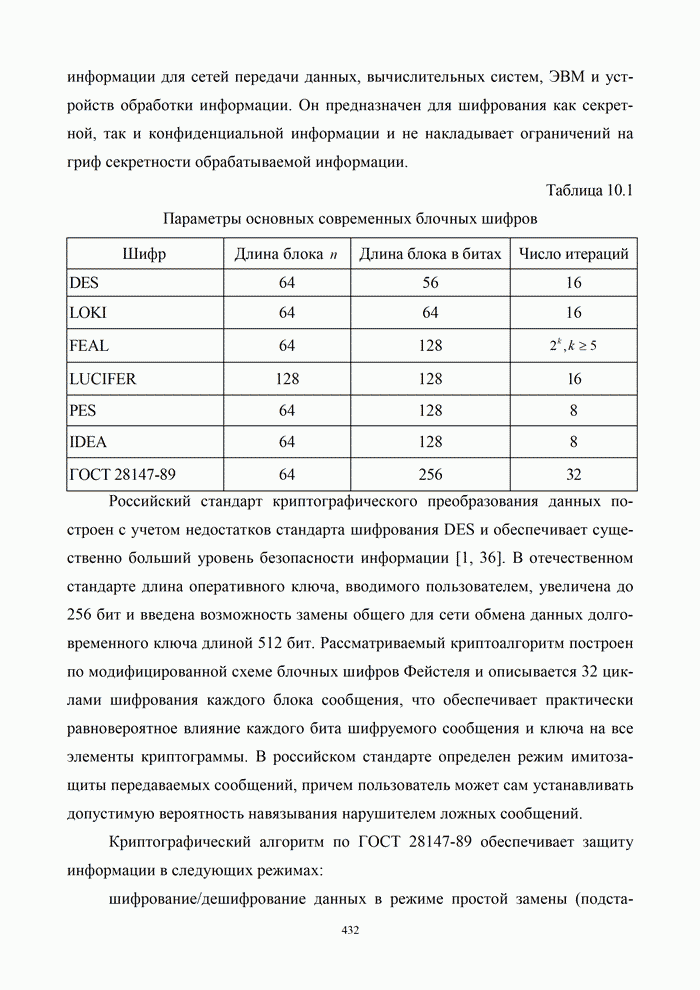
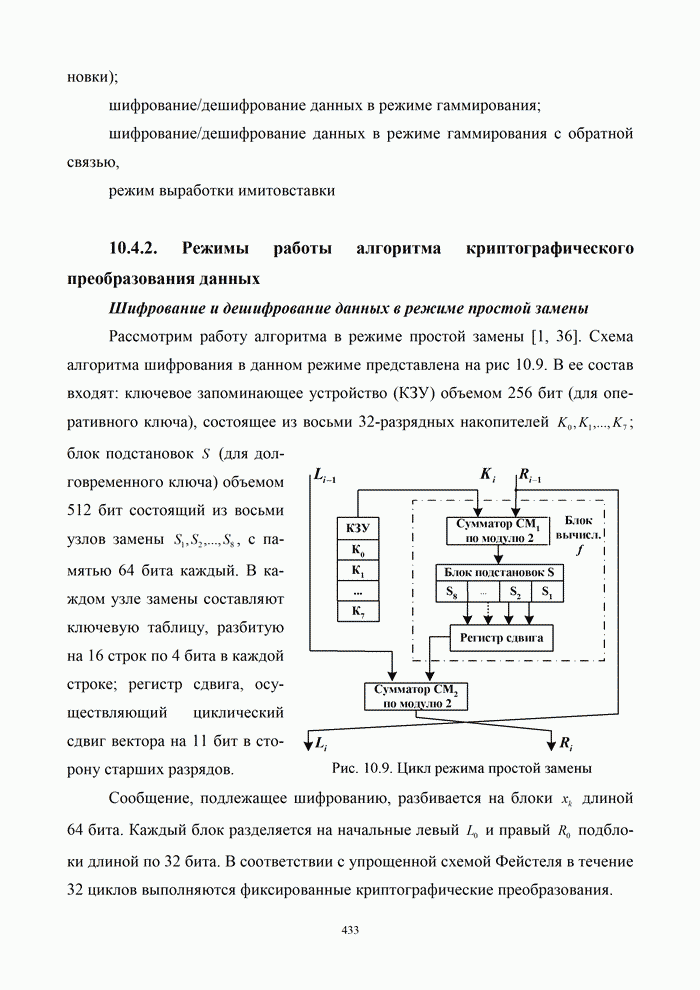
- 10.4.1. Алгоритм криптографической защиты информации согласно ГОСТ 28147-89
- Контрольные вопросы
- Заключение
- Список литературы



















































































































































































































































































































































































 ,
,
 ,
,
