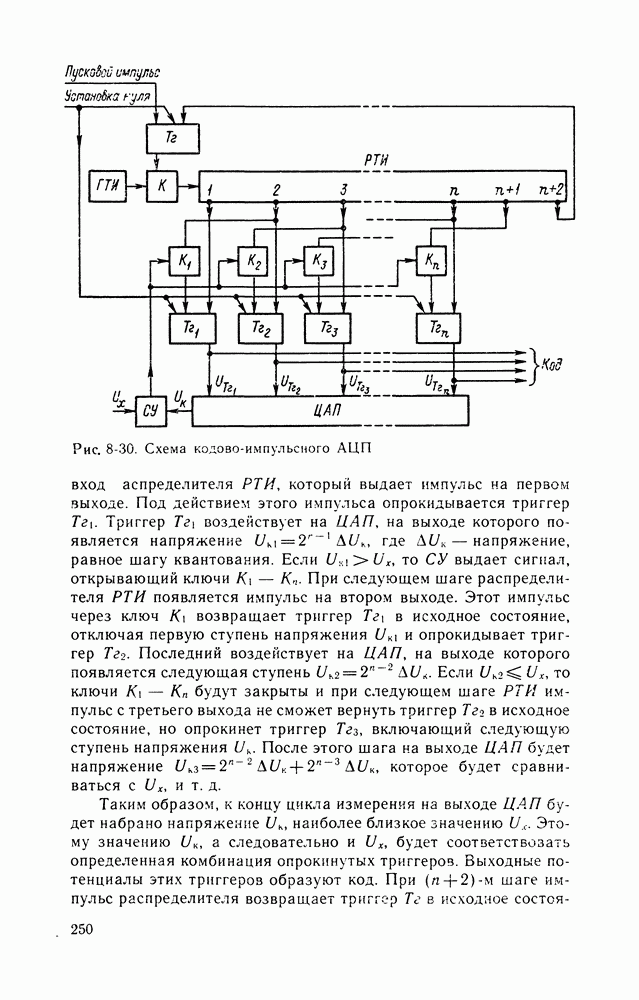
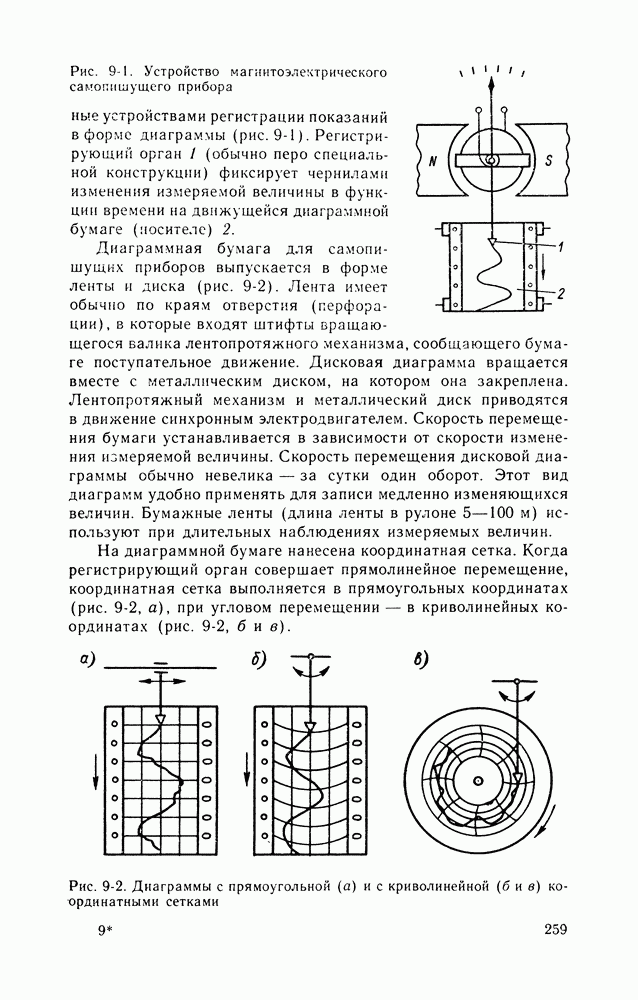
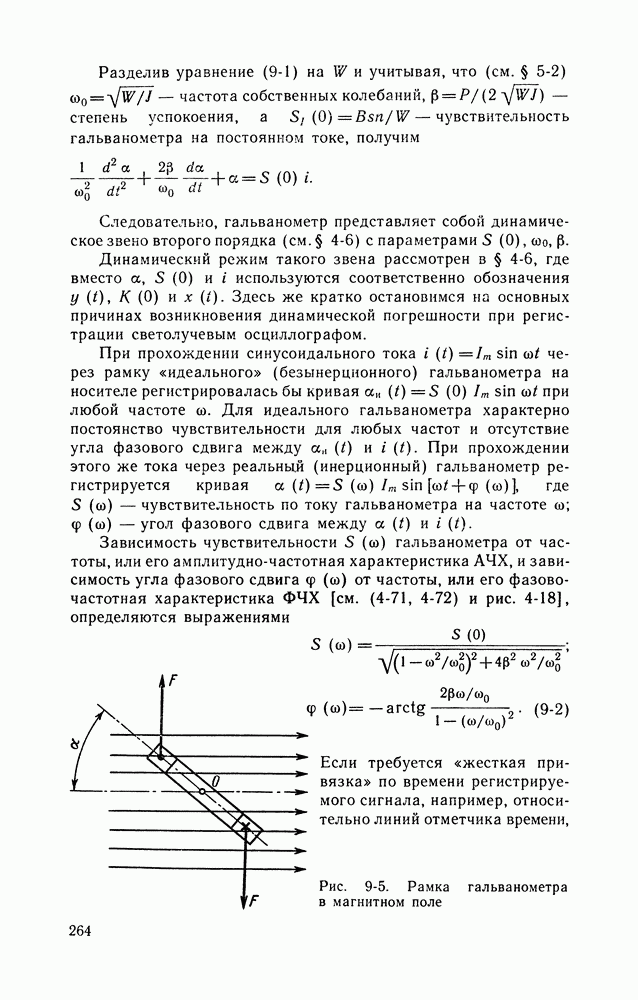
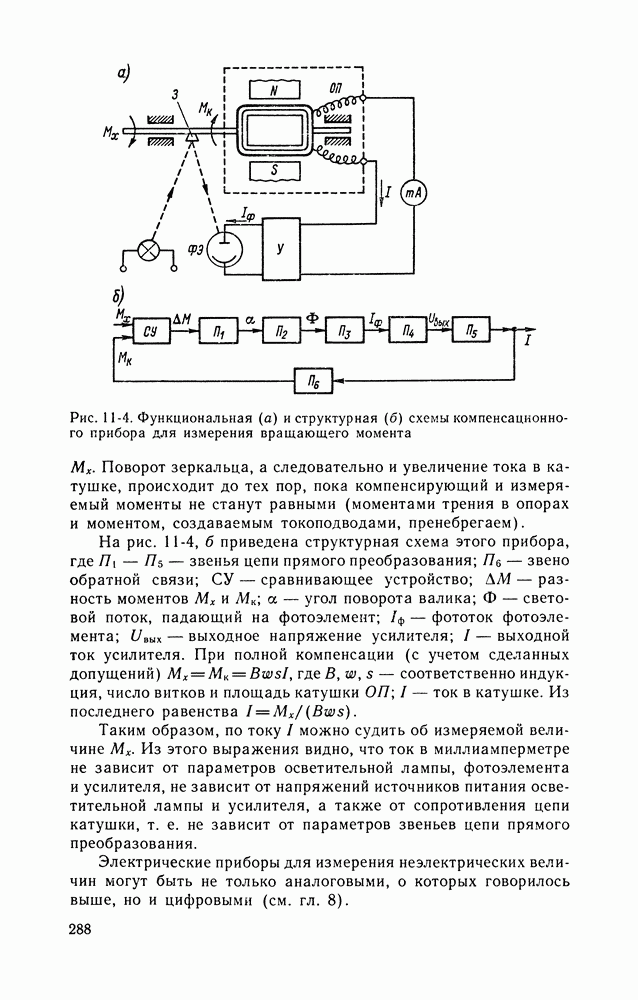
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Математические модели сигналов.
Под математической моделью понимают описание сигнала на формальном языке математики, т. е. с помощью формул, неравенств или логических соотношений. Для описания одних и тех же сигналов могут быть использованы различные математические модели. Выбор модели определяется адекватностью модели реальному сигналу, простотой математического описания, назначением модели и др.
Особенностью моделей сигналов измерительной информации является априорная (доопытная) неопределенность значений информативных параметров, обусловленная в общем случае неизвестными размерами измеряемых величин.
Существуют различные подходы к построению математических моделей сигналов.
1. Сигнал принимают квазидетерминированным. В этом случае для математического описания сигнала используют различные детерминированные функции времени. Модели таких сигналов называют квазидетерминированными (или детерминированными), подчеркивая тем самым, что вид функции, описывающей сигнал, известен, а неизвестными (информативными) являются ее параметры.
2. Сигнал рассматривают как случайный процесс. Описание таких сигналов основывается на теории вероятностей и теории случайных функций. В этом случае изменение сигнала во времени и пространстве характеризуется законом распределения, математическим ожиданием, дисперсией и корреляционной функцией. Модели таких сигналов называют случайными.
3. Сигналы представляют в виде комбинации случайной и детерминованной составляющих, в частности в виде суммы сигнала измерительной информации (квазидетерминированная составляющая) и помехи (случайная составляющая).
Модели квазидетерминированных сигналов. При построении таких моделей используется как временное, так и спектральное представление сигналов. Во временной области применяют некоторые функции  наиболее близко описывающие изменение сигнала во времени, в которых один из параметров
наиболее близко описывающие изменение сигнала во времени, в которых один из параметров  зависит от измеряемой величины
зависит от измеряемой величины  Такими функциями могут быть: функция включения, дельта-функция, тригонометрические и экспоненциальная функции, различные алгебраические полиномы и др.
Такими функциями могут быть: функция включения, дельта-функция, тригонометрические и экспоненциальная функции, различные алгебраические полиномы и др.
Рассмотрим некоторые примеры моделей квазидетерминированных сигналов.
А. При скачкообразном изменении измеряемой величины  сигнал
сигнал  на выходе безынерционного измерительного преобразователя может быть записан с использованием функции
на выходе безынерционного измерительного преобразователя может быть записан с использованием функции

Рис. 4-3. Функция включения (а) и последовательность прямоугольных импульсов (б)
включения. Функция включения (рис. 4-3, а), или единичный скачок, определяется системой равенств

С помощью этой функции сигнал измерительной информации может быть записан в виде

где  — коэффициент преобразования. Значение параметра а
— коэффициент преобразования. Значение параметра а  до опыта остается неизвестным, поэтому в рамках квазидетерминированной модели обычно оценивают диапазон Да изменения сигнала в зависимости от диапазона
до опыта остается неизвестным, поэтому в рамках квазидетерминированной модели обычно оценивают диапазон Да изменения сигнала в зависимости от диапазона  изменения измеряемой величины.
изменения измеряемой величины.
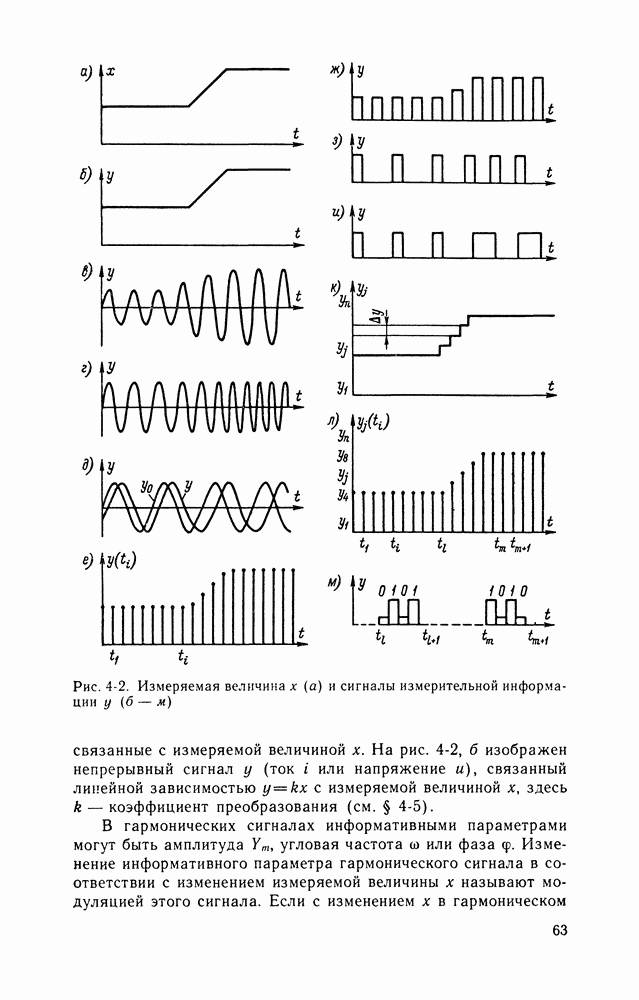
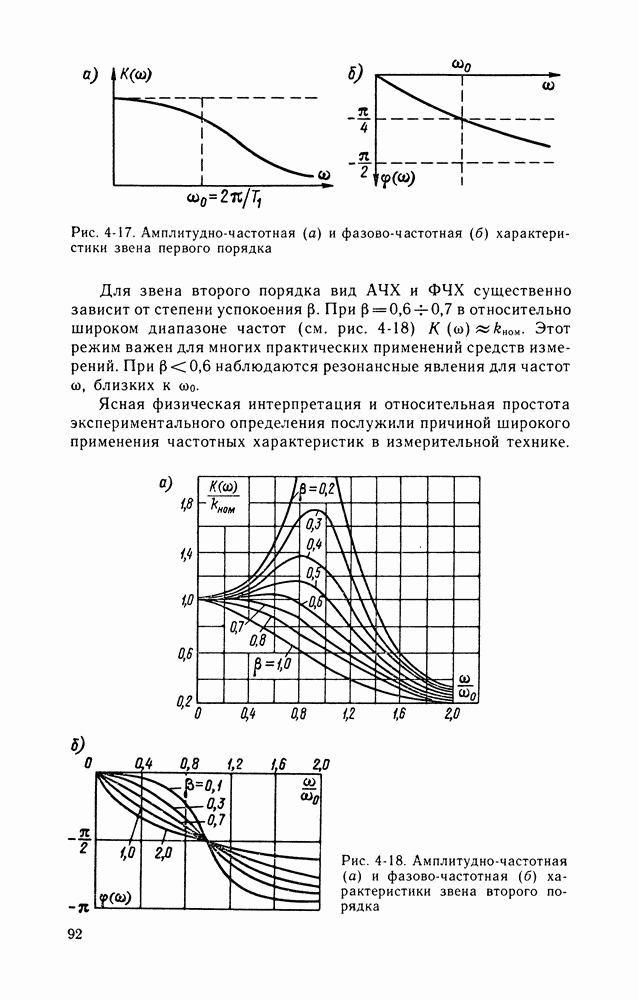
Б. Использование детерминированных моделей особенно удобно при описании периодических сигналов. Так, уравнение амплитудно-модулированного гармонического сигнала (рис. 4-2, в) имеет вид

где  — частота так называемых несущих колебаний;
— частота так называемых несущих колебаний;  — коэффициент амплитудной модуляции, определяющий влияние
— коэффициент амплитудной модуляции, определяющий влияние  на амплитуду
на амплитуду  синусоидальных колебаний. Диапазон изменения этой амплитуды характеризует глубину модуляции гармонического сигнала.
синусоидальных колебаний. Диапазон изменения этой амплитуды характеризует глубину модуляции гармонического сигнала.
В. Для описания периодической последовательности прямоугольных импульсов постоянного тока (рис. 4-3, б) применяют выражение

где  — амплитуда импульса;
— амплитуда импульса;  — длительность импульса;
— длительность импульса;  — период следования импульса. В этом случае аналитическое выражение для АИМ сигнала имеет вид
— период следования импульса. В этом случае аналитическое выражение для АИМ сигнала имеет вид

где  — коэффициент, характеризующий диапазон модуляции амплитуды
— коэффициент, характеризующий диапазон модуляции амплитуды 
Выражения (4-8) и (4-10) описывают амплитудную модуляцию периодических сигналов. Аналогично могут быть получены аналитические зависимости для ЧМ, ФМ, ЧИМ и ШИМ, в которых соответствующие параметры модели являются функциями 
Г. Сигналы измерительной информации могут иметь достаточно сложную структуру. Для точного описания таких сигналов (если оно принципиально возможно) приходится использовать сложные математические выражения. Часто оказывается удобным такие сигналы на интервале времени  описывать суммой некоторых относительно простых функций (аппроксимировать суммой функций). В общем случае для точного описания сигнала необходимо использовать бесконечный ряд
описывать суммой некоторых относительно простых функций (аппроксимировать суммой функций). В общем случае для точного описания сигнала необходимо использовать бесконечный ряд  где
где  — некоторые выбранные для аппроксимации функции (базисные функции); С, — весовые коэффициенты. На практике используют конечную сумму аппроксимируемых функций
— некоторые выбранные для аппроксимации функции (базисные функции); С, — весовые коэффициенты. На практике используют конечную сумму аппроксимируемых функций  что приводит к погрешности аппроксимации
что приводит к погрешности аппроксимации  так как аппроксимирующая функция
так как аппроксимирующая функция  не равна во всех точках
не равна во всех точках  (см. рис. 4-6). Погрешность
(см. рис. 4-6). Погрешность  зависит от вида функции и от интервала
зависит от вида функции и от интервала  представления сигнала, т. е. интервала, на котором
представления сигнала, т. е. интервала, на котором  аппроксимируется
аппроксимируется  . В качестве
. В качестве  нашли применение полиномы Лагранжа (см. стр. 72), Лежандра, Чебышева и др.
нашли применение полиномы Лагранжа (см. стр. 72), Лежандра, Чебышева и др.
Наряду с временным описанием сигналов широко используется их спектральное представление. Это представление основывается на преобразовании Фурье сигналов  Применяя разложение в ряд Фурье, периодический сигнал
Применяя разложение в ряд Фурье, периодический сигнал  может быть представлен суммой гармонических составляющих:
может быть представлен суммой гармонических составляющих:

где  — постоянная составляющая;
— постоянная составляющая;  — амплитуда и фаза
— амплитуда и фаза  гармонической составляющей сигнала;
гармонической составляющей сигнала;  — номер гармоники. Множество значений
— номер гармоники. Множество значений  образуют соответственно амплитудный и фазовый спектры сигнала. Такие спектры часто изображают графически.
образуют соответственно амплитудный и фазовый спектры сигнала. Такие спектры часто изображают графически.
Для непериодического сигнала у (0, используя интеграл Фурье, определяют его спектральную плотность

Спектральное представление сигналов позволяет оценить их частотный диапазон  т. е. такой диапазон частот, в котором заключены все или основные (имеющие наибольшие амплитуды) гармонические составляющие сигнала.
т. е. такой диапазон частот, в котором заключены все или основные (имеющие наибольшие амплитуды) гармонические составляющие сигнала.
Частотный диапазон является важной характеристикой сигналов, определяющей необходимую полосу пропускания средств измерений (см. § 4-6) для передачи сигналов с требуемой точностью. Так, для непрерывных сигналов  при линейной зависимости
при линейной зависимости  вид спектра сигнала повторяет спектр измеряемой величины
вид спектра сигнала повторяет спектр измеряемой величины  с точностью до постоянного множителя, равного
с точностью до постоянного множителя, равного  Следовательно, при таком сигнале средства измерений должны иметь полосу пропускания частот (см. § 4-6), определяемую спектром измеряемой величины
Следовательно, при таком сигнале средства измерений должны иметь полосу пропускания частот (см. § 4-6), определяемую спектром измеряемой величины 
При амплитудной модуляции гармонического сигнала спектр имеет более сложную зависимость от спектра входной величины  Если
Если  представляет собой гармоническое колебание с частотой
представляет собой гармоническое колебание с частотой  то на основании (4-8) и (4-11) получим
то на основании (4-8) и (4-11) получим

Спектр  такого сигнала показан на рис. 4-4, а. Для неискаженной передачи этого сигнала средство измерений должно иметь полосу пропускания частот в диапазоне от
такого сигнала показан на рис. 4-4, а. Для неискаженной передачи этого сигнала средство измерений должно иметь полосу пропускания частот в диапазоне от  до
до 
При модуляции импульсных сигналов спектр имеет достаточно сложную структуру. В качестве примера на рис.  показан вид спектра АИМ сигнала при
показан вид спектра АИМ сигнала при  Спектр такого сигнала бесконечен по частоте. В этом случае при определении требований к полосе пропускания соответствующих средств измерений исходят из допускаемой погрешности искажения сигнала за счет ограничения его частотного диапазона.
Спектр такого сигнала бесконечен по частоте. В этом случае при определении требований к полосе пропускания соответствующих средств измерений исходят из допускаемой погрешности искажения сигнала за счет ограничения его частотного диапазона.
Приведенные примеры показывают важность анализа частотных характеристик (спектров) сигналов измерительной информации.
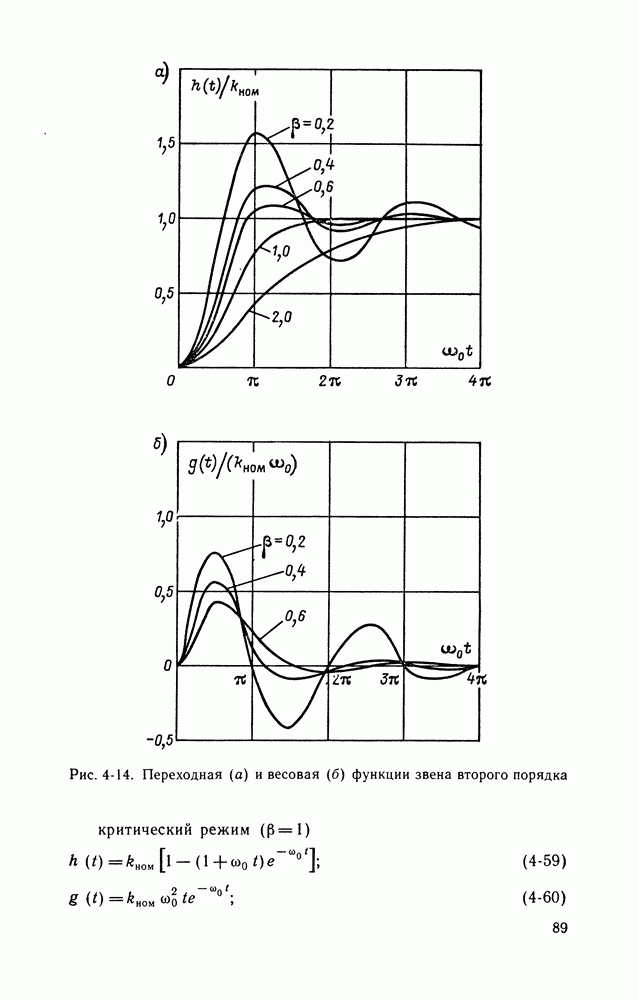
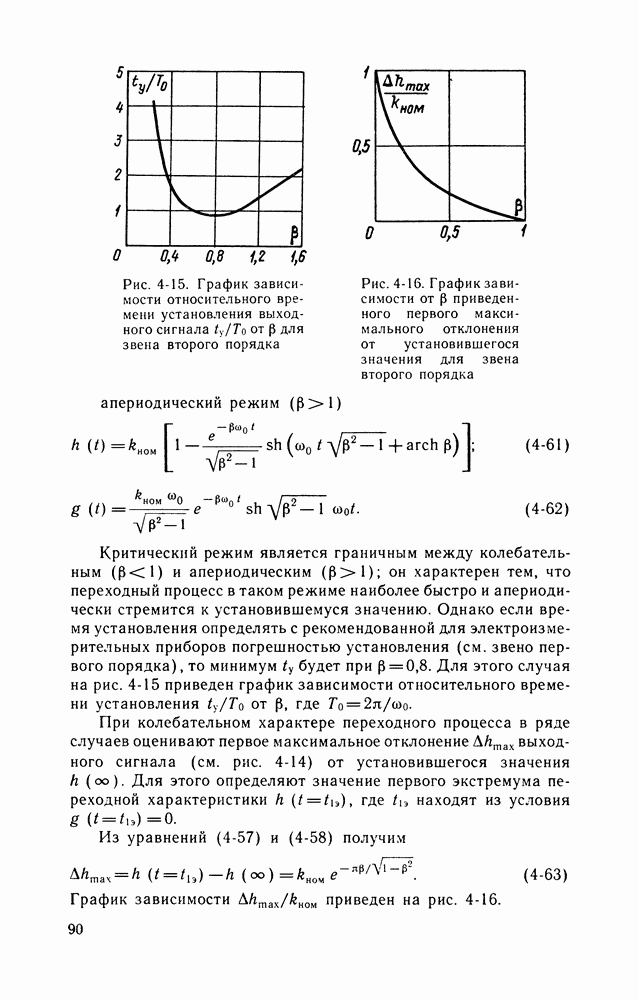
Таким образом, описание сигналов квазидетерминированными моделями дает хорошую математическую интерпретацию происходящих во времени процессов в средствах измерений. При известном  эти модели дают точное (в пределах принятой модели) описание сигнала
эти модели дают точное (в пределах принятой модели) описание сигнала  Однако поскольку измеряемая
Однако поскольку измеряемая

Рис. 4-4. Спектры амплитудной (а) и амплитудно-импульсной (б) модуляции сигналов при гармоническом модулирующем сигнале
величина  является неизвестной, то на основании этих моделей обычно определяют предельные характеристики сигналов
является неизвестной, то на основании этих моделей обычно определяют предельные характеристики сигналов  диапазон изменения сигнала и его информативного параметра, частотный диапазон и другие характеристики.
диапазон изменения сигнала и его информативного параметра, частотный диапазон и другие характеристики.
Модели случайных сигналов. Математические модели случайных сигналов основываются на использовании теории вероятностей и теории случайных процессов.
Во многих приложениях сигнал измерительной информации можно рассматривать как случайную величину. Например, последовательно измеряя сопротивления нескольких резисторов одного номинала, можно получить некоторый «разброс» в результатах измерений, обусловленный, в частности, технологией изготовления резисторов. Такой «разброс» нельзя описать детерминированными функциями. В подобных случаях для описания сигналов применяют такие характеристики, которые используют для описания случайных величин (см. § 3-2) — законы распределения, математическое ожидание и среднее квадратическое отклонение. Эти характеристики определяют либо опытным путем, либо на основании теоретических предпосылок о возможных изменениях измеряемой величины.
В наиболее общем виде сигналы измерительной информации могут быть представлены как случайные процессы. Например, регистрируя с помощью самопишущего прибора силу тока, потребляемого некоторым большим промышленным объектом, на диаграмме прибора получаем сложную кривую, определяемую случайным характером изменения нагрузки питающей сети. Делая повторно такие эксперименты, каждый раз будем получать новые кривые, отличающиеся друг от друга.
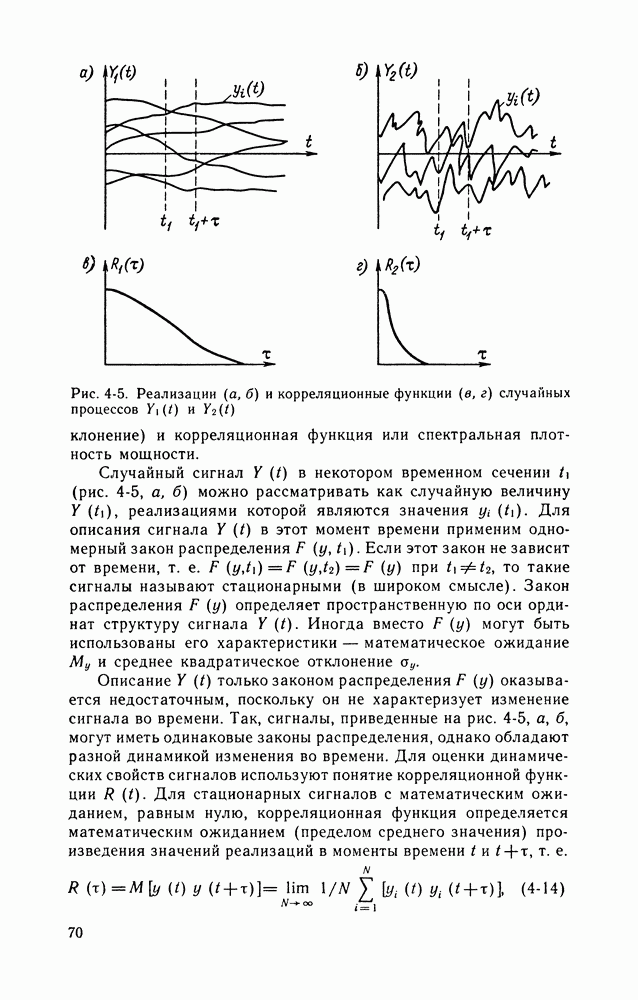
Семейство возможных реализаций  сигналов, подчиненное определенным вероятностным характеристикам, образует случайный сигнал
сигналов, подчиненное определенным вероятностным характеристикам, образует случайный сигнал  (рис. 4-5, а, б). Такими характеристиками могут быть закон распределения или его числовые характеристики (математическое ожидание и среднее квадратическое
(рис. 4-5, а, б). Такими характеристиками могут быть закон распределения или его числовые характеристики (математическое ожидание и среднее квадратическое

Рис. 4-5. Реализации (а, б) и корреляционные функции (в, г) случайных процессов 
отклонение) и корреляционная функция или спектральная плотность мощности.
Случайный сигнал  в некотором временном сечении
в некотором временном сечении  (рис. 4-5, а, б) можно рассматривать как случайную величину
(рис. 4-5, а, б) можно рассматривать как случайную величину  реализациями которой являются значения
реализациями которой являются значения  Для описания сигнала
Для описания сигнала  в этот момент времени применим одномерный закон распределения
в этот момент времени применим одномерный закон распределения  Если этот закон не зависит от времени, т. е.
Если этот закон не зависит от времени, т. е.  при
при  то такие сигналы называют стационарными (в широком смысле). Закон распределения
то такие сигналы называют стационарными (в широком смысле). Закон распределения  определяет пространственную по оси ординат структуру сигнала
определяет пространственную по оси ординат структуру сигнала  Иногда вместо
Иногда вместо  могут быть использованы его характеристики — математическое ожидание
могут быть использованы его характеристики — математическое ожидание  и среднее квадратическое отклонение
и среднее квадратическое отклонение 
Описание  только законом распределения
только законом распределения  оказывается недостаточным, поскольку он не характеризует изменение сигнала во времени. Так, сигналы, приведенные на рис. 4-5, а, б, могут иметь одинаковые законы распределения, однако обладают разной динамикой изменения во времени. Для оценки динамических свойств сигналов используют понятие корреляционной функции
оказывается недостаточным, поскольку он не характеризует изменение сигнала во времени. Так, сигналы, приведенные на рис. 4-5, а, б, могут иметь одинаковые законы распределения, однако обладают разной динамикой изменения во времени. Для оценки динамических свойств сигналов используют понятие корреляционной функции  Для стационарных сигналов с математическим ожиданием, равным нулю, корреляционная функция определяется математическим ожиданием (пределом среднего значения) произведения значений реализаций в моменты времени
Для стационарных сигналов с математическим ожиданием, равным нулю, корреляционная функция определяется математическим ожиданием (пределом среднего значения) произведения значений реализаций в моменты времени  и
и  т. е.
т. е.

где  — число реализаций случайного сигнала.
— число реализаций случайного сигнала.
Корреляционная функция характеризует статистическую связь между мгновенными значениями случайного сигнала в различные моменты времени. Чем меньше значение корреляционной функции, тем меньше в среднем «зависит» значение сигнала  в момент времени
в момент времени  от значения
от значения  в момент времени
в момент времени  На рис. 4-5, в, г качественно изображены корреляционные функции
На рис. 4-5, в, г качественно изображены корреляционные функции  соответствующие сигналам
соответствующие сигналам  Корреляционная функция
Корреляционная функция  относительно слабо затухает с увеличением
относительно слабо затухает с увеличением  что говорит о сильной корреляции
что говорит о сильной корреляции  для
для  На реализациях это отражается в относительно плавном изменении сигнала во времени.
На реализациях это отражается в относительно плавном изменении сигнала во времени.
Для эргодических сигналов (см. § 16-1) корреляционная функция может быть определена усреднением произведения  по времени для одной реализации:
по времени для одной реализации: 

При  корреляционная функция равна дисперсии сигнала:
корреляционная функция равна дисперсии сигнала: 

На практике часто используют понятие нормированной корреляционной функции

Для характеристики частотных свойств случайных сигналов используют спектральную плотность мощности  которая определяет распределение средней мощности сигнала по его частотам. Значения
которая определяет распределение средней мощности сигнала по его частотам. Значения  равны средней мощности, приходящейся на единицу полосы частот (иначе — плотности средней мощности) при различных частотах
равны средней мощности, приходящейся на единицу полосы частот (иначе — плотности средней мощности) при различных частотах  .
.
Спектральная плотность мощности  и корреляционная функция
и корреляционная функция  связаны соотношениями:
связаны соотношениями:

Таким образом, для описания случайных сигналов измерительной информации применяют некоторую совокупность его

Рис. 4-6. Исходная кривая  сигнала и восстановленная (аппроксимирующая) кривая
сигнала и восстановленная (аппроксимирующая) кривая  полиномами Лагранжа нулевой (а) и первой (б) степени
полиномами Лагранжа нулевой (а) и первой (б) степени
вероятностных характеристик. Так, если рассматривать сигнал как случайную величину, то его характеристикой будет закон распределения или его числовые характеристики. Если сигнал рассматривать как случайный процесс, то, кроме закона распределения, необходимо знать его корреляционную функцию или спектральную плотность мощности.
При описании случайных сигналов получили распространение нормальный и равномерный законы распределения и некоторые корреляционные функции, например  где
где  , а — параметры корреляционных функций, зависящие от динамических свойств случайных сигналов.
, а — параметры корреляционных функций, зависящие от динамических свойств случайных сигналов.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Раздел А. ОБЩИЕ СВЕДЕНИЯ ОБ ИЗМЕРИТЕЛЬНОЙ ТЕХНИКЕ
- Глава первая. ОСНОВНЫЕ ПОНЯТИЯ ИЗМЕРИТЕЛЬНОЙ ТЕХНИКИ И КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ
- 1-2. ВИДЫ И МЕТОДЫ ИЗМЕРЕНИЙ
- Глава вторая. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
- 2-1. ОСНОВНЫЕ ПОНЯТИЯ И ВИДЫ ПОГРЕШНОСТЕЙ
- 2-2. ВЕРОЯТНОСТНЫЙ ПОДХОД К ОПИСАНИЮ ПОГРЕШНОСТЕЙ
- 2-3. ВЕРОЯТНОСТНЫЕ ОЦЕНКИ ПОГРЕШНОСТЕЙ
- Глава третья. ОСНОВЫ МЕТРОЛОГИЧЕСКОГО ОБЕСПЕЧЕНИЯ
- 3-2. ЭТАЛОНЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН
- 3-3. ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ
- Раздел Б. ЭЛЕКТРИЧЕСКИЕ СРЕДСТВА ИЗМЕРЕНИЙ
- Глава четвертая. ОБЩИЕ СВЕДЕНИЯ О СРЕДСТВАХ ИЗМЕРЕНИЙ
- 4-2. ГОСУДАРСТВЕННАЯ СИСТЕМА ПРИБОРОВ
- 4-3. ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
- 4-4. СИГНАЛЫ ИЗМЕРИТЕЛЬНОЙ ИНФОРМАЦИИ
- Математические модели сигналов.
- Дискретизация сигналов.
- 4-5. СТРУКТУРНЫЕ СХЕМЫ И СВОЙСТВА СРЕДСТВ ИЗМЕРЕНИЙ В СТАТИЧЕСКОМ РЕЖИМЕ
- Средства измерений прямого преобразования.
- Средства измерений уравновешивающего преобразования.
- 4-6. СРЕДСТВА ИЗМЕРЕНИЙ В ДИНАМИЧЕСКОМ РЕЖИМЕ
- Переходные и импульсные переходные характеристики.
- Частотные характеристики.
- Передаточные функции.
- Глава пятая. МЕРЫ, ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ
- 5-2. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 5-3. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ
- МАГНИТОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ
- Амперметры и вольтметры.
- Омметры.
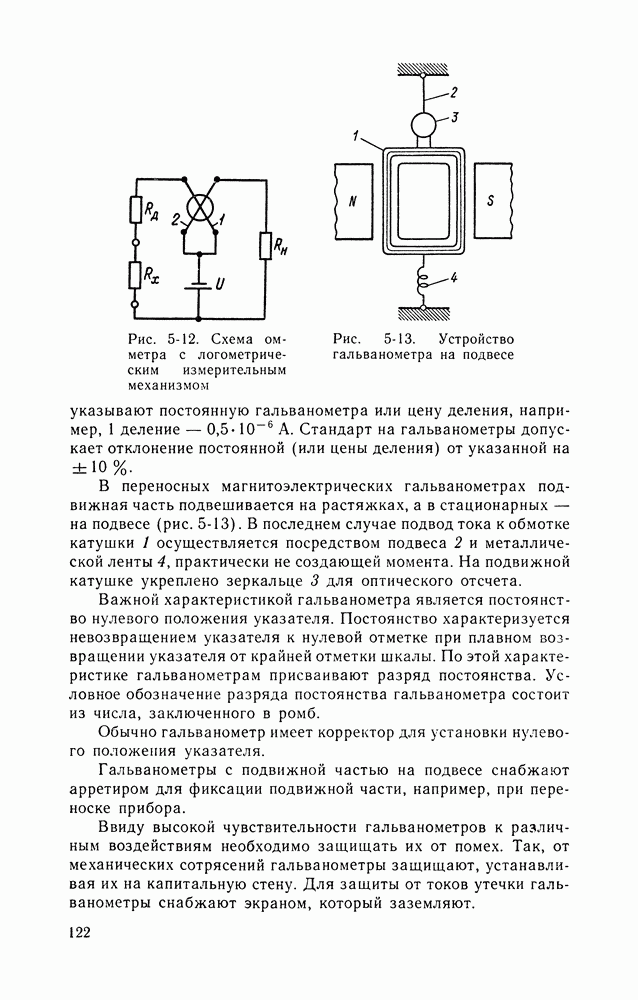
- Гальванометры.
- Баллистические гальванометры.
- Кулонметры.
- Вибрационные гальванометры.
- ЭЛЕКТРОДИНАМИЧЕСКИЕ И ФЕРРОДИНАМИЧЕСКИЕ ПРИБОРЫ
- ЭЛЕКТРОМАГНИТНЫЕ ПРИБОРЫ
- ЭЛЕКТРОСТАТИЧЕСКИЕ ПРИБОРЫ
- ИНДУКЦИОННЫЕ ПРИБОРЫ
- 5-4. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ С ПРЕОБРАЗОВАТЕЛЯМИ
- Глава шестая. ЭЛЕКТРОННЫЕ АНАЛОГОВЫЕ ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ
- 6-2. ЭЛЕКТРОННЫЕ ВОЛЬТМЕТРЫ
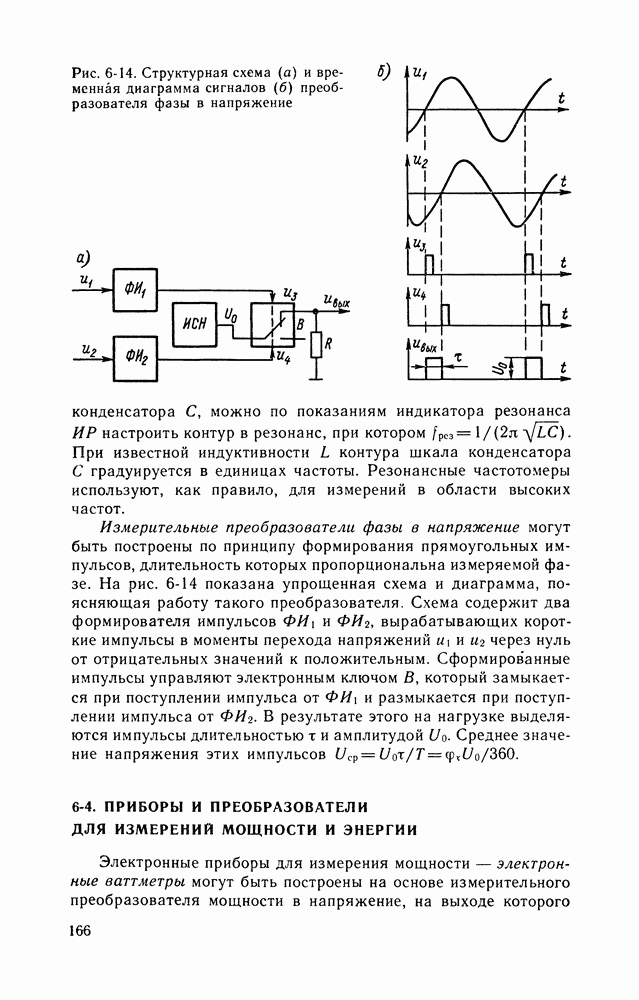
- 6-3. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ ЧАСТОТЫ И ФАЗЫ
- 6-4. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ МОЩНОСТИ И ЭНЕРГИИ
- 6-5. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ПАРАМЕТРОВ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 6-6. ЭЛЕКТРОННО ЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 6-7. АНАЛИЗАТОРЫ СПЕКТРА, ИЗМЕРИТЕЛИ НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ
- Глава седьмая. МОСТЫ И КОМПЕНСАТОРЫ
- 7-2. ТЕОРИЯ МОСТОВЫХ СХЕМ
- 7-3. МОСТЫ ДЛЯ ИЗМЕРЕНИЙ СОПРОТИВЛЕНИЯ НА ПОСТОЯННОМ ТОКЕ
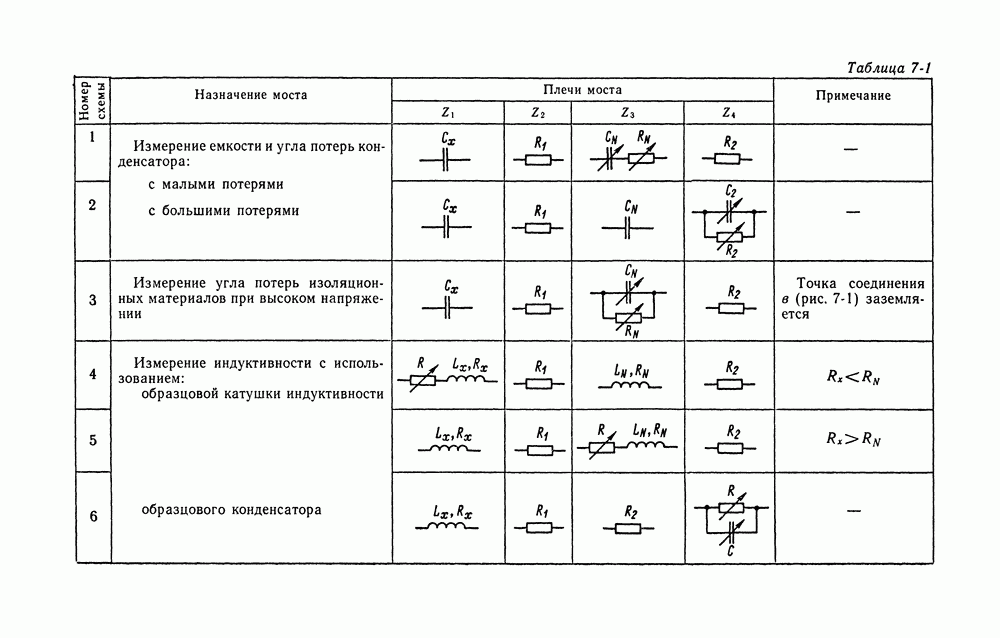
- 7-4. МОСТЫ ПЕРЕМЕННОГО ТОКА ДЛЯ ИЗМЕРЕНИЙ ЕМКОСТИ, УГЛА ПОТЕРЬ, ИНДУКТИВНОСТИ И ДОБРОТНОСТИ
- 7-5. КОМПЕНСАТОРЫ ПОСТОЯННОГО ТОКА
- 7-6. КОМПЕНСАТОРЫ ПЕРЕМЕННОГО ТОКА
- 7-7. АВТОМАТИЧЕСКИЕ МОСТЫ И КОМПЕНСАТОРЫ
- Глава восьмая. ЦИФРОВЫЕ ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ
- 8-2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 8-3. УЗЛЫ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 8-4. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА ПОСЛЕДОВАТЕЛЬНОГО СЧЕТА
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД ЧАСТОТЫ
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД НАПРЯЖЕНИЯ ПОСТОЯННОГО ТОКА
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД ПЕРЕМЕЩЕНИЯ
- 8-5. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА ПОСЛЕДОВАТЕЛЬНОГО ПРИБЛИЖЕНИЯ
- 8-6. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА СЧИТЫВАНИЯ
- 8-7. ХАРАКТЕРИСТИКА СОВРЕМЕННЫХ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ПЕРСПЕКТИВЫ ИХ РАЗВИТИЯ
- Глава девятая. РЕГИСТРИРУЮЩИЕ ПРИБОРЫ И УСТРОЙСТВА
- 9-2. САМОПИШУЩИЕ ПРИБОРЫ ПРЯМОГО ПРЕОБРАЗОВАНИЯ
- 9-3. СВЕТОЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 9-4. МАГНИТОГРАФЫ, ГРАФОПОСТРОИТЕЛИ, ЭЛЕКТРОННЫЕ ОСЦИЛЛОГРАФЫ, ЦИФРОПЕЧАТАЮЩИЕ УСТРОЙСТВА
- Глава десятая. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНЫХ ВЕЛИЧИН
- 10-2. МАГНИТОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНОГО ПОТОКА
- ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНОЙ ИНДУКЦИИ И НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ
- 10-3. АППАРАТУРА ДЛЯ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- Глава одиннадцатая. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 11-2. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- ГЕНЕРАТОРНЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
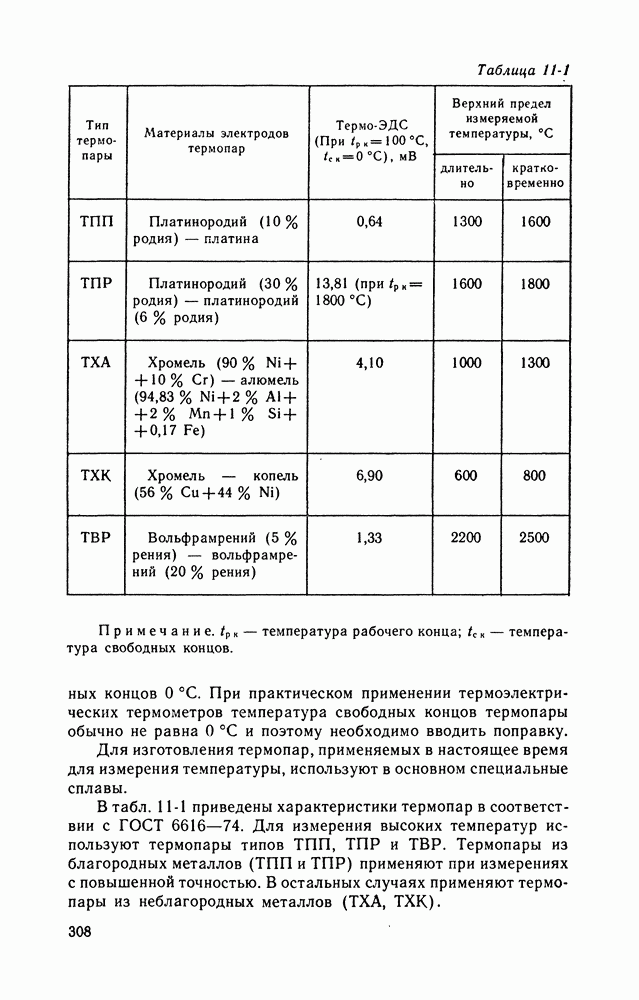
- 11-3. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ТЕМПЕРАТУРЫ
- 11-4. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ГЕОМЕТРИЧЕСКИХ И МЕХАНИЧЕСКИХ ВЕЛИЧИН
- 11-5. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ КОНЦЕНТРАЦИИ ЖИДКОЙ И ГАЗООБРАЗНОЙ СРЕДЫ
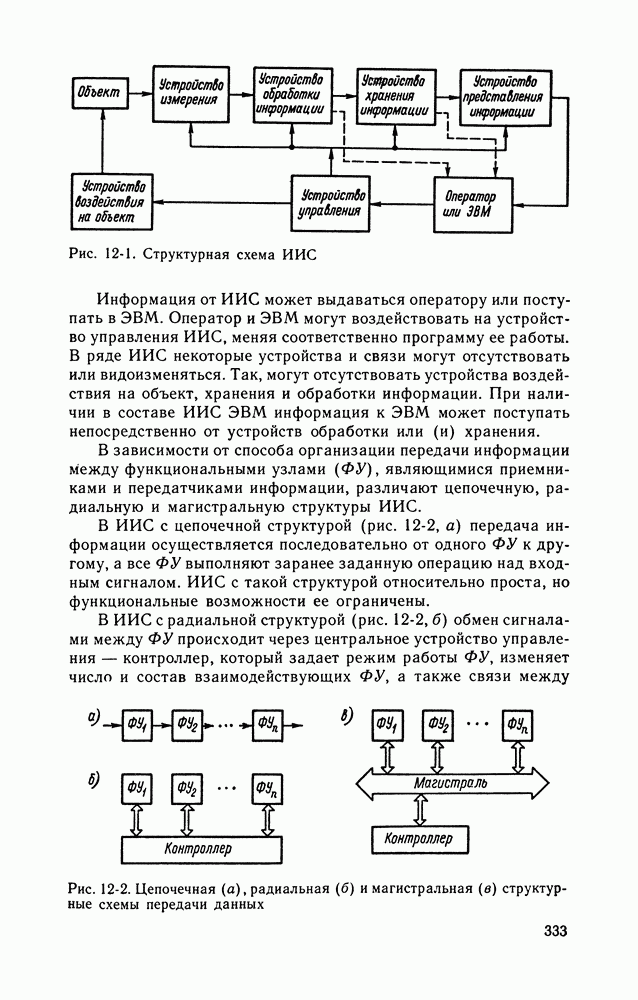
- Глава двенадцатая. ИЗМЕРИТЕЛЬНЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ
- 12-2. ИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ
- 12-3. ТЕЛЕИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ
- 12-4. СИСТЕМЫ АВТОМАТИЧЕСКОГО КОНТРОЛЯ И ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ
- 12-5. ИЗМЕРИТЕЛЬНЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ НА ОСНОВЕ АГРЕГАТНЫХ КОМПЛЕКСОВ ГОСУДАРСТВЕННОЙ СИСТЕМЫ ПРИБОРОВ И СРЕДСТВ АВТОМАТИЗАЦИИ
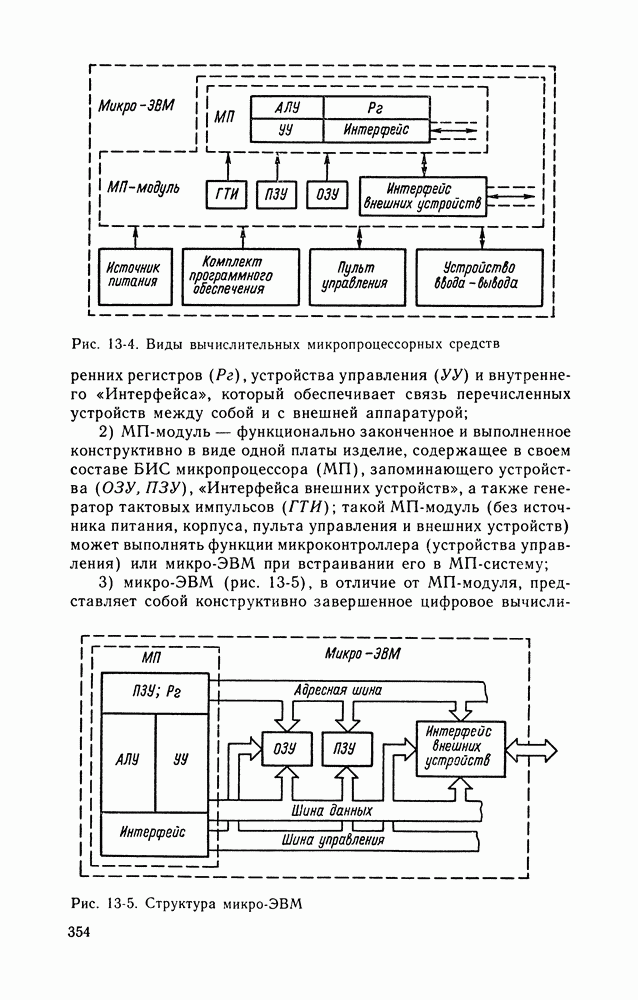
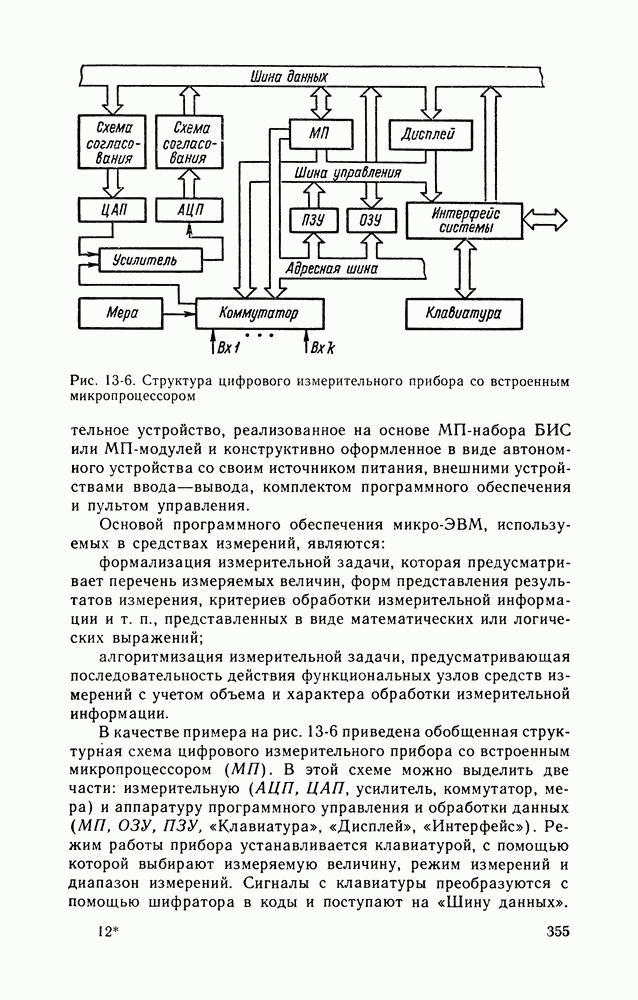
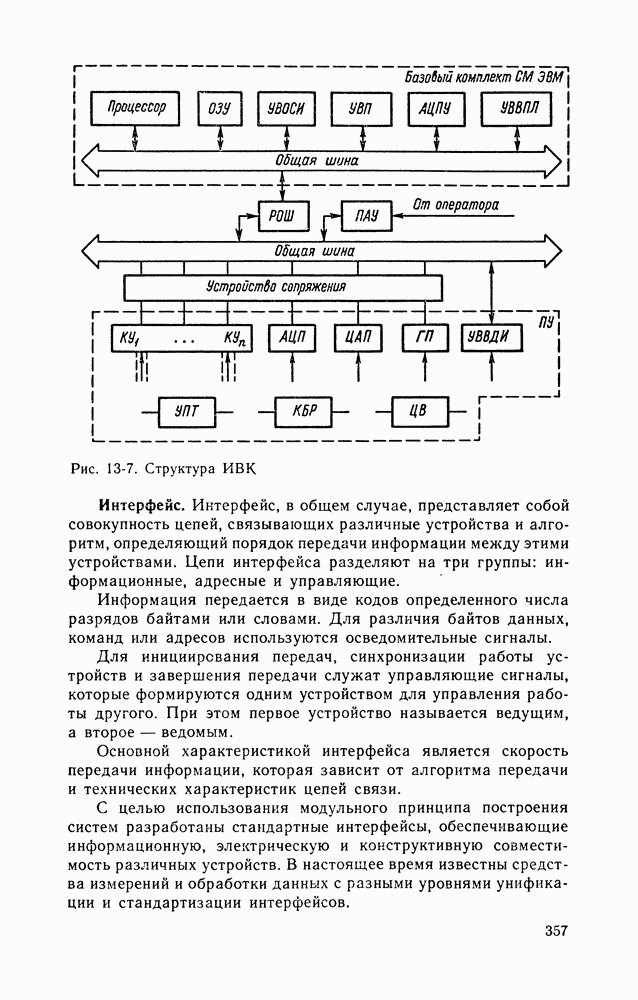
- Глава тринадцатая. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ СРЕДСТВА
- 13-2. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ СРЕДСТВА СИСТЕМНОГО ПРИМЕНЕНИЯ
- 13-3. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ КОМПЛЕКСЫ
- Раздел В. ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
- Глава четырнадцатая. ПОДГОТОВКА ИЗМЕРИТЕЛЬНОГО ЭКСПЕРИМЕНТА И ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- 14-2. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- 14-3. СУММИРОВАНИЕ ПОГРЕШНОСТЕЙ
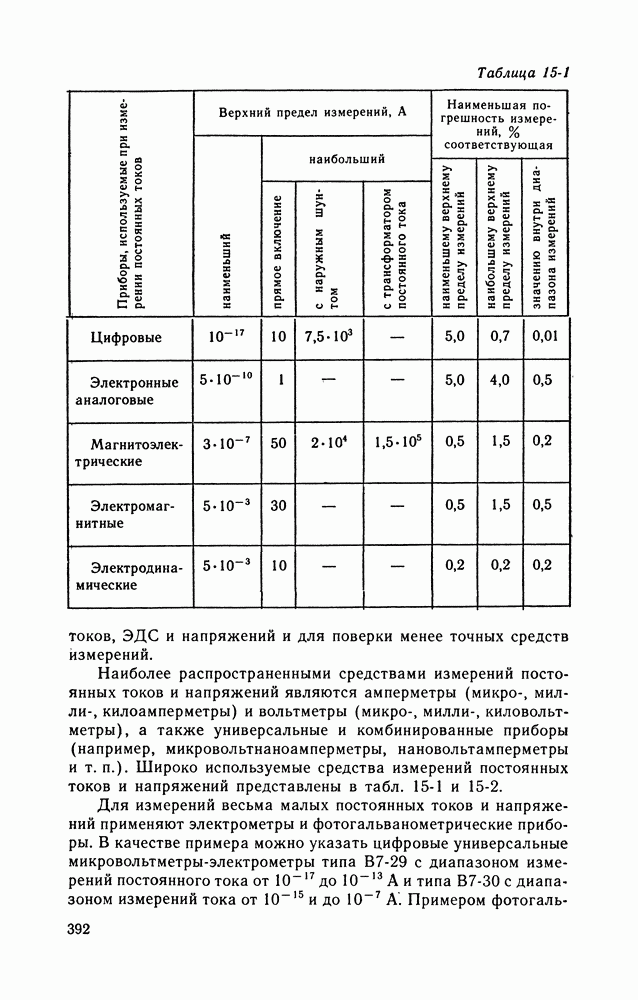
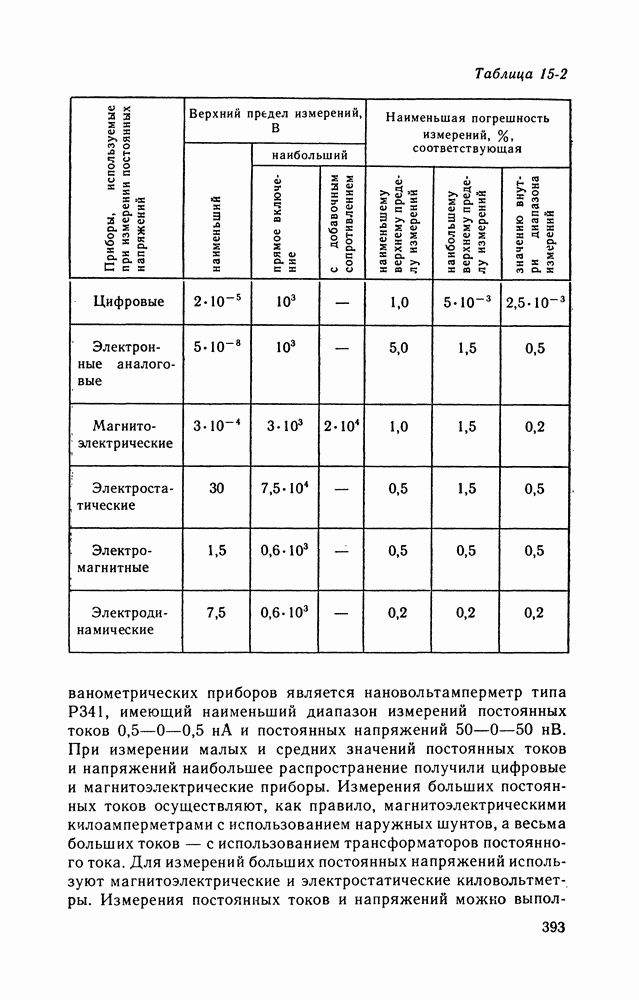
- Глава пятнадцатая. ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ, МАГНИТНЫХ И НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 15-2. ИЗМЕРЕНИЯ МОЩНОСТИ, ЭНЕРГИИ И КОЛИЧЕСТВА ЭЛЕКТРИЧЕСТВА
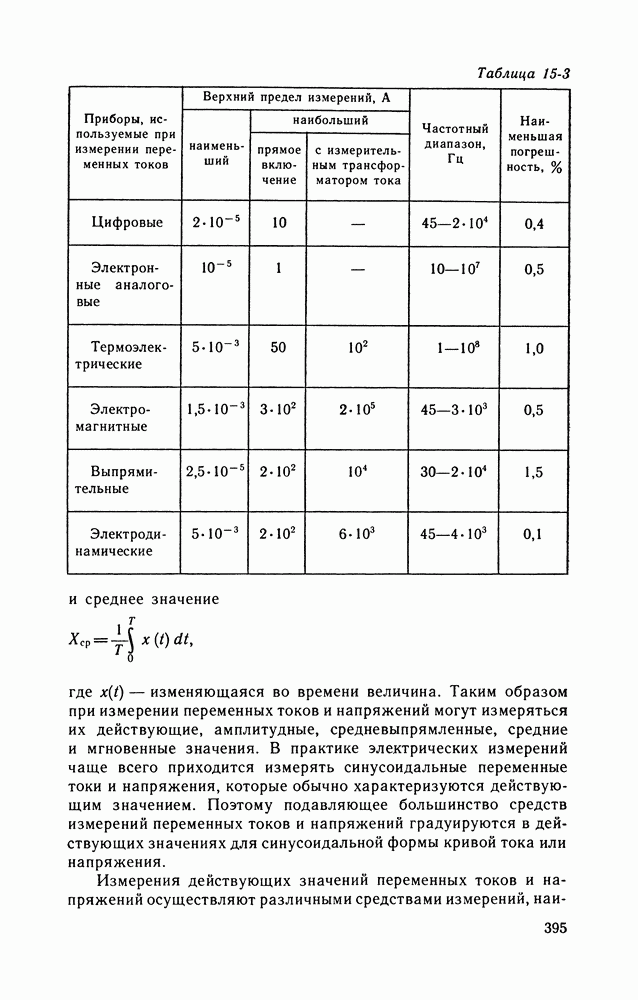
- 15-3. ИЗМЕРЕНИЯ ЧАСТОТЫ, ФАЗЫ, ВРЕМЕННЫХ ИНТЕРВАЛОВ, АНАЛИЗ СПЕКТРА ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
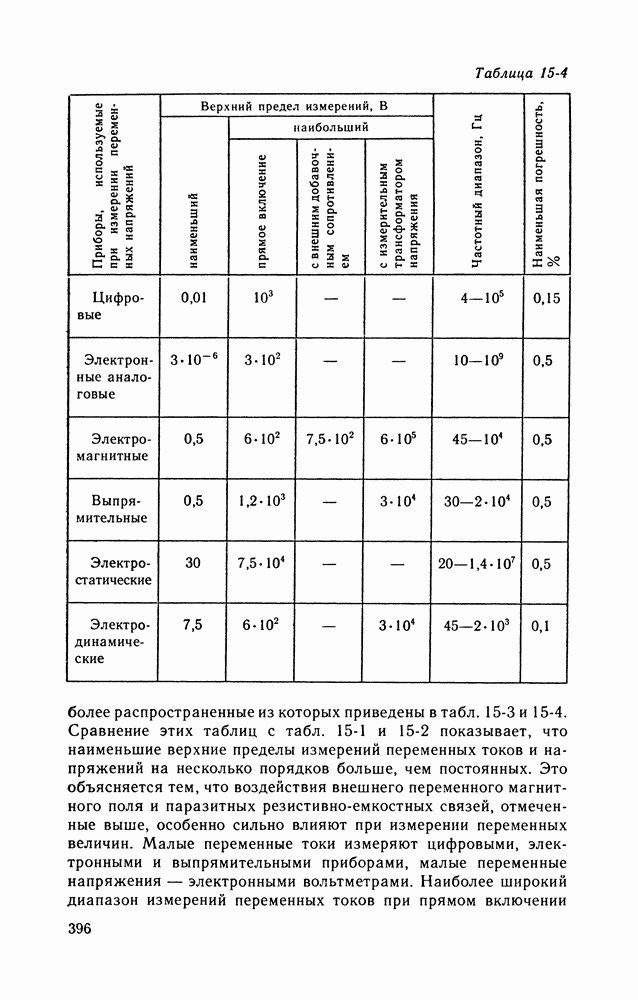
- 15-4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ЦЕПЕЙ ПОСТОЯННОГО И ПЕРЕМЕННОГО ТОКА
- 15-5. ИЗМЕРЕНИЯ ПАРАМЕТРОВ МАГНИТНОГО ПОЛЯ, ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
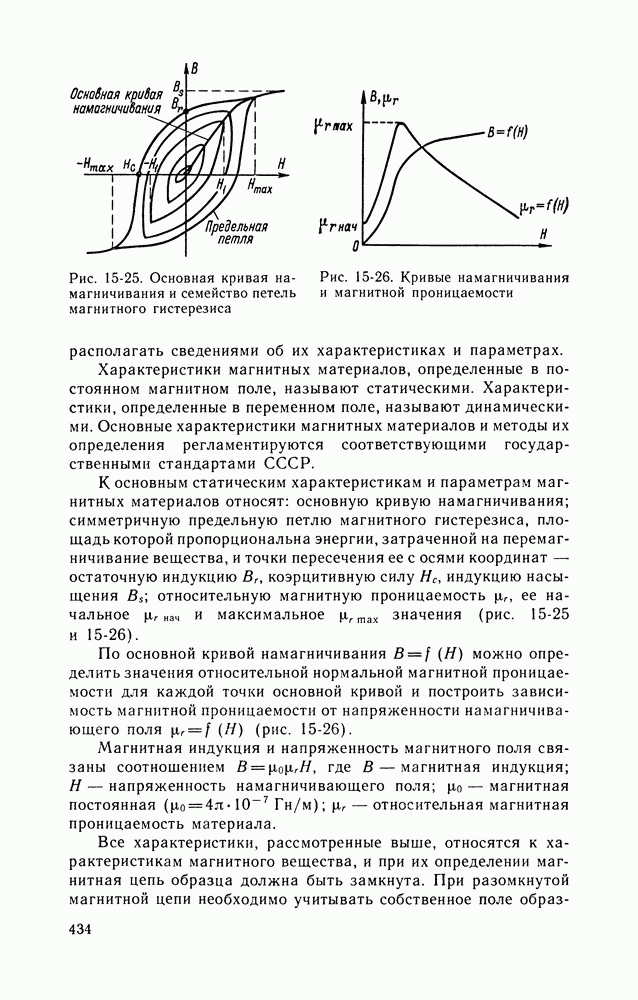
- МАГНИТНЫЕ МАТЕРИАЛЫ И ИХ ХАРАКТЕРИСТИКИ
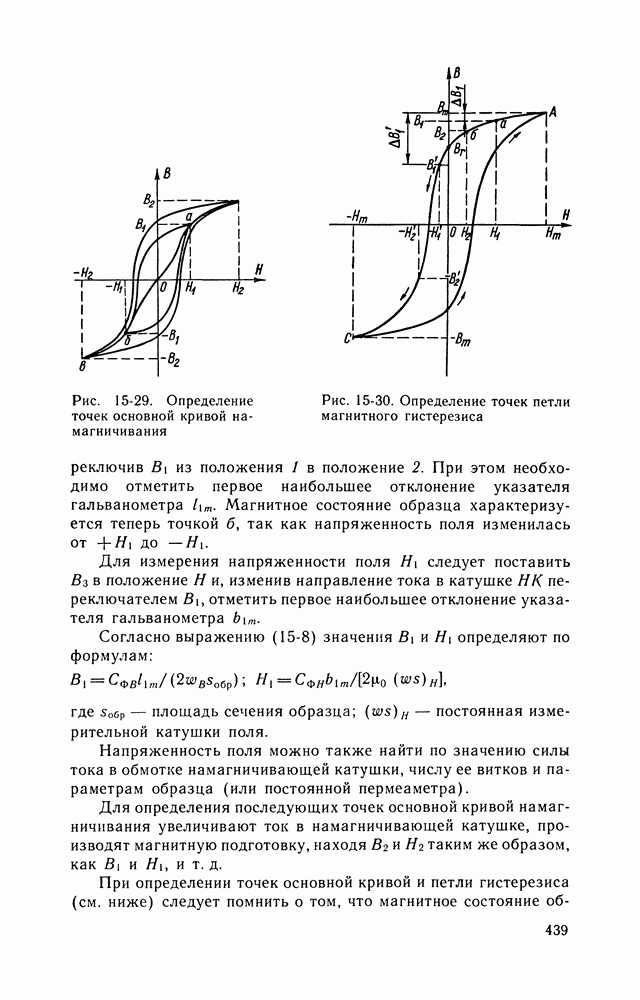
- ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- 15-6. ИЗМЕРЕНИЯ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
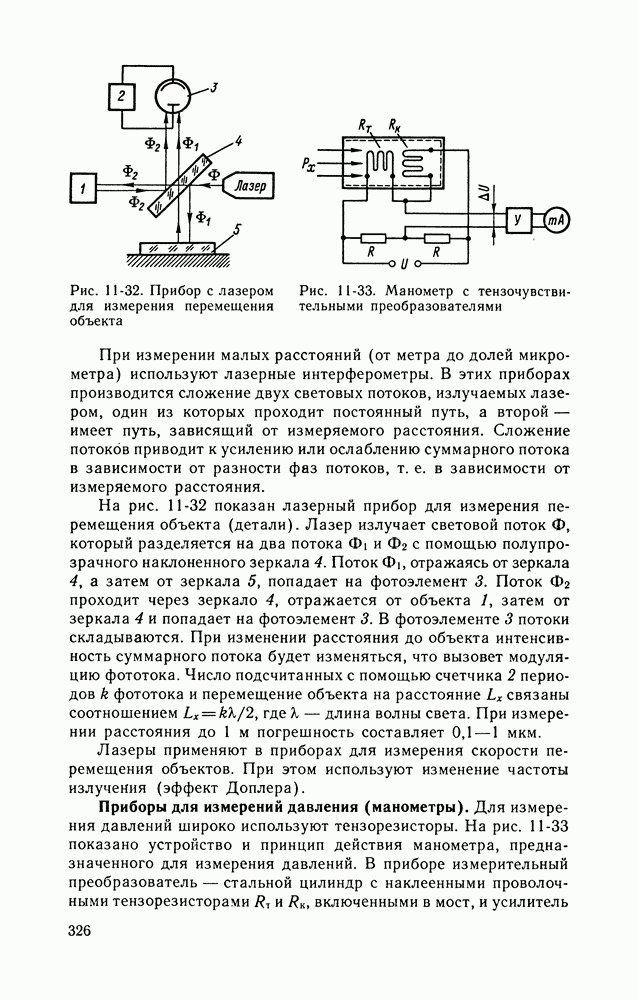
- ИЗМЕРЕНИЯ ДАВЛЕНИЙ, ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ И РАССТОЯНИЙ
- Глава шестнадцатая. ИЗМЕРЕНИЯ ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ПРОЦЕССОВ
- 16-2. ИЗМЕРЕНИЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ДИСПЕРСИИ СЛУЧАЙНОГО ПРОЦЕССА
- 16-3. ИЗМЕРЕНИЕ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
- 16-4. ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННОЙ ФУНКЦИИ
- 16-5. АНАЛИЗ СПЕКТРА МОЩНОСТИ
- Список литературы