| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава шестнадцатая. ИЗМЕРЕНИЯ ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ПРОЦЕССОВ
16-1. ОБЩИЕ СВЕДЕНИЯ
Измерения вероятностных характеристик случайных процессов (статистические измерения) составляют один из наиболее быстро развивающихся разделов измерительной техники. В настоящее время область распространения статистических методов исследования и обработки сигналов измерительной информации практически безгранична. Связь, навигация, управление, диагностика (техническая, медицинская), исследование среды и многие другие области немыслимы без знания и использования свойств сигналов и помех, описываемых их вероятностными характеристиками.
Потребность в изучении свойств случайных процессов привела к развитию соответствующих методов и средств (преимущественно электрических). Появление анализаторов функций распределения вероятностей, коррелометров, измерителей математического ожидания, дисперсиометров и других видов измерителен вероятностных характеристик открыло новые возможности в области создания современной информационной и управляющей техники.
Рассмотрим необходимые исходные определения и общие сведения о статистических измерениях (см. также § 2-2, 4-4).
В теории статистических измерений используют следующие понятия и их аналоги, заимствованные из теории случайных функций (аналоги из математической статистики): реализация случайного процесса (выборочная функция), мгновенное значение (выборочное значение), совокупность мгновенных значений (выборка), вероятностная характеристика (предел выборочного среднего).
Введем следующие обозначения:  — случайный процесс;
— случайный процесс;  — порядковый номер реализации случайного процесса
— порядковый номер реализации случайного процесса  — мгновенное значение процесса
— мгновенное значение процесса  соответствующее значению
соответствующее значению  реализации в
реализации в  момент времени. Случайным называют процесс
момент времени. Случайным называют процесс  мгновенные значения которого
мгновенные значения которого  суть случайные величины.
суть случайные величины.
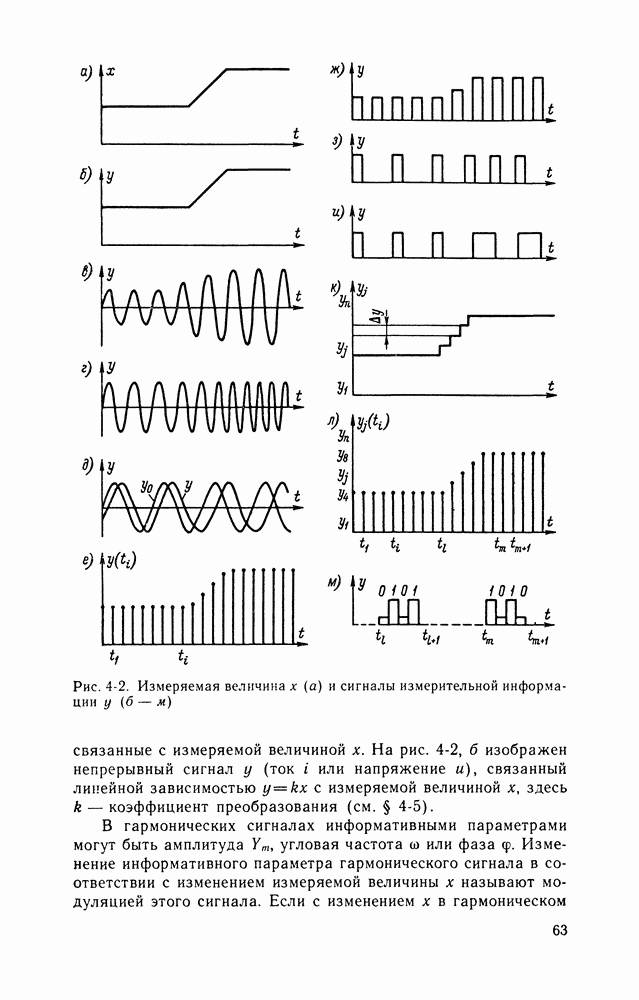
На рис. 16-1 представлена в качестве примера совокупность реализаций случайного процесса, воспроизводящих зависимости некоторого параметра X от времени 

Рис. 16-1. Совокупность реализаций случайного процесса
В теории случайных процессов их полное описание производится с помощью систем вероятностных характеристик: многомерных функций распределения вероятности, моментных функций, характеристических функций и т. п. В теории статистических измерений исследуемый случайный процесс представляется своими реализациями, причем полное представление осуществляется с помощью так называемого ансамбля, т. е. бесконечной совокупностью реализаций. Ансамбль — математическая абстракция, модель рассматриваемого процесса, но конкретные реализации, используемые в измерительном эксперименте, представляют собой физические объекты или явления и входят в ансамбль как его неотъемлемая часть.
Если случайный процесс представлен ансамблем реализаций  то вероятностная характеристика 0 может быть определена усреднением по совокупности, т. е.
то вероятностная характеристика 0 может быть определена усреднением по совокупности, т. е.

где  некоторое преобразование, лежащее в основе определения вероятностной характеристики 0. Так, например, при определении дисперсии
некоторое преобразование, лежащее в основе определения вероятностной характеристики 0. Так, например, при определении дисперсии  При этом полагаем, что процесс характеризуется нулевым математическим ожиданием.
При этом полагаем, что процесс характеризуется нулевым математическим ожиданием.
Вместо усреднения по совокупности может быть использовано усреднение по времени с использованием  реализации
реализации  и тогда
и тогда

Например, при определении математического ожидания

В общем случае результаты усреднения по совокупности (16-1) и по времени (16-2) неодинаковы. Предел выборочного среднего по совокупности (16-1) представляет собой вероятностную характеристику, выражающую зависимость вероятностных свойств процесса от текущего времени. Предел выборочного среднего по времени (16-2) представляет собой вероятностную характеристику, выражающую зависимость вероятностных свойств процесса от номера реализации.
Наличие и отсутствие зависимости вероятностных характеристик от времени или от номера реализации определяет такие фундаментальные свойства процесса, как стационарность и эргодичность. Стационарным называется процесс, вероятностные характеристики которого не зависят от времени; соответственно эргодическим называется процесс, вероятностные характеристики которого не зависят от номера реализации.
Следовательно, стационарный неэргодический случайный процесс — это такой процесс, у которого эквивалентны временные сечения (вероятностные характеристики не зависят от текущего времени), но не эквивалентны реализации (вероятностные характеристики зависят от номера реализации). Нестационарный эргодический процесс — это процесс, у которого эквивалентны реализации (вероятностные характеристики не зависят от номера реализации), но не эквивалентны временные сечения (вероятностные характеристики зависят от текущего времени).
Классифицируя случайные процессы на основе этих признаков (стационарность и эргодичность), получаем следующие четыре класса процессов: стационарные эргодические, стационарные неэргодические, нестационарные эргодические, нестационарные неэргодические.
Учет и использование описанных свойств случайных процессов играет большую роль при планировании эксперимента по определению их вероятностных характеристик.
Поскольку измерение представляет собой процедуру нахождения величины опытным путем с помощью специальных технических средств, реализующих алгоритм, включающий в себя операцию сравнения с известной величиной, в статических измерениях должна применяться мера, воспроизводящая известную величину.
Типовые алгоритмы измерений вероятностных характеристик случайных процессов, различающиеся способом применения меры в процессе измерений, представляются в следующем виде:

Рис. 16-2. Средства измерений вероятностных характеристик случайных процессов, когда сравнение с образцовой мерой является заключительной (а), выполняется до усреднения (б) и является начальной (в) операцией

где  — оператор усреднения; К — оператор сравнения;
— оператор усреднения; К — оператор сравнения;  - результат измерения характеристики
- результат измерения характеристики 
Данные алгоритмы различаются порядком выполнения операций. Операция сравнения с образцовой мерой  может быть заключительной [см. (16-4)], выполняться после реализации оператора
может быть заключительной [см. (16-4)], выполняться после реализации оператора  но до усреднения [см. (16-5)] и, наконец, быть начальной [см. (16-6)]. Соответствующие обобщенные структурные схемы средств измерений значений вероятностных характеристик представлены на рис. 16-2.
но до усреднения [см. (16-5)] и, наконец, быть начальной [см. (16-6)]. Соответствующие обобщенные структурные схемы средств измерений значений вероятностных характеристик представлены на рис. 16-2.
На этих рисунках для обозначения блоков, реализующих операторы, входящие в выражения (16-4) — (16-6), используются те же обозначения. Так,  — устройство, выполняющее преобразование, лежащее в основе определения вероятностной характеристики
— устройство, выполняющее преобразование, лежащее в основе определения вероятностной характеристики  — устройство усреднения (сумматор или интегратор); К — компаратор (сравнивающее устройство),
— устройство усреднения (сумматор или интегратор); К — компаратор (сравнивающее устройство), 
мера, с помощью которой формируется известная величина  или
или 
Представленное на рис. 16-2, а средство измерений реализует следующую процедуру: на вход поступает совокупность реализаций  (при использовании усреднения по времени — одна реализация
(при использовании усреднения по времени — одна реализация  на выходе узла
на выходе узла  имеем совокупность преобразованных реализаций
имеем совокупность преобразованных реализаций  после усреднения получаем величину
после усреднения получаем величину  которая поступает на компаратор, осуществляющий сравнение с известной величиной
которая поступает на компаратор, осуществляющий сравнение с известной величиной  в результате чего получаем значение измеряемой вероятностной характеристики в
в результате чего получаем значение измеряемой вероятностной характеристики в 
Отличие процедуры, реализуемой средством измерений, представленным на рис. 16-2, б, заключается в том, что послеформирования совокупности  она поступает не на усреднитель, а на компаратор, который выполняет сравнение с известной величиной
она поступает не на усреднитель, а на компаратор, который выполняет сравнение с известной величиной  на выходе компаратора формируется числовой массив
на выходе компаратора формируется числовой массив  и усреднение выполняется в числовой форме. На выходе усреднителя
и усреднение выполняется в числовой форме. На выходе усреднителя  имеем результат измерения
имеем результат измерения 
Средство измерений (рис. 16-2, в) основано на формировании массива числовых эквивалентов мгновенных значений реализаций случайного процесса  после чего преобразование
после чего преобразование  и усреднение выполняются в числовой форме. Это устройство эквивалентно последовательному соединению аналого-цифрового преобразователя (АЦП) и вычислительного устройства (процессора). На выходе АЦП формируется массив мгновенных значений, а процессор по определенной программе обеспечивает реализацию операторов
и усреднение выполняются в числовой форме. Это устройство эквивалентно последовательному соединению аналого-цифрового преобразователя (АЦП) и вычислительного устройства (процессора). На выходе АЦП формируется массив мгновенных значений, а процессор по определенной программе обеспечивает реализацию операторов  и
и 
Погрешность результата измерения вероятностной характеристики случайного процесса

Для статистических измерений характерно обязательное наличие составляющей методической погрешности, обусловленной конечностью объема выборочных данных о мгновенных значениях реализаций случайного процесса, ибо при проведении физического эксперимента принципиально не может быть использован бесконечный ансамбль реализаций или бесконечный временной интервал. Соотношение (16-7) определяет результирующую погрешность, включающую в себя как методическую, так и инструментальную составляющие. В дальнейшем будут приводиться соотношения только для определения специфической для статистических измерений методической погрешности, обусловленной конечностью числа реализаций и временного интервала.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Раздел А. ОБЩИЕ СВЕДЕНИЯ ОБ ИЗМЕРИТЕЛЬНОЙ ТЕХНИКЕ
- Глава первая. ОСНОВНЫЕ ПОНЯТИЯ ИЗМЕРИТЕЛЬНОЙ ТЕХНИКИ И КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ
- 1-2. ВИДЫ И МЕТОДЫ ИЗМЕРЕНИЙ
- Глава вторая. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
- 2-1. ОСНОВНЫЕ ПОНЯТИЯ И ВИДЫ ПОГРЕШНОСТЕЙ
- 2-2. ВЕРОЯТНОСТНЫЙ ПОДХОД К ОПИСАНИЮ ПОГРЕШНОСТЕЙ
- 2-3. ВЕРОЯТНОСТНЫЕ ОЦЕНКИ ПОГРЕШНОСТЕЙ
- Глава третья. ОСНОВЫ МЕТРОЛОГИЧЕСКОГО ОБЕСПЕЧЕНИЯ
- 3-2. ЭТАЛОНЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН
- 3-3. ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ
- Раздел Б. ЭЛЕКТРИЧЕСКИЕ СРЕДСТВА ИЗМЕРЕНИЙ
- Глава четвертая. ОБЩИЕ СВЕДЕНИЯ О СРЕДСТВАХ ИЗМЕРЕНИЙ
- 4-2. ГОСУДАРСТВЕННАЯ СИСТЕМА ПРИБОРОВ
- 4-3. ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
- 4-4. СИГНАЛЫ ИЗМЕРИТЕЛЬНОЙ ИНФОРМАЦИИ
- Математические модели сигналов.
- Дискретизация сигналов.
- 4-5. СТРУКТУРНЫЕ СХЕМЫ И СВОЙСТВА СРЕДСТВ ИЗМЕРЕНИЙ В СТАТИЧЕСКОМ РЕЖИМЕ
- Средства измерений прямого преобразования.
- Средства измерений уравновешивающего преобразования.
- 4-6. СРЕДСТВА ИЗМЕРЕНИЙ В ДИНАМИЧЕСКОМ РЕЖИМЕ
- Переходные и импульсные переходные характеристики.
- Частотные характеристики.
- Передаточные функции.
- Глава пятая. МЕРЫ, ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ
- 5-2. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 5-3. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ
- МАГНИТОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ
- Амперметры и вольтметры.
- Омметры.
- Гальванометры.
- Баллистические гальванометры.
- Кулонметры.
- Вибрационные гальванометры.
- ЭЛЕКТРОДИНАМИЧЕСКИЕ И ФЕРРОДИНАМИЧЕСКИЕ ПРИБОРЫ
- ЭЛЕКТРОМАГНИТНЫЕ ПРИБОРЫ
- ЭЛЕКТРОСТАТИЧЕСКИЕ ПРИБОРЫ
- ИНДУКЦИОННЫЕ ПРИБОРЫ
- 5-4. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ С ПРЕОБРАЗОВАТЕЛЯМИ
- Глава шестая. ЭЛЕКТРОННЫЕ АНАЛОГОВЫЕ ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ
- 6-2. ЭЛЕКТРОННЫЕ ВОЛЬТМЕТРЫ
- 6-3. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ ЧАСТОТЫ И ФАЗЫ
- 6-4. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ МОЩНОСТИ И ЭНЕРГИИ
- 6-5. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ПАРАМЕТРОВ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 6-6. ЭЛЕКТРОННО ЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 6-7. АНАЛИЗАТОРЫ СПЕКТРА, ИЗМЕРИТЕЛИ НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ
- Глава седьмая. МОСТЫ И КОМПЕНСАТОРЫ
- 7-2. ТЕОРИЯ МОСТОВЫХ СХЕМ
- 7-3. МОСТЫ ДЛЯ ИЗМЕРЕНИЙ СОПРОТИВЛЕНИЯ НА ПОСТОЯННОМ ТОКЕ
- 7-4. МОСТЫ ПЕРЕМЕННОГО ТОКА ДЛЯ ИЗМЕРЕНИЙ ЕМКОСТИ, УГЛА ПОТЕРЬ, ИНДУКТИВНОСТИ И ДОБРОТНОСТИ
- 7-5. КОМПЕНСАТОРЫ ПОСТОЯННОГО ТОКА
- 7-6. КОМПЕНСАТОРЫ ПЕРЕМЕННОГО ТОКА
- 7-7. АВТОМАТИЧЕСКИЕ МОСТЫ И КОМПЕНСАТОРЫ
- Глава восьмая. ЦИФРОВЫЕ ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ
- 8-2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 8-3. УЗЛЫ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 8-4. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА ПОСЛЕДОВАТЕЛЬНОГО СЧЕТА
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД ЧАСТОТЫ
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД НАПРЯЖЕНИЯ ПОСТОЯННОГО ТОКА
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД ПЕРЕМЕЩЕНИЯ
- 8-5. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА ПОСЛЕДОВАТЕЛЬНОГО ПРИБЛИЖЕНИЯ
- 8-6. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА СЧИТЫВАНИЯ
- 8-7. ХАРАКТЕРИСТИКА СОВРЕМЕННЫХ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ПЕРСПЕКТИВЫ ИХ РАЗВИТИЯ
- Глава девятая. РЕГИСТРИРУЮЩИЕ ПРИБОРЫ И УСТРОЙСТВА
- 9-2. САМОПИШУЩИЕ ПРИБОРЫ ПРЯМОГО ПРЕОБРАЗОВАНИЯ
- 9-3. СВЕТОЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 9-4. МАГНИТОГРАФЫ, ГРАФОПОСТРОИТЕЛИ, ЭЛЕКТРОННЫЕ ОСЦИЛЛОГРАФЫ, ЦИФРОПЕЧАТАЮЩИЕ УСТРОЙСТВА
- Глава десятая. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНЫХ ВЕЛИЧИН
- 10-2. МАГНИТОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНОГО ПОТОКА
- ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНОЙ ИНДУКЦИИ И НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ
- 10-3. АППАРАТУРА ДЛЯ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- Глава одиннадцатая. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 11-2. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- ГЕНЕРАТОРНЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
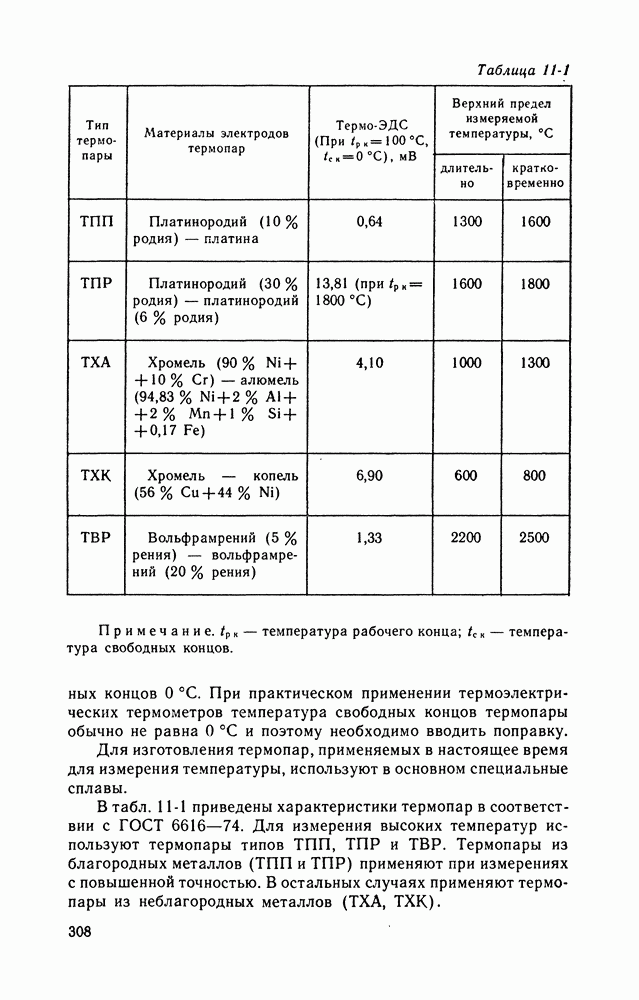
- 11-3. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ТЕМПЕРАТУРЫ
- 11-4. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ГЕОМЕТРИЧЕСКИХ И МЕХАНИЧЕСКИХ ВЕЛИЧИН
- 11-5. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ КОНЦЕНТРАЦИИ ЖИДКОЙ И ГАЗООБРАЗНОЙ СРЕДЫ
- Глава двенадцатая. ИЗМЕРИТЕЛЬНЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ
- 12-2. ИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ
- 12-3. ТЕЛЕИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ
- 12-4. СИСТЕМЫ АВТОМАТИЧЕСКОГО КОНТРОЛЯ И ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ
- 12-5. ИЗМЕРИТЕЛЬНЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ НА ОСНОВЕ АГРЕГАТНЫХ КОМПЛЕКСОВ ГОСУДАРСТВЕННОЙ СИСТЕМЫ ПРИБОРОВ И СРЕДСТВ АВТОМАТИЗАЦИИ
- Глава тринадцатая. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ СРЕДСТВА
- 13-2. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ СРЕДСТВА СИСТЕМНОГО ПРИМЕНЕНИЯ
- 13-3. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ КОМПЛЕКСЫ
- Раздел В. ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
- Глава четырнадцатая. ПОДГОТОВКА ИЗМЕРИТЕЛЬНОГО ЭКСПЕРИМЕНТА И ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- 14-2. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- 14-3. СУММИРОВАНИЕ ПОГРЕШНОСТЕЙ
- Глава пятнадцатая. ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ, МАГНИТНЫХ И НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 15-2. ИЗМЕРЕНИЯ МОЩНОСТИ, ЭНЕРГИИ И КОЛИЧЕСТВА ЭЛЕКТРИЧЕСТВА
- 15-3. ИЗМЕРЕНИЯ ЧАСТОТЫ, ФАЗЫ, ВРЕМЕННЫХ ИНТЕРВАЛОВ, АНАЛИЗ СПЕКТРА ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- 15-4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ЦЕПЕЙ ПОСТОЯННОГО И ПЕРЕМЕННОГО ТОКА
- 15-5. ИЗМЕРЕНИЯ ПАРАМЕТРОВ МАГНИТНОГО ПОЛЯ, ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
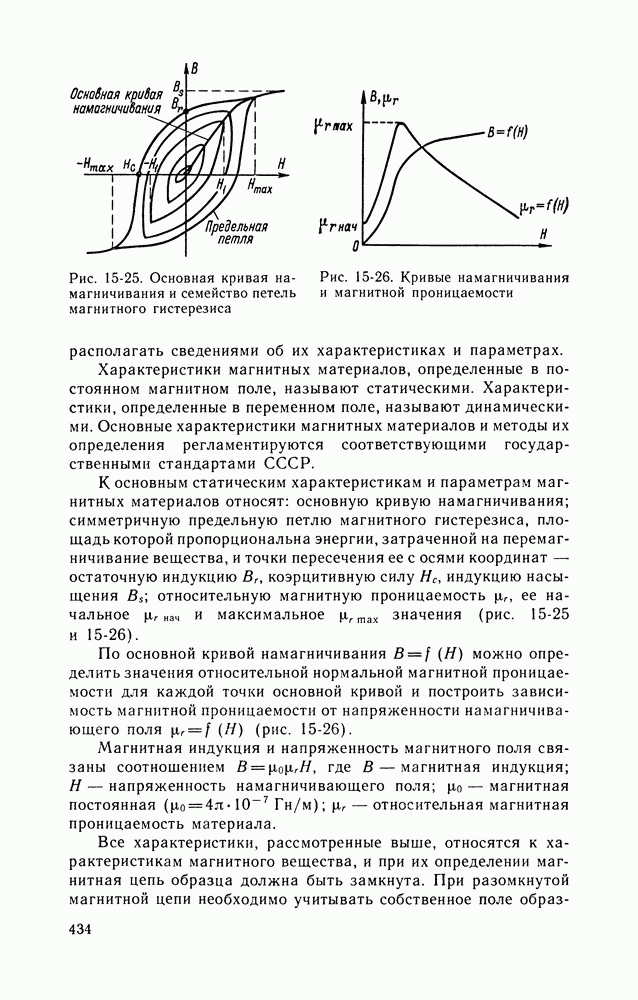
- МАГНИТНЫЕ МАТЕРИАЛЫ И ИХ ХАРАКТЕРИСТИКИ
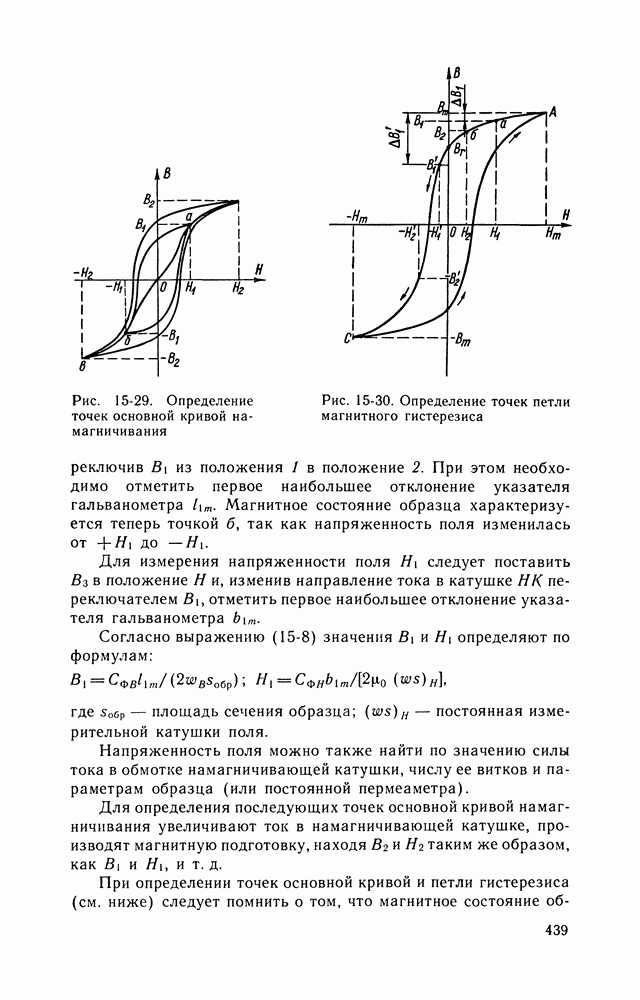
- ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- 15-6. ИЗМЕРЕНИЯ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- ИЗМЕРЕНИЯ ДАВЛЕНИЙ, ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ И РАССТОЯНИЙ
- Глава шестнадцатая. ИЗМЕРЕНИЯ ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ПРОЦЕССОВ
- 16-2. ИЗМЕРЕНИЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ДИСПЕРСИИ СЛУЧАЙНОГО ПРОЦЕССА
- 16-3. ИЗМЕРЕНИЕ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
- 16-4. ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННОЙ ФУНКЦИИ
- 16-5. АНАЛИЗ СПЕКТРА МОЩНОСТИ
- Список литературы