| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Передаточные функции.
Используя преобразование Лапласа, запишем уравнение (4-39) в операторной форме

где  — изображения по Лапласу
— изображения по Лапласу  Отношение изображений выходного и входного сигналов
Отношение изображений выходного и входного сигналов

называют передаточной функцией. Передаточная функция является полной математической моделью средства измерений. При
известном входном сигнале  и его изображении
и его изображении  изображение выходного сигнала определяется из соотношения
изображение выходного сигнала определяется из соотношения

Передаточную функцию (4-78) можно представить в виде произведения

где  — корни знаменателя выражения (4-78). Такая форма записи имеет известную физическую интерпретацию: сложное средство измерений с передаточной функцией типа (4-78) может быть представлено последовательным соединением простейших звеньев. Такие звенья имеют следующие передаточные функции:
— корни знаменателя выражения (4-78). Такая форма записи имеет известную физическую интерпретацию: сложное средство измерений с передаточной функцией типа (4-78) может быть представлено последовательным соединением простейших звеньев. Такие звенья имеют следующие передаточные функции:
идеальное звено

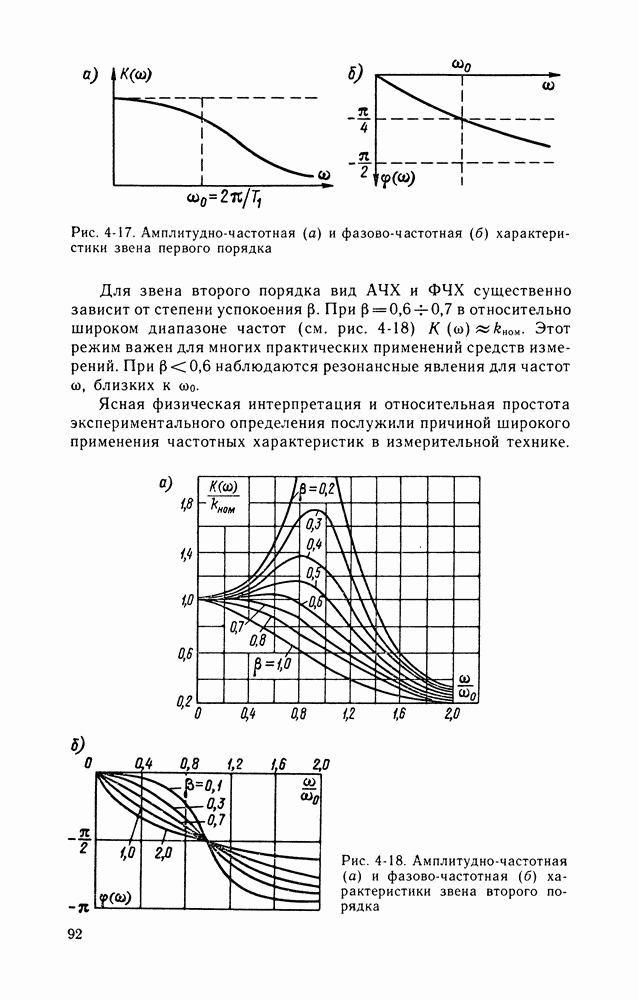
звено первого порядка

звено второго порядка

Динамические свойства таких звеньев, как было показано выше, хорошо изучены. При известных сведениях о входных сигналах — диапазоне изменения сигнала, частотном диапазоне, форме сигнала (например, прямоугольные импульсы) и других — для таких звеньев могут быть оценены динамические погрешности. Следует подчеркнуть, что при анализе динамического режима средств измерений чаще всего определяют некоторые оценки динамической погрешности при ограничениях на входные сигналы. Это объясняется тем, что точное решение в общем виде основной измерительной задачи — нахождение  по наблюдаемому сигналу
по наблюдаемому сигналу  — наталкивается на серьезные математические трудности. Так, формальная запись уравнения (4-79) в виде
— наталкивается на серьезные математические трудности. Так, формальная запись уравнения (4-79) в виде  приводит к необходимости решения так называемых некорректно поставленных обратных задач. Дело в том, что передаточная функция
приводит к необходимости решения так называемых некорректно поставленных обратных задач. Дело в том, что передаточная функция  описывает принципиально неустойчивое динамическое звено. Вследствие этого небольшим погрешностям исходных данных, а
описывает принципиально неустойчивое динамическое звено. Вследствие этого небольшим погрешностям исходных данных, а  всегда определяется с некоторой погрешностью, могут соответствовать настолько большие погрешности решения, что последние оказываются лишенными физического смысла. В настоящее время используют
всегда определяется с некоторой погрешностью, могут соответствовать настолько большие погрешности решения, что последние оказываются лишенными физического смысла. В настоящее время используют
специальные методы решения таких задач — методы регуляризации.  фективность этих методов существенно зависит от характера и объема априорной информации об исходном решении.
фективность этих методов существенно зависит от характера и объема априорной информации об исходном решении.
Подводя итоги рассмотрению динамического режима средств измерений, отметим следующее. При измерении переменных во времени величин  в реальных средствах измерений возникает динамическая погрешность. Эта погрешность определяется динамическими свойствами средств измерений и характером изменения внешних воздействий (см. § 2-1).
в реальных средствах измерений возникает динамическая погрешность. Эта погрешность определяется динамическими свойствами средств измерений и характером изменения внешних воздействий (см. § 2-1).
Динамические свойства средств измерений могут быть описаны полными динамическими характеристиками: дифференциальными уравнениями, переходными характеристиками, частотными характеристиками, передаточными функциями, а также частными динамическими характеристиками: временем установления  (временем реакции), постоянной времени
(временем реакции), постоянной времени  частотой собственных колебаний
частотой собственных колебаний  коэффициентом демпфирования (затухания)
коэффициентом демпфирования (затухания)  и некоторыми другими.
и некоторыми другими.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- Раздел А. ОБЩИЕ СВЕДЕНИЯ ОБ ИЗМЕРИТЕЛЬНОЙ ТЕХНИКЕ
- Глава первая. ОСНОВНЫЕ ПОНЯТИЯ ИЗМЕРИТЕЛЬНОЙ ТЕХНИКИ И КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ
- 1-2. ВИДЫ И МЕТОДЫ ИЗМЕРЕНИЙ
- Глава вторая. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
- 2-1. ОСНОВНЫЕ ПОНЯТИЯ И ВИДЫ ПОГРЕШНОСТЕЙ
- 2-2. ВЕРОЯТНОСТНЫЙ ПОДХОД К ОПИСАНИЮ ПОГРЕШНОСТЕЙ
- 2-3. ВЕРОЯТНОСТНЫЕ ОЦЕНКИ ПОГРЕШНОСТЕЙ
- Глава третья. ОСНОВЫ МЕТРОЛОГИЧЕСКОГО ОБЕСПЕЧЕНИЯ
- 3-2. ЭТАЛОНЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН
- 3-3. ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ
- Раздел Б. ЭЛЕКТРИЧЕСКИЕ СРЕДСТВА ИЗМЕРЕНИЙ
- Глава четвертая. ОБЩИЕ СВЕДЕНИЯ О СРЕДСТВАХ ИЗМЕРЕНИЙ
- 4-2. ГОСУДАРСТВЕННАЯ СИСТЕМА ПРИБОРОВ
- 4-3. ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
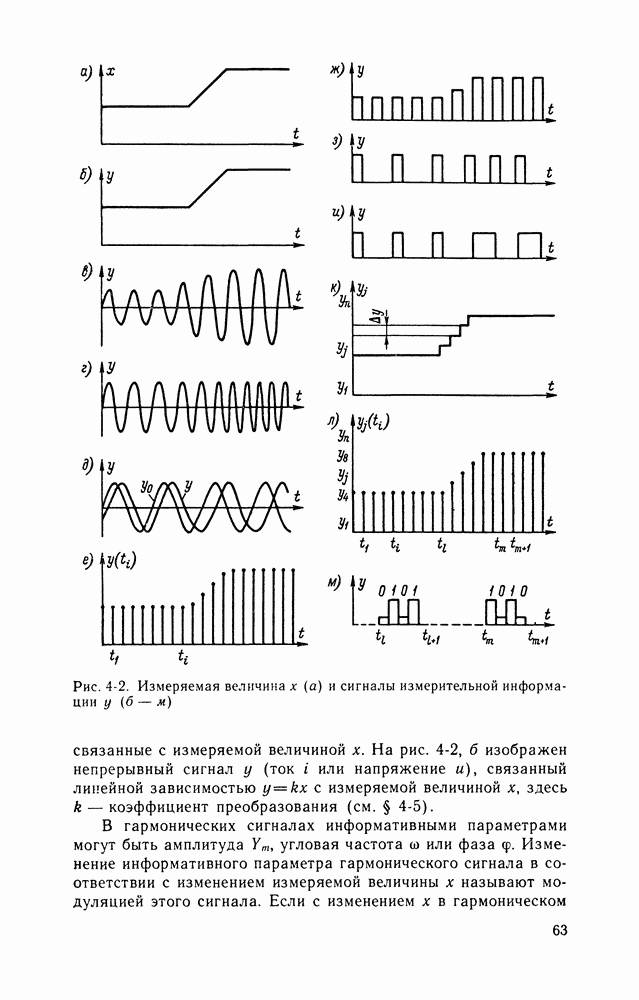
- 4-4. СИГНАЛЫ ИЗМЕРИТЕЛЬНОЙ ИНФОРМАЦИИ
- Математические модели сигналов.
- Дискретизация сигналов.
- 4-5. СТРУКТУРНЫЕ СХЕМЫ И СВОЙСТВА СРЕДСТВ ИЗМЕРЕНИЙ В СТАТИЧЕСКОМ РЕЖИМЕ
- Средства измерений прямого преобразования.
- Средства измерений уравновешивающего преобразования.
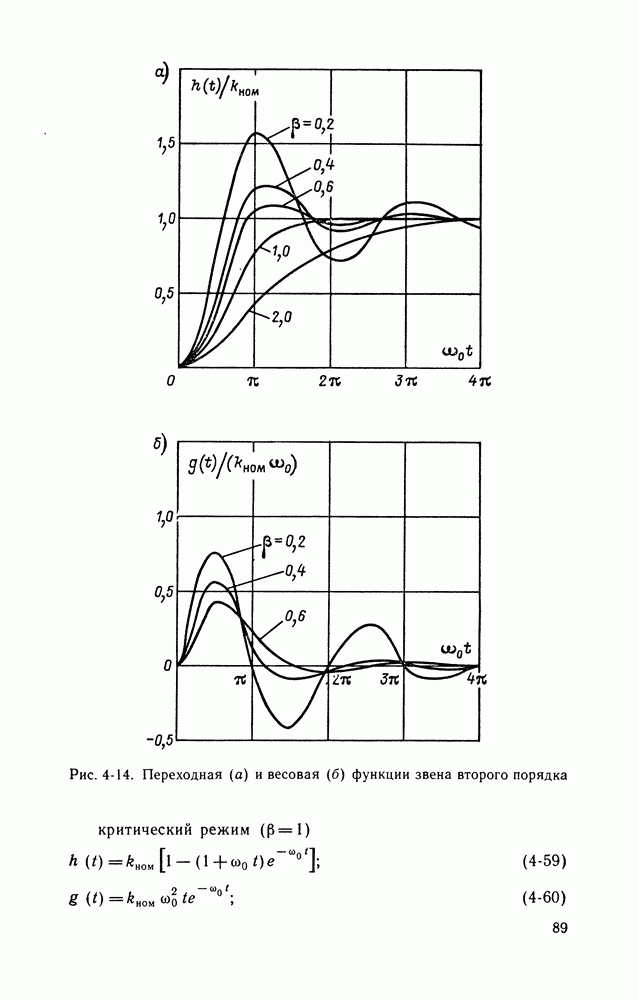
- 4-6. СРЕДСТВА ИЗМЕРЕНИЙ В ДИНАМИЧЕСКОМ РЕЖИМЕ
- Переходные и импульсные переходные характеристики.
- Частотные характеристики.
- Передаточные функции.
- Глава пятая. МЕРЫ, ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ
- 5-2. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 5-3. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ
- МАГНИТОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ
- Амперметры и вольтметры.
- Омметры.
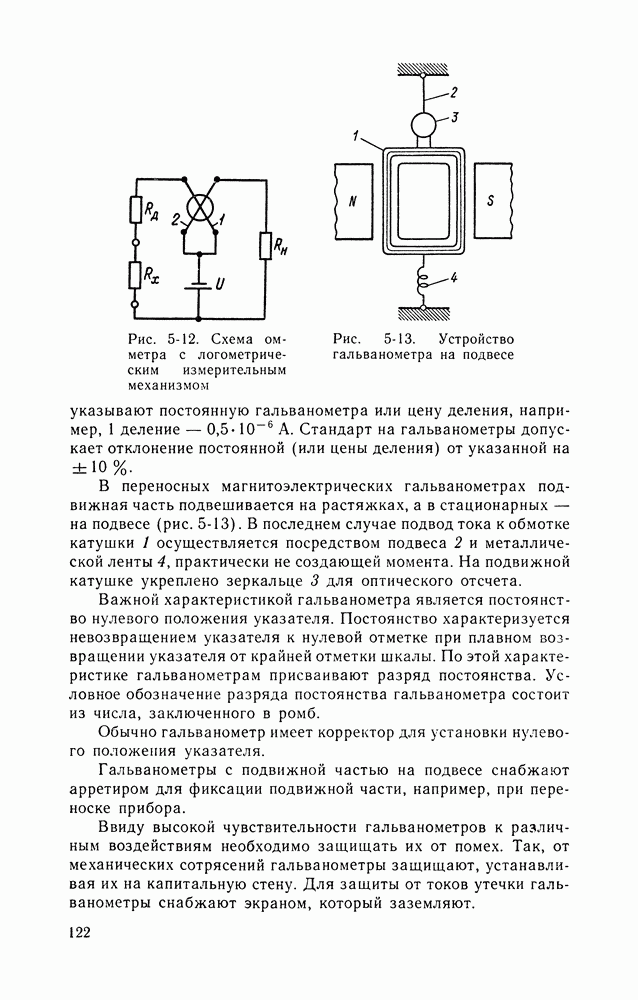
- Гальванометры.
- Баллистические гальванометры.
- Кулонметры.
- Вибрационные гальванометры.
- ЭЛЕКТРОДИНАМИЧЕСКИЕ И ФЕРРОДИНАМИЧЕСКИЕ ПРИБОРЫ
- ЭЛЕКТРОМАГНИТНЫЕ ПРИБОРЫ
- ЭЛЕКТРОСТАТИЧЕСКИЕ ПРИБОРЫ
- ИНДУКЦИОННЫЕ ПРИБОРЫ
- 5-4. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ С ПРЕОБРАЗОВАТЕЛЯМИ
- Глава шестая. ЭЛЕКТРОННЫЕ АНАЛОГОВЫЕ ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ
- 6-2. ЭЛЕКТРОННЫЕ ВОЛЬТМЕТРЫ
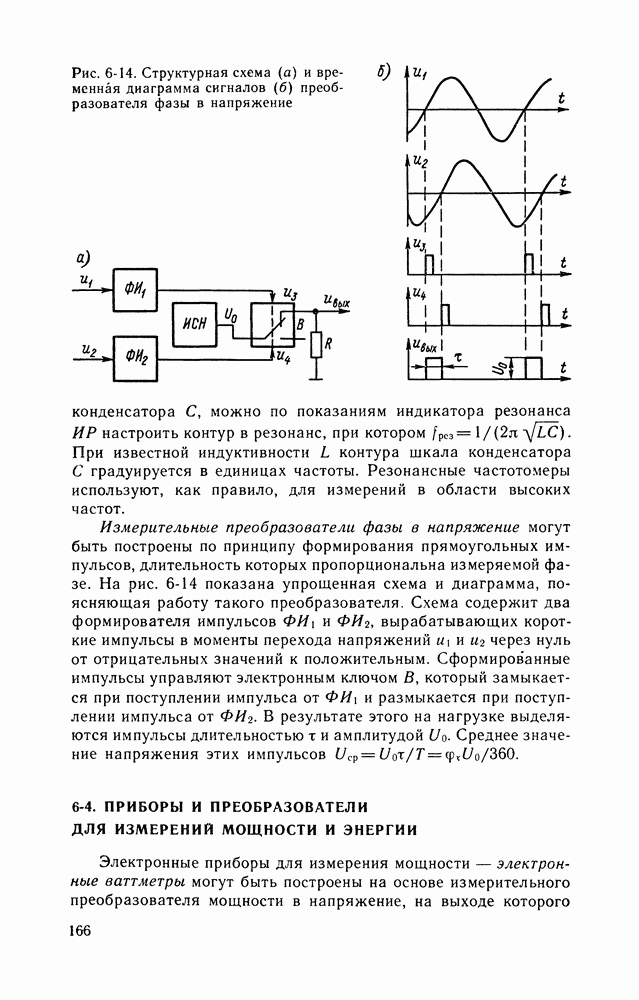
- 6-3. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ ЧАСТОТЫ И ФАЗЫ
- 6-4. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ МОЩНОСТИ И ЭНЕРГИИ
- 6-5. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ПАРАМЕТРОВ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 6-6. ЭЛЕКТРОННО ЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 6-7. АНАЛИЗАТОРЫ СПЕКТРА, ИЗМЕРИТЕЛИ НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ
- Глава седьмая. МОСТЫ И КОМПЕНСАТОРЫ
- 7-2. ТЕОРИЯ МОСТОВЫХ СХЕМ
- 7-3. МОСТЫ ДЛЯ ИЗМЕРЕНИЙ СОПРОТИВЛЕНИЯ НА ПОСТОЯННОМ ТОКЕ
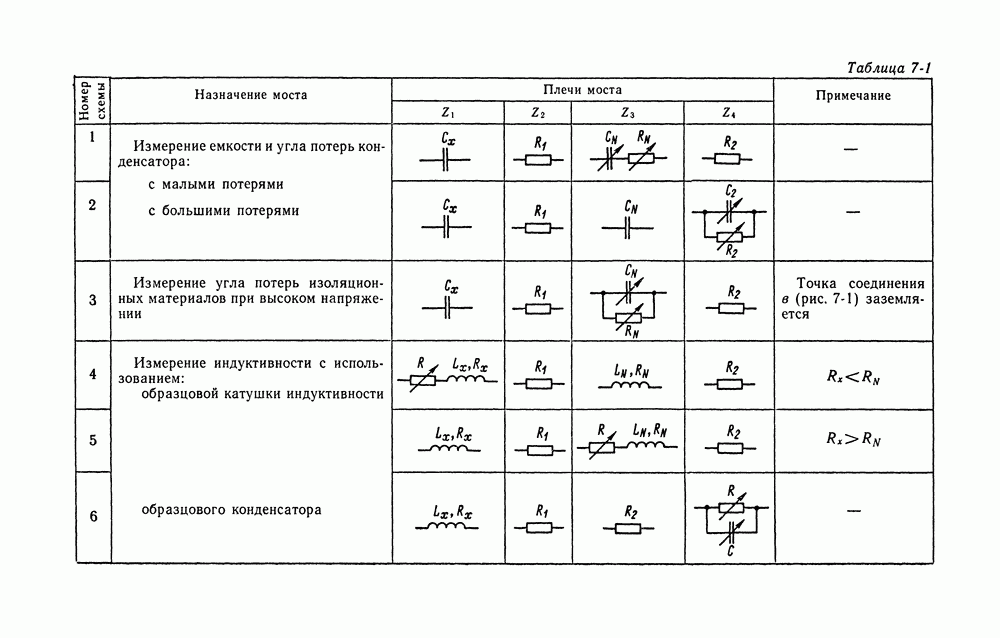
- 7-4. МОСТЫ ПЕРЕМЕННОГО ТОКА ДЛЯ ИЗМЕРЕНИЙ ЕМКОСТИ, УГЛА ПОТЕРЬ, ИНДУКТИВНОСТИ И ДОБРОТНОСТИ
- 7-5. КОМПЕНСАТОРЫ ПОСТОЯННОГО ТОКА
- 7-6. КОМПЕНСАТОРЫ ПЕРЕМЕННОГО ТОКА
- 7-7. АВТОМАТИЧЕСКИЕ МОСТЫ И КОМПЕНСАТОРЫ
- Глава восьмая. ЦИФРОВЫЕ ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ
- 8-2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 8-3. УЗЛЫ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 8-4. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА ПОСЛЕДОВАТЕЛЬНОГО СЧЕТА
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД ЧАСТОТЫ
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД НАПРЯЖЕНИЯ ПОСТОЯННОГО ТОКА
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД ПЕРЕМЕЩЕНИЯ
- 8-5. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА ПОСЛЕДОВАТЕЛЬНОГО ПРИБЛИЖЕНИЯ
- 8-6. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА СЧИТЫВАНИЯ
- 8-7. ХАРАКТЕРИСТИКА СОВРЕМЕННЫХ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ПЕРСПЕКТИВЫ ИХ РАЗВИТИЯ
- Глава девятая. РЕГИСТРИРУЮЩИЕ ПРИБОРЫ И УСТРОЙСТВА
- 9-2. САМОПИШУЩИЕ ПРИБОРЫ ПРЯМОГО ПРЕОБРАЗОВАНИЯ
- 9-3. СВЕТОЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 9-4. МАГНИТОГРАФЫ, ГРАФОПОСТРОИТЕЛИ, ЭЛЕКТРОННЫЕ ОСЦИЛЛОГРАФЫ, ЦИФРОПЕЧАТАЮЩИЕ УСТРОЙСТВА
- Глава десятая. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНЫХ ВЕЛИЧИН
- 10-2. МАГНИТОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНОГО ПОТОКА
- ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНОЙ ИНДУКЦИИ И НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ
- 10-3. АППАРАТУРА ДЛЯ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- Глава одиннадцатая. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 11-2. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- ГЕНЕРАТОРНЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 11-3. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ТЕМПЕРАТУРЫ
- 11-4. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ГЕОМЕТРИЧЕСКИХ И МЕХАНИЧЕСКИХ ВЕЛИЧИН
- 11-5. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ КОНЦЕНТРАЦИИ ЖИДКОЙ И ГАЗООБРАЗНОЙ СРЕДЫ
- Глава двенадцатая. ИЗМЕРИТЕЛЬНЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ
- 12-2. ИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ
- 12-3. ТЕЛЕИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ
- 12-4. СИСТЕМЫ АВТОМАТИЧЕСКОГО КОНТРОЛЯ И ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ
- 12-5. ИЗМЕРИТЕЛЬНЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ НА ОСНОВЕ АГРЕГАТНЫХ КОМПЛЕКСОВ ГОСУДАРСТВЕННОЙ СИСТЕМЫ ПРИБОРОВ И СРЕДСТВ АВТОМАТИЗАЦИИ
- Глава тринадцатая. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ СРЕДСТВА
- 13-2. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ СРЕДСТВА СИСТЕМНОГО ПРИМЕНЕНИЯ
- 13-3. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ КОМПЛЕКСЫ
- Раздел В. ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
- Глава четырнадцатая. ПОДГОТОВКА ИЗМЕРИТЕЛЬНОГО ЭКСПЕРИМЕНТА И ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- 14-2. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- 14-3. СУММИРОВАНИЕ ПОГРЕШНОСТЕЙ
- Глава пятнадцатая. ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ, МАГНИТНЫХ И НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 15-2. ИЗМЕРЕНИЯ МОЩНОСТИ, ЭНЕРГИИ И КОЛИЧЕСТВА ЭЛЕКТРИЧЕСТВА
- 15-3. ИЗМЕРЕНИЯ ЧАСТОТЫ, ФАЗЫ, ВРЕМЕННЫХ ИНТЕРВАЛОВ, АНАЛИЗ СПЕКТРА ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- 15-4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ЦЕПЕЙ ПОСТОЯННОГО И ПЕРЕМЕННОГО ТОКА
- 15-5. ИЗМЕРЕНИЯ ПАРАМЕТРОВ МАГНИТНОГО ПОЛЯ, ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- МАГНИТНЫЕ МАТЕРИАЛЫ И ИХ ХАРАКТЕРИСТИКИ
- ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- 15-6. ИЗМЕРЕНИЯ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- ИЗМЕРЕНИЯ ДАВЛЕНИЙ, ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ И РАССТОЯНИЙ
- Глава шестнадцатая. ИЗМЕРЕНИЯ ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ПРОЦЕССОВ
- 16-2. ИЗМЕРЕНИЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ДИСПЕРСИИ СЛУЧАЙНОГО ПРОЦЕССА
- 16-3. ИЗМЕРЕНИЕ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
- 16-4. ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННОЙ ФУНКЦИИ
- 16-5. АНАЛИЗ СПЕКТРА МОЩНОСТИ
- Список литературы