| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
14-2. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Общие сведения.
Целью обработки результатов измерений (наблюдений) является установление значения измеряемой величины и оценка погрешности полученного результата измерения. Методы обработки результатов наблюдений могут быть разными в зависимости от предварительной информации, которой располагает экспериментатор об источниках и характере проявления погрешностей, условиях эксперимента, свойствах используемых средств измерений, от вида измерений, числа выполненных наблюдений и других причин.
Погрешность измерения проявляет себя как случайная величина (см. § 2-2). Следовательно, и результаты отдельных измерений одного и того же значения измеряемой величины случайны Если систематическая погрешность при измерении этой величины постоянна, что является весьма распространенным случаем на практике, то вид закона распределения отдельных результатов измерения определяется видом закона распределения случайных погрешностей. При этом математическое ожидание этого закона распределения смещено с истинного значения измеряемой величины на систематическую погрешность, а дисперсия этого закона распределения равна дисперсии случайной составляющей погрешности. Отсюда следует, что для получения оценки измеряемой величины, максимально близкой к истинному значению, необходимо по экспериментальным данным найти оценку математического ожидания отдельных результатов наблюдений, оценить систематическую погрешность и исключить ее из оценки
математического ожидания. В более общем случае, когда отдельные результаты измерений содержат разные систематические погрешности, необходимо оценить каждую из этих погрешностей, исключив ее из соответствующего результата измерения и получив таким образом ряд наблюдений, не содержащих систематических погрешностей, и на основании этого оценить математическое ожидание.
Точность оценки математического ожидания ряда наблюдений зависит от количества выполненных измерений и от дисперсии случайной составляющей погрешности. Поэтому по экспериментальным данным приходится оценивать не только математическое ожидание, но и дисперсию.
При обработке результатов наблюдений необходимо пользоваться следующими основными правилами, разработанными в теории вероятностей и математической статистике:
1. Математическое ожидание суммы (разности) случайных величин равно сумме (разности) математических ожиданий этих величин

2. Постоянное (неслучайное) число можно выносить за знак математического ожидания:

3. Математическое ожидание постоянного (неслучайного) числа равно этому числу:

4. Дисперсия суммы (разности) случайных величин определяется выражением

где  коэффициенты корреляции соответствующих пар
коэффициенты корреляции соответствующих пар  случайных величин, входящих в рассматриваемую сумму (разность) этих величин; знак
случайных величин, входящих в рассматриваемую сумму (разность) этих величин; знак  или
или  перед коэффициентами корреляции определяется знаком произведения соответствующей пары
перед коэффициентами корреляции определяется знаком произведения соответствующей пары  Если все величины, входящие в сумму (разность), независимы, то для любой пары коэффициент корреляции равен нулю и, следовательно, дисперсия суммы (разности) независимых случайных величин равна сумме их дисперсий.
Если все величины, входящие в сумму (разность), независимы, то для любой пары коэффициент корреляции равен нулю и, следовательно, дисперсия суммы (разности) независимых случайных величин равна сумме их дисперсий.
5. Постоянное (неслучайное) число можно выносить за знак дисперсии, возведя это число в квадрат:

6. Дисперсия постоянного (неслучайного) числа равна нулю:

7. Оценкой математического ожидания случайной величины х по результатам отдельных наблюдений  этой величины является среднее арифметическое:
этой величины является среднее арифметическое:

где  — число наблюдений величины х.
— число наблюдений величины х.
При неограниченно большом числе наблюдений х стремится к математическому ожиданию 
При ограниченном числе  что всегда имеет место на практике, х является случайной величиной, основные характеристики которой (математическое ожидание и дисперсия) можно получить на основании сформулированных выше правил:
что всегда имеет место на практике, х является случайной величиной, основные характеристики которой (математическое ожидание и дисперсия) можно получить на основании сформулированных выше правил:

Последнее выражение справедливо при независимости 
8. Оценку дисперсии случайной величины х по результатам отдельных наблюдений  этой величины можно найти по формуле
этой величины можно найти по формуле

Оценка среднего квадратического отклонения случайной величины х равна  со знаком «плюс».
со знаком «плюс».
При неограниченно большом числе наблюдений оценки  стремятся, соответственно, к
стремятся, соответственно, к  При ограниченном
При ограниченном  эти оценки являются случайными величинами.
эти оценки являются случайными величинами.
Сформулированные правила позволяют оценить результат измерения и дисперсию случайной составляющей погрешности.
Что касается систематической погрешности, то следует иметь в виду, что обнаружить и оценить ее в общем случае непросто, особенно если причины возникновения этой погрешности неизвестны. Например, постоянная систематическая погрешность от эксперимента к эксперименту может не проявляться, оставаясь не обнаруженной. Для обнаружения систематической погрешности, природа которой неизвестна, необходима постановка специального эксперимента для измерения искомой величины того же размера с использованием более точных методов и средств измерений. Сравнение результатов измерения  полученных в первом и во втором (более точном) эксперименте, позволяет оценить систематическую погрешность первого эксперимента. Если результат измерения
полученных в первом и во втором (более точном) эксперименте, позволяет оценить систематическую погрешность первого эксперимента. Если результат измерения  содержит только постоянную систематическую погрешность, то она может быть оценена по однократным результатам измерения
содержит только постоянную систематическую погрешность, то она может быть оценена по однократным результатам измерения  как
как  Погрешность этой оценки определяется погрешностью результата измерения
Погрешность этой оценки определяется погрешностью результата измерения 
Если результат измерения  кроме систематической погрешности содержит и случайную составляющую погрешности, то
кроме систематической погрешности содержит и случайную составляющую погрешности, то  — случайная величина, математическим ожиданием которой (см. § 2-1) и является систематическая погрешность
— случайная величина, математическим ожиданием которой (см. § 2-1) и является систематическая погрешность 
Погрешность этой оценки определяется погрешностью оценок математических ожиданий результатов измерения в первом и втором экспериментах.
Если причины возникновения систематической погрешности известны, то в первую очередь необходимо постараться исключить или уменьшить влияние этих причин. При невозможности устранения источников погрешности необходимо на основании теоретического анализа или путем постановки специальных экспериментов получить количественные оценки систематических погрешностей. Например, путем предварительной поверки используемых средств измерений можно выявить систематическую погрешность этих средств при разных значениях измеряемой величины. Анализируя влияние внешних факторов, можно составить таблицы или графики зависимости систематической погрешности от внешних факторов. В этом случае для введения поправки на систематическую погрешность необходимо в процессе измерения контролировать значение соответствующего влияющего внешнего фактора.
Существуют приемы, позволяющие путем постановки специальных экспериментов исключить систематическую погрешность, не производя ее количественной оценки. Наиболее распространены следующие способы исключения из результата измерения
постоянной систематической погрешности: замещение, компенсация погрешности по знаку, противопоставление.
При способе замещения сначала получают результат измерения  при подключенном объекте исследования. Затем вместо объекта исследования подключают регулируемую меру, изменением параметра которой добиваются точно такого же результата измерения
при подключенном объекте исследования. Затем вместо объекта исследования подключают регулируемую меру, изменением параметра которой добиваются точно такого же результата измерения  За окончательный результат измерения принимают значение меры
За окончательный результат измерения принимают значение меры 
Способ компенсации погрешности по знаку предполагает измерение одной и той же величины два раза при изменении условий эксперимента второго измерения таким образом, чтобы систематическая погрешность проявлялась в нем с противоположным знаком. Примером этого способа является исключение погрешности, обусловленной влиянием постоянного внешнего магнитного поля. Результат первого измерения  получают при произвольном положении прибора; результат второго измерения
получают при произвольном положении прибора; результат второго измерения  получают, изменив положение прибора в горизонтальной плоскости на 180°. Так как оба результата измерения искажены одной и той же систематической погрешностью, но с разными знаками, то среднее значение этих результатов
получают, изменив положение прибора в горизонтальной плоскости на 180°. Так как оба результата измерения искажены одной и той же систематической погрешностью, но с разными знаками, то среднее значение этих результатов  не содержит систематической погрешности, обусловленной влиянием внешнего магнитного поля.
не содержит систематической погрешности, обусловленной влиянием внешнего магнитного поля.
Способ противопоставления также предполагает двукратное измерение одной и той же величины. Условия экспериментов должны различаться таким образом, чтобы по известным закономерностям возникновения систематической погрешности ее можно было исключить. Примером может быть измерение сопротивления  по схеме моста постоянного тока (см. § 7-1). Результат измерения
по схеме моста постоянного тока (см. § 7-1). Результат измерения  может содержать систематическую погрешность вследствие отличия сопротивлений резисторов
может содержать систематическую погрешность вследствие отличия сопротивлений резисторов  от их номинальных значений. Эту погрешность можно исключить, если при тех же резисторах
от их номинальных значений. Эту погрешность можно исключить, если при тех же резисторах  поменять местами плечи
поменять местами плечи  и снова уравновесить мост резистором
и снова уравновесить мост резистором  получив выражение
получив выражение  где
где  — сопротивление плеча
— сопротивление плеча  при новом равновесии моста. Исключив из полученных выражений отношение плеч
при новом равновесии моста. Исключив из полученных выражений отношение плеч  , следовательно, систематическую погрешность, обусловленную неточностью этого отношения, получим
, следовательно, систематическую погрешность, обусловленную неточностью этого отношения, получим 
Если систематическую погрешность удалось оценить, то ее сразу нужно исключить из результата измерения. При необходимости следует оценить погрешность найденной оценки систематической погрешности, что позволит установить границы неисключенного остатка систематической погрешности. Если систематическую погрешность оценить не удается, то для нее также нужно оценить границы возможных ее значений.
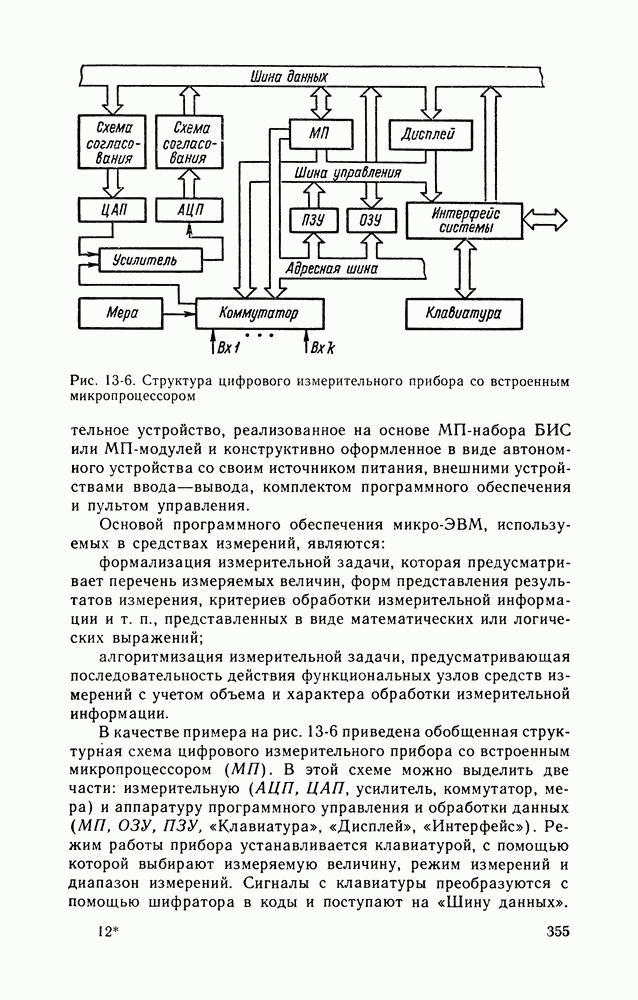
Рассмотрим наиболее характерные случаи обработки результатов наблюдений при различных видах измерений.
Прямые измерения.
Предположим, что при многократном измерении интересующей нас величины получили  отдельных результатов наблюдений. Исключив систематическую погрешность из каждого наблюдения, получаем исправленный ряд значений
отдельных результатов наблюдений. Исключив систематическую погрешность из каждого наблюдения, получаем исправленный ряд значений  математеческим ожиданием которого является истинное значение измеряемой величины
математеческим ожиданием которого является истинное значение измеряемой величины  За действительное значение измеряемой величины принимаем среднее арифметическое
За действительное значение измеряемой величины принимаем среднее арифметическое  определяемое по формуле (14-7), в которой х, — исправленное значение ряда наблюдений.
определяемое по формуле (14-7), в которой х, — исправленное значение ряда наблюдений.
Отклонения между отдельными значениями наблюдений и средним арифметическим (разности  называются случайными отклонениями результатов наблюдений (или остаточными погрешностями). Они могут быть как положительными, так и отрицательными. На основании свойства среднего арифметического алгебраическая сумма остаточные погрешностей равна нулю, т. е.
называются случайными отклонениями результатов наблюдений (или остаточными погрешностями). Они могут быть как положительными, так и отрицательными. На основании свойства среднего арифметического алгебраическая сумма остаточные погрешностей равна нулю, т. е.  этим следует пользоваться для контроля правильности подсчета х.
этим следует пользоваться для контроля правильности подсчета х.
Если дисперсия  полученного ряда наблюдений известна из предыдущих экспериментов или из технической документации на применяемые средства измерений, то дисперсия среднего арифметического на основании выражения
полученного ряда наблюдений известна из предыдущих экспериментов или из технической документации на применяемые средства измерений, то дисперсия среднего арифметического на основании выражения  где
где  — дисперсия исправленного ряда наблюдений;
— дисперсия исправленного ряда наблюдений;  — дисперсия действительного значения (среднего арифметического) измеряемой величины этого ряда.
— дисперсия действительного значения (среднего арифметического) измеряемой величины этого ряда.
Если дисперсия ряда неизвестна, то на основании соотношения (14-9) ее нужно оценить по формуле  где
где  — остаточные погрешности исправленного ряда наблюдений. В этом случае за оценку дисперсии действительного значения измеряемой величины нужно принять
— остаточные погрешности исправленного ряда наблюдений. В этом случае за оценку дисперсии действительного значения измеряемой величины нужно принять

Для нахождения доверительного интервала погрешности измерения необходимо найти закон распределения для величины

при известной дисперсии или для величины

при неизвестной дисперсии.
Так как в выражение (14-11) входит только одна случайная величина х, то вид закона распределения величины,
определяемой этим выражением, определяется видом закона распределения величины х. При нормальном законе распределения отдельных результатов закон распределения х тоже нормальный. Это объясняется известным из теории вероятностей свойством устойчивости нормального закона, заключающемся в том, что сумма случайных величин, распределенных по нормальному закону, дает случайную величину, распределенную по нормальному закону. Таким образом, при нормальном законе распределения  случайная величина, определяемая выражением (14-11), имеет нормальный закон распределения с математическим ожиданием, равным нулю, и дисперсией, равной единице, в чем можно убедиться, применяя к соотношению (14-11) сформулированные выше основные правила (14-1) — (14-6). Случайную величину с таким нормальным законом распределения обозначим
случайная величина, определяемая выражением (14-11), имеет нормальный закон распределения с математическим ожиданием, равным нулю, и дисперсией, равной единице, в чем можно убедиться, применяя к соотношению (14-11) сформулированные выше основные правила (14-1) — (14-6). Случайную величину с таким нормальным законом распределения обозначим 
Выражение (14-12) содержит две случайные величины  поэтому закон распределения величины, определяемой этим выражением, отличается от закона распределения величины, определяемой выражением (14-11). В теории вероятностей доказансэ, что при нормальном законе распределения
поэтому закон распределения величины, определяемой этим выражением, отличается от закона распределения величины, определяемой выражением (14-11). В теории вероятностей доказансэ, что при нормальном законе распределения  случайная величина, определяемая выражением (14-12), имеет закон распределения Стьюдента. Случайную величину, распределенную по закону Стьюдента, обозначим
случайная величина, определяемая выражением (14-12), имеет закон распределения Стьюдента. Случайную величину, распределенную по закону Стьюдента, обозначим  Для
Для  и
и  существуют таблицы, по которым можно найти значения
существуют таблицы, по которым можно найти значения  определяющие с доверительной вероятностью Р границы доверительного интервала для величин
определяющие с доверительной вероятностью Р границы доверительного интервала для величин  и
и  соответственно. Число
соответственно. Число  называется числом степеней свободы; для рассматриваемого случая
называется числом степеней свободы; для рассматриваемого случая 
Чем больше число измерений в ряду наблюдений, тем ближе оценка  совпадает с действительным средним квадратическим отклонением о
совпадает с действительным средним квадратическим отклонением о  Следовательно, с увеличением числа наблюдений закон распределения Стьюдента приближается к нормальному закону. Практически при
Следовательно, с увеличением числа наблюдений закон распределения Стьюдента приближается к нормальному закону. Практически при 
Зная  или
или  на основании выражений (14-11) и (14-12) с учетом (14-8) и (14-10), результат измерения с доверительной вероятностью Р можно записать в виде
на основании выражений (14-11) и (14-12) с учетом (14-8) и (14-10), результат измерения с доверительной вероятностью Р можно записать в виде

при известной дисперсии или в виде

при неизвестной дисперсии.
Если закон распределения отдельных результатов измерения  отличается от нормального, то найти закон распределения случайных величин, определяемых выражениями (14-11) и
отличается от нормального, то найти закон распределения случайных величин, определяемых выражениями (14-11) и
(14-12), затруднительно. В этом случае могут быть даны следующие рекомендации. Вид закона распределения для х определяется законом распределения суммы независимых случайных величин  среди которых нет преобладающих (все имеют один и тот же закон распределения). На основании центральной предельной теоремы (см. § 2-2) закон распределения х с увеличением числа наблюдений стремится к нормальному закону. Практически при
среди которых нет преобладающих (все имеют один и тот же закон распределения). На основании центральной предельной теоремы (см. § 2-2) закон распределения х с увеличением числа наблюдений стремится к нормальному закону. Практически при  можно считать, что закон распределения х близок к нормальному закону и при известном
можно считать, что закон распределения х близок к нормальному закону и при известном  для приближенной оценки доверительного интервала можно пользоваться выражением (14-13). Если дисперсия
для приближенной оценки доверительного интервала можно пользоваться выражением (14-13). Если дисперсия  неизвестна, то необходимо увеличить число наблюдений
неизвестна, то необходимо увеличить число наблюдений  так чтобы оценка
так чтобы оценка  была близка к
была близка к  Практически это условие выполняется при
Практически это условие выполняется при  . В этом случае для приближенной оценки доверительного интервала можно также пользоваться выражением (14-13).
. В этом случае для приближенной оценки доверительного интервала можно также пользоваться выражением (14-13).
Если ряд наблюдений  содержит результат
содержит результат  существенно отличающийся от остальных, то необходимо проверить, не является ли он промахом. При нормальном законе распределения отдельных результатов измерения
существенно отличающийся от остальных, то необходимо проверить, не является ли он промахом. При нормальном законе распределения отдельных результатов измерения  обнаружение промаха сводится к проверке неравенства
обнаружение промаха сводится к проверке неравенства

при известной дисперсии или

при неизвестной дисперсии.
В этих выражениях Р — вероятность, с которой обнаруживается промах;  — граница доверительного интервала нормально распределенной величины
— граница доверительного интервала нормально распределенной величины  при доверительной вероятности
при доверительной вероятности  — граница доверительного интервала случайной величины
— граница доверительного интервала случайной величины  имеющей специальное распределение, зависящее от
имеющей специальное распределение, зависящее от  , при доверительной вероятности Р. Если неравенства (14-15) и (14-16) не выполняются, то
, при доверительной вероятности Р. Если неравенства (14-15) и (14-16) не выполняются, то  следует считать промахом. Его необходимо исключить из ряда наблюдений, и для оценки результата измерения необходимо заново пересчитать
следует считать промахом. Его необходимо исключить из ряда наблюдений, и для оценки результата измерения необходимо заново пересчитать 
На практике часто встречается однократное измерение, когда измеряемая величина оценивается по результату одного наблюдения. Этот случай можно рассматривать как частный случай
многократных измерений  Тогда выражения (14-13) и (14-14) примут вид:
Тогда выражения (14-13) и (14-14) примут вид:

Здесь за действительное значение х измеряемой величины следует принять результат однократного измерения, из которого исключена систематическая погрешность. Нужно иметь в виду, что по однократному измерению нельзя определить  (или S). Поэтому для того чтобы можно было записать результат измерения в виде (14-17), среднее квадратическое отклонение а нужно знать на основании предварительных измерений или из технической документации на применяемое средство измерений. Если вместо о известна его оценка
(или S). Поэтому для того чтобы можно было записать результат измерения в виде (14-17), среднее квадратическое отклонение а нужно знать на основании предварительных измерений или из технической документации на применяемое средство измерений. Если вместо о известна его оценка  найденная по некоторому числу предварительных измерений, то для определения
найденная по некоторому числу предварительных измерений, то для определения  в выражении (14-18) число степеней свободы
в выражении (14-18) число степеней свободы  нужно взять равным этому числу предварительных измерений минус единица.
нужно взять равным этому числу предварительных измерений минус единица.
Сравнение выражений (14-13), (14-14) и (14-17), (14-18) показывает, что увеличение числа наблюдений позволяет получить более точную оценку истинного значения измеряемой величины. Однако следует иметь в виду, что число наблюдений  не может быть сколь угодно большим, так как в течение длительного времени, необходимого для получения большого числа результатов наблюдений, нельзя гарантировать неизменность не только условий проведения эксперимента, но и размера самой измеряемой величины. Практически
не может быть сколь угодно большим, так как в течение длительного времени, необходимого для получения большого числа результатов наблюдений, нельзя гарантировать неизменность не только условий проведения эксперимента, но и размера самой измеряемой величины. Практически  следует ограничивать таким значением, при котором случайная составляющая погрешности результата измерения будет существенно меньше неисключенных остатков систематических погрешностей отдельных результатов наблюдений.
следует ограничивать таким значением, при котором случайная составляющая погрешности результата измерения будет существенно меньше неисключенных остатков систематических погрешностей отдельных результатов наблюдений.
Косвенные измерения.
Допустим, что измеряемая величина у является функцией аргументов  измеряемых прямыми измерениями, т. е.
измеряемых прямыми измерениями, т. е.  Проведя обработку ряда наблюдений для каждого аргумента методом, изложенным для прямых измерений, можно найти действительные значения аргументов
Проведя обработку ряда наблюдений для каждого аргумента методом, изложенным для прямых измерений, можно найти действительные значения аргументов

и оценки дисперсий 

где  число измерений соответствующего аргумента.
число измерений соответствующего аргумента.
Дальнейшую обработку результатов наблюдений можно проводить по-разному. Наиболее распространенным является метод линеаризации, основанный на разложении функциональной зависимости  в ряд Тейлора с ограничением ряда членами, содержащими только первые производные:
в ряд Тейлора с ограничением ряда членами, содержащими только первые производные:

где  — истинные значения аргументов.
— истинные значения аргументов.
Запишем выражение (14-19) в более компактной форме:

где  — истинное значение косвенно измеряемой величины;
— истинное значение косвенно измеряемой величины;  погрешности результата измерения соответствующего аргумента;
погрешности результата измерения соответствующего аргумента;  значения частных производных от функции по соответствующему аргументу в точке, где аргументы имеют истинное значение. В правой части выражения (14-20) случайными величинами являются
значения частных производных от функции по соответствующему аргументу в точке, где аргументы имеют истинное значение. В правой части выражения (14-20) случайными величинами являются  Если результаты измерения аргументов независимы друг от друга (что чаще всего и бывает на практике), то эти случайные величины являются независимыми.
Если результаты измерения аргументов независимы друг от друга (что чаще всего и бывает на практике), то эти случайные величины являются независимыми.
Применяя к выражению (14-20) сформулированные выше правила, найдем математическое ожидание и дисперсию случайной величины К, полученной при подстановке в функциональную зависимость значений аргументов 

где  дисперсии значений
дисперсии значений  аргументов.
аргументов.
Если при определении действительных значений аргументов  систематические погрешности были исключены, то
систематические погрешности были исключены, то  . В этом случае
. В этом случае  , следовательно, значение
, следовательно, значение  можно принять за оценку действительного значения косвенно измеряемой величины. Что касается дисперсии полученного результата К, то вычислить ее непосредственно по выражению (14-22) нельзя, так как для расчета значений частных производных требуется знание истинных значений аргументов. Вместо истинных значений аргументов известны их оценки
можно принять за оценку действительного значения косвенно измеряемой величины. Что касается дисперсии полученного результата К, то вычислить ее непосредственно по выражению (14-22) нельзя, так как для расчета значений частных производных требуется знание истинных значений аргументов. Вместо истинных значений аргументов известны их оценки  Поэтому вместо значений
Поэтому вместо значений  нужно использовать их оценки
нужно использовать их оценки  вычисляя производные в точке, где аргументы принимают значения
вычисляя производные в точке, где аргументы принимают значения 
Если дисперсии аргументов известны, то оценка дисперсии результата измерения  для косвенно измеряемой величины вычисляется по формуле
для косвенно измеряемой величины вычисляется по формуле

Если вместо дисперсий аргументов известны их оценки  то оценку дисперсии величины
то оценку дисперсии величины  нужно определять по формуле, аналогичной (14-23), т. е.
нужно определять по формуле, аналогичной (14-23), т. е.

Для того чтобы найти доверительный интервал погрешности результата косвенного измерения, нужно определить закон распределения величины  или
или 
Закон распределения этих величин может быть весьма сложным даже при нормальном законе распределения случайных погрешностей аргументов.
Если систематические погрешности при измерении аргументов не исключаются, то результат измерения  косвенно измеряемой величины тоже содержит систематическую
косвенно измеряемой величины тоже содержит систематическую
погрешность, равную математическому ожиданию погрешности  На основании (14-21) эту погрешность можно представить в виде
На основании (14-21) эту погрешность можно представить в виде

где  систематическая погрешность результата измерения соответствующего аргумента. Заменяя значения частных производных, входящих в выражение (14-24), на значения этих производных в точке, где аргументы принимают значения
систематическая погрешность результата измерения соответствующего аргумента. Заменяя значения частных производных, входящих в выражение (14-24), на значения этих производных в точке, где аргументы принимают значения  получим выражение для оценки систематической погрешности результата косвенного измерения в виде
получим выражение для оценки систематической погрешности результата косвенного измерения в виде

При этом необходимо иметь в виду следующее. Очевидно, что оценить систематическую погрешность результата косвенного измерения по выражению (14-25) невозможно, не зная оценок систематических погрешностей измерения аргументов. Но если они известны, то их необходимо сразу исключить из результатов измерения аргументов и оценивать результат косвенного измерения по значениям аргументов, не содержащих систематических погрешностей. Поэтому выражением (14-25) следует пользоваться в том случае, когда систематические погрешности измерения аргументов не могли быть выявлены и оценены в процессе эксперимента, а были оценены лишь после него. Это выражение может использоваться также при подготовке к эксперименту. Например, если предполагается, что погрешность результата косвенного измерения определяется только погрешностью средств измерений аргументов, причем у этих средств преобладающей является систематическая погрешность (случайной погрешностью можно пренебречь), то, пользуясь выражением (14-25), можно выбрать средства измерений с такими допустимыми предельными значениями систематических погрешностей, чтобы погрешность результата измерения косвенно измеряемой величины не превысила заданного значения.
При однократных измерениях аргументов процедура определения результата косвенно измеряемой величины сохраняется такой же, как и при многократных измерениях, с учетом замечаний, сделанных при рассмотрении однократных прямых измерений.
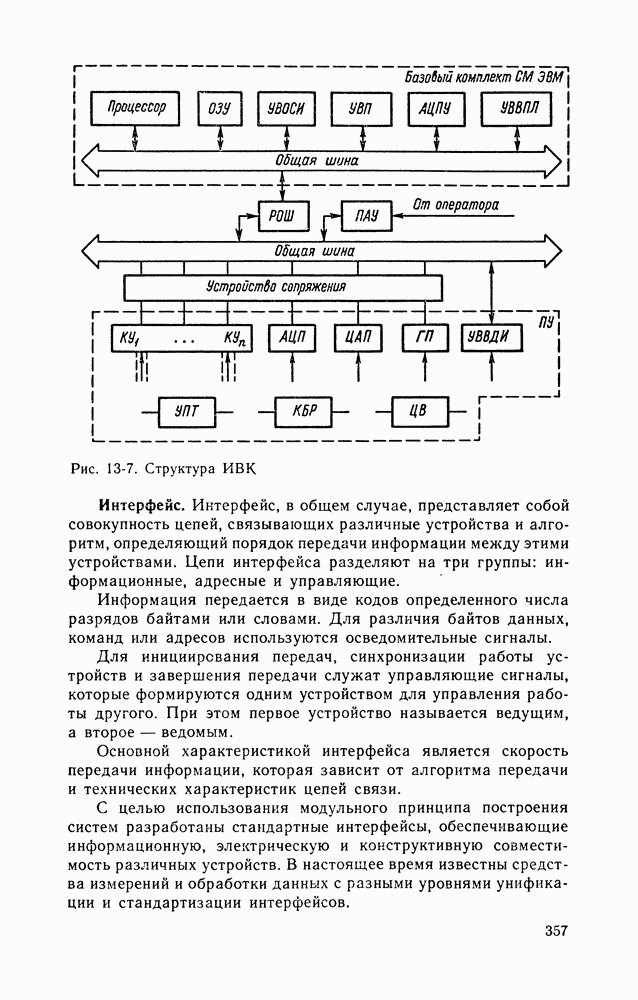
Совместные измерения.
Целью совместных измерений является установление функциональной зависимости между величинами, например зависимости сопротивления от температуры. Отыскивая зависимость между величинами  необходимо
необходимо
устанавливать и измерять различные размеры величины а и одновременно измерять величину  Таким образом, можно получить координаты исследуемой зависимости
Таким образом, можно получить координаты исследуемой зависимости  Так как результаты измерения этих величин содержат погрешности, то полученные координаты не будут принадлежать истинной исследуемой зависимости. Исключив систематическую погрешность из каждого результата измерения, можно уточнить эти координаты, но и уточненные координаты все-таки будут отклоняться (рассеиваться) относительно истинной зависимости из-за случайных погрешностей.
Так как результаты измерения этих величин содержат погрешности, то полученные координаты не будут принадлежать истинной исследуемой зависимости. Исключив систематическую погрешность из каждого результата измерения, можно уточнить эти координаты, но и уточненные координаты все-таки будут отклоняться (рассеиваться) относительно истинной зависимости из-за случайных погрешностей.
Степень рассеивания характеризуется дисперсией. Правильной зависимостью, построенной по полученным координатным точкам, следует считать такую зависимость, при которой дисперсия координатных точек относительно этой зависимости будет минимальной. Для оценки дисперсии нужно вычислить сумму квадратов отклонений координатных точек от истинной зависимости. Минимальной дисперсии будет соответствовать минимальное значение суммы квадратов этих отклонений. Поэтому метод, с помощью которого отыскивается истинная зависимость, называется методом наименьших квадратов.
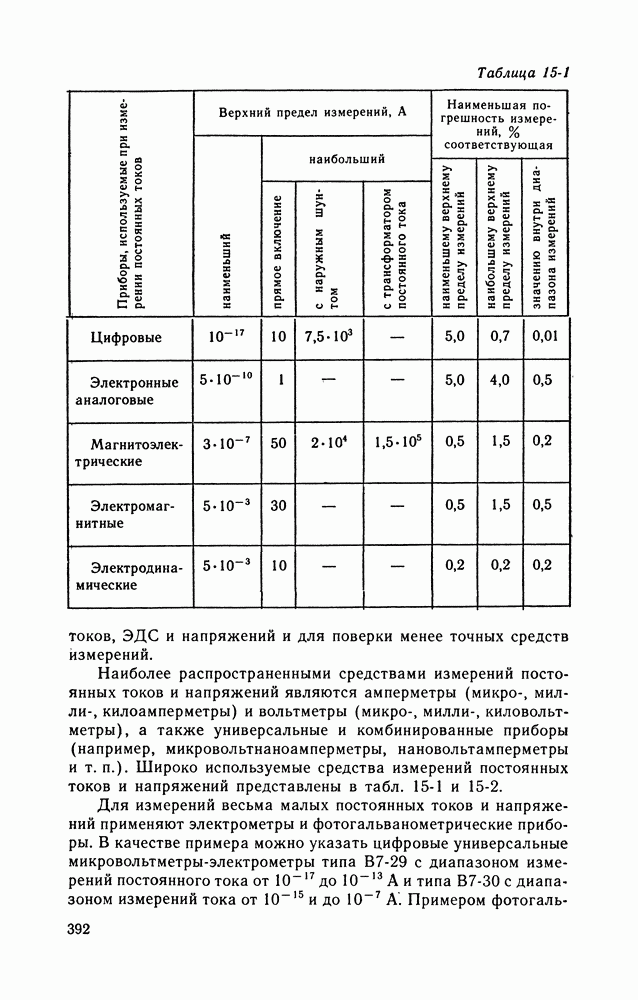
Рассмотрим применение этого метода на примере линейной зависимости между  Предположим, нам известно, что зависимость между
Предположим, нам известно, что зависимость между  должна описываться уравнением
должна описываться уравнением

Результаты эксперимента после исключения систематических погрешностей дают нам координаты исследуемой зависимости  Необходимо решить, как провести прямую линию, наилучшим образом согласующуюся с полученными координатами. Иными словами, зная координаты, полученные экспериментально, и вид функции, нужно определить коэффициенты
Необходимо решить, как провести прямую линию, наилучшим образом согласующуюся с полученными координатами. Иными словами, зная координаты, полученные экспериментально, и вид функции, нужно определить коэффициенты  в уравнении (14-26).
в уравнении (14-26).
В соответствии с уравнением (14-26), если  принимает значение
принимает значение  то значение а должно быть равно
то значение а должно быть равно  , а эксперимент дает значение
, а эксперимент дает значение  Следовательно, экспериментальная точка отклоняется от истинной точки на значение
Следовательно, экспериментальная точка отклоняется от истинной точки на значение  . Сумму квадратов отклонений экспериментальных точек от истинной зависимости можно найти по выражению
. Сумму квадратов отклонений экспериментальных точек от истинной зависимости можно найти по выражению

где  — число экспериментальных точек.
— число экспериментальных точек.
Найдем значения коэффициентов  обращающие выражение (14-27) в минимум. Для этого продифференцируем это выражение по
обращающие выражение (14-27) в минимум. Для этого продифференцируем это выражение по  и приравняем производные нулю:
и приравняем производные нулю:

Систему уравнений (14-28) с учетом (14-26) приведем к виду

Решая эту систему уравнений, получим выражение для коэффициента 

а зная  находим выражение для а:
находим выражение для а:

Полученные значения  в общем случае отличаются от истинных значений коэффициентов уравнения
в общем случае отличаются от истинных значений коэффициентов уравнения  и являются случайными величинами, так как координаты
и являются случайными величинами, так как координаты  искаженные случайными погрешностями, тоже являются случайными величинами. Погрешностями определения коэффициентов являются
искаженные случайными погрешностями, тоже являются случайными величинами. Погрешностями определения коэффициентов являются  и
и  Дисперсии этих погрешностей равны дисперсиям соответствующих коэффициентов, т. е.
Дисперсии этих погрешностей равны дисперсиям соответствующих коэффициентов, т. е.  Найдем эти дисперсии.
Найдем эти дисперсии.
Сначала рассмотрим влияние погрешностей измерения  на рассеивание экспериментальных точек относительно исследуемой зависимости. Предположим, что мы хотим измерить величину а при
на рассеивание экспериментальных точек относительно исследуемой зависимости. Предположим, что мы хотим измерить величину а при  Если измерения выполняются без погрешностей, то, установив значение
Если измерения выполняются без погрешностей, то, установив значение  получим значение величины а, соответствующее координатной точке 1 (рис. 14-1), лежащей на исследуемой зависимости. Теперь допустим, что величина а измеряется без погрешности, а величина
получим значение величины а, соответствующее координатной точке 1 (рис. 14-1), лежащей на исследуемой зависимости. Теперь допустим, что величина а измеряется без погрешности, а величина  с погрешностью. Тогда при установке значения
с погрешностью. Тогда при установке значения  истинное значение величины
истинное значение величины  может оказаться равным
может оказаться равным  за счет погрешности
за счет погрешности  Значение величины а при этом будет соответствовать координатной точке 2, лежащей на исследуемой зависимости. Однако полагая, что мы установили значение
Значение величины а при этом будет соответствовать координатной точке 2, лежащей на исследуемой зависимости. Однако полагая, что мы установили значение  вместо координатной точки 2 мы будем рассматривать координатную точку 2, которая смещена с исследуемой
вместо координатной точки 2 мы будем рассматривать координатную точку 2, которая смещена с исследуемой

Рис. 14-1. Рассеивание экспериментальных точек из-за погрешностей измерения величин 
зависимости на  где
где  — истинный коэффициент наклона исследуемой зависимости. Если же и величина а измеряется с погрешностью, то координатная точка 2 сместится на величину этой погрешности
— истинный коэффициент наклона исследуемой зависимости. Если же и величина а измеряется с погрешностью, то координатная точка 2 сместится на величину этой погрешности  и окажется в точке 3. Именно эту точку мы и рассматриваем как точку с координатами
и окажется в точке 3. Именно эту точку мы и рассматриваем как точку с координатами  Точка 3 смещена с исследуемой зависимости на
Точка 3 смещена с исследуемой зависимости на  Очевидно, что экспериментальная точка 3 не изменит своего положения, если при изменении погрешностей
Очевидно, что экспериментальная точка 3 не изменит своего положения, если при изменении погрешностей  и
и  значение Да будет оставаться неизменным. При этом значения коэффициентов
значение Да будет оставаться неизменным. При этом значения коэффициентов  и а, рассчитанных по выражениям (14-30) и (14-31), будут одни и те же, так как они определяются только положением экспериментальных точек. Поэтому мы можем считать, что измерение величины
и а, рассчитанных по выражениям (14-30) и (14-31), будут одни и те же, так как они определяются только положением экспериментальных точек. Поэтому мы можем считать, что измерение величины  осуществляется без погрешности, а рассеивание экспериментальных точек относительно исследуемой зависимости обусловлено только погрешностью измерения величины а, причем эта погрешность
осуществляется без погрешности, а рассеивание экспериментальных точек относительно исследуемой зависимости обусловлено только погрешностью измерения величины а, причем эта погрешность  Погрешности
Погрешности  и
и  являются независимыми случайными величинами. Применяя правила нахождения дисперсий, устанавливаем, что дисперсия, характеризующая рассеивание экспериментальных точек,
являются независимыми случайными величинами. Применяя правила нахождения дисперсий, устанавливаем, что дисперсия, характеризующая рассеивание экспериментальных точек,  Считаем, что эта дисперсия одинакова при измерении любых значений
Считаем, что эта дисперсия одинакова при измерении любых значений 
Перейдем теперь к непосредственной оценке дисперсий коэффициентов  и а. Считая, что величина
и а. Считая, что величина  измеряется без погрешности, мы имеем право рассматривать любые значения
измеряется без погрешности, мы имеем право рассматривать любые значения  входящие в выражения для рассчета коэффициентов, как неслучайные числа.
входящие в выражения для рассчета коэффициентов, как неслучайные числа.
Выражение (14-30) путем алгебраических преобразований можно привести к виду

где  — среднее арифметическое значение координат величины
— среднее арифметическое значение координат величины 
Так как все  — независимые случайные величины с дисперсией
— независимые случайные величины с дисперсией  то дисперсию коэффициента
то дисперсию коэффициента  согласно (14-4) и (14-5) можно найти по выражению
согласно (14-4) и (14-5) можно найти по выражению

Для нахождения дисперсии коэффициента а удобнее вместо выражения (14-31) использовать выражение, которое можно получить, исключая из системы уравнений (14-29) коэффициент  и решая эту систему относительно коэффициента а:
и решая эту систему относительно коэффициента а:

Отсюда находим дисперсию коэффициента а:

Для расчета дисперсий по выражениям (14-32) и (14-33) необходимо знать дисперсию рассеивания экспериментальных точек  Точное значение этой дисперсии найти нельзя даже при известных дисперсиях погрешностей измерения величин
Точное значение этой дисперсии найти нельзя даже при известных дисперсиях погрешностей измерения величин  так как еще необходимо знать истинный коэффициент наклона
так как еще необходимо знать истинный коэффициент наклона  Поэтому вместо дисперсий
Поэтому вместо дисперсий  получают их оценки
получают их оценки  используя вместо
используя вместо  одну из следующих ее оценок:
одну из следующих ее оценок:
1) при известных дисперсиях погрешностей измерения 

2) при известных оценках дисперсий погрешностей измерения 

3) при отсутствии предварительной информации о дисперсиях погрешностей или их оценках

Последнее выражение является аналогом выражения (14-9). В числителе этих выражений стоят суммы квадратов отклонений
отдельных результатов измерения от оценок их истинных значений, в знаменателе — число степеней свободы. В математической статистике доказано, что при обработке совместных измерений число степеней свободы определяется числом координатных точек  минус число неизвестных коэффициентов
минус число неизвестных коэффициентов  в исследуемой функциональной зависимости. В рассматриваемом случае
в исследуемой функциональной зависимости. В рассматриваемом случае  (коэффициенты
(коэффициенты  ), поэтому число степеней свободы равно
), поэтому число степеней свободы равно 
Совокупные измерения.
Если число проведенных различных совокупных измерений равно числу измеряемых величин, то по результатам измерений можно составить систему уравнений, в которой число уравнений равно числу измеряемых величин. Решая систему уравнений, каждую измеряемую величину можно косвенно выразить через результаты совокупных измерений. Дальнейшую обработку можно проводить по правилам обработки результатов наблюдений при косвенных измерениях. Если число различных совокупных измерений больше числа измеряемых величин, то обработку результатов измерения проводят с помощью метода наименьших квадратов.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Раздел А. ОБЩИЕ СВЕДЕНИЯ ОБ ИЗМЕРИТЕЛЬНОЙ ТЕХНИКЕ
- Глава первая. ОСНОВНЫЕ ПОНЯТИЯ ИЗМЕРИТЕЛЬНОЙ ТЕХНИКИ И КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ
- 1-2. ВИДЫ И МЕТОДЫ ИЗМЕРЕНИЙ
- Глава вторая. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
- 2-1. ОСНОВНЫЕ ПОНЯТИЯ И ВИДЫ ПОГРЕШНОСТЕЙ
- 2-2. ВЕРОЯТНОСТНЫЙ ПОДХОД К ОПИСАНИЮ ПОГРЕШНОСТЕЙ
- 2-3. ВЕРОЯТНОСТНЫЕ ОЦЕНКИ ПОГРЕШНОСТЕЙ
- Глава третья. ОСНОВЫ МЕТРОЛОГИЧЕСКОГО ОБЕСПЕЧЕНИЯ
- 3-2. ЭТАЛОНЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН
- 3-3. ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ
- Раздел Б. ЭЛЕКТРИЧЕСКИЕ СРЕДСТВА ИЗМЕРЕНИЙ
- Глава четвертая. ОБЩИЕ СВЕДЕНИЯ О СРЕДСТВАХ ИЗМЕРЕНИЙ
- 4-2. ГОСУДАРСТВЕННАЯ СИСТЕМА ПРИБОРОВ
- 4-3. ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
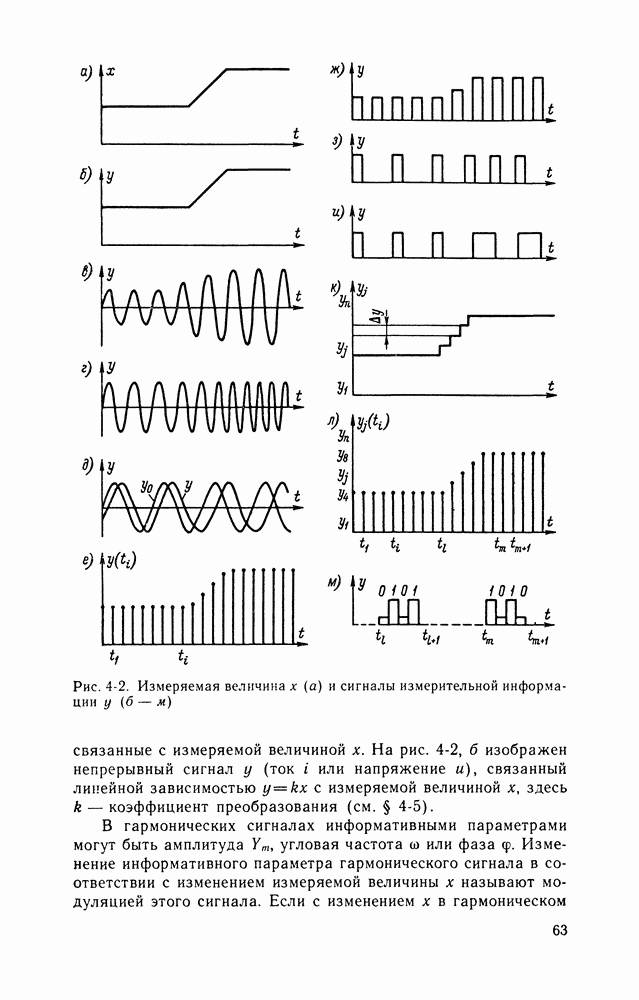
- 4-4. СИГНАЛЫ ИЗМЕРИТЕЛЬНОЙ ИНФОРМАЦИИ
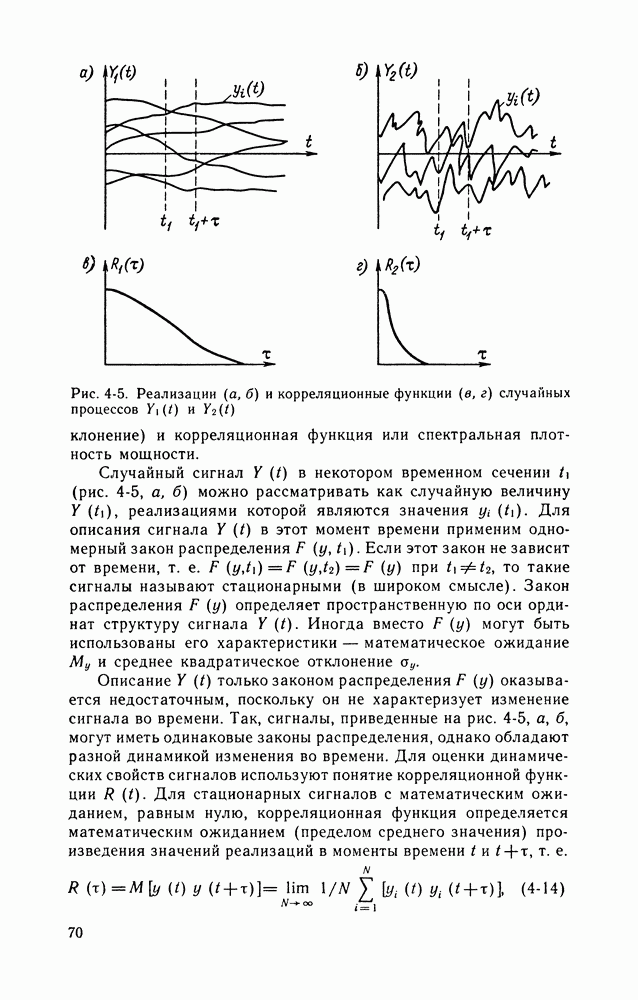
- Математические модели сигналов.
- Дискретизация сигналов.
- 4-5. СТРУКТУРНЫЕ СХЕМЫ И СВОЙСТВА СРЕДСТВ ИЗМЕРЕНИЙ В СТАТИЧЕСКОМ РЕЖИМЕ
- Средства измерений прямого преобразования.
- Средства измерений уравновешивающего преобразования.
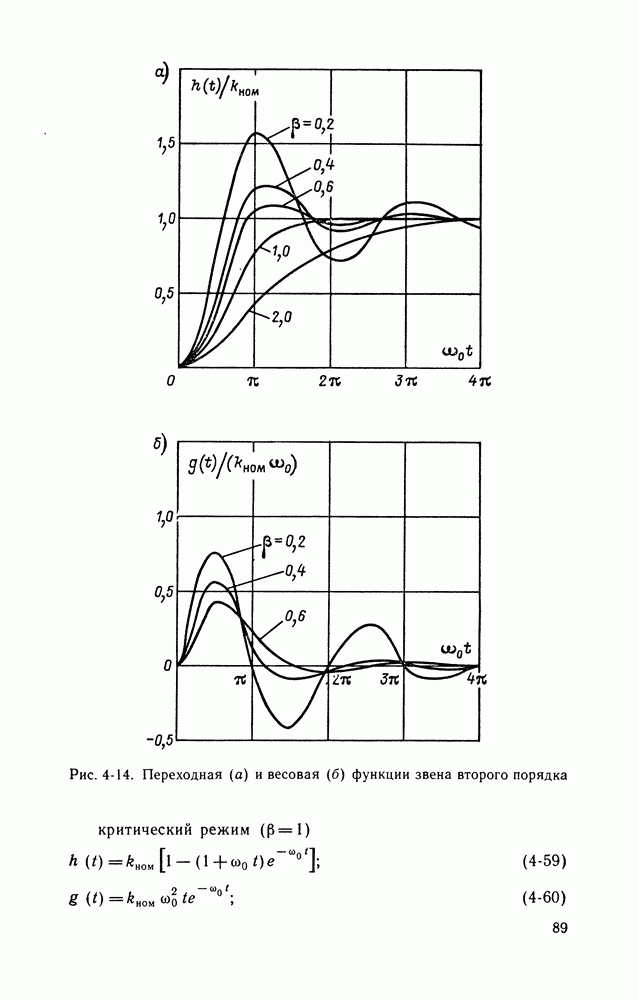
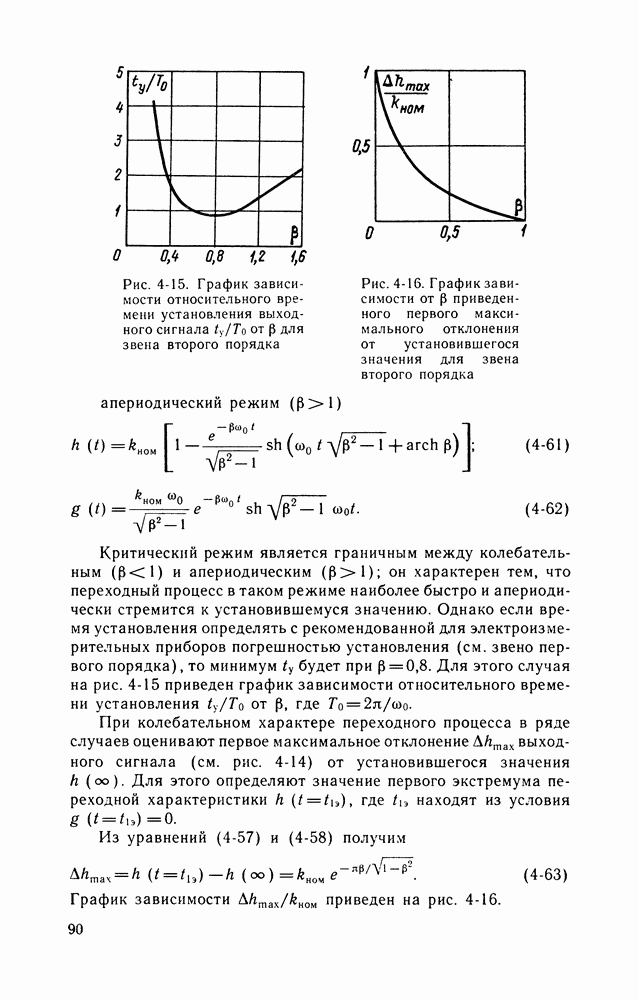
- 4-6. СРЕДСТВА ИЗМЕРЕНИЙ В ДИНАМИЧЕСКОМ РЕЖИМЕ
- Переходные и импульсные переходные характеристики.
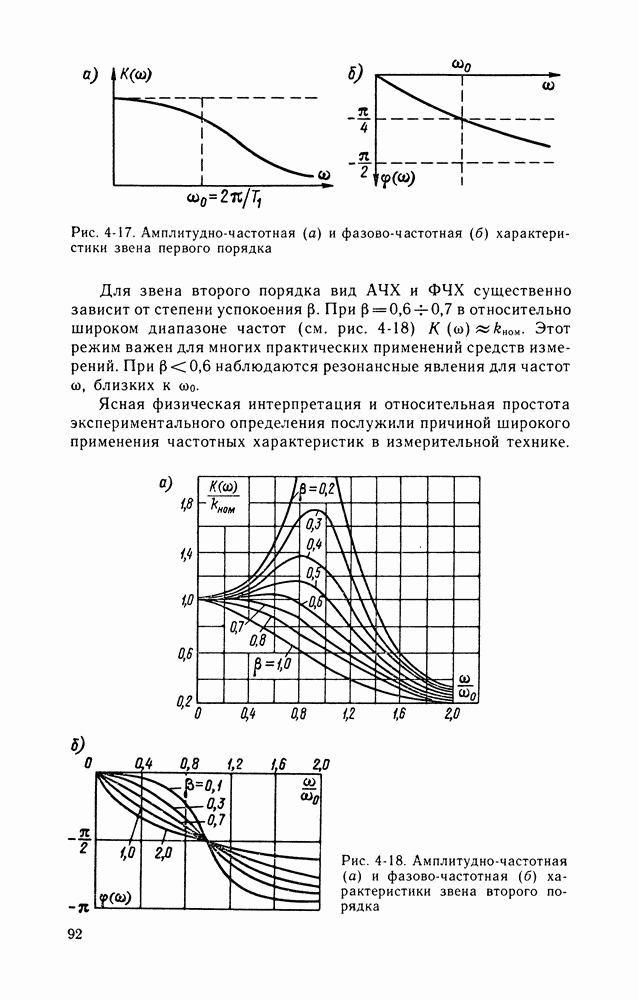
- Частотные характеристики.
- Передаточные функции.
- Глава пятая. МЕРЫ, ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ
- 5-2. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 5-3. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ
- МАГНИТОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ
- Амперметры и вольтметры.
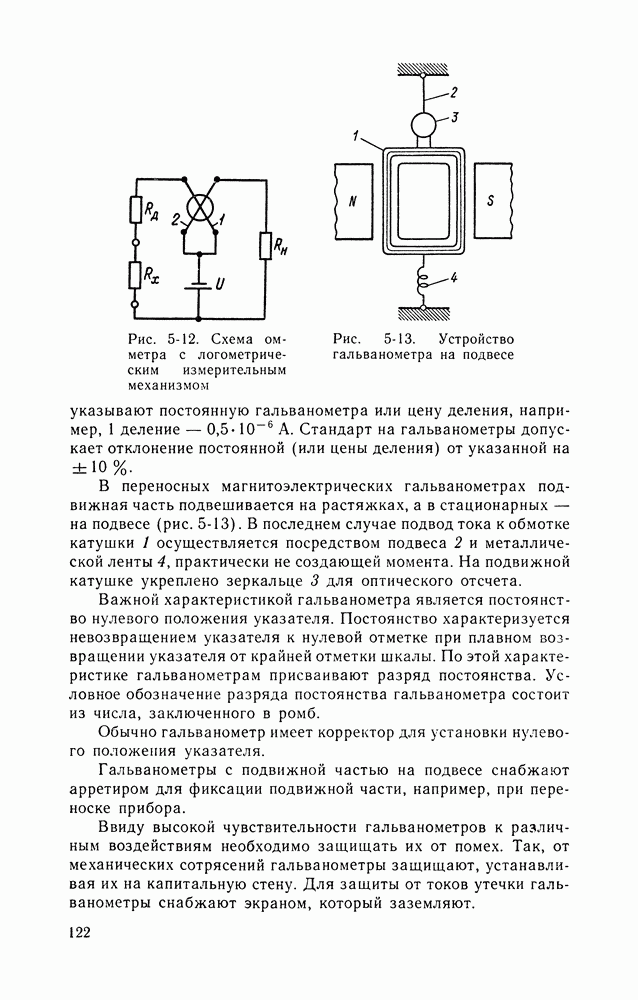
- Омметры.
- Гальванометры.
- Баллистические гальванометры.
- Кулонметры.
- Вибрационные гальванометры.
- ЭЛЕКТРОДИНАМИЧЕСКИЕ И ФЕРРОДИНАМИЧЕСКИЕ ПРИБОРЫ
- ЭЛЕКТРОМАГНИТНЫЕ ПРИБОРЫ
- ЭЛЕКТРОСТАТИЧЕСКИЕ ПРИБОРЫ
- ИНДУКЦИОННЫЕ ПРИБОРЫ
- 5-4. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ С ПРЕОБРАЗОВАТЕЛЯМИ
- Глава шестая. ЭЛЕКТРОННЫЕ АНАЛОГОВЫЕ ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ
- 6-2. ЭЛЕКТРОННЫЕ ВОЛЬТМЕТРЫ
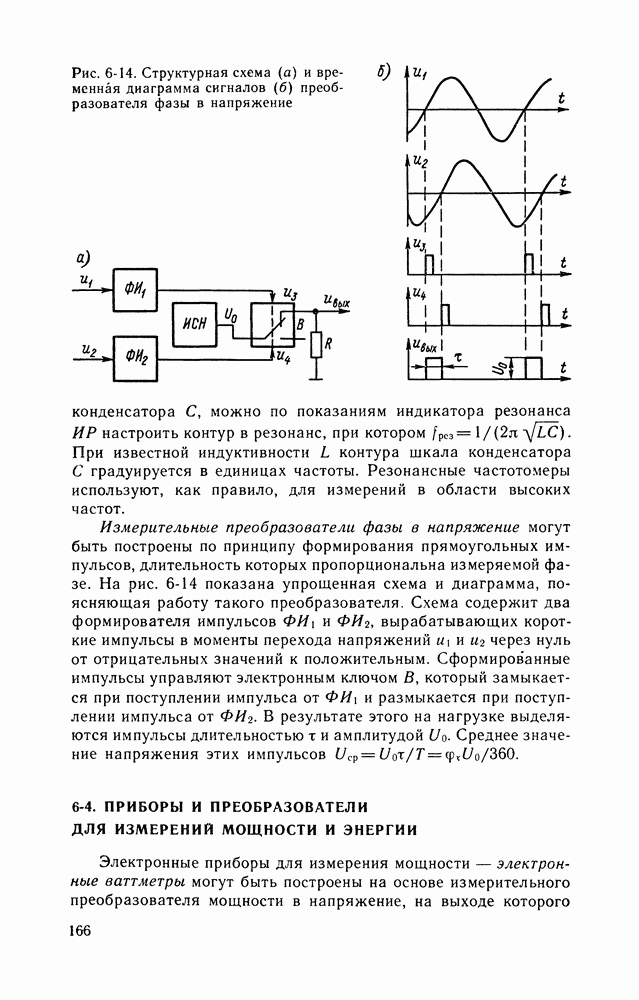
- 6-3. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ ЧАСТОТЫ И ФАЗЫ
- 6-4. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ МОЩНОСТИ И ЭНЕРГИИ
- 6-5. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ПАРАМЕТРОВ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 6-6. ЭЛЕКТРОННО ЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 6-7. АНАЛИЗАТОРЫ СПЕКТРА, ИЗМЕРИТЕЛИ НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ
- Глава седьмая. МОСТЫ И КОМПЕНСАТОРЫ
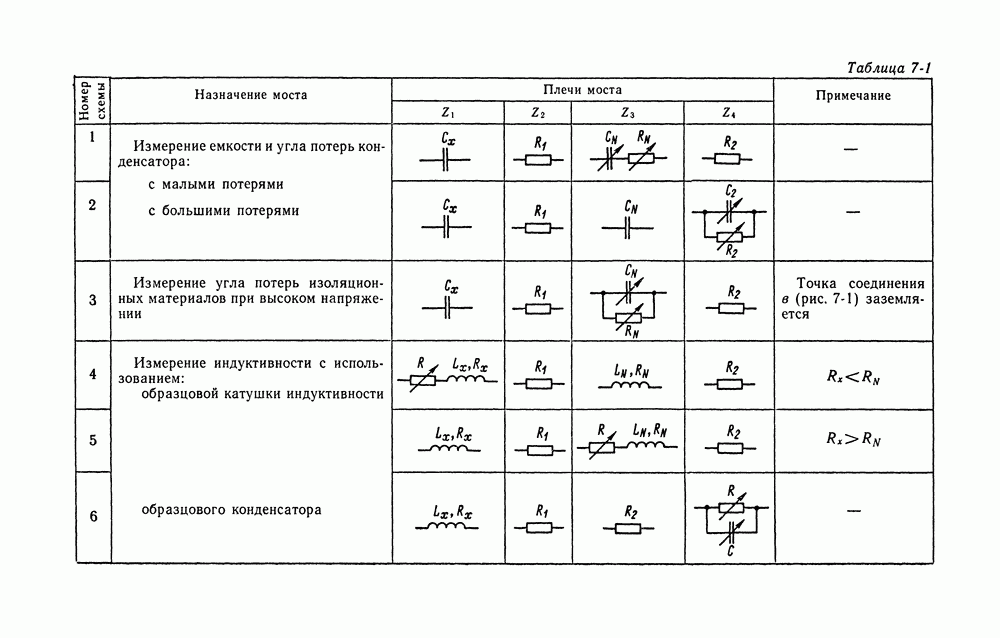
- 7-2. ТЕОРИЯ МОСТОВЫХ СХЕМ
- 7-3. МОСТЫ ДЛЯ ИЗМЕРЕНИЙ СОПРОТИВЛЕНИЯ НА ПОСТОЯННОМ ТОКЕ
- 7-4. МОСТЫ ПЕРЕМЕННОГО ТОКА ДЛЯ ИЗМЕРЕНИЙ ЕМКОСТИ, УГЛА ПОТЕРЬ, ИНДУКТИВНОСТИ И ДОБРОТНОСТИ
- 7-5. КОМПЕНСАТОРЫ ПОСТОЯННОГО ТОКА
- 7-6. КОМПЕНСАТОРЫ ПЕРЕМЕННОГО ТОКА
- 7-7. АВТОМАТИЧЕСКИЕ МОСТЫ И КОМПЕНСАТОРЫ
- Глава восьмая. ЦИФРОВЫЕ ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ
- 8-2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 8-3. УЗЛЫ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 8-4. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА ПОСЛЕДОВАТЕЛЬНОГО СЧЕТА
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД ЧАСТОТЫ
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД НАПРЯЖЕНИЯ ПОСТОЯННОГО ТОКА
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД ПЕРЕМЕЩЕНИЯ
- 8-5. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА ПОСЛЕДОВАТЕЛЬНОГО ПРИБЛИЖЕНИЯ
- 8-6. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА СЧИТЫВАНИЯ
- 8-7. ХАРАКТЕРИСТИКА СОВРЕМЕННЫХ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ПЕРСПЕКТИВЫ ИХ РАЗВИТИЯ
- Глава девятая. РЕГИСТРИРУЮЩИЕ ПРИБОРЫ И УСТРОЙСТВА
- 9-2. САМОПИШУЩИЕ ПРИБОРЫ ПРЯМОГО ПРЕОБРАЗОВАНИЯ
- 9-3. СВЕТОЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 9-4. МАГНИТОГРАФЫ, ГРАФОПОСТРОИТЕЛИ, ЭЛЕКТРОННЫЕ ОСЦИЛЛОГРАФЫ, ЦИФРОПЕЧАТАЮЩИЕ УСТРОЙСТВА
- Глава десятая. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНЫХ ВЕЛИЧИН
- 10-2. МАГНИТОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНОГО ПОТОКА
- ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНОЙ ИНДУКЦИИ И НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ
- 10-3. АППАРАТУРА ДЛЯ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- Глава одиннадцатая. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 11-2. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- ГЕНЕРАТОРНЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
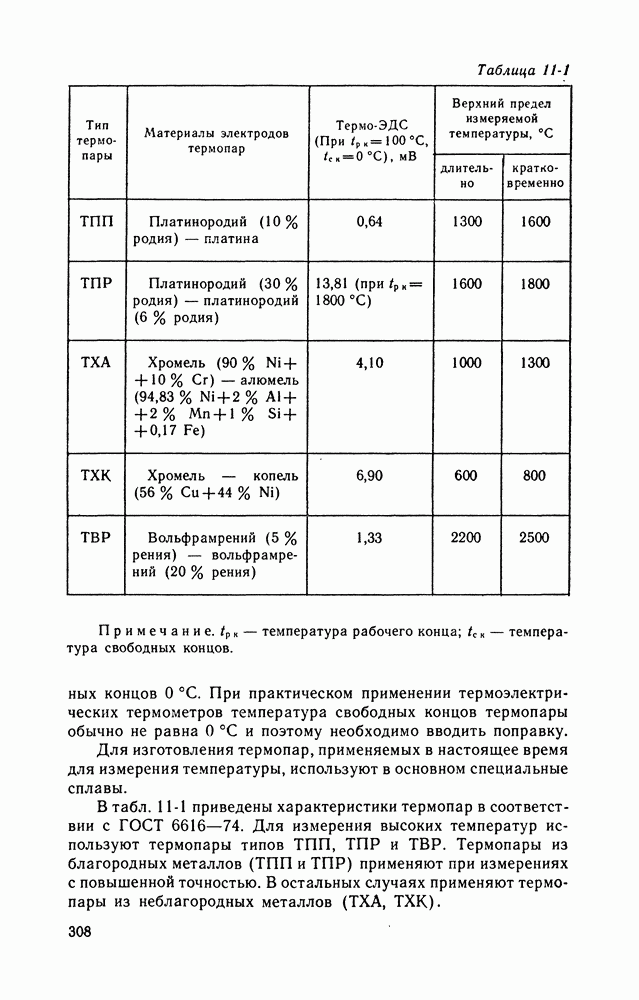
- 11-3. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ТЕМПЕРАТУРЫ
- 11-4. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ГЕОМЕТРИЧЕСКИХ И МЕХАНИЧЕСКИХ ВЕЛИЧИН
- 11-5. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ КОНЦЕНТРАЦИИ ЖИДКОЙ И ГАЗООБРАЗНОЙ СРЕДЫ
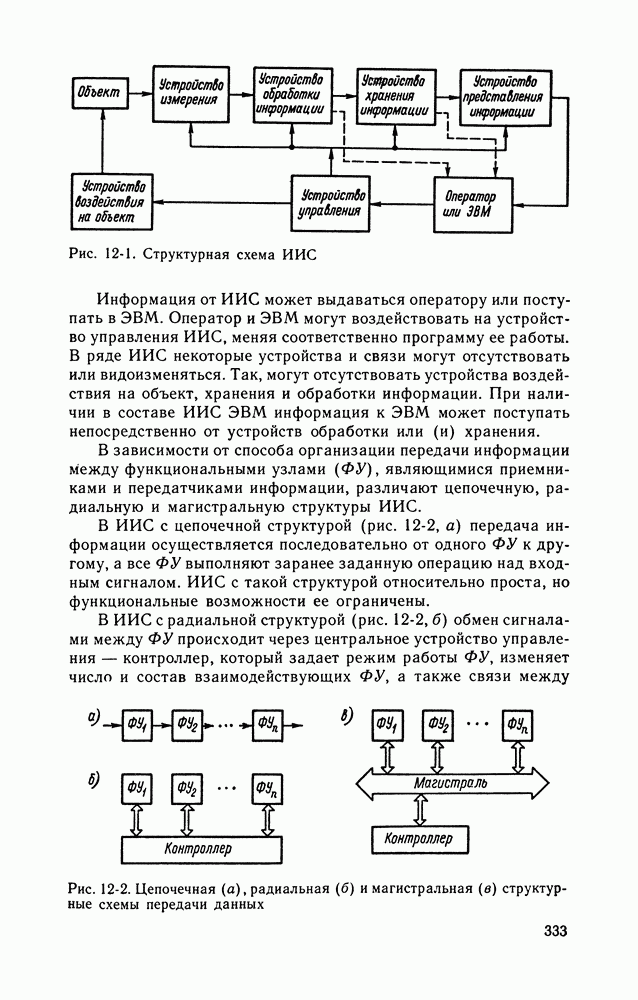
- Глава двенадцатая. ИЗМЕРИТЕЛЬНЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ
- 12-2. ИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ
- 12-3. ТЕЛЕИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ
- 12-4. СИСТЕМЫ АВТОМАТИЧЕСКОГО КОНТРОЛЯ И ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ
- 12-5. ИЗМЕРИТЕЛЬНЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ НА ОСНОВЕ АГРЕГАТНЫХ КОМПЛЕКСОВ ГОСУДАРСТВЕННОЙ СИСТЕМЫ ПРИБОРОВ И СРЕДСТВ АВТОМАТИЗАЦИИ
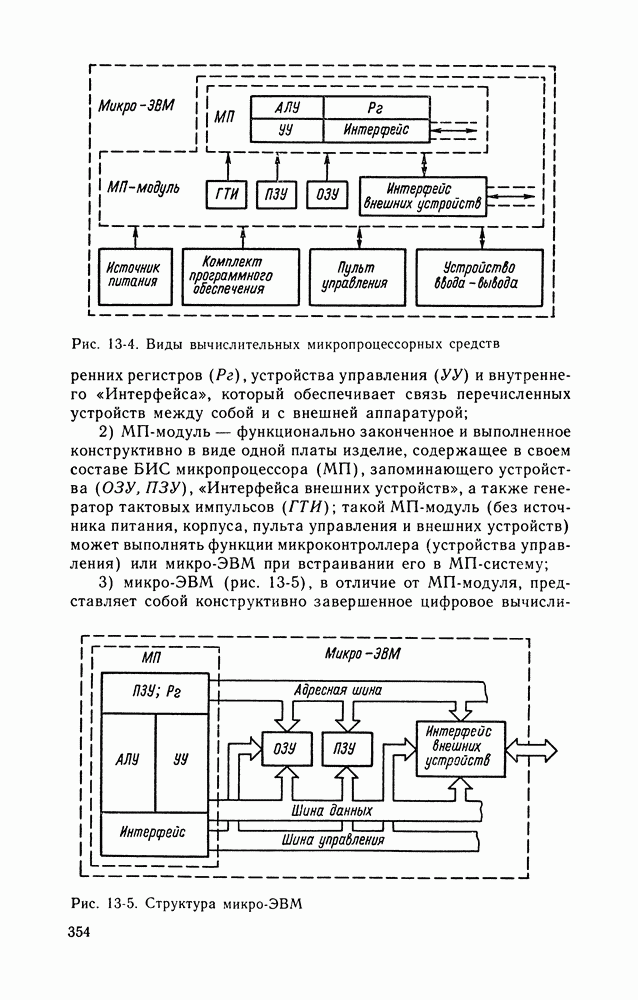
- Глава тринадцатая. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ СРЕДСТВА
- 13-2. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ СРЕДСТВА СИСТЕМНОГО ПРИМЕНЕНИЯ
- 13-3. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ КОМПЛЕКСЫ
- Раздел В. ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
- Глава четырнадцатая. ПОДГОТОВКА ИЗМЕРИТЕЛЬНОГО ЭКСПЕРИМЕНТА И ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- 14-2. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- 14-3. СУММИРОВАНИЕ ПОГРЕШНОСТЕЙ
- Глава пятнадцатая. ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ, МАГНИТНЫХ И НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
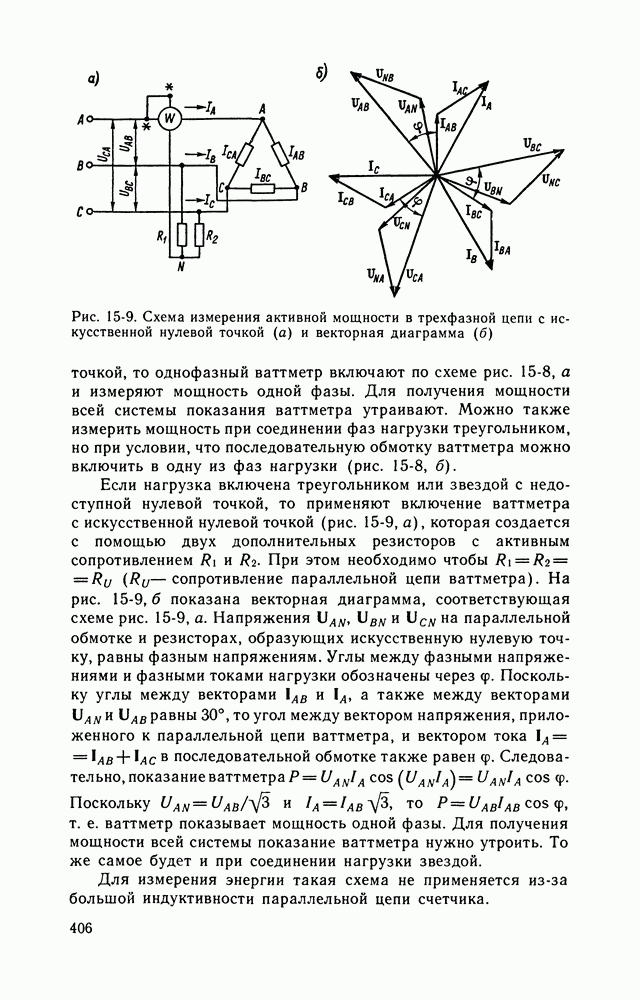
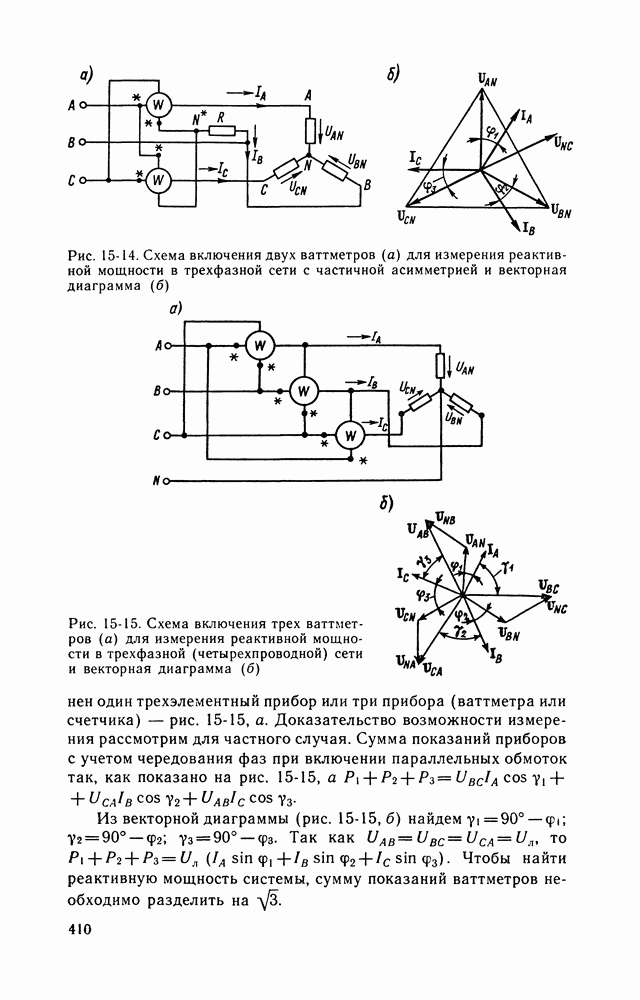
- 15-2. ИЗМЕРЕНИЯ МОЩНОСТИ, ЭНЕРГИИ И КОЛИЧЕСТВА ЭЛЕКТРИЧЕСТВА
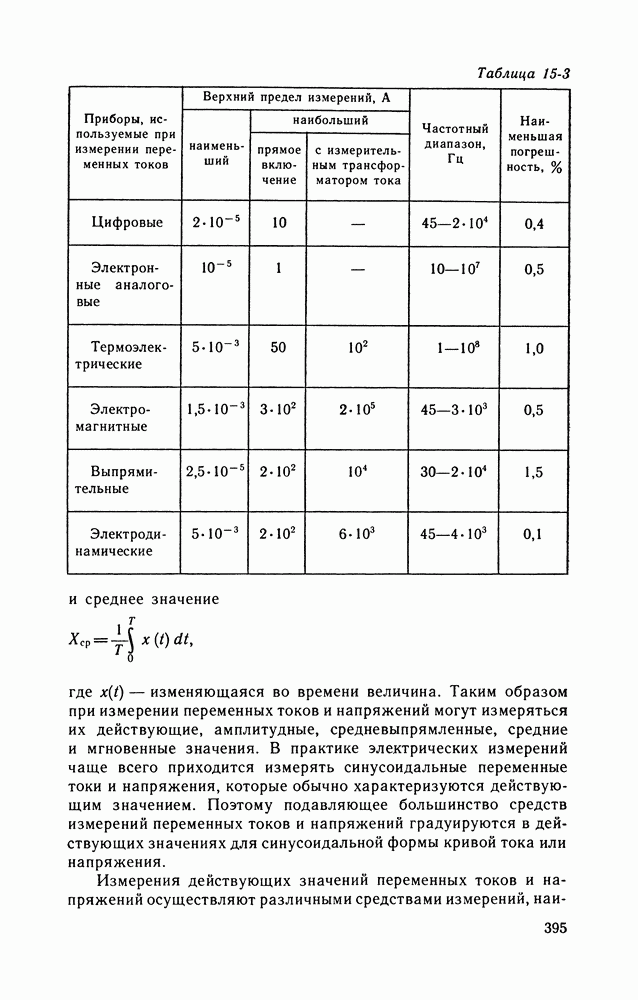
- 15-3. ИЗМЕРЕНИЯ ЧАСТОТЫ, ФАЗЫ, ВРЕМЕННЫХ ИНТЕРВАЛОВ, АНАЛИЗ СПЕКТРА ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
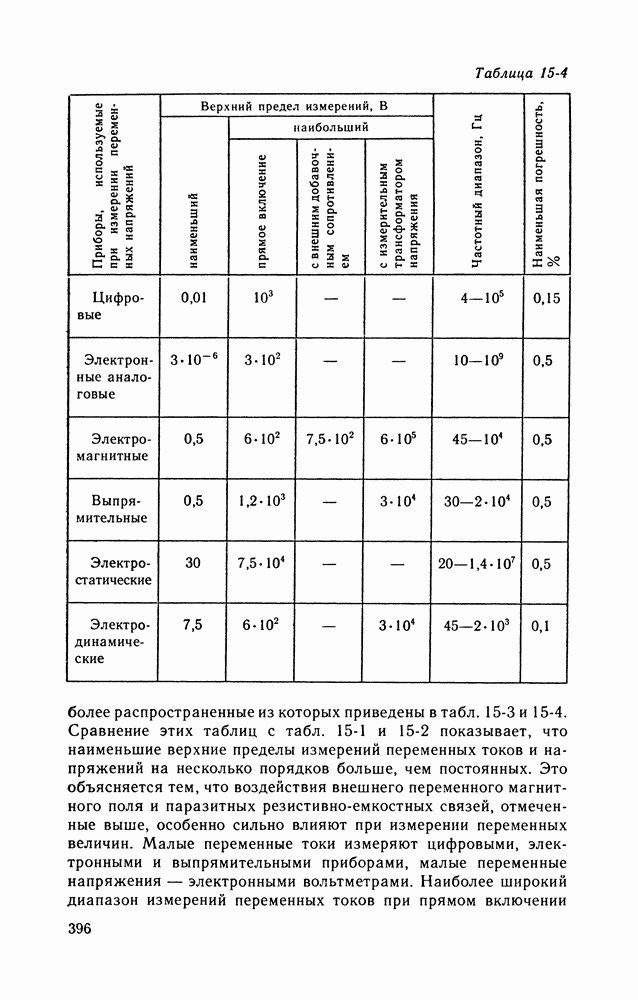
- 15-4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ЦЕПЕЙ ПОСТОЯННОГО И ПЕРЕМЕННОГО ТОКА
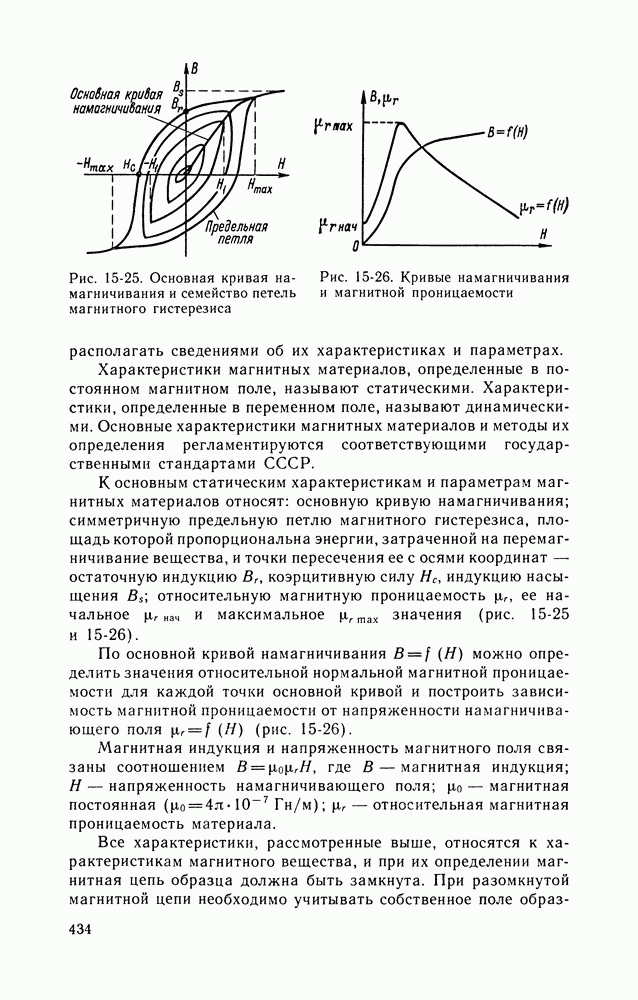
- 15-5. ИЗМЕРЕНИЯ ПАРАМЕТРОВ МАГНИТНОГО ПОЛЯ, ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- МАГНИТНЫЕ МАТЕРИАЛЫ И ИХ ХАРАКТЕРИСТИКИ
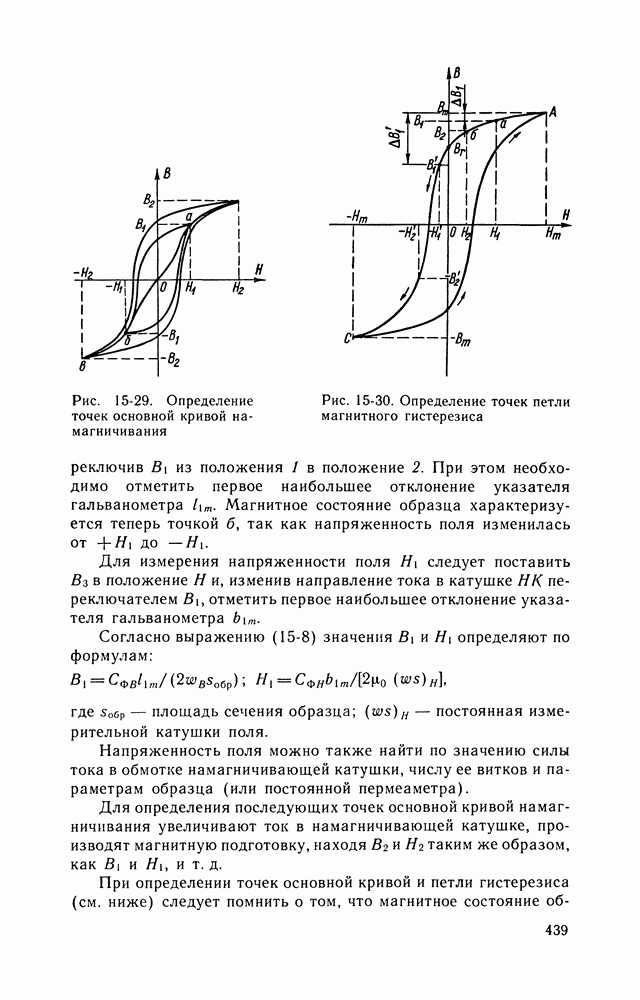
- ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
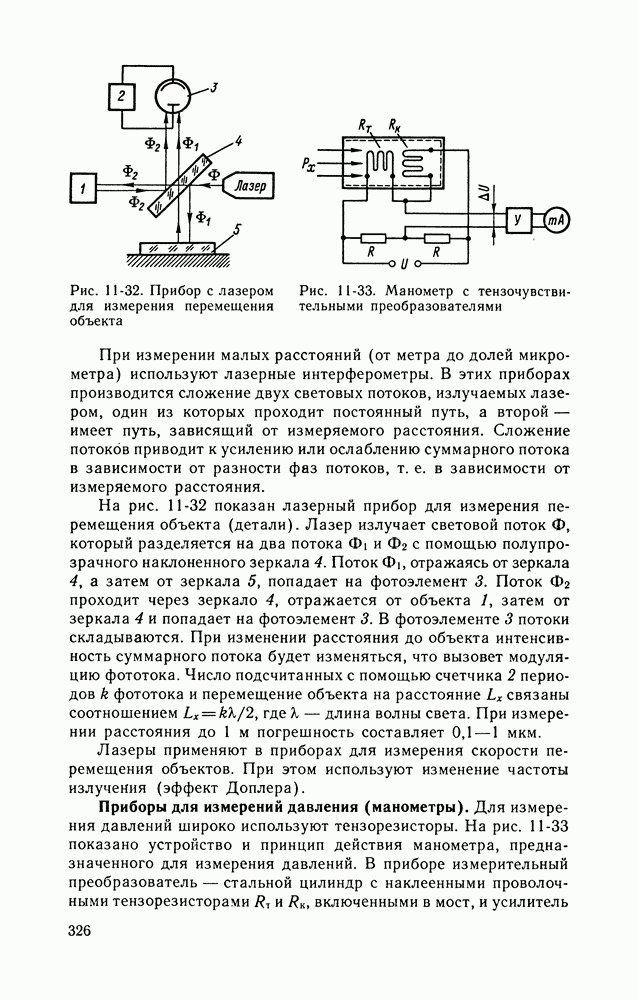
- 15-6. ИЗМЕРЕНИЯ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- ИЗМЕРЕНИЯ ДАВЛЕНИЙ, ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ И РАССТОЯНИЙ
- Глава шестнадцатая. ИЗМЕРЕНИЯ ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ПРОЦЕССОВ
- 16-2. ИЗМЕРЕНИЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ДИСПЕРСИИ СЛУЧАЙНОГО ПРОЦЕССА
- 16-3. ИЗМЕРЕНИЕ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
- 16-4. ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННОЙ ФУНКЦИИ
- 16-5. АНАЛИЗ СПЕКТРА МОЩНОСТИ
- Список литературы