| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4-6. СРЕДСТВА ИЗМЕРЕНИЙ В ДИНАМИЧЕСКОМ РЕЖИМЕ
Изменение во времени измеряемой величины  приводит к динамическому режиму (см. § 4-3) работы средств измерений. В таком режиме точность измерений во многом зависит от динамических свойств средств измерений и от характера изменения измеряемой величины.
приводит к динамическому режиму (см. § 4-3) работы средств измерений. В таком режиме точность измерений во многом зависит от динамических свойств средств измерений и от характера изменения измеряемой величины.
Для того чтобы выходной сигнал  некоторого (идеального) средства измерений точно отображал во времени измеряемую величину
некоторого (идеального) средства измерений точно отображал во времени измеряемую величину  независимо от характера ее изменения, необходимо соблюдение условия
независимо от характера ее изменения, необходимо соблюдение условия

где  — номинальный коэффициент преобразования. Для упрощения анализа динамического режима примем, что средство измерений не имеет статической погрешности, т. е. реальный коэффициент преобразования
— номинальный коэффициент преобразования. Для упрощения анализа динамического режима примем, что средство измерений не имеет статической погрешности, т. е. реальный коэффициент преобразования  во всем диапазоне изменения
во всем диапазоне изменения  Уравнение (4-43) соответствует идеальному безынерционному линейному преобразованию. Из этого уравнения следует, что измеряемая величина
Уравнение (4-43) соответствует идеальному безынерционному линейному преобразованию. Из этого уравнения следует, что измеряемая величина  может быть определена по выходному (наблюдаемому, регистрируемому) сигналу
может быть определена по выходному (наблюдаемому, регистрируемому) сигналу  из соотношения
из соотношения  При этом отсутствует какая-либо погрешность определения
При этом отсутствует какая-либо погрешность определения  обусловленная изменением входной величины во времени.
обусловленная изменением входной величины во времени.
Реальные средства измерений обладают динамическими (инерционными) свойствами из-за наличия элементов, запасающих энергию, например подвижных элементов, обладающих определенной массой, и упругих элементов в электромеханических приборах, емкостей и индуктивностей в измерительных цепях и т. д., что приводит к более сложной зависимости между 
Существуют различные способы описания динамических свойств средств измерений и оценки погрешностей, возникающих в динамическом режиме. Наиболее полно эти свойства средств измерений могут быть описаны дифференциальными уравнениями,

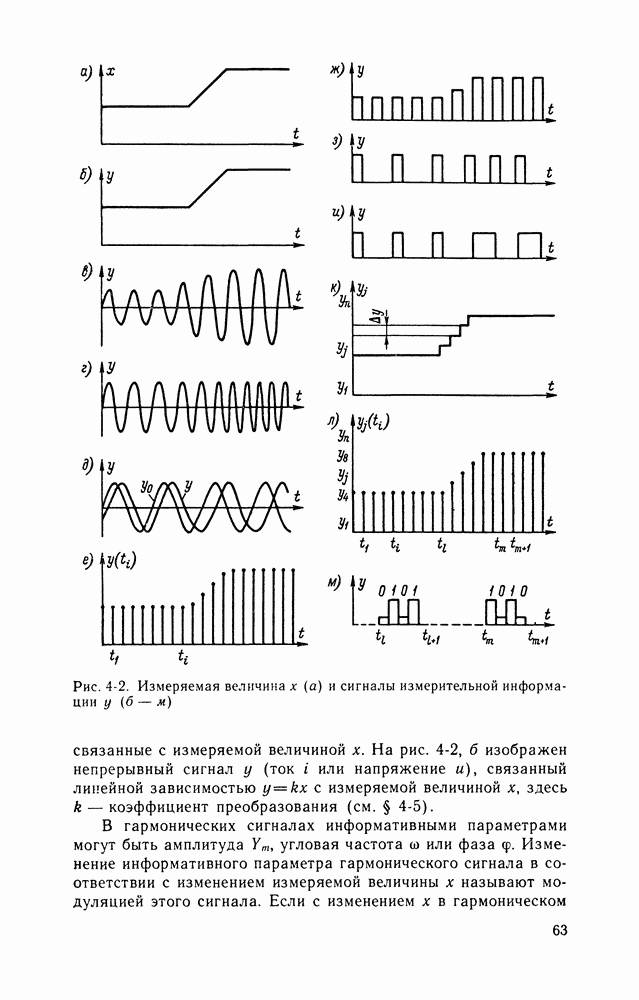
Рис. 4-11. Входной  и выходные
и выходные  сигналы некоторого реального и идеального (безынерционного) средств измерений
сигналы некоторого реального и идеального (безынерционного) средств измерений
переходными и импульсными переходными характеристиками, частотными характеристиками и передаточными функциями.
Дифференциальные уравнения.
Динамический режим широкого класса средств измерений может быть описан линейным неоднородным дифференциальным уравнением с постоянными коэффициентами

Это уравнение отличается от уравнения (4-43) наличием членов, содержащих производные от выходного сигнала  которые и определяют динамические свойства средств измерений. При равенстве нулю этих членов уравнение (4-44) вырождается в уравнение (4-43).
которые и определяют динамические свойства средств измерений. При равенстве нулю этих членов уравнение (4-44) вырождается в уравнение (4-43).
Решение  дифференциального уравнения (4-44) описывает выходной сигнал средства измерения при входном воздействии
дифференциального уравнения (4-44) описывает выходной сигнал средства измерения при входном воздействии  На рис. 4-11 показаны выходные сигналы у (О некоторого реального и
На рис. 4-11 показаны выходные сигналы у (О некоторого реального и  идеального (безынерционного) средства измерений при входном сигнале
идеального (безынерционного) средства измерений при входном сигнале  Погрешность по выходу средства измерений в динамическом режиме определяется выражением
Погрешность по выходу средства измерений в динамическом режиме определяется выражением

Погрешность в динамическом режиме представляет собой алгебраическую сумму динамической и статической погрешности. Поскольку статическая погрешность принята равной нулю, то выражение (4-45) определяет только динамическую погрешность.
В задачу измерений входит нахождение значений измеряемой величины  по значениям
по значениям  Если
Если  определять из соотношения
определять из соотношения  а такой способ является наиболее распространенным в измерительной технике, то динамическая погрешность по входу средства измерений
а такой способ является наиболее распространенным в измерительной технике, то динамическая погрешность по входу средства измерений

Следовательно, при таком подходе погрешности  различаются постоянным множителем
различаются постоянным множителем 
Вычитая из выражения (4-44) уравнение (4-43) с учетом (4-45), получим выражение для динамической погрешности по выходу средства измерений

Определение погрешности  по этому выражению хотя принципиально и возможно, однако на практике встречает трудности, поскольку аналитическое выражение для у (0, как правило, неизвестно, а определение производных от
по этому выражению хотя принципиально и возможно, однако на практике встречает трудности, поскольку аналитическое выражение для у (0, как правило, неизвестно, а определение производных от  например, графически по зарегистрированному выходному сигналу не может быть проведено с необходимой точностью. Поэтому часто применяют некоторые оценки динамической погрешности, характеризующие результат измерений переменной во времени величины
например, графически по зарегистрированному выходному сигналу не может быть проведено с необходимой точностью. Поэтому часто применяют некоторые оценки динамической погрешности, характеризующие результат измерений переменной во времени величины  При этом оказывается удобным оценивать динамические погрешности отдельно для переходного режима работы средства измерений и для установившегося.
При этом оказывается удобным оценивать динамические погрешности отдельно для переходного режима работы средства измерений и для установившегося.
Общее решение  неоднородного линейного дифференциального уравнения с постоянными коэффициентами определяется суммой:
неоднородного линейного дифференциального уравнения с постоянными коэффициентами определяется суммой:  где
где  — общее решение соответствующего однородного дифференциального уравнения;
— общее решение соответствующего однородного дифференциального уравнения;  — частное решение уравнения (4-44). Решение
— частное решение уравнения (4-44). Решение  описывает свободные колебания, определяемые динамическими характеристиками средства измерений. Для устойчивых средств измерений свободные колебания являются затухающими, т. е.
описывает свободные колебания, определяемые динамическими характеристиками средства измерений. Для устойчивых средств измерений свободные колебания являются затухающими, т. е.  а продолжительность этих колебаний определяет продолжительность переходного режима. В измерительной технике переходный режим принято оценивать временем установления
а продолжительность этих колебаний определяет продолжительность переходного режима. В измерительной технике переходный режим принято оценивать временем установления  (в более общей трактовке — временем реакции, см. § 4-3), которое, по существу, определяется временем затухания свободных колебаний до некоторой малой величины, при которой практически можно считать
(в более общей трактовке — временем реакции, см. § 4-3), которое, по существу, определяется временем затухания свободных колебаний до некоторой малой величины, при которой практически можно считать  Частное решение
Частное решение  описывает вынужденные колебания (установившийся режим), определяемые входным воздействием и динамическими свойствами средств измерений. Отсюда следует, что динамическая погрешность в переходном режиме
описывает вынужденные колебания (установившийся режим), определяемые входным воздействием и динамическими свойствами средств измерений. Отсюда следует, что динамическая погрешность в переходном режиме  определяется составляющими
определяется составляющими  а в установившемся
а в установившемся  — только составляющей
— только составляющей  Значения динамической погрешности при указанных режимах могут существенно различаться.
Значения динамической погрешности при указанных режимах могут существенно различаться.
Порядок уравнения (4-44) определяется динамическими свойствами средства измерений и в общем случае может быть высоким. Дифференциальные уравнения высокого порядка могут быть представлены системой дифференциальных уравнений более низкого порядка. По существу, это означает представление сложного в динамическом смысле средства измерений более простыми. Как показано в § 4-5, сложные средства измерений условно могут быть разбиты на звенья в зависимости от их свойств, в том числе и динамических. В этом случае для исследования динамических свойств средств измерений широко используются динамические звенья первого и второго порядков.
Динамическое звено первого порядка описывается уравнением

где  — постоянная времени звена первого порядка. Применяют также параметр
— постоянная времени звена первого порядка. Применяют также параметр  называемый граничной частотой. Для такого звена при известном
называемый граничной частотой. Для такого звена при известном  относительно просто определяется
относительно просто определяется 
При измерениях решается обратная задача — по реакции звена находится измеряемая величина  Рассмотрим одну из возможных оценок максимальной динамической погрешности при следующих ограничениях на входное воздействие: диапазон изменения входного сигнала от
Рассмотрим одну из возможных оценок максимальной динамической погрешности при следующих ограничениях на входное воздействие: диапазон изменения входного сигнала от  до
до  спектр входного сигнала ограничен частотой
спектр входного сигнала ограничен частотой  . Такая форма задания входных сигналов часто используется на практике.
. Такая форма задания входных сигналов часто используется на практике.
На основании уравнений (4-46) — (4-48) динамическая погрешность по входу звена первого порядка определяется выражением Да:  Максимальное значение модуля этой погрешности
Максимальное значение модуля этой погрешности  Для оценки
Для оценки  можно воспользоваться неравенством С. Н. Бернштейна (см. § 4-4):
можно воспользоваться неравенством С. Н. Бернштейна (см. § 4-4):  где
где  — модуль максимально возможного значения сигнала на выходе звена;
— модуль максимально возможного значения сигнала на выходе звена;  — максимально возможный коэффициент передачи для звена первого порядка. Для такого звена, как будет показано далее (см. стр. 91),
— максимально возможный коэффициент передачи для звена первого порядка. Для такого звена, как будет показано далее (см. стр. 91),  Следовательно
Следовательно

На основании этого выражения определим максимальную приведенную (к диапазону  изменения сигнала) погрешность
изменения сигнала) погрешность

Динамическое звено второго порядка описывается уравнением

где  — частота собственных колебаний звена;
— частота собственных колебаний звена;  — коэффициент демпфирования, или степень успокоения, — характеристика звена, значение которой существенно влияет на характер динамических процессов, протекающих в таком звене.
— коэффициент демпфирования, или степень успокоения, — характеристика звена, значение которой существенно влияет на характер динамических процессов, протекающих в таком звене.
Используя (4-51), (4-46) и неравенство  (см. § 4-4), можно записать выражения для динамической погрешности по входу звена второго порядка
(см. § 4-4), можно записать выражения для динамической погрешности по входу звена второго порядка

и ее максимальной оценки для указанных выше условий 

Значение коэффициента  соответствующего максимальному отклонению
соответствующего максимальному отклонению  здесь также неизвестно. Более того, для звена второго порядка в общем случае
здесь также неизвестно. Более того, для звена второго порядка в общем случае  может быть как меньше, так и больше
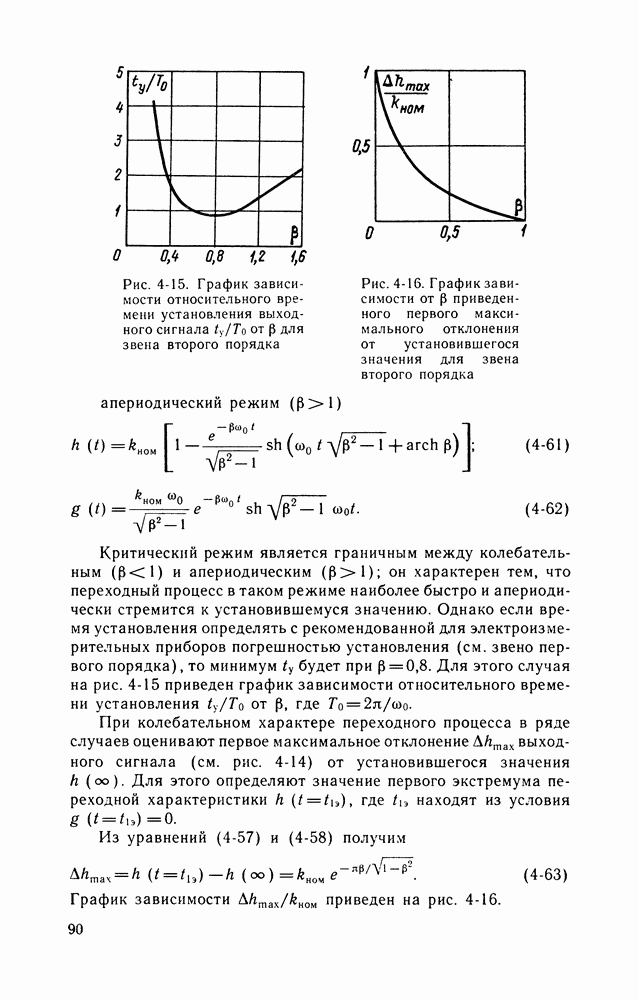
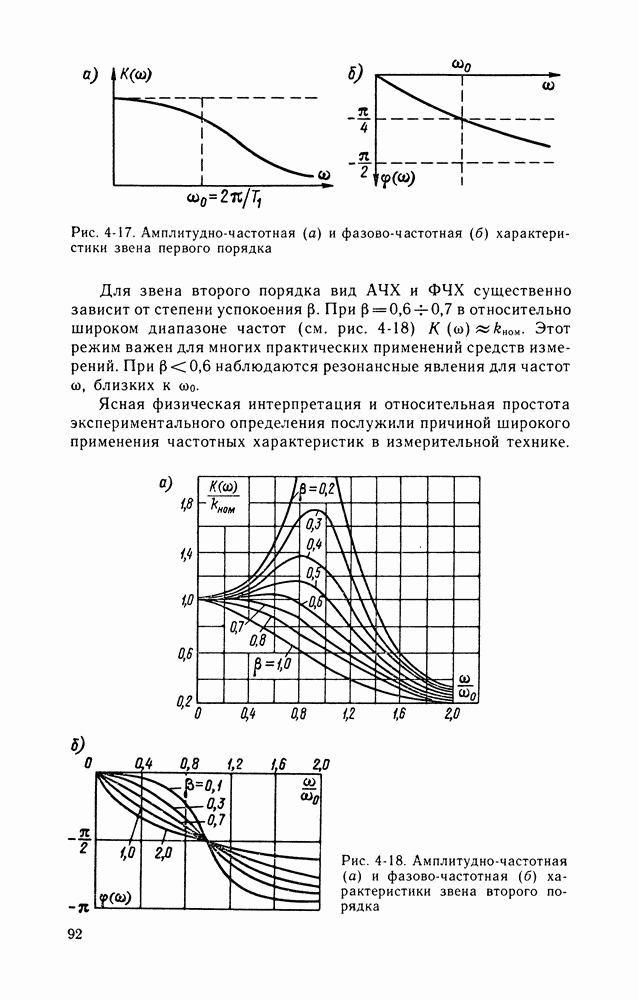
может быть как меньше, так и больше  (см. стр. 92). При принятых ограничениях на максимальную частоту спектра входных сигналов по амплитудно-частотным характеристикам (см. рис. 4-18) можно определить максимальное значение
(см. стр. 92). При принятых ограничениях на максимальную частоту спектра входных сигналов по амплитудно-частотным характеристикам (см. рис. 4-18) можно определить максимальное значение  в заданном диапазоне частот и подставить его в выражение (4-52) для оценки динамической погрешности. Приведем выражение для оценки максимальной приведенной погрешности звеньев, имеющих (30,7, для которых
в заданном диапазоне частот и подставить его в выражение (4-52) для оценки динамической погрешности. Приведем выражение для оценки максимальной приведенной погрешности звеньев, имеющих (30,7, для которых  Считая
Считая  и подставляя это значение в выражение (4-52), получим
и подставляя это значение в выражение (4-52), получим

Необходимо иметь в виду, что выражения (4-50) и (4-53) дают завышенную оценку (оценку сверху) максимальной динамической погрешности. Поэтому их следует применять при небольших отношениях  при которых значения погрешностей относительно невелики.
при которых значения погрешностей относительно невелики.

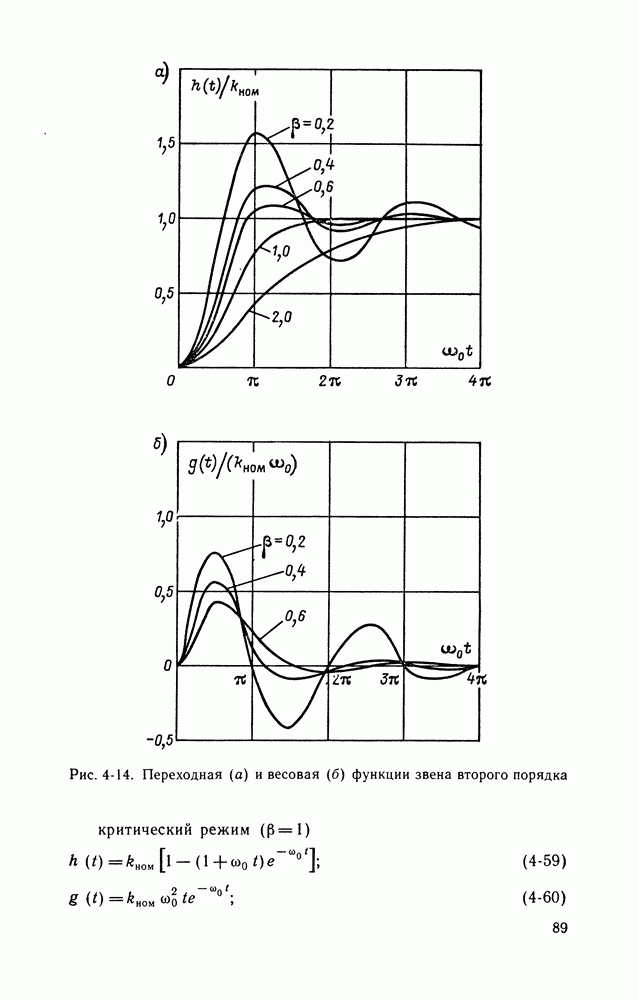
Рис. 4-12. Переходная (а) и весовая (б) функции некоторого средства измерений
Полученные оценки можно использовать для установившегося динамического режима при ограниченном спектре входного сигнала. Для переходного режима возникают трудности в определении максимальной частоты сот. Так, при подключении в некоторый момент времени  сигнала
сигнала  входное воздействие имеет неограниченный спектр. Кроме того, некоторые сигналы имеют в установившемся режиме
входное воздействие имеет неограниченный спектр. Кроме того, некоторые сигналы имеют в установившемся режиме  например когда входной сигнал по форме близок к прямоугольным импульсам. В этих случаях целесообразно использовать переходные и импульсные переходные характеристики.
например когда входной сигнал по форме близок к прямоугольным импульсам. В этих случаях целесообразно использовать переходные и импульсные переходные характеристики.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Раздел А. ОБЩИЕ СВЕДЕНИЯ ОБ ИЗМЕРИТЕЛЬНОЙ ТЕХНИКЕ
- Глава первая. ОСНОВНЫЕ ПОНЯТИЯ ИЗМЕРИТЕЛЬНОЙ ТЕХНИКИ И КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ
- 1-2. ВИДЫ И МЕТОДЫ ИЗМЕРЕНИЙ
- Глава вторая. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
- 2-1. ОСНОВНЫЕ ПОНЯТИЯ И ВИДЫ ПОГРЕШНОСТЕЙ
- 2-2. ВЕРОЯТНОСТНЫЙ ПОДХОД К ОПИСАНИЮ ПОГРЕШНОСТЕЙ
- 2-3. ВЕРОЯТНОСТНЫЕ ОЦЕНКИ ПОГРЕШНОСТЕЙ
- Глава третья. ОСНОВЫ МЕТРОЛОГИЧЕСКОГО ОБЕСПЕЧЕНИЯ
- 3-2. ЭТАЛОНЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН
- 3-3. ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ
- Раздел Б. ЭЛЕКТРИЧЕСКИЕ СРЕДСТВА ИЗМЕРЕНИЙ
- Глава четвертая. ОБЩИЕ СВЕДЕНИЯ О СРЕДСТВАХ ИЗМЕРЕНИЙ
- 4-2. ГОСУДАРСТВЕННАЯ СИСТЕМА ПРИБОРОВ
- 4-3. ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
- 4-4. СИГНАЛЫ ИЗМЕРИТЕЛЬНОЙ ИНФОРМАЦИИ
- Математические модели сигналов.
- Дискретизация сигналов.
- 4-5. СТРУКТУРНЫЕ СХЕМЫ И СВОЙСТВА СРЕДСТВ ИЗМЕРЕНИЙ В СТАТИЧЕСКОМ РЕЖИМЕ
- Средства измерений прямого преобразования.
- Средства измерений уравновешивающего преобразования.
- 4-6. СРЕДСТВА ИЗМЕРЕНИЙ В ДИНАМИЧЕСКОМ РЕЖИМЕ
- Переходные и импульсные переходные характеристики.
- Частотные характеристики.
- Передаточные функции.
- Глава пятая. МЕРЫ, ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ
- 5-2. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 5-3. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ
- МАГНИТОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ
- Амперметры и вольтметры.
- Омметры.
- Гальванометры.
- Баллистические гальванометры.
- Кулонметры.
- Вибрационные гальванометры.
- ЭЛЕКТРОДИНАМИЧЕСКИЕ И ФЕРРОДИНАМИЧЕСКИЕ ПРИБОРЫ
- ЭЛЕКТРОМАГНИТНЫЕ ПРИБОРЫ
- ЭЛЕКТРОСТАТИЧЕСКИЕ ПРИБОРЫ
- ИНДУКЦИОННЫЕ ПРИБОРЫ
- 5-4. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ С ПРЕОБРАЗОВАТЕЛЯМИ
- Глава шестая. ЭЛЕКТРОННЫЕ АНАЛОГОВЫЕ ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ
- 6-2. ЭЛЕКТРОННЫЕ ВОЛЬТМЕТРЫ
- 6-3. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ ЧАСТОТЫ И ФАЗЫ
- 6-4. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ МОЩНОСТИ И ЭНЕРГИИ
- 6-5. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ПАРАМЕТРОВ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 6-6. ЭЛЕКТРОННО ЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 6-7. АНАЛИЗАТОРЫ СПЕКТРА, ИЗМЕРИТЕЛИ НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ
- Глава седьмая. МОСТЫ И КОМПЕНСАТОРЫ
- 7-2. ТЕОРИЯ МОСТОВЫХ СХЕМ
- 7-3. МОСТЫ ДЛЯ ИЗМЕРЕНИЙ СОПРОТИВЛЕНИЯ НА ПОСТОЯННОМ ТОКЕ
- 7-4. МОСТЫ ПЕРЕМЕННОГО ТОКА ДЛЯ ИЗМЕРЕНИЙ ЕМКОСТИ, УГЛА ПОТЕРЬ, ИНДУКТИВНОСТИ И ДОБРОТНОСТИ
- 7-5. КОМПЕНСАТОРЫ ПОСТОЯННОГО ТОКА
- 7-6. КОМПЕНСАТОРЫ ПЕРЕМЕННОГО ТОКА
- 7-7. АВТОМАТИЧЕСКИЕ МОСТЫ И КОМПЕНСАТОРЫ
- Глава восьмая. ЦИФРОВЫЕ ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ
- 8-2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 8-3. УЗЛЫ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 8-4. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА ПОСЛЕДОВАТЕЛЬНОГО СЧЕТА
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД ЧАСТОТЫ
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД НАПРЯЖЕНИЯ ПОСТОЯННОГО ТОКА
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД ПЕРЕМЕЩЕНИЯ
- 8-5. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА ПОСЛЕДОВАТЕЛЬНОГО ПРИБЛИЖЕНИЯ
- 8-6. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА СЧИТЫВАНИЯ
- 8-7. ХАРАКТЕРИСТИКА СОВРЕМЕННЫХ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ПЕРСПЕКТИВЫ ИХ РАЗВИТИЯ
- Глава девятая. РЕГИСТРИРУЮЩИЕ ПРИБОРЫ И УСТРОЙСТВА
- 9-2. САМОПИШУЩИЕ ПРИБОРЫ ПРЯМОГО ПРЕОБРАЗОВАНИЯ
- 9-3. СВЕТОЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 9-4. МАГНИТОГРАФЫ, ГРАФОПОСТРОИТЕЛИ, ЭЛЕКТРОННЫЕ ОСЦИЛЛОГРАФЫ, ЦИФРОПЕЧАТАЮЩИЕ УСТРОЙСТВА
- Глава десятая. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНЫХ ВЕЛИЧИН
- 10-2. МАГНИТОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНОГО ПОТОКА
- ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНОЙ ИНДУКЦИИ И НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ
- 10-3. АППАРАТУРА ДЛЯ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- Глава одиннадцатая. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 11-2. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- ГЕНЕРАТОРНЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
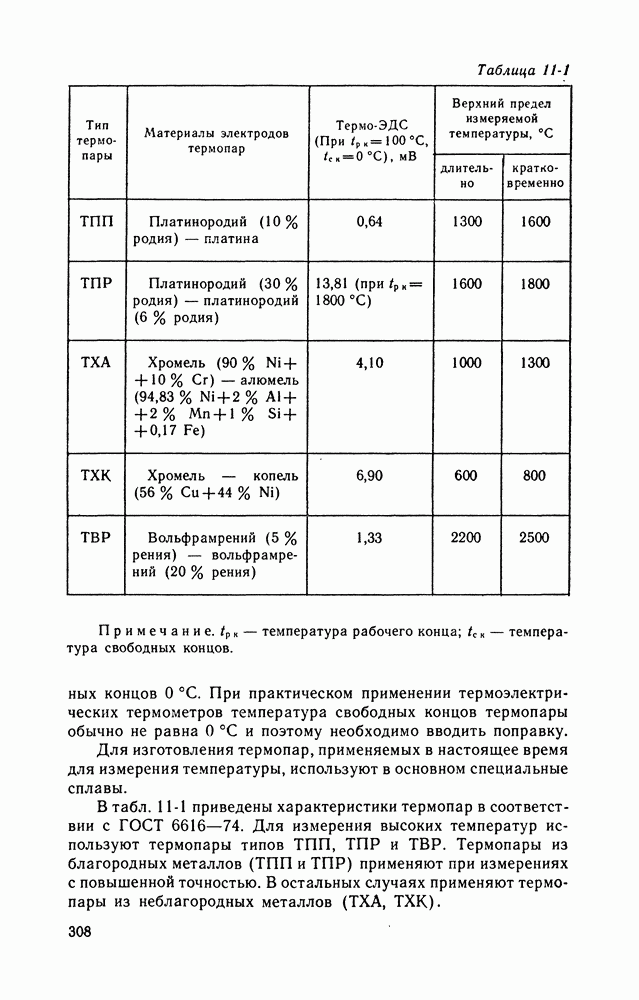
- 11-3. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ТЕМПЕРАТУРЫ
- 11-4. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ГЕОМЕТРИЧЕСКИХ И МЕХАНИЧЕСКИХ ВЕЛИЧИН
- 11-5. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ КОНЦЕНТРАЦИИ ЖИДКОЙ И ГАЗООБРАЗНОЙ СРЕДЫ
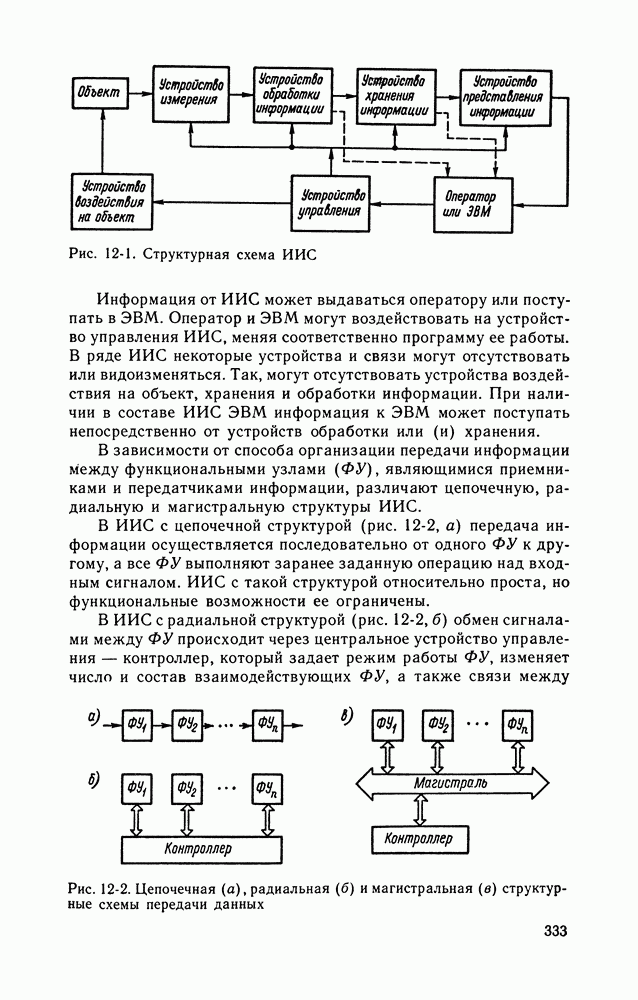
- Глава двенадцатая. ИЗМЕРИТЕЛЬНЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ
- 12-2. ИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ
- 12-3. ТЕЛЕИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ
- 12-4. СИСТЕМЫ АВТОМАТИЧЕСКОГО КОНТРОЛЯ И ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ
- 12-5. ИЗМЕРИТЕЛЬНЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ НА ОСНОВЕ АГРЕГАТНЫХ КОМПЛЕКСОВ ГОСУДАРСТВЕННОЙ СИСТЕМЫ ПРИБОРОВ И СРЕДСТВ АВТОМАТИЗАЦИИ
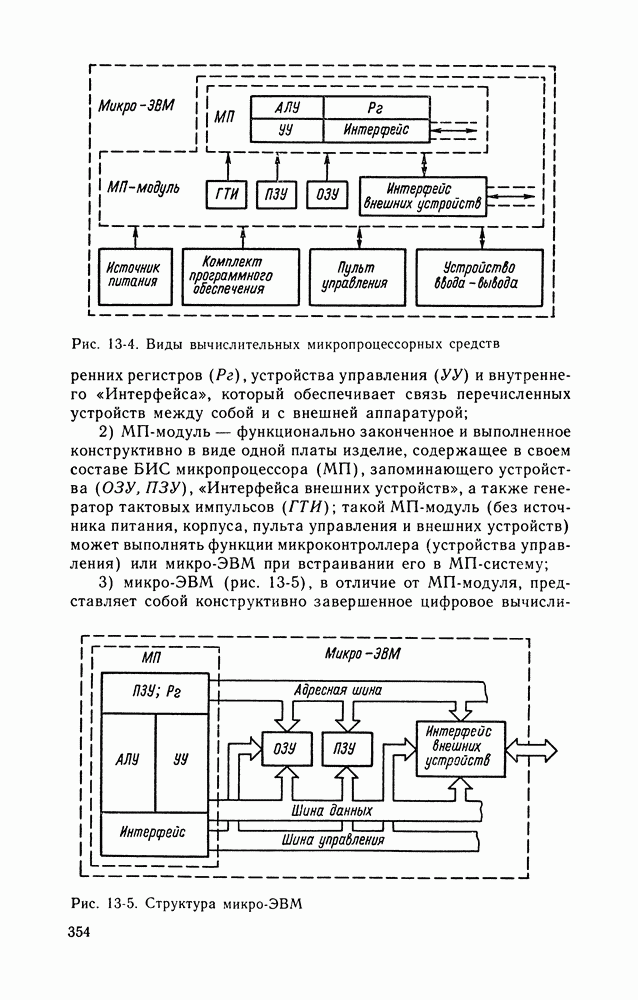
- Глава тринадцатая. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ СРЕДСТВА
- 13-2. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ СРЕДСТВА СИСТЕМНОГО ПРИМЕНЕНИЯ
- 13-3. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ КОМПЛЕКСЫ
- Раздел В. ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
- Глава четырнадцатая. ПОДГОТОВКА ИЗМЕРИТЕЛЬНОГО ЭКСПЕРИМЕНТА И ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- 14-2. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- 14-3. СУММИРОВАНИЕ ПОГРЕШНОСТЕЙ
- Глава пятнадцатая. ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ, МАГНИТНЫХ И НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 15-2. ИЗМЕРЕНИЯ МОЩНОСТИ, ЭНЕРГИИ И КОЛИЧЕСТВА ЭЛЕКТРИЧЕСТВА
- 15-3. ИЗМЕРЕНИЯ ЧАСТОТЫ, ФАЗЫ, ВРЕМЕННЫХ ИНТЕРВАЛОВ, АНАЛИЗ СПЕКТРА ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- 15-4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ЦЕПЕЙ ПОСТОЯННОГО И ПЕРЕМЕННОГО ТОКА
- 15-5. ИЗМЕРЕНИЯ ПАРАМЕТРОВ МАГНИТНОГО ПОЛЯ, ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- МАГНИТНЫЕ МАТЕРИАЛЫ И ИХ ХАРАКТЕРИСТИКИ
- ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- 15-6. ИЗМЕРЕНИЯ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- ИЗМЕРЕНИЯ ДАВЛЕНИЙ, ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ И РАССТОЯНИЙ
- Глава шестнадцатая. ИЗМЕРЕНИЯ ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ПРОЦЕССОВ
- 16-2. ИЗМЕРЕНИЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ДИСПЕРСИИ СЛУЧАЙНОГО ПРОЦЕССА
- 16-3. ИЗМЕРЕНИЕ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
- 16-4. ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННОЙ ФУНКЦИИ
- 16-5. АНАЛИЗ СПЕКТРА МОЩНОСТИ
- Список литературы