| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Частотные характеристики.
Частотные методы анализа основаны на исследовании прохождения гармонических колебаний различных частот через средства измерений. Если на вход линейного устройства подать сигнал  то выходной сигнал можно записать в виде
то выходной сигнал можно записать в виде  Отношение
Отношение

называют амплитудно-фазовой характеристикой. Амплитуднофазовую характеристику можно получить из дифференциального уравнения (4-44), подставив в него выражения  и решив полученное уравнение относительно
и решив полученное уравнение относительно 

Следует иметь в виду, что  представляет собой частное решение дифференциального уравнения и поэтому амплитуднофазовая характеристика
представляет собой частное решение дифференциального уравнения и поэтому амплитуднофазовая характеристика  непосредственно определяет только установившийся режим.
непосредственно определяет только установившийся режим.
На практике широкое распространение получила амплитудно-частотная характеристика 

и фазово-частотная характеристика 
Из выражения (4-65) получают выражения  для типовых звеньев.
для типовых звеньев.
Идеальное безынерционное звено имеет

Звено первого порядка (см. рис. 4-17)

Звено второго порядка (см. рис. 4-18)


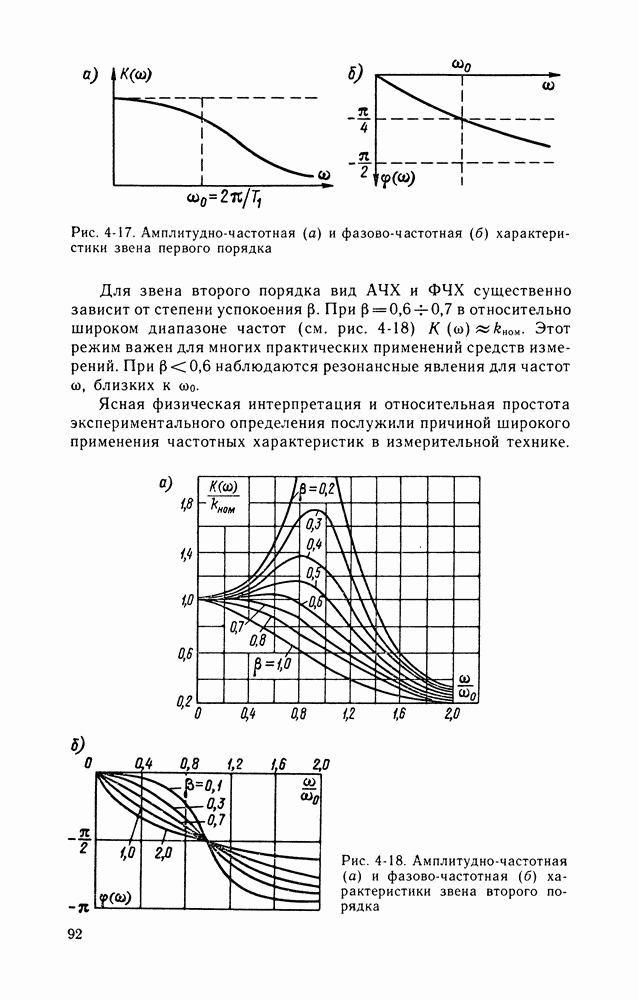
Рис. 4-17. Амплитудно-частотная (а) и фазово-частотная (б) характеристики звена первого порядка
Для звена второго порядка вид АЧХ и ФЧХ существенно зависит от степени успокоения  При
При  в относительно широком диапазоне частот (см. рис. 4-18) К
в относительно широком диапазоне частот (см. рис. 4-18) К  Этот режим важен для многих практических применений средств измерений. При
Этот режим важен для многих практических применений средств измерений. При  наблюдаются резонансные явления для частот
наблюдаются резонансные явления для частот  близких
близких 
Ясная физическая интерпретация и относительная простота экспериментального определения послужили причиной широкого применения частотных характеристик в измерительной технике.

Рис. 4-18. Амплитудно-частотная (а) и фазово-частотная (б) характеристики звена второго порядка

Рис. 4.19. Амплитудно-частотная (а) и фазово-частотная (б) характеристики некоторого средства измерений
Рассмотрим возможность оценки динамических погрешностей по известным АЧХ и ФЧХ средств измерений для сигнала  заданного диапазоном изменения от
заданного диапазоном изменения от  до
до  и частотным диапазоном
и частотным диапазоном  . Предположим, что средство измерений имеет такие АЧХ и
. Предположим, что средство измерений имеет такие АЧХ и  как показано на рис. 4-19. Для частот
как показано на рис. 4-19. Для частот
О — соср характеристики  , где
, где  — время задержки выходного сигнала. Частоту
— время задержки выходного сигнала. Частоту  называют частотой среза (на практике
называют частотой среза (на практике  с некоторой заданной погрешностью). Для частот
с некоторой заданной погрешностью). Для частот  характеристика
характеристика  имеет нелинейную зависимость от частоты.
имеет нелинейную зависимость от частоты.
Сначала оценим влияние на динамическую погрешность только  Для этого условно примем
Для этого условно примем  При
При  очевидно, погрешность не возникает, так как каждая гармоническая составляющая передается с одним и тем же коэффициентом
очевидно, погрешность не возникает, так как каждая гармоническая составляющая передается с одним и тем же коэффициентом  при сот
при сот  они передаются с
они передаются с  что приводит к искажению
что приводит к искажению  а следовательно, и появлению погрешности. Для каждой гармонической составляющей
а следовательно, и появлению погрешности. Для каждой гармонической составляющей  относительная погрешность
относительная погрешность

где  — значение АЧХ на частоте
— значение АЧХ на частоте  Можно показать, что для полигармонического сигнала при условии
Можно показать, что для полигармонического сигнала при условии  максимальная приведенная погрешность будет определяться выражением
максимальная приведенная погрешность будет определяться выражением

где  -максимальная разность коэффициентов передачи в пределах диапазона частот
-максимальная разность коэффициентов передачи в пределах диапазона частот  , определяемая по АЧХ средства измерений.
, определяемая по АЧХ средства измерений.
Теперь рассмотрим влияние ФЧХ на результаты измерений. Примем условно  во всем диапазоне
во всем диапазоне

Рис. 4-20. Выходные сигналы реального  и идеального
и идеального  средства измерений
средства измерений
рассматриваемых частот. При  имеем
имеем  . В тех случаях, когда требуется «жесткая привязка» результатов измерений во времени, возникает погрешность
. В тех случаях, когда требуется «жесткая привязка» результатов измерений во времени, возникает погрешность  вызванная фазовым сдвигом. Из рис. 4-20 видно, что при
вызванная фазовым сдвигом. Из рис. 4-20 видно, что при  эта погрешность максимальна при
эта погрешность максимальна при 

Если  представляет собой сумму
представляет собой сумму  гармонических составляющих
гармонических составляющих  при условии
при условии  то максимально возможная погрешность
то максимально возможная погрешность

где  — максимальный фазовый сдвиг в диапазоне частот
— максимальный фазовый сдвиг в диапазоне частот  , определяемый по
, определяемый по  Отсюда максимальная приведенная погрешность
Отсюда максимальная приведенная погрешность

В некоторых измерительных задачах задержка выходного сигнала во времени несущественна или она может быть учтена в процессе обработки результатов измерений. Важной в таких задачах является точная передача формы сигнала. Так, если сместить сигнал  (см. рис. 4-20), точно отражающий характер изменения
(см. рис. 4-20), точно отражающий характер изменения  на время
на время  то он полностью совпадает с сигналом
то он полностью совпадает с сигналом  и в этом смысле погрешность будет отсутствовать. Для сложного сигнала с диапазоном частот
и в этом смысле погрешность будет отсутствовать. Для сложного сигнала с диапазоном частот  , лежащим в пределах линейной фазовой характеристики
, лежащим в пределах линейной фазовой характеристики  , возникает аналогичная картина, поскольку каждая
, возникает аналогичная картина, поскольку каждая

Рис. 4-21. Аппроксимация фазово-частотной характеристики линейной зависимостью
гармоническая составляющая смещается во времени на постоянную величину 13 В этом случае считают, что динамическая погрешность равна нулю. Если фазовая характеристика нелинейна, то гармонические составляющие смещаются на различное время задержки  что приводит к искажению формы выходного сигнала, а следовательно, смещение в этом случае не исключает погрешности. Определить эту погрешность в общем случае достаточно сложно. Приближенно ее можно оценить, проводя некоторую линейную ФЧХ, аппроксимирующую реальную ФЧХ (рис. 4-21) с максимальными погрешностями
что приводит к искажению формы выходного сигнала, а следовательно, смещение в этом случае не исключает погрешности. Определить эту погрешность в общем случае достаточно сложно. Приближенно ее можно оценить, проводя некоторую линейную ФЧХ, аппроксимирующую реальную ФЧХ (рис. 4-21) с максимальными погрешностями  Такая ФЧХ будет соответствовать сдвигу сигнала на некоторое время, определяемое ее наклоном. Оценить погрешность, вызванную нелинейностью ФЧХ измерительного звена, можно по формуле (4-76), подставляя в нее
Такая ФЧХ будет соответствовать сдвигу сигнала на некоторое время, определяемое ее наклоном. Оценить погрешность, вызванную нелинейностью ФЧХ измерительного звена, можно по формуле (4-76), подставляя в нее  вместо
вместо 
В общем случае на динамическую погрешность влияет как АЧХ, так и ФЧХ измерительного звена. Точное определение суммарной погрешности является относительно сложной задачей. В качестве оценки сверху для общей динамической погрешности может быть принята сумма этих двух составляющих. Однако следует иметь в виду, что данная оценка является достаточно «грубой», поскольку во многих случаях общая погрешность принципиально меньше суммы рассматриваемых составляющих. Так, при моногармоническом сигнале максимальные значения этих составляющих всегда разнесены во времени и, следовательно, общая погрешность будет меньше суммы их максимальных значений.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Раздел А. ОБЩИЕ СВЕДЕНИЯ ОБ ИЗМЕРИТЕЛЬНОЙ ТЕХНИКЕ
- Глава первая. ОСНОВНЫЕ ПОНЯТИЯ ИЗМЕРИТЕЛЬНОЙ ТЕХНИКИ И КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ
- 1-2. ВИДЫ И МЕТОДЫ ИЗМЕРЕНИЙ
- Глава вторая. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
- 2-1. ОСНОВНЫЕ ПОНЯТИЯ И ВИДЫ ПОГРЕШНОСТЕЙ
- 2-2. ВЕРОЯТНОСТНЫЙ ПОДХОД К ОПИСАНИЮ ПОГРЕШНОСТЕЙ
- 2-3. ВЕРОЯТНОСТНЫЕ ОЦЕНКИ ПОГРЕШНОСТЕЙ
- Глава третья. ОСНОВЫ МЕТРОЛОГИЧЕСКОГО ОБЕСПЕЧЕНИЯ
- 3-2. ЭТАЛОНЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН
- 3-3. ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ
- Раздел Б. ЭЛЕКТРИЧЕСКИЕ СРЕДСТВА ИЗМЕРЕНИЙ
- Глава четвертая. ОБЩИЕ СВЕДЕНИЯ О СРЕДСТВАХ ИЗМЕРЕНИЙ
- 4-2. ГОСУДАРСТВЕННАЯ СИСТЕМА ПРИБОРОВ
- 4-3. ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
- 4-4. СИГНАЛЫ ИЗМЕРИТЕЛЬНОЙ ИНФОРМАЦИИ
- Математические модели сигналов.
- Дискретизация сигналов.
- 4-5. СТРУКТУРНЫЕ СХЕМЫ И СВОЙСТВА СРЕДСТВ ИЗМЕРЕНИЙ В СТАТИЧЕСКОМ РЕЖИМЕ
- Средства измерений прямого преобразования.
- Средства измерений уравновешивающего преобразования.
- 4-6. СРЕДСТВА ИЗМЕРЕНИЙ В ДИНАМИЧЕСКОМ РЕЖИМЕ
- Переходные и импульсные переходные характеристики.
- Частотные характеристики.
- Передаточные функции.
- Глава пятая. МЕРЫ, ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ
- 5-2. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 5-3. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ
- МАГНИТОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ
- Амперметры и вольтметры.
- Омметры.
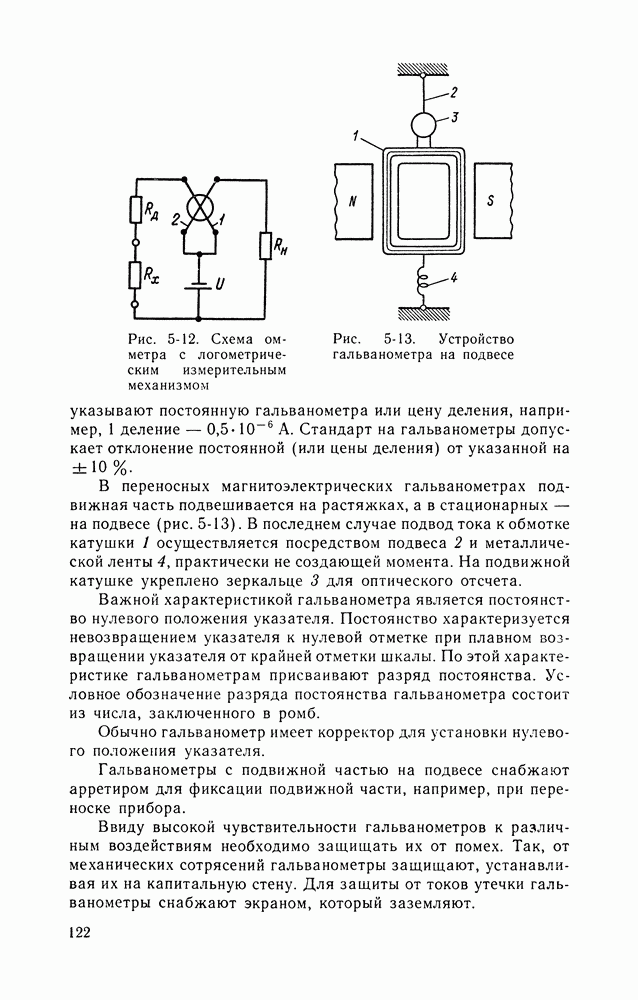
- Гальванометры.
- Баллистические гальванометры.
- Кулонметры.
- Вибрационные гальванометры.
- ЭЛЕКТРОДИНАМИЧЕСКИЕ И ФЕРРОДИНАМИЧЕСКИЕ ПРИБОРЫ
- ЭЛЕКТРОМАГНИТНЫЕ ПРИБОРЫ
- ЭЛЕКТРОСТАТИЧЕСКИЕ ПРИБОРЫ
- ИНДУКЦИОННЫЕ ПРИБОРЫ
- 5-4. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ С ПРЕОБРАЗОВАТЕЛЯМИ
- Глава шестая. ЭЛЕКТРОННЫЕ АНАЛОГОВЫЕ ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ
- 6-2. ЭЛЕКТРОННЫЕ ВОЛЬТМЕТРЫ
- 6-3. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ ЧАСТОТЫ И ФАЗЫ
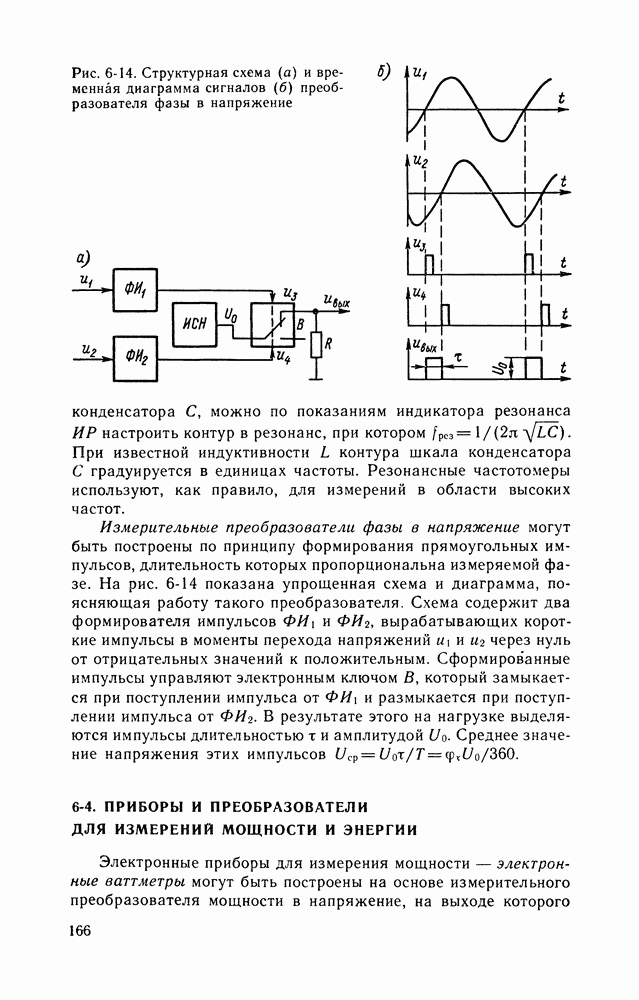
- 6-4. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ МОЩНОСТИ И ЭНЕРГИИ
- 6-5. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ПАРАМЕТРОВ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 6-6. ЭЛЕКТРОННО ЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 6-7. АНАЛИЗАТОРЫ СПЕКТРА, ИЗМЕРИТЕЛИ НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ
- Глава седьмая. МОСТЫ И КОМПЕНСАТОРЫ
- 7-2. ТЕОРИЯ МОСТОВЫХ СХЕМ
- 7-3. МОСТЫ ДЛЯ ИЗМЕРЕНИЙ СОПРОТИВЛЕНИЯ НА ПОСТОЯННОМ ТОКЕ
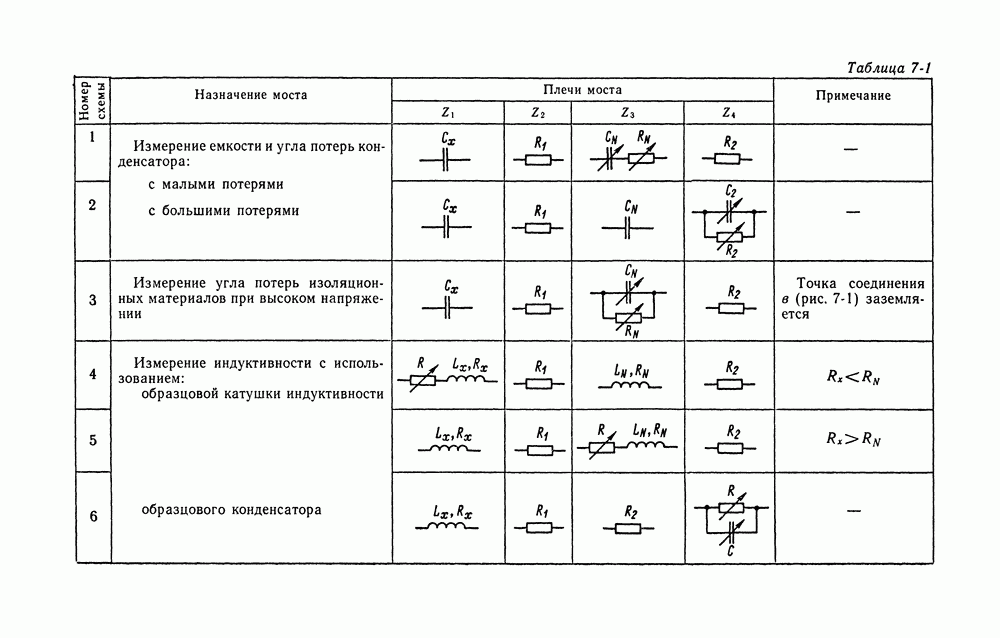
- 7-4. МОСТЫ ПЕРЕМЕННОГО ТОКА ДЛЯ ИЗМЕРЕНИЙ ЕМКОСТИ, УГЛА ПОТЕРЬ, ИНДУКТИВНОСТИ И ДОБРОТНОСТИ
- 7-5. КОМПЕНСАТОРЫ ПОСТОЯННОГО ТОКА
- 7-6. КОМПЕНСАТОРЫ ПЕРЕМЕННОГО ТОКА
- 7-7. АВТОМАТИЧЕСКИЕ МОСТЫ И КОМПЕНСАТОРЫ
- Глава восьмая. ЦИФРОВЫЕ ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ
- 8-2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 8-3. УЗЛЫ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 8-4. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА ПОСЛЕДОВАТЕЛЬНОГО СЧЕТА
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД ЧАСТОТЫ
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД НАПРЯЖЕНИЯ ПОСТОЯННОГО ТОКА
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД ПЕРЕМЕЩЕНИЯ
- 8-5. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА ПОСЛЕДОВАТЕЛЬНОГО ПРИБЛИЖЕНИЯ
- 8-6. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА СЧИТЫВАНИЯ
- 8-7. ХАРАКТЕРИСТИКА СОВРЕМЕННЫХ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ПЕРСПЕКТИВЫ ИХ РАЗВИТИЯ
- Глава девятая. РЕГИСТРИРУЮЩИЕ ПРИБОРЫ И УСТРОЙСТВА
- 9-2. САМОПИШУЩИЕ ПРИБОРЫ ПРЯМОГО ПРЕОБРАЗОВАНИЯ
- 9-3. СВЕТОЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 9-4. МАГНИТОГРАФЫ, ГРАФОПОСТРОИТЕЛИ, ЭЛЕКТРОННЫЕ ОСЦИЛЛОГРАФЫ, ЦИФРОПЕЧАТАЮЩИЕ УСТРОЙСТВА
- Глава десятая. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНЫХ ВЕЛИЧИН
- 10-2. МАГНИТОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНОГО ПОТОКА
- ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНОЙ ИНДУКЦИИ И НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ
- 10-3. АППАРАТУРА ДЛЯ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- Глава одиннадцатая. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 11-2. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- ГЕНЕРАТОРНЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 11-3. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ТЕМПЕРАТУРЫ
- 11-4. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ГЕОМЕТРИЧЕСКИХ И МЕХАНИЧЕСКИХ ВЕЛИЧИН
- 11-5. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ КОНЦЕНТРАЦИИ ЖИДКОЙ И ГАЗООБРАЗНОЙ СРЕДЫ
- Глава двенадцатая. ИЗМЕРИТЕЛЬНЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ
- 12-2. ИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ
- 12-3. ТЕЛЕИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ
- 12-4. СИСТЕМЫ АВТОМАТИЧЕСКОГО КОНТРОЛЯ И ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ
- 12-5. ИЗМЕРИТЕЛЬНЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ НА ОСНОВЕ АГРЕГАТНЫХ КОМПЛЕКСОВ ГОСУДАРСТВЕННОЙ СИСТЕМЫ ПРИБОРОВ И СРЕДСТВ АВТОМАТИЗАЦИИ
- Глава тринадцатая. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ СРЕДСТВА
- 13-2. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ СРЕДСТВА СИСТЕМНОГО ПРИМЕНЕНИЯ
- 13-3. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ КОМПЛЕКСЫ
- Раздел В. ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
- Глава четырнадцатая. ПОДГОТОВКА ИЗМЕРИТЕЛЬНОГО ЭКСПЕРИМЕНТА И ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- 14-2. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- 14-3. СУММИРОВАНИЕ ПОГРЕШНОСТЕЙ
- Глава пятнадцатая. ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ, МАГНИТНЫХ И НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 15-2. ИЗМЕРЕНИЯ МОЩНОСТИ, ЭНЕРГИИ И КОЛИЧЕСТВА ЭЛЕКТРИЧЕСТВА
- 15-3. ИЗМЕРЕНИЯ ЧАСТОТЫ, ФАЗЫ, ВРЕМЕННЫХ ИНТЕРВАЛОВ, АНАЛИЗ СПЕКТРА ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- 15-4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ЦЕПЕЙ ПОСТОЯННОГО И ПЕРЕМЕННОГО ТОКА
- 15-5. ИЗМЕРЕНИЯ ПАРАМЕТРОВ МАГНИТНОГО ПОЛЯ, ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
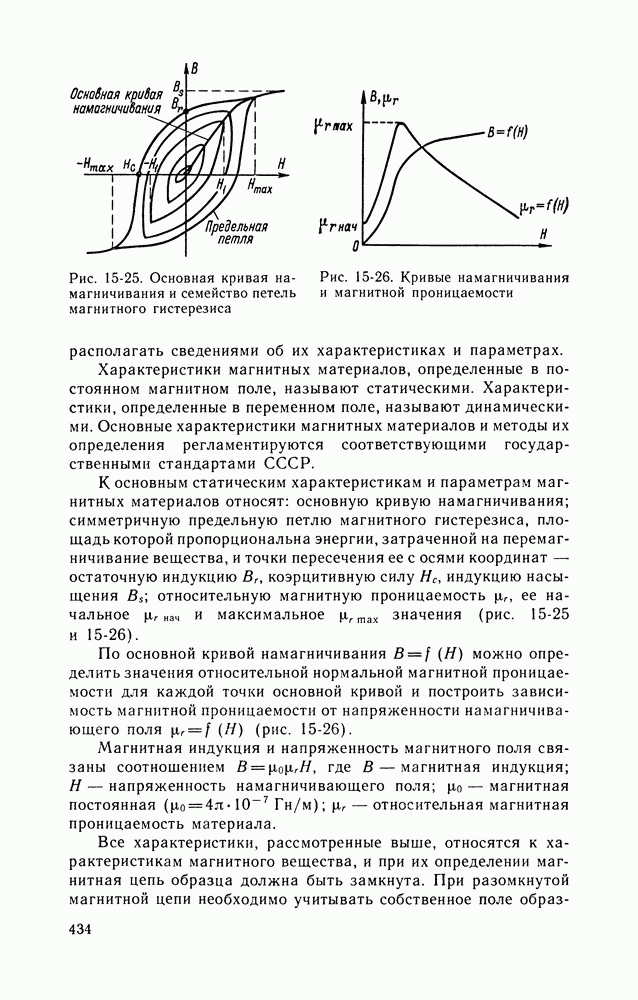
- МАГНИТНЫЕ МАТЕРИАЛЫ И ИХ ХАРАКТЕРИСТИКИ
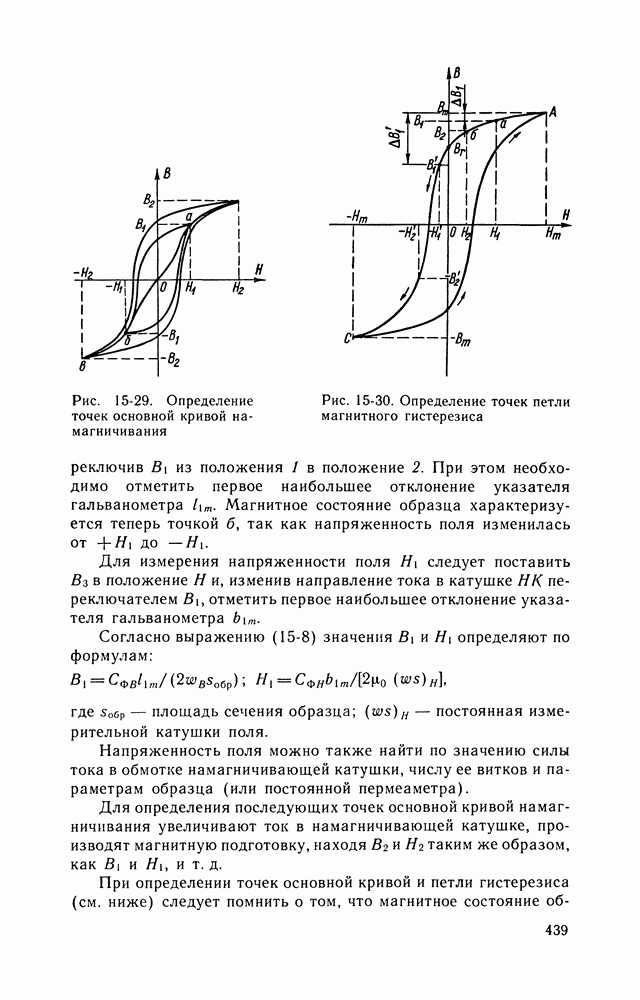
- ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- 15-6. ИЗМЕРЕНИЯ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- ИЗМЕРЕНИЯ ДАВЛЕНИЙ, ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ И РАССТОЯНИЙ
- Глава шестнадцатая. ИЗМЕРЕНИЯ ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ПРОЦЕССОВ
- 16-2. ИЗМЕРЕНИЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ДИСПЕРСИИ СЛУЧАЙНОГО ПРОЦЕССА
- 16-3. ИЗМЕРЕНИЕ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
- 16-4. ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННОЙ ФУНКЦИИ
- 16-5. АНАЛИЗ СПЕКТРА МОЩНОСТИ
- Список литературы