| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2-2. ВЕРОЯТНОСТНЫЙ ПОДХОД К ОПИСАНИЮ ПОГРЕШНОСТЕЙ
Полным описанием случайной величины, а следовательно и погрешности, является ее закон распределения, которым определяется характер появления различных результатов отдельных измерений.
В практике электрических измерений встречаются различные законы распределения, некоторые из которых рассмотрены ниже.
Нормальный закон распределения (закон Гаусса). Этот закон является одним из наиболее распространенных законов распределения погрешностей. Объясняется это тем, что во многих случаях погрешность измерения образуется под действием большой совокупности различных, независимых друг от друга причин. На основании центральной предельной теоремы теории вероятностей результатом действия этих причин будет погрешность, распределенная по нормальному закону при условии, что ни одна из этих причин не является существенно преобладающей.
Нормальный закон распределения погрешностей описывается формулой

где  — плотность вероятности погрешности
— плотность вероятности погрешности  — среднее квадратическое отклонение погрешности;
— среднее квадратическое отклонение погрешности;  — систематическая составляющая погрешности.
— систематическая составляющая погрешности.
Вид нормального закона, описываемого выражением (2-1), представлен на рис. 2-2, а для двух значений  Так как
Так как  то закон распределения случайной составляющей погрешности
то закон распределения случайной составляющей погрешности  имеет тот же вид (рис. 2-2, б) и описывается выражением, аналогичным (2-1), т. е.
имеет тот же вид (рис. 2-2, б) и описывается выражением, аналогичным (2-1), т. е.

где а  — среднее квадратическое отклонение случайной составляющей погрешности; о
— среднее квадратическое отклонение случайной составляющей погрешности; о 

Рис. 2-2. Нормальный закон распределения погрешности измерений (а) и случайной составляющей погрешности измерений (б)
Таким образом, закон распределения погрешности  отличается от закона распределения случайной составляющей погрешности
отличается от закона распределения случайной составляющей погрешности  только сдвигом по оси абсцисс на величину систематической составляющей погрешности
только сдвигом по оси абсцисс на величину систематической составляющей погрешности 
Из теории вероятностей известно, что площадь под кривой плотности вероятности характеризует вероятность появления погрешности. Из рис. 2-2, б видно, что вероятность Р появления погрешности в диапазоне  при
при  больше, чем при
больше, чем при  (площади, характеризующие эти вероятности, заштрихованы). Полная площадь под кривой распределения всегда равна 1, т. е. полной вероятности.
(площади, характеризующие эти вероятности, заштрихованы). Полная площадь под кривой распределения всегда равна 1, т. е. полной вероятности.
Учитывая это, можно утверждать, что погрешности, абсолютные значения которых превышают  появляются с вероятностью, равной
появляются с вероятностью, равной  которая при
которая при  меньше, чем при
меньше, чем при 
Следовательно, чем меньше  тем реже встречаются большие погрешности, тем точнее выполнены измерения. Таким образом, Среднее квадратическое отклонение
тем реже встречаются большие погрешности, тем точнее выполнены измерения. Таким образом, Среднее квадратическое отклонение  можно использовать для характеристики точности измерений:
можно использовать для характеристики точности измерений:
Равномерный закон распределения. Если погрешность измерений с одинаковой вероятностью может принимать любые значения, не выходящие за некоторые границы, то такая погрешность описывается равномерным законом распределения. При этом плотность вероятности погрешности  постоянна внутри этих границ и равна нулю вне этих границ. Равномерный закон распределения представлен на рис. 2-3. Аналитически он может быть записан так:
постоянна внутри этих границ и равна нулю вне этих границ. Равномерный закон распределения представлен на рис. 2-3. Аналитически он может быть записан так:


Рис. 2-3. Равномерный закон распределения

С таким законом распределения хорошо согласуется погрешность от трения в опорах электромеханических приборов, неисключенные остатки систематических погрешностей, погрешность дискретности в цифровых приборах (см. § 8-2) и др.
Трапециевидный закон распределения. Это распределение графически изображено на рис. 2-4, а. Погрешность имеет такой закон распределения, если она образуется из двух независимых составляющих, каждая из которых имеет равномерный закон распределения, но ширина интервала равномерных законов различна. Например, при последовательном соединении двух измерительных преобразователей, один из которых имеет погрешность, равномерно распределенную в интервале  а другой — равномерно распределенную в интервале
а другой — равномерно распределенную в интервале  суммарная погрешность преобразования будет описываться трапециевидным законом распределения.
суммарная погрешность преобразования будет описываться трапециевидным законом распределения.
Треугольный закон распределения (закон Симпсона). Это распределение (см. рис. 2-4, б) является частным случаем трапециевидного, когда составляющие имеют одинаковые равномерные законы распределения (см. § 8-2).
Двухмодальные законы распределения. В практике измерений встречаются двухмодальные законы распределения, т. е. законы распределения, имеющие два максимума плотности вероятности. В качестве примера на рис. 2-5 изображен двухмодальный закон распределения, который может быть в приборах, имеющих погрешность от люфта кинематических механизмов или от гистерезиса при перемагничивании деталей прибора.
Некоторые другие законы распределения погрешностей даны в ГОСТ 8.011-72 «Показатели точности измерений и формы представления результатов измерений».

Рис. 2-4. Трапециевидный (а) и треугольный (б) законы распределения

Рис. 2-5. Двухмодальный закон распределения
Если законы распределения погрешностей неизвестны, то они могут быть установлены на основании статистической обработки опытных данных. Однако экспериментальное определение законов распределения весьма трудоемко, поэтому к нему прибегают лишь при весьма ответственных измерениях.
Иногда закон распределения погрешности принимают, исходя из физического представления о причинах появления погрешностей и анализа составляющих погрешностей измерения. Так, например, если погрешность измерения образуется из пяти и более составляющих, среди которых нет существенно преобладающих, то закон распределения результирующей погрешности обычно принимают нормальным. В противном случае, анализируя составляющие погрешности, принимают для них вид законов распределения и методами теории вероятностей находят закон распределения для результирующей (суммарной) погрешности измерения (см. § 14-3).
Из сказанного следует, что точный вид закона распределения погрешностей обычно неизвестен. Реальные законы распределения даже в простейших случаях отличаются от теоретических стандартных законов распределения, рассмотренных выше и в ГОСТ 8.011-72, где они называются стандартными аппроксимациями функций плотности вероятности. Поэтому характеристики погрешности не удается найти точно. Однако практика показывает, что погрешность 10-20 % при определении самой погрешности зачастую вполне удовлетворительна. Поэтому никогда не следует указывать значение погрешности с большим количеством значащих цифр. Обычно погрешность достаточно выражать одной двумя значащими цифрами.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Раздел А. ОБЩИЕ СВЕДЕНИЯ ОБ ИЗМЕРИТЕЛЬНОЙ ТЕХНИКЕ
- Глава первая. ОСНОВНЫЕ ПОНЯТИЯ ИЗМЕРИТЕЛЬНОЙ ТЕХНИКИ И КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ
- 1-2. ВИДЫ И МЕТОДЫ ИЗМЕРЕНИЙ
- Глава вторая. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
- 2-1. ОСНОВНЫЕ ПОНЯТИЯ И ВИДЫ ПОГРЕШНОСТЕЙ
- 2-2. ВЕРОЯТНОСТНЫЙ ПОДХОД К ОПИСАНИЮ ПОГРЕШНОСТЕЙ
- 2-3. ВЕРОЯТНОСТНЫЕ ОЦЕНКИ ПОГРЕШНОСТЕЙ
- Глава третья. ОСНОВЫ МЕТРОЛОГИЧЕСКОГО ОБЕСПЕЧЕНИЯ
- 3-2. ЭТАЛОНЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН
- 3-3. ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ
- Раздел Б. ЭЛЕКТРИЧЕСКИЕ СРЕДСТВА ИЗМЕРЕНИЙ
- Глава четвертая. ОБЩИЕ СВЕДЕНИЯ О СРЕДСТВАХ ИЗМЕРЕНИЙ
- 4-2. ГОСУДАРСТВЕННАЯ СИСТЕМА ПРИБОРОВ
- 4-3. ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
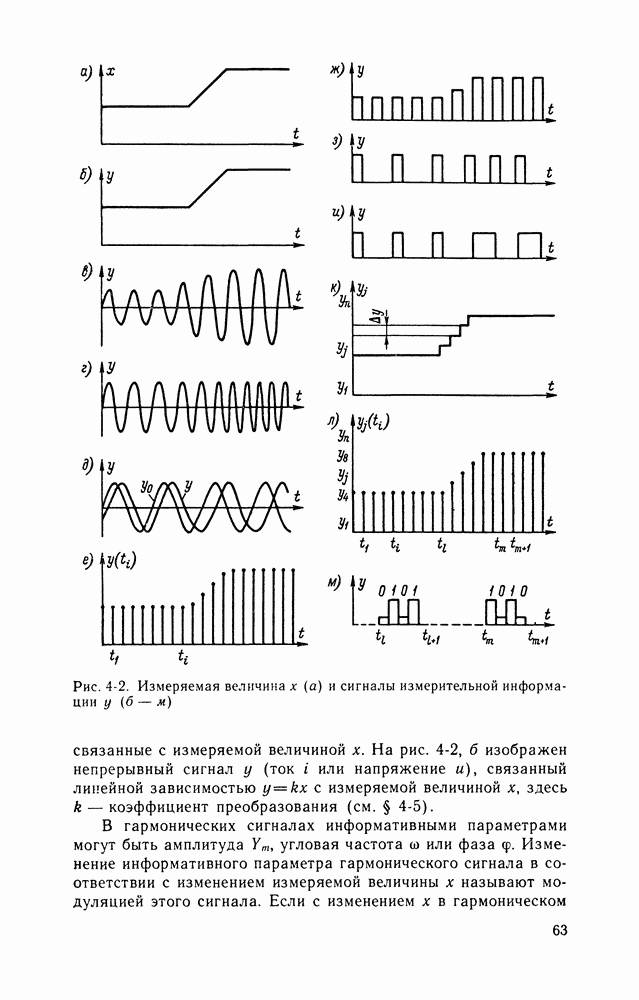
- 4-4. СИГНАЛЫ ИЗМЕРИТЕЛЬНОЙ ИНФОРМАЦИИ
- Математические модели сигналов.
- Дискретизация сигналов.
- 4-5. СТРУКТУРНЫЕ СХЕМЫ И СВОЙСТВА СРЕДСТВ ИЗМЕРЕНИЙ В СТАТИЧЕСКОМ РЕЖИМЕ
- Средства измерений прямого преобразования.
- Средства измерений уравновешивающего преобразования.
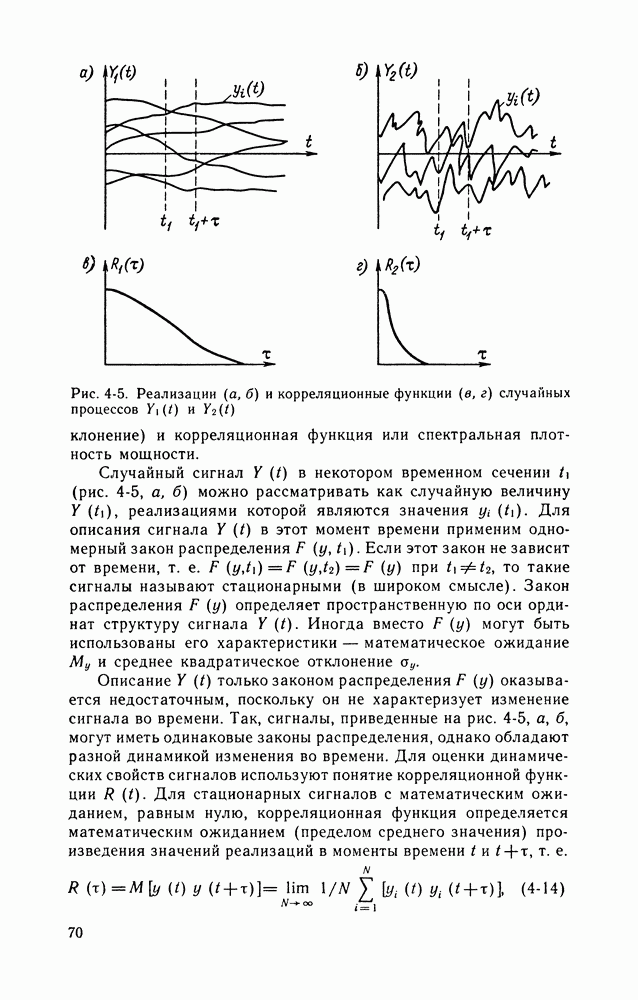
- 4-6. СРЕДСТВА ИЗМЕРЕНИЙ В ДИНАМИЧЕСКОМ РЕЖИМЕ
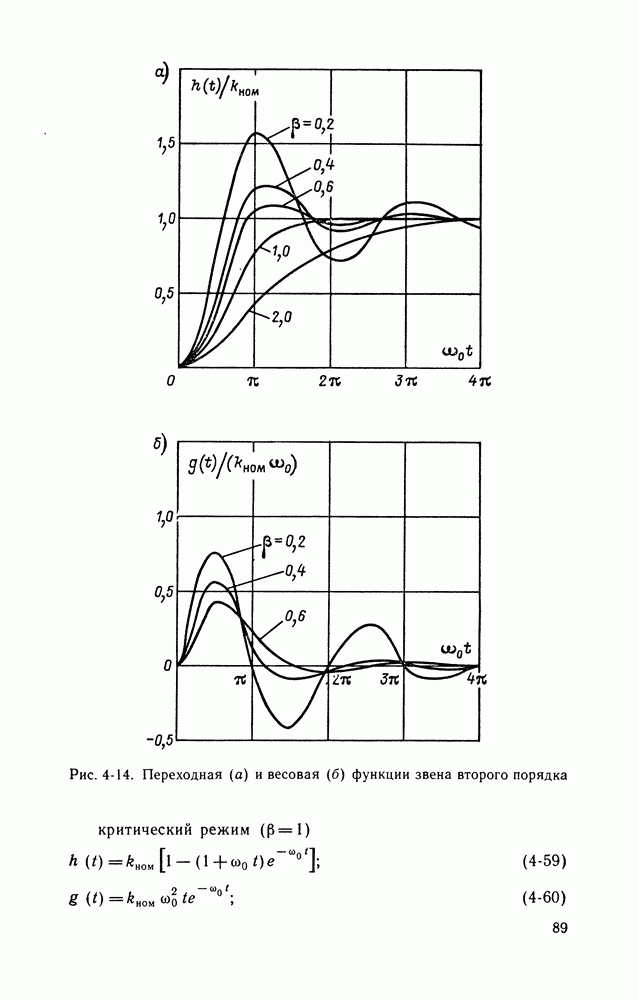
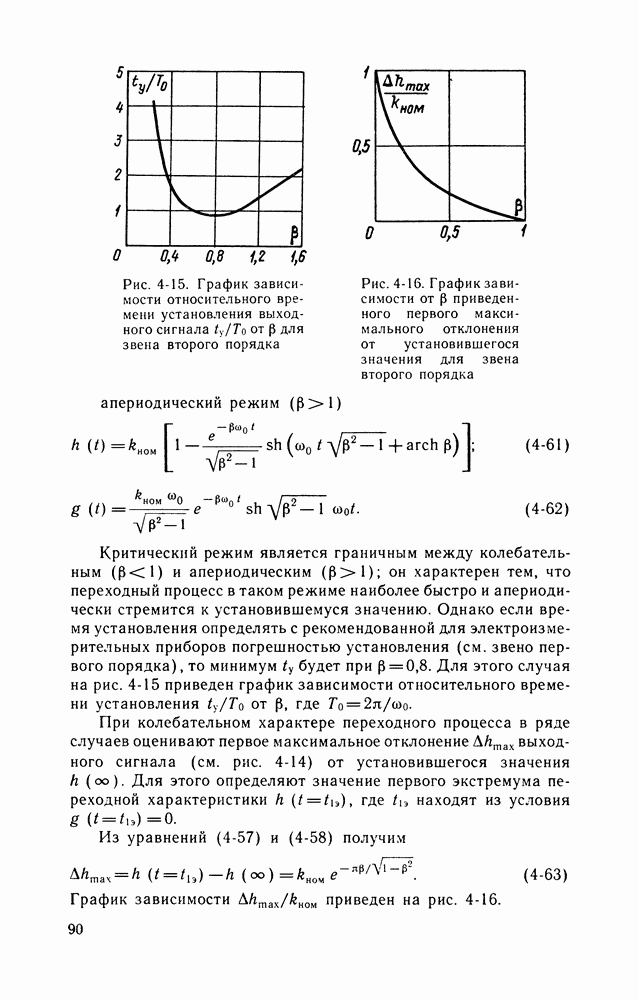
- Переходные и импульсные переходные характеристики.
- Частотные характеристики.
- Передаточные функции.
- Глава пятая. МЕРЫ, ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ
- 5-2. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 5-3. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ
- МАГНИТОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ
- Амперметры и вольтметры.
- Омметры.
- Гальванометры.
- Баллистические гальванометры.
- Кулонметры.
- Вибрационные гальванометры.
- ЭЛЕКТРОДИНАМИЧЕСКИЕ И ФЕРРОДИНАМИЧЕСКИЕ ПРИБОРЫ
- ЭЛЕКТРОМАГНИТНЫЕ ПРИБОРЫ
- ЭЛЕКТРОСТАТИЧЕСКИЕ ПРИБОРЫ
- ИНДУКЦИОННЫЕ ПРИБОРЫ
- 5-4. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ С ПРЕОБРАЗОВАТЕЛЯМИ
- Глава шестая. ЭЛЕКТРОННЫЕ АНАЛОГОВЫЕ ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ
- 6-2. ЭЛЕКТРОННЫЕ ВОЛЬТМЕТРЫ
- 6-3. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ ЧАСТОТЫ И ФАЗЫ
- 6-4. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ МОЩНОСТИ И ЭНЕРГИИ
- 6-5. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ПАРАМЕТРОВ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 6-6. ЭЛЕКТРОННО ЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 6-7. АНАЛИЗАТОРЫ СПЕКТРА, ИЗМЕРИТЕЛИ НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ
- Глава седьмая. МОСТЫ И КОМПЕНСАТОРЫ
- 7-2. ТЕОРИЯ МОСТОВЫХ СХЕМ
- 7-3. МОСТЫ ДЛЯ ИЗМЕРЕНИЙ СОПРОТИВЛЕНИЯ НА ПОСТОЯННОМ ТОКЕ
- 7-4. МОСТЫ ПЕРЕМЕННОГО ТОКА ДЛЯ ИЗМЕРЕНИЙ ЕМКОСТИ, УГЛА ПОТЕРЬ, ИНДУКТИВНОСТИ И ДОБРОТНОСТИ
- 7-5. КОМПЕНСАТОРЫ ПОСТОЯННОГО ТОКА
- 7-6. КОМПЕНСАТОРЫ ПЕРЕМЕННОГО ТОКА
- 7-7. АВТОМАТИЧЕСКИЕ МОСТЫ И КОМПЕНСАТОРЫ
- Глава восьмая. ЦИФРОВЫЕ ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ
- 8-2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 8-3. УЗЛЫ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 8-4. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА ПОСЛЕДОВАТЕЛЬНОГО СЧЕТА
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД ЧАСТОТЫ
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД НАПРЯЖЕНИЯ ПОСТОЯННОГО ТОКА
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД ПЕРЕМЕЩЕНИЯ
- 8-5. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА ПОСЛЕДОВАТЕЛЬНОГО ПРИБЛИЖЕНИЯ
- 8-6. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА СЧИТЫВАНИЯ
- 8-7. ХАРАКТЕРИСТИКА СОВРЕМЕННЫХ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ПЕРСПЕКТИВЫ ИХ РАЗВИТИЯ
- Глава девятая. РЕГИСТРИРУЮЩИЕ ПРИБОРЫ И УСТРОЙСТВА
- 9-2. САМОПИШУЩИЕ ПРИБОРЫ ПРЯМОГО ПРЕОБРАЗОВАНИЯ
- 9-3. СВЕТОЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 9-4. МАГНИТОГРАФЫ, ГРАФОПОСТРОИТЕЛИ, ЭЛЕКТРОННЫЕ ОСЦИЛЛОГРАФЫ, ЦИФРОПЕЧАТАЮЩИЕ УСТРОЙСТВА
- Глава десятая. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНЫХ ВЕЛИЧИН
- 10-2. МАГНИТОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНОГО ПОТОКА
- ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНОЙ ИНДУКЦИИ И НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ
- 10-3. АППАРАТУРА ДЛЯ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- Глава одиннадцатая. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 11-2. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- ГЕНЕРАТОРНЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
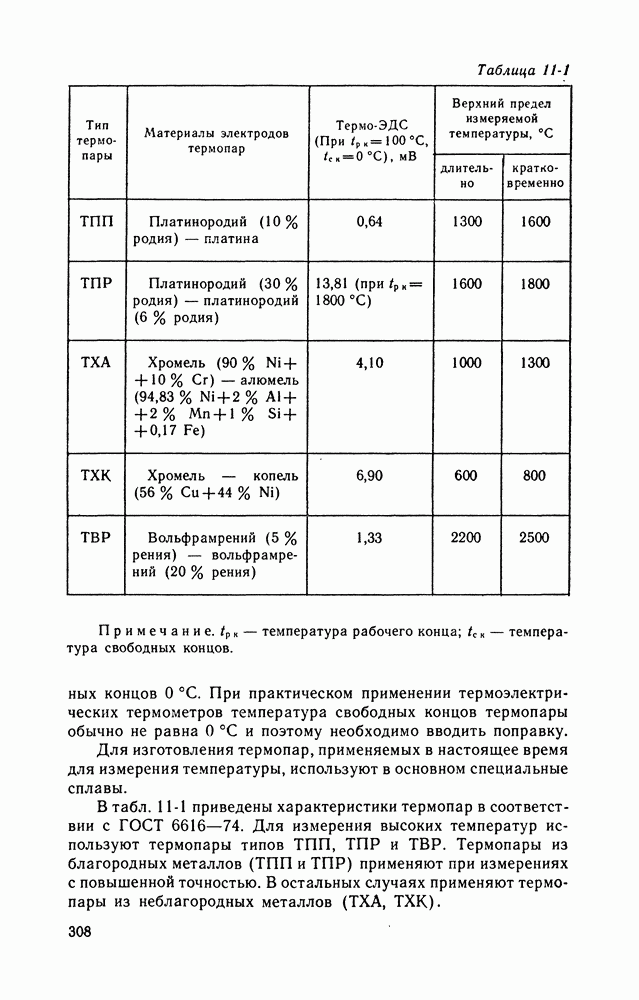
- 11-3. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ТЕМПЕРАТУРЫ
- 11-4. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ГЕОМЕТРИЧЕСКИХ И МЕХАНИЧЕСКИХ ВЕЛИЧИН
- 11-5. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ КОНЦЕНТРАЦИИ ЖИДКОЙ И ГАЗООБРАЗНОЙ СРЕДЫ
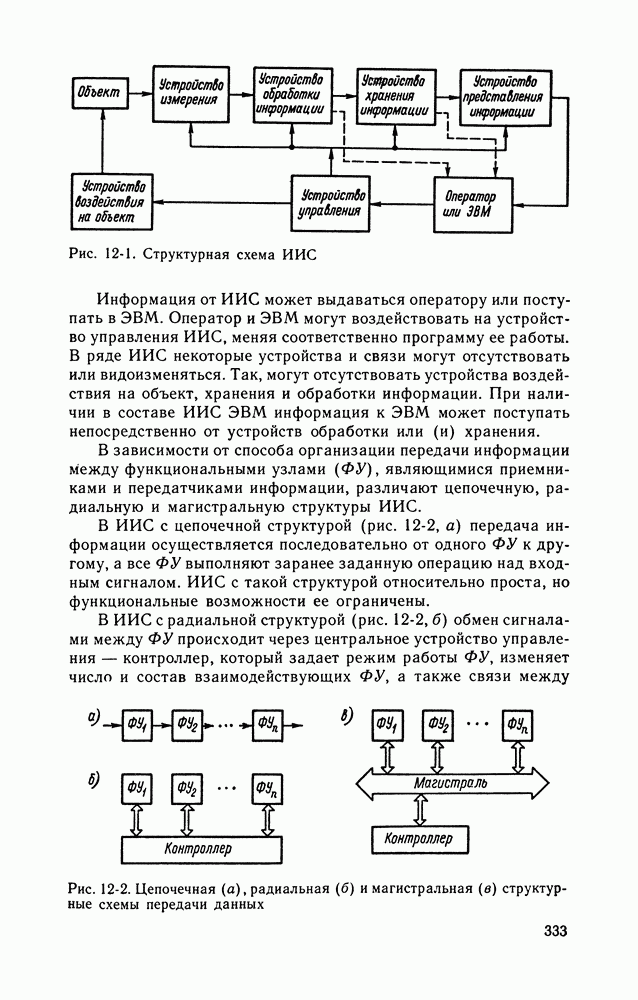
- Глава двенадцатая. ИЗМЕРИТЕЛЬНЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ
- 12-2. ИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ
- 12-3. ТЕЛЕИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ
- 12-4. СИСТЕМЫ АВТОМАТИЧЕСКОГО КОНТРОЛЯ И ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ
- 12-5. ИЗМЕРИТЕЛЬНЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ НА ОСНОВЕ АГРЕГАТНЫХ КОМПЛЕКСОВ ГОСУДАРСТВЕННОЙ СИСТЕМЫ ПРИБОРОВ И СРЕДСТВ АВТОМАТИЗАЦИИ
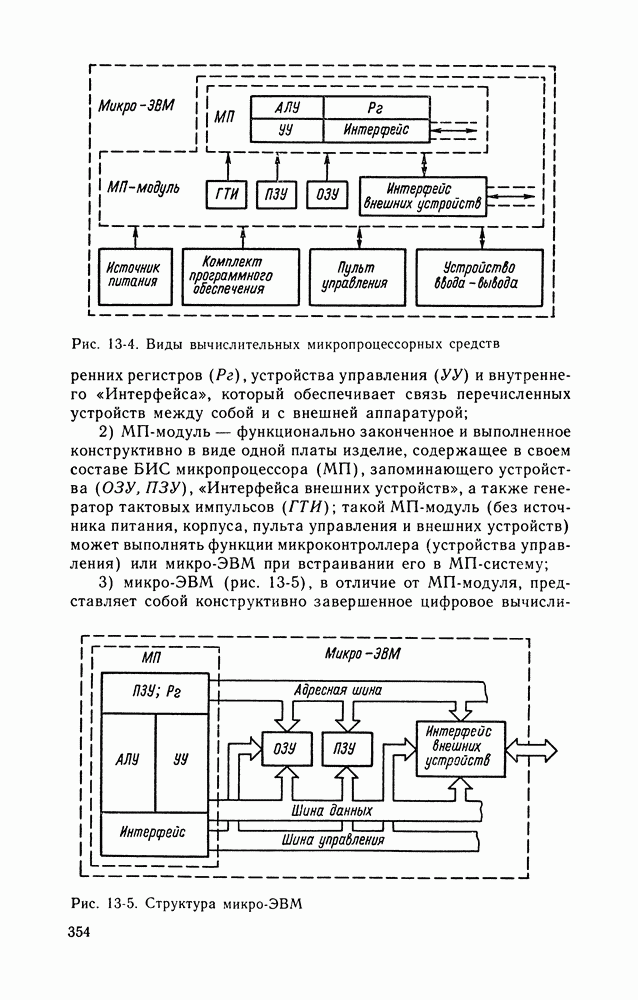
- Глава тринадцатая. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ СРЕДСТВА
- 13-2. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ СРЕДСТВА СИСТЕМНОГО ПРИМЕНЕНИЯ
- 13-3. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ КОМПЛЕКСЫ
- Раздел В. ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
- Глава четырнадцатая. ПОДГОТОВКА ИЗМЕРИТЕЛЬНОГО ЭКСПЕРИМЕНТА И ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- 14-2. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- 14-3. СУММИРОВАНИЕ ПОГРЕШНОСТЕЙ
- Глава пятнадцатая. ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ, МАГНИТНЫХ И НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 15-2. ИЗМЕРЕНИЯ МОЩНОСТИ, ЭНЕРГИИ И КОЛИЧЕСТВА ЭЛЕКТРИЧЕСТВА
- 15-3. ИЗМЕРЕНИЯ ЧАСТОТЫ, ФАЗЫ, ВРЕМЕННЫХ ИНТЕРВАЛОВ, АНАЛИЗ СПЕКТРА ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- 15-4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ЦЕПЕЙ ПОСТОЯННОГО И ПЕРЕМЕННОГО ТОКА
- 15-5. ИЗМЕРЕНИЯ ПАРАМЕТРОВ МАГНИТНОГО ПОЛЯ, ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
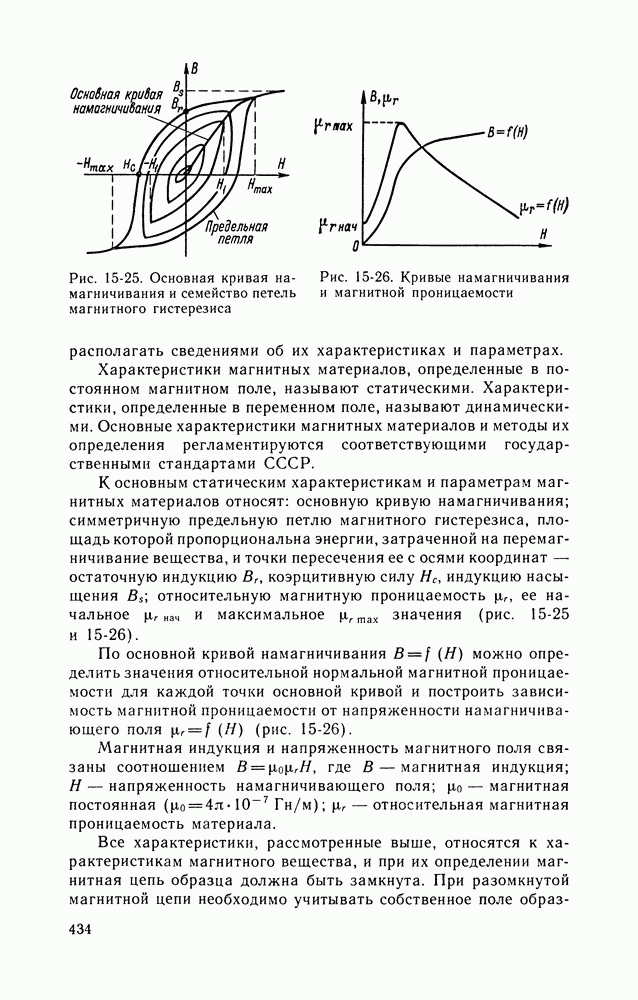
- МАГНИТНЫЕ МАТЕРИАЛЫ И ИХ ХАРАКТЕРИСТИКИ
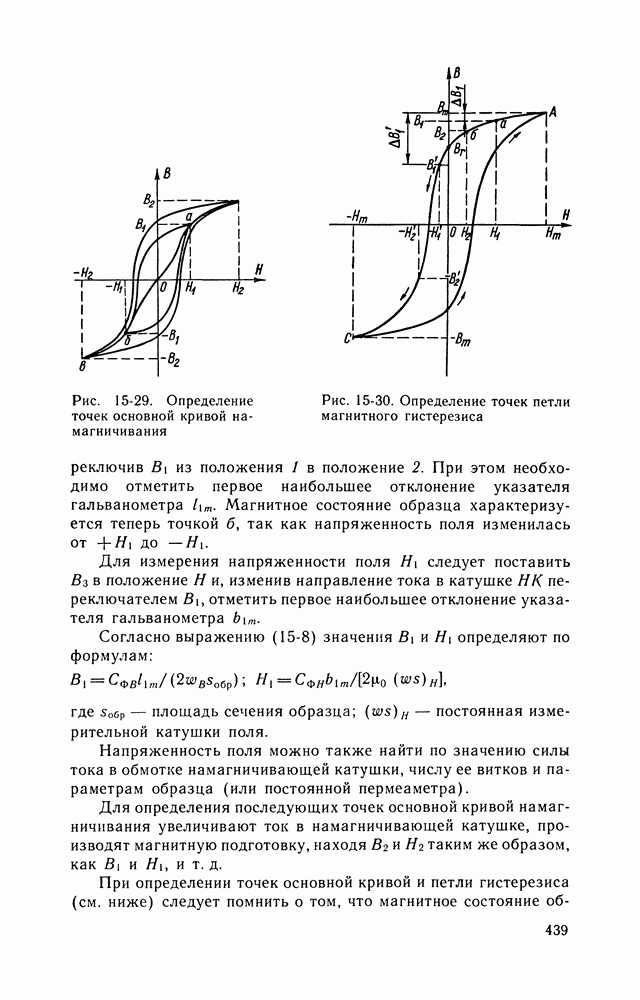
- ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- 15-6. ИЗМЕРЕНИЯ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- ИЗМЕРЕНИЯ ДАВЛЕНИЙ, ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ И РАССТОЯНИЙ
- Глава шестнадцатая. ИЗМЕРЕНИЯ ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ПРОЦЕССОВ
- 16-2. ИЗМЕРЕНИЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ДИСПЕРСИИ СЛУЧАЙНОГО ПРОЦЕССА
- 16-3. ИЗМЕРЕНИЕ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
- 16-4. ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННОЙ ФУНКЦИИ
- 16-5. АНАЛИЗ СПЕКТРА МОЩНОСТИ
- Список литературы