| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава восьмая. ЦИФРОВЫЕ ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ
8-1. ОБЩИЕ СВЕДЕНИЯ
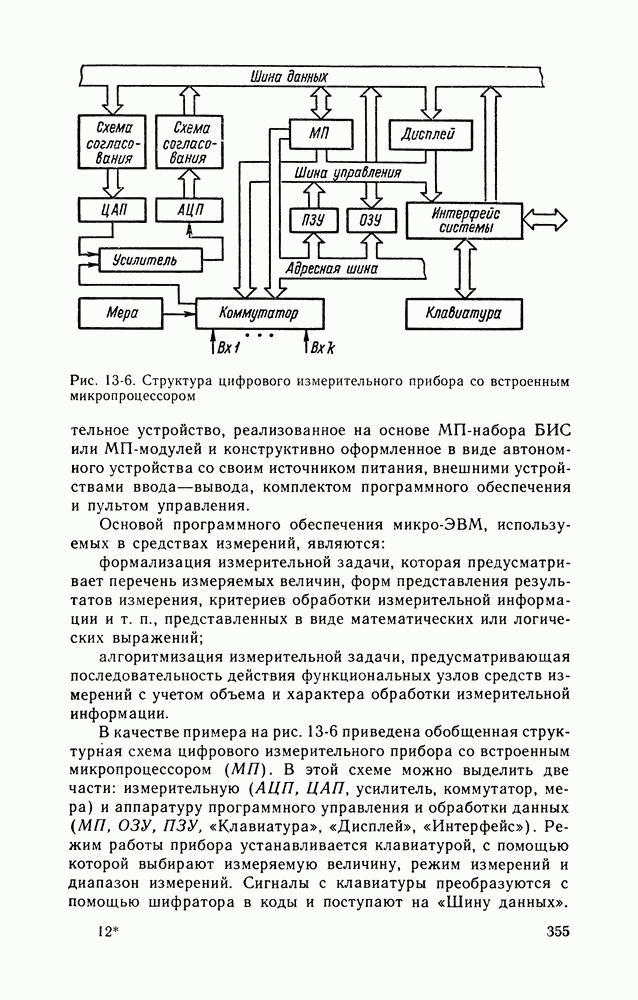
Основные понятия и определения. В настоящее время широко применяют цифровые измерительные приборы (ЦИП), имеющие ряд достоинств по сравнению с аналоговыми электроизмеритель ными приборами. Цифровыми называют приборы, автоматически вырабатывающие дискретные сигналы измерительной информации, показания которых представляются в цифровой форме. В цифровых приборах в соответствии с размером измеряемой величины образуется код (см. § 1-1), а затем в соответствии с кодом значение измеряемой величины представляется на отсчетном устройстве в цифровой форме. Применительно к цифровым приборам код — условные сигналы (обычно электрические) Код может подаваться в цифровое регистрирующее устройство, вычислительную машину или другие автоматические устройства.
Неавтоматические лабораторные компенсаторы и мосты с декадными магазинами сопротивлений по существу являются цифровыми приборами (неавтоматическими), так как в них положение ручек декадных магазинов сопротивления после уравновешивания (оператором) образует код и результат выражается в цифровой форме. Развитие электроизмерительной техники, а также других смежных областей привело к созданию автоматических цифровых приборов, которые рассматриваются в этой главе.
Цифровой прибор включает в себя два обязательных функциональных узла: аналого-цифровой преобразователь (АЦП) (см. § 4-1) и цифровое отсчетное устройство (ЦОУ).
АЦП выдает код в соответствии со значением измеряемой величины, а цифровое отсчетное устройство отражает это значение в цифровой форме.
АЦП являются не только составной частью ЦИП, они также используются в измерительных информационных, управляющих и других системах. АЦП выпускаются промышленностью и в качестве автономных устройств. Автономные АЦП в отличие от ЦИП не имеют десятичного отсчетного устройства, т. е. они дают на выходе только код; обычно они выполняются более быстродействующими, чем ЦИП, но менее точными; чаще всего они имеют один диапазон для одной измеряемой величины.
Кроме АЦП, к цифровым преобразователям относят цифро-аналоговые преобразователи (ЦАП), предназначенные для преобразования кода в аналоговую квантованную величину. ЦАП применяют не только как узел ЦИП и АЦП, но и как автономное устройство. В настоящее время промышленность выпускает АЦП и ЦАП не только в виде автономных средств измерений, но и в виде интегральных микросхем.
Кроме АЦП и ЦОУ, ЦИП может содержать предварительные аналоговые преобразователи, преобразующие измеряемую величину в другую величину, более удобную для преобразования в код. Например, аналоговыми преобразователями могут быть делители напряжения, усилители, преобразователи и т. п.
В настоящее время получили применение аналого-дискретные измерительные приборы (АДИП). В отличие от ЦИП в этих приборах используют квазианалоговые отсчетные устройства, т. е. устройства, в которых роль указателя выполняет светящаяся полоса или светящаяся точка, меняющие дискретно свою длину (полоса) или положение (точка) относительно шкалы. Квазианалоговые отсчетные устройства управляются кодом. Такие приборы сочетают в себе достоинства аналоговых приборов (аналоговые отсчетные устройства) и цифровых приборов (код на выходе).
При рассмотрении вопросов, общих для ЦИП, АЦП и АДИП, вводится понятие цифровое измерительное устройство (ЦИУ), под которым понимается любое из указанных средств измерений.
Для образования кода непрерывная измеряемая величина в ЦИУ дискретизируется во времени и квантуется по уровню.
Дискретизацией непрерывной во времени величины  называется операция ее преобразования в прерывную во времени, т. е. величину, значения которой отличны от нуля и совпадают с соответствующими значениями
называется операция ее преобразования в прерывную во времени, т. е. величину, значения которой отличны от нуля и совпадают с соответствующими значениями  только в определенные моменты времени. Промежуток между двумя соседними моментами времени дискретизации называют шагом дискретизации, который может быть постоянным или переменным.
только в определенные моменты времени. Промежуток между двумя соседними моментами времени дискретизации называют шагом дискретизации, который может быть постоянным или переменным.
Квантованием по уровню непрерывной по уровню величины  называют операцию ее преобразования в квантованную величину
называют операцию ее преобразования в квантованную величину  Фиксированные значения квантованной величины называют уровнями квантования, разность между двумя ближайшими уровнями — ступенью, или шагом квантования, или квантом.
Фиксированные значения квантованной величины называют уровнями квантования, разность между двумя ближайшими уровнями — ступенью, или шагом квантования, или квантом.
Код в ЦИУ вырабатывается в соответствии с квантованной величиной, принимаемой равной измеряемой величине. При преобразовании измеряемой величины в квантованную имеет значение правило установления равенства (способ отождествления) измеряемой и квантованной величины. Отождествление может производиться с ближайшим большим или равным, ближайшим меньшим или равным, а также с ближайшим уровнем квантования.
Число возможных уровней квантования определяется устройством ЦИУ. От числа уровней квантования зависит емкость (число возможных отсчетов) отсчетного устройства. Например, если у ЦИП отсчетное устройство имеет максимальное показание 999, то такой прибор бесконечное множество значений измеряемой величины в пределах от 0 до 999 отражает всего 1000 различными показаниями, т. е. в этом приборе измеряемая величина преобразуется в квантованную, имеющую 1000 уровней квантования.
В результате квантования измеряемой величины по уровню возникает погрешность дискретности (квантования по уровню), обусловленная тем, что бесконечное множество значений измеряемой величины отражается лишь ограниченным числом кодовых комбинаций ЦИУ. Возникновение погрешности дискретности иллюстрирует рис. 8-1, где  — график изменения измеряемой величины;
— график изменения измеряемой величины;  — ординаты, соответствующие кодам ЦИУ (показаниям ЦИП) при измерении
— ординаты, соответствующие кодам ЦИУ (показаниям ЦИП) при измерении  в моменты времени
в моменты времени  и при отождествлении с ближайшим уровнем квантования.
и при отождествлении с ближайшим уровнем квантования.
Как видно, в большинстве случаев измерений имеется разность между значениями кодовых комбинаций ЦИУ (показаниями ЦИП) и размерами измеряемой величины в моменты измерений. Эта разность есть абсолютная погрешность. При идеальном преобразовании измеряемой непрерывной величины в квантованную и в код полученная погрешность равна погрешности дискретности. Погрешность дискретности не является препятствием для увеличения точности ЦИУ, так как соответствующим выбором числа уровней квантования погрешность дискретности можно сделать достаточно малой,
Иногда возникает необходимость восстанавливать все значения непрерывной измеряемой величины по ряду измеренных

Рис. 8-1. Квантование по уровню и дискретизации во времени непрерывной измеряемой величины
мгновенных значений. Практически это удается сделать всегда с погрешностью, носящей название погрешности аппроксимации.
Если ЦИУ предназначены для получения результатов измерений, по которым будут восстанавливаться все промежуточные непрерывные значения измеряемой величины, то быстродействие таких приборов и преобразователей выбирают с учетом допускаемой погрешности аппроксимации, способа аппроксимации и характера изменения измеряемой величины.
Системы счисления, коды.
В ЦИУ кодирование производится по определенному правилу, например с использованием системы счисления.
В привычной для нас десятичной системе счисления любое целое число  может быть представлено в виде:
может быть представлено в виде:

где  — число разрядов;
— число разрядов;  — коэффициент, принимающий значения
— коэффициент, принимающий значения  (используется 10 различных символов). Например, число 902 можно представить в виде суммы:
(используется 10 различных символов). Например, число 902 можно представить в виде суммы:  . Для упрощения записи обычно пишут только значения коэффициентов (символов)
. Для упрощения записи обычно пишут только значения коэффициентов (символов)  располагая их слева направо по убывающим номерам. При такой записи положение коэффициента определяет его принадлежность к определенному разряду, т. е. определяет его «вес».
располагая их слева направо по убывающим номерам. При такой записи положение коэффициента определяет его принадлежность к определенному разряду, т. е. определяет его «вес».
Любое целое число  можно выразить также в двоичной системе:
можно выразить также в двоичной системе:

где  — число разрядов;
— число разрядов;  — коэффициент, принимающий значения 0 и 1 (используются два символа).
— коэффициент, принимающий значения 0 и 1 (используются два символа).
Например, то же число 902 в двоичной системе:  Для упрощения записи указывают только коэффициенты
Для упрощения записи указывают только коэффициенты 
располагаемые в соответствии с порядком следования разрядов т. е. в упрощенном виде число 902 в двоичной системе равно 1110000110.
Наиболее простая система счисления — единичная, имеющая один символ (цифра 1), при помощи которого можно выразить любое число, например, следующим образом:

Находят применение комбинации систем счисления. Например, двоично-десятичная система строится на сочетании признаков двоичной и десятичной систем. Расположение десятичных разрядов сохраняется, но цифра каждого десятичного разряда изображается в двоичной системе. Число 902 в двоично-десятичной системе: 1001 0000 0010.
Для образования кода используют также комбинации целых положительных чисел. Например, каждый десятичный разряд может быть выражен комбинацией целых положительных чисел  Эти числа выбирают так, чтобы их линейная комбинация
Эти числа выбирают так, чтобы их линейная комбинация  могла принимать любое целое число от 0 до 9 при
могла принимать любое целое число от 0 до 9 при  принимающих значения 0 или 1. Например,
принимающих значения 0 или 1. Например,  выбирают такими: 2, 4, 2, 1 или 5, 2, 1, 1 и т. д.
выбирают такими: 2, 4, 2, 1 или 5, 2, 1, 1 и т. д.
При образовании кодов каждому символу используемой системы счисления должен соответствовать свой элемент кода.
В зависимости от очередности передачи элементов кода все коды разделяют на последовательные и параллельные. У последовательного кода элементы кода передаются последовательно во времени, причем могут передаваться по одному каналу. У параллельного кода элементы кода передаются одновременно по различным каналам.
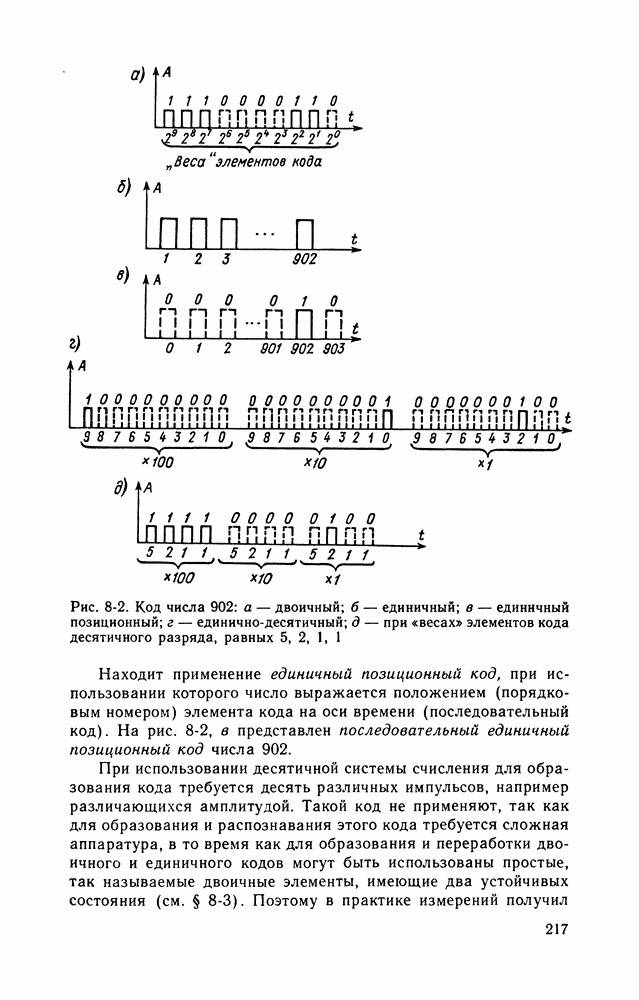
Если образовывать последовательный код импульсами постоянного тока и считать, что символу 1 двоичной системы счисления соответствует наличие импульса, а отсутствие импульса соответствует символу 0, то число 902 в двоичной системе счисления имеет вид, показанный на рис. 8-2, а. Каждый импульс кода в зависимости от места (во времени) имеет определенную значимость — «вес». Код, построенный с использованием двоичной системы, называют двоичным кодом.
На рис.  показан последовательный код в виде импульсов тока, представляющий число 902 в единичной системе счисления. Такой код носит название число-импульсного или единичного кода. Он более громоздок, чем двоичный, однако находит применение в тех случаях, когда измеряемая величина простыми средствами преобразуется в этот код. Достоинство этого кода заключается также в простоте суммирования импульсов кода с помощью пересчетных устройств (см. § 8-3).
показан последовательный код в виде импульсов тока, представляющий число 902 в единичной системе счисления. Такой код носит название число-импульсного или единичного кода. Он более громоздок, чем двоичный, однако находит применение в тех случаях, когда измеряемая величина простыми средствами преобразуется в этот код. Достоинство этого кода заключается также в простоте суммирования импульсов кода с помощью пересчетных устройств (см. § 8-3).

Рис. 8-2. Код числа 902: а — двоичный; б - единичный; в — единичный позиционный; г - единично-десятичный; д - при «весах» элементов кода десятичного разряда, равных 5, 2, 1, 1
Находит применение единичный позиционный код, при использовании которого число выражается положением (порядковым номером) элемента кода на оси времени (последовательный код). На рис. 8-2, в представлен последовательный единичный позиционный код числа 902.
При использовании десятичной системы счисления для образования кода требуется десять различных импульсов, например различающихся амплитудой. Такой код не применяют, так как для образования и распознавания этого кода требуется сложная аппаратура, в то время как для образования и переработки двоичного и единичного кодов могут быть использованы простые, так называемые двоичные элементы, имеющие два устойчивых состояния (см. § 8-3). Поэтому в практике измерений получил
применение единично-десятичный код, в котором для передачи значения десятичного разряда требуется десять элементов кода (десять мест расположения импульса) с весами  .
.
Двоичный код более компактен (экономичен), чем единичнодесятичный. Кроме того, двоичный код вследствие ряда достоинств используют в вычислительных, управляющих и других устройствах. По этой причине двоичный код применяют в АЦП, предназначенных для работы совместно с указанными устройствами. Однако двоичный код неудобен для управления десятичным отсчетным устройством. Поэтому в ЦИП находит применение двоично-десятичный код с «весами» элементов кода одного десятичного разряда, равными 8, 4, 2, 1, а также так называемые тетрадно-десятичные коды с «весами» 2, 4, 2, 1; 4, 2, 2, 1; 5, 2, 1, 1 и т. д. Эти коды более удобны для управления десятичным отсчетным устройством, чем двоичный код, и мало отличаются от двоичного по числу элементов кода. На рис. 8-2, д показан последовательный код числа 902 при «весах» элементов кода десятичного разряда, равных 5, 2, 1, 1.
Согласно требованию стандарта все ЦИП должны выдавать во внешние устройства двоично-десятичный код (8—4—2—1) независимо от кода, применяемого в процессе аналого-цифрового преобразования.
Наряду с указанными кодами находят применение так называемые циклические коды, один из которых будет рассмотрен при изучении ЦИУ считывания.
Основные методы преобразования непрерывных измеряемых величин в коды.
При аналого-цифровом преобразовании происходит определение отождествляемого уровня квантования, т. е. происходит преобразование непрерывной измеряемой величины в квантованную и образование кода, причем образование кода происходит, как правило, одновременно с преобразованием измеряемой величины в квантованную.
По способу преобразования выделяют три основных метода.
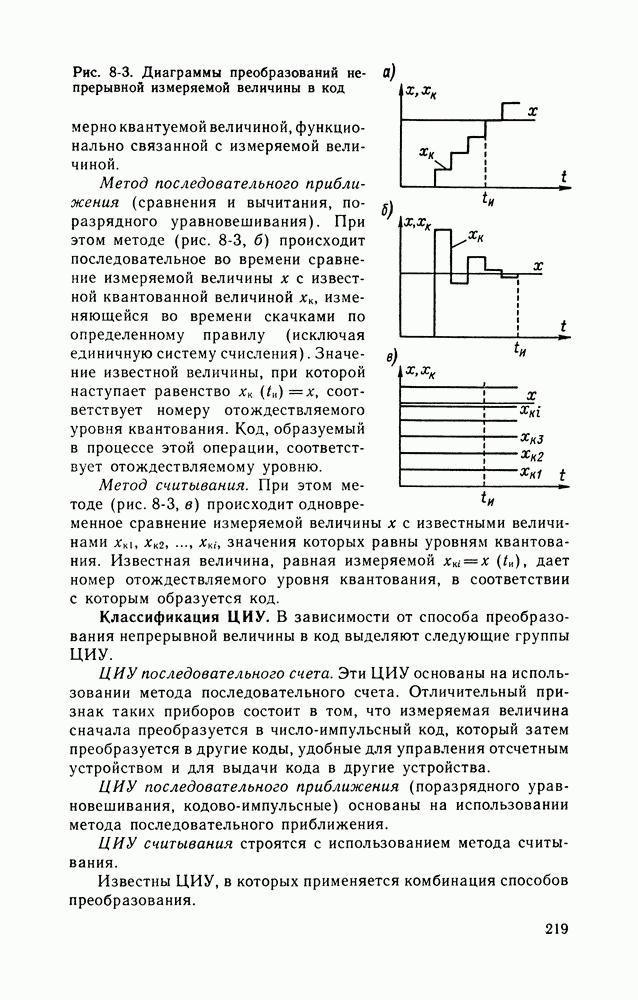
Метод последовательного счета. При этом методе (рис. 8-3, а) происходит последовательное во времени сравнение измеряемой величины х с известной квантованной величиной  изменяющейся (возрастающей или убывающей) во времени скачками, причем каждый скачок соответствует шагу (ступени) квантования по уровню. Число ступеней, при котором наступает равенство
изменяющейся (возрастающей или убывающей) во времени скачками, причем каждый скачок соответствует шагу (ступени) квантования по уровню. Число ступеней, при котором наступает равенство  (с некоторой погрешностью), равно номеру отождествляемого уровня квантования. В процессе сравнения образуется единичный код, соответствующий номеру отождествляемого уровня квантования. Возможно инверсное преобразование, при котором известная постоянная величина сравнивается с
(с некоторой погрешностью), равно номеру отождествляемого уровня квантования. В процессе сравнения образуется единичный код, соответствующий номеру отождествляемого уровня квантования. Возможно инверсное преобразование, при котором известная постоянная величина сравнивается с

Рис. 8-3. Диаграммы преобразований непрерывной измеряемой величины в код
равномерно квантуемой величиной, функционально связанной с измеряемой величиной.
Метод последовательного приближения (сравнения и вычитания, поразрядного уравновешивания). При этом методе (рис. 8-3, б) происходит последовательное во времени сравнение измеряемой величины х с известной квантованной величиной  изменяющейся во времени скачками по определенному правилу (исключая единичную систему счисления). Значение известной величины, при которой наступает равенство
изменяющейся во времени скачками по определенному правилу (исключая единичную систему счисления). Значение известной величины, при которой наступает равенство  соответствует номеру отождествляемого уровня квантования. Код, образуемый в процессе этой операции, соответствует отождествляемому уровню.
соответствует номеру отождествляемого уровня квантования. Код, образуемый в процессе этой операции, соответствует отождествляемому уровню.
Метод считывания. При этом методе (рис. 8-3, в) происходит одновременное сравнение измеряемой величины х с известными величинами  значения которых равны уровням квантования. Известная величина, равная измеряемой
значения которых равны уровням квантования. Известная величина, равная измеряемой  дает номер отождествляемого уровня квантования, в соответствии с которым образуется код.
дает номер отождествляемого уровня квантования, в соответствии с которым образуется код.
Классификация ЦИУ.
В зависимости от способа преобразования непрерывной величины в код выделяют следующие группы ЦИУ.
ЦИУ последовательного счета. Эти ЦИУ основаны на использовании метода последовательного счета. Отличительный признак таких приборов состоит в том, что измеряемая величина сначала преобразуется в число-импульсный код, который затем преобразуется в другие коды, удобные для управления отсчетным устройством и для выдачи кода в другие устройства.
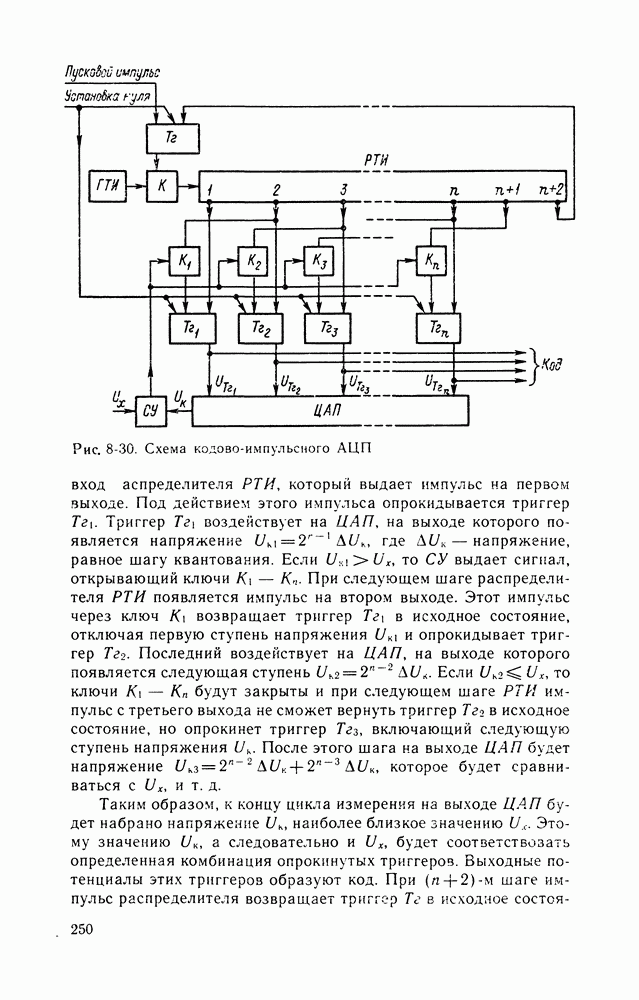
ЦИУ последовательного приближения (поразрядного уравновешивания, кодово-импульсные) основаны на использовании метода последовательного приближения.
ЦИУ считывания строятся с использованием метода считывания.
Известны ЦИУ, в которых применяется комбинация способов преобразования.
По измеряемой величине ЦИП разделяют на вольтметры, частотомеры, фазометры, омметры, вольтомметры и т. д. В зависимости от наличия усреднения измеряемой величины ЦИУ делят на приборы, измеряющие мгновенное значение, и приборы, измеряющие среднее значение за определенный интервал времени (интегрирующие). Кроме того, все ЦИУ делят на группы по точности, быстродействию, надежности. По режиму работы ЦИУ разделяют на циклические и следящие.
В циклических ЦИУ весь процесс преобразования протекает всегда независимо от размера измеряемой величины по заданной программе от начала до конца. В следящих ЦИУ процесс преобразования начинается только при отклонении измеряемой величины от ранее измеренного размера на определенное приращение. Характер процесса преобразования зависит от приращения измеряемой величины.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Раздел А. ОБЩИЕ СВЕДЕНИЯ ОБ ИЗМЕРИТЕЛЬНОЙ ТЕХНИКЕ
- Глава первая. ОСНОВНЫЕ ПОНЯТИЯ ИЗМЕРИТЕЛЬНОЙ ТЕХНИКИ И КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ
- 1-2. ВИДЫ И МЕТОДЫ ИЗМЕРЕНИЙ
- Глава вторая. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
- 2-1. ОСНОВНЫЕ ПОНЯТИЯ И ВИДЫ ПОГРЕШНОСТЕЙ
- 2-2. ВЕРОЯТНОСТНЫЙ ПОДХОД К ОПИСАНИЮ ПОГРЕШНОСТЕЙ
- 2-3. ВЕРОЯТНОСТНЫЕ ОЦЕНКИ ПОГРЕШНОСТЕЙ
- Глава третья. ОСНОВЫ МЕТРОЛОГИЧЕСКОГО ОБЕСПЕЧЕНИЯ
- 3-2. ЭТАЛОНЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН
- 3-3. ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ
- Раздел Б. ЭЛЕКТРИЧЕСКИЕ СРЕДСТВА ИЗМЕРЕНИЙ
- Глава четвертая. ОБЩИЕ СВЕДЕНИЯ О СРЕДСТВАХ ИЗМЕРЕНИЙ
- 4-2. ГОСУДАРСТВЕННАЯ СИСТЕМА ПРИБОРОВ
- 4-3. ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
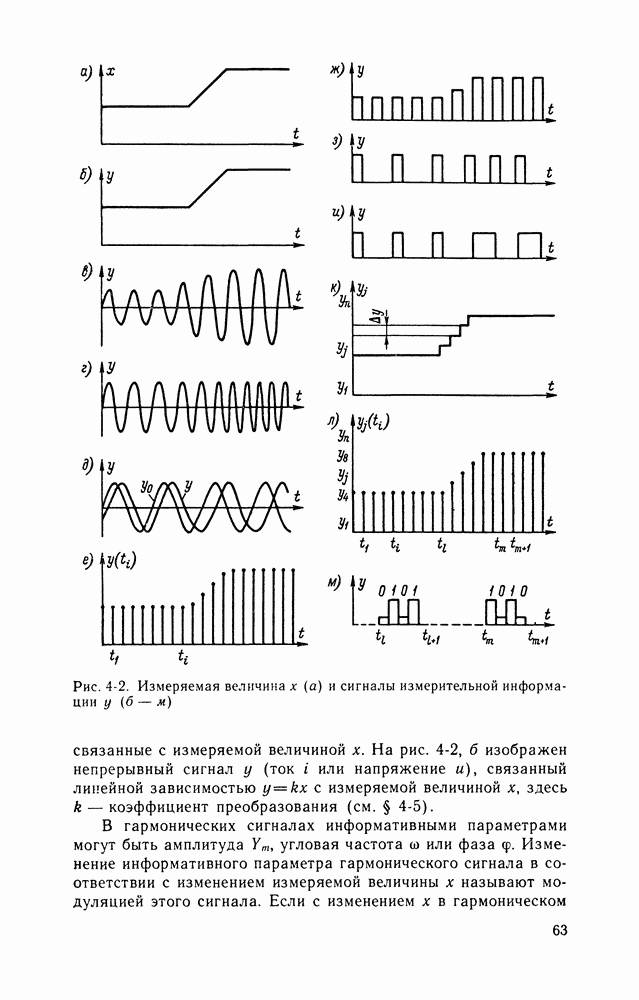
- 4-4. СИГНАЛЫ ИЗМЕРИТЕЛЬНОЙ ИНФОРМАЦИИ
- Математические модели сигналов.
- Дискретизация сигналов.
- 4-5. СТРУКТУРНЫЕ СХЕМЫ И СВОЙСТВА СРЕДСТВ ИЗМЕРЕНИЙ В СТАТИЧЕСКОМ РЕЖИМЕ
- Средства измерений прямого преобразования.
- Средства измерений уравновешивающего преобразования.
- 4-6. СРЕДСТВА ИЗМЕРЕНИЙ В ДИНАМИЧЕСКОМ РЕЖИМЕ
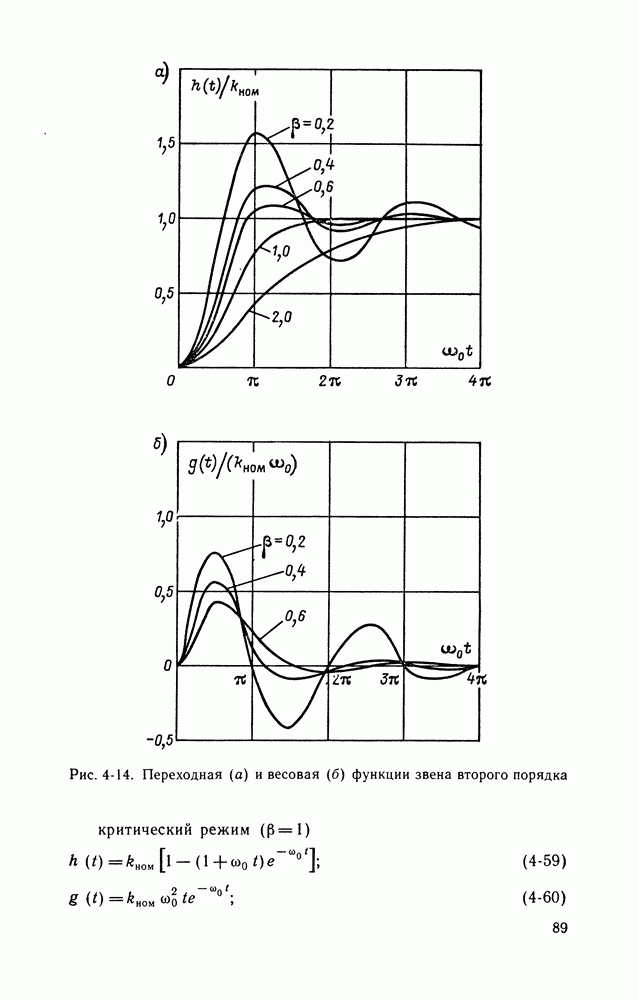
- Переходные и импульсные переходные характеристики.
- Частотные характеристики.
- Передаточные функции.
- Глава пятая. МЕРЫ, ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ И ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ
- 5-2. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 5-3. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ
- МАГНИТОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ
- Амперметры и вольтметры.
- Омметры.
- Гальванометры.
- Баллистические гальванометры.
- Кулонметры.
- Вибрационные гальванометры.
- ЭЛЕКТРОДИНАМИЧЕСКИЕ И ФЕРРОДИНАМИЧЕСКИЕ ПРИБОРЫ
- ЭЛЕКТРОМАГНИТНЫЕ ПРИБОРЫ
- ЭЛЕКТРОСТАТИЧЕСКИЕ ПРИБОРЫ
- ИНДУКЦИОННЫЕ ПРИБОРЫ
- 5-4. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРИБОРЫ С ПРЕОБРАЗОВАТЕЛЯМИ
- Глава шестая. ЭЛЕКТРОННЫЕ АНАЛОГОВЫЕ ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ
- 6-2. ЭЛЕКТРОННЫЕ ВОЛЬТМЕТРЫ
- 6-3. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ ЧАСТОТЫ И ФАЗЫ
- 6-4. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ МОЩНОСТИ И ЭНЕРГИИ
- 6-5. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ПАРАМЕТРОВ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 6-6. ЭЛЕКТРОННО ЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 6-7. АНАЛИЗАТОРЫ СПЕКТРА, ИЗМЕРИТЕЛИ НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ
- Глава седьмая. МОСТЫ И КОМПЕНСАТОРЫ
- 7-2. ТЕОРИЯ МОСТОВЫХ СХЕМ
- 7-3. МОСТЫ ДЛЯ ИЗМЕРЕНИЙ СОПРОТИВЛЕНИЯ НА ПОСТОЯННОМ ТОКЕ
- 7-4. МОСТЫ ПЕРЕМЕННОГО ТОКА ДЛЯ ИЗМЕРЕНИЙ ЕМКОСТИ, УГЛА ПОТЕРЬ, ИНДУКТИВНОСТИ И ДОБРОТНОСТИ
- 7-5. КОМПЕНСАТОРЫ ПОСТОЯННОГО ТОКА
- 7-6. КОМПЕНСАТОРЫ ПЕРЕМЕННОГО ТОКА
- 7-7. АВТОМАТИЧЕСКИЕ МОСТЫ И КОМПЕНСАТОРЫ
- Глава восьмая. ЦИФРОВЫЕ ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ
- 8-2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 8-3. УЗЛЫ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 8-4. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА ПОСЛЕДОВАТЕЛЬНОГО СЧЕТА
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД ЧАСТОТЫ
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД НАПРЯЖЕНИЯ ПОСТОЯННОГО ТОКА
- ЦИУ С НЕПОСРЕДСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ В КОД ПЕРЕМЕЩЕНИЯ
- 8-5. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА ПОСЛЕДОВАТЕЛЬНОГО ПРИБЛИЖЕНИЯ
- 8-6. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА СЧИТЫВАНИЯ
- 8-7. ХАРАКТЕРИСТИКА СОВРЕМЕННЫХ ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ПЕРСПЕКТИВЫ ИХ РАЗВИТИЯ
- Глава девятая. РЕГИСТРИРУЮЩИЕ ПРИБОРЫ И УСТРОЙСТВА
- 9-2. САМОПИШУЩИЕ ПРИБОРЫ ПРЯМОГО ПРЕОБРАЗОВАНИЯ
- 9-3. СВЕТОЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 9-4. МАГНИТОГРАФЫ, ГРАФОПОСТРОИТЕЛИ, ЭЛЕКТРОННЫЕ ОСЦИЛЛОГРАФЫ, ЦИФРОПЕЧАТАЮЩИЕ УСТРОЙСТВА
- Глава десятая. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНЫХ ВЕЛИЧИН
- 10-2. МАГНИТОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНОГО ПОТОКА
- ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ МАГНИТНОЙ ИНДУКЦИИ И НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ
- 10-3. АППАРАТУРА ДЛЯ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- Глава одиннадцатая. ПРИБОРЫ И ПРЕОБРАЗОВАТЕЛИ ДЛЯ ИЗМЕРЕНИЙ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 11-2. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- ГЕНЕРАТОРНЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 11-3. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ТЕМПЕРАТУРЫ
- 11-4. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ ГЕОМЕТРИЧЕСКИХ И МЕХАНИЧЕСКИХ ВЕЛИЧИН
- 11-5. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЙ КОНЦЕНТРАЦИИ ЖИДКОЙ И ГАЗООБРАЗНОЙ СРЕДЫ
- Глава двенадцатая. ИЗМЕРИТЕЛЬНЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ
- 12-2. ИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ
- 12-3. ТЕЛЕИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ
- 12-4. СИСТЕМЫ АВТОМАТИЧЕСКОГО КОНТРОЛЯ И ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ
- 12-5. ИЗМЕРИТЕЛЬНЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ НА ОСНОВЕ АГРЕГАТНЫХ КОМПЛЕКСОВ ГОСУДАРСТВЕННОЙ СИСТЕМЫ ПРИБОРОВ И СРЕДСТВ АВТОМАТИЗАЦИИ
- Глава тринадцатая. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ СРЕДСТВА
- 13-2. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ СРЕДСТВА СИСТЕМНОГО ПРИМЕНЕНИЯ
- 13-3. ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЕ КОМПЛЕКСЫ
- Раздел В. ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
- Глава четырнадцатая. ПОДГОТОВКА ИЗМЕРИТЕЛЬНОГО ЭКСПЕРИМЕНТА И ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- 14-2. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- 14-3. СУММИРОВАНИЕ ПОГРЕШНОСТЕЙ
- Глава пятнадцатая. ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ, МАГНИТНЫХ И НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 15-2. ИЗМЕРЕНИЯ МОЩНОСТИ, ЭНЕРГИИ И КОЛИЧЕСТВА ЭЛЕКТРИЧЕСТВА
- 15-3. ИЗМЕРЕНИЯ ЧАСТОТЫ, ФАЗЫ, ВРЕМЕННЫХ ИНТЕРВАЛОВ, АНАЛИЗ СПЕКТРА ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- 15-4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ЦЕПЕЙ ПОСТОЯННОГО И ПЕРЕМЕННОГО ТОКА
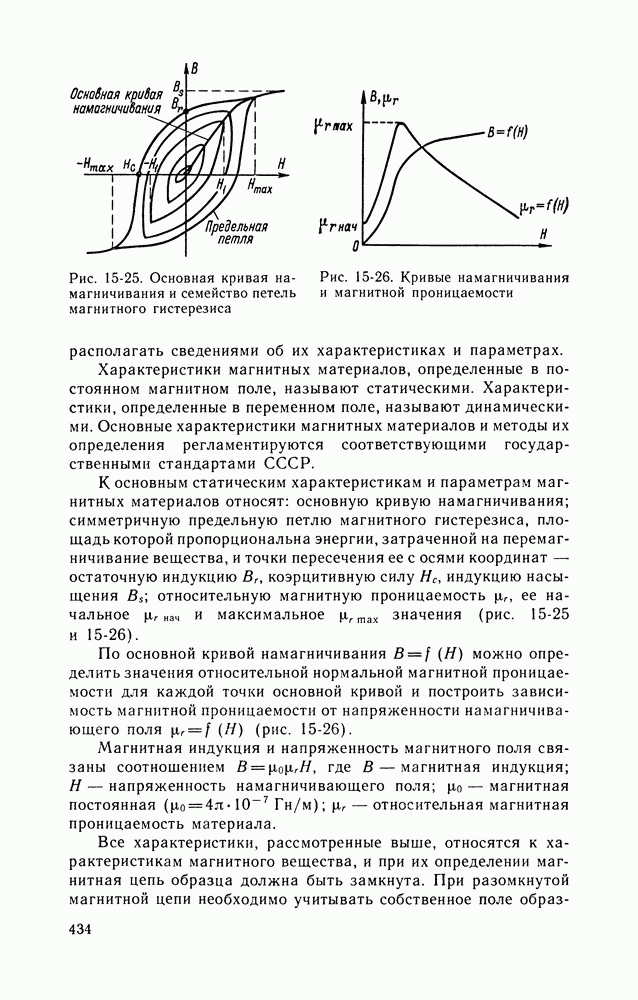
- 15-5. ИЗМЕРЕНИЯ ПАРАМЕТРОВ МАГНИТНОГО ПОЛЯ, ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- МАГНИТНЫЕ МАТЕРИАЛЫ И ИХ ХАРАКТЕРИСТИКИ
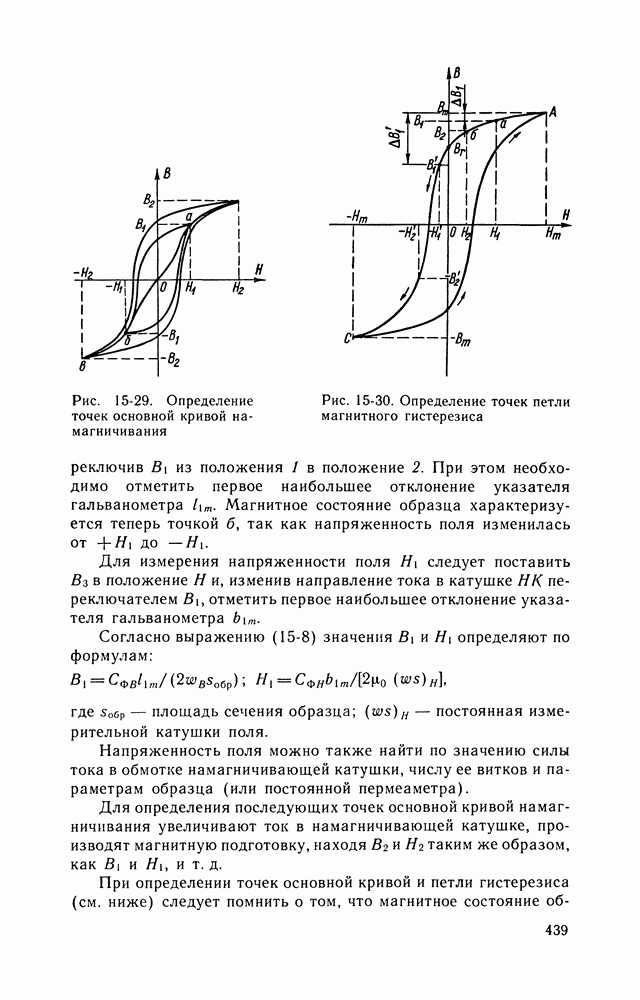
- ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ МАГНИТНЫХ МАТЕРИАЛОВ
- 15-6. ИЗМЕРЕНИЯ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- ИЗМЕРЕНИЯ ДАВЛЕНИЙ, ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ И РАССТОЯНИЙ
- Глава шестнадцатая. ИЗМЕРЕНИЯ ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ПРОЦЕССОВ
- 16-2. ИЗМЕРЕНИЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ДИСПЕРСИИ СЛУЧАЙНОГО ПРОЦЕССА
- 16-3. ИЗМЕРЕНИЕ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
- 16-4. ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННОЙ ФУНКЦИИ
- 16-5. АНАЛИЗ СПЕКТРА МОЩНОСТИ
- Список литературы