| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 7. Область, ограниченная изнутри круговым цилиндром из идеального проводника
Во многих задачах, имеющих практическое значение, например в задачах о нагреве подземных электрических кабелей, а также при измерении теплопроводности методом «зонда» металлический цилиндр окружен неограниченной средой (такой, как почва или горная порода) со значительно меньшей теплопроводностью. С хорошим приближением металл может рассматриваться как
идеальный проводник тепла — влияние конечности коэффициента теплопроводности можно оценить из более сложных результатов, приведенных в § 8 данной главы. В большинстве задач наиболее интересным оказывается вопрос о температуре материала внутри цилиндра. Последний либо имеет вначале температуру, равную единице (область вне цилиндра имеет температуру, равную нулю), либо в единицу времени к нему подводится постоянное количество тепла. Аналогичные задачи возникают в тех случаях, когда область  содержит хорошо перемешиваемую жидкость.
содержит хорошо перемешиваемую жидкость.
Во многих практических задачах между цилиндром и окружающей средой имеется контактное сопротивление. Такие задачи будут рассмотрены ниже (см. примеры III и IV данного параграфа). Однако в первую очередь мы обсудим более простой случай, когда контактное сопрстивление отсутствует.
1. Область  имеет в начальный момент времени температуру, равную нулю. На границе
имеет в начальный момент времени температуру, равную нулю. На границе  эта область соприкасается с идеальным проводником в виде цилиндра, обладающим теплоемкостью
эта область соприкасается с идеальным проводником в виде цилиндра, обладающим теплоемкостью  единицу длины цилиндра). Начальная температура проводника равна
единицу длины цилиндра). Начальная температура проводника равна  На границе
На границе  контактное сопротивление отсутствует.
контактное сопротивление отсутствует.
Обозначая температуру в области  через
через  получим, как и в примере V § 2 данной главы,
получим, как и в примере V § 2 данной главы,

где

является параметром, равным удвоенному отношению теплоемкости эквивалентного объема среды к теплоемкости идеального проводника. Отсюда следует, что

где

Температура V в области  равная значению (7.3) при
равная значению (7.3) при  , записывается в виде
, записывается в виде

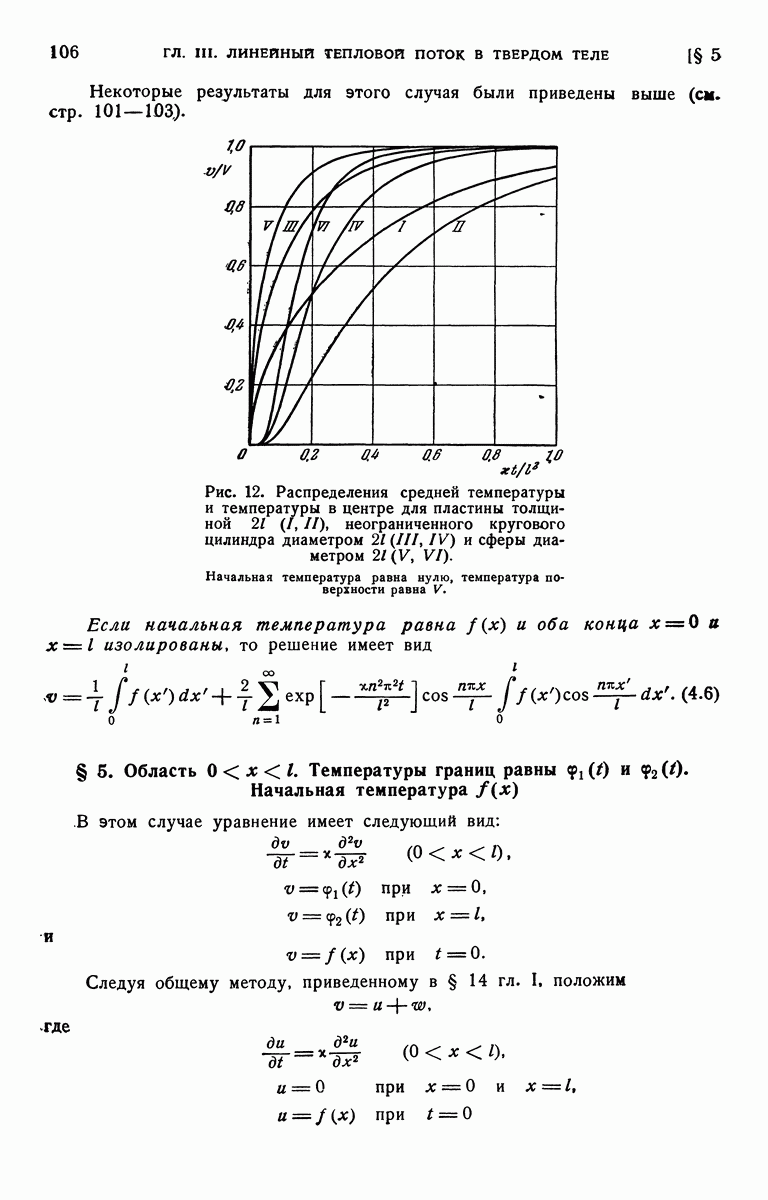
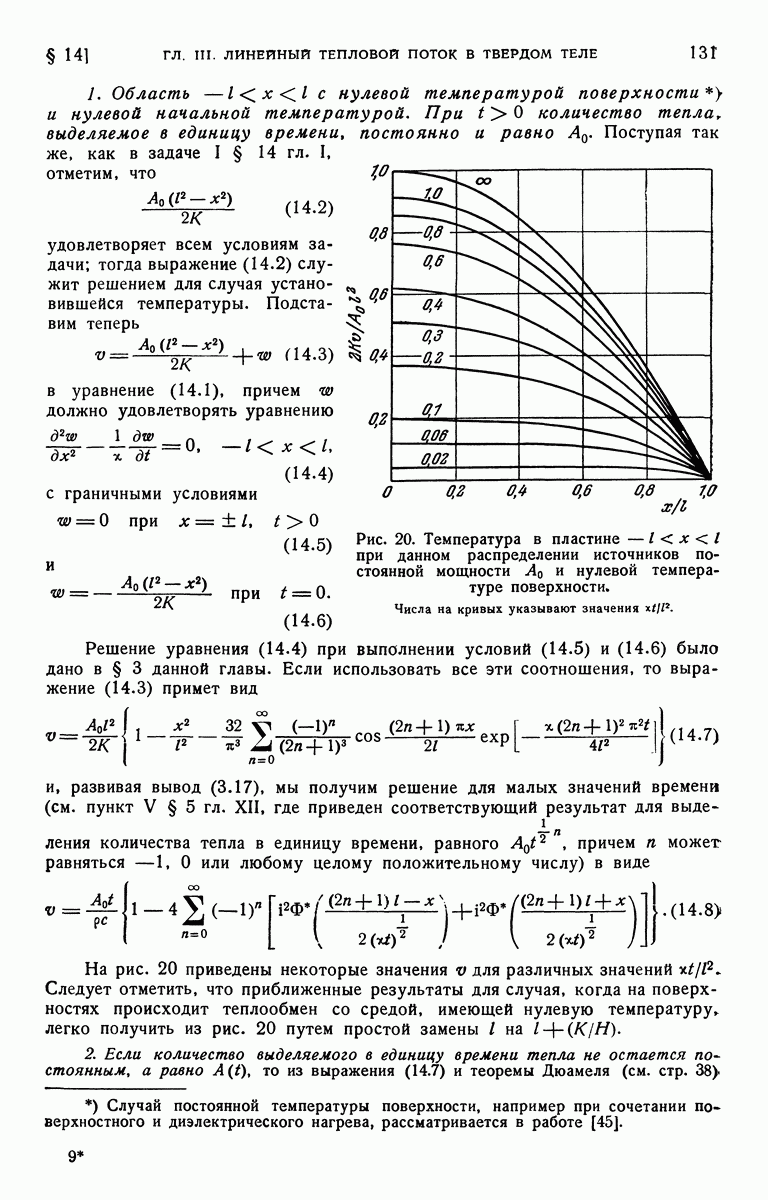
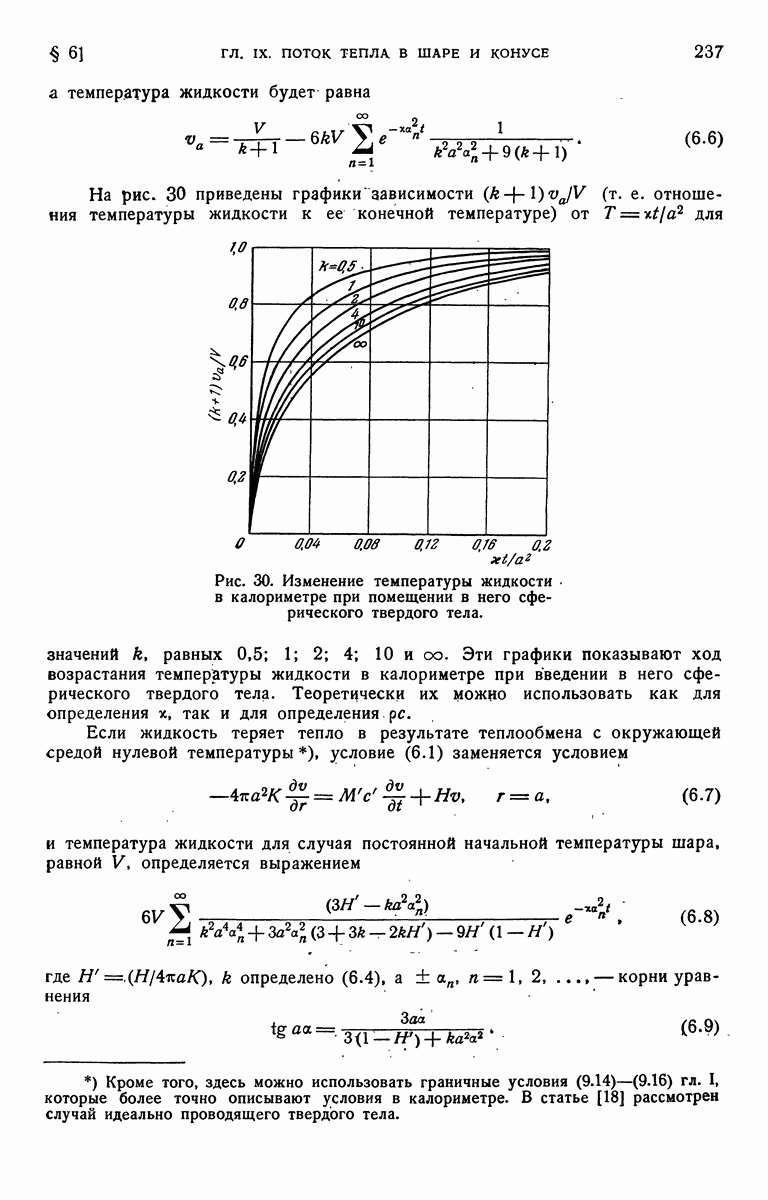
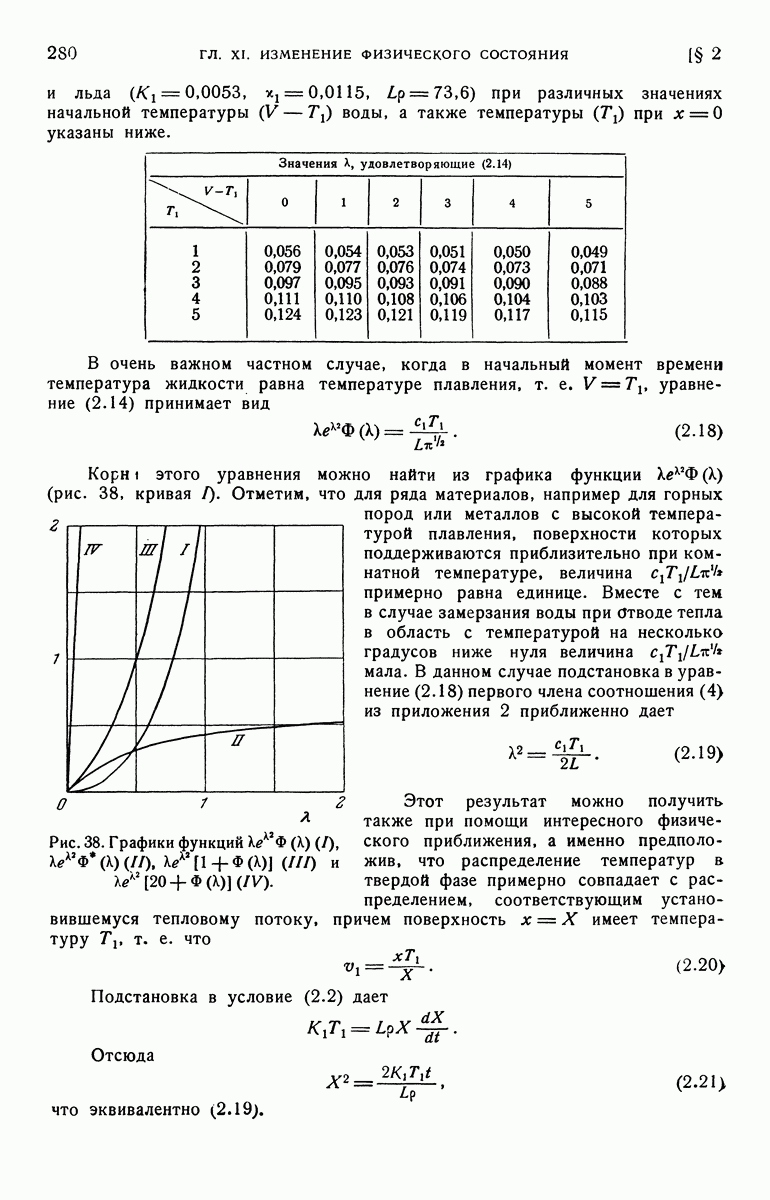
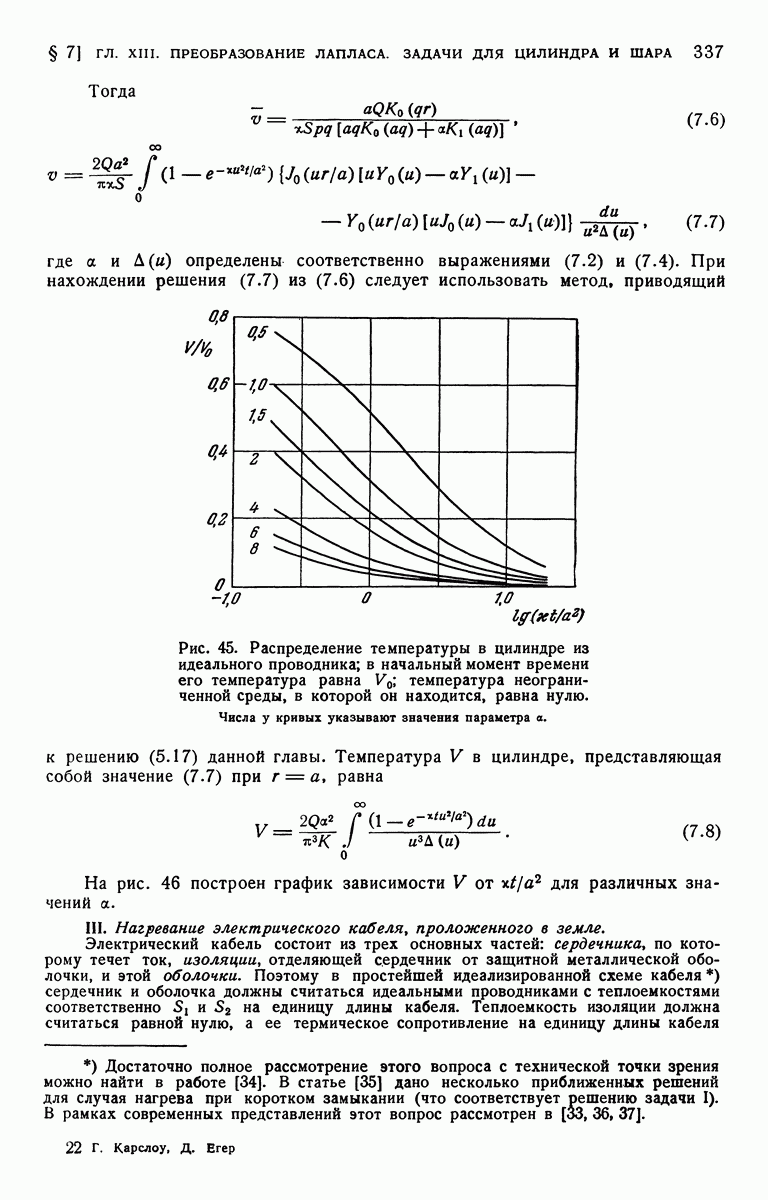
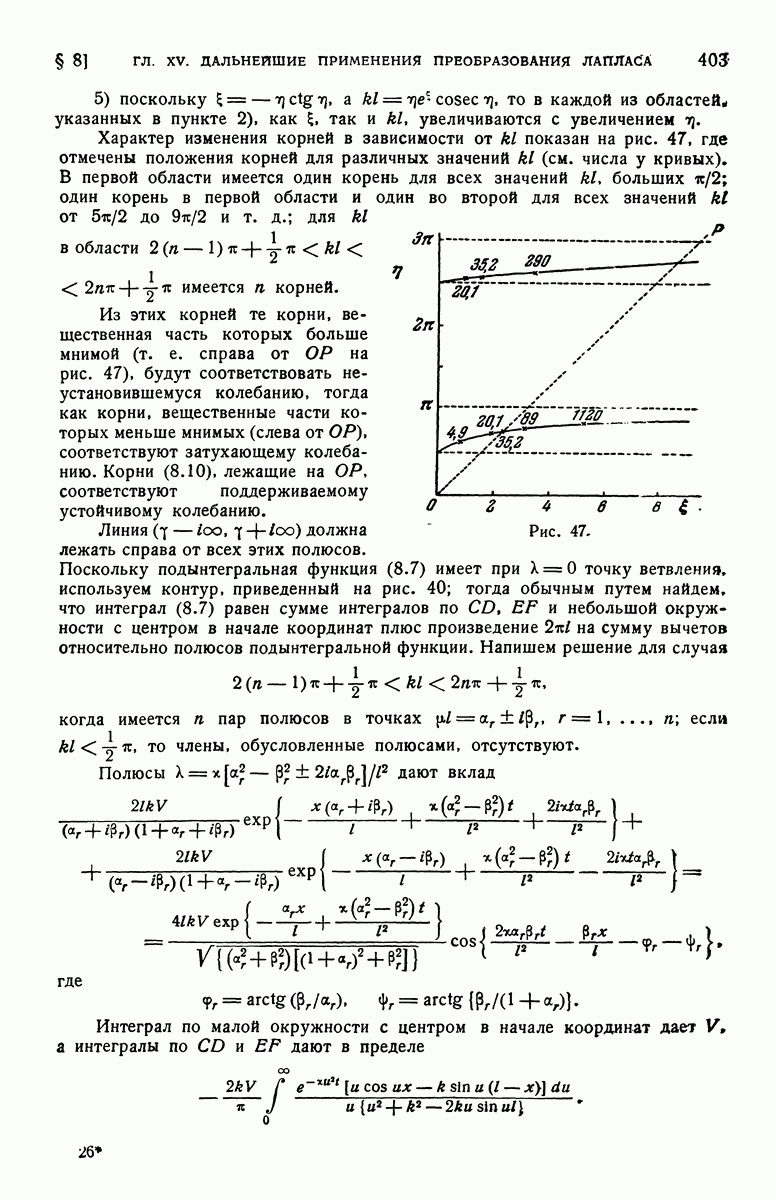
График зависимости V от  для различных значений а изображен на рис. 45.
для различных значений а изображен на рис. 45.
II. Та же задача, но цилиндр имеет нулевую начальную температуру и при  в него поступает количество тепла, равное в единицу времени на единицу длины величине
в него поступает количество тепла, равное в единицу времени на единицу длины величине 
Тогда

где  определены соответственно выражениями (7.2) и (7.4). При нахождении решения (7.7) из (7.6) следует использовать метод, приводящий к решению (5.17) данной главы.
определены соответственно выражениями (7.2) и (7.4). При нахождении решения (7.7) из (7.6) следует использовать метод, приводящий к решению (5.17) данной главы.

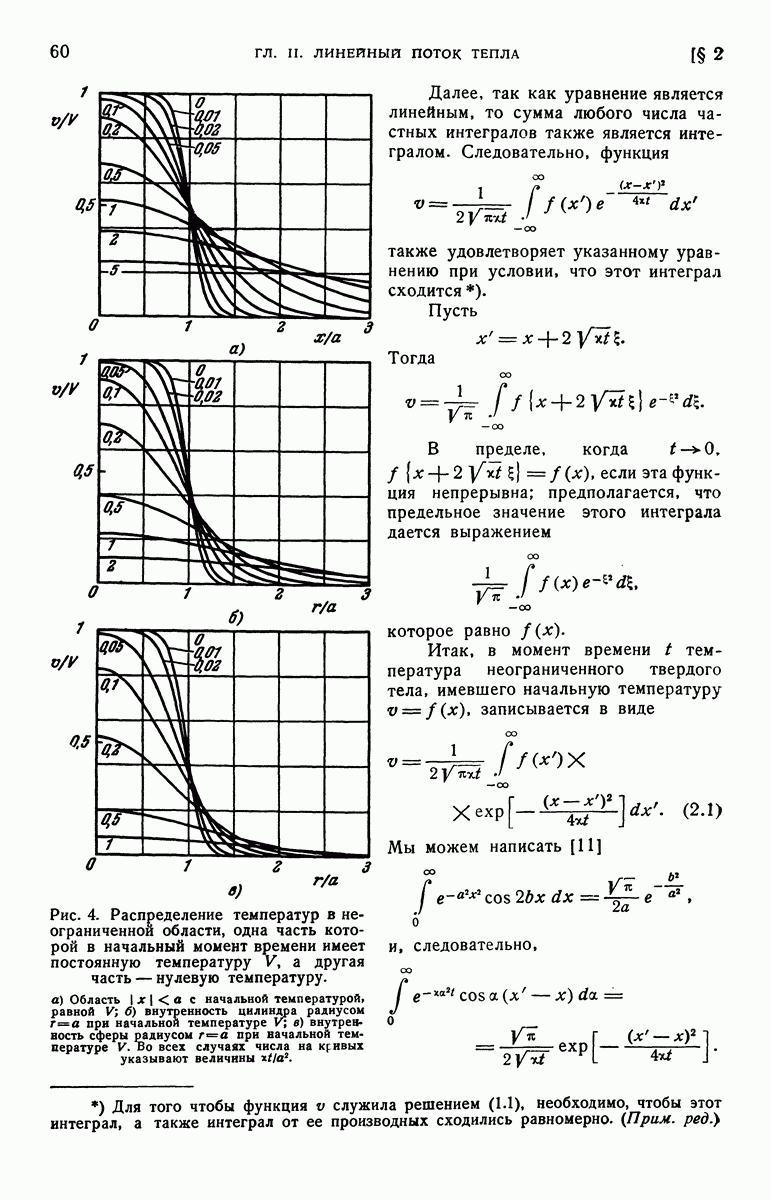
Рис. 45. Распределение температуры в цилиндре из идеального проводника; в начальный момент времени его температура равна  ; температура неограниченной среды, в которой он находится, равна нулю. Числа у кривых указывают значения параметра а.
; температура неограниченной среды, в которой он находится, равна нулю. Числа у кривых указывают значения параметра а.
Температура V в цилиндре, представляющая собой значение (7.7) при  равна
равна

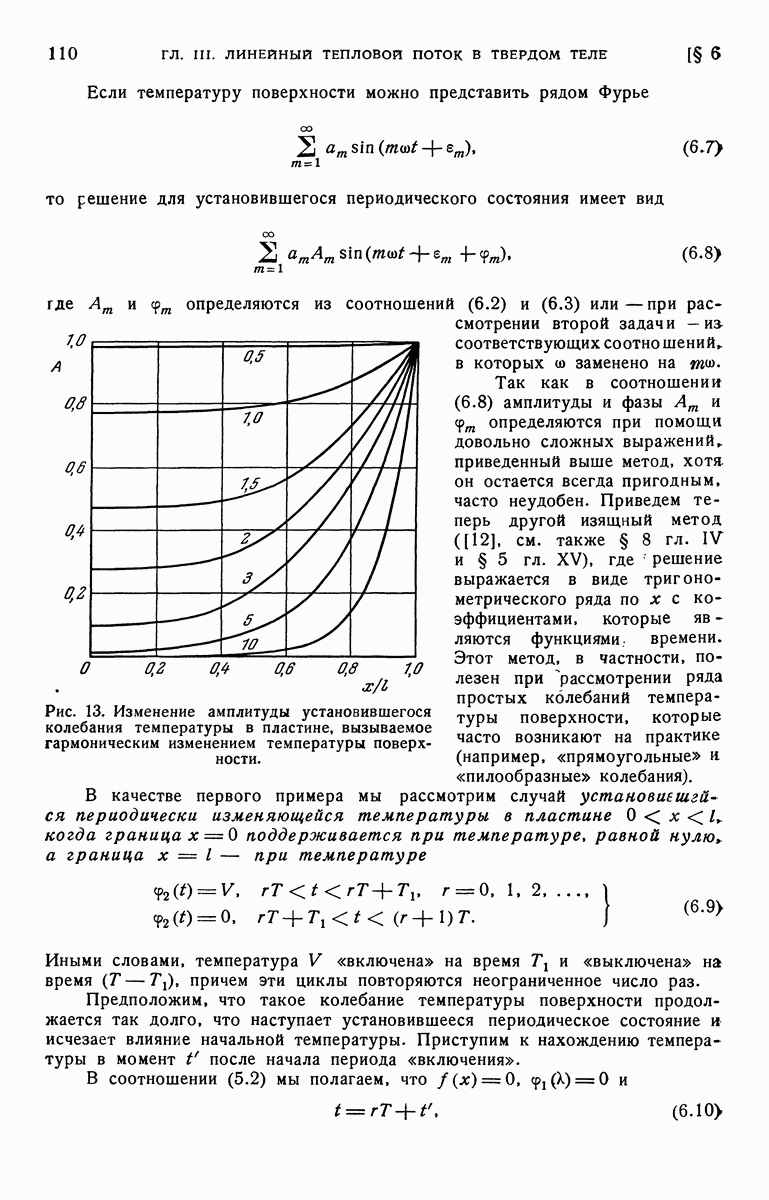
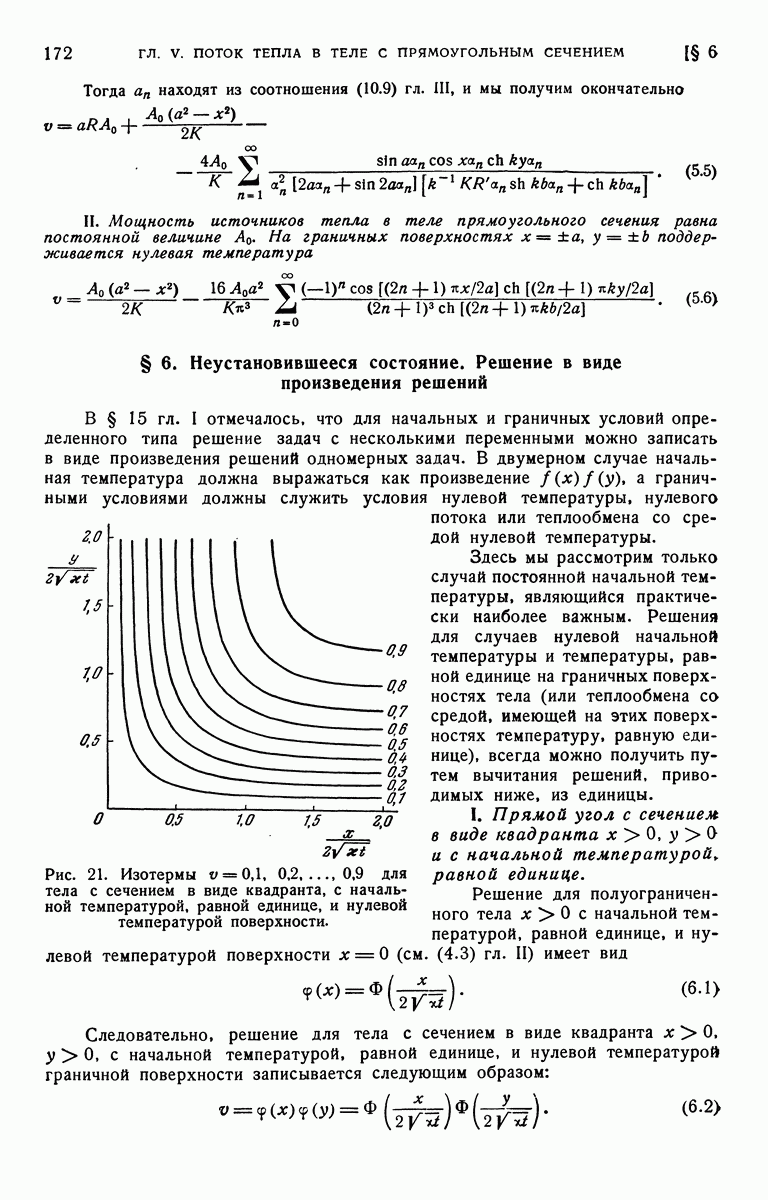
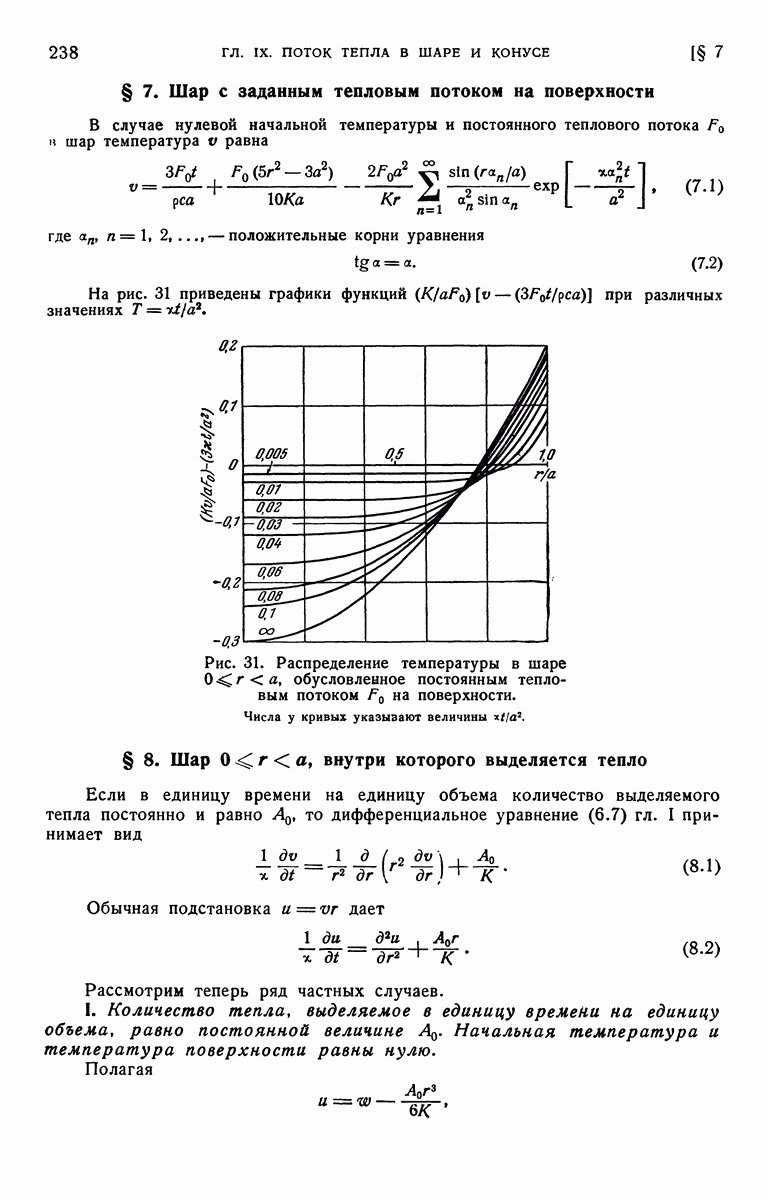
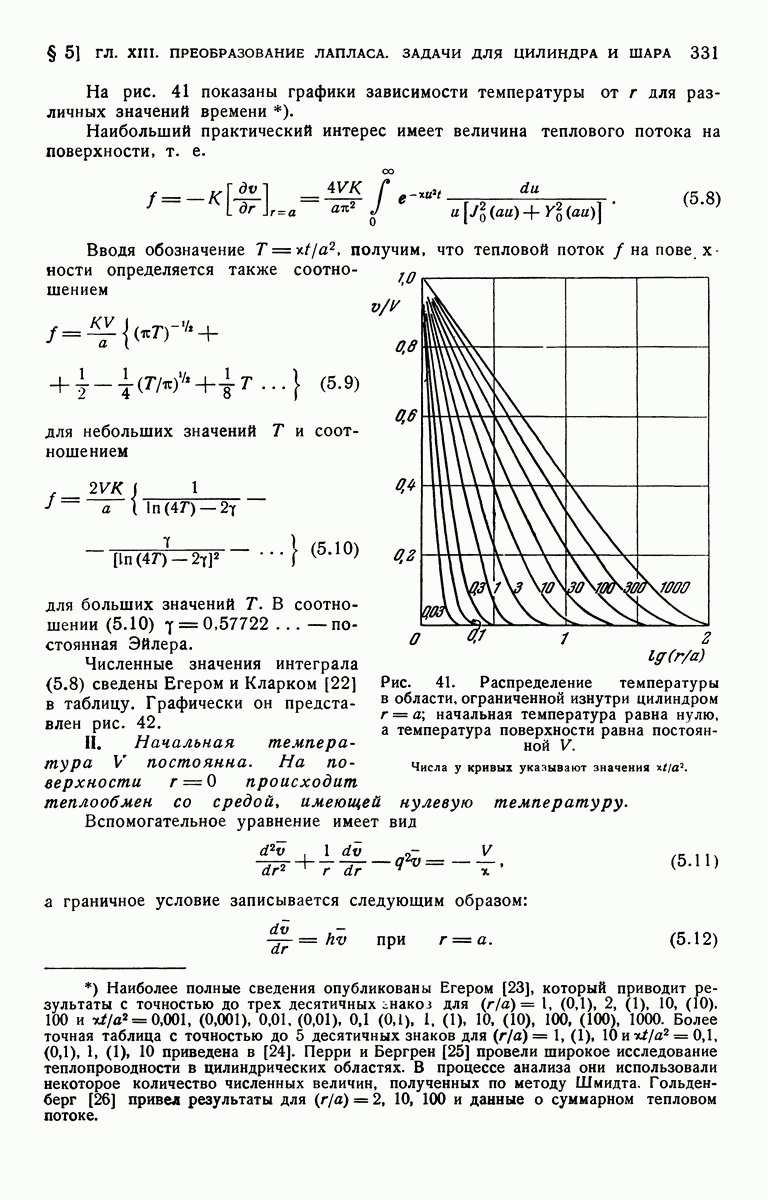
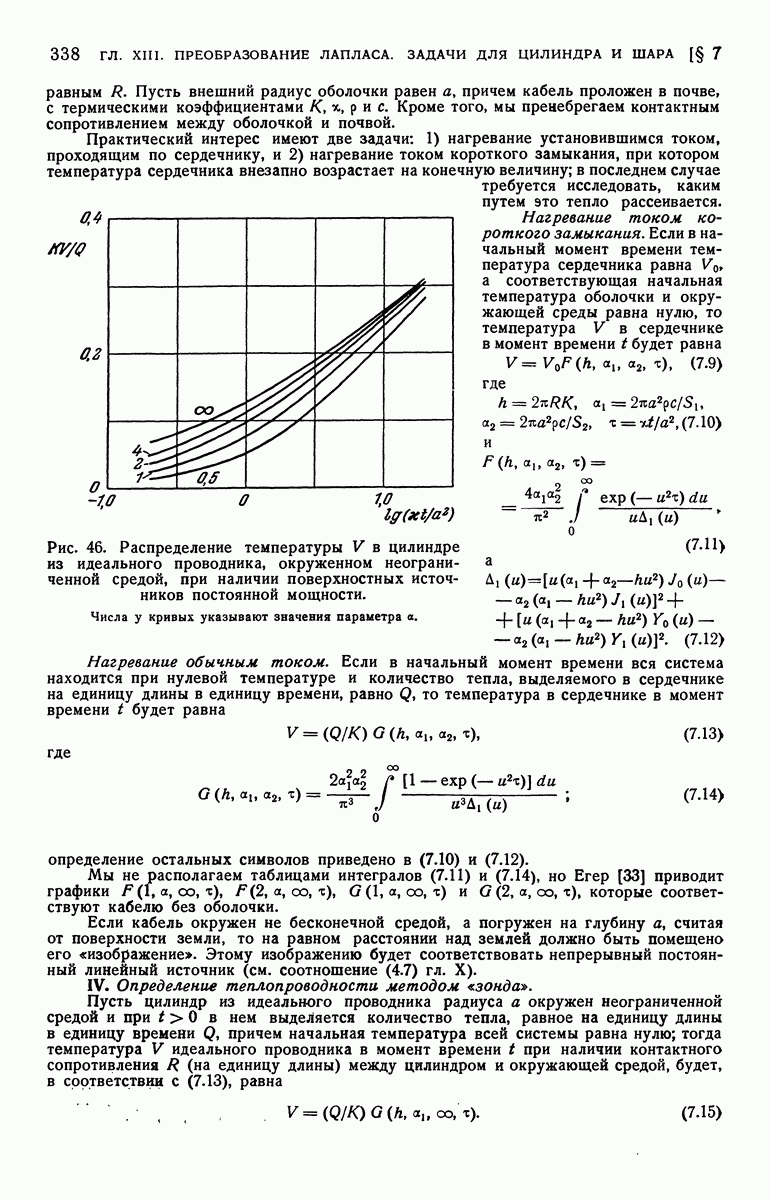
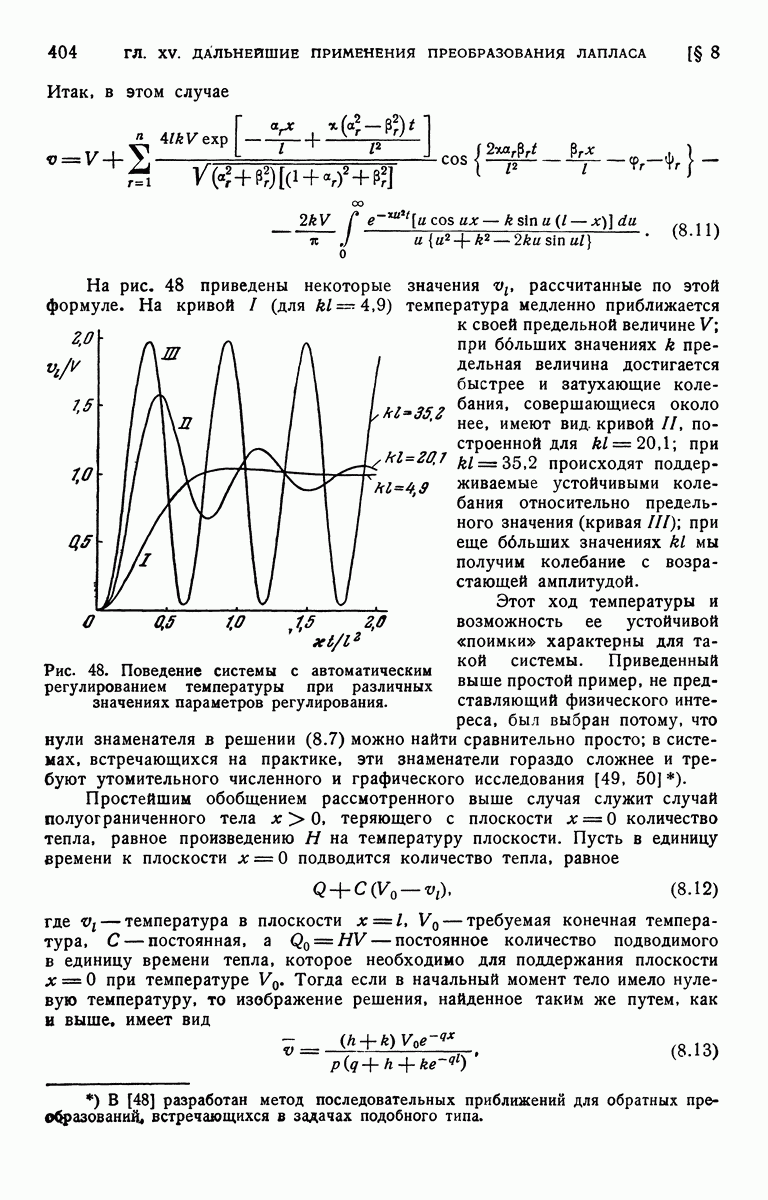
На рис. 46 построен график зависимости V от  для различных значений а.
для различных значений а.
III. Нагревание электрического кабеля, проложенного в земле.
Электрический кабель состоит из трех основных частей: сердечника, по которому течет ток, изоляции, отделяющей сердечник от защитной металлической оболочки, и этой оболочки. Поэтому в простейшей идеализированной схеме кабеля сердечник и оболочка должны считаться идеальными проводниками с теплоемкостями соответственно  на единицу длины кабеля. Теплоемкость изоляции должна считаться равной нулю, а ее термическое сопротивление на единицу длины кабеля
на единицу длины кабеля. Теплоемкость изоляции должна считаться равной нулю, а ее термическое сопротивление на единицу длины кабеля
равным  Пусть внешний радиус оболочки равен а, причем кабель проложен в почве, с термическими коэффициентами
Пусть внешний радиус оболочки равен а, причем кабель проложен в почве, с термическими коэффициентами  Кроме того, мы пренебрегаем контактным сопротивлением между оболочкой и почвой.
Кроме того, мы пренебрегаем контактным сопротивлением между оболочкой и почвой.
Практический интерес имеют две задачи: 1) нагревание установившимся током, проходящим по сердечнику, и 2) нагревание током короткого замыкания, при котором температура сердечника внезапно возрастает на конечную величину; в последнем случае требуется исследовать, каким путем это тепло рассеивается.

Рис. 46. Распределение температуры V в цилиндре из идеального проводника, окруженном неограниченной средой, при наличии поверхностных источников постоянной мощности.
Числа у кривых указывают значения параметра а.
Нагревание током короткого замыкания. Если в начальный момент времени температура сердечника равна  а соответствующая начальная температура оболочки и окружающей среды равна нулю, то температура V в сердечнике в момент времени
а соответствующая начальная температура оболочки и окружающей среды равна нулю, то температура V в сердечнике в момент времени  будет равна
будет равна

где

и

Нагревание обычным током. Если в начальный момент времени вся система находится при нулевой температуре и количество тепла, выделяемого в сердечнике на единицу длины в единицу времени, равно  то температура в сердечнике в момент времени
то температура в сердечнике в момент времени  будет равна
будет равна

где

определение остальных символов приведено в (7.10) и (7.12).
Мы не располагаем таблицами интегралов (7.11) и (7.14), но Егер [33] приводит графики  которые соответствуют кабелю без оболочки.
которые соответствуют кабелю без оболочки.
Если кабель окружен не бесконечной средой, а погружен на глубину  , считая от поверхности земли, то на равном расстоянии над землей должно быть помещено его «изображение». Этому изображению будет соответствовать непрерывный постоянный линейный источник (см. соотношение (4.7) гл. X).
, считая от поверхности земли, то на равном расстоянии над землей должно быть помещено его «изображение». Этому изображению будет соответствовать непрерывный постоянный линейный источник (см. соотношение (4.7) гл. X).
IV. Определение теплопроводности методом «зонда».
Пусть цилиндр из идеального проводника радиуса а окружен неограниченной средой и при  в нем выделяется количество тепла, равное на единицу длины в единицу времени
в нем выделяется количество тепла, равное на единицу длины в единицу времени  причем начальная температура всей системы равна нулю; тогда температура V идеального проводника в момент времени
причем начальная температура всей системы равна нулю; тогда температура V идеального проводника в момент времени  при наличии контактного сопротивления
при наличии контактного сопротивления  (на единицу длины) между цилиндром и окружающей средой, будет, в соответствии с (7.13), равна
(на единицу длины) между цилиндром и окружающей средой, будет, в соответствии с (7.13), равна

Отсюда, как и в § 3 данной главы, следует, что для небольших значений 

или

Для больших значений времени  (как и в предыдущем параграфе) можем написать
(как и в предыдущем параграфе) можем написать

где  постоянная Эйлера).
постоянная Эйлера).
Из соотношения (7.18) следует, что во всех случаях кривая зависимости V от  имеет прямолинейную асимптоту с угловым коэффициентом, равным
имеет прямолинейную асимптоту с угловым коэффициентом, равным  Поэтому, если известно
Поэтому, если известно  то можно сразу же определить
то можно сразу же определить  Если
Если  то к концу промежутка времени 10 мин
то к концу промежутка времени 10 мин  будет равняться 600, и следовательно, в этом случае быстро получается асимптота. Вместе с тем, если
будет равняться 600, и следовательно, в этом случае быстро получается асимптота. Вместе с тем, если  то
то  равно 6 и время, необходимое для достижения асимптотического значения, оказывается существенно большим.
равно 6 и время, необходимое для достижения асимптотического значения, оказывается существенно большим.
Методы зонда [38—41] очень удобны при измерении теплопроводности гранулированных материалов, почв и горных пород. В последнем случае зонд следует помещать в отверстие, просверленное в горной породе, и поэтому можно ожидать, что его радиус должен иметь порядок 1 см, и ввиду наличия воздушного зазора между зондом и породой термическое сопротивление окажется довольно значительным. Блэкуэлл [29, 42] подробно рассмотрел этот случай и указал на то, что, воспользовавшись соотношениями (7.16) и (7.18), можно из экспериментальных данных определить все три параметра 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- ГЛАВА I. ОБЩАЯ ТЕОРИЯ
- § 2. Теплопроводность
- § 3. Тепловой поток через произвольную поверхность
- § 4. Изотермические поверхности
- § 5. Теплопроводность изотропных тел
- § 6. Дифференциальное уравнение теплопроводности для изотропного твердого тела
- § 7. Дифференциальное уравнение теплопроводности для движущейся среды
- § 8. Преобразование координат
- § 9. Начальные и граничные условия
- § 10. Безразмерные параметры
- § 11. Экспериментальные методы определения теплопроводности
- § 12. Математическая интерпретация начальных и граничных условий
- § 13. Родственные дифференциальные уравнения
- § 14. Упрощение общей задачи теплопроводности
- § 15. Задачи, решения которых можно выразить в виде произведения решений более простых задач
- § 16. Единственность решения задачи теплопроводности
- § 17. Теплопроводность анизотропных твердых тел
- § 18. Дифференциальное уравнение теплопроводности для анизотропных твердых тел
- § 19. Теплопроводность тонкой кристаллической пластины
- § 20. Изменение теплопроводности и вектор теплового потока в анизотропных твердых телах
- ГЛАВА II. ЛИНЕЙНЫЙ ПОТОК ТЕПЛА. НЕОГРАНИЧЕННОЕ И ПОЛУОГРАНИЧЕННОЕ ТВЕРДОЕ ТЕЛО
- § 2. Неограниченное твердое тело. Решение Лапласа
- § 3. Использование интегралов Фурье и преобразований Фурье
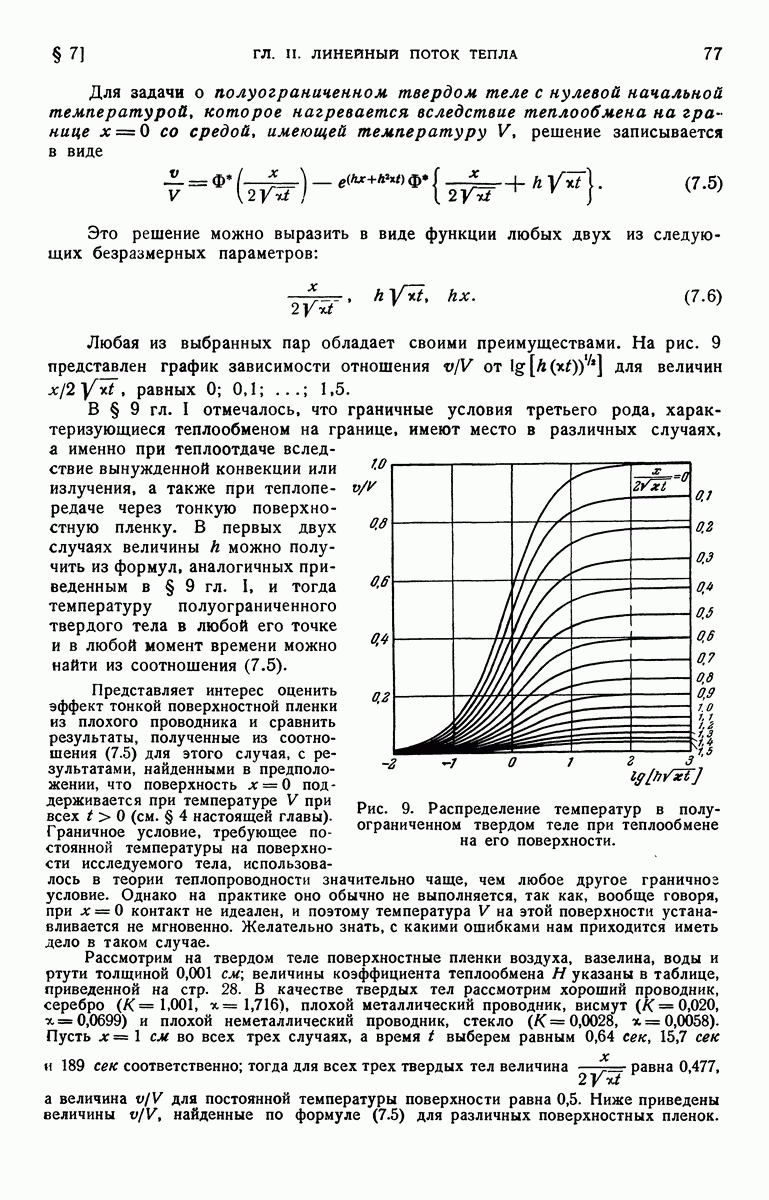
- § 4. Полуограниченное тело с начальной температурой f(x) и нулевой температурой поверхности
- § 5. Полуограниченное твердое тело. Начальная температура равна нулю. Поверхность находится при температуре …
- § 6. Полуограниченное твердое тело. Температура поверхности является гармонической функцией времени
- § 7. Полуограниченное твердое тело. Теплообмен на поверхности в среду с нулевой температурой. Начальная температура постоянна
- § 8. Полуограниченное твердое тело. Теплообмен на поверхности в среду с температурой f(t). Начальная температура равна нулю
- § 9. Полуограниченное тело. Тепловой поток на границе х = 0 является заданной функцией времени. Начальная температура равна нулю
- § 10. Применение полученных результатов к определению теплопроводности
- § 11. Полуограниченное твердое тело, внутри которого находится источник тепла
- § 12. Температура Земли и колебания температуры на ее поверхности
- § 13. Геотермический градиент и поток тепла
- § 14. Возраст Земли. Анализ Кельвина
- § 15. Неограниченное составное твердое тело
- § 16. Случай зависимости термических характеристик вещества от температуры
- ГЛАВА III. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В ТВЕРДОМ ТЕЛЕ, ОГРАНИЧЕННОМ ДВУМЯ ПАРАЛЛЕЛЬНЫМИ ПЛОСКОСТЯМИ
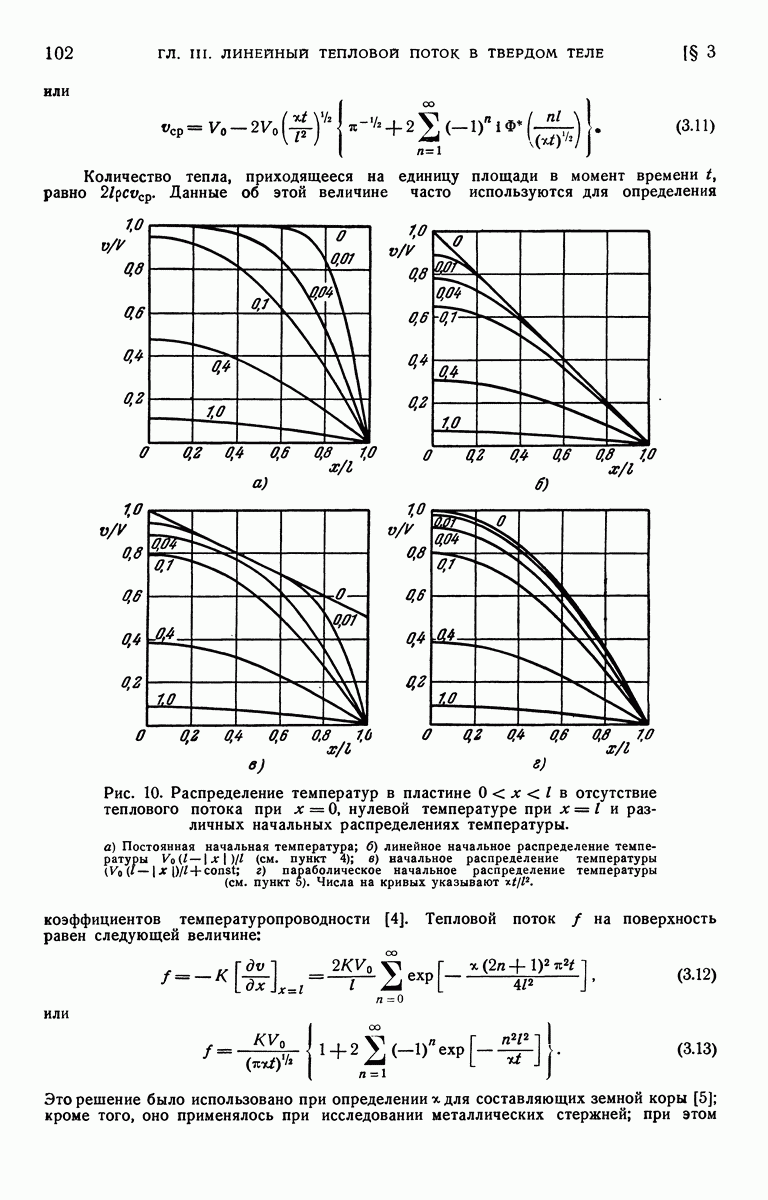
- § 3. Область [0, l]. Границы поддерживаются при нулевой температуре. Начальная температура f(x)
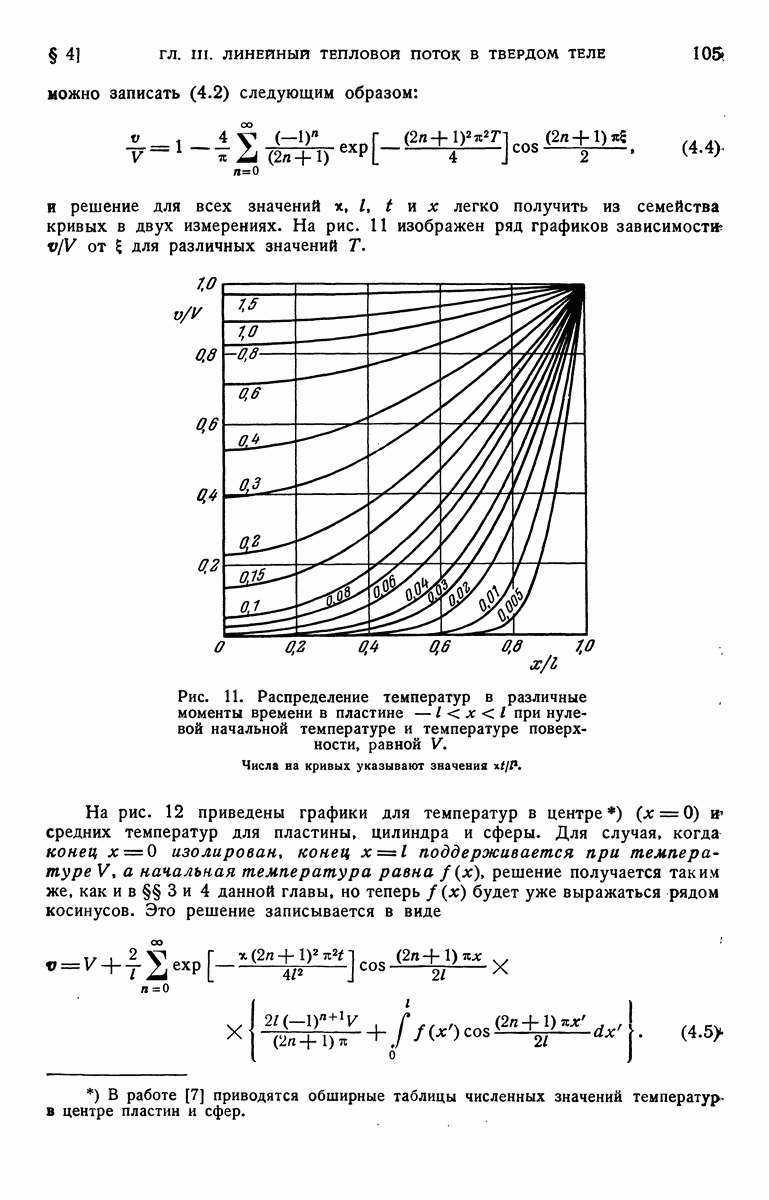
- § 4. Область [0, l] Начальная температура f(x). Границы поддерживаются при постоянной температуре или изолированы
- § 5. Область [0, l]. Температуры границ равны … Начальная температура f(x)
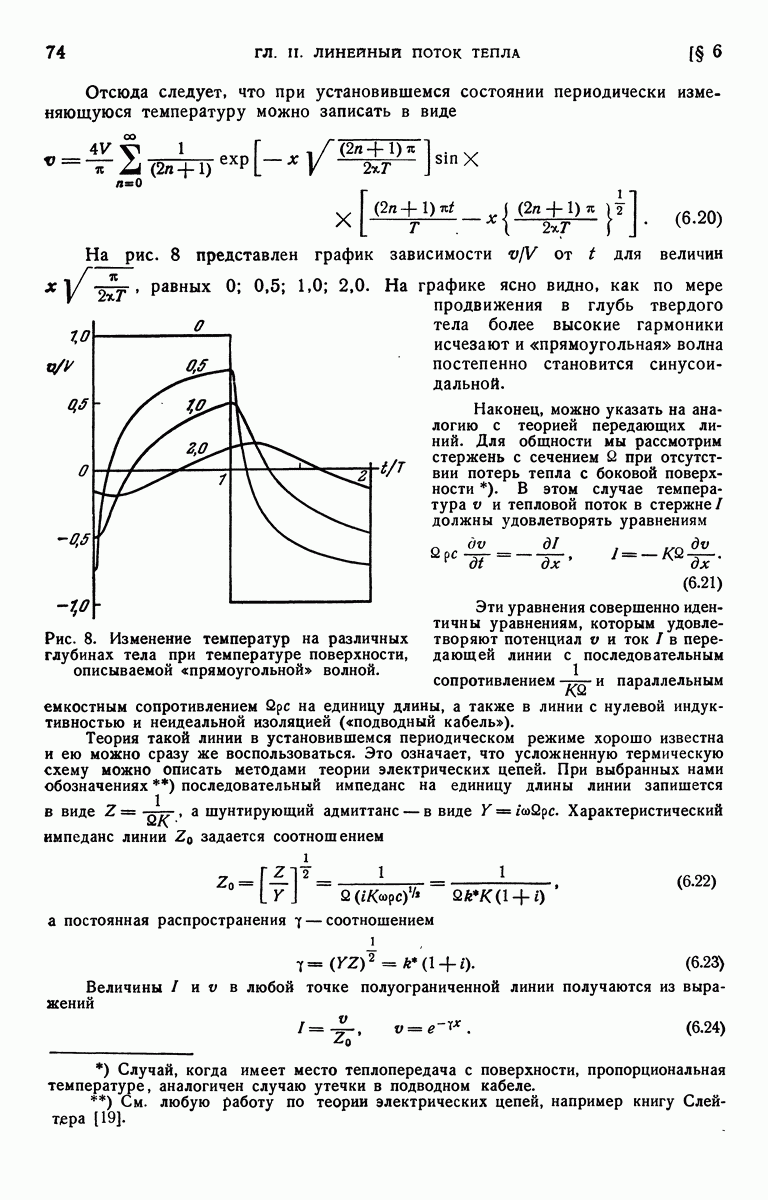
- § 6. Пластина с периодически изменяющейся температурой поверхности
- § 7. Установившаяся периодически изменяющаяся температура в составных пластинах
- § 8. Пластина с заданным тепловым потоком на ее границе
- § 9. Область [0, l]. Теплообмен на границах в среду с температурой, равной нулю. Начальная температура равна f(х)
- § 10. Область [-l, l]. На границах х=+l происходит теплообмен со средой нулевой температуры. Начальная температура f(x)
- § 11. Частные случаи и численные результаты для пластины с граничным условием третьего рода
- § 12. Область [-l, l] с нулевой начальной температурой и теплообменом на границах со средой, имеющей температуру …
- § 13. Пластина, одна из поверхностей которой соприкасается со слоем идеального проводника или хорошо перемешиваемой жидкости
- § 14. Пластина с внутренним источником тепла
- ГЛАВА IV. ЛИНЕЙНЫЙ ТЕПЛОВОЙ ПОТОК В СТЕРЖНЕ
- § 3. Полуограниченный стержень. Случай установившейся температуры. Метод Форбса
- § 4. Полуограниченный стержень. Периодически изменяющаяся температура. Метод Ангстрема [5—10]
- § 5. Ограниченный стержень, концы которого находятся при фиксированных температурах. Случай установившейся температуры
- § 6. Стержень переменного сечения с охлаждающимися ребрами. Случай установившейся температуры
- § 7. Ограниченный стержень при наличии теплообмена на его поверхности. Случай неустановившейся температуры
- § 8. Ограниченный стержень с периодически изменяющейся температурой концов. Метод Неймана
- § 9. Задачи по теплопроводности в движущемся стержне
- § 10. Уравнение теплопроводности для тонкой проволоки, нагреваемой постоянным электрическим током
- § 11. Установившаяся температура. Определение коэффициента теплопроводности
- § 12. Сильно нагретая проволока, по которой протекает электрический ток
- § 13. Установившийся поток тепла в составной проволоке
- § 14. Неустановившаяся температура в проволоке, по которой течет электрический ток
- § 15. Кольцо Фурье
- ГЛАВА V. ПОТОК ТЕПЛА В ТЕЛЕ С ПРЯМОУГОЛЬНЫМ СЕЧЕНИЕМ
- § 2. Неограниченное твердое тело прямоугольного сечения. Установившаяся температура
- § 3. Установившаяся температура в неограниченном теле прямоугольного сечения
- § 4. Тонкая пластина с прямоугольным сечением при наличии теплообмена на ее поверхности
- § 5. Установившаяся температура в теле прямоугольного сечения при наличии источника тепла
- § 6. Неустановившееся состояние. Решение в виде произведения решений
- § 7. Неустановившееся состояние. Произвольные начальные и граничные условия
- ГЛАВА VI. ТЕПЛОВОЙ ПОТОК В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ
- § 2. Установившаяся температура
- § 3. Двойные и кратные ряды Фурье
- § 4. Неустановившаяся температура. Решение в виде произведения решений
- § 5. Определение коэффициента теплопроводности и экстраполяция кривых охлаждения
- § 6. Неустановившаяся температура. Тройной ряд Фурье
- ГЛАВА VII. ТЕПЛОВОЙ ПОТОК В НЕОГРАНИЧЕННОМ ЦИЛИНДРЕ КРУГОВОГО СЕЧЕНИЯ
- § 2. Установившаяся температура. Радиальный поток
- § 3. Установившаяся, периодически изменяющаяся температура в круговых цилиндрах [19—22]
- § 4. Неограниченный цилиндр. Радиальный поток. Неустановившаяся температура
- § 5. Интегралы …
- § 6. Неограниченный цилиндр с температурой поверхности … и начальной температурой f(r)
- § 7. Неограниченный цилиндр с теплообменом на поверхности
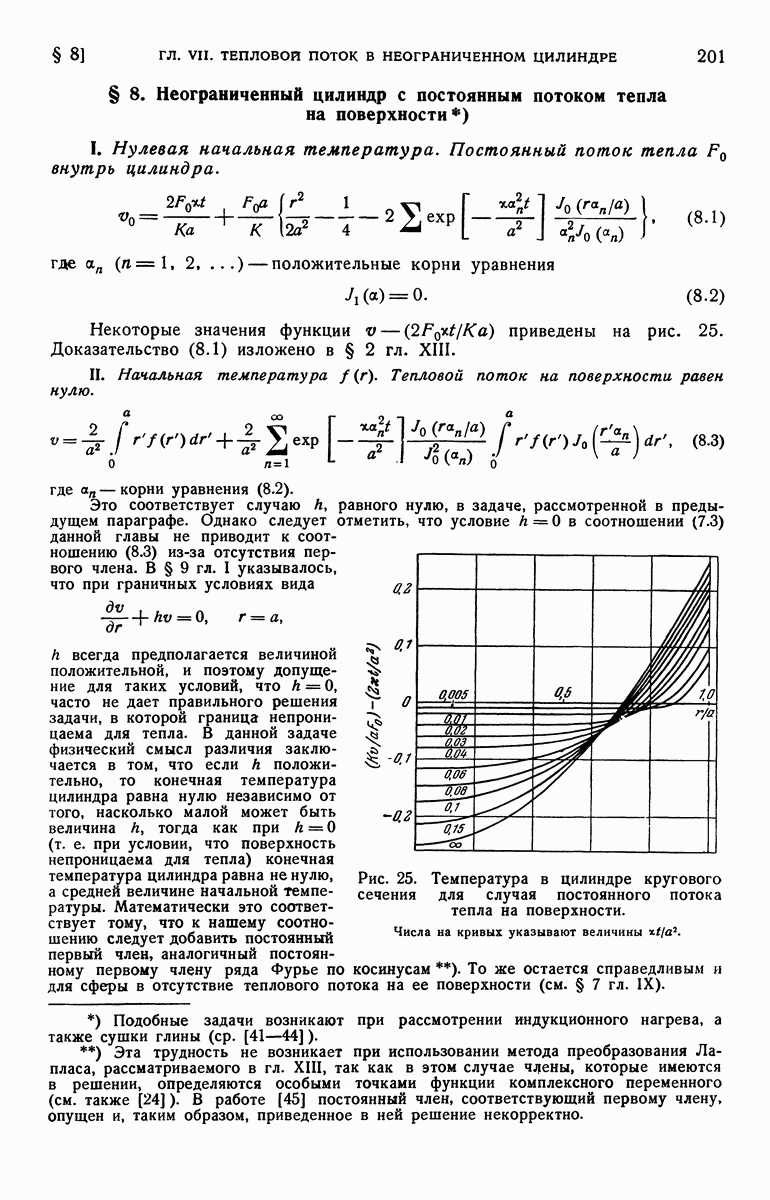
- § 8. Неограниченный цилиндр с постоянным потоком тепла на поверхности
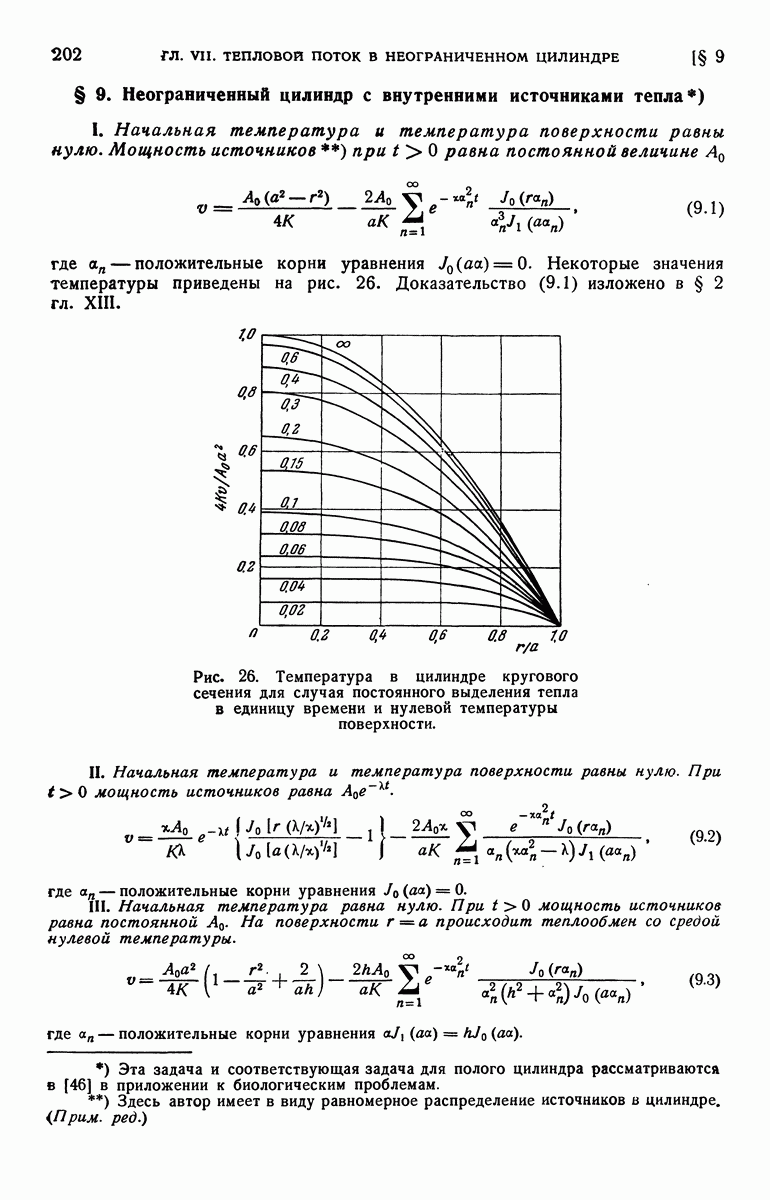
- § 9. Неограниченный цилиндр с внутренними источниками тепла
- § 10. Неограниченный полый цилиндр. Радиальный поток
- § 11. Неограниченный цилиндр. Установившаяся температура. Общий случай
- § 12. Неограниченный цилиндр. Неустановившаяся температура. Общий случай
- ГЛАВА VIII. ТЕПЛОВОЙ ПОТОК В ОБЛАСТЯХ, ОГРАНИЧЕННЫХ КООРДИНАТНЫМИ ПОВЕРХНОСТЯМИ ЦИЛИНДРИЧЕСКОЙ СИСТЕМЫ КООРДИНАТ
- § 3. Установившаяся температура в ограниченном и полуограниченном цилиндрах
- § 4. Неустановившееся состояние. Решения в форме произведений
- § 5. Определение теплопроводности вещества в форме цилиндра
- § 6. Ограниченный цилиндр с начальной температурой …
- § 7. Полуограниченный цилиндр
- ГЛАВА IX. ПОТОК ТЕПЛА В ШАРЕ И КОНУСЕ
- § 2. Установившаяся температура. Радиальный тепловой поток
- § 3. Шар с начальной температурой f(r) и температурой поверхности …
- § 4. Шар. Начальная температура f(r). На поверхности сферы происходит теплообмен
- § 5. Определение коэффициентов теплопроводности плохих проводников
- § 6. Случай шара, находящегося в контакте с хорошо перемешиваемой жидкостью
- § 7. Шар с заданным тепловым потоком на поверхности
- § 8. Шар, внутри которого выделяется тепло
- § 9. Полый шар
- § 10. Область, ограниченная изнутри сферической поверхностью r=a
- § 11. Шар с начальной температурой … Температура поверхности r=a равна нулю
- § 12. Поверхность шара r=a поддерживается при температуре …
- § 13. Часть шара, вырезаемая конусом … Температура поверхности равна нулю, начальная температура равна …
- § 14. Температура внутри Земли
- ГЛАВА Х. ПРИМЕНЕНИЕ МЕТОДА ИСТОЧНИКОВ И СТОКОВ К ЗАДАЧАМ С НЕУСТАНОВИВШЕЙСЯ ТЕМПЕРАТУРОЙ
- § 2. Мгновенный точечный источник
- § 3. Мгновенные источники; линейный, плоский и поверхностные цилиндрический и сферический источники
- § 4. Непрерывные и периодические источники
- § 5. Поверхностный нагрев полуограниченной области
- § 6. Выделение тепла в неограниченной среде
- § 7. Движущиеся источники тепла
- § 8. Дублеты
- § 9. Метод последовательных волн
- § 10. Метод изображений. Линейный тепловой поток
- § 11. Применение метода изображений к двумерным и трехмерным задачам
- § 12. Обобщение метода изображений Зоммерфельдом
- ГЛАВА XI. ИЗМЕНЕНИЕ ФИЗИЧЕСКОГО СОСТОЯНИЯ
- § 2. Одномерные случаи плавления и затвердевания. Решение Неймана и его обобщение
- § 3. Область … при других граничных условиях
- § 4. Методы интегрального уравнения. Рассмотрение задач затвердевания, предложенное Лайтфутом
- § 5. Решения в цилиндрических и сферических координатах
- § 6. Осесимметричные задачи о замерзании и плавлении
- ГЛАВА XII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЛИНЕЙНОГО ТЕПЛОВОГО ПОТОКА
- § 2. Преобразование Лапласа. Основные свойства
- § 3. Решение уравнения теплопроводности методом преобразования Лапласа
- § 4. Полуограниченная область. Решения, получаемые из таблицы изображений
- § 5. Ограниченная область (0, l). Решения, получаемые из таблицы изображений. Решения для небольших значений времени
- § 6. Ограниченная область (0, l). Применение теоремы обращения
- § 7. Полуограниченная область. Применение теоремы обращения
- § 8. Составные твердые тела
- ГЛАВА XIII. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА. ЗАДАЧИ ДЛЯ ЦИЛИНДРА И ШАРА
- § 3. Решения, применимые для малых интервалов времени
- § 4. Полый цилиндр
- § 5. Область ограничена изнутри цилиндром кругового сечения r=a
- § 6. Решения, применимые при больших значениях времени
- § 7. Область, ограниченная изнутри круговым цилиндром из идеального проводника
- § 8. Составная цилиндрическая область
- § 9. Шар. Радиальный тепловой поток
- ГЛАВА XIV. ПРИМЕНЕНИЕ ФУНКЦИЙ ГРИНА К РЕШЕНИЮ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 2. Линейный тепловой поток. Полуограниченное твердое тело
- § 3. Линейный тепловой поток в области (0, a)
- § 4. Двумерные задачи. Тела с прямоугольным сечением
- § 5. Прямоугольный параллелепипед
- § 6. Линейный тепловой поток. Составные твердые тела
- § 7. Шар. Радиальный поток тепла
- § 8. Цилиндр. Радиальный тепловой поток
- § 9. Полуограниченное твердое тело. Трехмерные задачи
- § 10. Область, ограниченная двумя параллельными плоскостями
- § 11. Полуограниченное твердое тело с тонкой пленкой на плоскости z=0 из материала, имеющего значительно большую теплопроводность. В точке … расположен единичный мгновенный источник
- § 12. Неограниченное составное твердое тело. В точке действует мгновенный единичный источник
- § 13. Области, ограниченные цилиндрической поверхностью r=a
- § 14 Клин
- § 15. Цилиндрическая область
- § 16. Области, ограниченные сферической поверхностью r=a
- § 17. Конус
- § 18. Непрерывные источники
- ГЛАВА XV. ДАЛЬНЕЙШИЕ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
- § 3. Тепловые регенераторы и теплообменники
- § 4. Тепловой поток в слоистых системах
- § 5. Установившийся периодический режим
- § 6. Линейная асимптотика и запаздывание
- § 7. Выделение тепла
- § 8. Система автоматического регулирования температуры
- § 9. Неоднородные тела
- § 11. Прямое применение метода преобразования Лапласа к двумерным и трехмерным задачам
- ГЛАВА XVI. УСТАНОВИВШАЯСЯ ТЕМПЕРАТУРА
- § 2. Источники и стоки при установившейся температуре
- § 3. Установившийся поток к почти плоской поверхности. Топографические поправки для геотермического потока
- § 4. Установившийся тепловой поток в составном теле
- § 5. Практические задачи
- § 6. Использование сопряженных гармонических функций в задачах с установившейся температурой
- § 7. Приложения этого метода [20, 21]
- § 8. Установившийся тепловой поток в многоугольнике
- § 9. Тепловой поток между изотермическими поверхностями
- ГЛАВА XVII. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
- § 2. Интегральные преобразования и формулы их обращения
- § 3. Неустановившийся тепловой поток
- § 4. Установившийся тепловой поток
- § 5. Конечные преобразования
- § 6. Последовательные преобразования
- ГЛАВА XVIII. ЧИСЛЕННЫЕ МЕТОДЫ
- § 3. Линейный тепловой поток в неограниченном пространстве
- § 4. Граничные условия
- § 5. Выделение тепла, переменная температуропроводность и скрытая теплота
- § 6. Релаксационные методы
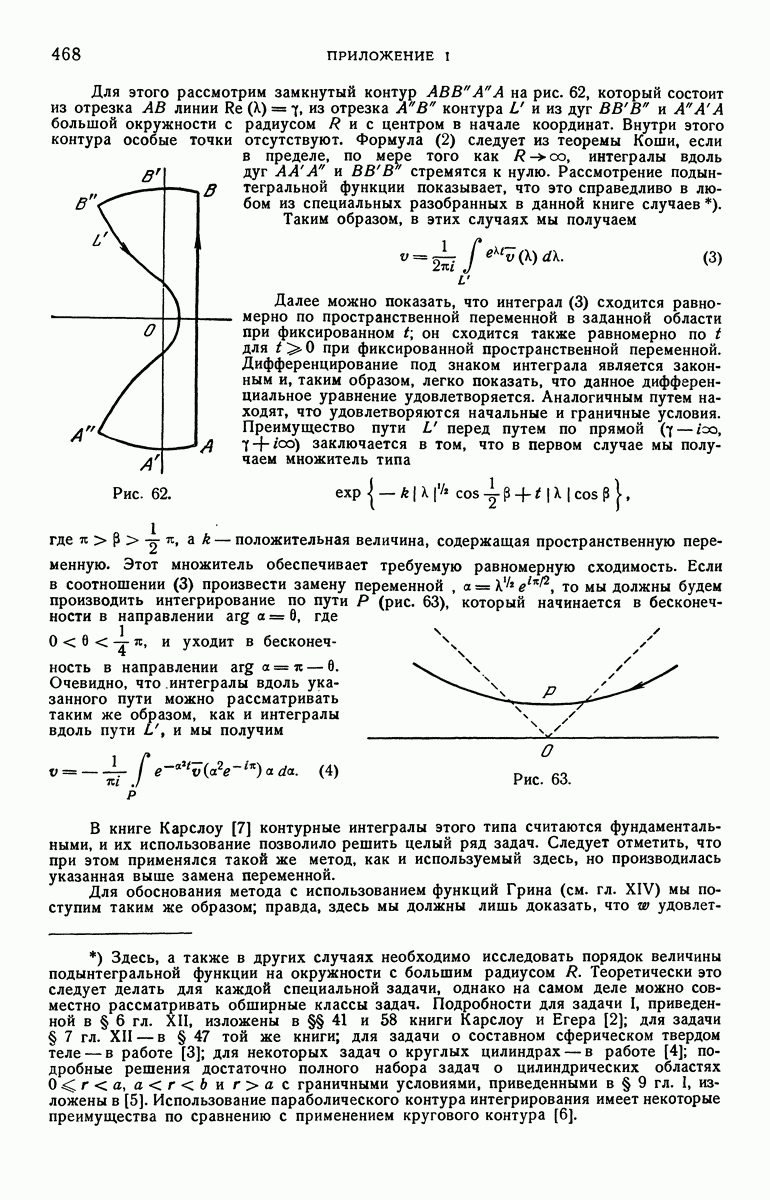
- ПРИЛОЖЕНИЕ 1. КОНТУРНЫЕ ИНТЕГРАЛЫ И ПРОВЕРКА РЕШЕНИЙ, ПОЛУЧЕННЫХ ПРИ ПОМОЩИ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
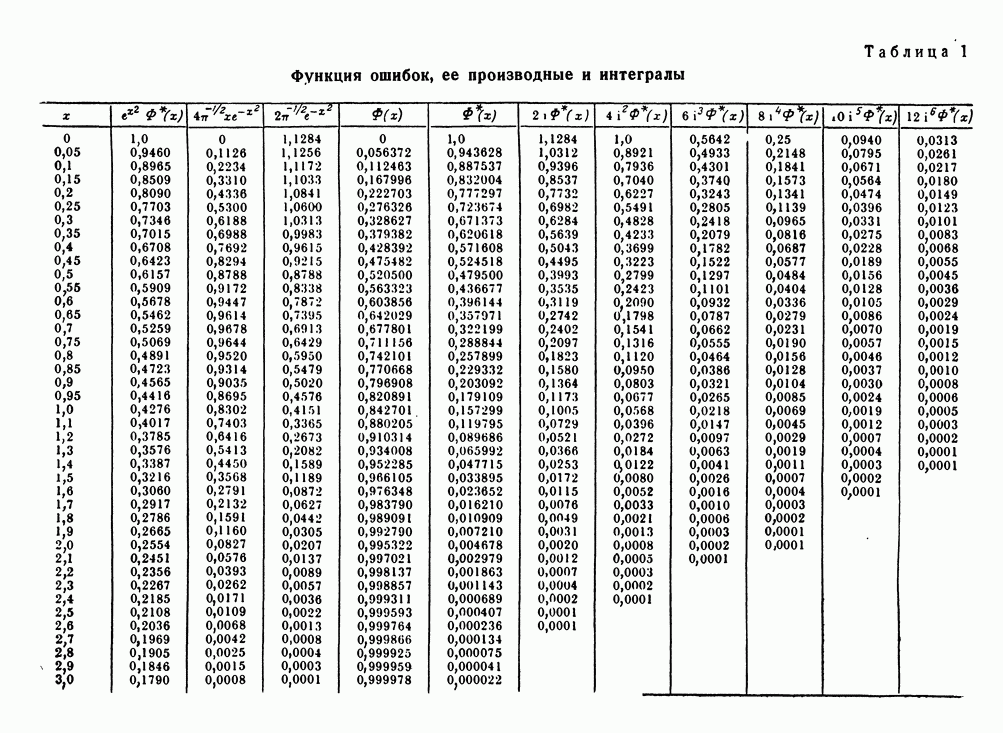
- ПРИЛОЖЕНИЕ 2. ФУНКЦИЯ ОШИБОК И РОДСТВЕННЫЕ ФУНКЦИИ
- ПРИЛОЖЕНИЕ 3. О ФУНКЦИЯХ БЕССЕЛЯ
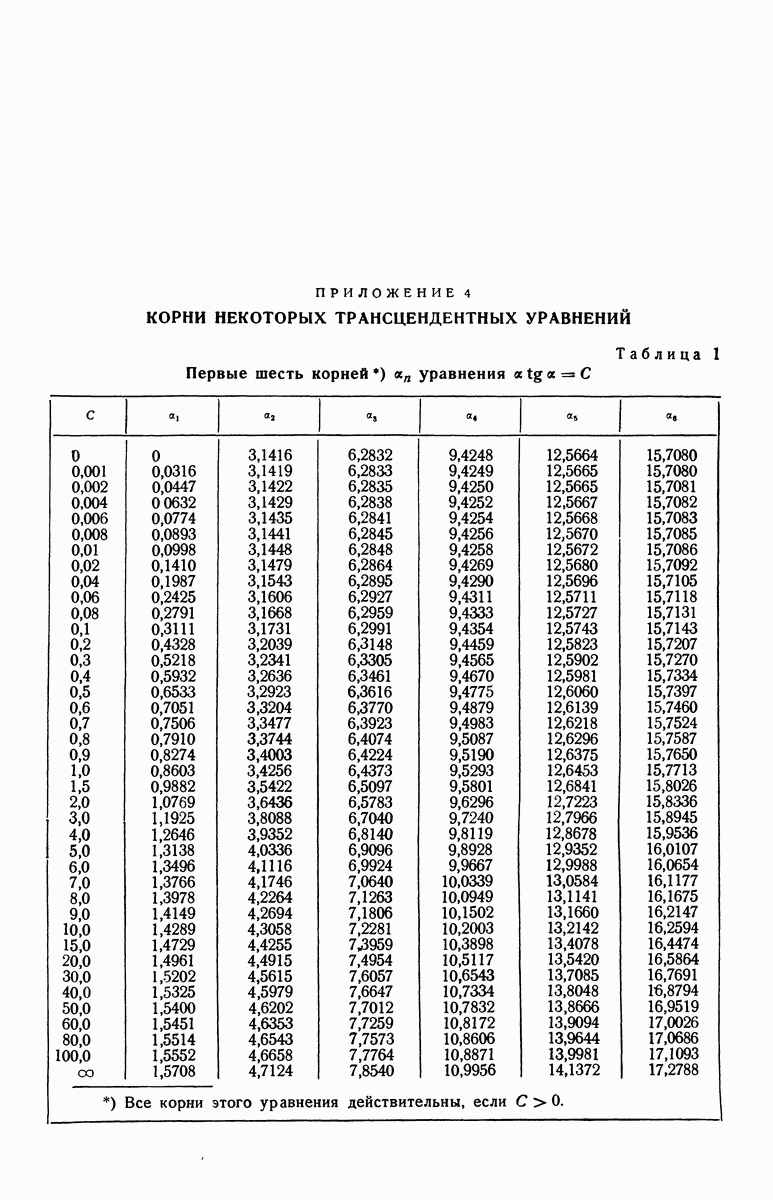
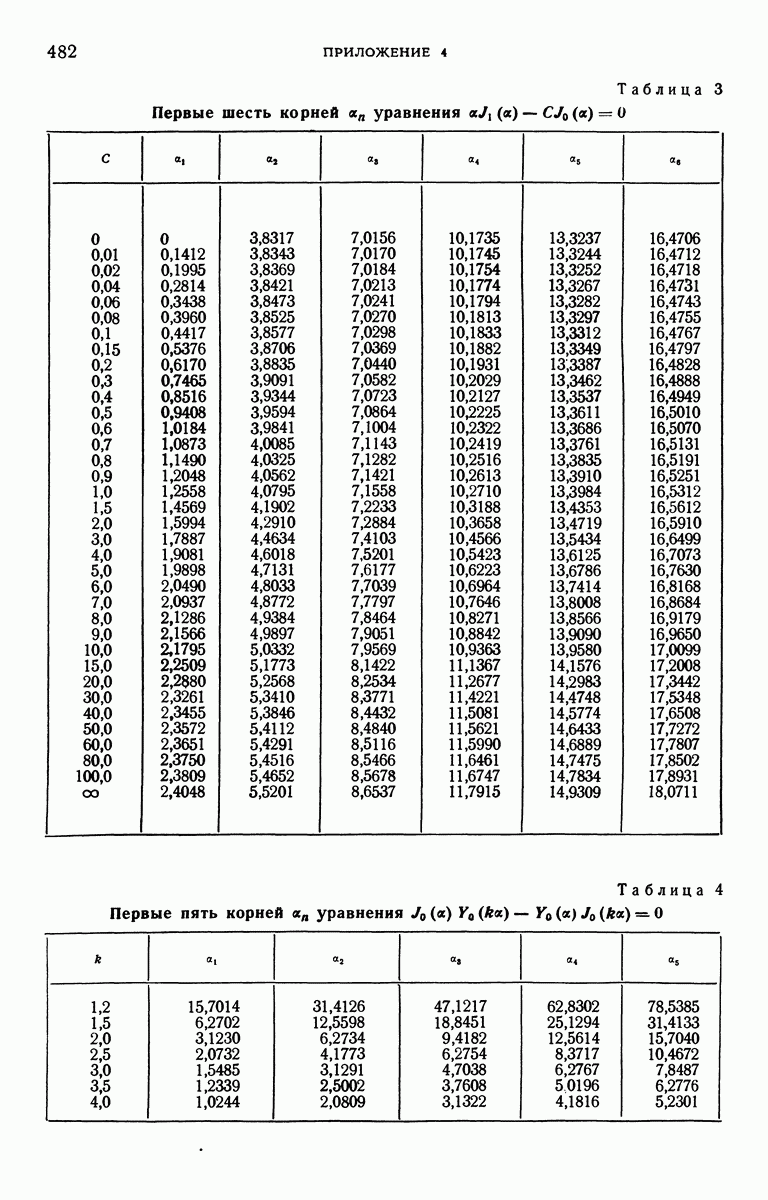
- ПРИЛОЖЕНИЕ 4. КОРНИ НЕКОТОРЫХ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
- ПРИЛОЖЕНИЕ 5. ТАБЛИЦА ПРЕОБРАЗОВАНИЙ ЛАПЛАСА …
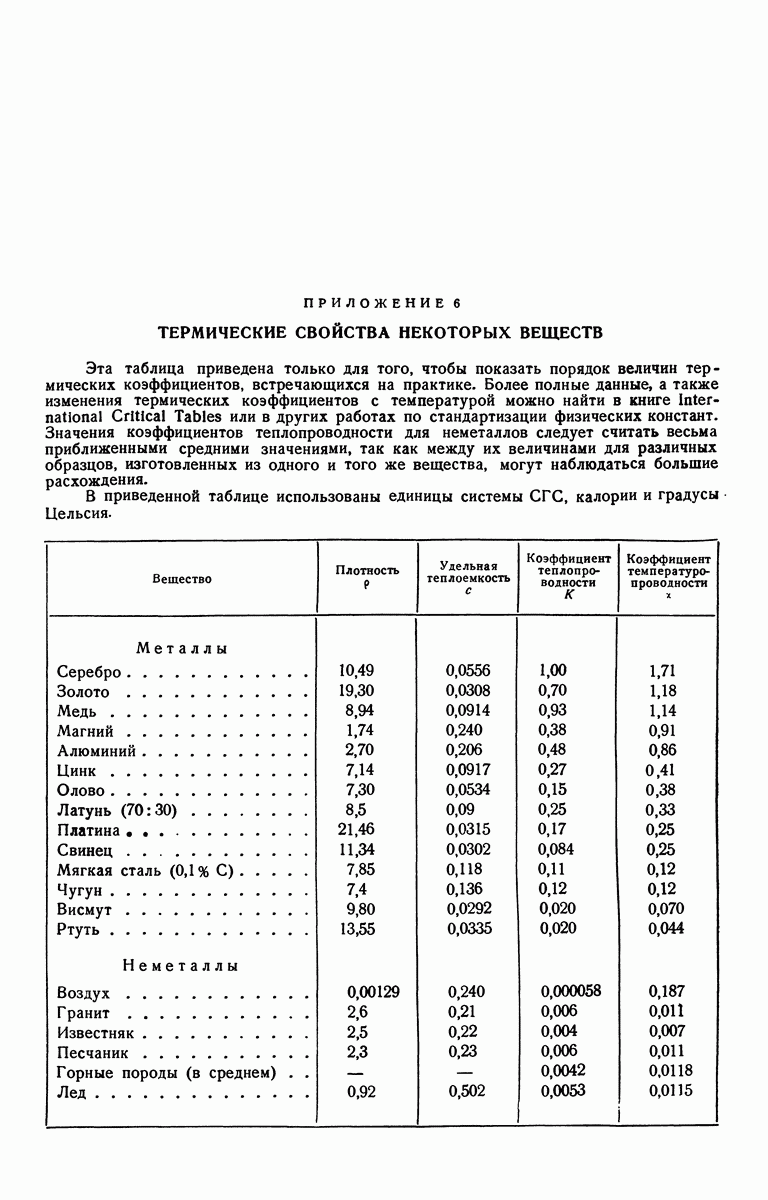
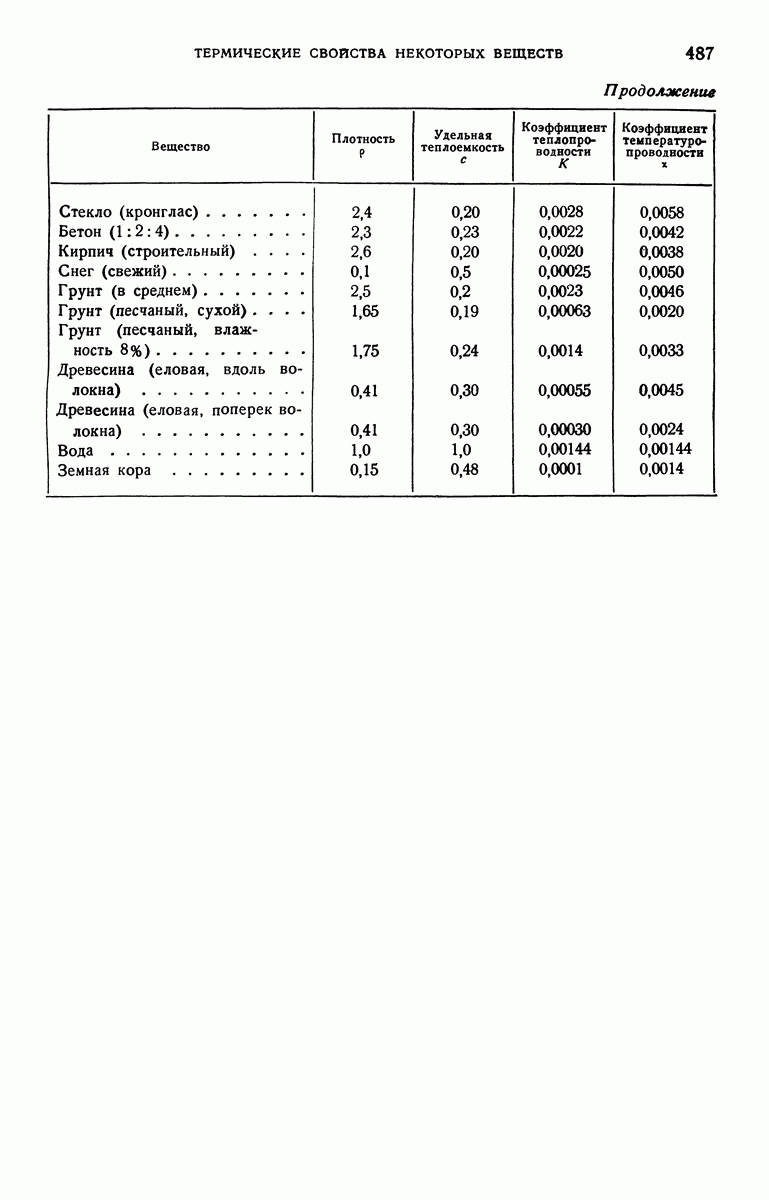
- ПРИЛОЖЕНИЕ 6. ТЕРМИЧЕСКИЕ СВОЙСТВА НЕКОТОРЫХ ВЕЩЕСТВ