| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.5. Алгоритм обратного распространения ошибки
Обсудим алгоритм обратного распространения ошибки [20], который позволяет обучать многослойные нейронные сети. Этот алгоритм считается наиболее известным и чаще всего применяемым в искусственных нейронных сетях.
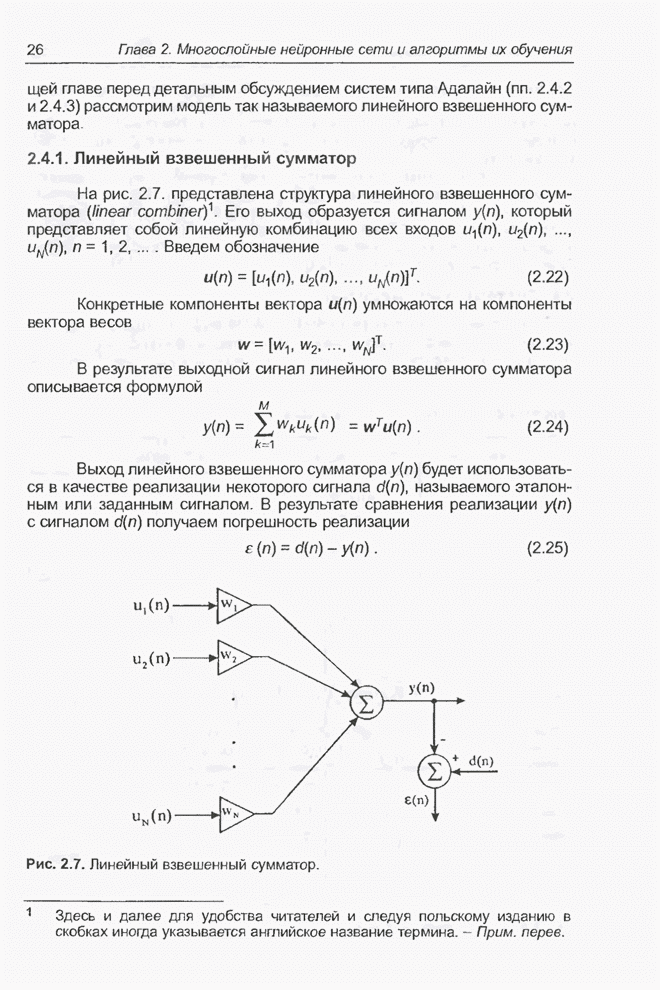
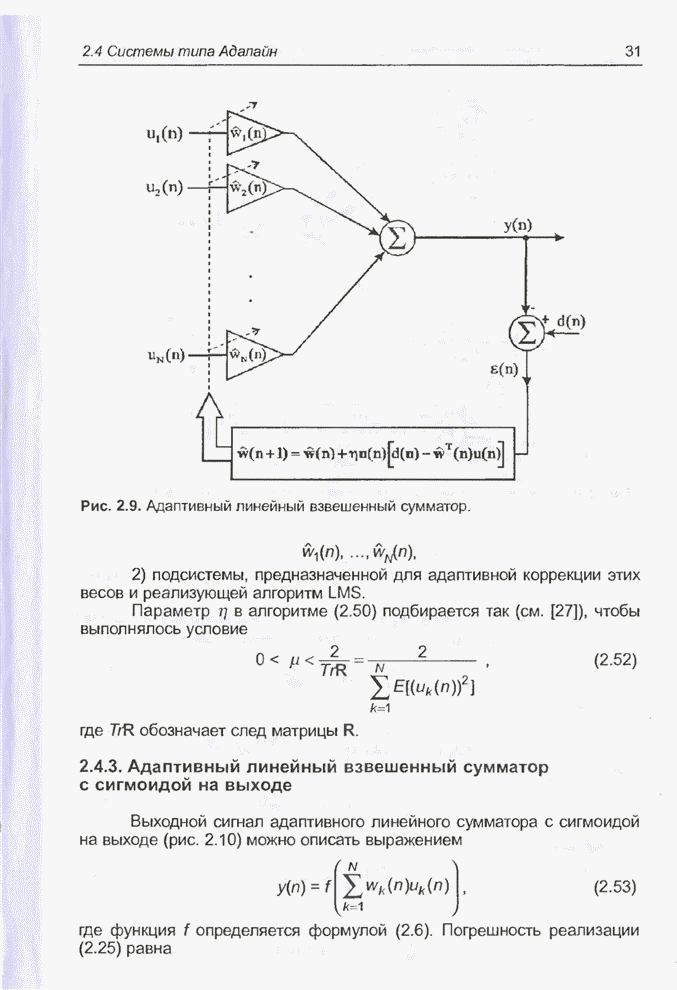
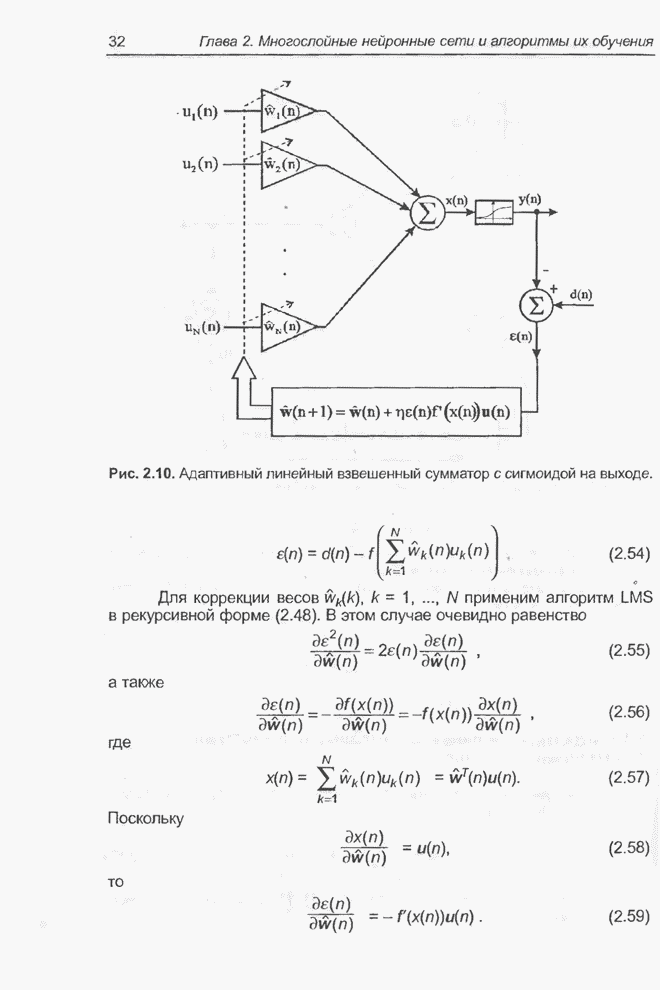
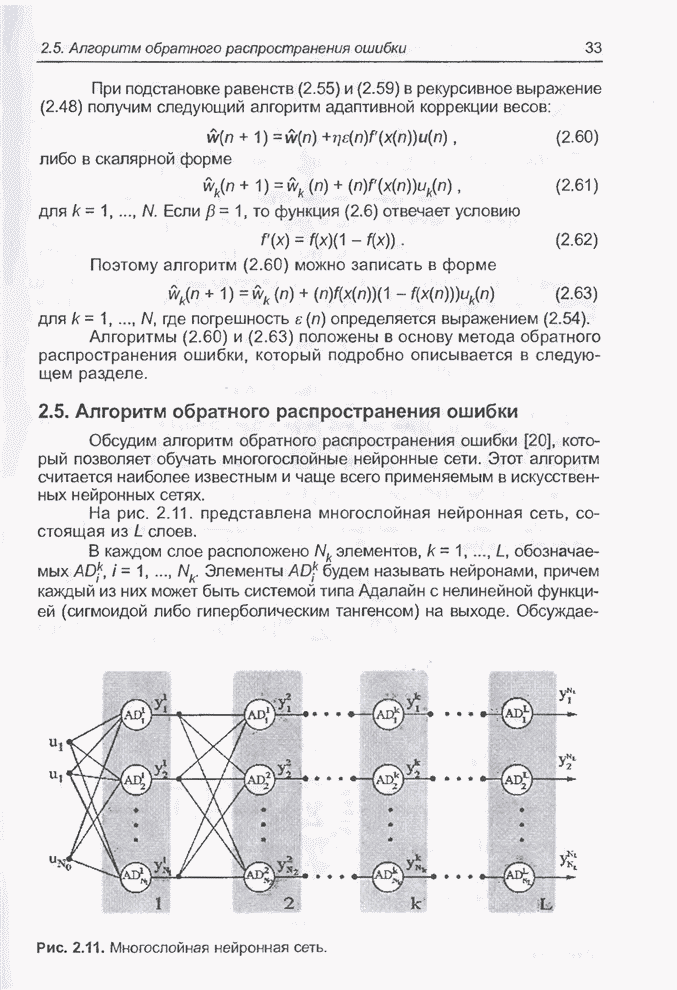
На рис. 2.11. представлена
многослойная нейронная сеть, состоящая из ![]() слоев.
слоев.

Рис. 2.11. Многослойная нейронная сеть.
В каждом слое расположено ![]() элементов,
элементов, ![]() , обозначаемых
, обозначаемых ![]() ,
, ![]() . Элементы
. Элементы ![]() будем называть нейронами,
причем каждый из них может быть системой типа Адалайн с нелинейной функцией
(сигмоидой либо гиперболическим тангенсом) на выходе. Обсуждаемая нейронная
сеть имеет
будем называть нейронами,
причем каждый из них может быть системой типа Адалайн с нелинейной функцией
(сигмоидой либо гиперболическим тангенсом) на выходе. Обсуждаемая нейронная
сеть имеет ![]() входов,
на которые подаются сигналы
входов,
на которые подаются сигналы ![]() , записываемые в векторной форме как
, записываемые в векторной форме как
![]() ,
,
![]() (2.64)
(2.64)
Выходной сигнал ![]() -го нейрона в
-го нейрона в ![]() -м слое обозначается
-м слое обозначается ![]() ,
, ![]() ,
, ![]() .
.
На рис. 2.12 показана детальная
структура ![]() -го
нейрона в
-го
нейрона в ![]() -м
слое.
-м
слое.
Нейрон ![]() имеет
имеет ![]() входов, образующих вектор
входов, образующих вектор
![]() , (2.65)
, (2.65)
причем
![]() для
для ![]() и
и ![]() . Обратим внимание на факт, что
входной сигнал нейрона
. Обратим внимание на факт, что
входной сигнал нейрона ![]() связан с выходным сигналом
связан с выходным сигналом ![]() слоя следующим
образом:
слоя следующим
образом:
 (2.66)
(2.66)
На
рис. 2.12 ![]() обозначает
вес связи
обозначает
вес связи ![]() -го
нейрона,
-го
нейрона, ![]() ,
расположенного в
,
расположенного в ![]() -м
слое, которая соединяет этот нейрон с
-м
слое, которая соединяет этот нейрон с ![]() -м входным сигналом
-м входным сигналом ![]() ,
, ![]() .
.

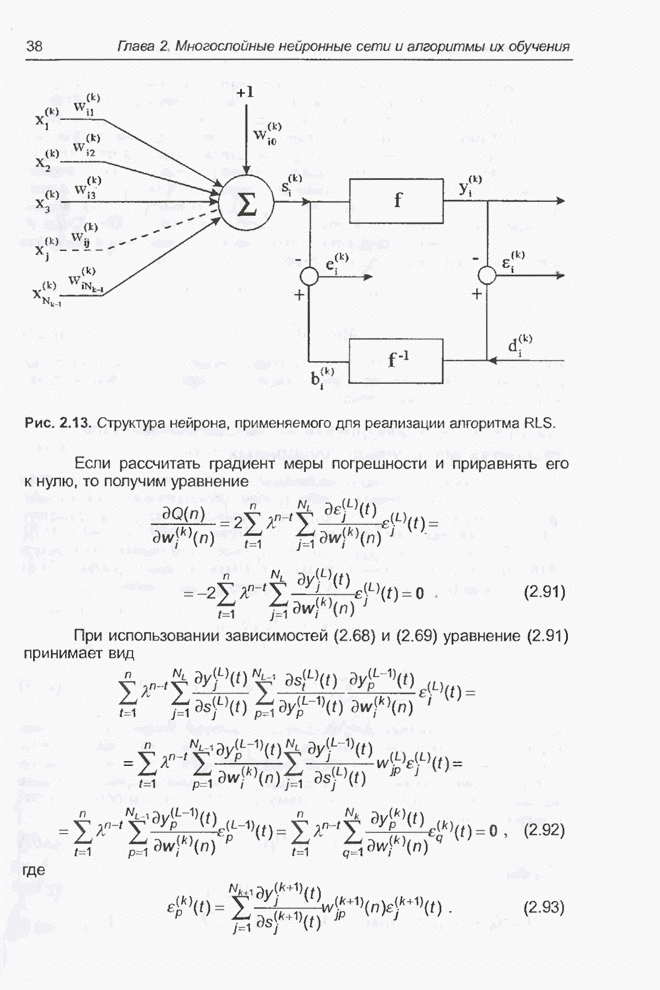
Рис. 2.12. Структура нейрона ![]() .
.
Вектор
весов нейрона ![]() обозначим
обозначим
![]() ,
,
![]() ,
, ![]() . (2.67)
. (2.67)
Выходной сигнал нейрона ![]() в
в ![]() -й момент времени,
-й момент времени, ![]() определяется как
определяется как
![]() , (2.68)
, (2.68)
причем
 . (2.69)
. (2.69)
Отметим,
что выходные сигналы нейронов в ![]() -м слое
-м слое
![]() (2.70)
(2.70)
одновременно являются выходными сигналами всей сети. Они сравниваются с так называемыми эталонными сигналами сети
![]() , (2.71)
, (2.71)
в результате чего получаем погрешность
![]() ,
,
![]() . (2.72)
. (2.72)
Можно сформулировать меру погрешности, основанную на сравнении сигналов (2.70) и (2.71), в виде суммы квадратов разностей (2.72), т.е.
 . (2.73)
. (2.73)
Из выражений (2.68) и (2.69)
следует, что мера погрешности (2.73) - это функция от весов сети. Обучение сети
основано на адаптивной коррекции всех весов ![]() таким образом, чтобы минимизировать ее
значение Для коррекции произвольного веса можно использовать правило
наискорейшего спуска, которое принимает вид
таким образом, чтобы минимизировать ее
значение Для коррекции произвольного веса можно использовать правило
наискорейшего спуска, которое принимает вид
 , (2.74)
, (2.74)
где
константа ![]() определяет
величину шага коррекции. Обратим внимание, что
определяет
величину шага коррекции. Обратим внимание, что
 . (2.75)
. (2.75)
Если ввести обозначение
 , (2.76)
, (2.76)
то получим равенство
 . (2.77)
. (2.77)
При этом алгоритм (2.74) принимает вид
![]() . (2.78)
. (2.78)
Способ расчета значения ![]() , заданного выражением
(2.76), зависит от номера слоя. Для последнего слоя получаем
, заданного выражением
(2.76), зависит от номера слоя. Для последнего слоя получаем


 . (2.79)
. (2.79)
Для произвольного слоя ![]() получаем
получаем


 . (2.80)
. (2.80)
Определим погрешность в ![]() -м (не последнем) слое
для
-м (не последнем) слое
для ![]() -го
нейрона в виде
-го
нейрона в виде
 ,
,
![]() . (2.81)
. (2.81)
Если подставить выражение (2.81) в формулу (2.80), то получим
![]() . (2.82)
. (2.82)
В результате алгоритм обратного распространения ошибки можно записать в виде
|
|
Название алгоритма связано со
способом расчета погрешностей в конкретных слоях. Вначале рассчитываются
погрешности в последнем слое (на основе выходных и эталонных сигналов), далее -
в предпоследнем и так вплоть до первого слоя. Начальные значения весов,
образующих сеть, выбираются случайным образом и, как правило, устанавливаются
близкими к нулю. Шаг коррекции ![]() чаще всего принимает большие значения
(близкие единице) на начальных этапах процесса обучения, но впоследствии его
следует уменьшать по мере того как веса приближаются к некоторым заранее
определенным значениям. В литературе, посвященной нейронным сетям (например, в
[3]), рекомендуются различные модификации алгоритма обратного распространения
ошибки. Одна из наиболее известных модификаций заключается во введении в
рекурсию (2.86) дополнительного члена, называемого моментом:
чаще всего принимает большие значения
(близкие единице) на начальных этапах процесса обучения, но впоследствии его
следует уменьшать по мере того как веса приближаются к некоторым заранее
определенным значениям. В литературе, посвященной нейронным сетям (например, в
[3]), рекомендуются различные модификации алгоритма обратного распространения
ошибки. Одна из наиболее известных модификаций заключается во введении в
рекурсию (2.86) дополнительного члена, называемого моментом:
![]()
![]() , (2.87)
, (2.87)
в
котором параметр ![]() .
Экспериментальные исследования показывают [24], что введение момента ускоряет
сходимость алгоритма обратного распространения ошибки.
.
Экспериментальные исследования показывают [24], что введение момента ускоряет
сходимость алгоритма обратного распространения ошибки.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Предисловие к русскому изданию
- ГЛАВА 1. ВВЕДЕНИЕ
- Список литературы
- ГЛАВА 2. МНОГОСЛОЙНЫЕ НЕЙРОННЫЕ СЕТИ И АЛГОРИТМЫ ИХ ОБУЧЕНИЯ
- 2.1. Введение
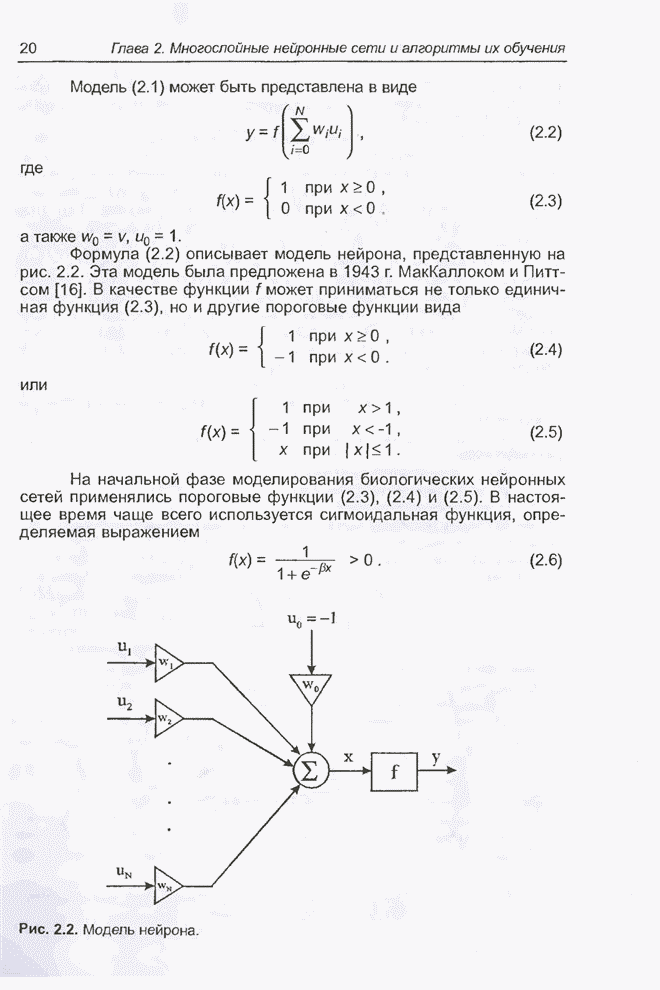
- 2.2. Нейрон и его модели
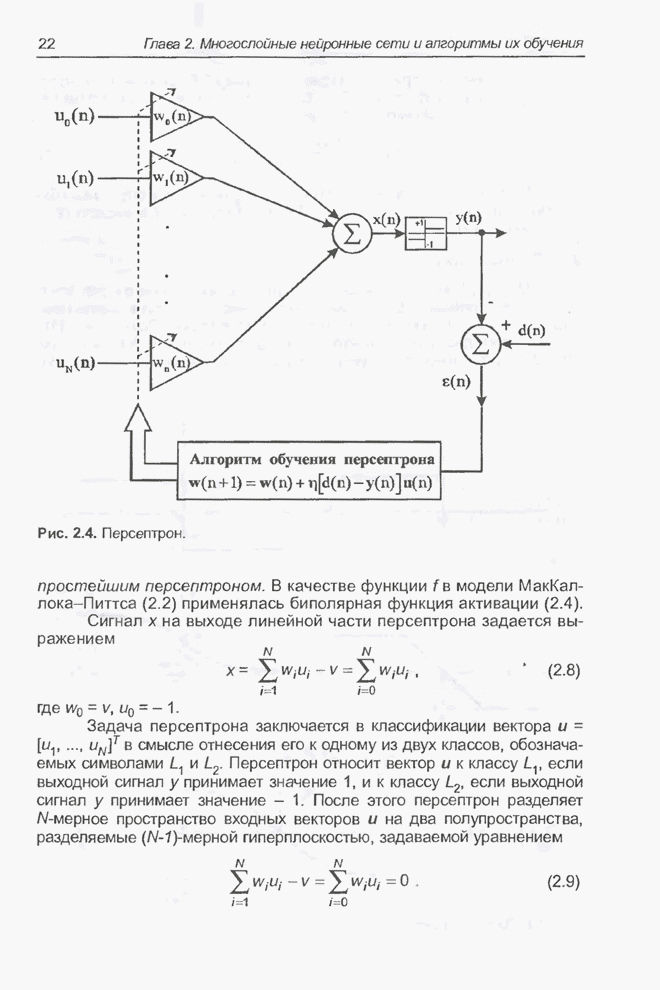
- 2.3. Персептрон
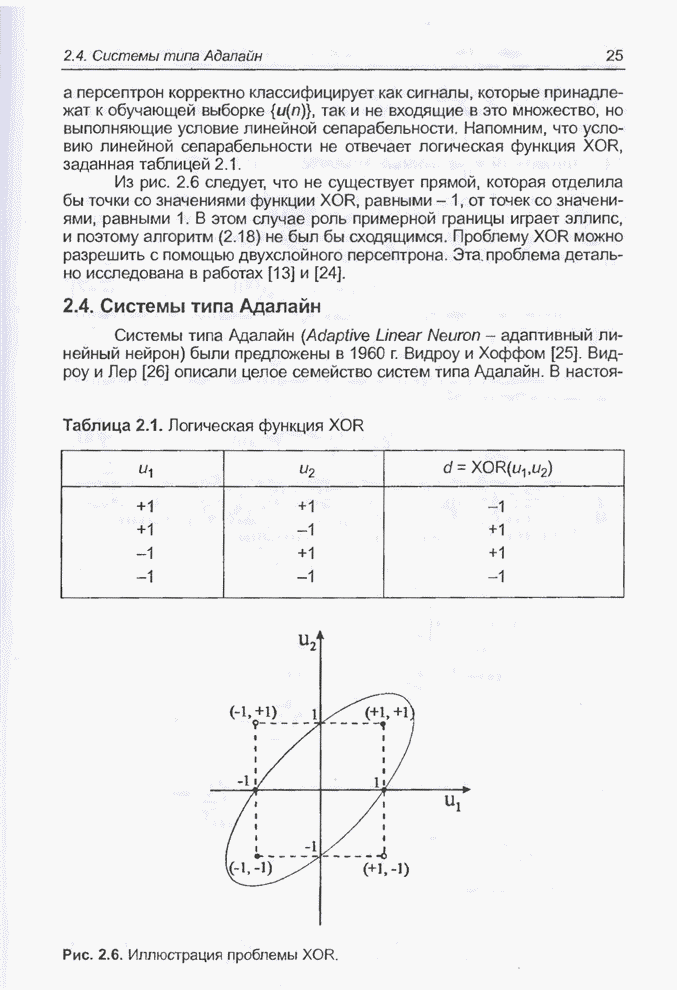
- 2.4. Системы типа Адалайн
- 2.4.1. Линейный взвешенный сумматор
- 2.4.2. Адаптивный линейный взвешенный сумматор
- 2.4.3. Адаптивный линейный взвешенный сумматор с сигмоидой на выходе
- 2.5. Алгоритм обратного распространения ошибки
- 2.6. Применение рекуррентного метода наименьших квадратов для обучения нейронных сетей
- Список литературы
- ГЛАВA3. НЕЧЕТКИЕ МНОЖЕСТВА И НЕЧЕТКИЙ ВЫВОД
- 3.1. Введение
- 3.2. Основные понятия и определения теории нечетких множеств
- 3.3. Операции на нечетких множествах
- 3.4. Принцип расширения
- 3.5. Нечеткие числа
- 3.6. Треугольные нормы
- 3.7. Нечеткие отношения и их свойства
- 3.8. Нечеткий вывод
- 3.9. Нечеткое управление
- 3.9.1. Классический модуль нечеткого управления
- 3.9.2. Метод нечеткого управления Такаги-Сугено
- 3.10. Проектирование базы нечетких правил на основе численных данных
- 3.10.1. Построение нечетких правил
- 3.10.2. Задача парковки грузовика
- 3.10.3. Примечание
- Список литературы
- ГЛАВА 4. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 4.1. Введение
- 4.2. Генетические алгоритмы и традиционные методы оптимизации
- 4.3. Основные понятия генетических алгоритмов
- 4.4. Классический генетический алгоритм
- 4.5. Иллюстрация выполнения классического генетического алгоритма
- 4.6. Кодирование параметров задачи в генетическом алгоритме
- 4.7. Основная теорема о генетических алгоритмах
- 4.8. Модификации классического генетического алгоритма
- 4.8.1. Методы селекции
- 4.8.2. Особые процедуры репродукции
- 4.8.3. Генетические операторы
- 4.8.4. Методы кодирования
- 4.8.5. Масштабирование функции приспособленности
- 4.8.6. Ниши в генетическом алгоритме
- 4.8.7. Генетические алгоритмы для многокритериальной оптимизации
- 4.8.8. Генетические микроалгоритмы
- 4.9. Примеры оптимизации функции с помощью программы FlexTool
- 4.10. Эволюционные алгоритмы
- 4.11. Приложения эволюционных алгоритмов
- 4.11.1. Примеры оптимизации функции с помощью программы Evolver
- 4.11.2. Решение комбинаторных задач с помощью программы Evolver
- 4.12. Эволюционные алгоритмы в нейронных сетях
- 4.12.1. Независимое применение генетических алгоритмов и нейронных сетей
- 4.12.2. Нейронные сети для поддержки генетических алгоритмов
- 4.12.3. Генетические алгоритмы для поддержки нейронных сетей
- 4.12.4. Применение генетических алгоритмов для обучения нейронных сетей
- 4.12.5. Генетические алгоритмы для выбора топологии нейронных сетей
- 4.12.6. Адаптивные взаимодействующие системы
- 4.12.7. Типовой цикл эволюции
- 4.12.7.1. Эволюция весов связей
- 4.12.7.2. Эволюция архитектуры сети
- 4.12.7.3. Эволюция правил обучения
- 4.13. Примеры моделирования эволюционных алгоритмов в приложении к нейронным сетям
- 4.13.1. Программы Evolver и BrainMaker
- 4.13.2. Программа GTO
- Список литературы
- ГЛАВА 5. МОДУЛИ НЕЧЕТКО-НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.1. Модуль нечеткого управления со структурой, определенной в процессе дефуззификации
- 5.1.2. Конструкция модуля
- 5.1.3. Структура модуля
- 5.1.4. Использование алгоритма обратного распространения ошибки
- 5.1.5. Модификации модуля
- 5.1.6. Применение модуля нечеткого управления для прогнозирования случайных временных рядов
- 5.1.7. Применение модуля нечеткого управления для решения задачи парковки грузовика
- 5.1.8. Примечание
- 5.2. Представление модуля нечеткого управления в виде стандартной нейронной сети
- 5.3. Модуль нечеткого управления с нейронной сетью для выполнения дефуззификации
- 5.3.1. Введение
- 5.3.2. Конструкция модуля
- 5.3.3. Структура модуля
- 5.3.4. Алгоритмы обучения модуля
- 5.3.5. Решение задачи стабилизации перевернутого маятника
- 5.3.6. Примечание
- 5.4. Модуль нечеткого управления с возможностью коррекции правил
- 5.4.1. Введение
- 5.4.2. Фаза обучения на основе самоорганизации
- 5.4.3. Фаза обучения с учителем
- 5.4.4. Примечание
- 5.5. Модуль нечеткого управления типа Такаги-Сугено
- 5.5.1. Введение
- 5.5.2. Нейронная реализация функции принадлежности
- 5.5.3. Модули Такаги-Сугено
- 5.5.4. Реализация условий
- 5.5.5. Реализация заключений
- 5.5.6. Примечание
- 5.6. Модуль нечеткого управления типа Такаги-Сугено: случай зависимых лингвистических переменных
- 5.6.1. Введение
- 5.6.2. Нейронные сети для нечеткого вывода
- 5.6.3. Структура системы
- 5.6.4. Способ обучения
- 5.6.5. Решение задачи парковки грузовика
- 5.6.6. Примечание
- Список литературы













































































































































































































































































 (2.84)
(2.84)
