| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.1.3. Структура модуля
Завершающий этап в процессе
проектирования нашего модуля нечеткого управления - это определение формы
представления нечетких множеств ![]() ,
, ![]() ;
; ![]() . Например, это может быть функция
. Например, это может быть функция
 , (5.12)
, (5.12)
где
параметры ![]() и
и
![]() имеют
физическую интерпретацию:
имеют
физическую интерпретацию: ![]() - это центр, а
- это центр, а ![]() - ширина гауссовской кривой.
- ширина гауссовской кривой.
Как будет показано ниже, эти параметры могут модифицироваться в процессе обучения, что позволяет изменять положение и структуру нечетких множеств.
Объединим теперь все представленные элементы. Воспользуемся методом дефуззификации (5.8), выводом согласно выражению (5.5), блоком фуззификации с операцией типа синглетон (5.6), а также гауссовской функцией принадлежности (5.12) и тогда модуль нечеткого управления приобретает окончательный вид
 . (5.13)
. (5.13)
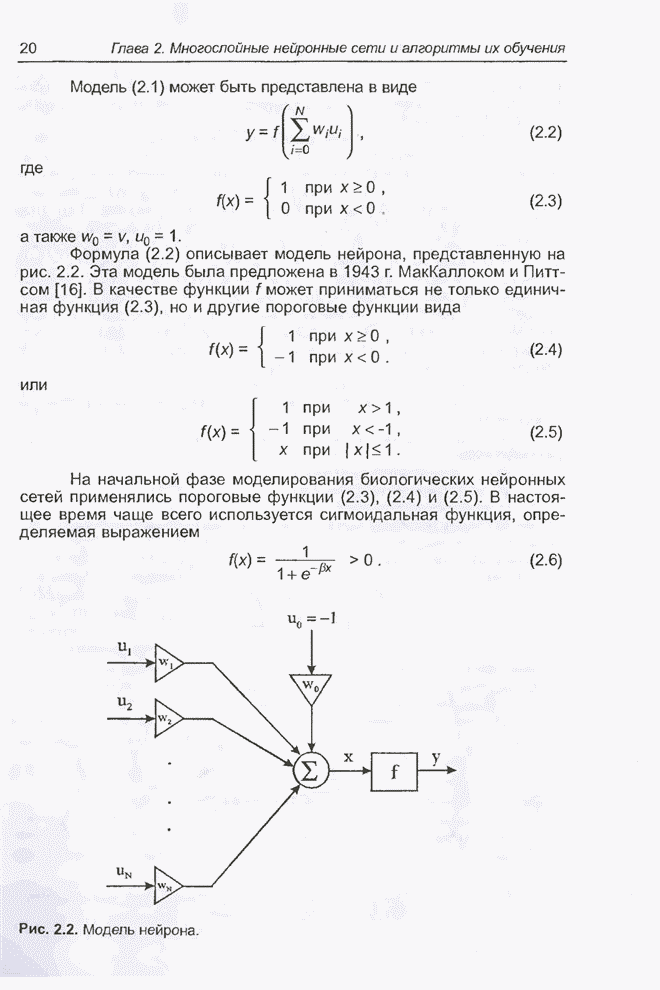
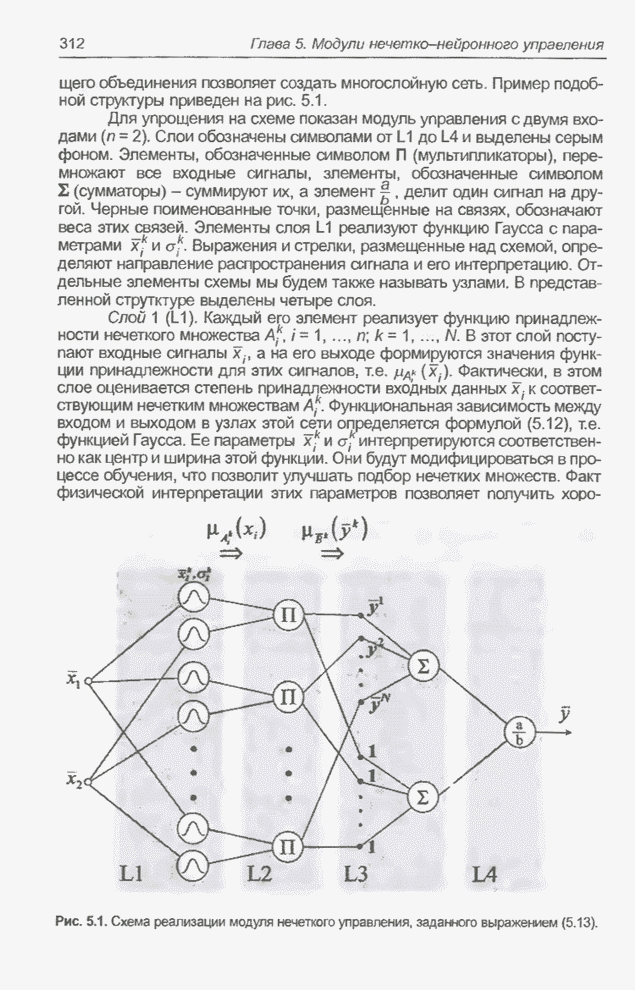
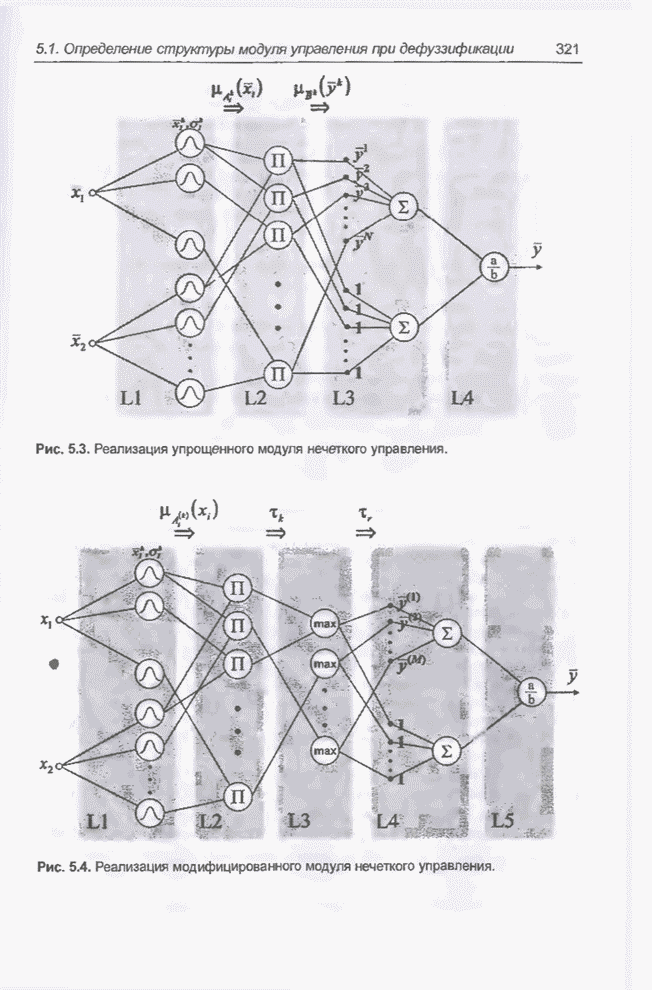
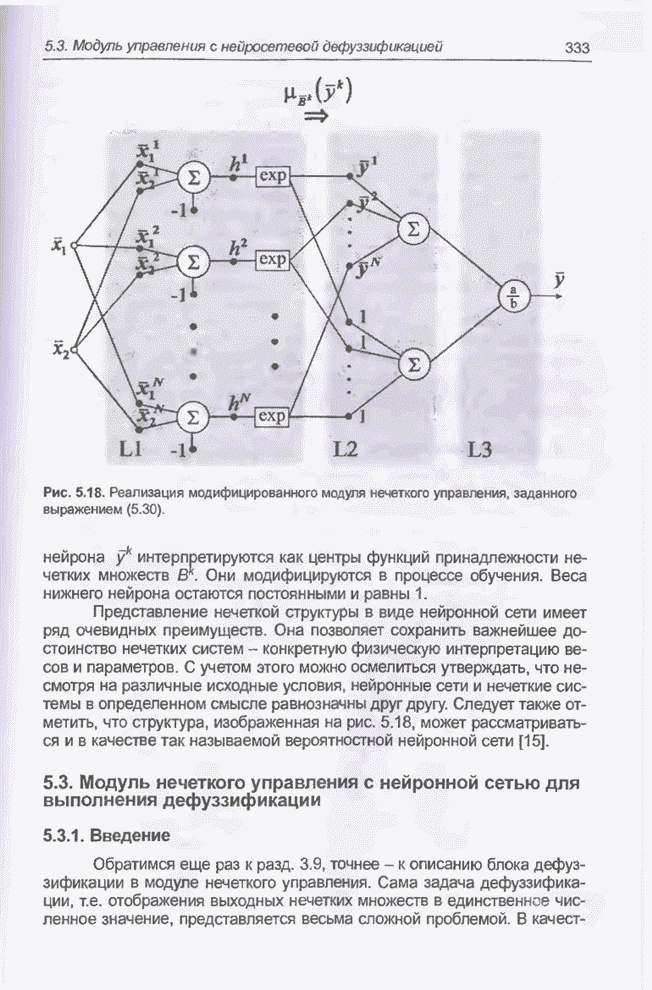
Приведенное выражение представляет собой один из наиболее известных и часто применяемых способов реализации нечетких систем. Каждый элемент этой формулы можно задать в форме функционального блока (сумма, произведение, функция Гаусса), что после соответствующего объединения позволяет создать многослойную сеть. Пример подобной структуры приведен на рис. 5.1.

Рис. 5.1. Схема реализации модуля нечеткого управления, заданного выражением (5.13).
Для упрощения на схеме показан
модуль управления с двумя входами ![]() . Слои обозначены символами от L1 до L4 и выделены серым фоном. Элементы, обозначенные
символом
. Слои обозначены символами от L1 до L4 и выделены серым фоном. Элементы, обозначенные
символом ![]() (мультипликаторы),
перемножают все входные сигналы, элементы, обозначенные символом
(мультипликаторы),
перемножают все входные сигналы, элементы, обозначенные символом ![]() (сумматоры) -
суммируют их, а элемент
(сумматоры) -
суммируют их, а элемент ![]() делит один сигнал на другой. Черные
поименованные точки, размещенные на связях, обозначают веса этих связей.
Элементы слоя L1 реализуют функцию Гаусса с
параметрами
делит один сигнал на другой. Черные
поименованные точки, размещенные на связях, обозначают веса этих связей.
Элементы слоя L1 реализуют функцию Гаусса с
параметрами ![]() и
и
![]() . Выражения
и стрелки, размещенные над схемой, определяют направление распространения
сигнала и его интерпретацию. Отдельные элементы схемы мы будем также называть
узлами. В представленной структуре выделены четыре слоя.
. Выражения
и стрелки, размещенные над схемой, определяют направление распространения
сигнала и его интерпретацию. Отдельные элементы схемы мы будем также называть
узлами. В представленной структуре выделены четыре слоя.
Слой 1 (L1). Каждый его элемент реализует функцию принадлежности
нечеткого множества ![]() ,
,
![]() ;
; ![]() . В этот слой
поступают входные сигналы
. В этот слой
поступают входные сигналы ![]() , а на его выходе формируются значения
функции принадлежности для этих сигналов, т.е.
, а на его выходе формируются значения
функции принадлежности для этих сигналов, т.е. ![]() . Фактически, в этом слое оценивается
степень принадлежности входных данных
. Фактически, в этом слое оценивается
степень принадлежности входных данных ![]() к соответствующим нечетким множествам
к соответствующим нечетким множествам ![]() . Функциональная
зависимость между входом и выходом в узлах этой сети определяется формулой
(5.12), т.е. функцией Гаусса. Ее параметры
. Функциональная
зависимость между входом и выходом в узлах этой сети определяется формулой
(5.12), т.е. функцией Гаусса. Ее параметры ![]() и
и ![]() интерпретируются соответственно как
центр и ширина этой функции. Они будут модифицироваться в процессе обучения,
что позволит улучшать подбор нечетких множеств. Факт физической интерпретации
этих параметров позволяет получить хорошее начальное размещение функции
принадлежности нечетких множеств, а также анализировать ее в процессе обучения.
Количество элементов слоя L1 равно количеству всех множеств
с принадлежностью
интерпретируются соответственно как
центр и ширина этой функции. Они будут модифицироваться в процессе обучения,
что позволит улучшать подбор нечетких множеств. Факт физической интерпретации
этих параметров позволяет получить хорошее начальное размещение функции
принадлежности нечетких множеств, а также анализировать ее в процессе обучения.
Количество элементов слоя L1 равно количеству всех множеств
с принадлежностью ![]() .
В случае
.
В случае ![]() нечетких
правил
нечетких
правил ![]() и
и ![]() входных переменных
входных переменных ![]() с учетом того, что в
каждом правиле любая входная переменная связана с другим нечетким множеством,
количество узлов (элементов слоя L1)
будет равно произведению количества входных переменных
с учетом того, что в
каждом правиле любая входная переменная связана с другим нечетким множеством,
количество узлов (элементов слоя L1)
будет равно произведению количества входных переменных ![]() и количества нечетких правил
и количества нечетких правил ![]() .
.
Слой 2 (L2). Конфигурация связей этого слоя соответствует
базе правил, а мультипликаторы - блоку вывода (см. формулы (5.7) и (5.10)). На
выходе слоя L2 формируется результат вывода в
виде значения функции принадлежности ![]() . Количество элементов этого слоя равно
количеству правил
. Количество элементов этого слоя равно
количеству правил ![]() .
Каждый узел связан с предыдущим слоем таким образом, что узел слоя L2, соответствующий
.
Каждый узел связан с предыдущим слоем таким образом, что узел слоя L2, соответствующий ![]() -му правилу, соединен
со всеми узлами слоя L1, соответствующими нечетким
множествам суждений этого правила. Применение мультипликаторов в качестве узлов
слоя L2 обусловлено тем фактом, что для
-му правилу, соединен
со всеми узлами слоя L1, соответствующими нечетким
множествам суждений этого правила. Применение мультипликаторов в качестве узлов
слоя L2 обусловлено тем фактом, что для
![]() -нормы,
декартова произведения множеств и нечеткой импликации используется операция
умножения. Следует отметить, что для реализации примера 3.32 достаточно
заменить операцию умножения операцией минимум (см. формулу 3.240).
-нормы,
декартова произведения множеств и нечеткой импликации используется операция
умножения. Следует отметить, что для реализации примера 3.32 достаточно
заменить операцию умножения операцией минимум (см. формулу 3.240).
Слои 3 (L3) и 4 (L4).
Оба слоя представляют собой реализацию блока дефуззификации, реализующего
зависимость (5.8). Веса связей, доходящих до верхнего узла слоя L3 и обозначенные ![]() , интерпретируются как
центры функций принадлежности нечетких множеств
, интерпретируются как
центры функций принадлежности нечетких множеств ![]() . Эти веса, также как и значения
параметров
. Эти веса, также как и значения
параметров ![]() и
и
![]() в слое L1, будут модифицироваться в
процессе обучения. На выходе слоя L4
формируется «четкое» (дефуззифицированное) выходное значение модуля управления
в слое L1, будут модифицироваться в
процессе обучения. На выходе слоя L4
формируется «четкое» (дефуззифицированное) выходное значение модуля управления ![]() . Представленная на
рис. 5.1 структура имеет много общего с нейронными сетями - она представляет
собой многослойную сеть, основанную на идее нечеткого вывода. В отличие от
«чистых» нейронных сетей, каждый слой в целом и отдельные составляющие его
элементы, также как и конфигурация связей, все параметры и веса имеют
физическую интерпретацию. Это свойство оказывается необычайно важным, поскольку
знания не распределяются по сети и могут быть легко локализованы и при
необходимости откорректированы экспертом-наблюдателем.
. Представленная на
рис. 5.1 структура имеет много общего с нейронными сетями - она представляет
собой многослойную сеть, основанную на идее нечеткого вывода. В отличие от
«чистых» нейронных сетей, каждый слой в целом и отдельные составляющие его
элементы, также как и конфигурация связей, все параметры и веса имеют
физическую интерпретацию. Это свойство оказывается необычайно важным, поскольку
знания не распределяются по сети и могут быть легко локализованы и при
необходимости откорректированы экспертом-наблюдателем.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Предисловие к русскому изданию
- ГЛАВА 1. ВВЕДЕНИЕ
- Список литературы
- ГЛАВА 2. МНОГОСЛОЙНЫЕ НЕЙРОННЫЕ СЕТИ И АЛГОРИТМЫ ИХ ОБУЧЕНИЯ
- 2.1. Введение
- 2.2. Нейрон и его модели
- 2.3. Персептрон
- 2.4. Системы типа Адалайн
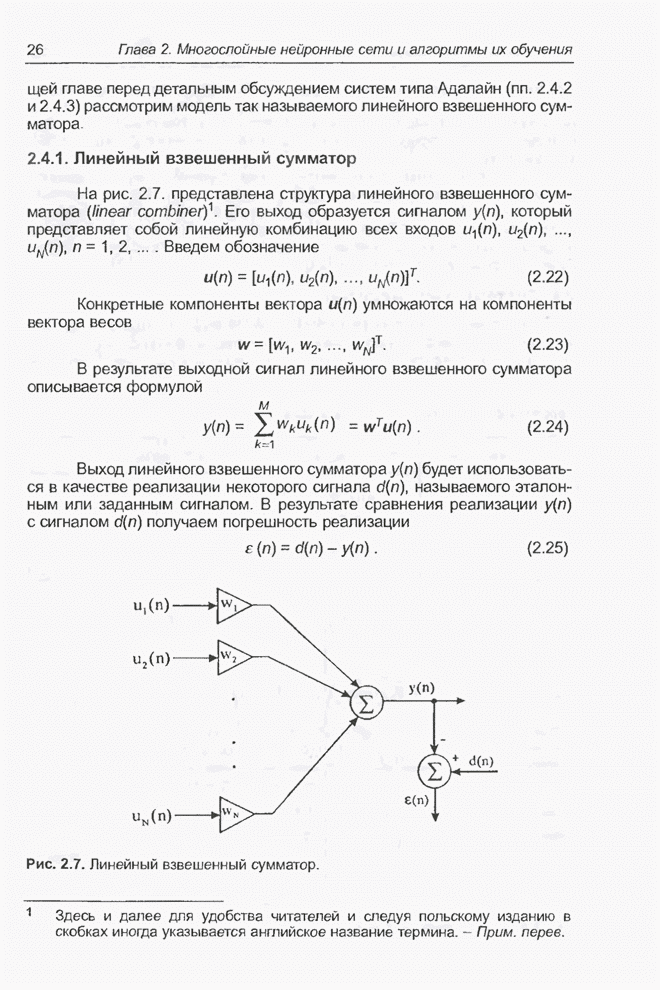
- 2.4.1. Линейный взвешенный сумматор
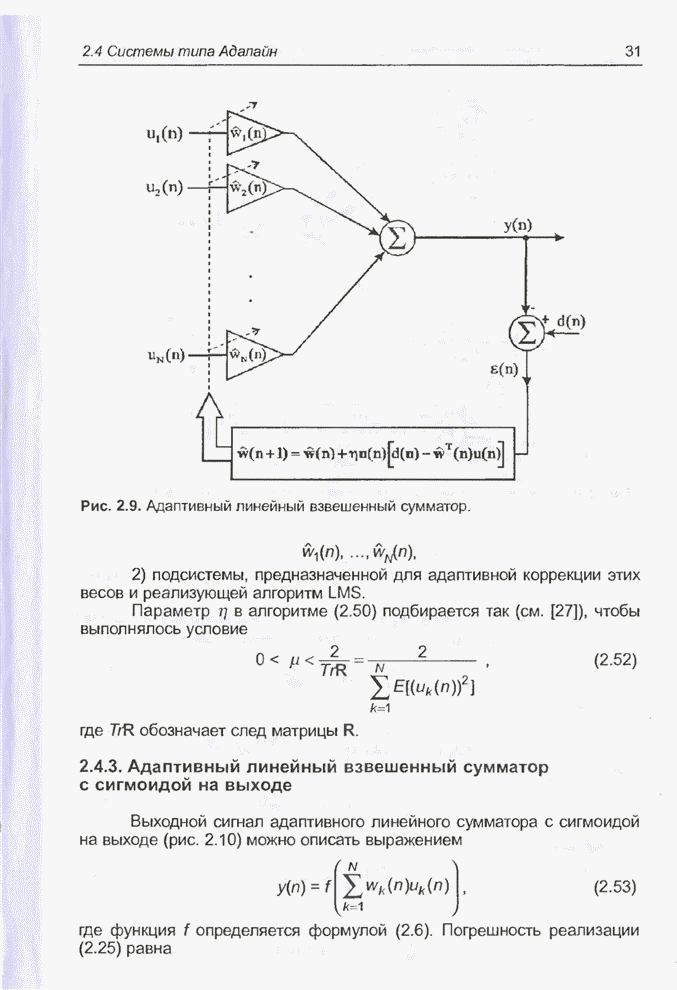
- 2.4.2. Адаптивный линейный взвешенный сумматор
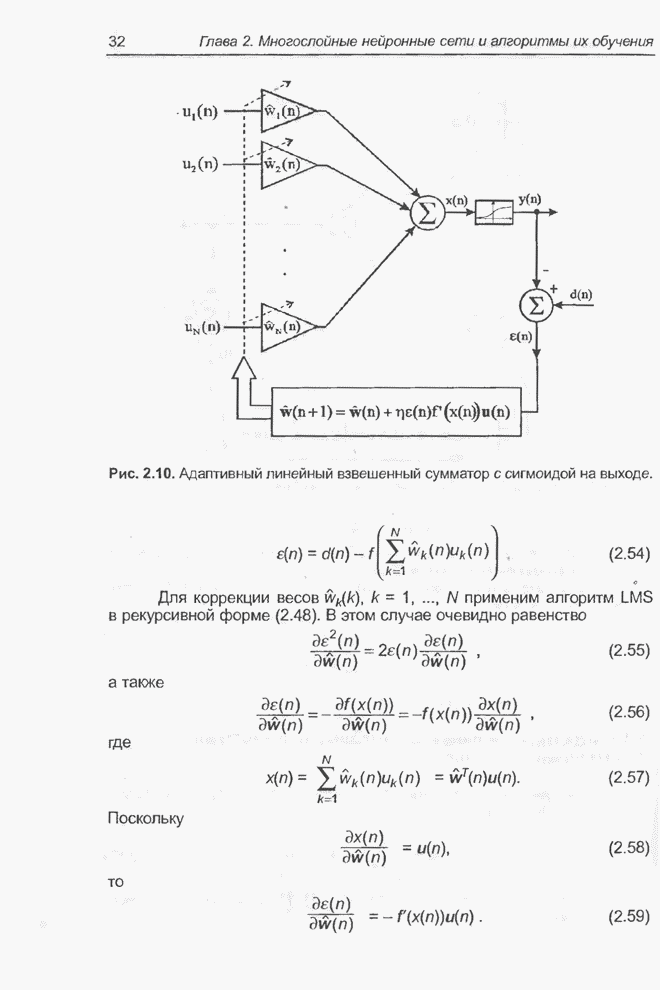
- 2.4.3. Адаптивный линейный взвешенный сумматор с сигмоидой на выходе
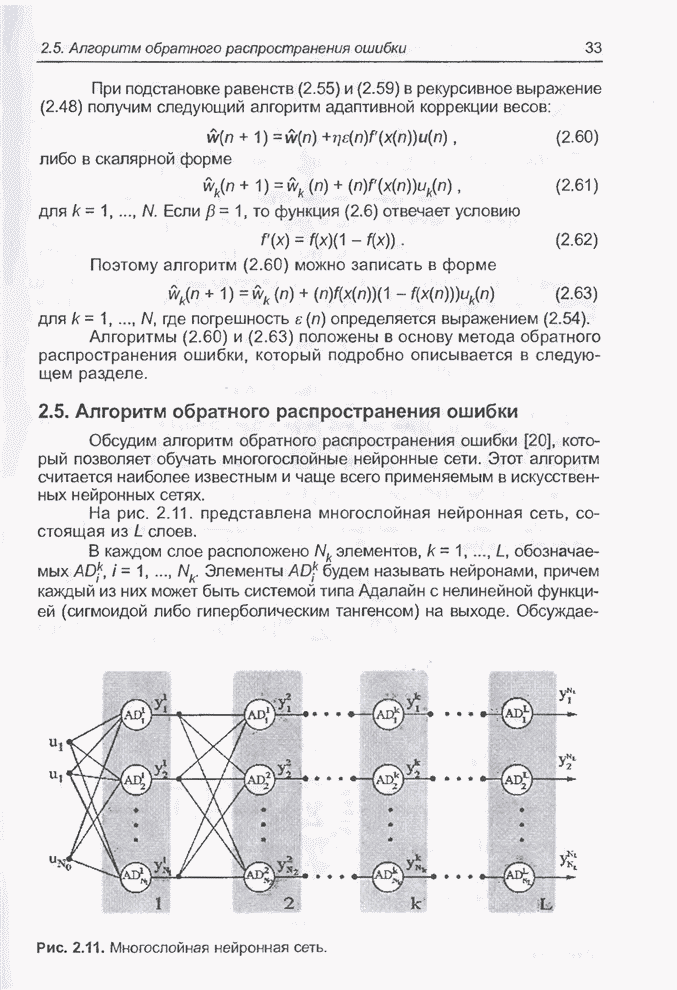
- 2.5. Алгоритм обратного распространения ошибки
- 2.6. Применение рекуррентного метода наименьших квадратов для обучения нейронных сетей
- Список литературы
- ГЛАВA3. НЕЧЕТКИЕ МНОЖЕСТВА И НЕЧЕТКИЙ ВЫВОД
- 3.1. Введение
- 3.2. Основные понятия и определения теории нечетких множеств
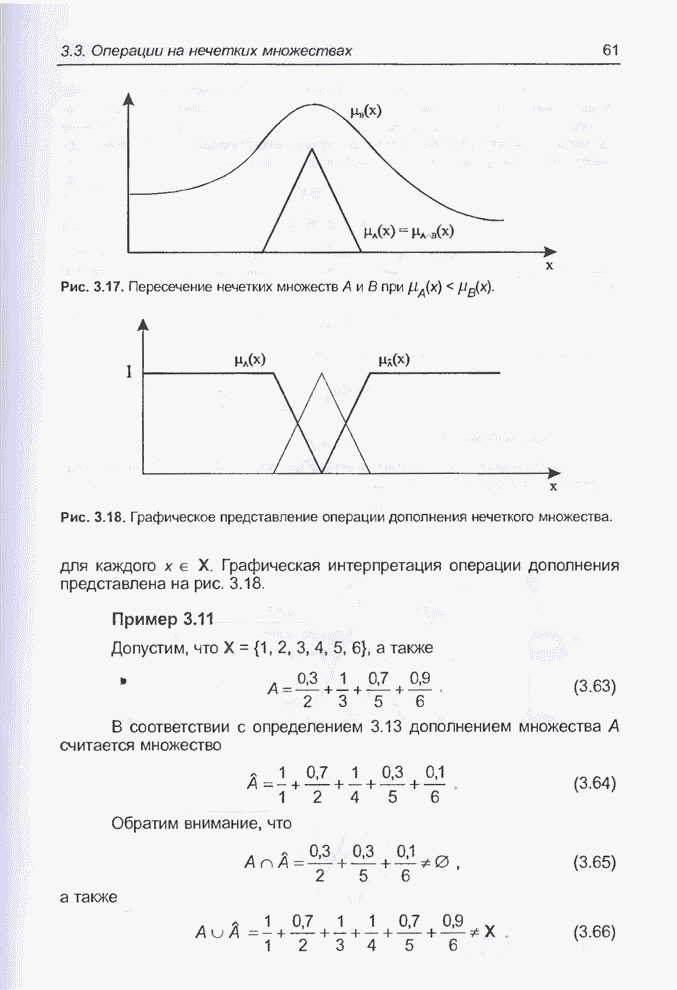
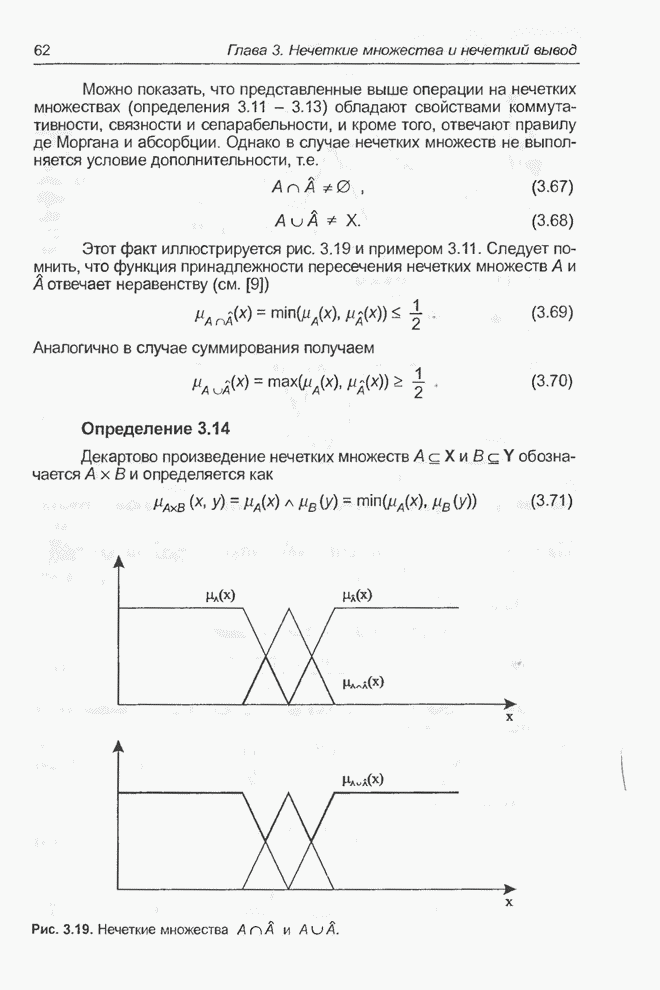
- 3.3. Операции на нечетких множествах
- 3.4. Принцип расширения
- 3.5. Нечеткие числа
- 3.6. Треугольные нормы
- 3.7. Нечеткие отношения и их свойства
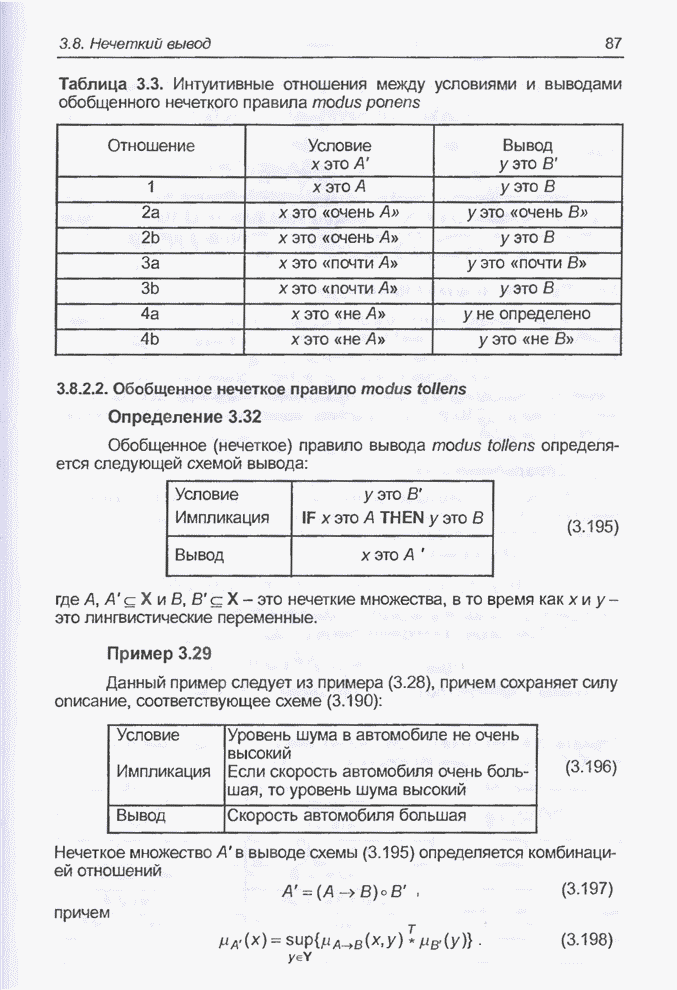
- 3.8. Нечеткий вывод
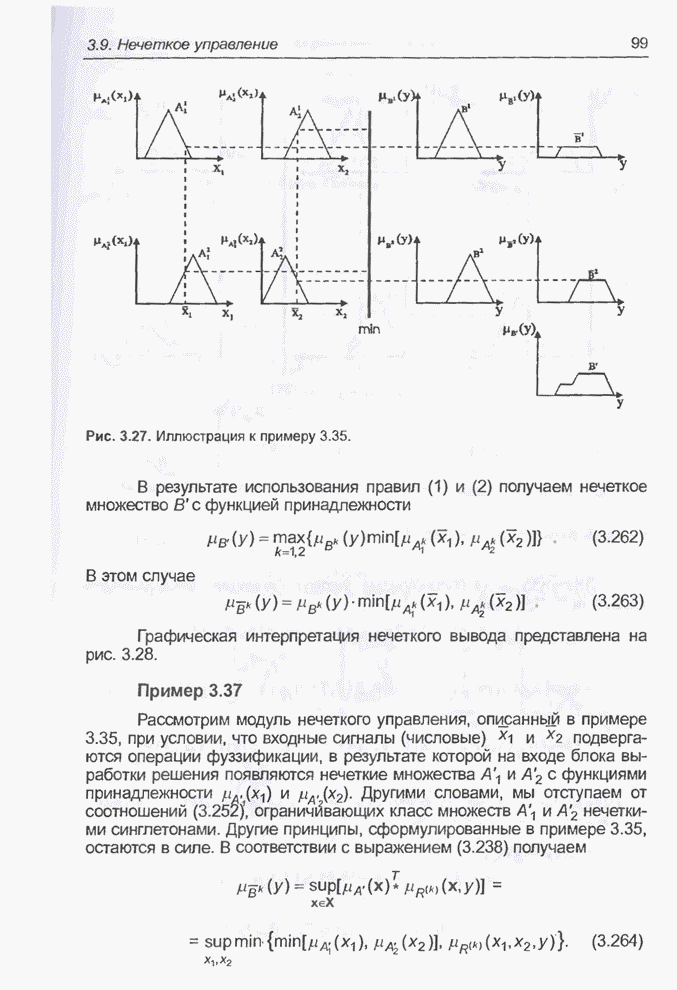
- 3.9. Нечеткое управление
- 3.9.1. Классический модуль нечеткого управления
- 3.9.2. Метод нечеткого управления Такаги-Сугено
- 3.10. Проектирование базы нечетких правил на основе численных данных
- 3.10.1. Построение нечетких правил
- 3.10.2. Задача парковки грузовика
- 3.10.3. Примечание
- Список литературы
- ГЛАВА 4. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 4.1. Введение
- 4.2. Генетические алгоритмы и традиционные методы оптимизации
- 4.3. Основные понятия генетических алгоритмов
- 4.4. Классический генетический алгоритм
- 4.5. Иллюстрация выполнения классического генетического алгоритма
- 4.6. Кодирование параметров задачи в генетическом алгоритме
- 4.7. Основная теорема о генетических алгоритмах
- 4.8. Модификации классического генетического алгоритма
- 4.8.1. Методы селекции
- 4.8.2. Особые процедуры репродукции
- 4.8.3. Генетические операторы
- 4.8.4. Методы кодирования
- 4.8.5. Масштабирование функции приспособленности
- 4.8.6. Ниши в генетическом алгоритме
- 4.8.7. Генетические алгоритмы для многокритериальной оптимизации
- 4.8.8. Генетические микроалгоритмы
- 4.9. Примеры оптимизации функции с помощью программы FlexTool
- 4.10. Эволюционные алгоритмы
- 4.11. Приложения эволюционных алгоритмов
- 4.11.1. Примеры оптимизации функции с помощью программы Evolver
- 4.11.2. Решение комбинаторных задач с помощью программы Evolver
- 4.12. Эволюционные алгоритмы в нейронных сетях
- 4.12.1. Независимое применение генетических алгоритмов и нейронных сетей
- 4.12.2. Нейронные сети для поддержки генетических алгоритмов
- 4.12.3. Генетические алгоритмы для поддержки нейронных сетей
- 4.12.4. Применение генетических алгоритмов для обучения нейронных сетей
- 4.12.5. Генетические алгоритмы для выбора топологии нейронных сетей
- 4.12.6. Адаптивные взаимодействующие системы
- 4.12.7. Типовой цикл эволюции
- 4.12.7.1. Эволюция весов связей
- 4.12.7.2. Эволюция архитектуры сети
- 4.12.7.3. Эволюция правил обучения
- 4.13. Примеры моделирования эволюционных алгоритмов в приложении к нейронным сетям
- 4.13.1. Программы Evolver и BrainMaker
- 4.13.2. Программа GTO
- Список литературы
- ГЛАВА 5. МОДУЛИ НЕЧЕТКО-НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.1. Модуль нечеткого управления со структурой, определенной в процессе дефуззификации
- 5.1.2. Конструкция модуля
- 5.1.3. Структура модуля
- 5.1.4. Использование алгоритма обратного распространения ошибки
- 5.1.5. Модификации модуля
- 5.1.6. Применение модуля нечеткого управления для прогнозирования случайных временных рядов
- 5.1.7. Применение модуля нечеткого управления для решения задачи парковки грузовика
- 5.1.8. Примечание
- 5.2. Представление модуля нечеткого управления в виде стандартной нейронной сети
- 5.3. Модуль нечеткого управления с нейронной сетью для выполнения дефуззификации
- 5.3.1. Введение
- 5.3.2. Конструкция модуля
- 5.3.3. Структура модуля
- 5.3.4. Алгоритмы обучения модуля
- 5.3.5. Решение задачи стабилизации перевернутого маятника
- 5.3.6. Примечание
- 5.4. Модуль нечеткого управления с возможностью коррекции правил
- 5.4.1. Введение
- 5.4.2. Фаза обучения на основе самоорганизации
- 5.4.3. Фаза обучения с учителем
- 5.4.4. Примечание
- 5.5. Модуль нечеткого управления типа Такаги-Сугено
- 5.5.1. Введение
- 5.5.2. Нейронная реализация функции принадлежности
- 5.5.3. Модули Такаги-Сугено
- 5.5.4. Реализация условий
- 5.5.5. Реализация заключений
- 5.5.6. Примечание
- 5.6. Модуль нечеткого управления типа Такаги-Сугено: случай зависимых лингвистических переменных
- 5.6.1. Введение
- 5.6.2. Нейронные сети для нечеткого вывода
- 5.6.3. Структура системы
- 5.6.4. Способ обучения
- 5.6.5. Решение задачи парковки грузовика
- 5.6.6. Примечание
- Список литературы