| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
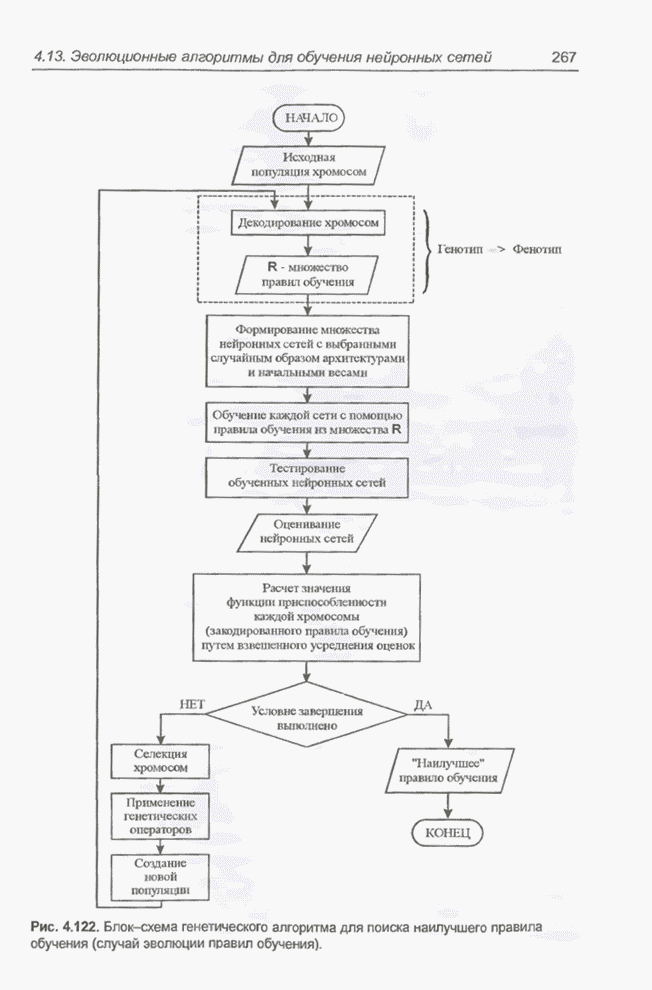
4.13. Примеры моделирования эволюционных алгоритмов в приложении к нейронным сетям
Представленные в п. 4.11.1 примеры 4.23 - 4.27, а также пример 4.20 из разд. 4.9 можно рассматривать как иллюстрацию возможности применения генетического (в частности, эволюционного) алгоритма для подбора весов нейронной сети. Этот алгоритм будет применяться в перечисленных примерах вместо традиционного метода обучения, например, вместо алгоритма обратного распространения ошибки (backpropagation). Очень часто применяется так называемый гибридный подход, состоящий в объединении обоих методов. Как правило, вначале при помощи генетического алгоритма находится решение, достаточно близкое к оптимальному, и затем оно рассматривается как отправная точка для традиционного поиска оптимальной точки, например, по методу обратного распространения ошибки.
4.13.1. Программы Evolver и BrainMaker
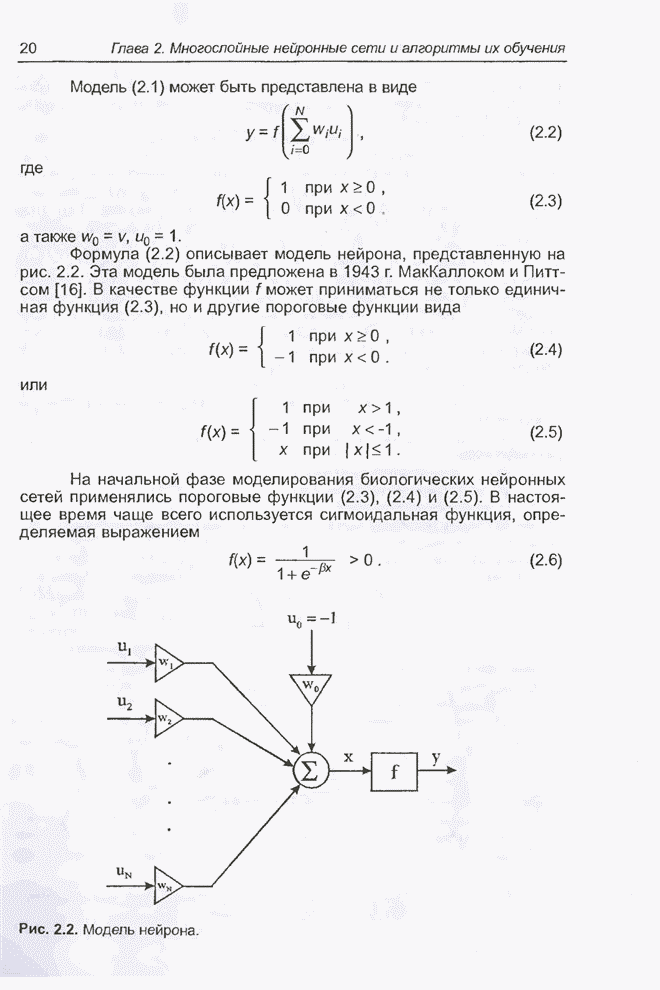
Метод обратного распространения ошибки применяется для обучения нейронных сетей в программе BrainMaker [50]. В примере 4.30 с использованием этой программы тестируется нейронная сеть, реализующая логическую систему XOR со значениями весов, рассчитанными в п. 4.11.1 с помощью программы Evolver. При решении примеров 4.31 и 4.32 демонстрируется гибридный подход, т.е. обучение этой же нейронной сети программой BrainMaker, но при начальных значениях весов, рассчитанных генетическим алгоритмом программы Evolver. В свою очередь, пример 4.33 иллюстрирует обучение нейронной сети, реализующей логическую систему XOR, при использовании только программы BrainMaker.
Пример 4.30
Протестировать с помощью программы BrainMaker нейронную сеть, реализующую логическую систему XOR (рис. 4.2) с весами, рассчитанными в примере 4.27 генетическим алгоритмом программы Evolver и представленными на рис. 4.101.
На рис. 4.123 показаны значения
весов, введенные в программу BrainMaker. Они сгруппированы в два блока,
разделенные пустой строкой. Первый блок содержит веса связей между входным и
скрытым слоем так, что для каждого из двух нейронов скрытого слоя приведены
веса связей со всеми входами, а последние элементы строк - это ![]() и
и ![]() . Второй блок содержит веса
связей между скрытым и выходным слоем, т.е. три веса выходного нейрона, причем
последним указан вес
. Второй блок содержит веса
связей между скрытым и выходным слоем, т.е. три веса выходного нейрона, причем
последним указан вес ![]() . В примере использовался интервал
значений весов
. В примере использовался интервал
значений весов ![]() .
.

Рис. 4.123. Показанные на рис. 4.101 веса нейронной сети, реализующей систему XOR (рис. 42) и подготовленной к тестированию программой BrainMaker.
Результаты тестирования сети
приведены на рис. 4.124 - 4.127. Можно сделать вывод о хорошей обученности
сети. Значения на выходах для четырех пар входных значений практически
совпадают с показанными на рис. 4.101. Абсолютная разность между заданным
значением ![]() и
выходным значением
и
выходным значением ![]() для
каждой пары входов
для
каждой пары входов ![]() и
и
![]() (рис. 4.124
- 4.127) оказалась меньше 0,025, поэтому сеть может считаться хорошо обученной
с толерантностью 0,025 и тем более - с толерантностью 0,1. Понижение порога
толерантности до 0,02 означало бы, что эта сеть не считается хорошо обученной и
что требуемый уровень обучения не может быть достигнут. Дальнейшее обучение при
толерантности, равной или меньшей 0,02, не изменяет значений весов, показанных
на рис. 4.123. Однако, как будет видно из примера 4.31, уменьшение
толерантности до 0,022 принесло бы эффект в виде «дообучения» сети.
(рис. 4.124
- 4.127) оказалась меньше 0,025, поэтому сеть может считаться хорошо обученной
с толерантностью 0,025 и тем более - с толерантностью 0,1. Понижение порога
толерантности до 0,02 означало бы, что эта сеть не считается хорошо обученной и
что требуемый уровень обучения не может быть достигнут. Дальнейшее обучение при
толерантности, равной или меньшей 0,02, не изменяет значений весов, показанных
на рис. 4.123. Однако, как будет видно из примера 4.31, уменьшение
толерантности до 0,022 принесло бы эффект в виде «дообучения» сети.

Рис. 4.124. Результат
тестирования программой BrainMaker нейронной сети из рис. 4.2 с начальными
значениями весов, представленными на рис. 4.123, для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.125. Результат
тестирования программой BrainMaker нейронной сети из рис 4.2 с начальными
значениями весов, представленными на рис. 4.123, для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.126. Результат
тестирования программой BrainMaker нейронной сети из рис. 4.2 с начальными
значениями весов, представленными на рис. 4.123, для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.127. Результат
тестирования программой BrainMaker нейронной сети из рис. 4.2 с начальными
значениями весов, представленными на рис. 4.123, для ![]() ,
, ![]() и
и ![]() .
.
Пример 4.31
Обучить с помощью программы BrainMaker нейронную сеть, реализующую логическую систему XOR (рис. 4.2) с весами, рассчитанными в примере 4.27 генетическим алгоритмом программы Evolver и представленными на рис. 4.100.
Вначале с помощью программы BrainMaker была протестирована нейронная сеть, показанная на рис. 4.2. В качестве начальных значений для алгоритма обучения программы BrainMaker использовались веса, рассчитанные генетическим алгоритмом программы Evolver. Следовательно, это типичный пример гибридного подхода, поскольку генетический алгоритм используется для нахождения начальных значений весов для градиентного алгоритма обратного распространения ошибки (backpropagation). Эти начальные значения в формате программы BrainMaker представлены на рис. 4.128, а соответствующие результаты тестирования сети - на рис. 4.129 - 4.132.

Рис. 4.128. Показанные на рис. 4.100 веса нейронной сети, реализующей систему XOR и подготовленной к обучению программой BrainMaker.

Рис. 4.129. Результат
тестирования нейронной сети из рис. 4.2 с начальными значениями весов,
представленными на рис. 4.128, для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.130. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.131. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.132. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.
Анализ результатов тестирования
свидетельствует о том, что они оказываются хуже, чем показанные на рис. 4.124 -
4.127, поскольку в предыдущем примере не было ни одной ошибки, а в текущем
примере в пяти случаях из 22 сеть дала неверный ответ. Кроме того, видно, что
толерантность выходного значения на рис. 4.130 превышает уровень 0,1.
Впоследствии сеть подверглась обучению с помощью программы BrainMaker с
толерантностью, равной 0,1. Результаты обучения иллюстрирует рис. 4.133. На
нижнем графике заметно уменьшение среднеквадратичной погрешности RMS (Root Mean
Squared) при выполнении 10 реализаций (runs) алгоритма. Погрешность RMS
отличается от погрешности ![]() , минимизировавшейся в примере 4.27, тем,
что
, минимизировавшейся в примере 4.27, тем,
что
 ,
,
 ,
,
где
![]() , а значение
, а значение
![]() в примере
4.27 равно 4.
в примере
4.27 равно 4.

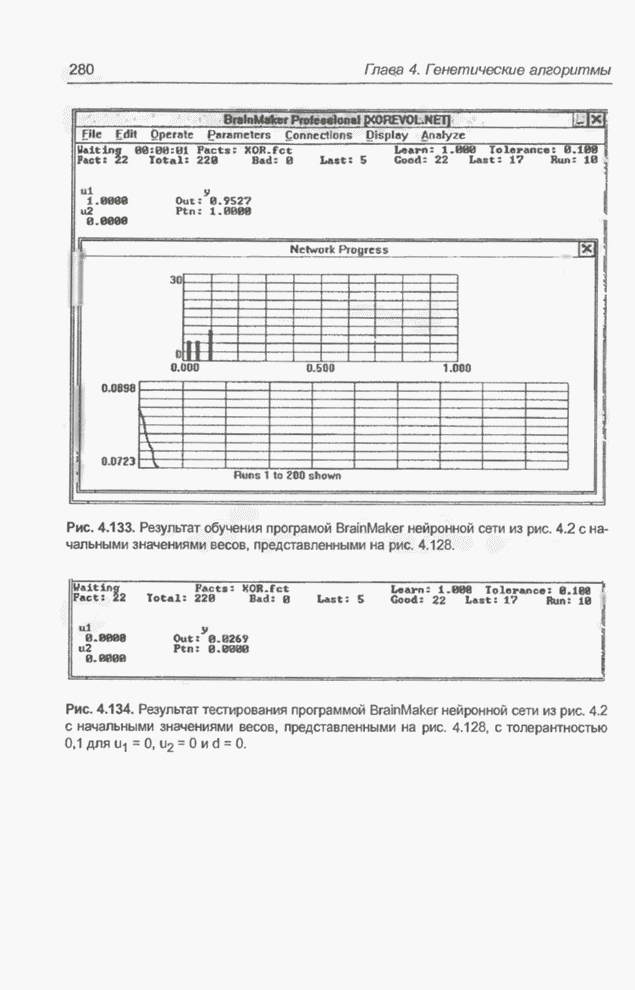
Рис. 4.133. Результат обучения программой BrainMaker нейронной сети из рис. 4.2 с начальными значениями весов, представленными на рис. 4.128.
С учетом различий, связанных с
взятием квадратного корня при расчете RMS, можно сравнить эту погрешность со
значением ![]() из
примера 4.27. Верхний график на рис. 4.133 представляет собой гистограмму
распределения погрешности рассчитанной как абсолютная разность между заданным
из
примера 4.27. Верхний график на рис. 4.133 представляет собой гистограмму
распределения погрешности рассчитанной как абсолютная разность между заданным ![]() и фактическим
и фактическим ![]() выходным значением
для каждой пары входов
выходным значением
для каждой пары входов ![]() и
и ![]() . На горизонтальной оси отложены значения
этой погрешности, а на вертикальной оси - количество выходных значений с такой
погрешностью. Представлены три уровня погрешности с толерантностью 0,1. В
верхней части рис. 4.133 указано значение
. На горизонтальной оси отложены значения
этой погрешности, а на вертикальной оси - количество выходных значений с такой
погрешностью. Представлены три уровня погрешности с толерантностью 0,1. В
верхней части рис. 4.133 указано значение ![]() для
для ![]() ,
, ![]() и
и ![]() (для упрощения здесь опущен индекс
(для упрощения здесь опущен индекс ![]() ). Результаты
тестирования этой сети для трех остальных комбинаций входных значений (для
системы XOR) приведены на рис. 4.134 - 4.136. Абсолютная разность между
эталонным (Ptn) и выходным (Out) значениями для рис. 4.133 равна 0,0473, для
рис. 4.134 - 0,0269, для рис. 4.135 - 0,0998 и для рис. 4.136 - 0,0979. Из
гистограммы на рис. 4.133 следует, что для шести из 22 входных пар
). Результаты
тестирования этой сети для трех остальных комбинаций входных значений (для
системы XOR) приведены на рис. 4.134 - 4.136. Абсолютная разность между
эталонным (Ptn) и выходным (Out) значениями для рис. 4.133 равна 0,0473, для
рис. 4.134 - 0,0269, для рис. 4.135 - 0,0998 и для рис. 4.136 - 0,0979. Из
гистограммы на рис. 4.133 следует, что для шести из 22 входных пар ![]() ,
, ![]() эта погрешность равна 0,0269,
такое же количество входных пар имеет погрешность 0,0473, а для оставшихся
входных пар эта погрешность составила около 0,099. Веса обученной таким образом
сети показаны на рис. 4.137.
эта погрешность равна 0,0269,
такое же количество входных пар имеет погрешность 0,0473, а для оставшихся
входных пар эта погрешность составила около 0,099. Веса обученной таким образом
сети показаны на рис. 4.137.

Рис. 4.134. Результат
тестирования программой BrainMaker нейронной сети из рис. 4.2 с начальными
значениями весов, представленными на рис. 4.128, с толерантностью 0,1 для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.135. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.136. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.137. Веса нейронной сети, обученной программой BrainMaker с толерантностью 0,1.
Сеть обучена с толерантностью
0,1. Это означает, что выходные значения должны не более чем на 10% отличаться
от значений 0 и 1 для того, чтобы модель системы XOR была признана корректной.
Следовательно, при подаче эталона 0 считаются правильными значения ![]() , меньшие или равные
0,1, а при подаче эталона 1 правильными будут значения
, меньшие или равные
0,1, а при подаче эталона 1 правильными будут значения ![]() , большие или равные 0,9.
, большие или равные 0,9.
Конечно, показанные на рис. 4.137 значения весов не могут рассматриваться в качестве оптимальных для системы XOR. Поэтому толерантность была уменьшена до 0,025, и процесс обучения продолжился. Полученные результаты приведены на рис. 4.138.

Рис. 4.138. Итоговая фаза последующего обучения программой BrainMaker сети с весами, показанными на рис. 4.137, при уровне толерантности 0,025.
Интересно сравнить достигнутое значение погрешности RMS с аналогичным показателем на рис. 4.133. Результаты тестирования обученной сети представлены на рис. 4.139 - 4.142. Значение абсолютной разности между эталоном и фактическим выходным значением на следующих друг за другом рисунках составляет 0,0252, 0,0246, 0,0239, 0,0247 соответственно, что отражает гистограмма на рис. 4.138.

Рис. 4.139. Результат
тестирования нейронной сети, обученной программой BrainMaker с толерантностью
0,025 (рис. 4.138), для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.140. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.141. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.142. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.
Значения весов для сети, обученной с толерантностью 0,025, приведены на рис. 4.143. Интересно сравнить его с рис. 4.137. Более поздние результаты оказываются гораздо ближе к оптимальным. Далее была предпринята попытка еще лучше обучить сеть с уменьшением толерантности до 0,02. К сожалению, эта попытка завершилась неудачей, поскольку способности сети к обучению оказались исчерпанными. Однако при фиксации толерантности на уровне 0,023 был достигнут конечный эффект, показанный на рис. 4.144. Результаты тестирования сети, обученной подобным образом, представлены на рис. 4.145 - 4.148, а значения весов этой сети - на рис. 4.149. Еще лучший результат обучения, который иллюстрируется рис. 4.150, удалось получить при толерантности 0,022. Результаты тестирования сети, обученной подобным образом, представлены на рис. 4.151 - 4.154, а значения весов этой сети - на рис. 4.155.

Рис. 4.143. Веса нейронной сети, обученной программой BrainMaker с толерантностью 0,025 (рис. 4.138).

Рис. 4.144. Итоговая фаза последующего обучения программой BrainMaker сети с весами, показанными на рис. 4.143, при уровне толерантности 0,023.

Рис. 4.145. Результат
тестирования нейронной сети, обученной программой BrainMaker с толерантностью
0,023 (рис. 4.144), для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.146. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.147. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.148. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.149. Веса нейронной сети, обученной программой BrainMaker с толерантностью 0,023 (рис. 4.144).

Рис. 4.150. Итоговая фаза последующего обучения программой BrainMaker сети с весами, показанными на рис. 4.149, при уровне толерантности 0,022.

Рис. 4.151. Результат
тестирования нейронной сети, обученной программой BrainMaker с толерантностью
0.022 (рис. 4.150), для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.152. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.153. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.154. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.155. Веса нейронной сети, обученной программой BrainMaker с толерантностью 0.022 (рис. 4.150).
Дальнейшее снижение уровня толерантности до 0,021, к сожалению, уже не ведет к большей обученности сети, даже если бы программа работала еще в течение многих часов. Таким образом, наилучшим решением считается сеть со значениями весов, показанными на рис. 4.155, которые следует сравнить с набором весов для примера 4.27, приведенными на рис. 4.101. Нетрудно заметить, что объединение генетического алгоритма программы Evolver с программой BrainMaker дало лучшие результаты, чем на рис. 4.101. Если бы вычисления сразу проводились с толерантностью 0,022, а в качестве начальных весов принимались значения с рис. 4.128, то результат был бы лучше, чем на рис. 4.101. Аналогичный результат можно было ожидать и в примере 4.30 при установлении уровня толерантности, равным 0,022.
Пример 4.32
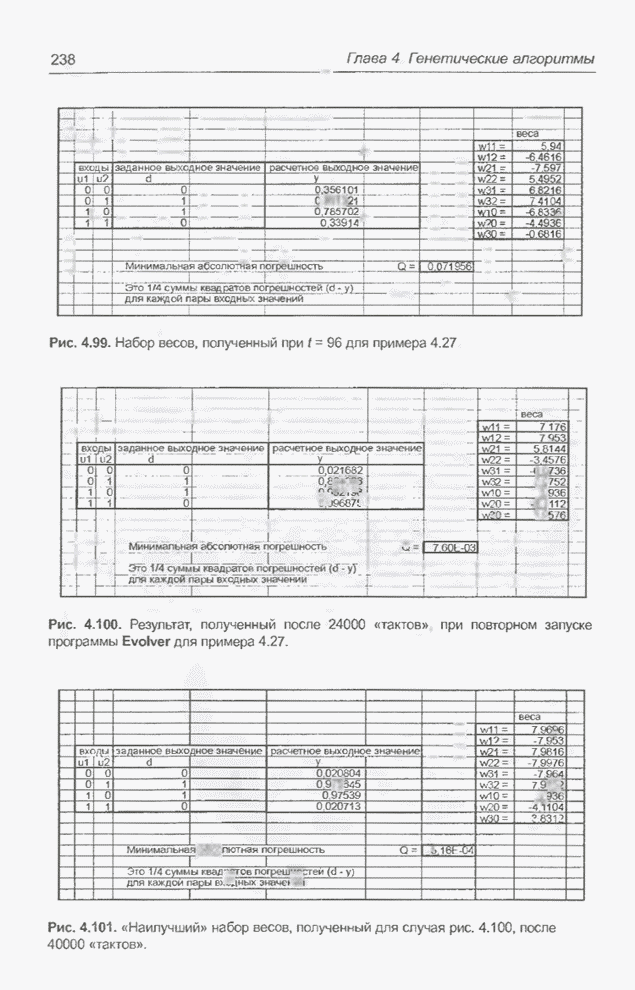
Обучить с помощью программы BrainMaker нейронную сеть, реализующую логическую систему XOR (рис. 4.2) с начальными значениями весов, рассчитанными в примере 4.27 генетическим алгоритмом программы Evolver и представленными на рис. 4.99. Это еще один пример гибридного подхода к обучению весов нейронной сети, реализующей логическую систему XOR. Он очень похож на предыдущий пример, однако отличается набором начальных значений весов, полученных за меньшее время выполнения генетического алгоритма и, следовательно, более далеких от оптимальных.
Толерантность погрешности принята
равной 0,025, что означает 2,5% допустимой погрешности, т.е. разницы между
фактическим выходным значением и заданным значением - эталоном. Поэтому для
эталона, равного 0, корректным будет признаваться выходное значение от 0 до
0,025, а для эталона, равного 0 - значение от 0,975 до 1. Начальный набор весов
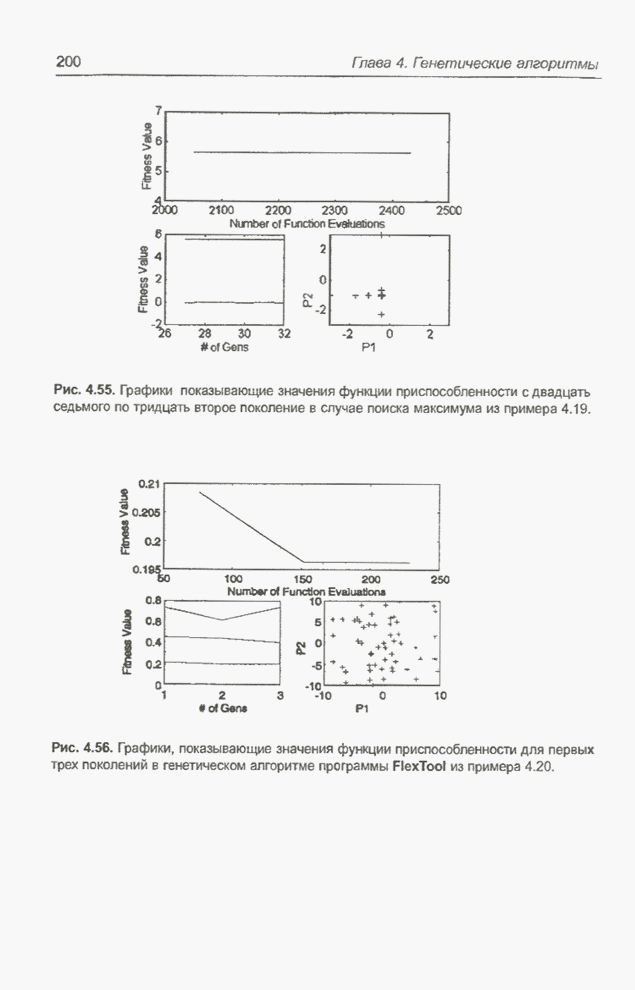
для программы BrainMaker представлен на рис. 4.156, а на рис. 4.157 - 4.160
показаны результаты тестирования сети. Видно, что выходные значения ![]() для конкретных пар
входов весьма близки к приведенным на рис. 4.99. Сеть не может считаться
обученной. На 22 тестирующих выборках только 5 раз реакция на выходе была
корректной, а в 17 случаях - ошибочной. Набор весов с рис. 4.156 был получен
после всего лишь 96 «тактов» функционирования программы Evolver (что
соответствует менее чем 2 итерациям классического генетического алгоритма).
Результаты обучения нейронной сети с этими весами программой BrainMaker с
толерантностью погрешности, равной 0,025, представлены на рис. 4.161. Значение
погрешности RMS с графика этого рисунка легко сравнить со значением погрешности
для конкретных пар
входов весьма близки к приведенным на рис. 4.99. Сеть не может считаться
обученной. На 22 тестирующих выборках только 5 раз реакция на выходе была
корректной, а в 17 случаях - ошибочной. Набор весов с рис. 4.156 был получен
после всего лишь 96 «тактов» функционирования программы Evolver (что
соответствует менее чем 2 итерациям классического генетического алгоритма).
Результаты обучения нейронной сети с этими весами программой BrainMaker с
толерантностью погрешности, равной 0,025, представлены на рис. 4.161. Значение
погрешности RMS с графика этого рисунка легко сравнить со значением погрешности
![]() на рис.
4.99, 4.100 и 4.101. Заметно, что выходные значения
на рис.
4.99, 4.100 и 4.101. Заметно, что выходные значения ![]() для каждой пары входов системы
XOR укладываются в границы 2,5% толерантности. Сеть обучилась достаточно быстро
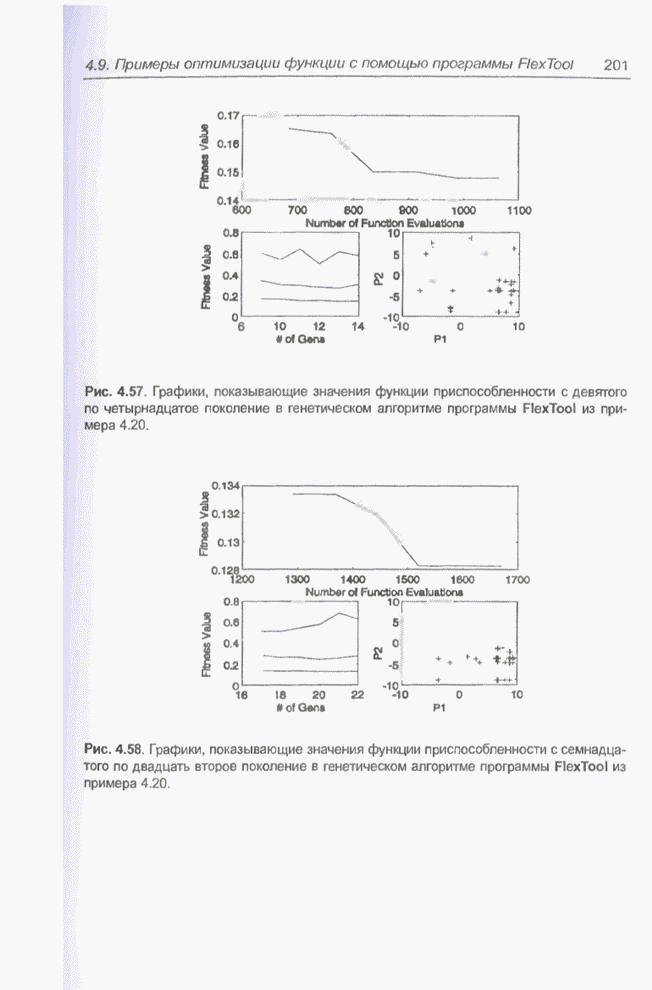
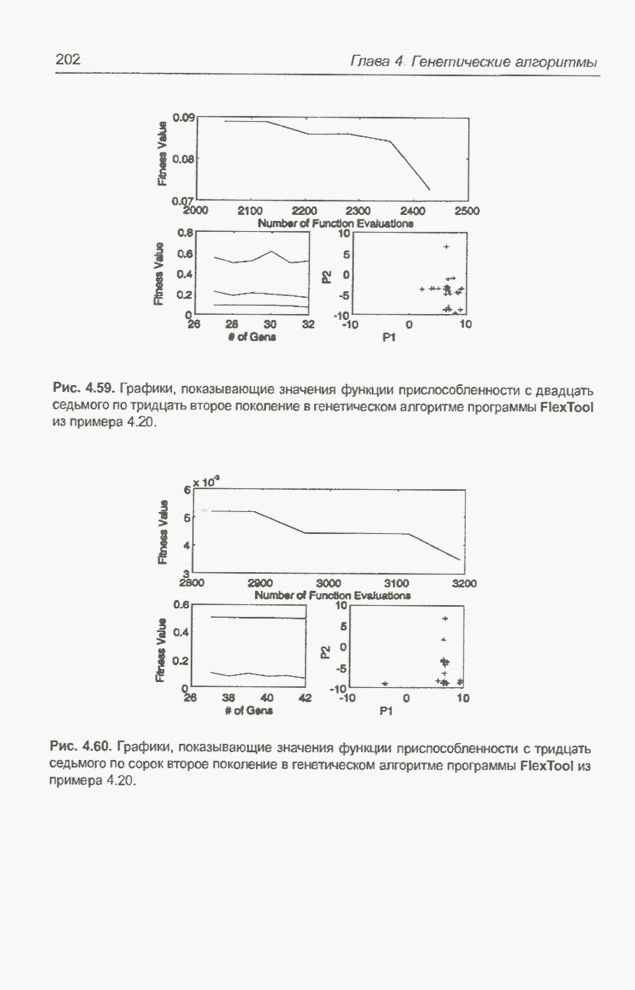
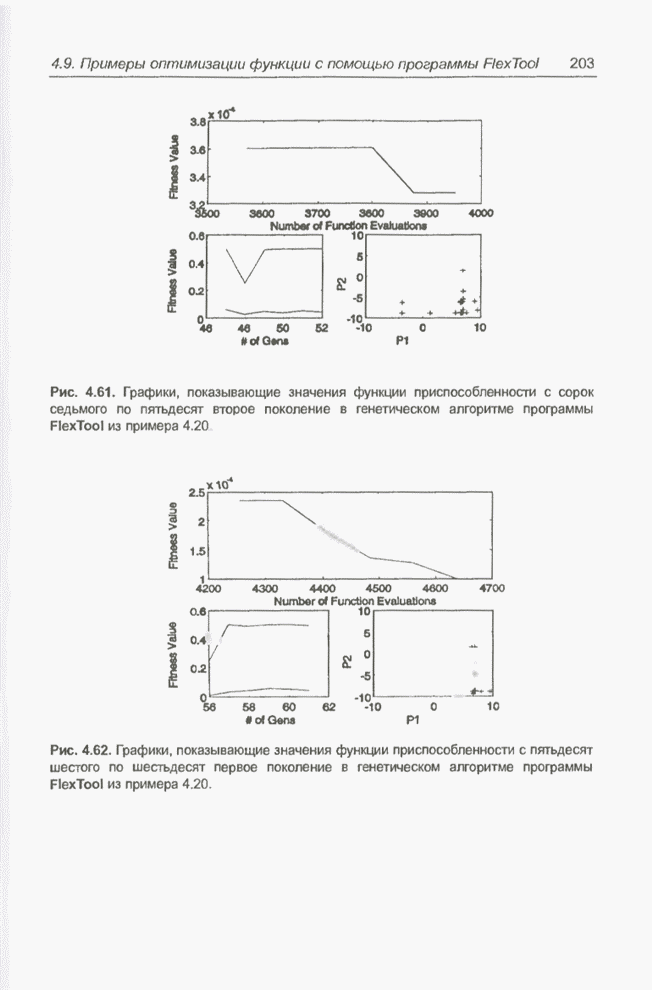
- за 104 прогона (runs). На рис. 4.165 представлены веса обученной сети, а на
рис. 4.161 - 4.164 - результаты ее тестирования. Представляет интерес
сопоставление рис. 4.165 и 4.143, поскольку они отражают обучение с одной и той
же толерантностью, равной 0,025. Если продолжить обучение сети при меньшем
значении толерантности, то (по аналогии с примером 4.31) можно найти значения
весов, еще более близкие к оптимальным и практически совпадающие с показанными
на рис. 4.155.
для каждой пары входов системы
XOR укладываются в границы 2,5% толерантности. Сеть обучилась достаточно быстро
- за 104 прогона (runs). На рис. 4.165 представлены веса обученной сети, а на
рис. 4.161 - 4.164 - результаты ее тестирования. Представляет интерес
сопоставление рис. 4.165 и 4.143, поскольку они отражают обучение с одной и той
же толерантностью, равной 0,025. Если продолжить обучение сети при меньшем
значении толерантности, то (по аналогии с примером 4.31) можно найти значения
весов, еще более близкие к оптимальным и практически совпадающие с показанными
на рис. 4.155.

Рис. 4.156. Исходное множество весов для программы BrainMaker. полученное с помощью генетического алгоритма программы Evolver.

Рис. 4.157. Результат
тестирования нейронной сети с весами, показанными на рис. 4.156, для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.158. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.159. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.160. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

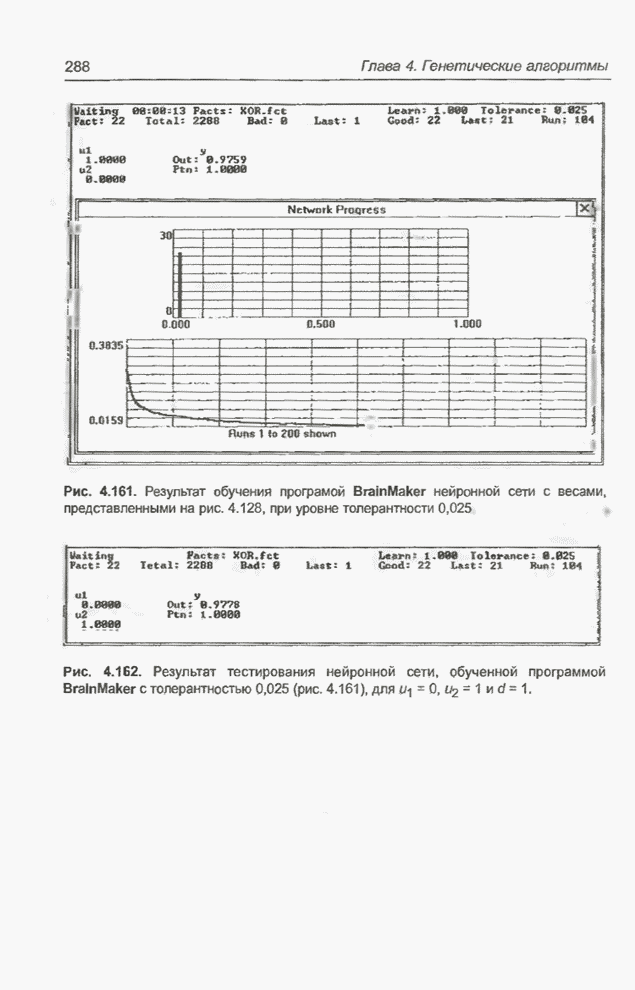
Рис. 4.161. Результат обучения программой BrainMaker нейронной сети с весами, представленными на рис. 4.128, при уровне толерантности 0,025

Рис. 4.162. Результат
тестирования нейронной сети, обученной программой BrainMaker с толерантностью
0,025 (рис. 4.161), для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.163. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.164. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.165. Веса нейронной сети (при начальных значениях, показанных на рис 4.156), обученной программой BrainMaker с толерантностью 0,025 .
Рассмотрим теперь эффект обучения нейронной сети, реализующей логическую систему XOR, с помощью только программы BrainMaker без применения генетического алгоритма.
Пример 4.33
Обучить с помощью программы BrainMaker нейронную сеть, реализующую логическую систему XOR (рис. 4.2) с начальными значениями весов, представленными на рис. 4.96.
Показанные на рис. 4.96 значения
весов сгенерированы случайным образом. На рис. 4.166 эти веса представлены в
формате программы BrainMaker. Нейронная сеть с этими весами не может считаться
обученной. Результаты ее тестирования приведены на рис. 4.167 - 4.170. Заметно,
что выходные значения ![]() совершенно не соответствуют эталону 1, а
для эталона 0 выходные значения также не попадают в границы 10% толерантности.
Для всех 22 тестирующих выборок получены ошибочные выходные сигналы.
совершенно не соответствуют эталону 1, а
для эталона 0 выходные значения также не попадают в границы 10% толерантности.
Для всех 22 тестирующих выборок получены ошибочные выходные сигналы.

Рис. 4.166. Сгенерированный случайным образом исходный набор весов для нейронной сети, реализующей систему XOR.

Рис. 4.167. Результат
тестирования нейронной сети с весами, показанными на рис. 4.166, для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.168. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.169. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис 4.170. Результат тестирования
той же сети для ![]() ,
,
![]() и
и ![]() .
.
Вначале обучение сети проводилось
с толерантностью погрешности, равной 0,1. Процесс обучения иллюстрируют графики
на рис. 4.171. На рис. 4.172 показаны значения весов, полученные после 191
прогона (runs) алгоритма. Продолжение графика с рис. 4.171 демонстрируется на
рис. 4.173, а его завершение - на рис. 4.174. Полученные значения весов
нейронной сети с толерантностью погрешности, равной 0,1, представлены на рис.
4.175. Заметим, что значение погрешности RMS для этого случая (см. рис. 4.174)
достаточно близко к значению погрешности ![]() , рассчитанному программой Evolver в
примерах 4.23 - 4.27 для значений весов с рис. 4.175 (среднеквадратичная
погрешность
, рассчитанному программой Evolver в
примерах 4.23 - 4.27 для значений весов с рис. 4.175 (среднеквадратичная
погрешность ![]() ).
).

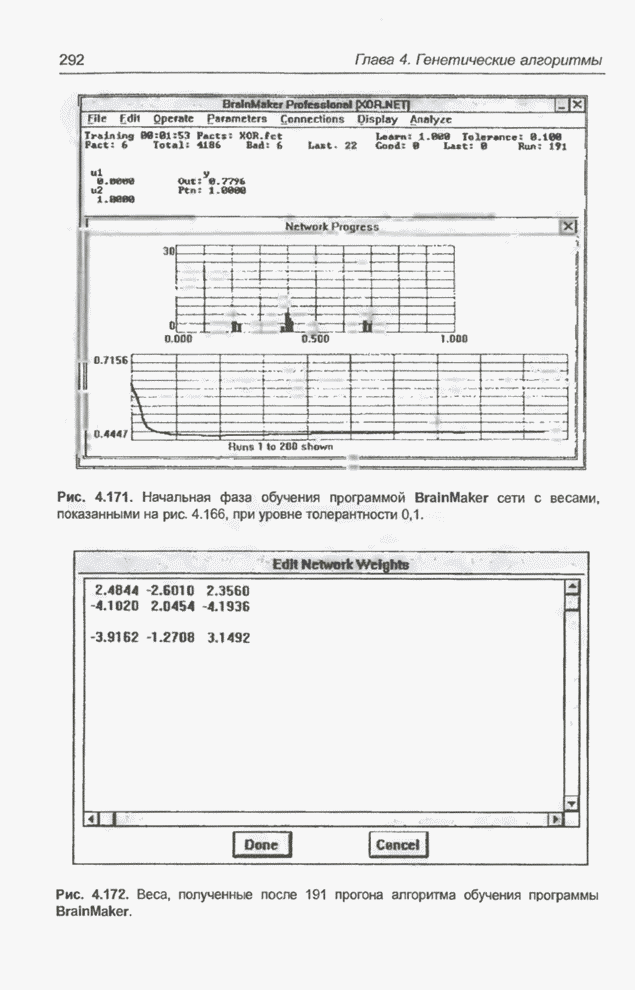
Рис. 4.171. Начальная фаза обучения программой BrainMaker сети с весами, показанными на рис. 4.166, при уровне толерантности 0,1.

Рис. 4.172. Веса, полученные после 191 прогона алгоритма обучения программы BrainMaker.

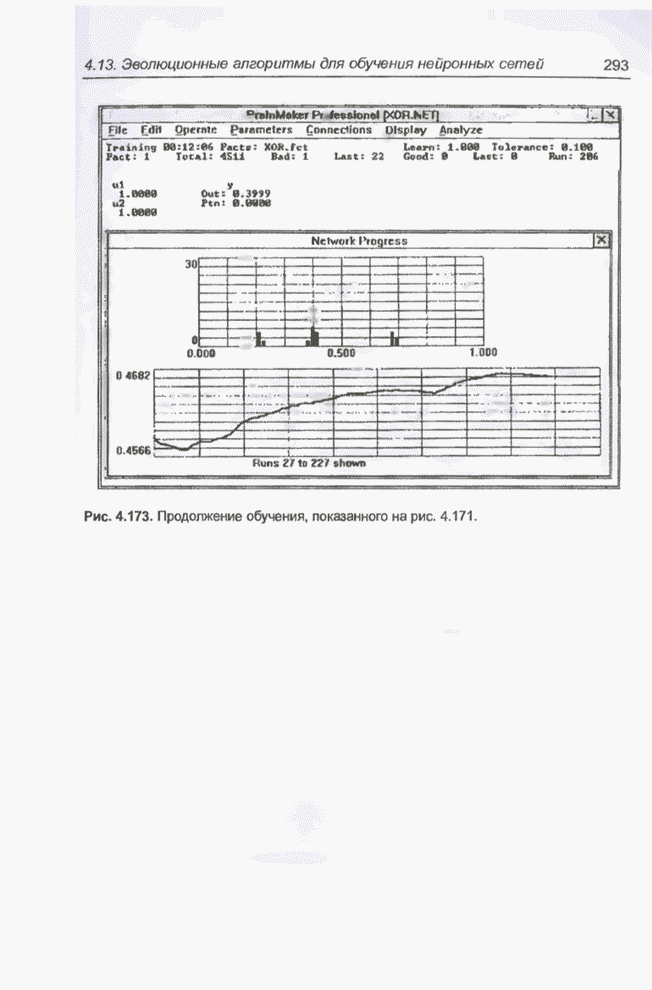
Рис. 4.173. Продолжение обучения, показанного на рис. 4.171.

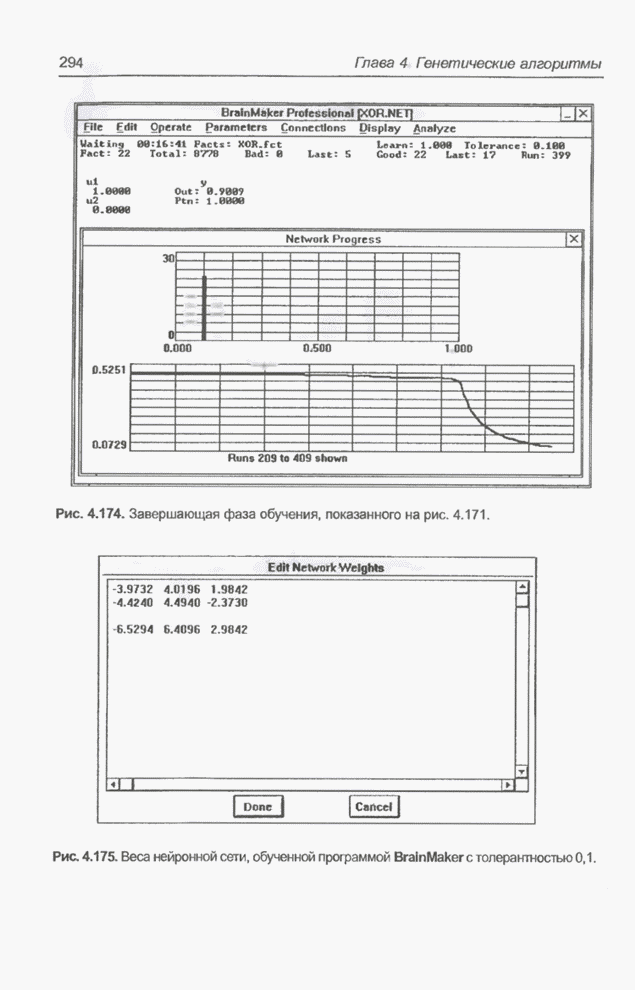
Рис. 4.174. Завершающая фаза обучения, показанного на рис. 4.171.

Рис. 4.175. Веса нейронной сети, обученной программой BrainMaker с толерантностью 0,1.
Нейронная сеть с весами,
показанными на рис. 4.166, была обучена с толерантностью погрешности 0,1 за 399
прогонов алгоритма программы BrainMaker. Результаты тестирования сформированной
сети представлены на рис. 4.176-4.178. Для входов ![]() и
и ![]() решение приведено на рис. 4.174. Сеть
может считаться обученной, поскольку в ходе тестирования не зарегистрированы
ошибочные отклики. Далее обучение сети продолжилось с толерантностью
погрешности, равной 0.025. После 510 прогонов получены графики, изображенные на
рис. 4.179, и значения весов, приведенные на рис. 4.180. Значение погрешности
RMS для этой комбинации весов можно получить с графика на рис. 4.179. При
толерантности погрешности 0,025 сеть плохо поддавалась обучению, поэтому после
4000 прогонов уровень толерантности был увеличен до 0,03. Графики и значения
весов на момент изменения уровня показаны на рис. 4.181 и 4.182 соответственно.
После увеличения значения толерантности выполнение программы очень быстро -
после 402 прогонов - завершилось. Достигнутый эффект можно наблюдать на рис.
4.183, а полученные значения весов - на рис. 4.184.
решение приведено на рис. 4.174. Сеть
может считаться обученной, поскольку в ходе тестирования не зарегистрированы
ошибочные отклики. Далее обучение сети продолжилось с толерантностью
погрешности, равной 0.025. После 510 прогонов получены графики, изображенные на
рис. 4.179, и значения весов, приведенные на рис. 4.180. Значение погрешности
RMS для этой комбинации весов можно получить с графика на рис. 4.179. При
толерантности погрешности 0,025 сеть плохо поддавалась обучению, поэтому после
4000 прогонов уровень толерантности был увеличен до 0,03. Графики и значения
весов на момент изменения уровня показаны на рис. 4.181 и 4.182 соответственно.
После увеличения значения толерантности выполнение программы очень быстро -
после 402 прогонов - завершилось. Достигнутый эффект можно наблюдать на рис.
4.183, а полученные значения весов - на рис. 4.184.

Рис. 4.176. Результат
тестирования нейронной сети, обученной программой BrainMaker с толерантностью
0,025, для ![]() ,
,
![]() и
и ![]() .
.

Рис. 4.177. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.178. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

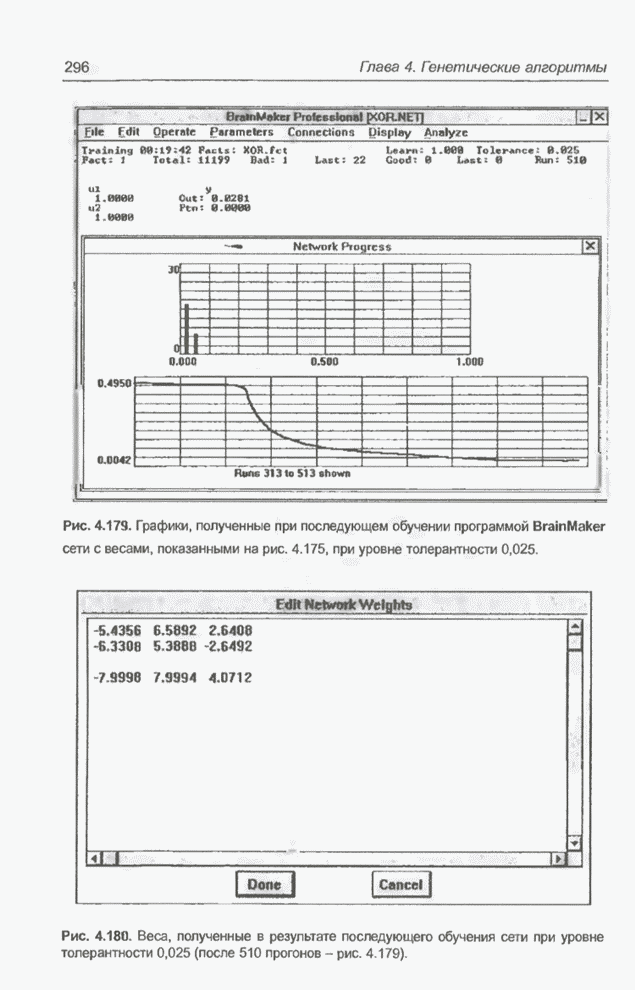
Рис. 4.179. Графики, полученные при последующем обучении программой BrainMaker сети с весами, показанными на рис. 4.175, при уровне толерантности 0,025.

Рис. 4.180. Веса, полученные в результате последующего обучения сети при уровне толерантности 0,025 (после 510 прогонов - рис. 4.179).

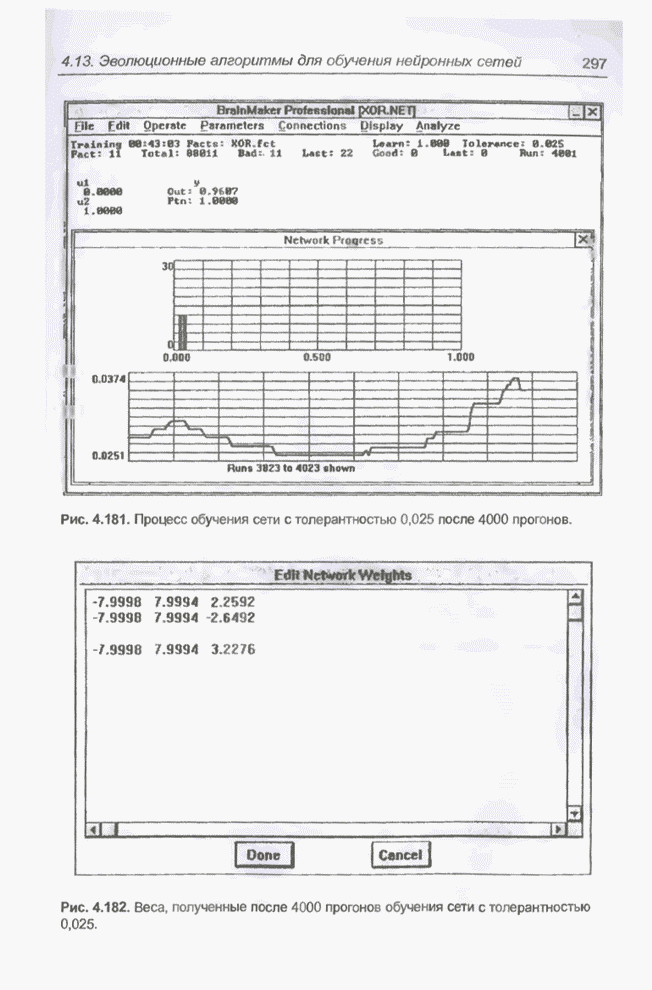
Рис. 4.181. Процесс обучения сети с толерантностью 0,025 после 4000 прогонов.

Рис. 4.182. Веса, полученные после 4000 прогонов обучения сети с толерантностью 0,025.

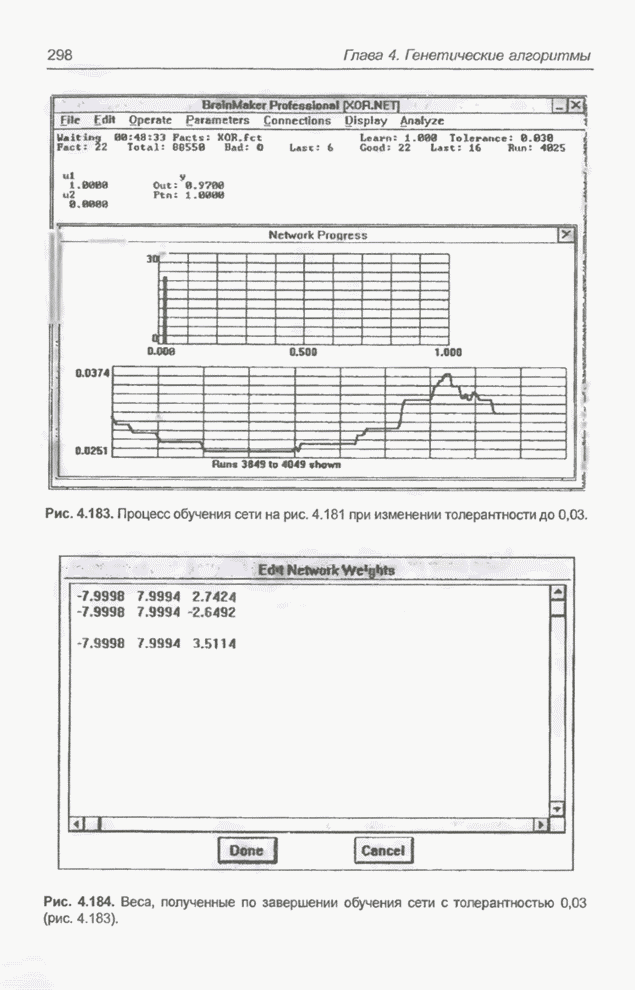
Рис. 4.183. Процесс обучения сети на рис. 4.181 при изменении толерантности до 0,03.

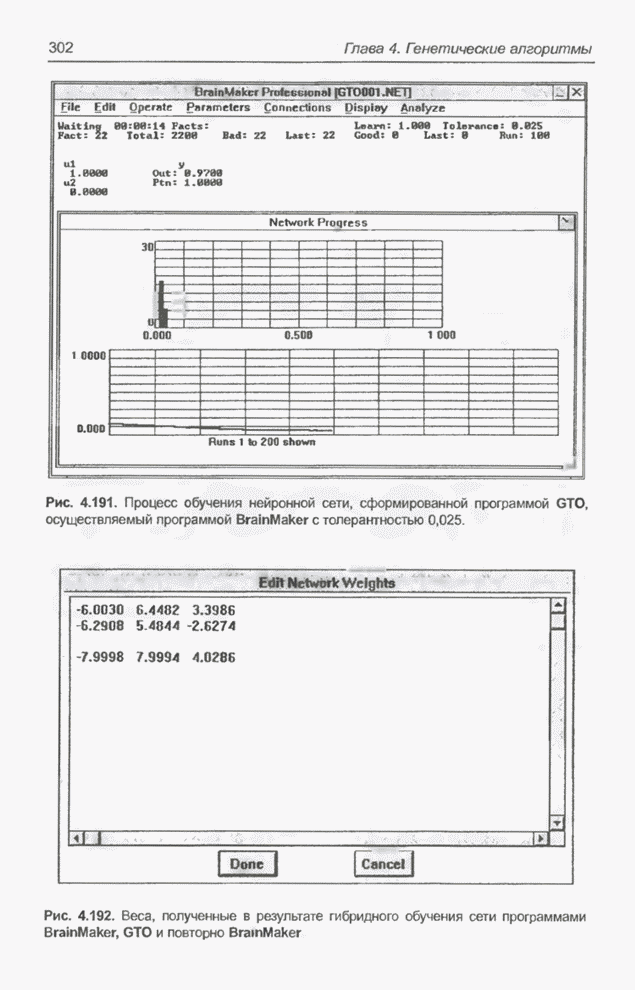
Рис. 4.184. Веса, полученные по завершении обучения сети с толерантностью 0,03 (рис. 4.183).
В результате обучения нейронной
сети, реализующей логическую систему XOR с начальными значениями весов,
представленными на рис. 4.166 и 4.96, была найдена еще одна комбинация весов,
подобная полученным при минимизации погрешности ![]() с помощью программы Evolver. В принципе,
сформированный в текущем примере и представленный на рис. 4.184 набор весов
сети, обученной с помощью программы BrainMaker, отличается от двух аналогичных
комбинаций «наилучших» весов из примера 4.27 только знаками. Например, если
сравнить веса с рис. 4.184 с весами, показанными на рис 4.101, то можно
зафиксировать, что веса
с помощью программы Evolver. В принципе,
сформированный в текущем примере и представленный на рис. 4.184 набор весов
сети, обученной с помощью программы BrainMaker, отличается от двух аналогичных
комбинаций «наилучших» весов из примера 4.27 только знаками. Например, если
сравнить веса с рис. 4.184 с весами, показанными на рис 4.101, то можно
зафиксировать, что веса ![]() ,
, ![]() ,
, ![]() ,
, ![]() изменили знаки на противоположные, а
веса
изменили знаки на противоположные, а
веса ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() имеют в обоих случаях одни и те же
знаки, т.е.
имеют в обоих случаях одни и те же
знаки, т.е. ![]() и
и
![]() остались
отрицательными, a
остались
отрицательными, a ![]() ,
,
![]() ,
, ![]() - положительными.
Результаты тестирования сформированной сети (с весами на рис. 4.184) для входов
- положительными.
Результаты тестирования сформированной сети (с весами на рис. 4.184) для входов
![]() и
и ![]() приведены на рис.
4.183. Для пары входов
приведены на рис.
4.183. Для пары входов ![]() и
и ![]() значение
значение ![]() осталось неизменным, т.е. равным 0,9700.
осталось неизменным, т.е. равным 0,9700.
Для ![]() и
и ![]() , а также для
, а также для ![]() и
и ![]() выходное значение
выходное значение ![]() равно 0,0301.
равно 0,0301.
Рассмотренные примеры иллюстрируют гибридный подход, основанный на объединении двух различных методов - генетического алгоритма и градиентного метода обучения весов нейронной сети, известного под названием обратного распространения ошибки. В примере 4.27 для обучения нейронной сети применялся генетический алгоритм программы Evolver. После 40 000 «тактов» функционирования этого алгоритма (что соответствует 800 поколениям классического генетического алгоритма) получено близкое к оптимальному решение. Однако, как показывают примеры 4.30 и 4.31, этот результат можно еще улучшить за счет «дообучения» с помощью градиентного алгоритма.
Примеры 4.31 и 4.32 представляют типичный способ такого гибридного подхода, когда генетический алгоритм применяется только для выбора начальной точки (в данном случае - исходного множества весов) для градиентного метода. В примере 4.31 генетический алгоритм функционировал дольше, чем в примере 4.32, поэтому начальная точка для метода обратного распространения ошибки в примере 4.32 находится на большем расстоянии от точки оптимального решения, чем в примере 4.31. Следует обратить внимание на факт, что длительность «дообучения» не имеет большого значения. Градиентный алгоритм выполняется быстрее генетического, так как в последнем предполагается просмотр всей популяции возможных решений.
В примере 4.33 продемонстрирован способ обучения нейронной сети методом обратного распространения ошибки (программа BrainMaker). Полученный результат оказался еще более близким к оптимальному, чем при использовании только генетического алгоритма (пример 4.30). Однако необходимо подчеркнуть, что градиентный метод не всегда приводит к достижению ожидаемого результата, который зависит от начальной точки. При другом, сгенерированном случайным образом исходном множестве весов сеть может оказаться «необучаемой», что встречается довольно часто. Кроме того, принципиальным недостатком градиентных методов оказывается их «застревание» в локальных оптимумах. Это можно предотвратить применением генетического алгоритма - только для того, чтобы найти какую-либо точку, настолько близкую к глобальному оптимуму, что градиентный алгоритм при старте из этой точки не «застрянет» ни в каком локальном оптимуме и быстро найдет глобальное решение.
В рассмотренных примерах использовался генетический (эволюционный) алгоритм программы Evolver. Конечно, для достижения тех же целей можно было применять и программу FlexTool (п. 4.9), которая допускает такой же интервал изменения значений весов от -7 до 8, как и программа BrainMaker. Для выбора исходного множества весов нейронной сети также пригодны и другие реализации генетического (эволюционного) алгоритма.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Предисловие к русскому изданию
- ГЛАВА 1. ВВЕДЕНИЕ
- Список литературы
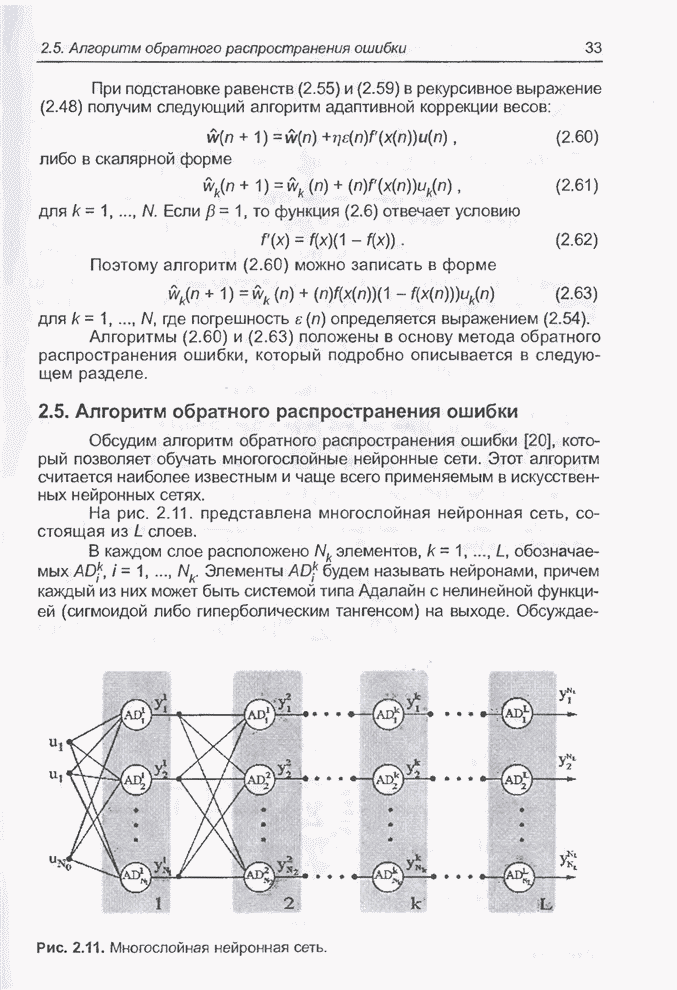
- ГЛАВА 2. МНОГОСЛОЙНЫЕ НЕЙРОННЫЕ СЕТИ И АЛГОРИТМЫ ИХ ОБУЧЕНИЯ
- 2.1. Введение
- 2.2. Нейрон и его модели
- 2.3. Персептрон
- 2.4. Системы типа Адалайн
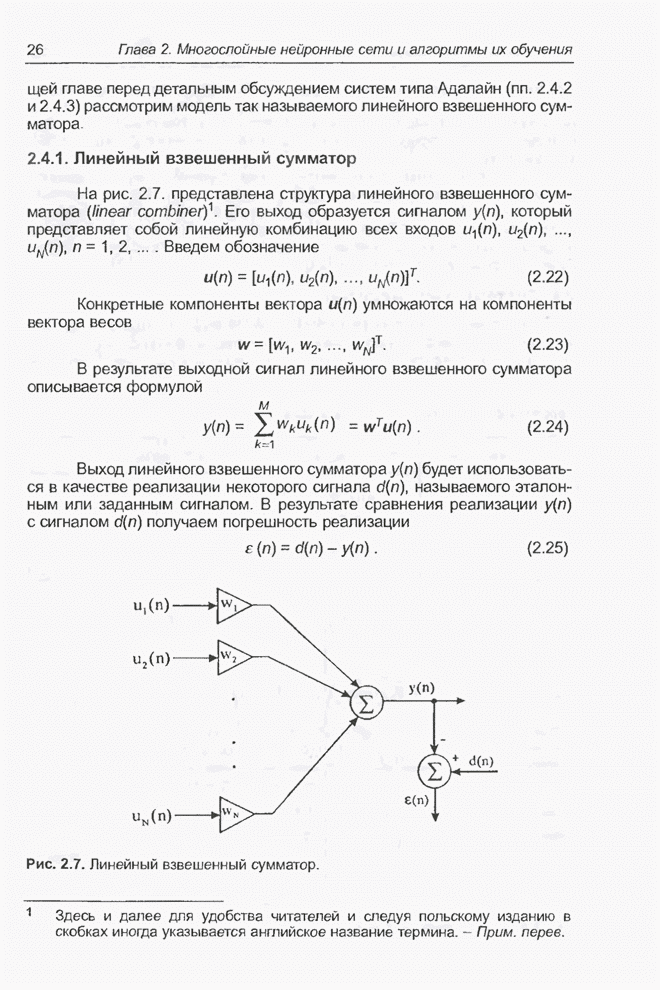
- 2.4.1. Линейный взвешенный сумматор
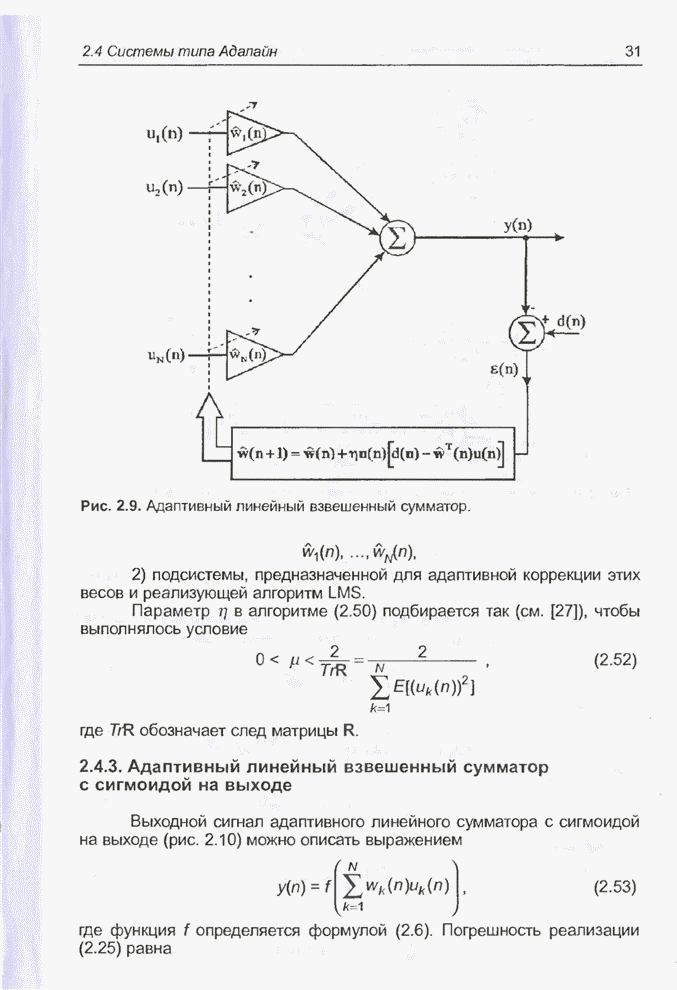
- 2.4.2. Адаптивный линейный взвешенный сумматор
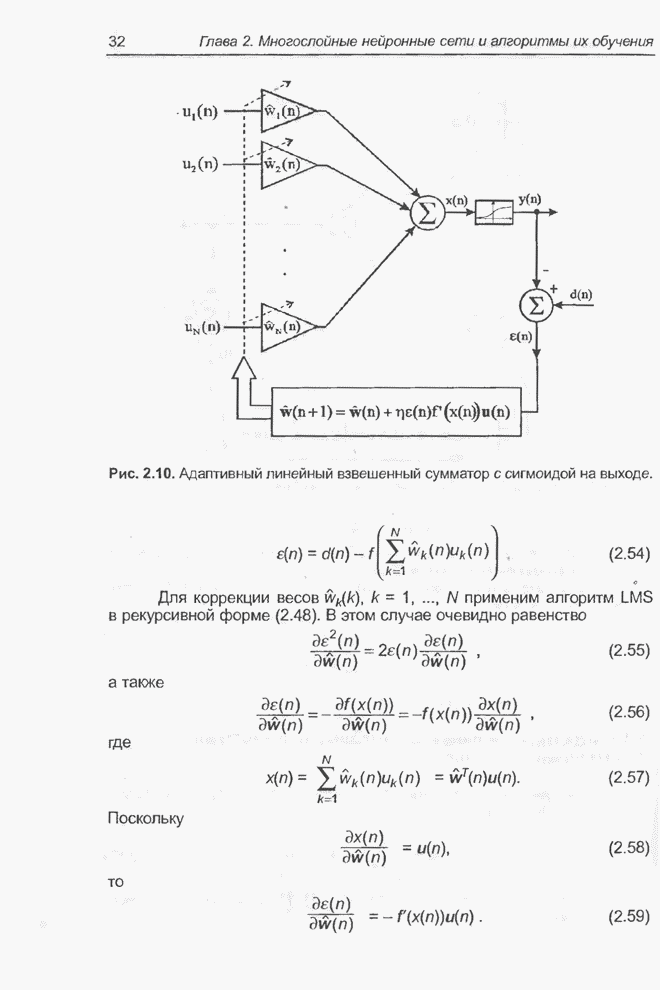
- 2.4.3. Адаптивный линейный взвешенный сумматор с сигмоидой на выходе
- 2.5. Алгоритм обратного распространения ошибки
- 2.6. Применение рекуррентного метода наименьших квадратов для обучения нейронных сетей
- Список литературы
- ГЛАВA3. НЕЧЕТКИЕ МНОЖЕСТВА И НЕЧЕТКИЙ ВЫВОД
- 3.1. Введение
- 3.2. Основные понятия и определения теории нечетких множеств
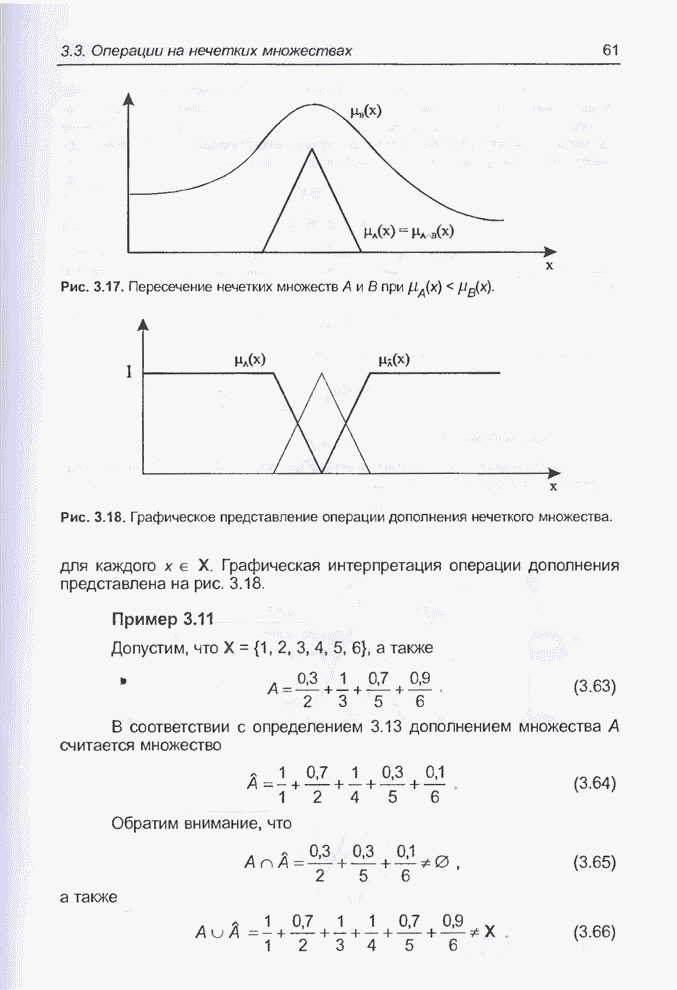
- 3.3. Операции на нечетких множествах
- 3.4. Принцип расширения
- 3.5. Нечеткие числа
- 3.6. Треугольные нормы
- 3.7. Нечеткие отношения и их свойства
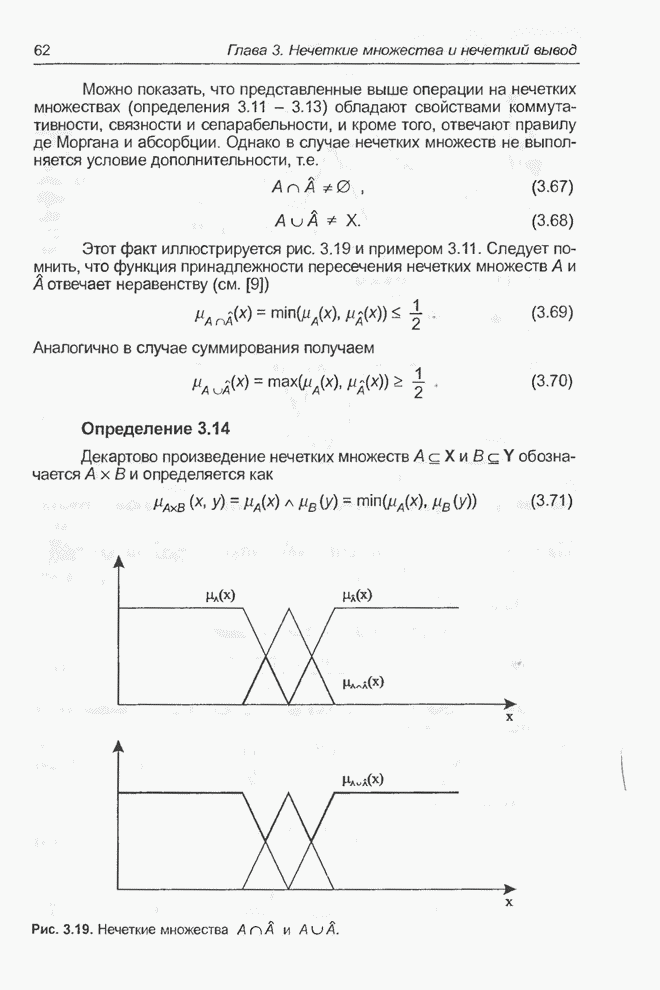
- 3.8. Нечеткий вывод
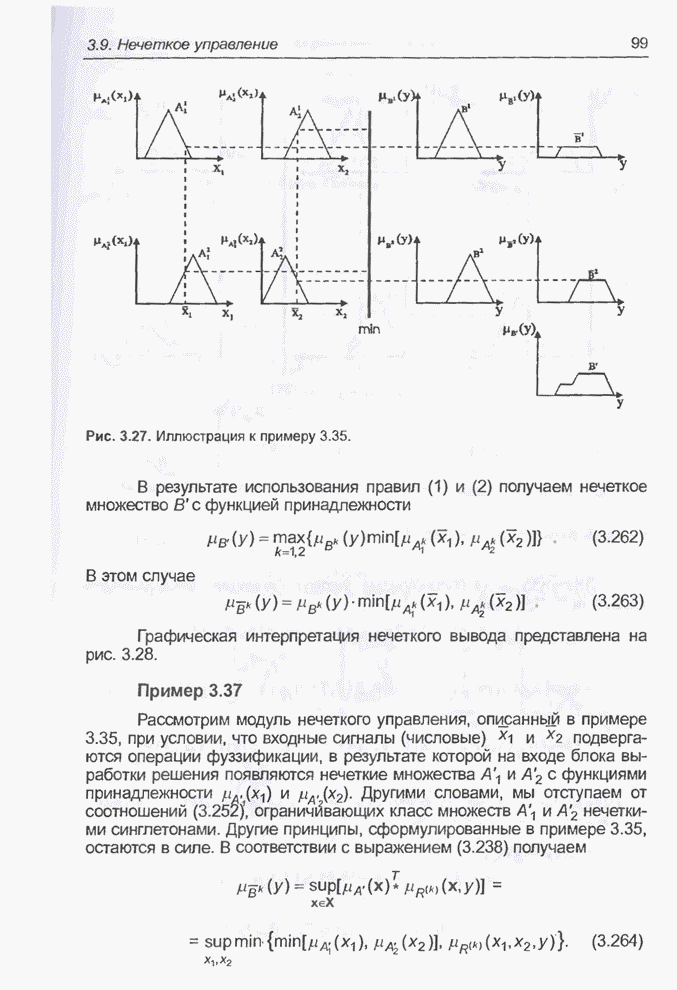
- 3.9. Нечеткое управление
- 3.9.1. Классический модуль нечеткого управления
- 3.9.2. Метод нечеткого управления Такаги-Сугено
- 3.10. Проектирование базы нечетких правил на основе численных данных
- 3.10.1. Построение нечетких правил
- 3.10.2. Задача парковки грузовика
- 3.10.3. Примечание
- Список литературы
- ГЛАВА 4. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 4.1. Введение
- 4.2. Генетические алгоритмы и традиционные методы оптимизации
- 4.3. Основные понятия генетических алгоритмов
- 4.4. Классический генетический алгоритм
- 4.5. Иллюстрация выполнения классического генетического алгоритма
- 4.6. Кодирование параметров задачи в генетическом алгоритме
- 4.7. Основная теорема о генетических алгоритмах
- 4.8. Модификации классического генетического алгоритма
- 4.8.1. Методы селекции
- 4.8.2. Особые процедуры репродукции
- 4.8.3. Генетические операторы
- 4.8.4. Методы кодирования
- 4.8.5. Масштабирование функции приспособленности
- 4.8.6. Ниши в генетическом алгоритме
- 4.8.7. Генетические алгоритмы для многокритериальной оптимизации
- 4.8.8. Генетические микроалгоритмы
- 4.9. Примеры оптимизации функции с помощью программы FlexTool
- 4.10. Эволюционные алгоритмы
- 4.11. Приложения эволюционных алгоритмов
- 4.11.1. Примеры оптимизации функции с помощью программы Evolver
- 4.11.2. Решение комбинаторных задач с помощью программы Evolver
- 4.12. Эволюционные алгоритмы в нейронных сетях
- 4.12.1. Независимое применение генетических алгоритмов и нейронных сетей
- 4.12.2. Нейронные сети для поддержки генетических алгоритмов
- 4.12.3. Генетические алгоритмы для поддержки нейронных сетей
- 4.12.4. Применение генетических алгоритмов для обучения нейронных сетей
- 4.12.5. Генетические алгоритмы для выбора топологии нейронных сетей
- 4.12.6. Адаптивные взаимодействующие системы
- 4.12.7. Типовой цикл эволюции
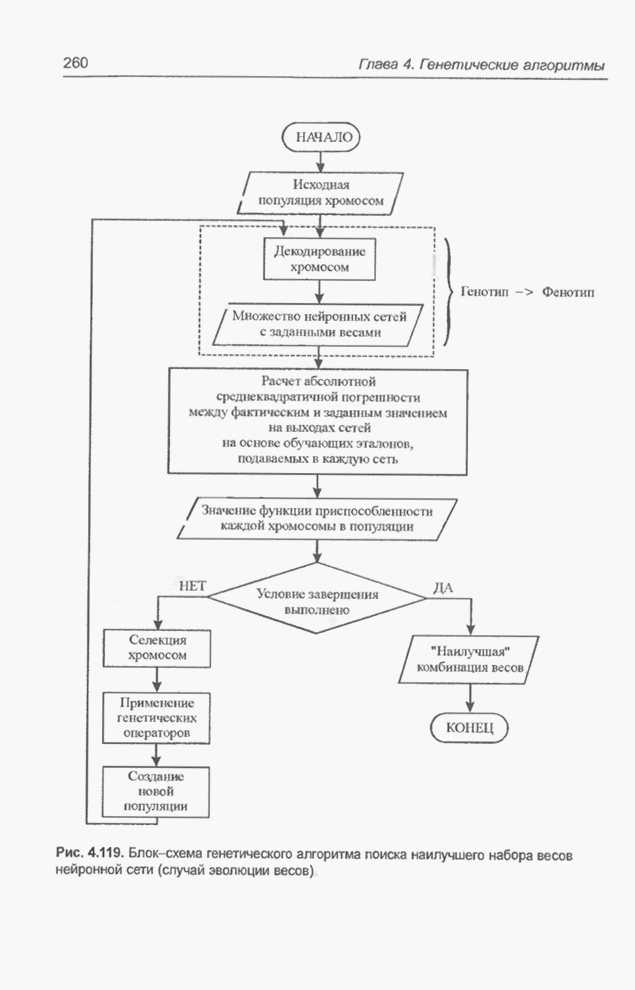
- 4.12.7.1. Эволюция весов связей
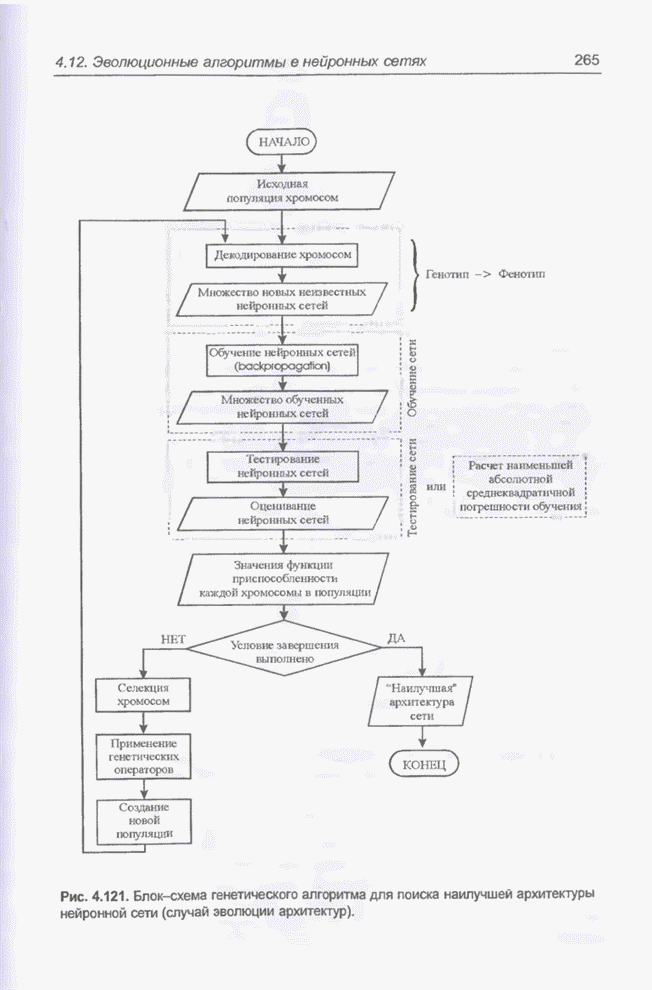
- 4.12.7.2. Эволюция архитектуры сети
- 4.12.7.3. Эволюция правил обучения
- 4.13. Примеры моделирования эволюционных алгоритмов в приложении к нейронным сетям
- 4.13.1. Программы Evolver и BrainMaker
- 4.13.2. Программа GTO
- Список литературы
- ГЛАВА 5. МОДУЛИ НЕЧЕТКО-НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.1. Модуль нечеткого управления со структурой, определенной в процессе дефуззификации
- 5.1.2. Конструкция модуля
- 5.1.3. Структура модуля
- 5.1.4. Использование алгоритма обратного распространения ошибки
- 5.1.5. Модификации модуля
- 5.1.6. Применение модуля нечеткого управления для прогнозирования случайных временных рядов
- 5.1.7. Применение модуля нечеткого управления для решения задачи парковки грузовика
- 5.1.8. Примечание
- 5.2. Представление модуля нечеткого управления в виде стандартной нейронной сети
- 5.3. Модуль нечеткого управления с нейронной сетью для выполнения дефуззификации
- 5.3.1. Введение
- 5.3.2. Конструкция модуля
- 5.3.3. Структура модуля
- 5.3.4. Алгоритмы обучения модуля
- 5.3.5. Решение задачи стабилизации перевернутого маятника
- 5.3.6. Примечание
- 5.4. Модуль нечеткого управления с возможностью коррекции правил
- 5.4.1. Введение
- 5.4.2. Фаза обучения на основе самоорганизации
- 5.4.3. Фаза обучения с учителем
- 5.4.4. Примечание
- 5.5. Модуль нечеткого управления типа Такаги-Сугено
- 5.5.1. Введение
- 5.5.2. Нейронная реализация функции принадлежности
- 5.5.3. Модули Такаги-Сугено
- 5.5.4. Реализация условий
- 5.5.5. Реализация заключений
- 5.5.6. Примечание
- 5.6. Модуль нечеткого управления типа Такаги-Сугено: случай зависимых лингвистических переменных
- 5.6.1. Введение
- 5.6.2. Нейронные сети для нечеткого вывода
- 5.6.3. Структура системы
- 5.6.4. Способ обучения
- 5.6.5. Решение задачи парковки грузовика
- 5.6.6. Примечание
- Список литературы