| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.9. Примеры оптимизации функции с помощью программы FlexTool
Применение генетического алгоритма для оптимизации различных функций будем иллюстрировать примерами, реализованными на IBM PC совместимом компьютере с использованием программы FlexTool [48].
Программа FlexTool позволяет выбирать различные варианты генетического алгоритма - такие, как классический (regular), с частичной заменой популяции (steady-state) или микроалгоритм (micro). Помимо того, предоставляется возможность выбрать метод селекции (рулетка, турнирный или ранговый), а также количество точек скрещивания и способ кодирования (двоичное или логарифмическое). В данном случае под двоичным кодированием понимается способ, применявшийся в примерах 4.1, 4.5 и 4.6, а логарифмическое кодирование было представлено в п. 4.8.4. Программа FlexTool также позволяет одновременно оптимизировать несколько функций и содержит алгоритм создания ниш для нахождения более чем одного оптимума (помимо единственного глобального решения). FlexTool взаимодействует с программой MATLAB и запускается в ее окне. Для определения оптимизируемых функций используются файлы с расширением .m (так называемые m-файлы), служащие для записи математических функций в программе MATLAB. В рабочем окне MATLAB'a также можно считывать значения различных переменных, используемых программой FlexTool, что дает, в частности, возможность просмотра популяций хромосом.
Программа FlexTool требует от пользователя ввести размерность популяций, вероятности скрещивания и мутации, интервалы изменения параметров задачи (пространства поиска), а также условия останова алгоритма. Предоставляется возможность прервать выполнение алгоритма в произвольный момент времени с последующим возобновлением ею работы с точки прерывания (так называемый warm-start) либо с начальной точки (cold-start).
Рассмотрим примеры оптимизации функции одной, двух и нескольких переменных. В качестве иллюстраций берутся графики большинства оптимизируемых функций (полученные средствами программы MATLAB) и сформированные программой FlexTool графики функций приспособленности для конкретных итераций генетического алгоритма.
Пример 4.12 демонстрирует способ решения задачи, рассмотренной в примере 4.5, но при использовании генетического алгоритма, реализованного в программе FlexTool. Для такой простой задачи лучше всего подходит генетический микроалгоритм, представленный в п. 4.8.8. В отличие от примера 4.5, в примере 4.12 ищется минимум функции, заданной формулой (4.1).
Пример 4.12
С помощью генетического микроалгоритма программы FlexTool найти минимум функции, заданной формулой (4.1), т.е.
![]()
для
целых значений ![]() в
интервале от 0 до 31.
в
интервале от 0 до 31.
Генетический микроалгоритм программы FlexTool выполняется на популяции с размерностью, равной пяти. Селекция производится детерминированным турнирным методом с применением элитарной стратегии, благодаря которой лучшая хромосома текущей популяции всегда переходит в следующее поколение. Производится одноточечное скрещивание. Вероятность скрещивания принимается равной 1, а вероятность мутации - равной 0.
Длина хромосом равна пяти, что
очевидно следует из возможности кодирования 32 целых чисел (для указанного
интервала изменения переменной ![]() ) пятью битами двоичной
последовательности. В программе FlexTool применяется двоичное кодирование,
аналогичное представленному в примерах 4.1 и 4.5, однако для удобства
программной реализации используется обратный код, т.е. на первой позиции
находится наименее значащий бит, а на последней - наиболее значащий. Такой
способ записи прямо противоположен повсеместно распространенной форме записи
двоичных чисел.
) пятью битами двоичной
последовательности. В программе FlexTool применяется двоичное кодирование,
аналогичное представленному в примерах 4.1 и 4.5, однако для удобства
программной реализации используется обратный код, т.е. на первой позиции
находится наименее значащий бит, а на последней - наиболее значащий. Такой
способ записи прямо противоположен повсеместно распространенной форме записи
двоичных чисел.
Существенным элементом выполнения генетического микроалгоритма считается процедура «рестарта», т.е. запуска его с начальной точки при обнаружении сходимости (п. 4.8.8). В программе FlexTool рестарт производится периодически после выполнения установленного количества итераций. По умолчанию оно равно 7, примеры выполнялись именно при этом значении.
Исходная популяция - на первой итерации генетического микроалгоритма - состоит из следующих хромосом:
![]()
![]()
![]()
![]()
![]()
со значениями фенотипов
6 3 30 21 19,
которые являются действительными целыми числами из интервала от 0 до 31.
Наименьшее значение функции приспособленности в этой популяции имеет стоящая на втором месте хромосома с фенотипом, равным трем. Оно равно 19. Наибольшее значение функции приспособленности у стоящей на третьем месте хромосомы с фенотипом, равным 30, составляет 1801. Легко подсчитать, что среднее значение функции приспособленности будет равно 699,8.
Популяция, полученная в результате селекции и скрещивания, становится текущей для следующей (второй) итерации. Она характеризуется средним значением функции приспособленности, равным 173,8. Заметно, что это значение меньше, чем рассчитанное для первого поколения. Наибольшее значение функции приспособленности, равное 723, имеет хромосома с фенотипом 19. Это наихудшая особь данной популяции. «Наилучшая к текущему моменту» хромосома с фенотипом, равным двум, имеет минимальное значение функции приспособленности, которое равно девяти.
В третьем поколении среднее значение функции приспособленности уменьшается до 13. Наибольшее значение для хромосомы с фенотипом, равным трем, составляет 19, а наименьшее значение функции приспособленности для этой популяции, также, как и для предыдущей, равно девяти. «Наилучшей к текущему моменту» продолжает оставаться хромосома с фенотипом, равным двум.
В следующих четырех поколениях (от четвертого до седьмого) среднее значение функции приспособленности по популяции совпадает с наибольшим и наименьшим значениями, равными девяти. Это означает, что популяция состоит из одинаковых хромосом с фенотипами, равными двум. Следовательно, наблюдается сходимость к решению, которое не является оптимальным.
До этого момента алгоритм выполнялся аналогично классическому генетическому алгоритму, причем селекция проводилась детерминированным турнирным методом с сохранением наилучшей хромосомы из популяции (элитарная стратегия).
После семи итераций начинается новый цикл выполнения генетического микроалгоритма. Производится его «рестарт», т.е. повторный запуск алгоритма с начальной точки - случайного выбора четырех новых хромосом для включения в популяцию. Из особей предыдущего поколения сохраняется только одна - «наилучшая к текущему моменту» хромосома с фенотипом, равным двум.
После селекции и скрещивания в очередном (девятом) поколении получаем популяцию со средним значением функции приспособленности, равным 481,4. Наибольшее значение функции приспособленности, равное 1579, имеет хромосома с фенотипом 28, а наименьшее значение, равное девяти, - с фенотипом, равным двум.
На следующих пяти итерациях второго цикла генетического микроалгоритма мы вновь получаем популяцию, состоящую из одинаковых хромосом с фенотипом, равным двум, для которых среднее, наибольшее и наименьшее значения функции приспособленности равны девяти. Следовательно, опять наблюдается сходимость к решению, которое не является оптимальным
С пятнадцатого поколения начинается очередной (третий) цикл выполнения генетического микроалгоритма. Он также открывается случайным выбором четырех новых хромосом и формированием популяции с сохранением «наилучшей к текущему моменту» особи с фенотипом, равным двум.
На девятнадцатой итерации генетического микроалгоритма, т.е. в пятом поколении третьего цикла (состоящего из семи итераций) возникает сходимость к оптимальному решению, которым оказывается хромосома с фенотипом, равным 0. Среднее, наибольшее и наименьшее значения функции приспособленности по всей популяции с 19 по 21 поколение остается равным 1.
Далее выполняются очередные циклы по семь итераций, начинающиеся «рестартом» алгоритма, и в каждом из них наблюдается сходимость к оптимальному решению, т.е. к хромосоме с фенотипом, равным 0.
Конечно, задачу из примера 4.12 можно решить с применением генетического алгоритма с произвольной размерностью популяций, при задании пользователем значений вероятностей скрещивания и мутации, а также при выборе им одного из методов селекции (рулетки, турнирного или рангового). Таким образом, вместо микроалгоритма можно применить реализованный в программе FlexTool обычный генетический алгоритм (regular). Однако необходимо отметить, что при его использовании на популяциях малой размерности с вероятностями скрещивания и мутации, соответственно равными 1 и 0, а также при выполнении селекции методом рулетки (так, как в примере 4.5) весьма часто встает проблема преждевременной сходимости этого алгоритма. Результат значительно улучшается, если вероятность мутации отличается от нуля (например, если она принимается равной 0,1). Несмотря на то, что мутация играет определенно второстепенную роль по отношению к скрещиванию, она оказывается необходимой, поскольку обеспечивает разнообразие хромосом в популяции.
Следует еще раз подчеркнуть, что при выполнении генетического микроалгоритма разнообразие в популяции достигается благодаря процедуре рестарта алгоритма в случае обнаружения его сходимости. В этом случае мутация оказывается излишней.
Следующий пример относится к
задаче, похожей на задачу примера 4.12. Минимизируется та же функция, однако
переменная ![]() принимает
действительные значения из интервала
принимает
действительные значения из интервала ![]() . По этой причине пространство поиска
оказывается большим, чем в примере 4.12. Для решения данной задачи применим
обычный генетический алгоритм программы FlexTool и селекцию методом рулетки.
Заметим, что этот метод, который пригоден и для селекции в случае максимизации
функции, в программе FlexTool может использоваться только для задач
минимизации. Это обусловлено адаптацией программы к требованиям пользователей,
которые чаще решают задачи минимизации (например, погрешностей, затрат и т.п.),
чем задачи максимизации.
. По этой причине пространство поиска
оказывается большим, чем в примере 4.12. Для решения данной задачи применим
обычный генетический алгоритм программы FlexTool и селекцию методом рулетки.
Заметим, что этот метод, который пригоден и для селекции в случае максимизации
функции, в программе FlexTool может использоваться только для задач
минимизации. Это обусловлено адаптацией программы к требованиям пользователей,
которые чаще решают задачи минимизации (например, погрешностей, затрат и т.п.),
чем задачи максимизации.
Пример 4.13
С помощью генетического алгоритма
программы FlexTool найти минимум функции, заданной формулой (4.1) для ![]() с точностью до 0,1.
с точностью до 0,1.
Поставленная задача решается путем использования обычного генетического алгоритма (regular) с селекцией методом рулетки. Заметим, что поиск проводится в пространстве, состоящем из 100 возможных решений. Длина хромосом (в соответствии с формулой 4.4)) должна быть равной семи. Пусть размерность популяции составляет 11 особей. Будем применять одноточечное скрещивание с вероятностью 0,9, а вероятность мутации установим равной 0,1.
Исходная популяция состоит из 11 хромосом длиной семь битов, соответствующих следующим фенотипам:
3,4 2,4 2,0 5,0 1,4 0,1 3,0 -2,3 2,3 5,0 -4,8
Наилучшее решение, т.е. хромосома с фенотипом, равным 0, для которой значение функции приспособленности составляет 1, получено на седьмой итерации алгоритма. На первой итерации наибольшее значение функции приспособленности по всей популяции равно 51, среднее - 22,0745, а наименьшее - 1,02. Однако в седьмом поколении наибольшее значение функции приспособленности равно 45,18, среднее по популяции составляет 5,9909, а наименьшее значение соответствует лучшей хромосоме и равно 1. График на рис. 4.18 показывает наименьшее значение функции приспособленности в популяции на последовательных итерациях генетического алгоритма.

Рис. 4.18. Наименьшее значение функции приспособленности в популяции на последовательных итерациях генетического алгоритма для примера 4.13.
Аналогично можно применять генетический алгоритм для нахождения решения с еще большей точностью, например, для двух или трех знаков после запятой. При этом будет соответственно расширяться пространство поиска и увеличиваться длина хромосом.
Следующий пример относится к задаче нахождения максимума функции, имеющей локальные максимумы. Покажем, что генетический алгоритм находит глобальный оптимум. Для поиска максимума будем применять реализованный в программе FlexTool турнирный метод, поскольку метод колеса рулетки в ней работает только для задач минимизации.
В программе FlexTool по умолчанию приняты следующие (наилучшие для большинства решаемых задач) значения параметров генетического алгоритма:
- размерность популяции = 77,
- вероятность скрещивания = 0,77,
- вероятность мутации = 0,0077.
В приводимых далее примерах используются указанные вероятности скрещивания и мутации, однако размерность популяций будет выбираться в зависимости от размерности решаемых задач.
Пример 4.14
С помощью генетического алгоритма программы FlexTool найти минимум функции, заданной формулой

для
![]() с точностью
до 0,01.
с точностью
до 0,01.
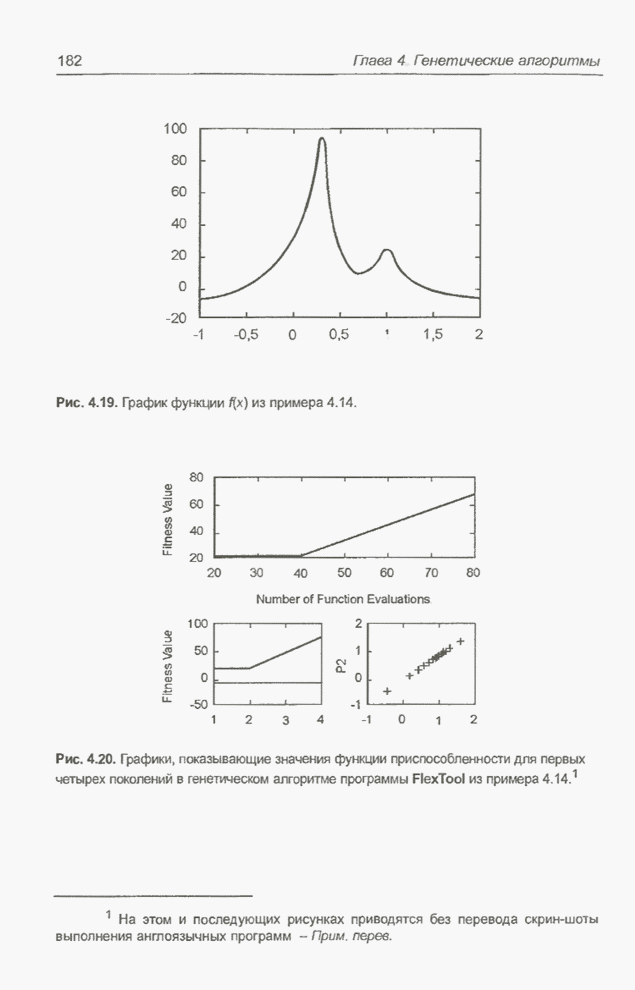
График оптимизируемой функции представлен на рис. 4.19. Обратим внимание на то, что функция имеет не только глобальный максимум, но и локальные оптимумы. Для нахождения глобального максимума применяется генетический алгоритм с турнирной селекцией в подгруппах по две особи. Размерность популяции равна 21; вероятности скрещивания и мутации составляют, соответственно 0,77 и 0,0077; используется одна точка скрещивания.

Рис. 4.19. График функции ![]() из примера 4.14.
из примера 4.14.
Хромосомы состоят из девяти генов со значениями 0 или 1. На рисунке 4.20 более светлой линией показана динамика изменения «наилучшего», в рассматриваемом случае - максимального значения функции приспособленности в популяции при увеличении количества поколений. Более темная линия на втором графике иллюстрирует изменение «наихудшего» значения функции приспособленности в популяции при последовательной смене поколений. На оси ординат обоих графиков указаны значения функции приспособленности (fitness value). На оси абсцисс второго графика указаны номера поколений, которые соответствуют числам на оси абсцисс первого графика, умноженным на размерность популяции, т.е. на 21.

Рис. 4.20. Графики, показывающие значения функции приспособленности для первых четырех поколений в генетическом алгоритме программы FlexTool из примера 4.14.1.
Из графиков видно, что
«наилучшая» хромосома в первом и втором поколениях характеризуется значением
функции приспособленности, близким к 20. В то же время значение функции
приспособленности «наихудшей» хромосомы примерно равно -5. В четвертом
поколении это значение приблизилось к -4, а значение функции приспособленности
«наилучшей» хромосомы возросло до 70. В нижней правой части рис. 4.20 показаны
значения параметра задачи, т.е. переменной ![]() со значениями в интервале от -1 до 2;
другими словами, это фенотипы, соответствующие отдельным хромосомам
рассматриваемой популяции. Заметно, что популяция характеризуется значительным
разнообразием. На рис. 4.21 популяция более однородна, а на рис. 4.22 зафиксировано
только одно значение параметра, равное 0,3; это означает, что все хромосомы в
популяции равны между собой. В рассматриваемом примере мы имеем дело только с
одним параметром задачи
со значениями в интервале от -1 до 2;
другими словами, это фенотипы, соответствующие отдельным хромосомам
рассматриваемой популяции. Заметно, что популяция характеризуется значительным
разнообразием. На рис. 4.21 популяция более однородна, а на рис. 4.22 зафиксировано
только одно значение параметра, равное 0,3; это означает, что все хромосомы в
популяции равны между собой. В рассматриваемом примере мы имеем дело только с
одним параметром задачи ![]() , который совпадает с
, который совпадает с ![]() , поэтому все точки
располагаются вдоль прямой так, как это показано на рис. 4.20 и 4.21.
, поэтому все точки
располагаются вдоль прямой так, как это показано на рис. 4.20 и 4.21.

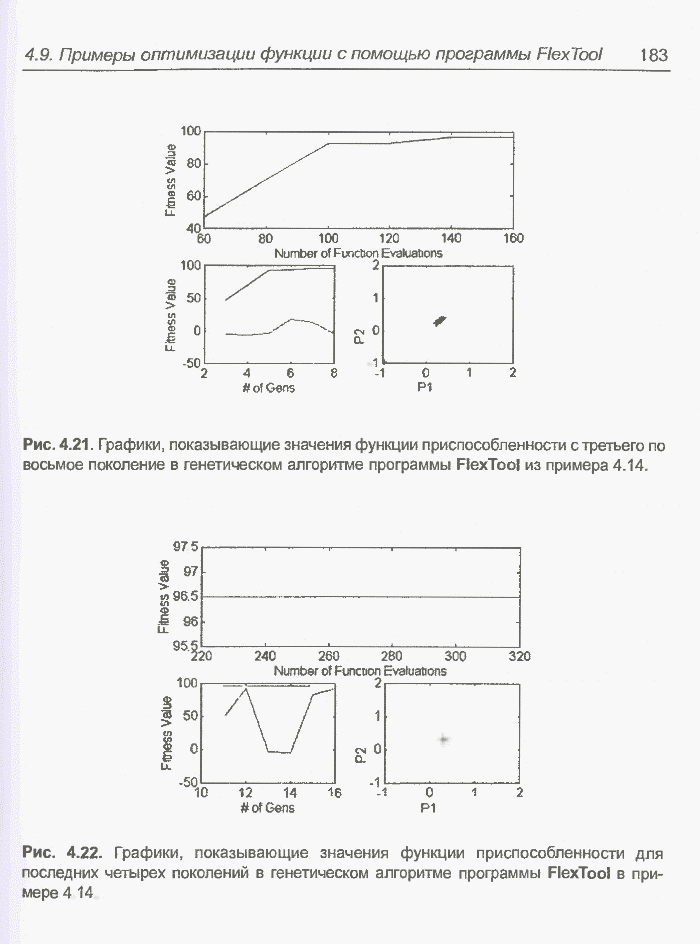
Рис. 4.21. Графики, показывающие значения функции приспособленности с третьего по восьмое поколение в генетическом алгоритме программы FlexTool из примера 4.14.
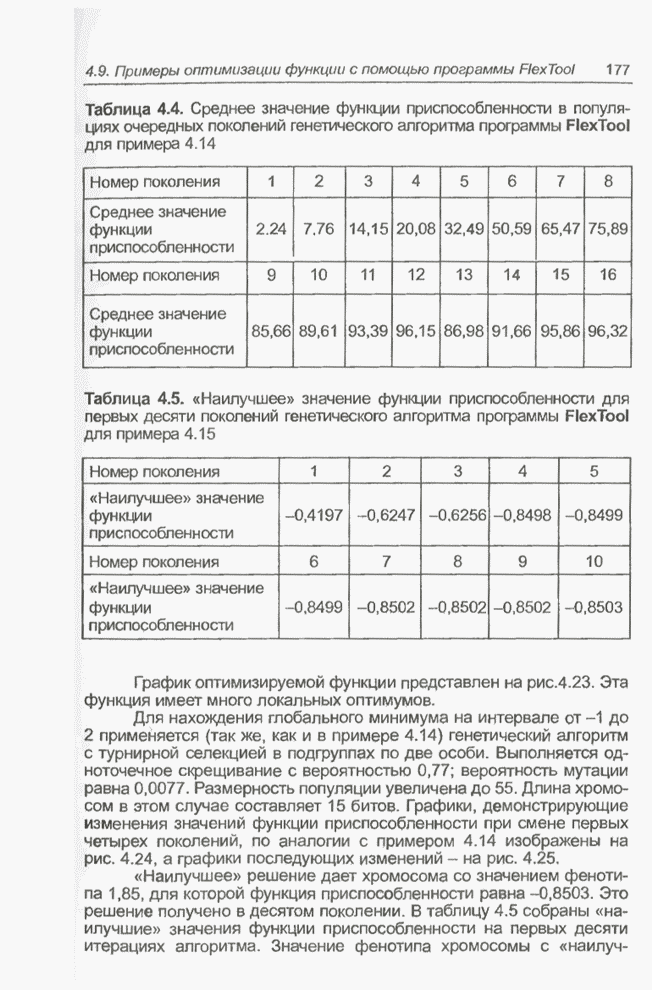
Графики на рис. 4.21 демонстрируют увеличение «наилучшего» значения функции приспособленности от около 47 в третьем поколении до примерно 70 в четвертом и примерно 93 - в пятом поколении, а в седьмом поколении достигается значение, равное 96,5. Это максимальная величина, которая остается неизменной в следующих поколениях, что видно на рис. 4.22. Таким образом, на седьмой итерации алгоритма найдено «наилучшее» решение - хромосома со значением фенотипа, равным 0,3, для которого значение функции приспособленности составляет 96,5. Нижние графики на рис. 4.21 и 4.22 также показывают, как изменяется «наихудшее» значение функции приспособленности от 3 до 16 поколения. В шестнадцатом поколении это значение равно 92,81. Среднее значение функции приспособленности в популяциях очередных поколений изменяется от 2,24 на первой итерации алгоритма до 96,32 на шестнадцатой итерации, что показывает таблица 4.4.

Рис. 4.22. Графики, показывающие значения функции приспособленности для последних четырех поколений в генетическом алгоритме программы FlexTool в примере 4.14.
Таблица 4.4. Среднее значение функции приспособленности в популяциях очередных поколений генетического алгоритма программы FlexTool для примера 4.14
|
Номер поколения |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Среднее значение функции приспособленности |
2,24 |
7,76 |
14,15 |
20,08 |
32,49 |
50,59 |
65,47 |
75,89 |
|
Номер поколения |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
Среднее значение функции приспособленности |
85,66 |
89,61 |
93,39 |
96,15 |
86,98 |
91,66 |
95,86 |
96,32 |
Пример 4.15
С помощью генетического алгоритма программы FlexTool найти минимум функции, заданной формулой
![]()
для
![]() с точностью
до 0,0001.
с точностью
до 0,0001.
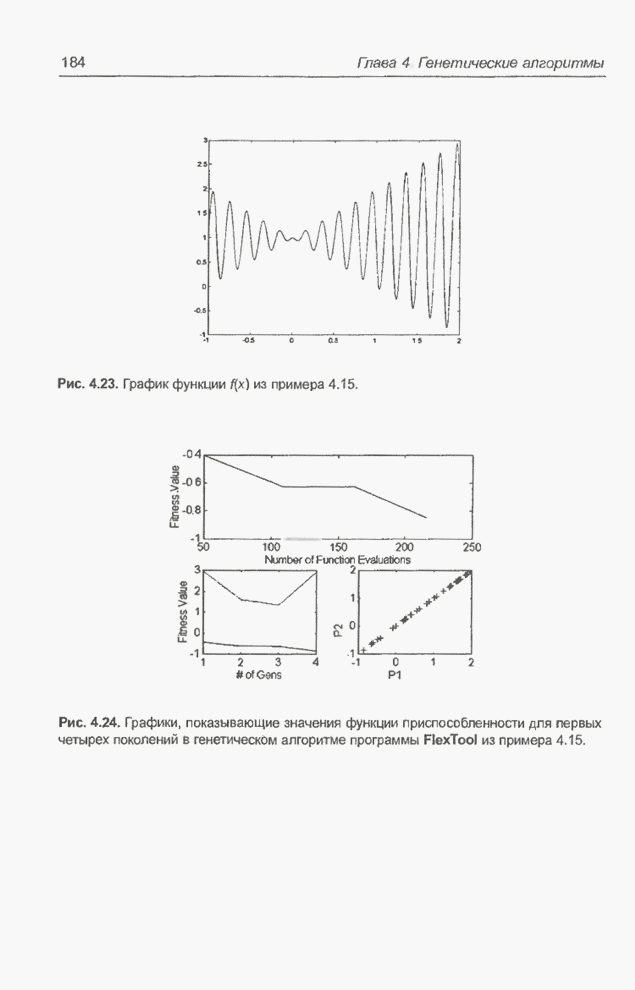
График оптимизируемой функции представлен на рис. 4.23. Эта функция имеет много локальных оптимумов.

Рис. 4.23. График функции ![]() из примера 4.15.
из примера 4.15.
Для нахождения глобального минимума на интервале от -1 до 2 применяется (так же, как и в примере 4.14) генетический алгоритм с турнирной селекцией в подгруппах по две особи. Выполняется одноточечное скрещивание с вероятностью 0,77; вероятность мутации равна 0,0077. Размерность популяции увеличена до 55. Длина хромосом в этом случае составляет 15 битов. Графики, демонстрирующие изменения значений функции приспособленности при смене первых четырех поколений, по аналогии с примером 4.14 изображены на рис. 4.24, а графики последующих изменений - на рис. 4.25.

Рис. 4.24. Графики, показывающие значения функции приспособленности для первых четырех поколений в генетическом алгоритме программы FlexTool из примера 4.15.

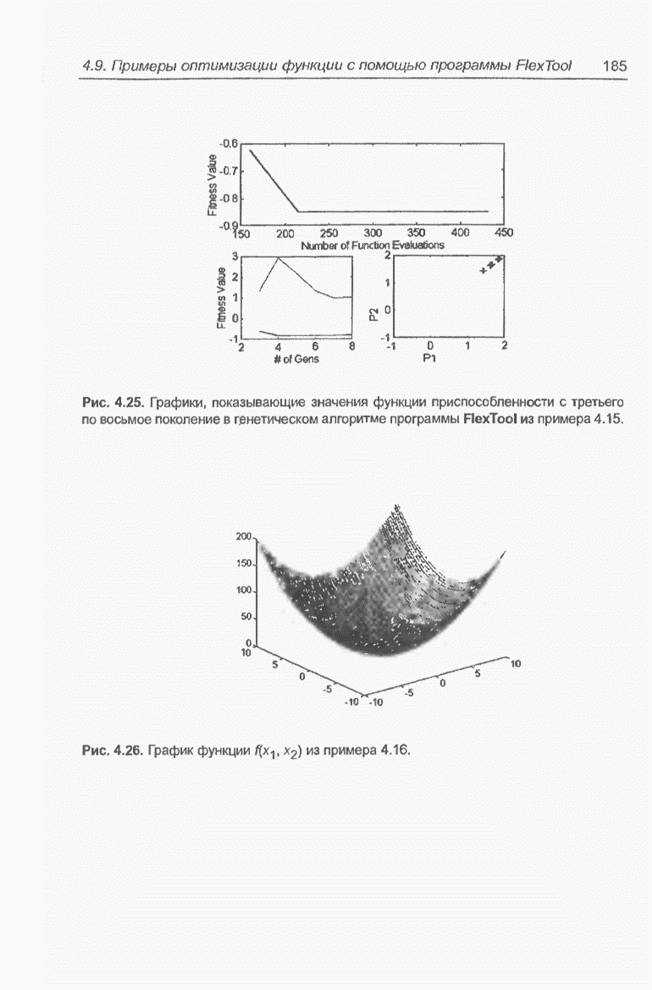
Рис. 4.25. Графики, показывающие значения функции приспособленности с третьего по восьмое поколение в генетическом алгоритме программы FlexTool из примера 4.15.
«Наилучшее» решение дает хромосома со значением фенотипа 1,85, для которой функция приспособленности равна -0,8503. Это решение получено в десятом поколении. В таблицу 4.5 собраны «наилучшие» значения функции приспособленности на первых десяти итерациях алгоритма. Значение фенотипа хромосомы с «наилучшим» значением функции приспособленности для второго поколения равно 1,645, а для четвертого и последующих поколений - 1,85.
Таблица 4.5. «Наилучшее» значение функции приспособленности для первых десяти поколений генетического алгоритма программы FlexTool для примера 4.15
|
Номер поколения |
1 |
2 |
3 |
4 |
5 |
|
«Наилучшее» значение функции приспособленности |
-0,4197 |
-0,6247 |
-0,6256 |
-0,8498 |
-0,8499 |
|
Номер поколения |
6 |
7 |
8 |
9 |
10 |
|
«Наилучшее» значение функции приспособленности |
-0,8499 |
-0,8502 |
-0,8502 |
-0,8502 |
-0,8503 |
Пример 4.16
С помощью генетического алгоритма программы FlexTool найти минимум функции двух переменных
![]()
для
![]() с
точностью до 0,0001.
с
точностью до 0,0001.
График оптимизируемой функции
представлен на рис. 4.26. Эта функция имеет один минимум, равный 0, в точке ![]() .
.

Рис. 4.26. График функции ![]() из примера 4.16.
из примера 4.16.
Применяется генетический алгоритм с турнирной селекцией в подгруппах по две особи, с одной точкой скрещивания и принятыми по умолчанию значениями вероятностей скрещивания 0,77 и мутации 0,0077, а также с размерностью популяции, равной 77.
Длина хромосом составляет 36
битов, при этом каждую переменную ![]() ,
, ![]() представляют 18 генов. Графики, демонстрирующие
изменения значений функции приспособленности при смене первых четырех поколений
при выполнении генетического алгоритма, изображены на рис. 4.27, а графики
последующих изменений - на рис. 4.28 - 4.31. По верхнему графику видно, как
изменяется «наилучшее» значение функции приспособленности - от значения 4,3543
в первом поколении (по 77 расчетным точкам) до нулевого значения. Во втором и
третьем поколениях эта функция имела значение 0,0608, в четвертом и пятом -
0,0586, в шестом - 0,0421, в седьмом - 0,0397, в восьмом - 0,0278, в девятом -
0,0192, в десятом и одиннадцатом - 0,0191, в двенадцатом - 0,0119, в
тринадцатом - 0,0105, с четырнадцатого по шестнадцатое - 0,0050, в семнадцатом
и восемнадцатом - 0,0011, в девятнадцатом - 0,0001, а в двадцатом и последующих
поколениях - значение 0,0000. Весь комплекс изменений показан на рис. 4.33, а
перечисленные «наилучшие» значения функции приспособленности выделены на рис.
4.32. Таким образом, в результате выполнения генетического алгоритма
«наилучшее» решение найдено в двадцатом поколении.
представляют 18 генов. Графики, демонстрирующие
изменения значений функции приспособленности при смене первых четырех поколений
при выполнении генетического алгоритма, изображены на рис. 4.27, а графики
последующих изменений - на рис. 4.28 - 4.31. По верхнему графику видно, как
изменяется «наилучшее» значение функции приспособленности - от значения 4,3543
в первом поколении (по 77 расчетным точкам) до нулевого значения. Во втором и
третьем поколениях эта функция имела значение 0,0608, в четвертом и пятом -
0,0586, в шестом - 0,0421, в седьмом - 0,0397, в восьмом - 0,0278, в девятом -
0,0192, в десятом и одиннадцатом - 0,0191, в двенадцатом - 0,0119, в
тринадцатом - 0,0105, с четырнадцатого по шестнадцатое - 0,0050, в семнадцатом
и восемнадцатом - 0,0011, в девятнадцатом - 0,0001, а в двадцатом и последующих
поколениях - значение 0,0000. Весь комплекс изменений показан на рис. 4.33, а
перечисленные «наилучшие» значения функции приспособленности выделены на рис.
4.32. Таким образом, в результате выполнения генетического алгоритма
«наилучшее» решение найдено в двадцатом поколении.

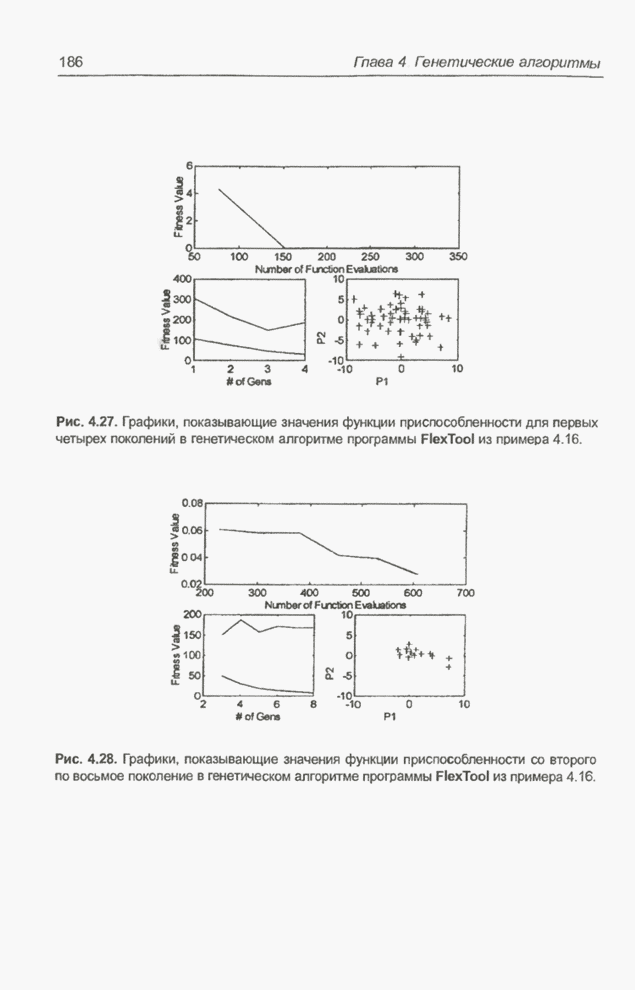
Рис. 4.27. Графики, показывающие значения функции приспособленности для первых четырех поколений в генетическом алгоритме программы FlexTool из примера 4.16.

Рис. 4.28. Графики, показывающие значения функции приспособленности со второго по восьмое поколение в генетическом алгоритме программы FlexTool из примера 4.16.

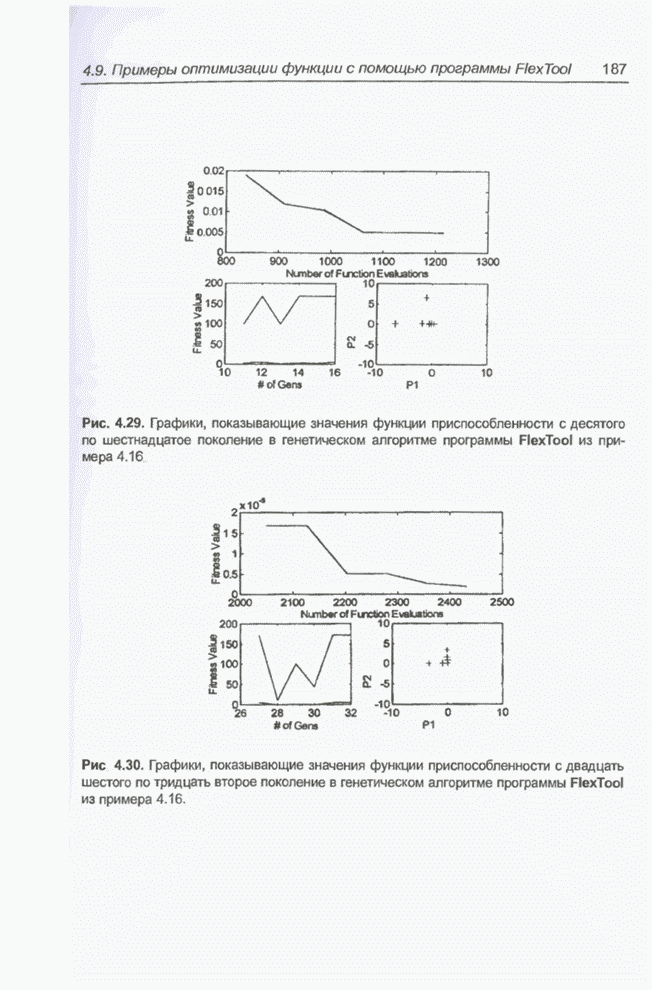
Рис. 4.29. Графики, показывающие значения функции приспособленности с десятого по шестнадцатое поколение в генетическом алгоритме программы FlexTool из примера 4.16.

Рис 4.30. Графики, показывающие значения функции приспособленности с двадцать шестого по тридцать второе поколение в генетическом алгоритме программы FlexTool из примера 4.16.

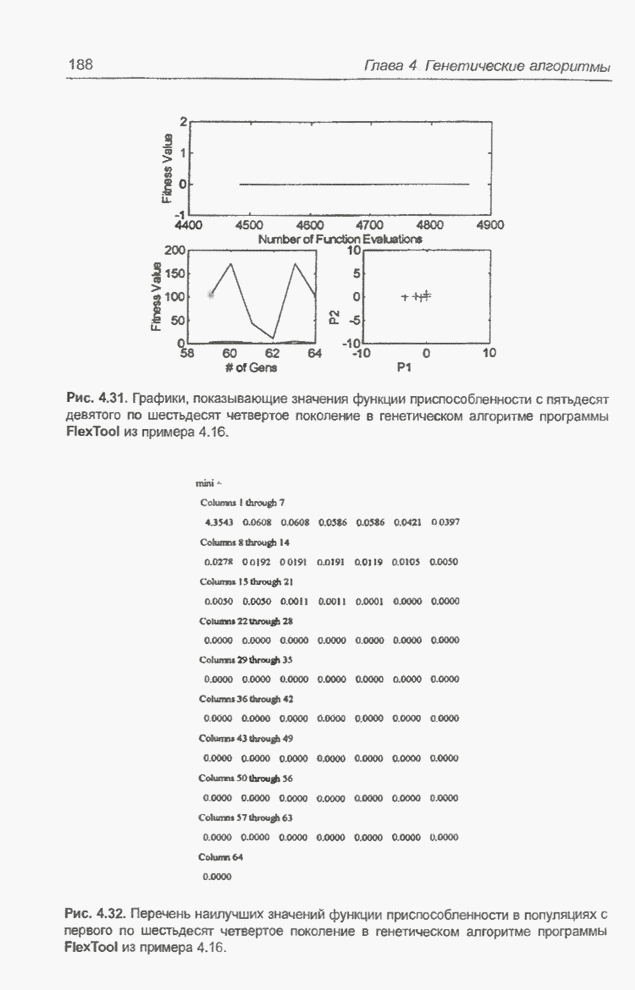
Рис. 4.31. Графики, показывающие значения функции приспособленности с пятьдесят девятого по шестьдесят четвертое поколение в генетическом алгоритме программы FlexTool из примера 4.16.

Рис. 4.32. Перечень наилучших значений функции приспособленности в популяциях с первого по шестьдесят четвертое поколение в генетическом алгоритме программы FlexTool из примера 4.16.

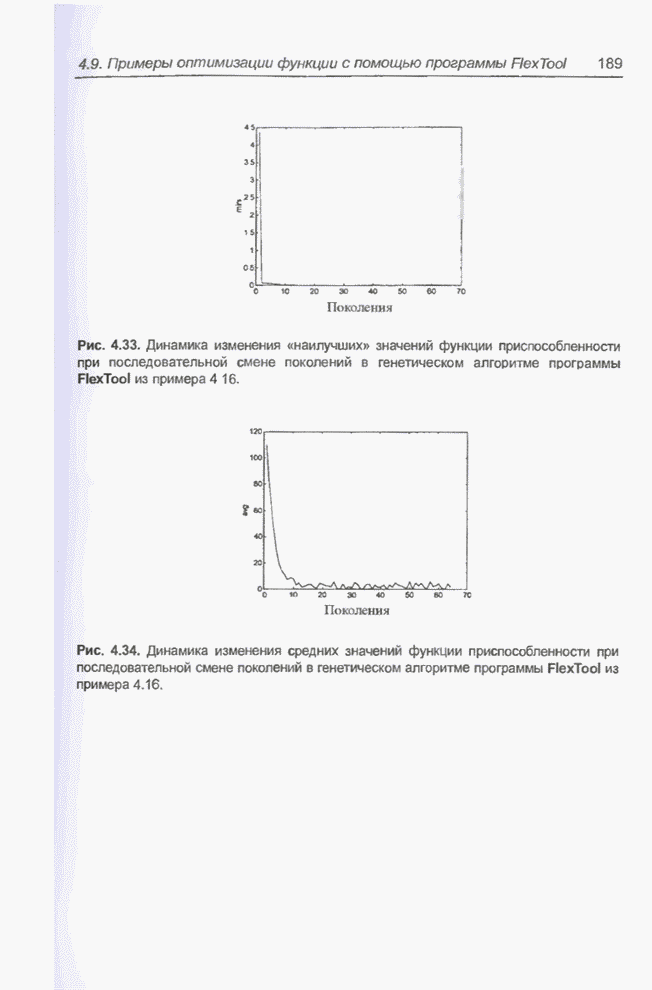
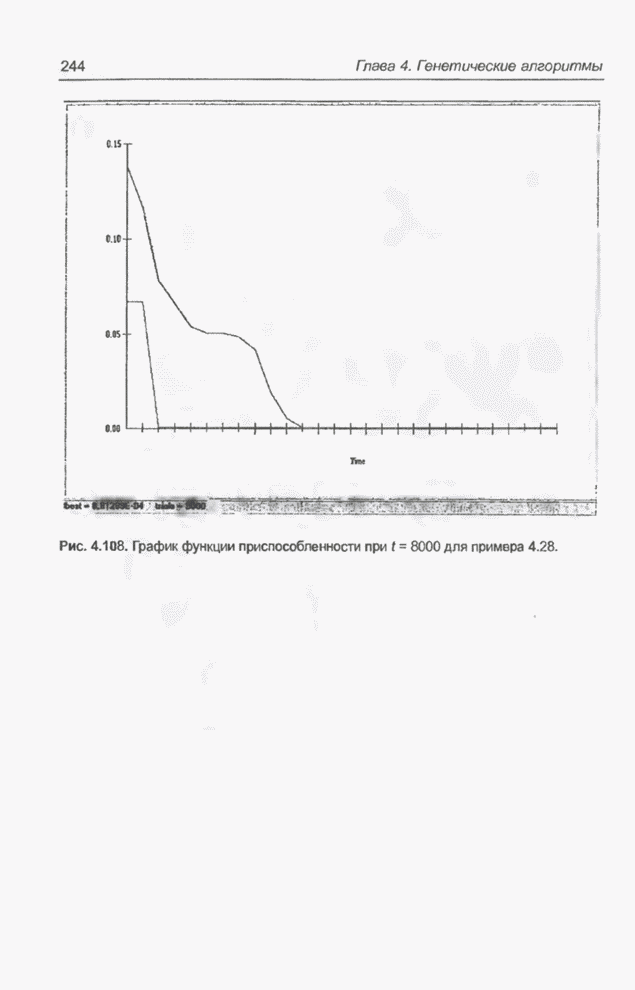
Рис. 4.33. Динамика изменения «наилучших» значений функции приспособленности при последовательной смене поколений в генетическом алгоритме программы FlexTool из примера 4.16.
Нижние левые графики на рис. 4.27 - 4.31 показывают изменения «наихудшего» (верхняя кривая) и среднего значения функции приспособленности особей популяции при смене поколений. Изменение «наилучшего» значения функции приспособленности на этих графиках почти незаметно, поскольку соответствующая кривая практически совпадает с горизонтальной осью, так как значения близки к 0. Комплексная динамика средних значений функции приспособленности на протяжении всех поколений демонстрируется на рис. 4.34. Обратим внимание на то, что значения функции приспособленности «наихудших» хромосом в отдельных популяциях довольно велики и, очевидно, значительно отличаются от оптимального значения. Динамика изменения «наихудших» значений функции приспособленности при смене поколений показана на рис. 4.35.

Рис. 4.34. Динамика изменения средних значений функции приспособленности при последовательной смене поколений в генетическом алгоритме программы FlexTool из примера 4.16.

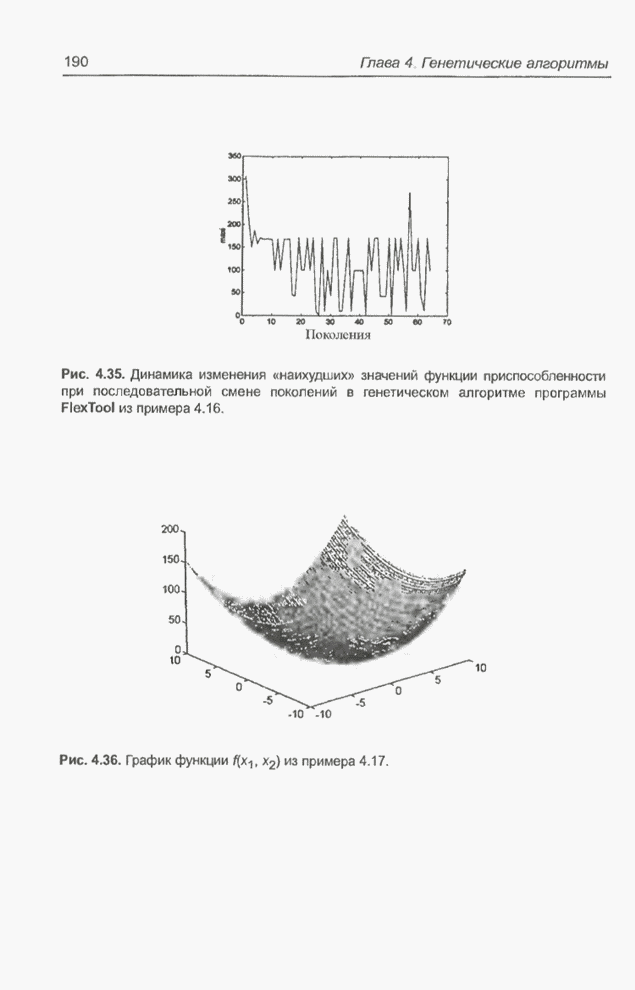
Рис. 4.35. Динамика изменения «наихудших» значений функции приспособленности при последовательной смене поколений в генетическом алгоритме программы FlexTool из примера 4.16.
На правых нижних графиках
рисунков 4.27 - 4.31 показаны значения параметров задачи ![]() и
и ![]() , соответствующих переменным
, соответствующих переменным ![]() ,
, ![]() , т.е. фенотипы (в интервале от
-10 до 10). Наибольшее разнообразие особей наблюдается в начальных поколениях.
В последующем в составе популяций появляется все больше одинаковых хромосом.
, т.е. фенотипы (в интервале от
-10 до 10). Наибольшее разнообразие особей наблюдается в начальных поколениях.
В последующем в составе популяций появляется все больше одинаковых хромосом.
Напомним, что «наилучшее»
решение, равное 0,0000, получено в двадцатом поколении (рис. 4.32). Однако
следует обратить внимание на динамику изменения «наилучшего» значения функции
приспособленности, показанную на рис. 4.30. Это значение находилось в интервале
от 0 до 0,0002, начиная с 27 и по 32 поколение (т.е. с 27*77 до 32*77 расчетной
точки функции приспособленности). Для «наилучшей» хромосомы со значениями
фенотипов (после 64 поколений), равными 0,0000 и 0,0001, значение функции ![]() составляет 0,00000001.
составляет 0,00000001.
Пример 4.17
С помощью генетического алгоритма программы FlexTool найти минимум функции двух переменных
![]()
для
![]() с
точностью до 0,001.
с
точностью до 0,001.
Данная задача аналогична предыдущей (пример 4.16). График оптимизируемой функции представлен на рис. 4.36. Эта функция имеет один минимум, равный 3, в точке (0, 0).

Рис. 4.36. График функции ![]() из примера 4.17.
из примера 4.17.
Применяется генетический алгоритм с турнирной селекцией в подгруппах по две особи с одной или двумя точками скрещивания, а также с селекцией по методу рулетки с одной точкой скрещивания. Также как и в предыдущем примере, используются принятые по умолчанию значения вероятностей скрещивания 0,77 и мутации 0,0077, а также размерность популяции, равная 77. В этом случае с учетом меньшей требуемой точности длина хромосом составляет 22 бита - по 11 генов на каждую переменную.
Ввиду сходства рассматриваемого и предыдущего примеров графики изменения значений функции приспособленности для конкретных поколений не приводятся. Они аналогичны графикам на рис. 4.27 - 4.31. Принципиальное различие заключается в том, что в данном случае «наименьшее» значение функции приспособленности стремится к значению, равному 3.
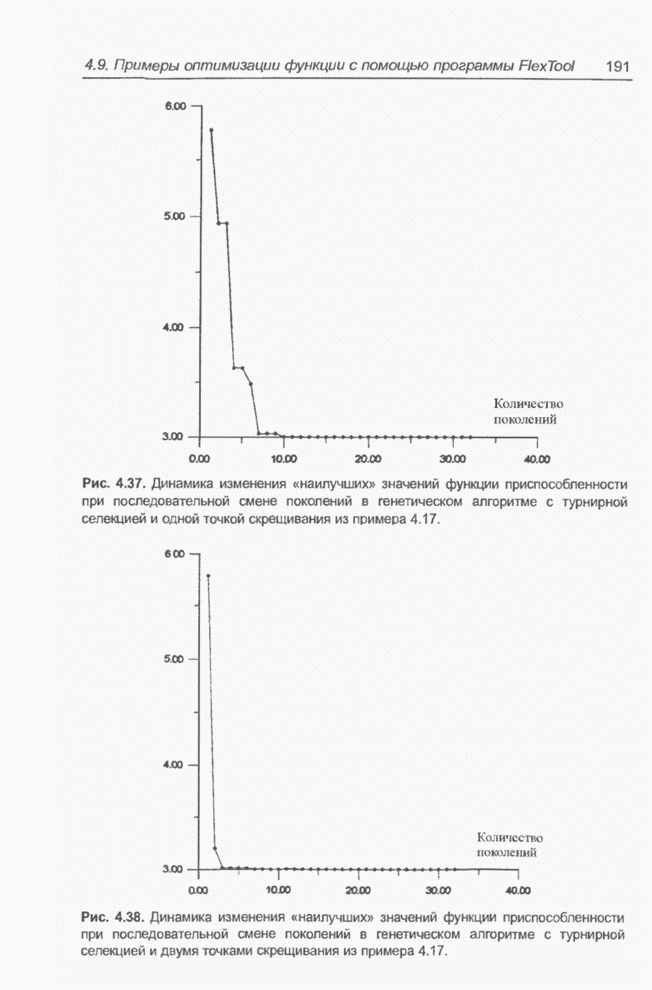
В данном случае представляют интерес графики общей динамики изменения «наилучшего» значения функции приспособленности (подобные графику на рис. 4.33) для использованных методов селекции. График для турнирной селекции с одной точкой скрещивания показан на рис. 4.37, а с двумя точками скрещивания - на рис. 4.38. Заметно, что во втором случае «наилучшее» решение (т.е. значение функции приспособленности, равное 3) было найдено быстрее. Аналогичный график для селекции методом рулетки представлен на рис. 4.39. Можно сделать вывод, что турнирный метод позволяет быстрее находить минимальное значение оптимизируемой функции, чем метод рулетки.

Рис. 4.37. Динамика изменения «наилучших» значений функции приспособленности при последовательной смене поколений в генетическом алгоритме с турнирной селекцией и одной точкой скрещивания из примера 4.17.

Рис. 4.38. Динамика изменения «наилучших» значений функции приспособленности при последовательной смене поколений в генетическом алгоритме с турнирной селекцией и двумя точками скрещивания из примера 4.17.

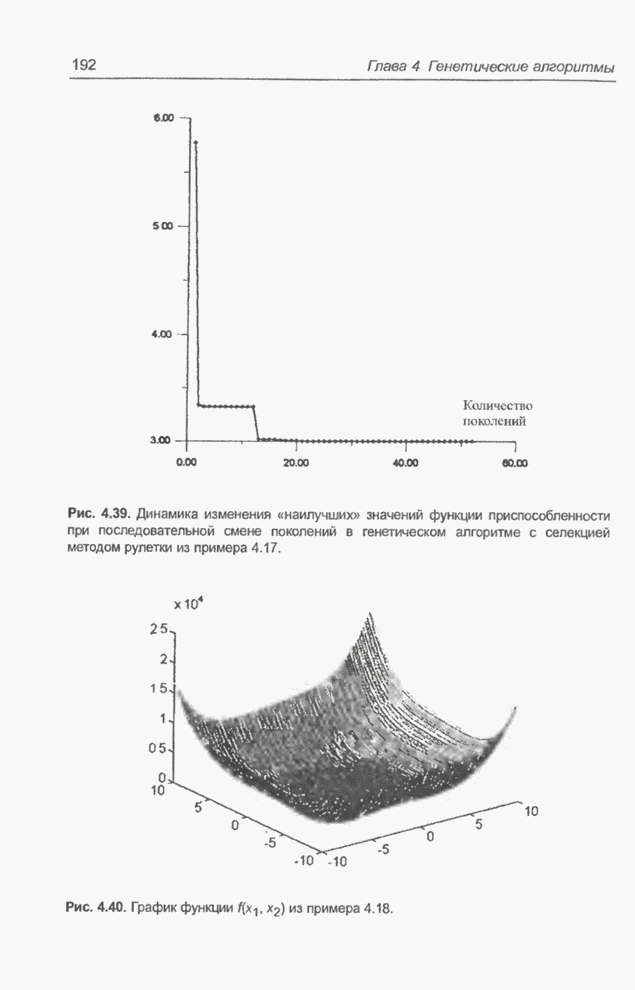
Рис. 4.39. Динамика изменения «наилучших» значений функции приспособленности при последовательной смене поколений в генетическом алгоритме с селекцией методом рулетки из примера 4.17.
Пример 4.18
С помощью генетического алгоритма программы FlexTool найти минимум функции двух переменных
![]()
для
![]() с
точностью до 0,001.
с
точностью до 0,001.
График оптимизируемой функции
представлен на рис. 4.40. Эта функция имеет минимум, равный 0, в следующих
точках: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

Рис. 4.40. График функции ![]() из примера 4.18.
из примера 4.18.
В случае, когда функция имеет минимальное (или максимальное) значение в нескольких различных точках, и это значение является глобальным оптимумом, генетический алгоритм находит, как правило, одну из этих точек. Повторный запуск алгоритма может принести тот же самый результат либо обнаружить координаты другой точки с таким же оптимальным значением функции.
В примере вначале применялся
генетический алгоритм с турнирной селекцией в подгруппах по две особи с одной
точкой скрещивания и принятые по умолчанию значения вероятностей скрещивания
0,77 и мутации 0,0077, а также размерность популяции, равная 77. Наилучшим
решением, найденным в этих условиях, стала точка с координатами ![]() .
.
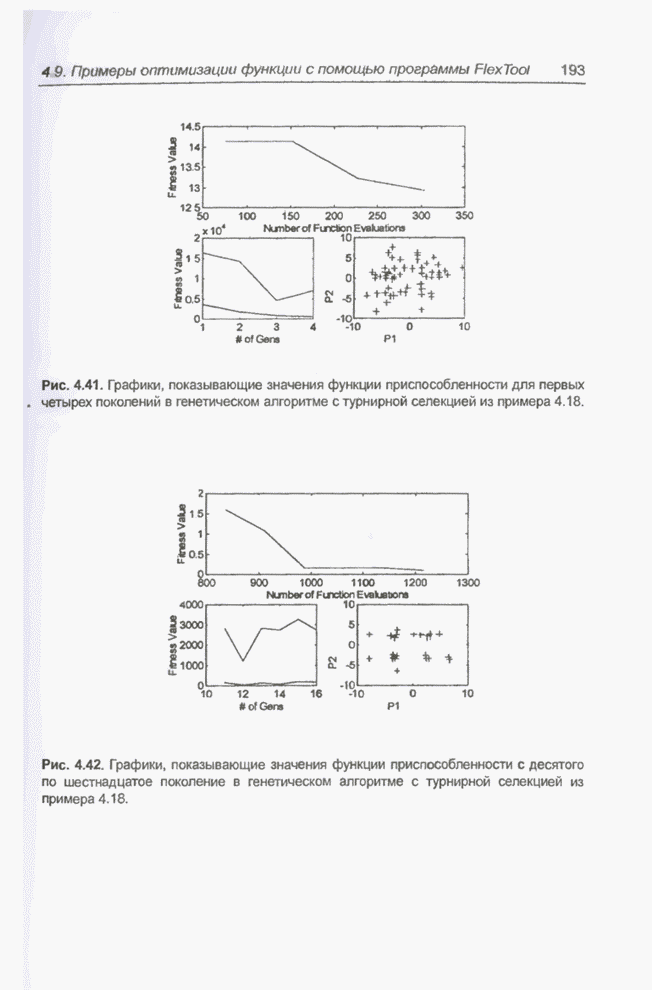
Динамику изменения «наилучшего»
значения функции приспособленности показывают графики на рис. 4.41 - 4.43. Для
32 поколений это значение равно 0,0474, а в 46 поколениях достигается величина
0,0005. На этих же рисунках представлено и изменение «наихудшего» и среднего
значений функции приспособленности по популяции при последовательной смене
поколений, а также распределение особей в популяции (параметры ![]() и
и ![]() ).
).

Рис. 4.41. Графики, показывающие значения функции приспособленности для первых четырех поколений в генетическом алгоритме с турнирной селекцией из примера 4.18.

Рис. 4.42. Графики, показывающие значения функции приспособленности с десятого по шестнадцатое поколение в генетическом алгоритме с турнирной селекцией из примера 4.18.

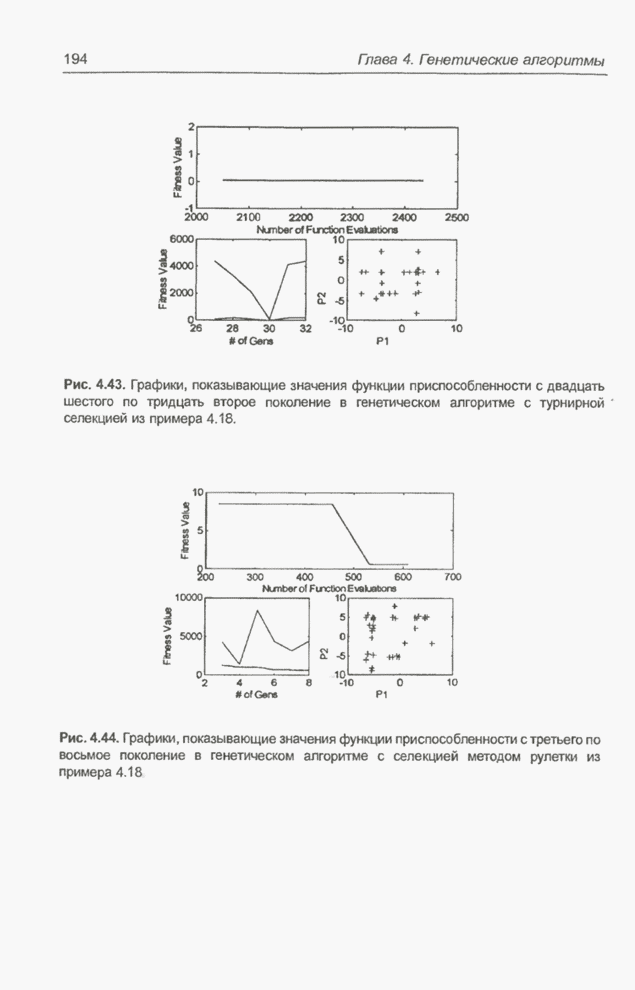
Рис. 4.43. Графики, показывающие значения функции приспособленности с двадцать шестого по тридцать второе поколение в генетическом алгоритме с турнирной селекцией из примера 4.18.
В дальнейшем алгоритм был
выполнен еще один раз, причем для эксперимента применялась селекция методом
рулетки, а вероятности скрещивания и мутации были установлены равными 0,6 и
0,001 соответственно. Графики, иллюстрирующие изменение значений функции
приспособленности при последовательной смене поколений, представлены на рис.
4.44 и 4.45. «Наилучшее» значение функции приспособленности в 70 поколениях
равно 0,0038, а начиная с 83 поколения оно составляет 0,0009. «Наилучшей»
особью оказалась хромосома со значениями фенотипов -2,80 и 3,13. Таким образом,
в этом эксперименте была найдена другая точка с координатами ![]() , в которой
минимизируемая функция принимает нулевое значение.
, в которой
минимизируемая функция принимает нулевое значение.

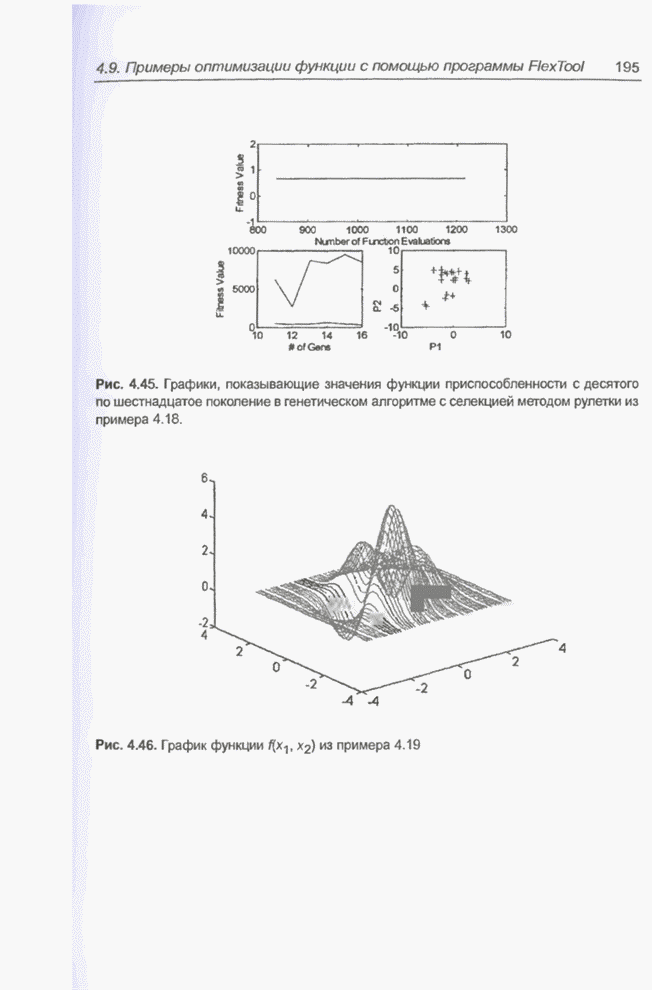
Рис. 4.44. Графики, показывающие значения функции приспособленности с третьего по восьмое поколение в генетическом алгоритме с селекцией методом рулетки из примера 4.18.

Рис. 4.45. Графики, показывающие значения функции приспособленности с десятого по шестнадцатое поколение в генетическом алгоритме с селекцией методом рулетки из примера 4.18.
Попытки поиска других оптимальных точек, соответствующих «наилучшему» решению, можно продолжать с применением того же алгоритма либо с использованием альтернативных методов селекции. Иногда такие попытки приходится повторять по несколько раз, если они приводят к полученным ранее решениям.
Пример 4.19
С помощью генетического алгоритма программы FlexTool найти минимум и максимум функции
![]()
для
![]() с точностью
до 0,01.
с точностью
до 0,01.
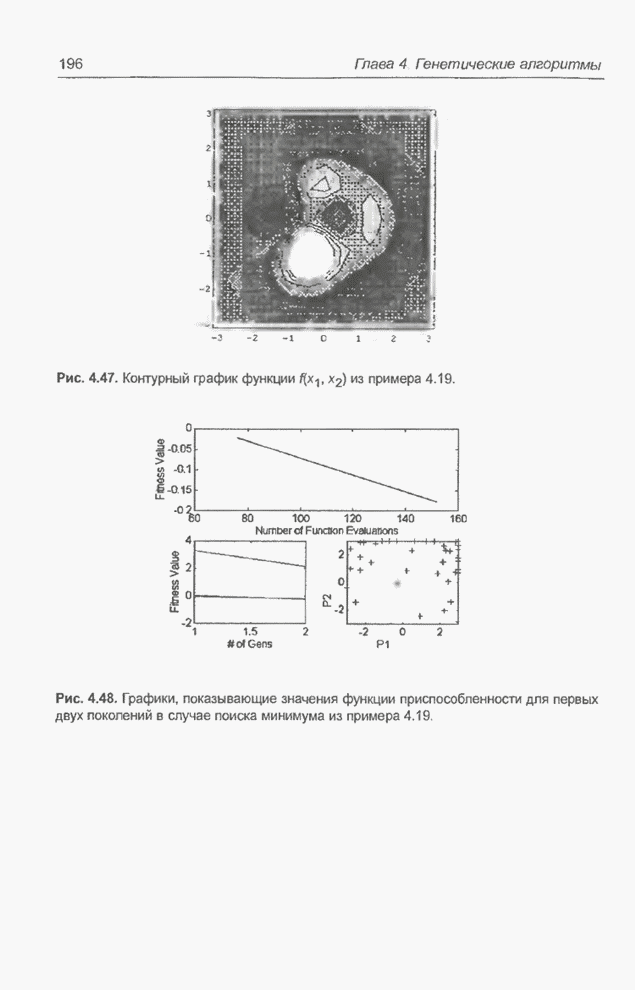
График оптимизируемой функции представлен на рис. 4.46. Эта функция двух переменных имеет несколько так называемых пиков. Ее контурный график изображен на рис. 4.47.

Рис. 4.46. График функции ![]() из примера 4.19.
из примера 4.19.

Рис. 4.47. Контурный график
функции ![]() из
примера 4.19.
из
примера 4.19.
Применяется генетический алгоритм
с турнирной селекцией в подгруппах по две особи с одной точкой скрещивания; по
умолчанию приняты значения вероятностей скрещивания 0,77 и мутации 0,0077, а
также размерность популяции, равная 77. В точке ![]() найден минимум, равный -1,907, а в точке
найден минимум, равный -1,907, а в точке
![]() -
максимум, равный 5,638. Точнее говоря, при минимизации наилучшим решением
оказалась хромосома со значениями фенотипов -1,4 и 0,17, для которой значение
функции приспособленности составляет -1,907, а при максимизации - хромосома со
значениями фенотипов -0,39 и -0,99 со значением функции приспособленности
5,638. Динамика изменения значений функции приспособленности при
последовательной смене поколений для случая минимизации показана на рис. 4.48 -
4.52, а для случая максимизации - на рис. 4.53 - 4.55.
-
максимум, равный 5,638. Точнее говоря, при минимизации наилучшим решением
оказалась хромосома со значениями фенотипов -1,4 и 0,17, для которой значение
функции приспособленности составляет -1,907, а при максимизации - хромосома со
значениями фенотипов -0,39 и -0,99 со значением функции приспособленности
5,638. Динамика изменения значений функции приспособленности при
последовательной смене поколений для случая минимизации показана на рис. 4.48 -
4.52, а для случая максимизации - на рис. 4.53 - 4.55.

Рис. 4.48. Графики, показывающие значения функции приспособленности для первых двух поколений в случае поиска минимума из примера 4.19.

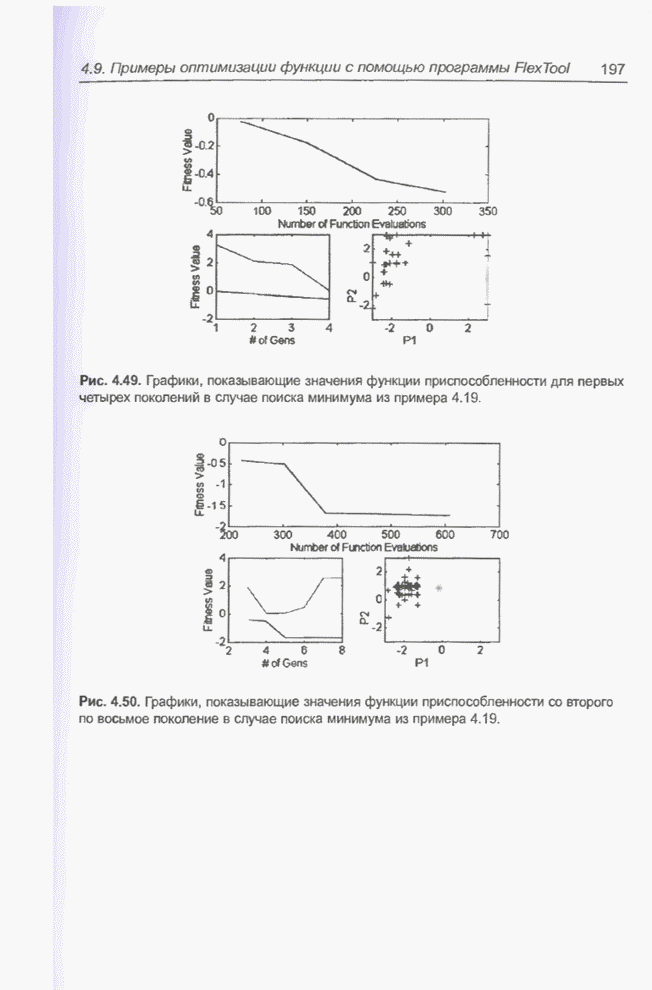
Рис. 4.49. Графики, показывающие значения функции приспособленности для первых четырех поколений в случае поиска минимума из примера 4.19.

Рис. 4.50. Графики, показывающие значения функции приспособленности со второго по восьмое поколение в случае поиска минимума из примера 4.19.

Рис. 4.51. Графики, показывающие значения функции приспособленности с десятого по шестнадцатое поколение в случае поиска минимума из примера 4.19.

Рис. 4.52. Графики, показывающие значения функции приспособленности с двадцать шестого по тридцать второе поколение в случае поиска минимума из примера 4.19.

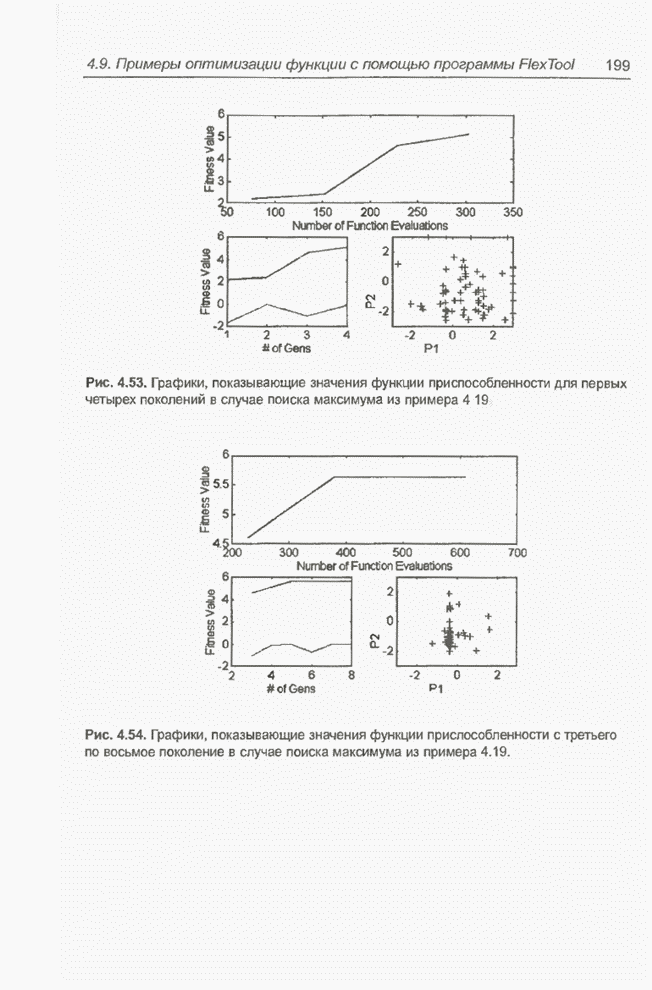
Рис. 4.53. Графики, показывающие знамения функции приспособленности для первых четырех поколений в случае поиска максимума из примера 4.19.

Рис. 4.54. Графики, показывающие значения функции приспособленности с третьего по восьмое поколение в случае поиска максимума из примера 4.19.

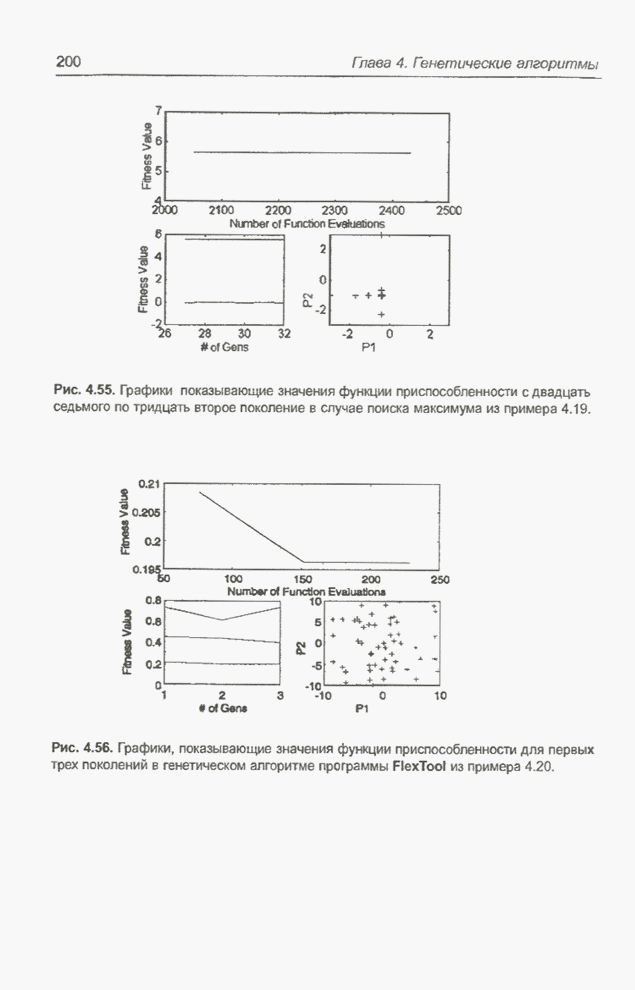
Рис. 4.55. Графики показывающие значения функции приспособленности с двадцать седьмого по тридцать второе поколение в случае поиска максимума из примера 4.19.
Обратим внимание на распределение
особей в популяции в зависимости от номера поколения. Вначале (рис. 4.48)
заметно довольно большое разнообразие и относительно равномерное распределение
отдельных точек на плоскости, заданной осями ![]() и
и ![]() в интервале от -3 до 3. На рис. 4.49
(четвертое поколение) наблюдается отчетливое их смещение в направлении значений
в интервале от -3 до 3. На рис. 4.49
(четвертое поколение) наблюдается отчетливое их смещение в направлении значений
![]() , близких к
-2, а на рис. 4.50 - группирование поблизости значений
, близких к
-2, а на рис. 4.50 - группирование поблизости значений ![]() , примерно равных 0,5. На рис.
4.51 большинство точек находится в окрестности оптимального решения с
координатами
, примерно равных 0,5. На рис.
4.51 большинство точек находится в окрестности оптимального решения с
координатами ![]() и
и
![]() . Из рис.
4.52 следует, что большинство хромосом в популяции совпадает с «наилучшей»
особью, для которой функция приспособленности принимает минимальное значение,
равное -1,907. Также необходимо добавить, что этого минимального значения
функция приспособленности достигла в шестнадцатом поколении выполнения
генетического алгоритма. Верхние графики на рис. 4.48 - 4.52 иллюстрируют
изменение «наилучшего» значения функции приспособленности при последовательной
смене поколений (числа на оси абсцисс соответствуют номерам поколений,
умноженным на 77). Нижние левые графики на этих рисунках отображают динамику
изменения «наилучшего» и «наихудшего» значений функции приспособленности при
последовательной смене поколений.
. Из рис.
4.52 следует, что большинство хромосом в популяции совпадает с «наилучшей»
особью, для которой функция приспособленности принимает минимальное значение,
равное -1,907. Также необходимо добавить, что этого минимального значения
функция приспособленности достигла в шестнадцатом поколении выполнения
генетического алгоритма. Верхние графики на рис. 4.48 - 4.52 иллюстрируют
изменение «наилучшего» значения функции приспособленности при последовательной
смене поколений (числа на оси абсцисс соответствуют номерам поколений,
умноженным на 77). Нижние левые графики на этих рисунках отображают динамику
изменения «наилучшего» и «наихудшего» значений функции приспособленности при
последовательной смене поколений.
Аналогичные графики приведены на
рис. 4.53 - 4.55; они демонстрируют, как изменяются «наилучшее» и «наихудшее»
значения функции приспособленности при последовательной смене поколений в
случае поиска максимума. На этих рисунках можно проследить уменьшение
разнообразия хромосом в популяции. На рис. 4.55 практически все особи одинаковы
и равны «наилучшей» хромосоме со значениями фенотипов -0,39 и -0,99 Функция
приспособленности этой хромосомы равна 5,638. Эта точка максимума функции ![]() найдена (также, как и
в случае минимизации) в шестнадцатом поколении выполнения генетического
алгоритма.
найдена (также, как и
в случае минимизации) в шестнадцатом поколении выполнения генетического
алгоритма.
Пример 4.20
С помощью генетического алгоритма
программы FlexTool найти оптимальный набор весов ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() в диапазоне от -10 до 10 для нейронной
сети, изображенной на рис. 4.2.
в диапазоне от -10 до 10 для нейронной
сети, изображенной на рис. 4.2.
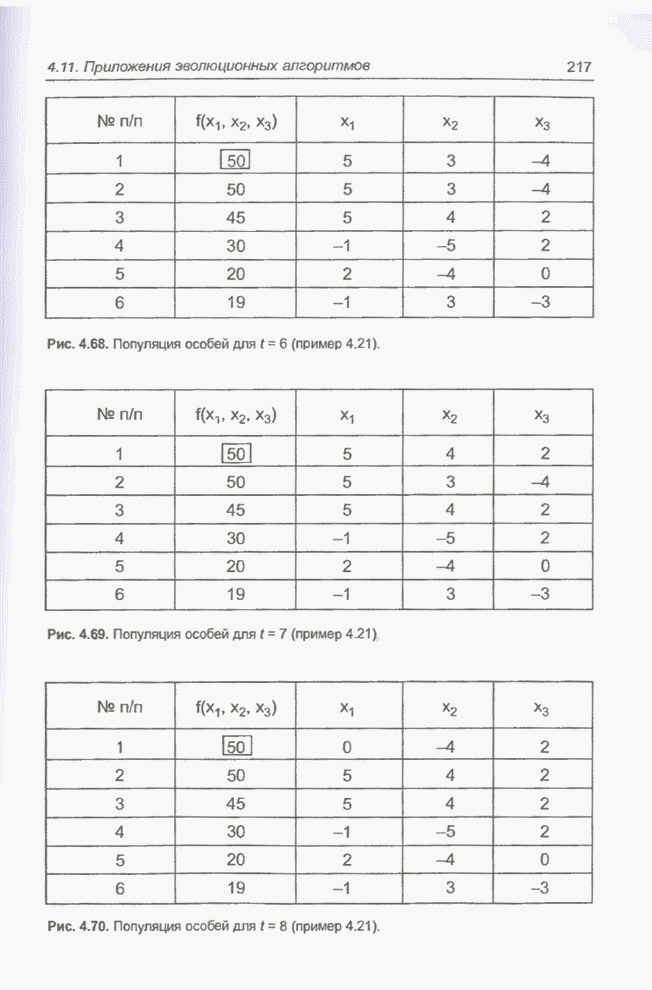
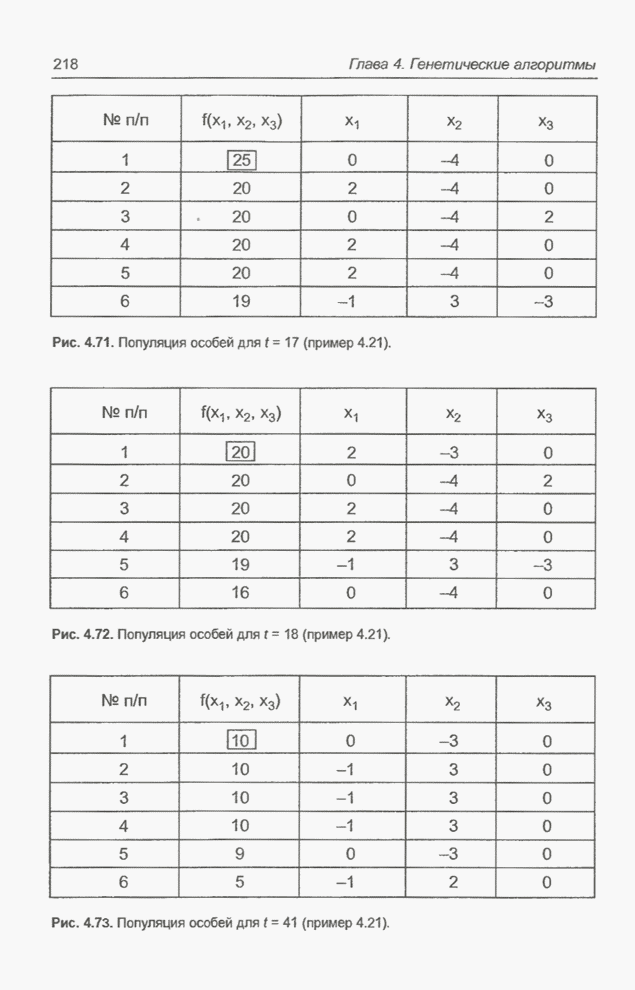
Итак, необходимо решить задачу,
поставленную в примере 4.3, т.е. найти значения девяти переменных, обозначающих
веса нейронной сети, для которых функция погрешности ![]() достигает минимального
значения, равного 0. Для сети, реализующей логическую систему XOR, функцию
погрешности можно определить в виде
достигает минимального
значения, равного 0. Для сети, реализующей логическую систему XOR, функцию
погрешности можно определить в виде
 ,
,
где

для
![]() . Значения
. Значения ![]() ,
, ![]() и
и ![]() приведены в таблице 2.1.
Предполагается, что
приведены в таблице 2.1.
Предполагается, что ![]() .
.
Применяется генетический алгоритм с турнирной селекцией в подгруппах по две особи с одной точкой скрещивания. По умолчанию приняты установленные в программе FlexTool значения вероятностей скрещивания 0,77 и мутации 0,0077, а также размерность популяции, равная 77. Длина хромосом для решаемой задачи равна 99 битам - по 11 генов на каждую переменную.
Динамика изменения значений
функции приспособленности при последовательной смене поколений иллюстрируется
графиками на рис. 4.56 - 4.64. На них также показано распределение особей в
зависимости от номера поколения, причем отмечены только параметры ![]() и
и ![]() , соответствующие переменным
, соответствующие переменным ![]() и
и ![]() . «Наилучшее» значение функции
приспособленности изменяется от значения, примерно равного 0,21, до 0,00007.
Напомним, что функция приспособленности соответствует функции погрешности
. «Наилучшее» значение функции
приспособленности изменяется от значения, примерно равного 0,21, до 0,00007.
Напомним, что функция приспособленности соответствует функции погрешности ![]() , значение которой
может изменяться от 1 до 0.
, значение которой
может изменяться от 1 до 0.

Рис. 4.56. Графики, показывающие значения функции приспособленности для первых трех поколений в генетическом алгоритме программы FlexTool из примера 4.20.

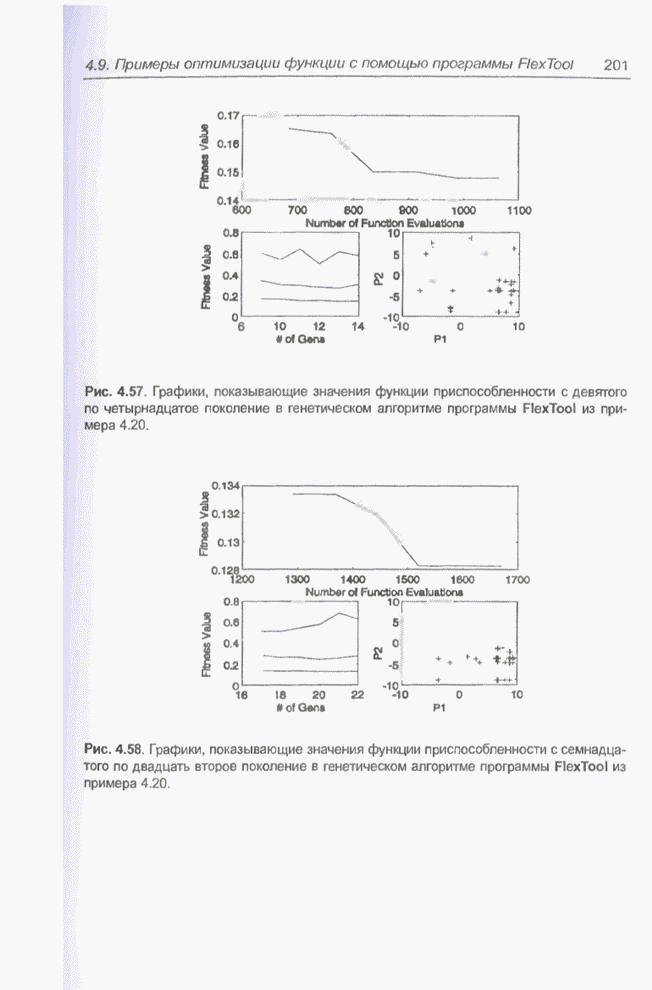
Рис. 4.57. Графики, показывающие значения функции приспособленности с девятого по четырнадцатое поколение в генетическом алгоритме программы FlexTool из примера 4.20.

Рис. 4.58. Графики, показывающие значения функции приспособленности с семнадцатого по двадцать второе поколение в генетическом алгоритме программы FlexTool из примера 4.20.

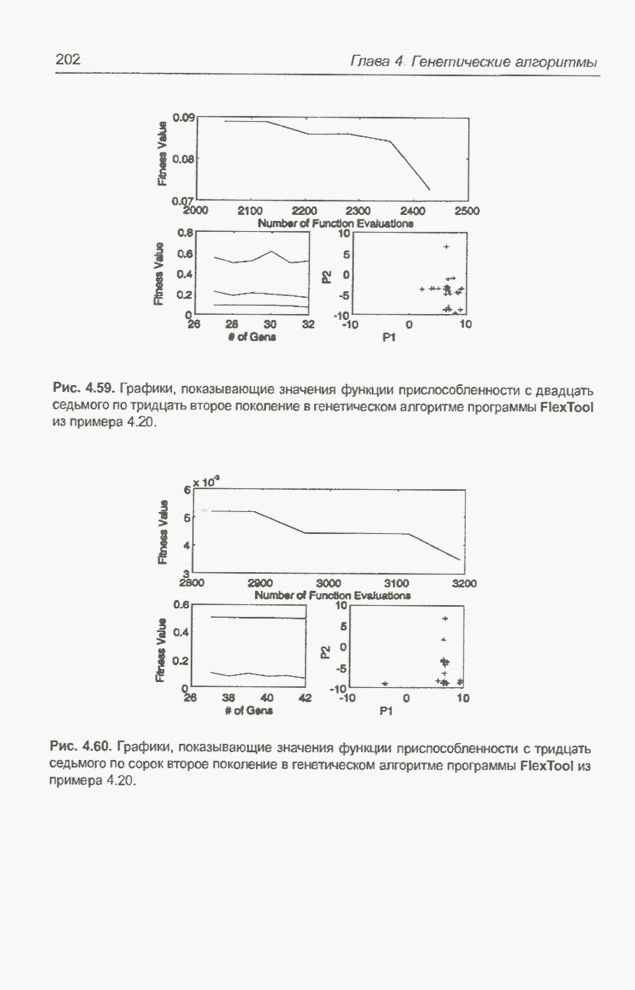
Рис. 4.59. Графики, показывающие значения функции приспособленности с двадцать седьмого по тридцать второе поколение в генетическом алгоритме программы FlexTool из примера 4.20.

Рис. 4.60. Графики, показывающие значения функции приспособленности с тридцать седьмого по сорок второе поколение в генетическом алгоритме программы FlexTool из примера 4.20.

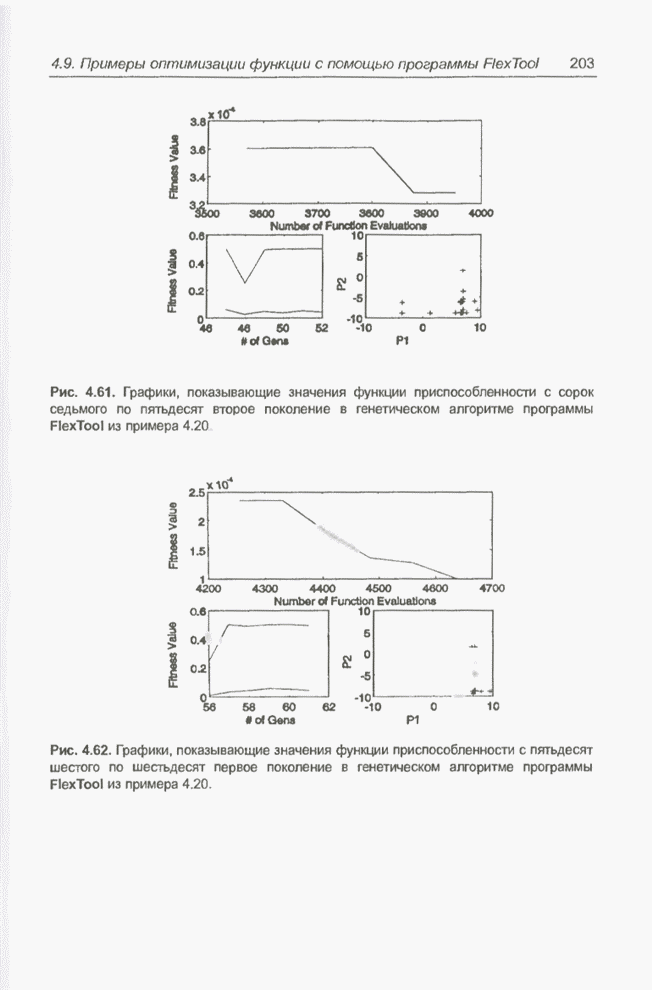
Рис. 4.61. Графики, показывающие значения функции приспособленности с сорок седьмого по пятьдесят второе поколение в генетическом алгоритме программы FlexTool из примера 4.20.

Рис. 4.62. Графики, показывающие значения функции приспособленности с пятьдесят шестого по шестьдесят первое поколение в генетическом алгоритме программы FlexTool из примера 4.20.

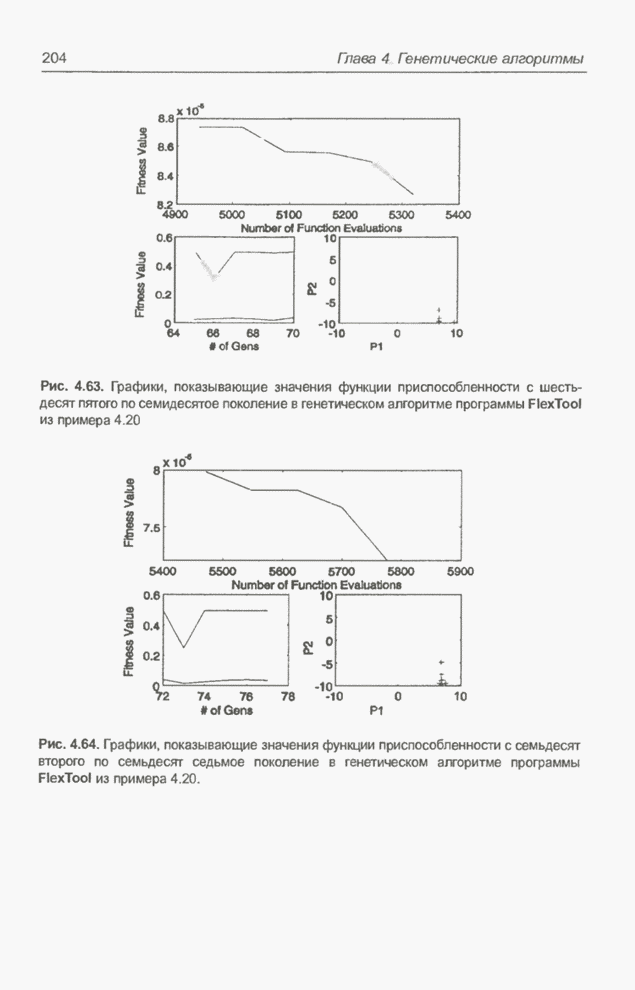
Рис. 4.63. Графики, показывающие значения функции приспособленности с шестьдесят пятого по семидесятое поколение в генетическом алгоритме программы FlexTool из примера 4.20.

Рис. 4.64. Графики, показывающие значения функции приспособленности с семьдесят второго по семьдесят седьмое поколение в генетическом алгоритме программы FlexTool из примера 4.20.
Нижние левые графики иллюстрируют
динамику изменения «наилучшего» (нижняя кривая), «наихудшего» (верхняя кривая) и
среднего (средняя кривая) значений функции приспособленности в популяции при
последовательной смене поколений. На рис. 4.61 - 4.64 «наилучшее» значение
функции приспособленности принимает настолько малое значение, что оно
становится незаметным на графиках. В 75-м поколении оно становится равным ![]() , т.е. таким, которое
принимается в качестве минимального значения. Таким образом, эта величина может
считаться значением функции приспособленности «наилучшей» хромосомы со
следующими фенотипами - значениями отдельных переменных, обозначающих веса
нейронной сети:
, т.е. таким, которое
принимается в качестве минимального значения. Таким образом, эта величина может
считаться значением функции приспособленности «наилучшей» хромосомы со
следующими фенотипами - значениями отдельных переменных, обозначающих веса
нейронной сети:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
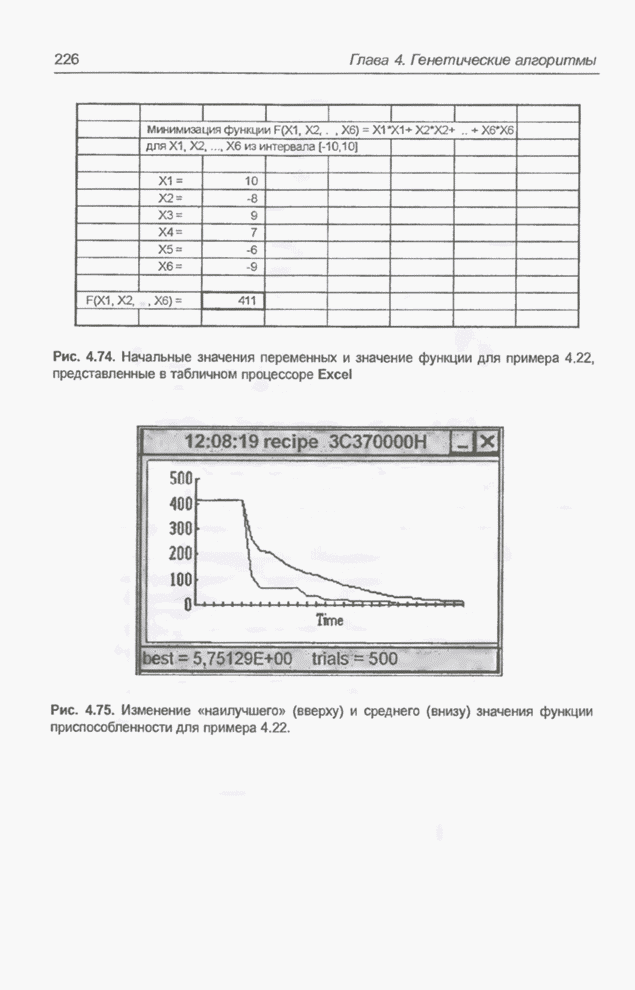
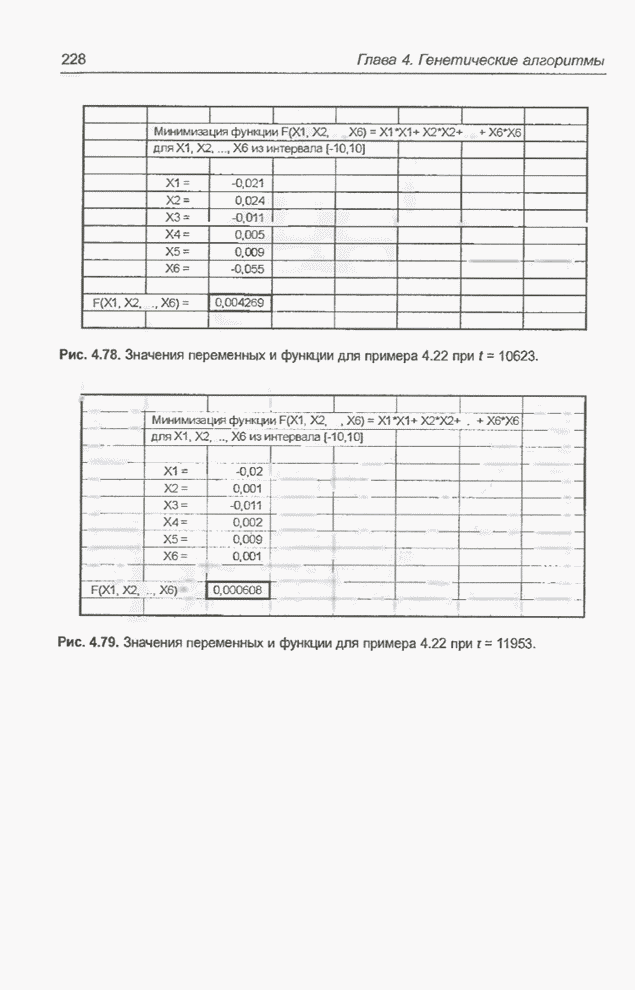
Вычисления были завершены после
77 итераций алгоритма. В случае их продолжения можно было бы ожидать получение
результата, более близкого к представленному на рис. 4.83 и 4.84, т.е. значения
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() оказались бы примерно равны
соответственно 10, -10, -10, 10, -10, -10, a
оказались бы примерно равны
соответственно 10, -10, -10, 10, -10, -10, a ![]() ,
, ![]() ,
, ![]() - величине -5. Также очевидно, что
уменьшилось бы и значение погрешности
- величине -5. Также очевидно, что
уменьшилось бы и значение погрешности ![]() ; скорее всего, оно приблизилось бы к
величине, полученной с помощью программы Evolver (пример 4.24) и показанной на
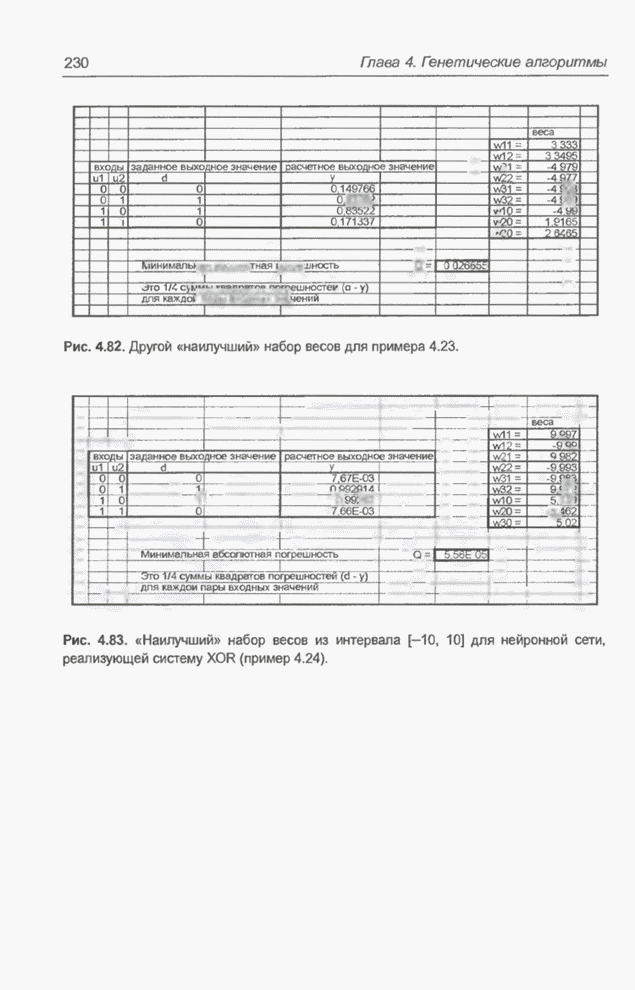
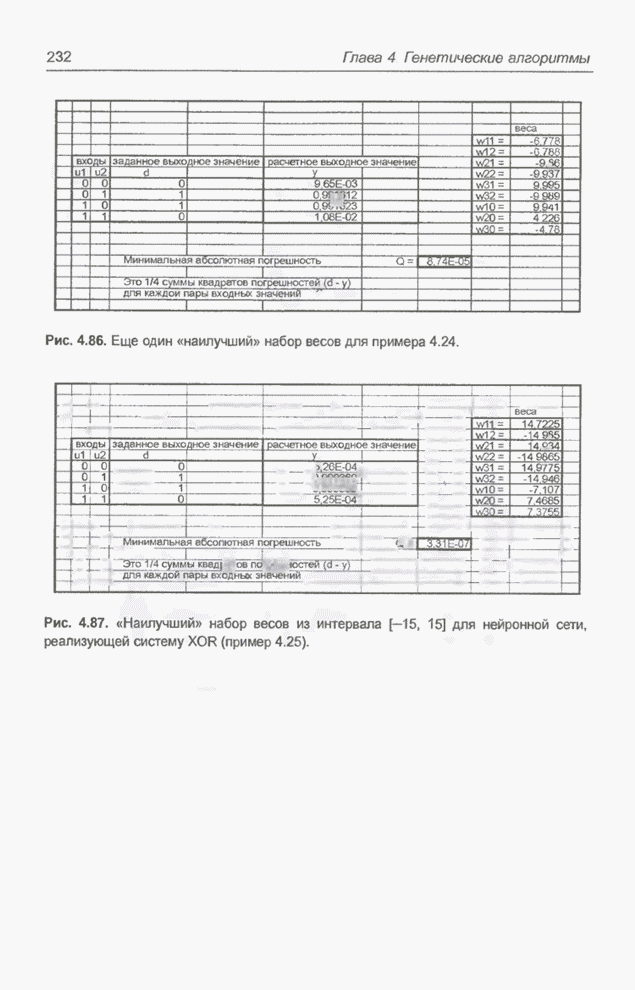
рис. 4.83 и 4.84. Рассчитанные значения представляют собой одну из возможных
комбинаций весов для нейронной сети, реализующей логическую систему XOR и
изображенной на рис. 4.2 [31]. В разд. 4.11 будут представлены примеры,
относящиеся к этой же задаче, решаемой с помощью программы Evolver [49] при
различных интервалах весов.
; скорее всего, оно приблизилось бы к
величине, полученной с помощью программы Evolver (пример 4.24) и показанной на
рис. 4.83 и 4.84. Рассчитанные значения представляют собой одну из возможных
комбинаций весов для нейронной сети, реализующей логическую систему XOR и
изображенной на рис. 4.2 [31]. В разд. 4.11 будут представлены примеры,
относящиеся к этой же задаче, решаемой с помощью программы Evolver [49] при
различных интервалах весов.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Предисловие к русскому изданию
- ГЛАВА 1. ВВЕДЕНИЕ
- Список литературы
- ГЛАВА 2. МНОГОСЛОЙНЫЕ НЕЙРОННЫЕ СЕТИ И АЛГОРИТМЫ ИХ ОБУЧЕНИЯ
- 2.1. Введение
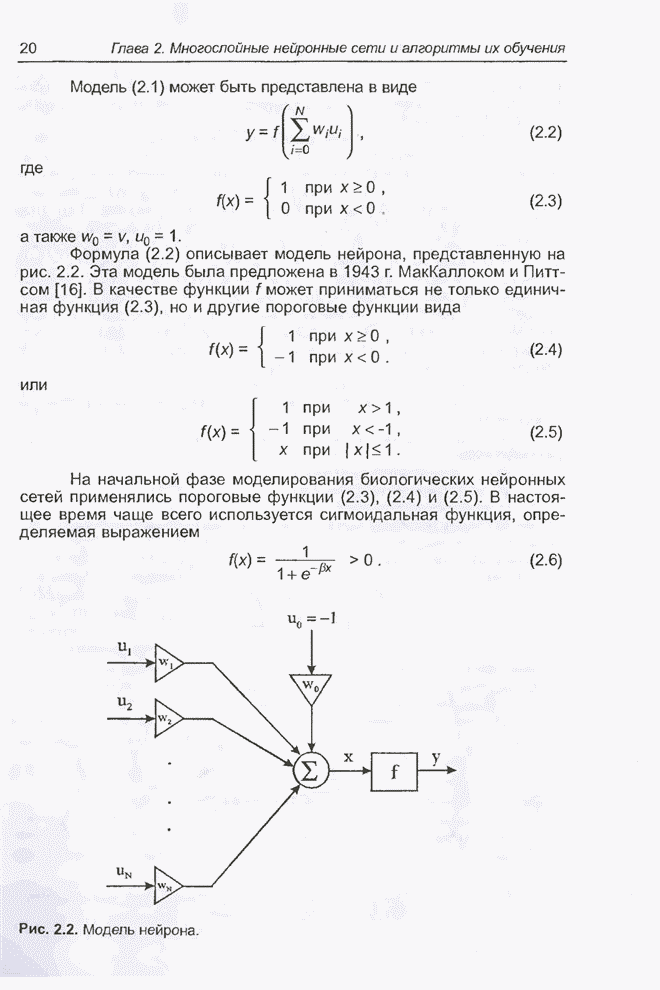
- 2.2. Нейрон и его модели
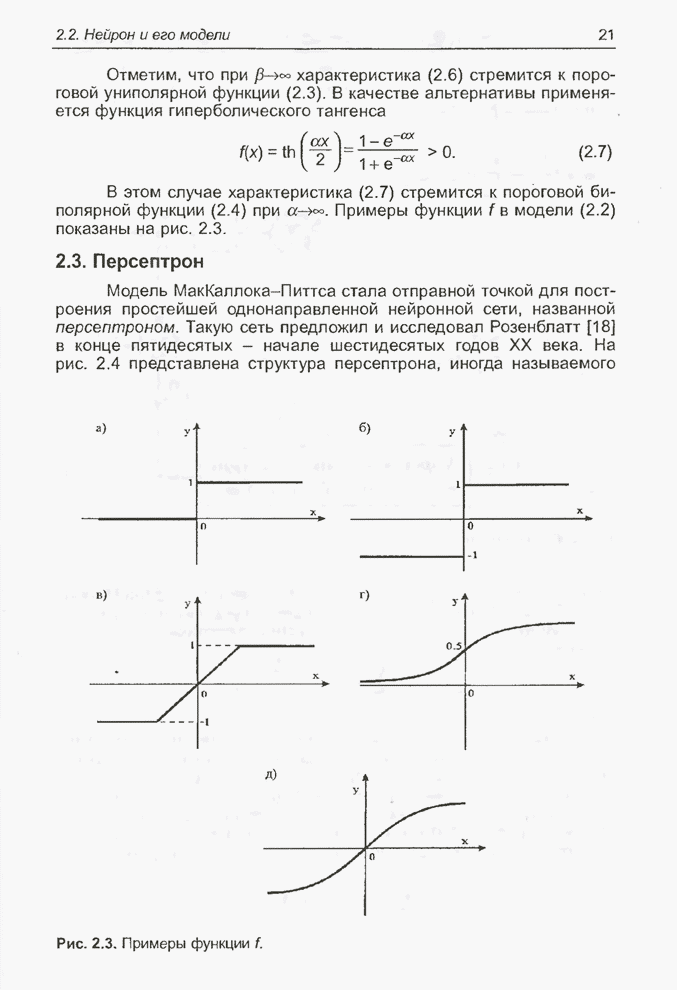
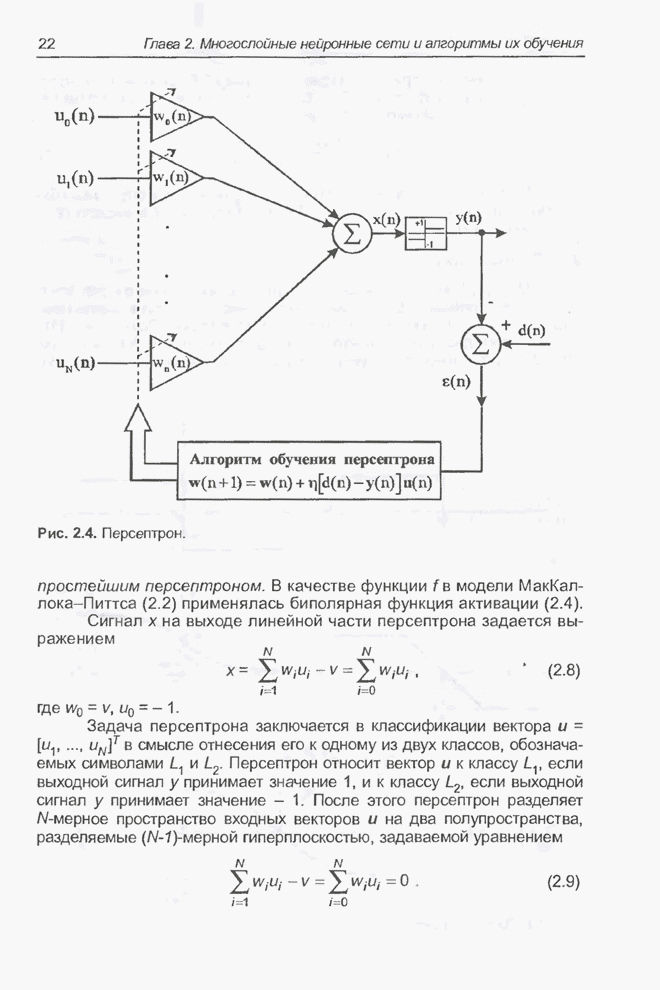
- 2.3. Персептрон
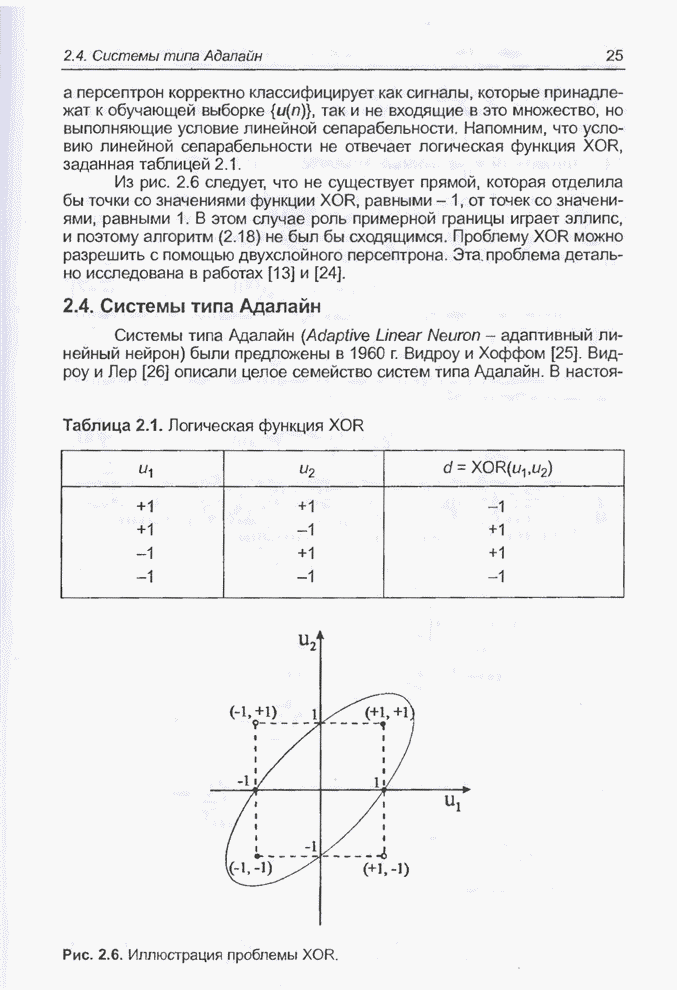
- 2.4. Системы типа Адалайн
- 2.4.1. Линейный взвешенный сумматор
- 2.4.2. Адаптивный линейный взвешенный сумматор
- 2.4.3. Адаптивный линейный взвешенный сумматор с сигмоидой на выходе
- 2.5. Алгоритм обратного распространения ошибки
- 2.6. Применение рекуррентного метода наименьших квадратов для обучения нейронных сетей
- Список литературы
- ГЛАВA3. НЕЧЕТКИЕ МНОЖЕСТВА И НЕЧЕТКИЙ ВЫВОД
- 3.1. Введение
- 3.2. Основные понятия и определения теории нечетких множеств
- 3.3. Операции на нечетких множествах
- 3.4. Принцип расширения
- 3.5. Нечеткие числа
- 3.6. Треугольные нормы
- 3.7. Нечеткие отношения и их свойства
- 3.8. Нечеткий вывод
- 3.9. Нечеткое управление
- 3.9.1. Классический модуль нечеткого управления
- 3.9.2. Метод нечеткого управления Такаги-Сугено
- 3.10. Проектирование базы нечетких правил на основе численных данных
- 3.10.1. Построение нечетких правил
- 3.10.2. Задача парковки грузовика
- 3.10.3. Примечание
- Список литературы
- ГЛАВА 4. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 4.1. Введение
- 4.2. Генетические алгоритмы и традиционные методы оптимизации
- 4.3. Основные понятия генетических алгоритмов
- 4.4. Классический генетический алгоритм
- 4.5. Иллюстрация выполнения классического генетического алгоритма
- 4.6. Кодирование параметров задачи в генетическом алгоритме
- 4.7. Основная теорема о генетических алгоритмах
- 4.8. Модификации классического генетического алгоритма
- 4.8.1. Методы селекции
- 4.8.2. Особые процедуры репродукции
- 4.8.3. Генетические операторы
- 4.8.4. Методы кодирования
- 4.8.5. Масштабирование функции приспособленности
- 4.8.6. Ниши в генетическом алгоритме
- 4.8.7. Генетические алгоритмы для многокритериальной оптимизации
- 4.8.8. Генетические микроалгоритмы
- 4.9. Примеры оптимизации функции с помощью программы FlexTool
- 4.10. Эволюционные алгоритмы
- 4.11. Приложения эволюционных алгоритмов
- 4.11.1. Примеры оптимизации функции с помощью программы Evolver
- 4.11.2. Решение комбинаторных задач с помощью программы Evolver
- 4.12. Эволюционные алгоритмы в нейронных сетях
- 4.12.1. Независимое применение генетических алгоритмов и нейронных сетей
- 4.12.2. Нейронные сети для поддержки генетических алгоритмов
- 4.12.3. Генетические алгоритмы для поддержки нейронных сетей
- 4.12.4. Применение генетических алгоритмов для обучения нейронных сетей
- 4.12.5. Генетические алгоритмы для выбора топологии нейронных сетей
- 4.12.6. Адаптивные взаимодействующие системы
- 4.12.7. Типовой цикл эволюции
- 4.12.7.1. Эволюция весов связей
- 4.12.7.2. Эволюция архитектуры сети
- 4.12.7.3. Эволюция правил обучения
- 4.13. Примеры моделирования эволюционных алгоритмов в приложении к нейронным сетям
- 4.13.1. Программы Evolver и BrainMaker
- 4.13.2. Программа GTO
- Список литературы
- ГЛАВА 5. МОДУЛИ НЕЧЕТКО-НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.1. Модуль нечеткого управления со структурой, определенной в процессе дефуззификации
- 5.1.2. Конструкция модуля
- 5.1.3. Структура модуля
- 5.1.4. Использование алгоритма обратного распространения ошибки
- 5.1.5. Модификации модуля
- 5.1.6. Применение модуля нечеткого управления для прогнозирования случайных временных рядов
- 5.1.7. Применение модуля нечеткого управления для решения задачи парковки грузовика
- 5.1.8. Примечание
- 5.2. Представление модуля нечеткого управления в виде стандартной нейронной сети
- 5.3. Модуль нечеткого управления с нейронной сетью для выполнения дефуззификации
- 5.3.1. Введение
- 5.3.2. Конструкция модуля
- 5.3.3. Структура модуля
- 5.3.4. Алгоритмы обучения модуля
- 5.3.5. Решение задачи стабилизации перевернутого маятника
- 5.3.6. Примечание
- 5.4. Модуль нечеткого управления с возможностью коррекции правил
- 5.4.1. Введение
- 5.4.2. Фаза обучения на основе самоорганизации
- 5.4.3. Фаза обучения с учителем
- 5.4.4. Примечание
- 5.5. Модуль нечеткого управления типа Такаги-Сугено
- 5.5.1. Введение
- 5.5.2. Нейронная реализация функции принадлежности
- 5.5.3. Модули Такаги-Сугено
- 5.5.4. Реализация условий
- 5.5.5. Реализация заключений
- 5.5.6. Примечание
- 5.6. Модуль нечеткого управления типа Такаги-Сугено: случай зависимых лингвистических переменных
- 5.6.1. Введение
- 5.6.2. Нейронные сети для нечеткого вывода
- 5.6.3. Структура системы
- 5.6.4. Способ обучения
- 5.6.5. Решение задачи парковки грузовика
- 5.6.6. Примечание
- Список литературы