| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.7. Нечеткие отношения и их свойства
Одним из основных понятий теории
нечетких множеств считается понятие нечеткого отношения. Эти отношения позволяют
формализовать неточные утверждения типа «![]() почти равно
почти равно ![]() » или «
» или «![]() значительно больше чем
значительно больше чем ![]() ». Приведем определение
нечеткого отношения и комбинации нечетких отношений.
». Приведем определение
нечеткого отношения и комбинации нечетких отношений.
Определение 3.26
Нечеткое отношение ![]() между двумя непустыми
множествами (четкими)
между двумя непустыми
множествами (четкими) ![]() и
и ![]() будем называть нечеткое множество,
определенное на декартовом произведении
будем называть нечеткое множество,
определенное на декартовом произведении ![]() , т.е.
, т.е.
![]() . (3.157)
. (3.157)
Другими словами, нечеткое отношение - множество пар
![]() , (3.158)
, (3.158)
где
![]() (3.159)
(3.159)
-
это функция принадлежности, которая каждой паре ![]() приписывает ее степень принадлежности
приписывает ее степень принадлежности ![]() , которая
интерпретируется как сила связи между элементами
, которая
интерпретируется как сила связи между элементами ![]() и
и ![]() . В соответствии с принятым соглашением
(п. 3.2) нечеткое отношение можно представить в виде
. В соответствии с принятым соглашением
(п. 3.2) нечеткое отношение можно представить в виде
 (3.160)
(3.160)
или
 . (3.161)
. (3.161)
Пример 3.22
Применим определение 3.26 для
формализации неточного утверждения «![]() примерно равно
примерно равно ![]() ». Пусть
». Пусть ![]() и
и ![]() . Отношение
. Отношение ![]() можно определить следующим
образом:
можно определить следующим
образом:
![]() . (3.162)
. (3.162)
Следовательно, функция
принадлежности ![]() отношения
отношения
![]() имеет вид
имеет вид
 (3.163)
(3.163)
Отношение ![]() можно также задать в виде
матрицы
можно также задать в виде
матрицы
 , (3.164)
, (3.164)
где
![]() ,
, ![]() ,
, ![]() , а
, а ![]() ,
, ![]() ,
, ![]() .
.
Пример 3.23
Пусть ![]() - это длительность жизни
человека. В этом случае отношение
- это длительность жизни
человека. В этом случае отношение ![]() с функцией принадлежности
с функцией принадлежности
 (3.165)
(3.165)
представляет
неточное утверждение «особа ![]() намного старше особы
намного старше особы ![]() ».
».
Следует подчеркнуть, что нечеткое
отношение ![]() -
это нечеткое множество, поэтому сохраняют силу введенные в п. 3.3 определения
операций пересечения, суммирования и дополнения:
-
это нечеткое множество, поэтому сохраняют силу введенные в п. 3.3 определения
операций пересечения, суммирования и дополнения:
![]() , (3.166)
, (3.166)
![]() , (3.167)
, (3.167)
![]() . (3.168)
. (3.168)
В теории нечетких множеств важную
роль играет понятие комбинации двух нечетких отношений. Рассмотрим три четких
множества ![]() ,
, ![]() ,
, ![]() и два нечетких отношения
и два нечетких отношения ![]() и
и ![]() c функциями принадлежности
c функциями принадлежности ![]() и
и ![]() .
.
Определение 3.27
Комбинацией типа ![]() нечетких отношений
нечетких отношений ![]() и
и ![]() называется нечеткое отношение
называется нечеткое отношение ![]() с функцией
принадлежности
с функцией
принадлежности
![]() . (3.169)
. (3.169)
Конкретная форма функции
принадлежности ![]() комбинации
комбинации
![]() зависит от
зависит от ![]() -нормы, используемой в
формуле (3.169). Если в качестве
-нормы, используемой в
формуле (3.169). Если в качестве ![]() -нормы применяется
-нормы применяется ![]() , т.е.
, т.е. ![]() , то равенство (3.169) можно
представить в виде
, то равенство (3.169) можно
представить в виде
![]() . (3.170)
. (3.170)
Формула
(3.170) известна в литературе под названием «комбинация типа sup-min». Если
множество ![]() имеет
конечное количество элементов, то комбинация типа sup-min сводится к комбинации
типа max-min в форме
имеет
конечное количество элементов, то комбинация типа sup-min сводится к комбинации
типа max-min в форме
![]() . (3.171)
. (3.171)
Пример 3.24
Допустим, что отношения ![]() и
и ![]() представлены матрицами
представлены матрицами
![]() ,
, ![]() , (3.172)
, (3.172)
причем
![]() ,
, ![]() ,
, ![]() . Комбинация типа max-min
отношений
. Комбинация типа max-min
отношений ![]() и
и
![]() имеет вид
имеет вид
 , (3.173)
, (3.173)
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Поэтому
![]() . (3.174)
. (3.174)
В таблице 3.2 собраны важнейшие
свойства нечетких отношений, причем ![]() означает единичную матрицу, а
означает единичную матрицу, а ![]() - нулевую матрицу.
- нулевую матрицу.
Таблица 3.2. Важнейшие свойства нечетких отношений
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
Как отмечалось в начале п. 3.6,
для практических приложений особенно важна комбинация нечеткого множества с
нечетким отношением. Комбинация этого типа будет многократно использоваться в
последующем изложении. Рассмотрим нечеткое множество ![]() и нечеткое отношение
и нечеткое отношение ![]() с функциями
принадлежности
с функциями
принадлежности ![]() и
и
![]() .
.
Определение 3.28
Комбинация нечеткого множества ![]() и нечеткого отношения
и нечеткого отношения
![]() обозначается
обозначается
![]() и
определяется как нечеткое множество
и
определяется как нечеткое множество ![]() .
.
![]() (3.175)
(3.175)
с функцией принадлежности
![]() . (3.176)
. (3.176)
Конкретная форма записи выражения
(3.176) зависит от используемой ![]() -нормы и от свойств множества
-нормы и от свойств множества ![]() . Выделим 4 случая:
. Выделим 4 случая:
1)
если ![]() , то
получаем комбинацию типа sup-min
, то
получаем комбинацию типа sup-min
![]() , (3.177)
, (3.177)
2)
если ![]() и
и ![]() представляет собой
множество с конечным количеством элементов, то получаем комбинацию типа max-min
представляет собой
множество с конечным количеством элементов, то получаем комбинацию типа max-min
![]() , (3.178)
, (3.178)
3)
если ![]() , то
получаем комбинацию типа sup-произведение (sup-product)
, то
получаем комбинацию типа sup-произведение (sup-product)
![]() , (3.179)
, (3.179)
4)
если ![]() и
и ![]() представляет собой
множество с конечным количеством элементов, то получаем комбинацию типа mах-произведение (max-product)
представляет собой
множество с конечным количеством элементов, то получаем комбинацию типа mах-произведение (max-product)
![]() . (3.180)
. (3.180)
Пример 3.25
Допустим, что ![]() ,
, ![]() и
и ![]() имеет вид
имеет вид
![]() , (3.181)
, (3.181)
тогда
как отношение ![]() представлено
матрицей
представлено
матрицей
 . (3.182)
. (3.182)
Комбинацию ![]() типа max-min рассчитываем по
формуле (3.178). Результат комбинации - это нечеткое множество
типа max-min рассчитываем по
формуле (3.178). Результат комбинации - это нечеткое множество ![]() вида
вида
![]() , (3.183)
, (3.183)
причем
![]() , (3.184)
, (3.184)
![]() . (3.185)
. (3.185)
Поэтому
![]() . (3.186)
. (3.186)
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Предисловие к русскому изданию
- ГЛАВА 1. ВВЕДЕНИЕ
- Список литературы
- ГЛАВА 2. МНОГОСЛОЙНЫЕ НЕЙРОННЫЕ СЕТИ И АЛГОРИТМЫ ИХ ОБУЧЕНИЯ
- 2.1. Введение
- 2.2. Нейрон и его модели
- 2.3. Персептрон
- 2.4. Системы типа Адалайн
- 2.4.1. Линейный взвешенный сумматор
- 2.4.2. Адаптивный линейный взвешенный сумматор
- 2.4.3. Адаптивный линейный взвешенный сумматор с сигмоидой на выходе
- 2.5. Алгоритм обратного распространения ошибки
- 2.6. Применение рекуррентного метода наименьших квадратов для обучения нейронных сетей
- Список литературы
- ГЛАВA3. НЕЧЕТКИЕ МНОЖЕСТВА И НЕЧЕТКИЙ ВЫВОД
- 3.1. Введение
- 3.2. Основные понятия и определения теории нечетких множеств
- 3.3. Операции на нечетких множествах
- 3.4. Принцип расширения
- 3.5. Нечеткие числа
- 3.6. Треугольные нормы
- 3.7. Нечеткие отношения и их свойства
- 3.8. Нечеткий вывод
- 3.9. Нечеткое управление
- 3.9.1. Классический модуль нечеткого управления
- 3.9.2. Метод нечеткого управления Такаги-Сугено
- 3.10. Проектирование базы нечетких правил на основе численных данных
- 3.10.1. Построение нечетких правил
- 3.10.2. Задача парковки грузовика
- 3.10.3. Примечание
- Список литературы
- ГЛАВА 4. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 4.1. Введение
- 4.2. Генетические алгоритмы и традиционные методы оптимизации
- 4.3. Основные понятия генетических алгоритмов
- 4.4. Классический генетический алгоритм
- 4.5. Иллюстрация выполнения классического генетического алгоритма
- 4.6. Кодирование параметров задачи в генетическом алгоритме
- 4.7. Основная теорема о генетических алгоритмах
- 4.8. Модификации классического генетического алгоритма
- 4.8.1. Методы селекции
- 4.8.2. Особые процедуры репродукции
- 4.8.3. Генетические операторы
- 4.8.4. Методы кодирования
- 4.8.5. Масштабирование функции приспособленности
- 4.8.6. Ниши в генетическом алгоритме
- 4.8.7. Генетические алгоритмы для многокритериальной оптимизации
- 4.8.8. Генетические микроалгоритмы
- 4.9. Примеры оптимизации функции с помощью программы FlexTool
- 4.10. Эволюционные алгоритмы
- 4.11. Приложения эволюционных алгоритмов
- 4.11.1. Примеры оптимизации функции с помощью программы Evolver
- 4.11.2. Решение комбинаторных задач с помощью программы Evolver
- 4.12. Эволюционные алгоритмы в нейронных сетях
- 4.12.1. Независимое применение генетических алгоритмов и нейронных сетей
- 4.12.2. Нейронные сети для поддержки генетических алгоритмов
- 4.12.3. Генетические алгоритмы для поддержки нейронных сетей
- 4.12.4. Применение генетических алгоритмов для обучения нейронных сетей
- 4.12.5. Генетические алгоритмы для выбора топологии нейронных сетей
- 4.12.6. Адаптивные взаимодействующие системы
- 4.12.7. Типовой цикл эволюции
- 4.12.7.1. Эволюция весов связей
- 4.12.7.2. Эволюция архитектуры сети
- 4.12.7.3. Эволюция правил обучения
- 4.13. Примеры моделирования эволюционных алгоритмов в приложении к нейронным сетям
- 4.13.1. Программы Evolver и BrainMaker
- 4.13.2. Программа GTO
- Список литературы
- ГЛАВА 5. МОДУЛИ НЕЧЕТКО-НЕЙРОННОГО УПРАВЛЕНИЯ
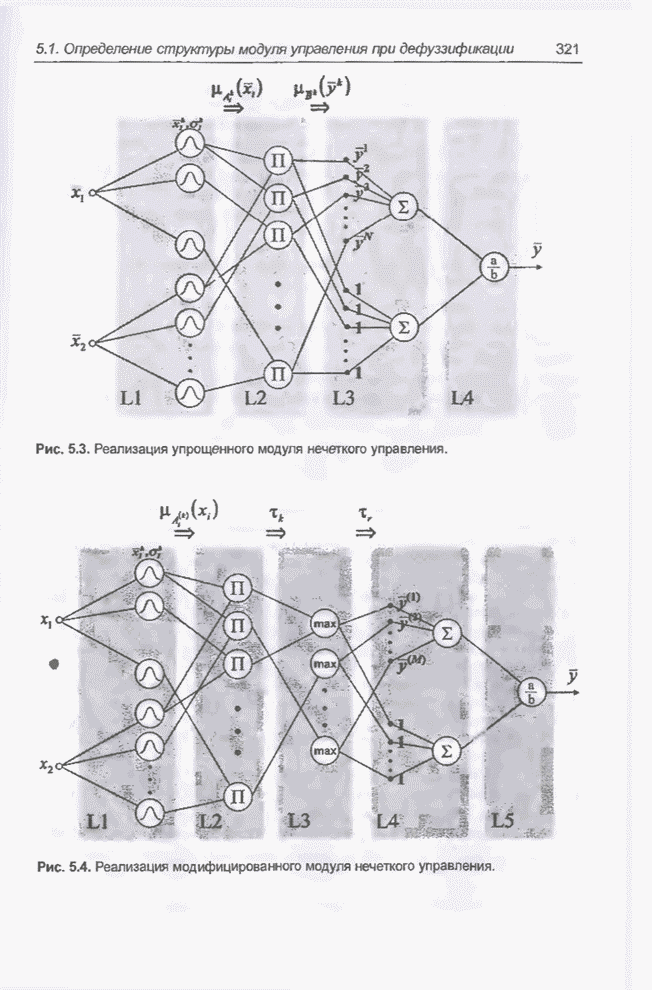
- 5.1. Модуль нечеткого управления со структурой, определенной в процессе дефуззификации
- 5.1.2. Конструкция модуля
- 5.1.3. Структура модуля
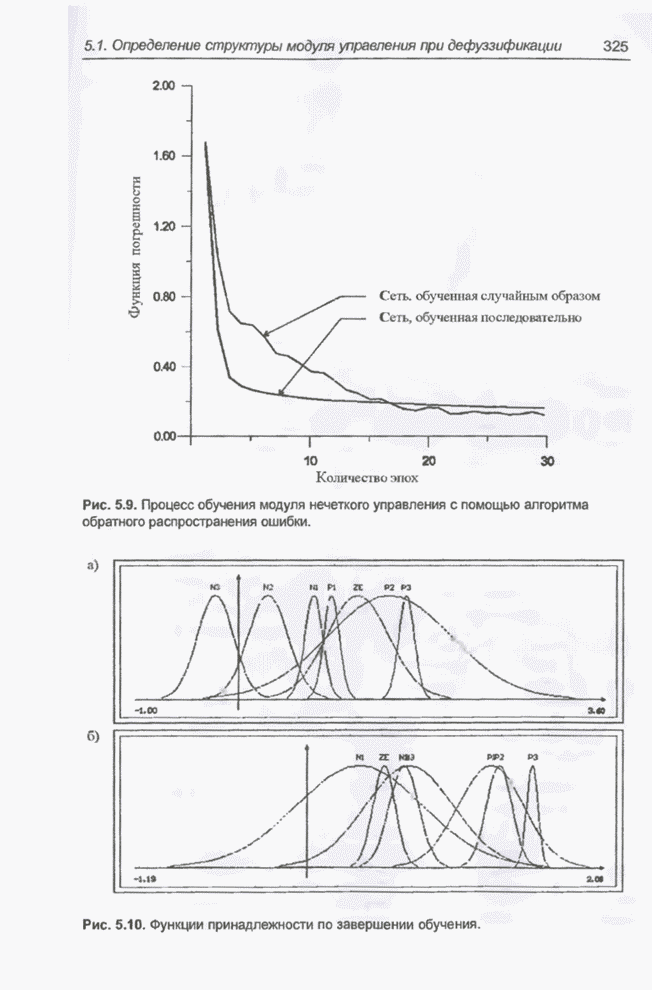
- 5.1.4. Использование алгоритма обратного распространения ошибки
- 5.1.5. Модификации модуля
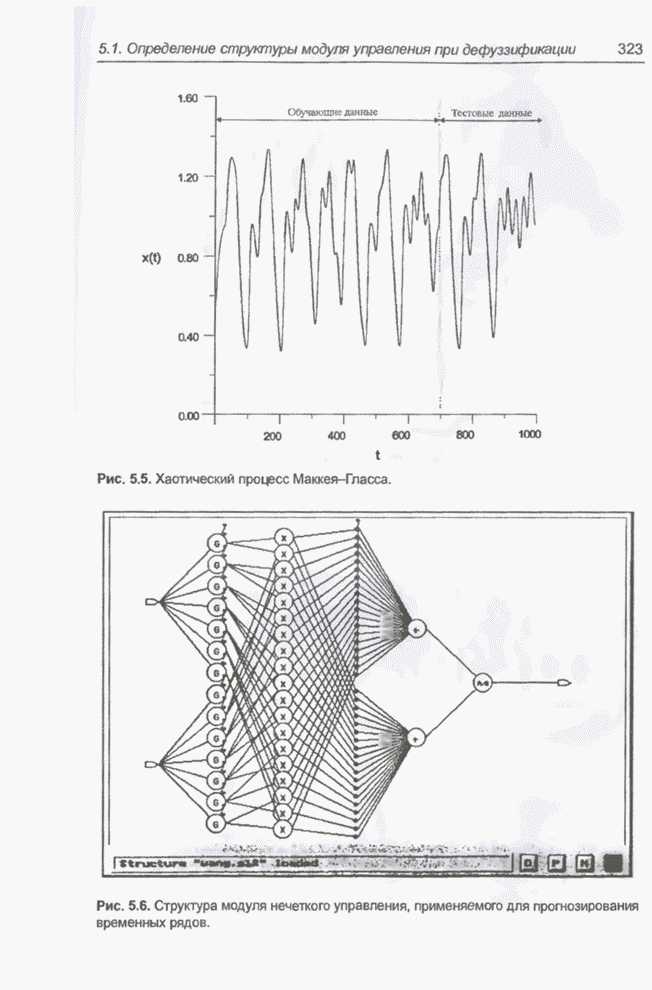
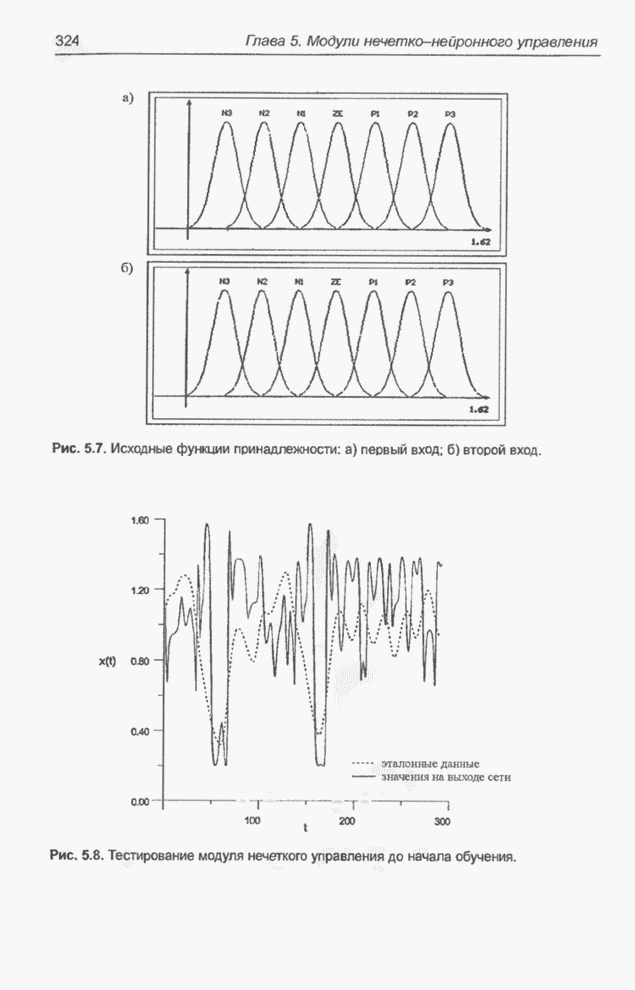
- 5.1.6. Применение модуля нечеткого управления для прогнозирования случайных временных рядов
- 5.1.7. Применение модуля нечеткого управления для решения задачи парковки грузовика
- 5.1.8. Примечание
- 5.2. Представление модуля нечеткого управления в виде стандартной нейронной сети
- 5.3. Модуль нечеткого управления с нейронной сетью для выполнения дефуззификации
- 5.3.1. Введение
- 5.3.2. Конструкция модуля
- 5.3.3. Структура модуля
- 5.3.4. Алгоритмы обучения модуля
- 5.3.5. Решение задачи стабилизации перевернутого маятника
- 5.3.6. Примечание
- 5.4. Модуль нечеткого управления с возможностью коррекции правил
- 5.4.1. Введение
- 5.4.2. Фаза обучения на основе самоорганизации
- 5.4.3. Фаза обучения с учителем
- 5.4.4. Примечание
- 5.5. Модуль нечеткого управления типа Такаги-Сугено
- 5.5.1. Введение
- 5.5.2. Нейронная реализация функции принадлежности
- 5.5.3. Модули Такаги-Сугено
- 5.5.4. Реализация условий
- 5.5.5. Реализация заключений
- 5.5.6. Примечание
- 5.6. Модуль нечеткого управления типа Такаги-Сугено: случай зависимых лингвистических переменных
- 5.6.1. Введение
- 5.6.2. Нейронные сети для нечеткого вывода
- 5.6.3. Структура системы
- 5.6.4. Способ обучения
- 5.6.5. Решение задачи парковки грузовика
- 5.6.6. Примечание
- Список литературы