| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
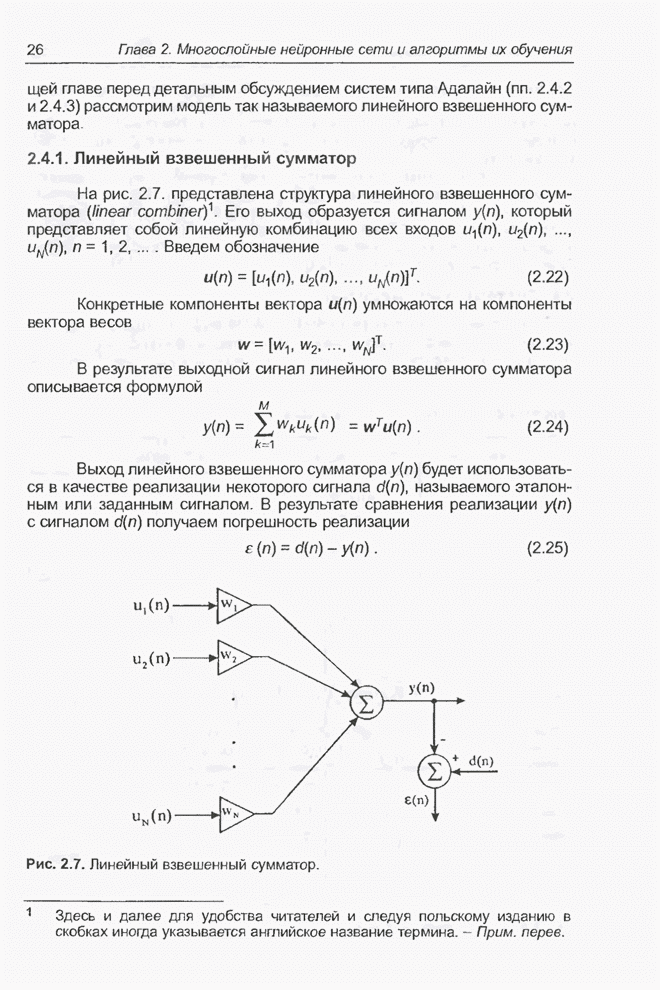
2.4.1. Линейный взвешенный сумматор
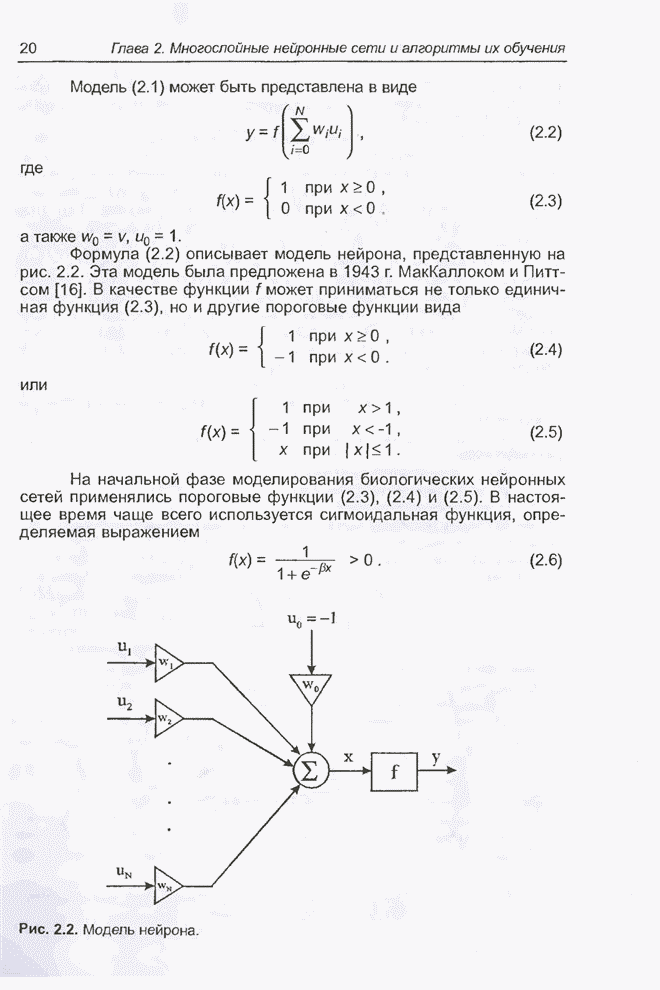
На рис. 2.7. представлена
структура линейного взвешенного сумматора (linear combiner). Его выход
образуется сигналом ![]() ,
который представляет собой линейную комбинацию всех входов
,
который представляет собой линейную комбинацию всех входов ![]() ,
, ![]() . Введем обозначение
. Введем обозначение
![]() . (2.22)
. (2.22)
Конкретные компоненты вектора ![]() умножаются на
компоненты вектора весов
умножаются на
компоненты вектора весов
![]() . (2.23)
. (2.23)
В результате выходной сигнал линейного взвешенного сумматора описывается формулой
 . (2.24)
. (2.24)
Выход линейного взвешенного
сумматора ![]() будет
использоваться в качестве реализации некоторого сигнала
будет
использоваться в качестве реализации некоторого сигнала ![]() , называемого эталонным или
заданным сигналом. В результате сравнения реализации
, называемого эталонным или
заданным сигналом. В результате сравнения реализации ![]() с сигналом
с сигналом ![]() получаем погрешность реализации
получаем погрешность реализации
![]() . (2.25)
. (2.25)

Рис. 2.7. Линейный взвешенный сумматор.
Веса линейного взвешенного
сумматора ![]() будут
подбираться так, чтобы минимизировать меру погрешности
будут
подбираться так, чтобы минимизировать меру погрешности

![]() . (2.26)
. (2.26)
Предположим, что входной сигнал ![]() и эталонный сигнал
и эталонный сигнал ![]() - это реализации
дискретных стохастических процессов
- это реализации
дискретных стохастических процессов ![]() и
и ![]() совместно стационарных в широком смысле,
т.е.
совместно стационарных в широком смысле,
т.е.
1) ![]() -
стационарный в широком смысле стохастический процесс;
-
стационарный в широком смысле стохастический процесс;
2) ![]() -
стационарный в широком смысле стохастический процесс;
-
стационарный в широком смысле стохастический процесс;
3)
функция взаимной корреляции процессов ![]() и
и ![]() зависит только от значения
зависит только от значения ![]() .
.
Мера погрешности (2.26)
называется среднеквадратичной погрешностью реализации. Обозначим ![]() вектор весов,
минимизирующих погрешность (2.26). Представленная на рис. 2.7 система, веса
которой принимают значения
вектор весов,
минимизирующих погрешность (2.26). Представленная на рис. 2.7 система, веса
которой принимают значения ![]() , называется пространственным фильтром
Винера (spatial filter). Процесс фильтрации заключается в умножении входов
, называется пространственным фильтром
Винера (spatial filter). Процесс фильтрации заключается в умножении входов ![]() на соответствующее им
множество весов
на соответствующее им
множество весов ![]() последующим
суммированием отдельных произведений для получения реализации
последующим
суммированием отдельных произведений для получения реализации ![]() эталонного сигнала
эталонного сигнала ![]() . Покажем, что
среднеквадратичная погрешность реализации (2.26) - это функция второго порядка
вектора весов
. Покажем, что
среднеквадратичная погрешность реализации (2.26) - это функция второго порядка
вектора весов ![]() .
.
Поскольку
![]() , (2.27)
, (2.27)
то формула (2.26) принимает вид
![]() . (2.28)
. (2.28)
В последнем слагаемом выражения (2.28) можно выделить матрицу автокорреляции компонентов входного вектора
 , (2.29)
, (2.29)
а
также вектор взаимной корреляции между сигналами ![]() и
и ![]()
 . (2.30)
. (2.30)
С использованием обозначений (2.29) и (2.30) среднеквадратичная погрешность реализации (2.28) может быть записана в виде
![]() . (2.31)
. (2.31)
Из выражения (2.31) следует, что
среднеквадратичная погрешность реализации ![]() - это функция второго порядка вектора
весов
- это функция второго порядка вектора
весов ![]() . С
геометрической точки зрения
. С
геометрической точки зрения ![]() представляется гиперпараболоидом, имеющим
единственный глобальный экстремум
представляется гиперпараболоидом, имеющим
единственный глобальный экстремум ![]() . Этот гиперпараболоид называется
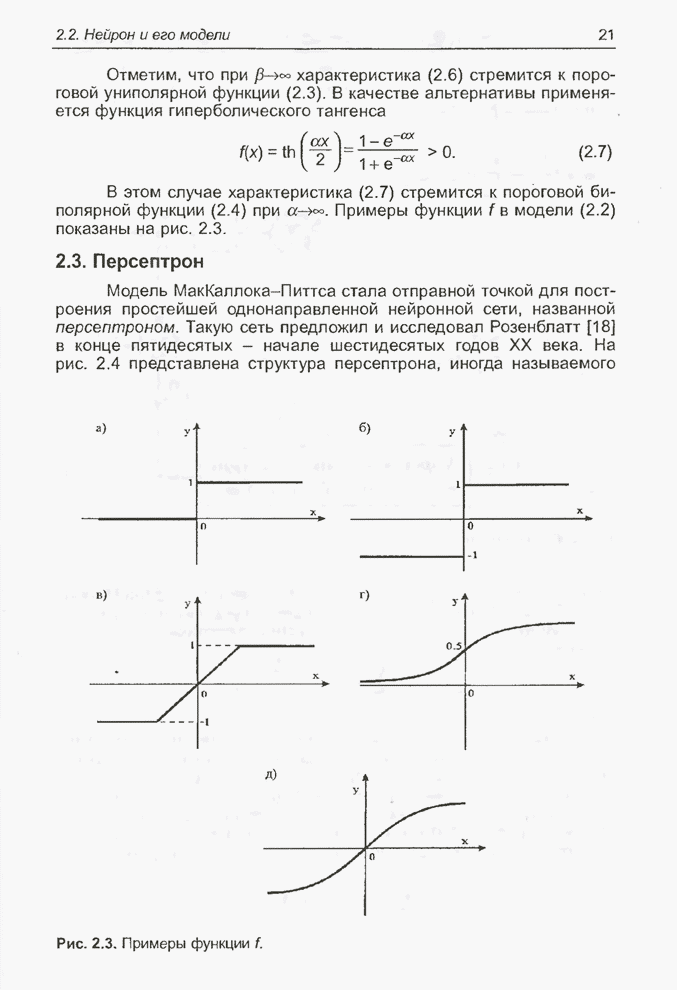
поверхностью среднеквадратичной погрешности. Рис. 2.8 представляет фрагмент
типовой поверхности среднеквадратичной погрешности для
. Этот гиперпараболоид называется
поверхностью среднеквадратичной погрешности. Рис. 2.8 представляет фрагмент
типовой поверхности среднеквадратичной погрешности для ![]() (в этом случае это параболоид).
(в этом случае это параболоид).

Рис. 2.8. Поверхность среднеквадратичной погрешности.
Поверхность среднеквадратичной
погрешности, описываемая уравнением (2.31), имеет единственный глобальный
экстремум ![]() ,
достигаемый при оптимальных значениях весов
,
достигаемый при оптимальных значениях весов ![]() . Вычисление оптимальных значений весов
сводится к определению вектора градиента
. Вычисление оптимальных значений весов
сводится к определению вектора градиента ![]() функции
функции ![]() и приравниванию полученного результата к
нулю:
и приравниванию полученного результата к
нулю:
 , (2.32)
, (2.32)
где
![]() есть
есть ![]() -мерный нулевой вектор.
Допустим, что гессиан
-мерный нулевой вектор.
Допустим, что гессиан
![]() (2.33)
(2.33)
это
положительно определенная матрица. В этом случае вектор весов ![]() минимизирует
среднеквадратичную погрешность реализации (2.31). Из уравнения (2.32) следует,
что для этого вектора справедливо равенство
минимизирует
среднеквадратичную погрешность реализации (2.31). Из уравнения (2.32) следует,
что для этого вектора справедливо равенство
![]() . (2.34)
. (2.34)
Равенство (2.34) называется
нормальным уравнением. Если ![]() , то его решением оказывается вектор
, то его решением оказывается вектор
![]() . (2.35)
. (2.35)
При ![]() погрешность принимает минимальное
значение, обозначаемое
погрешность принимает минимальное
значение, обозначаемое ![]() и равное
и равное
![]() . (2.36)
. (2.36)
Если подставить равенство (2.34) в выражение (2.36), то получим формулу для расчета минимальной среднеквадратичной погрешности реализации
![]() . (2.37)
. (2.37)
Для нахождения оптимального
вектора весов ![]() ,
удовлетворяющего нормальному уравнению (2.34), требуется инвертировать матрицу
автокорреляции
,
удовлетворяющего нормальному уравнению (2.34), требуется инвертировать матрицу
автокорреляции ![]() .
Вместо этого можно использовать метод наискорейшего спуска (см., например, [2,
6]), который широко применяется в теории оптимизации. В этом методе
предусматривается итеративный расчет последовательных приближений оптимального
вектора
.
Вместо этого можно использовать метод наискорейшего спуска (см., например, [2,
6]), который широко применяется в теории оптимизации. В этом методе
предусматривается итеративный расчет последовательных приближений оптимального
вектора ![]() .
Обозначим
.
Обозначим ![]() приближение,
рассчитанное на
приближение,
рассчитанное на ![]() -й
итерации
-й
итерации
![]() . (2.38)
. (2.38)
Очередные коррекции компонентов
вектора весов ![]() должны
производиться в направлении, противоположном знаку компонентов вектора
градиента
должны
производиться в направлении, противоположном знаку компонентов вектора
градиента
 (2.39)
(2.39)
Алгоритм наискорейшего спуска можно представить в виде
 . (2.40)
. (2.40)
При подстановке формулы (2.32) в зависимость (2.40) получаем рекурсию
![]() , (2.41)
, (2.41)
где
константа ![]() определяет
величину шага коррекции.
определяет
величину шага коррекции.
Можно показать (см., например, [8, 19]), что алгоритм наискорейшего спуска (2.41) сходится, т.е.
![]() , (2.42)
, (2.42)
если
шаг коррекции ![]() лежит
в пределах
лежит
в пределах
![]() , (2.43)
, (2.43)
где
![]() - это
наибольшее собственное значение матрицы автокорреляции
- это
наибольшее собственное значение матрицы автокорреляции ![]() .
.
Кроме того, доказано, что
скорость сходимости алгоритма наискорейшего спуска зависит от отношения
наименьшего и наибольшего собственных значений матрицы ![]() . Если
. Если
![]() , (2.44)
, (2.44)
то алгоритм наискорейшего спуска сходится быстро. Если же
![]() , (2.45)
, (2.45)
то алгоритм наискорейшего спуска сходится медленно.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Предисловие к русскому изданию
- ГЛАВА 1. ВВЕДЕНИЕ
- Список литературы
- ГЛАВА 2. МНОГОСЛОЙНЫЕ НЕЙРОННЫЕ СЕТИ И АЛГОРИТМЫ ИХ ОБУЧЕНИЯ
- 2.1. Введение
- 2.2. Нейрон и его модели
- 2.3. Персептрон
- 2.4. Системы типа Адалайн
- 2.4.1. Линейный взвешенный сумматор
- 2.4.2. Адаптивный линейный взвешенный сумматор
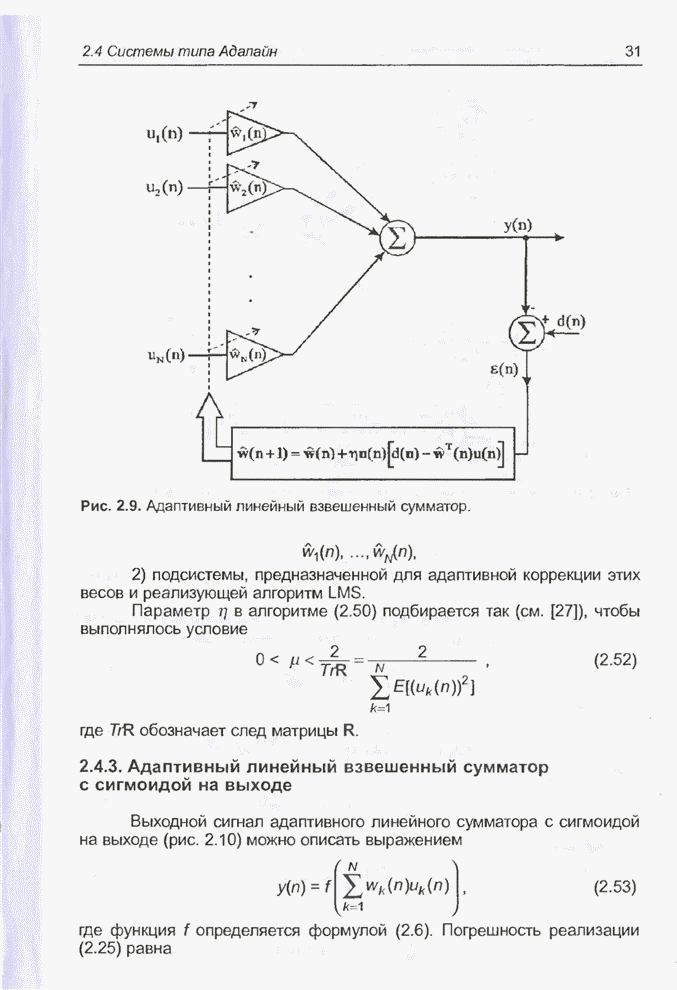
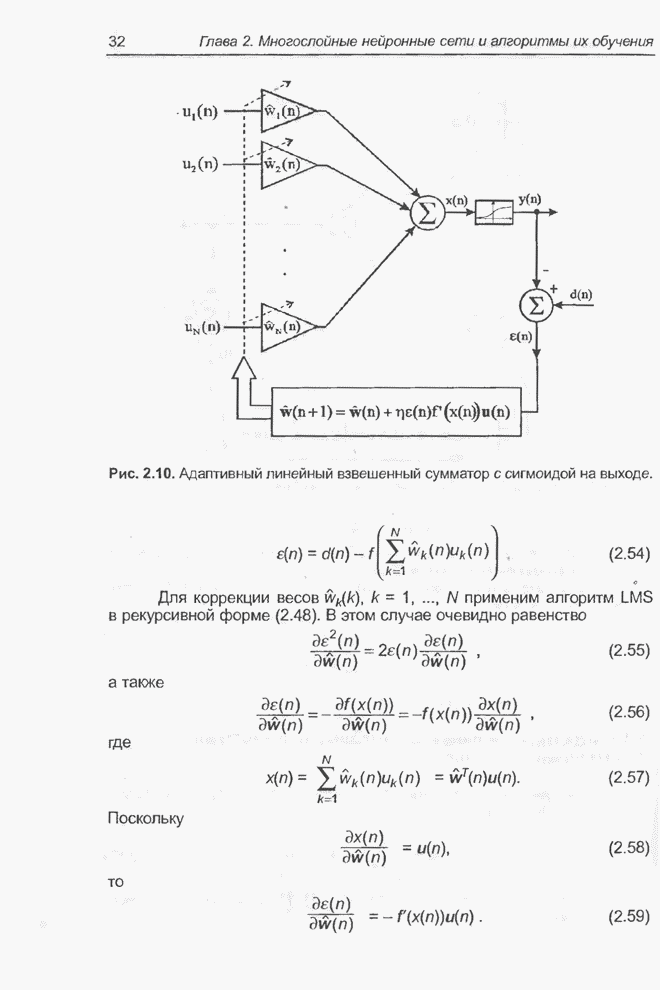
- 2.4.3. Адаптивный линейный взвешенный сумматор с сигмоидой на выходе
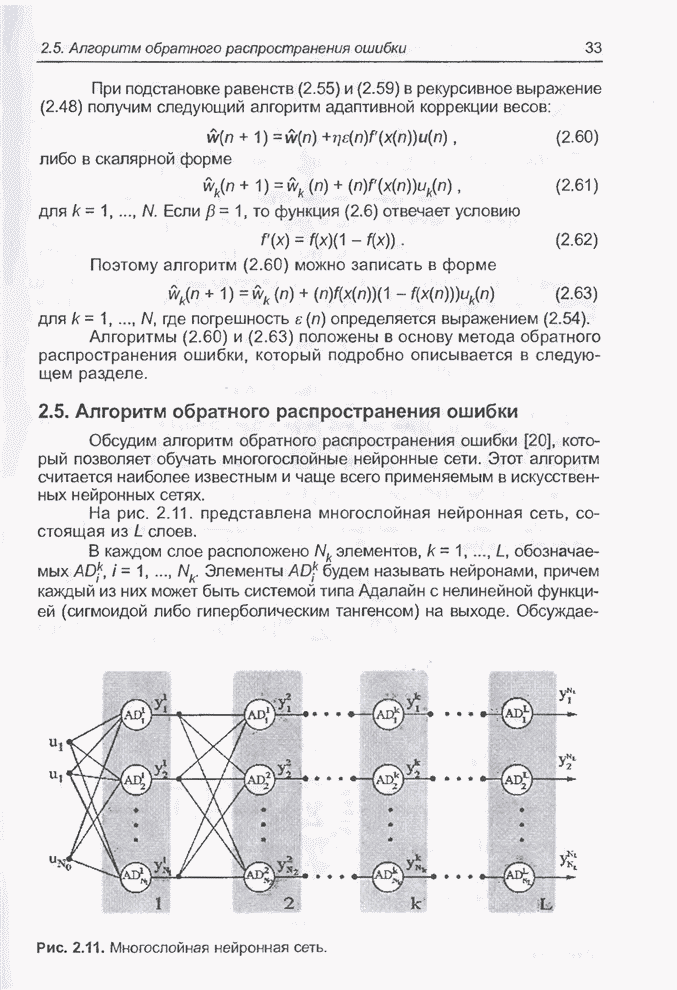
- 2.5. Алгоритм обратного распространения ошибки
- 2.6. Применение рекуррентного метода наименьших квадратов для обучения нейронных сетей
- Список литературы
- ГЛАВA3. НЕЧЕТКИЕ МНОЖЕСТВА И НЕЧЕТКИЙ ВЫВОД
- 3.1. Введение
- 3.2. Основные понятия и определения теории нечетких множеств
- 3.3. Операции на нечетких множествах
- 3.4. Принцип расширения
- 3.5. Нечеткие числа
- 3.6. Треугольные нормы
- 3.7. Нечеткие отношения и их свойства
- 3.8. Нечеткий вывод
- 3.9. Нечеткое управление
- 3.9.1. Классический модуль нечеткого управления
- 3.9.2. Метод нечеткого управления Такаги-Сугено
- 3.10. Проектирование базы нечетких правил на основе численных данных
- 3.10.1. Построение нечетких правил
- 3.10.2. Задача парковки грузовика
- 3.10.3. Примечание
- Список литературы
- ГЛАВА 4. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 4.1. Введение
- 4.2. Генетические алгоритмы и традиционные методы оптимизации
- 4.3. Основные понятия генетических алгоритмов
- 4.4. Классический генетический алгоритм
- 4.5. Иллюстрация выполнения классического генетического алгоритма
- 4.6. Кодирование параметров задачи в генетическом алгоритме
- 4.7. Основная теорема о генетических алгоритмах
- 4.8. Модификации классического генетического алгоритма
- 4.8.1. Методы селекции
- 4.8.2. Особые процедуры репродукции
- 4.8.3. Генетические операторы
- 4.8.4. Методы кодирования
- 4.8.5. Масштабирование функции приспособленности
- 4.8.6. Ниши в генетическом алгоритме
- 4.8.7. Генетические алгоритмы для многокритериальной оптимизации
- 4.8.8. Генетические микроалгоритмы
- 4.9. Примеры оптимизации функции с помощью программы FlexTool
- 4.10. Эволюционные алгоритмы
- 4.11. Приложения эволюционных алгоритмов
- 4.11.1. Примеры оптимизации функции с помощью программы Evolver
- 4.11.2. Решение комбинаторных задач с помощью программы Evolver
- 4.12. Эволюционные алгоритмы в нейронных сетях
- 4.12.1. Независимое применение генетических алгоритмов и нейронных сетей
- 4.12.2. Нейронные сети для поддержки генетических алгоритмов
- 4.12.3. Генетические алгоритмы для поддержки нейронных сетей
- 4.12.4. Применение генетических алгоритмов для обучения нейронных сетей
- 4.12.5. Генетические алгоритмы для выбора топологии нейронных сетей
- 4.12.6. Адаптивные взаимодействующие системы
- 4.12.7. Типовой цикл эволюции
- 4.12.7.1. Эволюция весов связей
- 4.12.7.2. Эволюция архитектуры сети
- 4.12.7.3. Эволюция правил обучения
- 4.13. Примеры моделирования эволюционных алгоритмов в приложении к нейронным сетям
- 4.13.1. Программы Evolver и BrainMaker
- 4.13.2. Программа GTO
- Список литературы
- ГЛАВА 5. МОДУЛИ НЕЧЕТКО-НЕЙРОННОГО УПРАВЛЕНИЯ
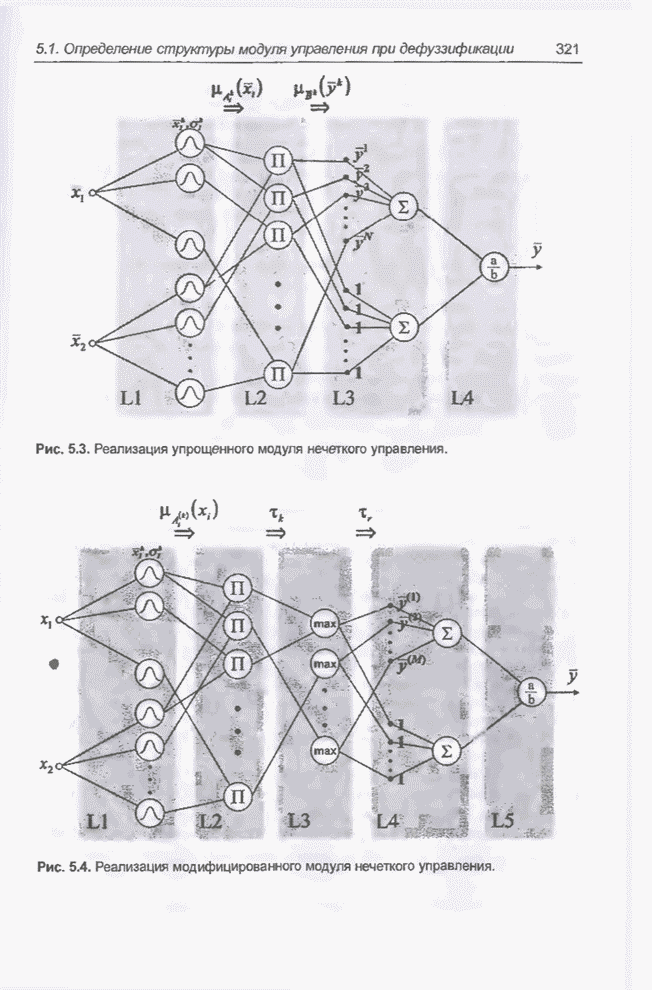
- 5.1. Модуль нечеткого управления со структурой, определенной в процессе дефуззификации
- 5.1.2. Конструкция модуля
- 5.1.3. Структура модуля
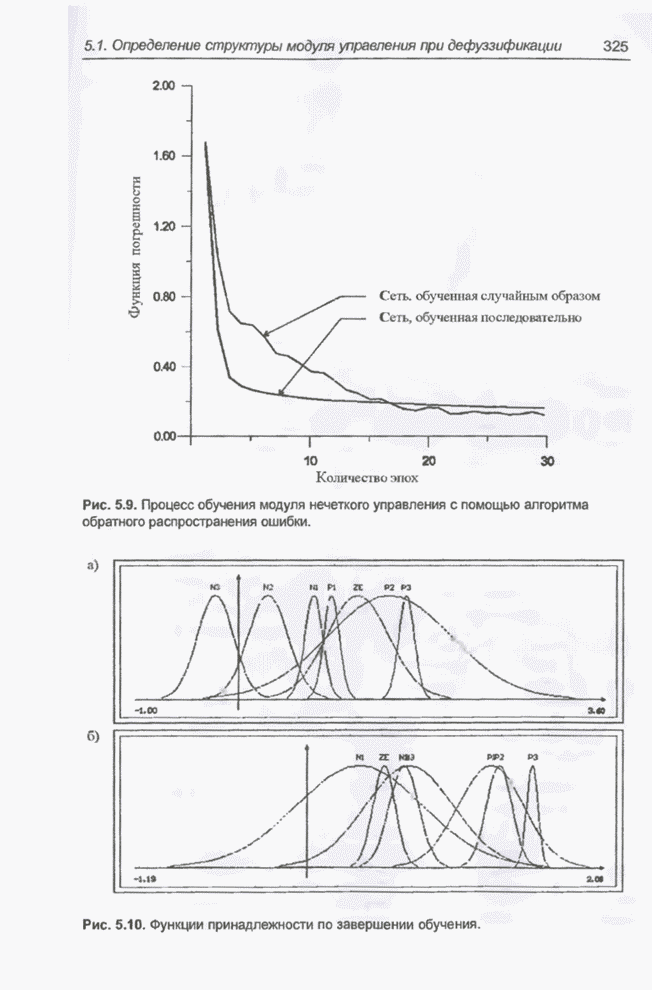
- 5.1.4. Использование алгоритма обратного распространения ошибки
- 5.1.5. Модификации модуля
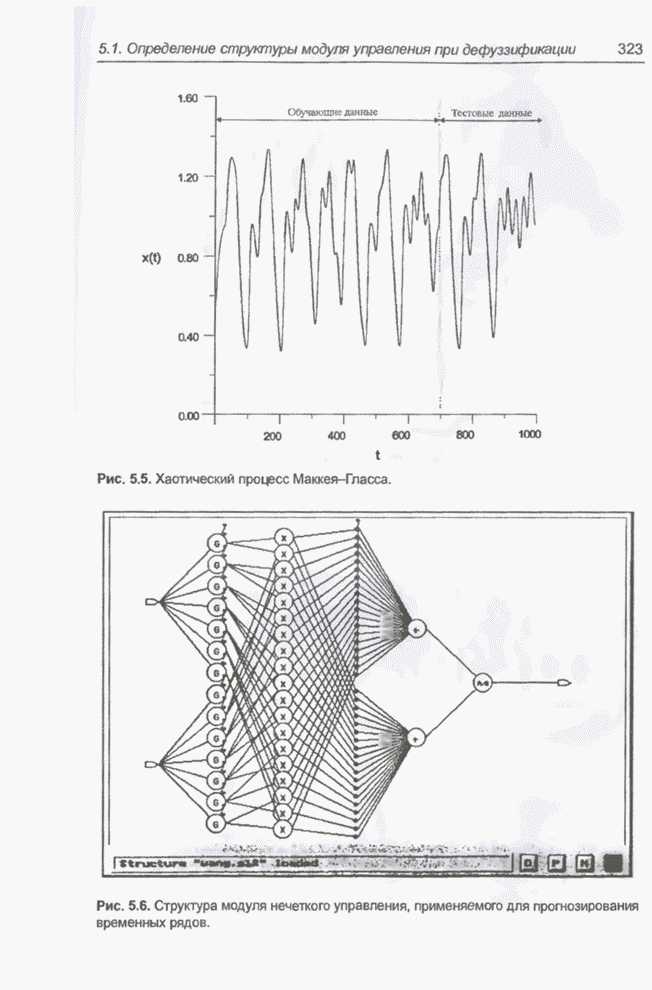
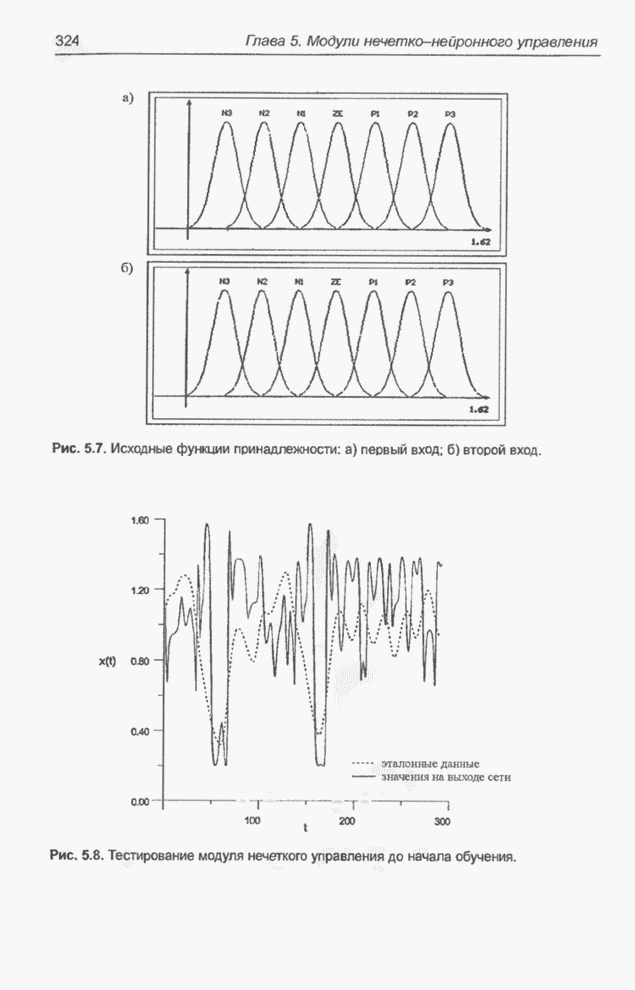
- 5.1.6. Применение модуля нечеткого управления для прогнозирования случайных временных рядов
- 5.1.7. Применение модуля нечеткого управления для решения задачи парковки грузовика
- 5.1.8. Примечание
- 5.2. Представление модуля нечеткого управления в виде стандартной нейронной сети
- 5.3. Модуль нечеткого управления с нейронной сетью для выполнения дефуззификации
- 5.3.1. Введение
- 5.3.2. Конструкция модуля
- 5.3.3. Структура модуля
- 5.3.4. Алгоритмы обучения модуля
- 5.3.5. Решение задачи стабилизации перевернутого маятника
- 5.3.6. Примечание
- 5.4. Модуль нечеткого управления с возможностью коррекции правил
- 5.4.1. Введение
- 5.4.2. Фаза обучения на основе самоорганизации
- 5.4.3. Фаза обучения с учителем
- 5.4.4. Примечание
- 5.5. Модуль нечеткого управления типа Такаги-Сугено
- 5.5.1. Введение
- 5.5.2. Нейронная реализация функции принадлежности
- 5.5.3. Модули Такаги-Сугено
- 5.5.4. Реализация условий
- 5.5.5. Реализация заключений
- 5.5.6. Примечание
- 5.6. Модуль нечеткого управления типа Такаги-Сугено: случай зависимых лингвистических переменных
- 5.6.1. Введение
- 5.6.2. Нейронные сети для нечеткого вывода
- 5.6.3. Структура системы
- 5.6.4. Способ обучения
- 5.6.5. Решение задачи парковки грузовика
- 5.6.6. Примечание
- Список литературы