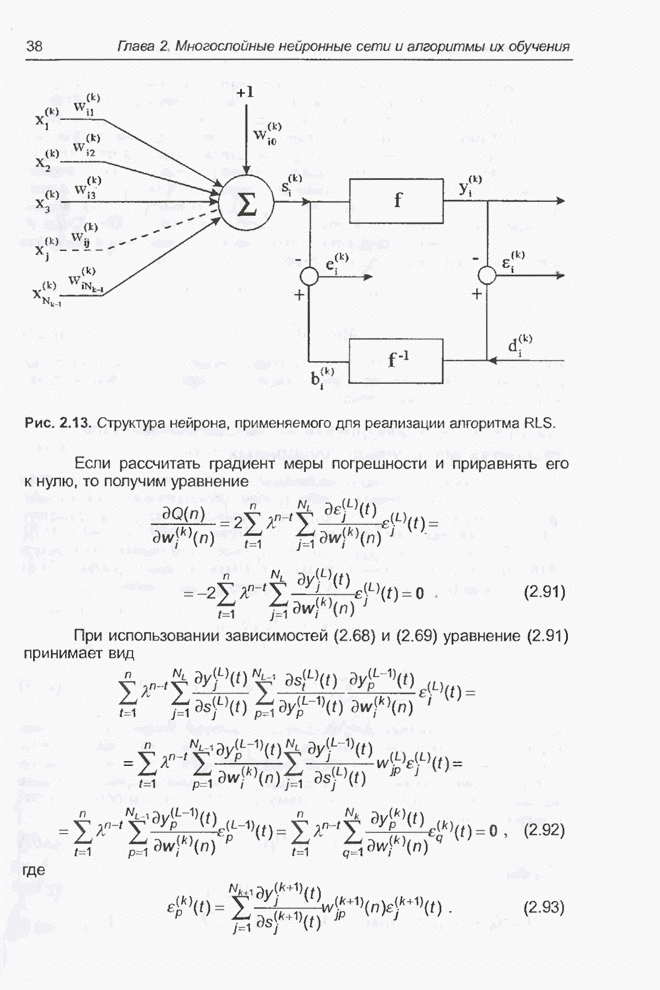
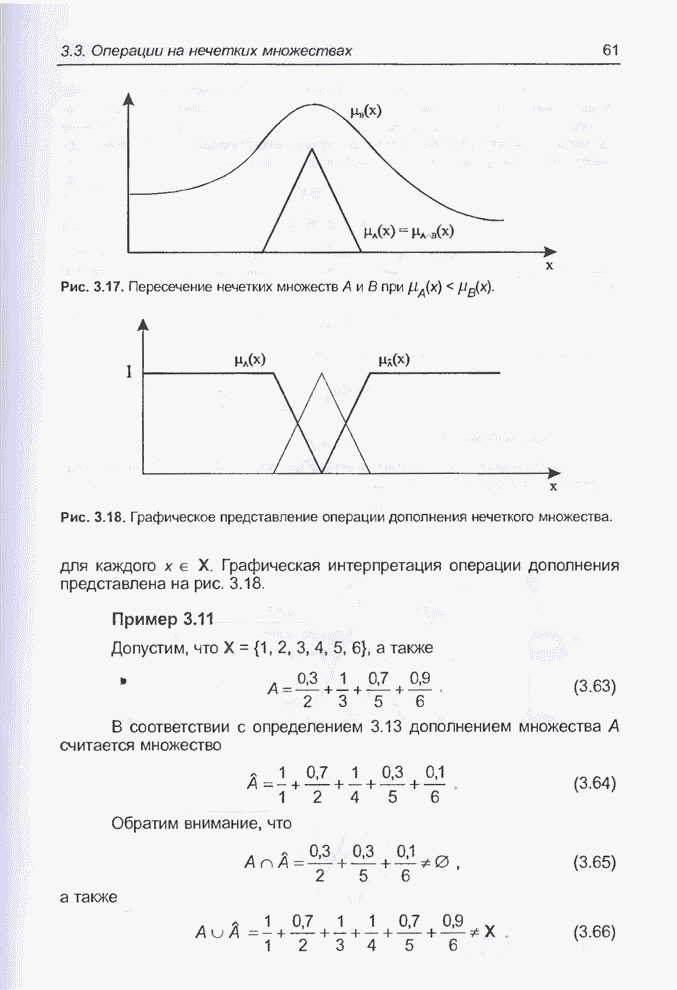
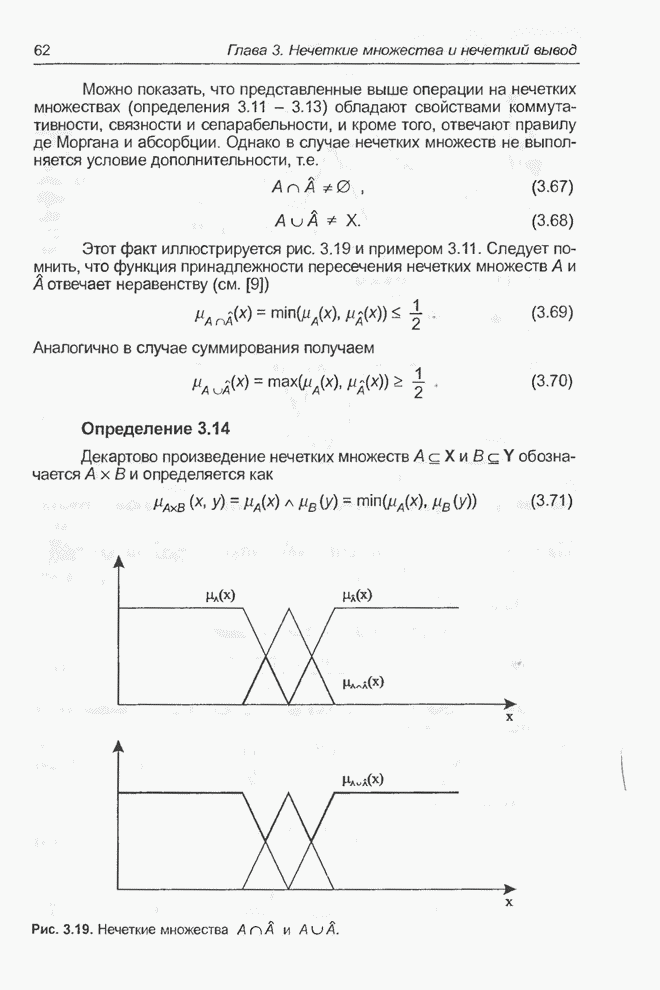
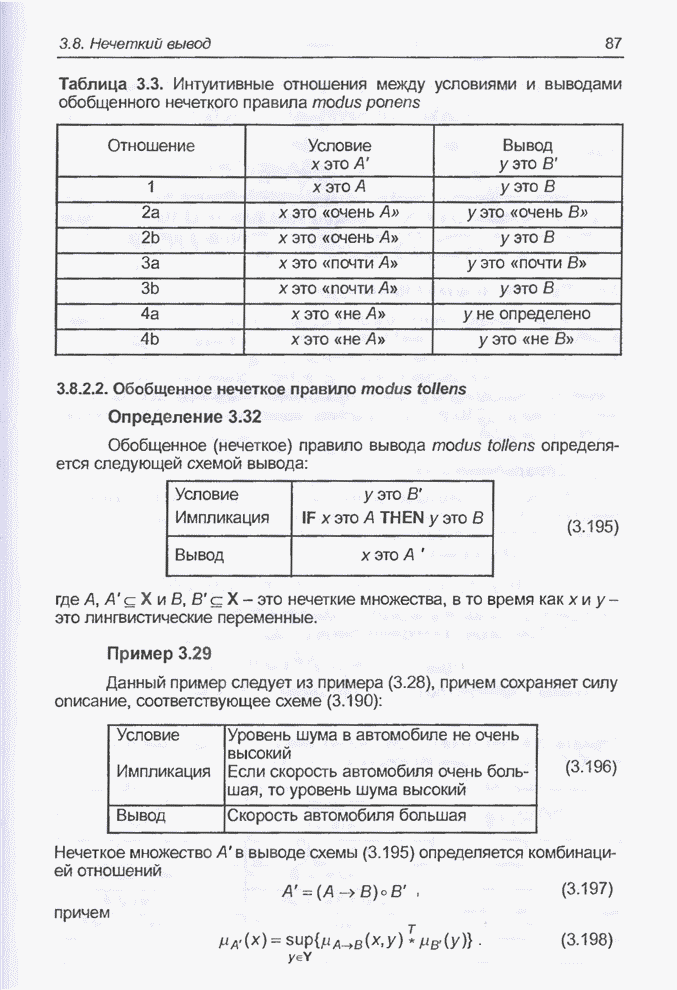
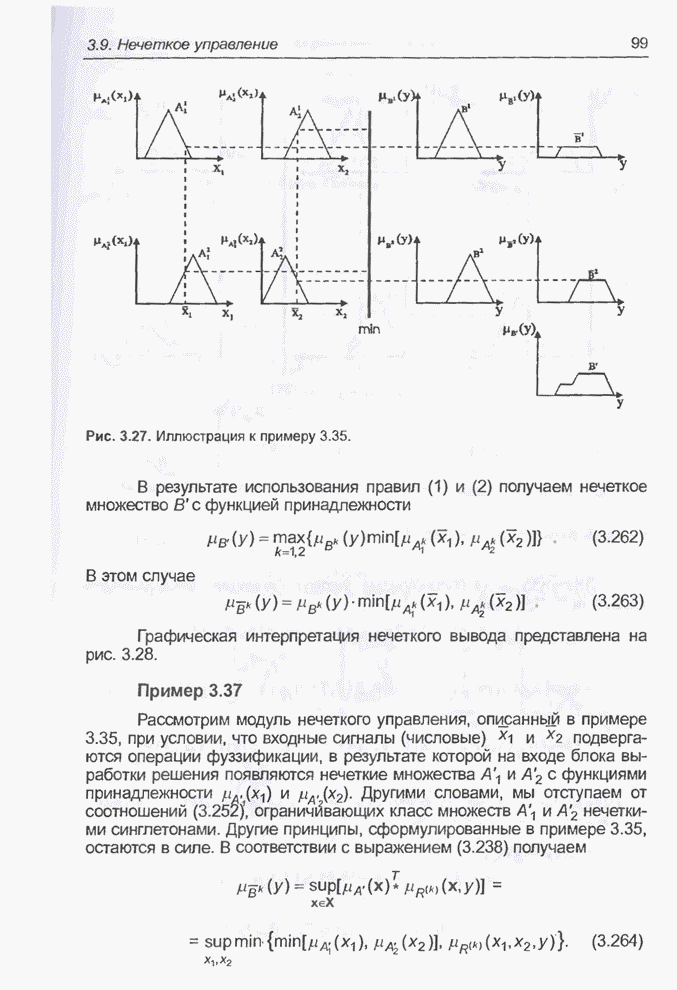
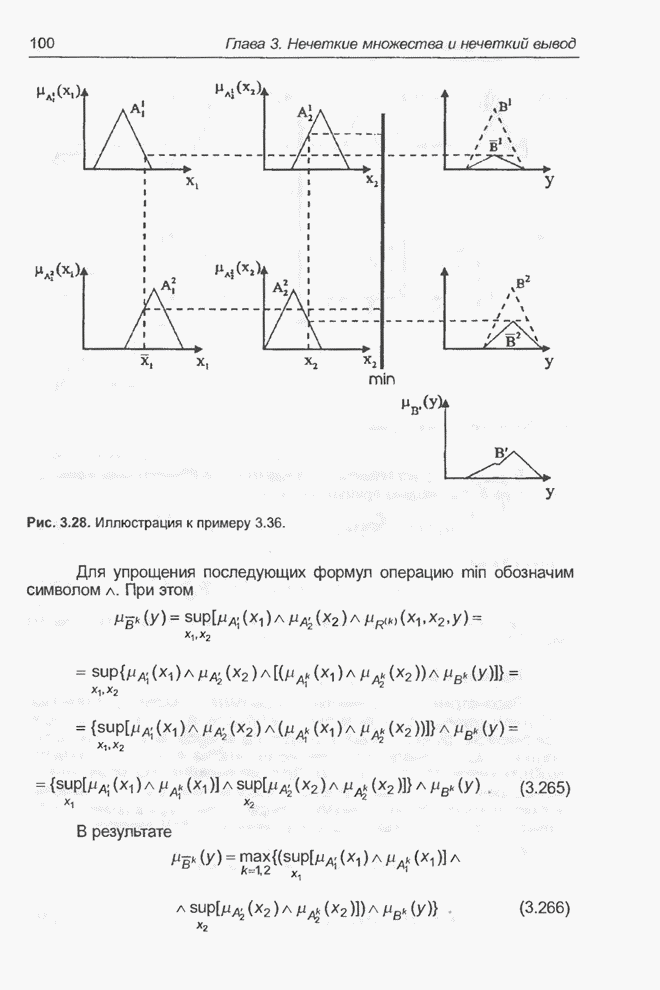
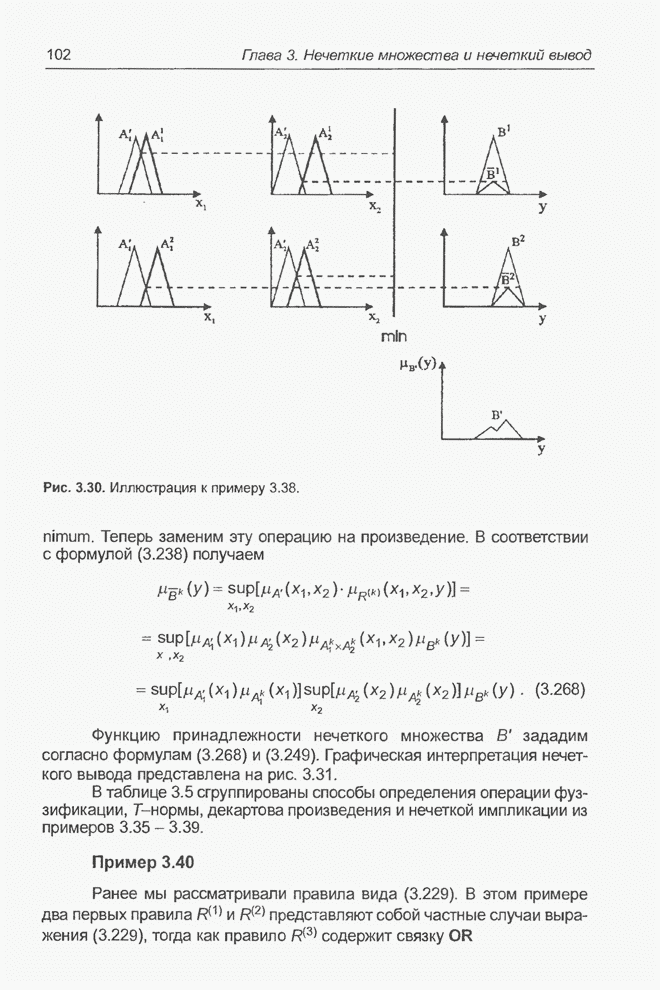
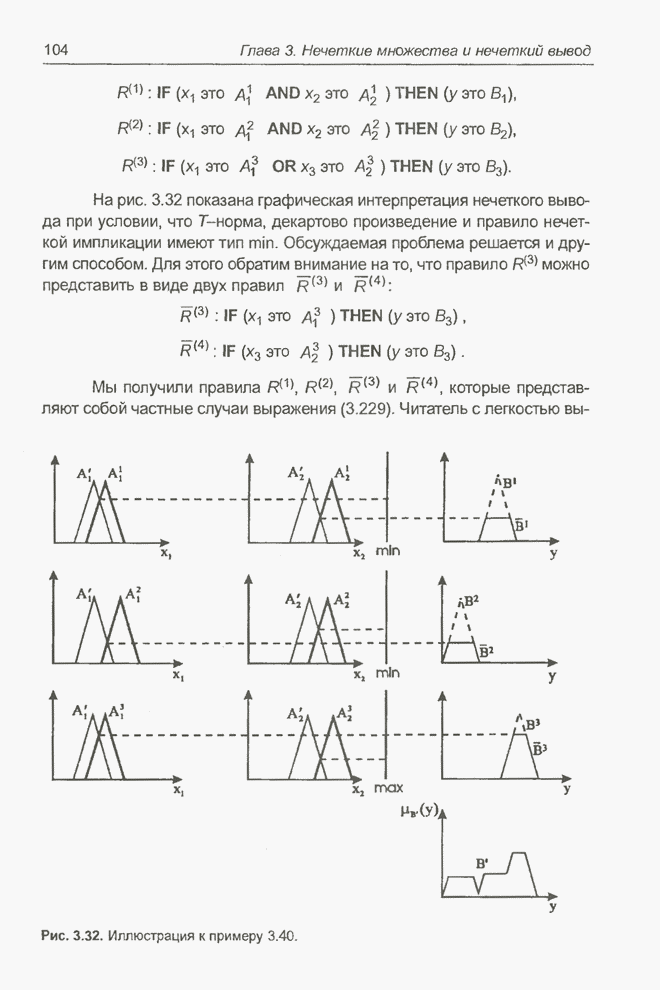
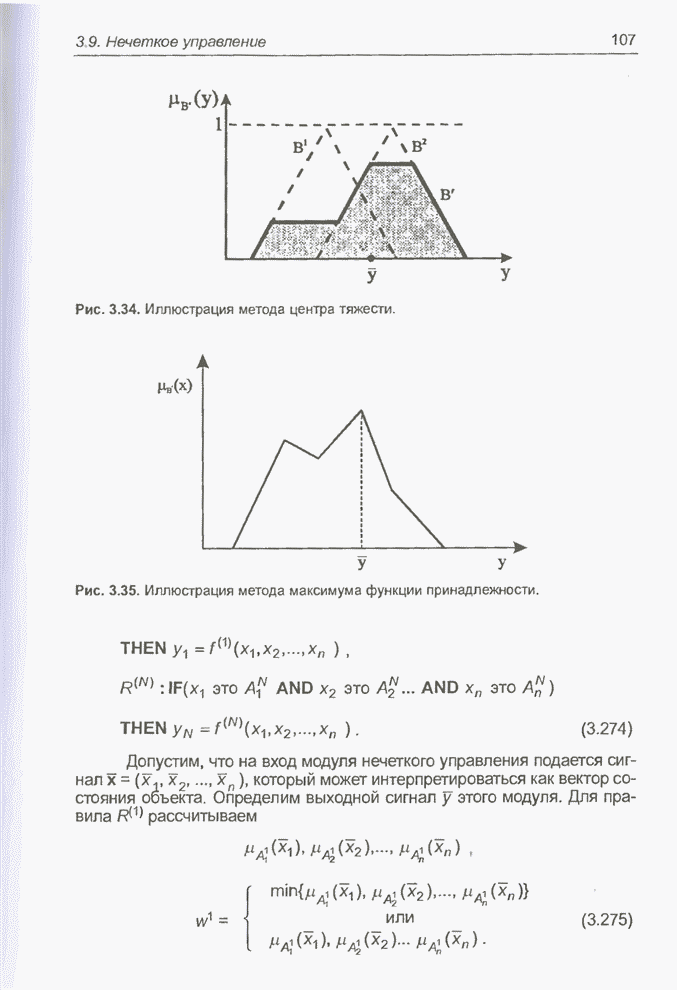
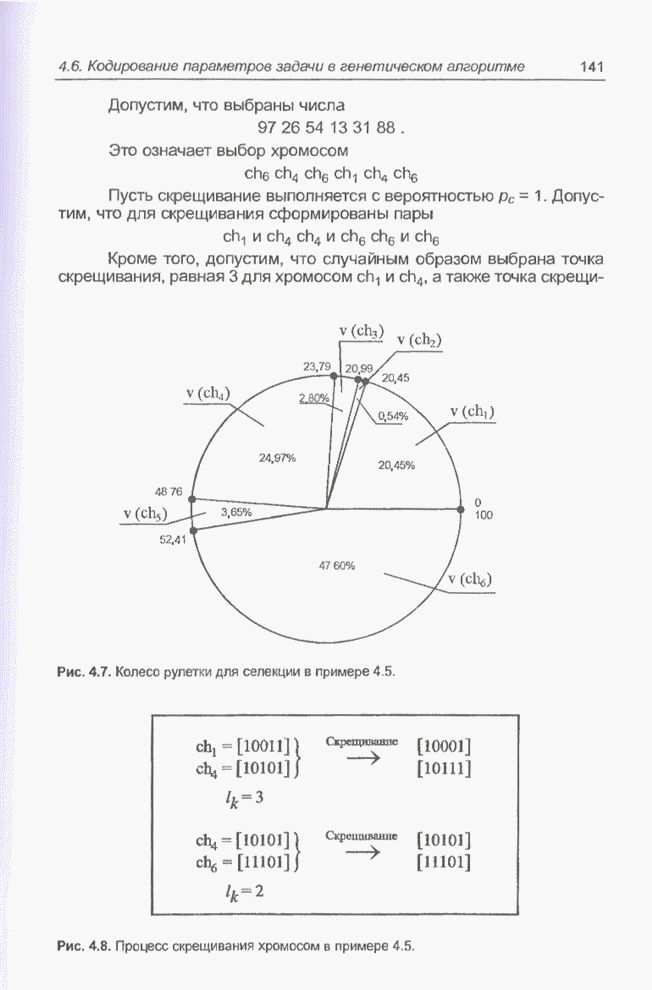
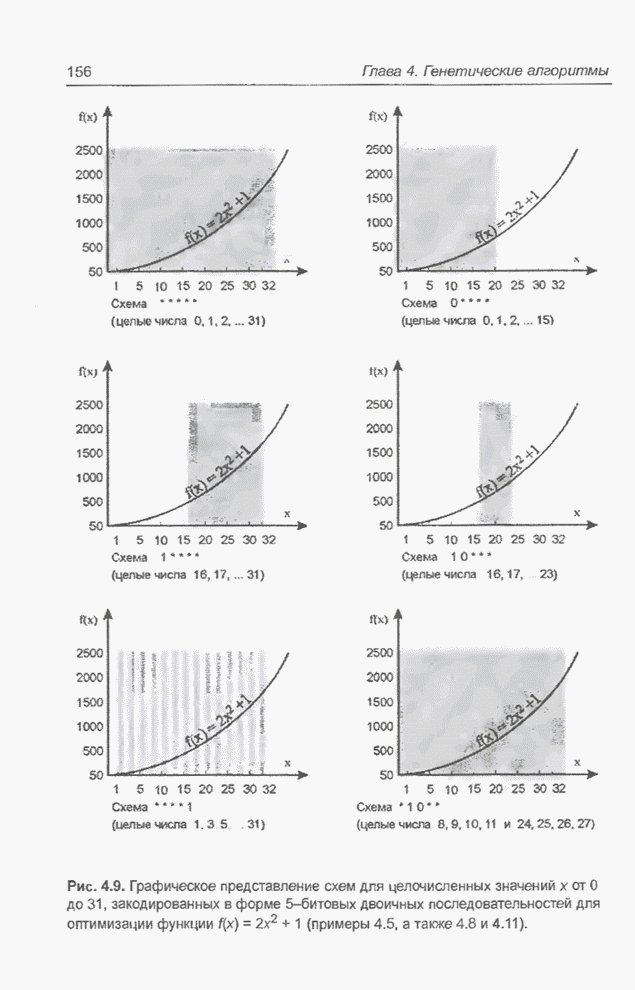
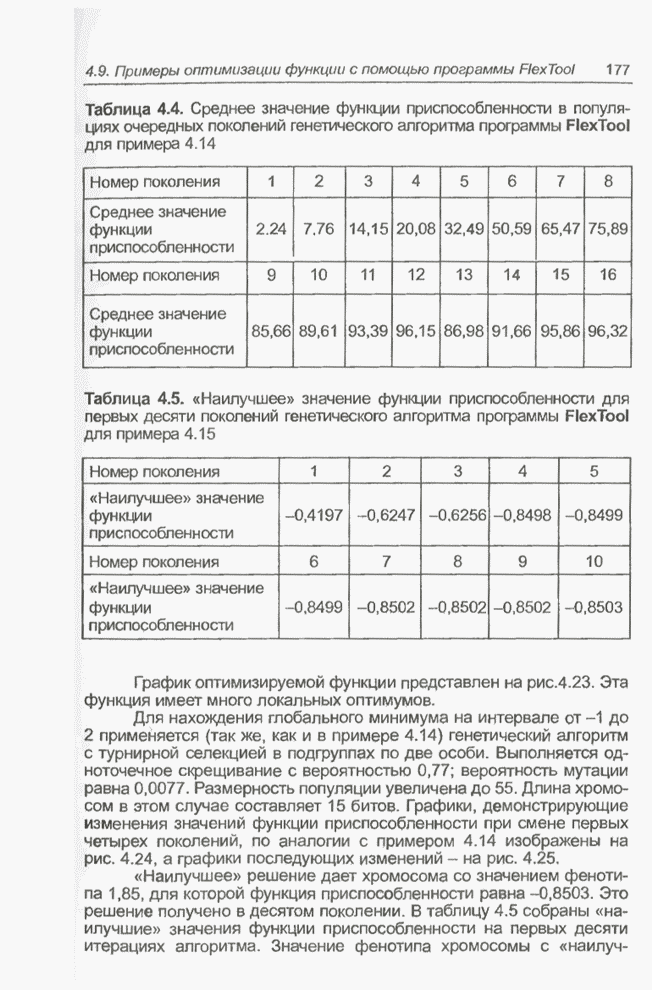
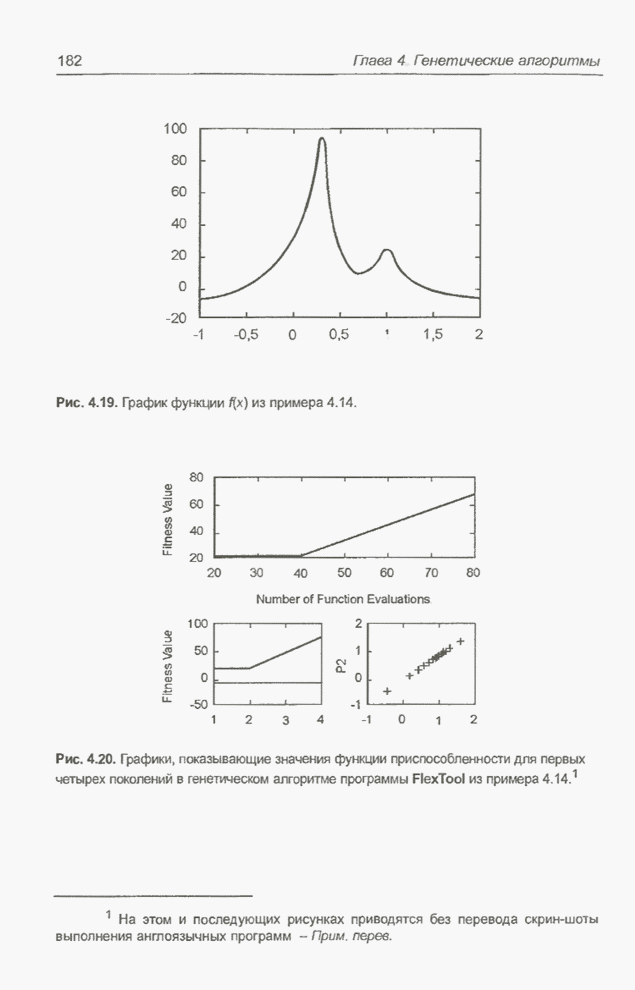
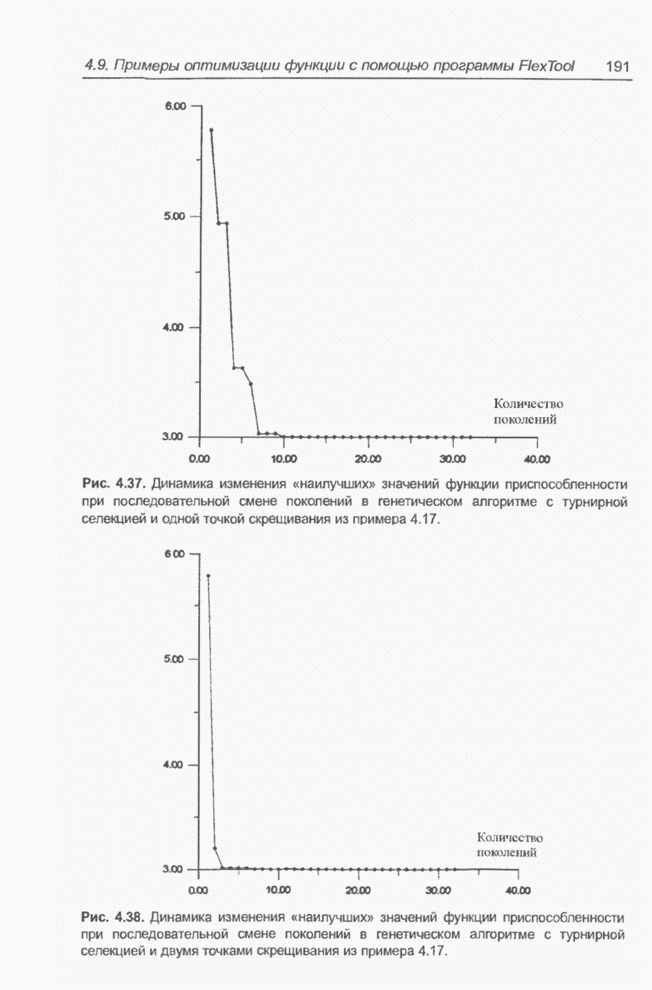
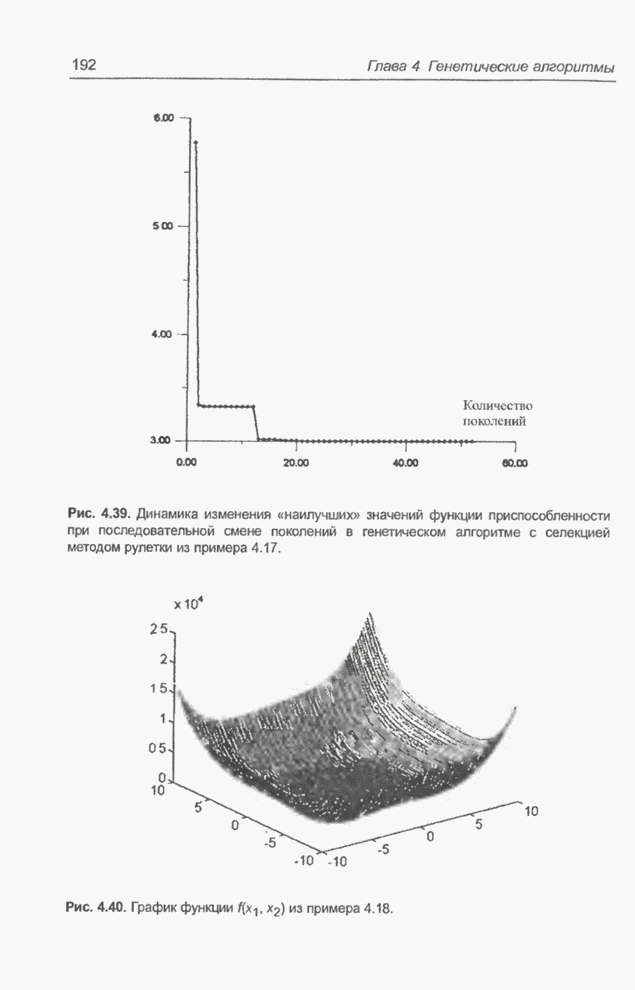
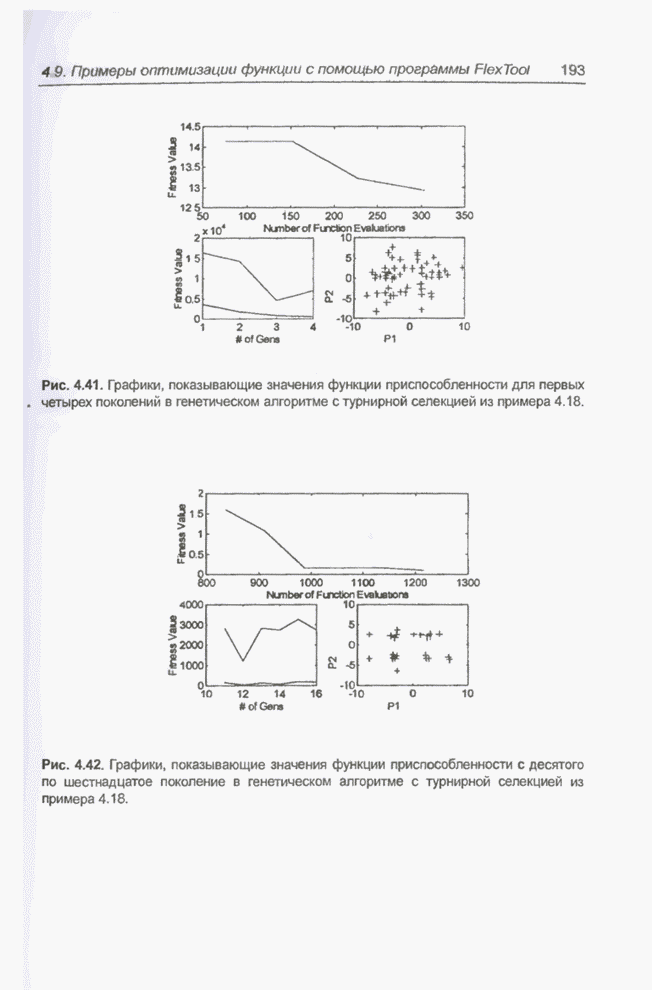
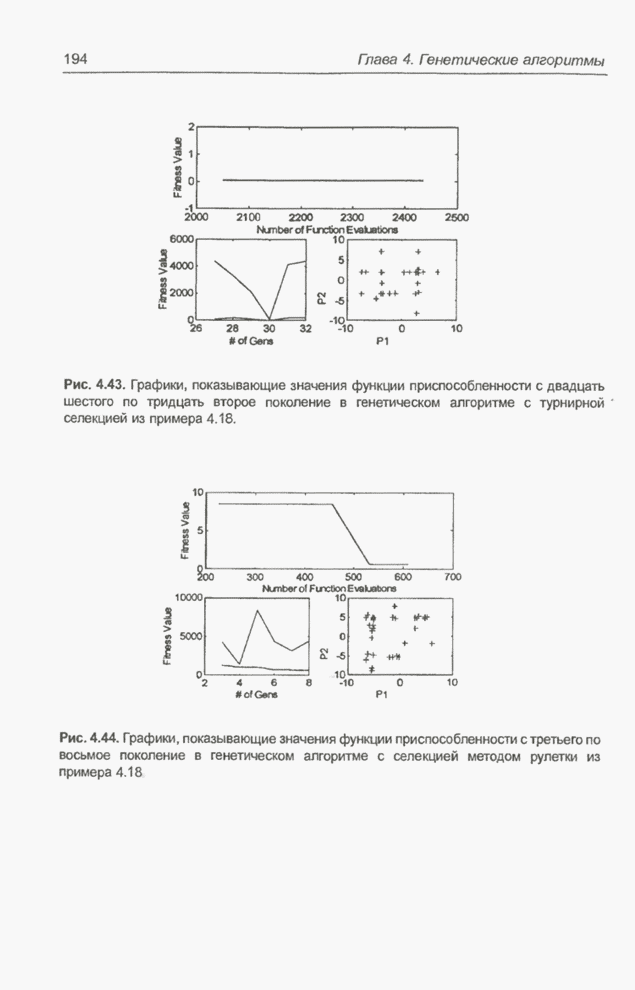
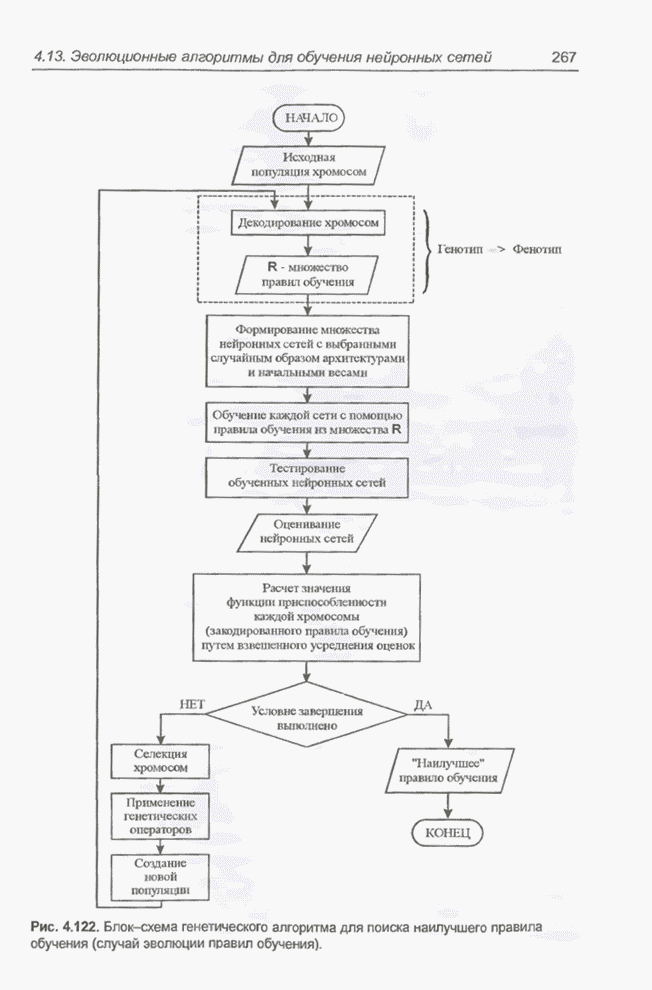
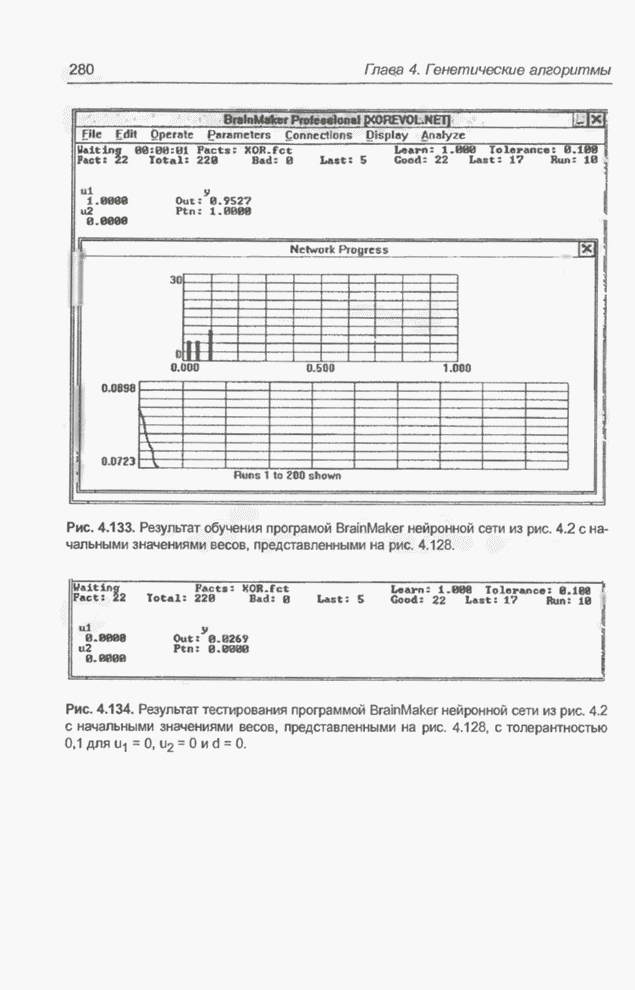
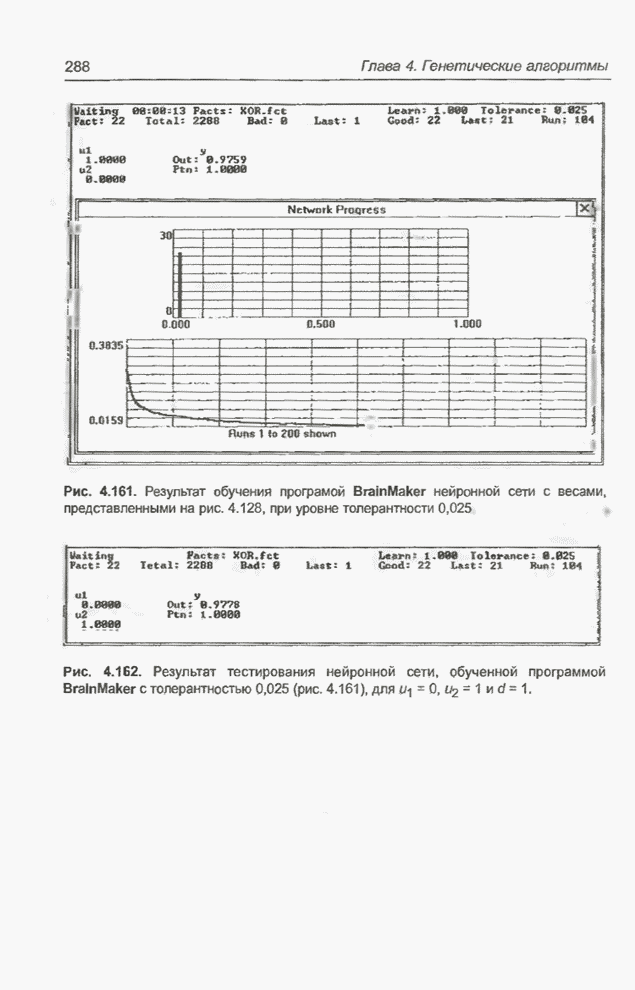
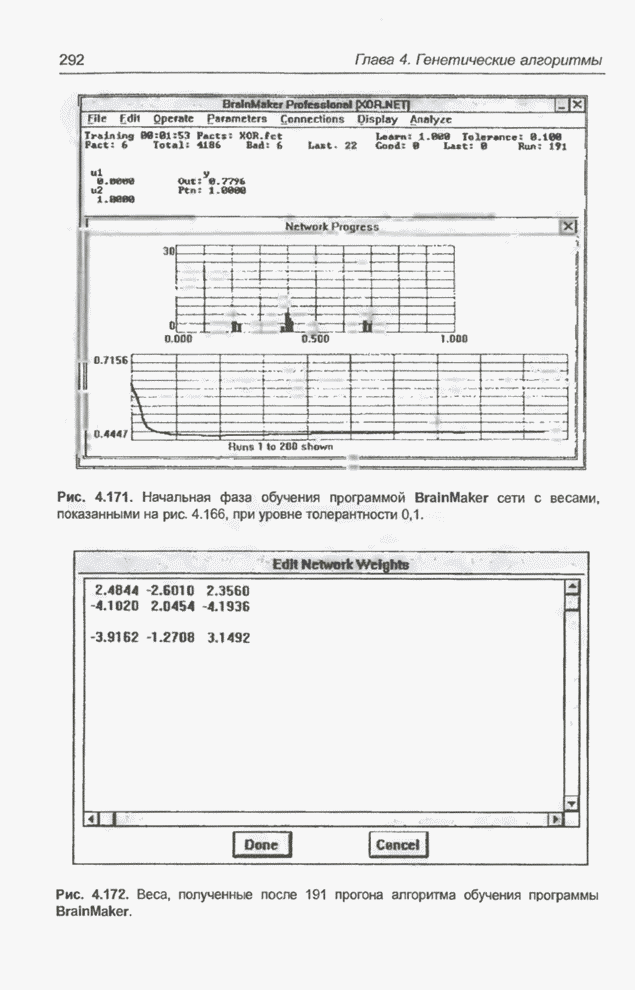
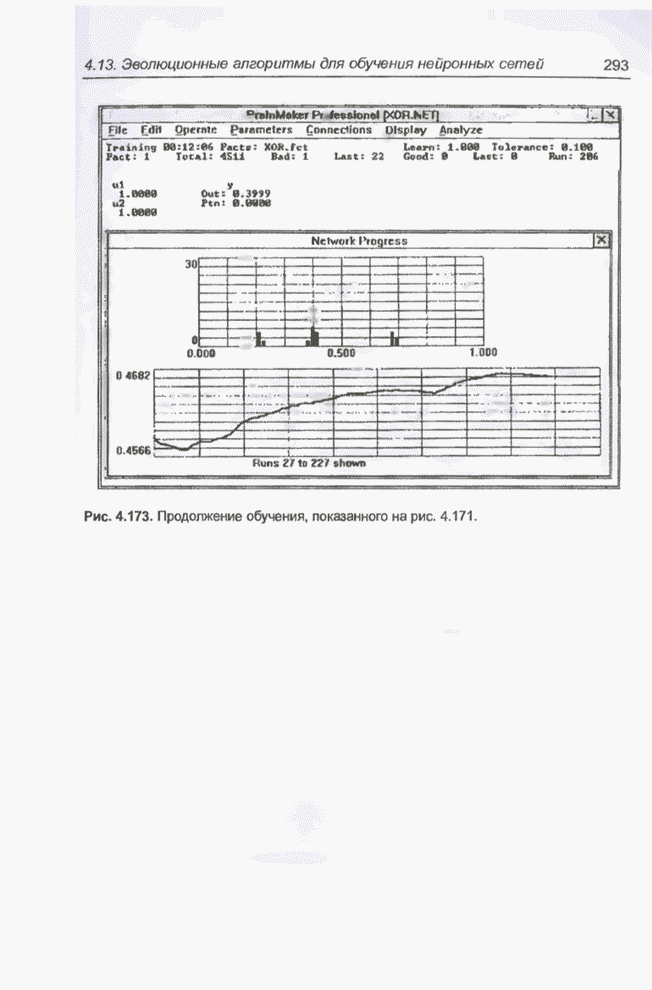
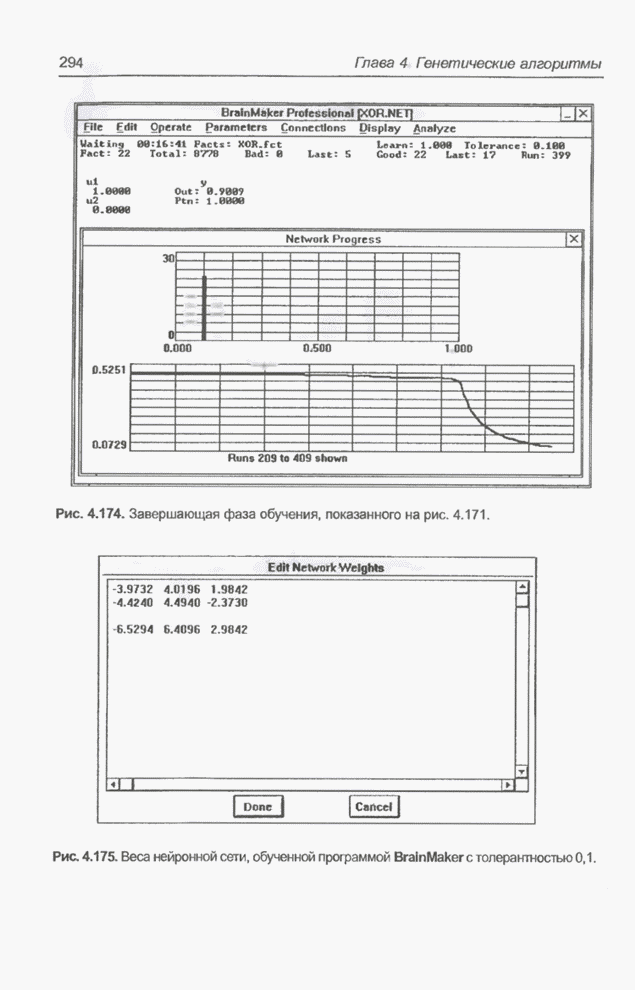
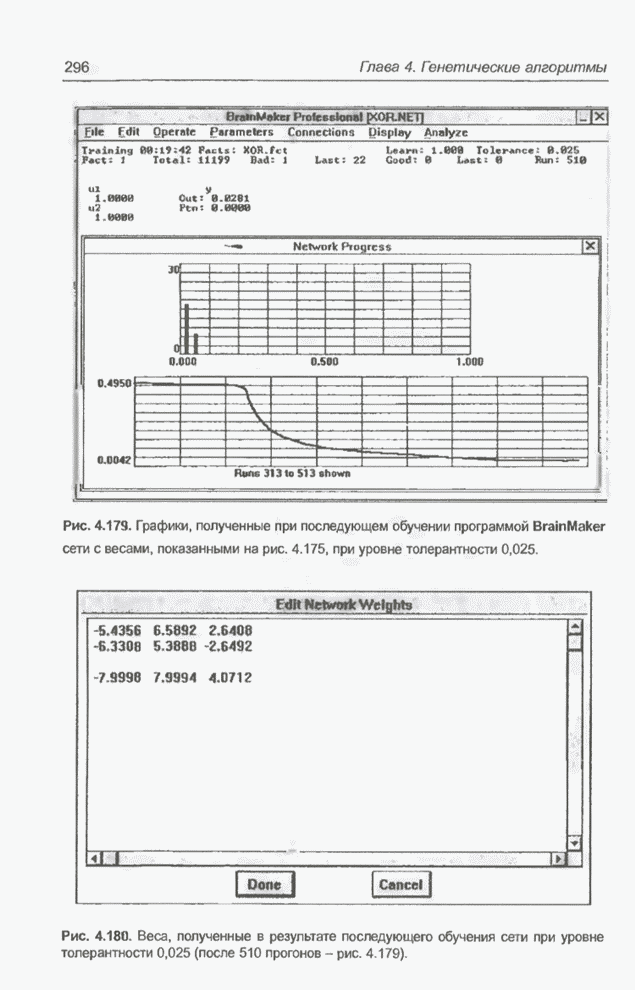
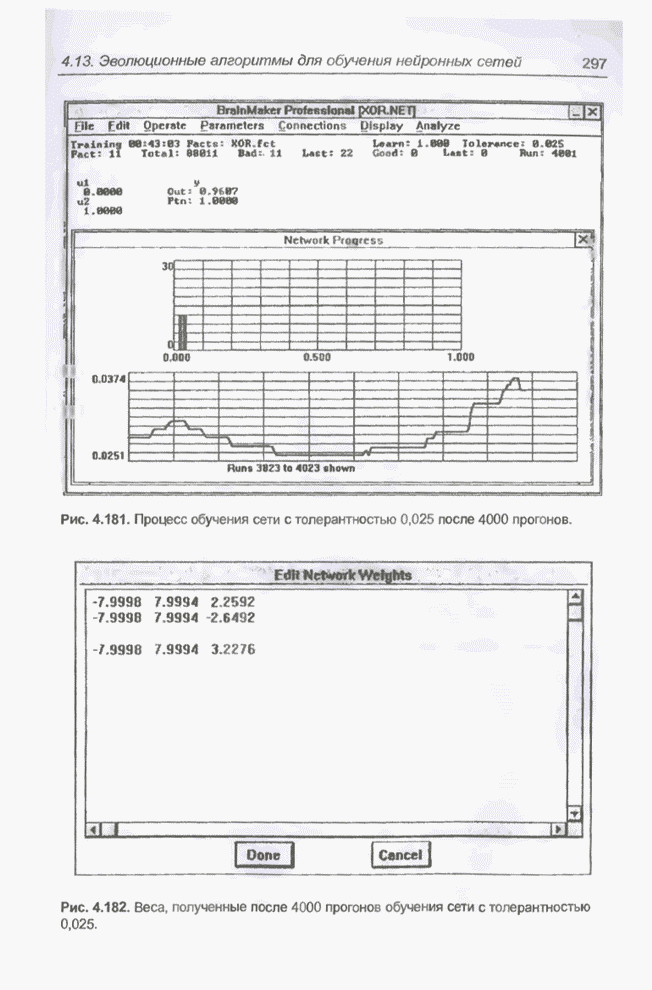
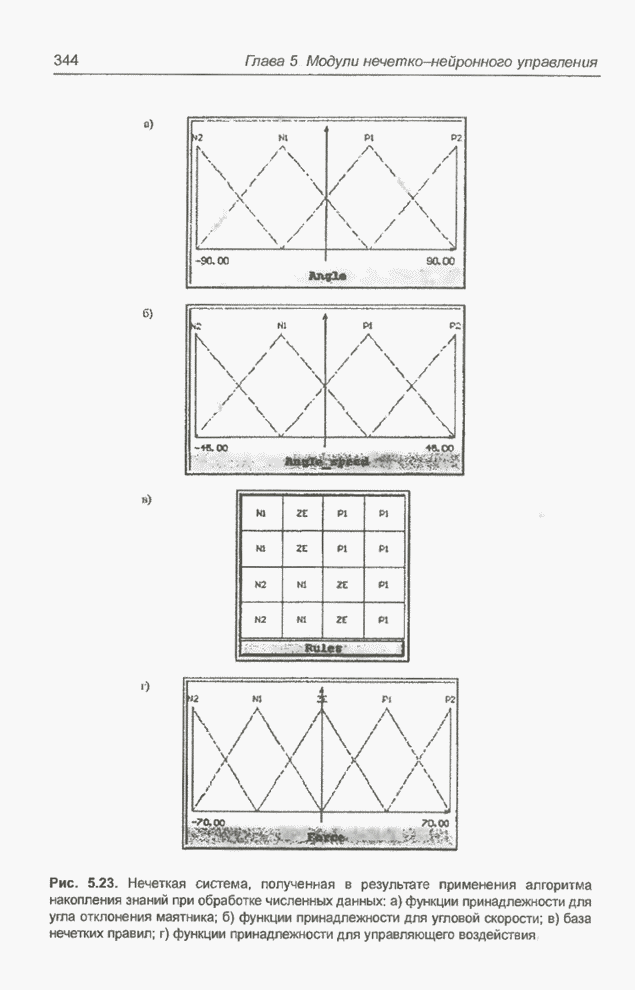
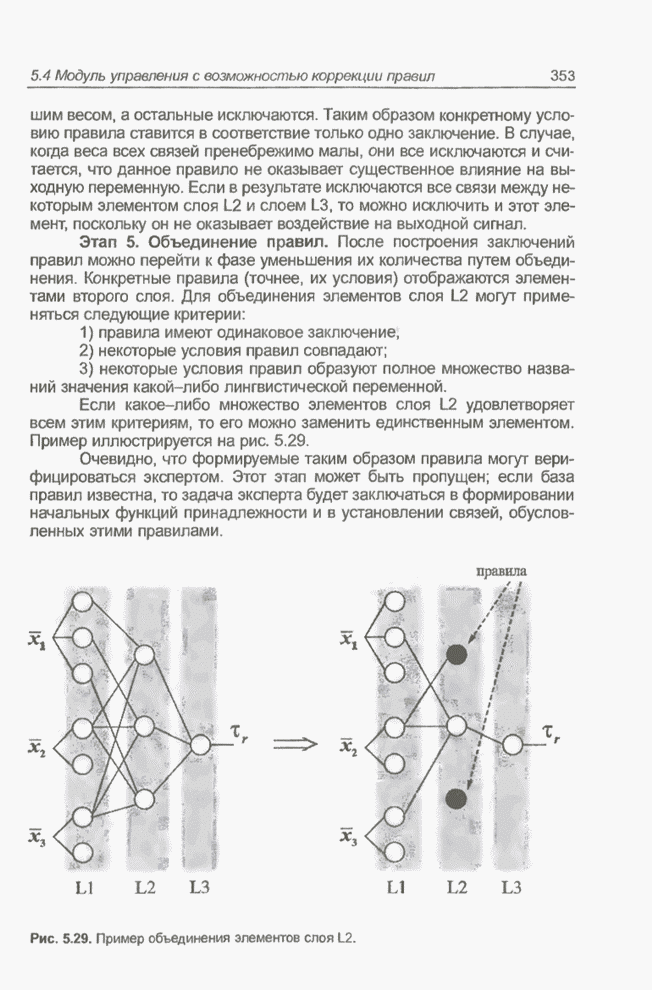
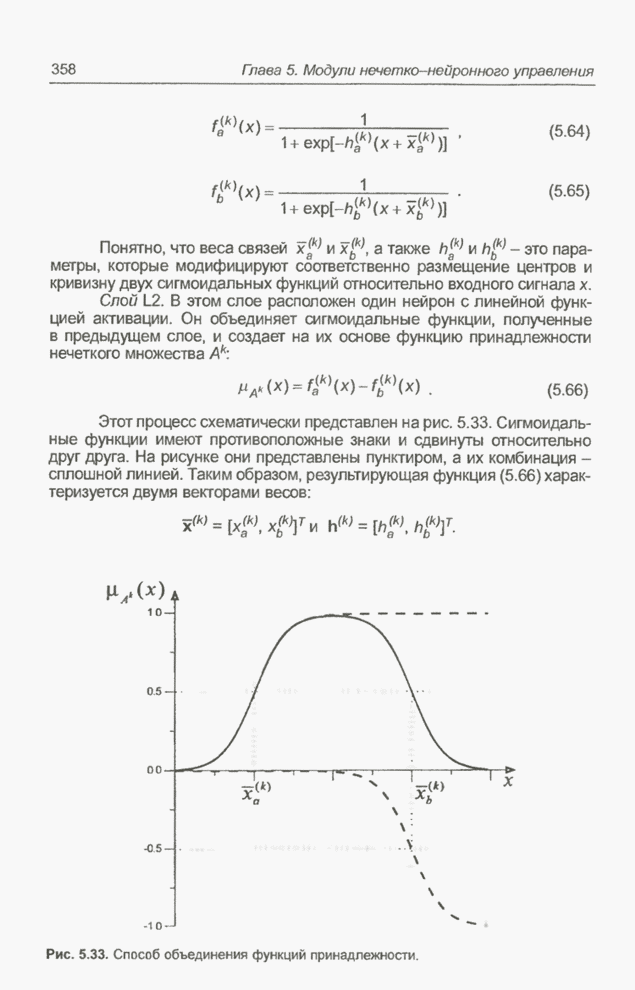
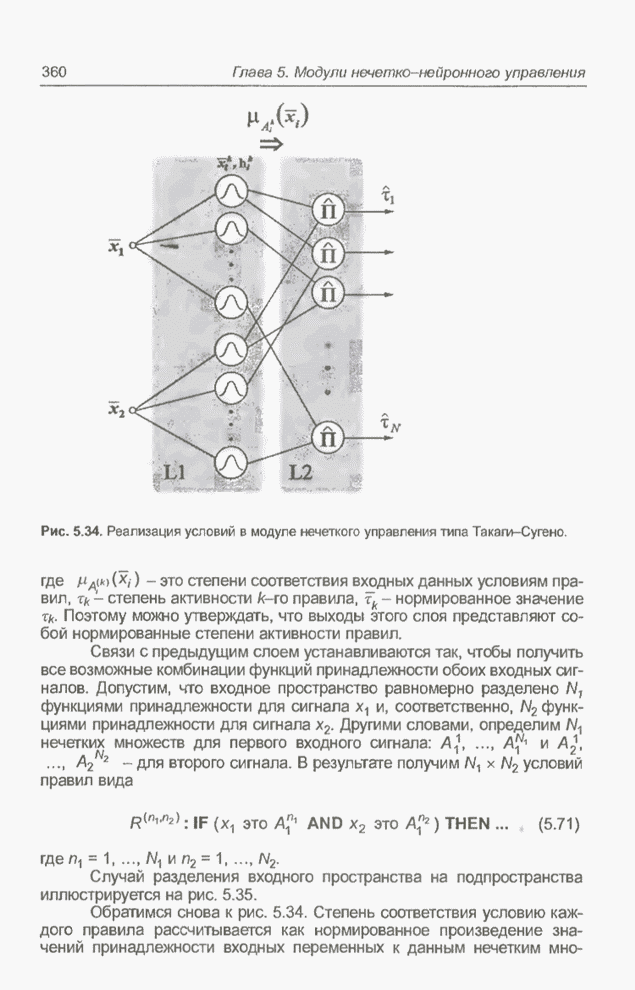
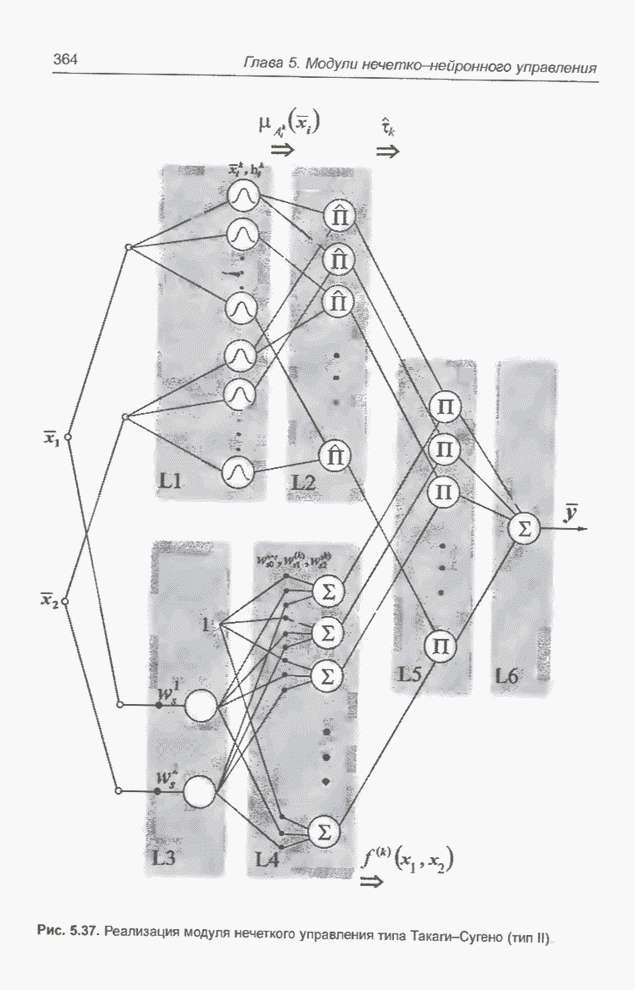
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
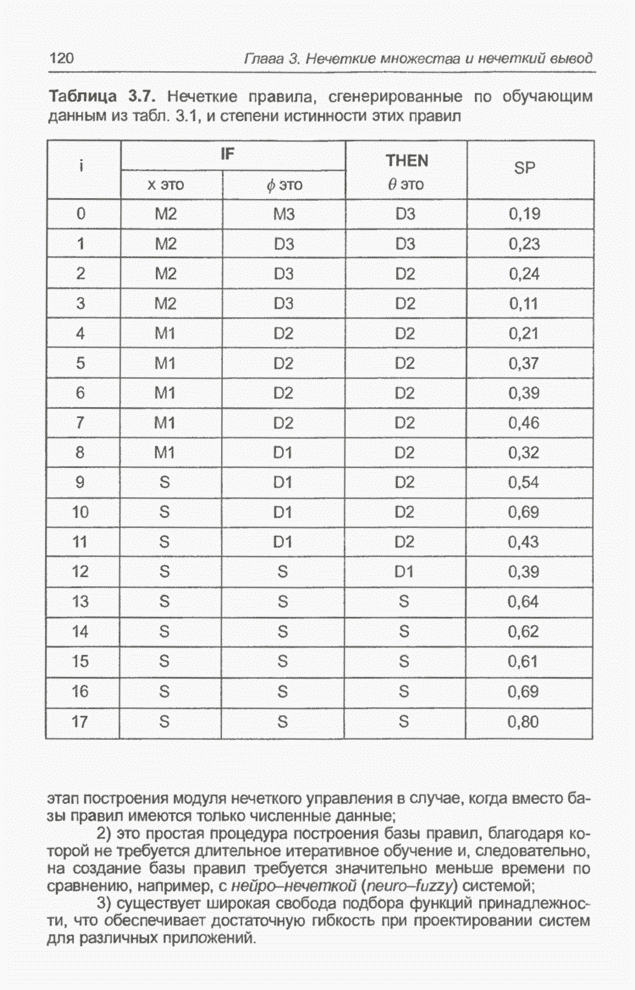
5.1.6. Применение модуля нечеткого управления для прогнозирования случайных временных рядов
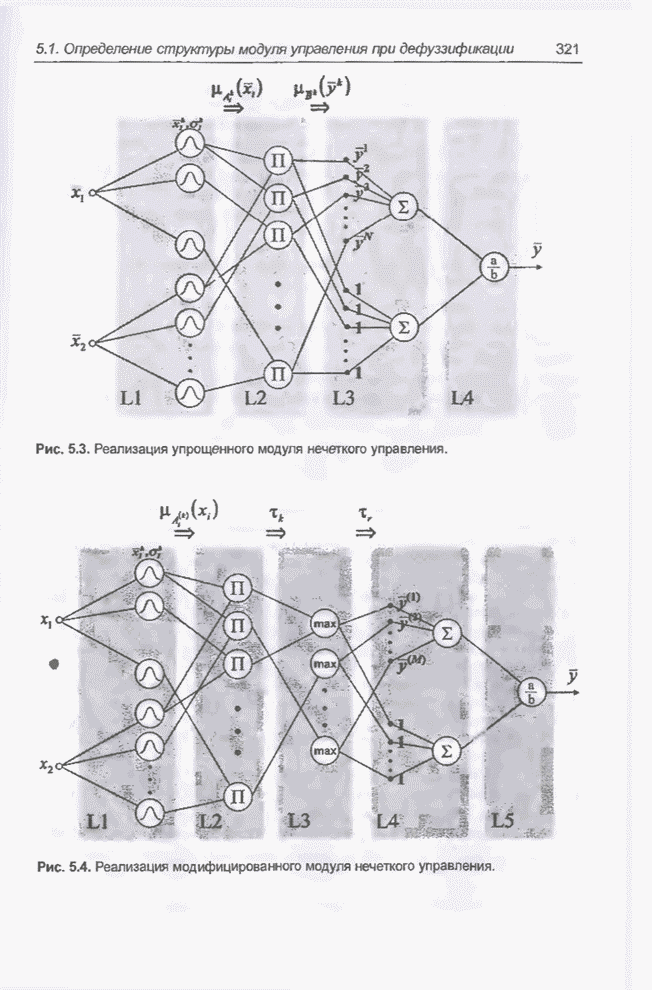
Прогнозирование временных рядов считается чрезвычайно важной задачей, возникающей в области экономики, финансового планирования, управления производством, предсказания погоды, обработки сигналов, управления в технических системах и т.п. В настоящем подразделе будет моделироваться поведение модуля нечеткого управления (5.13) в задаче прогнозирования временного ряда Маккея-Гласса (Mackey-Glass), который описывается дифференциальным уравнением вида
 .
.
При ![]() рассматриваемый ряд ведет себя
хаотически. Чем больше значение
рассматриваемый ряд ведет себя
хаотически. Чем больше значение ![]() , тем более хаотичным становится характер
ряда. Для моделирования установим
, тем более хаотичным становится характер
ряда. Для моделирования установим ![]() . На рис. 5.5 представлен пример развития
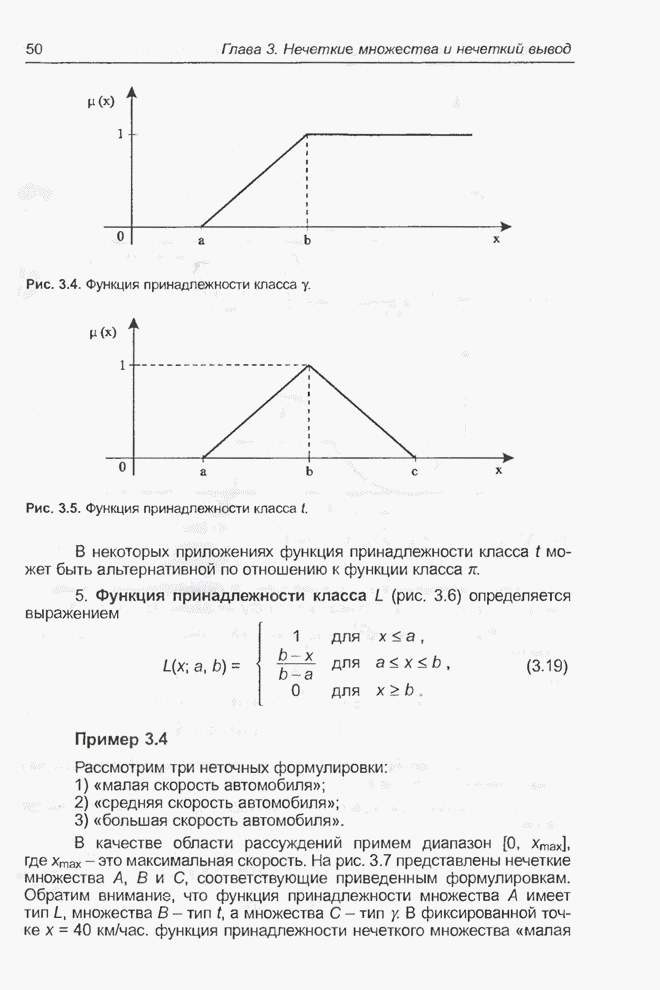
процесса для 1000 точек ряда Маккея-Гласса. Допустим, что первые 700 точек
будут использоваться в качестве обучающей выборки, а последние 300 точек - в
качестве тестовых данных. На рис. 5.6 представлена структура модуля нечеткого
управления. Он построен на базе 19 правил, предложенных экспертом. Эти правила
можно сформулировать и другими способами - например, методом, описанным в разд.
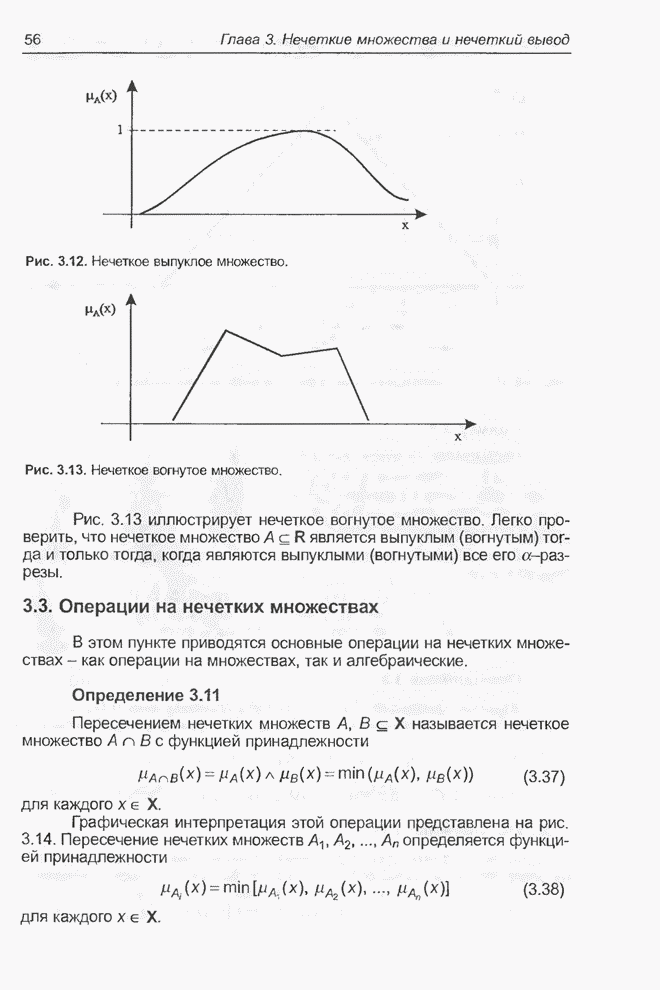
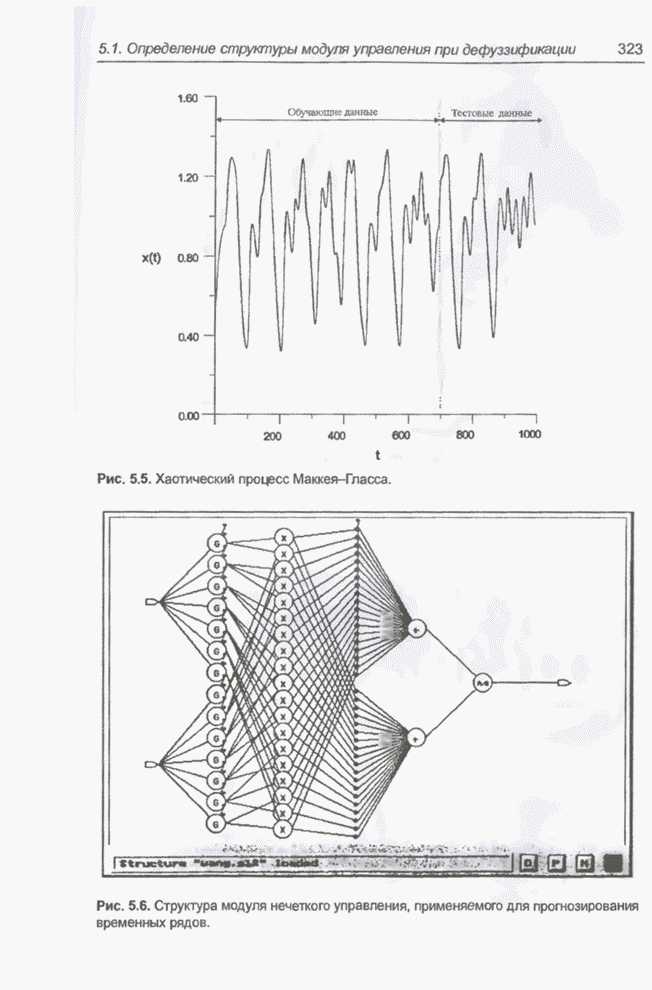
3.10. Форма функции принадлежности для обоих входных сигналов показана на рис.
5.7 (на нем используются следующие обозначения:
. На рис. 5.5 представлен пример развития
процесса для 1000 точек ряда Маккея-Гласса. Допустим, что первые 700 точек
будут использоваться в качестве обучающей выборки, а последние 300 точек - в
качестве тестовых данных. На рис. 5.6 представлена структура модуля нечеткого
управления. Он построен на базе 19 правил, предложенных экспертом. Эти правила
можно сформулировать и другими способами - например, методом, описанным в разд.
3.10. Форма функции принадлежности для обоих входных сигналов показана на рис.
5.7 (на нем используются следующие обозначения: ![]() - отрицательный,
- отрицательный, ![]() - нулевой,
- нулевой, ![]() - положительный). На первый
вход подается значение ряда в момент
- положительный). На первый
вход подается значение ряда в момент ![]() , а на второй вход - значение в момент
, а на второй вход - значение в момент ![]() . Задача модуля
нечеткого управления заключается в определении значения ряда в момент
. Задача модуля
нечеткого управления заключается в определении значения ряда в момент ![]() .
.

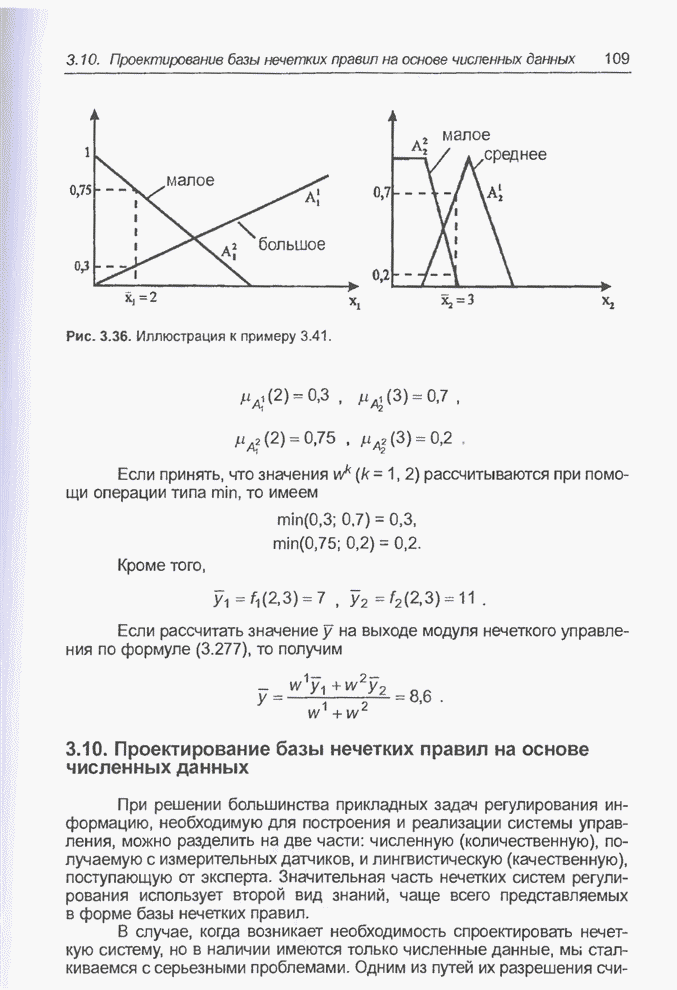
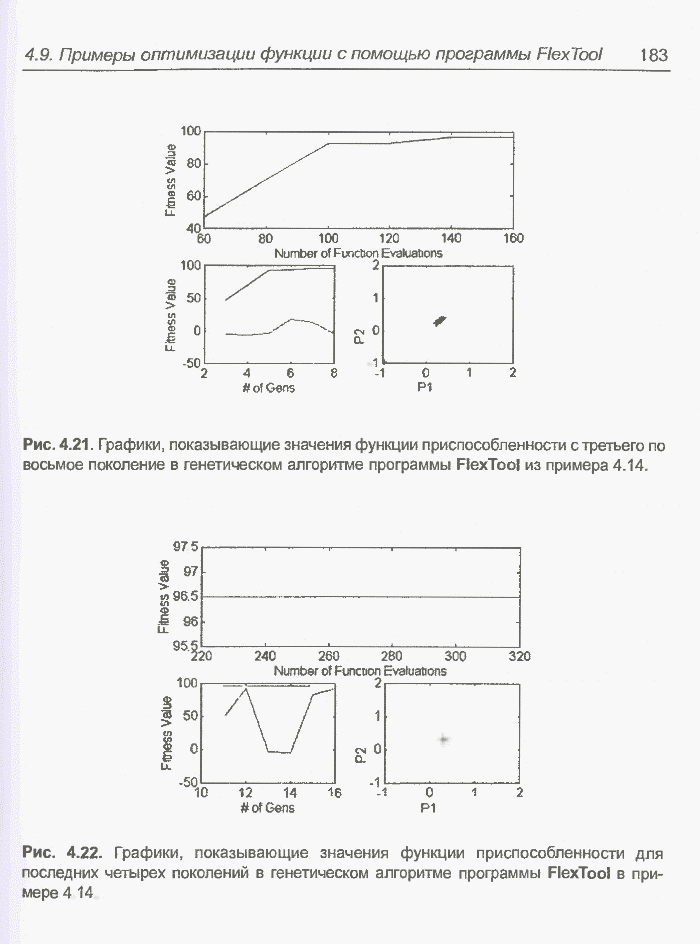
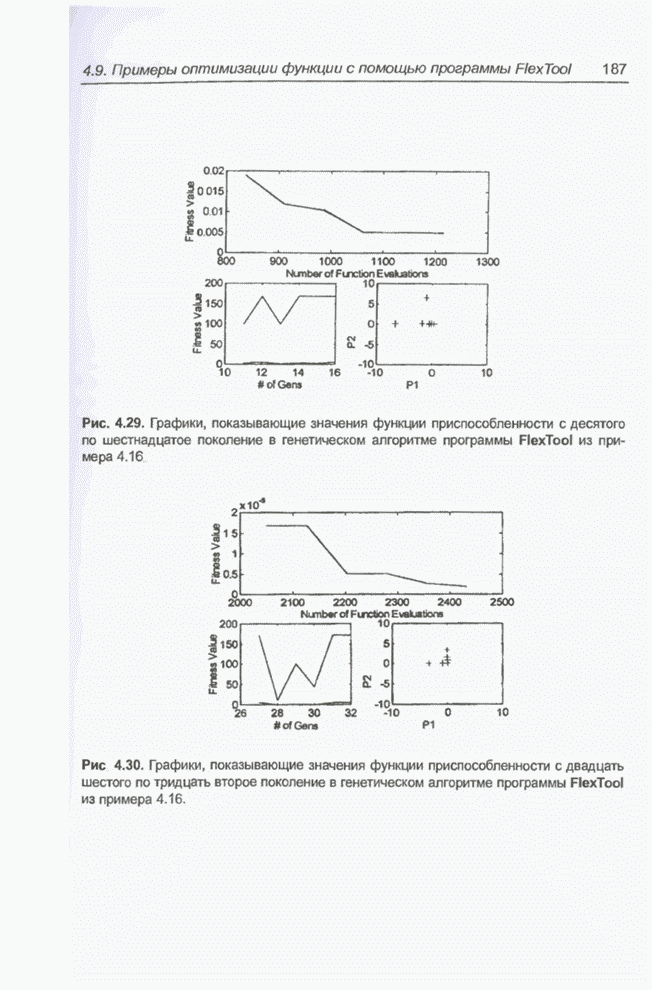
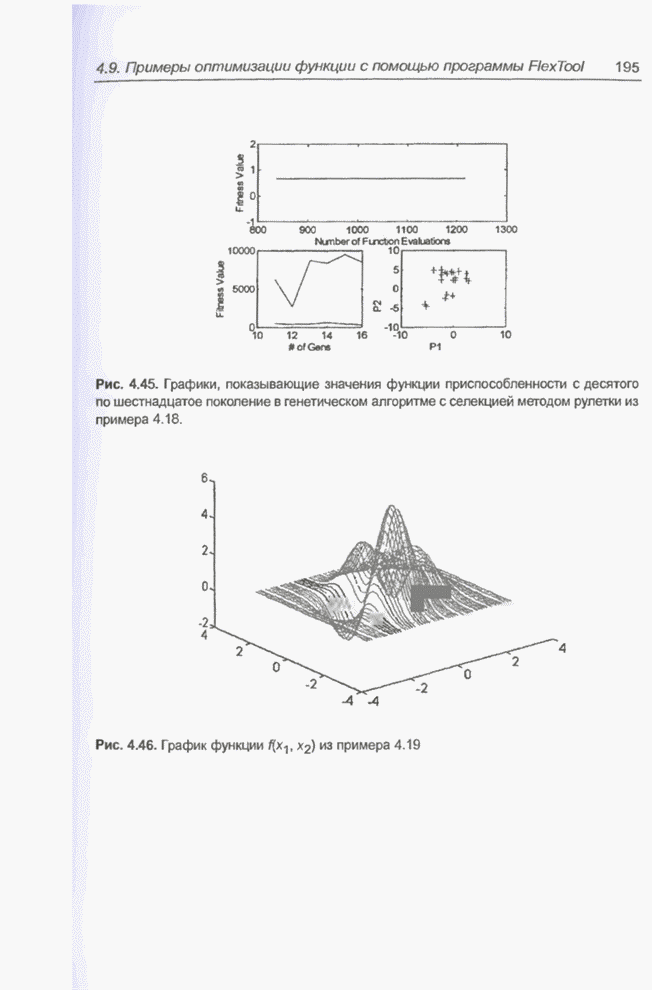
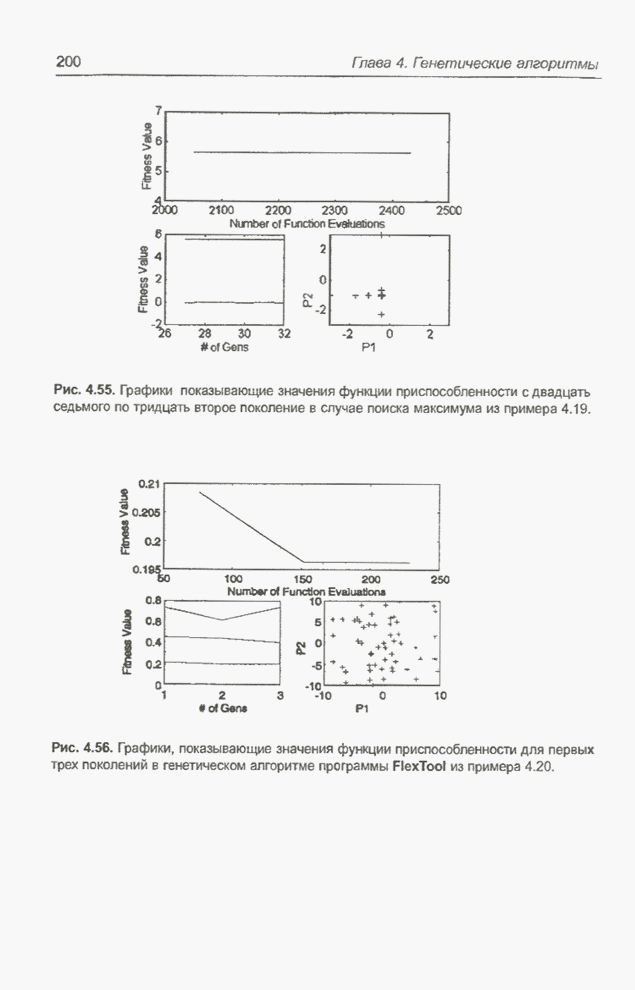
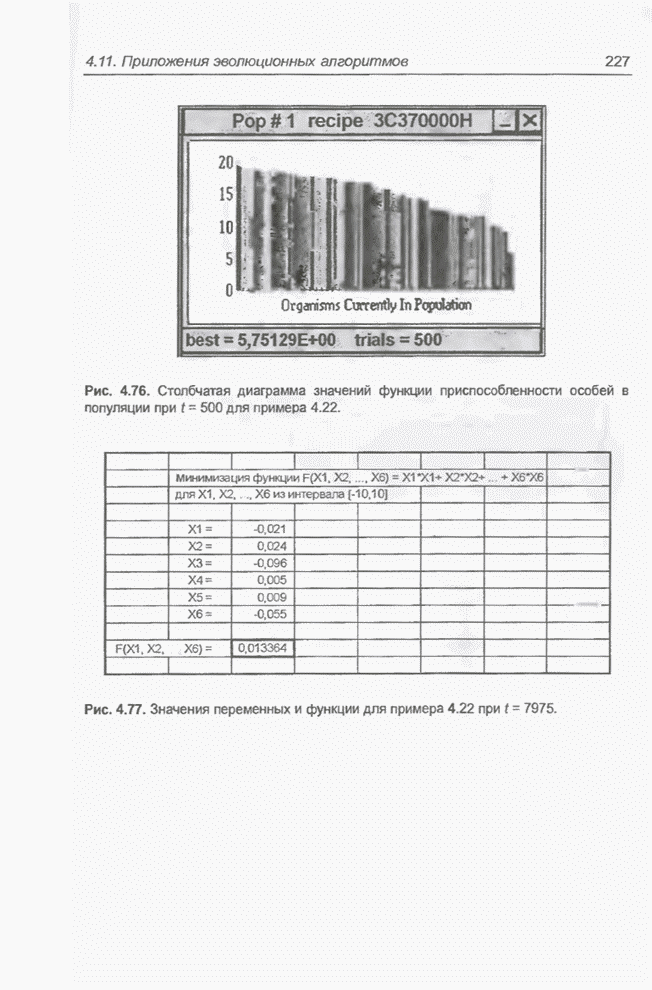
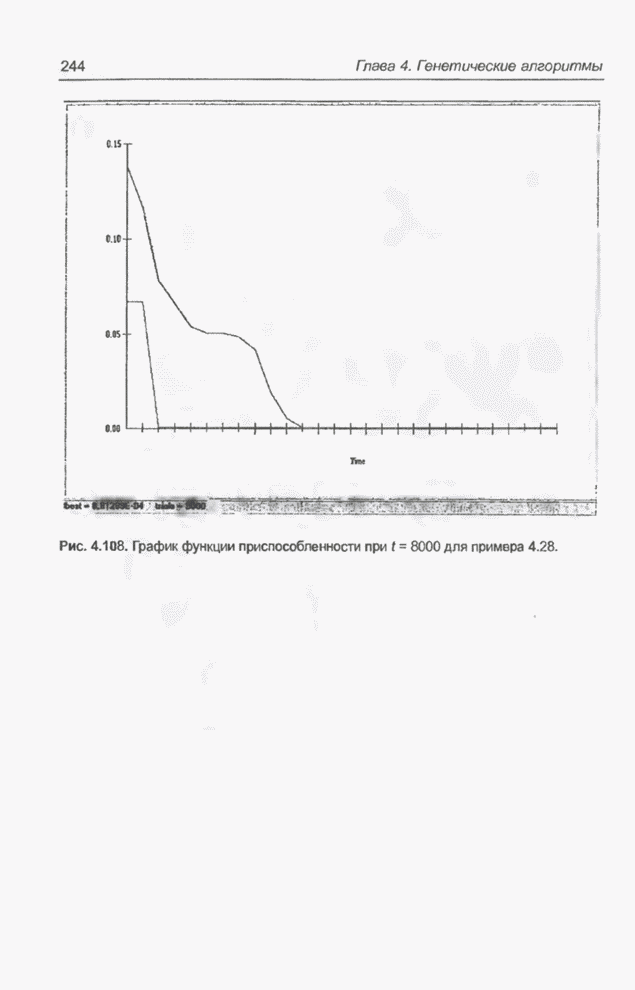
Рис. 5.5. Хаотический процесс Маккея-Гласса.

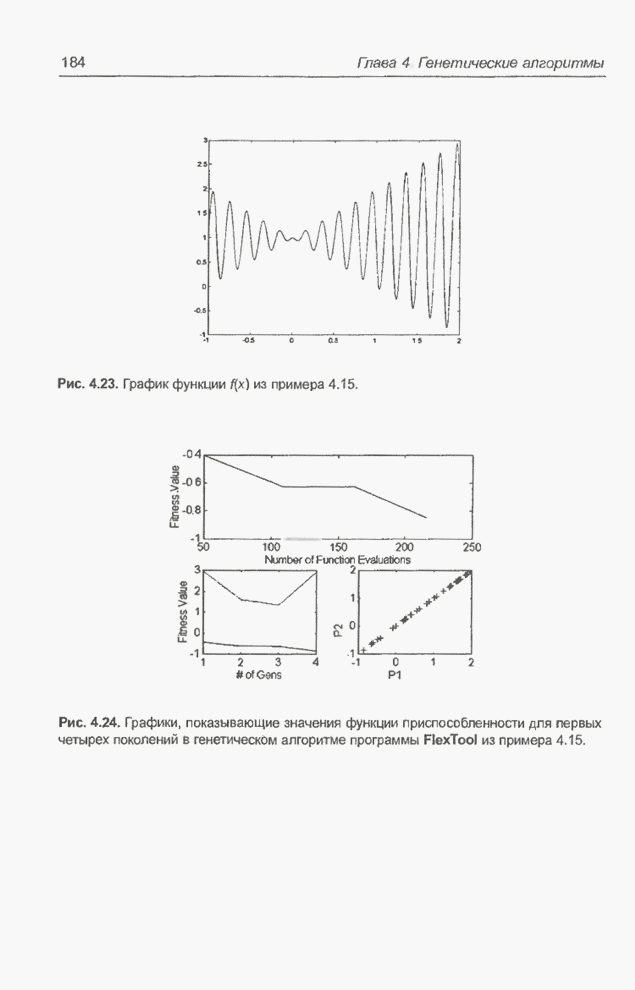
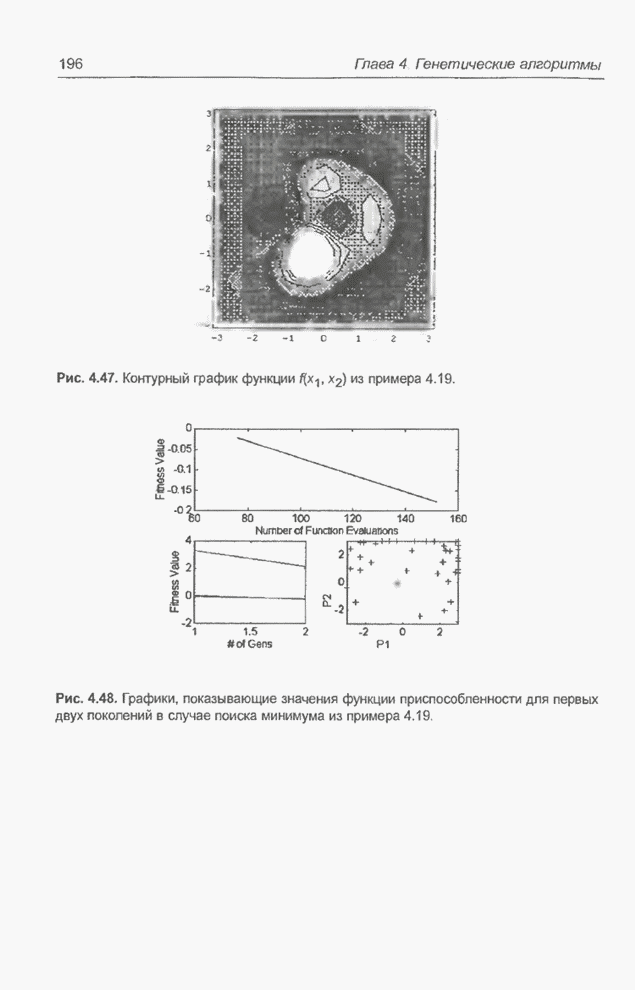
Рис. 5.6. Структура модуля нечеткого управления, применяемого для прогнозирования временных рядов.

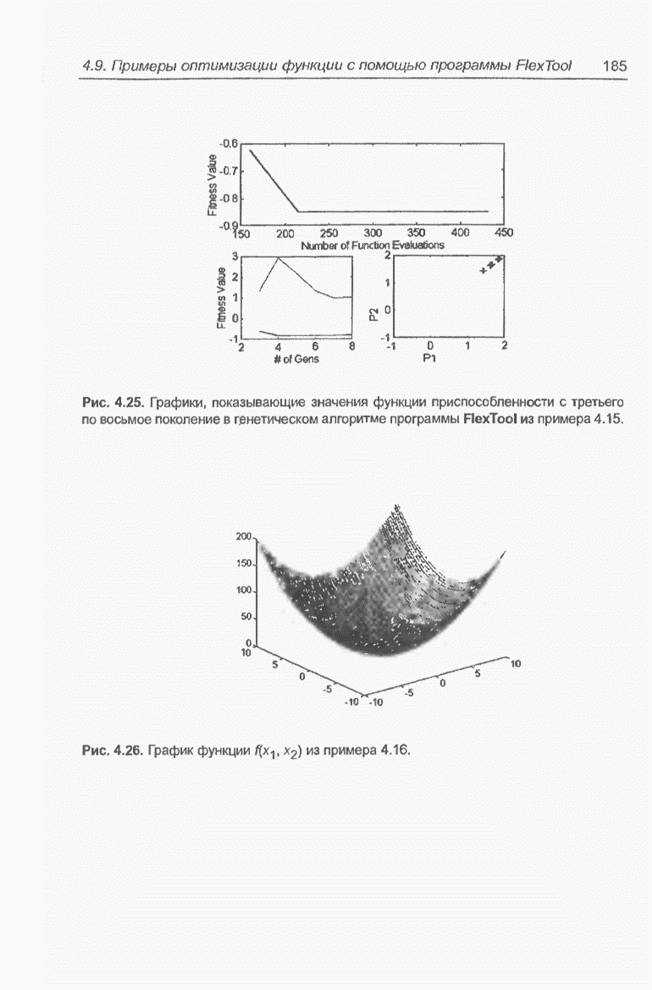
Рис. 5.7. Исходные функции принадлежности: а) первый вход; б) второй вход.
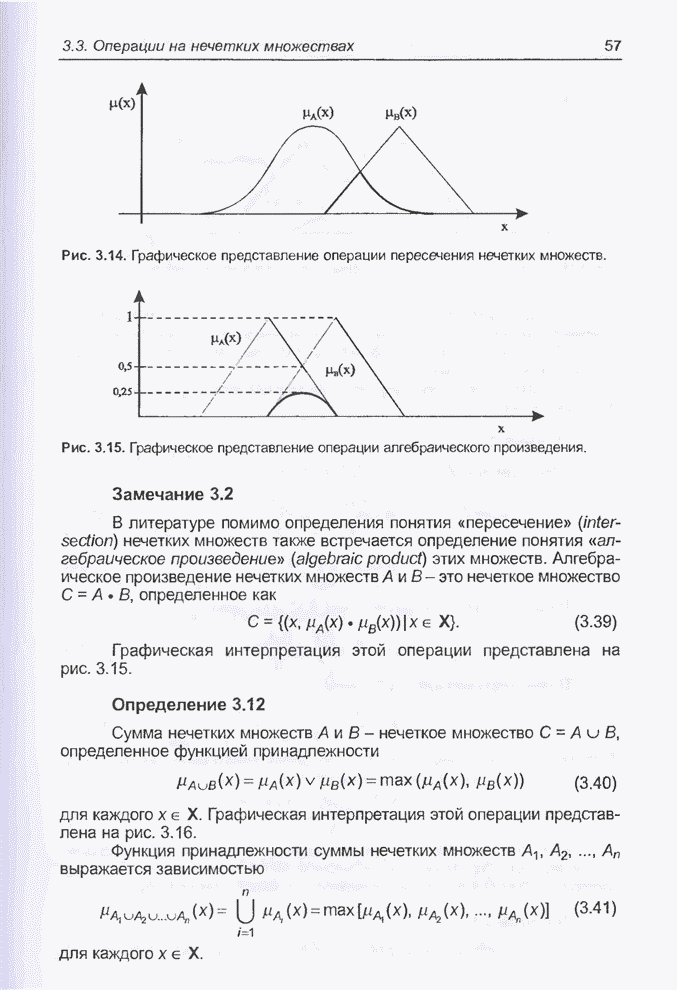
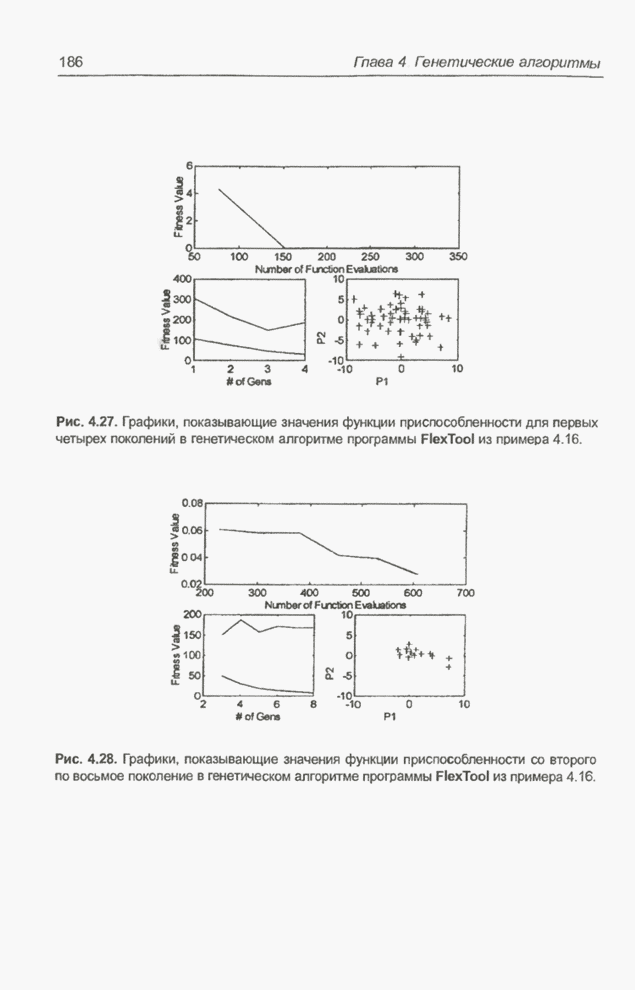
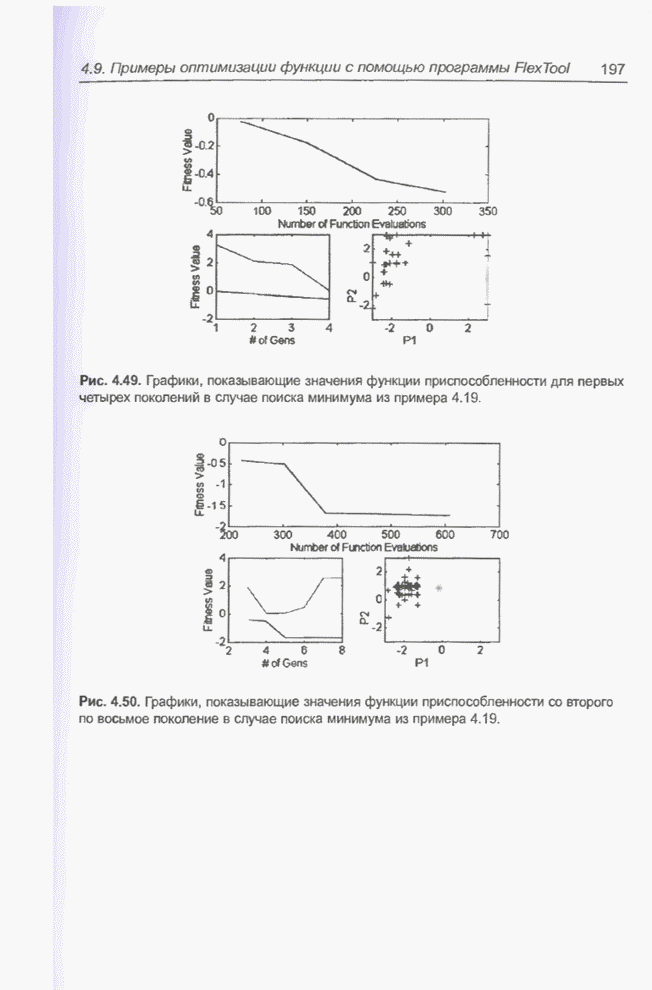
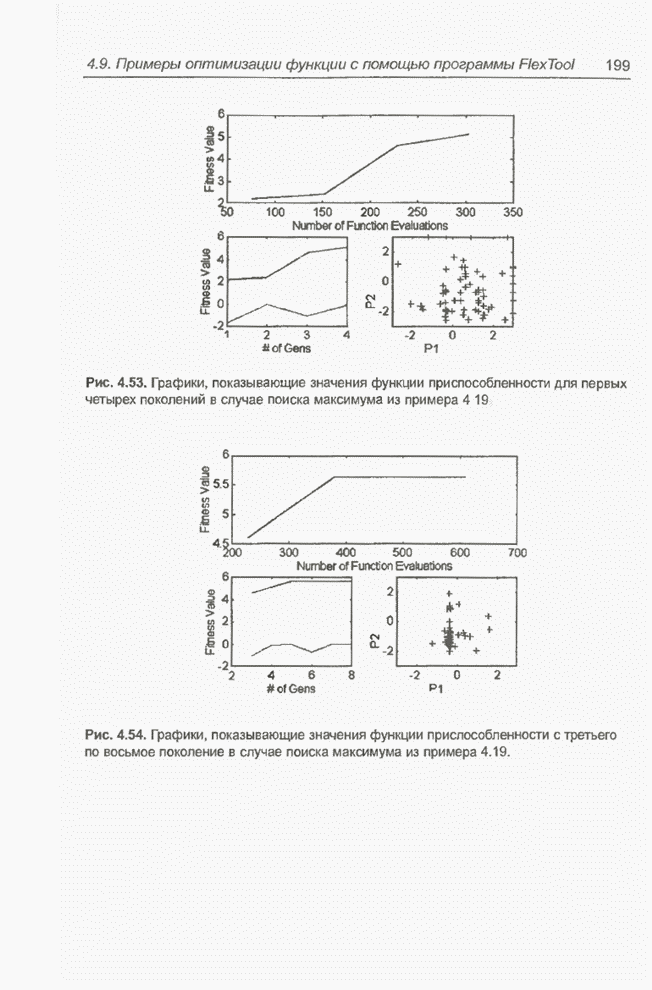
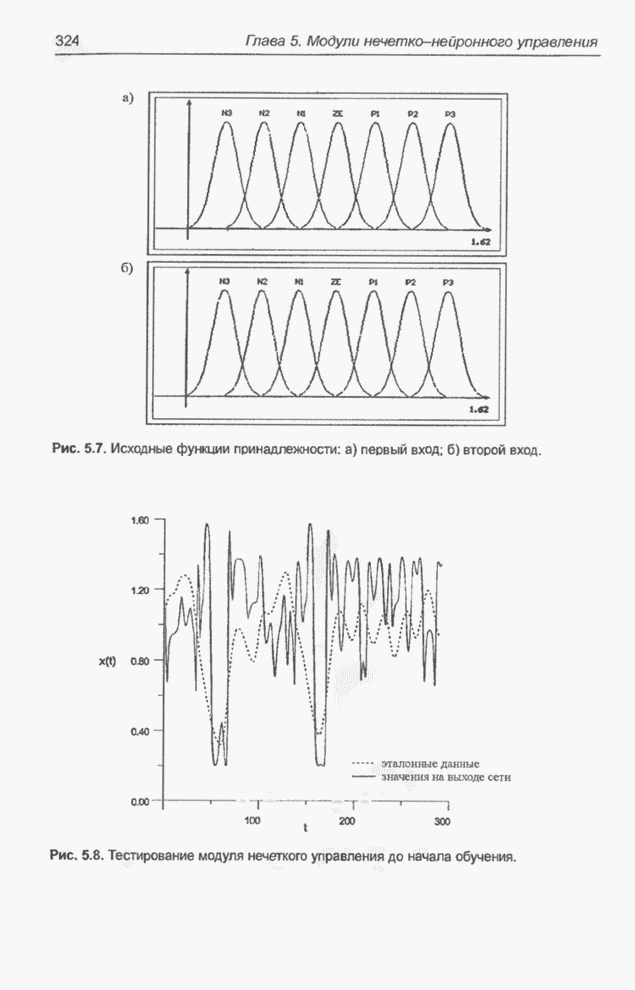
После проведения моделирования выяснилось, что предсказываемые значения сильно отличаются от тестовых данных (см. рис. 5.8). Поэтому модуль был подвергнут обучению. Как уже отмечалось, в качестве обучающей выборки использовались первые 700 значений временного ряда. На рис. 5.9 представлены два варианта процесса обучения сети: а) когда обучающая последовательность предъявлялась строго последовательно и б) когда обучающие данные выбирались случайным образом. Представленная на рисунке мера погрешности была задана в алгоритме обратного распространения ошибки формулой
![]() ,
,
где
![]() - выходной
сигнал модуля нечеткого управления, a
- выходной
сигнал модуля нечеткого управления, a ![]() - эталонный сигнал. Обучение проводилось
на протяжении 30 эпох.
- эталонный сигнал. Обучение проводилось
на протяжении 30 эпох.

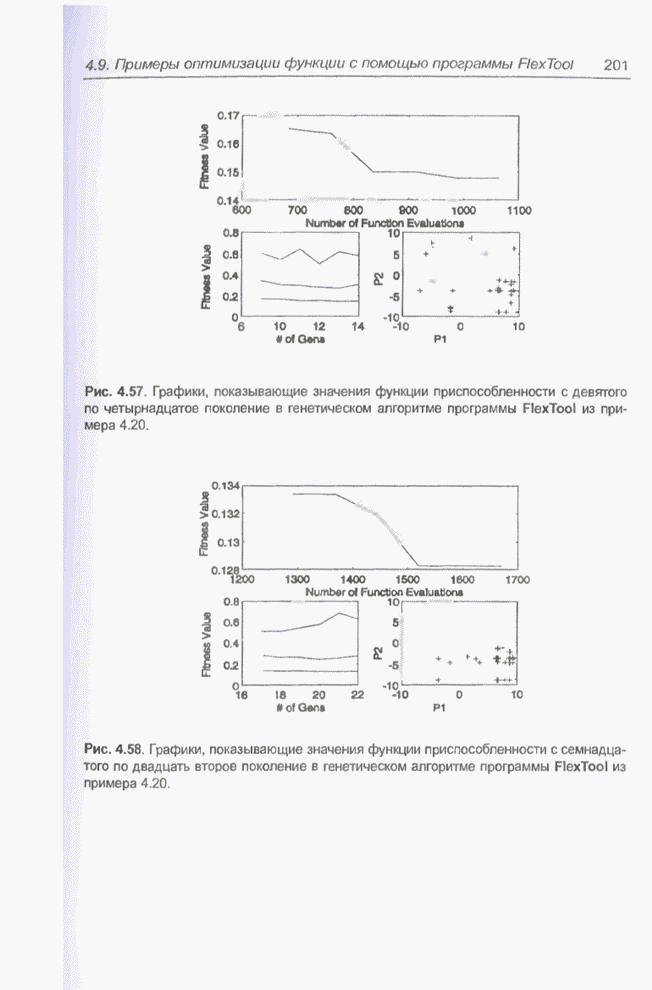
Рис. 5.8. Тестирование модуля нечеткого управления до начала обучения.

Рис. 5.9. Процесс обучения модуля нечеткого управления с помощью алгоритма обратного распространения ошибки.
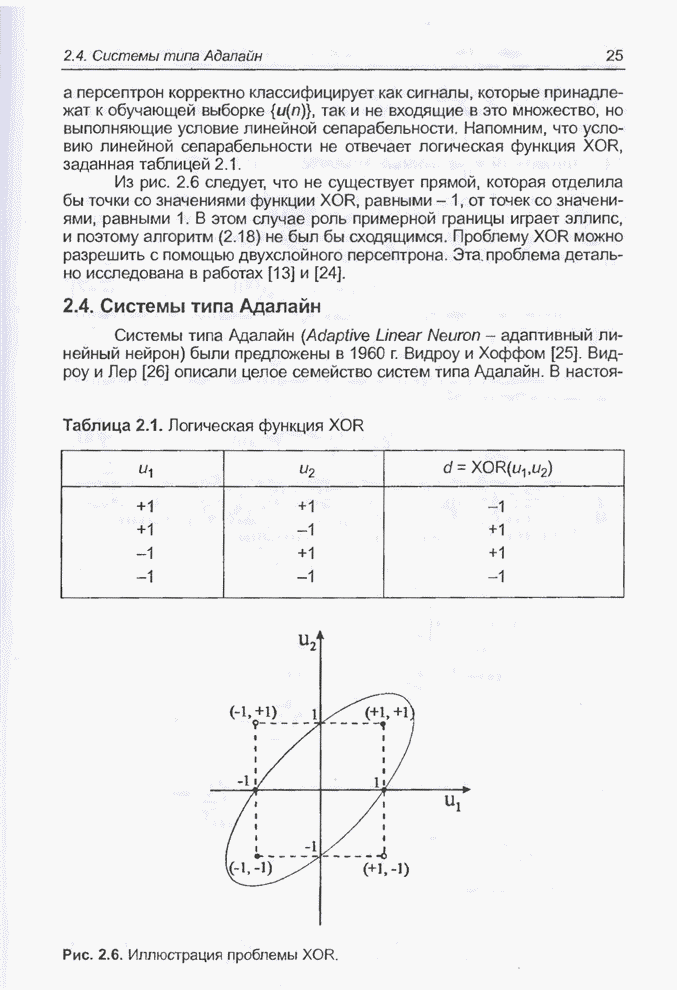
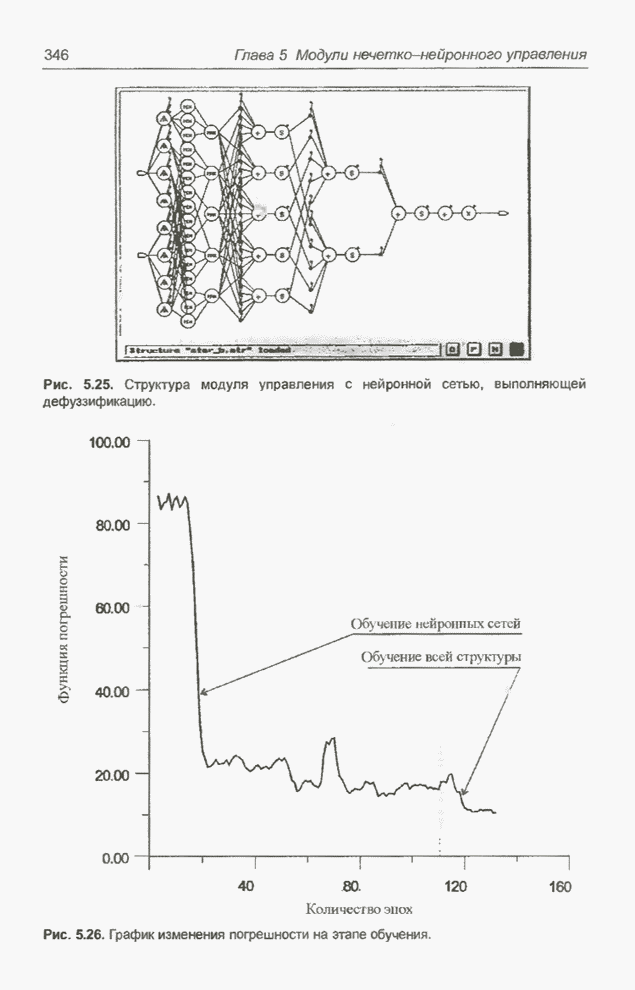
Тот факт, что последовательность предъявления обучающих данных имеет существенное значение, не является неожиданным. Интересно то, что обучение нечетко-нейронной сети данными, предъявляемыми строго последовательно, в начальной фазе оказывается значительно более эффективным. Аналогичный эффект зарегистрирован и при проведении других экспериментов.
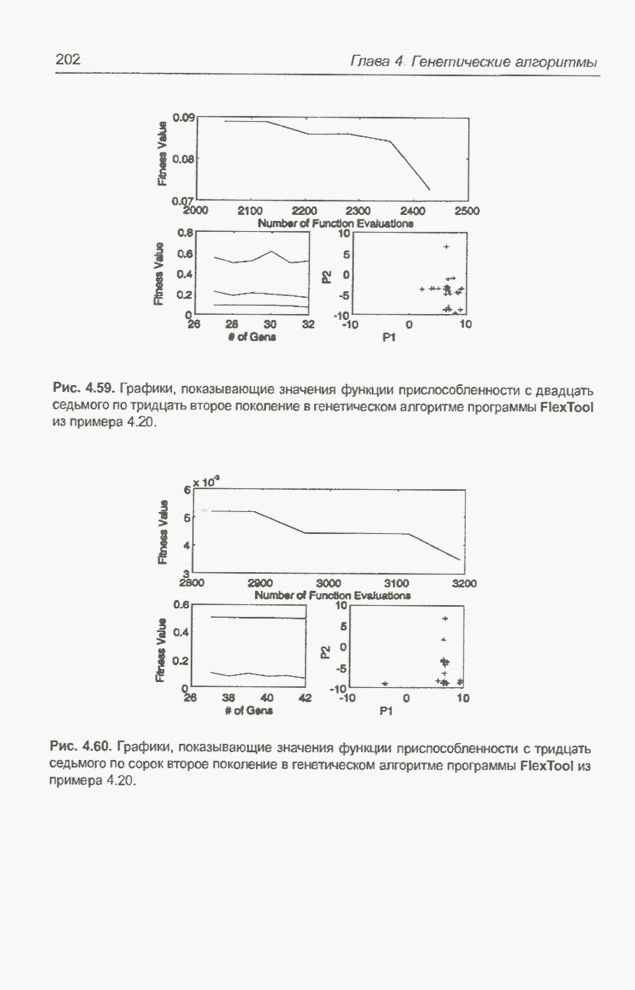
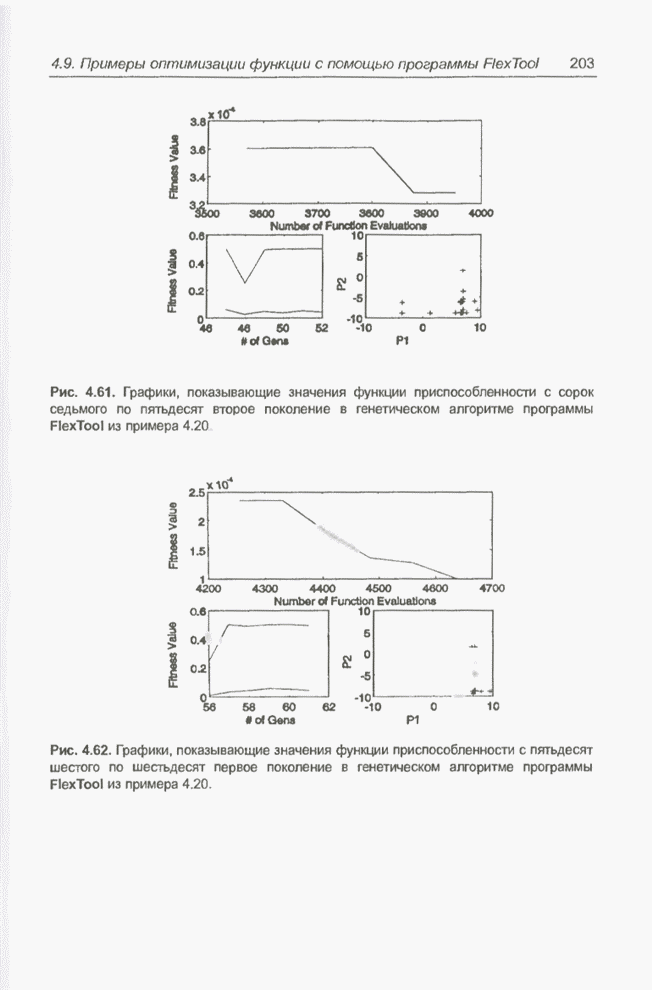
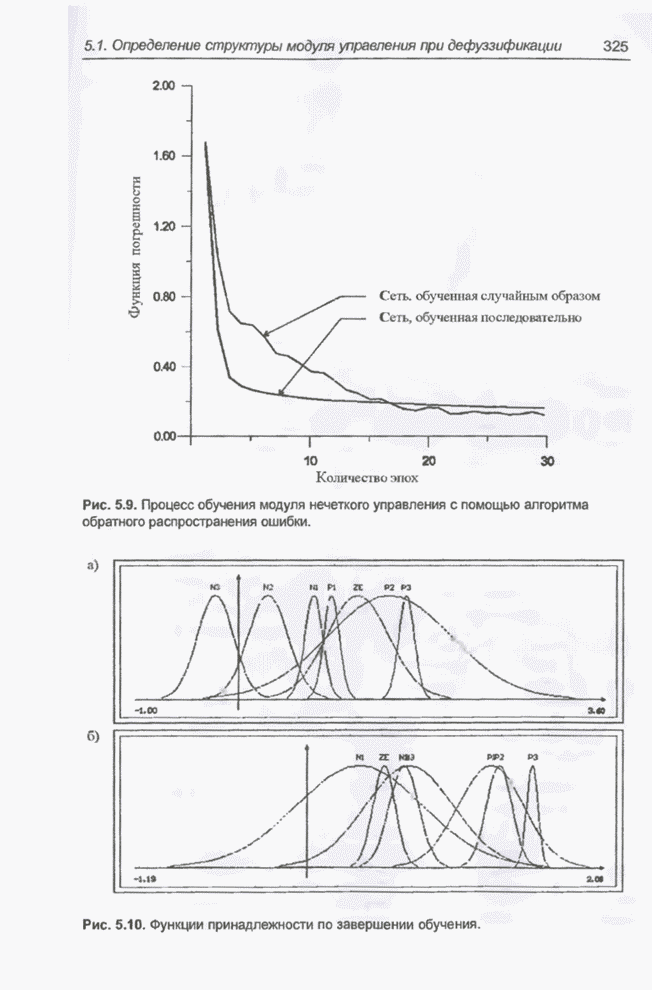
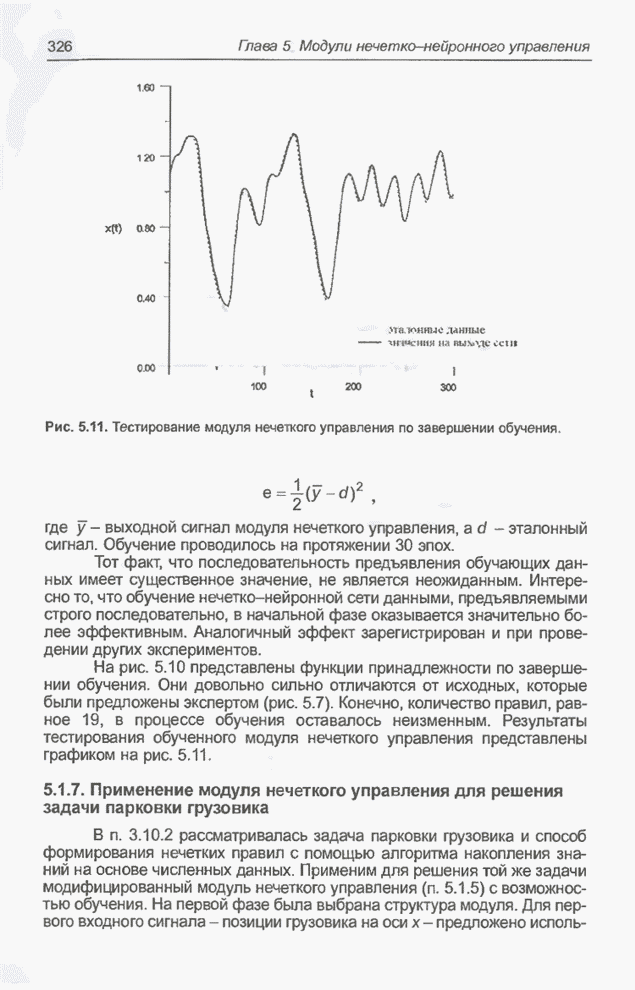
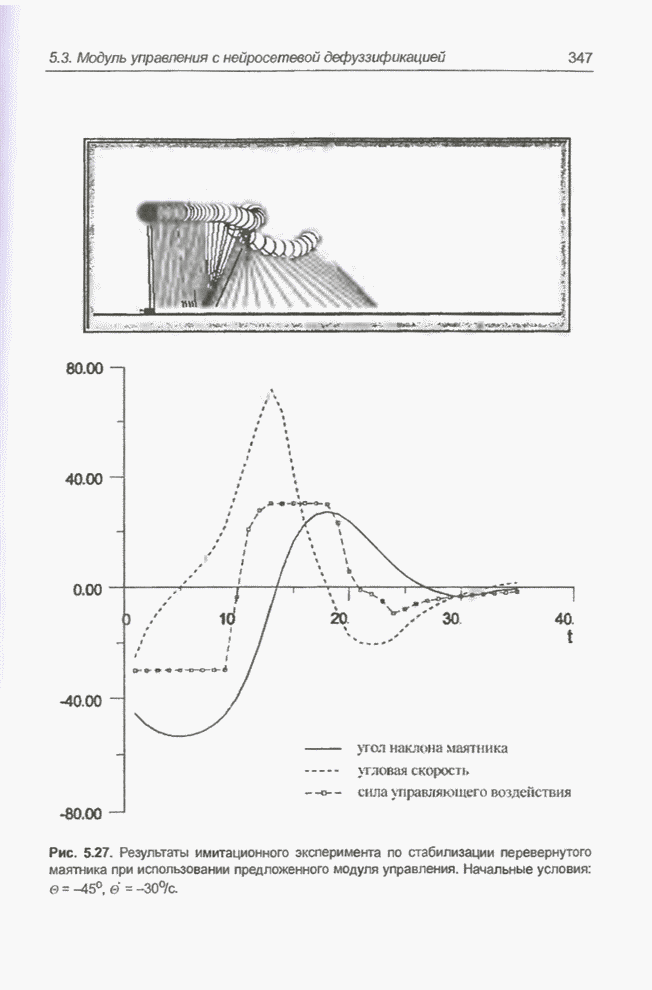
На рис. 5.10 представлены функции принадлежности по завершении обучения. Они довольно сильно отличаются от исходных, которые были предложены экспертом (рис. 5.7). Конечно, количество правил, равное 19, в процессе обучения оставалось неизменным. Результаты тестирования обученного модуля нечеткого управления представлены графиком на рис. 5.11.

Рис. 5.10. Функции принадлежности по завершении обучения.

Рис. 5.11. Тестирование модуля нечеткого управления по завершении обучения.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Предисловие к русскому изданию
- ГЛАВА 1. ВВЕДЕНИЕ
- Список литературы
- ГЛАВА 2. МНОГОСЛОЙНЫЕ НЕЙРОННЫЕ СЕТИ И АЛГОРИТМЫ ИХ ОБУЧЕНИЯ
- 2.1. Введение
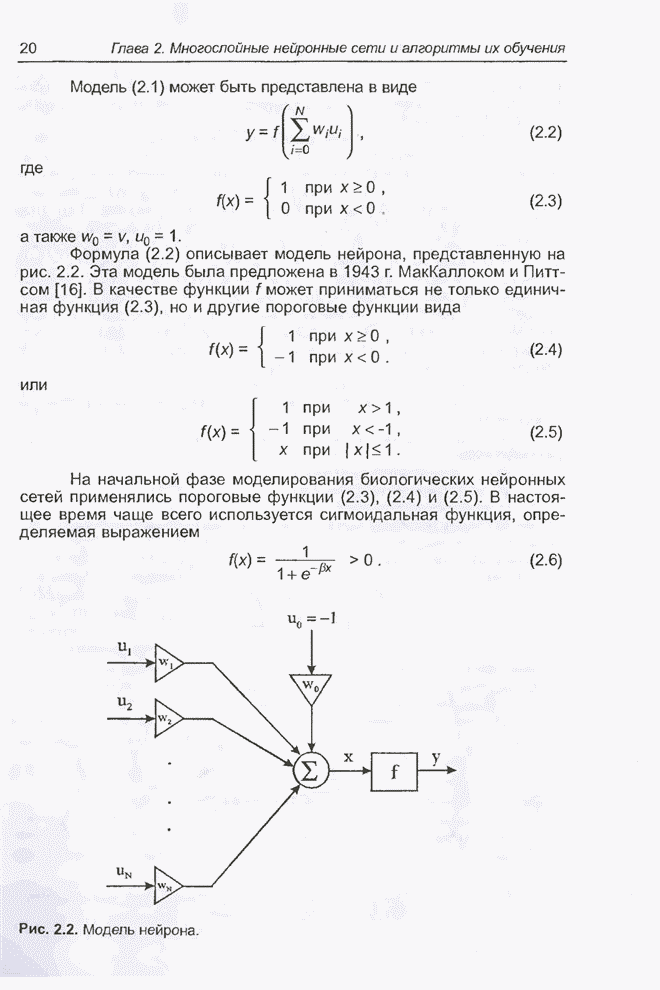
- 2.2. Нейрон и его модели
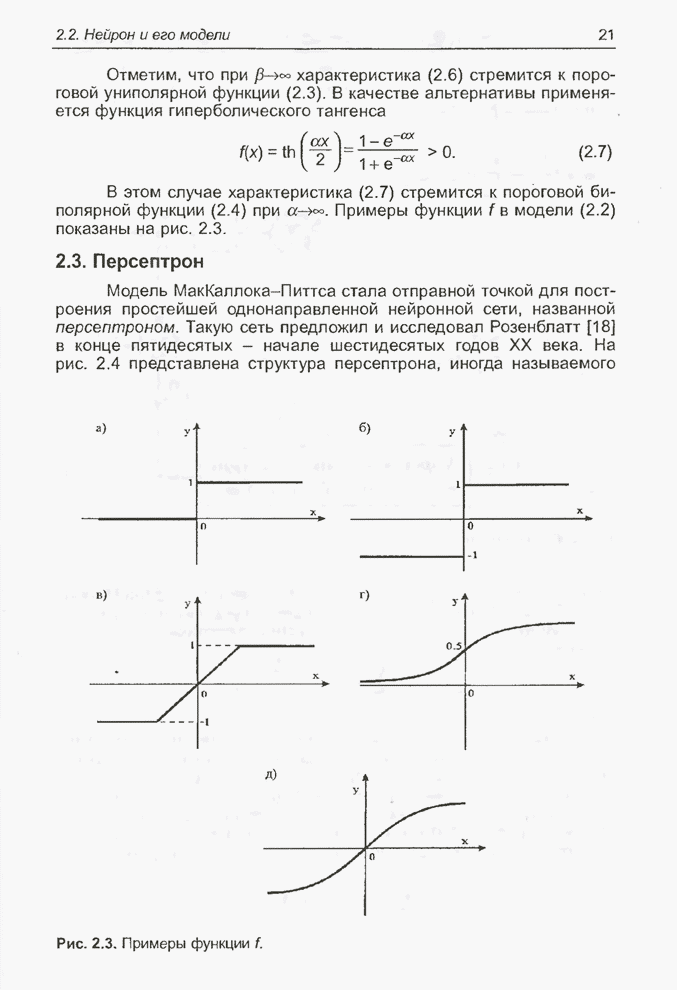
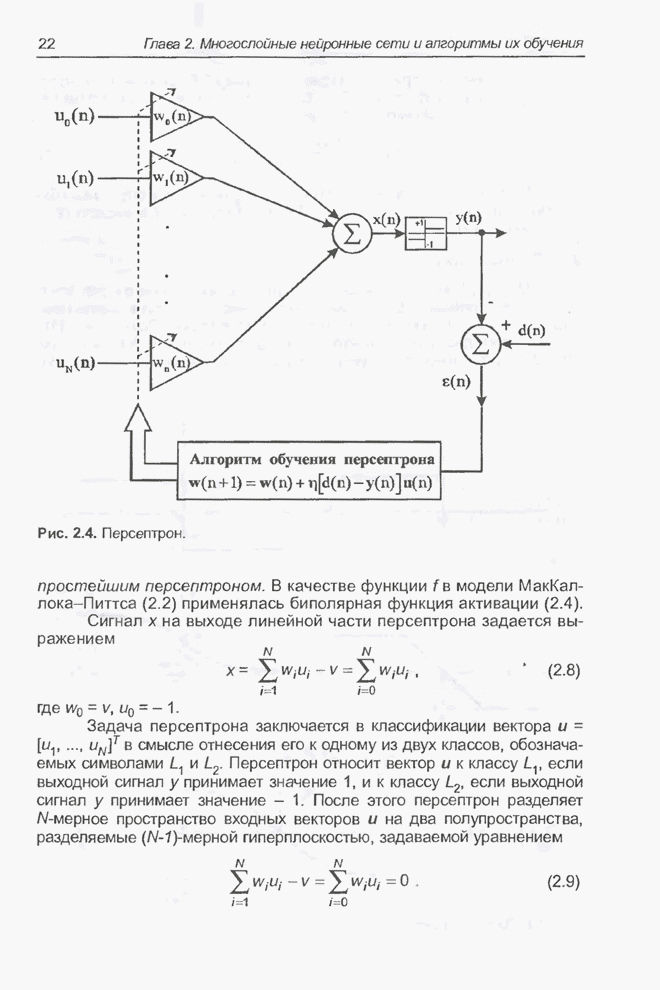
- 2.3. Персептрон
- 2.4. Системы типа Адалайн
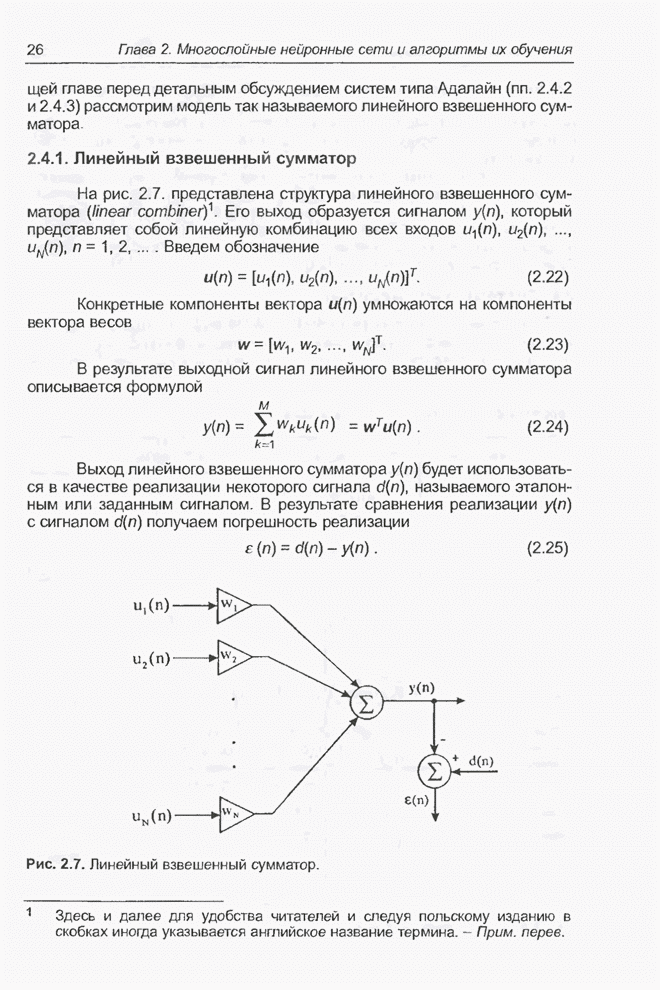
- 2.4.1. Линейный взвешенный сумматор
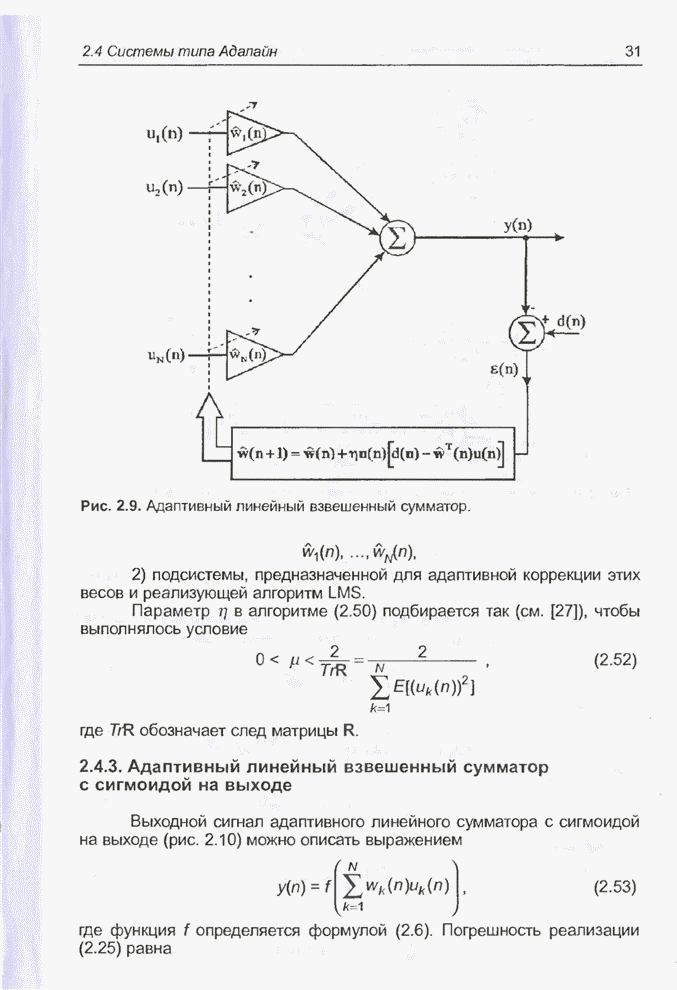
- 2.4.2. Адаптивный линейный взвешенный сумматор
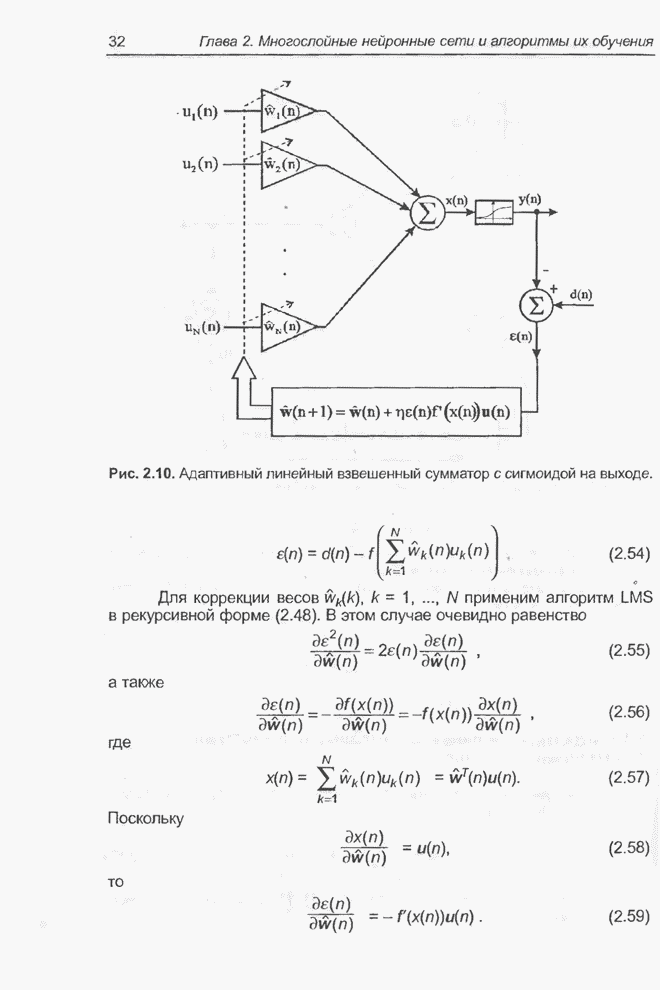
- 2.4.3. Адаптивный линейный взвешенный сумматор с сигмоидой на выходе
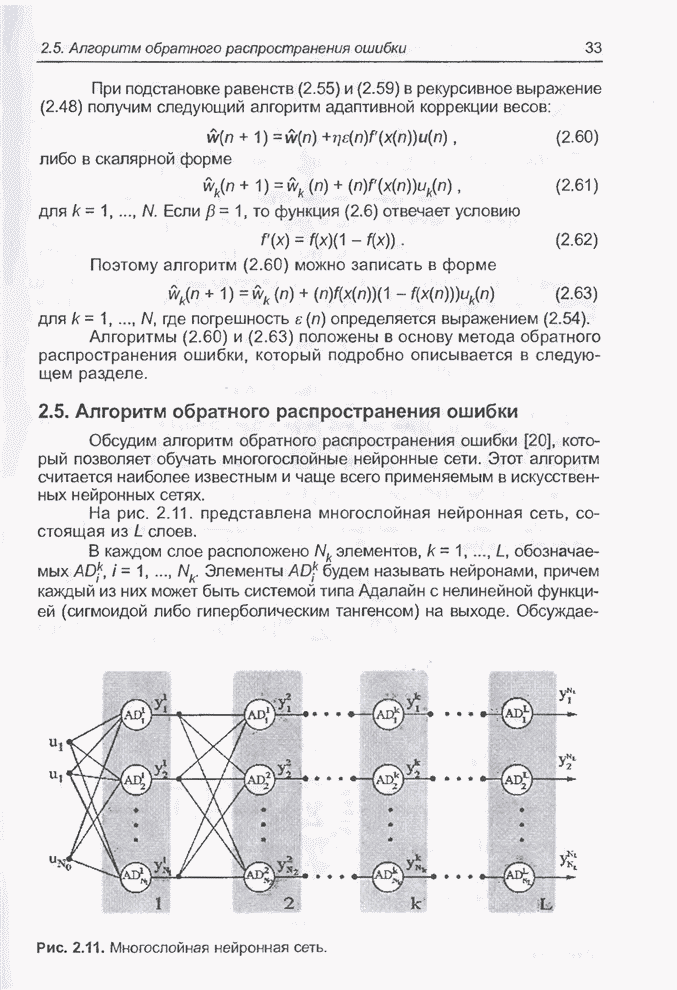
- 2.5. Алгоритм обратного распространения ошибки
- 2.6. Применение рекуррентного метода наименьших квадратов для обучения нейронных сетей
- Список литературы
- ГЛАВA3. НЕЧЕТКИЕ МНОЖЕСТВА И НЕЧЕТКИЙ ВЫВОД
- 3.1. Введение
- 3.2. Основные понятия и определения теории нечетких множеств
- 3.3. Операции на нечетких множествах
- 3.4. Принцип расширения
- 3.5. Нечеткие числа
- 3.6. Треугольные нормы
- 3.7. Нечеткие отношения и их свойства
- 3.8. Нечеткий вывод
- 3.9. Нечеткое управление
- 3.9.1. Классический модуль нечеткого управления
- 3.9.2. Метод нечеткого управления Такаги-Сугено
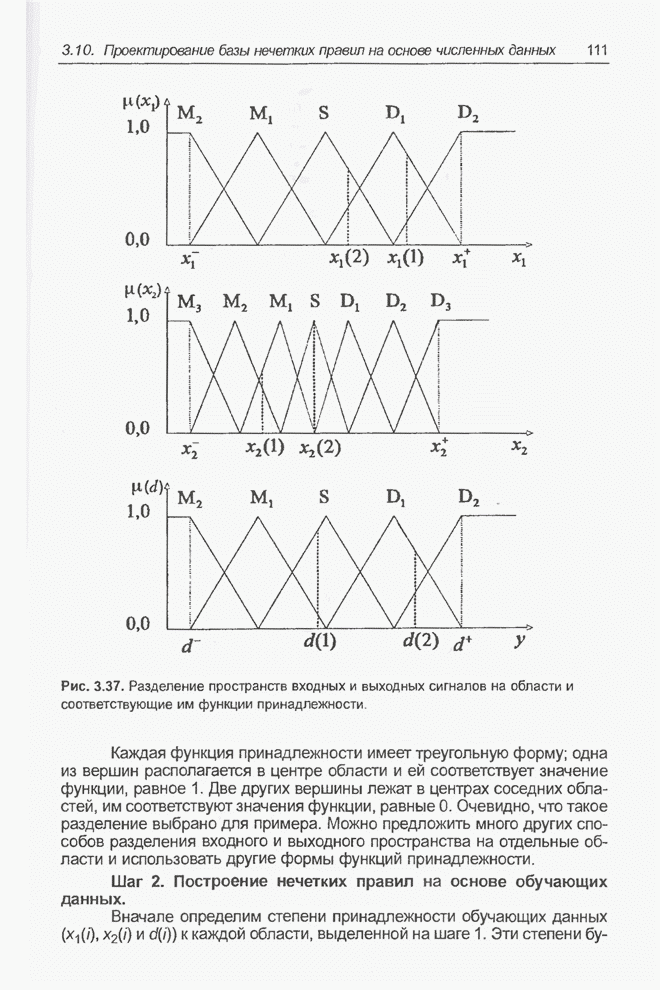
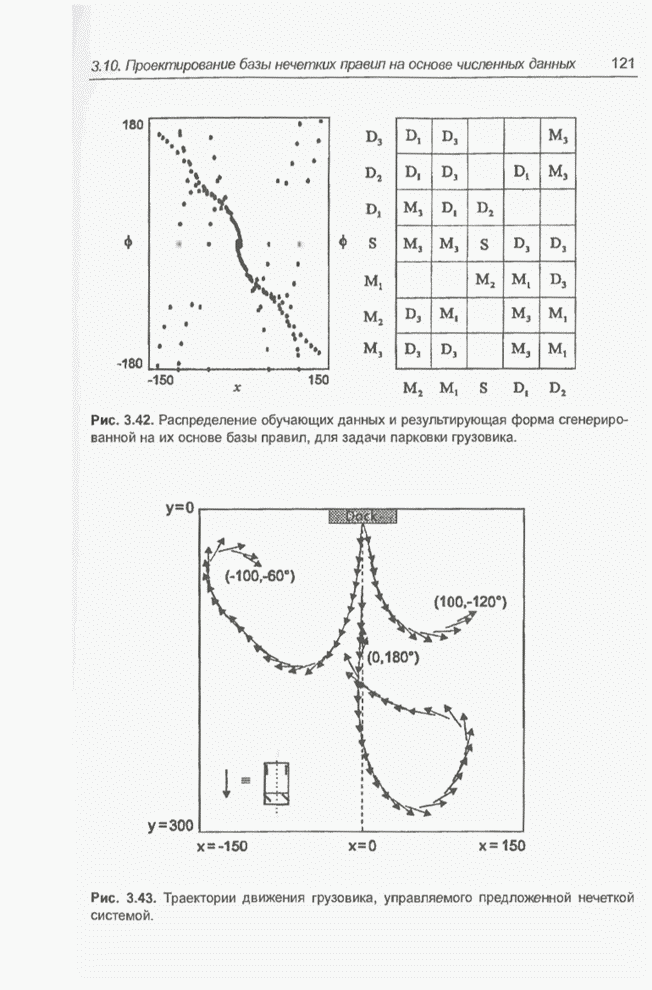
- 3.10. Проектирование базы нечетких правил на основе численных данных
- 3.10.1. Построение нечетких правил
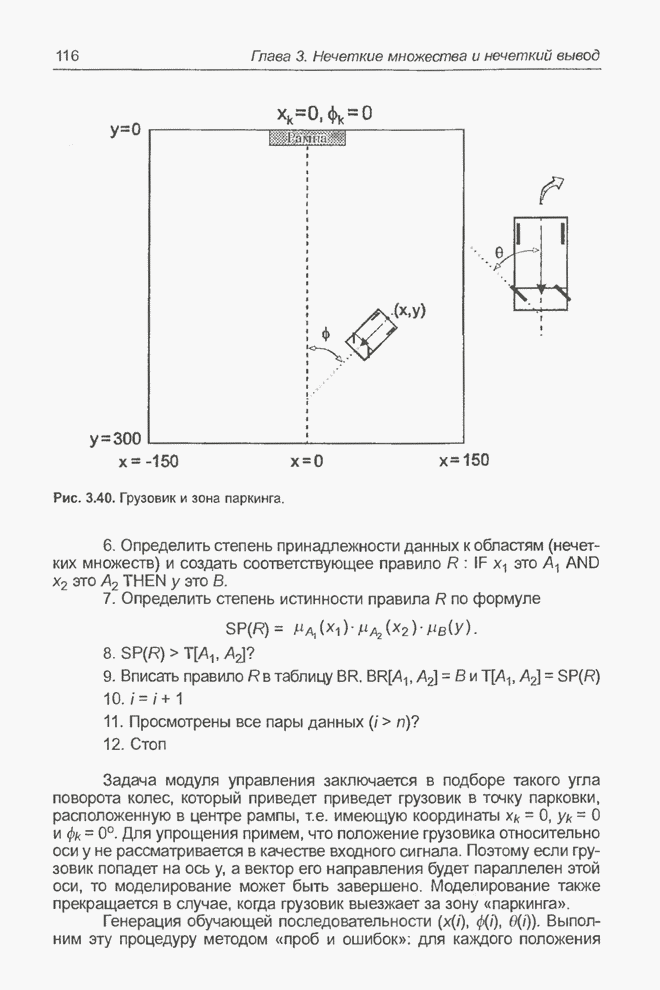
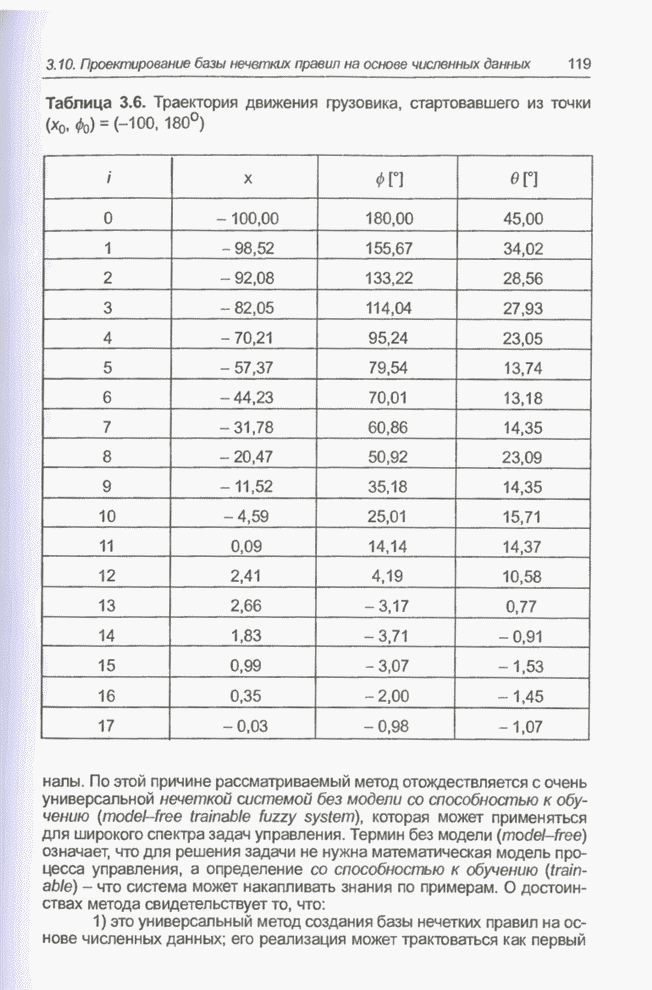
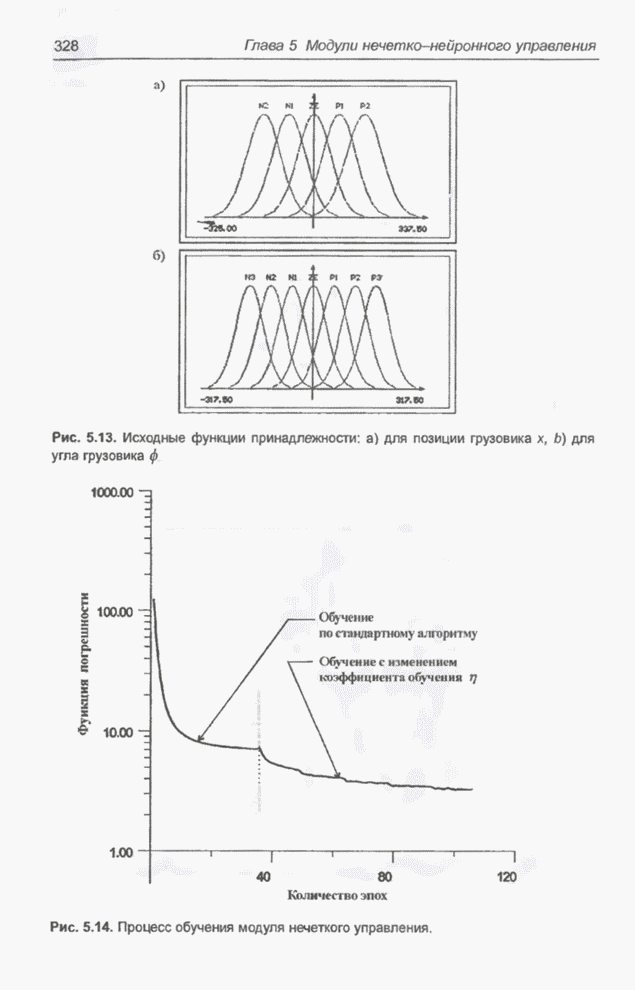
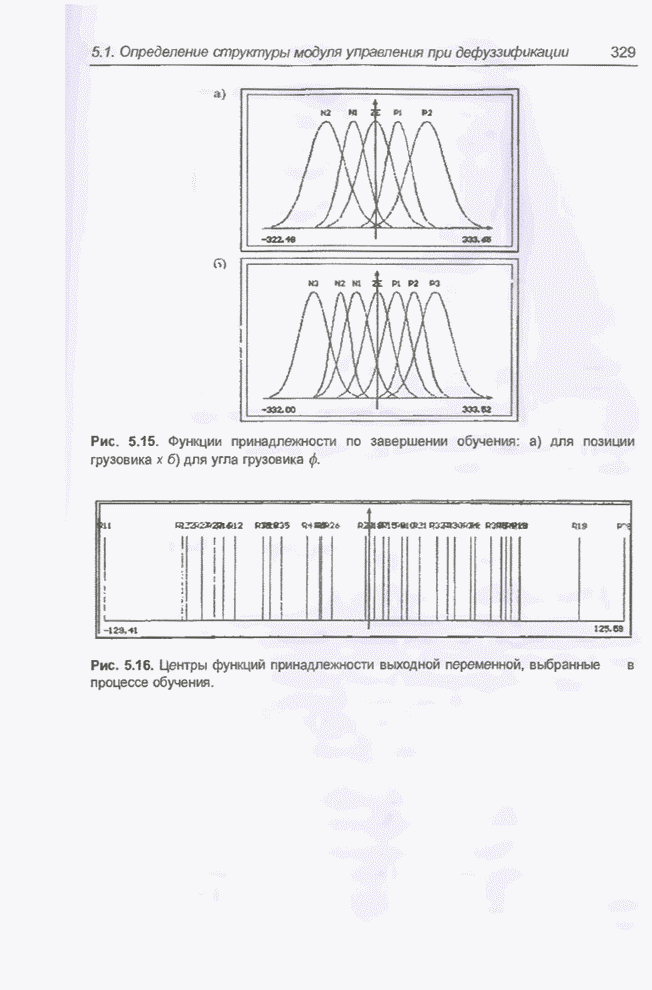
- 3.10.2. Задача парковки грузовика
- 3.10.3. Примечание
- Список литературы
- ГЛАВА 4. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 4.1. Введение
- 4.2. Генетические алгоритмы и традиционные методы оптимизации
- 4.3. Основные понятия генетических алгоритмов
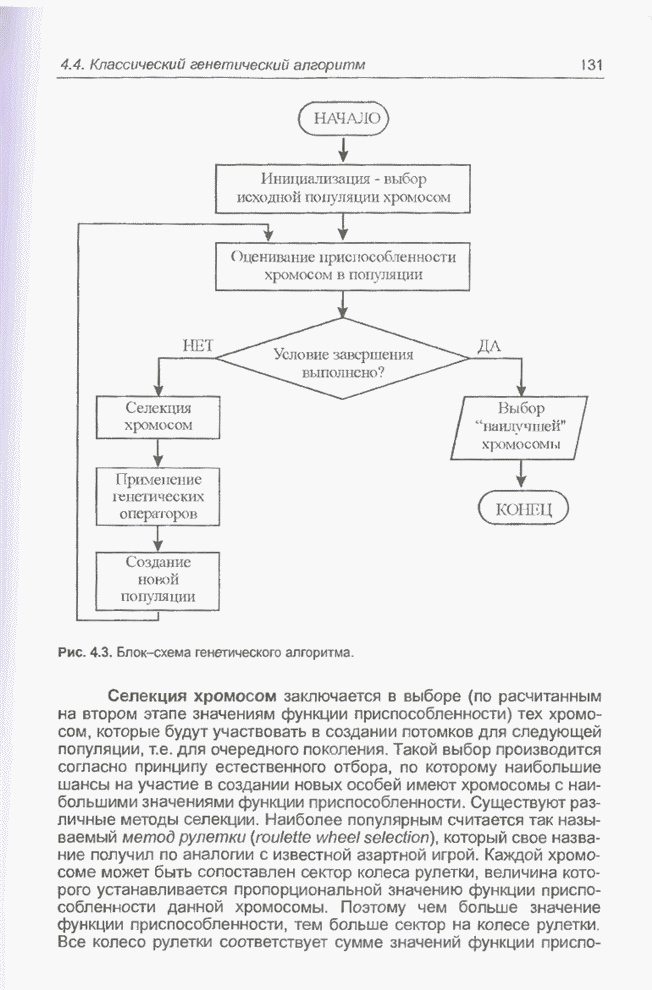
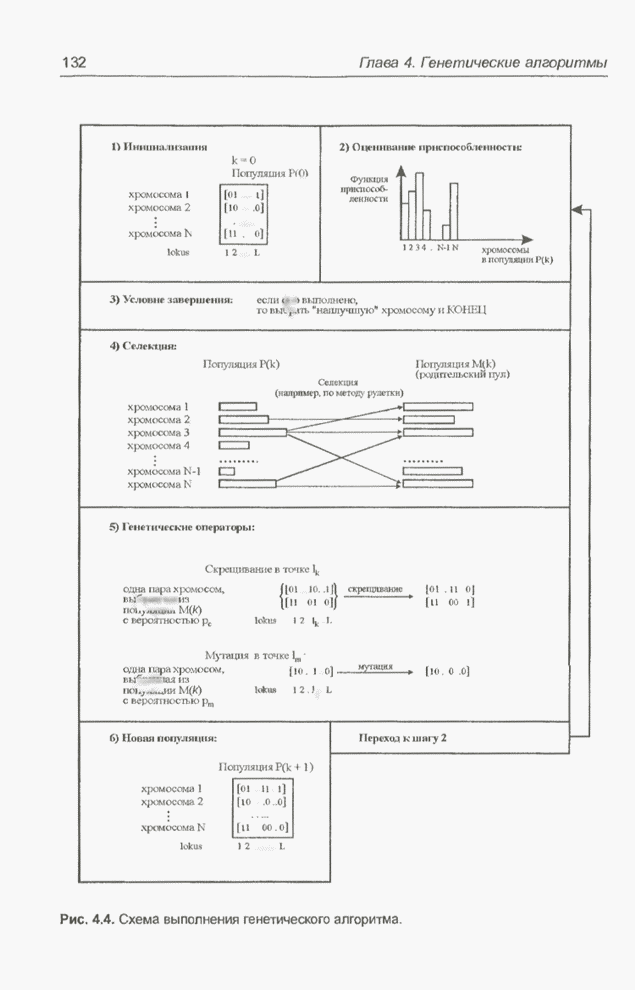
- 4.4. Классический генетический алгоритм
- 4.5. Иллюстрация выполнения классического генетического алгоритма
- 4.6. Кодирование параметров задачи в генетическом алгоритме
- 4.7. Основная теорема о генетических алгоритмах
- 4.8. Модификации классического генетического алгоритма
- 4.8.1. Методы селекции
- 4.8.2. Особые процедуры репродукции
- 4.8.3. Генетические операторы
- 4.8.4. Методы кодирования
- 4.8.5. Масштабирование функции приспособленности
- 4.8.6. Ниши в генетическом алгоритме
- 4.8.7. Генетические алгоритмы для многокритериальной оптимизации
- 4.8.8. Генетические микроалгоритмы
- 4.9. Примеры оптимизации функции с помощью программы FlexTool
- 4.10. Эволюционные алгоритмы
- 4.11. Приложения эволюционных алгоритмов
- 4.11.1. Примеры оптимизации функции с помощью программы Evolver
- 4.11.2. Решение комбинаторных задач с помощью программы Evolver
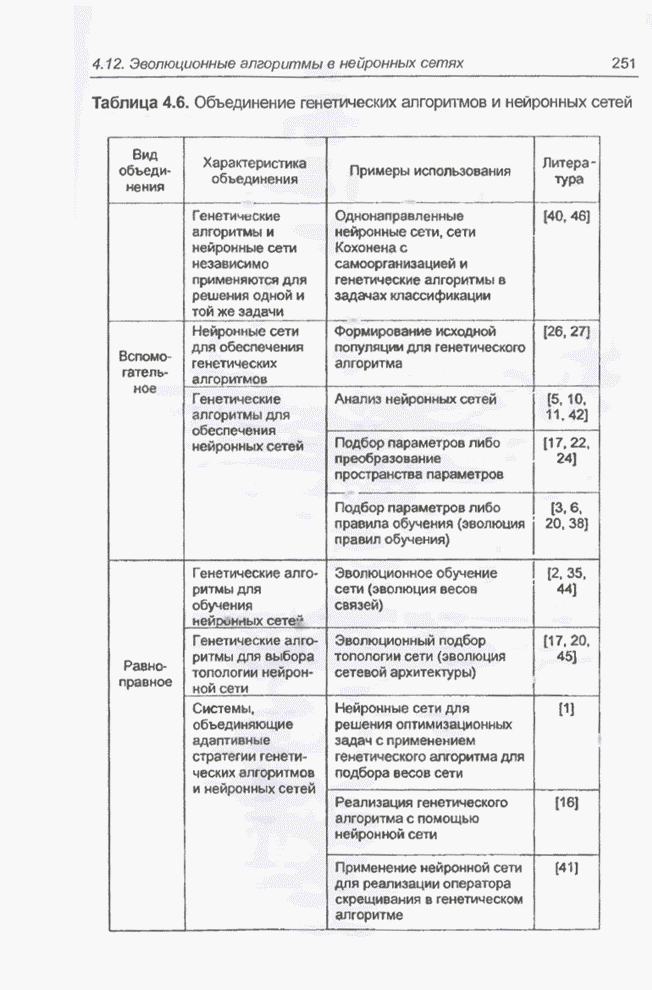
- 4.12. Эволюционные алгоритмы в нейронных сетях
- 4.12.1. Независимое применение генетических алгоритмов и нейронных сетей
- 4.12.2. Нейронные сети для поддержки генетических алгоритмов
- 4.12.3. Генетические алгоритмы для поддержки нейронных сетей
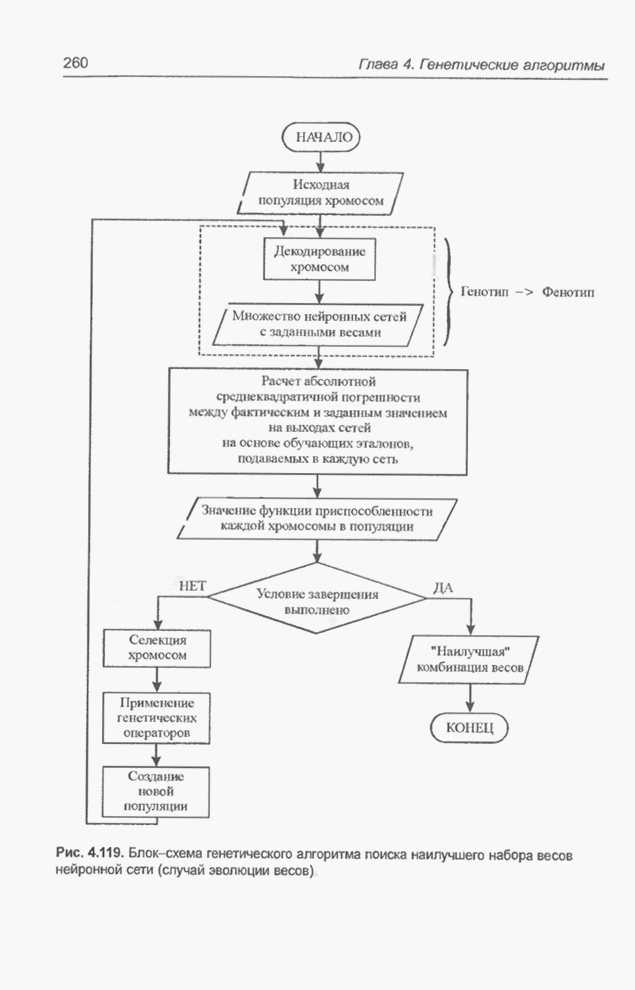
- 4.12.4. Применение генетических алгоритмов для обучения нейронных сетей
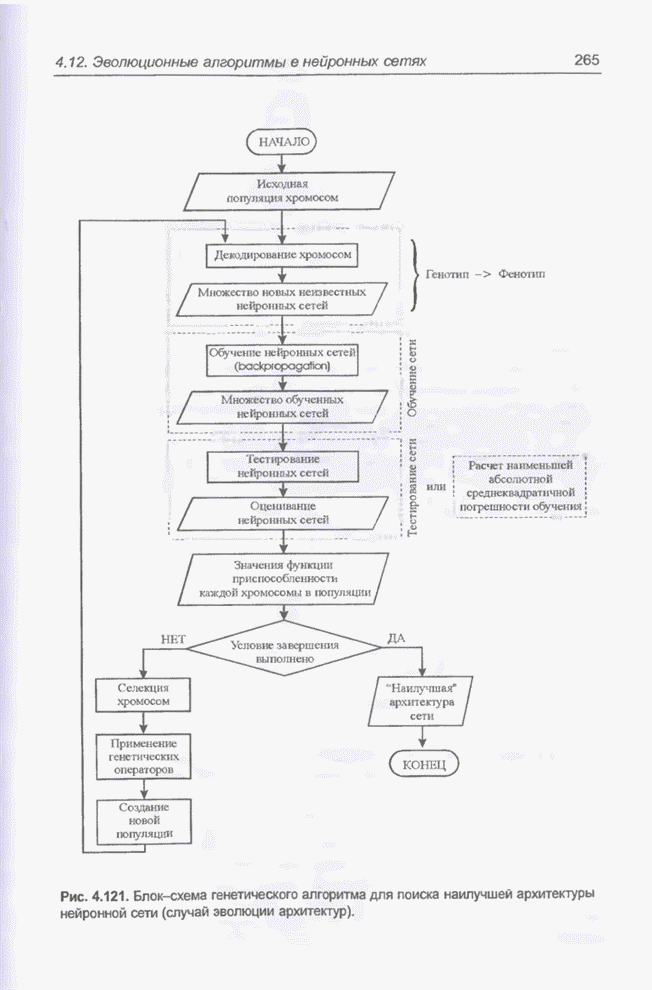
- 4.12.5. Генетические алгоритмы для выбора топологии нейронных сетей
- 4.12.6. Адаптивные взаимодействующие системы
- 4.12.7. Типовой цикл эволюции
- 4.12.7.1. Эволюция весов связей
- 4.12.7.2. Эволюция архитектуры сети
- 4.12.7.3. Эволюция правил обучения
- 4.13. Примеры моделирования эволюционных алгоритмов в приложении к нейронным сетям
- 4.13.1. Программы Evolver и BrainMaker
- 4.13.2. Программа GTO
- Список литературы
- ГЛАВА 5. МОДУЛИ НЕЧЕТКО-НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.1. Модуль нечеткого управления со структурой, определенной в процессе дефуззификации
- 5.1.2. Конструкция модуля
- 5.1.3. Структура модуля
- 5.1.4. Использование алгоритма обратного распространения ошибки
- 5.1.5. Модификации модуля
- 5.1.6. Применение модуля нечеткого управления для прогнозирования случайных временных рядов
- 5.1.7. Применение модуля нечеткого управления для решения задачи парковки грузовика
- 5.1.8. Примечание
- 5.2. Представление модуля нечеткого управления в виде стандартной нейронной сети
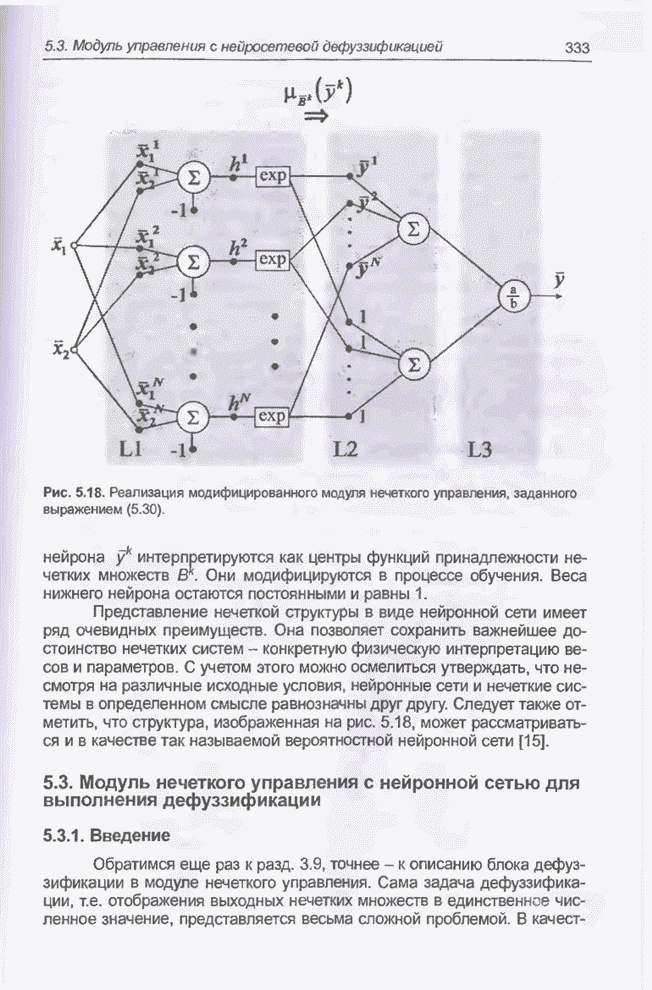
- 5.3. Модуль нечеткого управления с нейронной сетью для выполнения дефуззификации
- 5.3.1. Введение
- 5.3.2. Конструкция модуля
- 5.3.3. Структура модуля
- 5.3.4. Алгоритмы обучения модуля
- 5.3.5. Решение задачи стабилизации перевернутого маятника
- 5.3.6. Примечание
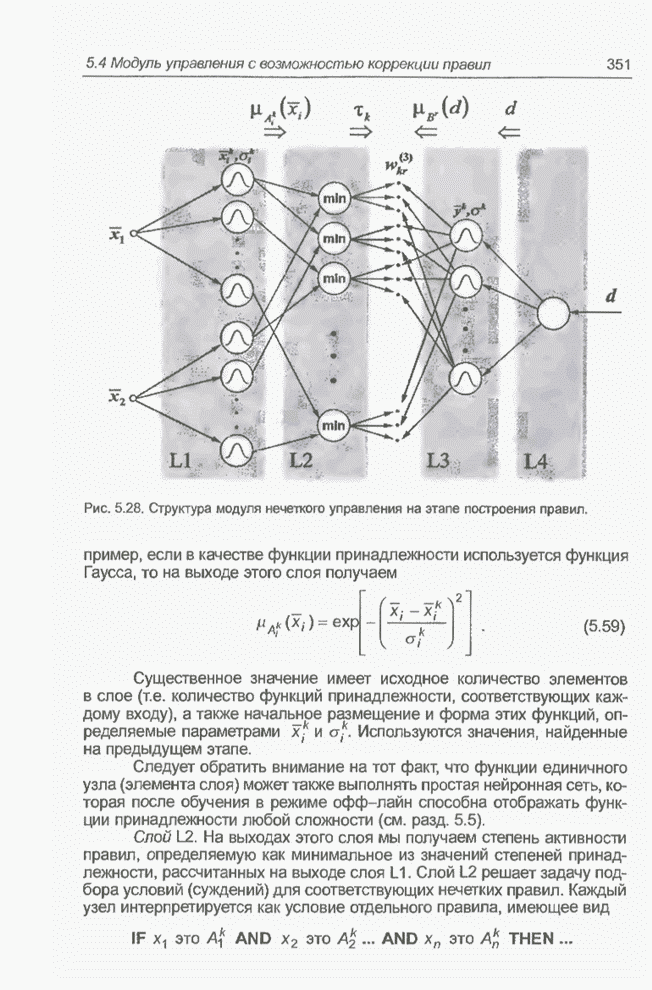
- 5.4. Модуль нечеткого управления с возможностью коррекции правил
- 5.4.1. Введение
- 5.4.2. Фаза обучения на основе самоорганизации
- 5.4.3. Фаза обучения с учителем
- 5.4.4. Примечание
- 5.5. Модуль нечеткого управления типа Такаги-Сугено
- 5.5.1. Введение
- 5.5.2. Нейронная реализация функции принадлежности
- 5.5.3. Модули Такаги-Сугено
- 5.5.4. Реализация условий
- 5.5.5. Реализация заключений
- 5.5.6. Примечание
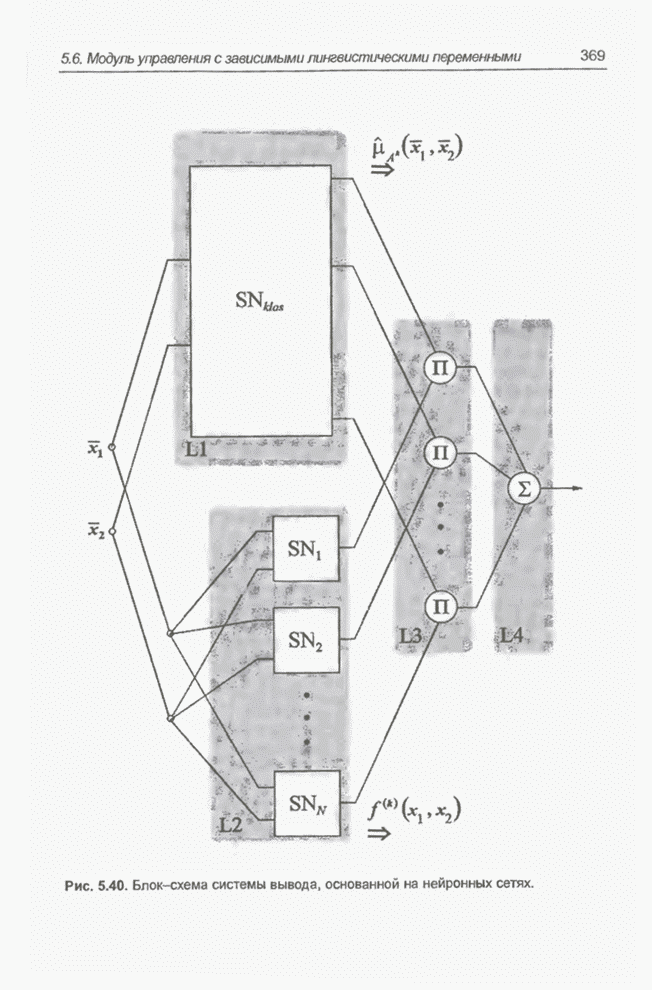
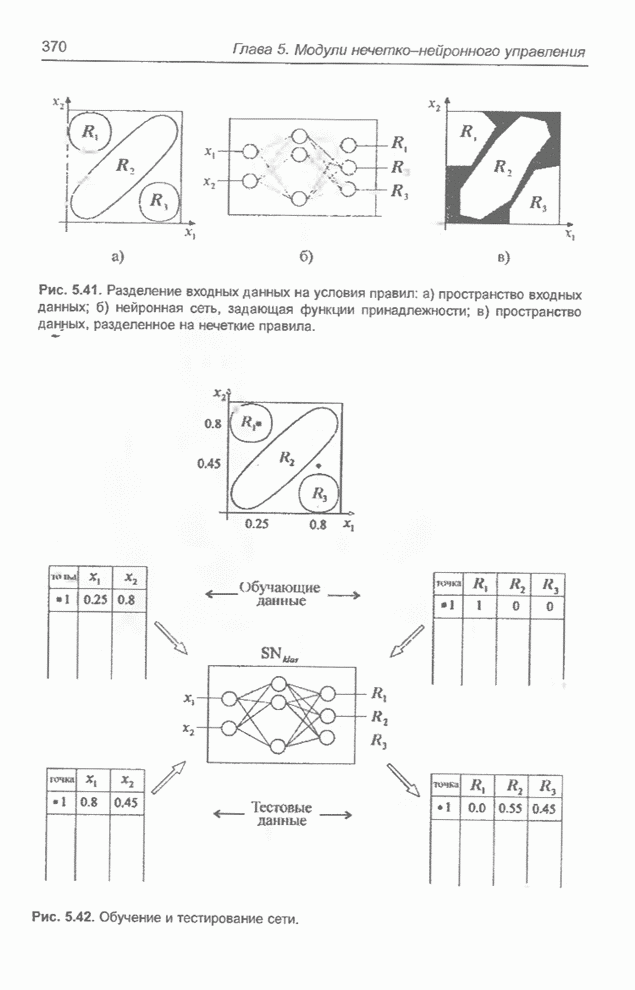
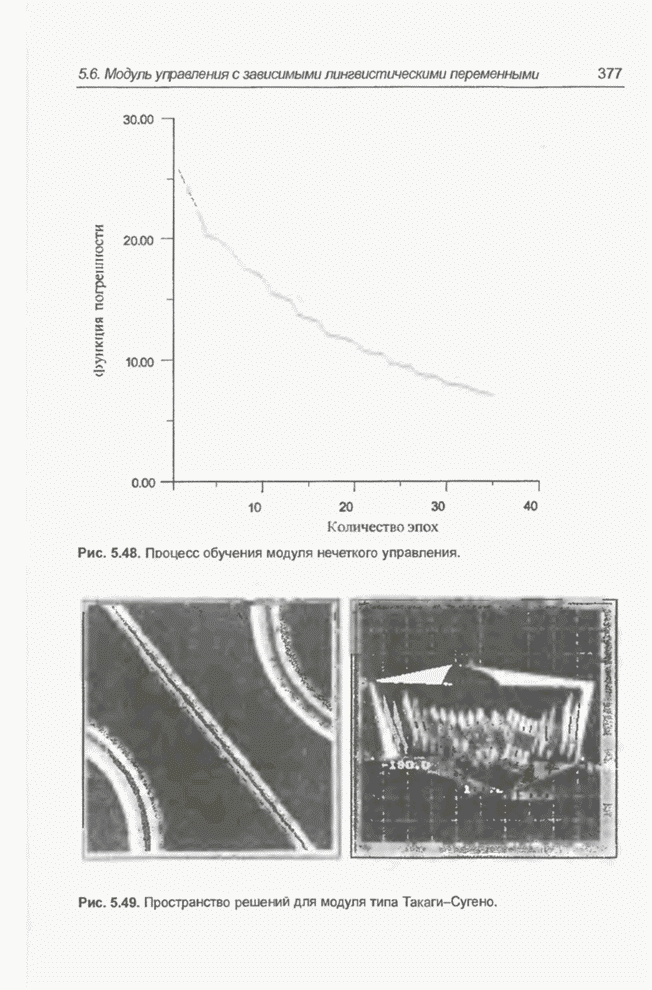
- 5.6. Модуль нечеткого управления типа Такаги-Сугено: случай зависимых лингвистических переменных
- 5.6.1. Введение
- 5.6.2. Нейронные сети для нечеткого вывода
- 5.6.3. Структура системы
- 5.6.4. Способ обучения
- 5.6.5. Решение задачи парковки грузовика
- 5.6.6. Примечание
- Список литературы