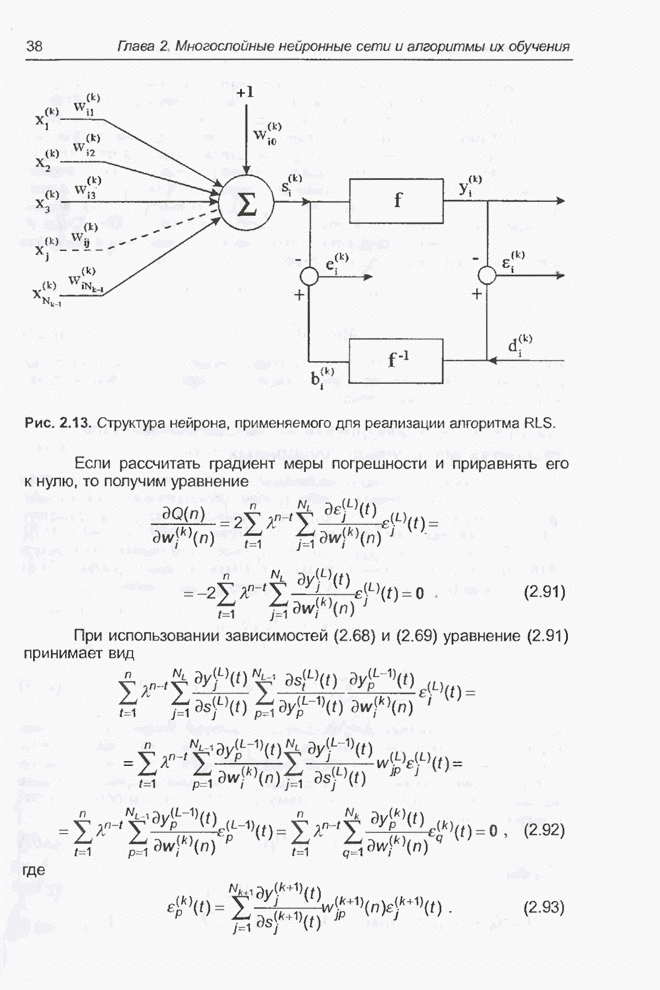
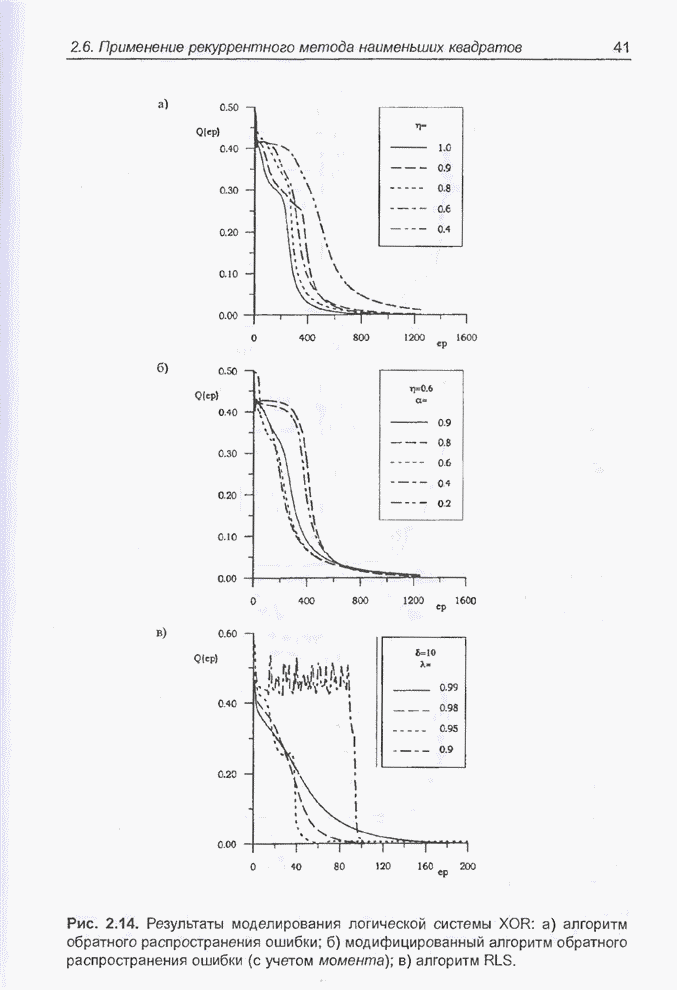
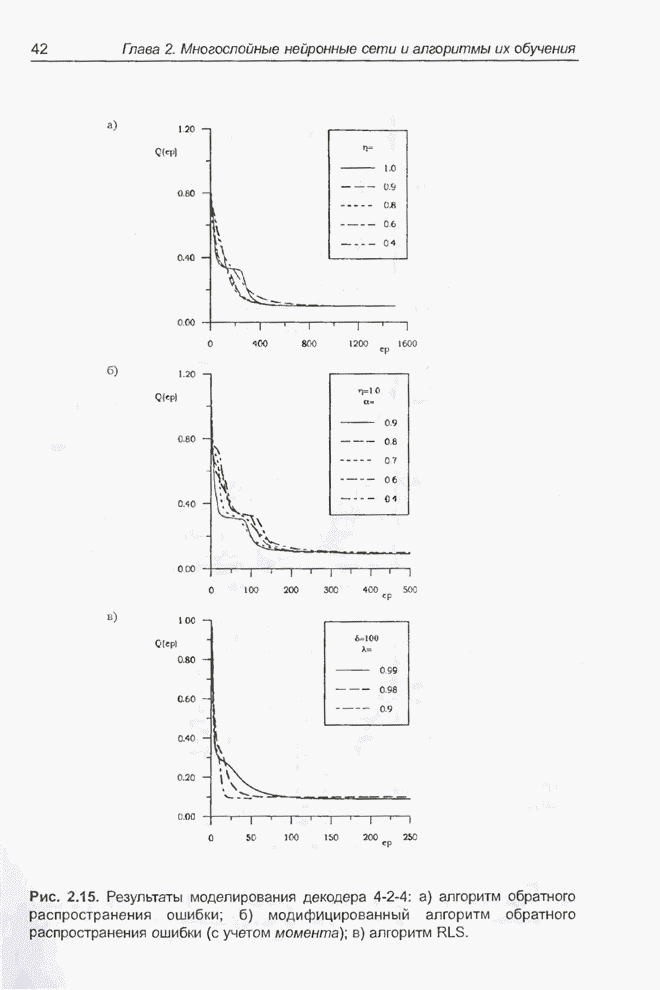
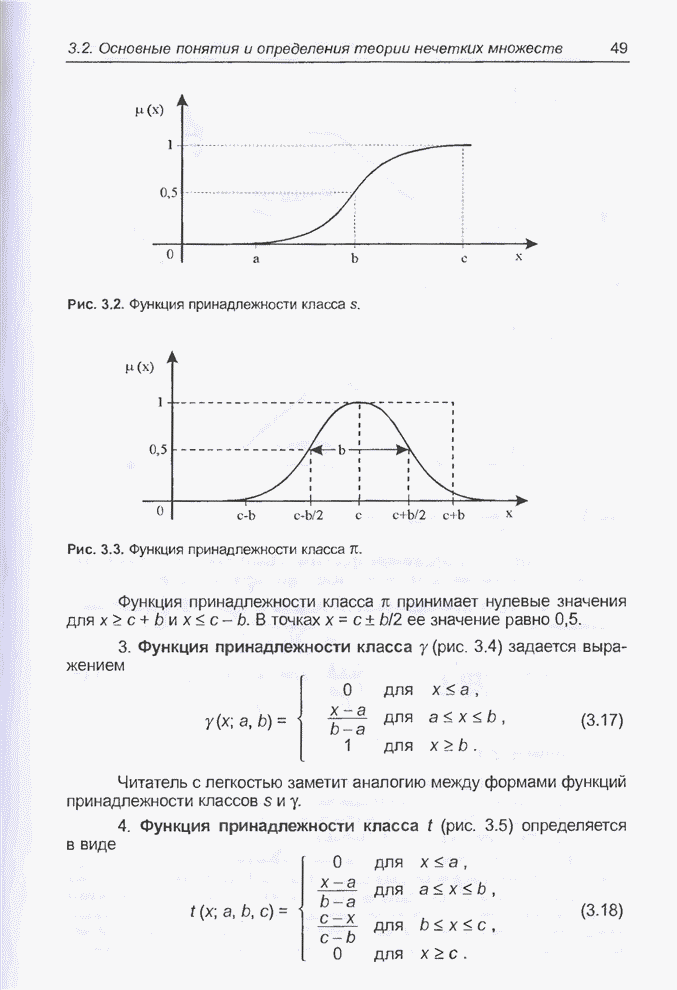
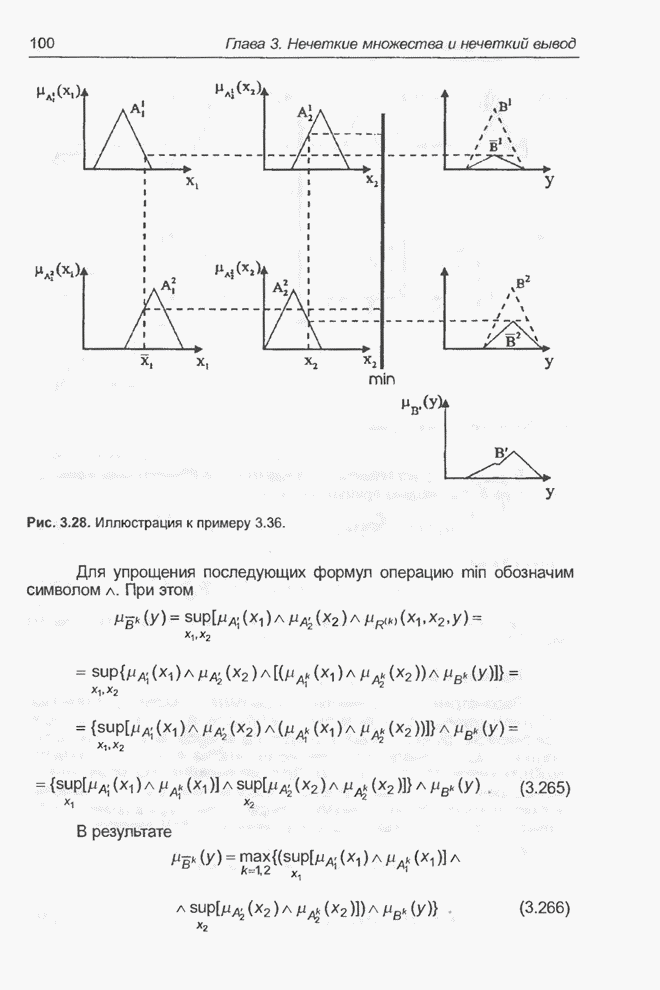
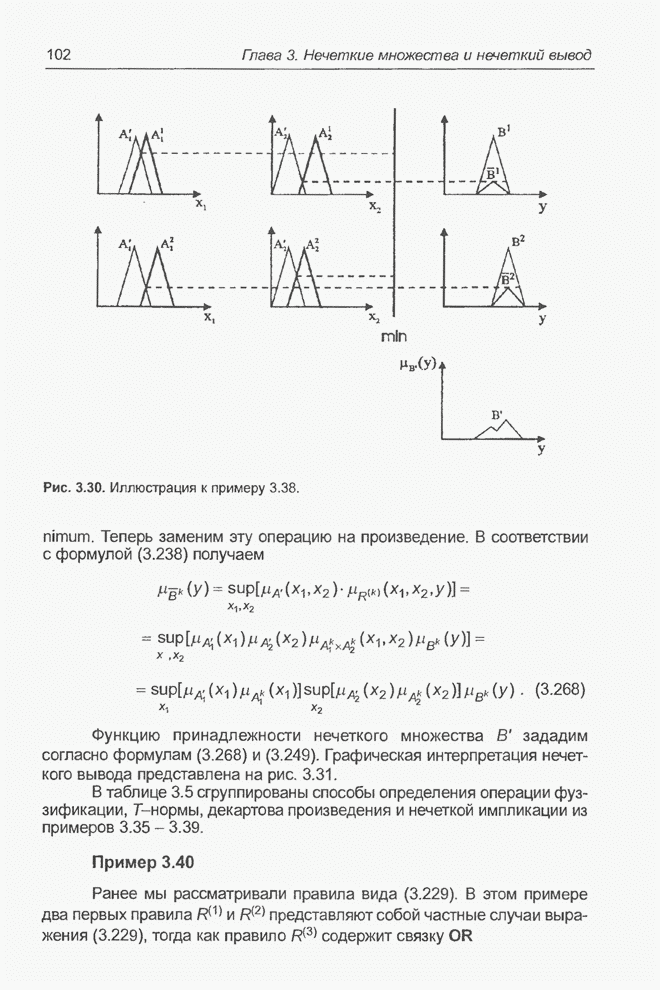
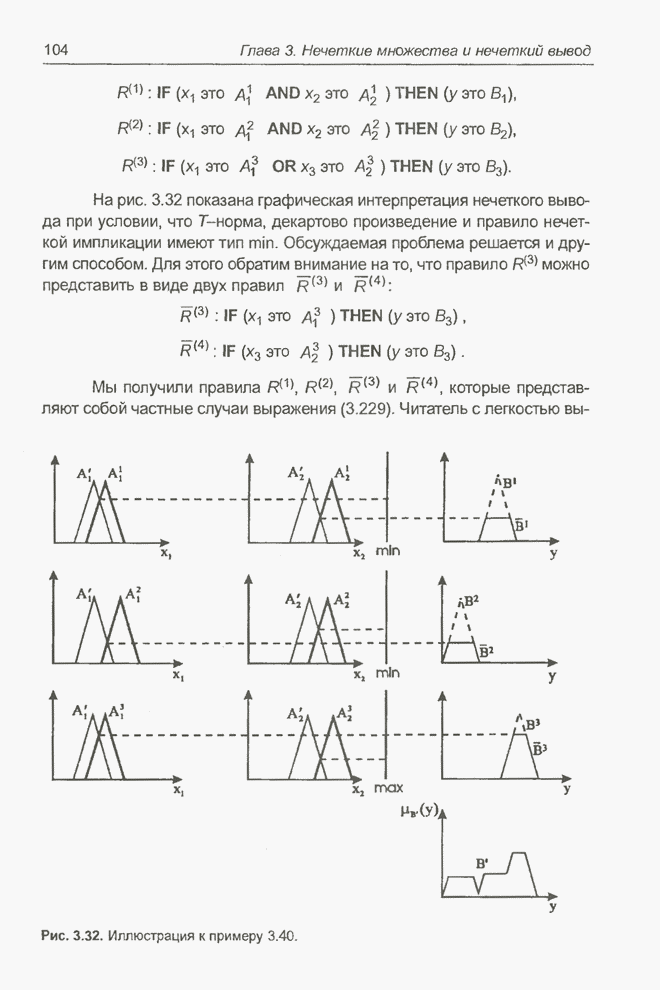
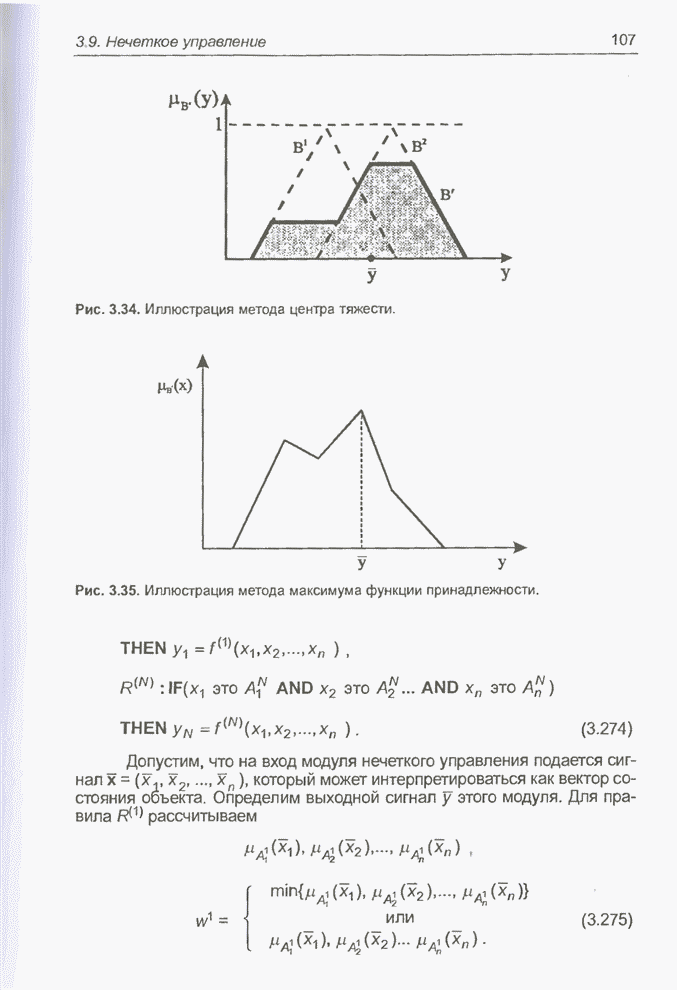
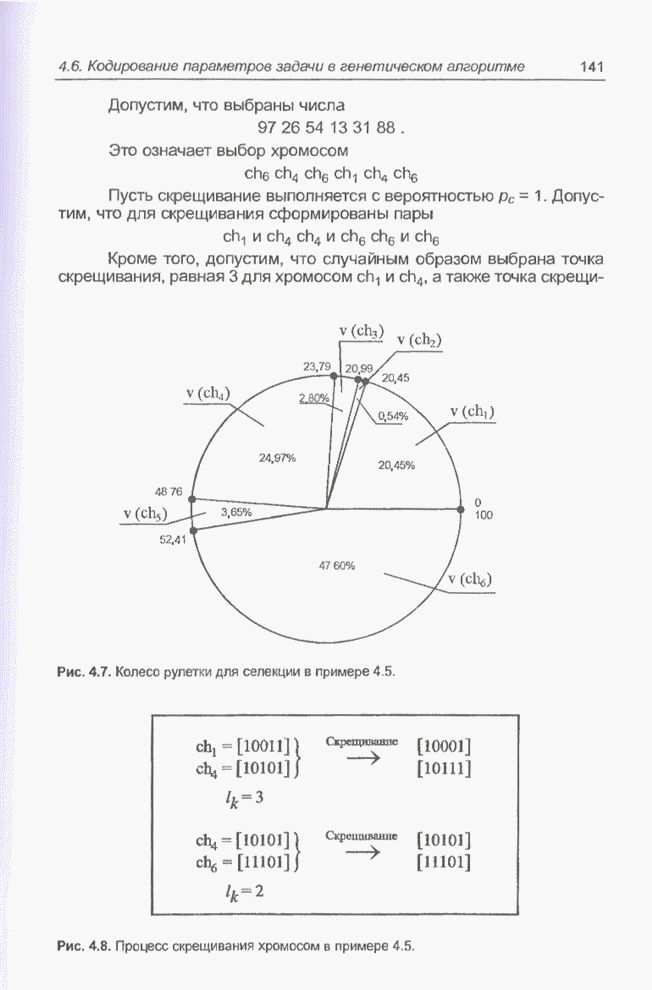
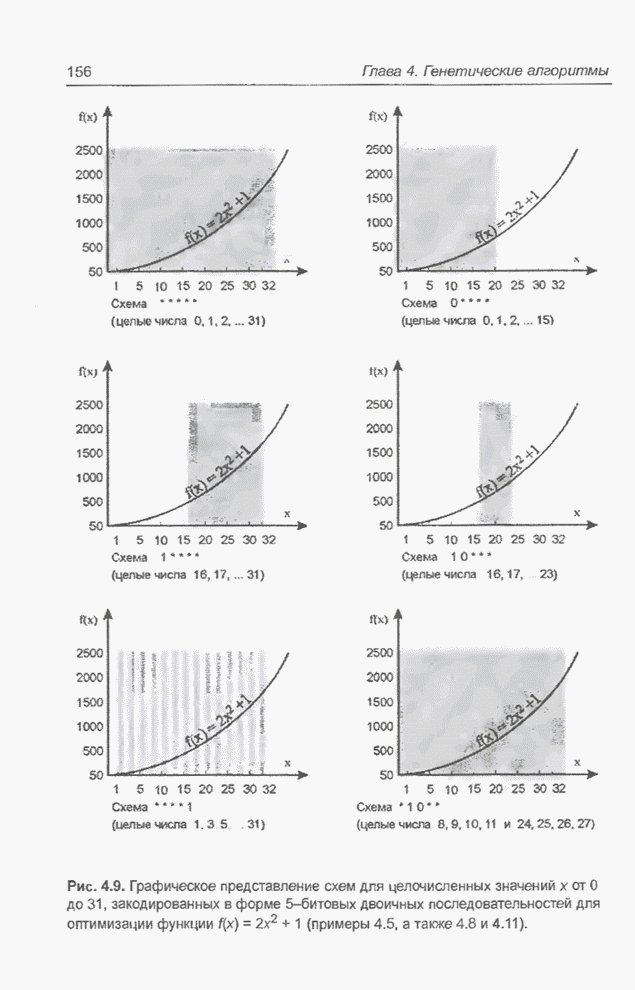
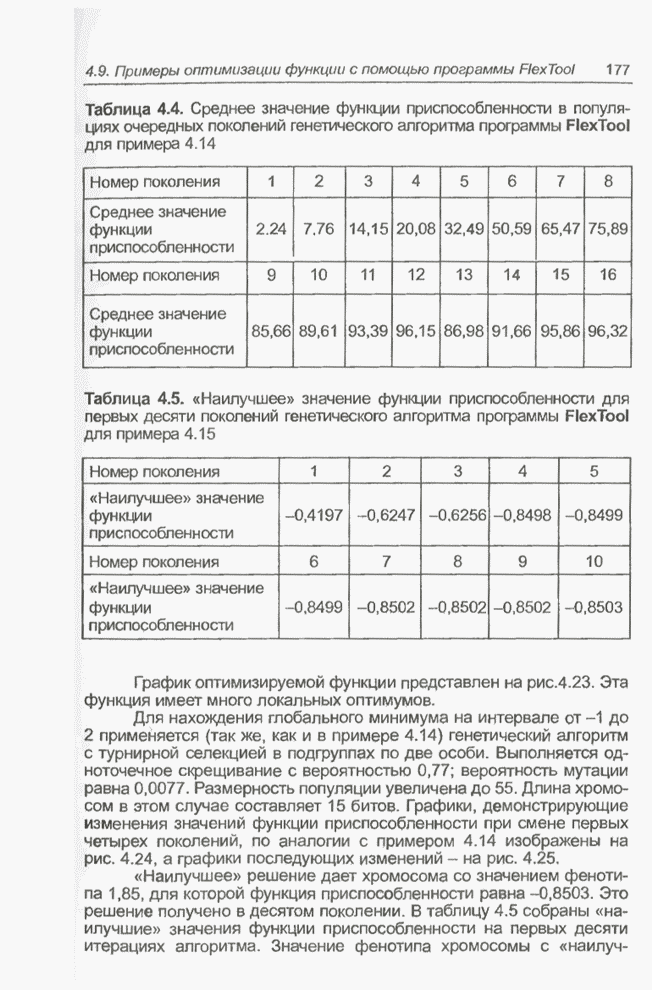
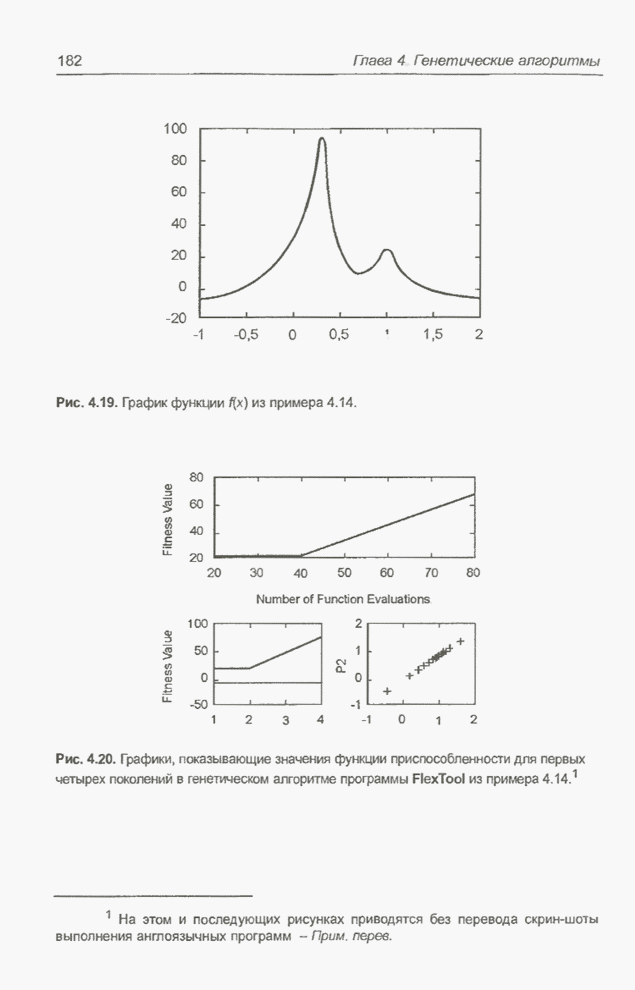
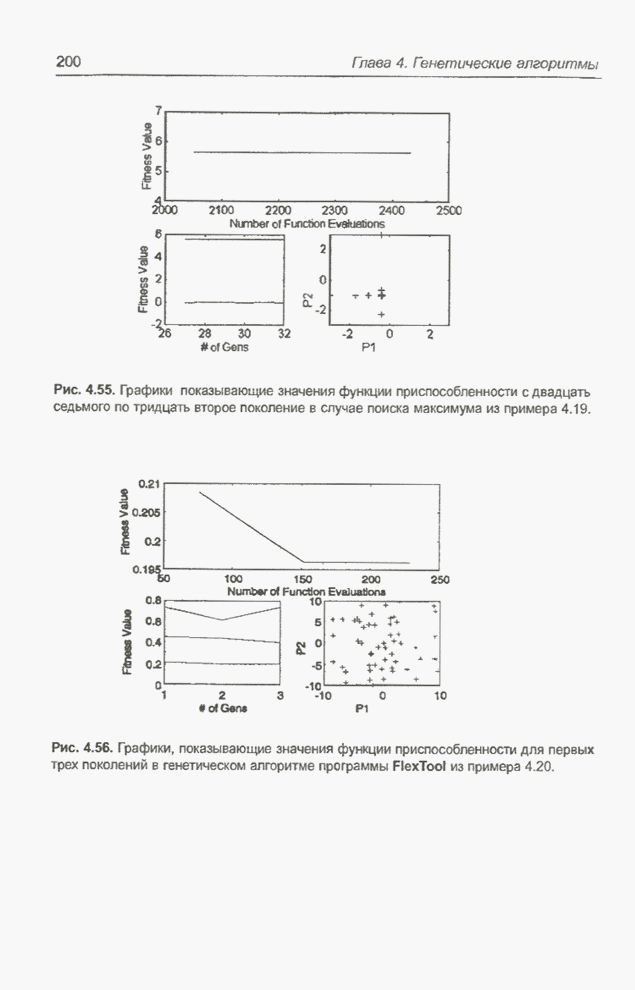
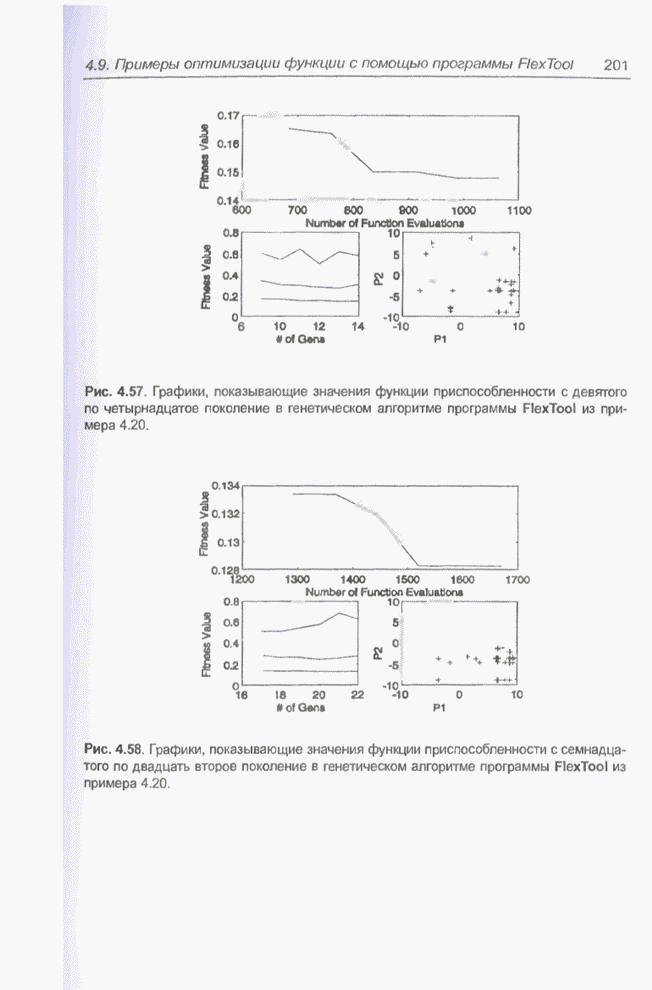
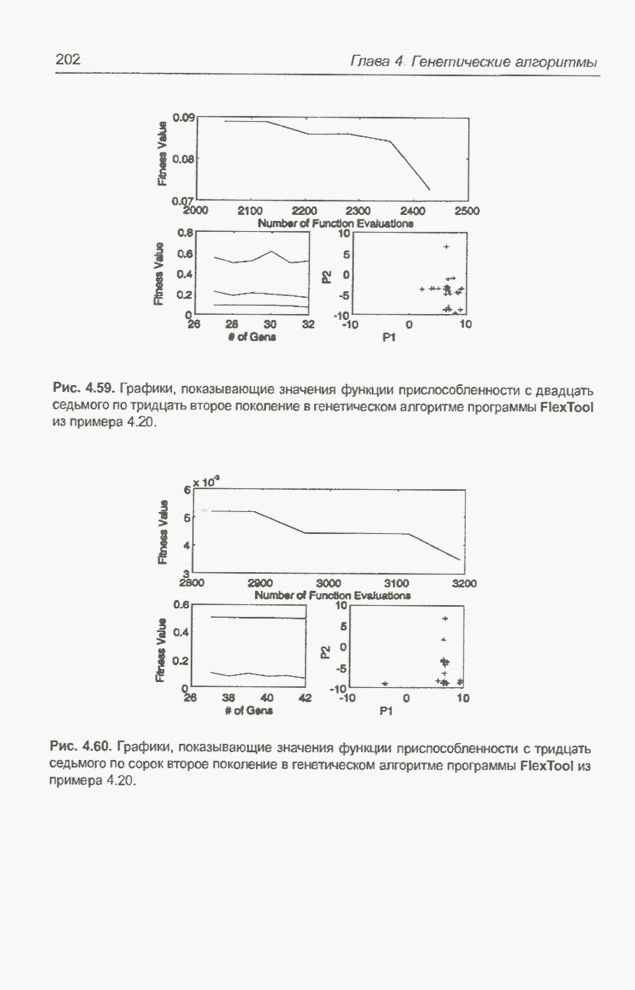
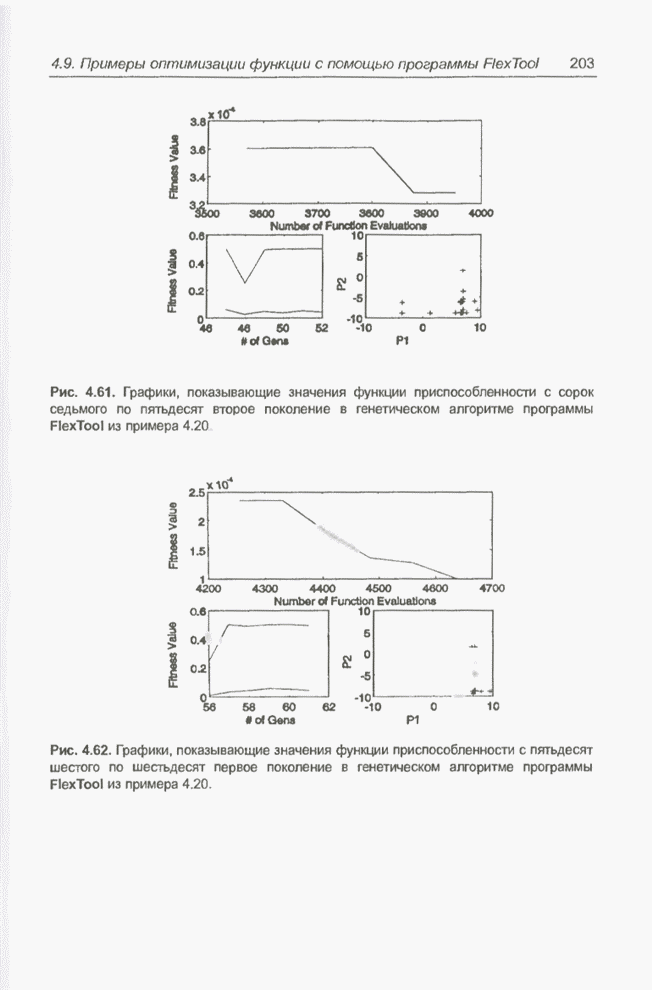
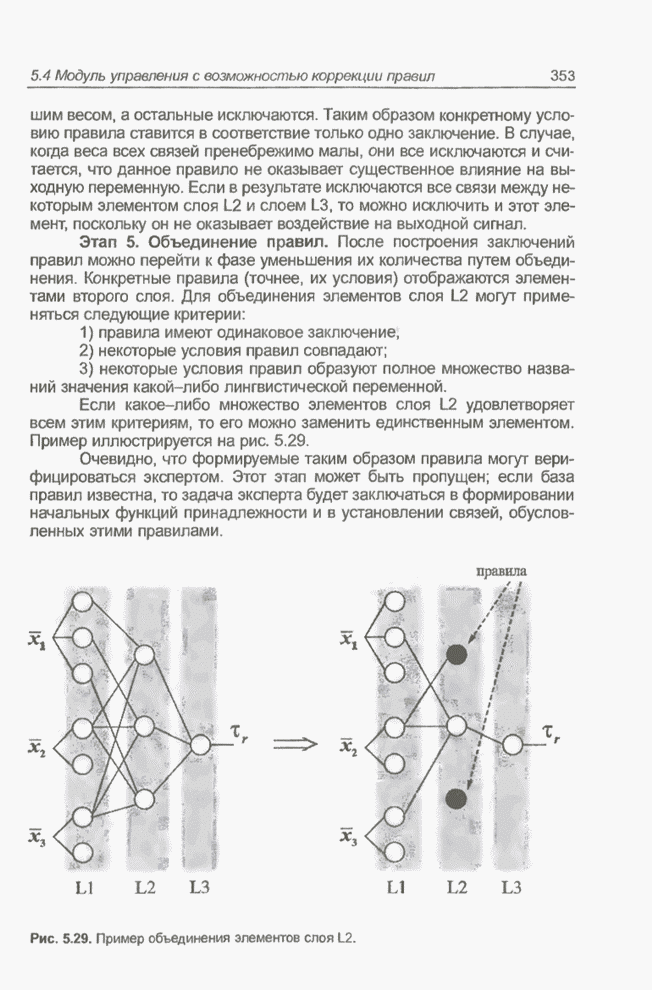
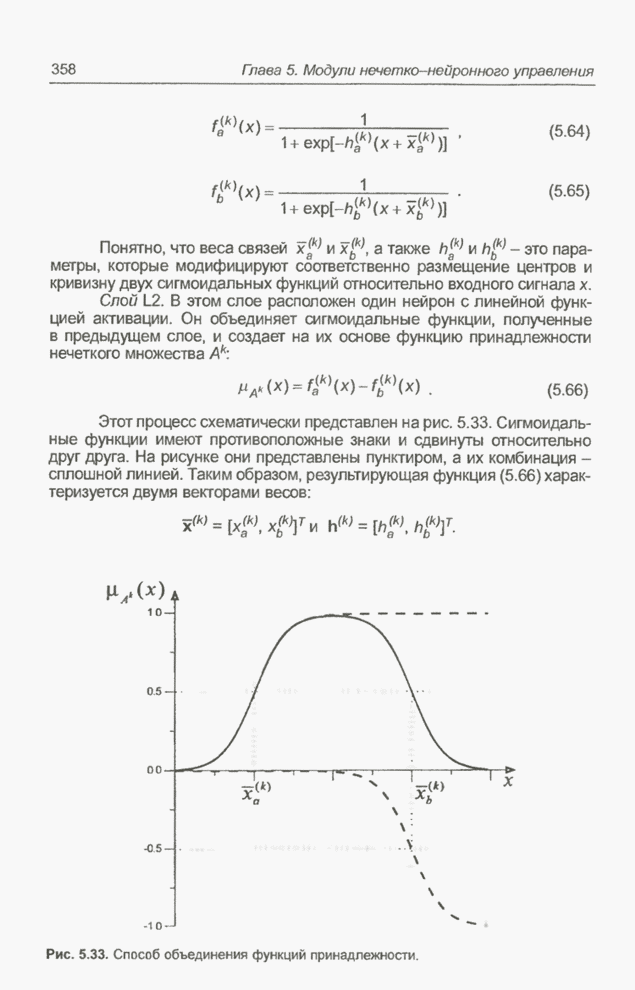
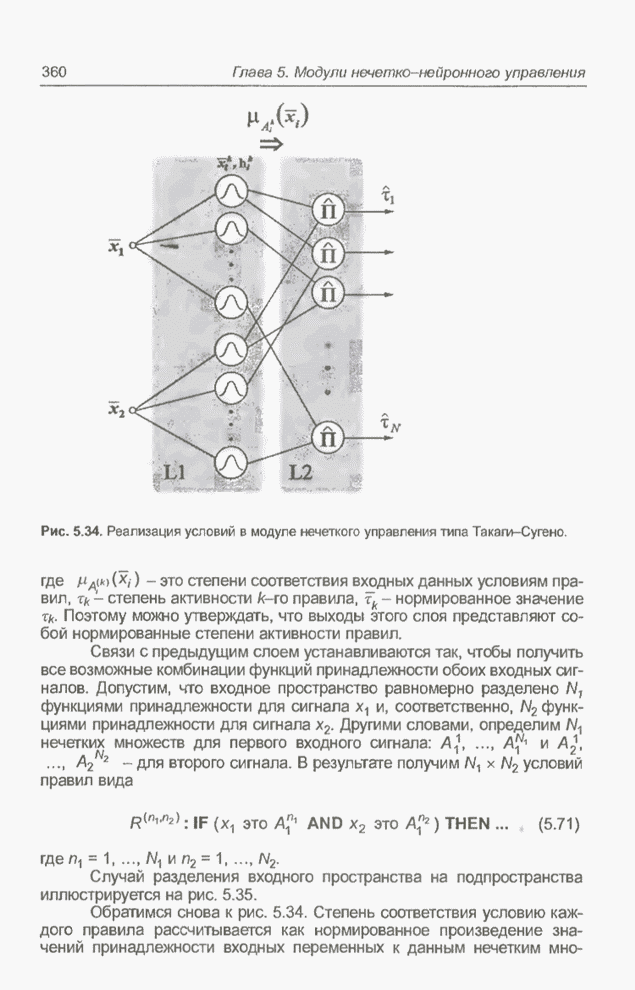
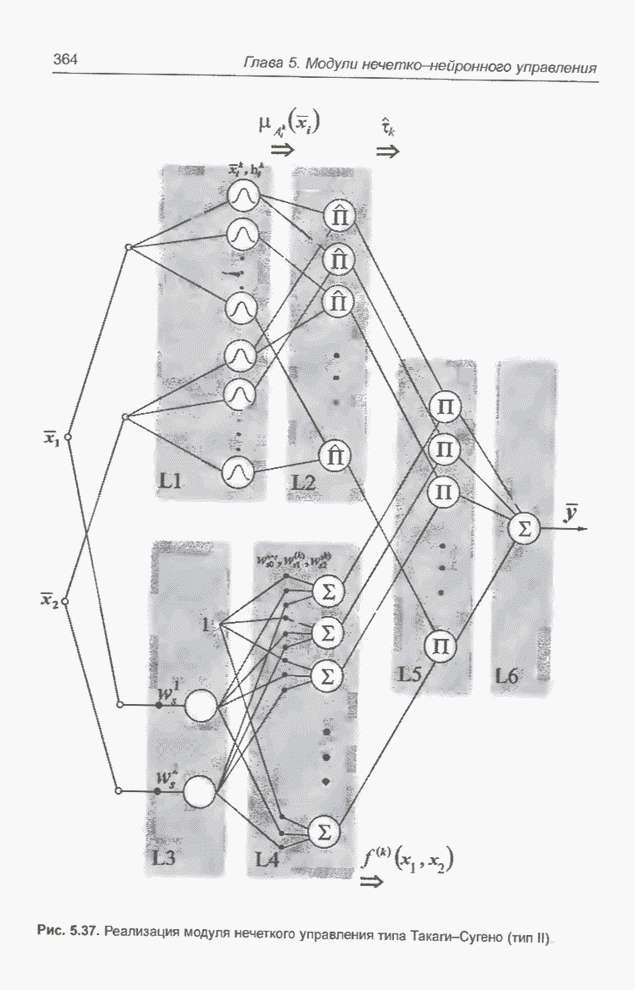
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
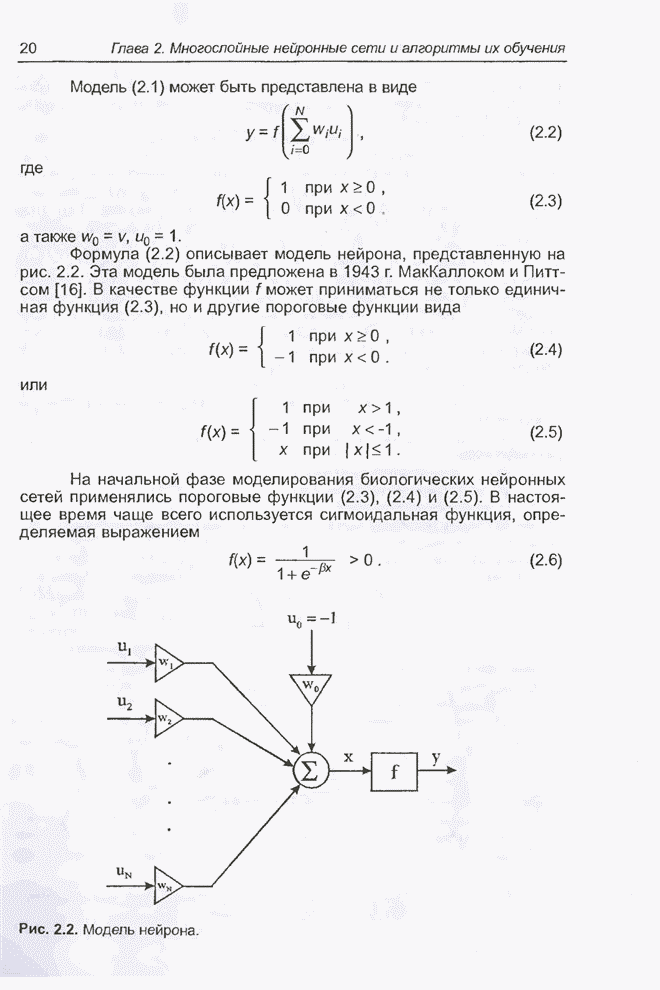
5.2. Представление модуля нечеткого управления в виде стандартной нейронной сети
Покажем теперь, что модуль нечеткого управления, описанный в разд. 5.1, можно представить в виде стандартной нейронной сети.
С учетом формул (5.10) и (5.12)
преобразуем выражение (5.7), описывающее функцию принадлежности нечеткого
множества ![]() ,
к форме
,
к форме
 . (5.23)
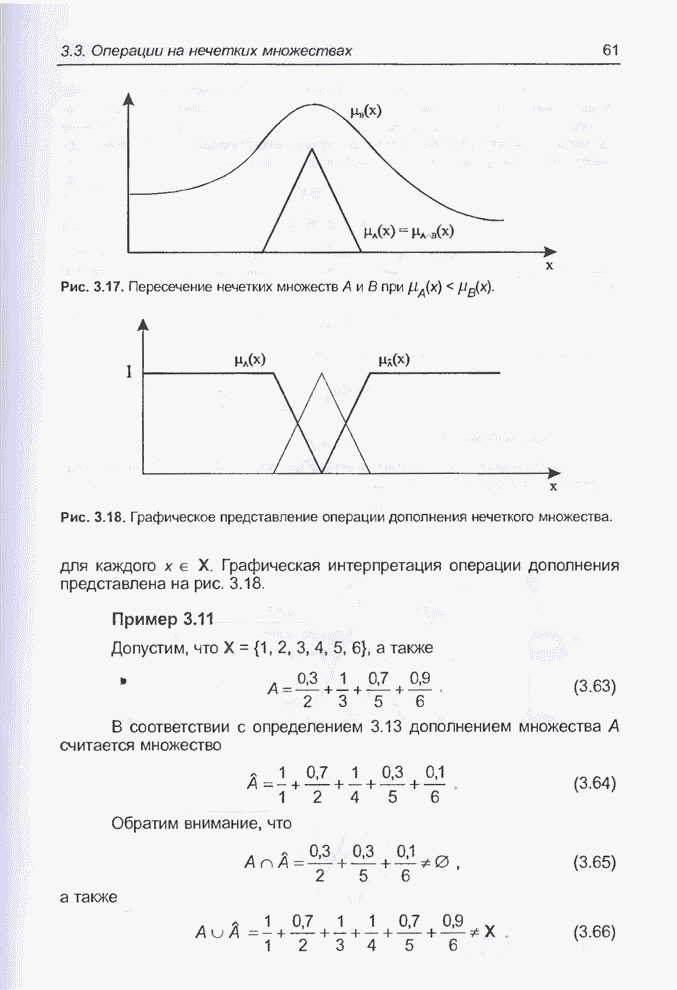
. (5.23)
При подстановке базовой зависимости

в выражение (5.23) получим
 . (5.24)
. (5.24)
Для упрощения будем считать, что
ширина функции Гаусса остается постоянной для любого ![]() , т.е.
, т.е. ![]() . Следовательно, можно записать
. Следовательно, можно записать
 . (5.25)
. (5.25)
Продолжим преобразования:
 . (5.26)
. (5.26)
Для упрощения приведенного
уравнения можно нормализовать векторы ![]() и
и ![]() , т.е. допустить, что их длина равна 1:
, т.е. допустить, что их длина равна 1:
 и
и  . (5.27)
. (5.27)
В этом случае зависимость (5.27) можно преобразовать к виду
 . (5.28)
. (5.28)
В итоге
 ,
где
,
где  . (5.29)
. (5.29)
При подстановке приведенного выражения в формулу, описывающую операцию дефуззификации (5.8), получим
 . (5.30)
. (5.30)
Полученное решение представляет
собой модификацию уравнения (5.13). Следует подчеркнуть тот факт, что его вывод
обусловлен нормализацией векторов ![]() и
и ![]() , а также что параметр
, а также что параметр ![]() имеет постоянное
значение для любого
имеет постоянное
значение для любого ![]() .
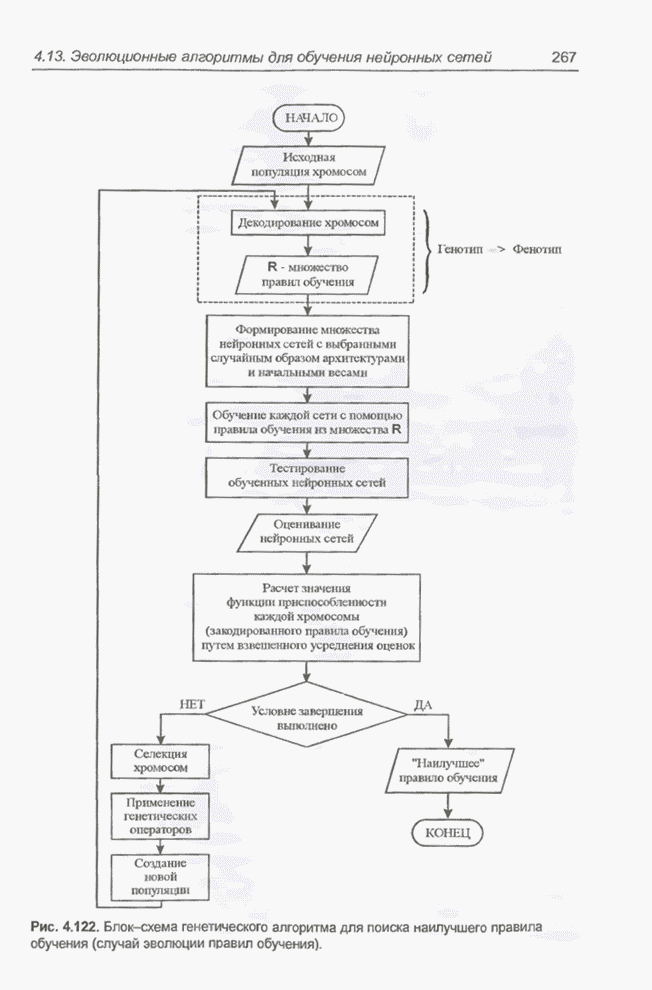
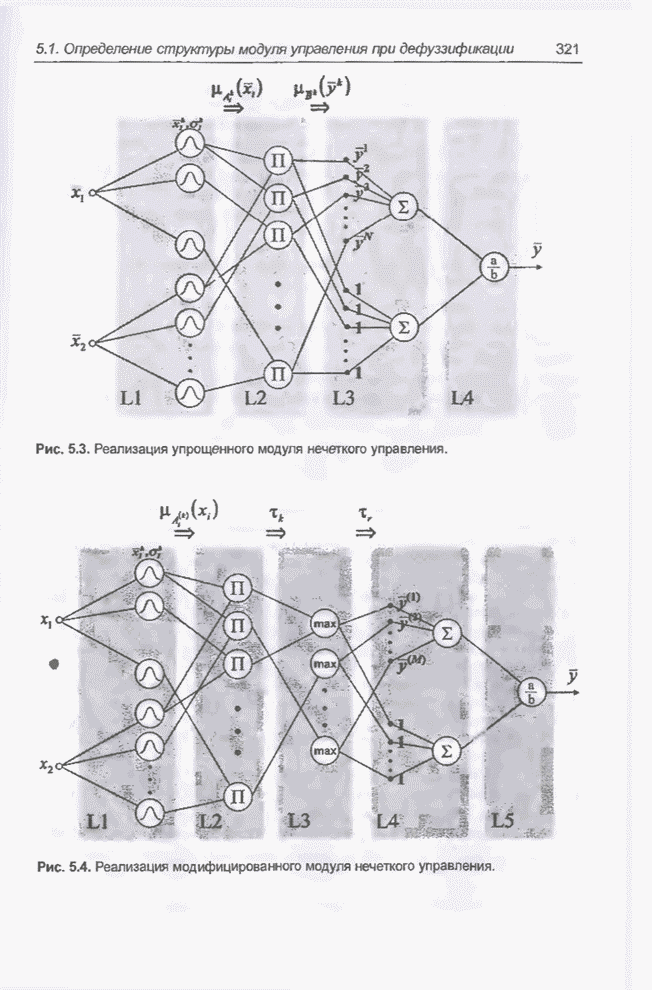
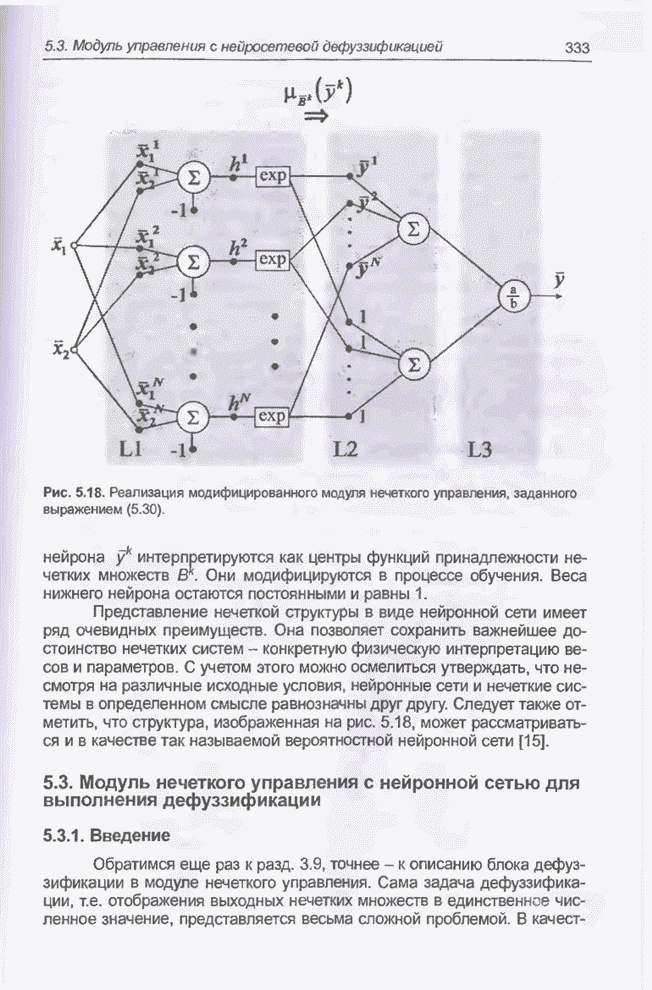
Новый подход требует формирования новой структуры. Она показана на рис. 5.18. С
учетом принятых допущений практическая реализация этой структуры вызывает
большие сомнения, однако она демонстрирует принципиальную возможность
представления нечеткой системы в виде нейронной сети. В такой сети выделяются
три слоя.
.
Новый подход требует формирования новой структуры. Она показана на рис. 5.18. С
учетом принятых допущений практическая реализация этой структуры вызывает
большие сомнения, однако она демонстрирует принципиальную возможность
представления нечеткой системы в виде нейронной сети. В такой сети выделяются
три слоя.

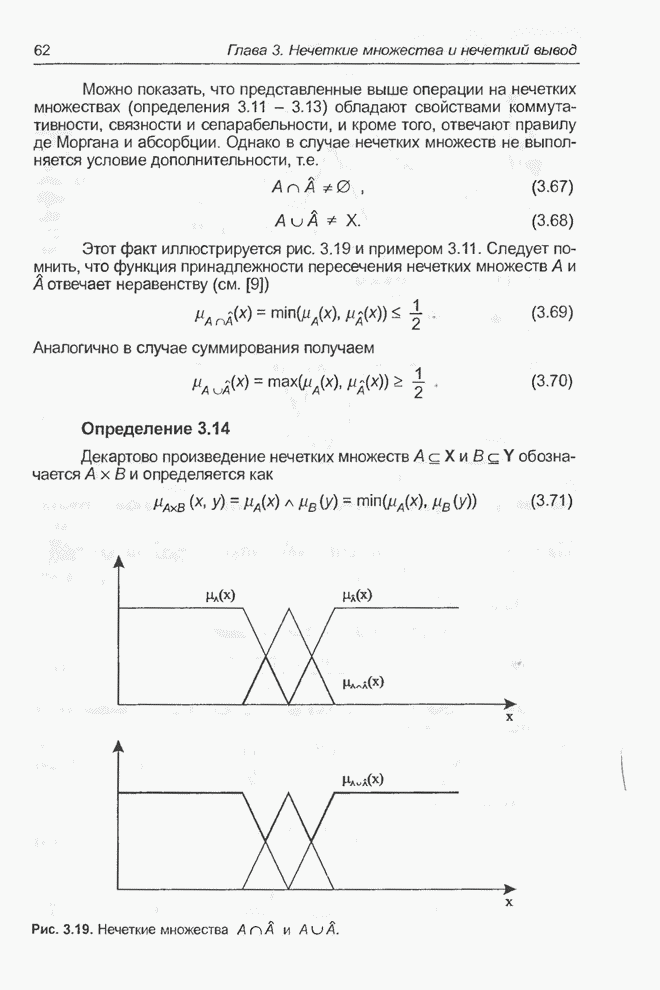
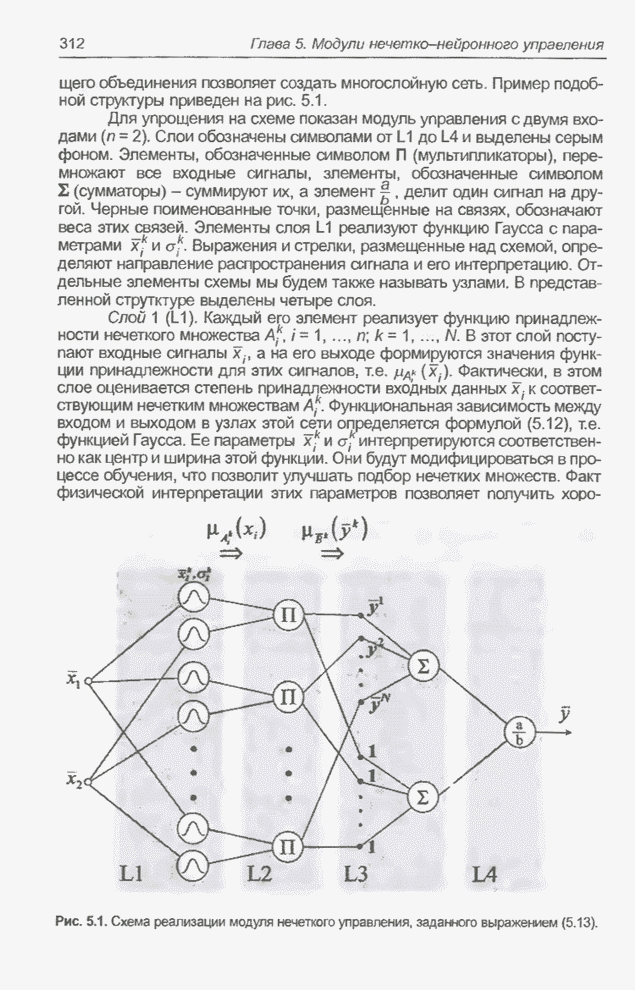
Рис. 5.18. Реализация модифицированного модуля нечеткого управления, заданного выражением (5.30).
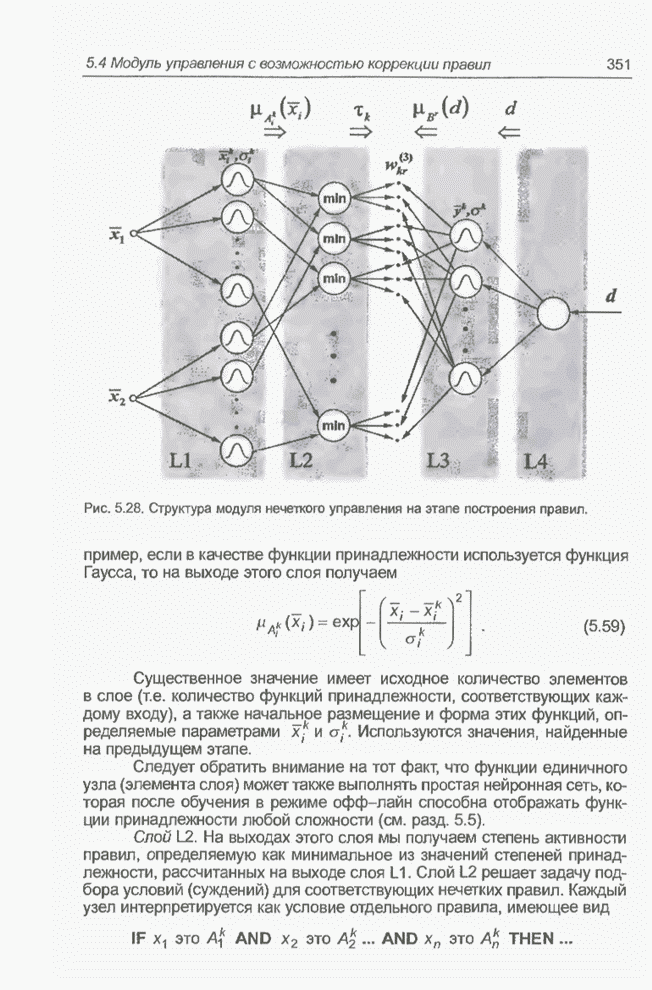
Слой 1 (L1). Первый слой возник в результате объединения и
модификации первого и второго слоев эталонной структуры (рис. 5.1). В качестве
элементов этого слоя выступают классические нейроны с взвешенной суммой входов,
поляризацией постоянным числом (bias) и экспоненциальной функцией активации с
параметром ![]() .
В отличие от «обычных» нейронных сетей, как веса, так и параметры этого слоя
имеют конкретную интерпретацию:
.
В отличие от «обычных» нейронных сетей, как веса, так и параметры этого слоя
имеют конкретную интерпретацию: ![]() представляет центр функции
принадлежности нечеткого множества, соответствующего
представляет центр функции
принадлежности нечеткого множества, соответствующего ![]() -й входной переменной в
-й входной переменной в ![]() -м правиле, a
-м правиле, a ![]() - ширину этих
функций. Каждый нейрон соответствует одному нечеткому правилу.
- ширину этих
функций. Каждый нейрон соответствует одному нечеткому правилу.
Слои 2 (L2) и 3 (L3). Легко
заметить, что эти слои идентичны слоям L3 и L4 эталонной структуры (рис. 5.1).
Они так же реализуют операцию дефуззификации, определенную выражением (5.8).
Слой L2 состоит из двух нейронов с линейной функцией активации. Веса связей
верхнего нейрона ![]() интерпретируются
как центры функций принадлежности нечетких множеств
интерпретируются
как центры функций принадлежности нечетких множеств ![]() . Они модифицируются в процессе
обучения. Веса нижнего нейрона остаются постоянными и равны 1.
. Они модифицируются в процессе
обучения. Веса нижнего нейрона остаются постоянными и равны 1.
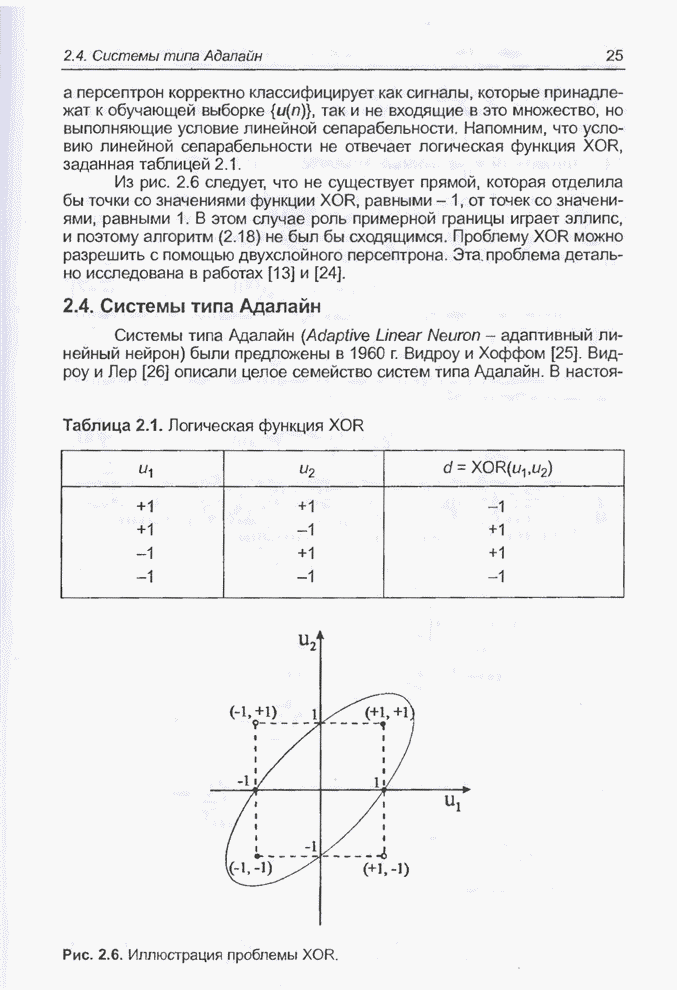
Представление нечеткой структуры в виде нейронной сети имеет ряд очевидных преимуществ. Она позволяет сохранить важнейшее достоинство нечетких систем - конкретную физическую интерпретацию весов и параметров. С учетом этого можно осмелиться утверждать, что, несмотря на различные исходные условия, нейронные сети и нечеткие системы в определенном смысле равнозначны друг другу. Следует также отметить, что структура, изображенная на рис. 5.18, может рассматриваться и в качестве так называемой вероятностной нейронной сети [15].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Предисловие к русскому изданию
- ГЛАВА 1. ВВЕДЕНИЕ
- Список литературы
- ГЛАВА 2. МНОГОСЛОЙНЫЕ НЕЙРОННЫЕ СЕТИ И АЛГОРИТМЫ ИХ ОБУЧЕНИЯ
- 2.1. Введение
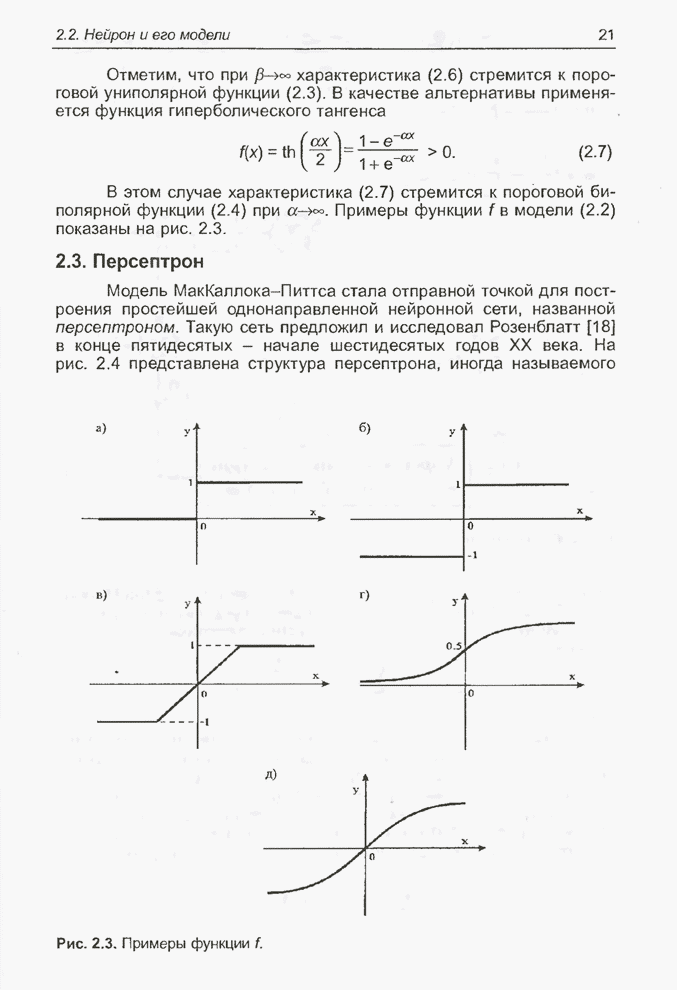
- 2.2. Нейрон и его модели
- 2.3. Персептрон
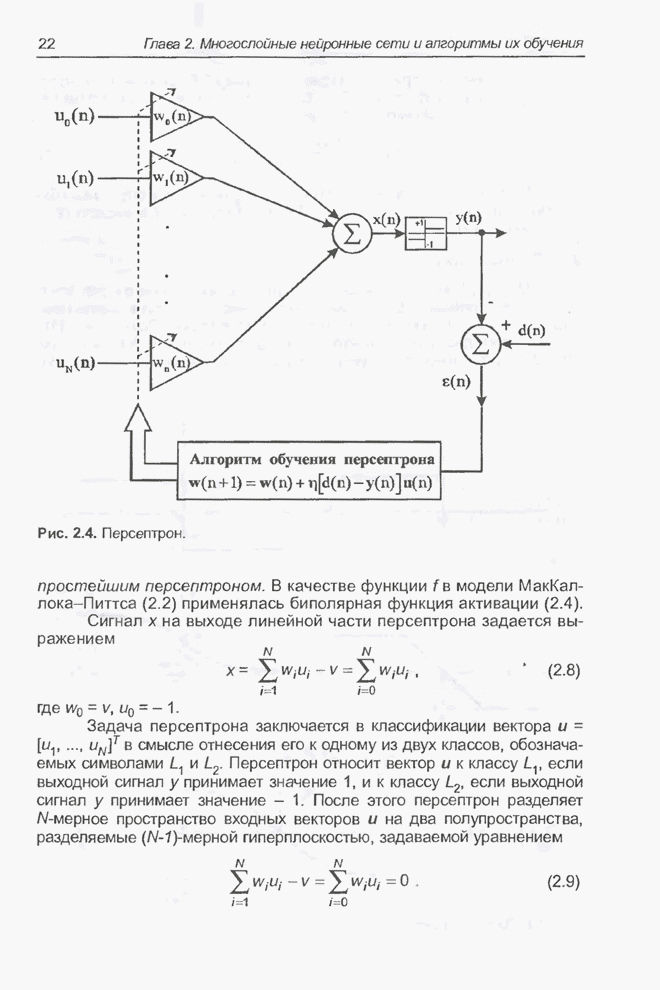
- 2.4. Системы типа Адалайн
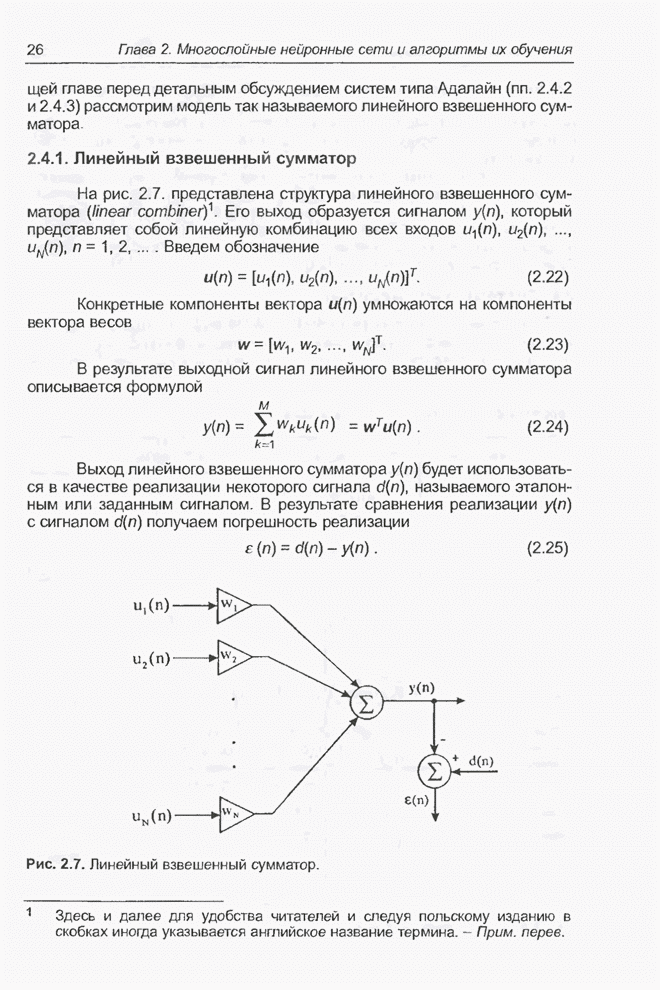
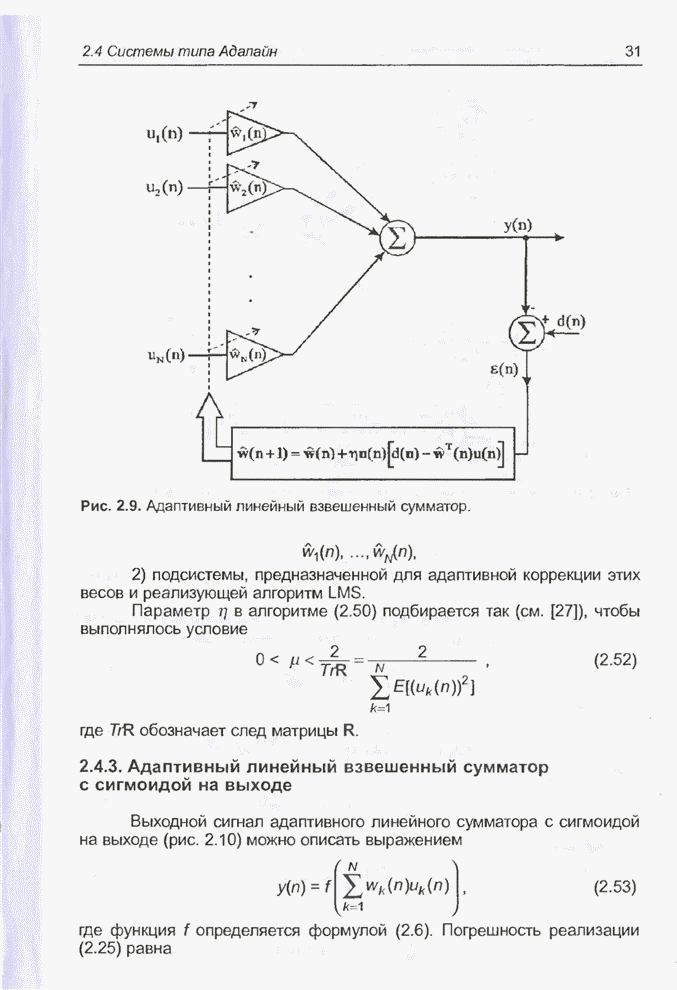
- 2.4.1. Линейный взвешенный сумматор
- 2.4.2. Адаптивный линейный взвешенный сумматор
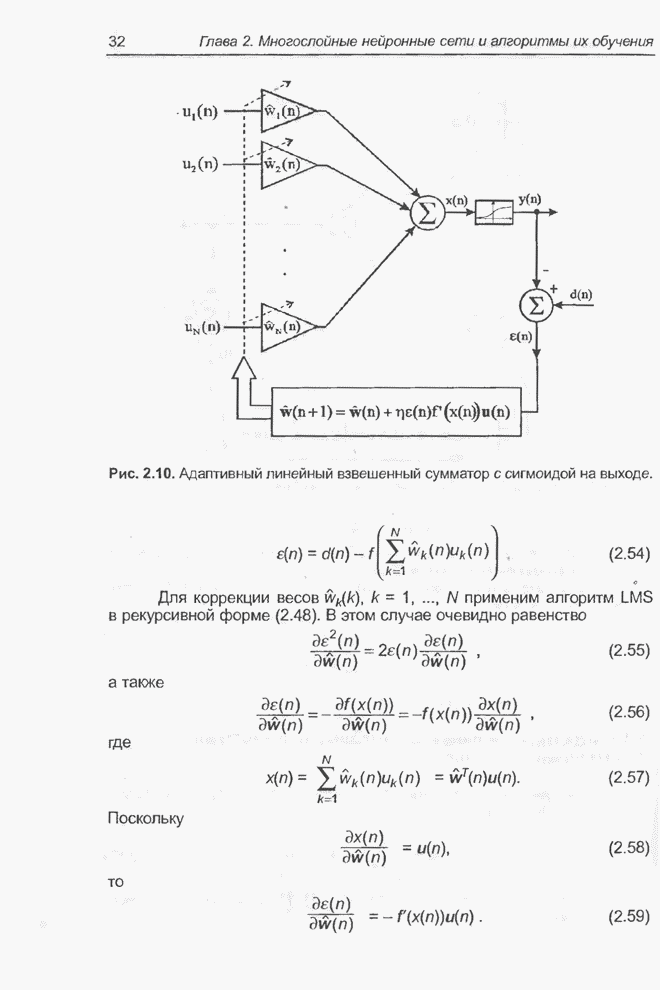
- 2.4.3. Адаптивный линейный взвешенный сумматор с сигмоидой на выходе
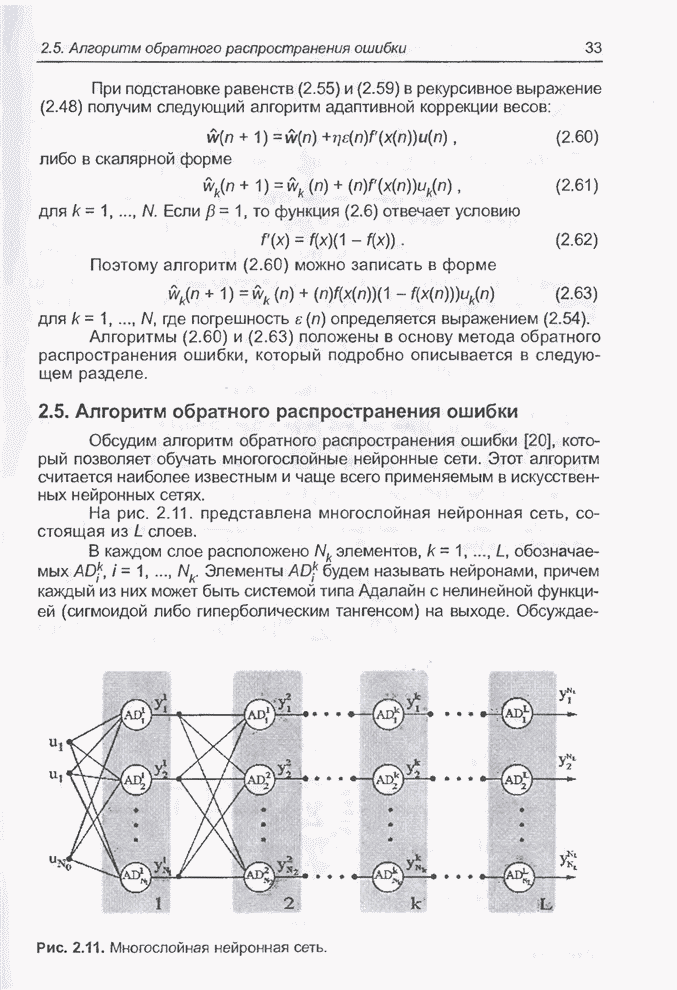
- 2.5. Алгоритм обратного распространения ошибки
- 2.6. Применение рекуррентного метода наименьших квадратов для обучения нейронных сетей
- Список литературы
- ГЛАВA3. НЕЧЕТКИЕ МНОЖЕСТВА И НЕЧЕТКИЙ ВЫВОД
- 3.1. Введение
- 3.2. Основные понятия и определения теории нечетких множеств
- 3.3. Операции на нечетких множествах
- 3.4. Принцип расширения
- 3.5. Нечеткие числа
- 3.6. Треугольные нормы
- 3.7. Нечеткие отношения и их свойства
- 3.8. Нечеткий вывод
- 3.9. Нечеткое управление
- 3.9.1. Классический модуль нечеткого управления
- 3.9.2. Метод нечеткого управления Такаги-Сугено
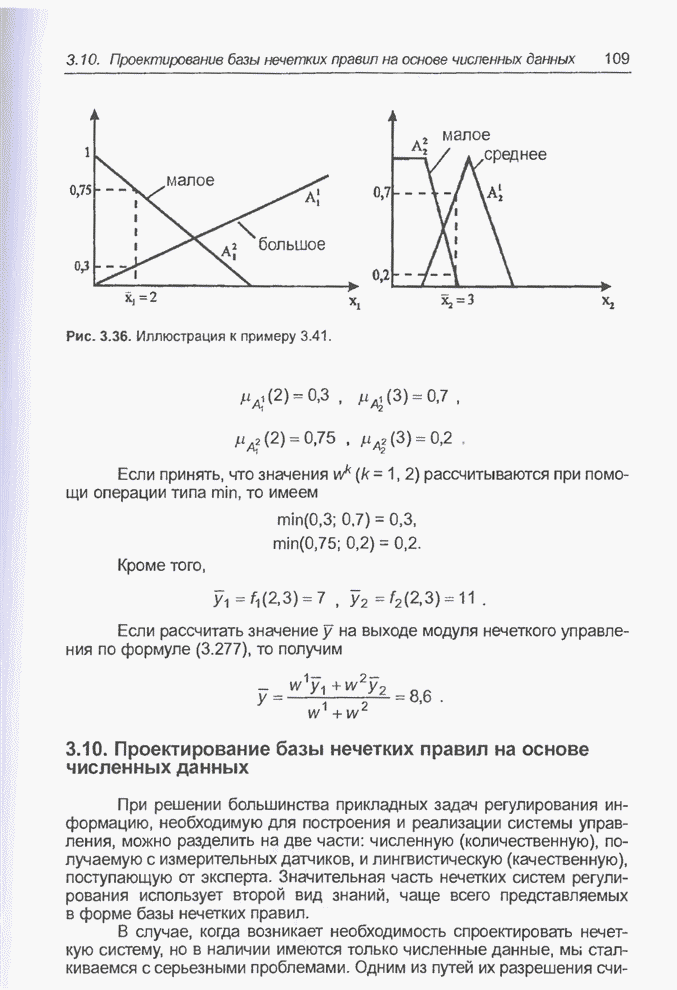
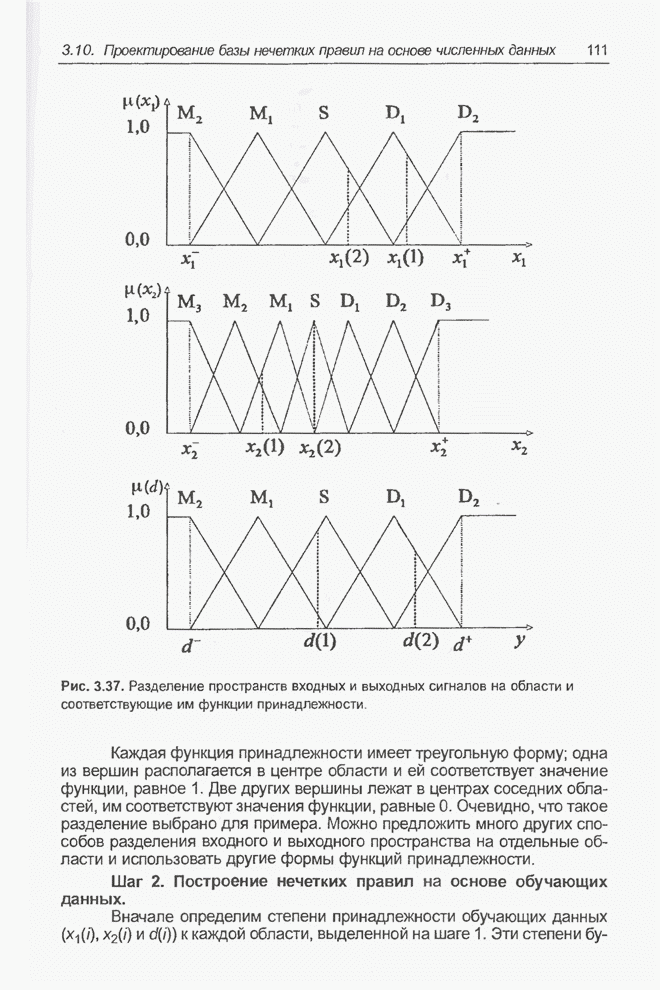
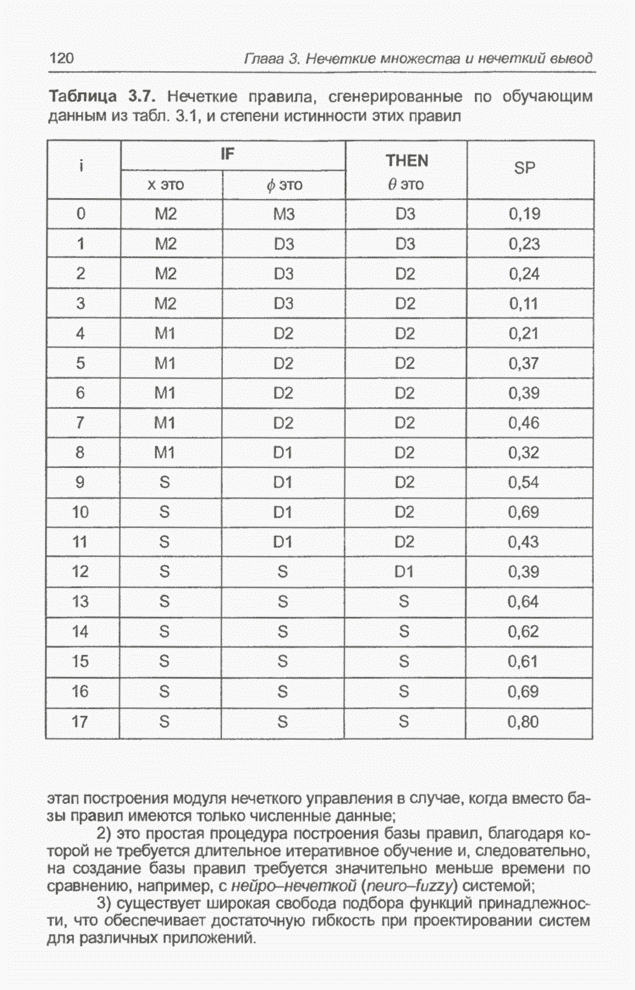
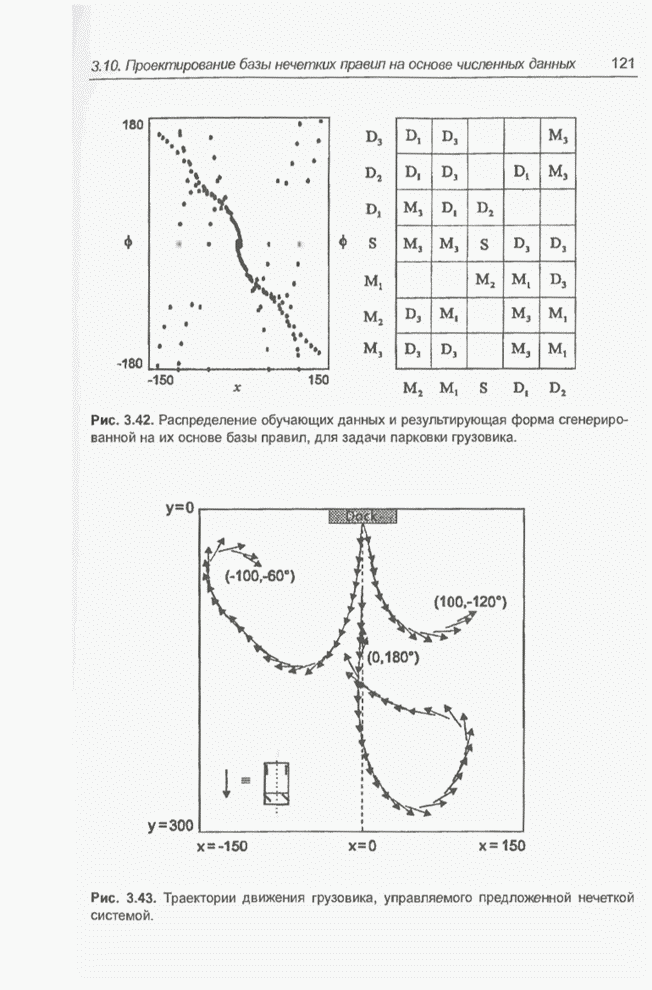
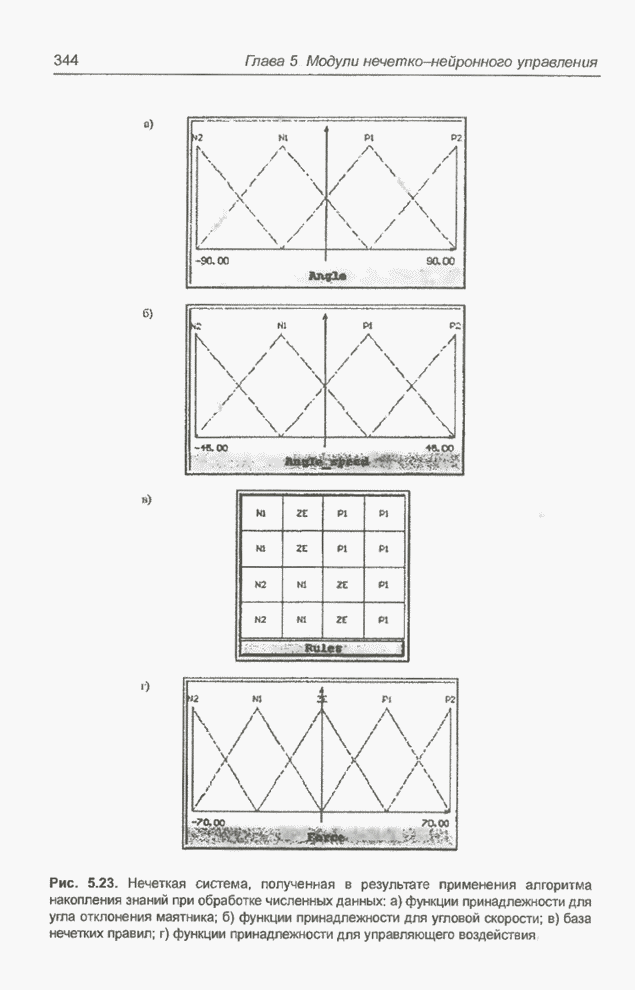
- 3.10. Проектирование базы нечетких правил на основе численных данных
- 3.10.1. Построение нечетких правил
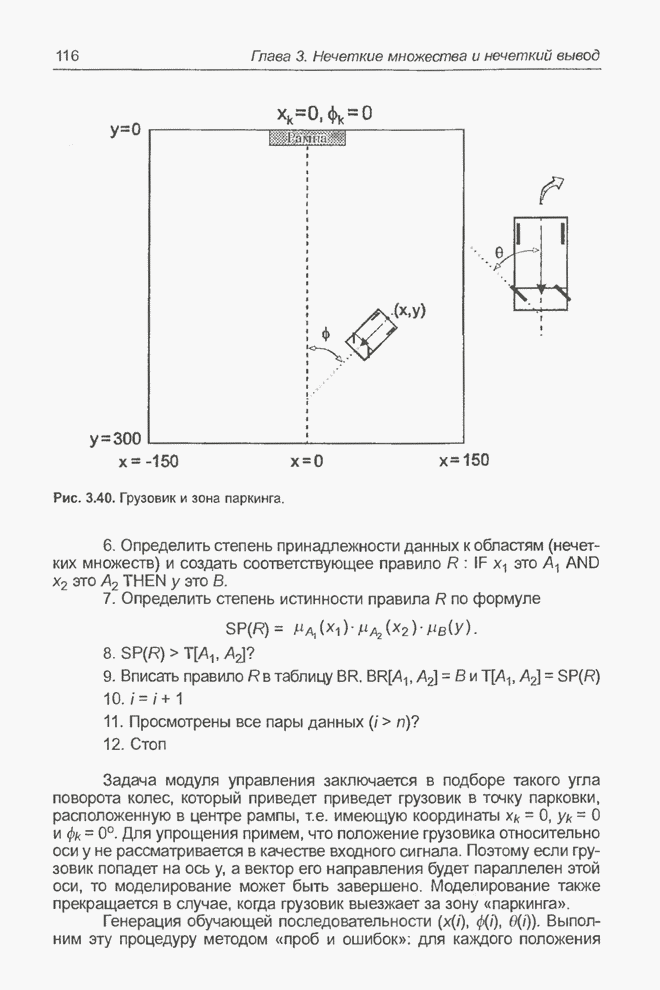
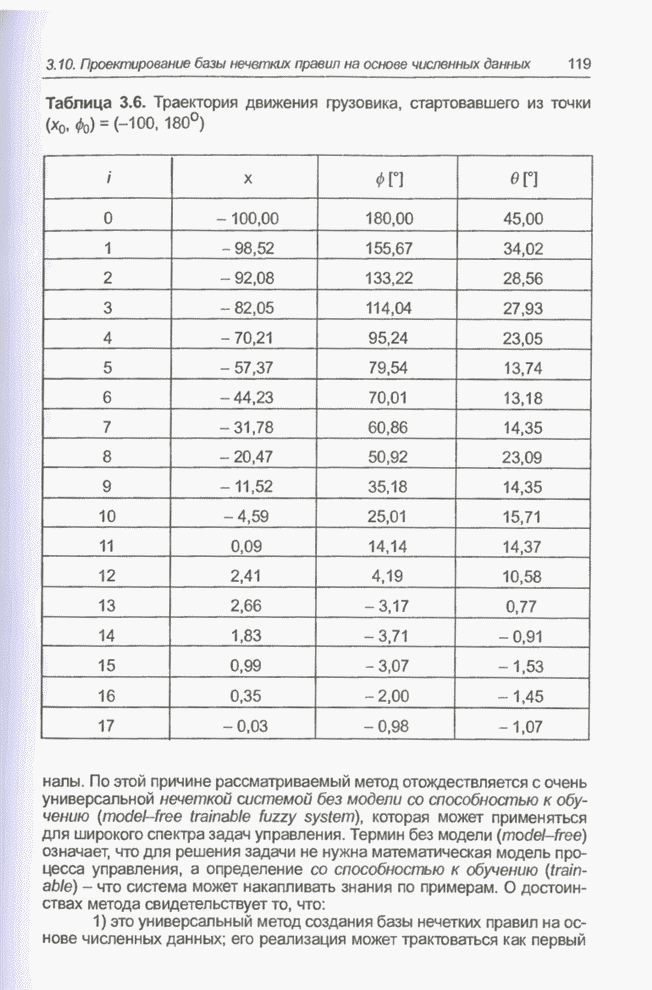
- 3.10.2. Задача парковки грузовика
- 3.10.3. Примечание
- Список литературы
- ГЛАВА 4. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 4.1. Введение
- 4.2. Генетические алгоритмы и традиционные методы оптимизации
- 4.3. Основные понятия генетических алгоритмов
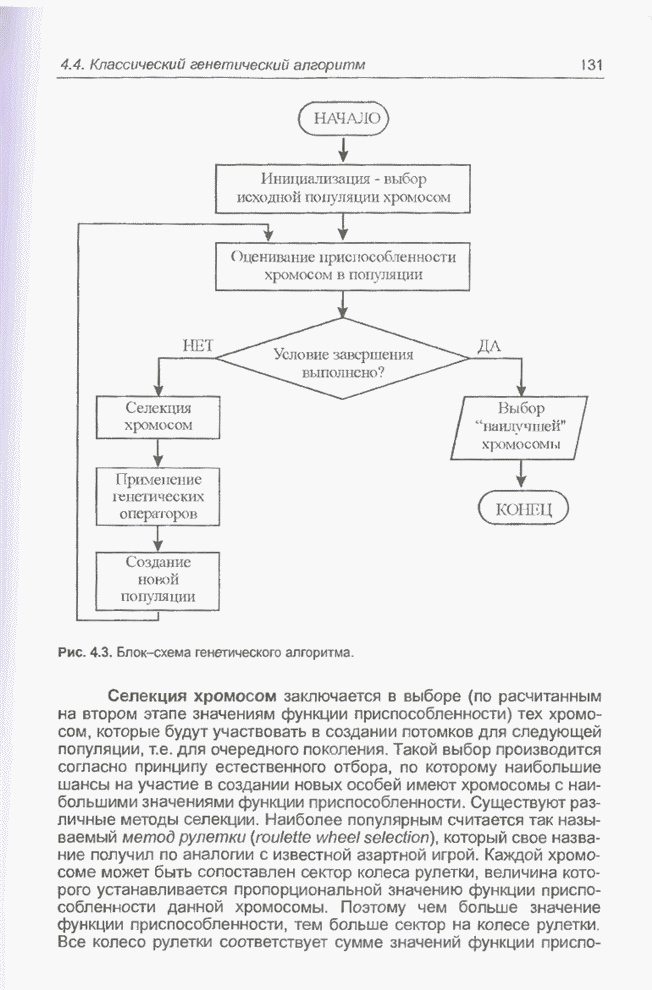
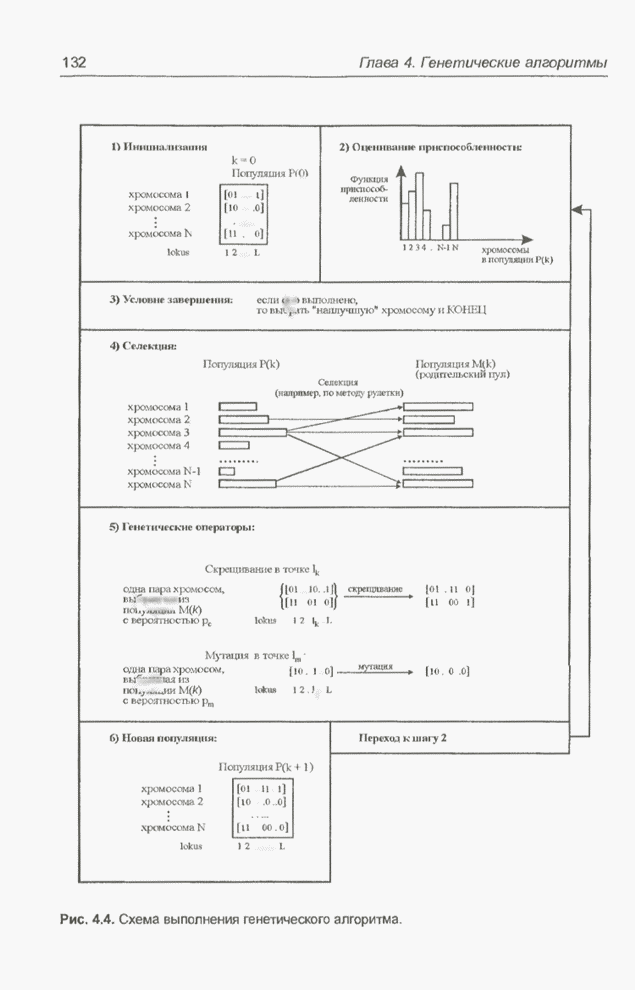
- 4.4. Классический генетический алгоритм
- 4.5. Иллюстрация выполнения классического генетического алгоритма
- 4.6. Кодирование параметров задачи в генетическом алгоритме
- 4.7. Основная теорема о генетических алгоритмах
- 4.8. Модификации классического генетического алгоритма
- 4.8.1. Методы селекции
- 4.8.2. Особые процедуры репродукции
- 4.8.3. Генетические операторы
- 4.8.4. Методы кодирования
- 4.8.5. Масштабирование функции приспособленности
- 4.8.6. Ниши в генетическом алгоритме
- 4.8.7. Генетические алгоритмы для многокритериальной оптимизации
- 4.8.8. Генетические микроалгоритмы
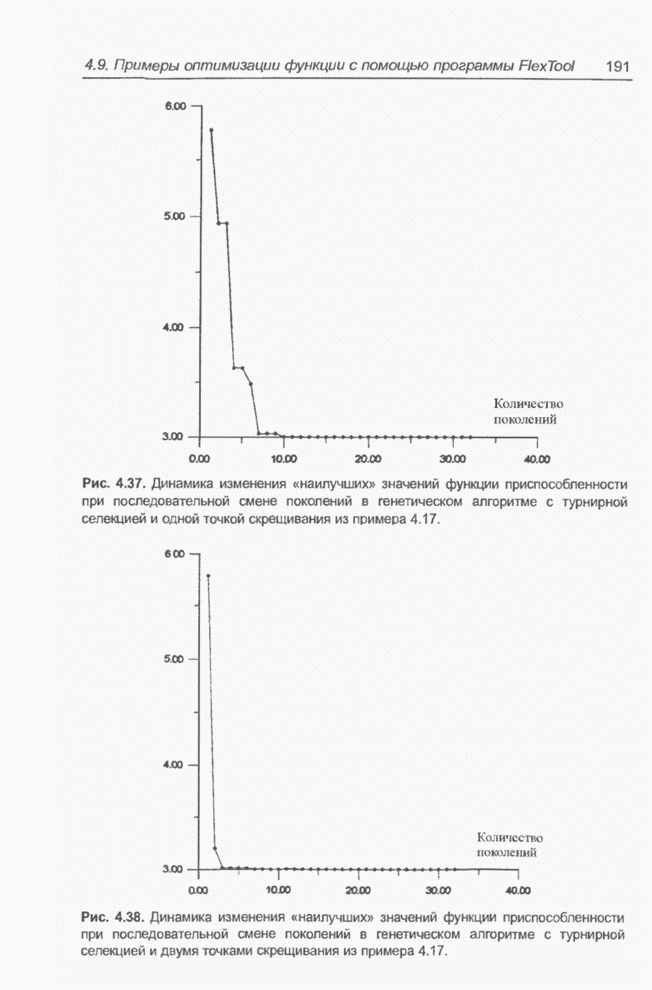
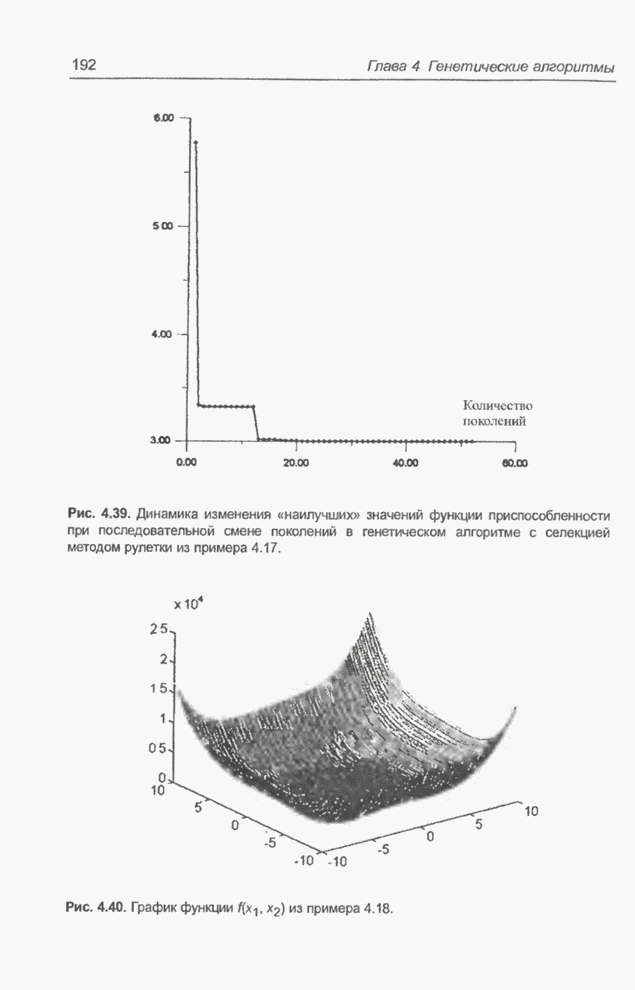
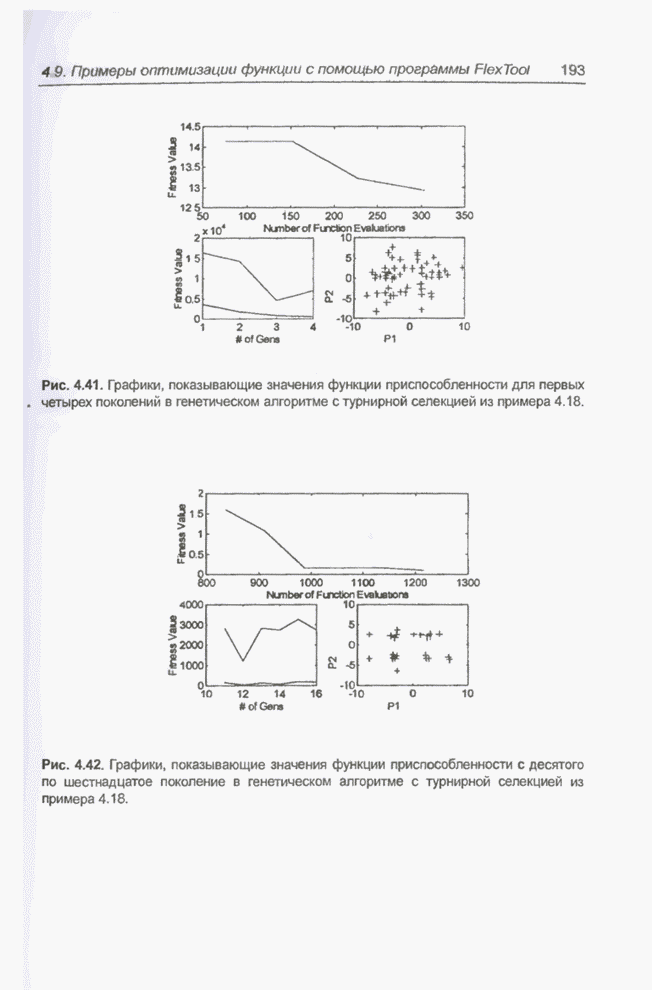
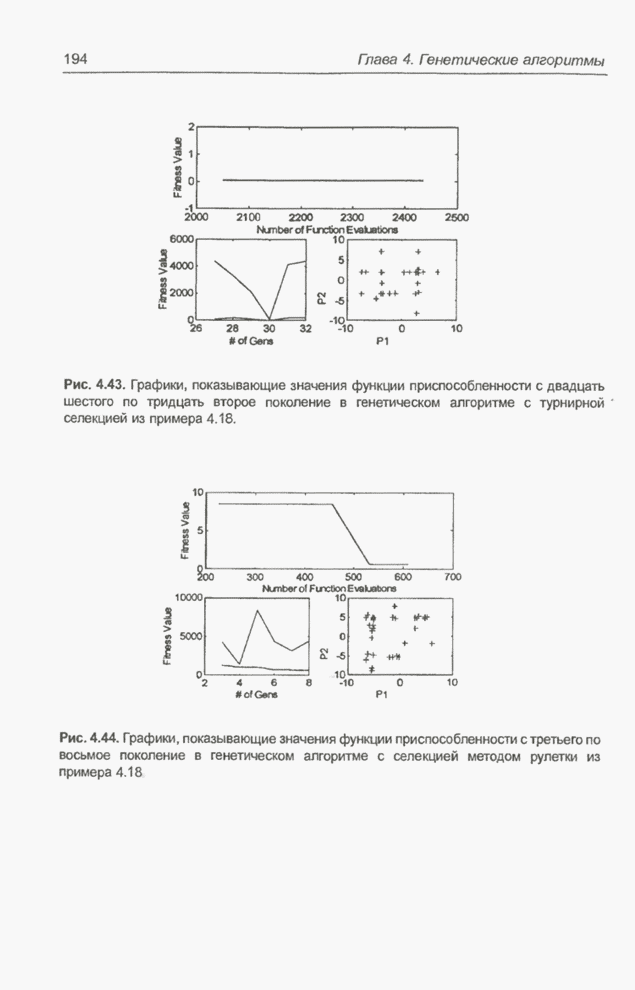
- 4.9. Примеры оптимизации функции с помощью программы FlexTool
- 4.10. Эволюционные алгоритмы
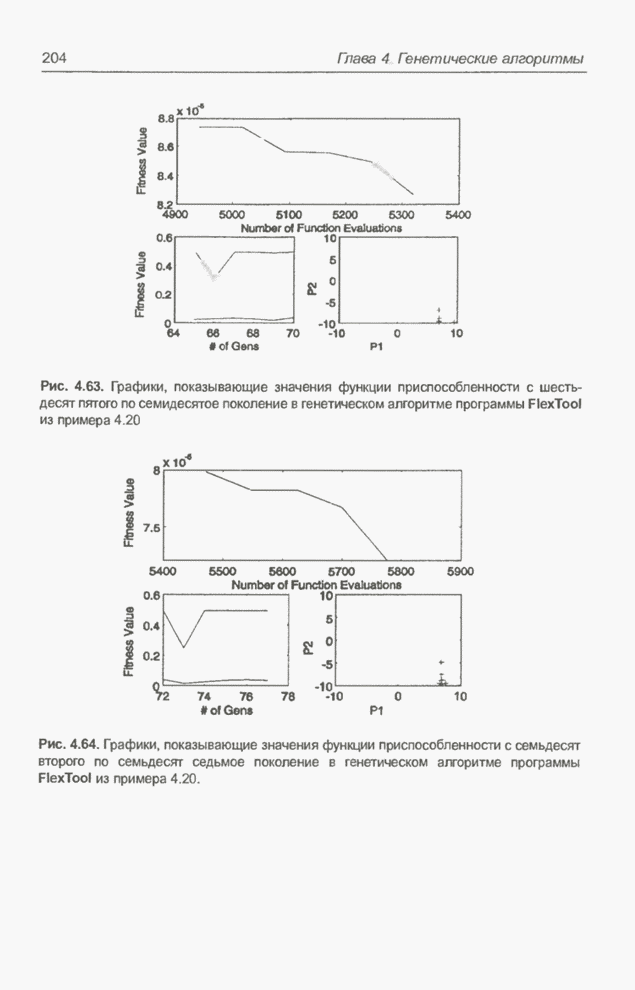
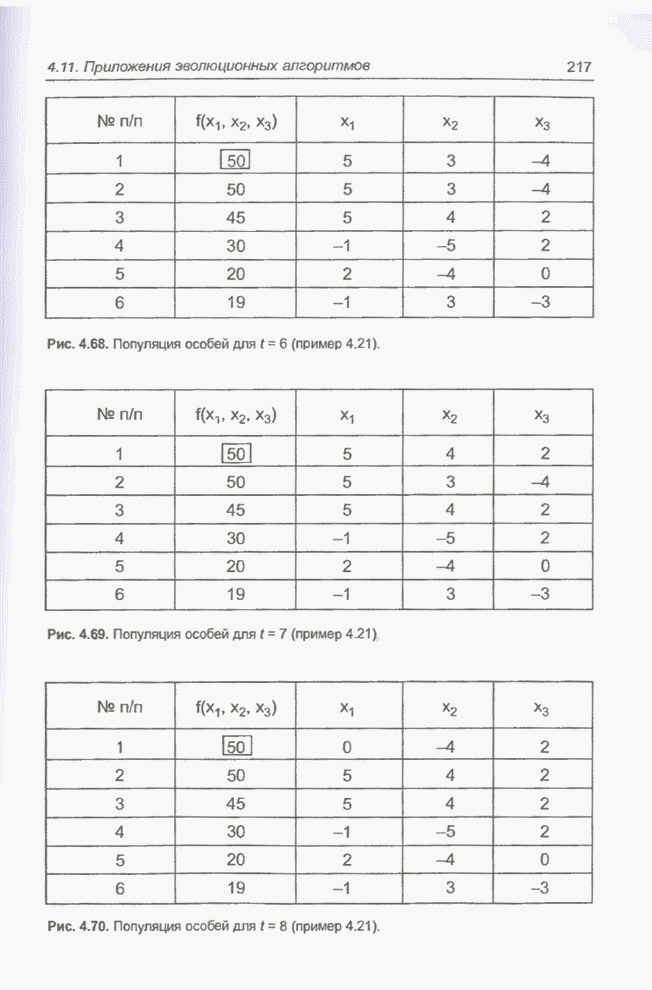
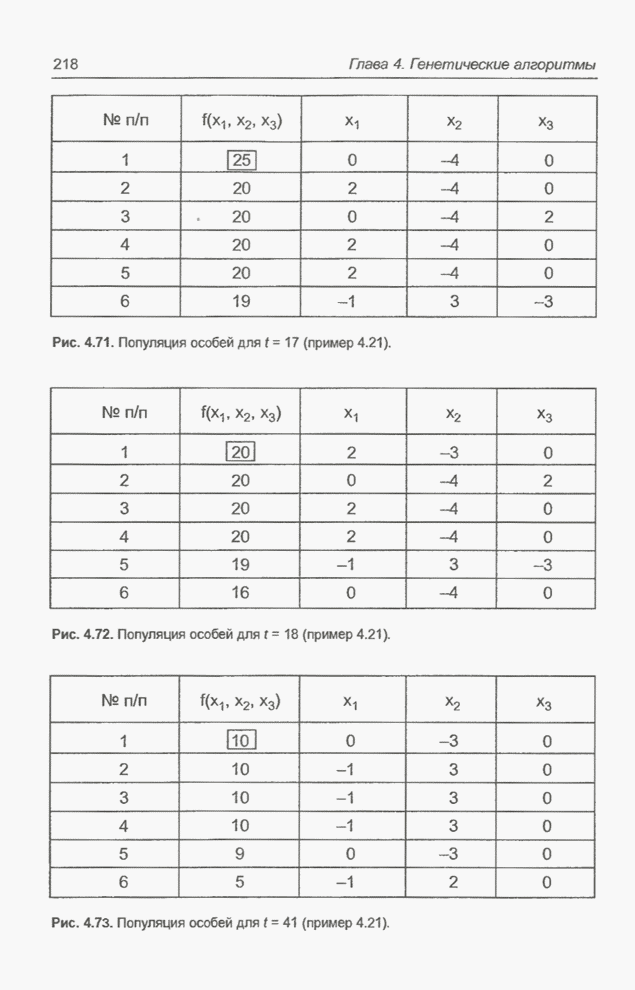
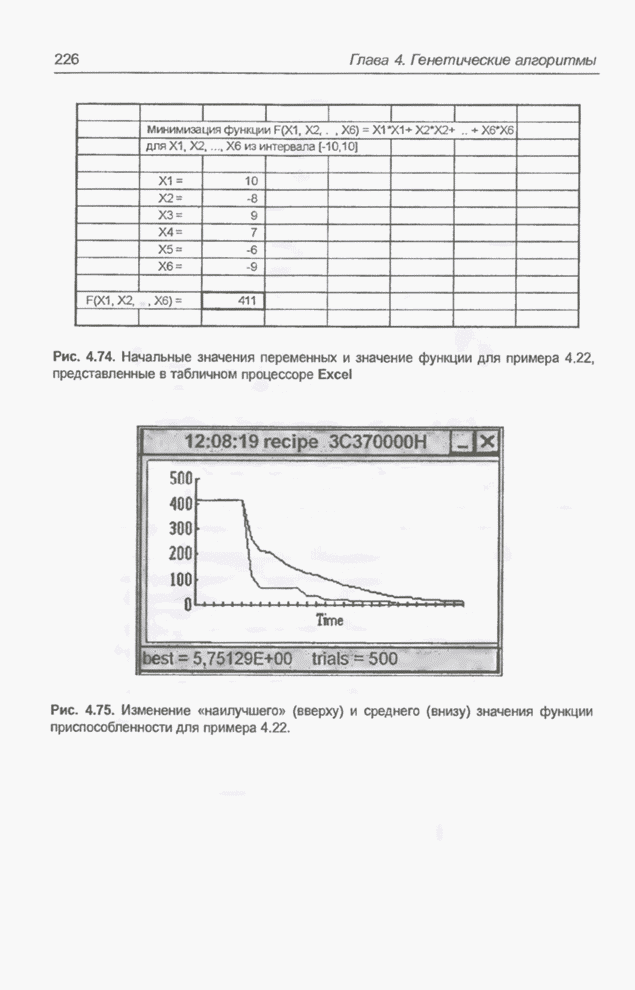
- 4.11. Приложения эволюционных алгоритмов
- 4.11.1. Примеры оптимизации функции с помощью программы Evolver
- 4.11.2. Решение комбинаторных задач с помощью программы Evolver
- 4.12. Эволюционные алгоритмы в нейронных сетях
- 4.12.1. Независимое применение генетических алгоритмов и нейронных сетей
- 4.12.2. Нейронные сети для поддержки генетических алгоритмов
- 4.12.3. Генетические алгоритмы для поддержки нейронных сетей
- 4.12.4. Применение генетических алгоритмов для обучения нейронных сетей
- 4.12.5. Генетические алгоритмы для выбора топологии нейронных сетей
- 4.12.6. Адаптивные взаимодействующие системы
- 4.12.7. Типовой цикл эволюции
- 4.12.7.1. Эволюция весов связей
- 4.12.7.2. Эволюция архитектуры сети
- 4.12.7.3. Эволюция правил обучения
- 4.13. Примеры моделирования эволюционных алгоритмов в приложении к нейронным сетям
- 4.13.1. Программы Evolver и BrainMaker
- 4.13.2. Программа GTO
- Список литературы
- ГЛАВА 5. МОДУЛИ НЕЧЕТКО-НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.1. Модуль нечеткого управления со структурой, определенной в процессе дефуззификации
- 5.1.2. Конструкция модуля
- 5.1.3. Структура модуля
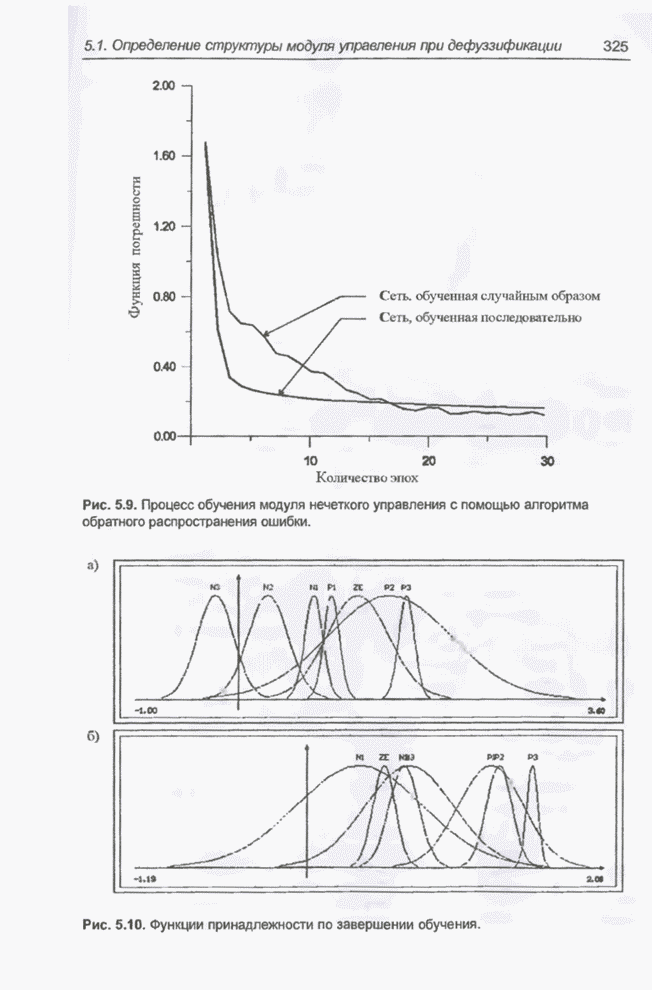
- 5.1.4. Использование алгоритма обратного распространения ошибки
- 5.1.5. Модификации модуля
- 5.1.6. Применение модуля нечеткого управления для прогнозирования случайных временных рядов
- 5.1.7. Применение модуля нечеткого управления для решения задачи парковки грузовика
- 5.1.8. Примечание
- 5.2. Представление модуля нечеткого управления в виде стандартной нейронной сети
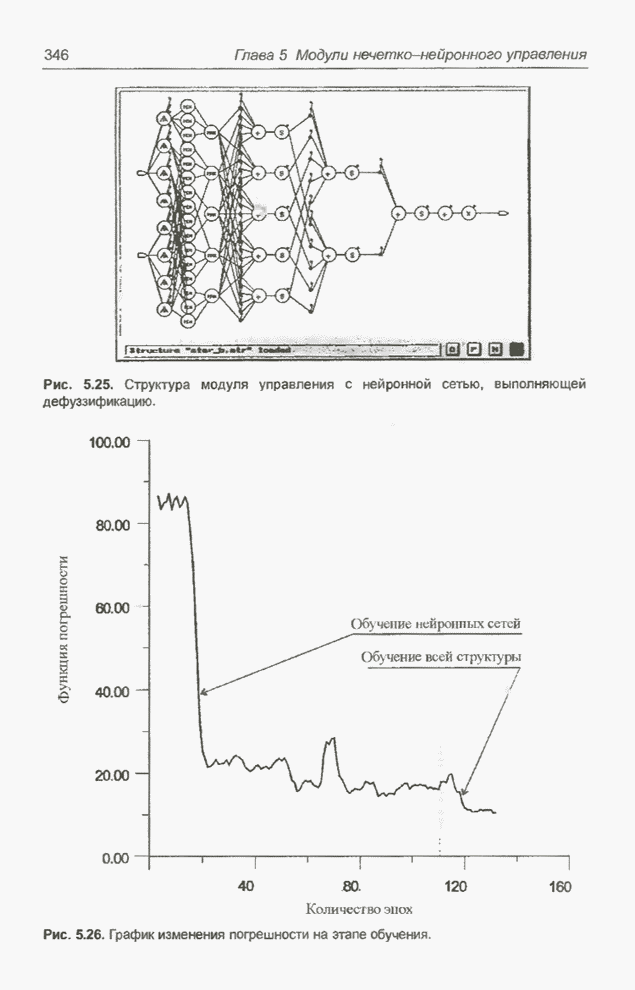
- 5.3. Модуль нечеткого управления с нейронной сетью для выполнения дефуззификации
- 5.3.1. Введение
- 5.3.2. Конструкция модуля
- 5.3.3. Структура модуля
- 5.3.4. Алгоритмы обучения модуля
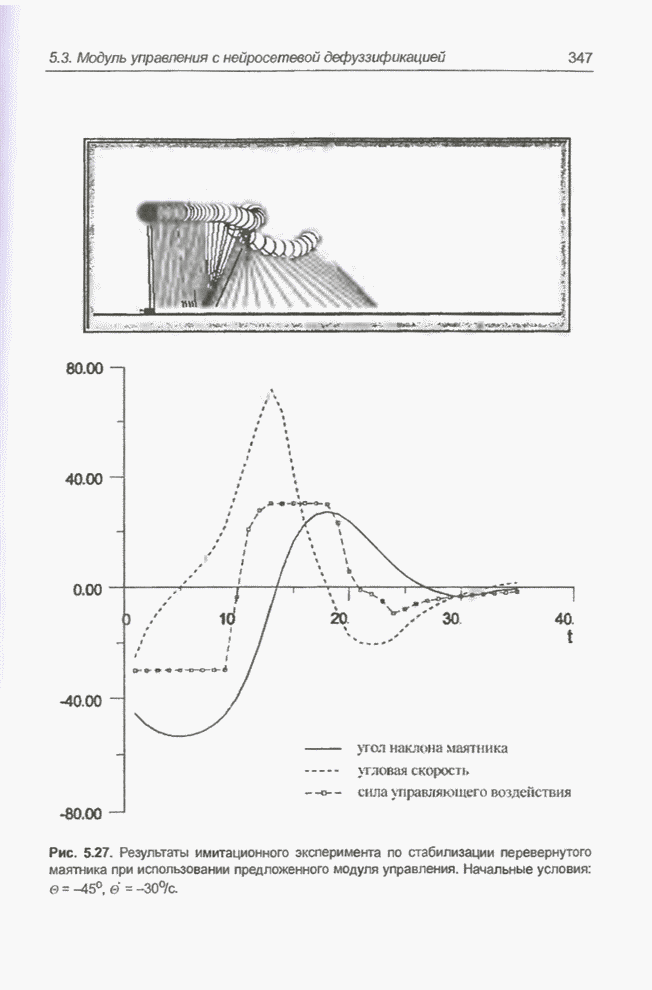
- 5.3.5. Решение задачи стабилизации перевернутого маятника
- 5.3.6. Примечание
- 5.4. Модуль нечеткого управления с возможностью коррекции правил
- 5.4.1. Введение
- 5.4.2. Фаза обучения на основе самоорганизации
- 5.4.3. Фаза обучения с учителем
- 5.4.4. Примечание
- 5.5. Модуль нечеткого управления типа Такаги-Сугено
- 5.5.1. Введение
- 5.5.2. Нейронная реализация функции принадлежности
- 5.5.3. Модули Такаги-Сугено
- 5.5.4. Реализация условий
- 5.5.5. Реализация заключений
- 5.5.6. Примечание
- 5.6. Модуль нечеткого управления типа Такаги-Сугено: случай зависимых лингвистических переменных
- 5.6.1. Введение
- 5.6.2. Нейронные сети для нечеткого вывода
- 5.6.3. Структура системы
- 5.6.4. Способ обучения
- 5.6.5. Решение задачи парковки грузовика
- 5.6.6. Примечание
- Список литературы