| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.13.2. Программа GTO
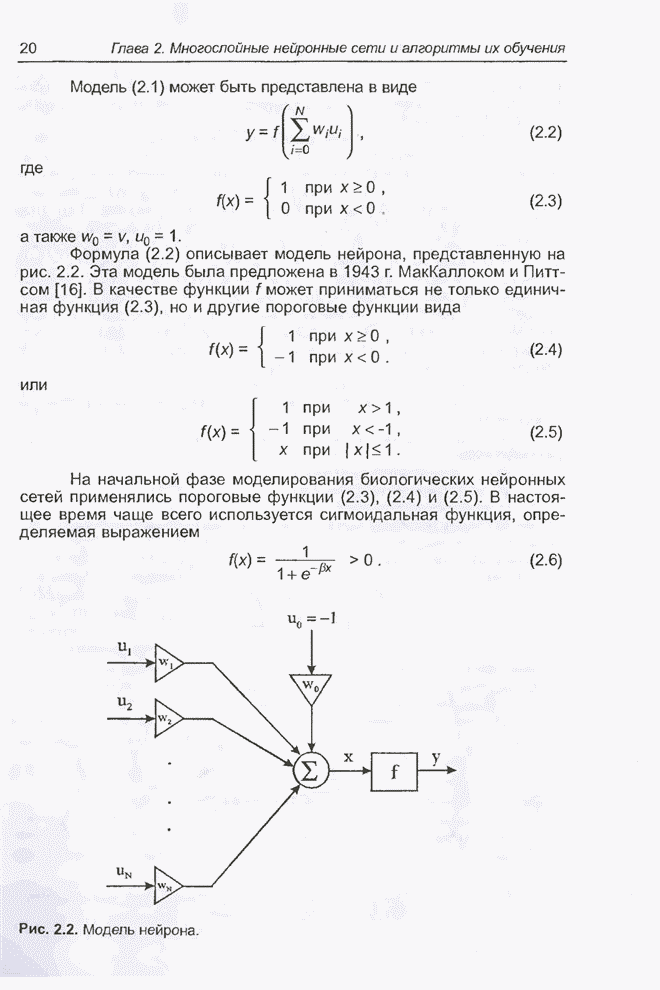
Программа GTO (Genetic Training Option - Режим Генетического Обучения) взаимодействует с программой BrainMaker. В ней реализован эволюционный алгоритм с соответственно определенными операторами мутации и скрещивания. Мутация изменяет значения весов избранного нейрона, а скрещивание заключается в обмене весов избранных нейронов у пары родителей. Например, для нейронной сети, изображенной на рис. 4.2, можно получить потомка, имеющего веса первого нейрона, унаследованные от первого родителя, и веса второго и третьего нейронов - от второго родителя. Выраженные в процентах показатели мутации (mutation rate) и скрещивания (crossover rate) определяют количество нейронов, подвергающихся мутации или скрещиванию. Пользователь также может ввести значения дополнительных параметров скрещивания и мутации. Они относятся к так называемому полному скрещиванию либо к определенным функциям распределения показателей скрещивания и/или мутации [51].
Пример 4.34
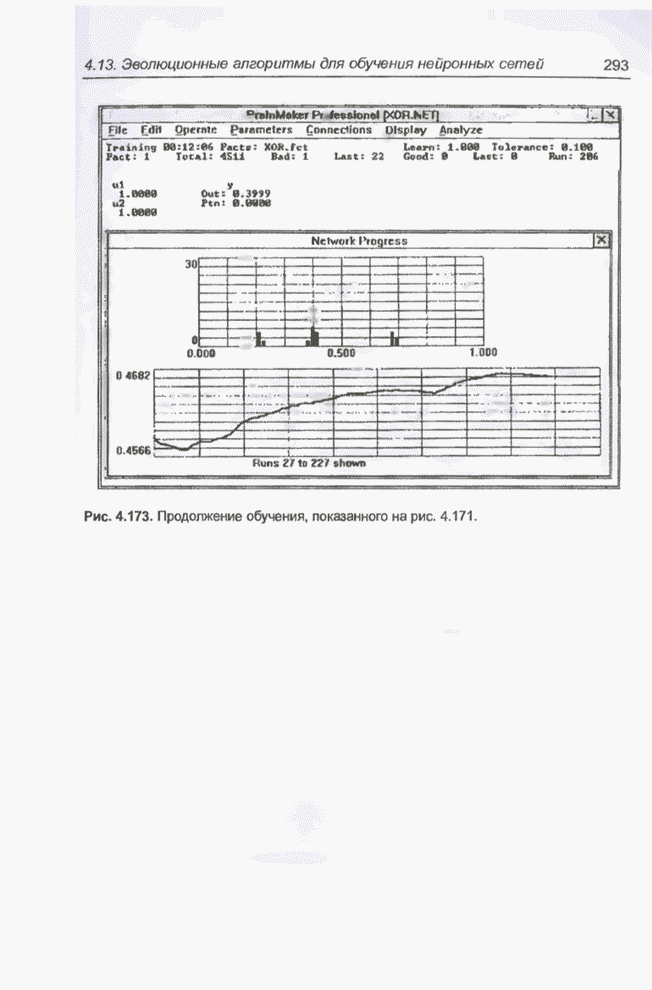
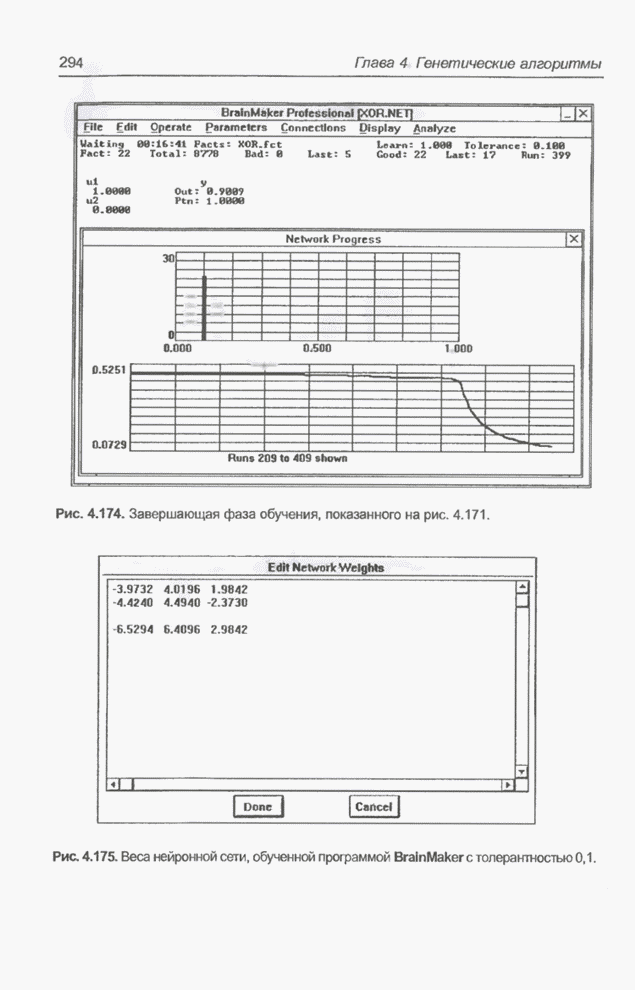
Применить программу GTO для нейронной сети, реализующей логическую систему XOR (рис. 4.2) с начальными значениями весов, представленными на рис. 4.166, которая после обучения программой BrainMaker с толерантностью погрешности, равной 0,1 (пример 4.33) имеет веса, представленные на рис. 4.175.
Все параметры программы GTO имели
значения, установленные по умолчанию. В частности, предусматривалось обучение
каждой сети программой BrainMaker в течение 100 прогонов (runs) и смена 30
поколений. Для оценки приспособленности сети использовались результаты как
обучения, и тестирования уже обученной сети. Показатели мутации и скрещивания
были равны соответственно 10 и 50. Это означает, что 50% всех нейронов сети
подвергалось скрещиванию, а 10% - мутации. Также принималось, что все
скрещиваемые нейроны подвергаются полному скрещиванию, т.е. потомок наследует
все веса нейрона от второго родителя. Помимо того, все подлежащие мутации
нейроны мутировали в соответствии с распределением Гаусса с показателем 0,25.
Это означает, что к весу добавлялась некоторая величина, выбиравшаяся по
распределению Гаусса. В качестве критерия оценивания потомков применялся ![]() , где
, где ![]() (также, как и в
примере 4.31) означал погрешность, рассчитанную как квадратный корень из суммы
квадратов разностей между заданным (эталонным) и выходным значением, деленный
на количество эталонов. В результате выполнения программы GTO при ее
взаимодействии с программой BrainMaker рассчитаны значения указанной выше
погрешности для конкретных сетей, упорядоченные в порядке их уменьшения, т.е.
от «наилучшей» сети к «наихудшей» (рис. 4.185).
(также, как и в
примере 4.31) означал погрешность, рассчитанную как квадратный корень из суммы
квадратов разностей между заданным (эталонным) и выходным значением, деленный
на количество эталонов. В результате выполнения программы GTO при ее
взаимодействии с программой BrainMaker рассчитаны значения указанной выше
погрешности для конкретных сетей, упорядоченные в порядке их уменьшения, т.е.
от «наилучшей» сети к «наихудшей» (рис. 4.185).

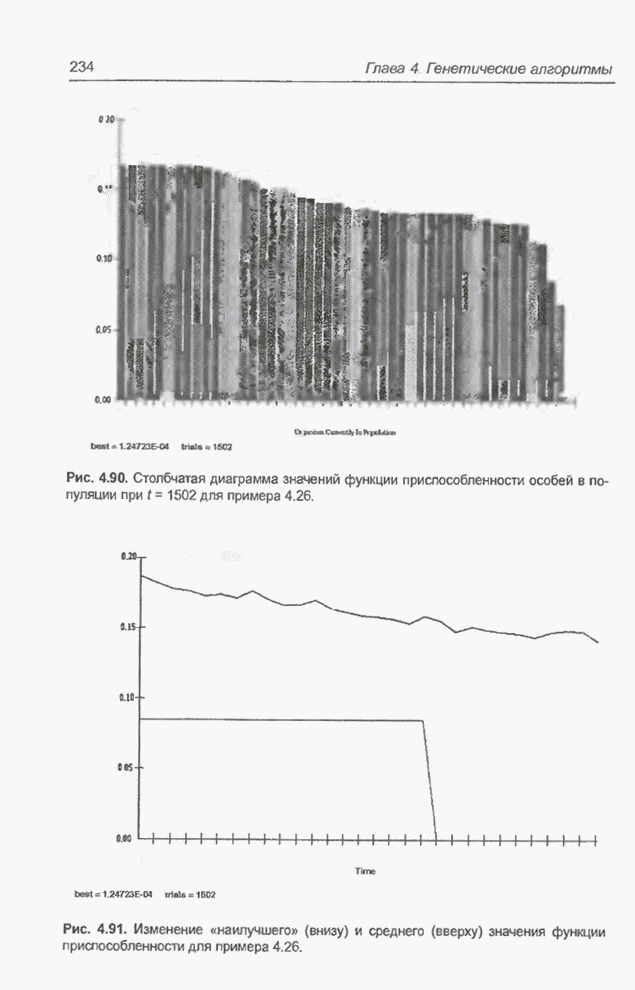
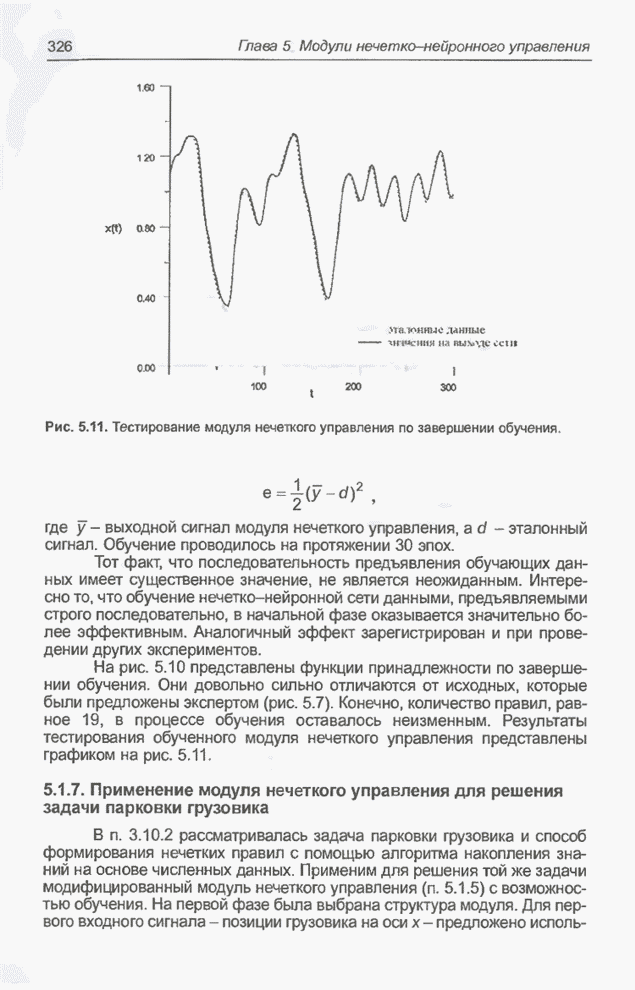
Рис. 4.185. Список нейронных сетей, сформированных программой GTO для примера 4.34 и упорядоченных в последовательности от «наилучшей» до «наихудшей».
Наилучшей из 30 сформированных
программой GTO нейронных сетей со структурой, показанной на рис. 4.2, оказалась
сеть, для которой значение ![]() было равно 0,9139. Значения весов этой
сети представлены на рис. 4.186, а результаты ее тестирования программой
BrainMaker - на рис. 4.187 - 4.190. Заметим, что значение погрешности
было равно 0,9139. Значения весов этой
сети представлены на рис. 4.186, а результаты ее тестирования программой
BrainMaker - на рис. 4.187 - 4.190. Заметим, что значение погрешности ![]() , рассчитываемой
программой Evolver, для сети с весами, показанными на рис. 4.186, равно 0,007451.
Эта погрешность меньше значения
, рассчитываемой
программой Evolver, для сети с весами, показанными на рис. 4.186, равно 0,007451.
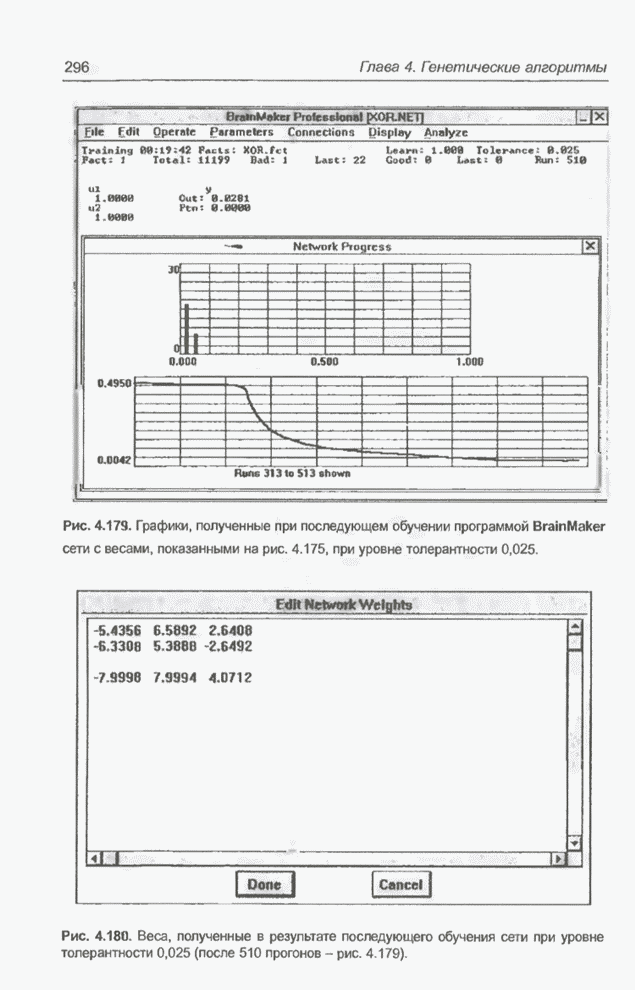
Эта погрешность меньше значения ![]() , рассчитанного для сети из примера 4.33
(веса см. на рис. 4.175). Конечно, новая сеть ненамного лучше сети из примера
4.33. Теперь следует вновь применить программу BrainMaker для проверки - можно
ли улучшить характеристики сети, полученной в результате выполнения программы
GTO. Очевидно, что попытка дообучения этой сети с толерантностью погрешности
0,1 ничего не изменит. Однако при задании уровня толерантности 0,025 мы
получаем процесс, показанный на рис. 4.191 и значения весов, представленные на
рис. 4.192. Выходное значение
, рассчитанного для сети из примера 4.33
(веса см. на рис. 4.175). Конечно, новая сеть ненамного лучше сети из примера
4.33. Теперь следует вновь применить программу BrainMaker для проверки - можно
ли улучшить характеристики сети, полученной в результате выполнения программы
GTO. Очевидно, что попытка дообучения этой сети с толерантностью погрешности
0,1 ничего не изменит. Однако при задании уровня толерантности 0,025 мы
получаем процесс, показанный на рис. 4.191 и значения весов, представленные на
рис. 4.192. Выходное значение ![]() для
для ![]() и
и ![]() также приведено на рис. 4.191.
также приведено на рис. 4.191.

Рис. 4.186. Веса нейронной сети, реализующей систему XOR, полученные программой GTO (пример 4.34).

Рис. 4.187. Результат
тестирования сформированной программой GTO нейронной сети с весами, показанными
на рис. 4.186, для ![]() ,
,
![]() и
и ![]() .
.

Рис. 4.188. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.189. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

Рис. 4.190. Результат
тестирования той же сети для ![]() ,
, ![]() и
и ![]() .
.

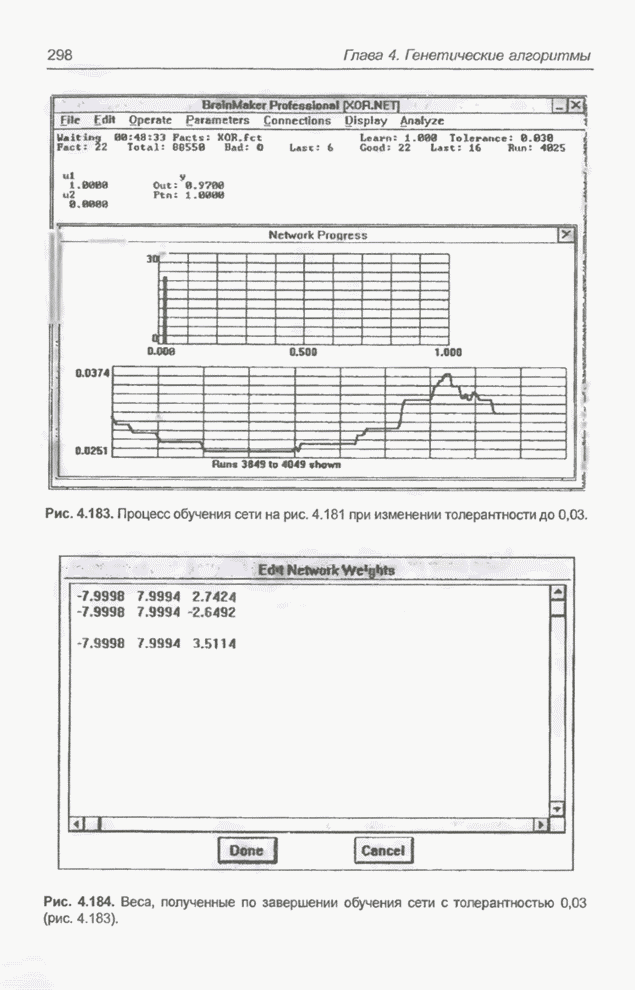
Рис. 4.191. Процесс обучения нейронной сети, сформированной программой GTO, осуществляемый программой BrainMaker с толерантностью 0,025.

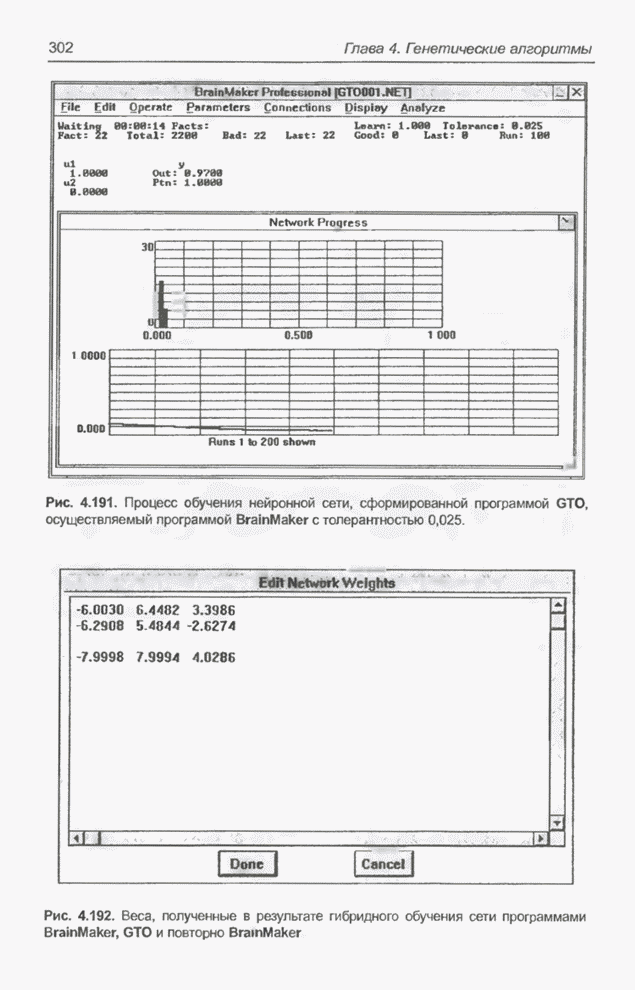
Рис. 4.192. Веса, полученные в результате гибридного обучения сети программами BrainMaker, GTO и повторно BrainMaker.
Пример 4.34 иллюстрирует следующее объединение традиционного (градиентного) алгоритма обучения, реализованного в программе BrainMaker, с генетическим алгоритмом программы GTO:
1) обучение нейронной сети программой BrainMaker;
2) применение программы GTO к сети, обученной в п.1;
3) продолжение обучения наилучшей сети, полученной в п.2, программой BrainMaker;
Следует отметить, что п.2 предполагает использование как генетического алгоритма программы GTO, так и соответствующей процедуры программы BrainMaker, вызываемой программой GTO.
Можно предложить и другой подход:
1) использование программы BrainMaker только для формирования сети со значениями весов, выбираемыми случайным образом;
2) применение программы GTO для поиска наилучших весов;
3) применение программы BrainMaker для завершения обучения
Второй подход основан на обработке программой GTO сети со случайными значениями весов. При отключении опции обучения каждой вновь формируемой сети программой BrainMaker программа GTO вызывает ее только для тестирования сети. В последующем наилучшая из созданных таким образом сетей «дообучается» программой BrainMaker (п. 3). Такая методика подобна применявшейся в примерах 4.31 и 4.32 - вначале выполняется генетический, а затем - традиционный алгоритм обучения. В программе GTO дополнительно возможно обучение каждой вновь сформированной сети (потомка) за определенное количество прогонов с последующим ее тестированием. Это пример подхода, состоящего в «дообучении» нейронных сетей традиционным (в частности, градиентным) методом каждый раз перед оцениванием приспособленности [43]. Программа GTO также предоставляет возможность выбрать один из нескольких критериев оценивания нейронных сетей (функцию их приспособленности). Решение о применении одного из двух рассмотренных гибридных подходов к совместному применению программ GTO и BrainMaker зависит от поставленной задачи и, как правило, принимается методом проб и ошибок. Как справедливо отмечается в [51], практически невозможно априорно оценить - какой подход окажется лучшим для конкретной задачи.
Применительно к нейронной сети, предназначенной для реализации логической системы XOR, наилучшие результаты можно было бы ожидать от применения второго подхода. Однако с учетом ограниченного объема настоящей работы мы не будем рассматривать дополнительные примеры, демонстрирующие различные возможности его реализации с использованием программы GTO
Наиболее важные замечания относительно гибридного подхода, состоящего в объединении генетического алгоритма с градиентным методом обучения нейронных сетей (программа BrainMaker) представлены в п. 4.13.1. Программа GTO представляет собой пример равноправного объединения обоих методов, при котором в соответствии с типовым циклом эволюции (п. 4.12.7) приспособленность особей популяции рассчитывается генетическим алгоритмом по результатам обучения нейронных сетей. Существование такой программы, как GTO, подтверждает практическое применение гибридного подхода, объединяющего достоинства двух оптимизационных методов: генетического алгоритма, который легко находит точку, близкую к оптимальному решению, и градиентного алгоритма, который стартует из найденной точки и быстро приводит к настоящему оптимуму.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Предисловие к русскому изданию
- ГЛАВА 1. ВВЕДЕНИЕ
- Список литературы
- ГЛАВА 2. МНОГОСЛОЙНЫЕ НЕЙРОННЫЕ СЕТИ И АЛГОРИТМЫ ИХ ОБУЧЕНИЯ
- 2.1. Введение
- 2.2. Нейрон и его модели
- 2.3. Персептрон
- 2.4. Системы типа Адалайн
- 2.4.1. Линейный взвешенный сумматор
- 2.4.2. Адаптивный линейный взвешенный сумматор
- 2.4.3. Адаптивный линейный взвешенный сумматор с сигмоидой на выходе
- 2.5. Алгоритм обратного распространения ошибки
- 2.6. Применение рекуррентного метода наименьших квадратов для обучения нейронных сетей
- Список литературы
- ГЛАВA3. НЕЧЕТКИЕ МНОЖЕСТВА И НЕЧЕТКИЙ ВЫВОД
- 3.1. Введение
- 3.2. Основные понятия и определения теории нечетких множеств
- 3.3. Операции на нечетких множествах
- 3.4. Принцип расширения
- 3.5. Нечеткие числа
- 3.6. Треугольные нормы
- 3.7. Нечеткие отношения и их свойства
- 3.8. Нечеткий вывод
- 3.9. Нечеткое управление
- 3.9.1. Классический модуль нечеткого управления
- 3.9.2. Метод нечеткого управления Такаги-Сугено
- 3.10. Проектирование базы нечетких правил на основе численных данных
- 3.10.1. Построение нечетких правил
- 3.10.2. Задача парковки грузовика
- 3.10.3. Примечание
- Список литературы
- ГЛАВА 4. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 4.1. Введение
- 4.2. Генетические алгоритмы и традиционные методы оптимизации
- 4.3. Основные понятия генетических алгоритмов
- 4.4. Классический генетический алгоритм
- 4.5. Иллюстрация выполнения классического генетического алгоритма
- 4.6. Кодирование параметров задачи в генетическом алгоритме
- 4.7. Основная теорема о генетических алгоритмах
- 4.8. Модификации классического генетического алгоритма
- 4.8.1. Методы селекции
- 4.8.2. Особые процедуры репродукции
- 4.8.3. Генетические операторы
- 4.8.4. Методы кодирования
- 4.8.5. Масштабирование функции приспособленности
- 4.8.6. Ниши в генетическом алгоритме
- 4.8.7. Генетические алгоритмы для многокритериальной оптимизации
- 4.8.8. Генетические микроалгоритмы
- 4.9. Примеры оптимизации функции с помощью программы FlexTool
- 4.10. Эволюционные алгоритмы
- 4.11. Приложения эволюционных алгоритмов
- 4.11.1. Примеры оптимизации функции с помощью программы Evolver
- 4.11.2. Решение комбинаторных задач с помощью программы Evolver
- 4.12. Эволюционные алгоритмы в нейронных сетях
- 4.12.1. Независимое применение генетических алгоритмов и нейронных сетей
- 4.12.2. Нейронные сети для поддержки генетических алгоритмов
- 4.12.3. Генетические алгоритмы для поддержки нейронных сетей
- 4.12.4. Применение генетических алгоритмов для обучения нейронных сетей
- 4.12.5. Генетические алгоритмы для выбора топологии нейронных сетей
- 4.12.6. Адаптивные взаимодействующие системы
- 4.12.7. Типовой цикл эволюции
- 4.12.7.1. Эволюция весов связей
- 4.12.7.2. Эволюция архитектуры сети
- 4.12.7.3. Эволюция правил обучения
- 4.13. Примеры моделирования эволюционных алгоритмов в приложении к нейронным сетям
- 4.13.1. Программы Evolver и BrainMaker
- 4.13.2. Программа GTO
- Список литературы
- ГЛАВА 5. МОДУЛИ НЕЧЕТКО-НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.1. Модуль нечеткого управления со структурой, определенной в процессе дефуззификации
- 5.1.2. Конструкция модуля
- 5.1.3. Структура модуля
- 5.1.4. Использование алгоритма обратного распространения ошибки
- 5.1.5. Модификации модуля
- 5.1.6. Применение модуля нечеткого управления для прогнозирования случайных временных рядов
- 5.1.7. Применение модуля нечеткого управления для решения задачи парковки грузовика
- 5.1.8. Примечание
- 5.2. Представление модуля нечеткого управления в виде стандартной нейронной сети
- 5.3. Модуль нечеткого управления с нейронной сетью для выполнения дефуззификации
- 5.3.1. Введение
- 5.3.2. Конструкция модуля
- 5.3.3. Структура модуля
- 5.3.4. Алгоритмы обучения модуля
- 5.3.5. Решение задачи стабилизации перевернутого маятника
- 5.3.6. Примечание
- 5.4. Модуль нечеткого управления с возможностью коррекции правил
- 5.4.1. Введение
- 5.4.2. Фаза обучения на основе самоорганизации
- 5.4.3. Фаза обучения с учителем
- 5.4.4. Примечание
- 5.5. Модуль нечеткого управления типа Такаги-Сугено
- 5.5.1. Введение
- 5.5.2. Нейронная реализация функции принадлежности
- 5.5.3. Модули Такаги-Сугено
- 5.5.4. Реализация условий
- 5.5.5. Реализация заключений
- 5.5.6. Примечание
- 5.6. Модуль нечеткого управления типа Такаги-Сугено: случай зависимых лингвистических переменных
- 5.6.1. Введение
- 5.6.2. Нейронные сети для нечеткого вывода
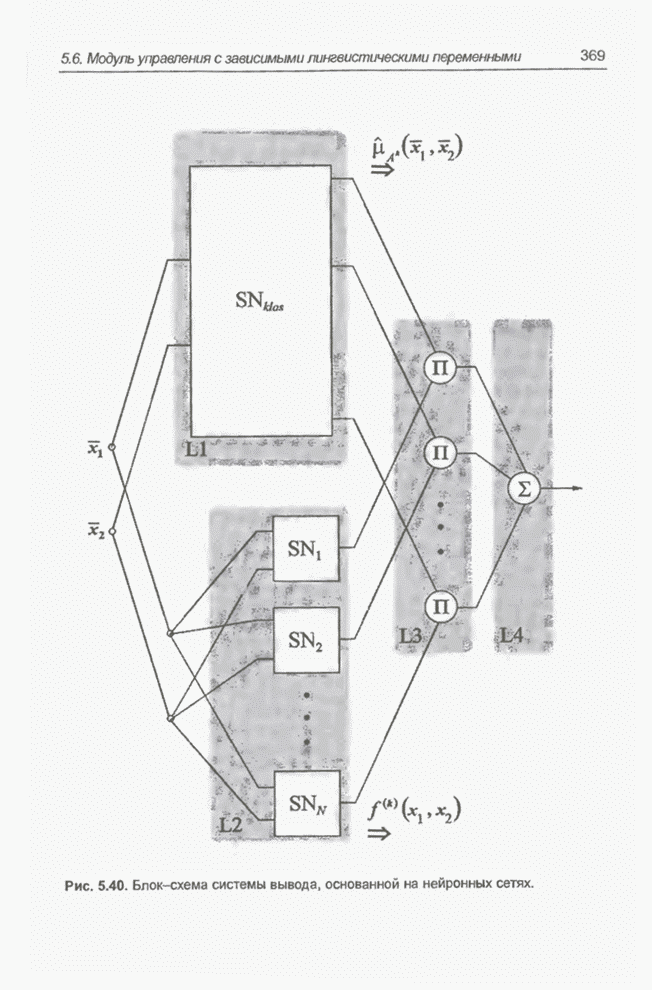
- 5.6.3. Структура системы
- 5.6.4. Способ обучения
- 5.6.5. Решение задачи парковки грузовика
- 5.6.6. Примечание
- Список литературы