| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.9.1. Классический модуль нечеткого управления
На рис. 3.26 представлена типовая структура модуля нечеткого управления. Он состоит из следующих компонентов: базы правил, блока фуззификации (fuzzification), блока выработки решения, блока дефуззификации.

Рис. 3.26. Модуль нечеткого управления.
3.9.1.1. База правил
База правил, иногда называемая
лингвистической моделью, представляет собой множество нечетких правил ![]() ,
, ![]() , вида
, вида
![]() :
IF (
:
IF (![]() это
это
![]() AND
AND ![]() это
это ![]() … AND
… AND ![]() это
это
![]() )
)
THEN (![]() это
это ![]() AND
AND ![]() это
это ![]() … AND
… AND ![]() это
это ![]() ), (3.224)
), (3.224)
где
![]() - количество
нечетких правил,
- количество
нечетких правил, ![]() -
нечеткие множества
-
нечеткие множества
![]() ,
,
![]() , (3.225)
, (3.225)
![]() -
нечеткие множества
-
нечеткие множества
![]() ,
,
![]() , (3.226)
, (3.226)
![]() -
входные переменные лингвистической модели, причем
-
входные переменные лингвистической модели, причем
![]() , (3.227)
, (3.227)
![]() -
входные переменные лингвистической модели, причем
-
входные переменные лингвистической модели, причем
![]() . (3.228)
. (3.228)
Символами ![]() ,
, ![]() и
и ![]() ,
, ![]() обозначаются соответственно пространства
входных и выходных переменных.
обозначаются соответственно пространства
входных и выходных переменных.
Для дальнейших рассуждений
примем, что конкретные правила ![]() ,
, ![]() связаны между собой логическим
оператором «ИЛИ». Кроме того, допустим, что выходы
связаны между собой логическим
оператором «ИЛИ». Кроме того, допустим, что выходы ![]() взаимно независимы. Поэтому
без утраты общности будем использовать нечеткие правила со скалярным выходом в
форме
взаимно независимы. Поэтому
без утраты общности будем использовать нечеткие правила со скалярным выходом в
форме
![]() :
IF (
:
IF (![]() это
это ![]() AND
AND ![]() это
это ![]() … AND
… AND ![]() это
это ![]() )
)
THEN (![]() это
это ![]() ), (3.229)
), (3.229)
где
![]() и
и ![]() .
.
Заметим, что каждое правило вида
(3.229) состоит из части IF, называемой посылкой (antecedent), и части THEN,
называемой следствием (consequent). Посылка правила содержит набор условий,
тогда как следствие содержит вывод. Переменные ![]() и
и ![]() могут принимать как лингвистические
(например, «малый», «средний», «большой»), так и числовые значения. Если ввести
обозначения
могут принимать как лингвистические
(например, «малый», «средний», «большой»), так и числовые значения. Если ввести
обозначения
![]() , (3.230)
, (3.230)
![]() , (3.231)
, (3.231)
то правило (3.229) можно представить в виде нечеткой импликации
![]() ,
,
![]() . (3.232)
. (3.232)
Обратим внимание, что правило
также можно интерпретировать как нечеткое отношение, определенное на множестве ![]() , т.е.
, т.е. ![]() - это нечеткое
множество с функцией принадлежности
- это нечеткое
множество с функцией принадлежности
![]() . (3.233)
. (3.233)
При проектировании модулей нечеткого управления следует оценивать достаточность количества нечетких правил, их непротиворечивость и наличие корреляции между отдельными правилами. Эти проблемы детально обсуждаются в работах [5, 7, 26].
3.9.1.2. Блок фуззификации
Система управления с нечеткой
логикой оперирует нечеткими множествами. Поэтому конкретное значение ![]() входного сигнала
модуля нечеткого управления подлежит операции фуззификации, в результате
которой ему будет сопоставлено нечеткое множество
входного сигнала
модуля нечеткого управления подлежит операции фуззификации, в результате
которой ему будет сопоставлено нечеткое множество ![]() . В задачах управления чаще
всего применяется операция фуззификации типа синглетон (singleton):
. В задачах управления чаще
всего применяется операция фуззификации типа синглетон (singleton):
 (3.234)
(3.234)
Нечеткое множество ![]() подается на вход
блока выработки решения. Если входной сигнал поступает зашумленным, то нечеткое
множество
подается на вход
блока выработки решения. Если входной сигнал поступает зашумленным, то нечеткое
множество ![]() можно
определить функцией принадлежности
можно
определить функцией принадлежности
 , (3.235)
, (3.235)
где
![]() . В этом
случае операция фуззификации имеет тип non-singleton.
. В этом
случае операция фуззификации имеет тип non-singleton.
3.9.1.3. Блок выработки решения
Допустим, что на вход блока
выработки решения подано нечеткое множество ![]() . На выходе этого блока также появится
соответствующее нечеткое множество. Рассмотрим два случая, которым будут
соответствовать различные методы дефуззификации (п. 3.9.1.4).
. На выходе этого блока также появится
соответствующее нечеткое множество. Рассмотрим два случая, которым будут
соответствовать различные методы дефуззификации (п. 3.9.1.4).
Случай 1
На выходе блока выработки решения
в соответствии с обобщенным нечетким правилом modus ponens получаем ![]() нечетких множеств
нечетких множеств ![]() .
.
|
Условие
Импликация
|
|
(3.236) |
|
Вывод |
|
Нечеткое множество ![]() определяется
комбинацией нечеткого множества
определяется
комбинацией нечеткого множества ![]() и отношения
и отношения ![]() , т.е.
, т.е.
![]() ,
,
![]() . (3.237)
. (3.237)
При использовании определения
3.28 можно задать функцию принадлежности нечеткого множества ![]() в виде
в виде
![]() . (3.238)
. (3.238)
Конкретная форма функции ![]() зависит от
применяемой
зависит от
применяемой ![]() -нормы
(п. 3.6), определения нечеткой импликации
-нормы
(п. 3.6), определения нечеткой импликации ![]() (п. 3.8.3) и от способа определения
декартова произведения нечетких множеств (определение 3.14). Следует отметить,
что если выполняется операция фуззификации типа синглетон (3.234), то выражение
(3.238) принимает вид
(п. 3.8.3) и от способа определения
декартова произведения нечетких множеств (определение 3.14). Следует отметить,
что если выполняется операция фуззификации типа синглетон (3.234), то выражение
(3.238) принимает вид
![]() . (3.239)
. (3.239)
Пример 3.32
Если ![]() ,
, ![]() -норма имеет тип min, нечеткая импликация
определяется правилом типа min и декартово произведение нечетких множеств
задано формулой (3.71), то выражение (3.238) принимает вид
-норма имеет тип min, нечеткая импликация
определяется правилом типа min и декартово произведение нечетких множеств
задано формулой (3.71), то выражение (3.238) принимает вид
 (3.240)
(3.240)
Последнее равенство следует из того, что
![]() (3.241)
(3.241)
и
![]() . (3.242)
. (3.242)
Пример 3.33
Если ![]() ,
, ![]() -норма имеет тип произведение, нечеткая
импликация определяется правилом типа произведение и декартово произведение
нечетких множеств задано формулой (3.72), то выражение (3.238) принимает вид
-норма имеет тип произведение, нечеткая
импликация определяется правилом типа произведение и декартово произведение
нечетких множеств задано формулой (3.72), то выражение (3.238) принимает вид
 (3.243)
(3.243)
Пример 3.34
Если ![]() ,
, ![]() -норма имеет тип min, нечеткая импликация
определяется правилом типа произведение и декартово произведение нечетких
множеств задано формулой (3.72), то получаем выражение
-норма имеет тип min, нечеткая импликация
определяется правилом типа произведение и декартово произведение нечетких
множеств задано формулой (3.72), то получаем выражение
 (3.244)
(3.244)
Случай 2
На выходе блока выработки решения
получаем одно нечеткое множество ![]() по обобщенному нечеткому правилу modus
ponens, которое принимает вид
по обобщенному нечеткому правилу modus
ponens, которое принимает вид
|
Условие
Импликация
|
|
(3.245) |
|
Вывод |
|
При использовании комбинированного правила вывода получаем
 , (3.246)
, (3.246)
где
 . В силу
определений 3.12 и 3.28 получаем
. В силу
определений 3.12 и 3.28 получаем
![]() . (3.247)
. (3.247)
Заметим, что вывод по схеме
(3.245) - это результат комбинирования посылки ![]() и глобального правила (отношения)
и глобального правила (отношения) ![]() , которое представляет
собой обобщение отдельных правил
, которое представляет
собой обобщение отдельных правил ![]() ,
, ![]() . Будем называть такой прием глобальным
подходом к проблеме синтеза блока выработки решения.
. Будем называть такой прием глобальным
подходом к проблеме синтеза блока выработки решения.
Допустим теперь, что выполняется равенство
 . (3.248)
. (3.248)
Легко проверить [22], что
равенство (2.248) соблюдается, если правила нечеткой импликации (п. 3.8.3)
определены ![]() -нормой
типа min или произведение. При использовании определений 3.12 и 3.28 получаем
функцию принадлежности нечеткого множества
-нормой
типа min или произведение. При использовании определений 3.12 и 3.28 получаем
функцию принадлежности нечеткого множества ![]() в виде
в виде
![]() , (3.249)
, (3.249)
причем
функция принадлежности ![]() задается выражением (3.238).
задается выражением (3.238).
В этом случае вывод по схеме
(3.245) представляет собой результат локального комбинирования (3.238) посылки ![]() и правила
и правила ![]() ,
, ![]() с последующим агрегированием,
которое определяется равенством (3.249). Будем называть такой прием локальным
подходом к проблеме синтеза блока выработки решения.
с последующим агрегированием,
которое определяется равенством (3.249). Будем называть такой прием локальным
подходом к проблеме синтеза блока выработки решения.
Пример 3.35
Рассмотрим модуль нечеткого управления с базой правил
![]() :
IF (
:
IF (![]() это
это
![]() AND
AND ![]() это
это ![]() ) THEN (
) THEN (![]() это
это ![]() ), (3.250)
), (3.250)
![]() :
IF(
:
IF(![]() это
это ![]() AND
AND ![]() это
это ![]() ) THEN (
) THEN (![]() это
это ![]() ). (3.251)
). (3.251)
На его вход подан сигнал ![]() . После выполнения
фуззификации типа синглетон на входе блока выработки решения получаем нечеткие
множества
. После выполнения
фуззификации типа синглетон на входе блока выработки решения получаем нечеткие
множества ![]() и
и
![]() , причем
, причем
![]() ,
,
![]() . (3.252)
. (3.252)
Обозначим выходной сигнал модуля
нечеткого управления символом ![]() . Воспользуемся выражением (3.238),
которое принимает вид
. Воспользуемся выражением (3.238),
которое принимает вид
![]() . (3.253)
. (3.253)
В качестве ![]() -нормы будем применять операцию
minimum. Кроме того, допустим, что
-нормы будем применять операцию
minimum. Кроме того, допустим, что
![]() (3.254)
(3.254)
В этом случае
![]() (3.255)
(3.255)
В качестве нечеткой импликации
![]() (3.256)
(3.256)
можно применить одно из десяти правил, представленных в п. 3.8.3. При использовании правила типа minimum получаем
![]() . (3.257)
. (3.257)
Кроме того,
![]() . (3.258)
. (3.258)
В результате
 (3.259)
(3.259)
![]() . (3.260)
. (3.260)
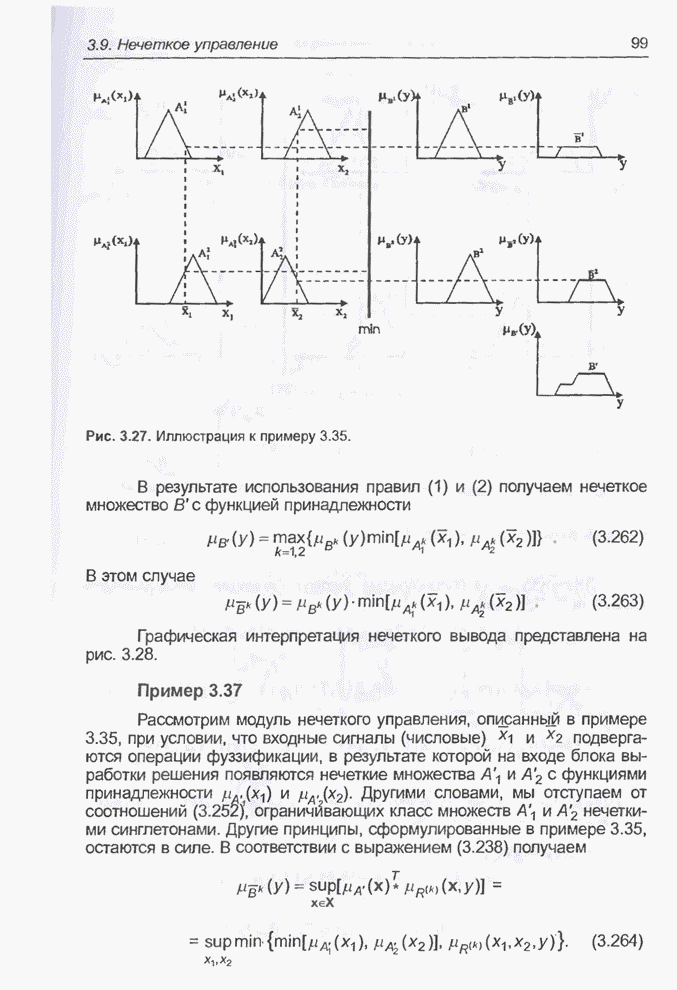
На рис. 3.27 представлена графическая интерпретация нечеткого вывода.

Рис. 3.27. Иллюстрация к примеру 3.35.
Пример 3.36
В этом примере мы повторим рассуждения, проведенные в примере 3.35, однако вместо нечеткой импликации (3.257) применим правило типа «произведение», т.е.
![]() . (3.261)
. (3.261)
В результате использования правил
(1) и (2) получаем нечеткое множество ![]() с функцией принадлежности
с функцией принадлежности
![]() . (3.262)
. (3.262)
В этом случае
![]() . (3.263)
. (3.263)
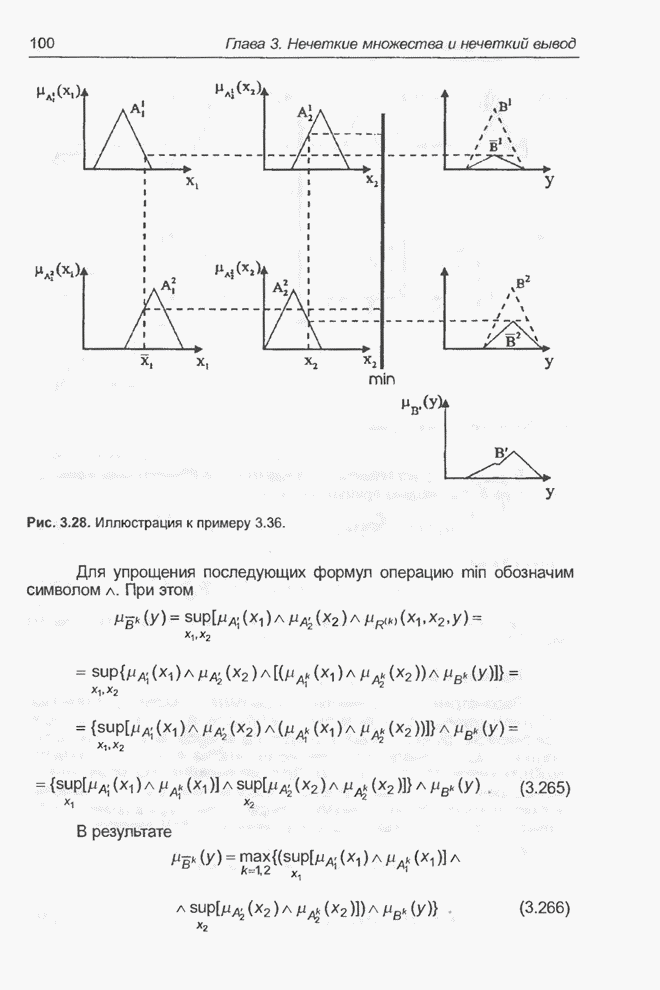
Графическая интерпретация нечеткого вывода представлена на рис. 3.28.

Рис. 3.28. Иллюстрация к примеру 3.36.
Пример 3.37
Рассмотрим модуль нечеткого
управления, описанный в примере 3.35, при условии, что входные сигналы
(числовые) ![]() и
и
![]() подвергаются
операции фуззификации, в результате которой на входе блока выработки решения
появляются нечеткие множества
подвергаются
операции фуззификации, в результате которой на входе блока выработки решения
появляются нечеткие множества ![]() и
и ![]() с функциями принадлежности
с функциями принадлежности ![]() и
и ![]() . Другими словами, мы отступаем
от соотношений (3.252), ограничивающих класс множеств
. Другими словами, мы отступаем
от соотношений (3.252), ограничивающих класс множеств ![]() и
и ![]() нечеткими синглетонами. Другие
принципы, сформулированные в примере 3.35, остаются в силе. В соответствии с
выражением (3.238) получаем
нечеткими синглетонами. Другие
принципы, сформулированные в примере 3.35, остаются в силе. В соответствии с
выражением (3.238) получаем
 (3.264)
(3.264)
Для упрощения последующих формул
операцию min обозначим символом ![]() . При этом
. При этом
 (3.265)
(3.265)
В результате
 (3.266)
(3.266)
Графическая интерпретация нечеткого вывода представлена на рис. 3.29.

Рис. 3.29. Иллюстрация к примеру 3.37.
Пример 3.38
В примере 3.37 мы предположили, что нечеткая импликация имеет тип minimum, т.е.
![]() .
.
Применим теперь импликацию типа «произведение»
![]() .
.
Остальные условия такие же, как в примере 3.37. По аналогии с предыдущим примером получаем
 (3.267)
(3.267)
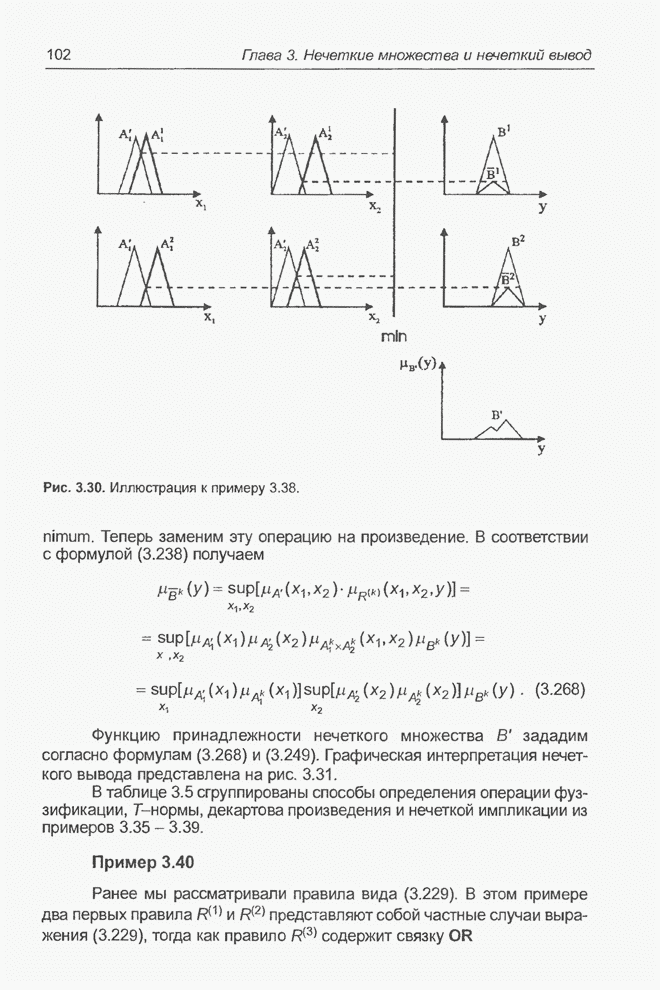
Графическая интерпретация нечеткого вывода представлена на рис. 3.30.

Рис. 3.30. Иллюстрация к примеру 3.38.
Пример 3.39
В примере 3.37 мы предположили,
что ![]() -норма,
декартово произведение и нечеткая импликация определяются с помощью операции minimum.
Теперь заменим эту операцию на произведение. В соответствии с формулой (3.238)
получаем
-норма,
декартово произведение и нечеткая импликация определяются с помощью операции minimum.
Теперь заменим эту операцию на произведение. В соответствии с формулой (3.238)
получаем
 (3.268)
(3.268)
Функцию принадлежности нечеткого
множества ![]() зададим
согласно формулам (3.268) и (3.249). Графическая интерпретация нечеткого вывода
представлена на рис. 3.31.
зададим
согласно формулам (3.268) и (3.249). Графическая интерпретация нечеткого вывода
представлена на рис. 3.31.

Рис. 3.31. Иллюстрация к примеру 3.39.
В таблице 3.5 сгруппированы
способы определения операции фуззификации, ![]() -нормы, декартова произведения и нечеткой
импликации из примеров 3.35 - 3.39.
-нормы, декартова произведения и нечеткой
импликации из примеров 3.35 - 3.39.
Таблица
3.5. Способы определения операции фуззификации, ![]() -нормы, декартова произведения и нечеткой
импликации из примеров 3.35 - 3.39
-нормы, декартова произведения и нечеткой
импликации из примеров 3.35 - 3.39
|
Пример |
Операция фуззификации |
|
Определение нечеткой импликации |
Правило |
Рисунок |
|
3.35 |
синглетон |
min |
min |
min |
3.27 |
|
3.36 |
синглетон |
min |
min |
произведение |
3.28 |
|
3.37 |
не синглетон |
min |
min |
min |
3.29 |
|
3.38 |
не синглетон |
min |
min |
произведение |
3.30 |
|
3.39 |
|
произведение |
произведение |
произведение |
3.31 |
Пример 3.40
Ранее мы рассматривали правила
вида (3.229). В этом примере два первых правила ![]() и
и ![]() представляют собой частные случаи
выражения (3.229), тогда как правило
представляют собой частные случаи
выражения (3.229), тогда как правило ![]() содержит связку OR
содержит связку OR
![]() :
IF (
:
IF (![]() это
это ![]() AND
AND
![]() это
это ![]() ) THEN (
) THEN (![]() это
это ![]() ),
),
![]() :
IF (
:
IF (![]() это
это ![]() AND
AND
![]() это
это ![]() ) THEN (
) THEN (![]() это
это ![]() ),
),
![]() :
IF (
:
IF (![]() это
это ![]() OR
OR ![]() это
это ![]() ) THEN (
) THEN (![]() это
это ![]() ).
).
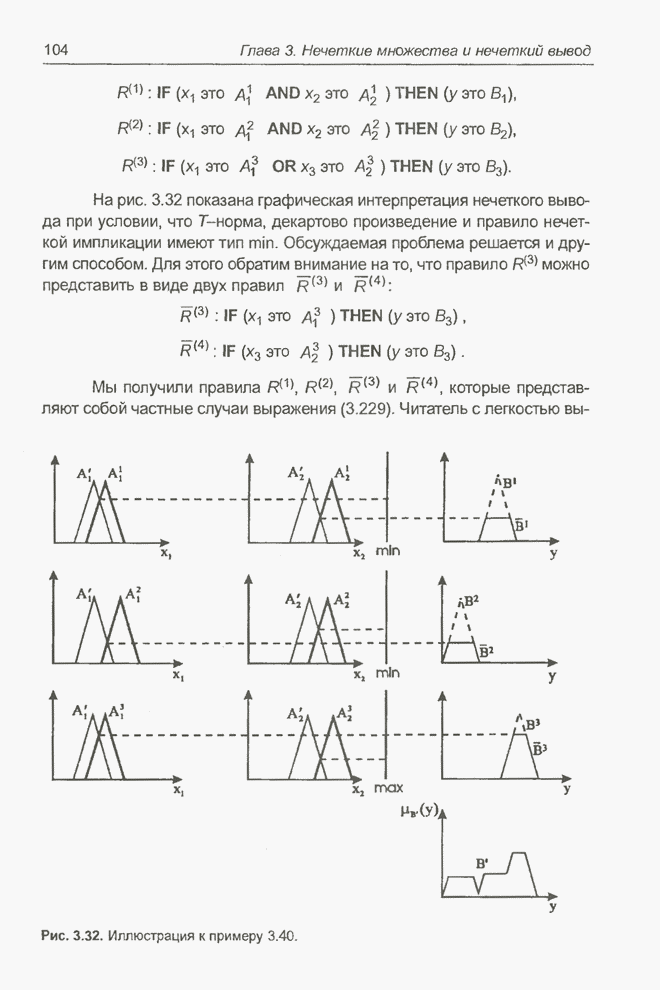
На рис. 3.32 показана графическая
интерпретация нечеткого вывода при условии, что ![]() -норма, декартово произведение и правило
нечеткой импликации имеют тип min. Обсуждаемая проблема решается и другим
способом. Для этого обратим внимание на то, что правило можно представить в
виде двух правил
-норма, декартово произведение и правило
нечеткой импликации имеют тип min. Обсуждаемая проблема решается и другим
способом. Для этого обратим внимание на то, что правило можно представить в
виде двух правил ![]() и
и
![]() :
:
![]() :
IF (
:
IF (![]() это
это ![]() ) THEN (
) THEN (![]() это
это ![]() ),
),
![]() :
IF (
:
IF (![]() это
это ![]() ) THEN
(
) THEN
(![]() это
это ![]() ).
).

Рис. 3.32. Иллюстрация к примеру 3.40.
Мы получили правила ![]() ,
, ![]() ,
, ![]() и
и ![]() , которые представляют собой частные
случаи выражения (3.229). Читатель с легкостью выведет аналитическую форму
функции принадлежности множества
, которые представляют собой частные
случаи выражения (3.229). Читатель с легкостью выведет аналитическую форму
функции принадлежности множества ![]() , базируясь на результатах примера 3.37.
, базируясь на результатах примера 3.37.
3.9.1.4. Блок дефуззификации
На выходе блока выработки решения
формируется либо ![]() нечетких
множеств
нечетких
множеств ![]() (случай
1, п. 3.9.1.3) с функциями принадлежности
(случай
1, п. 3.9.1.3) с функциями принадлежности ![]() ,
, ![]() , либо одно нечеткое множество
, либо одно нечеткое множество ![]() (случай 2, п.
3.9.1.3) с функцией принадлежности
(случай 2, п.
3.9.1.3) с функцией принадлежности ![]() . Встает задача отображения нечетких
множеств
. Встает задача отображения нечетких
множеств ![]() (либо
нечеткого множества
(либо
нечеткого множества ![]() )
в единственное значение
)
в единственное значение ![]() , которое представляет собой управляющее
воздействие, подаваемое на вход объекта. Такое отображение называется
дефуззификацией (defuzzification), и реализуется оно в одноименном блоке.
, которое представляет собой управляющее
воздействие, подаваемое на вход объекта. Такое отображение называется
дефуззификацией (defuzzification), и реализуется оно в одноименном блоке.
Если на выходе блока выработки
решения формируется ![]() нечетких
множеств
нечетких
множеств ![]() ,
то значение
,
то значение ![]() можно
рассчитать с помощью различных методов.
можно
рассчитать с помощью различных методов.
1.
Метод дефуззификации по среднему центру (сenter average defuzzification).
Значение ![]() рассчитывается
по формуле
рассчитывается
по формуле
 , (3.269)
, (3.269)
где
![]() - это
точка, в которой функция
- это
точка, в которой функция ![]() принимает максимальное значение, т.е.
принимает максимальное значение, т.е.
![]() . (3.270)
. (3.270)
Точка ![]() называется центром (center)
нечеткого множества
называется центром (center)
нечеткого множества ![]() .
.
На рис. 3.33 представлена идея
этого метода для ![]() .
Обратим внимание, что значение
.
Обратим внимание, что значение ![]() не зависит от формы и носителя функции
принадлежности
не зависит от формы и носителя функции
принадлежности ![]() .
.

Рис. 3.33. Иллюстрация метода дефуззификации по среднему центру.
2.
Метод дефуззификации по сумме центров (center of sums defuzzification).
Значение ![]() рассчитывается
следующим образом:
рассчитывается
следующим образом:
 . (3.271)
. (3.271)
Если выходное значение блока
выработки решения представляет собой единственное нечеткое множество ![]() , то значение
, то значение ![]() можно определить с
применением следующих двух методов.
можно определить с
применением следующих двух методов.
3. Метод
центра тяжести (center of gravity method, center of area method). Значение ![]() рассчитывается как центр
тяжести функции принадлежности
рассчитывается как центр
тяжести функции принадлежности ![]() , т.е.
, т.е.
 (3.272)
(3.272)
при
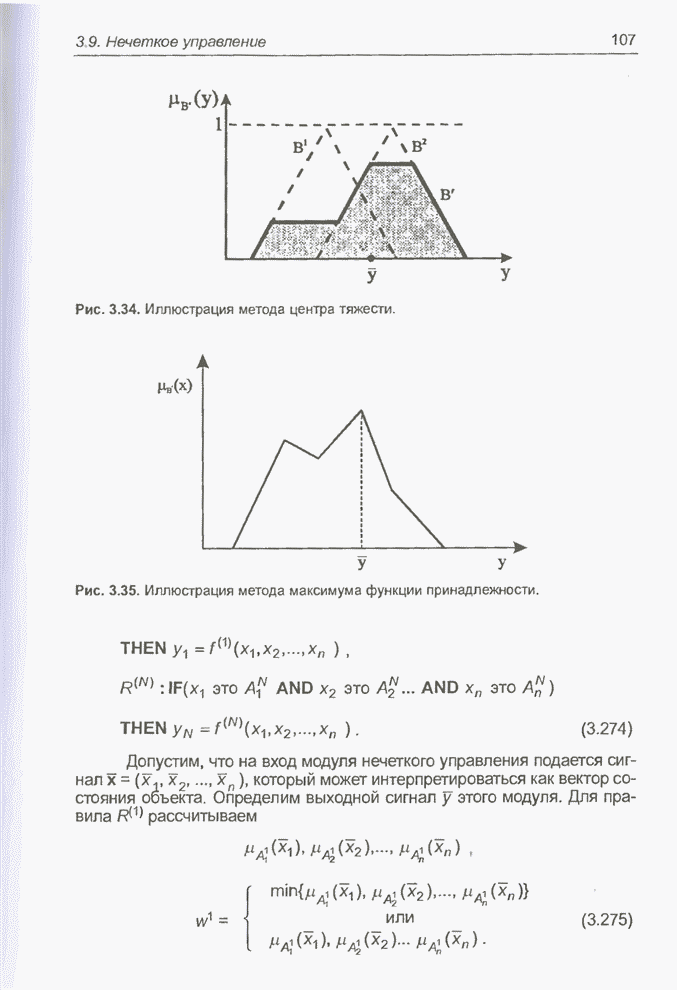
условии, что оба интеграла в приведенном выражении существуют. На рис. 3.34
иллюстрируется способ определения значения ![]() по методу центра тяжести.
по методу центра тяжести.

Рис. 3.34. Иллюстрация метода центра тяжести.
4.
Метод максимума функции принадлежности. Значение ![]() рассчитывается в соответствии с формулой
рассчитывается в соответствии с формулой
![]() (3.273)
(3.273)
при
условии, что ![]() -
это унимодальная функция. Этот метод не учитывает форму функции принадлежности,
что иллюстрируется на рис. 3.35.
-
это унимодальная функция. Этот метод не учитывает форму функции принадлежности,
что иллюстрируется на рис. 3.35.

Рис. 3.35. Иллюстрация метода максимума функции принадлежности.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Предисловие к русскому изданию
- ГЛАВА 1. ВВЕДЕНИЕ
- Список литературы
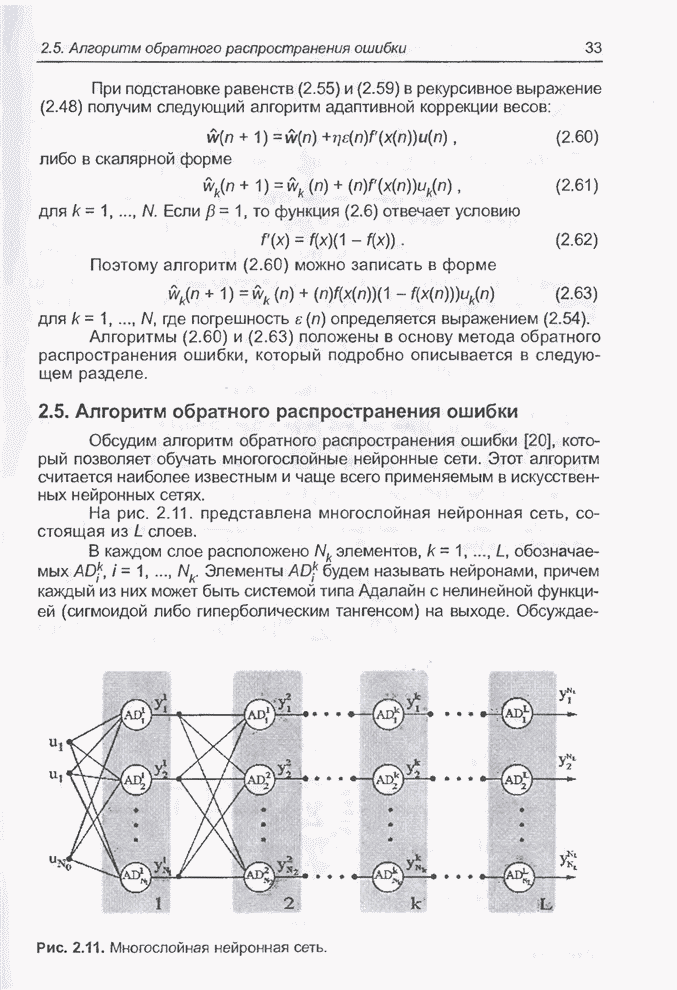
- ГЛАВА 2. МНОГОСЛОЙНЫЕ НЕЙРОННЫЕ СЕТИ И АЛГОРИТМЫ ИХ ОБУЧЕНИЯ
- 2.1. Введение
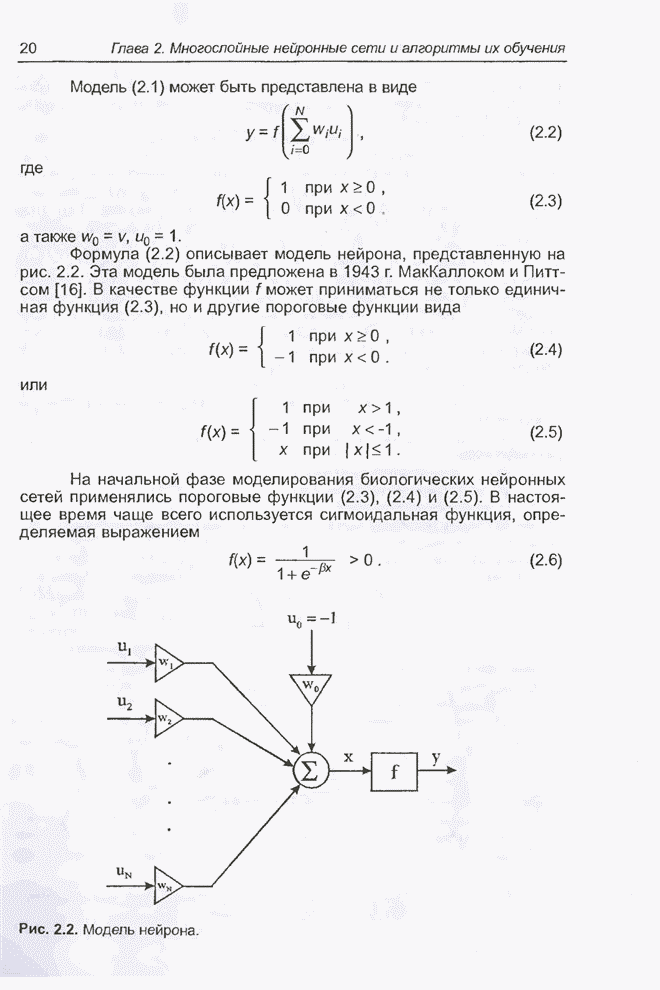
- 2.2. Нейрон и его модели
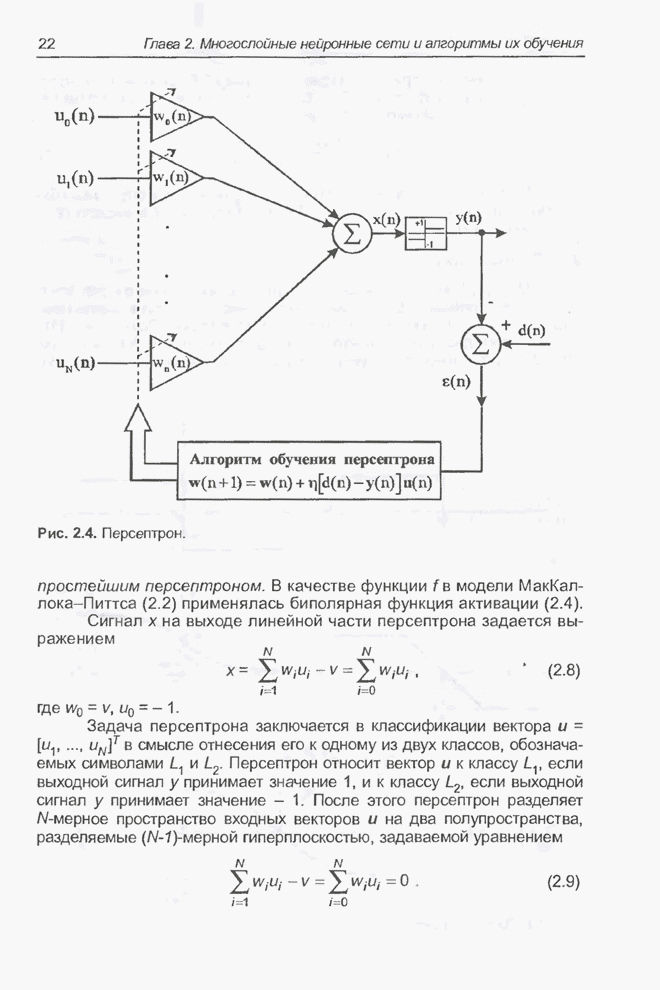
- 2.3. Персептрон
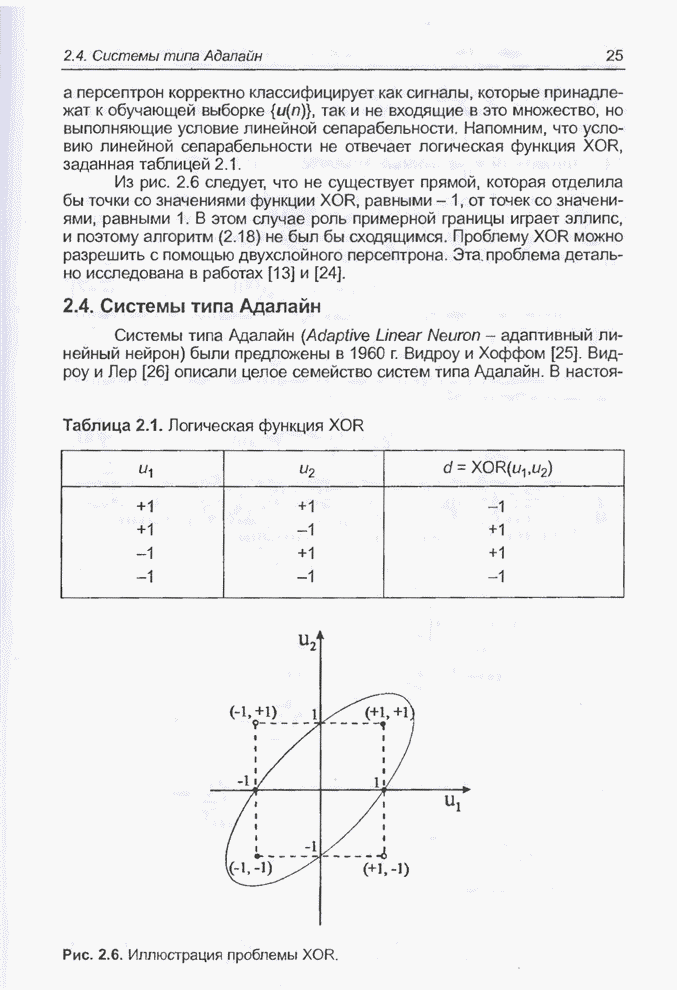
- 2.4. Системы типа Адалайн
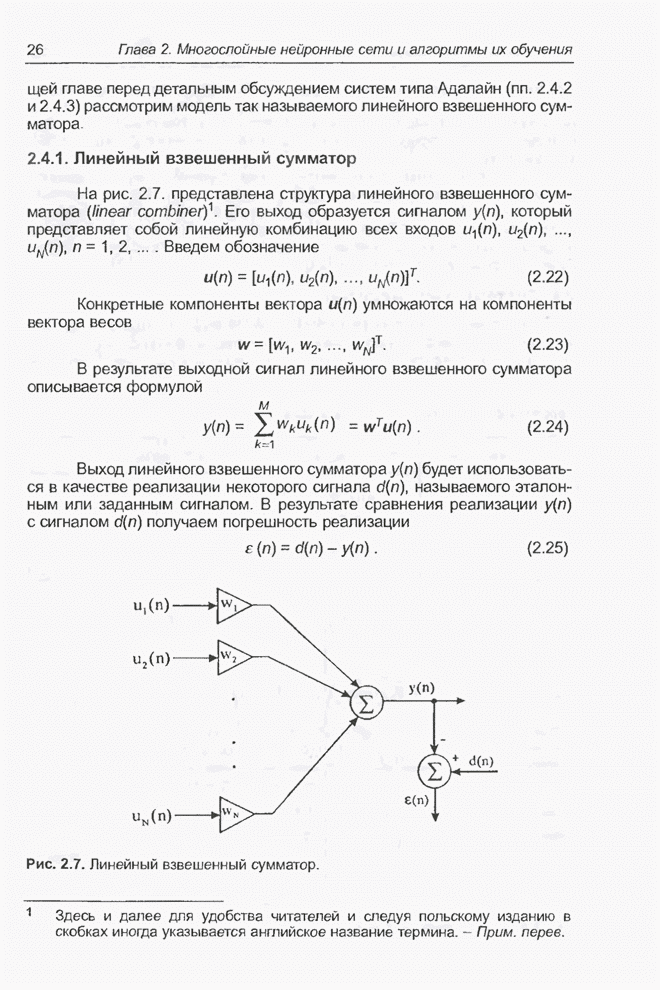
- 2.4.1. Линейный взвешенный сумматор
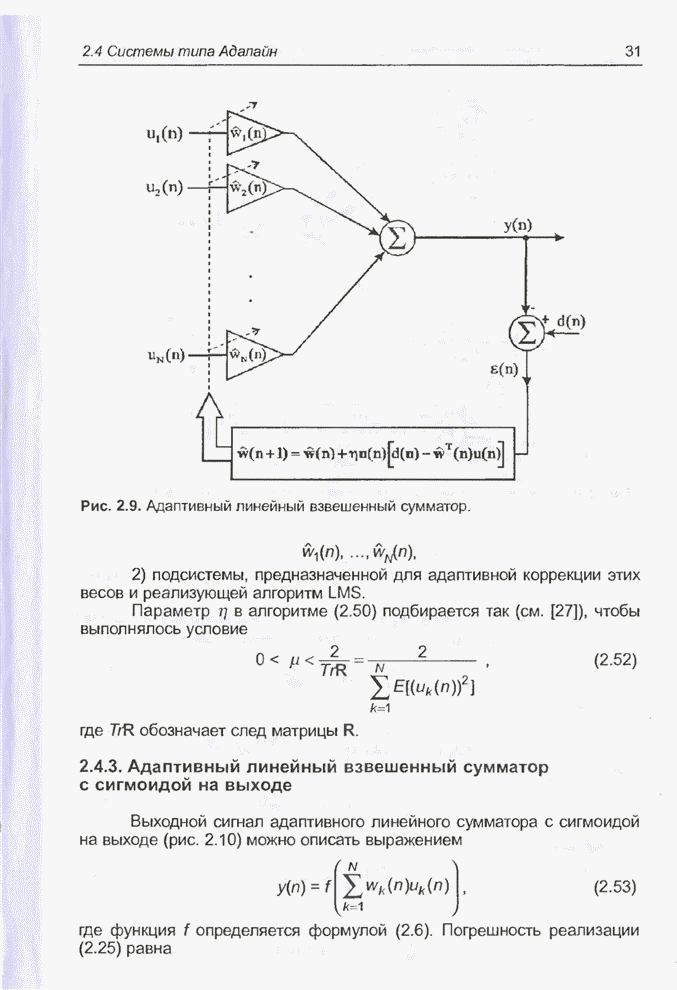
- 2.4.2. Адаптивный линейный взвешенный сумматор
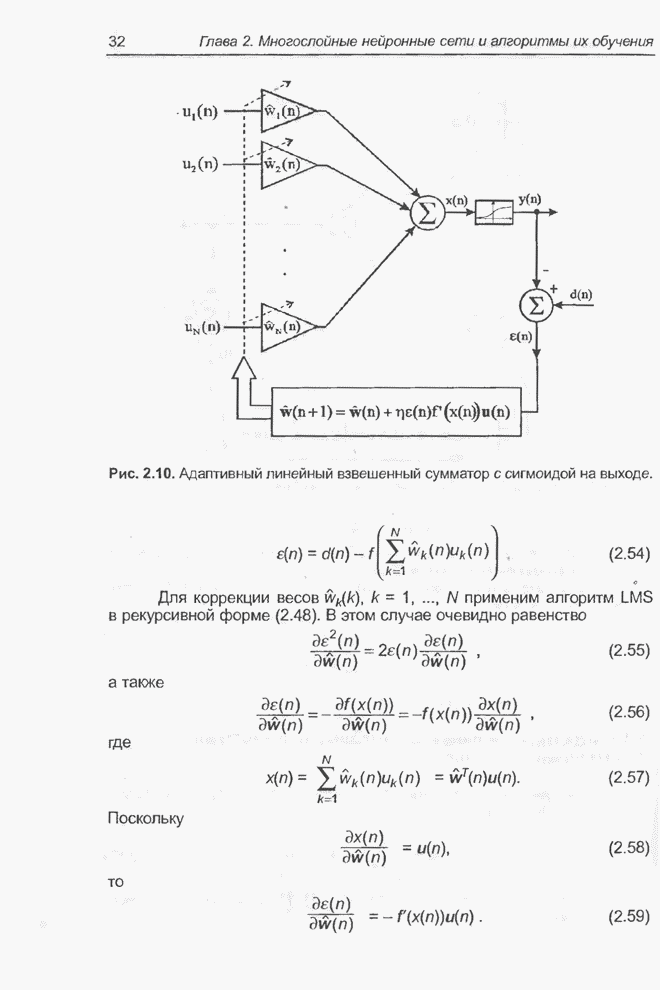
- 2.4.3. Адаптивный линейный взвешенный сумматор с сигмоидой на выходе
- 2.5. Алгоритм обратного распространения ошибки
- 2.6. Применение рекуррентного метода наименьших квадратов для обучения нейронных сетей
- Список литературы
- ГЛАВA3. НЕЧЕТКИЕ МНОЖЕСТВА И НЕЧЕТКИЙ ВЫВОД
- 3.1. Введение
- 3.2. Основные понятия и определения теории нечетких множеств
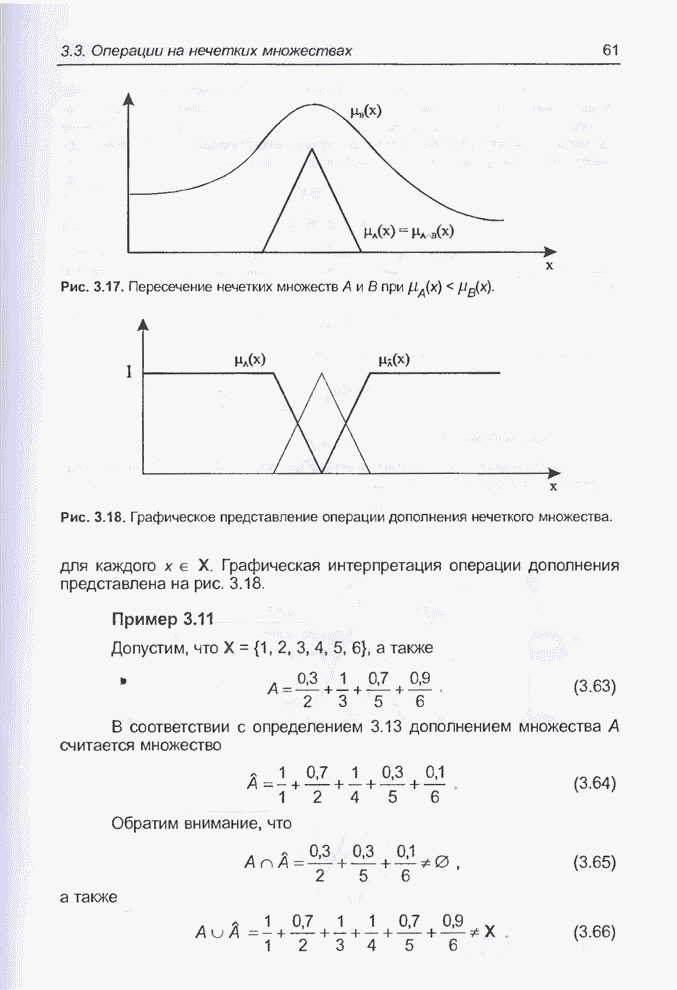
- 3.3. Операции на нечетких множествах
- 3.4. Принцип расширения
- 3.5. Нечеткие числа
- 3.6. Треугольные нормы
- 3.7. Нечеткие отношения и их свойства
- 3.8. Нечеткий вывод
- 3.9. Нечеткое управление
- 3.9.1. Классический модуль нечеткого управления
- 3.9.2. Метод нечеткого управления Такаги-Сугено
- 3.10. Проектирование базы нечетких правил на основе численных данных
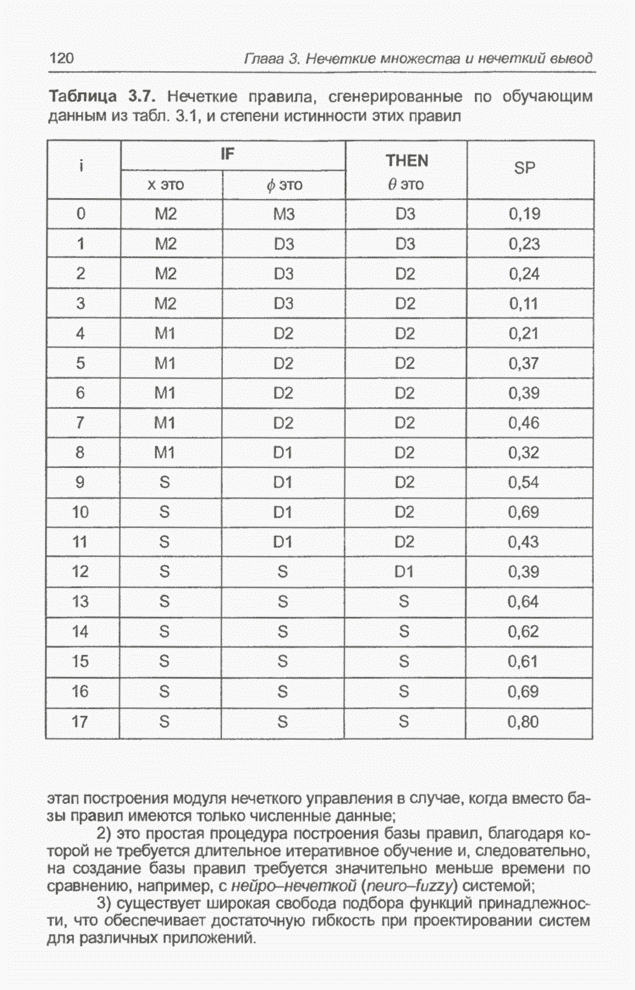
- 3.10.1. Построение нечетких правил
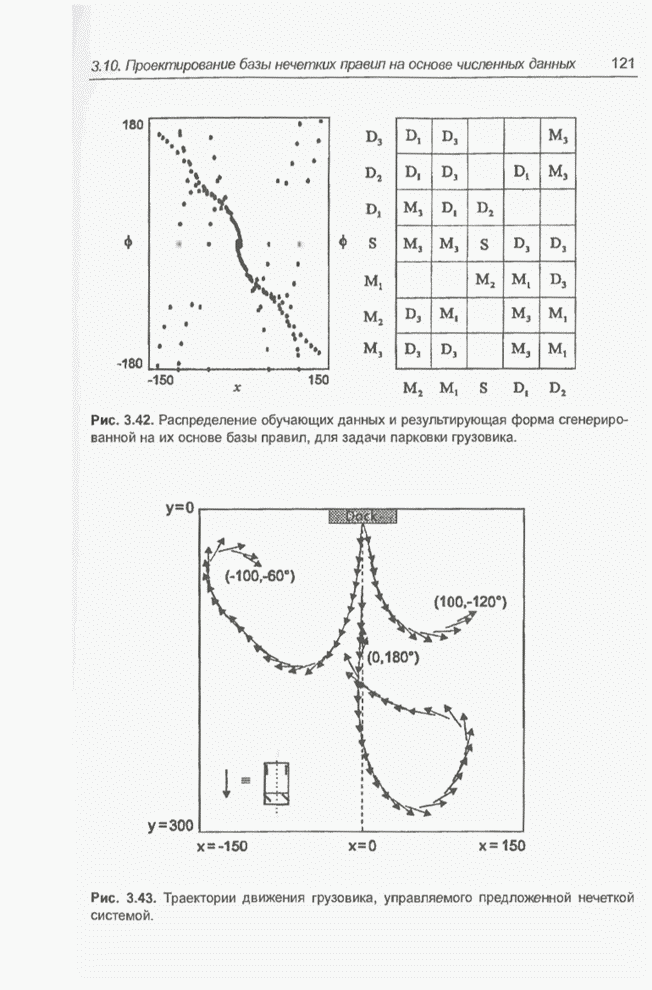
- 3.10.2. Задача парковки грузовика
- 3.10.3. Примечание
- Список литературы
- ГЛАВА 4. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 4.1. Введение
- 4.2. Генетические алгоритмы и традиционные методы оптимизации
- 4.3. Основные понятия генетических алгоритмов
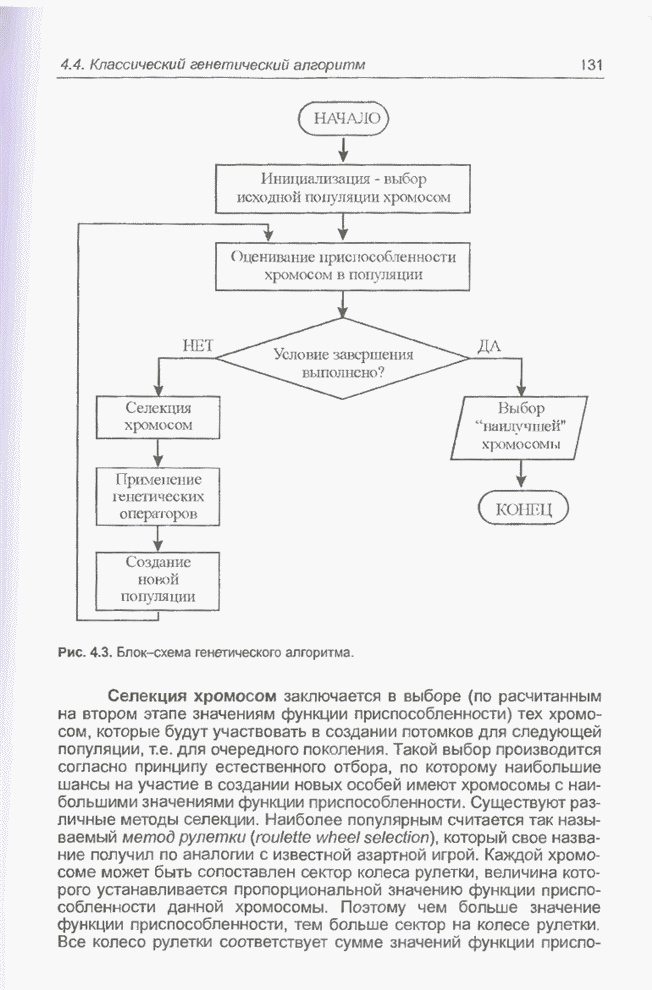
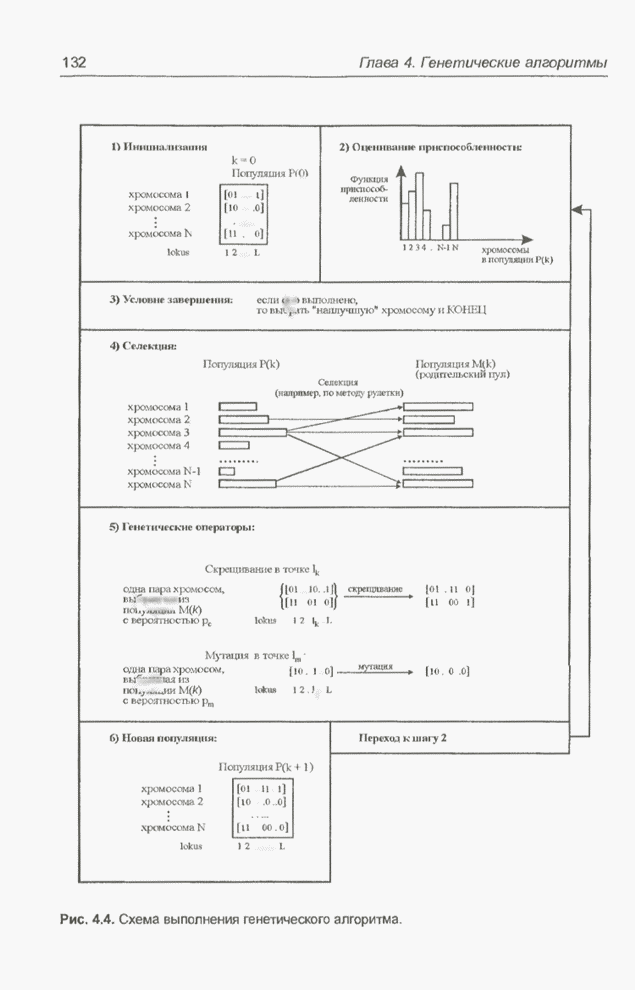
- 4.4. Классический генетический алгоритм
- 4.5. Иллюстрация выполнения классического генетического алгоритма
- 4.6. Кодирование параметров задачи в генетическом алгоритме
- 4.7. Основная теорема о генетических алгоритмах
- 4.8. Модификации классического генетического алгоритма
- 4.8.1. Методы селекции
- 4.8.2. Особые процедуры репродукции
- 4.8.3. Генетические операторы
- 4.8.4. Методы кодирования
- 4.8.5. Масштабирование функции приспособленности
- 4.8.6. Ниши в генетическом алгоритме
- 4.8.7. Генетические алгоритмы для многокритериальной оптимизации
- 4.8.8. Генетические микроалгоритмы
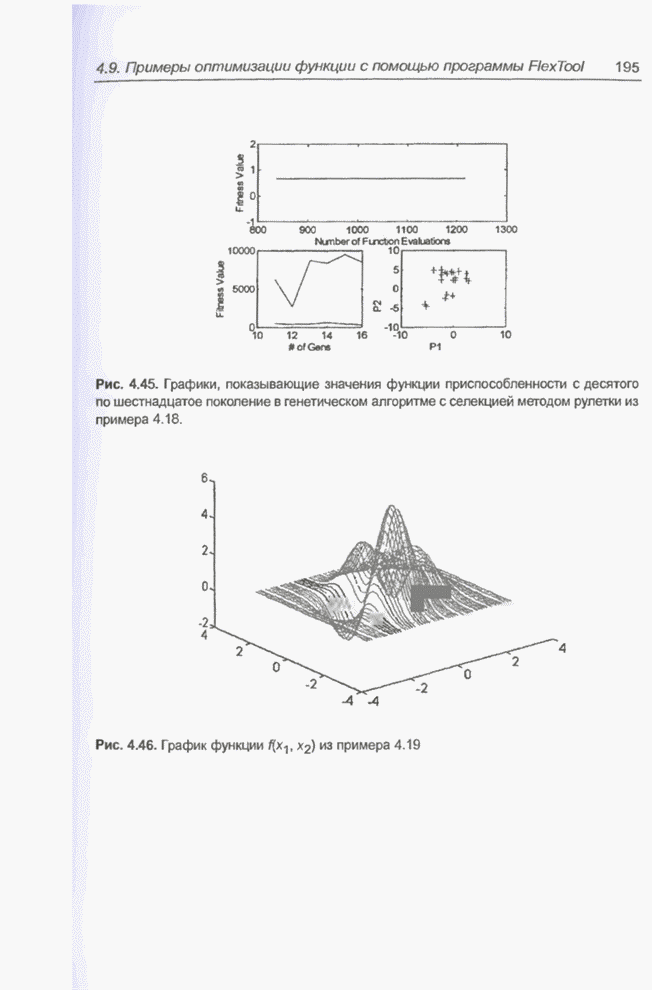
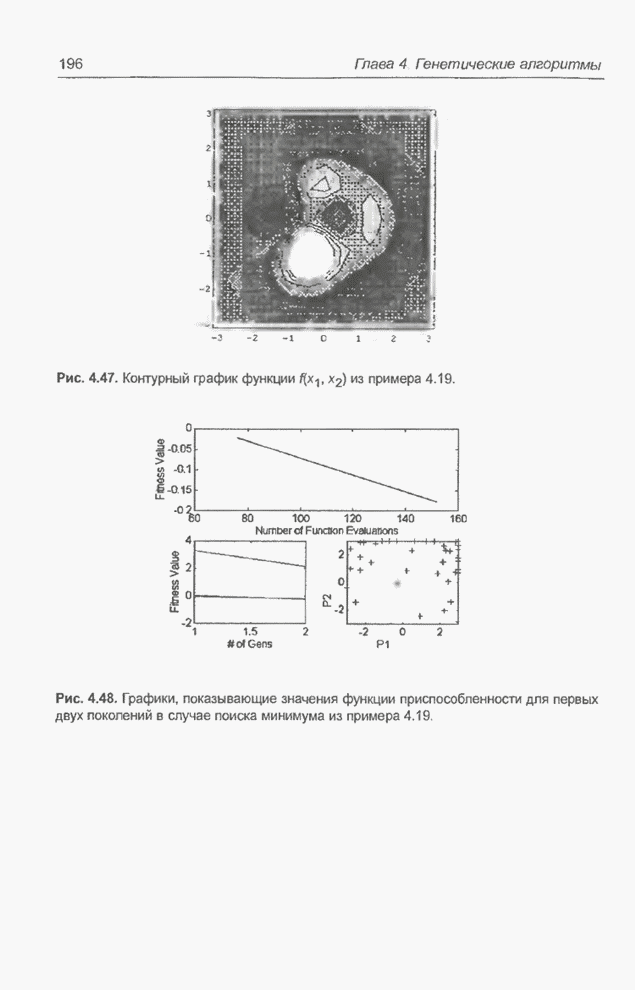
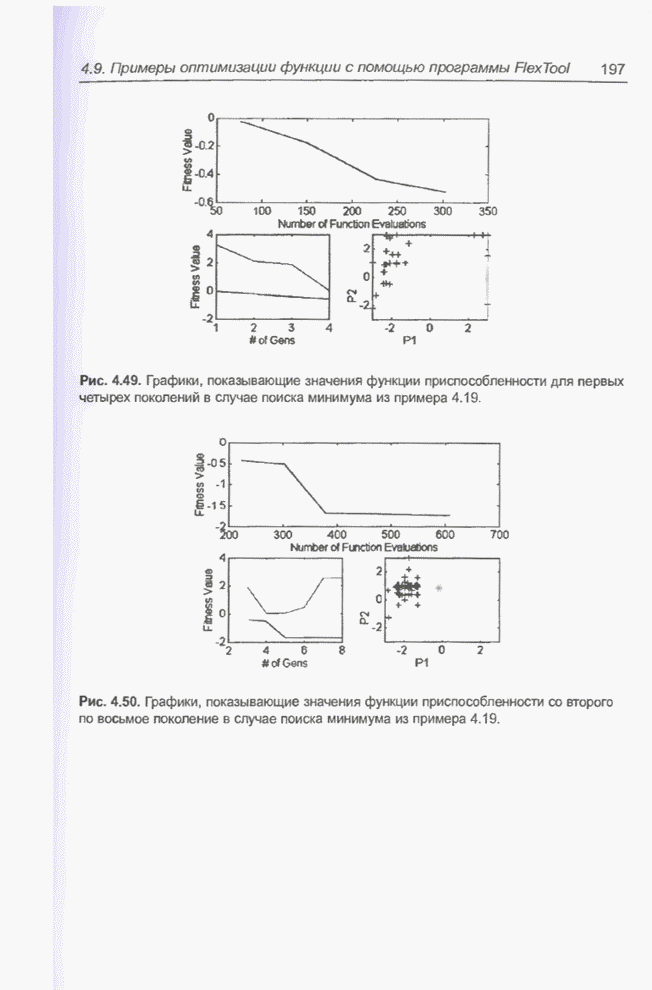
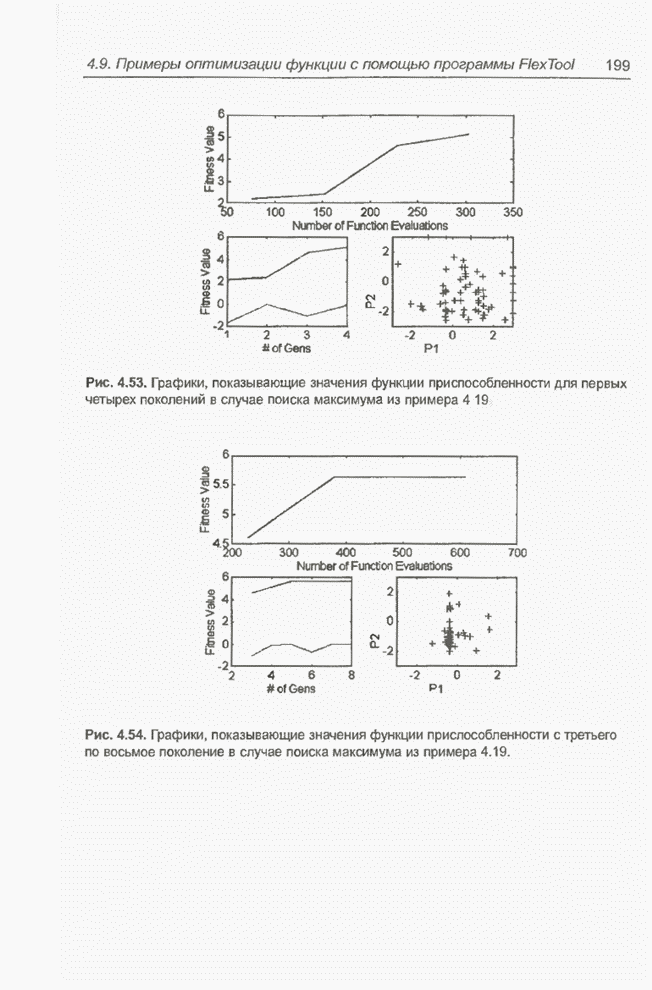
- 4.9. Примеры оптимизации функции с помощью программы FlexTool
- 4.10. Эволюционные алгоритмы
- 4.11. Приложения эволюционных алгоритмов
- 4.11.1. Примеры оптимизации функции с помощью программы Evolver
- 4.11.2. Решение комбинаторных задач с помощью программы Evolver
- 4.12. Эволюционные алгоритмы в нейронных сетях
- 4.12.1. Независимое применение генетических алгоритмов и нейронных сетей
- 4.12.2. Нейронные сети для поддержки генетических алгоритмов
- 4.12.3. Генетические алгоритмы для поддержки нейронных сетей
- 4.12.4. Применение генетических алгоритмов для обучения нейронных сетей
- 4.12.5. Генетические алгоритмы для выбора топологии нейронных сетей
- 4.12.6. Адаптивные взаимодействующие системы
- 4.12.7. Типовой цикл эволюции
- 4.12.7.1. Эволюция весов связей
- 4.12.7.2. Эволюция архитектуры сети
- 4.12.7.3. Эволюция правил обучения
- 4.13. Примеры моделирования эволюционных алгоритмов в приложении к нейронным сетям
- 4.13.1. Программы Evolver и BrainMaker
- 4.13.2. Программа GTO
- Список литературы
- ГЛАВА 5. МОДУЛИ НЕЧЕТКО-НЕЙРОННОГО УПРАВЛЕНИЯ
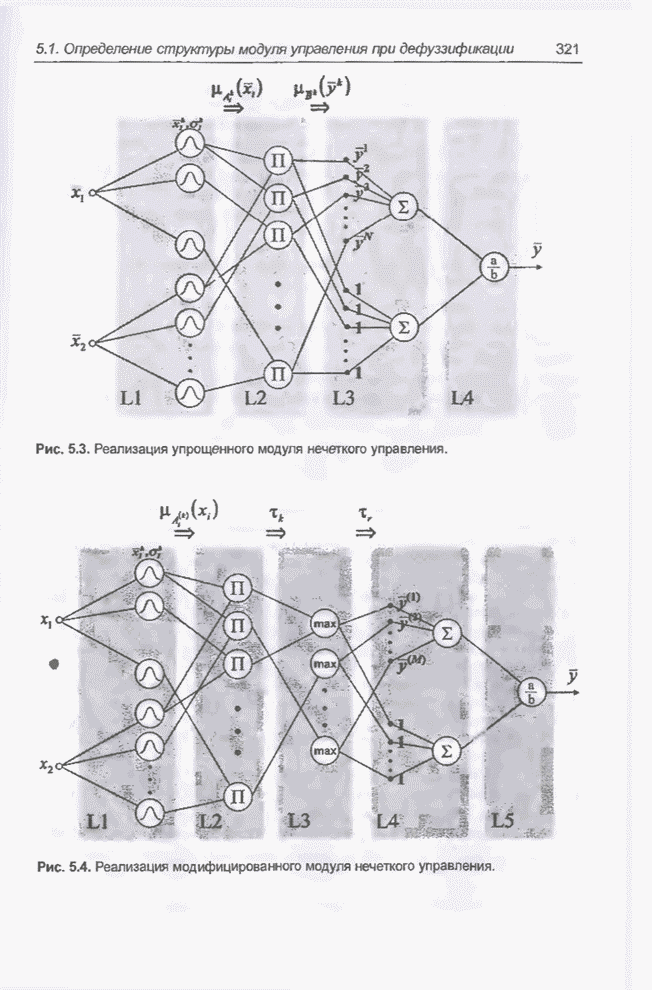
- 5.1. Модуль нечеткого управления со структурой, определенной в процессе дефуззификации
- 5.1.2. Конструкция модуля
- 5.1.3. Структура модуля
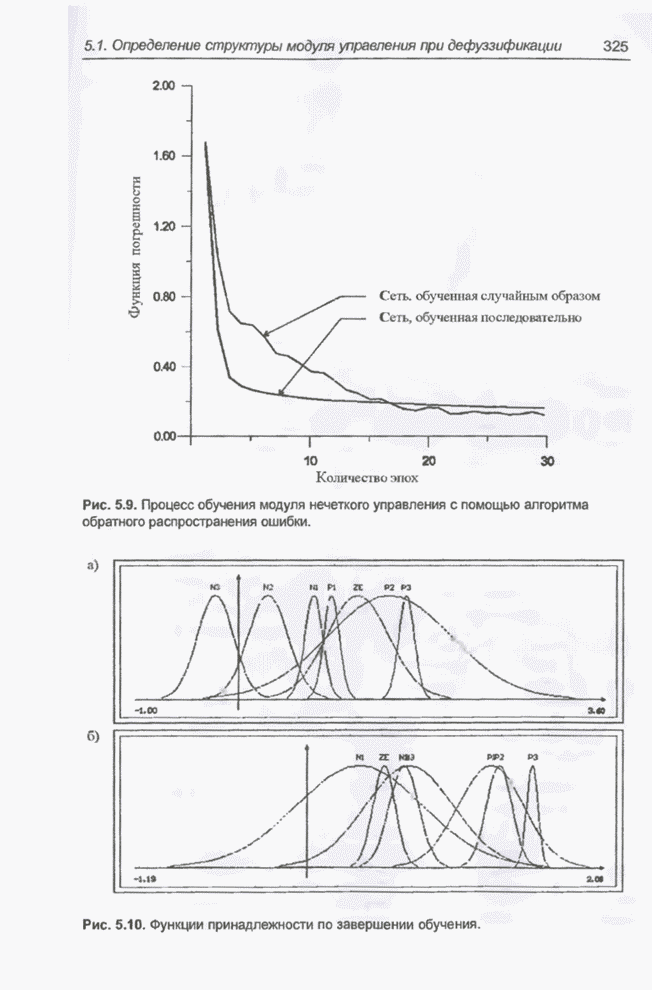
- 5.1.4. Использование алгоритма обратного распространения ошибки
- 5.1.5. Модификации модуля
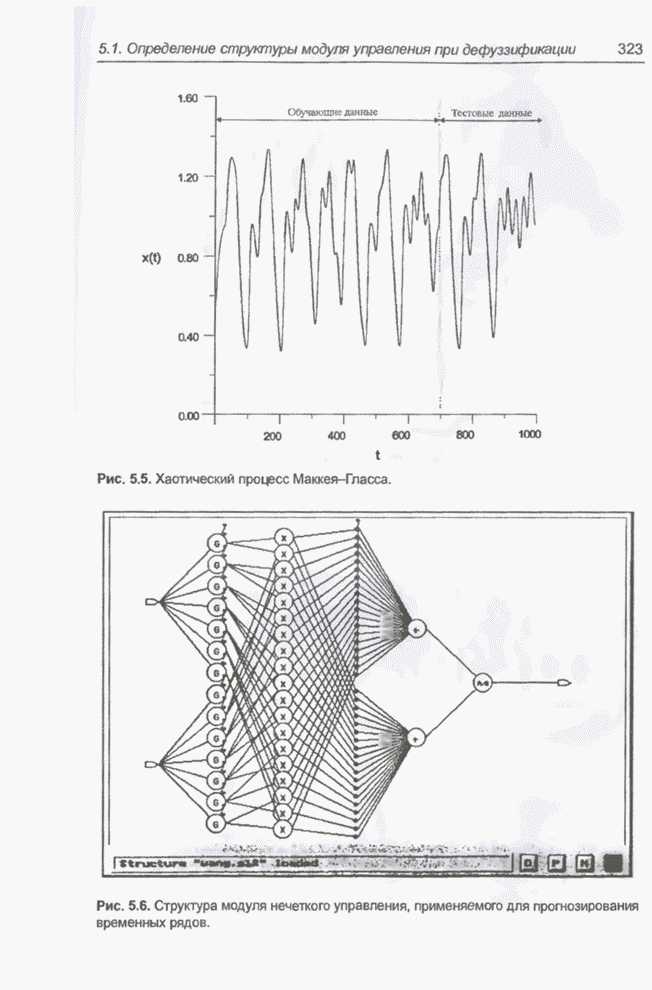
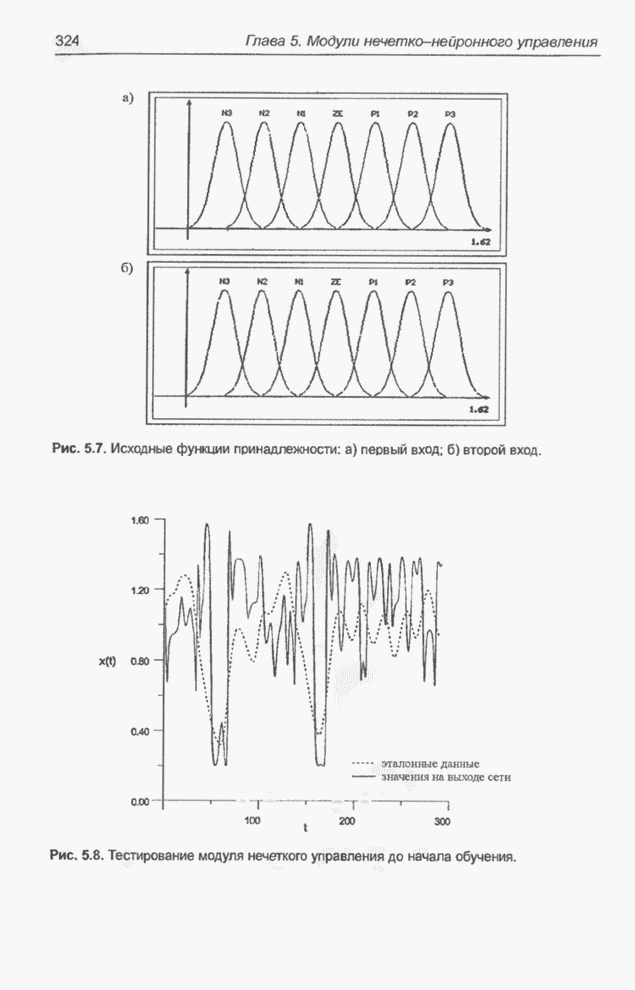
- 5.1.6. Применение модуля нечеткого управления для прогнозирования случайных временных рядов
- 5.1.7. Применение модуля нечеткого управления для решения задачи парковки грузовика
- 5.1.8. Примечание
- 5.2. Представление модуля нечеткого управления в виде стандартной нейронной сети
- 5.3. Модуль нечеткого управления с нейронной сетью для выполнения дефуззификации
- 5.3.1. Введение
- 5.3.2. Конструкция модуля
- 5.3.3. Структура модуля
- 5.3.4. Алгоритмы обучения модуля
- 5.3.5. Решение задачи стабилизации перевернутого маятника
- 5.3.6. Примечание
- 5.4. Модуль нечеткого управления с возможностью коррекции правил
- 5.4.1. Введение
- 5.4.2. Фаза обучения на основе самоорганизации
- 5.4.3. Фаза обучения с учителем
- 5.4.4. Примечание
- 5.5. Модуль нечеткого управления типа Такаги-Сугено
- 5.5.1. Введение
- 5.5.2. Нейронная реализация функции принадлежности
- 5.5.3. Модули Такаги-Сугено
- 5.5.4. Реализация условий
- 5.5.5. Реализация заключений
- 5.5.6. Примечание
- 5.6. Модуль нечеткого управления типа Такаги-Сугено: случай зависимых лингвистических переменных
- 5.6.1. Введение
- 5.6.2. Нейронные сети для нечеткого вывода
- 5.6.3. Структура системы
- 5.6.4. Способ обучения
- 5.6.5. Решение задачи парковки грузовика
- 5.6.6. Примечание
- Список литературы













































































































































































































































































 ,
, 