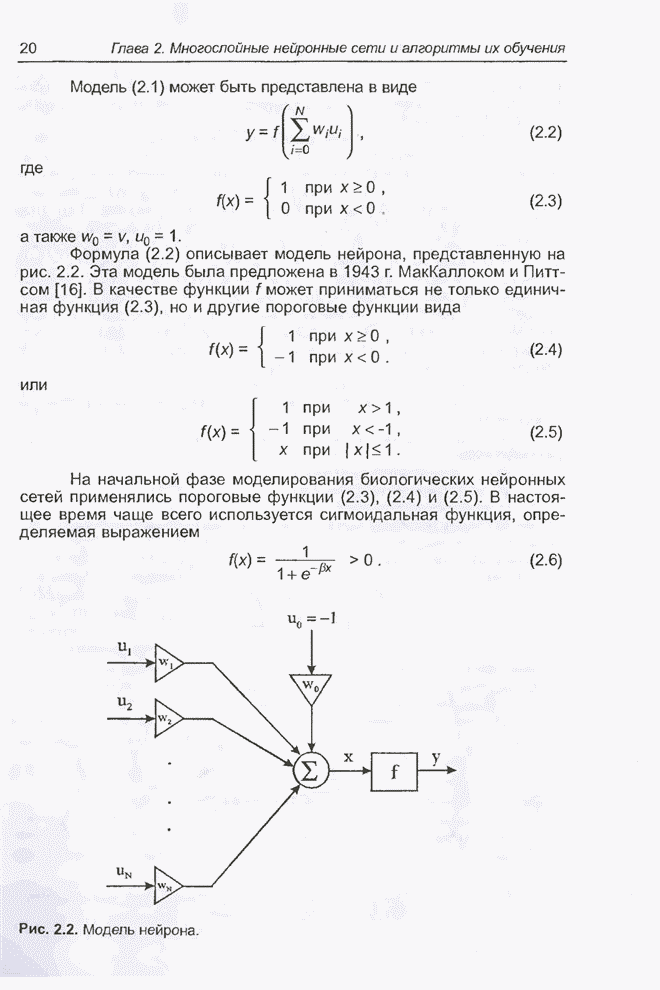
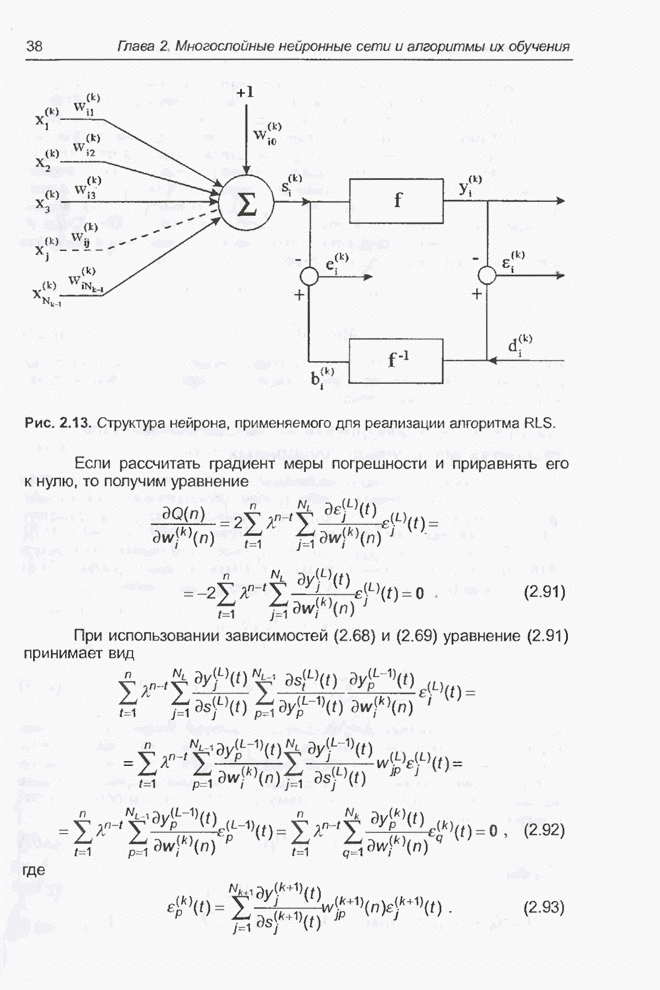
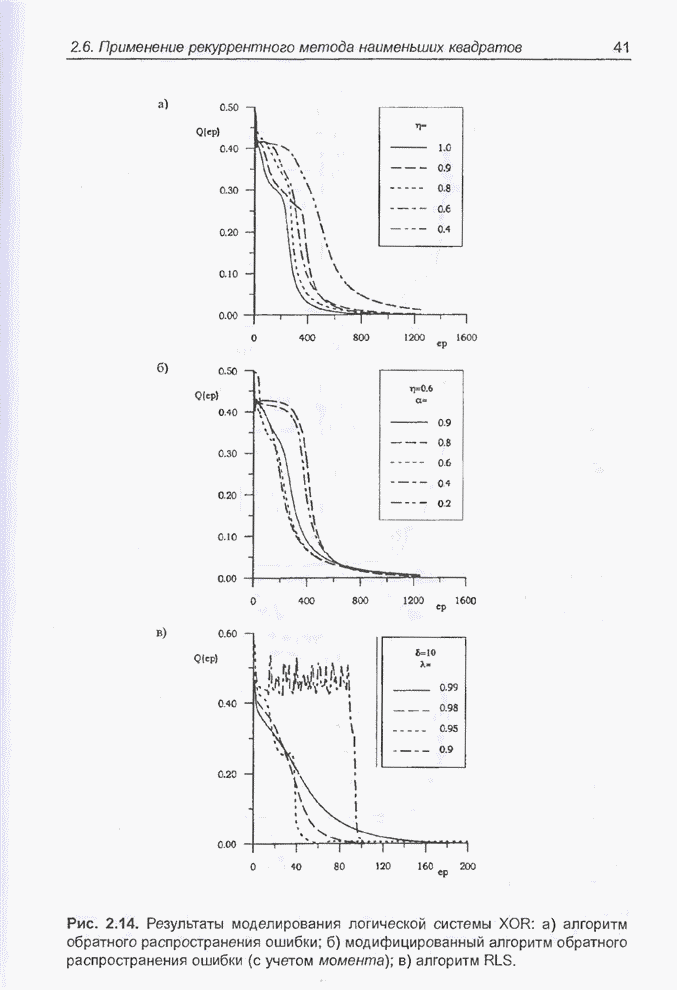
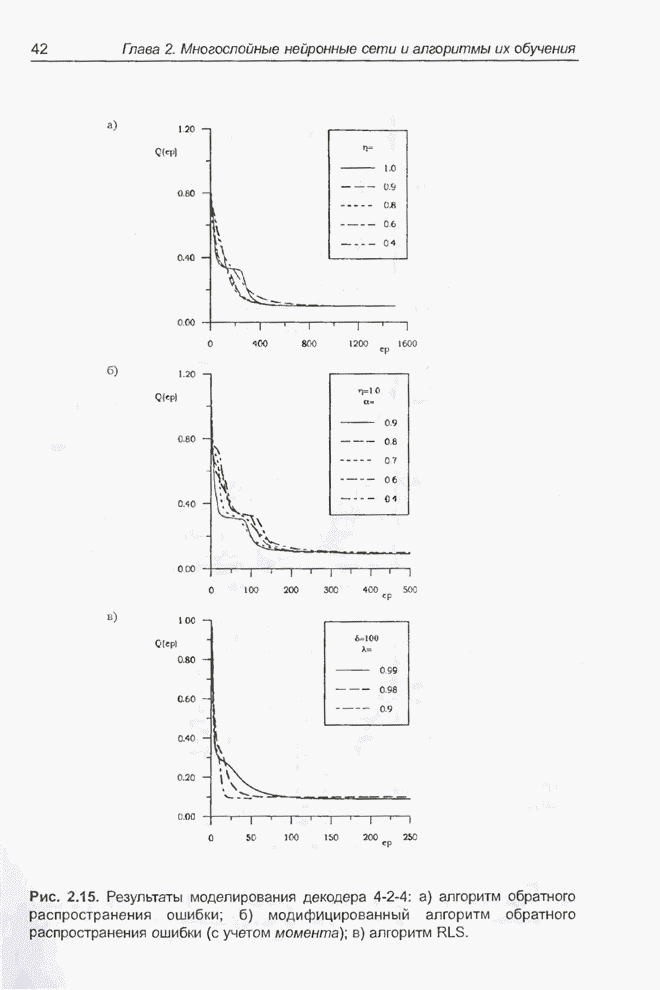
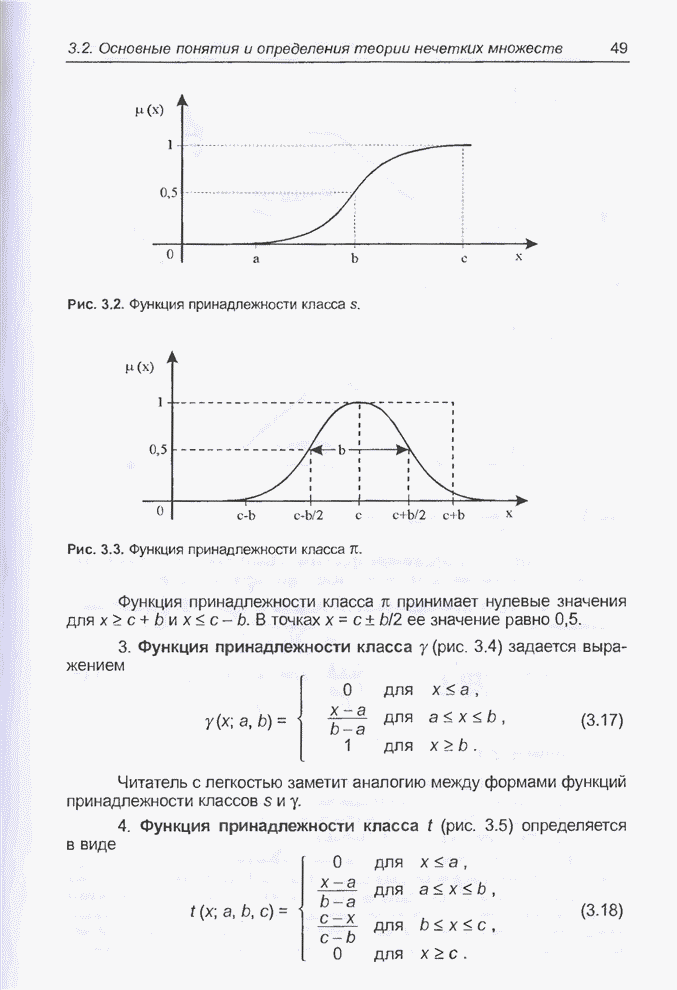
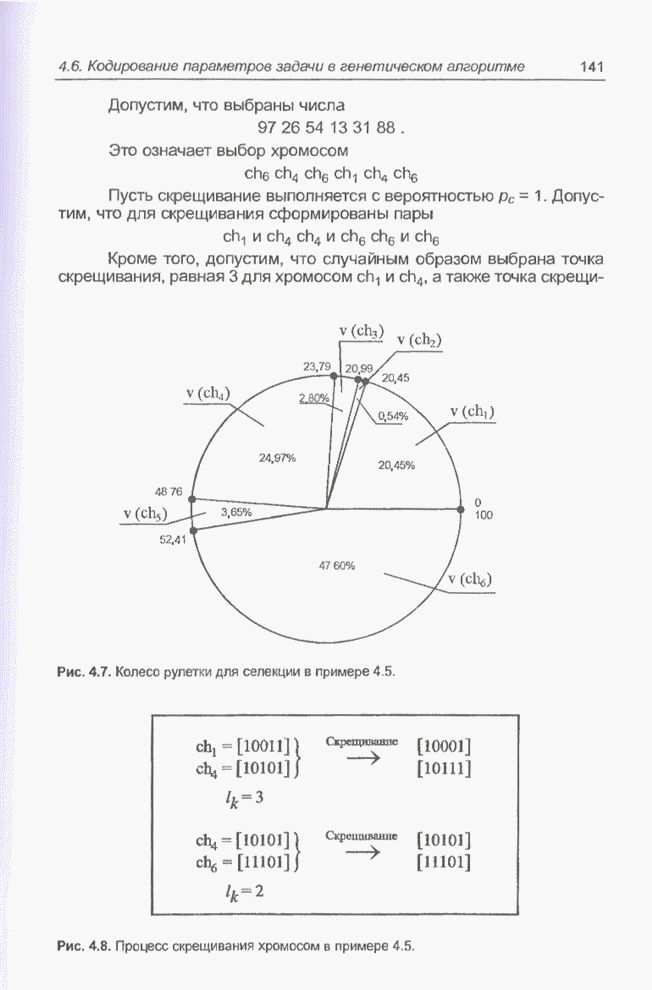
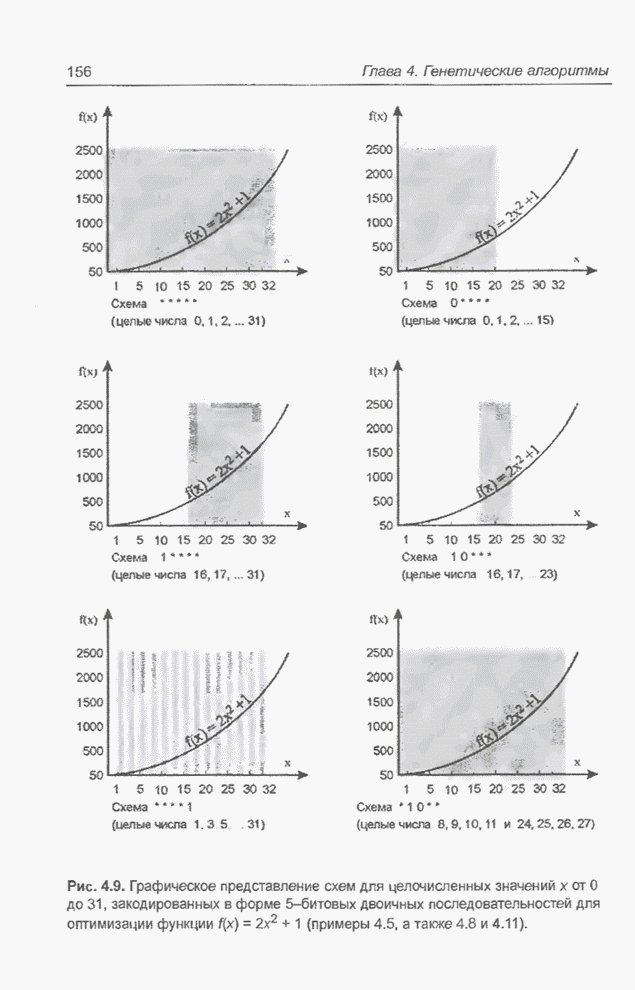
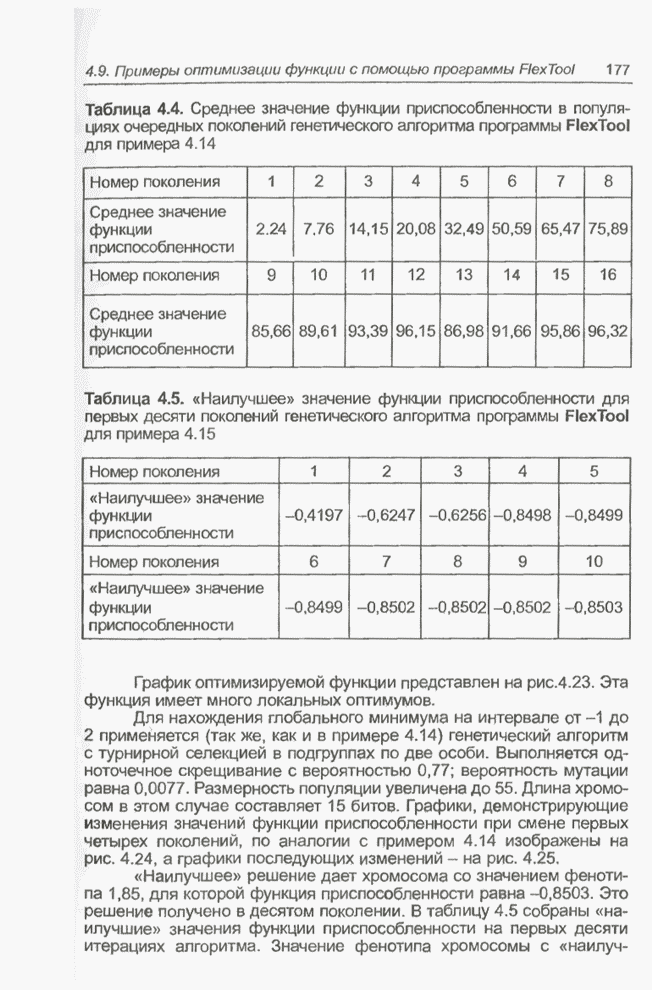
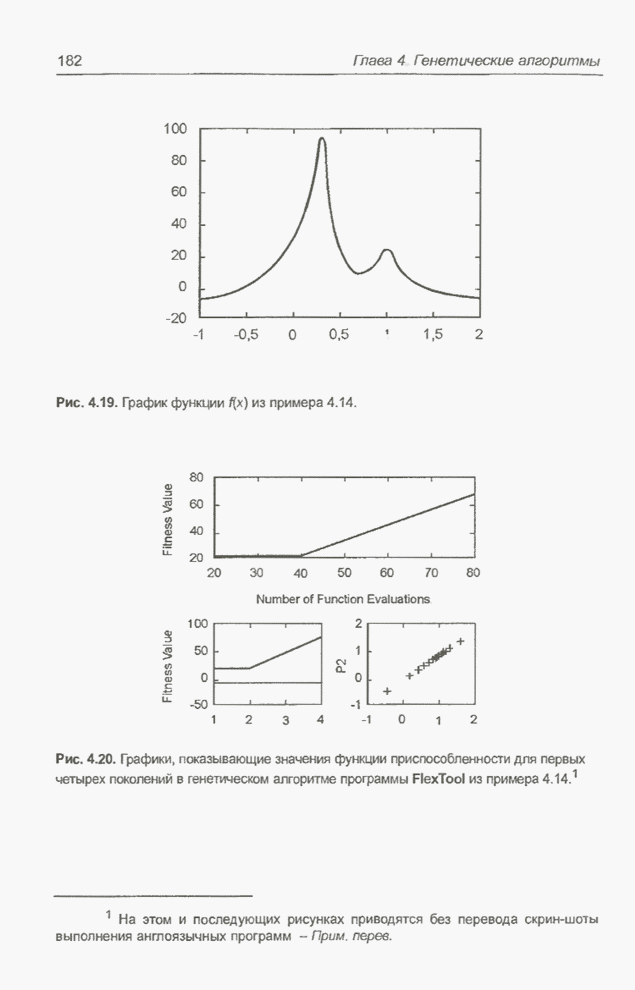
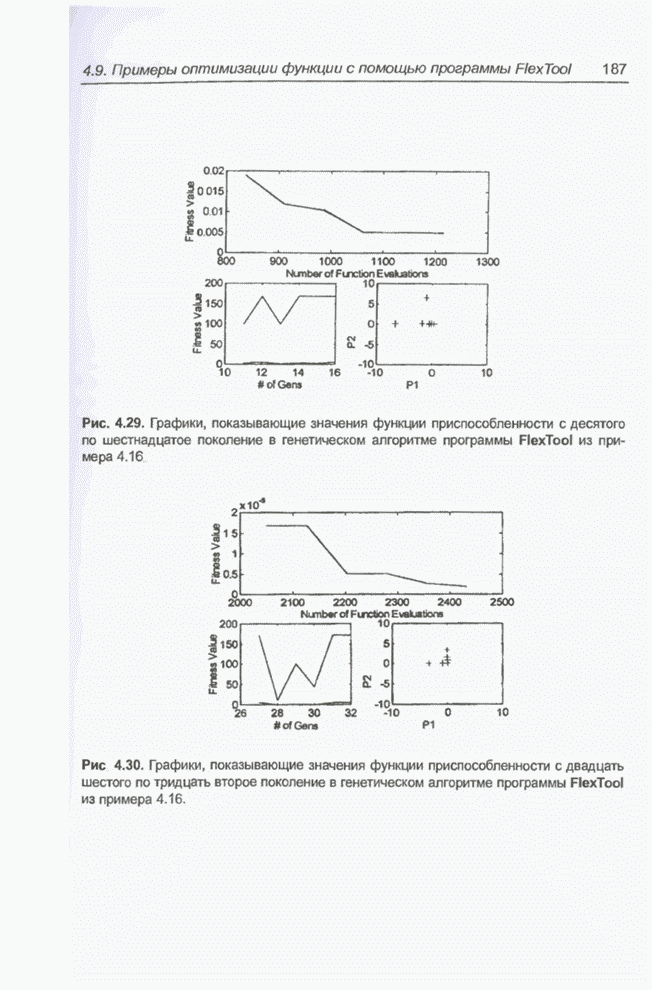
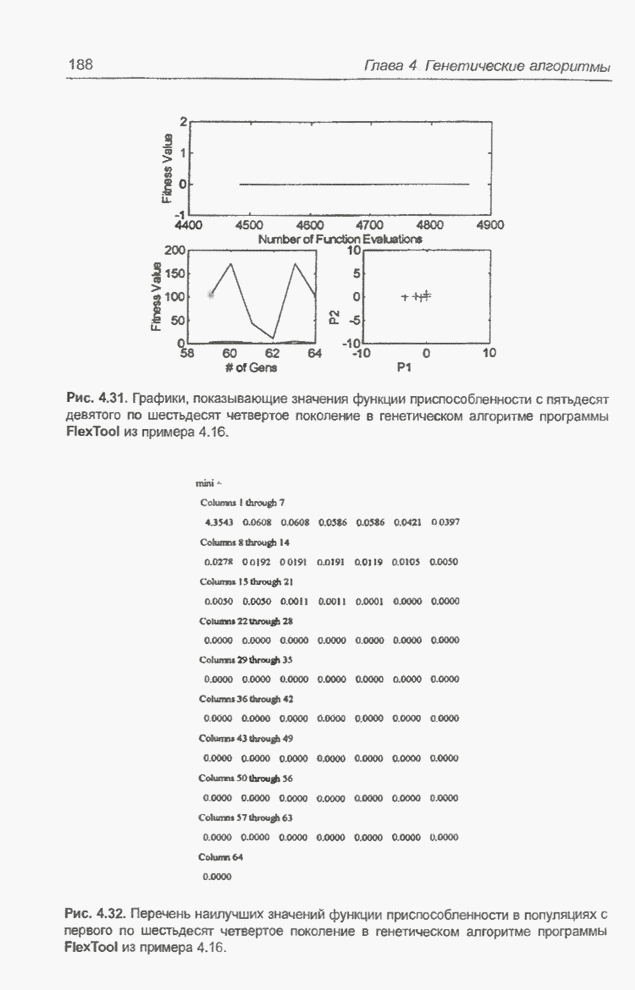
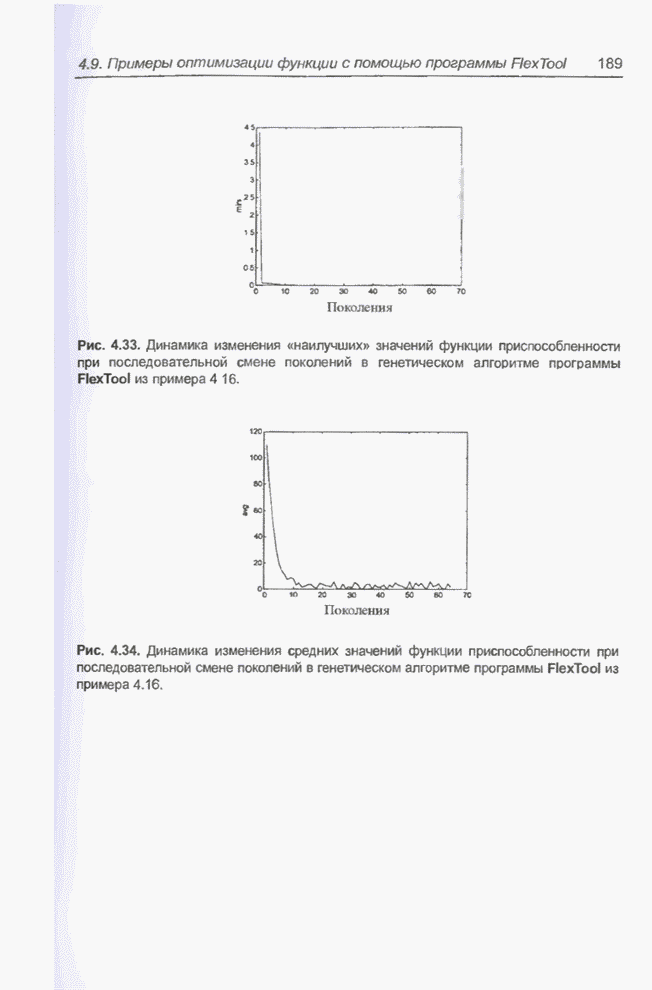
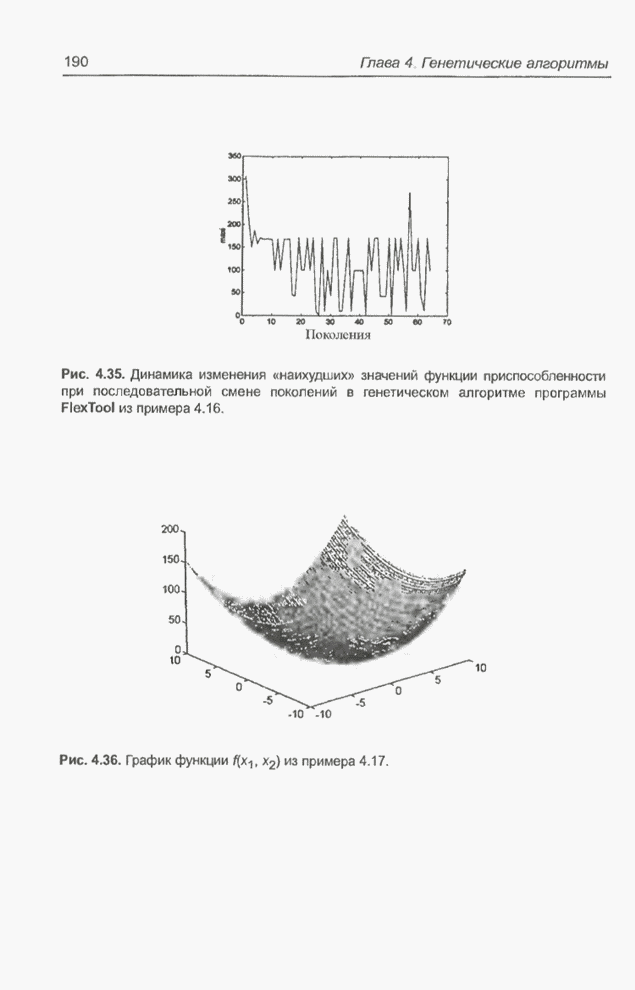
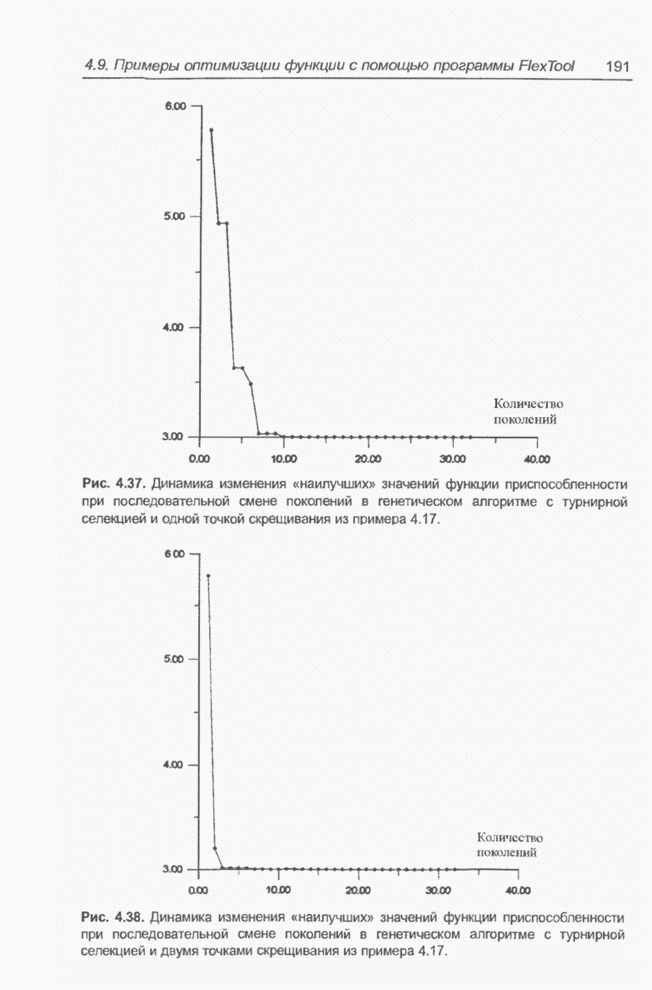
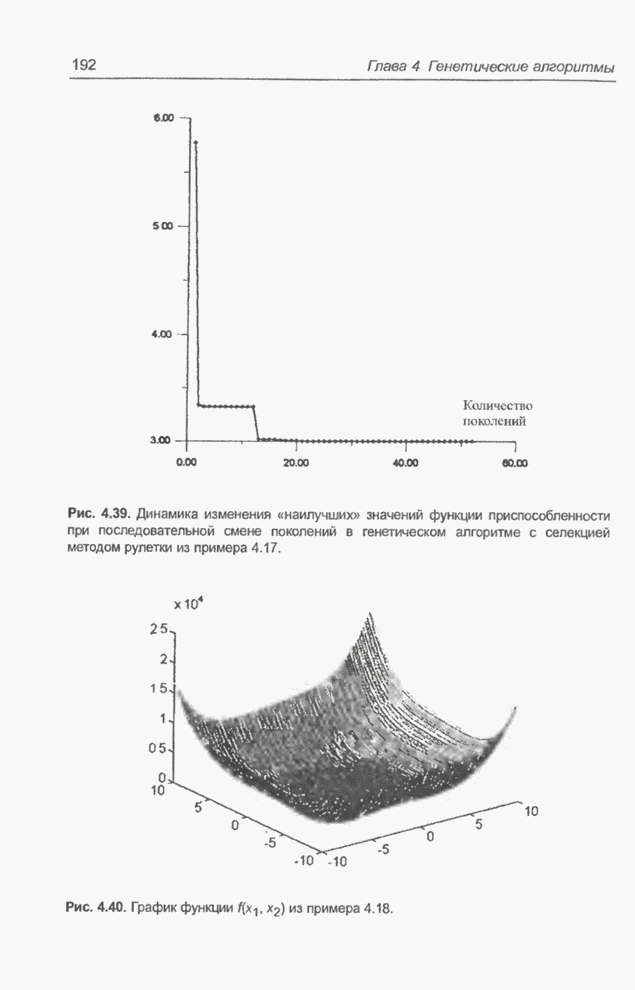
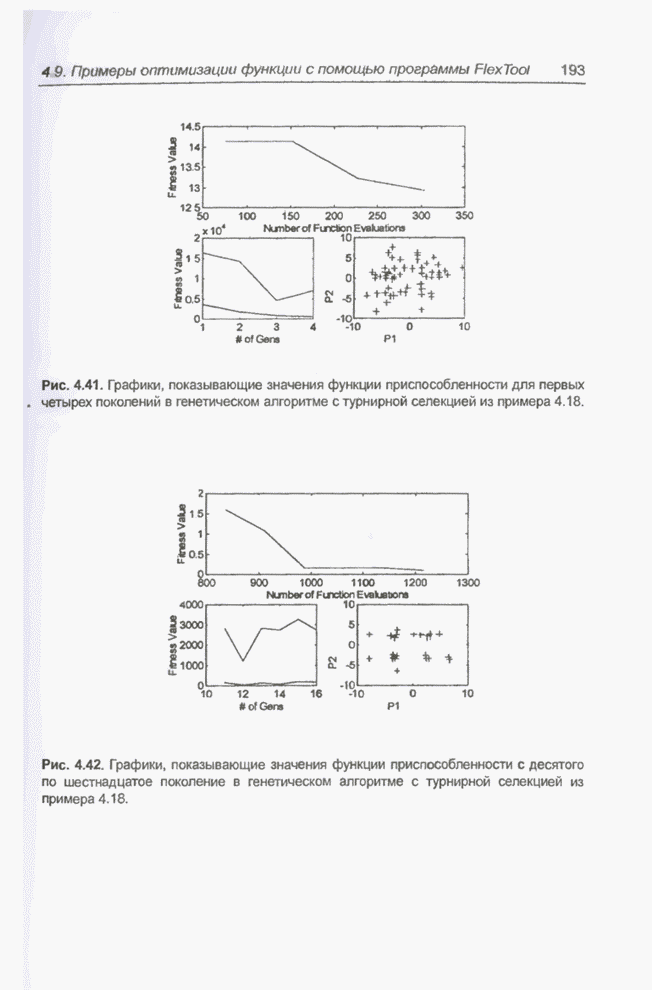
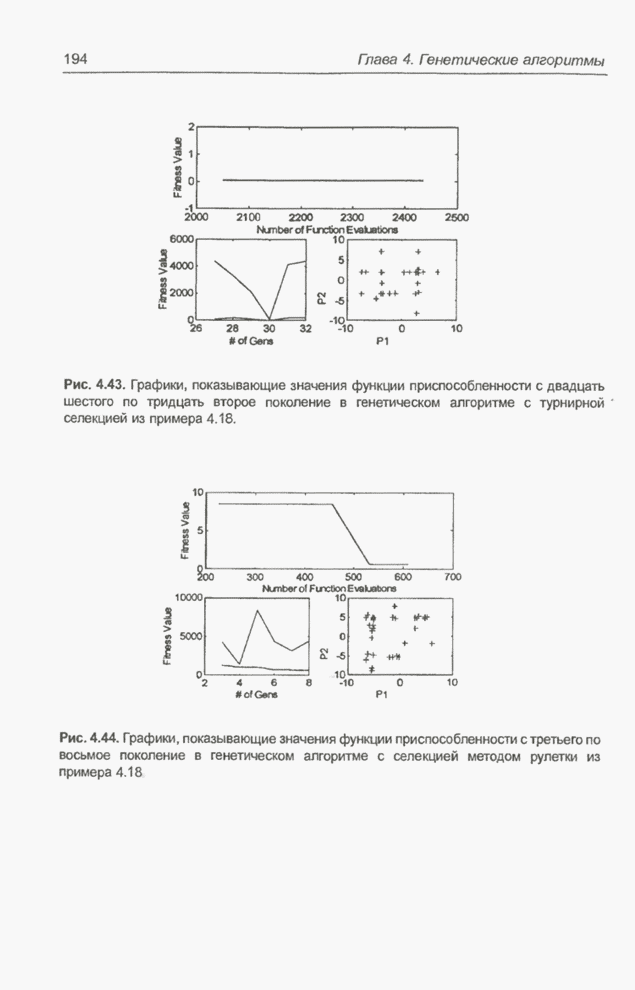
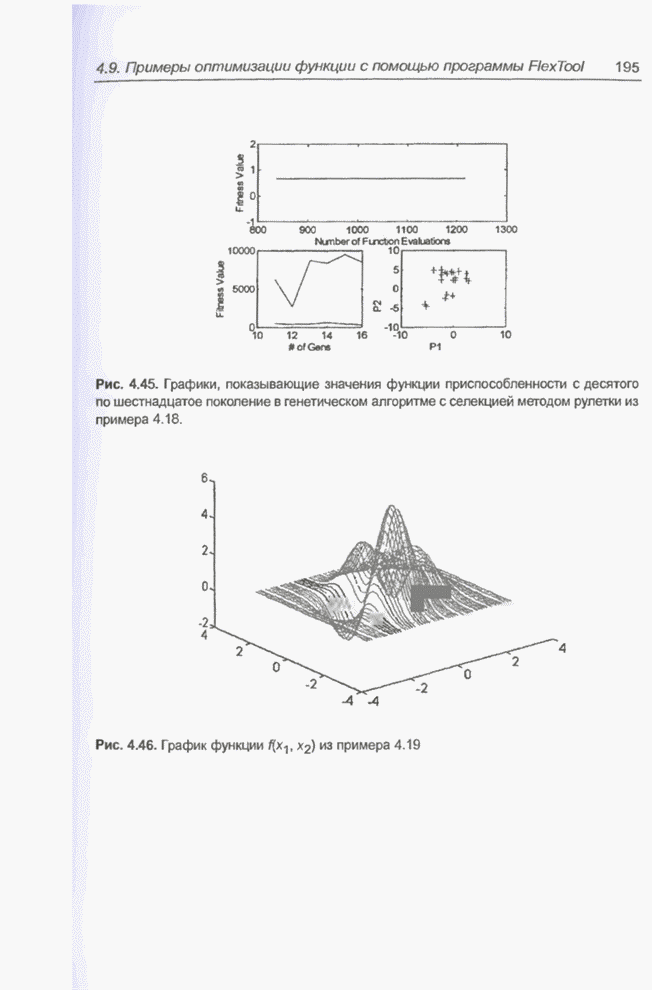
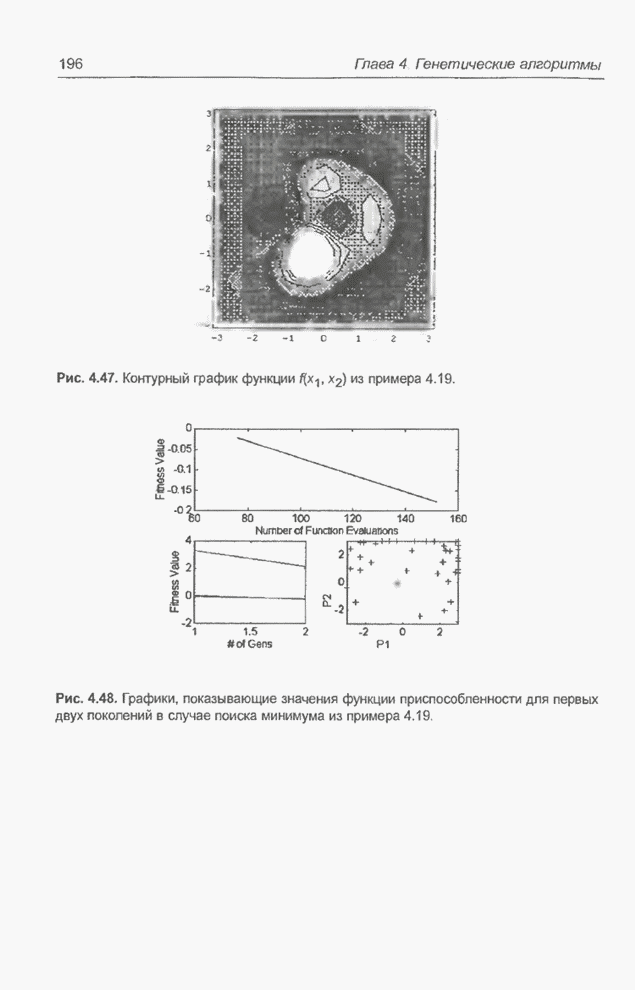
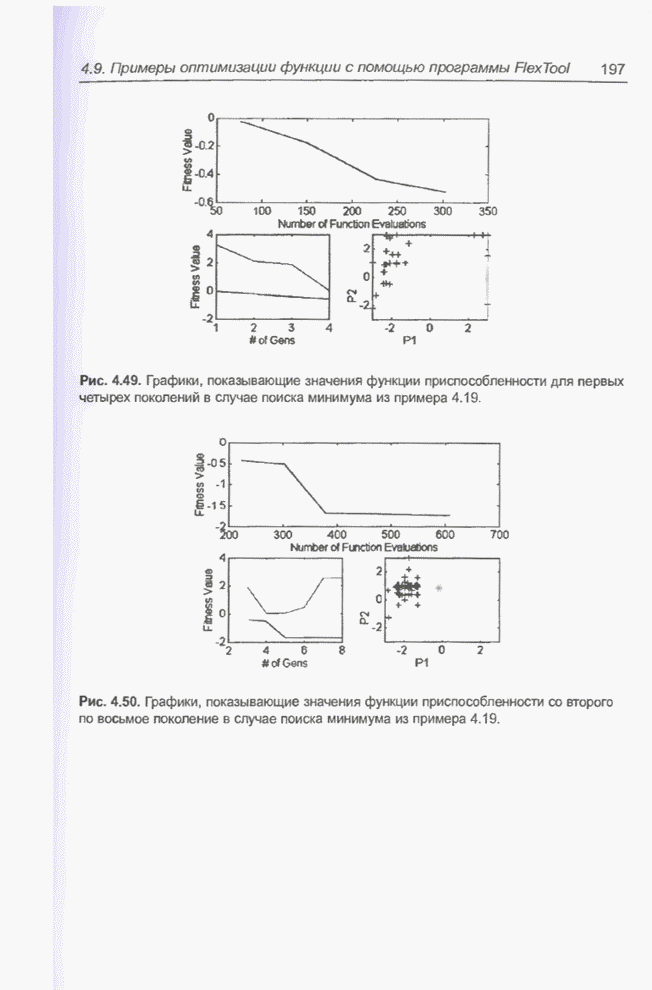
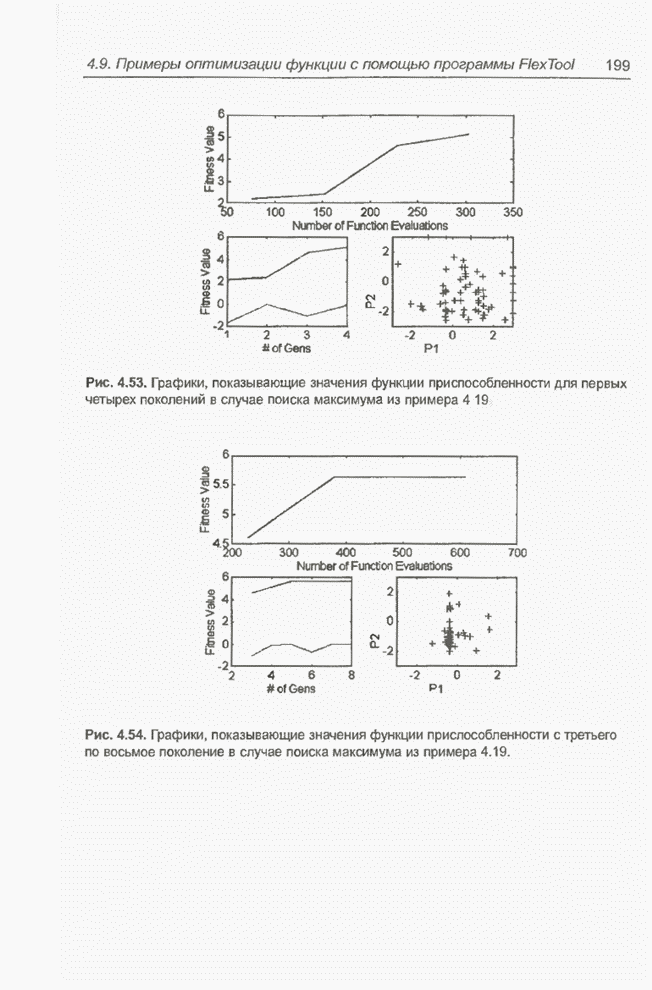
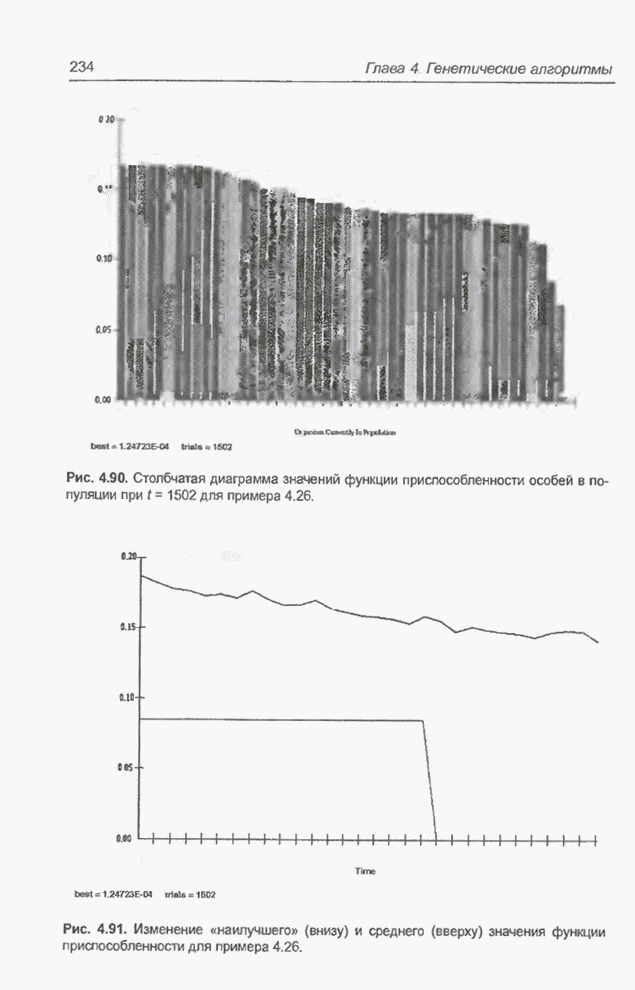
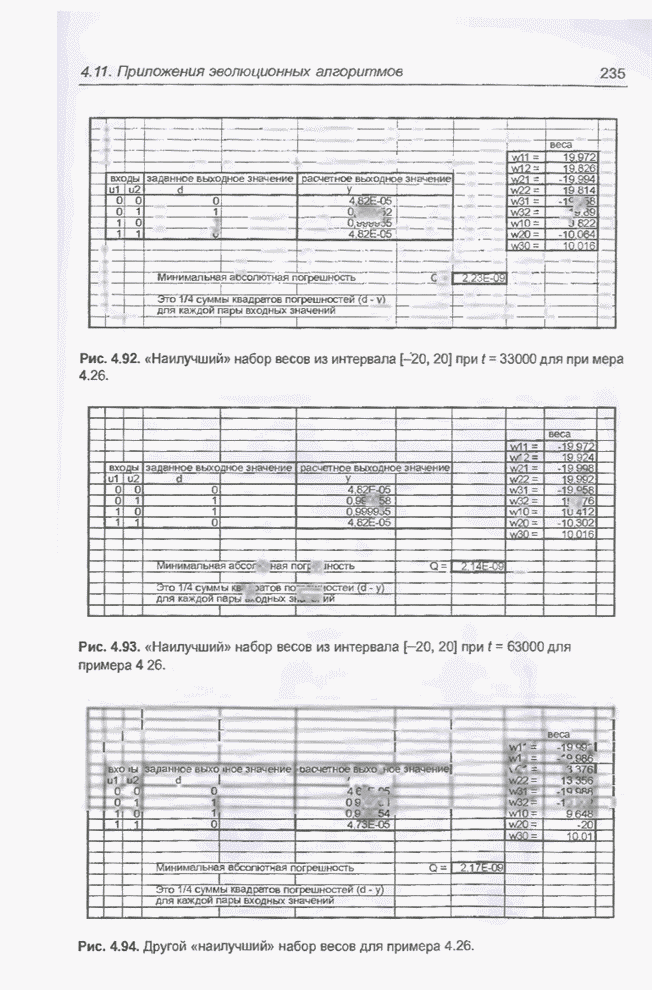
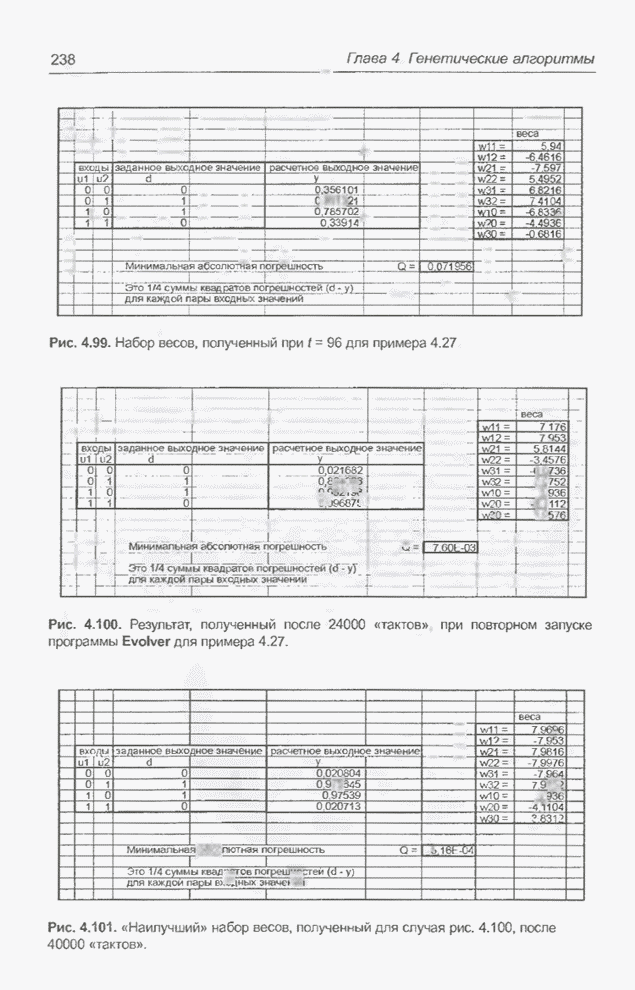
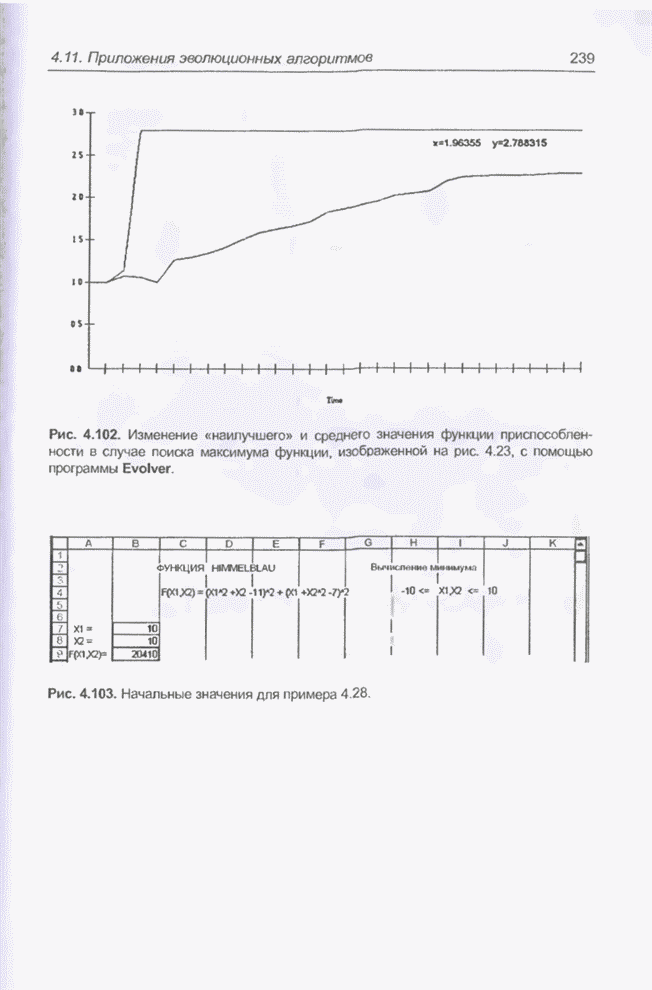
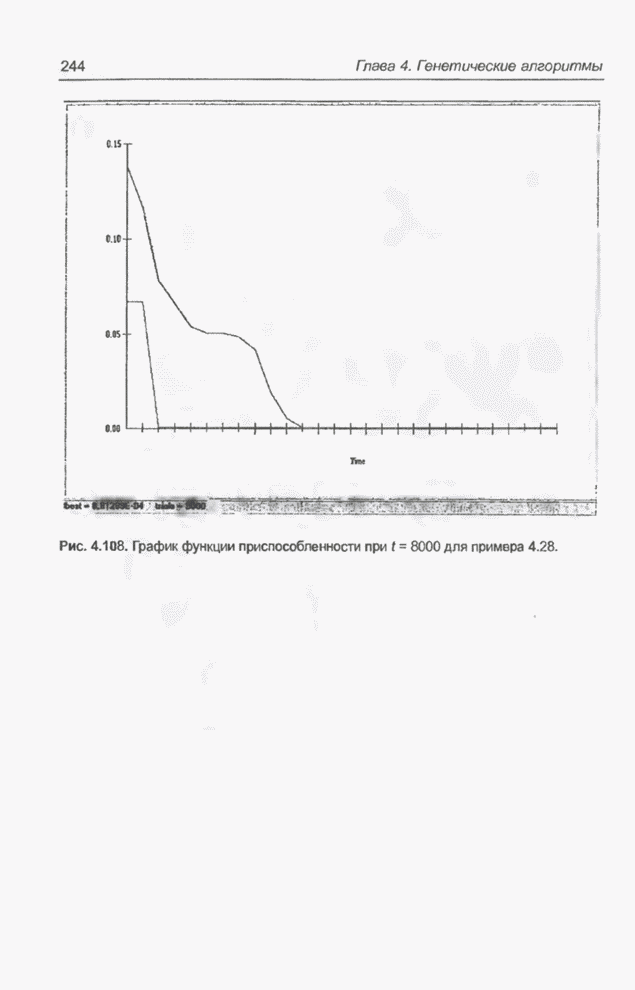
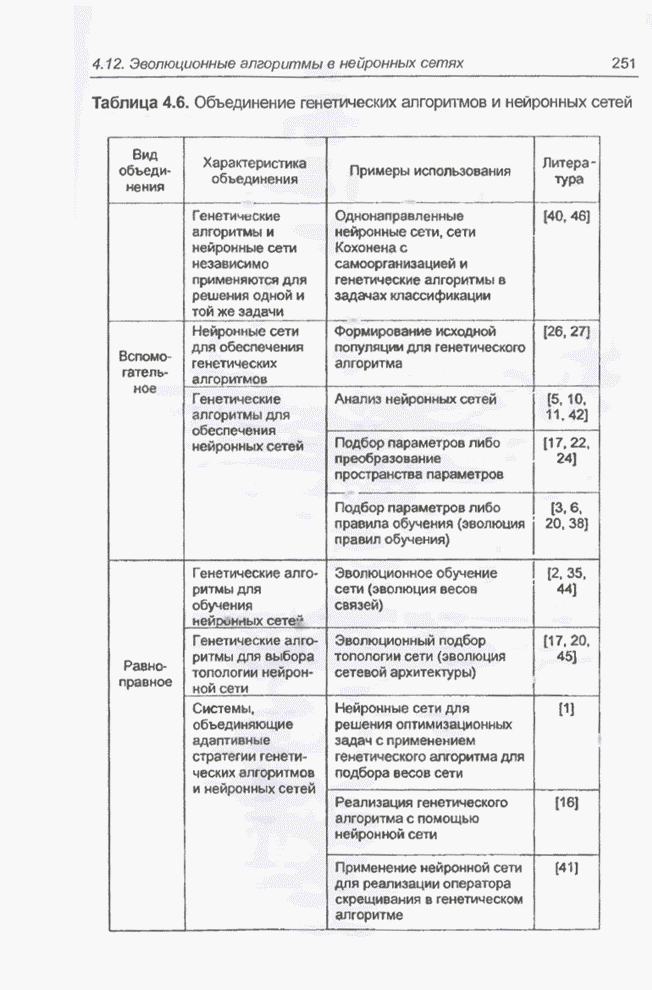
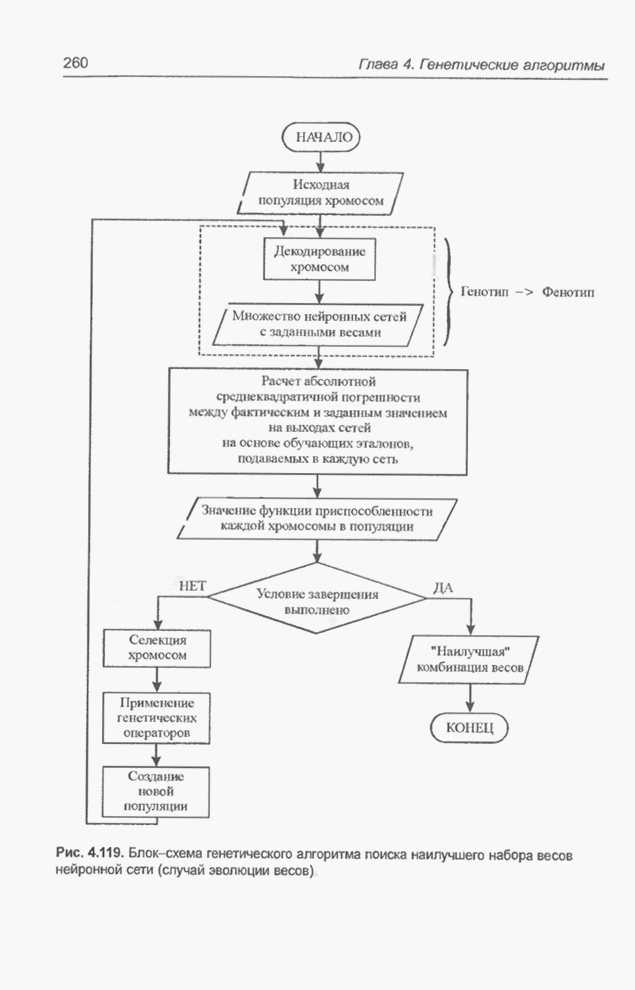
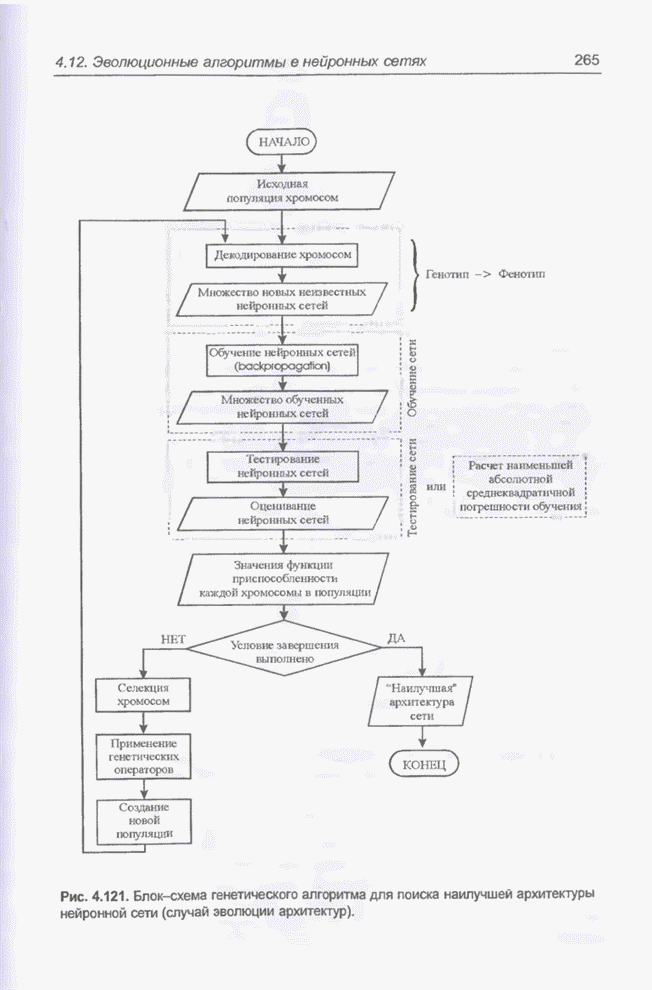
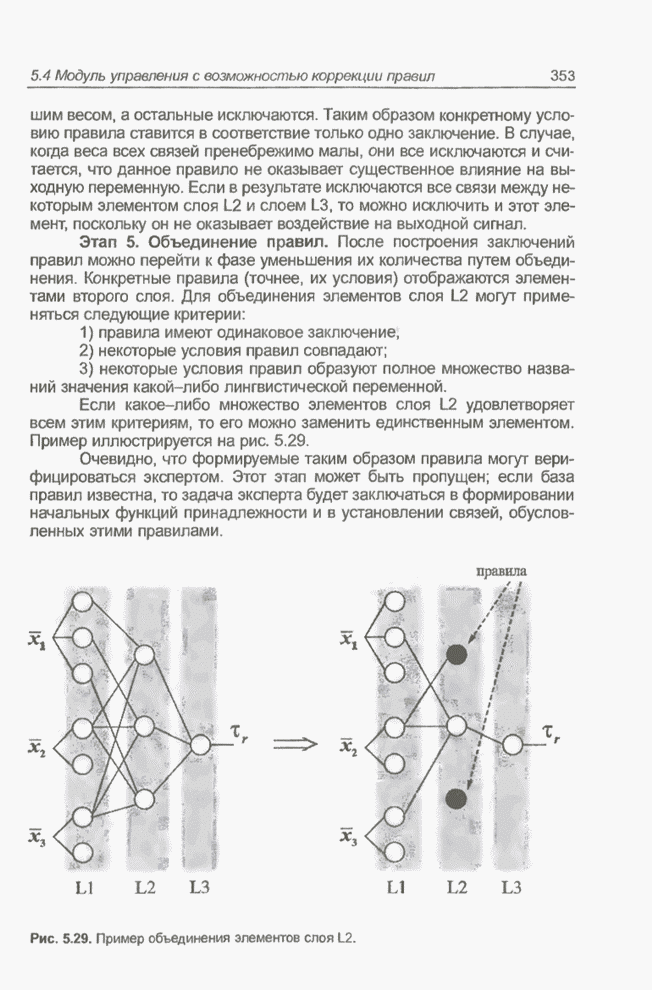
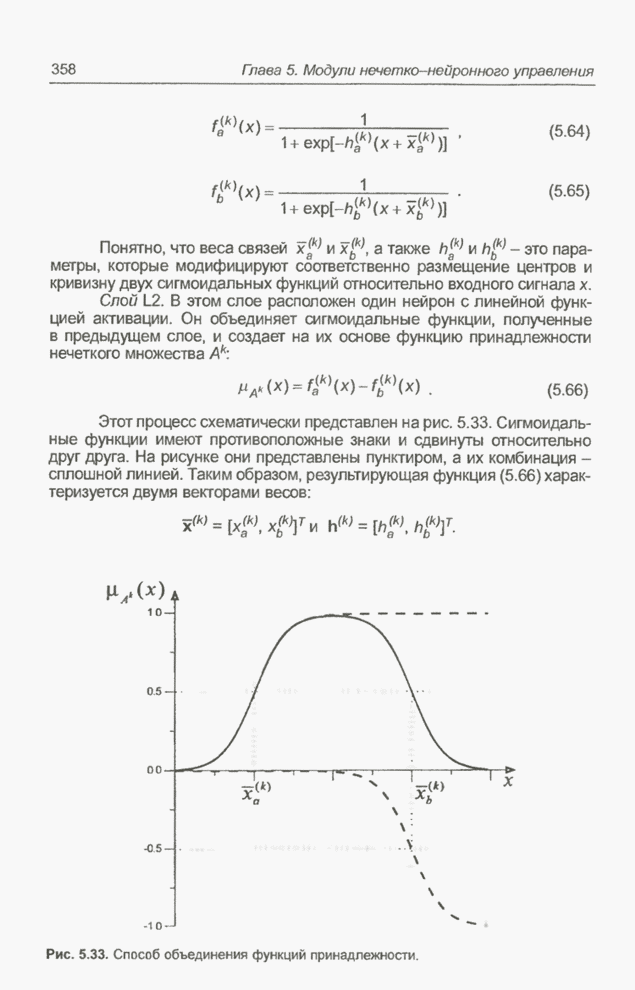
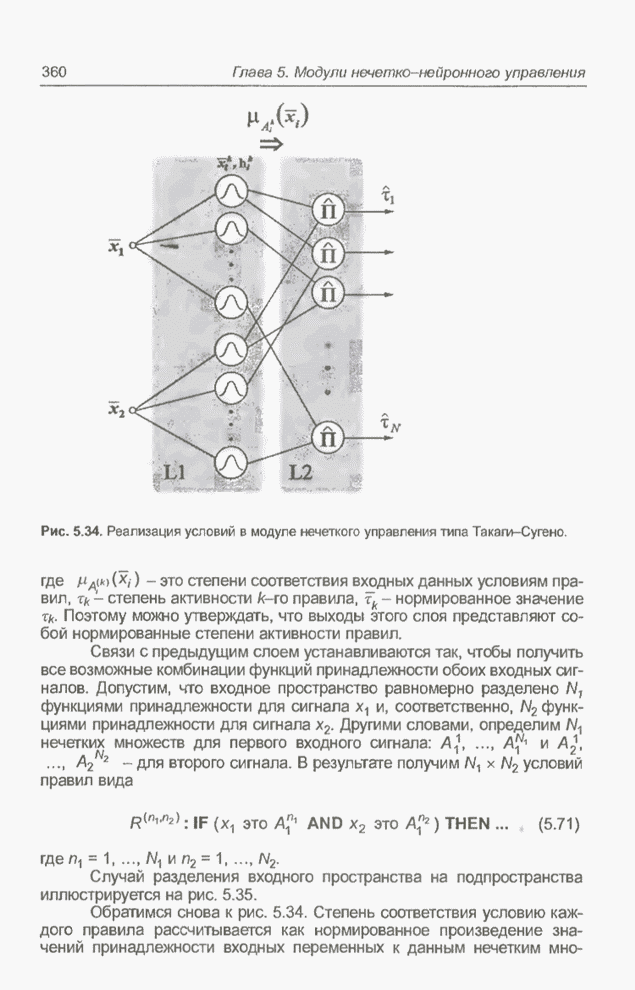
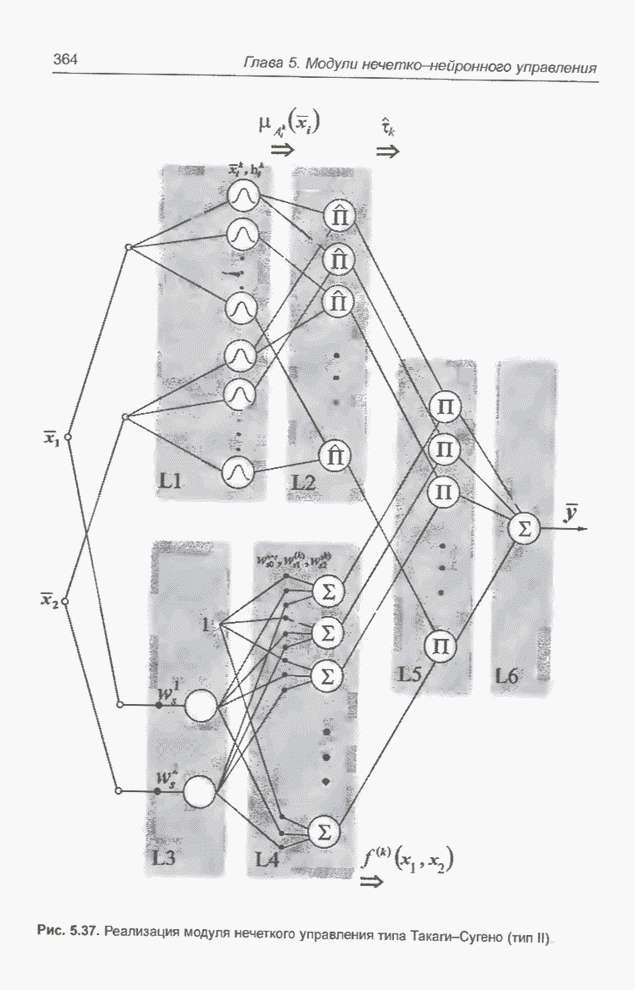
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.3. Основные понятия генетических алгоритмов
При описании генетических алгоритмов используются определения, заимствованные из генетики. Например, речь идет о популяции особей, а в качестве базовых понятий применяются ген, хромосома, генотип, фенотип, аллель. Также используются соответствующие этим терминам определения из технического лексикона, в частности, цепь, двоичная последовательность, структура.
Популяция - это конечное множество особей.
Особи, входящие в популяцию, в генетических алгоритмах представляются хромосомами с закодированным в них множествами параметров задачи, т.е. решений, которые иначе называются точками в пространстве поиска (search points). В некоторых работах особи называются организмами.
Хромосомы (другие названия - цепочки или кодовые последовательности) - это упорядоченные последовательности генов.
Ген (также называемый свойством, знаком или детектором) - это атомарный элемент генотипа, в частности, хромосомы.
Генотип или структура - это набор хромосом данной особи. Следовательно, особями популяции могут быть генотипы либо единичные хромосомы (в довольно распространенном случае, когда генотип состоит из одной хромосомы).
Фенотип - это набор значений, соответствующих данному генотипу, т.е. декодированная структура или множество параметров задачи (решение, точка пространства поиска).
Аллель - это значение конкретного гена, также определяемое как значение свойства или вариант свойства.
Локус или позиция указывает место размещения данного гена в хромосоме (цепочке). Множество позиций генов - это локи.
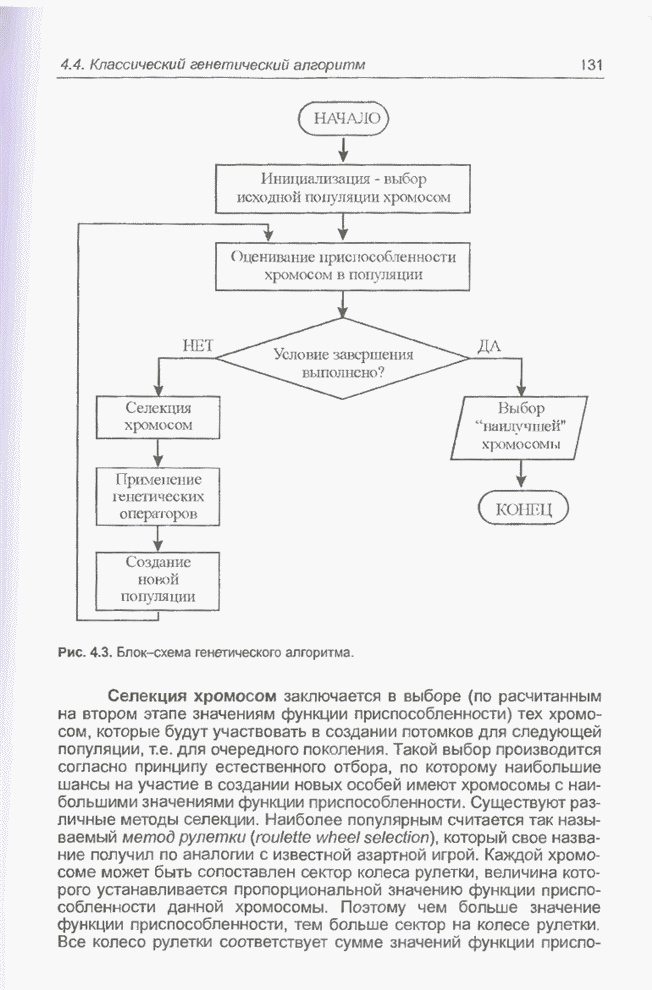
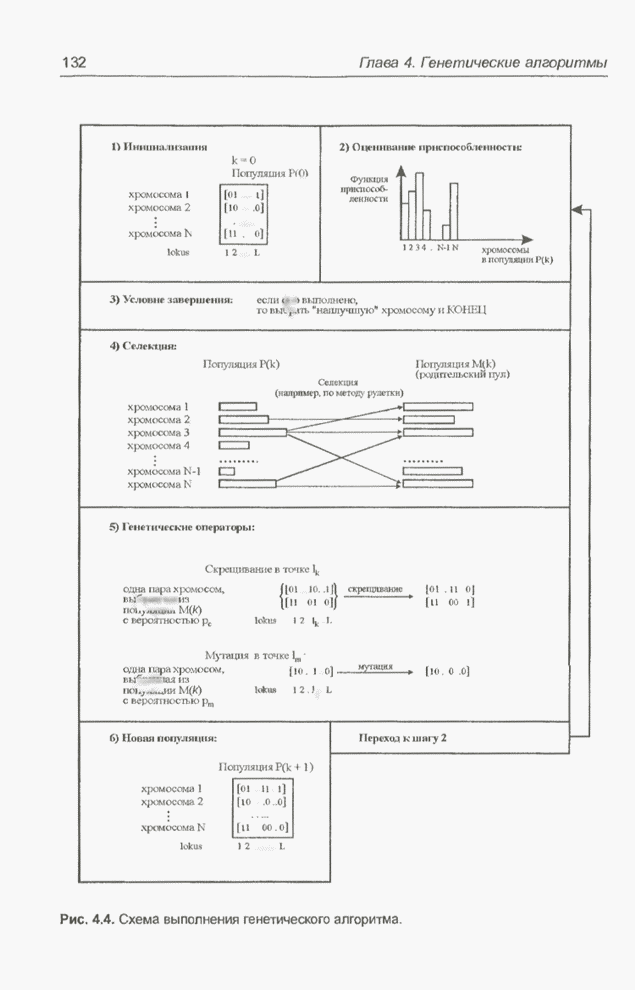
Очень важным понятием в генетических алгоритмах считается функция приспособленности (fitness function), иначе называемая функцией оценки. Она представляет меру приспособленности данной особи в популяции. Эта функция играет важнейшую роль, поскольку позволяет оценить степень приспособленности конкретных особей в популяции и выбрать из них наиболее приспособленные (т.е. имеющие наибольшие значения функции приспособленности) в соответствии с эволюционным принципом выживания «сильнейших» (лучше всего приспособившихся). Функция приспособленности также получила свое название непосредственно из генетики. Она оказывает сильное влияние на функционирование генетических алгоритмов и должна иметь точное и корректное определение. В задачах оптимизации функция приспособленности, как правило, оптимизируется (точнее говоря, максимизируется) и называется целевой функцией. В задачах минимизации целевая функция преобразуется, и проблема сводится к максимизации. В теории управления функция приспособленности может принимать вид функции погрешности, а в теории игр - стоимостной функции. На каждой итерации генетического алгоритма приспособленность каждой особи данной популяции оценивается при помощи функции приспособленности, и на этой основе создается следующая популяция особей, составляющих множество потенциальных решений проблемы, например, задачи оптимизации.
Очередная популяция в генетическом алгоритме называется поколением, а к вновь создаваемой популяции особей применяется термин «новое поколение» или «поколение потомков».
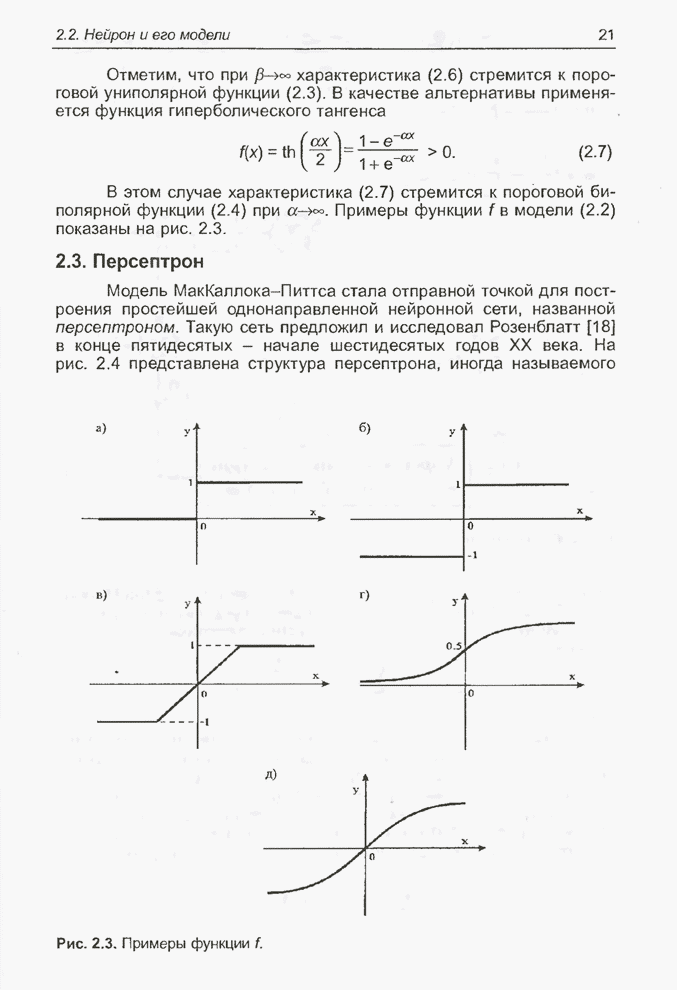
Пример 4.1
Рассмотрим функцию
![]() (4.1)
(4.1)
и
допустим, что ![]() принимает
целые значения из интервала от 0 до 15. Задача оптимизации этой функции
заключается в перемещении по пространству, состоящему из 16 точек со значениями
принимает
целые значения из интервала от 0 до 15. Задача оптимизации этой функции
заключается в перемещении по пространству, состоящему из 16 точек со значениями
![]() для
обнаружения той точки, в которой функция принимает максимальное (или
минимальное) значение.
для
обнаружения той точки, в которой функция принимает максимальное (или
минимальное) значение.
В этом случае в качестве
параметра задачи выступает переменная ![]() . Множество
. Множество ![]() составляет пространство поиска и
одновременно - множество потенциальных решений задачи. Каждое из 16 чисел,
принадлежащих к этому множеству, называется точкой пространства поиска,
решением, значением параметра, фенотипом. Следует отметить, что решение,
оптимизирующее функцию, называется наилучшим или оптимальным решением. Значения
параметра
составляет пространство поиска и
одновременно - множество потенциальных решений задачи. Каждое из 16 чисел,
принадлежащих к этому множеству, называется точкой пространства поиска,
решением, значением параметра, фенотипом. Следует отметить, что решение,
оптимизирующее функцию, называется наилучшим или оптимальным решением. Значения
параметра ![]() от
0 до 15 можно закодировать следующим образом:
от
0 до 15 можно закодировать следующим образом:
0000 0001 0010 0011 0100 0101 0110 0111
1000 1001 1010 1011 1100 1101 1110 1111
Это
широко известный способ двоичного кодирования, связанный с записью десятичных
цифр в двоичной системе. Представленные кодовые последовательности также
называются цепями или хромосомами. В рассматриваемом примере они выступают и в
роли генотипов. Каждая из хромосом состоит из 4 генов (иначе можно сказать, что
двоичные последовательности состоят из 4 битов). Значение гена в конкретной
позиции называется аллелью, принимающей в данном случае значения 0 или 1.
Популяция состоит из особей, выбираемых среди этих 16 хромосом. Примером
популяции с численностью, равной 6, может быть, например, множество хромосом ![]() , представляющих
собой закодированную форму следующих фенотипов:
, представляющих
собой закодированную форму следующих фенотипов: ![]() . Функция приспособленности в этом
примере задается выражением (4.1). Приспособленность отдельных хромосом в
популяции определяется значением этой функции для значений
. Функция приспособленности в этом
примере задается выражением (4.1). Приспособленность отдельных хромосом в
популяции определяется значением этой функции для значений ![]() , соответствующих этим
хромосомам, т.е. для фенотипов, соответствующих определенным генотипам.
, соответствующих этим
хромосомам, т.е. для фенотипов, соответствующих определенным генотипам.
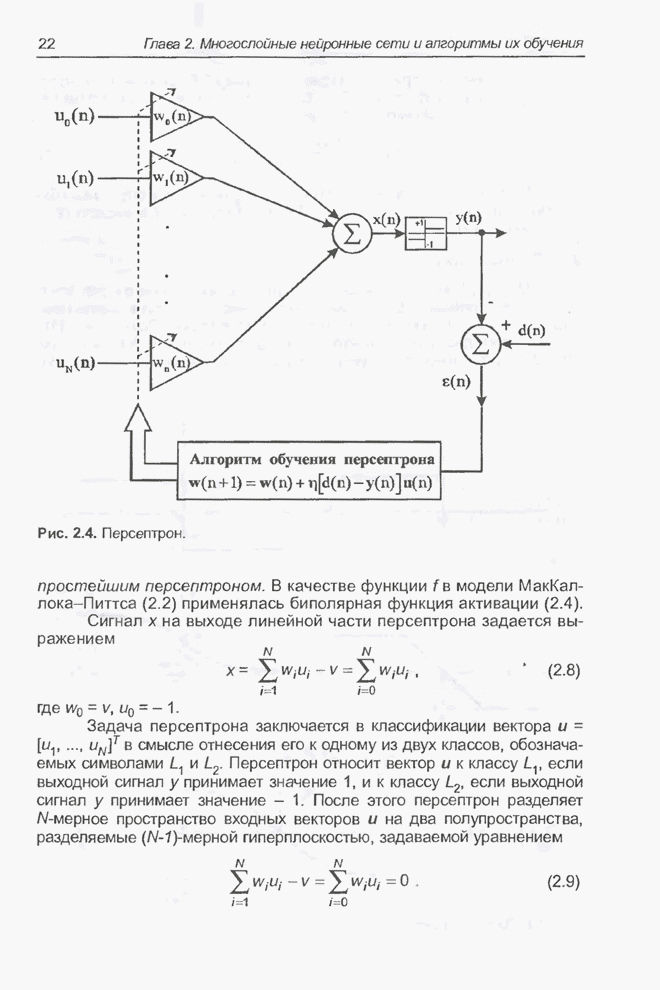
Пример 4.2
Рассмотрим следующий пример постановки оптимизационной задачи. Для системы, изображенной на рис. 4.1, следует найти
 ,
,
где
![]() .
.

Рис. 4.1. Схема оптимизационной двухпараметрической системы.
В роли параметров этой задачи
выступают ![]() и
и
![]() .
Пространство поиска должно содержать конечное количество точек, которые можно
закодировать в виде хромосом. Параметры
.
Пространство поиска должно содержать конечное количество точек, которые можно
закодировать в виде хромосом. Параметры ![]() и
и ![]() дискретизированы; множество их значений
во всем диапазоне от минимального
дискретизированы; множество их значений
во всем диапазоне от минимального ![]() до максимального
до максимального ![]() отображаются на
соответствующие двоичные кодовые последовательности. При этом значению
отображаются на
соответствующие двоичные кодовые последовательности. При этом значению ![]() сопоставлена кодовая
последовательность, состоящая из одних нулей, а значению
сопоставлена кодовая
последовательность, состоящая из одних нулей, а значению ![]() - кодовая последовательность,
состоящая из одних единиц. Длина этих кодовых последовательностей зависит от
значений
- кодовая последовательность,
состоящая из одних единиц. Длина этих кодовых последовательностей зависит от
значений ![]() и
и ![]() , а также от частоты
дискретизации интервала
, а также от частоты
дискретизации интервала ![]() .
.
Допустим, что ![]() , а
, а ![]() и для каждого из параметров
и для каждого из параметров ![]() и
и ![]() применяются кодовые
последовательности длиной 10. Пример популяции, состоящей из 10 особей,
приведен в таблице 4.1.
применяются кодовые
последовательности длиной 10. Пример популяции, состоящей из 10 особей,
приведен в таблице 4.1.
Таблица 4.1. Популяция особей (для примера 4.2)
|
Генотипы |
Фенотипы |
|
|
00000000000000000000 |
–25,00 |
–25,00 |
|
10100010010011001011 |
6,72 |
–15,08 |
|
01101000101111010010 |
–4,57 |
22,8. |
|
11011010011110000111 |
17,67 |
19,13 |
|
00011011000000010001 |
–19,72 |
–24,17 |
|
00110000101011111010 |
–15,52 |
12,24 |
|
11111111111111111111 |
25,00 |
25,00 |
Первые 10 генов каждого генотипа
соответствуют параметру ![]() , а последние 10 генов - параметру
, а последние 10 генов - параметру ![]() . Таким образом, длина
хромосом равна 20.
. Таким образом, длина
хромосом равна 20.
Способ кодирования значений
параметров ![]() и
и
![]() в виде
хромосом будет подробно изложен в разд. 4.6.
в виде
хромосом будет подробно изложен в разд. 4.6.
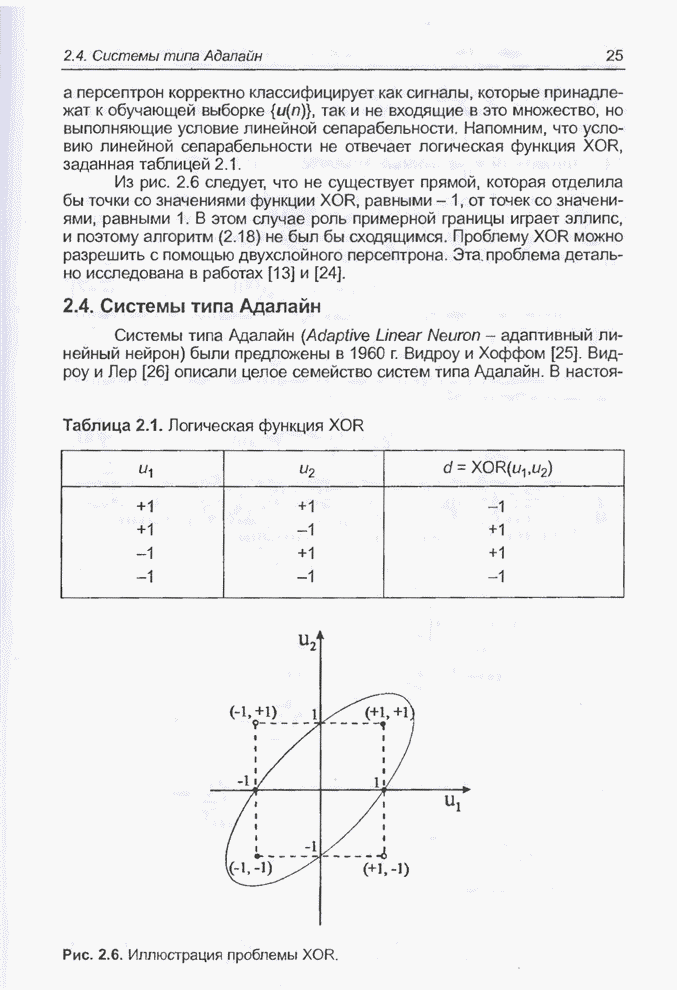
Пример 4.3
Рассмотрим нейронную сеть,
представленную на рис. 4.2, для которой необходимо подобрать оптимальные веса ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() , минимизирующих значение погрешности
, минимизирующих значение погрешности
 .
.

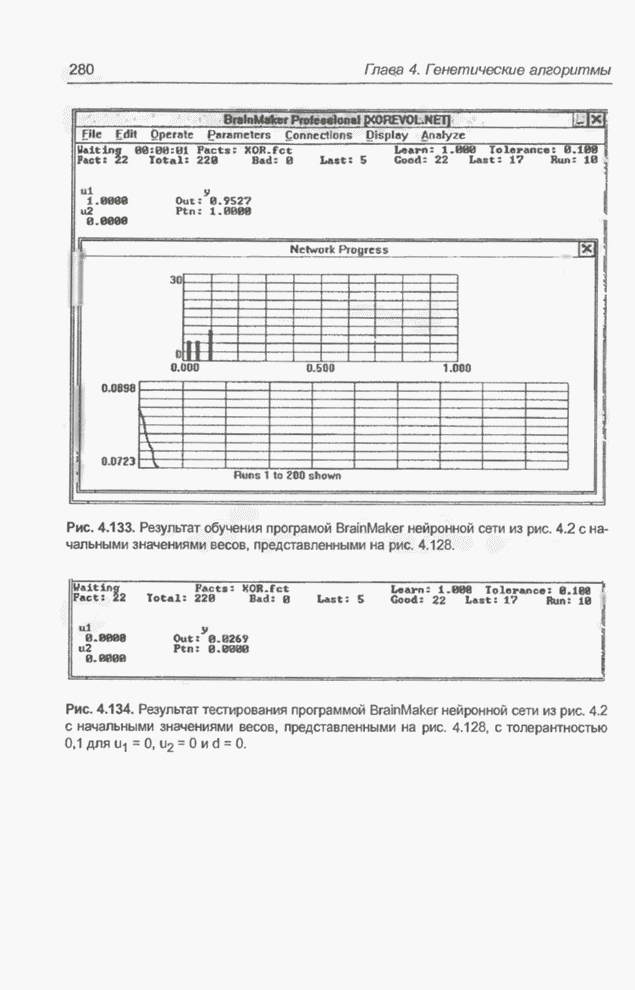
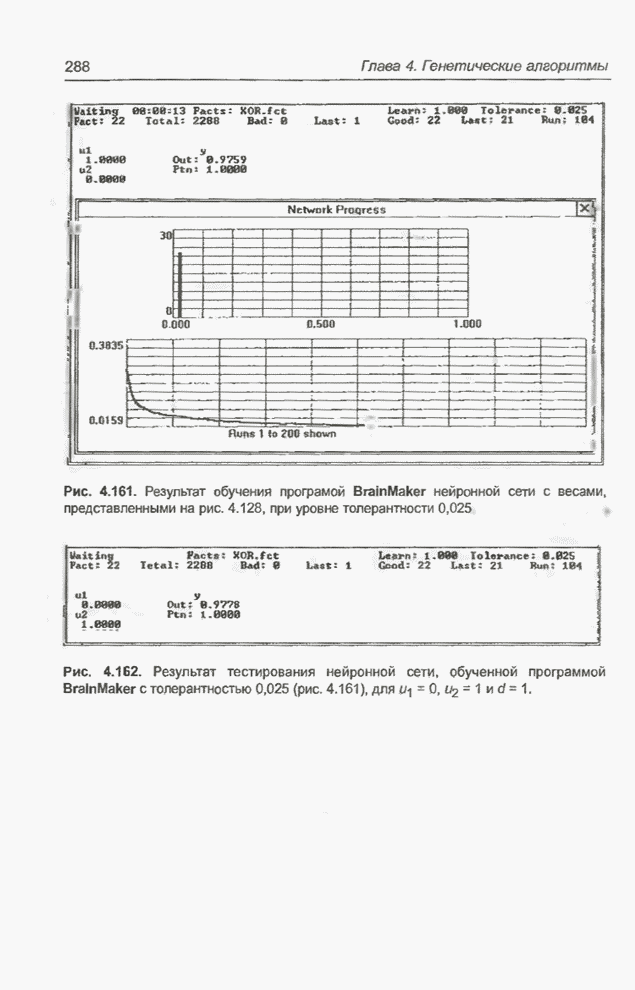
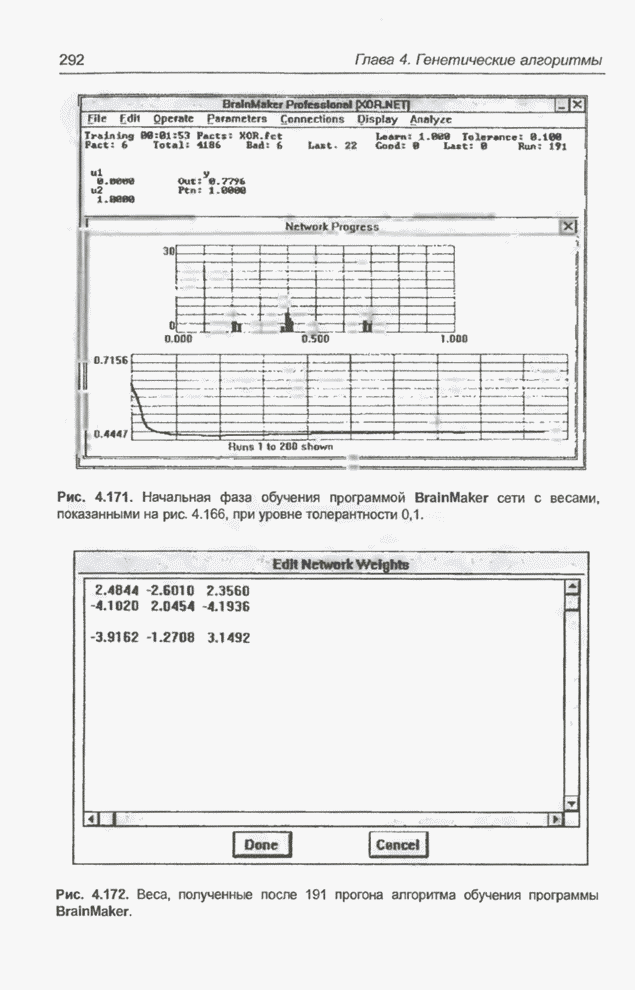
Рис. 4.2. Нейронная сеть, реализующая операцию XOR.
Это сеть, реализующая систему
XOR, поэтому значения ![]() и
и ![]() , а также
, а также ![]() для
для ![]() принимают значения, приведенные в табл.
2.1. В качестве параметров рассматриваемой задачи выступают перечисленные выше
веса, т.е. задача имеет 9 параметров. В данном примере набор из этих 9
параметров определяет точку пространства поиска и, следовательно, представляет
собой возможное решение. Допустим, что веса могут принимать значения из
интервала
принимают значения, приведенные в табл.
2.1. В качестве параметров рассматриваемой задачи выступают перечисленные выше
веса, т.е. задача имеет 9 параметров. В данном примере набор из этих 9
параметров определяет точку пространства поиска и, следовательно, представляет
собой возможное решение. Допустим, что веса могут принимать значения из
интервала ![]() .
Тогда каждая хромосома будет комбинацией из 9 двоичных последовательностей,
кодирующих конкретные веса. Это, очевидно, и есть генотипы. Соответствующие им
фенотипы представлены значениями отдельных весов, т.е. множествами
соответствующих действительных чисел из интервала
.
Тогда каждая хромосома будет комбинацией из 9 двоичных последовательностей,
кодирующих конкретные веса. Это, очевидно, и есть генотипы. Соответствующие им
фенотипы представлены значениями отдельных весов, т.е. множествами
соответствующих действительных чисел из интервала ![]() .
.
В приведенных примерах (4.1 - 4.3) хромосомы и генотипы обозначают одно и то же - фенотипы особей популяции, закодированные в форме упорядоченных последовательностей генов со значениями (аллелями), равными 0 или 1.
В генетике генотип задает генетическую структуру особи, которая может включать более одной хромосомы. Например, клетки человека содержат 46 хромосом. В генетических алгоритмах генотип определяется аналогичным образом, однако чаще всего он состоит всего из одной хромосомы, которая и выступает в роли особи популяции.
Длина хромосом зависит от условий задачи (см. разд. 4.6). Следует заметить, что в естественных организмах хромосома может состоять из нескольких сотен и даже тысяч генов. У человека имеется около 100 000 генов, хотя их точное количество до сих пор неизвестно.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Предисловие к русскому изданию
- ГЛАВА 1. ВВЕДЕНИЕ
- Список литературы
- ГЛАВА 2. МНОГОСЛОЙНЫЕ НЕЙРОННЫЕ СЕТИ И АЛГОРИТМЫ ИХ ОБУЧЕНИЯ
- 2.1. Введение
- 2.2. Нейрон и его модели
- 2.3. Персептрон
- 2.4. Системы типа Адалайн
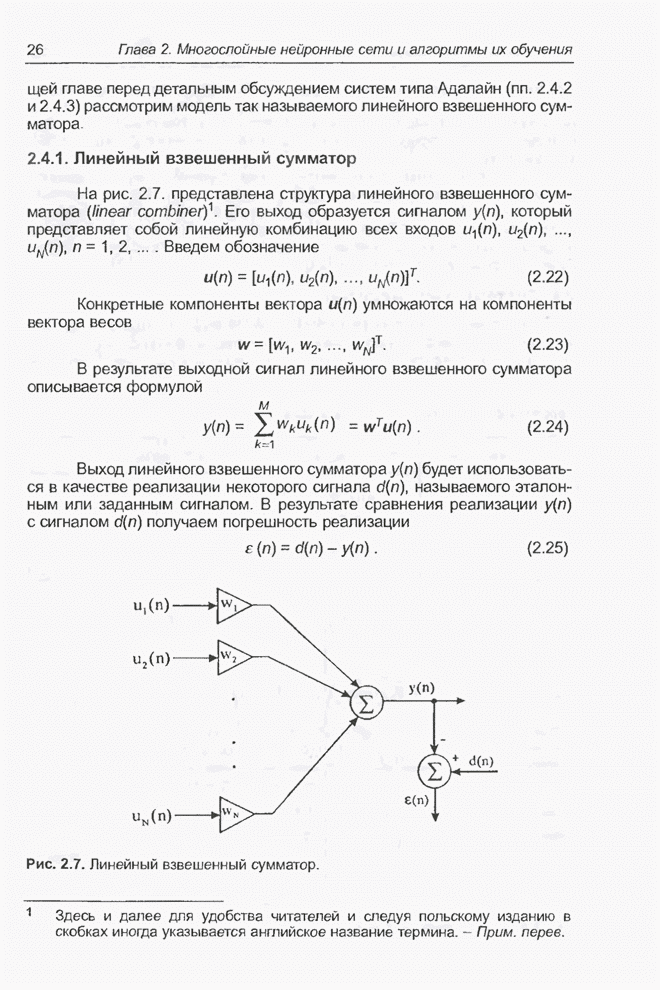
- 2.4.1. Линейный взвешенный сумматор
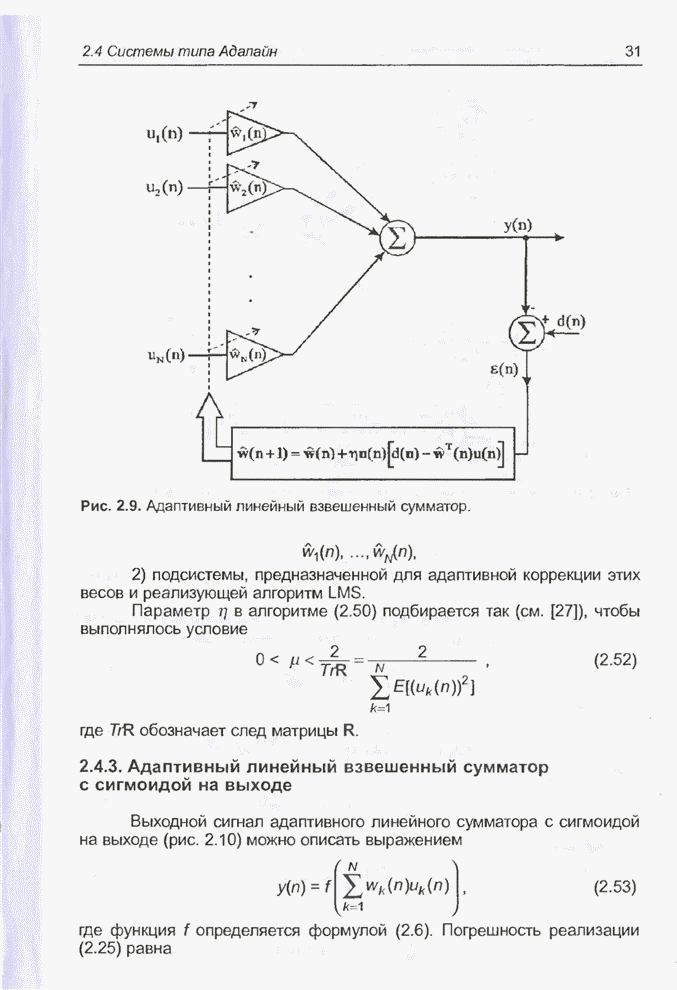
- 2.4.2. Адаптивный линейный взвешенный сумматор
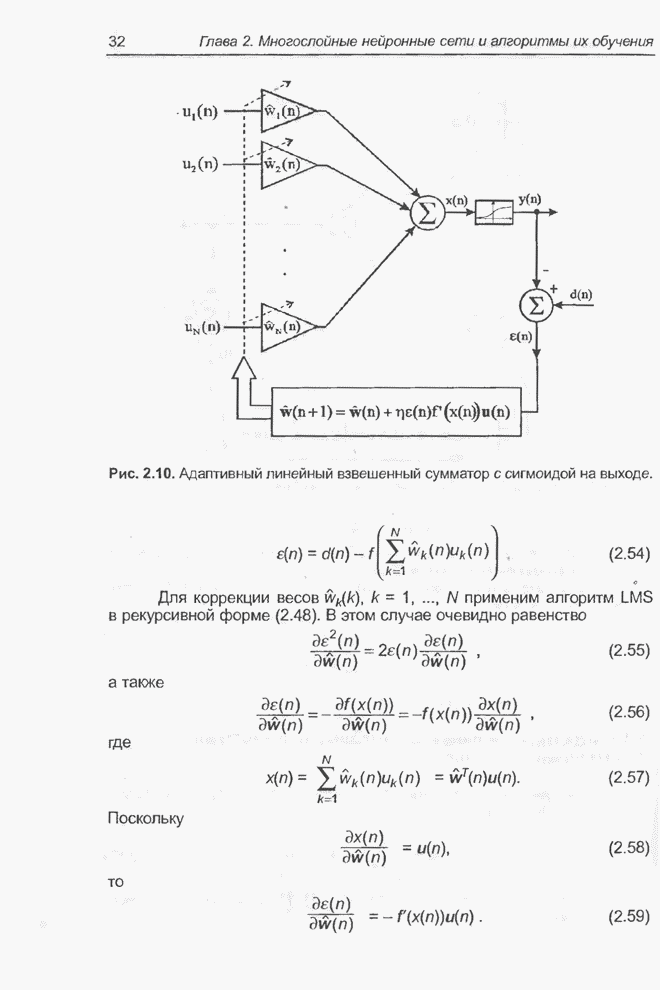
- 2.4.3. Адаптивный линейный взвешенный сумматор с сигмоидой на выходе
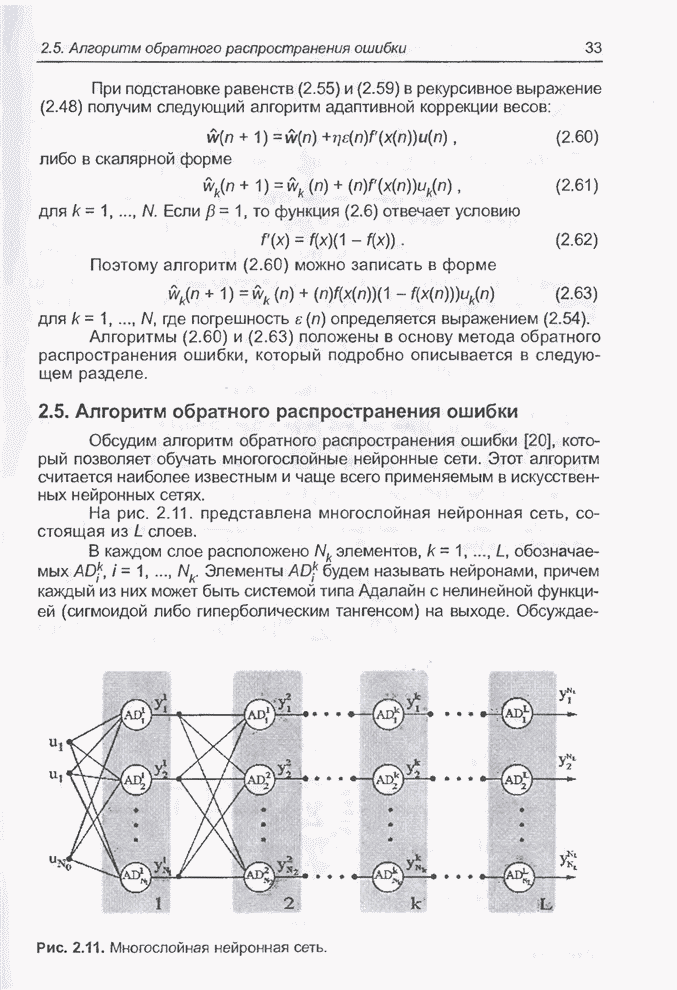
- 2.5. Алгоритм обратного распространения ошибки
- 2.6. Применение рекуррентного метода наименьших квадратов для обучения нейронных сетей
- Список литературы
- ГЛАВA3. НЕЧЕТКИЕ МНОЖЕСТВА И НЕЧЕТКИЙ ВЫВОД
- 3.1. Введение
- 3.2. Основные понятия и определения теории нечетких множеств
- 3.3. Операции на нечетких множествах
- 3.4. Принцип расширения
- 3.5. Нечеткие числа
- 3.6. Треугольные нормы
- 3.7. Нечеткие отношения и их свойства
- 3.8. Нечеткий вывод
- 3.9. Нечеткое управление
- 3.9.1. Классический модуль нечеткого управления
- 3.9.2. Метод нечеткого управления Такаги-Сугено
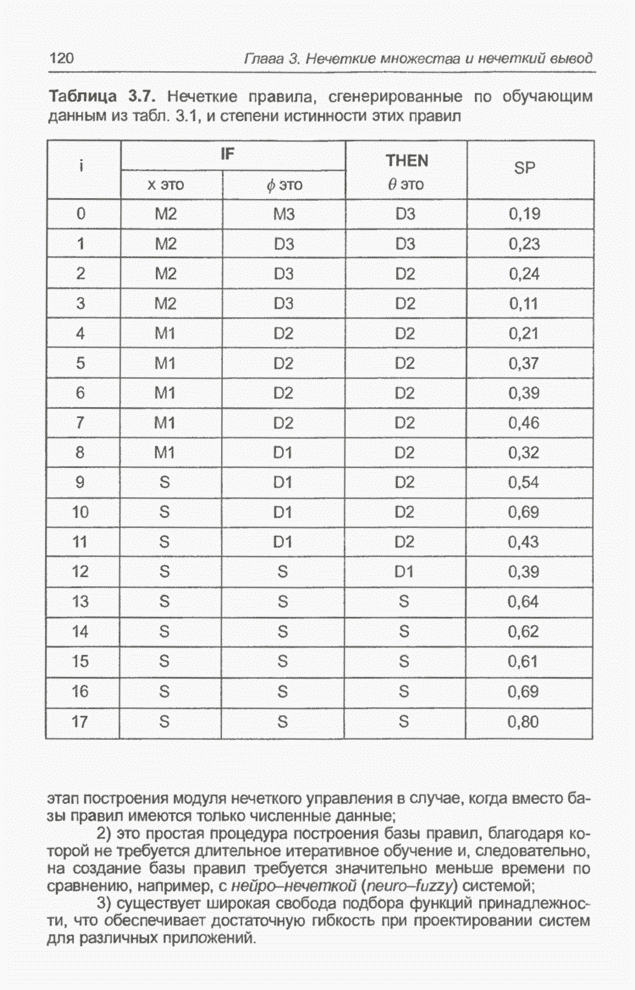
- 3.10. Проектирование базы нечетких правил на основе численных данных
- 3.10.1. Построение нечетких правил
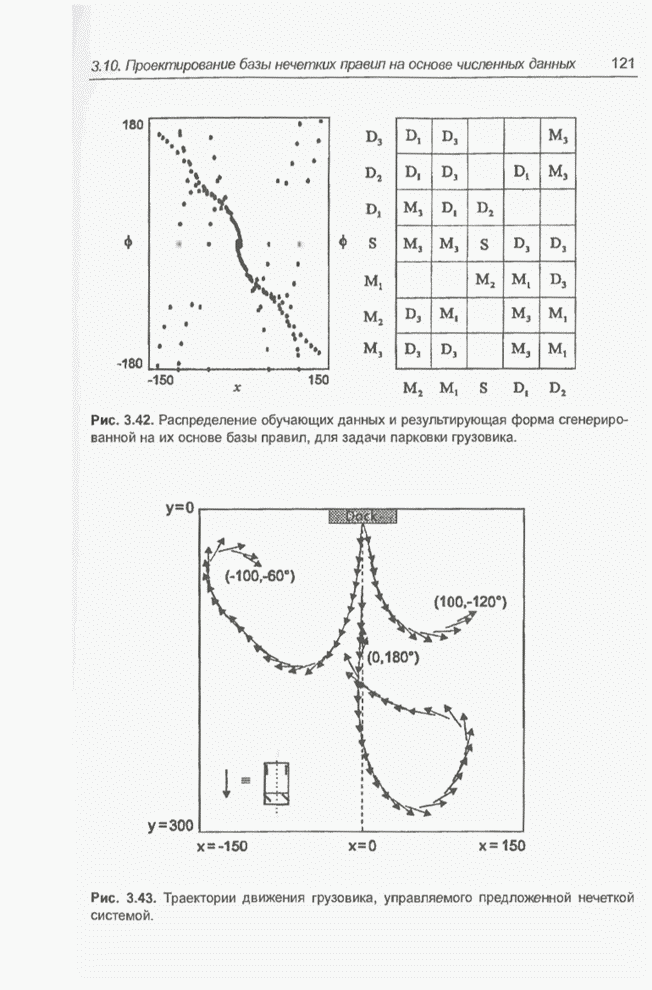
- 3.10.2. Задача парковки грузовика
- 3.10.3. Примечание
- Список литературы
- ГЛАВА 4. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 4.1. Введение
- 4.2. Генетические алгоритмы и традиционные методы оптимизации
- 4.3. Основные понятия генетических алгоритмов
- 4.4. Классический генетический алгоритм
- 4.5. Иллюстрация выполнения классического генетического алгоритма
- 4.6. Кодирование параметров задачи в генетическом алгоритме
- 4.7. Основная теорема о генетических алгоритмах
- 4.8. Модификации классического генетического алгоритма
- 4.8.1. Методы селекции
- 4.8.2. Особые процедуры репродукции
- 4.8.3. Генетические операторы
- 4.8.4. Методы кодирования
- 4.8.5. Масштабирование функции приспособленности
- 4.8.6. Ниши в генетическом алгоритме
- 4.8.7. Генетические алгоритмы для многокритериальной оптимизации
- 4.8.8. Генетические микроалгоритмы
- 4.9. Примеры оптимизации функции с помощью программы FlexTool
- 4.10. Эволюционные алгоритмы
- 4.11. Приложения эволюционных алгоритмов
- 4.11.1. Примеры оптимизации функции с помощью программы Evolver
- 4.11.2. Решение комбинаторных задач с помощью программы Evolver
- 4.12. Эволюционные алгоритмы в нейронных сетях
- 4.12.1. Независимое применение генетических алгоритмов и нейронных сетей
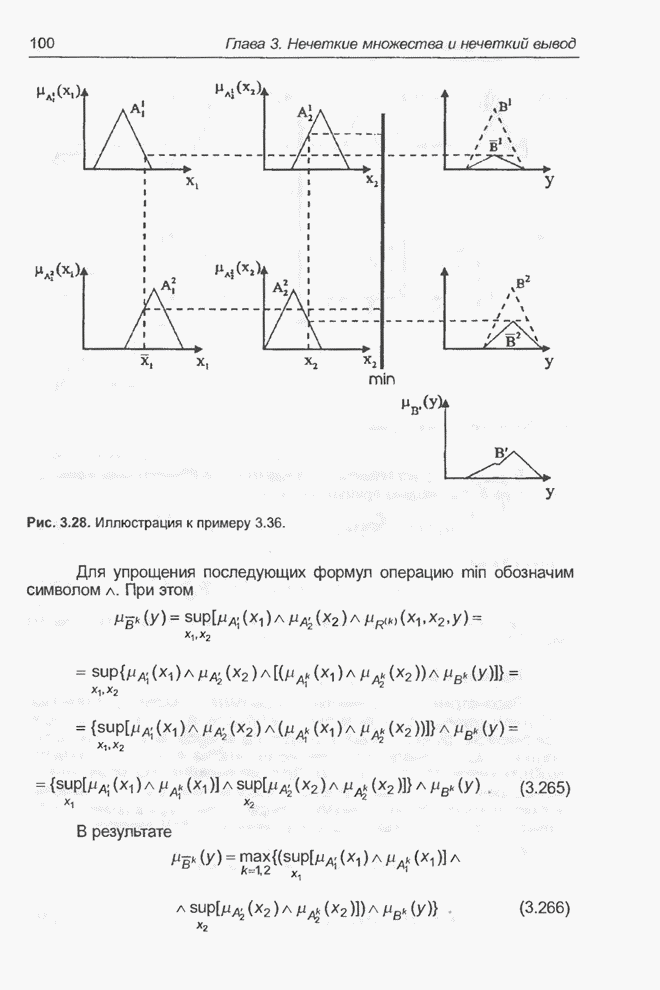
- 4.12.2. Нейронные сети для поддержки генетических алгоритмов
- 4.12.3. Генетические алгоритмы для поддержки нейронных сетей
- 4.12.4. Применение генетических алгоритмов для обучения нейронных сетей
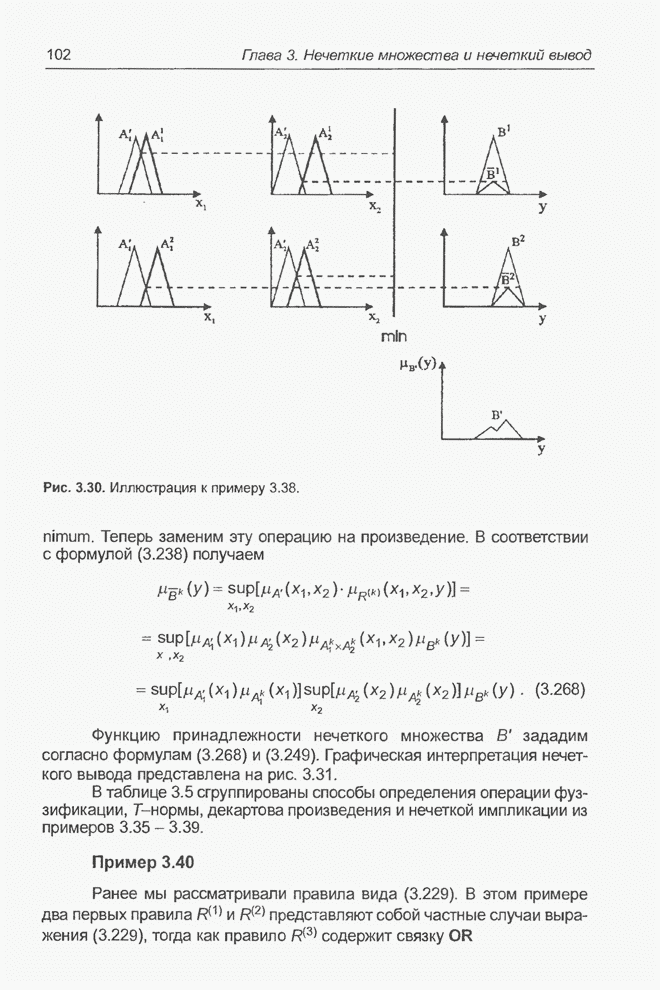
- 4.12.5. Генетические алгоритмы для выбора топологии нейронных сетей
- 4.12.6. Адаптивные взаимодействующие системы
- 4.12.7. Типовой цикл эволюции
- 4.12.7.1. Эволюция весов связей
- 4.12.7.2. Эволюция архитектуры сети
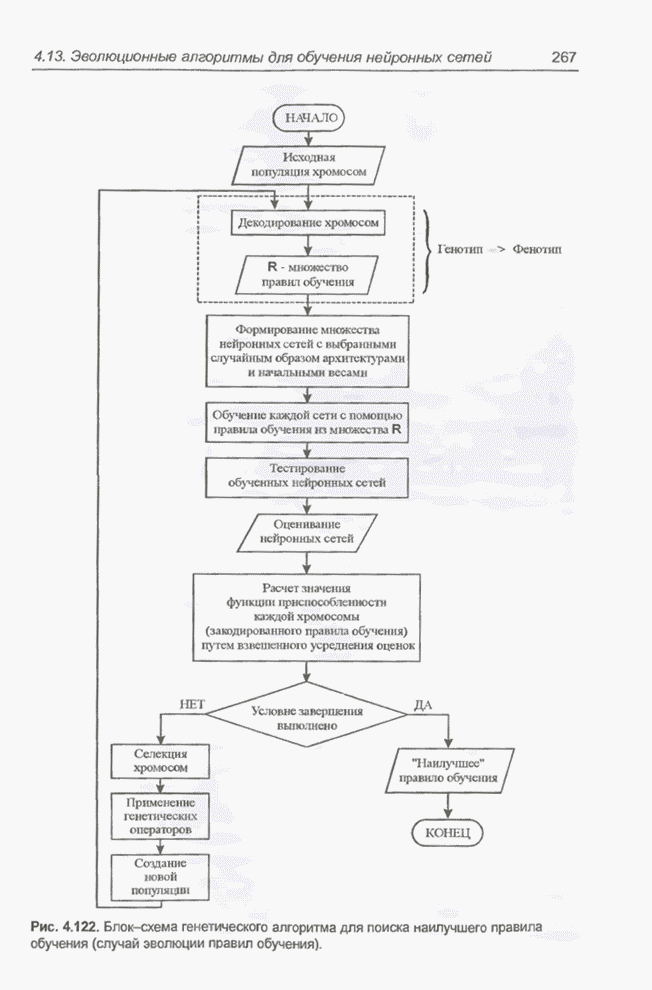
- 4.12.7.3. Эволюция правил обучения
- 4.13. Примеры моделирования эволюционных алгоритмов в приложении к нейронным сетям
- 4.13.1. Программы Evolver и BrainMaker
- 4.13.2. Программа GTO
- Список литературы
- ГЛАВА 5. МОДУЛИ НЕЧЕТКО-НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.1. Модуль нечеткого управления со структурой, определенной в процессе дефуззификации
- 5.1.2. Конструкция модуля
- 5.1.3. Структура модуля
- 5.1.4. Использование алгоритма обратного распространения ошибки
- 5.1.5. Модификации модуля
- 5.1.6. Применение модуля нечеткого управления для прогнозирования случайных временных рядов
- 5.1.7. Применение модуля нечеткого управления для решения задачи парковки грузовика
- 5.1.8. Примечание
- 5.2. Представление модуля нечеткого управления в виде стандартной нейронной сети
- 5.3. Модуль нечеткого управления с нейронной сетью для выполнения дефуззификации
- 5.3.1. Введение
- 5.3.2. Конструкция модуля
- 5.3.3. Структура модуля
- 5.3.4. Алгоритмы обучения модуля
- 5.3.5. Решение задачи стабилизации перевернутого маятника
- 5.3.6. Примечание
- 5.4. Модуль нечеткого управления с возможностью коррекции правил
- 5.4.1. Введение
- 5.4.2. Фаза обучения на основе самоорганизации
- 5.4.3. Фаза обучения с учителем
- 5.4.4. Примечание
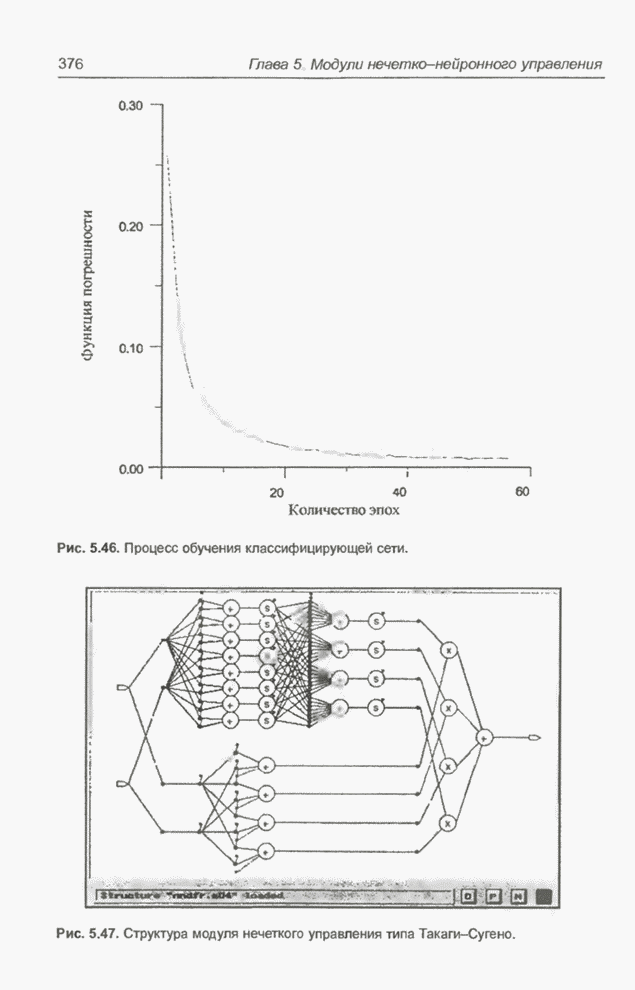
- 5.5. Модуль нечеткого управления типа Такаги-Сугено
- 5.5.1. Введение
- 5.5.2. Нейронная реализация функции принадлежности
- 5.5.3. Модули Такаги-Сугено
- 5.5.4. Реализация условий
- 5.5.5. Реализация заключений
- 5.5.6. Примечание
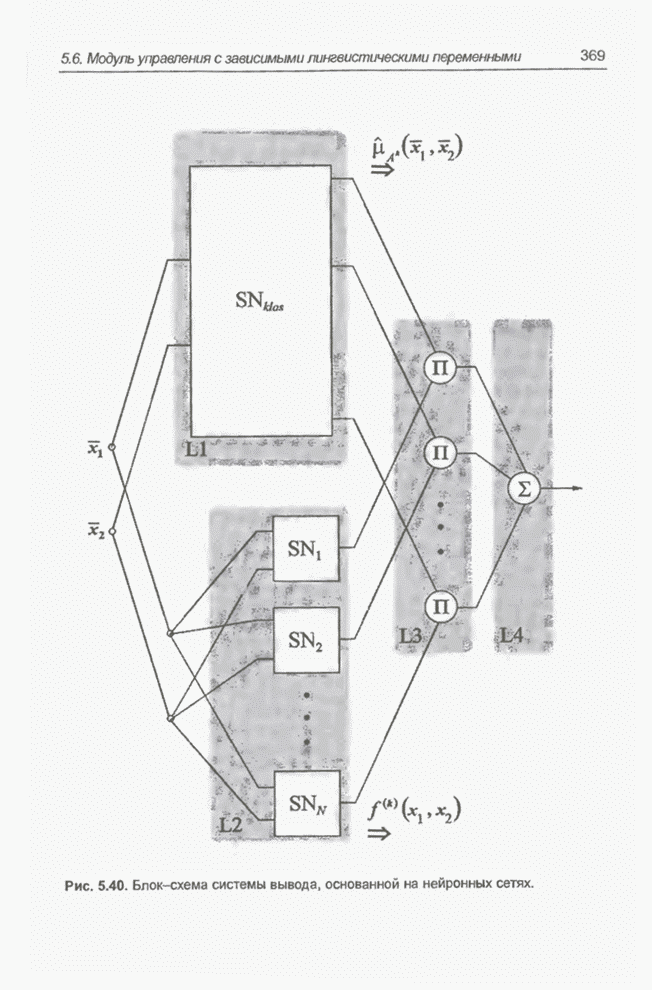
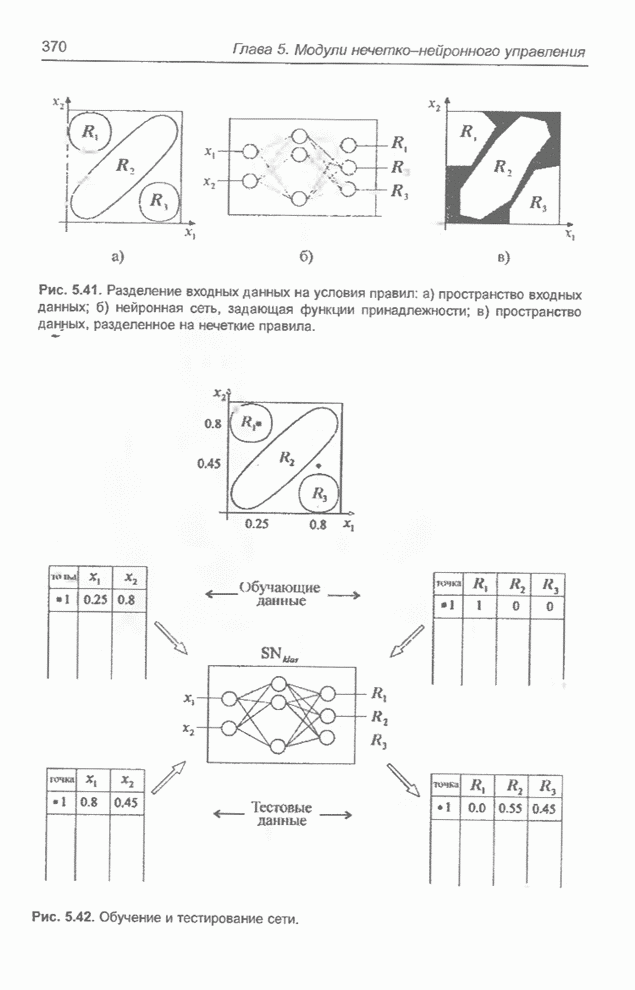
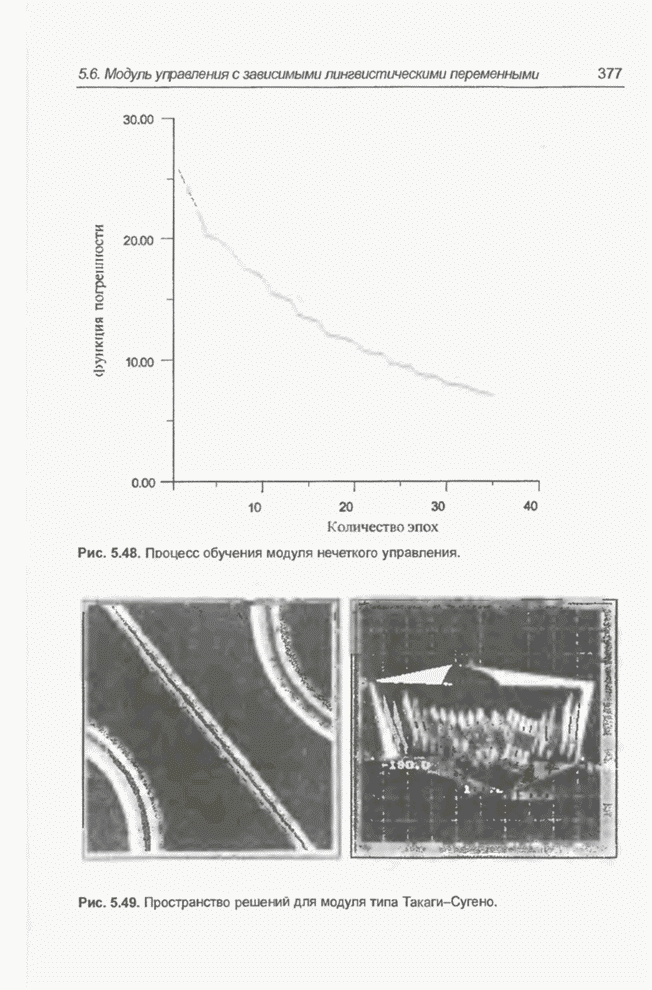
- 5.6. Модуль нечеткого управления типа Такаги-Сугено: случай зависимых лингвистических переменных
- 5.6.1. Введение
- 5.6.2. Нейронные сети для нечеткого вывода
- 5.6.3. Структура системы
- 5.6.4. Способ обучения
- 5.6.5. Решение задачи парковки грузовика
- 5.6.6. Примечание
- Список литературы