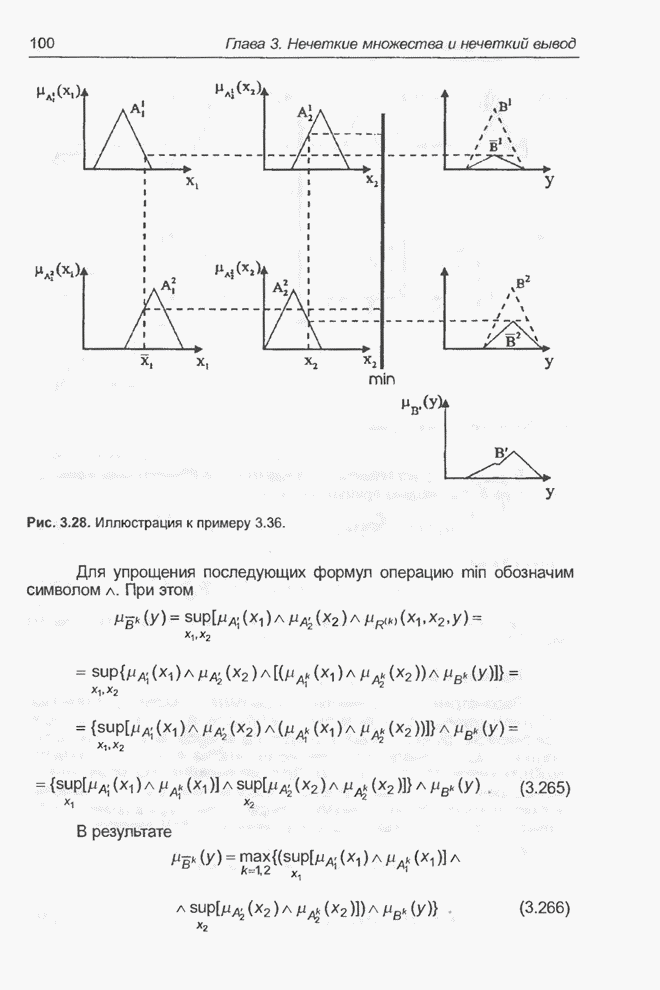
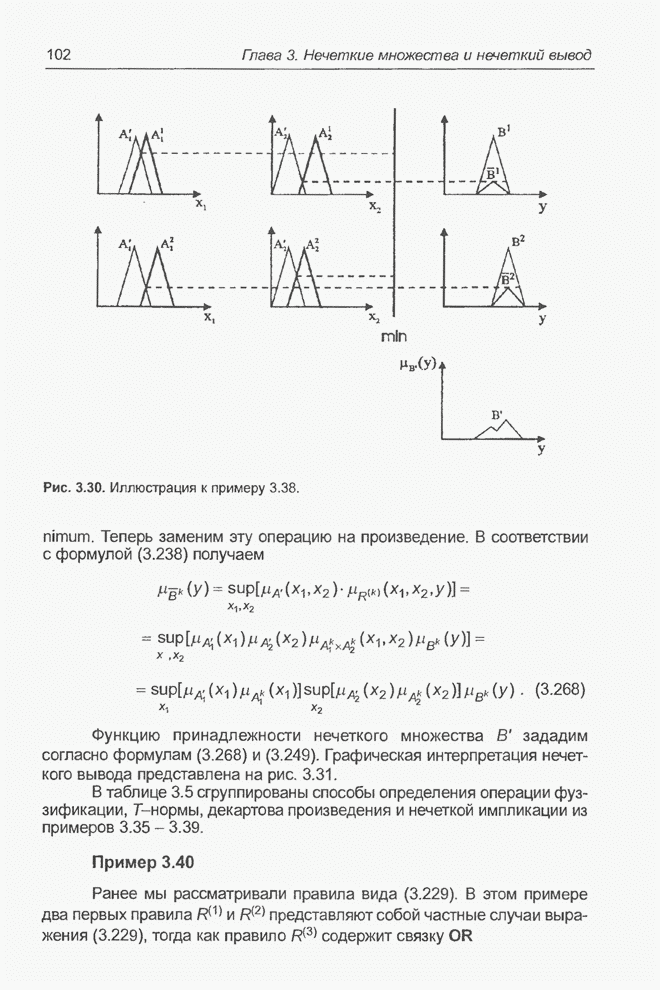
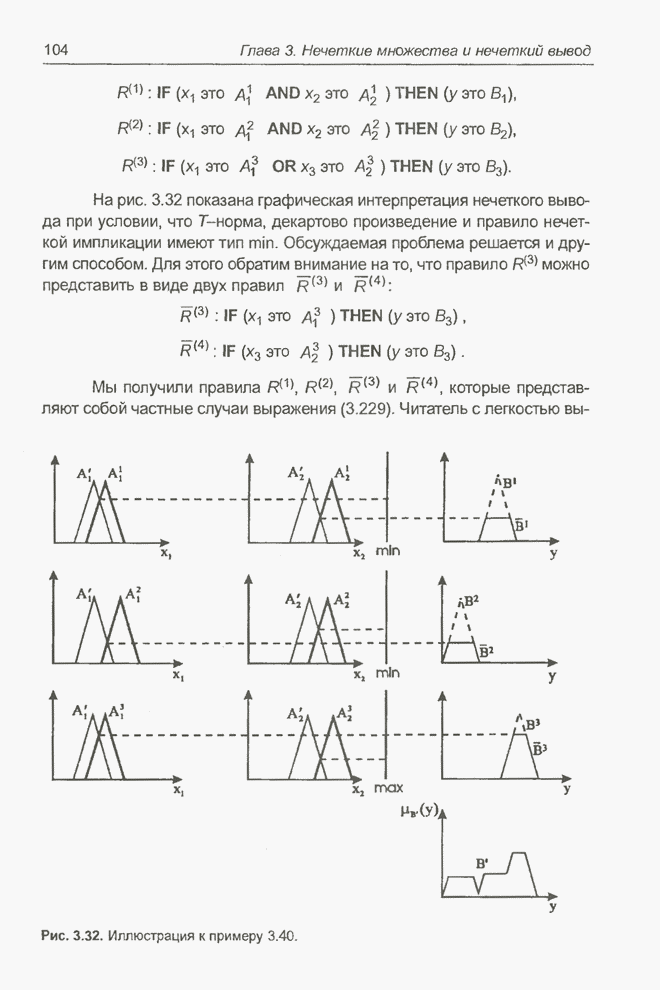
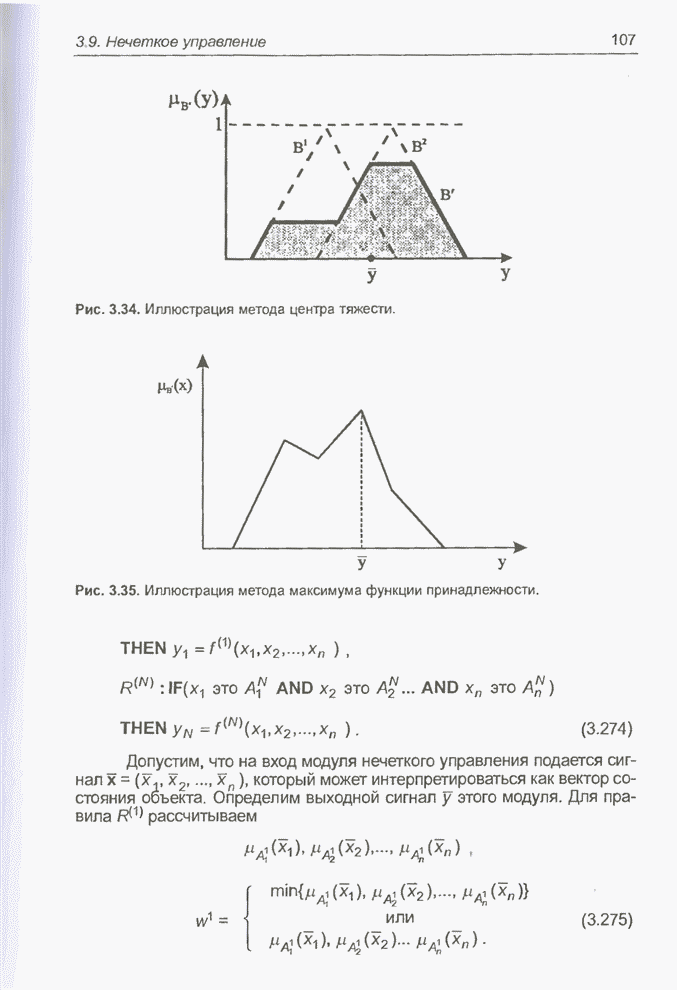
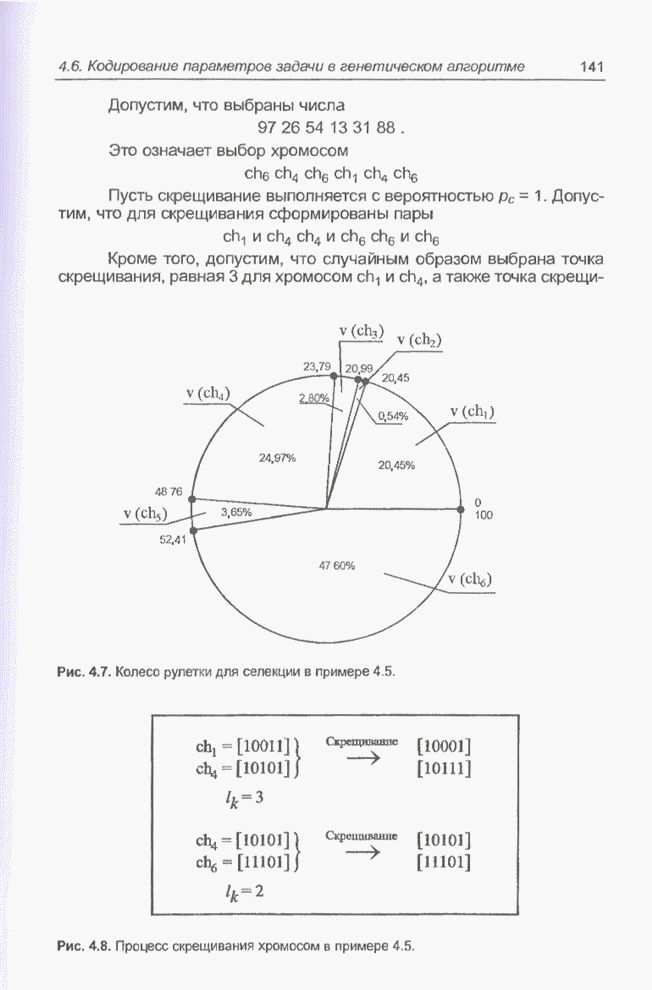
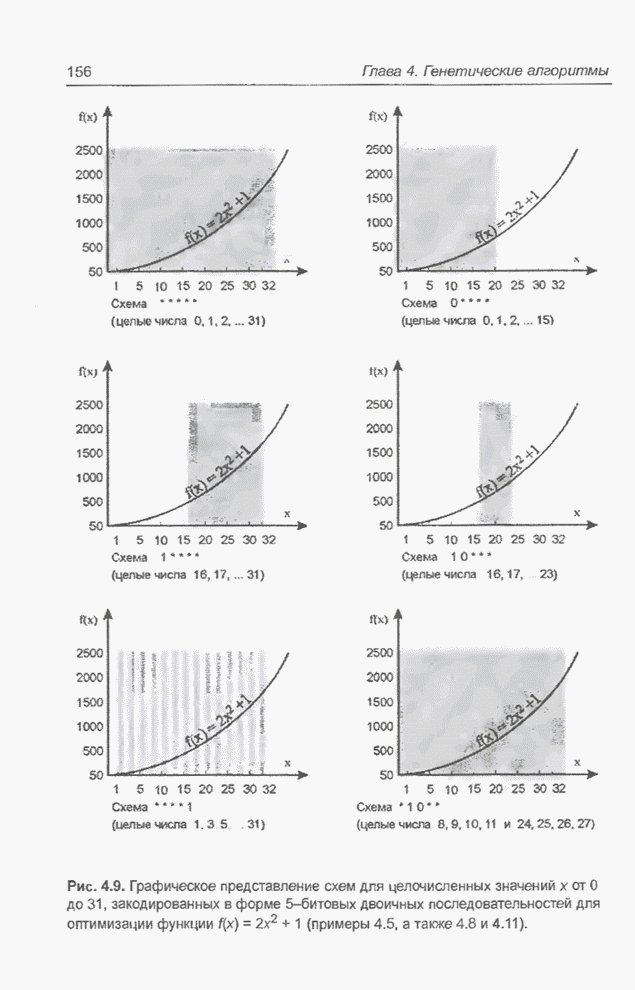
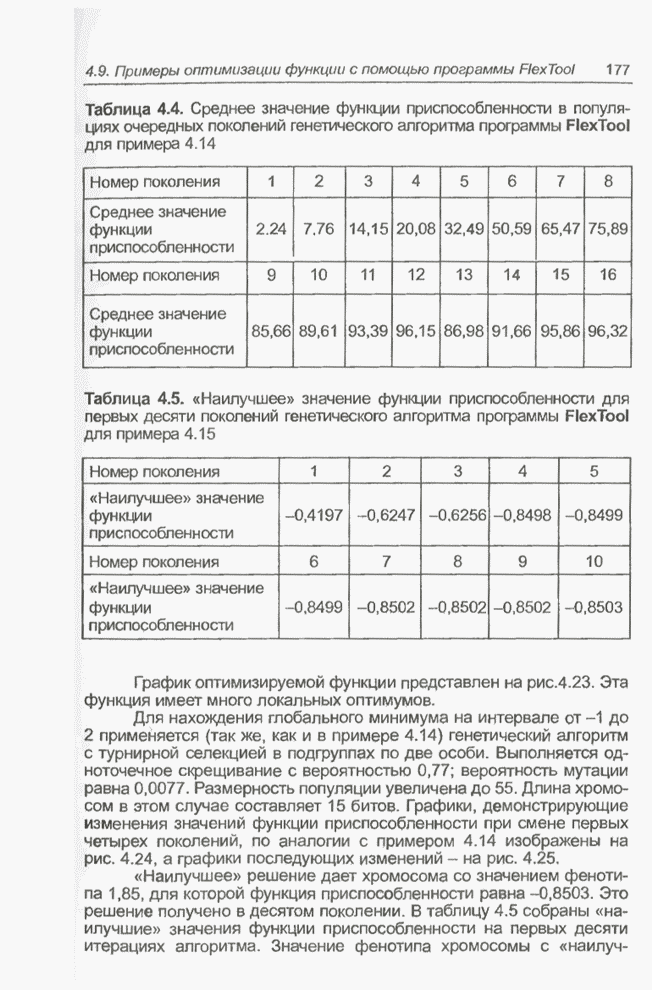
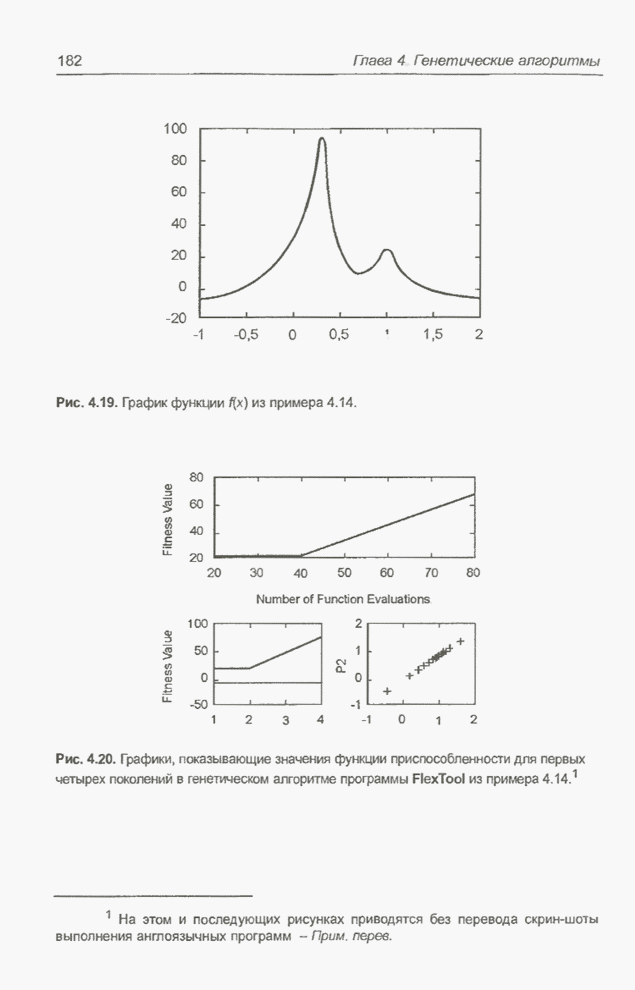
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
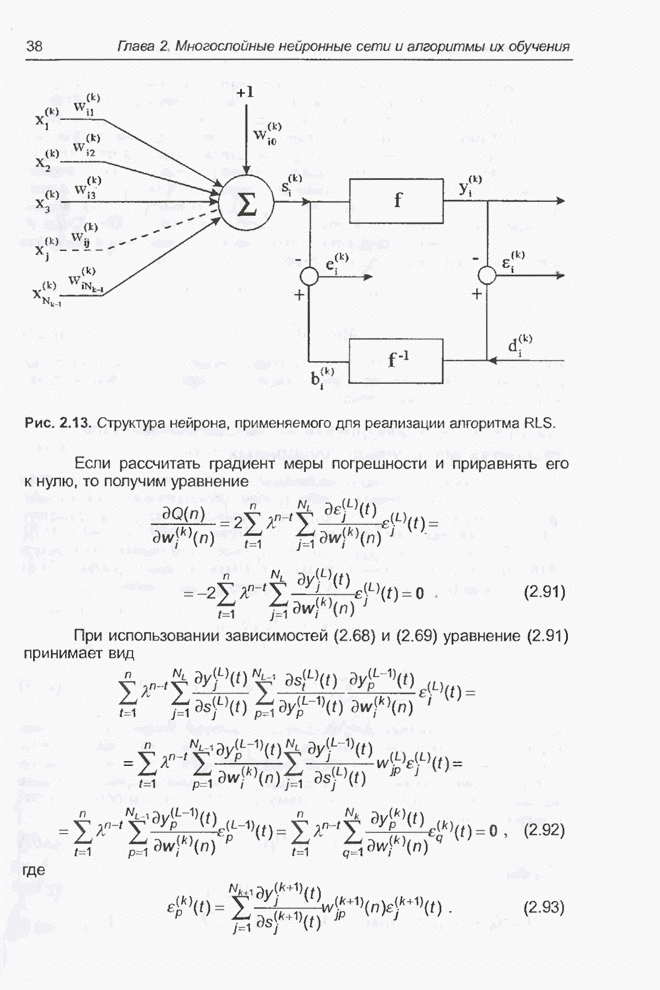
2.4.2. Адаптивный линейный взвешенный сумматор
Применение алгоритма (2.41)
предполагает знание матрицы ![]() и вектора
и вектора ![]() . В случае, когда эти величины неизвестны,
следует заменить градиент (2.39) его приближением. Запишем рекурсивное
выражение (2.40) в виде
. В случае, когда эти величины неизвестны,
следует заменить градиент (2.39) его приближением. Запишем рекурсивное
выражение (2.40) в виде
 . (2.46)
. (2.46)
Если в этой формуле заменить градиент его приближенным локальным значением (instantaneous estimate), т.е.
 , (2.47)
, (2.47)
то получим рекурсию вида
 . (2.48)
. (2.48)
Из выражений (2.24) и (2.25) следует, что
 . (2.49)
. (2.49)
При подстановке зависимости (2.49) в формулу (2.48) получаем так называемый алгоритм LMS (Least Mean Square) в векторной форме
![]() (2.50)
(2.50)
или в скалярной форме
 (2.51)
(2.51)
для
![]() .
.
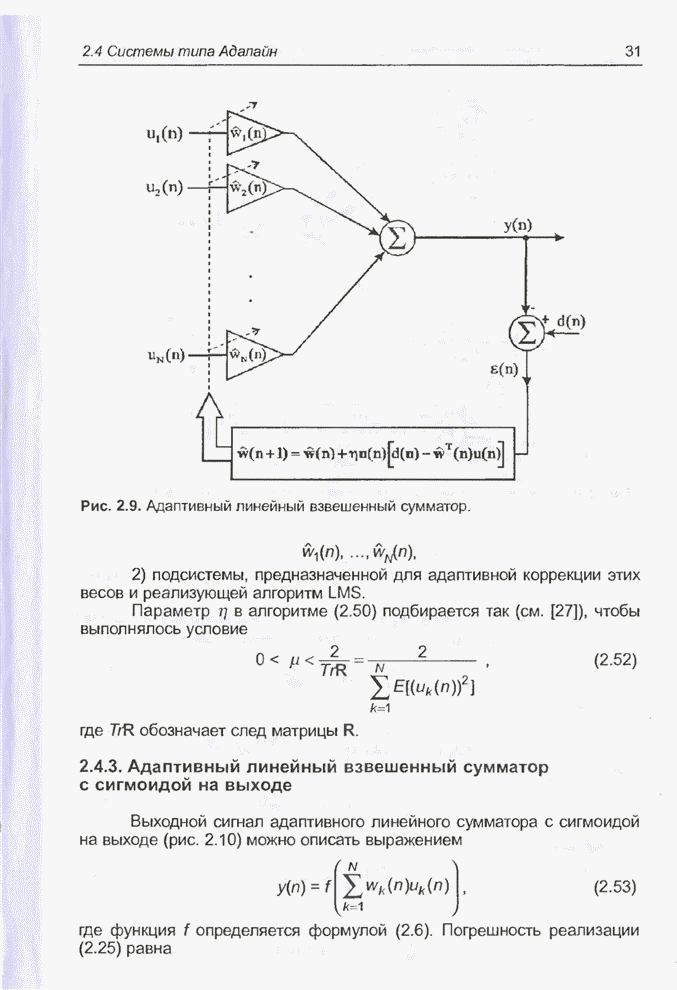
На рис. 2.9 представлен адаптивный линейный взвешенный сумматор, известный в литературе под названием Адалайн (Adaptive Linear Neuron). Он состоит из двух основных частей:
1) линейного взвешенного сумматора с адаптивно корректируемыми весами
![]() ,
,
2) подсистемы, предназначенной для адаптивной коррекции этих весов и реализующей алгоритм LMS.

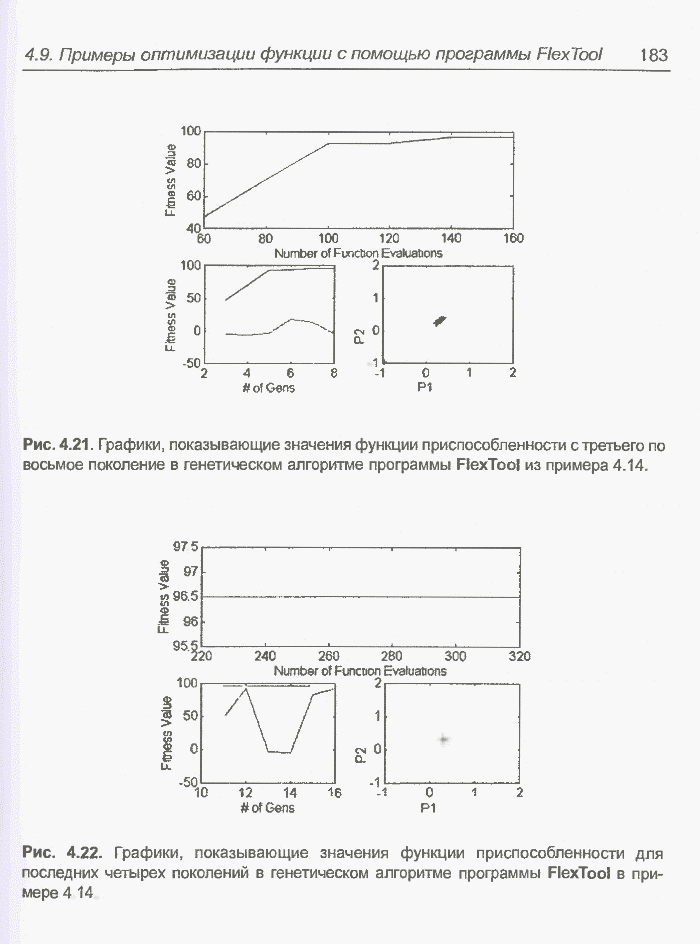
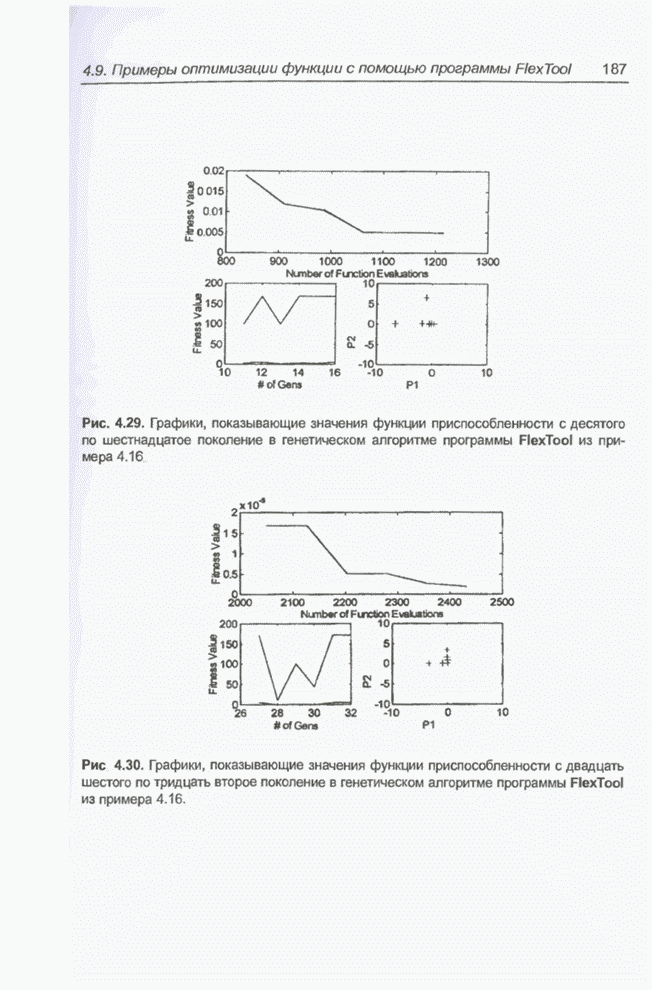
Рис. 2.9. Адаптивный линейный взвешенный сумматор.
Параметр ![]() в алгоритме (2.50) подбирается
так (см. [27]), чтобы выполнялось условие
в алгоритме (2.50) подбирается
так (см. [27]), чтобы выполнялось условие
 , (2.52)
, (2.52)
где
![]() обозначает
след матрицы
обозначает
след матрицы ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Предисловие к русскому изданию
- ГЛАВА 1. ВВЕДЕНИЕ
- Список литературы
- ГЛАВА 2. МНОГОСЛОЙНЫЕ НЕЙРОННЫЕ СЕТИ И АЛГОРИТМЫ ИХ ОБУЧЕНИЯ
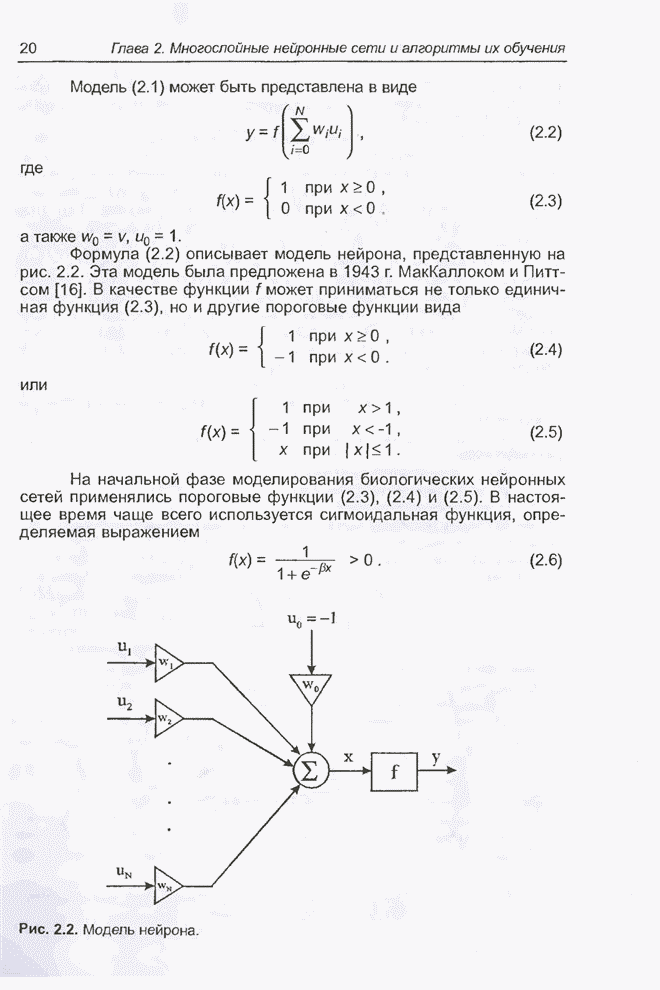
- 2.1. Введение
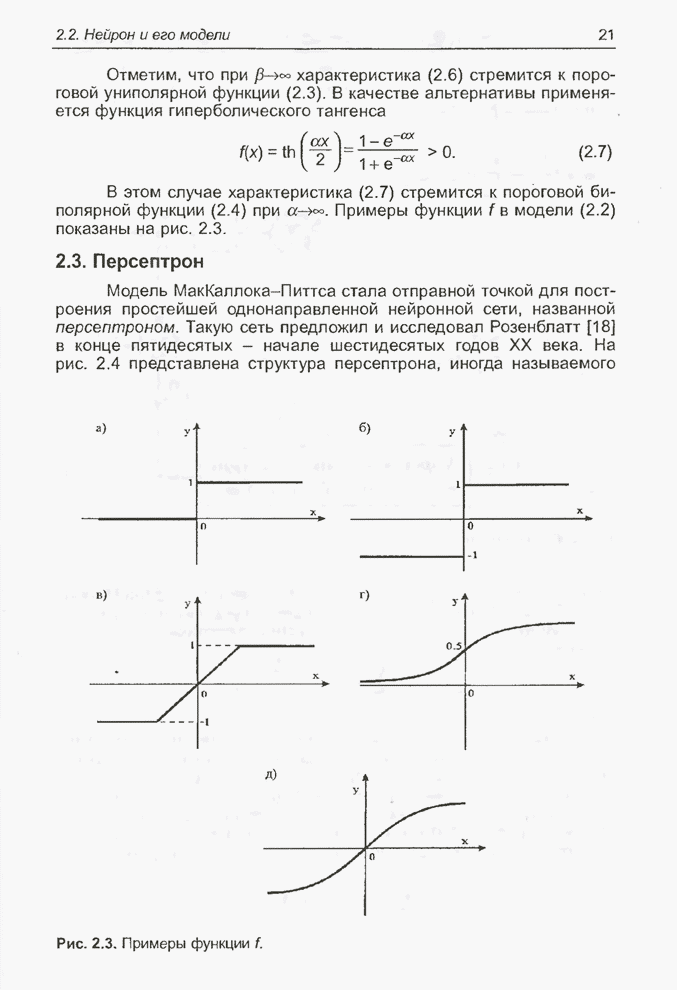
- 2.2. Нейрон и его модели
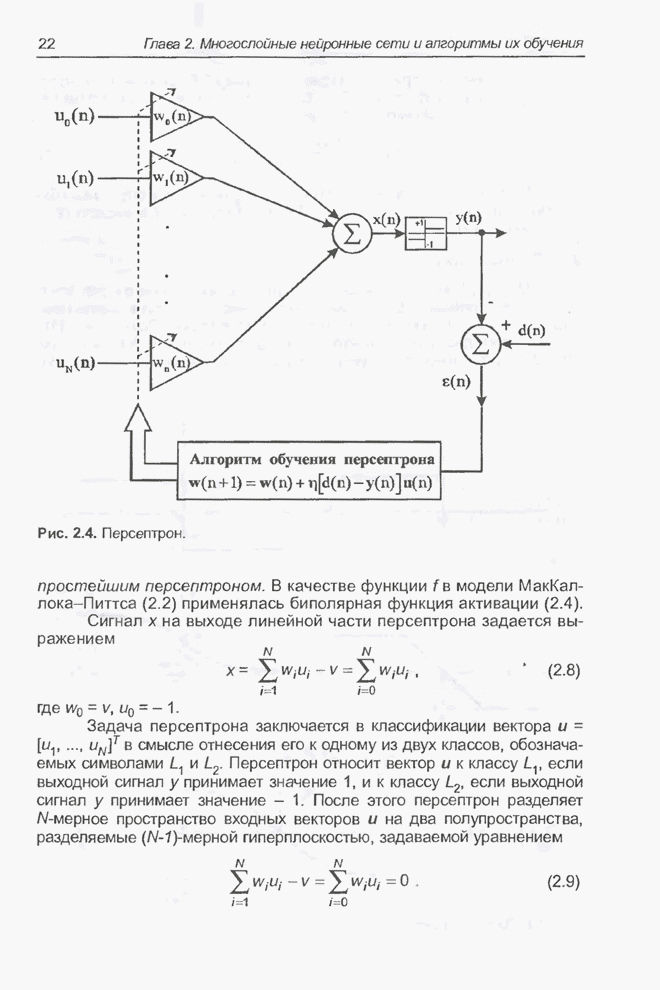
- 2.3. Персептрон
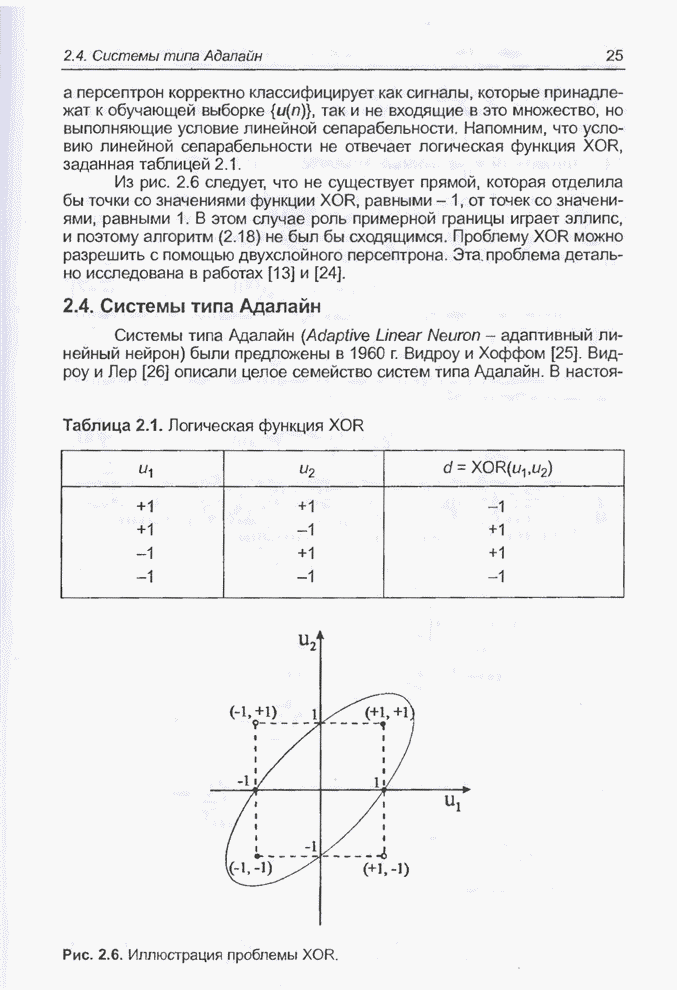
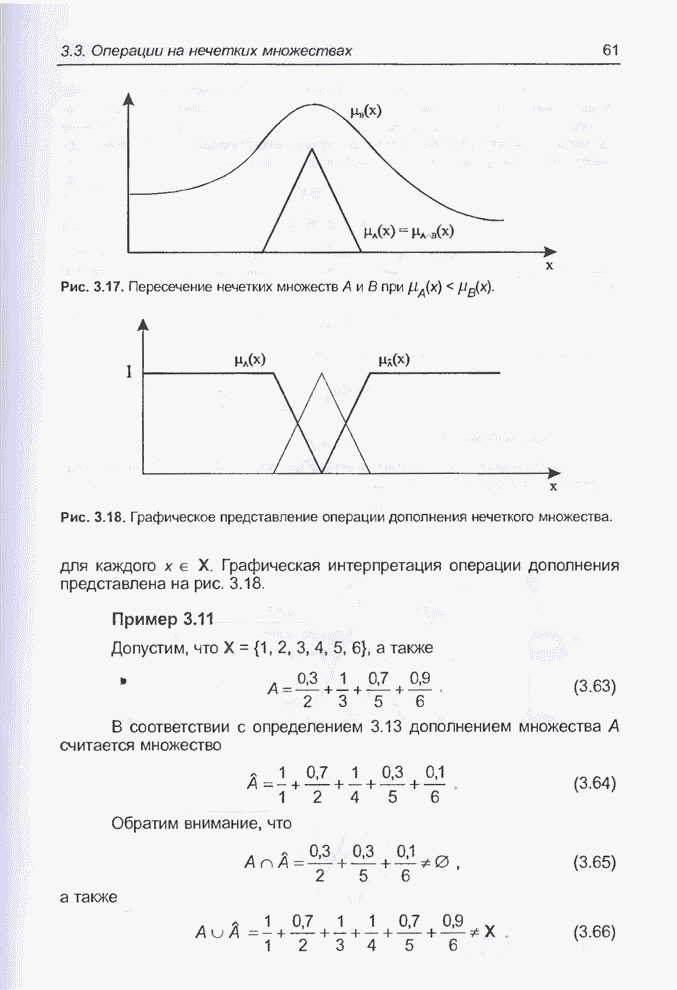
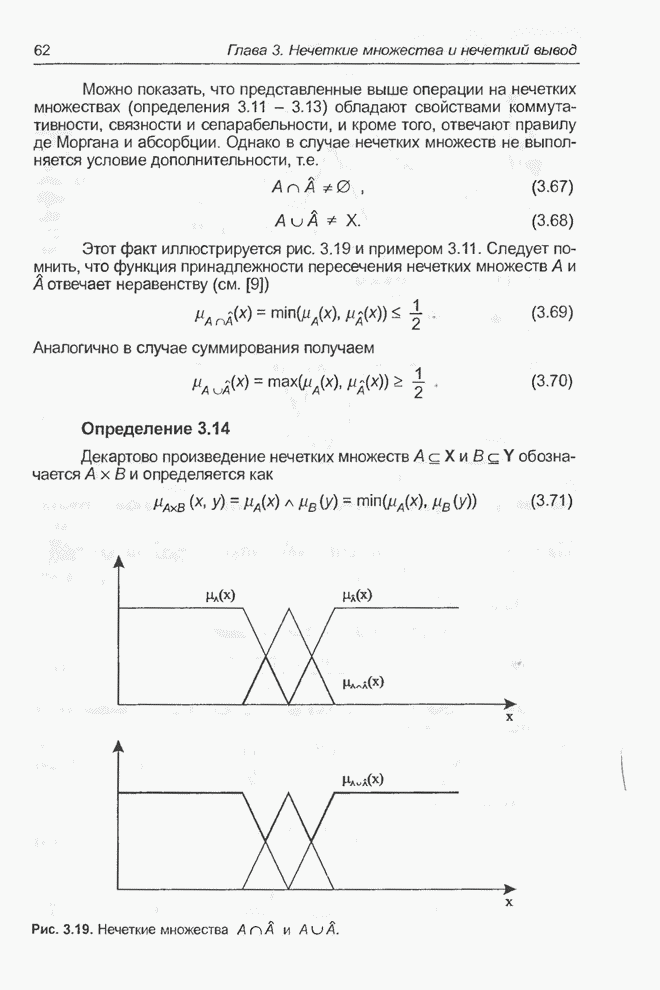
- 2.4. Системы типа Адалайн
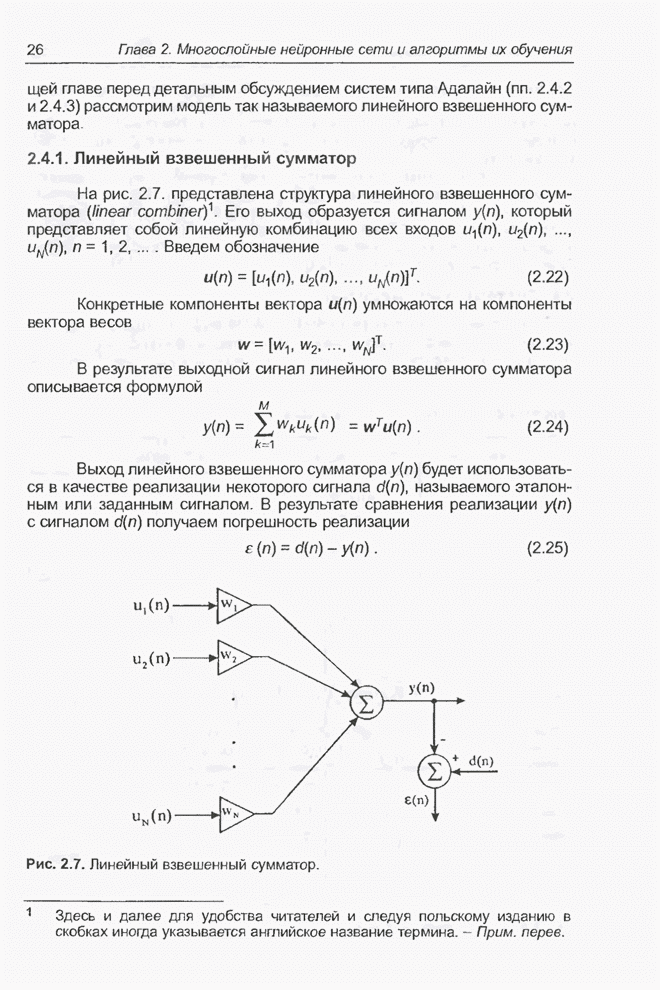
- 2.4.1. Линейный взвешенный сумматор
- 2.4.2. Адаптивный линейный взвешенный сумматор
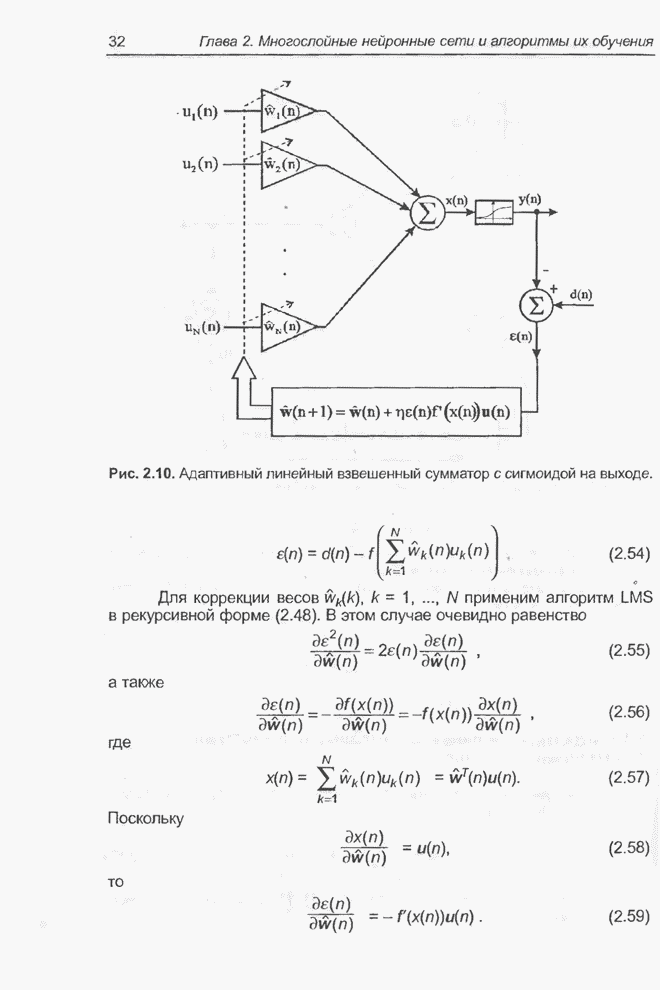
- 2.4.3. Адаптивный линейный взвешенный сумматор с сигмоидой на выходе
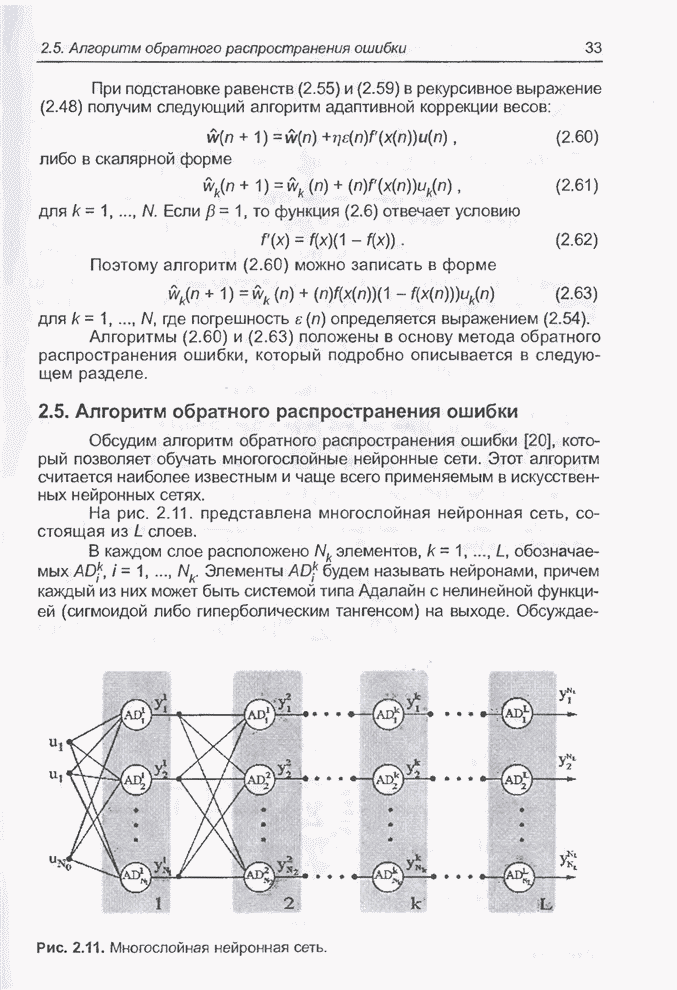
- 2.5. Алгоритм обратного распространения ошибки
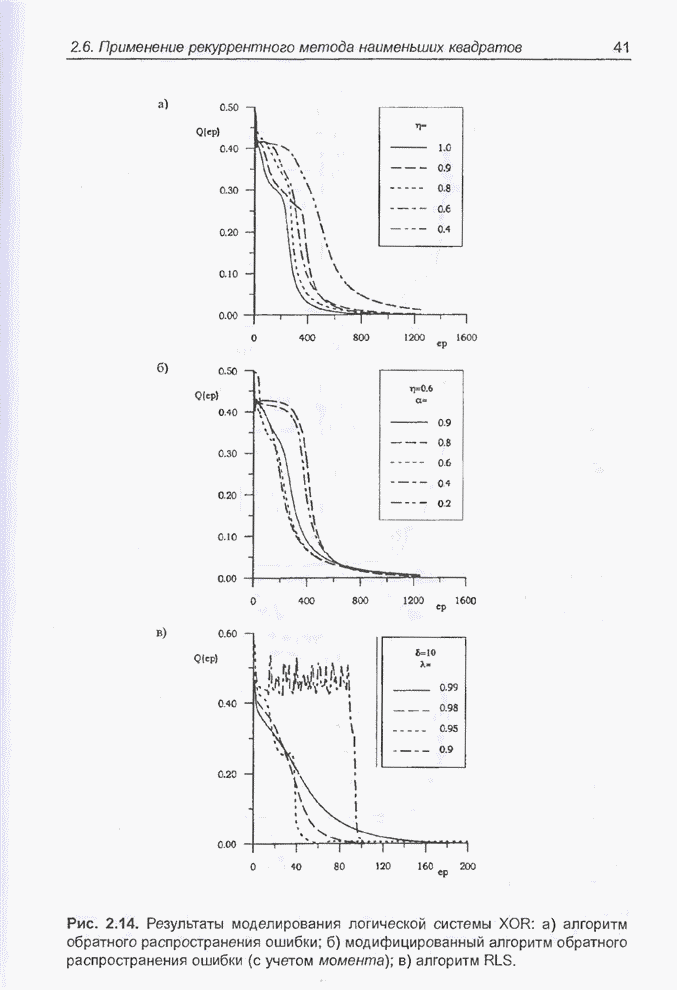
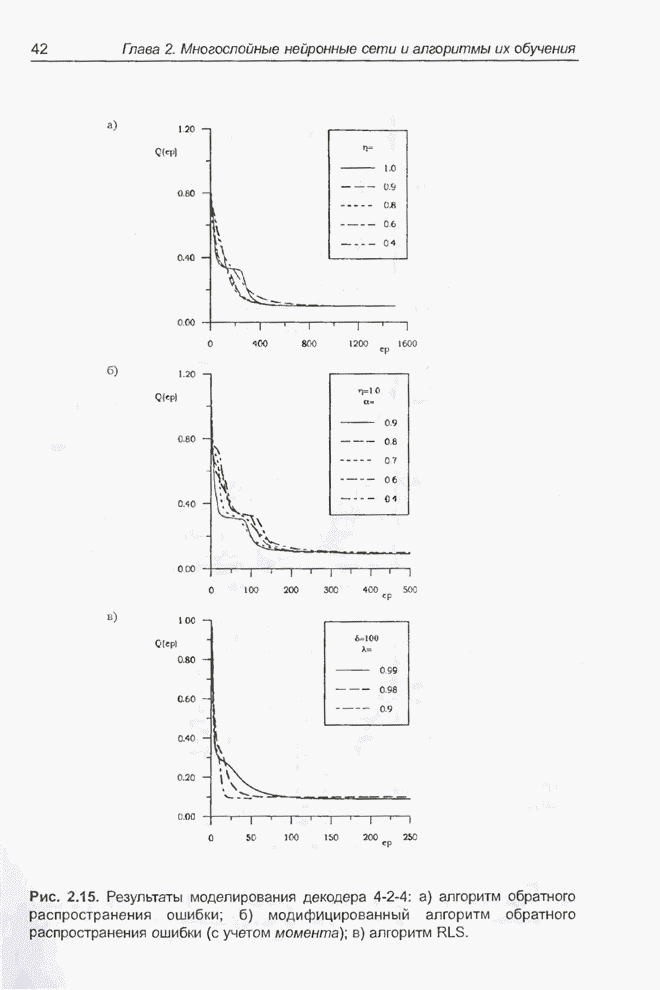
- 2.6. Применение рекуррентного метода наименьших квадратов для обучения нейронных сетей
- Список литературы
- ГЛАВA3. НЕЧЕТКИЕ МНОЖЕСТВА И НЕЧЕТКИЙ ВЫВОД
- 3.1. Введение
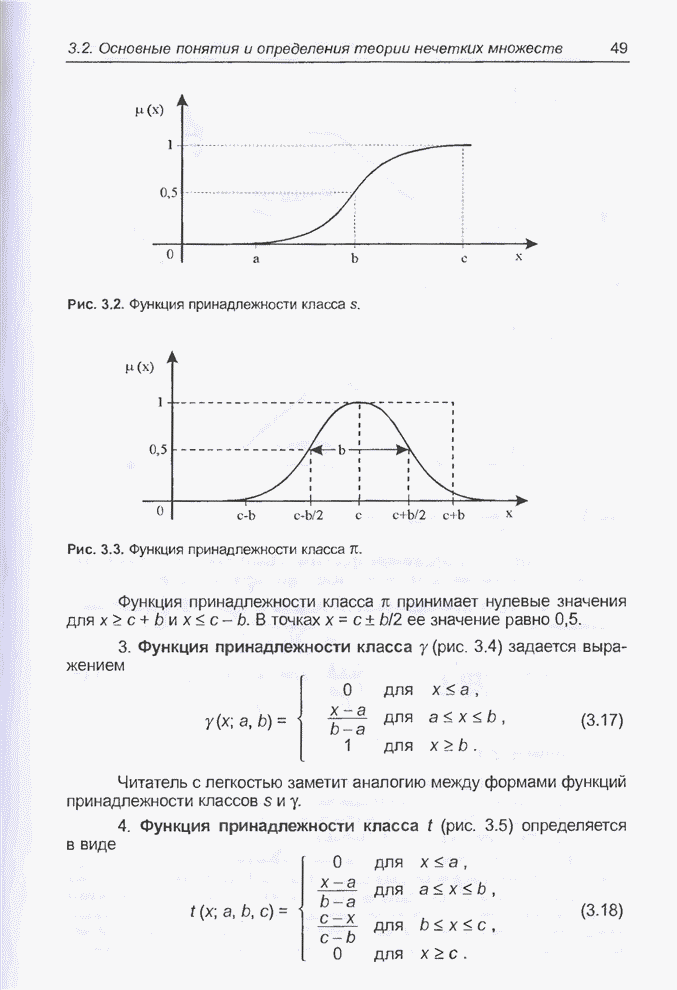
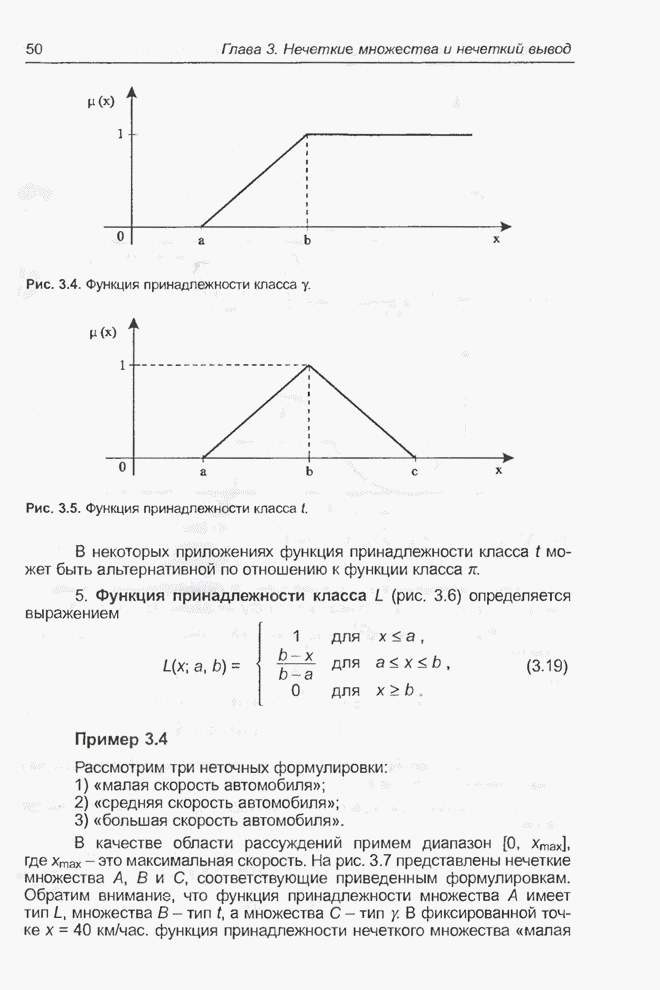
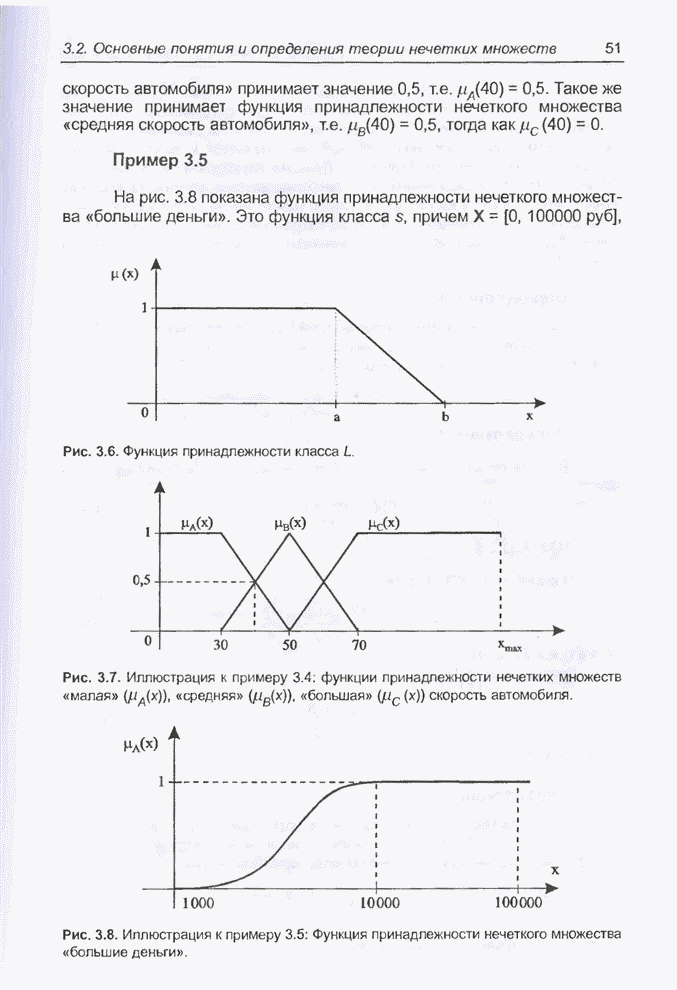
- 3.2. Основные понятия и определения теории нечетких множеств
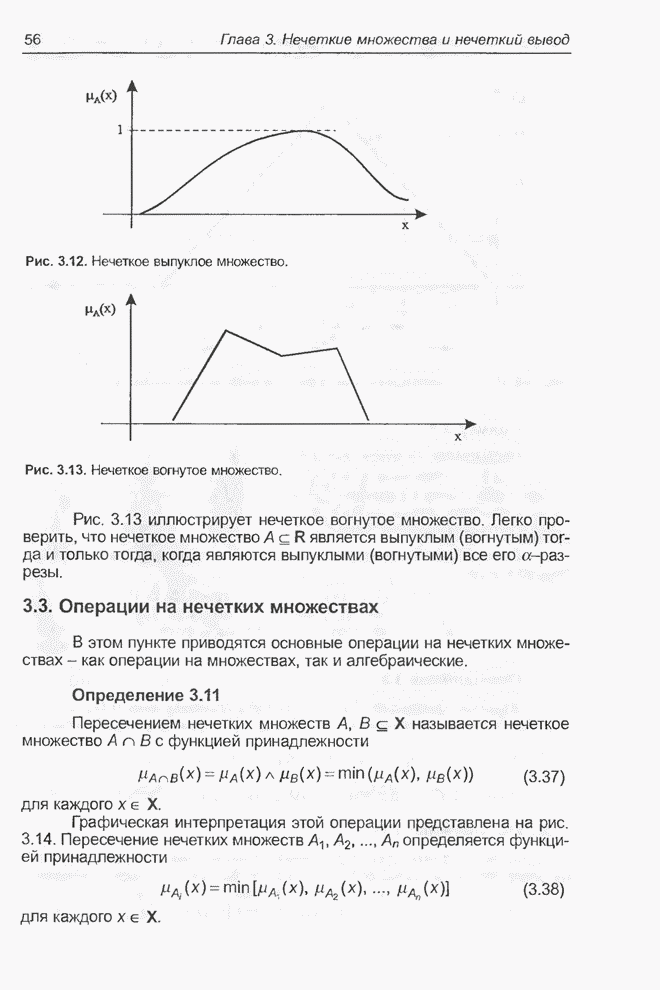
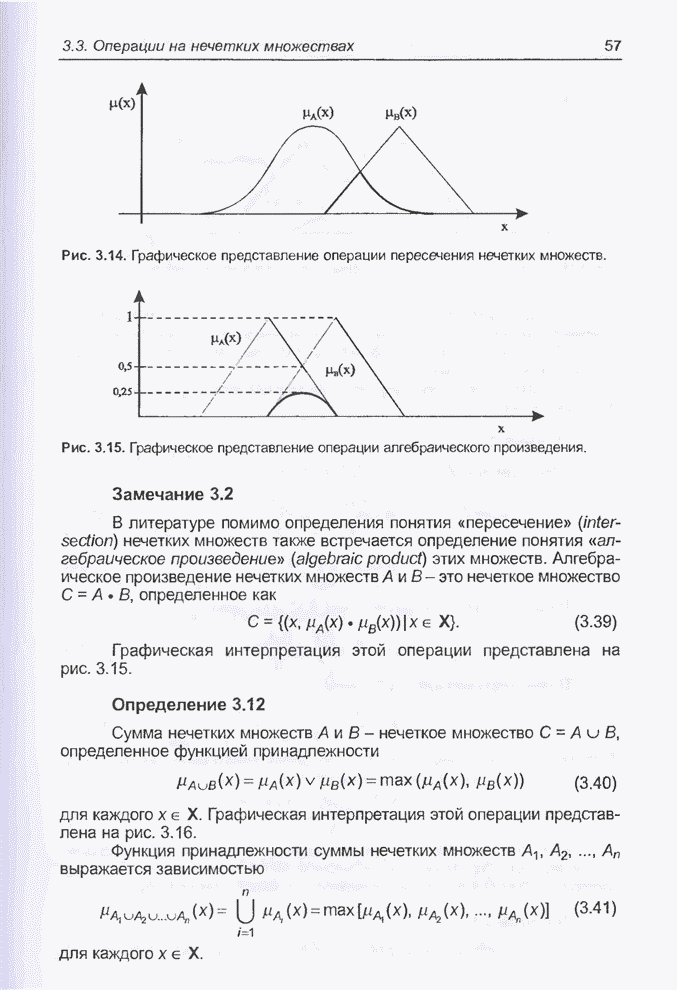
- 3.3. Операции на нечетких множествах
- 3.4. Принцип расширения
- 3.5. Нечеткие числа
- 3.6. Треугольные нормы
- 3.7. Нечеткие отношения и их свойства
- 3.8. Нечеткий вывод
- 3.9. Нечеткое управление
- 3.9.1. Классический модуль нечеткого управления
- 3.9.2. Метод нечеткого управления Такаги-Сугено
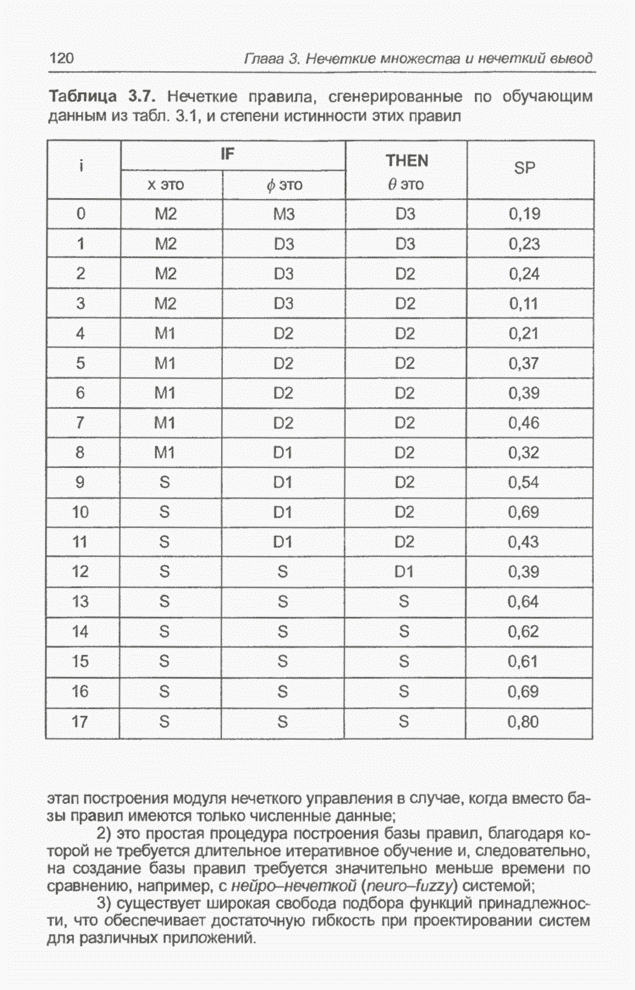
- 3.10. Проектирование базы нечетких правил на основе численных данных
- 3.10.1. Построение нечетких правил
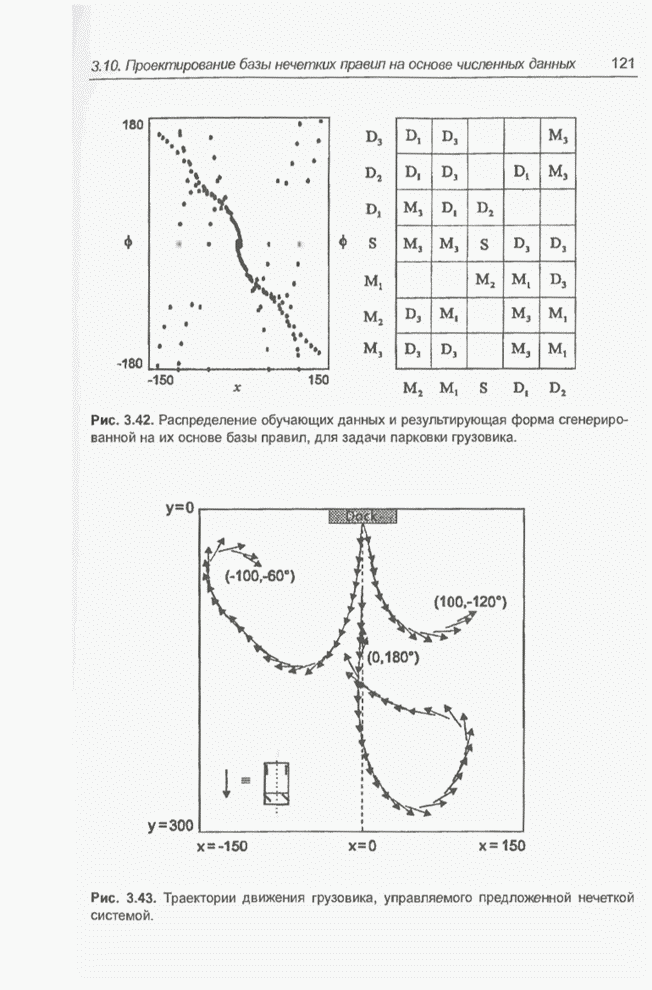
- 3.10.2. Задача парковки грузовика
- 3.10.3. Примечание
- Список литературы
- ГЛАВА 4. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 4.1. Введение
- 4.2. Генетические алгоритмы и традиционные методы оптимизации
- 4.3. Основные понятия генетических алгоритмов
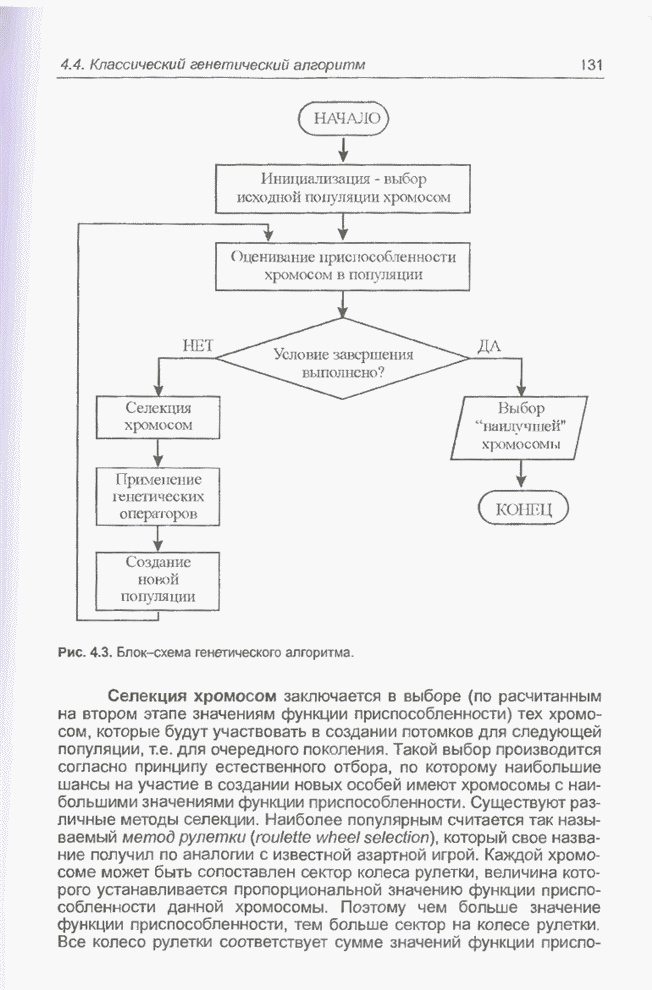
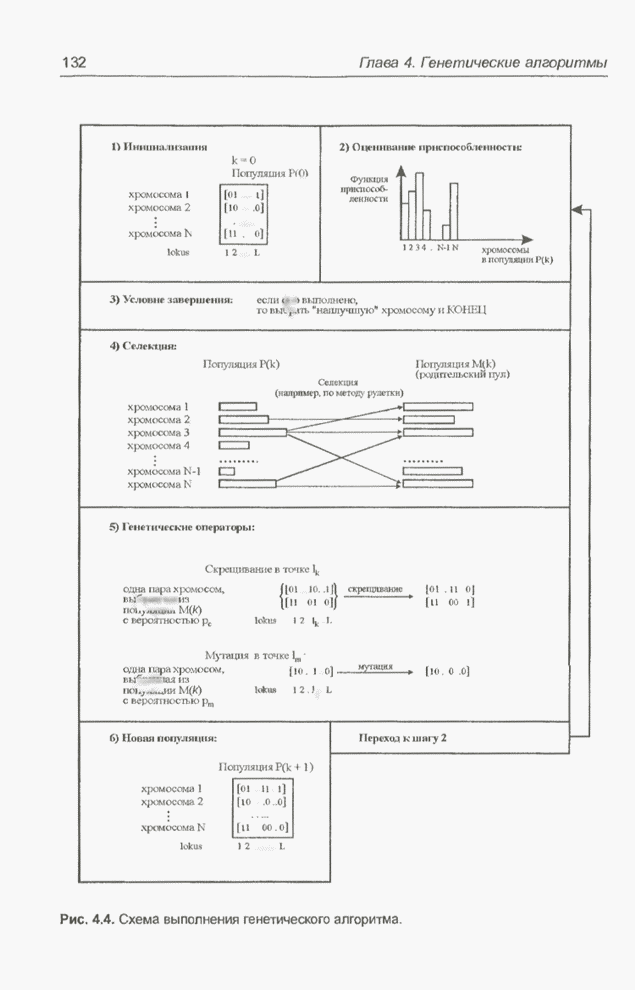
- 4.4. Классический генетический алгоритм
- 4.5. Иллюстрация выполнения классического генетического алгоритма
- 4.6. Кодирование параметров задачи в генетическом алгоритме
- 4.7. Основная теорема о генетических алгоритмах
- 4.8. Модификации классического генетического алгоритма
- 4.8.1. Методы селекции
- 4.8.2. Особые процедуры репродукции
- 4.8.3. Генетические операторы
- 4.8.4. Методы кодирования
- 4.8.5. Масштабирование функции приспособленности
- 4.8.6. Ниши в генетическом алгоритме
- 4.8.7. Генетические алгоритмы для многокритериальной оптимизации
- 4.8.8. Генетические микроалгоритмы
- 4.9. Примеры оптимизации функции с помощью программы FlexTool
- 4.10. Эволюционные алгоритмы
- 4.11. Приложения эволюционных алгоритмов
- 4.11.1. Примеры оптимизации функции с помощью программы Evolver
- 4.11.2. Решение комбинаторных задач с помощью программы Evolver
- 4.12. Эволюционные алгоритмы в нейронных сетях
- 4.12.1. Независимое применение генетических алгоритмов и нейронных сетей
- 4.12.2. Нейронные сети для поддержки генетических алгоритмов
- 4.12.3. Генетические алгоритмы для поддержки нейронных сетей
- 4.12.4. Применение генетических алгоритмов для обучения нейронных сетей
- 4.12.5. Генетические алгоритмы для выбора топологии нейронных сетей
- 4.12.6. Адаптивные взаимодействующие системы
- 4.12.7. Типовой цикл эволюции
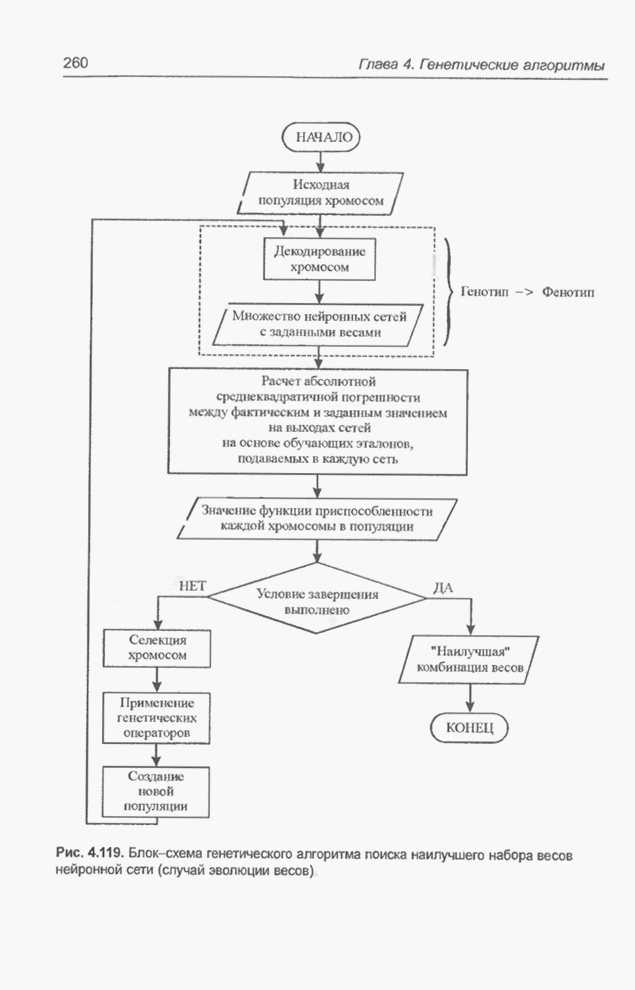
- 4.12.7.1. Эволюция весов связей
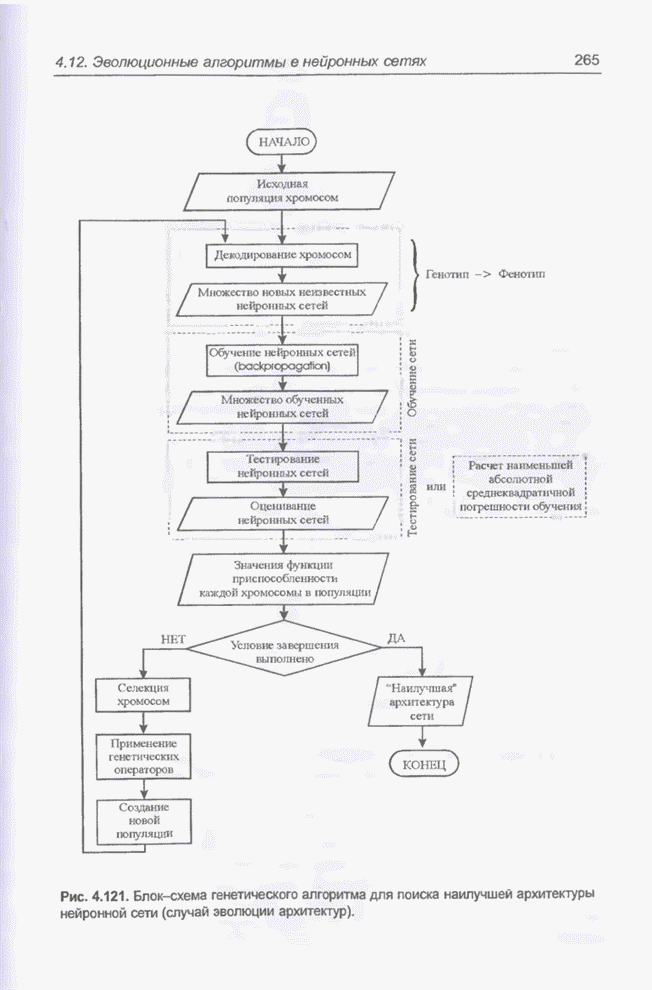
- 4.12.7.2. Эволюция архитектуры сети
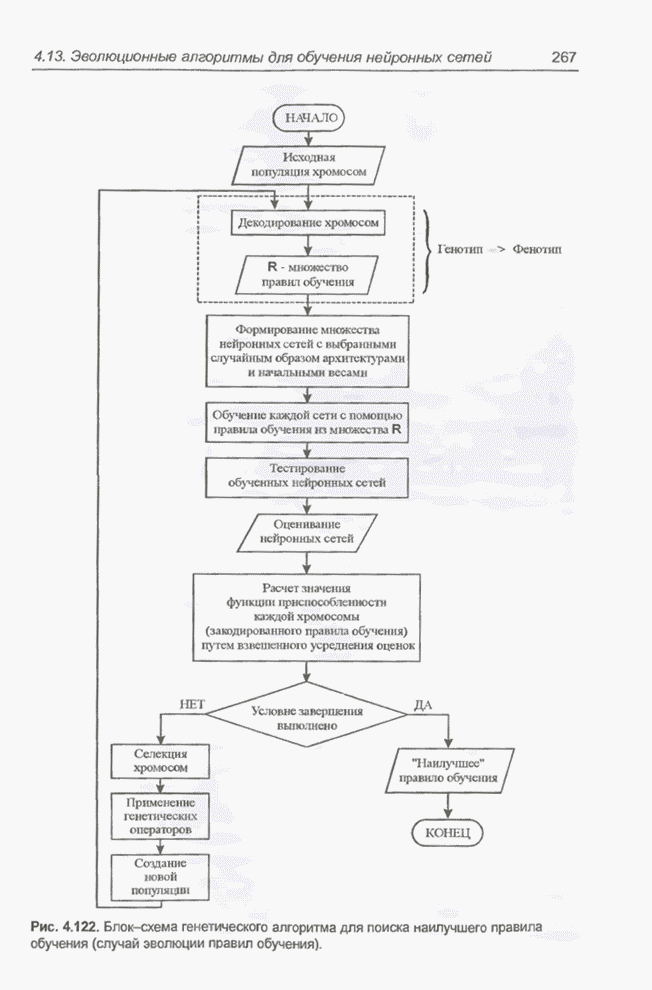
- 4.12.7.3. Эволюция правил обучения
- 4.13. Примеры моделирования эволюционных алгоритмов в приложении к нейронным сетям
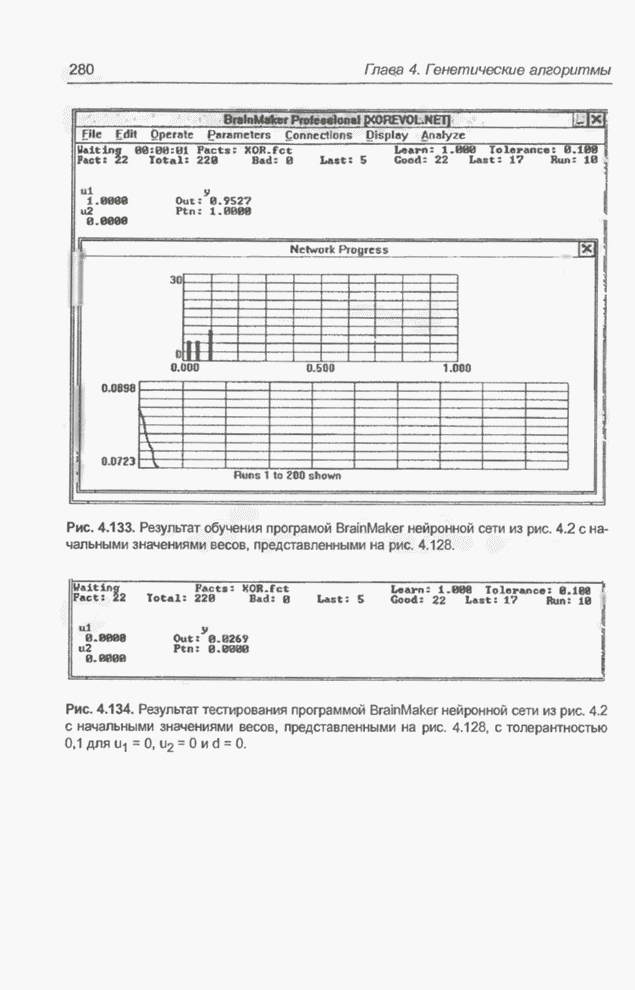
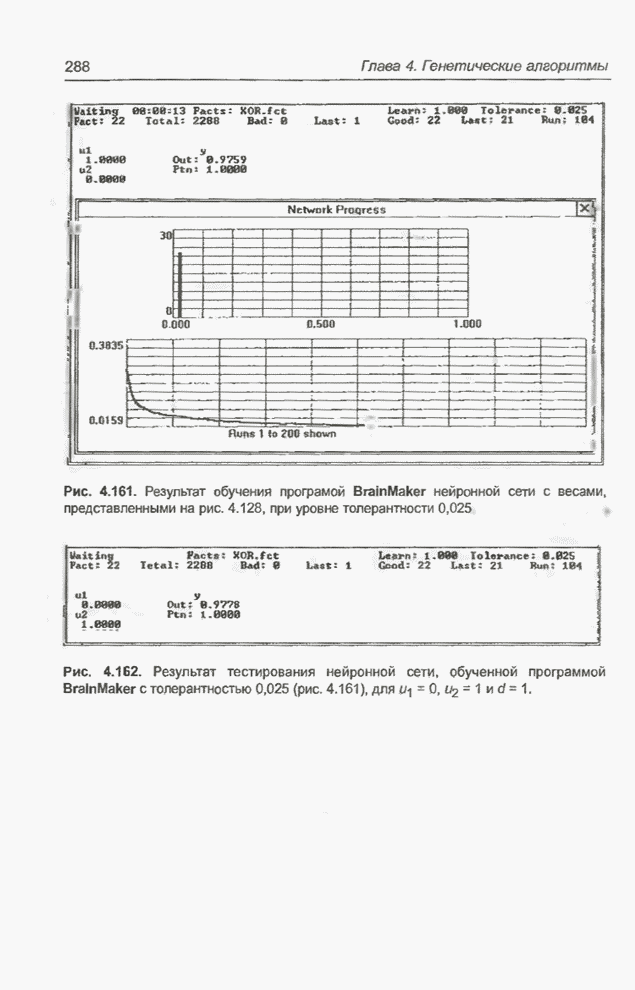
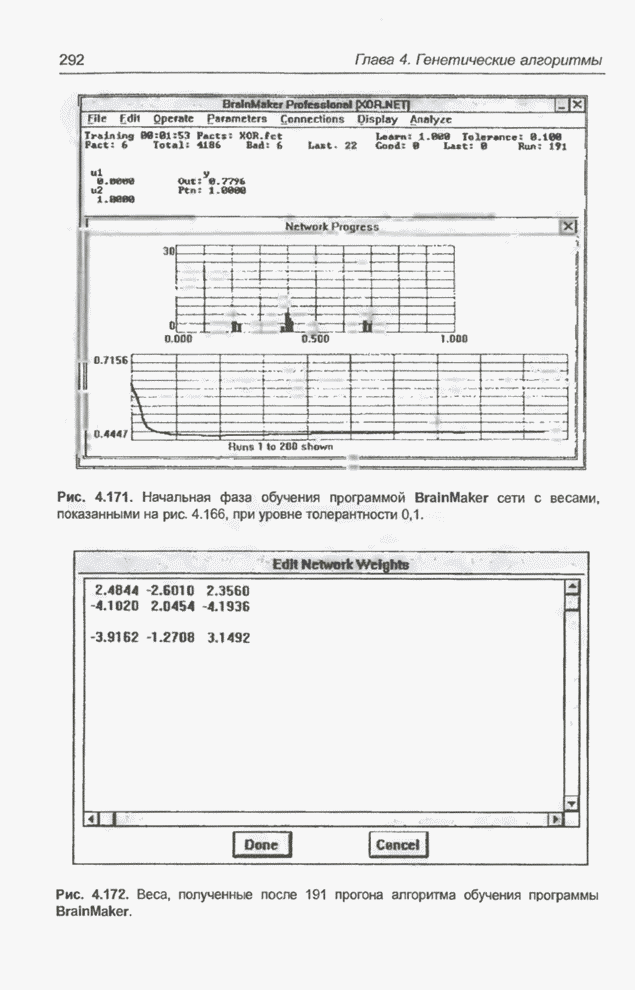
- 4.13.1. Программы Evolver и BrainMaker
- 4.13.2. Программа GTO
- Список литературы
- ГЛАВА 5. МОДУЛИ НЕЧЕТКО-НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.1. Модуль нечеткого управления со структурой, определенной в процессе дефуззификации
- 5.1.2. Конструкция модуля
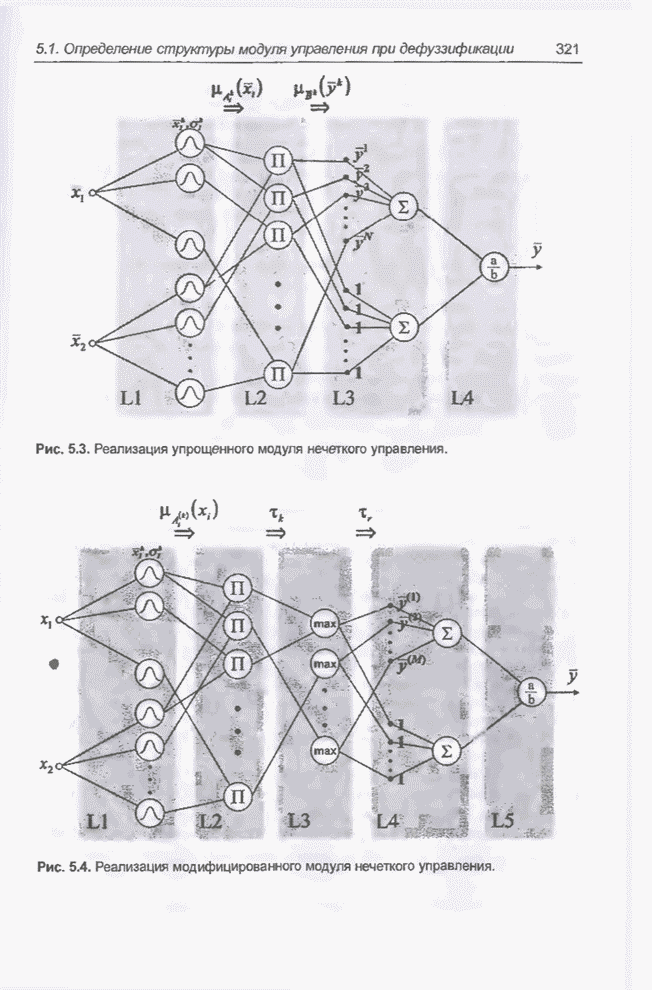
- 5.1.3. Структура модуля
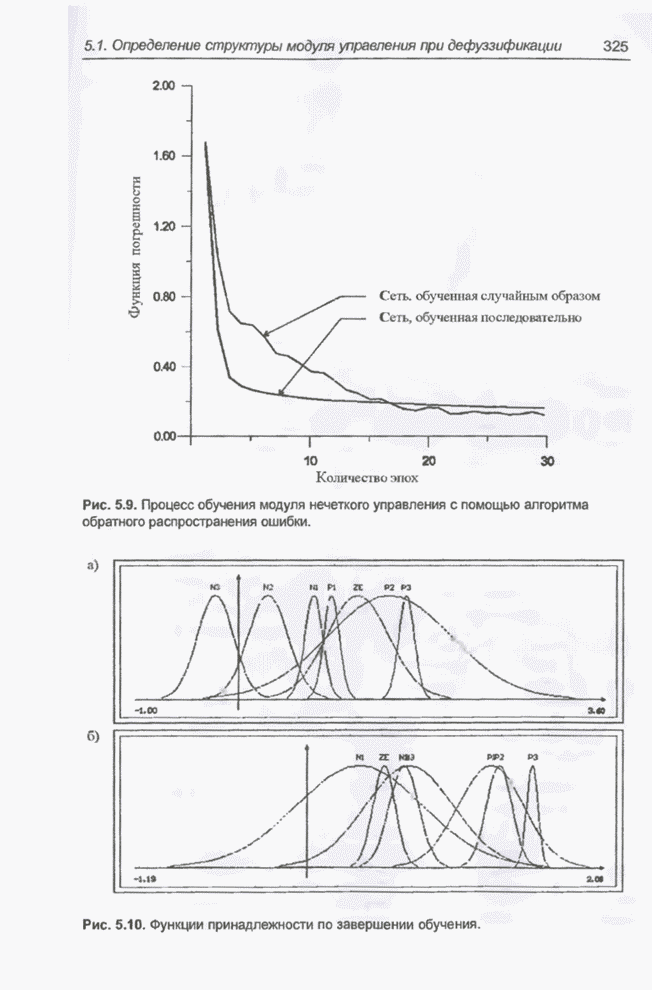
- 5.1.4. Использование алгоритма обратного распространения ошибки
- 5.1.5. Модификации модуля
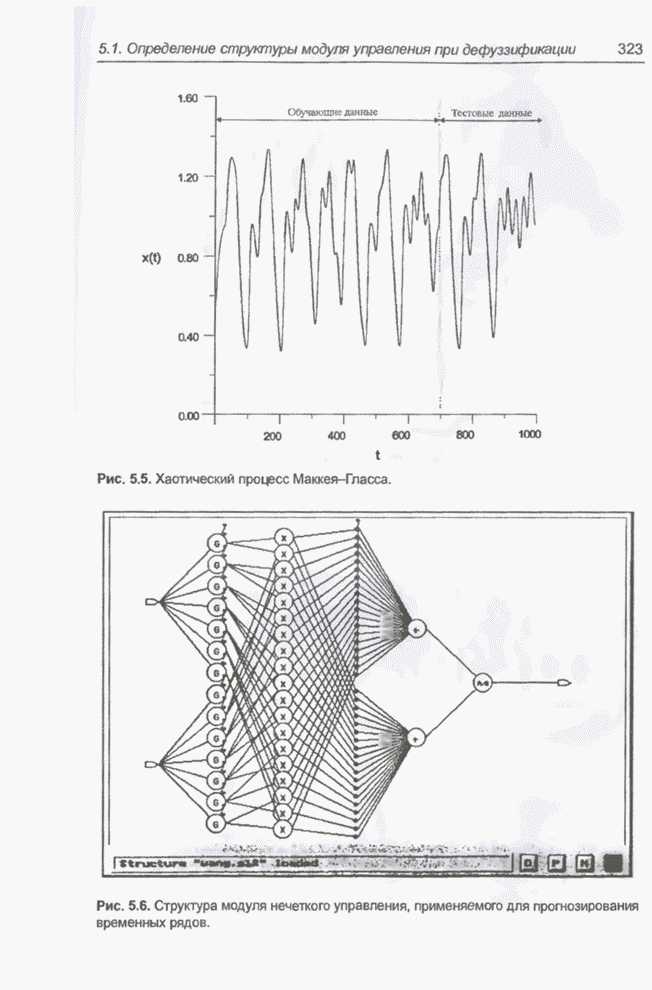
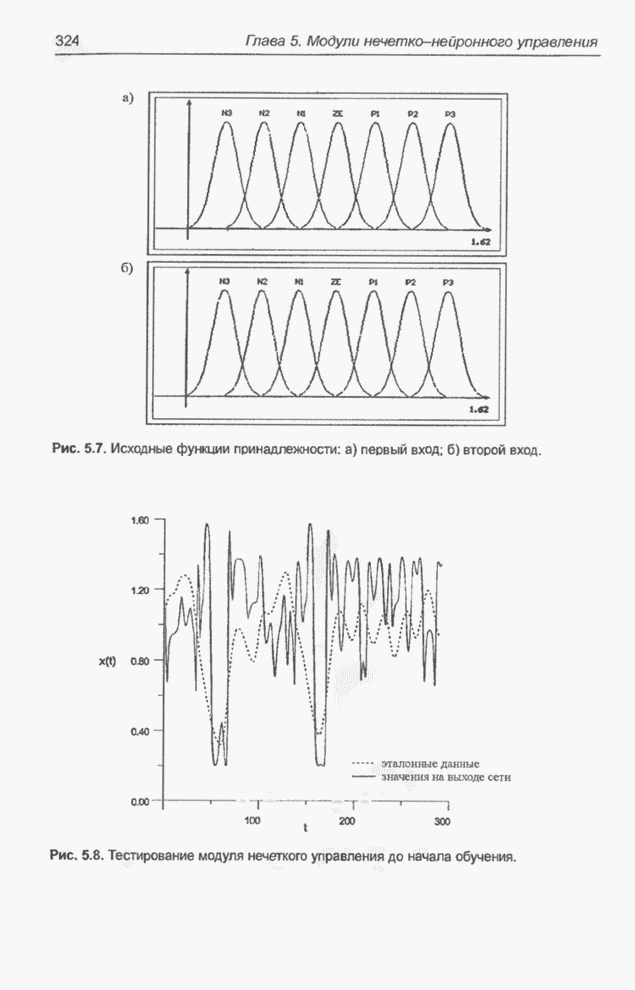
- 5.1.6. Применение модуля нечеткого управления для прогнозирования случайных временных рядов
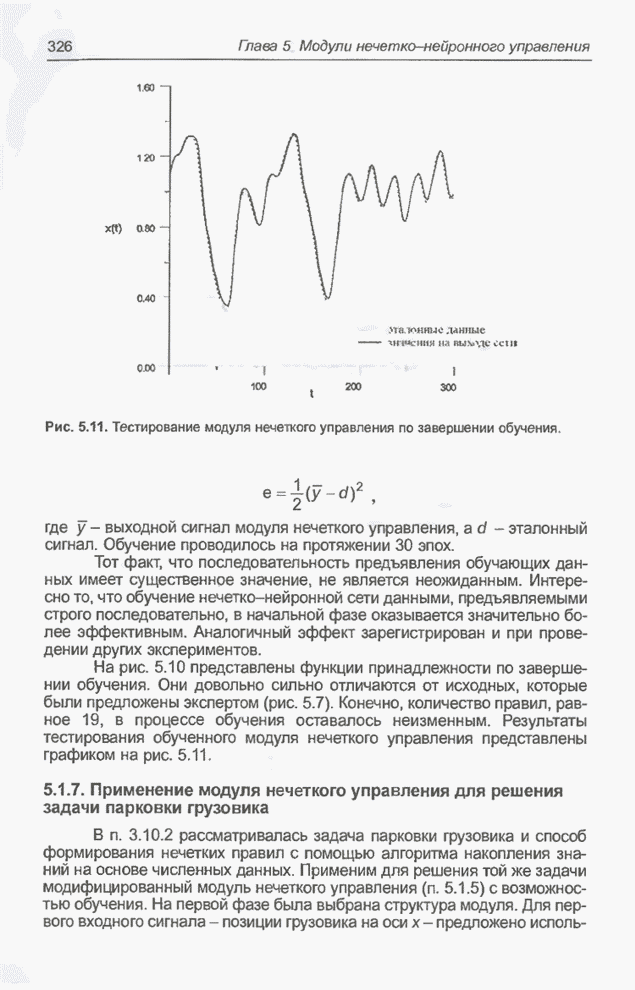
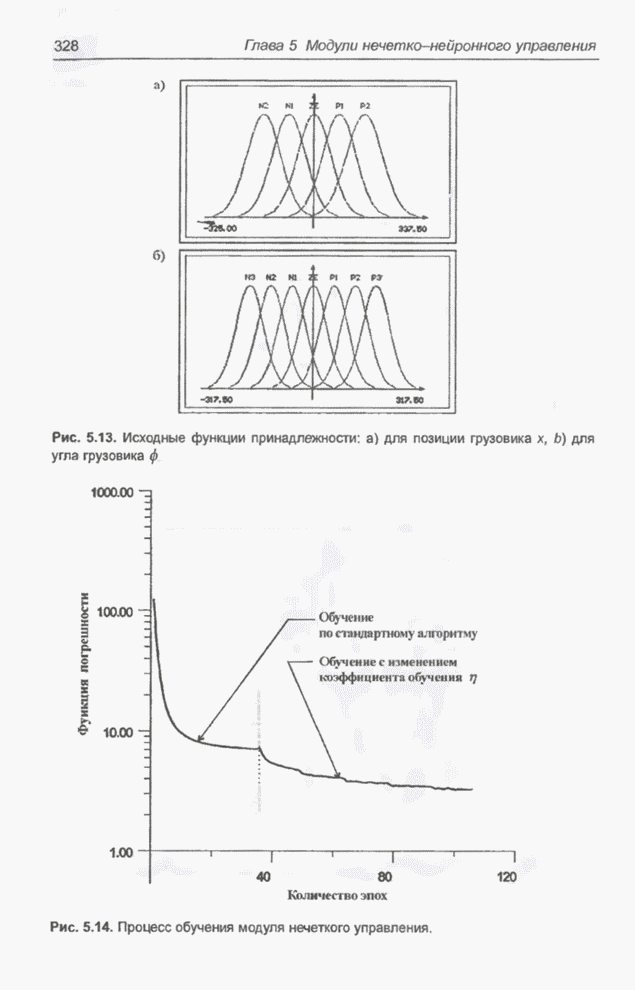
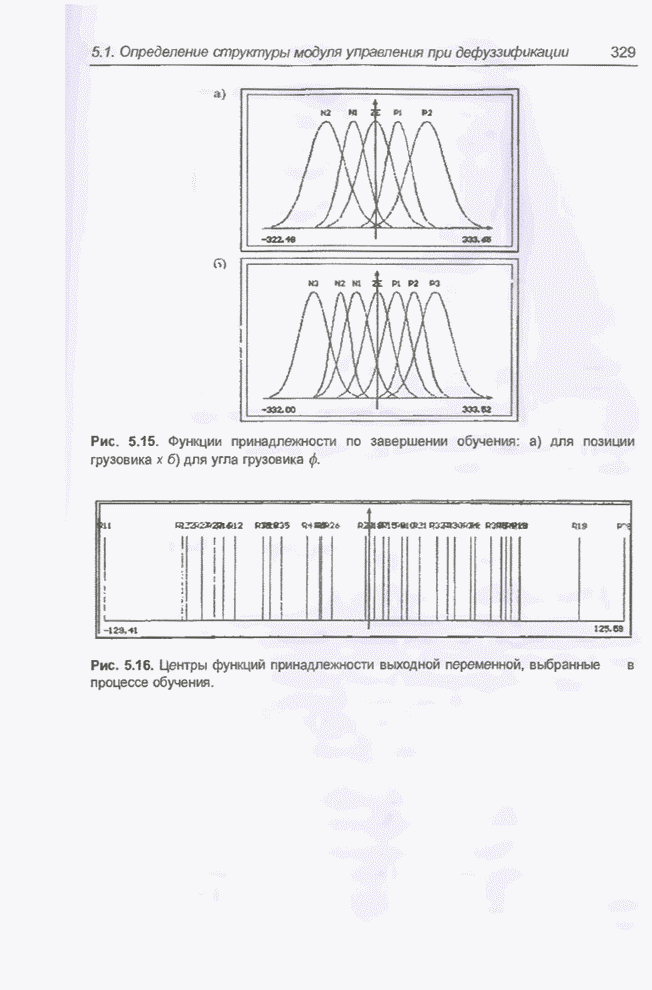
- 5.1.7. Применение модуля нечеткого управления для решения задачи парковки грузовика
- 5.1.8. Примечание
- 5.2. Представление модуля нечеткого управления в виде стандартной нейронной сети
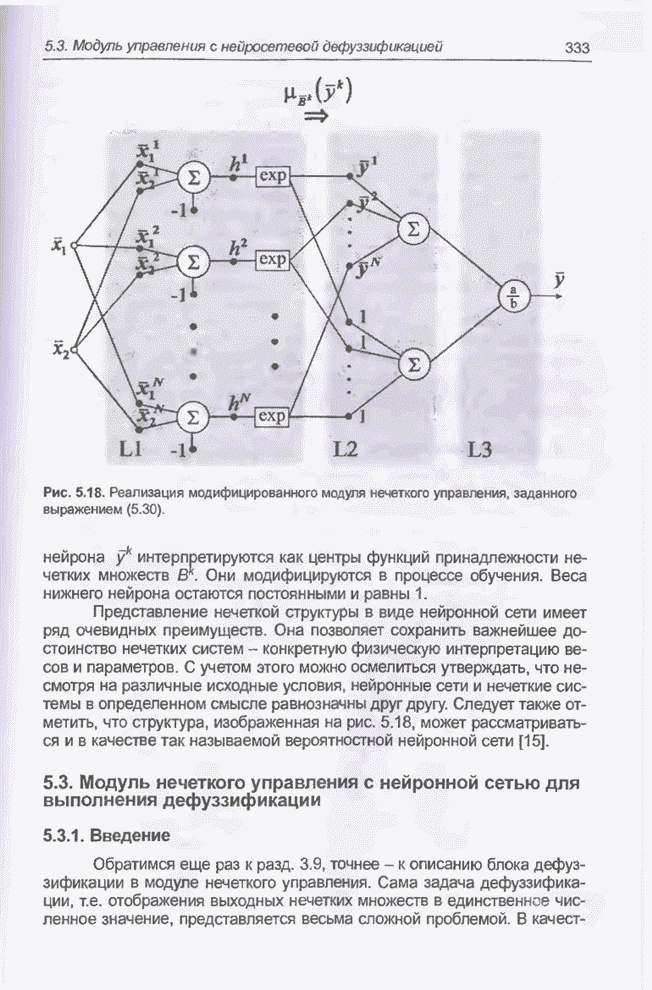
- 5.3. Модуль нечеткого управления с нейронной сетью для выполнения дефуззификации
- 5.3.1. Введение
- 5.3.2. Конструкция модуля
- 5.3.3. Структура модуля
- 5.3.4. Алгоритмы обучения модуля
- 5.3.5. Решение задачи стабилизации перевернутого маятника
- 5.3.6. Примечание
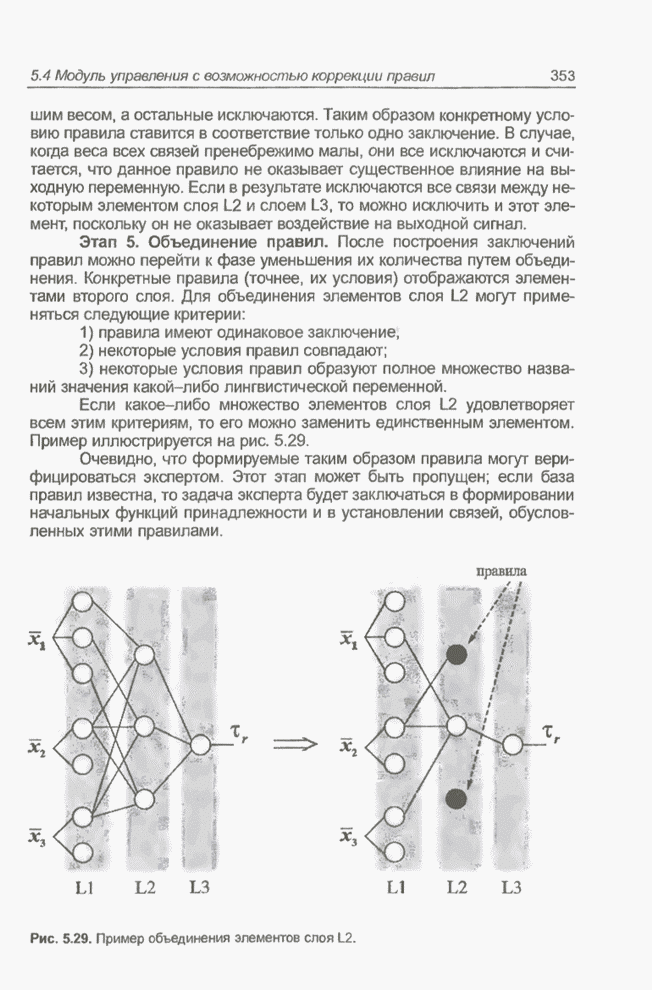
- 5.4. Модуль нечеткого управления с возможностью коррекции правил
- 5.4.1. Введение
- 5.4.2. Фаза обучения на основе самоорганизации
- 5.4.3. Фаза обучения с учителем
- 5.4.4. Примечание
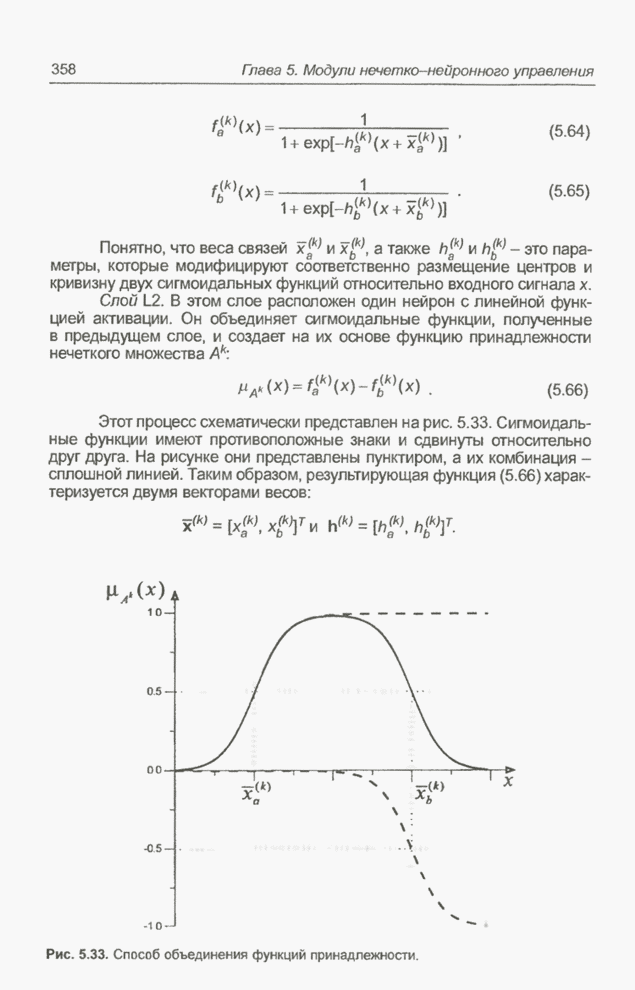
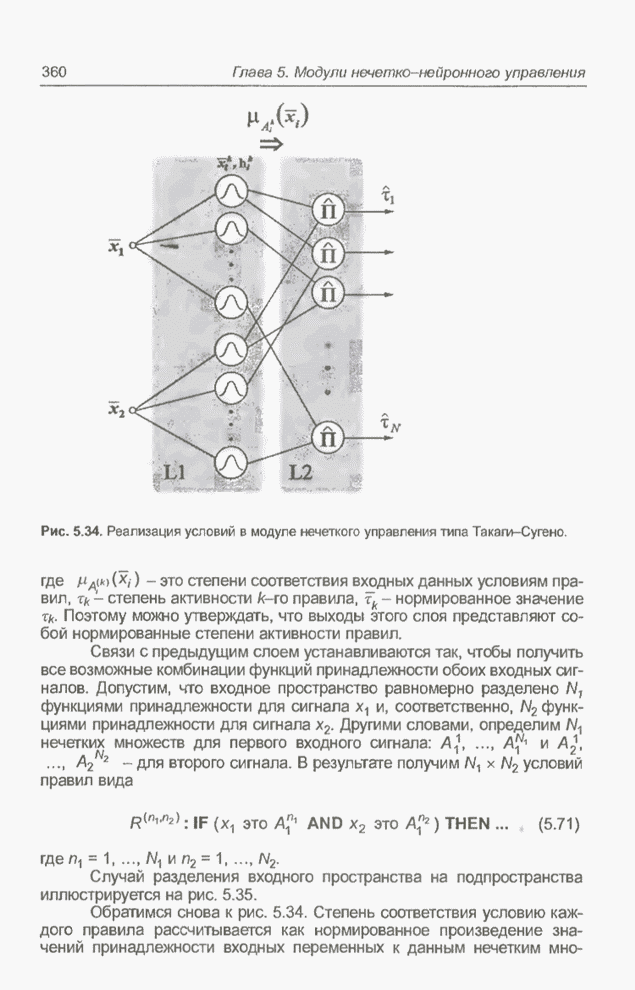
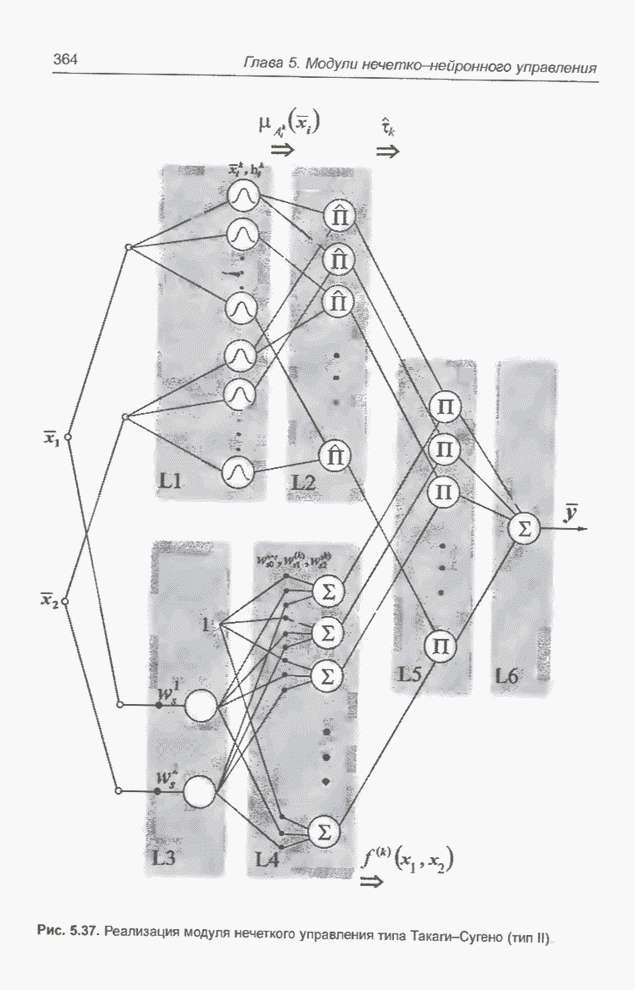
- 5.5. Модуль нечеткого управления типа Такаги-Сугено
- 5.5.1. Введение
- 5.5.2. Нейронная реализация функции принадлежности
- 5.5.3. Модули Такаги-Сугено
- 5.5.4. Реализация условий
- 5.5.5. Реализация заключений
- 5.5.6. Примечание
- 5.6. Модуль нечеткого управления типа Такаги-Сугено: случай зависимых лингвистических переменных
- 5.6.1. Введение
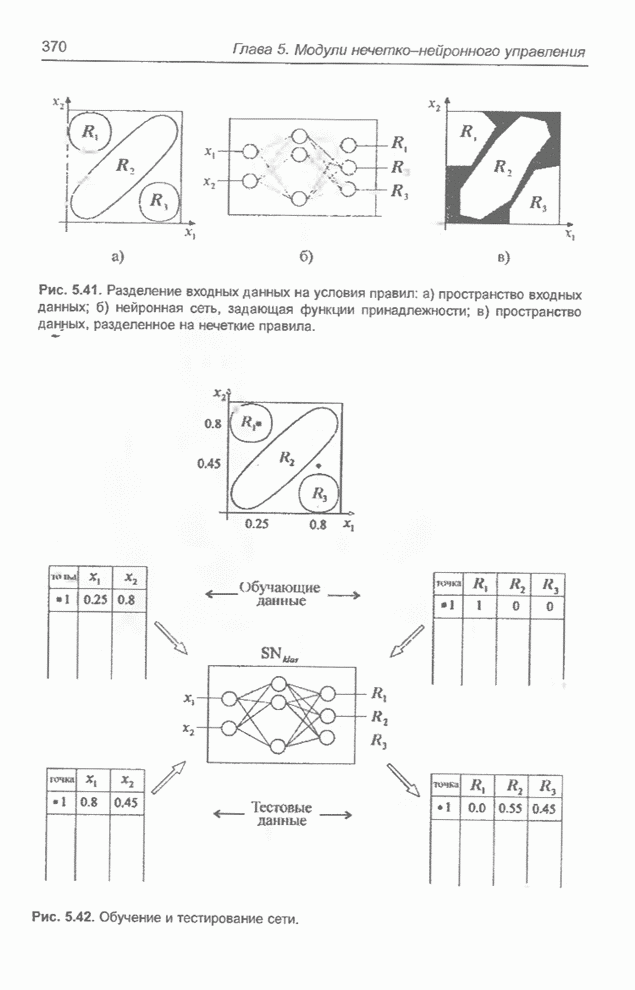
- 5.6.2. Нейронные сети для нечеткого вывода
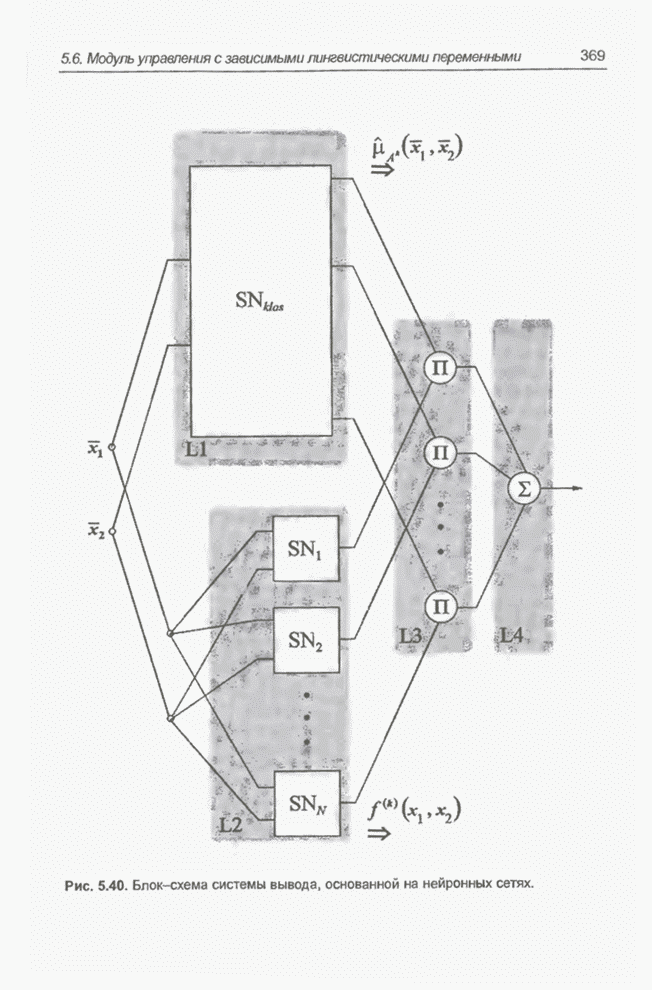
- 5.6.3. Структура системы
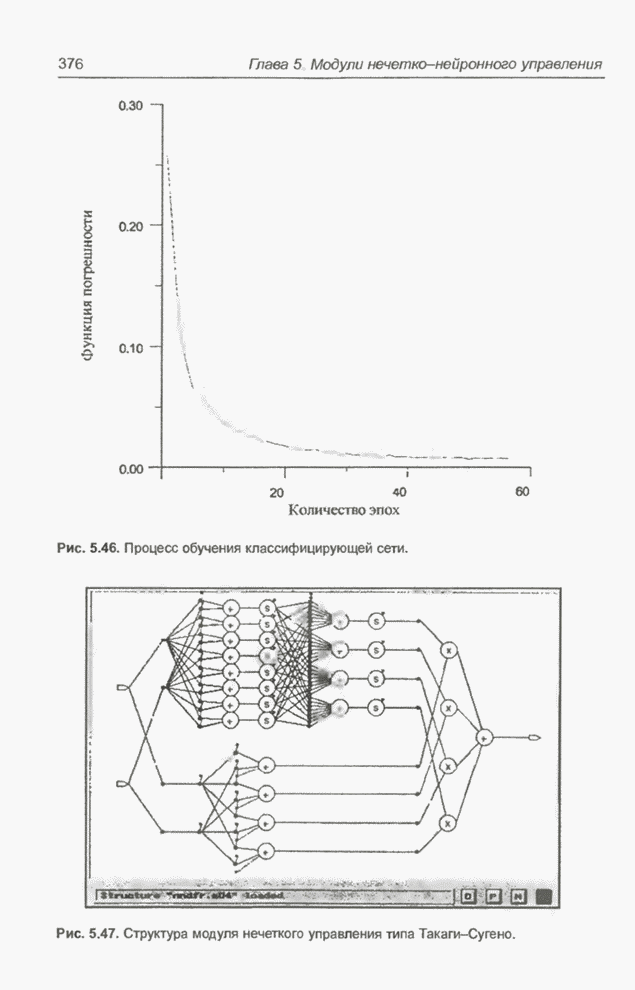
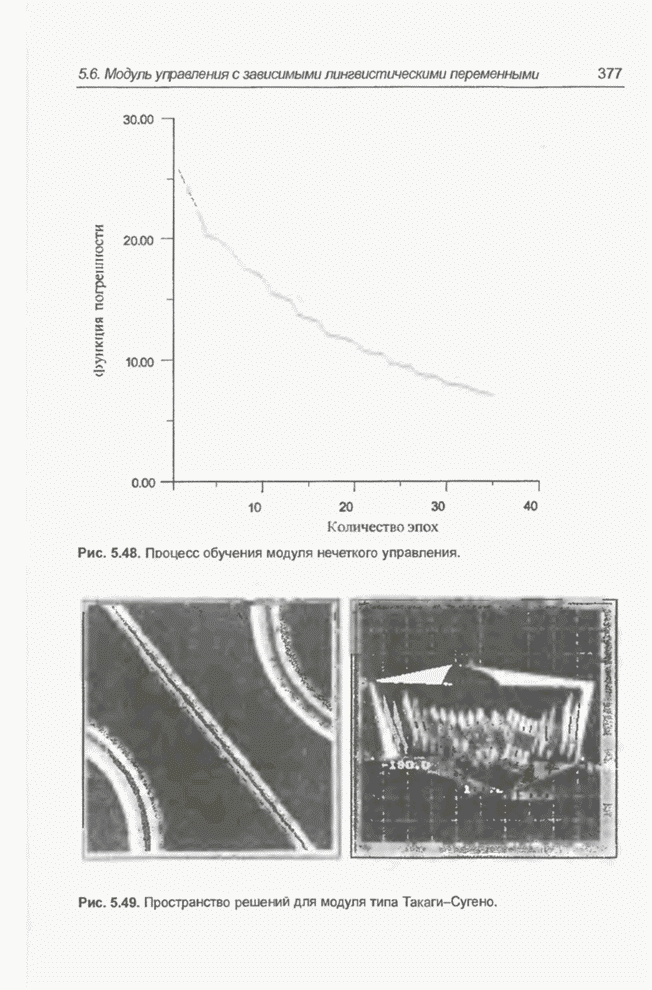
- 5.6.4. Способ обучения
- 5.6.5. Решение задачи парковки грузовика
- 5.6.6. Примечание
- Список литературы