| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.1.4. Использование алгоритма обратного распространения ошибки
Поскольку обсуждаемая нами
структура представляет собой многослойную сеть и, как уже отмечалось, алгоритм
обратного распространения ошибки можно обобщить на любую сеть с прямым
распространением сигнала, то ничто не препятствует тому, чтобы предлагаемый модуль
нечеткого управления обучать также, как и обычную нейронную сеть. Для этого
потребуется обучающая выборка в виде пар ![]() , где
, где ![]() - это входной вектор, a
- это входной вектор, a ![]() - эталонный сигнал.
Задача заключается в такой модификации (коррекции) параметров модуля нечеткого
управления, описанного выражением (5.13), чтобы мера погрешности, задаваемая
выражением
- эталонный сигнал.
Задача заключается в такой модификации (коррекции) параметров модуля нечеткого
управления, описанного выражением (5.13), чтобы мера погрешности, задаваемая
выражением
![]() (5.14)
(5.14)
была
минимальной. Значение выходного сигнала ![]() для заданного входного сигнала
для заданного входного сигнала ![]() будем для упрощения
обозначать
будем для упрощения
обозначать ![]() .
.
Допустим, что количество правил ![]() известно (его можно
задать). В этом случае остается подобрать три параметра:
известно (его можно
задать). В этом случае остается подобрать три параметра: ![]() ,
, ![]() и
и ![]() для
для ![]() .
.
Начнем с весов ![]() в слое L3. Напомним (разд. 2.5), что
алгоритм обратного распространения ошибки относится к классу так называемых
градиентных алгоритмов. Их идея заключается в уменьшении предыдущего значения
веса на величину производной от меры погрешности (5.14), умноженную на некоторый
коэффициент. Процесс должен длиться так долго, чтобы погрешность на выходе
системы достигла априорно установленной минимальной величины. Для веса
в слое L3. Напомним (разд. 2.5), что
алгоритм обратного распространения ошибки относится к классу так называемых
градиентных алгоритмов. Их идея заключается в уменьшении предыдущего значения
веса на величину производной от меры погрешности (5.14), умноженную на некоторый
коэффициент. Процесс должен длиться так долго, чтобы погрешность на выходе
системы достигла априорно установленной минимальной величины. Для веса ![]() выражение,
определяющее способ модификации, будет иметь вид
выражение,
определяющее способ модификации, будет иметь вид
 , (5.15)
, (5.15)
где
![]() обозначает
номер итерации (
обозначает
номер итерации (![]() - начальное значение веса), а константа
- начальное значение веса), а константа ![]() интерпретируется как коэффициент,
определяющий скорость обучения (он также называется шагом коррекции).
интерпретируется как коэффициент,
определяющий скорость обучения (он также называется шагом коррекции).
В формуле (5.14), задающей меру погрешности, содержится выходной сигнал системы (модуля управления). Представим уравнение (5.13) в виде
 ,
где
,
где  . (5.16)
. (5.16)
Легко заметить, что значение ![]() и, следовательно,
также мера погрешности
и, следовательно,
также мера погрешности ![]() зависит от веса
зависит от веса ![]() только в числителе (т.е. в
части
только в числителе (т.е. в
части ![]() ).
Если применить правило дифференцирования сложной функции, то можно рассчитать
производную меры погрешности относительно веса
).
Если применить правило дифференцирования сложной функции, то можно рассчитать
производную меры погрешности относительно веса ![]()
 . (5.17)
. (5.17)
Исключение зависимости (5.17). При подстановке выражения (5.14) в формулу (5.17) получаем выражение
 .
.
Поскольку эталонный сигнал ![]() не зависит от веса
не зависит от веса ![]() , то можно
рассматривать его в качестве константы:
, то можно
рассматривать его в качестве константы:
 .
.
Применяя формулу для расчета производной от сложной функции, получаем
 .
.
С учетом того, что  , можно определить
производную
, можно определить
производную ![]() в
виде
в
виде
 .
.
Отдельные веса сети независимы друг от друга, поэтому
 .
.
Следовательно,
 .
.
И окончательно
 .
.
При подстановке полученной
формулы в выражение (5.15), определяющее способ модификации веса ![]() , получаем алгоритм
обучения
, получаем алгоритм
обучения
 , (5.18)
, (5.18)
который с учетом выведенных выше зависимостей представляется в виде
 .
.
Для упрощения записи в
приведенной формуле зависимость отдельных ее параметров от номера итерации ![]() ,
, ![]() обозначена символически.
Процесс обучения подразделяется на два этапа. Вначале на вход модуля управления
подается значение сигнала
обозначена символически.
Процесс обучения подразделяется на два этапа. Вначале на вход модуля управления
подается значение сигнала ![]() , входящее в обучающую выборку; на его
основе формируется выходное управляющее воздействие. Этот сигнал
распространяется по сети в прямом направлении, и последовательно рассчитываются
значения
, входящее в обучающую выборку; на его
основе формируется выходное управляющее воздействие. Этот сигнал
распространяется по сети в прямом направлении, и последовательно рассчитываются
значения ![]()
![]() ,
, ![]() ,
, ![]() и, наконец,
и, наконец, ![]() . Затем выполняется второй
этап: обратное распространение ошибки. При этом выходная реакция
. Затем выполняется второй
этап: обратное распространение ошибки. При этом выходная реакция ![]() сравнивается с
эталонным значением
сравнивается с
эталонным значением ![]() ,
и по результатам сравнения модифицируются значения весов
,
и по результатам сравнения модифицируются значения весов ![]() .
.
Аналогично рассчитываются
остальные параметры: ![]() и
и ![]() . Для
. Для ![]() применяется рекурсия
применяется рекурсия
 , (5.19)
, (5.19)
где
![]() ,
, ![]() ,
, ![]() . Из уравнения (5.16) следует,
что выходная величина
. Из уравнения (5.16) следует,
что выходная величина ![]() (и, соответственно, мера погрешности
(и, соответственно, мера погрешности ![]() ) зависит от
) зависит от ![]() только через
только через ![]() . При использовании,
как и прежде, формулы для расчета производной от составной функции, получаем
. При использовании,
как и прежде, формулы для расчета производной от составной функции, получаем
 . (5.20)
. (5.20)
Исключение зависимости (5.20). Так же как и в случае с формулой (5.17), будем основываться на уравнении, определяющем производную от меры погрешности
 .
.
С учетом того, что от параметра ![]() зависит только
значение выходного сигнала
зависит только
значение выходного сигнала ![]() , согласно формуле для расчета
производной от сложной функции имеем
, согласно формуле для расчета
производной от сложной функции имеем
 .
.
Поскольку ![]() , причем
, причем ![]() и
и ![]() зависят от
зависят от ![]() , определим первую из
производных в виде
, определим первую из
производных в виде
 .
.
После подстановки вместо ![]() и
и ![]() соответствующих выражений и
взятия производных получаем
соответствующих выражений и
взятия производных получаем
 .
.
В результате замены  , где
, где  можно рассчитать
можно рассчитать

и далее
 ,
,
а также
 .
.
После этого
 ,
,
что в итоге приводит к формуле
 .
.
При подстановке равенства (5.20)
в выражение (5.19), получаем алгоритм обучения для параметра ![]() в виде
в виде
 , (5.21)
, (5.21)
где
![]() и
и ![]() определяются по
формуле (5.16).
определяются по
формуле (5.16).
При использовании такой же
методики можно получить алгоритм обучения для параметра ![]() в виде
в виде
 . (5.22)
. (5.22)
Представленные зависимости
(5.18), (5.21) и (5.22) определяют способ модификации весов и параметров на
основе алгоритма обратного распространения ошибки. На первом этапе входной
вектор ![]() распространяется
по сети в прямом направлении, и последовательно рассчитываются значения
распространяется
по сети в прямом направлении, и последовательно рассчитываются значения ![]()
![]() ,
, ![]() ,
, ![]() и, наконец,
и, наконец, ![]() . На втором этапе с
использованием представленных формул рассчитываются новые значения весов связей
. На втором этапе с
использованием представленных формул рассчитываются новые значения весов связей
![]() ,
, ![]() и
и ![]() для
для ![]() ;
; ![]() , после чего старые значения заменяются
новыми, и счетчик количества итераций
, после чего старые значения заменяются
новыми, и счетчик количества итераций ![]() увеличивается на 1. Такая
последовательность имеет существенное значение, поскольку, например, в формуле
расчета «нового» значения веса
увеличивается на 1. Такая
последовательность имеет существенное значение, поскольку, например, в формуле
расчета «нового» значения веса ![]() содержатся «старые» (точнее -
рассчитанные на предыдущем шаге) значения весов
содержатся «старые» (точнее -
рассчитанные на предыдущем шаге) значения весов ![]() ,
, ![]() и
и ![]() .
.
Заметим, что во всех формулах
фигурирует «нормализованная» погрешность ![]() . Она распространяется в обратном
направлении до третьего слоя (L3), в котором находятся веса
связей
. Она распространяется в обратном
направлении до третьего слоя (L3), в котором находятся веса
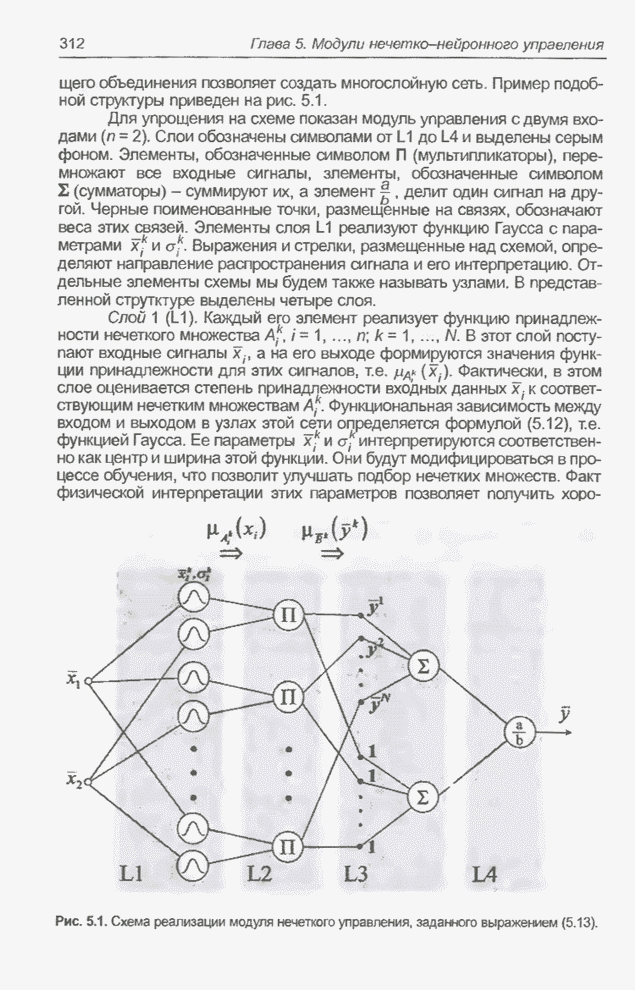
связей ![]() (см.
рис. 5.1). Впоследствии каждый вес
(см.
рис. 5.1). Впоследствии каждый вес ![]() модифицируется согласно алгоритму
(5.18), причем следует отметить, что значения
модифицируется согласно алгоритму
(5.18), причем следует отметить, что значения ![]() уже определены ранее на первом этапе
(это сигналы, выходящие из предыдущего слоя). Для обучения параметров
уже определены ранее на первом этапе
(это сигналы, выходящие из предыдущего слоя). Для обучения параметров ![]() и
и ![]() та же «нормализованная»
погрешность
та же «нормализованная»
погрешность ![]() умножается
на разность
умножается
на разность ![]() и
на значение
и
на значение ![]() ,
после чего распространяется в обратном направлении до первого слоя (L1). Параметры
,
после чего распространяется в обратном направлении до первого слоя (L1). Параметры ![]() и
и ![]() модифицируются по алгоритмам
(5.21) и (5.22) соответственно. Это доказывает, что они с полным основанием
могут называться «алгоритмами обратного распространения ошибки».
модифицируются по алгоритмам
(5.21) и (5.22) соответственно. Это доказывает, что они с полным основанием
могут называться «алгоритмами обратного распространения ошибки».
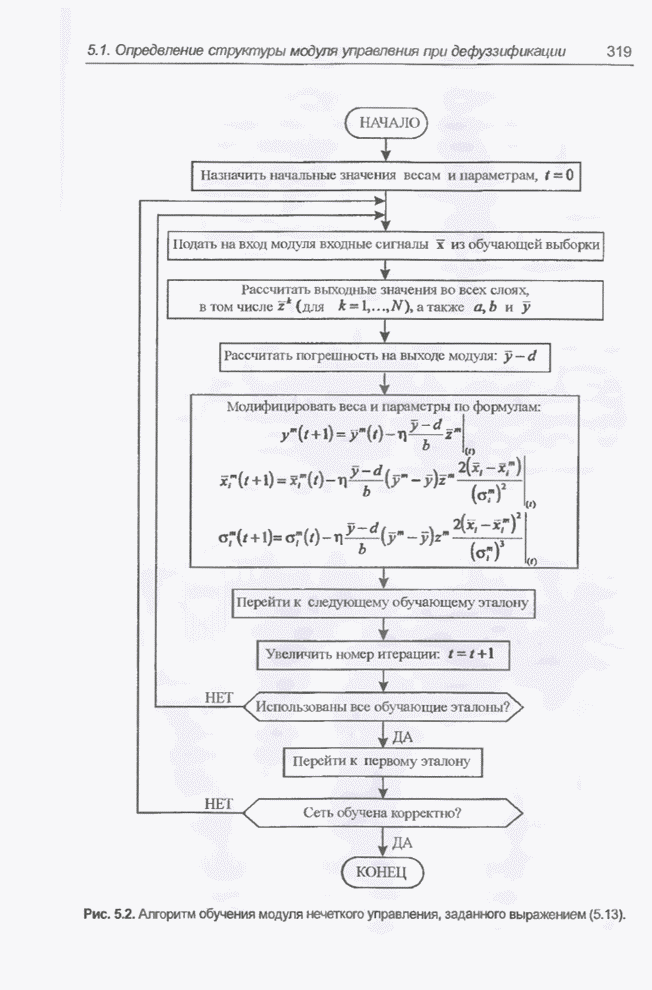
Алгоритм обучения обсуждаемой сети представлен на рис. 5.2 в виде блок-схемы. В принципе, он не требует дополнительных комментариев, можно добавить лишь несколько слов о принятых на этом рисунке упрощениях.

Рис. 52. Алгоритм обучения модуля нечеткого управления, заданного выражением (5.13).
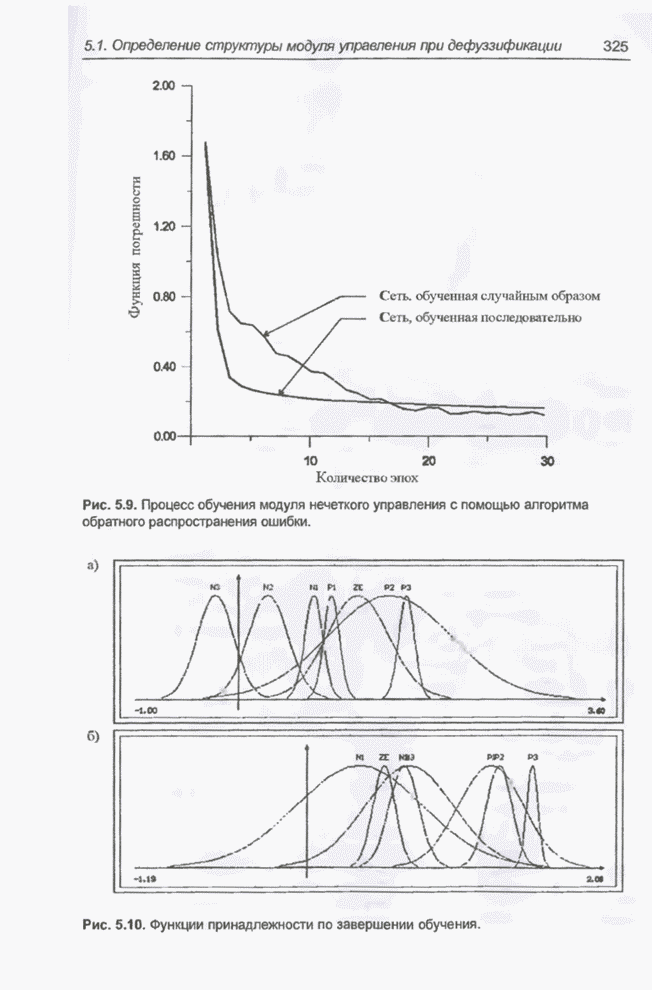
Во-первых, как определить, насколько корректно обучена сеть? Для этого созданы различные методы, и одним из простейших считается расчет значения средней погрешности для всех эпох (epoch) с последующим сравнением результата с некоторым заданным значением. Напомним, что эпохой называется количество итераций, равное числу пар векторов входных и эталонных сигналов (т.е. один цикл предъявления обучающей выборки).
Во-вторых, на схеме предполагается, что обучающие эталоны предъявляются строго последовательно. В принципе, для простейших сетей это не имеет особого значения, однако в общем случае выдвигается условие, чтобы в рамках каждой эпохи данные выбирались случайным образом.
Программная реализация приведенного алгоритма не представляет проблему даже для начинающего программиста. Однако следует помнить очень важное правило: на каждом шаге вначале рассчитываются поправки для всех весов в каждом слое, и только после этого корректируются значения самих весов.
Следует обратить внимание на то,
что в формулах для расчета очередных значений параметров ![]() и
и ![]() имеются «старые» значения
имеются «старые» значения ![]() ,
, ![]() и
и ![]() из предыдущей итерации; их
преждевременное изменение могло бы ухудшить качество обучения сети.
из предыдущей итерации; их
преждевременное изменение могло бы ухудшить качество обучения сети.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Предисловие к русскому изданию
- ГЛАВА 1. ВВЕДЕНИЕ
- Список литературы
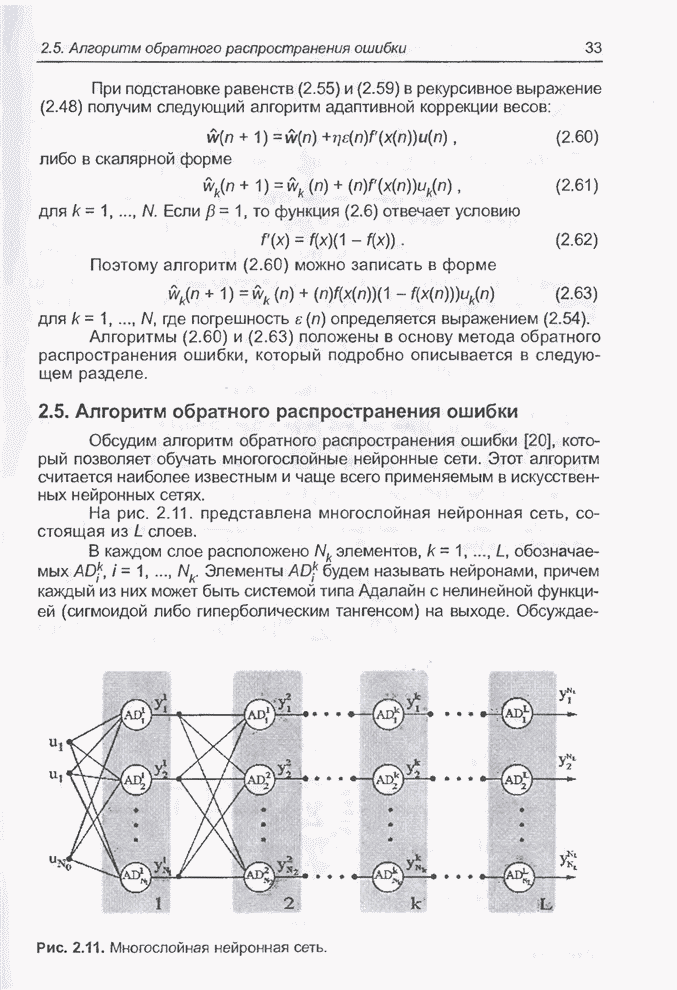
- ГЛАВА 2. МНОГОСЛОЙНЫЕ НЕЙРОННЫЕ СЕТИ И АЛГОРИТМЫ ИХ ОБУЧЕНИЯ
- 2.1. Введение
- 2.2. Нейрон и его модели
- 2.3. Персептрон
- 2.4. Системы типа Адалайн
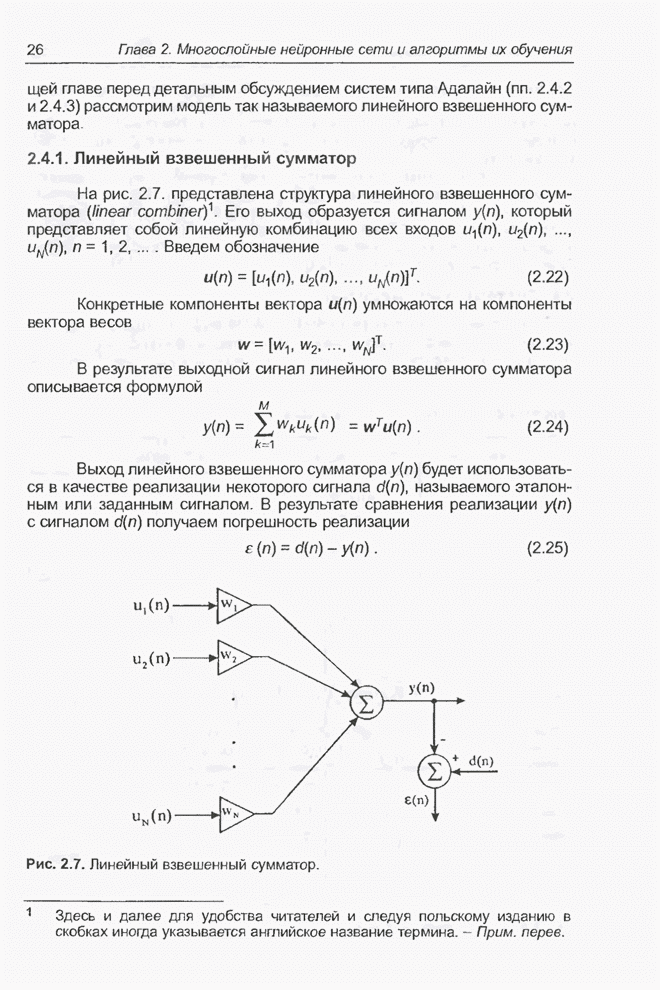
- 2.4.1. Линейный взвешенный сумматор
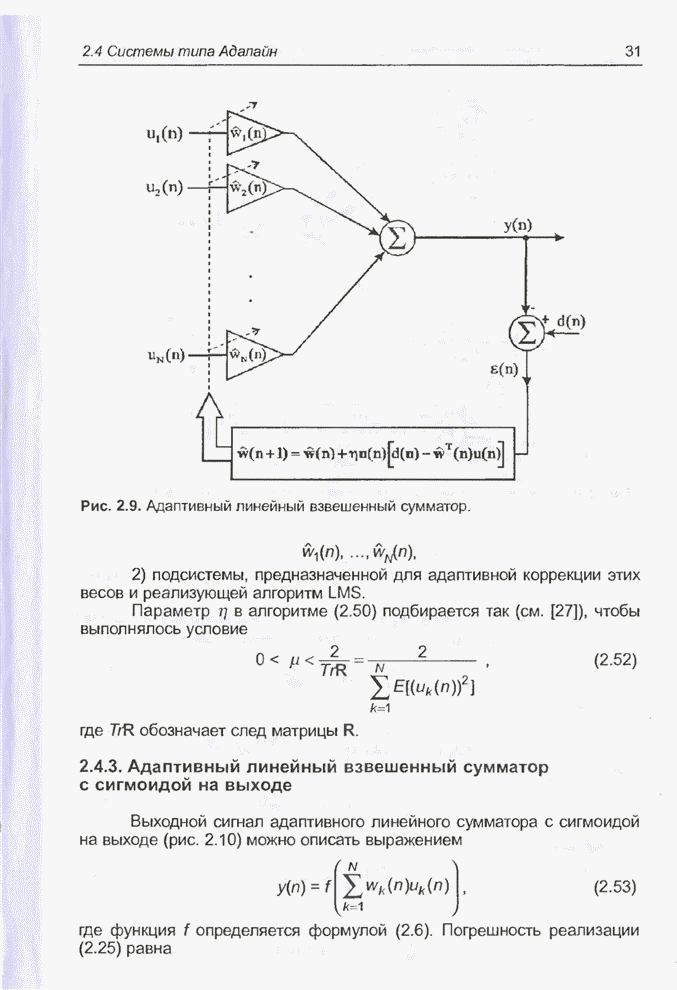
- 2.4.2. Адаптивный линейный взвешенный сумматор
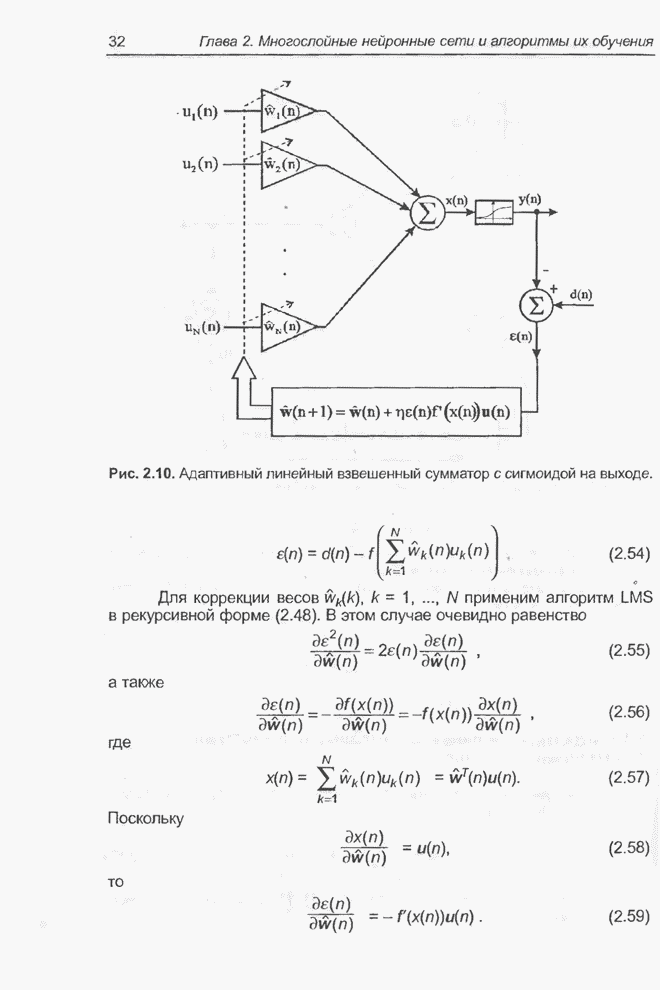
- 2.4.3. Адаптивный линейный взвешенный сумматор с сигмоидой на выходе
- 2.5. Алгоритм обратного распространения ошибки
- 2.6. Применение рекуррентного метода наименьших квадратов для обучения нейронных сетей
- Список литературы
- ГЛАВA3. НЕЧЕТКИЕ МНОЖЕСТВА И НЕЧЕТКИЙ ВЫВОД
- 3.1. Введение
- 3.2. Основные понятия и определения теории нечетких множеств
- 3.3. Операции на нечетких множествах
- 3.4. Принцип расширения
- 3.5. Нечеткие числа
- 3.6. Треугольные нормы
- 3.7. Нечеткие отношения и их свойства
- 3.8. Нечеткий вывод
- 3.9. Нечеткое управление
- 3.9.1. Классический модуль нечеткого управления
- 3.9.2. Метод нечеткого управления Такаги-Сугено
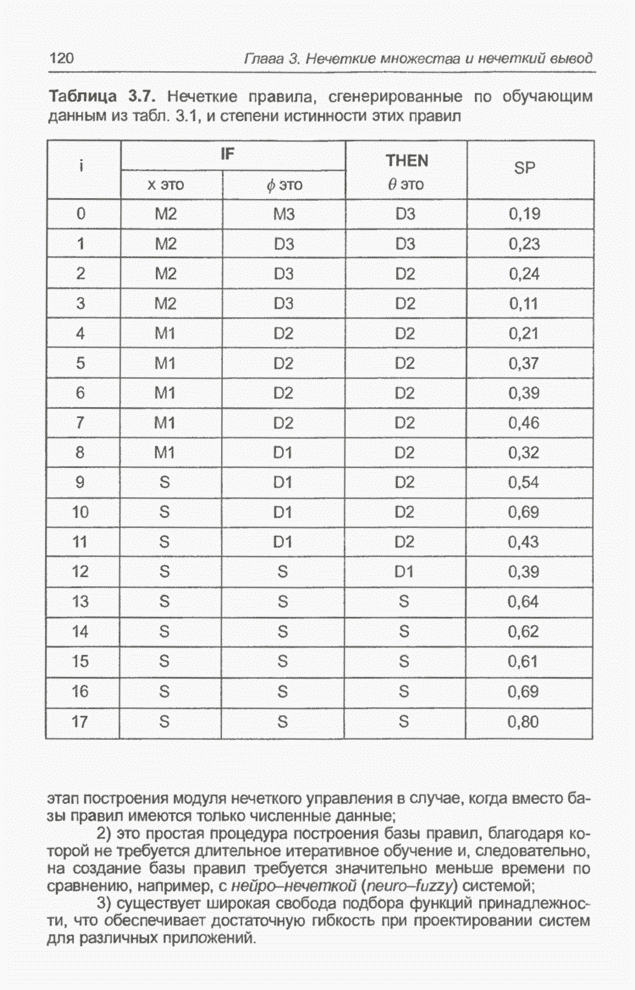
- 3.10. Проектирование базы нечетких правил на основе численных данных
- 3.10.1. Построение нечетких правил
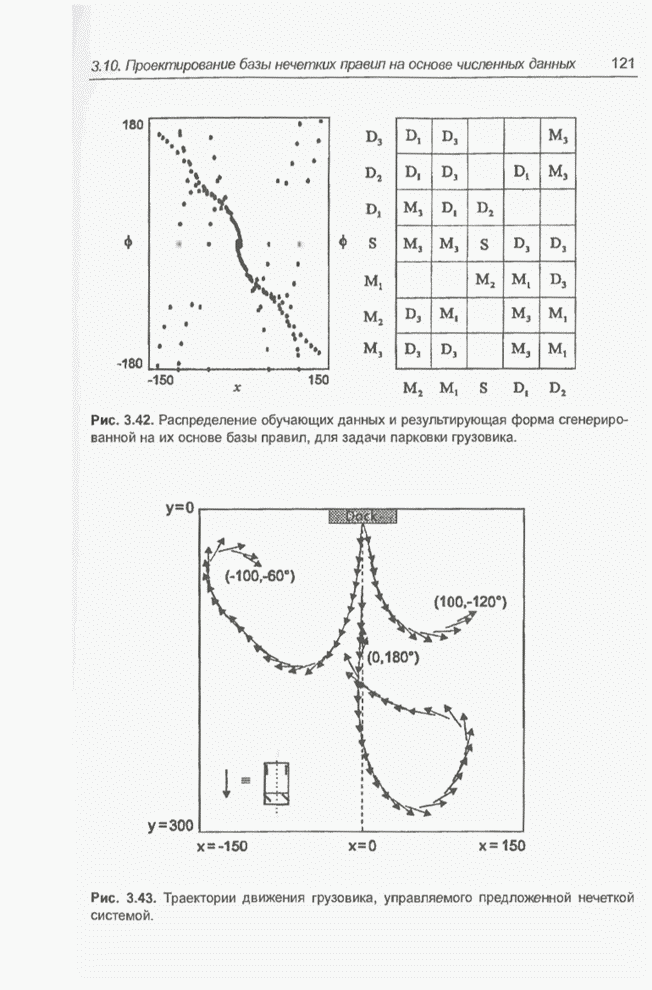
- 3.10.2. Задача парковки грузовика
- 3.10.3. Примечание
- Список литературы
- ГЛАВА 4. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 4.1. Введение
- 4.2. Генетические алгоритмы и традиционные методы оптимизации
- 4.3. Основные понятия генетических алгоритмов
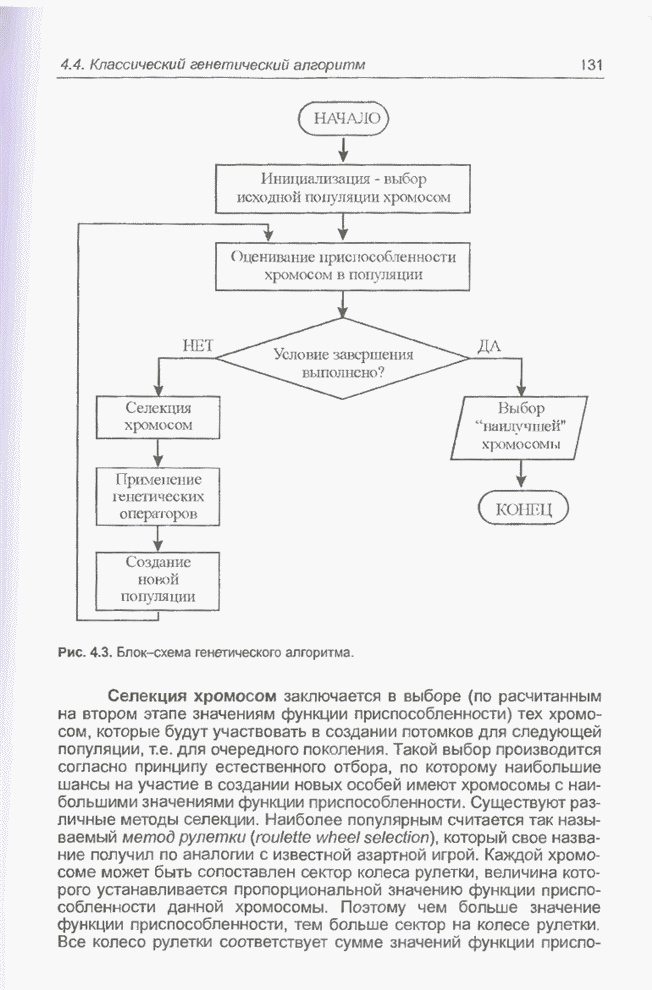
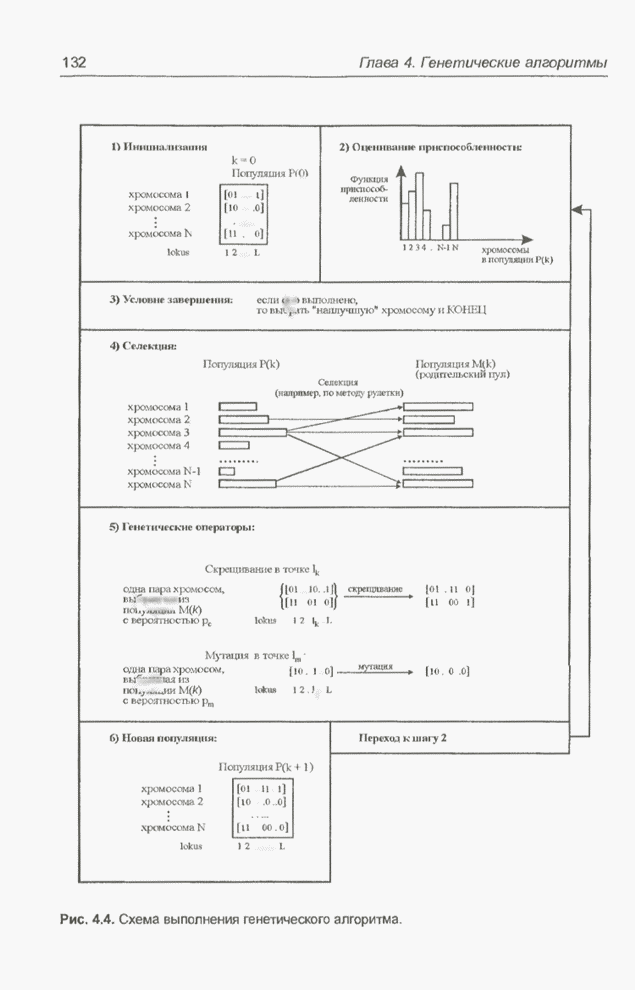
- 4.4. Классический генетический алгоритм
- 4.5. Иллюстрация выполнения классического генетического алгоритма
- 4.6. Кодирование параметров задачи в генетическом алгоритме
- 4.7. Основная теорема о генетических алгоритмах
- 4.8. Модификации классического генетического алгоритма
- 4.8.1. Методы селекции
- 4.8.2. Особые процедуры репродукции
- 4.8.3. Генетические операторы
- 4.8.4. Методы кодирования
- 4.8.5. Масштабирование функции приспособленности
- 4.8.6. Ниши в генетическом алгоритме
- 4.8.7. Генетические алгоритмы для многокритериальной оптимизации
- 4.8.8. Генетические микроалгоритмы
- 4.9. Примеры оптимизации функции с помощью программы FlexTool
- 4.10. Эволюционные алгоритмы
- 4.11. Приложения эволюционных алгоритмов
- 4.11.1. Примеры оптимизации функции с помощью программы Evolver
- 4.11.2. Решение комбинаторных задач с помощью программы Evolver
- 4.12. Эволюционные алгоритмы в нейронных сетях
- 4.12.1. Независимое применение генетических алгоритмов и нейронных сетей
- 4.12.2. Нейронные сети для поддержки генетических алгоритмов
- 4.12.3. Генетические алгоритмы для поддержки нейронных сетей
- 4.12.4. Применение генетических алгоритмов для обучения нейронных сетей
- 4.12.5. Генетические алгоритмы для выбора топологии нейронных сетей
- 4.12.6. Адаптивные взаимодействующие системы
- 4.12.7. Типовой цикл эволюции
- 4.12.7.1. Эволюция весов связей
- 4.12.7.2. Эволюция архитектуры сети
- 4.12.7.3. Эволюция правил обучения
- 4.13. Примеры моделирования эволюционных алгоритмов в приложении к нейронным сетям
- 4.13.1. Программы Evolver и BrainMaker
- 4.13.2. Программа GTO
- Список литературы
- ГЛАВА 5. МОДУЛИ НЕЧЕТКО-НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.1. Модуль нечеткого управления со структурой, определенной в процессе дефуззификации
- 5.1.2. Конструкция модуля
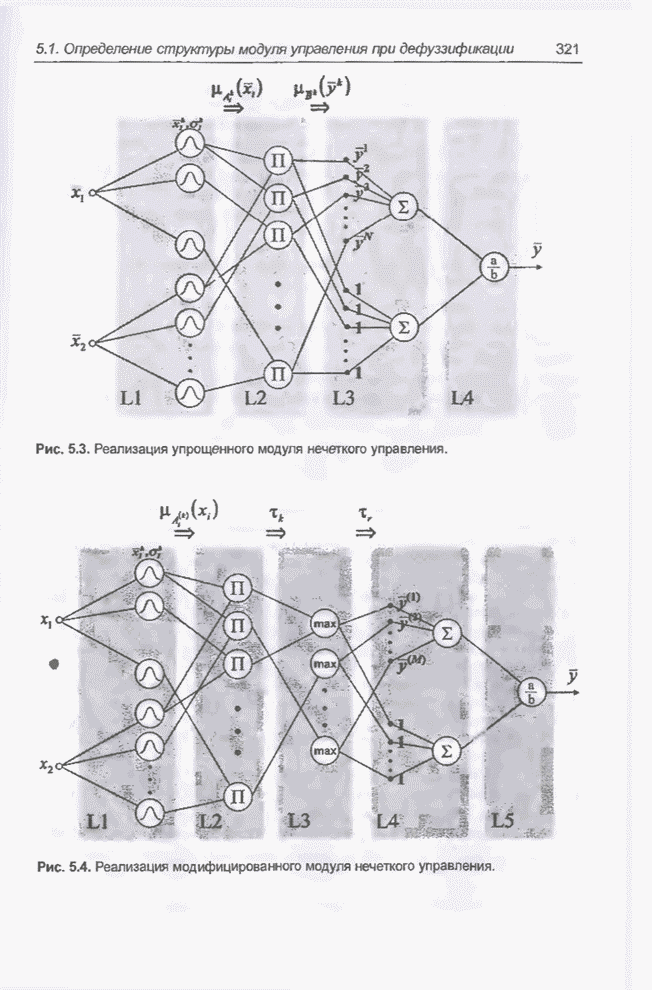
- 5.1.3. Структура модуля
- 5.1.4. Использование алгоритма обратного распространения ошибки
- 5.1.5. Модификации модуля
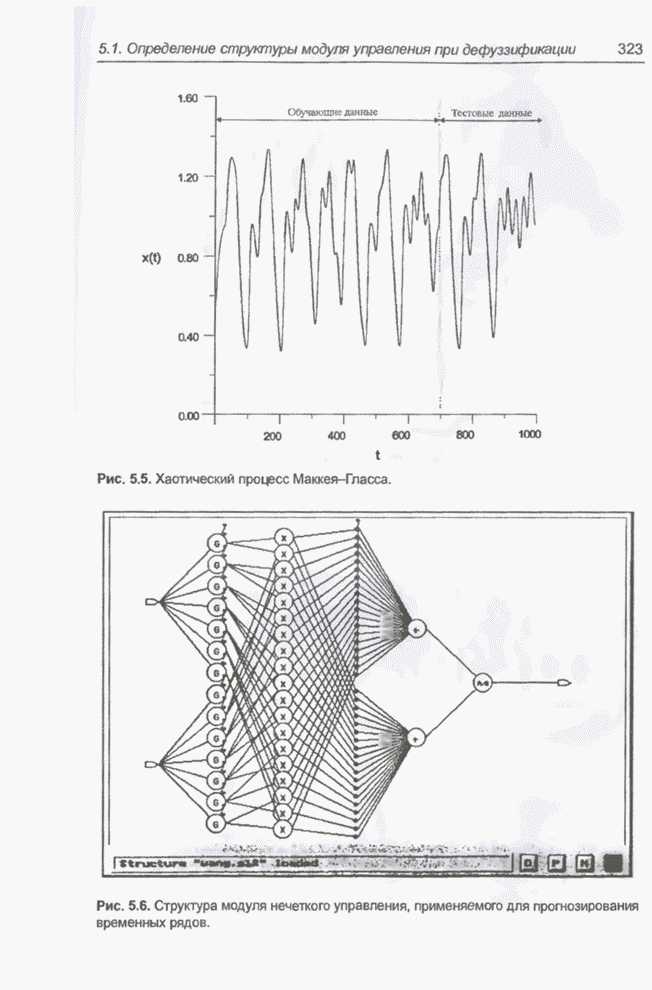
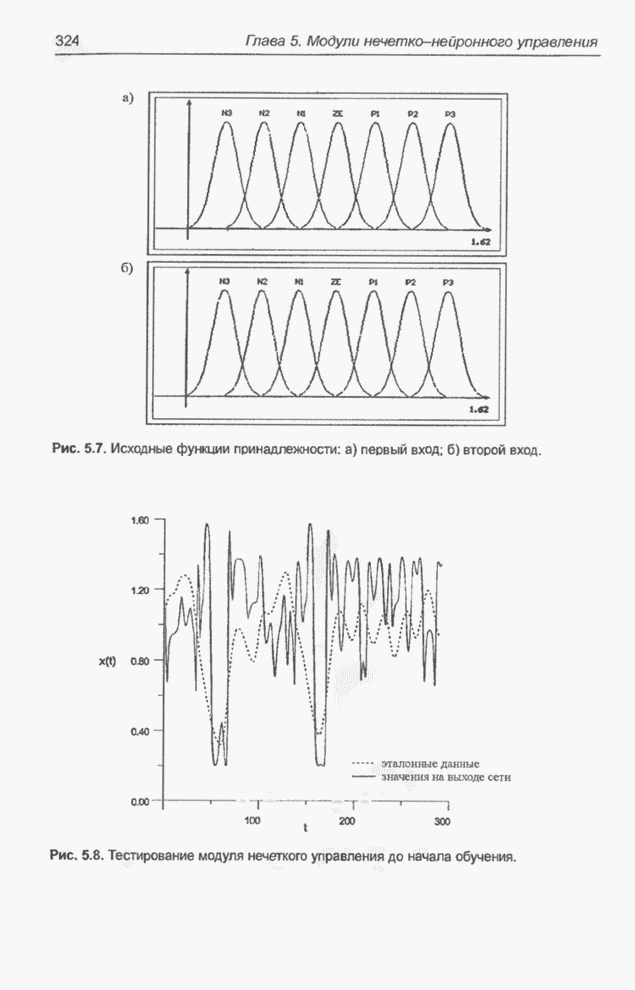
- 5.1.6. Применение модуля нечеткого управления для прогнозирования случайных временных рядов
- 5.1.7. Применение модуля нечеткого управления для решения задачи парковки грузовика
- 5.1.8. Примечание
- 5.2. Представление модуля нечеткого управления в виде стандартной нейронной сети
- 5.3. Модуль нечеткого управления с нейронной сетью для выполнения дефуззификации
- 5.3.1. Введение
- 5.3.2. Конструкция модуля
- 5.3.3. Структура модуля
- 5.3.4. Алгоритмы обучения модуля
- 5.3.5. Решение задачи стабилизации перевернутого маятника
- 5.3.6. Примечание
- 5.4. Модуль нечеткого управления с возможностью коррекции правил
- 5.4.1. Введение
- 5.4.2. Фаза обучения на основе самоорганизации
- 5.4.3. Фаза обучения с учителем
- 5.4.4. Примечание
- 5.5. Модуль нечеткого управления типа Такаги-Сугено
- 5.5.1. Введение
- 5.5.2. Нейронная реализация функции принадлежности
- 5.5.3. Модули Такаги-Сугено
- 5.5.4. Реализация условий
- 5.5.5. Реализация заключений
- 5.5.6. Примечание
- 5.6. Модуль нечеткого управления типа Такаги-Сугено: случай зависимых лингвистических переменных
- 5.6.1. Введение
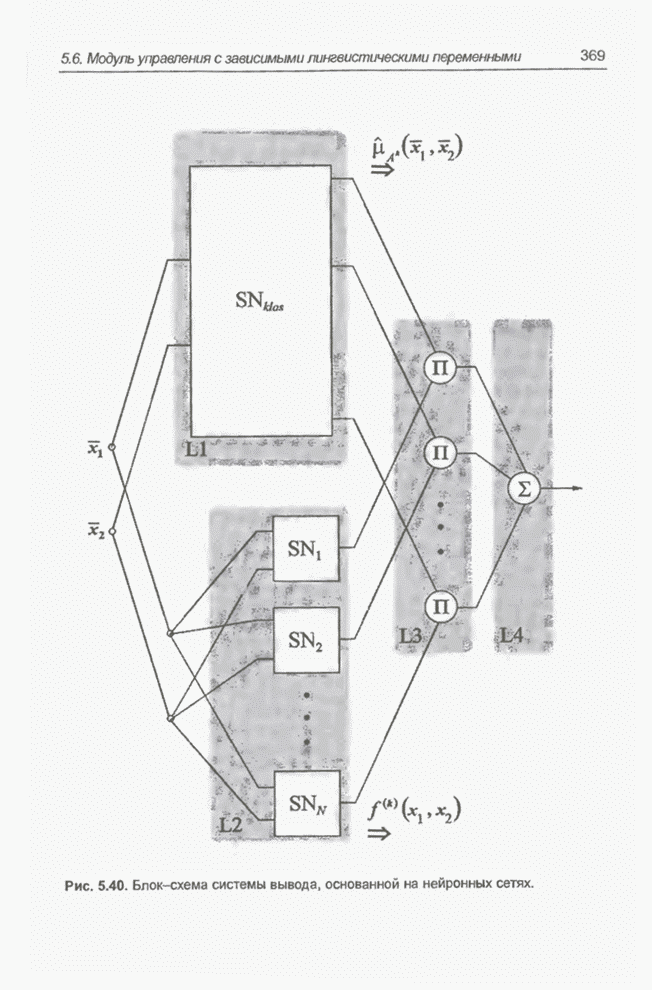
- 5.6.2. Нейронные сети для нечеткого вывода
- 5.6.3. Структура системы
- 5.6.4. Способ обучения
- 5.6.5. Решение задачи парковки грузовика
- 5.6.6. Примечание
- Список литературы