| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
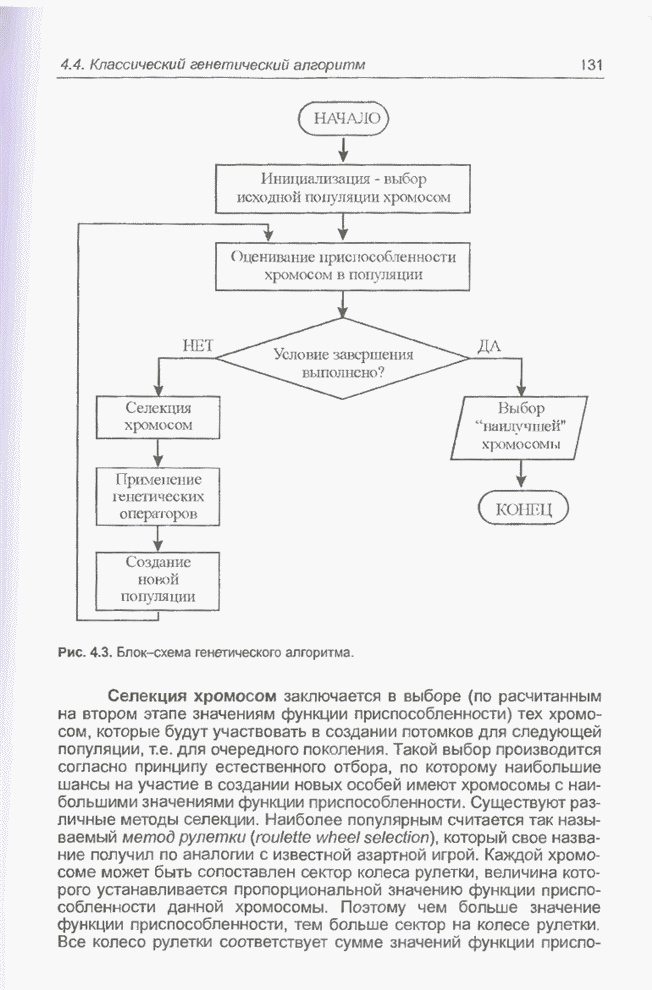
4.7. Основная теорема о генетических алгоритмах
Для того чтобы лучше понять
функционирование генетического алгоритма, будем использовать понятие схема и
сформулируем основную теорему, относящуюся к генетическим алгоритмам и
называемую теоремой о схемах [7, 15, 21, 33]. Понятие схема было введено для определения
множества хромосом, обладающих некоторыми общими свойствами, т.е. подобных друг
другу. Если аллели принимают значения 0 или 1 (рассматриваются хромосомы с
двоичным алфавитом), то схема представляет собой множество хромосом, содержащих
нули и единицы на некоторых заранее определенных позициях. При рассмотрении
схем удобно использовать расширенный алфавит ![]() , в который помимо 0 и 1 введен
дополнительный символ *, обозначающий любое допустимое значение, т.е. 0 или 1;
символ * в конкретной позиции означает «все равно» (don't саге). Например,
, в который помимо 0 и 1 введен
дополнительный символ *, обозначающий любое допустимое значение, т.е. 0 или 1;
символ * в конкретной позиции означает «все равно» (don't саге). Например,
![]()
![]() .
.
Считается, что хромосома
принадлежит к данной схеме, если для каждой ![]() -й позиции (локуса),
-й позиции (локуса), ![]() , где
, где ![]() - длина хромосомы; символ,
занимающий
- длина хромосомы; символ,
занимающий ![]() -ю
позицию хромосомы, соответствует символу, занимающему
-ю
позицию хромосомы, соответствует символу, занимающему ![]() -ю позицию схемы, причем
символу * соответствуют как 0, так и 1. То же самое означают утверждения
хромосома соответствует схеме и хромосома представляет схему. Отметим, что если
в схеме присутствует
-ю позицию схемы, причем
символу * соответствуют как 0, так и 1. То же самое означают утверждения
хромосома соответствует схеме и хромосома представляет схему. Отметим, что если
в схеме присутствует ![]() символов *, то эта схема содержит
символов *, то эта схема содержит ![]() хромосом. Кроме того,
каждая хромосома (цепочка) длиной
хромосом. Кроме того,
каждая хромосома (цепочка) длиной ![]() принадлежит к
принадлежит к ![]() схемам. В таблицах 4.2 и 4.3
представлены схемы, к которым принадлежат цепочки длиной 2 и 3 соответственно.
схемам. В таблицах 4.2 и 4.3
представлены схемы, к которым принадлежат цепочки длиной 2 и 3 соответственно.
Таблица 4.2. Схемы, к которым принадлежат цепочки длиной 2
|
Звенья |
Схемы |
|||
|
1 |
2 |
3 |
4 |
|
|
00 |
** |
*0 |
0* |
00 |
|
01 |
** |
*1 |
0* |
01 |
|
10 |
** |
*0 |
1* |
10 |
|
11 |
** |
*1 |
1* |
11 |
Таблица 4.3. Схемы, к которым принадлежат цепочки длиной 3
|
Звенья |
Схемы |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
000 |
*** |
**0 |
*0* |
0** |
*00 |
0*0 |
00* |
000 |
|
001 |
*** |
** |
*0* |
0** |
*01 |
0*1 |
00* |
001 |
|
010 |
*** |
**0 |
*1* |
0** |
*10 |
0*0 |
01* |
010 |
|
011 |
*** |
**1 |
*1* |
0** |
*11 |
0*1 |
01* |
011 |
|
100 |
*** |
**0 |
*0* |
1** |
*00 |
1*0 |
10* |
100 |
|
101 |
*** |
**1 |
*0* |
1** |
*01 |
1*1 |
10* |
101 |
|
110 |
*** |
**0 |
*1* |
1** |
*10 |
1*0 |
11* |
110 |
|
111 |
*** |
**1 |
*1* |
1** |
*11 |
1*1 |
11* |
111 |
Цепочки длиной 2 соответствуют четырем различным схемам, а цепочки длиной 3 - восьми схемам.
Генетический алгоритм базируется
на принципе трансформации наиболее приспособленных особей (хромосом). Пусть ![]() означает исходную
популяцию особей, а
означает исходную
популяцию особей, а ![]() -
текущую популяцию (на
-
текущую популяцию (на ![]() -й итерации алгоритма). Из каждой
популяции
-й итерации алгоритма). Из каждой
популяции ![]() ,
, ![]() методом селекции
выбираются хромосомы с наибольшей приспособленностью, которые включаются в так
называемый родительский пул (mating pool)
методом селекции
выбираются хромосомы с наибольшей приспособленностью, которые включаются в так
называемый родительский пул (mating pool) ![]() . Далее, в результате объединения особей
из популяции
. Далее, в результате объединения особей
из популяции ![]() в
родительские пары и выполнения операции скрещивания с вероятностью
в
родительские пары и выполнения операции скрещивания с вероятностью ![]() , а также операции
мутации с вероятностью
, а также операции
мутации с вероятностью ![]() формируется новая популяция
формируется новая популяция ![]() , в которую входят
потомки особей из популяции
, в которую входят
потомки особей из популяции ![]() .
.
Следовательно, для любой схемы,
представляющей хорошее решение, было бы желательным, чтобы количество хромосом,
соответствующих этой схеме, возрастало с увеличением количества итераций![]() .
.
На соответствующее преобразование схем в генетическом алгоритме оказывают влияние 3 фактора: селекция хромосом, скрещивание и мутация. Проанализируем воздействие каждого из них с точки зрения увеличения ожидаемого количества представителей отдельно взятой схемы.
Обозначим рассматриваемую схему
символом ![]() , а
количество хромосом популяции
, а
количество хромосом популяции ![]() , соответствующих этой схеме -
, соответствующих этой схеме - ![]() . Следовательно,
. Следовательно, ![]() можно считать
количеством элементов (т.е. мощностью) множества
можно считать
количеством элементов (т.е. мощностью) множества ![]() .
.
Начнем с исследования влияния
селекции. При выполнении этой операции хромосомы из популяции ![]() копируются в
родительский пул
копируются в
родительский пул ![]() с
вероятностью, определяемой выражением (4.3). Пусть
с
вероятностью, определяемой выражением (4.3). Пусть ![]() обозначает среднее значение
функции приспособленности хромосом из популяции
обозначает среднее значение
функции приспособленности хромосом из популяции ![]() , которые соответствуют схеме
, которые соответствуют схеме ![]() . Если
. Если
![]() ,
,
то
 . (4.6)
. (4.6)
Величина ![]() также называется
приспособленностью схемы
также называется
приспособленностью схемы ![]() на
на ![]() -й итерации.
-й итерации.
Пусть ![]() обозначает сумму значений
функций приспособленности хромосом из популяции
обозначает сумму значений
функций приспособленности хромосом из популяции ![]() мощностью
мощностью ![]() , т.е.
, т.е.
 . (4.7)
. (4.7)
Обозначим через ![]() среднее значение
функции приспособленности хромосом этой популяции, т.е.
среднее значение
функции приспособленности хромосом этой популяции, т.е.
![]() . (4.8)
. (4.8)
Пусть ![]() обозначает элемент
родительского пула
обозначает элемент
родительского пула ![]() .
Для каждого
.
Для каждого ![]() и
для каждого
и
для каждого ![]() вероятность
того, что
вероятность
того, что ![]() определяется
отношением
определяется
отношением ![]() .
Поэтому ожидаемое количество хромосом в популяции
.
Поэтому ожидаемое количество хромосом в популяции ![]() , которые равны
, которые равны ![]() , составит
, составит
 .
.
Таким образом, ожидаемое
количество хромосом из множества ![]() , отобранных для включения в родительский
пул
, отобранных для включения в родительский
пул ![]() , будет
равно
, будет
равно
 ,
,
что следует из выражения (4.6).
Поскольку каждая хромосома из
родительского пула ![]() одновременно
принадлежит популяции
одновременно
принадлежит популяции ![]() , то хромосомы, составляющие множество
, то хромосомы, составляющие множество ![]() - это те же самые
особи, которые были отобраны из множества
- это те же самые
особи, которые были отобраны из множества ![]() для включения в популяцию
для включения в популяцию ![]() . Если количество
хромосом родительского пула
. Если количество
хромосом родительского пула ![]() , соответствующих схеме
, соответствующих схеме ![]() (т.е. количество
элементов множества
(т.е. количество
элементов множества ![]() ),
обозначить
),
обозначить ![]() ,
то из приведенных рассуждений можно сделать следующий вывод:
,
то из приведенных рассуждений можно сделать следующий вывод:
Вывод 4.1
Ожидаемое значение ![]() , т.е. ожидаемое
значение количества хромосом родительского пула
, т.е. ожидаемое
значение количества хромосом родительского пула ![]() , соответствующих схеме
, соответствующих схеме ![]() , определяется
выражением
, определяется
выражением
 . (4.9)
. (4.9)
Из этого следует, что если схема ![]() содержит хромосомы со
значением функции приспособленности, превышающим среднее значение (т.е.
приспособленность схемы
содержит хромосомы со
значением функции приспособленности, превышающим среднее значение (т.е.
приспособленность схемы ![]() на
на ![]() -й итерации оказывается большей, чем
среднее значение функции приспособленности хромосом из популяции
-й итерации оказывается большей, чем
среднее значение функции приспособленности хромосом из популяции ![]() , и поэтому
, и поэтому ![]() ), то ожидаемое
количество хромосом из родительского пула
), то ожидаемое
количество хромосом из родительского пула ![]() , соответствующих схеме
, соответствующих схеме ![]() , будет больше
количества хромосом из популяции
, будет больше
количества хромосом из популяции ![]() , соответствующих схеме
, соответствующих схеме ![]() . Поэтому можно утверждать,
что селекция вызывает распространение схем с приспособленностью «лучше средней»
и исчезновение схем с «худшей» приспособленностью.
. Поэтому можно утверждать,
что селекция вызывает распространение схем с приспособленностью «лучше средней»
и исчезновение схем с «худшей» приспособленностью.
Прежде чем приступить к анализу
влияния генетических операторов скрещивания и мутации на хромосомы из
родительского пула, определим необходимые для дальнейших рассуждений понятия
порядка и охвата схемы. Пусть ![]() обозначает длину хромосом,
соответствующих схеме
обозначает длину хромосом,
соответствующих схеме ![]() .
.
Определение 4.1
Порядок (order) схемы ![]() , иначе называемый
счетностью схемы и обозначаемый
, иначе называемый
счетностью схемы и обозначаемый ![]() - это количество постоянных позиций в
схеме, т.е. нулей и единиц в случае алфавита
- это количество постоянных позиций в
схеме, т.е. нулей и единиц в случае алфавита ![]() . Например
. Например
![]() .
.
Порядок схемы ![]() равен длине
равен длине ![]() за вычетом количества
символов *, что легко проверить на представленных примерах (для
за вычетом количества
символов *, что легко проверить на представленных примерах (для ![]() с одним символом * и
для
с одним символом * и
для ![]() с
двумя, четырьмя и тремя символами *). Легко заметить, что порядок схемы,
состоящей исключительно из символов *, равен нулю, т.е.
с
двумя, четырьмя и тремя символами *). Легко заметить, что порядок схемы,
состоящей исключительно из символов *, равен нулю, т.е. ![]() , а порядок схемы без единого
символа * равен
, а порядок схемы без единого
символа * равен ![]() ;
например,
;
например, ![]() .
Порядок схемы
.
Порядок схемы ![]() -
это всегда целое число из интервала
-
это всегда целое число из интервала ![]() .
.
Определение 4.2
Охват (defining length) схемы ![]() , называемый также
длиной схемы (не путать с длиной
, называемый также
длиной схемы (не путать с длиной ![]() ) и обозначаемый
) и обозначаемый ![]() - это расстояние между первым
и последним постоянным символом (т.е. разность между правой и левой крайними
позициями, содержащими постоянные символы). Например,
- это расстояние между первым
и последним постоянным символом (т.е. разность между правой и левой крайними
позициями, содержащими постоянные символы). Например,
![]()
![]()
![]()
![]() .
.
Охват схемы ![]() - это целое число из интервала
- это целое число из интервала
![]() . Отметим,
что охват схемы с постоянными символами на первой и последней позиции равен
. Отметим,
что охват схемы с постоянными символами на первой и последней позиции равен ![]() (как в первом из
приведенных примеров). Охват схемы с единственной постоянной позицией равен
нулю, в частности,
(как в первом из
приведенных примеров). Охват схемы с единственной постоянной позицией равен
нулю, в частности, ![]() .
Охват характеризует содержательность информации, заключенной в схеме.
.
Охват характеризует содержательность информации, заключенной в схеме.
Перейдем к рассуждениям о влиянии
операции скрещивания на обработку схем в генетическом алгоритме. Прежде всего
отметим, что одни схемы оказываются более подверженными уничтожению в процессе
скрещивания, чем другие. Например, рассмотрим схемы ![]() и
и ![]() , а также хромосому
, а также хромосому ![]() , соответствующую
обеим схемам. Видно, что схема
, соответствующую
обеим схемам. Видно, что схема ![]() имеет больше шансов «пережить» операцию
скрещивания, чем схема
имеет больше шансов «пережить» операцию
скрещивания, чем схема ![]() , которая больше подвержена «расщеплению»
в точках скрещивания 1, 2, 3, 4 и 5. Схему
, которая больше подвержена «расщеплению»
в точках скрещивания 1, 2, 3, 4 и 5. Схему ![]() можно разделить только при выборе точки
скрещивания, равной 3. Обратим внимание на охват обеих схем, который - это
очевидно оказывается существенным в процессе скрещивания.
можно разделить только при выборе точки
скрещивания, равной 3. Обратим внимание на охват обеих схем, который - это
очевидно оказывается существенным в процессе скрещивания.
В ходе анализа влияния операции
скрещивания на родительский пул ![]() рассмотрим некоторую хромосому из
множества
рассмотрим некоторую хромосому из
множества ![]() ,
т.е. хромосому из родительского пула, соответствующую схеме
,
т.е. хромосому из родительского пула, соответствующую схеме ![]() . Вероятность того, что эта
хромосома будет отобрана для скрещивания, равна
. Вероятность того, что эта
хромосома будет отобрана для скрещивания, равна ![]() . Если ни один из потомков этой хромосомы
не будет принадлежать к схеме
. Если ни один из потомков этой хромосомы
не будет принадлежать к схеме ![]() , то это означает, что точка скрещивания
должна находиться между первым и последним постоянным символом данной схемы.
Вероятность этого равна
, то это означает, что точка скрещивания
должна находиться между первым и последним постоянным символом данной схемы.
Вероятность этого равна ![]() . Из это можно сделать следующие выводы:
. Из это можно сделать следующие выводы:
Вывод 4.2 (влияние скрещивания)
Для некоторой хромосомы из ![]() вероятность того, что
она будет отобрана для скрещивания и ни один из ее потомков не будет
принадлежать к схеме
вероятность того, что
она будет отобрана для скрещивания и ни один из ее потомков не будет
принадлежать к схеме ![]() , ограничена сверху величиной
, ограничена сверху величиной
![]() .
.
Эта величина называется
вероятностью уничтожения схемы ![]() .
.
Вывод 4.3
Для некоторой хромосомы из ![]() вероятность того, что
она не будет отобрана для скрещивания либо, что хотя бы один из ее потомков
после скрещивания будет принадлежать к схеме
вероятность того, что
она не будет отобрана для скрещивания либо, что хотя бы один из ее потомков
после скрещивания будет принадлежать к схеме ![]() , ограничена снизу величиной
, ограничена снизу величиной
![]() .
.
Эта величина называется
вероятностью выживания схемы ![]() .
.
Легко показать, что если данная
хромосома принадлежит к схеме ![]() и отбирается для скрещивания, а вторая
родительская хромосома также принадлежит к схеме
и отбирается для скрещивания, а вторая
родительская хромосома также принадлежит к схеме ![]() , то оба их потомка тоже будут
принадлежать к схеме
, то оба их потомка тоже будут
принадлежать к схеме ![]() . Выводы 4.2 и 4.3 подтверждают
значимость показателя охвата схемы
. Выводы 4.2 и 4.3 подтверждают
значимость показателя охвата схемы ![]() для оценки вероятности уничтожения или
выживания схемы.
для оценки вероятности уничтожения или
выживания схемы.
Рассмотрим теперь влияние мутации
на родительский пул ![]() .
Оператор мутации с вероятностью
.
Оператор мутации с вероятностью ![]() случайным образом изменяет значение в
конкретной позиции с 0 на 1 и обратно. Очевидно, что схема переживет мутацию
только в том случае, когда все ее постоянные позиции останутся после выполнения
этой операции неизменными
случайным образом изменяет значение в
конкретной позиции с 0 на 1 и обратно. Очевидно, что схема переживет мутацию
только в том случае, когда все ее постоянные позиции останутся после выполнения
этой операции неизменными
Хромосома из родительского пула,
принадлежащая к схеме ![]() (т.е. хромосома из множества
(т.е. хромосома из множества ![]() ) останется в этой
схеме тогда и только тогда, когда ни один символ этой хромосомы,
соответствующий постоянным символам схемы
) останется в этой
схеме тогда и только тогда, когда ни один символ этой хромосомы,
соответствующий постоянным символам схемы ![]() , не изменится в процессе мутации.
Вероятность такого события равна
, не изменится в процессе мутации.
Вероятность такого события равна ![]() . Этот результат можно представить в
форме следующего вывода:
. Этот результат можно представить в
форме следующего вывода:
Вывод 4.4 (влияние мутации)
Вероятность того, что некоторая
хромосома из ![]() будет
принадлежать к схеме
будет
принадлежать к схеме ![]() после операции мутации, определяется
выражением
после операции мутации, определяется
выражением
![]() .
.
Эта величина называется
вероятностью выживания схемы ![]() после мутации.
после мутации.
Вывод 4.5
Если вероятность мутации ![]() мала
мала ![]() , то можно считать,
что вероятность выживания схемы
, то можно считать,
что вероятность выживания схемы ![]() после мутации, определенная в выводе
4.4, приближенно равна
после мутации, определенная в выводе
4.4, приближенно равна
![]() .
.
Эффект совместного воздействия
селекции, скрещивания и мутации (выводы 4.1 - 4.4) с учетом факта, что если
хромосома из множества ![]() дает потомка, соответствующего схеме
дает потомка, соответствующего схеме ![]() , то он будет
принадлежать к
, то он будет
принадлежать к ![]() ,
ведет к построению следующей схемы репродукции [7]:
,
ведет к построению следующей схемы репродукции [7]:
 . (4.10)
. (4.10)
Зависимость (4.10) показывает,
как изменяется от популяции к популяции количество хромосом, соответствующих
данной схеме. Это изменение вызывается тремя факторами, представленными в
правой части выражения (4.10), в частности: ![]() отражает роль среднего значения функции
приспособленности,
отражает роль среднего значения функции
приспособленности, ![]() показывает
влияние скрещивания и
показывает
влияние скрещивания и ![]() - влияние мутации. Чем больше значение
каждого из этих факторов, тем большим оказывается ожидаемое количество соответствий
схеме
- влияние мутации. Чем больше значение
каждого из этих факторов, тем большим оказывается ожидаемое количество соответствий
схеме ![]() в
следующей популяции. Вывод 4.5 позволяет представить зависимость (4.10) в виде
в
следующей популяции. Вывод 4.5 позволяет представить зависимость (4.10) в виде
 . (4.11)
. (4.11)
Для больших популяций зависимость (4.11) можно аппроксимировать выражением
 . (4.12)
. (4.12)
Из формул (4.11) и (4.12)
следует, что ожидаемое количество хромосом, соответствующих схеме ![]() в следующем
поколении, можно считать функцией от фактического количества хромосом,
принадлежащих этой схеме, относительной приспособленности схемы, а также
порядка и охвата схемы. Заметно, что схемы с приспособленностью выше средней и
с малым порядком и охватом характеризуются возрастанием количества своих
представителей в последующих популяциях. Подобный рост имеет показательный
характер, что следует из выражения (4.9). Для больших популяций эту формулу
можно заменить рекуррентной зависимостью вида [33]
в следующем
поколении, можно считать функцией от фактического количества хромосом,
принадлежащих этой схеме, относительной приспособленности схемы, а также
порядка и охвата схемы. Заметно, что схемы с приспособленностью выше средней и
с малым порядком и охватом характеризуются возрастанием количества своих
представителей в последующих популяциях. Подобный рост имеет показательный
характер, что следует из выражения (4.9). Для больших популяций эту формулу
можно заменить рекуррентной зависимостью вида [33]
 . (4.13)
. (4.13)
Если допустить, что схема ![]() имеет
приспособленность на
имеет
приспособленность на ![]() выше средней, т.е.
выше средней, т.е.
![]() , (4.14)
, (4.14)
то
при подстановке выражения (4.12) в неравенство (4.11) в предположении, что ![]() не изменяется во
времени, при старте от
не изменяется во
времени, при старте от ![]() получаем
получаем
![]() ,
,
![]() , (4.15)
, (4.15)
т.е.
![]() для схемы с
приспособленностью выше средней и
для схемы с
приспособленностью выше средней и ![]() - в противном случае.
- в противном случае.
Равенство (4.15) описывает
геометрическую прогрессию. Из этого следует, что в процессе репродукции схемы,
оказавшиеся лучше (хуже) средних, выбираются на очередных итерациях
генетического алгоритма в показательно возрастающих (убывающих) количествах.
Обратим внимание, что зависимости (4.9) - (4.13) основаны на предположении, что
функция приспособленности ![]() принимает только положительные значения.
При использовании генетических алгоритмов для решения оптимизационных задач, в
которых целевая функция может принимать и отрицательные значения, необходимы
некоторые дополнительные соотношения между оптимизируемой функцией и функцией
приспособленности. Конечный результат, получаемый из выражений (4.10) - (4.12),
можно сформулировать в форме теоремы. Это основная теорема генетических
алгоритмов, иначе называемая теоремой о схемах [21].
принимает только положительные значения.
При использовании генетических алгоритмов для решения оптимизационных задач, в
которых целевая функция может принимать и отрицательные значения, необходимы
некоторые дополнительные соотношения между оптимизируемой функцией и функцией
приспособленности. Конечный результат, получаемый из выражений (4.10) - (4.12),
можно сформулировать в форме теоремы. Это основная теорема генетических
алгоритмов, иначе называемая теоремой о схемах [21].
Теорема 4.1
Схемы малого порядка, с малым охватом и с приспособленностью выше средней формируют показательно возрастающее количество своих представителей в последующих поколениях генетического алгоритма.
В соответствии с приведенной теоремой важным вопросом становится кодирование, которое должно обеспечивать построение схем малого порядка, с малым охватом и с приспособленностью выше средней. Косвенным результатом теоремы 4.1 (о схемах) можно считать следующую гипотезу, называемую гипотезой о кирпичиках (либо о строительных блоках) [15, 33].
Гипотеза 4.1
Генетический алгоритм стремится достичь близкого к оптимальному результата за счет комбинирования хороших схем (с приспособленностью выше средней) малого порядка и малого охвата. Такие схемы называются кирпичиками (либо строительными блоками).
Гипотеза о строительных блоках выдвинута на основании теоремы о схемах с учетом того, что генетические алгоритмы исследуют пространство поиска с помощью схем малого порядка и малого охвата, которые впоследствии участвуют в обмене информацией при скрещивании.
Несмотря на то, что для доказательства этой гипотезы предпринимались определенные исследования, однако в большинстве нетривиальных приложений приходится опираться на эмпирические результаты. В течение последних двадцати лет опубликованы многочисленные работы, посвященные применениям генетических алгоритмов, подтверждающим эту гипотезу. Если она считается истинной, то проблема кодирования приобретает критическое значение для генетического алгоритма; кодирование должно реализовать концепцию малых строительных блоков. Качество, которое обеспечивает генетическим алгоритмам явное преимущество перед другими традиционными методами, несомненно заключается в обработке большого количества различных схем.
Обратимся снова к примерам 4.4 и 4.5 и на их основе проанализируем обработку схем генетическим алгоритмом.
Пример 4.7
В условиях примера 4.4 рассмотрим схему
![]()
и покажем, как изменяется количество представителей этой схемы и приспособленность в процессе выполнения генетического алгоритма.
Длина ![]() , а охват и порядок схемы
, а охват и порядок схемы ![]() составляют
соответственно
составляют
соответственно ![]() и
и
![]() . В исходной
популяции из примера 4.4 схеме
. В исходной
популяции из примера 4.4 схеме ![]() соответствуют две следующие хромосомы:
соответствуют две следующие хромосомы:
![]()
![]() .
.
Из формулы (4.10) следует, что
после селекции и скрещивания количество хромосом, соответствующих схеме ![]() , должно быть больше
или равно 2,5. Напомним, что вероятности скрещивания и мутации считаются
равными соответственно
, должно быть больше
или равно 2,5. Напомним, что вероятности скрещивания и мутации считаются
равными соответственно ![]() и
и ![]() . Приспособленность схемы
. Приспособленность схемы ![]() в исходной популяции,
обозначаемая
в исходной популяции,
обозначаемая ![]() ,
равна 8 и превышает среднюю приспособленность всех хромосом этой популяции
,
равна 8 и превышает среднюю приспособленность всех хромосом этой популяции ![]() , что легко рассчитать
по формулам (4.6) - (4.8).
, что легко рассчитать
по формулам (4.6) - (4.8).
В примере 4.4 после селекции и
скрещивания в новой популяции получены четыре хромосомы, соответствующие схеме ![]() :
:
![]()
![]()
![]()
![]() .
.
Приспособленность схемы ![]() в новой популяции,
т.е.
в новой популяции,
т.е. ![]() ,
составит 8,25, тогда как средняя приспособленность хромосом этой популяции
,
составит 8,25, тогда как средняя приспособленность хромосом этой популяции ![]() , что также следует из
формул (4.6) - (4.8). Новая популяция характеризуется большим средним значением
функции приспособленности особей по сравнению с предыдущей (исходной)
популяцией, что уже отмечалось в примере 4.4. Кроме того, в новой популяции
приспособленность схемы
, что также следует из
формул (4.6) - (4.8). Новая популяция характеризуется большим средним значением
функции приспособленности особей по сравнению с предыдущей (исходной)
популяцией, что уже отмечалось в примере 4.4. Кроме того, в новой популяции
приспособленность схемы ![]() оказывается лучшей, а количество
представителей этой схемы - большим по сравнению с предыдущей популяцией.
оказывается лучшей, а количество
представителей этой схемы - большим по сравнению с предыдущей популяцией.
Пример 4.8
В условиях примера 4.5 рассмотрим схему
![]()
и проследим ее обработку при выполнении генетического алгоритма.
В этом случае ![]() , а охват и порядок схемы
, а охват и порядок схемы ![]() составляют
составляют ![]() и
и ![]() соответственно. В исходной
популяции из примера 4.5 этой схеме соответствуют три хромосомы
соответственно. В исходной
популяции из примера 4.5 этой схеме соответствуют три хромосомы
![]()
![]()
![]() .
.
Приспособленность схемы ![]() в исходной популяции
в исходной популяции ![]() и превышает среднюю
приспособленность особей этой популяции
и превышает среднюю
приспособленность особей этой популяции ![]() , что следует из выражений (4.6) - (4.8).
На основе формулы (4.9) легко рассчитать ожидаемое количество хромосом
родительского пула, соответствующих схеме
, что следует из выражений (4.6) - (4.8).
На основе формулы (4.9) легко рассчитать ожидаемое количество хромосом
родительского пула, соответствующих схеме ![]() . Оно составит
. Оно составит ![]() . В примере 4.5 по результатам
селекции в родительский пул включены 6 таких хромосом:
. В примере 4.5 по результатам
селекции в родительский пул включены 6 таких хромосом: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Ожидаемое количество хромосом,
соответствующих схеме
. Ожидаемое количество хромосом,
соответствующих схеме ![]() , после скрещивания с вероятностью
, после скрещивания с вероятностью ![]() (вероятность мутации
(вероятность мутации ![]() ), как легко
рассчитать по формуле (4.10), должно превышать 5,58. В новую популяцию включены
6 представителей схемы
), как легко
рассчитать по формуле (4.10), должно превышать 5,58. В новую популяцию включены
6 представителей схемы ![]() . Это все хромосомы данной популяции.
. Это все хромосомы данной популяции.
Пример 4.9
В условиях примера 4.5 рассмотрим схему
![]()
и проследим ее обработку при выполнении генетического алгоритма.
Длина ![]() , а охват и порядок схемы
, а охват и порядок схемы ![]() составляют
составляют ![]() и
и ![]() соответственно. В исходной
популяции из примера 4.5 этой схеме соответствует одна хромосома
соответственно. В исходной
популяции из примера 4.5 этой схеме соответствует одна хромосома
![]() .
.
Поэтому приспособленность схемы ![]() в исходной популяции
равна функции приспособленности хромосомы
в исходной популяции
равна функции приспособленности хромосомы ![]() и составляет 1683. Она превышает среднюю
приспособленность особей исходной популяции, равную 589. По формуле (4.9)
рассчитываем ожидаемое количество хромосом родительского пула, соответствующих
схеме
и составляет 1683. Она превышает среднюю
приспособленность особей исходной популяции, равную 589. По формуле (4.9)
рассчитываем ожидаемое количество хромосом родительского пула, соответствующих
схеме ![]() . Оно
составит
. Оно
составит ![]() .
В примере 4.5 по результатам селекции в родительский пул включены 3 одинаковых
хромосомы
.
В примере 4.5 по результатам селекции в родительский пул включены 3 одинаковых
хромосомы ![]() ,
соответствующих схеме
,
соответствующих схеме ![]() . Ожидаемое количество хромосом в новой
популяции, соответствующих схеме
. Ожидаемое количество хромосом в новой
популяции, соответствующих схеме ![]() , после скрещивания с вероятностью
, после скрещивания с вероятностью ![]() (вероятность мутации
(вероятность мутации ![]() ), должно превышать 5,58.
В примере 4.5 в новую популяцию включены 3 хромосомы, соответствующих схеме
), должно превышать 5,58.
В примере 4.5 в новую популяцию включены 3 хромосомы, соответствующих схеме ![]() . Это
. Это
![]() .
.
Пример 4.10
В условиях примера 4.5 рассмотрим схему
![]()
и проследим ее обработку при выполнении генетического алгоритма.
Длина ![]() , а охват и порядок схемы
, а охват и порядок схемы ![]() составляют
составляют ![]() и
и ![]() соответственно. В исходной
популяции из примера 4.5 этой схеме соответствуют три хромосомы
соответственно. В исходной
популяции из примера 4.5 этой схеме соответствуют три хромосомы
![]()
![]()
![]() .
.
В отличие от примеров 4.8 и 4.9
приспособленность схемы ![]() в исходной популяции оказывается меньше
средней приспособленности особей этой популяции
в исходной популяции оказывается меньше
средней приспособленности особей этой популяции ![]() и составляет
и составляет ![]() . Ожидаемое количество хромосом
родительского пула, соответствующих схеме
. Ожидаемое количество хромосом
родительского пула, соответствующих схеме ![]() и рассчитанное по формуле (4.9), равно
и рассчитанное по формуле (4.9), равно ![]() . В примере 4.5 в
родительский пул была включена одна хромосома
. В примере 4.5 в
родительский пул была включена одна хромосома ![]() , соответствующая схеме
, соответствующая схеме ![]() . На основе формулы
(4.10) получаем значение 1,068, определяющее количество представителей схемы
. На основе формулы
(4.10) получаем значение 1,068, определяющее количество представителей схемы ![]() в новой популяции. В
примере 4.5 после скрещивания с вероятностью
в новой популяции. В
примере 4.5 после скрещивания с вероятностью ![]() (вероятность мутации
(вероятность мутации ![]() ) в новую популяцию была
включена одна хромосома, соответствующая схеме
) в новую популяцию была
включена одна хромосома, соответствующая схеме ![]() , т.е.
, т.е. ![]() .
.
Пример 4.11
В условиях примера 4.5 рассмотрим схему
![]()
и проследим ее обработку при выполнении генетического алгоритма.
Длина ![]() , а охват и порядок схемы
, а охват и порядок схемы ![]() составляют
составляют ![]() и
и ![]() соответственно. В исходной
популяции из примера 4.5 этой схеме соответствует только одна хромосома
соответственно. В исходной
популяции из примера 4.5 этой схеме соответствует только одна хромосома
![]() .
.
Поэтому приспособленность схемы ![]() в исходной популяции
равна значению функции приспособленности хромосомы
в исходной популяции
равна значению функции приспособленности хромосомы ![]() и составляет 129. Аналогично
примеру 4.10, она меньше средней приспособленности особей начальной популяции,
которая равна 589. Ожидаемое количество представителей схемы
и составляет 129. Аналогично
примеру 4.10, она меньше средней приспособленности особей начальной популяции,
которая равна 589. Ожидаемое количество представителей схемы ![]() в родительском пуле
составляет
в родительском пуле
составляет ![]() ,
что следует из формулы (4.9). В примере 4.5 родительский пул (после селекции)
не содержит ни одной хромосомы, соответствующей схеме
,
что следует из формулы (4.9). В примере 4.5 родительский пул (после селекции)
не содержит ни одной хромосомы, соответствующей схеме ![]() . При расчете ожидаемого
количества представителей схемы
. При расчете ожидаемого
количества представителей схемы ![]() в новой популяции по формуле (4.10) для
вероятности скрещивания
в новой популяции по формуле (4.10) для
вероятности скрещивания ![]() и вероятности мутации
и вероятности мутации ![]() получаем значение
0,165. В примере 4.5 после скрещивания в новую популяцию не была включена ни
одна хромосома, соответствующая схеме
получаем значение
0,165. В примере 4.5 после скрещивания в новую популяцию не была включена ни
одна хромосома, соответствующая схеме ![]() .
.
Из примеров 4.7 - 4.11, посвященных обработке схем, можно сделать следующие выводы. Эти примеры иллюстрируют основную теорему генетических алгоритмов - теорему о схемах. Они затрагивают обработку схем низкого (малого) порядка с малым охватом. Примеры 4.7 - 4.9 демонстрируют увеличение количества представителей данной схемы в следующем поколении для случая, когда приспособленность этой схемы превышает среднюю приспособленность всех особей популяции. Примеры 4.10 и 4.11 показывают ситуацию, когда приспособленность схемы оказывается меньше средней приспособленности особей популяции. Количество представителей таких схем в следующих поколениях не увеличивается, а наоборот - наблюдается уменьшение количества соответствующих им хромосом.
При анализе подобных примеров для схем большего порядка и большего охвата также не регистрируется увеличение количества их представителей в следующем поколении, что согласуется с теоремой о схемах.
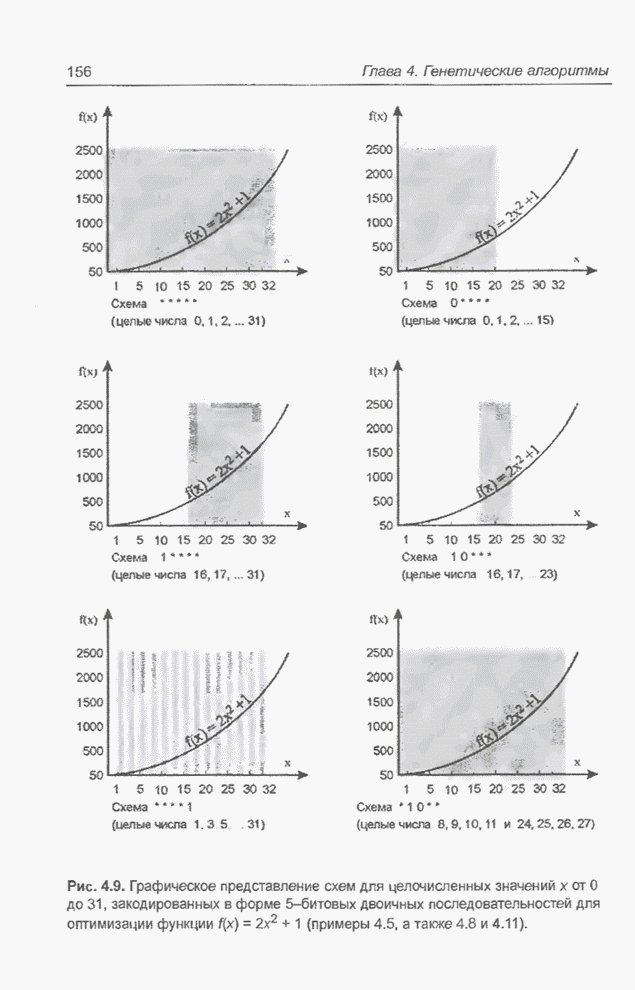
Графическая интерпретация схем, обсуждавшихся в примерах 4.8 и 4.11, представлена на рис. 4.9; аналогичным образом можно проиллюстрировать схемы из примеров 4.9 и 4.10, равно как и любые другие.

Рис. 4.9. Графическое
представление схем для целочисленных значений ![]() от 0 до 31, закодированных в форме
5-битовых двоичных последовательностей для оптимизации функции
от 0 до 31, закодированных в форме
5-битовых двоичных последовательностей для оптимизации функции ![]() (примеры 4.5, а также
4.8 и 4.11).
(примеры 4.5, а также
4.8 и 4.11).
На
рис. 4.9 видно, что к схеме 1**** (пример 4.8) в исходной популяции из примера
4.5 принадлежат хромосомы ![]() ,
, ![]() и
и ![]() с фенотипами 19, 21, 29 соответственно,
а после селекции и скрещивания к этой схеме уже принадлежат все включенные в
новую популяцию хромосомы, т.е.
с фенотипами 19, 21, 29 соответственно,
а после селекции и скрещивания к этой схеме уже принадлежат все включенные в
новую популяцию хромосомы, т.е. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() с фенотипами 17, 23, 21, 29, 29, 29
соответственно. В то же время к схеме *10** (пример 4.11) в исходной популяции
из примера 4.5 принадлежит только одна хромосома
с фенотипами 17, 23, 21, 29, 29, 29
соответственно. В то же время к схеме *10** (пример 4.11) в исходной популяции
из примера 4.5 принадлежит только одна хромосома ![]() , фенотип которой равен 8; в следующей
популяции уже нет ни одной хромосомы, принадлежащей этой схеме. Обратим
внимание (рис. 4.9), что оптимальное решение, которое максимизирует функцию,
заданную выражением (4.1), принадлежит к схеме 1* - и не соответствует схеме
*10**.
, фенотип которой равен 8; в следующей
популяции уже нет ни одной хромосомы, принадлежащей этой схеме. Обратим
внимание (рис. 4.9), что оптимальное решение, которое максимизирует функцию,
заданную выражением (4.1), принадлежит к схеме 1* - и не соответствует схеме
*10**.
Выполнение генетических алгоритмов основано на обработке схем. Схемы малого порядка, с малым охватом и приспособленностью выше средней выбираются, размножаются и комбинируются, в результате чего формируются все лучшие кодовые последовательности. Поэтому оптимальное решение строится (в соответствии с гипотезой кирпичиков) путем объединения наилучших из полученных к текущему моменту частичных решений. Простое скрещивание не слишком часто уничтожает схемы с малым охватом, однако ликвидирует схемы с достаточно большим охватом. Однако, невзирая на губительность операций скрещивания и мутации для схем высокого порядка и охвата, количество обрабатываемых схем настолько велико, что даже при относительно низком количестве хромосом в популяции достигаются весьма неплохие результаты выполнения генетического алгоритма.
Количество эффективно
обрабатываемых схем, рассчитанное Холландом [21], составляет ![]() . Это означает, что
для популяции мощностью
. Это означает, что
для популяции мощностью ![]() количество обрабатываемых в каждом
поколении схем имеет порядок
количество обрабатываемых в каждом
поколении схем имеет порядок ![]() .
.
Следует упомянуть о том, что в последнее время теорема Холланда о схемах и следующие из нее оценки количества схем, обрабатываемых генетическим алгоритмом, вызывают в научной среде определенные возражения [37].
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Предисловие к русскому изданию
- ГЛАВА 1. ВВЕДЕНИЕ
- Список литературы
- ГЛАВА 2. МНОГОСЛОЙНЫЕ НЕЙРОННЫЕ СЕТИ И АЛГОРИТМЫ ИХ ОБУЧЕНИЯ
- 2.1. Введение
- 2.2. Нейрон и его модели
- 2.3. Персептрон
- 2.4. Системы типа Адалайн
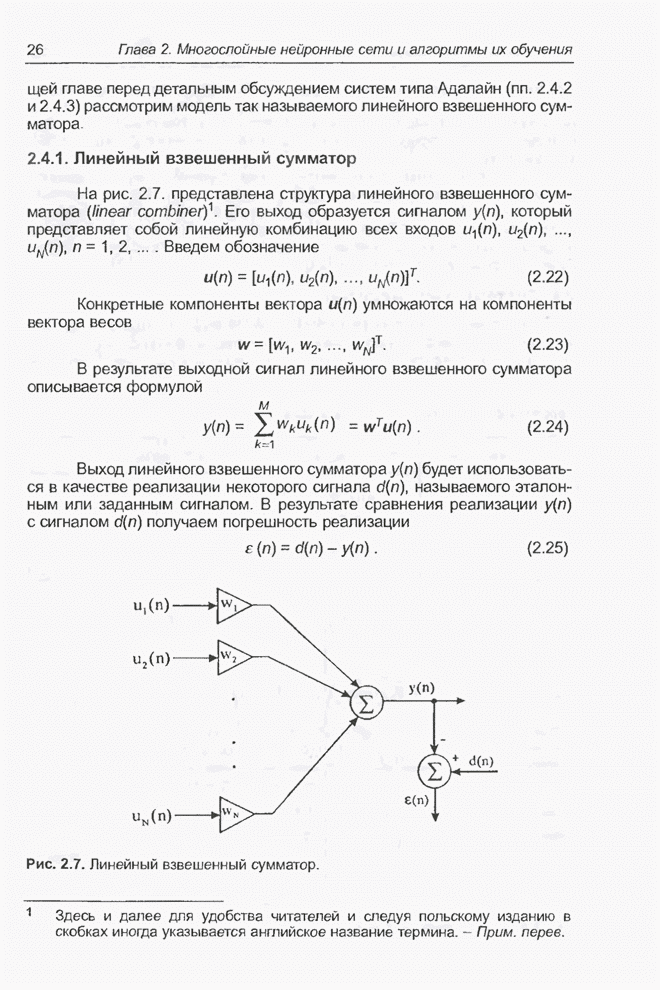
- 2.4.1. Линейный взвешенный сумматор
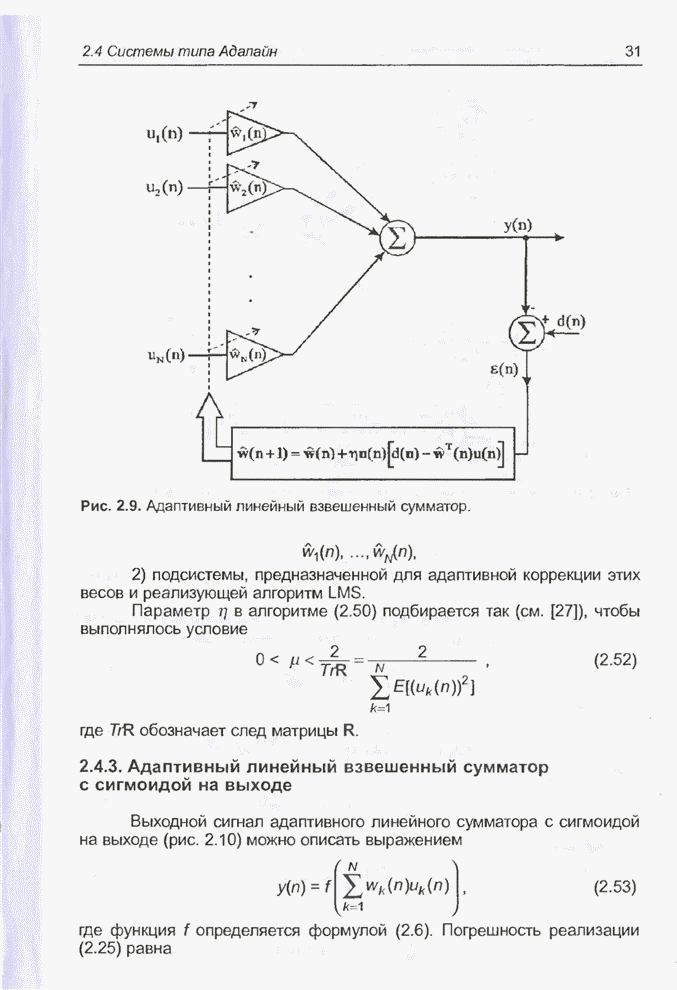
- 2.4.2. Адаптивный линейный взвешенный сумматор
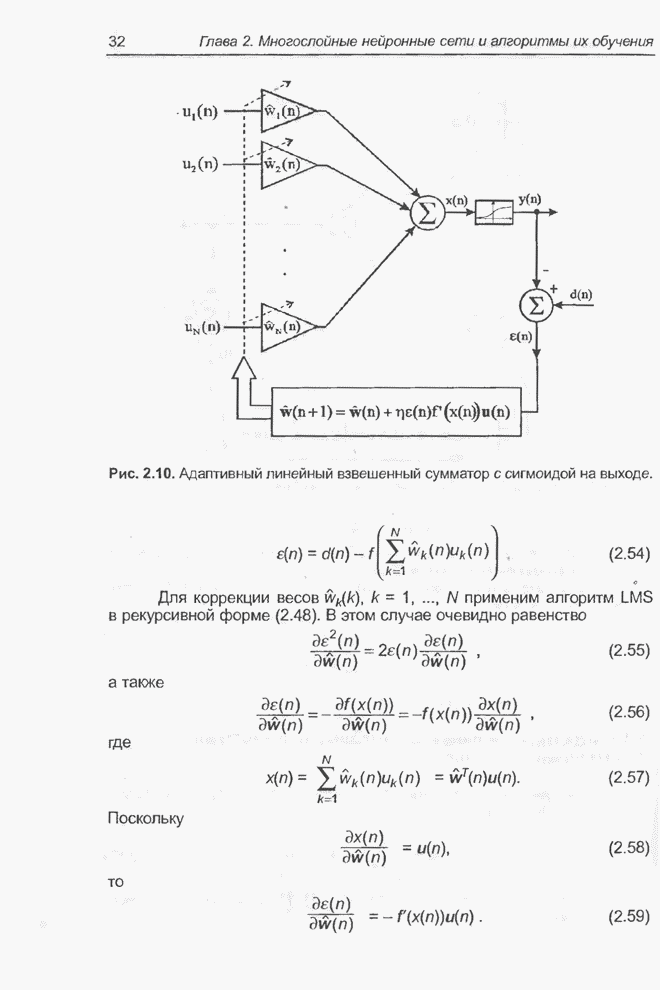
- 2.4.3. Адаптивный линейный взвешенный сумматор с сигмоидой на выходе
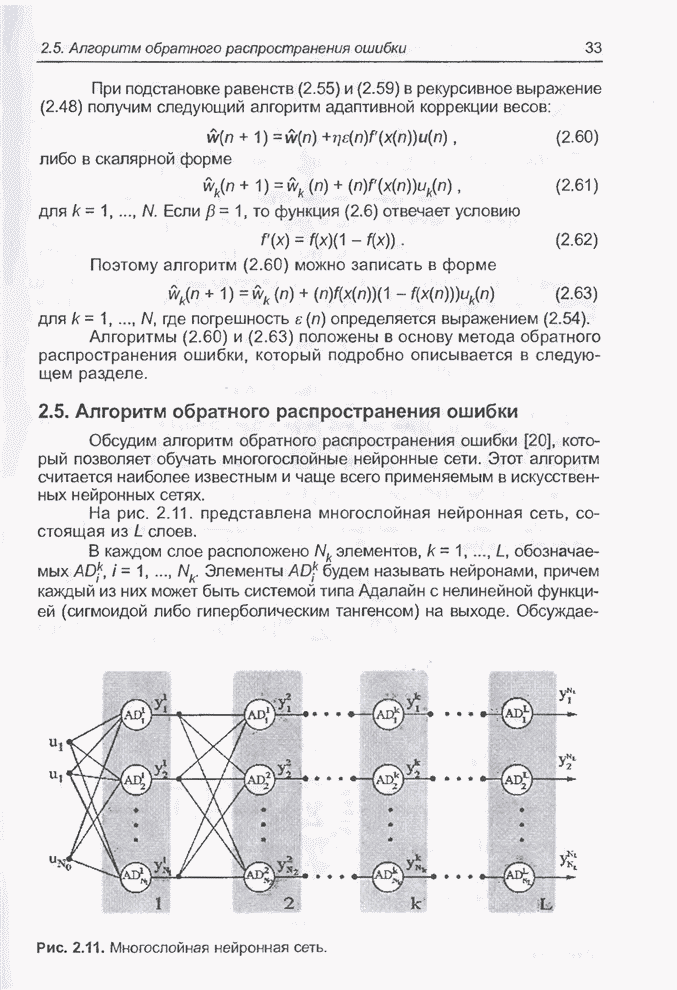
- 2.5. Алгоритм обратного распространения ошибки
- 2.6. Применение рекуррентного метода наименьших квадратов для обучения нейронных сетей
- Список литературы
- ГЛАВA3. НЕЧЕТКИЕ МНОЖЕСТВА И НЕЧЕТКИЙ ВЫВОД
- 3.1. Введение
- 3.2. Основные понятия и определения теории нечетких множеств
- 3.3. Операции на нечетких множествах
- 3.4. Принцип расширения
- 3.5. Нечеткие числа
- 3.6. Треугольные нормы
- 3.7. Нечеткие отношения и их свойства
- 3.8. Нечеткий вывод
- 3.9. Нечеткое управление
- 3.9.1. Классический модуль нечеткого управления
- 3.9.2. Метод нечеткого управления Такаги-Сугено
- 3.10. Проектирование базы нечетких правил на основе численных данных
- 3.10.1. Построение нечетких правил
- 3.10.2. Задача парковки грузовика
- 3.10.3. Примечание
- Список литературы
- ГЛАВА 4. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 4.1. Введение
- 4.2. Генетические алгоритмы и традиционные методы оптимизации
- 4.3. Основные понятия генетических алгоритмов
- 4.4. Классический генетический алгоритм
- 4.5. Иллюстрация выполнения классического генетического алгоритма
- 4.6. Кодирование параметров задачи в генетическом алгоритме
- 4.7. Основная теорема о генетических алгоритмах
- 4.8. Модификации классического генетического алгоритма
- 4.8.1. Методы селекции
- 4.8.2. Особые процедуры репродукции
- 4.8.3. Генетические операторы
- 4.8.4. Методы кодирования
- 4.8.5. Масштабирование функции приспособленности
- 4.8.6. Ниши в генетическом алгоритме
- 4.8.7. Генетические алгоритмы для многокритериальной оптимизации
- 4.8.8. Генетические микроалгоритмы
- 4.9. Примеры оптимизации функции с помощью программы FlexTool
- 4.10. Эволюционные алгоритмы
- 4.11. Приложения эволюционных алгоритмов
- 4.11.1. Примеры оптимизации функции с помощью программы Evolver
- 4.11.2. Решение комбинаторных задач с помощью программы Evolver
- 4.12. Эволюционные алгоритмы в нейронных сетях
- 4.12.1. Независимое применение генетических алгоритмов и нейронных сетей
- 4.12.2. Нейронные сети для поддержки генетических алгоритмов
- 4.12.3. Генетические алгоритмы для поддержки нейронных сетей
- 4.12.4. Применение генетических алгоритмов для обучения нейронных сетей
- 4.12.5. Генетические алгоритмы для выбора топологии нейронных сетей
- 4.12.6. Адаптивные взаимодействующие системы
- 4.12.7. Типовой цикл эволюции
- 4.12.7.1. Эволюция весов связей
- 4.12.7.2. Эволюция архитектуры сети
- 4.12.7.3. Эволюция правил обучения
- 4.13. Примеры моделирования эволюционных алгоритмов в приложении к нейронным сетям
- 4.13.1. Программы Evolver и BrainMaker
- 4.13.2. Программа GTO
- Список литературы
- ГЛАВА 5. МОДУЛИ НЕЧЕТКО-НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.1. Модуль нечеткого управления со структурой, определенной в процессе дефуззификации
- 5.1.2. Конструкция модуля
- 5.1.3. Структура модуля
- 5.1.4. Использование алгоритма обратного распространения ошибки
- 5.1.5. Модификации модуля
- 5.1.6. Применение модуля нечеткого управления для прогнозирования случайных временных рядов
- 5.1.7. Применение модуля нечеткого управления для решения задачи парковки грузовика
- 5.1.8. Примечание
- 5.2. Представление модуля нечеткого управления в виде стандартной нейронной сети
- 5.3. Модуль нечеткого управления с нейронной сетью для выполнения дефуззификации
- 5.3.1. Введение
- 5.3.2. Конструкция модуля
- 5.3.3. Структура модуля
- 5.3.4. Алгоритмы обучения модуля
- 5.3.5. Решение задачи стабилизации перевернутого маятника
- 5.3.6. Примечание
- 5.4. Модуль нечеткого управления с возможностью коррекции правил
- 5.4.1. Введение
- 5.4.2. Фаза обучения на основе самоорганизации
- 5.4.3. Фаза обучения с учителем
- 5.4.4. Примечание
- 5.5. Модуль нечеткого управления типа Такаги-Сугено
- 5.5.1. Введение
- 5.5.2. Нейронная реализация функции принадлежности
- 5.5.3. Модули Такаги-Сугено
- 5.5.4. Реализация условий
- 5.5.5. Реализация заключений
- 5.5.6. Примечание
- 5.6. Модуль нечеткого управления типа Такаги-Сугено: случай зависимых лингвистических переменных
- 5.6.1. Введение
- 5.6.2. Нейронные сети для нечеткого вывода
- 5.6.3. Структура системы
- 5.6.4. Способ обучения
- 5.6.5. Решение задачи парковки грузовика
- 5.6.6. Примечание
- Список литературы