| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.11.1. Примеры оптимизации функции с помощью программы Evolver
Прежде чем перейти к примерам, дадим характеристику генетическим операторам, используемым программой Evolver в задачах оптимизации функции.
Скрещивание. Это равномерное скрещивание (uniform crossover), определенное аналогично примененному в п. 4.8.3, но для хромосом, состоящих из генов с действительными аллелями.
Скрещивание производится в соответствии с так называемым показателем скрещивания (crossover rate), определяющим, какой процент генов потомок унаследует от каждого родителя. В программе Evolver показатель скрещивания вводится пользователем и представляет собой число из интервала от 0,01 до 1,0. Например, значение показателя скрещивания 0,8 означает, что потомок получит около 80 % генов со значениями (аллелями) такими же, как у первого родителя, а оставшееся количество (порядка 20 %) - унаследует от второго родителя. Если показатель скрещивания равен 1, то никакого скрещивания практически не происходит, а образуются только так называемые клоны, т.е. хромосомы, идентичные родителям. По умолчанию в программе Evolver применяется значение показателя скрещивания, равное 0,5, что означает наследование примерно одинакового количества генов от каждого родителя.
Мутация. Каждый ген в хромосоме представляет один параметр задачи. Следовательно, аллели соответствуют фенотипам, т.е. значениям конкретных переменных. Для каждого гена случайным образом выбирается число из интервала от 0 до 1, которое сравнивается с так называемым показателем мутации (mutation rate). Если разыгранное число меньше введенного значения показателя или равно ему, то выполняется мутация данного гена. Эта операция заключается в замене значения гена другим, случайно выбранным числом из области допустимых значений параметра, соответствующего мутирующему гену.
Вводимое пользователем значение
показателя мутации представляет собой число из интервала от 0,0 до 1,0. Чем
больше это значение, тем большее количество генов подвергается мутации. Если
показатель мутации равен 1, то мутации подвергаются 100% генов, выбираемых
случайным образом. С учетом того, что в программе Evolver мутация всегда
производится после скрещивания, задание показателя мутации равным 1 означает,
что в этом случае эффект скрещивания не имеет никакого значения. Очевидно, что
если показатель мутации равен 0, то мутация вообще не производится. Как
правило, значение показателя мутации задается в пределах от 0,06 до 0,2.
Отметим, что определяемый таким образом показатель мутации представляет собой
аналог вероятности мутации ![]() , описанной в разд. 4.4. В то же время
используемый в программе Evolver показатель скрещивания имеет смысл,
отличающийся от введенной в разд. 4.4 вероятности скрещивания
, описанной в разд. 4.4. В то же время
используемый в программе Evolver показатель скрещивания имеет смысл,
отличающийся от введенной в разд. 4.4 вероятности скрещивания ![]() . Значения как
показателя мутации, так и показателя скрещивания можно изменять в процессе
выполнения программы Evolver.
. Значения как
показателя мутации, так и показателя скрещивания можно изменять в процессе
выполнения программы Evolver.
В классическом генетическом
алгоритме на каждой итерации обновляется вся популяция, что соответствует
формированию очередного поколения. Применительно к программе Evolver можно
говорить о последовательных «тактах» (trials) ее выполнения, причем на каждом
такте изменяется только одна особь. Если популяция насчитывает ![]() хромосом (особей,
которые в описании программы называются организмами), то
хромосом (особей,
которые в описании программы называются организмами), то ![]() таких «тактов» составляют одну
итерацию классического генетического алгоритма. Поэтому для того, чтобы при
заданном количестве «тактов» выполнения программы Evolver найти соответствующее
ему количество поколений (в терминологии классического генетического
алгоритма), необходимо значение
таких «тактов» составляют одну
итерацию классического генетического алгоритма. Поэтому для того, чтобы при
заданном количестве «тактов» выполнения программы Evolver найти соответствующее
ему количество поколений (в терминологии классического генетического
алгоритма), необходимо значение ![]() разделить на количество особей в
популяции. В представляемых далее примерах «такты» будут обозначаться символом
разделить на количество особей в
популяции. В представляемых далее примерах «такты» будут обозначаться символом ![]() . Пример 4.21
демонстрирует применение программы Evolver для оптимизации функции трех
переменных.
. Пример 4.21
демонстрирует применение программы Evolver для оптимизации функции трех
переменных.
Пример 4.21
С помощью программы Evolver найти минимум функции
![]()
для
целочисленных ![]() ,
,
![]() ,
, ![]() в интервале
в интервале ![]() .
.
Вычисления производились для
популяции размерностью ![]() . Использовалось значение показателя
скрещивания равное 0,9. Это означает, что в результате скрещивания потомок
наследует приблизительно (с округлением до целого) 90 % генов от первого
родителя и остальные гены (около 10%) - от второго родителя. Заметим, что для
показателя скрещивания равного 1 будет наблюдаться такой же эффект, что и при
отсутствии скрещивания, поскольку потомок будет наследовать все гены только от
первого родителя. По этой причине при выбранном значении данного показателя,
равном 0,9, скрещивание либо не будет проводиться вообще (точнее говоря, потомок
окажется абсолютно идентичным своему первому родителю), либо скрещивание будет
выполнено, и потомок унаследует большую часть генов от первого родителя. Для
мутации выбрана величина показателя мутации равная 0,1, которая указывает, что
значения 10% генов (с округлением до целого) должны подвергнуться случайным
изменениям.
. Использовалось значение показателя
скрещивания равное 0,9. Это означает, что в результате скрещивания потомок
наследует приблизительно (с округлением до целого) 90 % генов от первого
родителя и остальные гены (около 10%) - от второго родителя. Заметим, что для
показателя скрещивания равного 1 будет наблюдаться такой же эффект, что и при
отсутствии скрещивания, поскольку потомок будет наследовать все гены только от
первого родителя. По этой причине при выбранном значении данного показателя,
равном 0,9, скрещивание либо не будет проводиться вообще (точнее говоря, потомок
окажется абсолютно идентичным своему первому родителю), либо скрещивание будет
выполнено, и потомок унаследует большую часть генов от первого родителя. Для
мутации выбрана величина показателя мутации равная 0,1, которая указывает, что
значения 10% генов (с округлением до целого) должны подвергнуться случайным
изменениям.
С помощью программы Evolver сформирована следующая исходная популяция:
![]()
![]()
![]()
![]()
![]()
![]() .
.
После шести «тактов», т.е. для ![]() , что соответствует
одной итерации классического генетического алгоритма, получена популяция
особей, упорядоченных по убыванию функции приспособленности так, как это
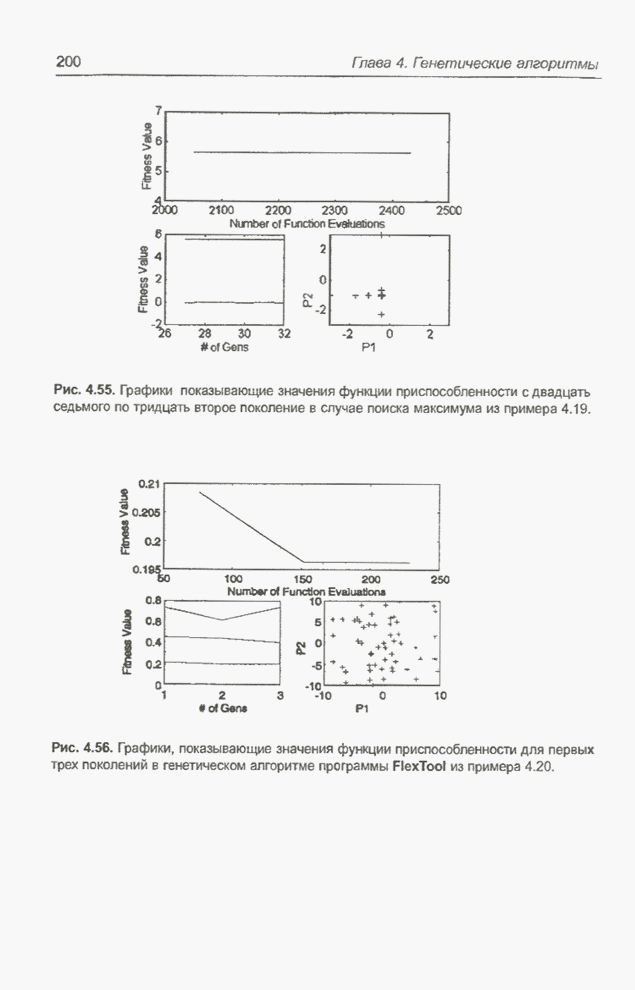
показано на рис. 4.68.
, что соответствует
одной итерации классического генетического алгоритма, получена популяция
особей, упорядоченных по убыванию функции приспособленности так, как это
показано на рис. 4.68.

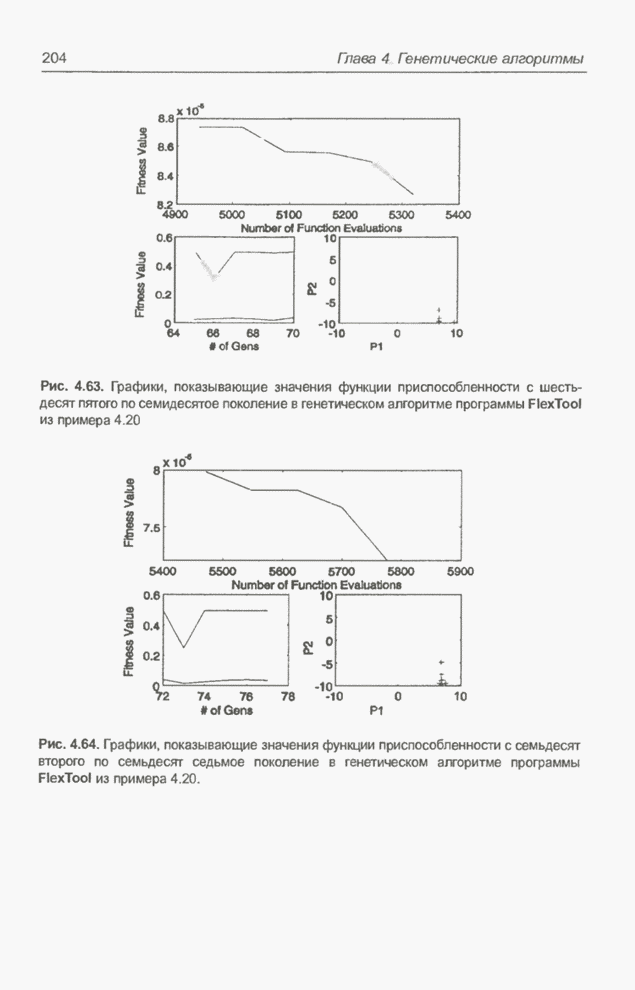
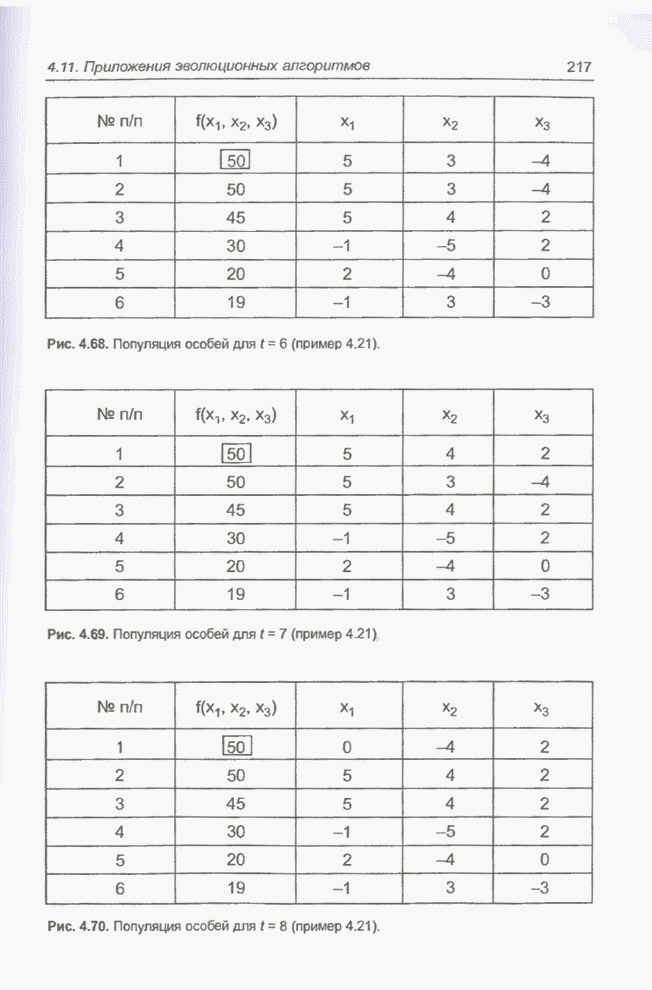
Рис. 4.68. Популяция особей для ![]() (пример 4.21).
(пример 4.21).
Отметим, что в популяцию не
входит особь ![]() со
значением функции приспособленности, равным 50. Она была исключена как
«наихудшая» особь (с наибольшим значением функции приспособленности), и на ее
место введена копия особи
со
значением функции приспособленности, равным 50. Она была исключена как
«наихудшая» особь (с наибольшим значением функции приспособленности), и на ее
место введена копия особи ![]() . Эта особь также оказывается
«наихудшей», поэтому она будет исключена на следующем «такте»
. Эта особь также оказывается
«наихудшей», поэтому она будет исключена на следующем «такте» ![]() . Популяции для
. Популяции для ![]() и
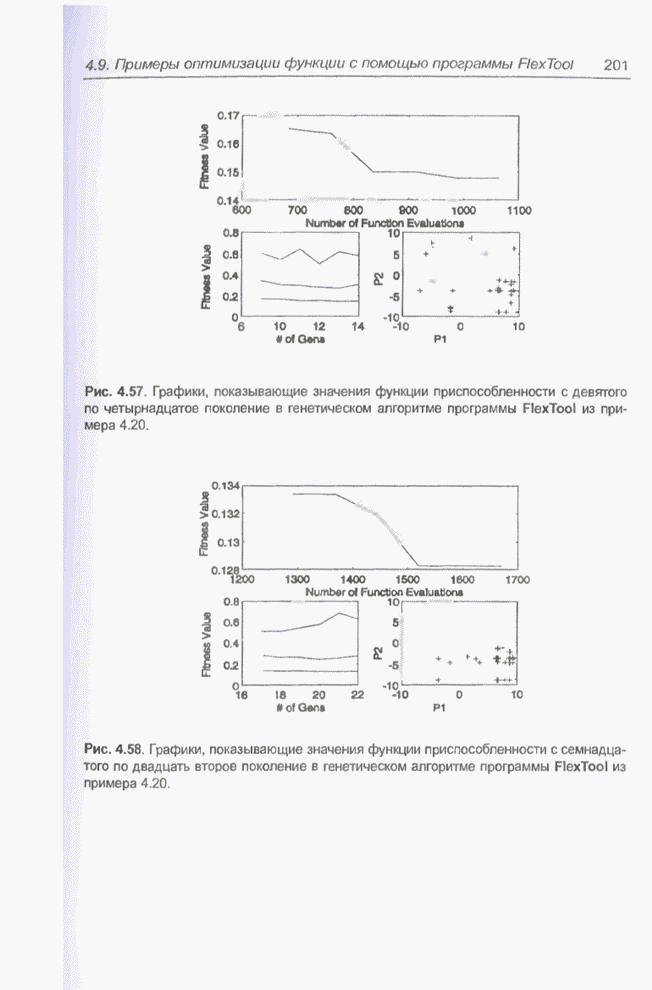
и ![]() представлены на рис. 4.69 и
4.70.
представлены на рис. 4.69 и
4.70.

Рис. 4.69. Популяция особей для ![]() (пример 4.21)
(пример 4.21)

Рис. 4.70. Популяция особей для ![]() (пример 4.21).
(пример 4.21).
На последнем месте (№ п/п = 6)
размещается «наилучшая к данному моменту» особь, имеющая наименьшее значение
функции приспособленности. На первом месте (№ п/п = 1) показана вновь введенная
в популяцию особь. На рис. 4.69 это копия особи ![]() из предыдущей популяции
из предыдущей популяции ![]() , а на рис. 4.70 -
новая особь
, а на рис. 4.70 -
новая особь ![]() ,
полученная в результате скрещивания с последующей мутацией от пары особей из
популяции для
,
полученная в результате скрещивания с последующей мутацией от пары особей из
популяции для ![]() .
Выделенное прямоугольником значение функции приспособленности в первой строке
таблицы относится к особи, исключаемой из популяции.
.
Выделенное прямоугольником значение функции приспособленности в первой строке
таблицы относится к особи, исключаемой из популяции.
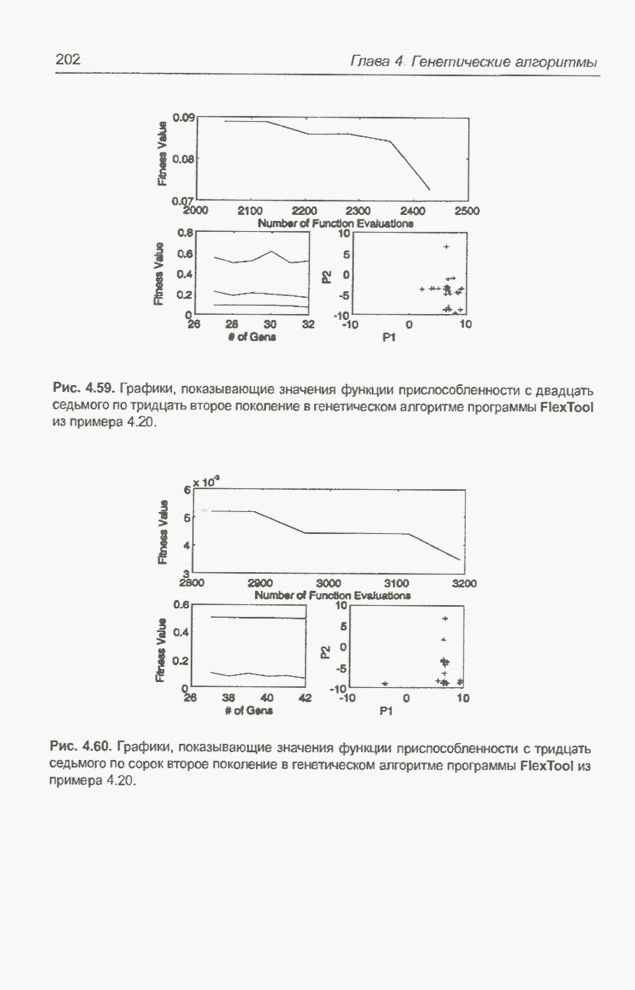
На рис. 4.71 и 4.72 представлены
популяции для ![]() и
и
![]() . Заметим,
что
. Заметим,
что ![]() соответствует
трем итерациям классического генетического алгоритма. Новая особь в популяции
на рис. 4.71 получена скрещиванием пары особей из предыдущей популяции (для
соответствует
трем итерациям классического генетического алгоритма. Новая особь в популяции
на рис. 4.71 получена скрещиванием пары особей из предыдущей популяции (для ![]() ), а новая особь в
популяции на рис. 4.72 сформирована в результате мутации среднего гена особи
), а новая особь в
популяции на рис. 4.72 сформирована в результате мутации среднего гена особи ![]() из предыдущей
популяции (для
из предыдущей
популяции (для ![]() ).
).

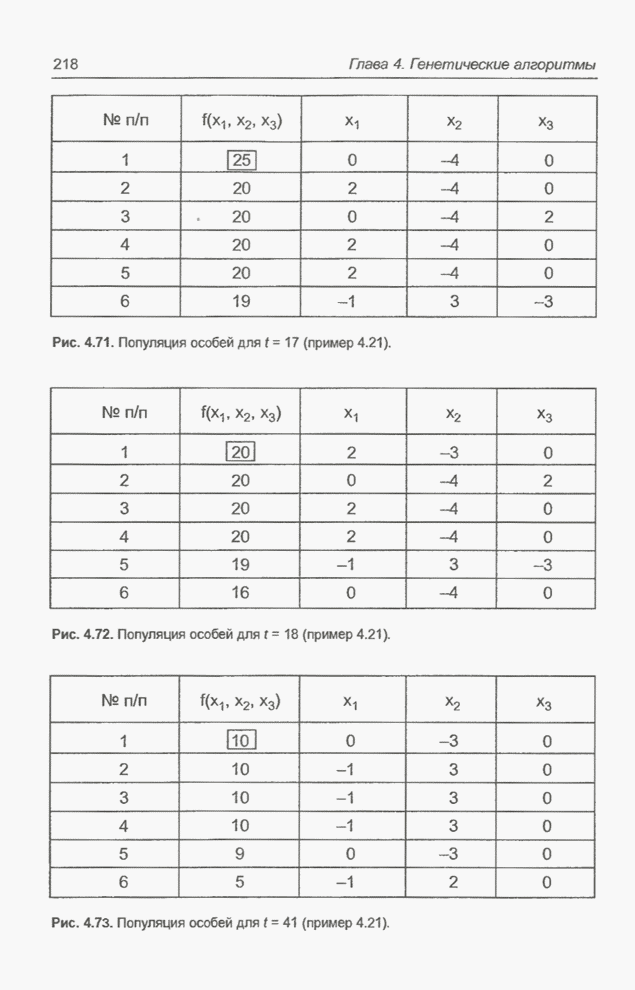
Рис. 4.71. Популяция особей для ![]() (пример 4.21).
(пример 4.21).

Рис. 4.72. Популяция особей для ![]() (пример 4.21).
(пример 4.21).
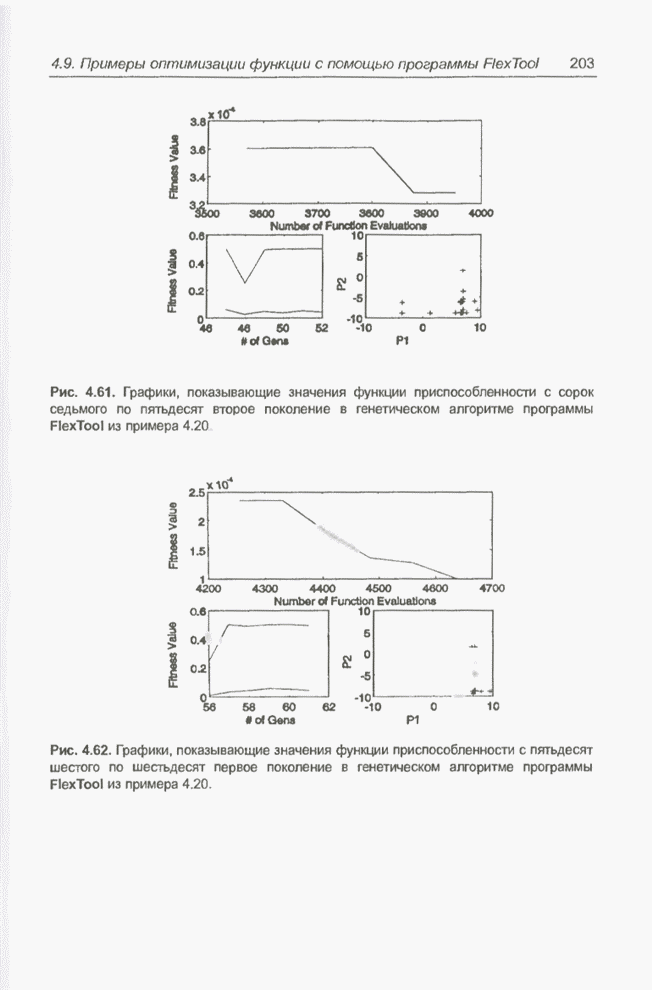
На рис. 4.73 показана популяция
для ![]() .
Обратим внимание, что
.
Обратим внимание, что ![]() соответствует семи итерациям
(поколениям) классического генетического алгоритма. «Наилучшее к данному
моменту» решение - это
соответствует семи итерациям
(поколениям) классического генетического алгоритма. «Наилучшее к данному
моменту» решение - это ![]() со значением функции приспособленности,
равным 5.
со значением функции приспособленности,
равным 5.

Рис. 4.73. Популяция особей для ![]() (пример 4.21).
(пример 4.21).
Получение «наилучшего» решения,
равного ![]() , с
нулевым значением функции приспособленности возможно в случае, если при дальнейшем
выполнении алгоритма произойдет мутация второго гена (замена -3, 3 или 2 на 0).
, с
нулевым значением функции приспособленности возможно в случае, если при дальнейшем
выполнении алгоритма произойдет мутация второго гена (замена -3, 3 или 2 на 0).
Следующий пример представляет собой обобщение предыдущего примера за счет увеличения количества переменных и расширения пространства поиска.
Пример 4.22
С помощью программы Evolver найти минимум функции
![]()
для
целочисленных ![]() в
интервале
в
интервале ![]() .
.
Вычисления производились для
популяции размерностью ![]() . Использовались принятые по умолчанию в
программе Evolver значения показателя скрещивания =0,5 и показателя мутации
=0,06. На рис. 4.74 представлена модель решения рассматриваемого примера в
табличном процессоре Excel, содержащая начальные значения переменных
. Использовались принятые по умолчанию в
программе Evolver значения показателя скрещивания =0,5 и показателя мутации
=0,06. На рис. 4.74 представлена модель решения рассматриваемого примера в
табличном процессоре Excel, содержащая начальные значения переменных ![]() .
.

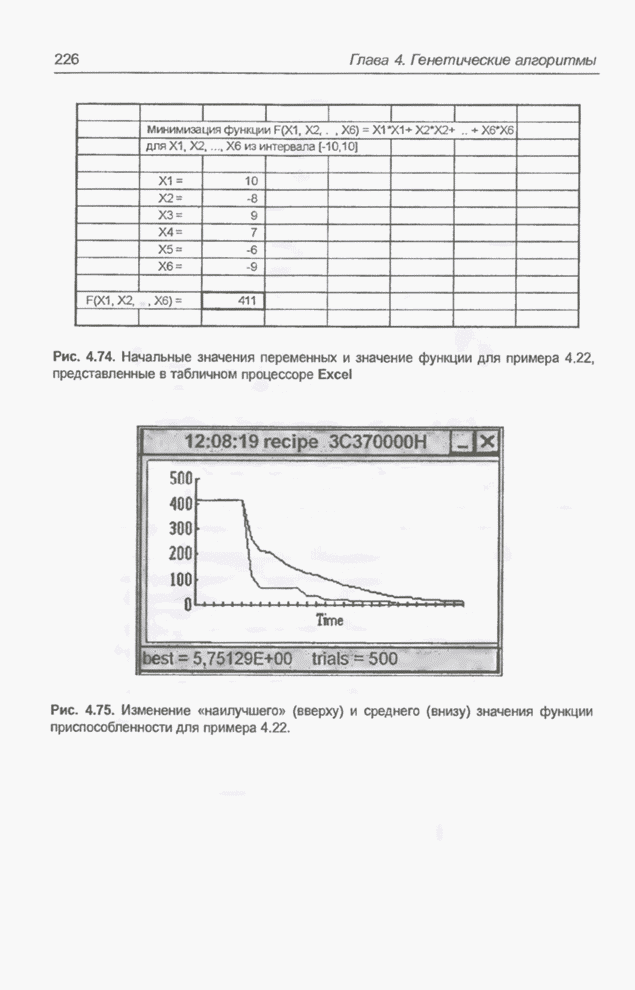
Рис. 4.74. Начальные значения переменных и значение функции для примера 4.22, представленные в табличном процессоре Excel.
В исходную популяцию включены 50
особей, первая из которых содержит гены со значениями, показанными на рис.
4.74, а остальные хромосомы сгенерированы случайным образом (гены имеют
действительные значения из интервала от -10 до 10). Длина каждой хромосомы
равна 6 и совпадает с количеством переменных ![]() . Заметно, что приведенные на рис. 4.74
начальные значения переменных
. Заметно, что приведенные на рис. 4.74
начальные значения переменных ![]() весьма далеки от оптимального решения,
которым для рассматриваемой задачи (также как и в примере 4.21) будет хромосома
с нулевыми значениями генов, т.е.
весьма далеки от оптимального решения,
которым для рассматриваемой задачи (также как и в примере 4.21) будет хромосома
с нулевыми значениями генов, т.е. ![]() . Поэтому не вызывает удивления то, что
хромосома с аллелями, показанными на рис. 4.74, очень быстро исключается из
популяции. На рис. 4.75 изображены графики изменения «наилучшего» (нижняя
кривая) и среднего (верхняя кривая) значения функции приспособленности с
течением времени (точнее, с увеличением количества «тактов»). На этом рисунке
един момент времени соответствует 20 «тактам». Для
. Поэтому не вызывает удивления то, что
хромосома с аллелями, показанными на рис. 4.74, очень быстро исключается из
популяции. На рис. 4.75 изображены графики изменения «наилучшего» (нижняя
кривая) и среднего (верхняя кривая) значения функции приспособленности с
течением времени (точнее, с увеличением количества «тактов»). На этом рисунке
един момент времени соответствует 20 «тактам». Для ![]() (через 500 «тактов») наилучшее
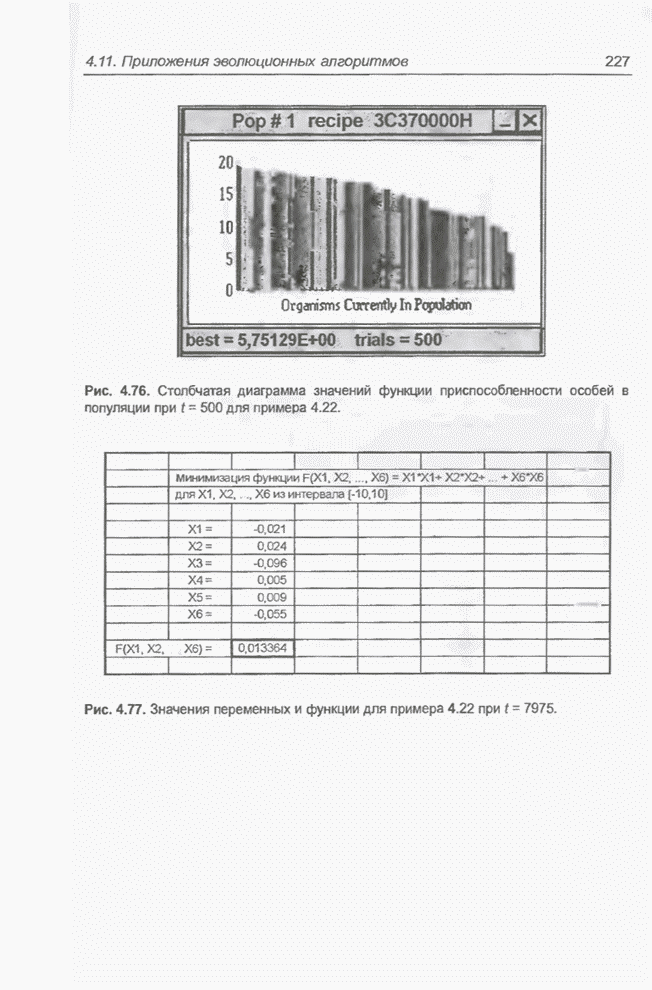
значение функции приспособленности было равно 5,75129. На рис. 4.76 в виде
столбчатой диаграммы показаны значения функции приспособленности всех особей
популяции для
(через 500 «тактов») наилучшее
значение функции приспособленности было равно 5,75129. На рис. 4.76 в виде
столбчатой диаграммы показаны значения функции приспособленности всех особей
популяции для ![]() .
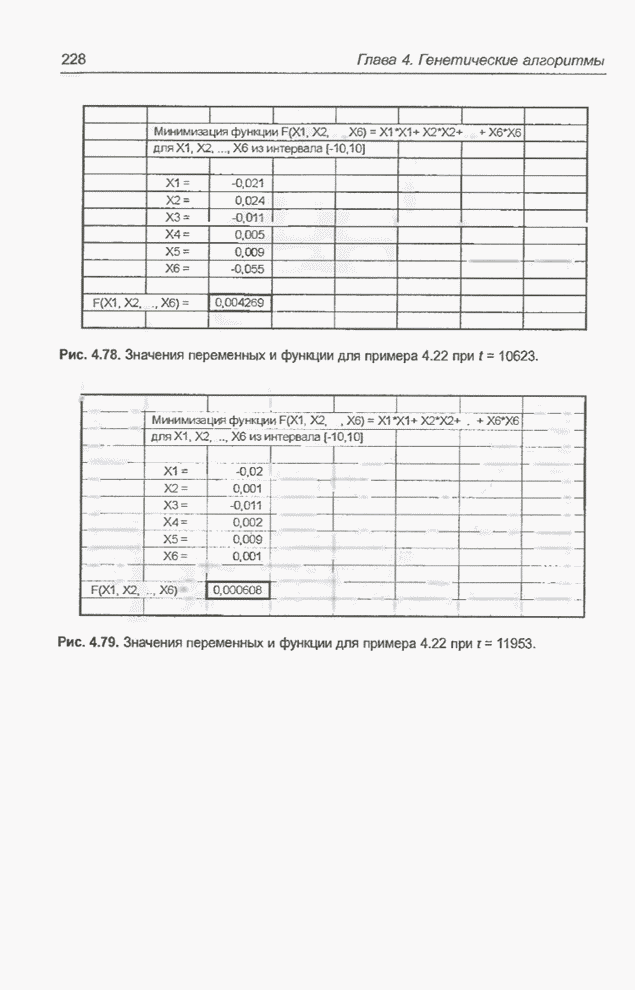
Рис. 4.77 представляет значения переменных
.
Рис. 4.77 представляет значения переменных ![]() и соответствующее им значение
минимизируемой функции, полученное после 7975 «тактов» выполнения программы
Evolver. На рис. 4.78 и 4.79 приведены аналогичные результаты, но после 10623 и
11953 «тактов». Их сопоставление показывает, как получаемые решения
приближаются к оптимальному. Рис. 4.80 демонстрирует «наилучшее решение»,
выработанное после примерно 15000 «тактов» выполнения программы Evolver.
Последующая работа программы уже не изменяет полученный результат. Итоговая
популяция содержит 50 особей со значениями
и соответствующее им значение
минимизируемой функции, полученное после 7975 «тактов» выполнения программы
Evolver. На рис. 4.78 и 4.79 приведены аналогичные результаты, но после 10623 и
11953 «тактов». Их сопоставление показывает, как получаемые решения
приближаются к оптимальному. Рис. 4.80 демонстрирует «наилучшее решение»,
выработанное после примерно 15000 «тактов» выполнения программы Evolver.
Последующая работа программы уже не изменяет полученный результат. Итоговая
популяция содержит 50 особей со значениями ![]() , показанными на рис. 4.80.
, показанными на рис. 4.80.

Рис. 4.75. Изменение «наилучшего» (вверху) и среднего (внизу) значения функции приспособленности для примера 4.22.

Рис. 4.76. Столбчатая диаграмма
значений функции приспособленности особей в популяции при ![]() для примера 4.22.
для примера 4.22.

Рис. 4.77. Значения переменных и
функции для примера 4.22 при ![]() .
.

Рис. 4.78. Значения переменных и
функции для примера 4.22 при ![]() .
.

Рис. 4.79. Значения переменных и
функции для примера 4.22 при ![]() .
.

Рис. 4.80. Значения переменных и
функции для примера 4.22 при ![]() .
.
Повторное возобновление этого
алгоритма при тех же начальных данных (рис. 4.74), но других случайных
значениях остальных членов исходной популяции дает совершенно иной набор
«наилучших» значений переменных ![]() , которые тоже близки к оптимальным.
, которые тоже близки к оптимальным.
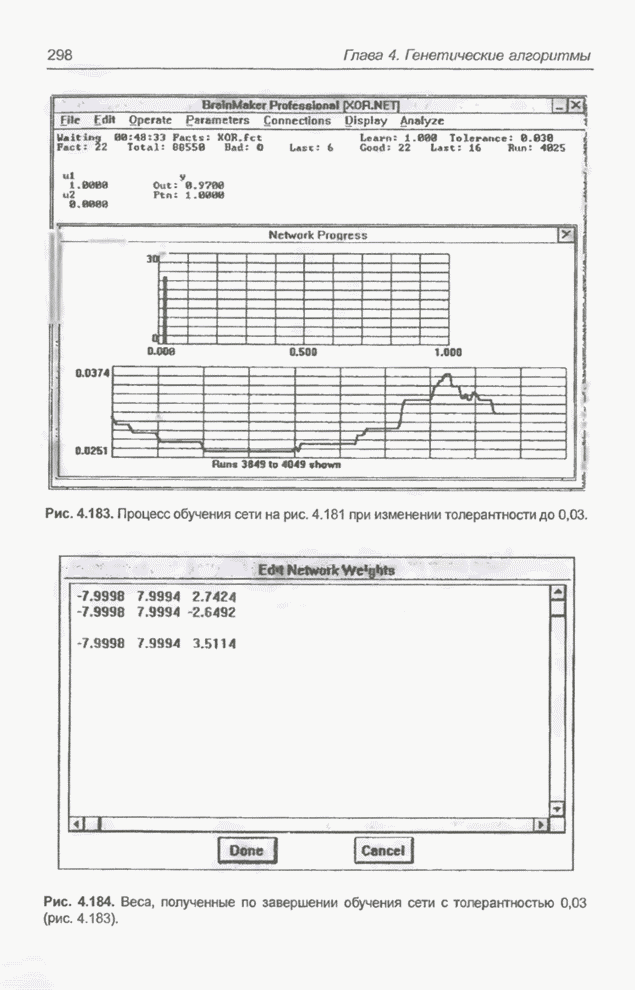
Следующие примеры связаны с минимизацией более сложной функции 9 переменных, а именно - функции погрешности нейронной сети, реализующей логическую систему XOR.
Пример 4.23
С помощью программы Evolver найти оптимальный набор весов нейронной сети, изображенной на рис. 4.2 (пример 4.3), если значения весов лежат в интервале от -5 до 5.
Решение этой задачи заключается в
подборе такого комплекса значений весов ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , a также
, a также ![]() ,
, ![]() ,
, ![]() , который минимизирует значение
погрешности
, который минимизирует значение
погрешности ![]() ,
заданной в примере 4.3. Это средняя сумма квадратов разностей между ожидаемым и
расчетным значением на выходе системы XOR для каждой из четырех пар входов,
указанных в табл. 2.1. Задача сводится к минимизации функции
,
заданной в примере 4.3. Это средняя сумма квадратов разностей между ожидаемым и
расчетным значением на выходе системы XOR для каждой из четырех пар входов,
указанных в табл. 2.1. Задача сводится к минимизации функции

относительно
определенных выше девяти весов, где ![]() для
для ![]() , а
, а ![]() рассчитывается по формуле
рассчитывается по формуле

Примем,
что ![]() .
.
Задача моделировалась в табличном
процессоре Excel, а оптимизация выполнялась при помощи генетического алгоритма
программы Evolver. Для популяции с размерностью, равной 50, при значениях
показателя скрещивания равного 0,5 и показателя мутации равного 0,06 после
примерно 30000 «тактов» получено «наилучшее решение» в виде набора весов,
показанного на рис. 4.81. Минимальное значение абсолютной погрешности ![]() для этих весов
составляет 0,015171.
для этих весов
составляет 0,015171.

Рис. 4.81. «Наилучший» набор
весов из интервала ![]() для
нейронной сети, реализующей систему XOR (пример 4.23).
для
нейронной сети, реализующей систему XOR (пример 4.23).
Необходимо отметить, что
полученное «наилучшее решение» близко набору весов ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , для которого
, для которого ![]() . Нейронная сеть (см. рис. 4.2)
с такими весами демонстрирует симметрию, характерную для системы XOR. Очевидно,
что найден не единственный оптимальный набор весов для сети этого типа [31].
При повторном запуске программы с той же самой размерностью популяции и такими
же показателями скрещивания и мутации, скорее всего, будет найдено «наилучшее
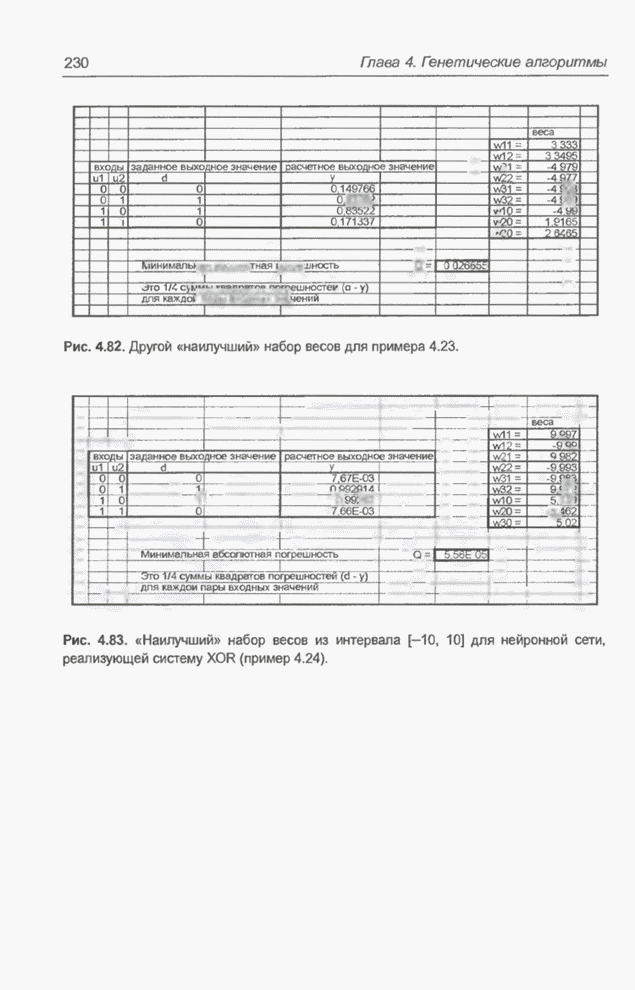
решение», содержащее иной «оптимальный» набор весов. На рис. 4.82 приведен
пример альтернативного «наилучшего» набора весов, полученного при повторном
выполнении генетического алгоритма программы Evolver и проведении вычислений на
протяжении 6000 «тактов». При известных допустимых комбинациях весов для
системы XOR [31], легко предсказать оптимальный набор весов, к которому
стремится решение при продолжении выполнения этого алгоритма.
. Нейронная сеть (см. рис. 4.2)
с такими весами демонстрирует симметрию, характерную для системы XOR. Очевидно,
что найден не единственный оптимальный набор весов для сети этого типа [31].
При повторном запуске программы с той же самой размерностью популяции и такими
же показателями скрещивания и мутации, скорее всего, будет найдено «наилучшее
решение», содержащее иной «оптимальный» набор весов. На рис. 4.82 приведен
пример альтернативного «наилучшего» набора весов, полученного при повторном
выполнении генетического алгоритма программы Evolver и проведении вычислений на
протяжении 6000 «тактов». При известных допустимых комбинациях весов для
системы XOR [31], легко предсказать оптимальный набор весов, к которому
стремится решение при продолжении выполнения этого алгоритма.

Рис. 4.82. Другой «наилучший» набор весов для примера 4.23.
Следующие примеры относятся к той же задаче, однако при расширенном диапазоне изменения весов.
Пример 4.24
С помощью программы Evolver найти оптимальный набор весов нейронной сети, изображенной на рис. 4.2 (пример 4.3), если значения весов лежат в интервале от -10 до 10.
При начальных значениях,
совпадающих с приведенными в примере 4.23, было проведено три сеанса
вычислений. Через 30000 «тактов» в первом, втором и третьем сеансах получены
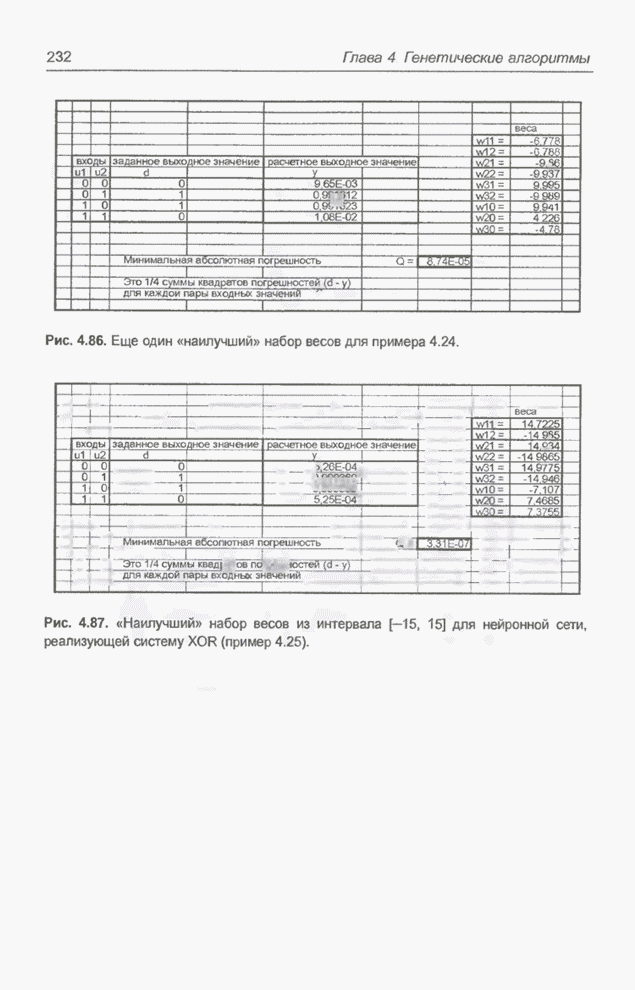
«наилучшие» решения, показанные на рис. 4.83, 4.84 и 4.86 соответственно. На
рис. 4.85 изображены графики изменения «наилучшего» (нижняя кривая) и среднего
(верхняя кривая) значения функции приспособленности для этого примера после 505
«тактов». Функция приспособленности для системы XOR задается формулой расчета
погрешности ![]() (см.
пример 4.23) и изменяется в пределах от 0 до 1. На рис. 4.85 заметно
стремительное уменьшение наилучшего значения функции приспособленности до
«наилучшего на данный момент» значения, равного 0,13159. Единица на временной
оси этого графика соответствует 20 «тактам». Набор весов, к которому стремится
«наилучшее решение», характеризуется тем, что
(см.
пример 4.23) и изменяется в пределах от 0 до 1. На рис. 4.85 заметно
стремительное уменьшение наилучшего значения функции приспособленности до
«наилучшего на данный момент» значения, равного 0,13159. Единица на временной
оси этого графика соответствует 20 «тактам». Набор весов, к которому стремится
«наилучшее решение», характеризуется тем, что ![]() и
и ![]() , что типично для логической системы XOR
[31]. Результаты, представленные на рис. 4.83 и 4.84, можно сравнить с
показанными на рис. 4.81 для примера 4.23, а информацию на рис. 4.86 -
сопоставить с рис. 4.82.
, что типично для логической системы XOR
[31]. Результаты, представленные на рис. 4.83 и 4.84, можно сравнить с
показанными на рис. 4.81 для примера 4.23, а информацию на рис. 4.86 -
сопоставить с рис. 4.82.

Рис. 4.83. «Наилучший» набор
весов из интервала ![]() для
нейронной сети, реализующей систему XOR (пример 4.24).
для
нейронной сети, реализующей систему XOR (пример 4.24).

Рис. 4.84. Другой «наилучший» набор весов для примера 4.24.

Рис. 4.85. Изменение «наилучшего» и среднего значения функции приспособленности для примера 4.22.

Рис. 4.86. Еще один «наилучший» набор весов для примера 4.24.
Заметим, что минимальная погрешность во всех трех случаях (рис. 4.83, 4.84 и 4.86) оказывается значительно меньше, чем для интервала изменения от -5 до 5, рассмотренного в примере 4.23 (рис. 4.81 и 4.82).
Пример 4.25
С помощью программы Evolver найти оптимальный набор весов нейронной сети, изображенной на рис. 4.2 (пример 4.3), если значения весов лежат в интервале от -15 до 15.
Применялся тот же генетический алгоритм программы Evolver, что и в предыдущих примерах, но для расширенного интервала изменения весов. После 30000 «тактов» получено «наилучшее решение», показанное на рис. 4.87.

Рис. 4.87. «Наилучший» набор
весов из интервала ![]() для
нейронной сети, реализующей систему XOR (пример 4.25).
для
нейронной сети, реализующей систему XOR (пример 4.25).
Повторное выполнение того же
алгоритма при тех же начальных условиях через 30000 «тактов» дало «наилучший»
набор весов, представленный на рис. 4.88. Главное различие между решениями на
рис. 4.87 и 4.88 заключается в том, что в первом случае веса ![]() и
и ![]() положительны, а веса
положительны, а веса ![]() и
и ![]() отрицательны, тогда как во
втором случае ситуация оказалась противоположной. В рассматриваемом примере
получены две из множества возможных комбинаций весов для нейронной сети,
реализующей систему XOR [31]. Еще одно альтернативное решение приведено на рис.
4.89. Значения входящих в него весов получены после примерно 12000 «тактов».
Несложно предугадать, как будут изменяться эти значения при увеличении
количества «тактов». Следовательно, это еще одна комбинация, подобная решениям
на рисунках 4.87 и 4.88, причем в данном случае веса
отрицательны, тогда как во
втором случае ситуация оказалась противоположной. В рассматриваемом примере
получены две из множества возможных комбинаций весов для нейронной сети,
реализующей систему XOR [31]. Еще одно альтернативное решение приведено на рис.
4.89. Значения входящих в него весов получены после примерно 12000 «тактов».
Несложно предугадать, как будут изменяться эти значения при увеличении
количества «тактов». Следовательно, это еще одна комбинация, подобная решениям
на рисунках 4.87 и 4.88, причем в данном случае веса ![]() ,
, ![]() ,
, ![]() и
и ![]() положительны, а веса
положительны, а веса ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() отрицательны.
отрицательны.

Рис. 4.88. Другой «наилучший» набор весов для примера 4.25.

Рис. 4.89. Еще один «наилучший» набор весов для примера 4.25 (получен после примерно 12000 «тактов»).
Пример 4.26
С помощью программы Evolver найти оптимальный набор весов нейронной сети, изображенной на рис. 4.2 (пример 4.3), если значения весов лежат в интервале от -20 до 20.
Это та же задача, что и в
предыдущих примерах, однако интервал изменения весов значительно расширен.
Задача решалась при той же размерности популяции и таких же значениях
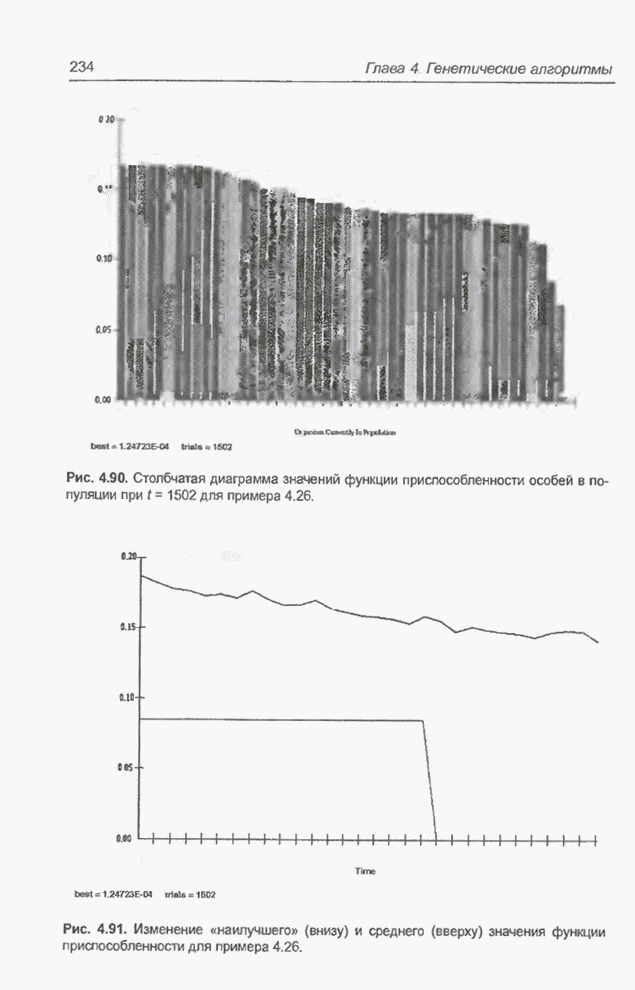
показателей скрещивания и мутации, как и в предыдущих примерах. Столбчатая
диаграмма на рис. 4.90 демонстрирует значения функции приспособленности особей
в популяции после примерно 1500 «тактов». Конечно, это значения в интервале от
0 до 1. На рис. 4.91 изображены графики изменения «наилучшего» (нижняя кривая)
и среднего (верхняя кривая) значения функции приспособленности для этого
примера после примерно 1500 «тактов». Единица на временной оси этого графика
соответствует 20 «тактам». «Наилучшее на данный момент» (после 1502 «тактов»)
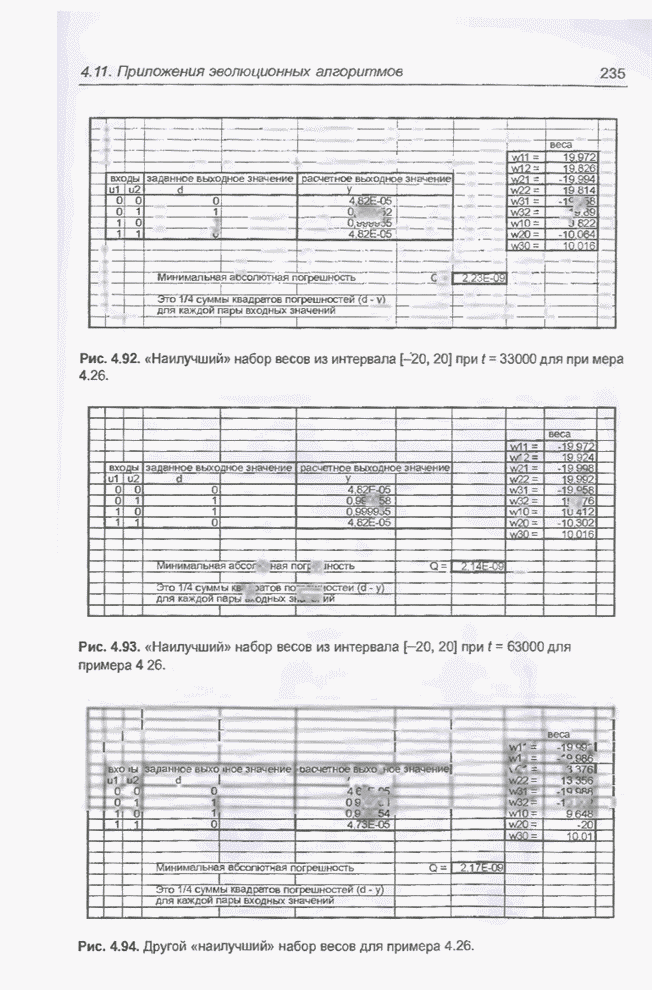
значение функции приспособленности составляет ![]() . Рис. 4.92 представляет «наилучший»
набор весов, полученный после 33000 «тактов», а рис. 4.93 - после 63000
«тактов». Заметно, что значения соединительных весов стремятся к 20 или к -20,
а значения
. Рис. 4.92 представляет «наилучший»
набор весов, полученный после 33000 «тактов», а рис. 4.93 - после 63000
«тактов». Заметно, что значения соединительных весов стремятся к 20 или к -20,
а значения ![]() ,
,
![]() и
и ![]() - соответственно к
10, -10, 10. Если продолжить выполнение алгоритма, то при дальнейшем увеличении
количества «тактов» некоторые веса примут значения, равные 20. Очевидно, что
наборы весов на рис. 4.92 и 4.93 представляют собой лишь два элемента из
множества допустимых комбинаций весов нейронной сети, реализующей логическую
систему XOR. На рис. 4.94 показан совершенно другой набор «наилучших» весов,
полученных при очередном возобновлении генетического алгоритма программы
Evolver. Результаты зафиксированы после примерно 15000 тактов при тех же, что и
прежде, размерности популяции, значениях показателей скрещивания и мутации и
интервале изменения весов.
- соответственно к
10, -10, 10. Если продолжить выполнение алгоритма, то при дальнейшем увеличении
количества «тактов» некоторые веса примут значения, равные 20. Очевидно, что
наборы весов на рис. 4.92 и 4.93 представляют собой лишь два элемента из
множества допустимых комбинаций весов нейронной сети, реализующей логическую
систему XOR. На рис. 4.94 показан совершенно другой набор «наилучших» весов,
полученных при очередном возобновлении генетического алгоритма программы
Evolver. Результаты зафиксированы после примерно 15000 тактов при тех же, что и
прежде, размерности популяции, значениях показателей скрещивания и мутации и
интервале изменения весов.

Рис. 4.90. Столбчатая диаграмма
значений функции приспособленности особей в популяции при ![]() для примера 4.26.
для примера 4.26.

Рис. 4.91. Изменение «наилучшего» (внизу) и среднего (вверху) значения функции приспособленности для примера 4.26.

Рис. 4.92. «Наилучший» набор
весов из интервала ![]() при
при
![]() для примера
4.26.
для примера
4.26.

Рис. 4.93. «Наилучший» набор
весов из интервала ![]() при
при
![]() для примера
4 26.
для примера
4 26.

Рис. 4.94. Другой «наилучший» набор весов для примера 4.26.
Отметим, что «наилучшее решение»
на рис. 4.94 тоже представляет собой одну из допустимых комбинаций весов
системы XOR [31], поскольку оно стремится к оптимальному решению, в котором ![]() и
и ![]() .
.
Из примеров 4.23 - 4.26 следует
вывод, что чем больше интервал изменения весов, тем меньше минимальное значение
погрешности. Поэтому для получения нейронной сети, которая сможет наиболее
точно реализовать систему XOR (т.е. для которой разность между эталонным и
расчетным выходными значениями будет минимальной), необходимо подбирать веса из
как можно более широкого интервала допустимых значений. Очевидно, что подбор
этих весов должен быть оптимальным и минимизировать погрешность так, как это
делалось в примерах 4.23 - 4.26. Если бы требовалось выбирать значения весов из
интервала, более узкого, чем ![]() , то обеспечить минимальную погрешность в
пределах, например, 0,1, оказалось бы еще сложнее. На рис. 4.95 показан
«наилучший» набор весов, найденный также как в примерах 4.23 - 4.26, но для
интервала
, то обеспечить минимальную погрешность в
пределах, например, 0,1, оказалось бы еще сложнее. На рис. 4.95 показан
«наилучший» набор весов, найденный также как в примерах 4.23 - 4.26, но для
интервала ![]() .
После 40000 «тактов» минимальное значение погрешности превышало 0,1. Заметим,
что для интервала изменения весов от -20 до 20 можно достичь погрешности
порядка
.
После 40000 «тактов» минимальное значение погрешности превышало 0,1. Заметим,
что для интервала изменения весов от -20 до 20 можно достичь погрешности
порядка ![]() уже
через 1500 «тактов» (рис. 4.90 и 4.91), а для интервала
уже
через 1500 «тактов» (рис. 4.90 и 4.91), а для интервала ![]() минимальная погрешность на
уровне 0,1 была достигнута уже через 500 «тактов» (рис. 4.85). В примерах 4.23
- 4.26 начальные значения весов, которые учитываются программой Evolver в
качестве генов одной из особей исходной популяции, в общем случае принимаются
равными 1. Для нейронной сети, изображенной на рис. 4.2, в этом случае величина
погрешности будет составлять
минимальная погрешность на
уровне 0,1 была достигнута уже через 500 «тактов» (рис. 4.85). В примерах 4.23
- 4.26 начальные значения весов, которые учитываются программой Evolver в
качестве генов одной из особей исходной популяции, в общем случае принимаются
равными 1. Для нейронной сети, изображенной на рис. 4.2, в этом случае величина
погрешности будет составлять ![]() , что сильно отличается от минимального
значения. Конечно, можно принять и другие начальные значения, далекие от
оптимальных.
, что сильно отличается от минимального
значения. Конечно, можно принять и другие начальные значения, далекие от
оптимальных.

Рис. 4.95. «Наилучший» набор
весов из интервала ![]() для
нейронной сети, реализующей систему XOR (пример 4.26).
для
нейронной сети, реализующей систему XOR (пример 4.26).
Пример 4.27
С помощью программы Evolver найти оптимальный набор весов нейронной сети, изображенной на рис. 4.2 (пример 4.3), если значения весов лежат в интервале от -7 до 8.
Начальные значения весов,
составляющие генотип одной из особей исходной популяции, представлены на рис.
4.96. Видно, что значения ![]() для конкретных пар входов совершенно не
соответствуют функции XOR. Значение погрешности
для конкретных пар входов совершенно не
соответствуют функции XOR. Значение погрешности ![]() считается абсолютно неудовлетворительным.
считается абсолютно неудовлетворительным.

Рис. 4.96. Начальные значения весов для примера 4.27.
Для решения задачи применялся тот же генетический алгоритм при той же размерности популяции и тех же показателях скрещивания и мутации, что и в предыдущих примерах. Всего лишь через 96 «тактов» получены наилучшие значения функции приспособленности конкретных особей в популяции, показанные на рис. 4.97 (столбчатая диаграмма). В свою очередь, на рис. 4.98 представлена таблица, содержащая генотипы всех 50 особей этой популяции (состоящие из девяти действительных чисел, соответствующих конкретным весам) и значения их функции приспособленности, размещенные в первой колонке.

Рис. 4.97. Столбчатая диаграмма
значений функции приспособленности особей в популяции при ![]() для примера 4.27.
для примера 4.27.

Рис. 4.98. Популяция особей при ![]() для примера 4.27.
для примера 4.27.
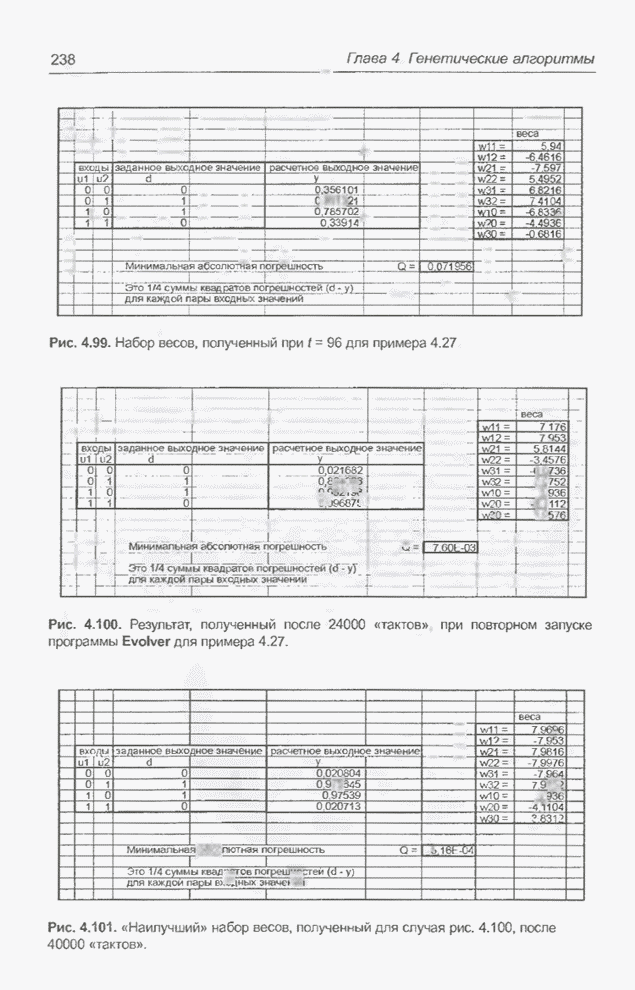
Обратим внимание на то, что начальная хромосома с аллелями, равными значениям весов из рис. 4.96, расположена в средней части этой таблицы и обозначена «Организм 25». Следует помнить, что особи в популяции упорядочены от «наихудшего» к «наилучшему». Последняя особь («Организм 50») – это хромосома, «наилучшая на данный момент», т.е. после 96 «тактов». Значения весов, входящих в состав этой хромосомы, показаны на рис. 4.99 вместе с выходными значениями для конкретных пар входов и значением минимизируемой погрешности. Итак, после 96 «тактов» получен исключительно хороший результат.

Рис. 4.99. Набор весов,
полученный при ![]() для
примера 4.27
для
примера 4.27
При повторном выполнении этой же
программы с самого начала при том же исходном наборе весов (рис. 4.96) через
примерно 10000 «тактов» получена погрешность ![]() , через 20000 «тактов» -
, через 20000 «тактов» - ![]() , а через 21000
«тактов» -
, а через 21000
«тактов» - ![]() .
После 24000 тактов эта погрешность уменьшилась до значения
.
После 24000 тактов эта погрешность уменьшилась до значения ![]() (рис. 4.100), а после 40000
«тактов» получен «наилучший» набор весов, показанный на рис. 4.101.
(рис. 4.100), а после 40000
«тактов» получен «наилучший» набор весов, показанный на рис. 4.101.

Рис. 4.100. Результат, полученный после 24000 «тактов» при повторном запуске программы Evolver для примера 4.27.

Рис. 4.101. «Наилучший» набор весов, полученный для случая рис. 4.100, после 40000 «тактов».
Таким образом, процессы выполнения одного и того же алгоритма при одинаковой размерности популяции и повторяющихся значениях показателей скрещивания и мутации оказываются совершенно различными. Это, конечно, определяется случайным набором особей исходной популяции и случайным проведением скрещивания и мутации.
Для случая на рис. 4.99 получен
результат, подобный представленному на рис. 4.101, причем веса ![]() ,
, ![]() ,
, ![]() , а также
, а также ![]() и
и ![]() имеют противоположные знаки.
имеют противоположные знаки.
При использовании генетического
алгоритма программы Evolver для решения задач, аналогичных рассмотренным в примерах
4.23 - 4.27, генетические операторы изменяют значения отдельных весов (мутация)
и осуществляют обмен значений весов, выбранных случайным образом, между двумя
хромосомами (скрещивание). В то же время, в программе FlexTool (пример 4.20)
генетические операторы рекомбинируют гены внутри хромосом, которые представляют
собой двоичные последовательности, соответствующие закодированным значениям
конкретных весов. В программе Evolver хромосомы состоят из генов, имеющих
действительные значения, совпадающие со значениями весов. Программа Evolver -
это прекрасный инструмент для оптимизации функции нескольких переменных, при
этом она может применяться для поиска максимума или минимума функции двух и
даже одной переменной. Заметим, что в случае только одной переменной
скрещивание практически не производится, и выполняется только операция мутации,
что характерно для так называемого эволюционного программирования (см. разд.
4.10). Все примеры, решенные в разд. 4.9 при помощи программы FlexTool, можно
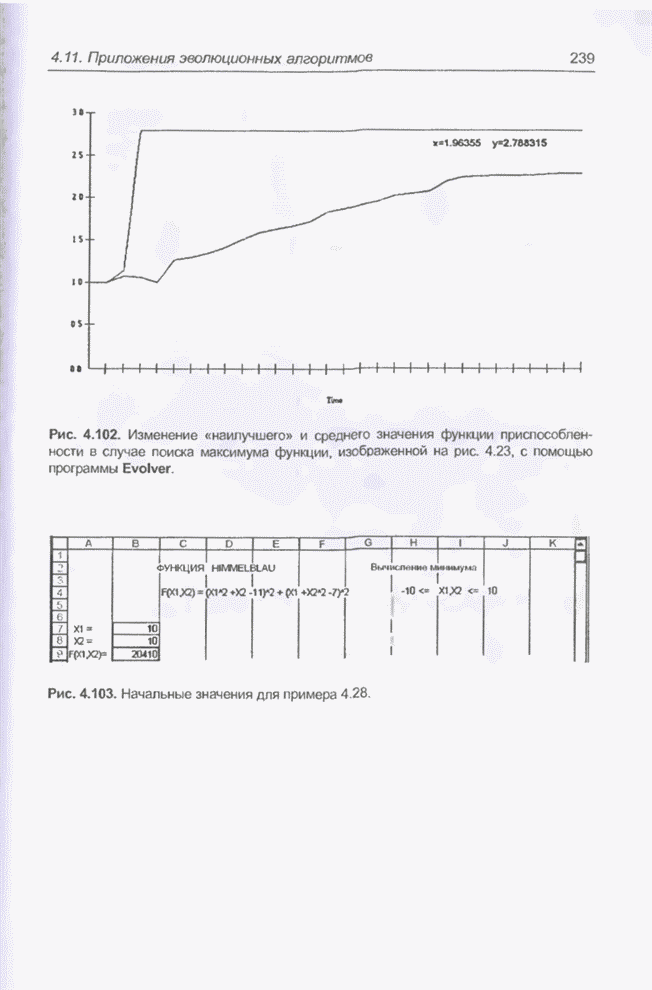
решать также и средствами программы Evolver. Например, на рис. 4.102 показано
изменение «наилучшего» и среднего значения функции приспособленности в случае
поиска максимума функции, представленной на рис. 4.23. Одно деление на
временной оси соответствует 20 «тактам». Вычисления проводились с принятыми по
умолчанию значениями показателей скрещивания (0,5) и мутации (0,06), а также
размерности популяции (50). Графики и «наилучшие» решения регистрировались
после 700 «тактов» ![]() .
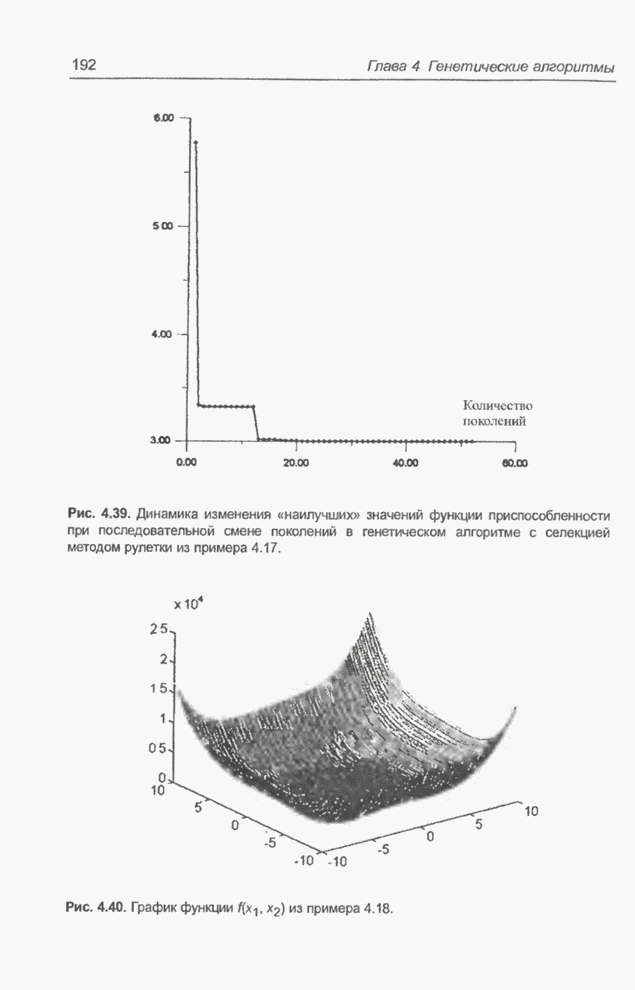
Пример 4.28 посвящен оптимизации функции двух переменных, график которой
изображен на рис. 4.40.
.
Пример 4.28 посвящен оптимизации функции двух переменных, график которой
изображен на рис. 4.40.

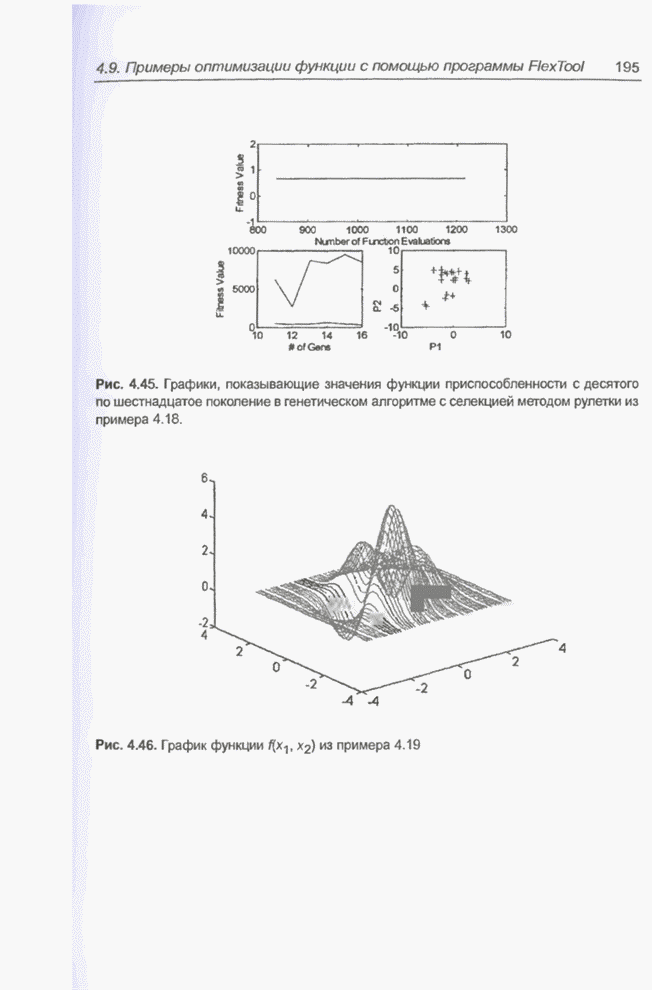
Рис. 4.102. Изменение «наилучшего» и среднего значения функции приспособленности в случае поиска максимума функции, изображенной на рис 4.23, с помощью программы Evolver.
Пример 4.28
С помощью программы Evolver найти минимум функции из примера 4.18.
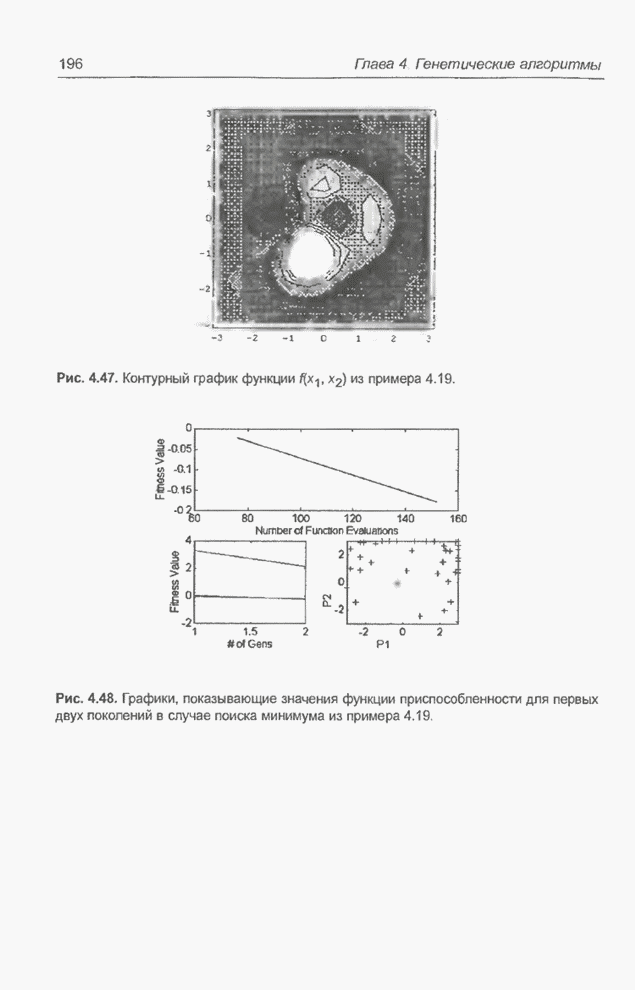
График этой функции изображен на
рис. 4.40. В примере 4.18 приведены координаты четырех точек, в которых эта
функция имеет минимальное значение, равное 0. Генетический алгоритм должен найти
одну из этих точек. Применяется программа Evolver с принятыми по умолчанию
значениями показателей скрещивания (0,5) и мутации (0,06). Размерность
популяции выбрана равной 30. На рис. 4.103 представлены начальные значения
переменных ![]() и
и
![]() , которые
введены в исходную популяцию в качестве генов одной из хромосом Значение
функции приспособленности для этой хромосомы очень велико - оно составляет
20410. Понятно, что данная хромосома будет очень скоро исключена из популяции,
что подтверждается рис. 4.104. На этом рисунке показаны хромосомы популяции для
, которые
введены в исходную популяцию в качестве генов одной из хромосом Значение
функции приспособленности для этой хромосомы очень велико - оно составляет
20410. Понятно, что данная хромосома будет очень скоро исключена из популяции,
что подтверждается рис. 4.104. На этом рисунке показаны хромосомы популяции для
![]() (после 30
«тактов»), что соответствует первой итерации (первому поколению) классического
генетического алгоритма. Переменные
(после 30
«тактов»), что соответствует первой итерации (первому поколению) классического
генетического алгоритма. Переменные ![]() и
и ![]() обозначают соответственно
обозначают соответственно ![]() и
и ![]() , первый столбец (result)
содержит значения функции приспособленности конкретных хромосом. Первое
значение (20410) принадлежит особи, исключенной из популяции. На ее место
вводится новая хромосома с аллелями, равными 7,89 и -1,537, для которой
значение функции приспособленности еще только предстоит рассчитать. В левом
нижнем углу рисунка демонстрируется разнородность особей этой популяции. В
данном случае она также довольно велика. На рис. 4.105 приведены аналогичные
графики для популяции после 60 «тактов»
, первый столбец (result)
содержит значения функции приспособленности конкретных хромосом. Первое
значение (20410) принадлежит особи, исключенной из популяции. На ее место
вводится новая хромосома с аллелями, равными 7,89 и -1,537, для которой
значение функции приспособленности еще только предстоит рассчитать. В левом
нижнем углу рисунка демонстрируется разнородность особей этой популяции. В
данном случае она также довольно велика. На рис. 4.105 приведены аналогичные
графики для популяции после 60 «тактов» ![]() , а также столбчатая диаграмма,
иллюстрирующая конкретные особи. «Наилучшее на данный момент» значение функции
приспособленности все еще слишком велико и составляет 28,3.
, а также столбчатая диаграмма,
иллюстрирующая конкретные особи. «Наилучшее на данный момент» значение функции
приспособленности все еще слишком велико и составляет 28,3.

Рис. 4.103. Начальные значения для примера 4.28.

Рис. 4.104. Популяция особей при ![]() для примера 4.28.
для примера 4.28.

Рис. 4.105. Популяция особей при ![]() для примера 4.28.
для примера 4.28.
На рис. 4.106 представлены те же
графики после 150 «тактов» ![]() , дополненные (в левом нижнем углу)
графиком изменения «наилучшего» значения функции приспособленности, которое
стремительно уменьшается. В средней части слева показана разнородность
популяции, которая также значительно снизилась.
, дополненные (в левом нижнем углу)
графиком изменения «наилучшего» значения функции приспособленности, которое
стремительно уменьшается. В средней части слева показана разнородность
популяции, которая также значительно снизилась.

Рис. 4.106. Популяция особей и
график функции приспособленности при ![]() для примера 4.28.
для примера 4.28.
Еще меньшая разнородность
популяции наблюдается на рис. 4.107, который содержит также столбчатую
диаграмму и значения генов конкретных хромосом популяции. «Наименьшее» значение
функции приспособленности здесь составляет 5,83 для ![]() , т.е. после 1080 «тактов». Это
значение все еще намного больше минимального. Графики в левой нижней части
рисунка показывают изменение среднего (верхняя кривая) и «наилучшего» (нижняя
кривая) значения функции приспособленности.
, т.е. после 1080 «тактов». Это
значение все еще намного больше минимального. Графики в левой нижней части
рисунка показывают изменение среднего (верхняя кривая) и «наилучшего» (нижняя
кривая) значения функции приспособленности.

Рис. 4.107. Популяция особей и
график функции приспособленности при ![]() для примера 4.28.
для примера 4.28.
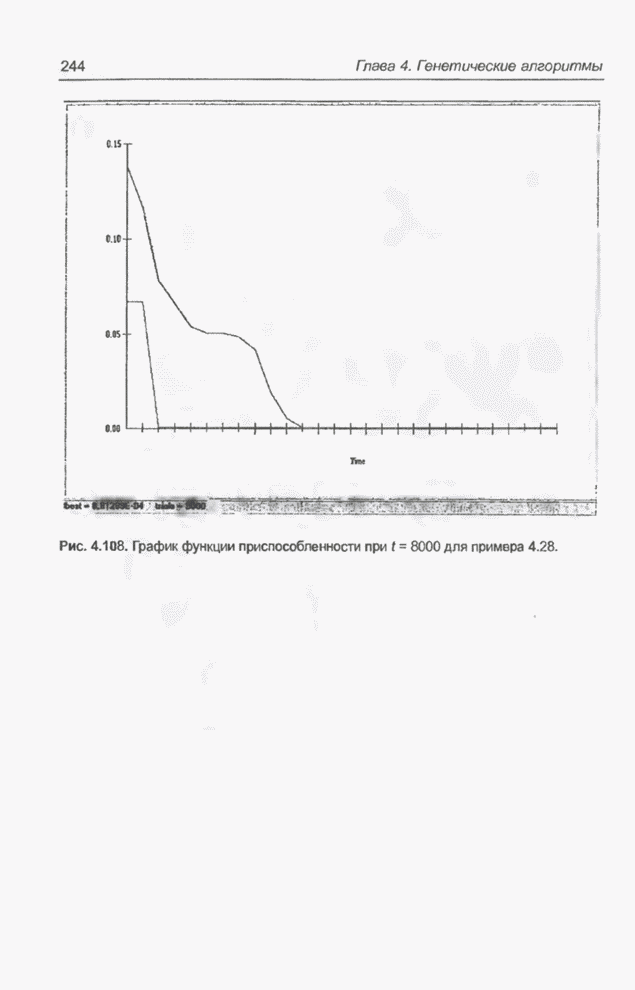
На рис. 4.108 представлены те же
графики после 8000 «тактов» ![]() . Заметно, что как «наилучшее», так и
среднее значение функции приспособленности в популяции принимают значения,
близкие к 0. На всех графиках одно деление на временной оси соответствует 20
«тактам».
. Заметно, что как «наилучшее», так и
среднее значение функции приспособленности в популяции принимают значения,
близкие к 0. На всех графиках одно деление на временной оси соответствует 20
«тактам».

Рис. 4.108. График функции
приспособленности при ![]() для примера 4.28.
для примера 4.28.
На рис. 4.109 изображена
столбчатая диаграмма особей популяции для ![]() . Заметно, что все хромосомы в популяции
стали одинаковыми. Значение их функции приспособленности, очевидно, такое же,
как и для «наилучшего» решения, т.е. равно 0,000881.
. Заметно, что все хромосомы в популяции
стали одинаковыми. Значение их функции приспособленности, очевидно, такое же,
как и для «наилучшего» решения, т.е. равно 0,000881.

Рис. 4.109. Столбчатая диаграмма
значений функции приспособленности особей в популяции при ![]() для примера 4.28.
для примера 4.28.
«Наилучшее» решение показано на
рис. 4.110. Это хромосома со значениями переменных ![]() и
и ![]() .
.

Рис. 4.110. «Наилучшее» решение
для примера 4.28 (полученное при ![]() ).
).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Предисловие к русскому изданию
- ГЛАВА 1. ВВЕДЕНИЕ
- Список литературы
- ГЛАВА 2. МНОГОСЛОЙНЫЕ НЕЙРОННЫЕ СЕТИ И АЛГОРИТМЫ ИХ ОБУЧЕНИЯ
- 2.1. Введение
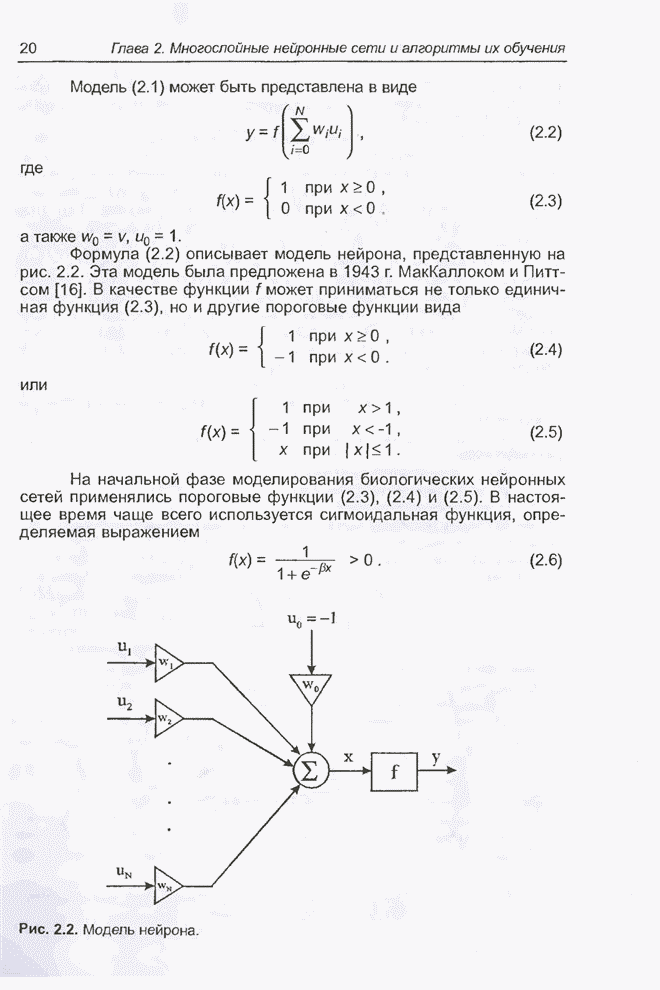
- 2.2. Нейрон и его модели
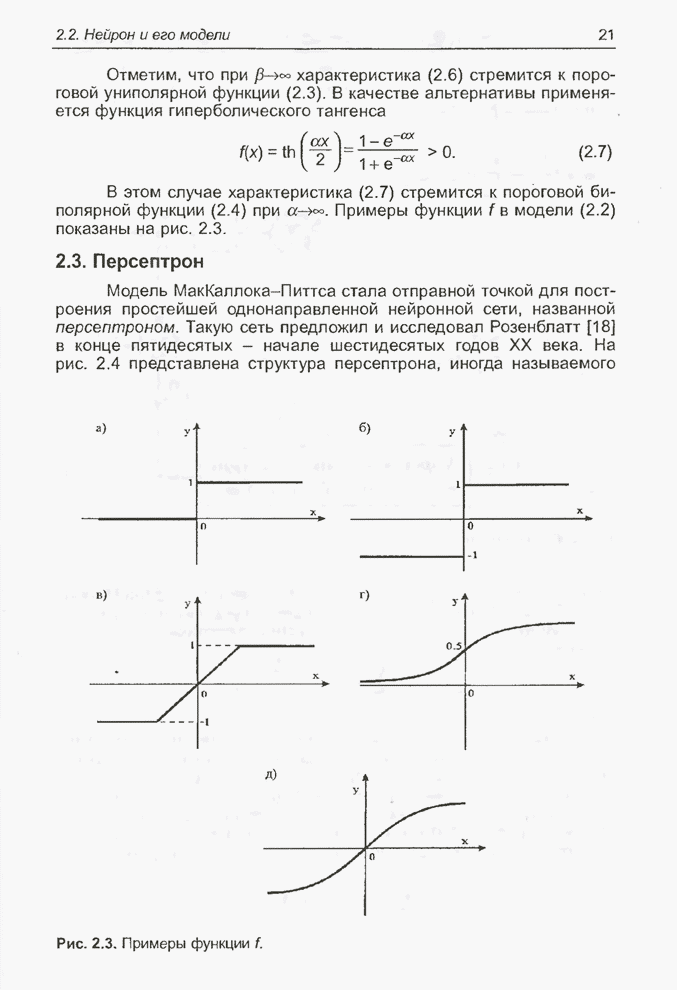
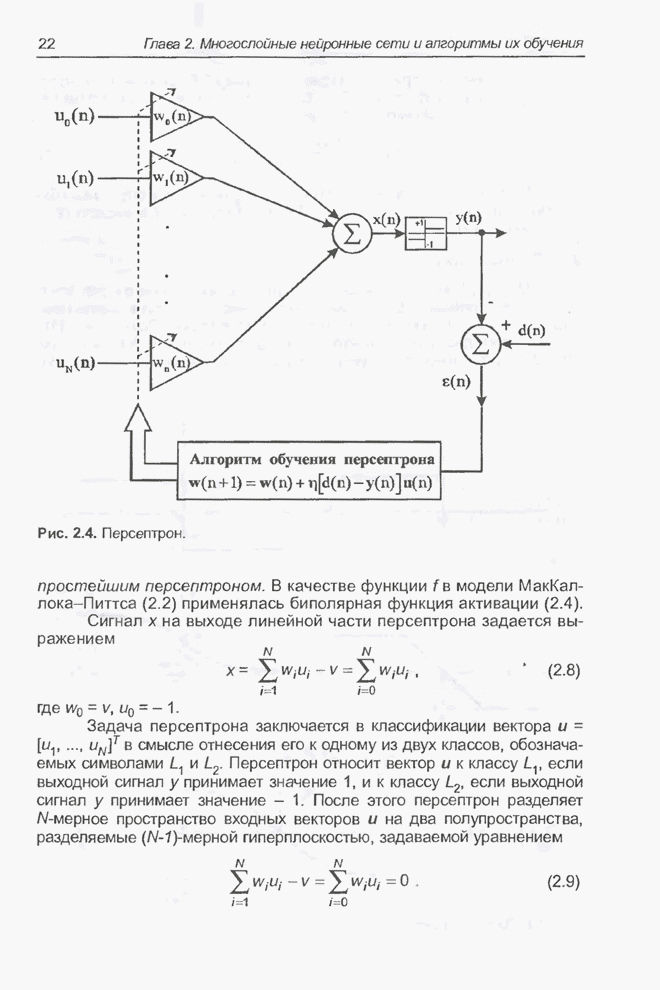
- 2.3. Персептрон
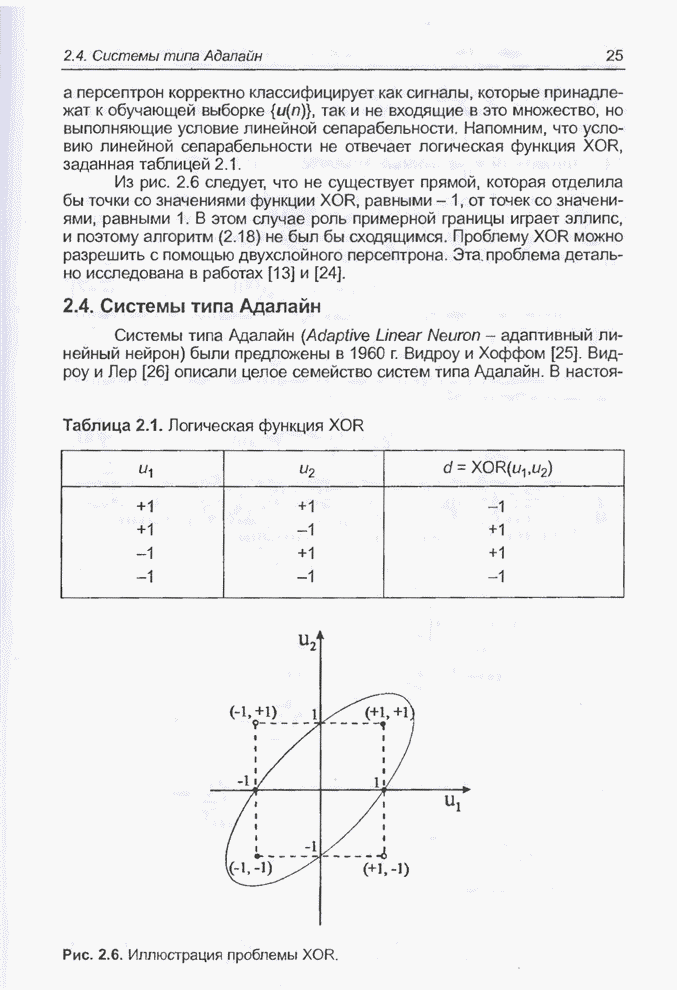
- 2.4. Системы типа Адалайн
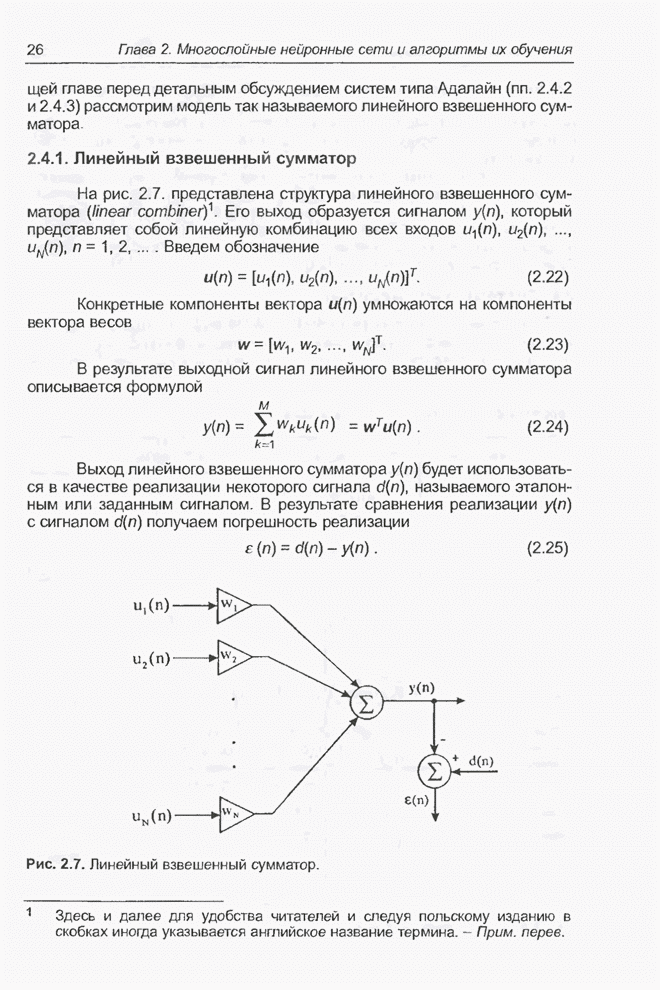
- 2.4.1. Линейный взвешенный сумматор
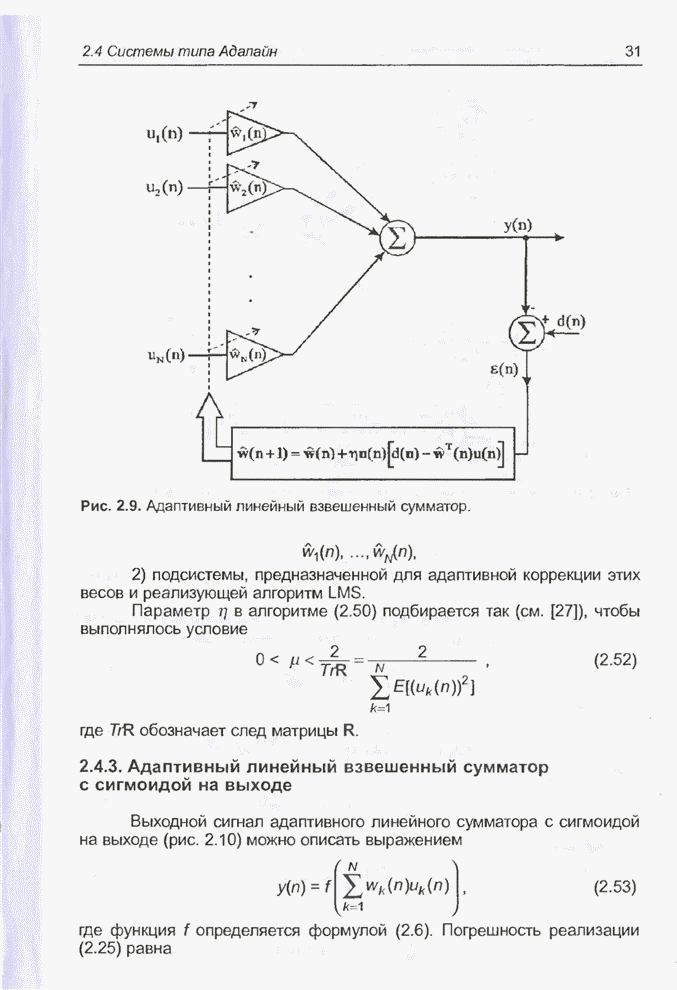
- 2.4.2. Адаптивный линейный взвешенный сумматор
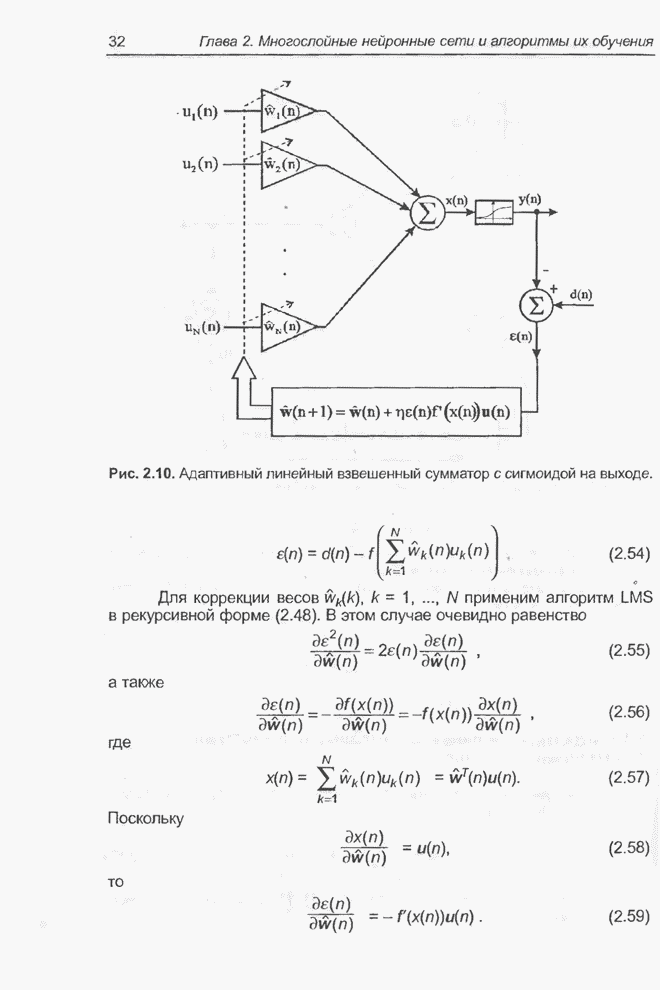
- 2.4.3. Адаптивный линейный взвешенный сумматор с сигмоидой на выходе
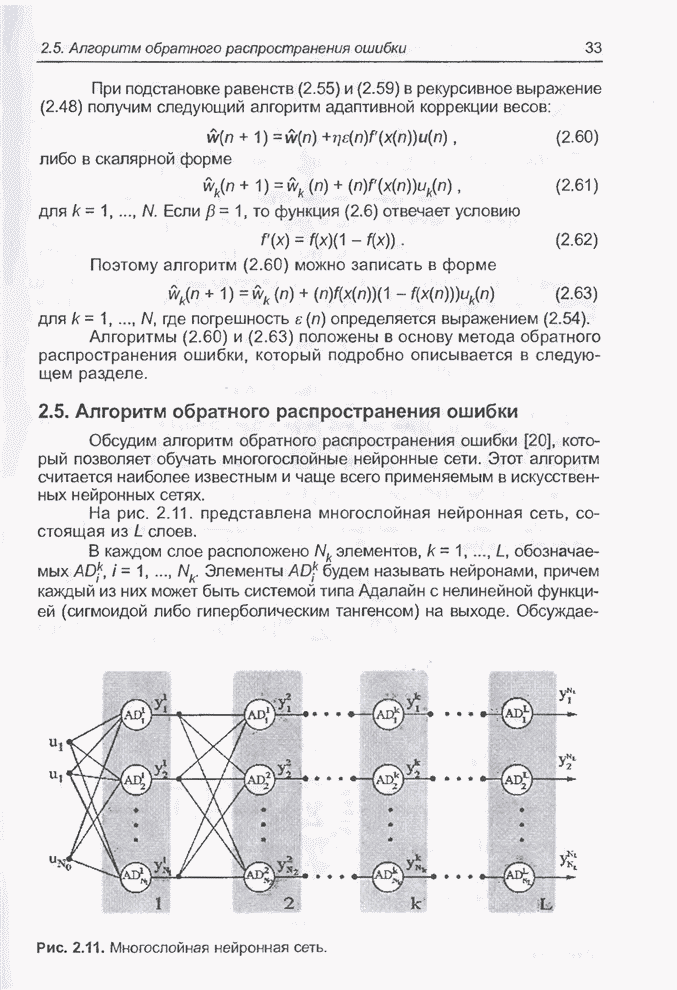
- 2.5. Алгоритм обратного распространения ошибки
- 2.6. Применение рекуррентного метода наименьших квадратов для обучения нейронных сетей
- Список литературы
- ГЛАВA3. НЕЧЕТКИЕ МНОЖЕСТВА И НЕЧЕТКИЙ ВЫВОД
- 3.1. Введение
- 3.2. Основные понятия и определения теории нечетких множеств
- 3.3. Операции на нечетких множествах
- 3.4. Принцип расширения
- 3.5. Нечеткие числа
- 3.6. Треугольные нормы
- 3.7. Нечеткие отношения и их свойства
- 3.8. Нечеткий вывод
- 3.9. Нечеткое управление
- 3.9.1. Классический модуль нечеткого управления
- 3.9.2. Метод нечеткого управления Такаги-Сугено
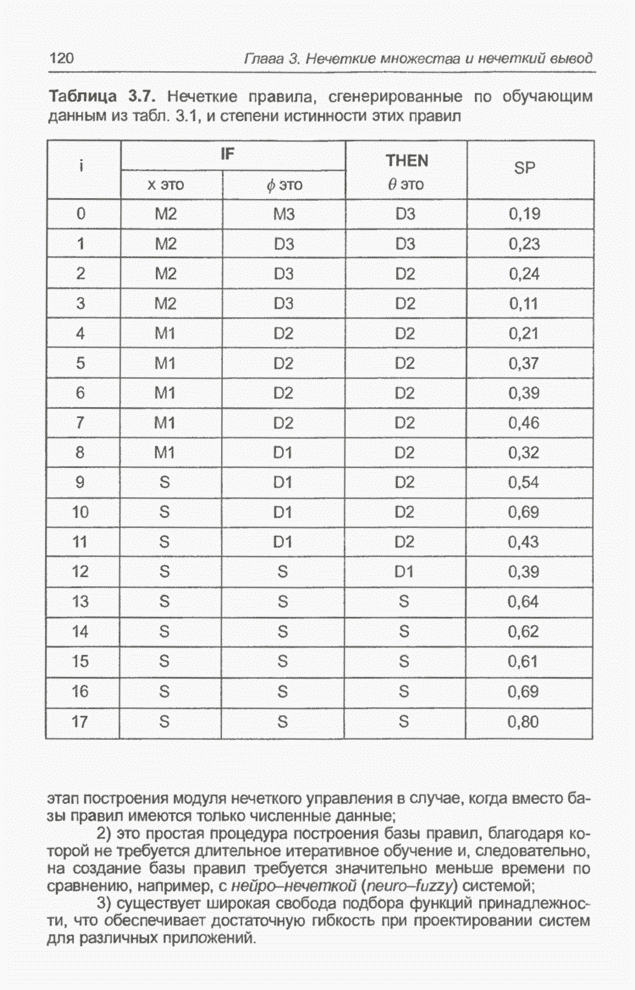
- 3.10. Проектирование базы нечетких правил на основе численных данных
- 3.10.1. Построение нечетких правил
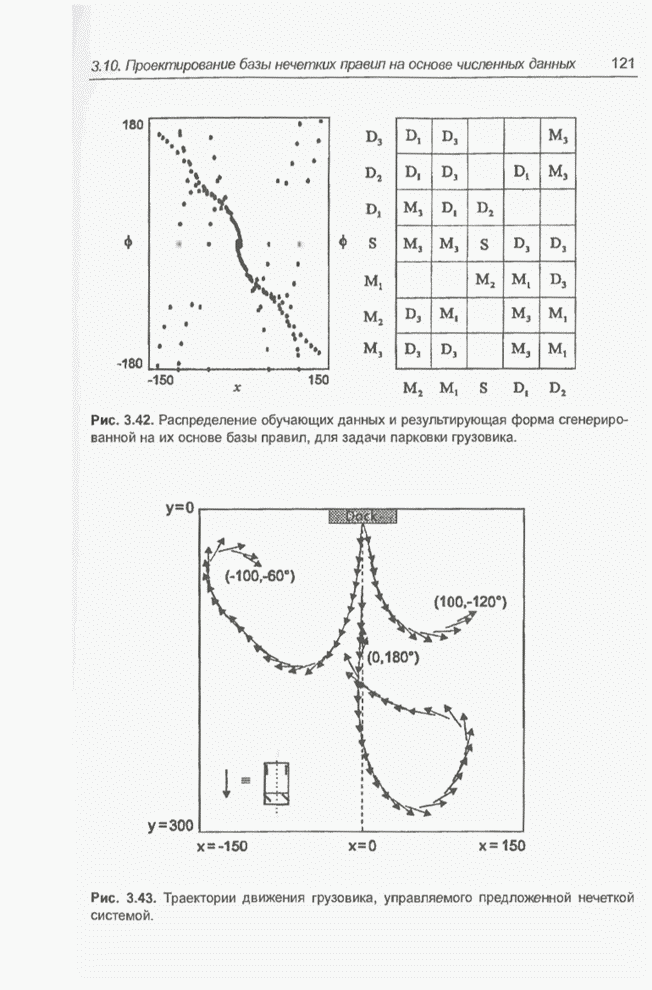
- 3.10.2. Задача парковки грузовика
- 3.10.3. Примечание
- Список литературы
- ГЛАВА 4. ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ
- 4.1. Введение
- 4.2. Генетические алгоритмы и традиционные методы оптимизации
- 4.3. Основные понятия генетических алгоритмов
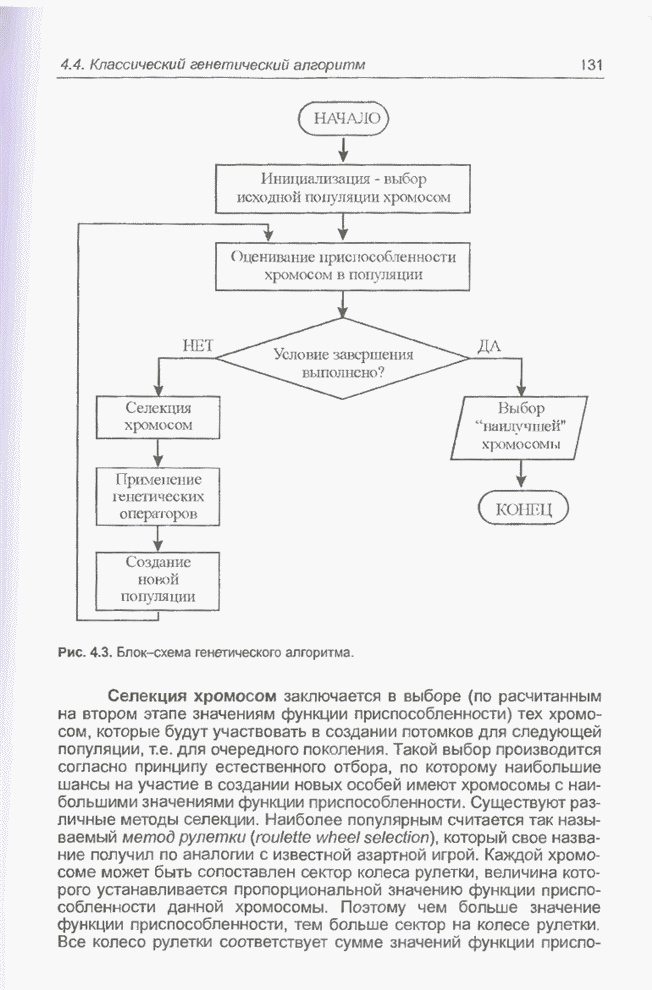
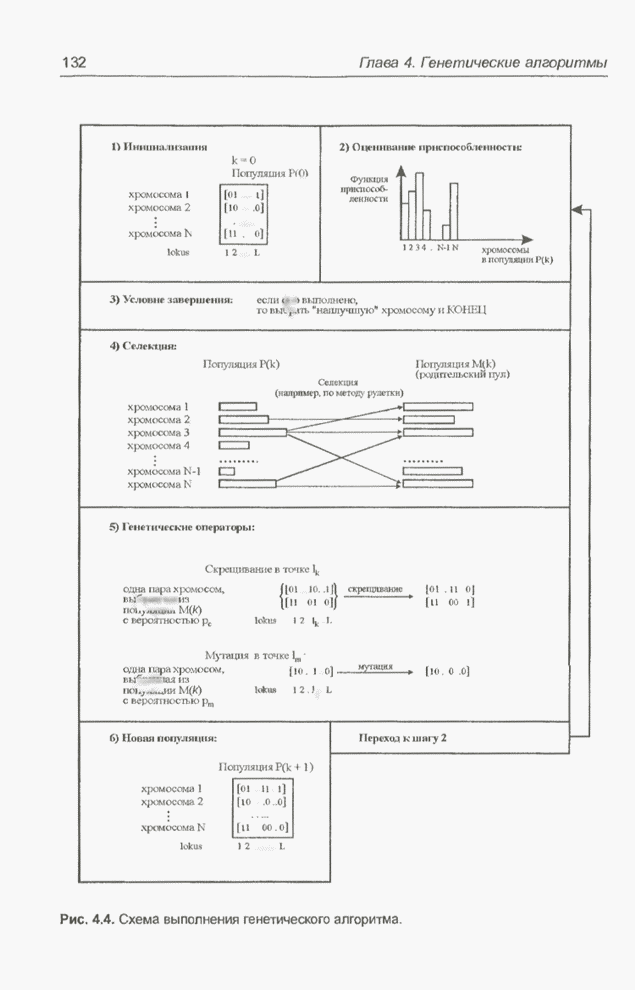
- 4.4. Классический генетический алгоритм
- 4.5. Иллюстрация выполнения классического генетического алгоритма
- 4.6. Кодирование параметров задачи в генетическом алгоритме
- 4.7. Основная теорема о генетических алгоритмах
- 4.8. Модификации классического генетического алгоритма
- 4.8.1. Методы селекции
- 4.8.2. Особые процедуры репродукции
- 4.8.3. Генетические операторы
- 4.8.4. Методы кодирования
- 4.8.5. Масштабирование функции приспособленности
- 4.8.6. Ниши в генетическом алгоритме
- 4.8.7. Генетические алгоритмы для многокритериальной оптимизации
- 4.8.8. Генетические микроалгоритмы
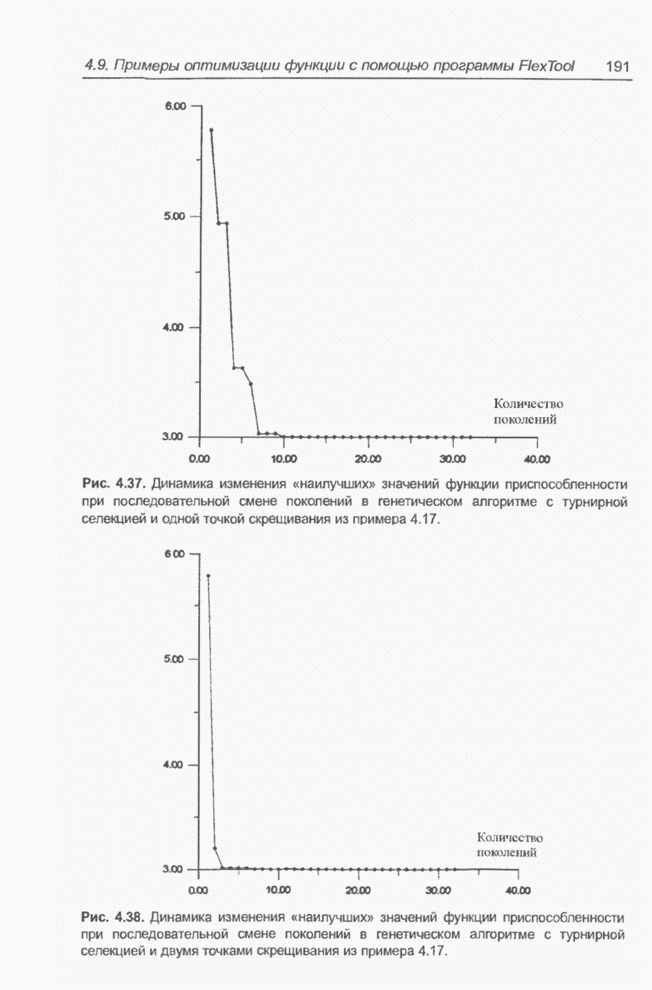
- 4.9. Примеры оптимизации функции с помощью программы FlexTool
- 4.10. Эволюционные алгоритмы
- 4.11. Приложения эволюционных алгоритмов
- 4.11.1. Примеры оптимизации функции с помощью программы Evolver
- 4.11.2. Решение комбинаторных задач с помощью программы Evolver
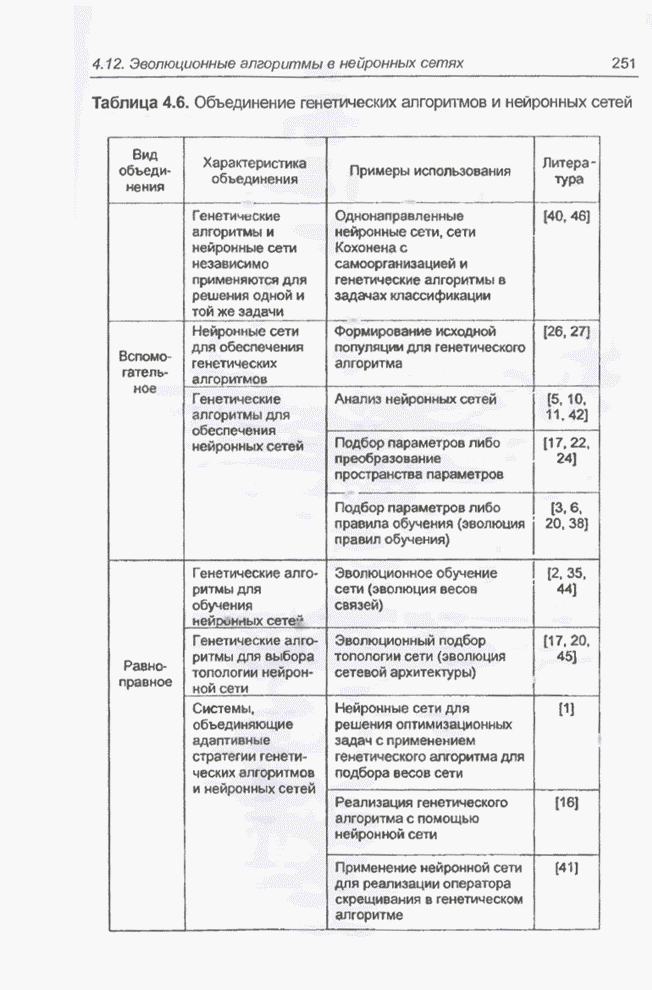
- 4.12. Эволюционные алгоритмы в нейронных сетях
- 4.12.1. Независимое применение генетических алгоритмов и нейронных сетей
- 4.12.2. Нейронные сети для поддержки генетических алгоритмов
- 4.12.3. Генетические алгоритмы для поддержки нейронных сетей
- 4.12.4. Применение генетических алгоритмов для обучения нейронных сетей
- 4.12.5. Генетические алгоритмы для выбора топологии нейронных сетей
- 4.12.6. Адаптивные взаимодействующие системы
- 4.12.7. Типовой цикл эволюции
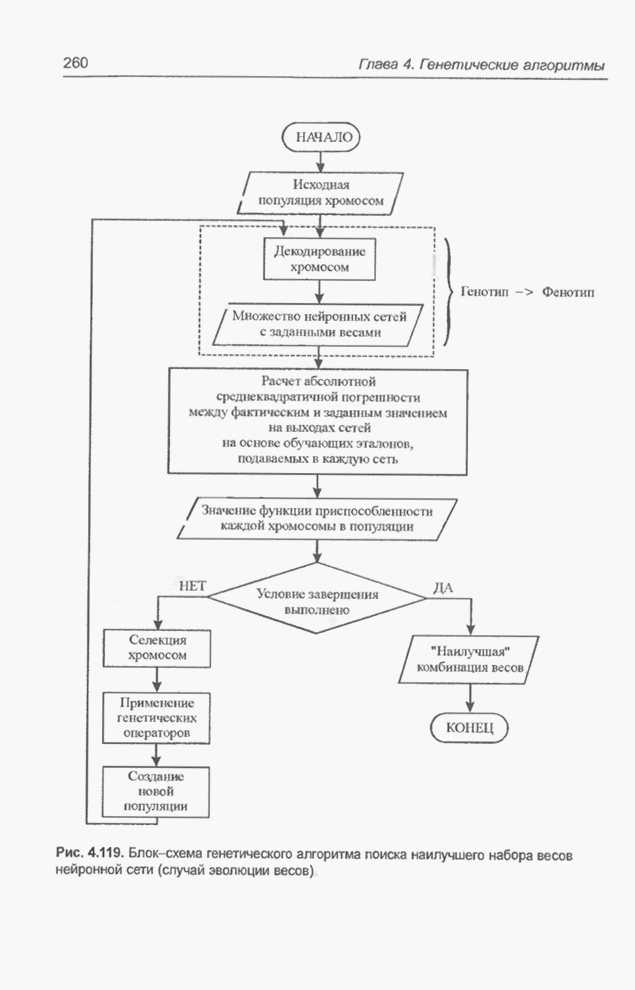
- 4.12.7.1. Эволюция весов связей
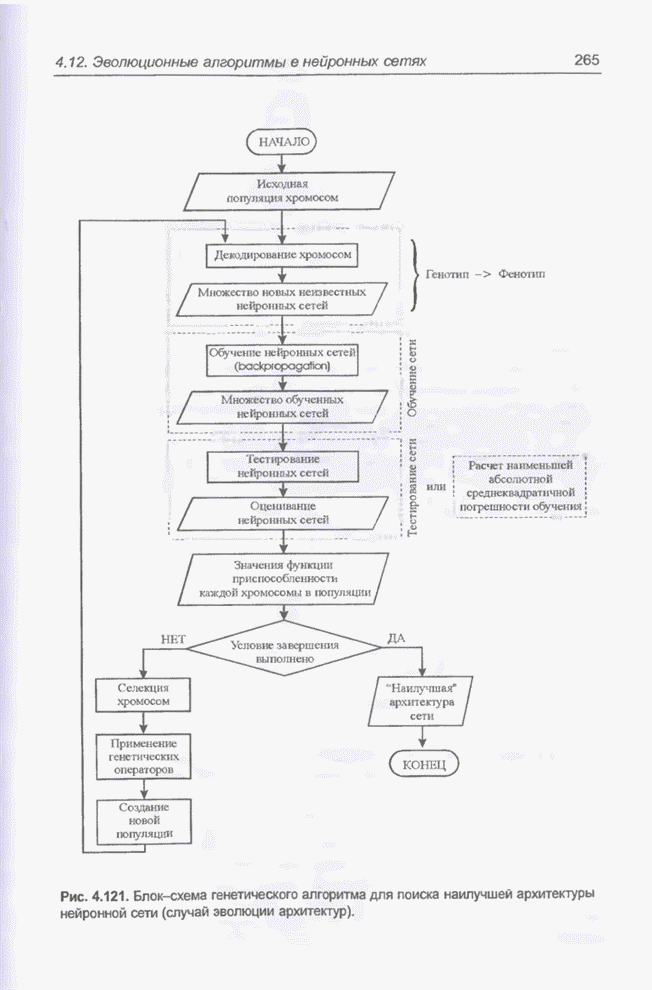
- 4.12.7.2. Эволюция архитектуры сети
- 4.12.7.3. Эволюция правил обучения
- 4.13. Примеры моделирования эволюционных алгоритмов в приложении к нейронным сетям
- 4.13.1. Программы Evolver и BrainMaker
- 4.13.2. Программа GTO
- Список литературы
- ГЛАВА 5. МОДУЛИ НЕЧЕТКО-НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.1. Модуль нечеткого управления со структурой, определенной в процессе дефуззификации
- 5.1.2. Конструкция модуля
- 5.1.3. Структура модуля
- 5.1.4. Использование алгоритма обратного распространения ошибки
- 5.1.5. Модификации модуля
- 5.1.6. Применение модуля нечеткого управления для прогнозирования случайных временных рядов
- 5.1.7. Применение модуля нечеткого управления для решения задачи парковки грузовика
- 5.1.8. Примечание
- 5.2. Представление модуля нечеткого управления в виде стандартной нейронной сети
- 5.3. Модуль нечеткого управления с нейронной сетью для выполнения дефуззификации
- 5.3.1. Введение
- 5.3.2. Конструкция модуля
- 5.3.3. Структура модуля
- 5.3.4. Алгоритмы обучения модуля
- 5.3.5. Решение задачи стабилизации перевернутого маятника
- 5.3.6. Примечание
- 5.4. Модуль нечеткого управления с возможностью коррекции правил
- 5.4.1. Введение
- 5.4.2. Фаза обучения на основе самоорганизации
- 5.4.3. Фаза обучения с учителем
- 5.4.4. Примечание
- 5.5. Модуль нечеткого управления типа Такаги-Сугено
- 5.5.1. Введение
- 5.5.2. Нейронная реализация функции принадлежности
- 5.5.3. Модули Такаги-Сугено
- 5.5.4. Реализация условий
- 5.5.5. Реализация заключений
- 5.5.6. Примечание
- 5.6. Модуль нечеткого управления типа Такаги-Сугено: случай зависимых лингвистических переменных
- 5.6.1. Введение
- 5.6.2. Нейронные сети для нечеткого вывода
- 5.6.3. Структура системы
- 5.6.4. Способ обучения
- 5.6.5. Решение задачи парковки грузовика
- 5.6.6. Примечание
- Список литературы