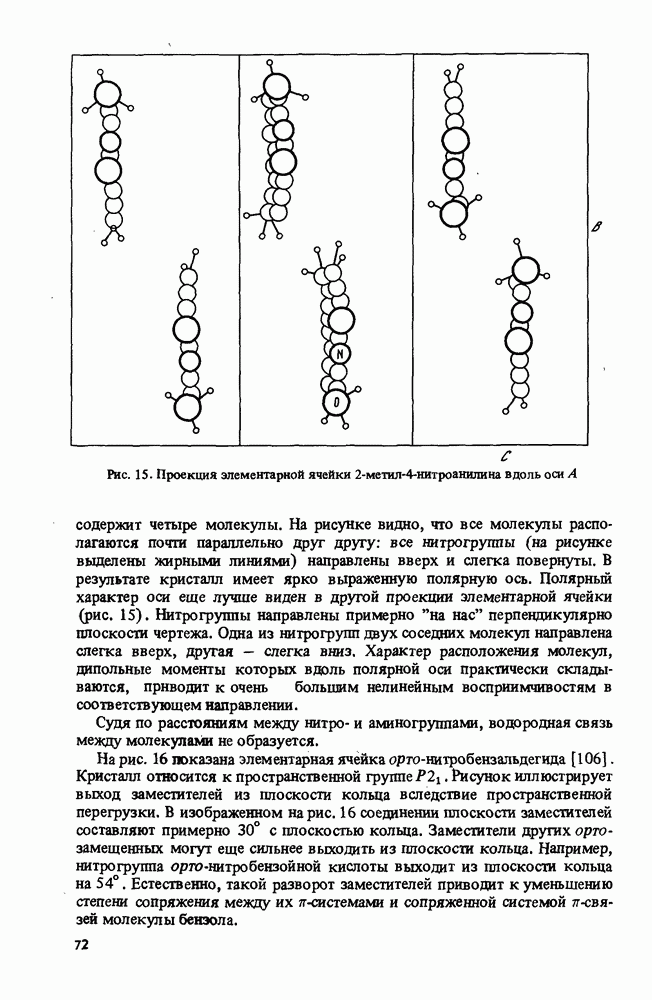
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.4. Измерение нелинейной восприимчивости
Методы измерения нелинейной восприимчивости молекулярных кристаллов ничем не отличаются от методов, применяемых при исследованиях неорганических материалов и полупроводников [137—139]. Все они основаны на измерении зависимости мощности сигнала на частоте преобразованного излучения от квадрата мощности падающего излучения. Действительно, отношение этих величин пропорционально 
Формула (14) описывает поляризацию бесконечной нелинейной среды. Для получения аналитического выражения мощности излучения второй гармоники на выходе из кристалла конечной толщины надо решить уравнения Максвелла с учетом нелинейной зависимости поляризации от полей [1, 137, 139]. При этом можно рассматривать распространение в среде двух волн второй гармоники: "свободной" и "связанной" (см. разд. 1.2), распространяющихся с разными скоростями: "свободная" волна распространяется со скоростью, характерной для волны частоты  "связанная" — со скоростью волны частоты
"связанная" — со скоростью волны частоты  Интерференция этих волн в отсутствие синхронизма приводит к колебаниям мощности излучения на выходе из кристалла [140]. Максимумы интенсивности соответствуют случаю, когда фазы волн совпадают, минимумы — когда волны в противофазе.
Интерференция этих волн в отсутствие синхронизма приводит к колебаниям мощности излучения на выходе из кристалла [140]. Максимумы интенсивности соответствуют случаю, когда фазы волн совпадают, минимумы — когда волны в противофазе.
Решение уравнения Максвелла позволяет получить следующее выражение для мощности излучения второй гармоники на расстоянии I от передней границы нелинейной среды при нормальном падении излучения:

Здесь  мощность основного излучения,
мощность основного излучения,  - показатели преломления среды на соответствующих частотах, С — коэффициент пропорциональности, в общем случае зависящий от формы и модового состава излучения [1, 137-139]. Изменение длины пути луча в кристалле, соответствующее двум последующим максимумам интенсивности, дается соотношением
- показатели преломления среды на соответствующих частотах, С — коэффициент пропорциональности, в общем случае зависящий от формы и модового состава излучения [1, 137-139]. Изменение длины пути луча в кристалле, соответствующее двум последующим максимумам интенсивности, дается соотношением

( длина волны излучения частоты
длина волны излучения частоты  в вакууме). Величину
в вакууме). Величину  иногда называют длиной когерентности.
иногда называют длиной когерентности.
При наклонном падении волны на кристалл выражение (98) усложняется. Появляются множители, зависящие от угла падения и от показателей преломления. Однако осциллирующий характер зависимости мощности от длины пути сохраняется. Длина когерентности определяется теперь выражением

где  углы преломления для соответствующих частот.
углы преломления для соответствующих частот.
Для абсолютных измерений  необходимо знать точное значение коэффициента С в формуле (98). Соответствующие выражения можно найти в [1, 137—139]. Для относительных измерений
необходимо знать точное значение коэффициента С в формуле (98). Соответствующие выражения можно найти в [1, 137—139]. Для относительных измерений  по значениям компонент этого тензора эталонного образца это часто не обязательно. Достаточно измерить длину когерентности и мощность излучения второй гармоники в максимумах интерференционной картины, регистрируемой для образца и эталона, при одном и том же модовом составе и интенсивности основного излучения. Затем относительное значение
по значениям компонент этого тензора эталонного образца это часто не обязательно. Достаточно измерить длину когерентности и мощность излучения второй гармоники в максимумах интерференционной картины, регистрируемой для образца и эталона, при одном и том же модовом составе и интенсивности основного излучения. Затем относительное значение  ляется по формуле
ляется по формуле

Формула (101) является очевидным следствием формулы (98) и справедлива при малых углах падения излучения на кристалл.
Для точных измерений  показатели преломления, прозрачность, длины когерентности и нелинейные восприимчивости образца и эталона должны быть сравнительно близки. Для материалов, прозрачных в видимой области спектра, в качестве эталонов используют кристаллический кварц, дигидрофосфат калия
показатели преломления, прозрачность, длины когерентности и нелинейные восприимчивости образца и эталона должны быть сравнительно близки. Для материалов, прозрачных в видимой области спектра, в качестве эталонов используют кристаллический кварц, дигидрофосфат калия  ниобат лития и иодат лития. Для кристаллов, прозрачных в инфракрасной области, в качестве эталона используют арсенид галлия. В этом случае нелинейная восприимчивость измеряется для длины волны
ниобат лития и иодат лития. Для кристаллов, прозрачных в инфракрасной области, в качестве эталона используют арсенид галлия. В этом случае нелинейная восприимчивость измеряется для длины волны 
Разные источники приводят различные значения нелинейных восприимчивостей эталонов. Мы здесь и далее будем использовать значения, приведенные в справочном издании [110]. Согласно [110],

Для измерения определенных компонент тензора  кристалл ориентируют относительно полей. Например, для измерения
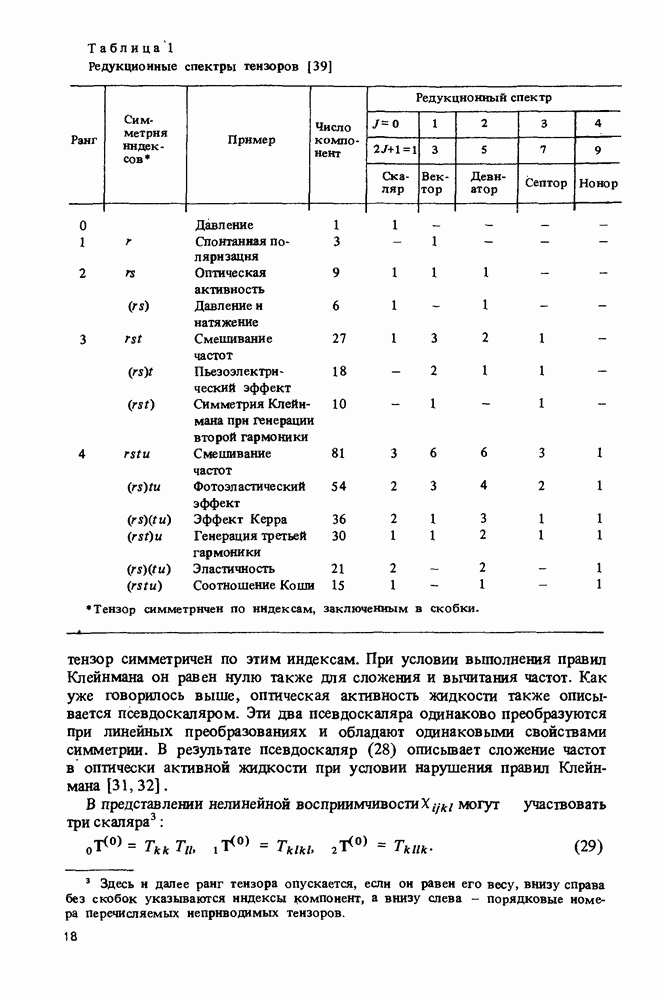
кристалл ориентируют относительно полей. Например, для измерения  в
в
соответсгвии с соотношением

надо, чтобы излучение частоты  было поляризовано по оси
было поляризовано по оси  измеряется мощность излучения второй гармоники, поляризованного по оси х. Если кристалл принадлежит к орторомбической сингонии, для этого достаточно вырезать пластину кристалла, параллельную плоскости
измеряется мощность излучения второй гармоники, поляризованного по оси х. Если кристалл принадлежит к орторомбической сингонии, для этого достаточно вырезать пластину кристалла, параллельную плоскости  и направить луч перпендикулярно этой пластине, т.е. по оси у кристалла, сориентировав соответствующим образом поляризацию лучей частоты
и направить луч перпендикулярно этой пластине, т.е. по оси у кристалла, сориентировав соответствующим образом поляризацию лучей частоты  и
и  Та же геометрия опыта может быть использована для получения компоненты
Та же геометрия опыта может быть использована для получения компоненты  входящей в соотношение
входящей в соотношение  Для этого кристалл достаточно повернуть на 45° вокруг кристаллографической оси у и измерять те же составляющие исходного и преобразованного излучения. Для измерения всех компонент тензора
Для этого кристалл достаточно повернуть на 45° вокруг кристаллографической оси у и измерять те же составляющие исходного и преобразованного излучения. Для измерения всех компонент тензора  двуосного кристалла нужно иметь по крайней мере два по-разному вырезанных кристалла.
двуосного кристалла нужно иметь по крайней мере два по-разному вырезанных кристалла.
Таким образом, измерение определенной составляющей  сводится к получению интерференционной картины ("полос Мейкера" [140]) и к измерению длины когерентности и интенсивности второй гармоники излучения в максимуме интерференционной картины. Для получения интерференционной картины необходимо менять длину пути луча в кристалле.
сводится к получению интерференционной картины ("полос Мейкера" [140]) и к измерению длины когерентности и интенсивности второй гармоники излучения в максимуме интерференционной картины. Для получения интерференционной картины необходимо менять длину пути луча в кристалле.
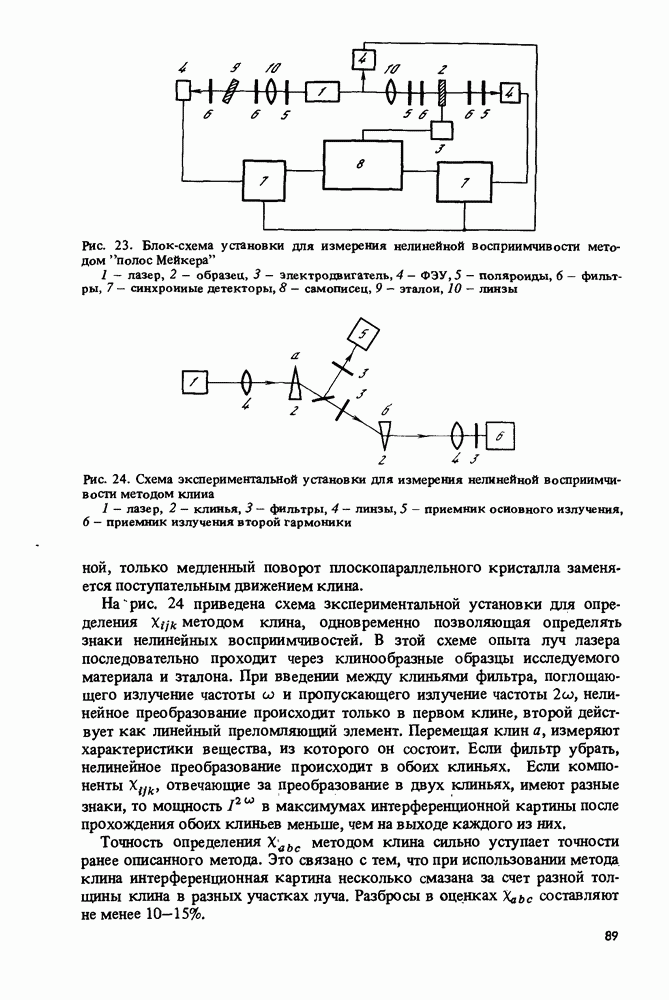
Используются два способа изменения этой длины: поворот плоскопараллельного кристалла и смещение клинообразного кристалла. Первый из них иногда называют методом "полос Мейкера", второй — методом клина.
Схема типичной установки для измерения первым способом дана на рис. 23. Излучение одного и того же источника направляется на образец и эталон; измеряется мощность второй гармоники после прохождения каждого кристалла. Толщина кристаллов, вырезанных в виде плоскопараллельных пластин, меняется за счет медленного вращения  скоростью 1— 20° С/мин). Чаще всего в качестве источника света используется импульсный лазер, но может быть использован и непрерывный лазер с внешним модулятором [141]. Точность определения
скоростью 1— 20° С/мин). Чаще всего в качестве источника света используется импульсный лазер, но может быть использован и непрерывный лазер с внешним модулятором [141]. Точность определения  этим методом зависит главным образом от качества изготовления и обработки поверхности кристалла.
этим методом зависит главным образом от качества изготовления и обработки поверхности кристалла.  могут быть измерены с точностью 1—2%. Если поверхность кристалла обработана с точностью до X, погрешность измерения
могут быть измерены с точностью 1—2%. Если поверхность кристалла обработана с точностью до X, погрешность измерения  может не превышать 2—3%. Так как молекулярные кристаллы пока не удается обрабатывать с такой тщательностью, наибольшая точность достигнутая при измерении
может не превышать 2—3%. Так как молекулярные кристаллы пока не удается обрабатывать с такой тщательностью, наибольшая точность достигнутая при измерении  составляет 5%.
составляет 5%.
Независимо от качества обработки поверхности погрешности измерений сильно увеличиваются, если исследуемый образец имеет большие показатели преломления и большие в нужном направлении. Это связано с тем, что при больших  для достаточного изменения длины путй луча приходится поворачивать кристалл на большие углы. В результате при больших показателях преломления сильно увеличиваются потери на отражение.
для достаточного изменения длины путй луча приходится поворачивать кристалл на большие углы. В результате при больших показателях преломления сильно увеличиваются потери на отражение.
Для измерения нелинейных восприимчивостей кристаллов, имеющих большие показатели преломления и длины когерентности, чаще используется метод клина [142-144]. Принципиальная схема измерения нелинейной восприимчивости зтим методом ничем не отличается от ранее

Рис. 23. Блок-схема установки для измерения нелинейной восприимчивости методом "полос Мейкера" 1 — лазер, 2 - образец, 3 - электродвигатель, 4 - ФЭУ, 5 - поляроиды, 6 — фильтры, 7 — синхронные детекторы, 8 — самописец, 9 - эталон, 10 — линзы

Рис. 24. Схема экспериментальной установки для измерения нелинейной восприимчивости методом клина 1 - лазер, 2 - клинья, 3 — фильтры, 4 — линзы, 5 - приемник основного излучения, 6 - приемник излучения второй гармоники
рассмотренной, только медленный поворот плоскопараллельного кристалла заменяется поступательным движением клина.
На рис, 24 приведена схема экспериментальной установки для определения  методом клина, одновременно позволяющая определять знаки нелинейных восприимчивостей. В этой схеме опыта луч лазера последовательно проходит через клинообразные образцы исследуемого материала и эталона. При введении между клиньями фильтра, поглощающего излучение частоты
методом клина, одновременно позволяющая определять знаки нелинейных восприимчивостей. В этой схеме опыта луч лазера последовательно проходит через клинообразные образцы исследуемого материала и эталона. При введении между клиньями фильтра, поглощающего излучение частоты  и пропускающего излучение частоты
и пропускающего излучение частоты  нелинейное преобразование происходит только в первом клине, второй действует как линейный преломляющий элемент. Перемещая клин а, измеряют характеристики вещества, из которого он состоит. Если фильтр убрать, нелинейное преобразование происходит в обоих клиньях. Если компоненты
нелинейное преобразование происходит только в первом клине, второй действует как линейный преломляющий элемент. Перемещая клин а, измеряют характеристики вещества, из которого он состоит. Если фильтр убрать, нелинейное преобразование происходит в обоих клиньях. Если компоненты  отвечающие за преобразование в двух клиньях, имеют разные знаки, то мощность
отвечающие за преобразование в двух клиньях, имеют разные знаки, то мощность  в максимумах интерференционной картины после прохождения обоих клиньев меньше, чем на выходе каждого из них.
в максимумах интерференционной картины после прохождения обоих клиньев меньше, чем на выходе каждого из них.
Точность определения  методом клина сильно уступает точности ранее описанного метода. Это связано с тем, что при использовании метода клина интерференционная картина несколько смазана за счет разной толщины клина в разных участках луча. Разбросы в оценках
методом клина сильно уступает точности ранее описанного метода. Это связано с тем, что при использовании метода клина интерференционная картина несколько смазана за счет разной толщины клина в разных участках луча. Разбросы в оценках  составляют не менее 10—15%.
составляют не менее 10—15%.
Описанные методы измерения  с помощью получения и исследования интерференционной картины ("полос Мейкера") позволяют измерить все компоненты тензора. Однако уровень мощности сигнала невысок, поэтому в качестве источников излучения используются мощные лазеры, а для регистрации — чувствительные приборы.
с помощью получения и исследования интерференционной картины ("полос Мейкера") позволяют измерить все компоненты тензора. Однако уровень мощности сигнала невысок, поэтому в качестве источников излучения используются мощные лазеры, а для регистрации — чувствительные приборы.
Ограничений по мощности можно избежать, если производить измерения в условиях синхронизма [144], т.е. если луч света распространяется по кристаллу в направлении, для которого фазовые скорости падающего и преобразованного излучения равны между собой. При этом мощность преобразованного излучения растет примерно пропорционально квадрату пути, пройденного в кристалле, и уровень мощности на выходе из кристалла может быть весьма значителен. Для определения нелинейной восприимчивости в направлении синхронизма достаточно измерить и толщину кристалла. Высокий уровень мощности преобразованного излучения позволяет использовать для измерений газовые лазеры, что существенно повышает точность измерения. Однако практически невозможно подобрать геометрию опыта таким образом, чтобы измерялась одна компонента тензора. Нелинейное преобразование в условиях синхронизма определяется значением эффективной нелинейной восприимчивости, зависящей от нескольких компонент тензора, согласно соотношению

Поэтому измерения в условиях синхронизма позволяют измерить лишь Хэфф [145].
В последнее время стал развиваться еще один метод измерения нелинейных восприимчивостей  [146,147], предложенный еще в работе [148]. Он основан на тщательном измерении формы линий и частот комбинационного рассеяния. Комбинационное рассеяние на продольных фононах связано с фононным вкладом в нелинейную восприимчивость (разд. 1.7); комбинационное рассеяние на поперечных фононах зависит как от фононного, так и от электронного вклада в нелинейную восприимчивость. Формулы, связывающие параметры рассеяния на поперечных фононах с
[146,147], предложенный еще в работе [148]. Он основан на тщательном измерении формы линий и частот комбинационного рассеяния. Комбинационное рассеяние на продольных фононах связано с фононным вкладом в нелинейную восприимчивость (разд. 1.7); комбинационное рассеяние на поперечных фононах зависит как от фононного, так и от электронного вклада в нелинейную восприимчивость. Формулы, связывающие параметры рассеяния на поперечных фононах с  на продольных - с
на продольных - с  в [146, 148]. Этот метод до сих пор использовался в основном для определения нелинейных восприимчивостей ионных кристаллов (фосфатов, ниобатов и т.д.). Согласие между значениями нелинейных восприимчивостей, определенных по комбинационному рассеянию, и значениями, полученными путем непосредственных измерений, является, на наш взгляд, даже слишком хорошим, если учесть допущения описываемого метода.
в [146, 148]. Этот метод до сих пор использовался в основном для определения нелинейных восприимчивостей ионных кристаллов (фосфатов, ниобатов и т.д.). Согласие между значениями нелинейных восприимчивостей, определенных по комбинационному рассеянию, и значениями, полученными путем непосредственных измерений, является, на наш взгляд, даже слишком хорошим, если учесть допущения описываемого метода.
При попытках применить этот метод к молекулярным кристаллам [147] было обнаружено, что частоты продольных и поперечных фононов практически совпадают (незначительные различия наблюдались лишь для трансляционных колебаний). Это объясняется тем, что как генерация суммарных частот, так и линейный злектрооптический эффект в молекулярных кристаллах связаны в основном с движением электронов (см. гл. 4). По-видимому, это сильно ограничивает возможности применения описанного метода для определения  молекулярных кристаллов.
молекулярных кристаллов.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. НЕЛИНЕЙНАЯ ВОСПРИИМЧИВОСТЬ
- 1.1. Электроны и нелинейная восприимчивость
- 1.2. Феноменологическое описание нелинейных эффектов. Нелинейная поляризация (одномерный случай)
- 1.3. Феноменологическое описание нелинейных эффектов (трехмерный случай). Симметрия
- 1.4. Описание нелинейных восприимчивостей с помощью неприводимых тензоров
- 1.5. Гиперполяризуемости. Связь с нелинейной восприимчивостью среды
- 1.6. Квантовомеханическое описание нелинейной восприимчивости. Двухуровневая и трехуровневая системы, двухзонная модель
- 1.7. Вклад фононов в нелинейную восприимчивость. Электрооптический эффект, электрохромизм
- ГЛАВА 2. МОЛЕКУЛЫ И МОЛЕКУЛЯРНЫЕ КРИСТАЛЛЫ
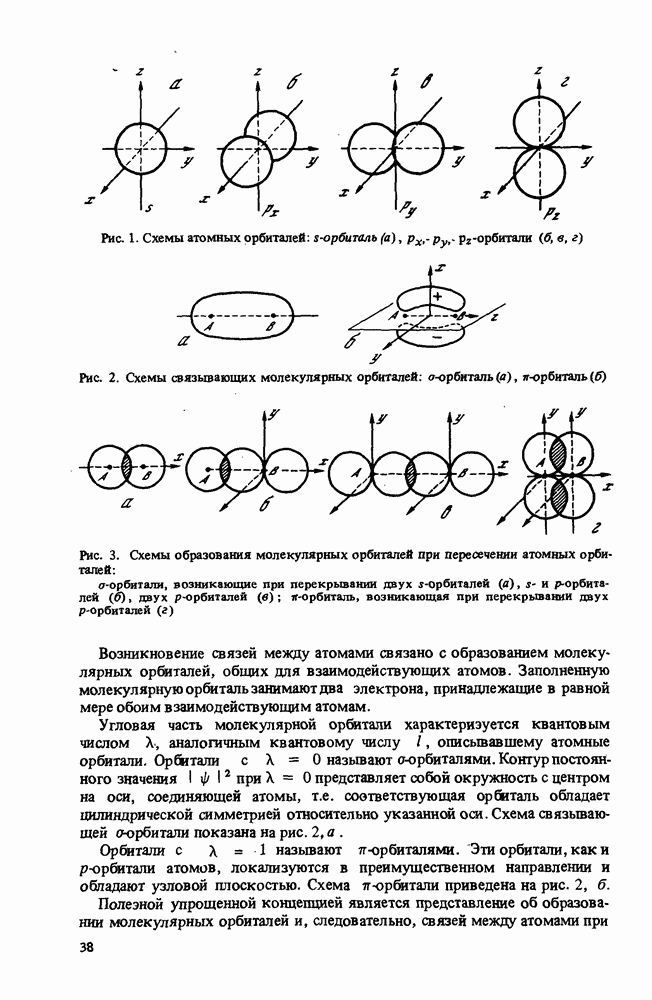
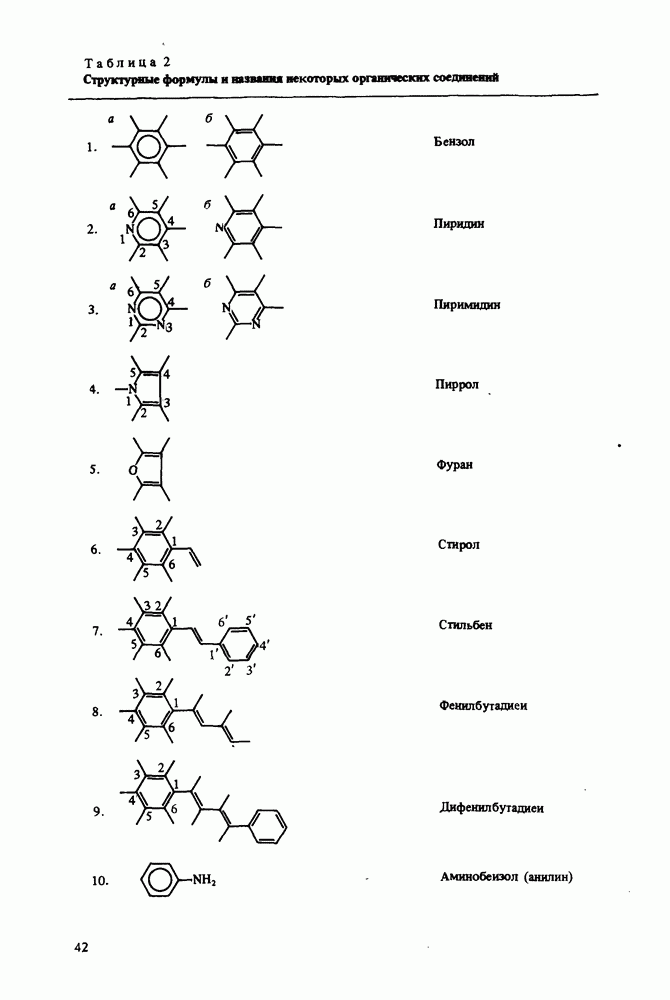
- 2.2. Электронные переходы в молекулах
- 2.3. Некоторые методы квантовой химии
- 2.4. Донорно-акцепторная сила заместителей, степень ПЗ
- 2.5. Комплексы переноса заряда
- 2.6. Молекулярные кристаллы
- 2.7. Структура конкретных молекулярных кристаллов
- 2.8. Механические и оптические свойства молекулярных кристаллов
- ГЛАВА 3. СИНТЕЗ И МЕТОДЫ ИССЛЕДОВАНИЯ МОЛЕКУЛЯРНЫХ КРИСТАЛЛОВ
- 3.1. Приготовление образцов для исследования оптических характеристик
- 3.2. Измерение коэффициентов преломления
- 3.3. Электрооптический эффект, электрохромизм, измерение дипольных моментов возбужденных состояний
- 3.4. Измерение нелинейной восприимчивости
- 3.5. Методы изучения синхронизма в монокристаллах
- 3.6. Оценка нелинейных восприимчивостей и наличия синхронизма порошковым методом
- 3.7. Измерение гиперполяризуемости
- ГЛАВА 4. ПРИРОДА НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СВОЙСТВ МОЛЕКУЛЯРНЫХ КРИСТАЛЛОВ
- 4.1 Происхождение нелинейной восприимчивости третьего порядка
- 4.2. Оценка различных методов экспериментального определения нелинейной восприимчивости второго порядка
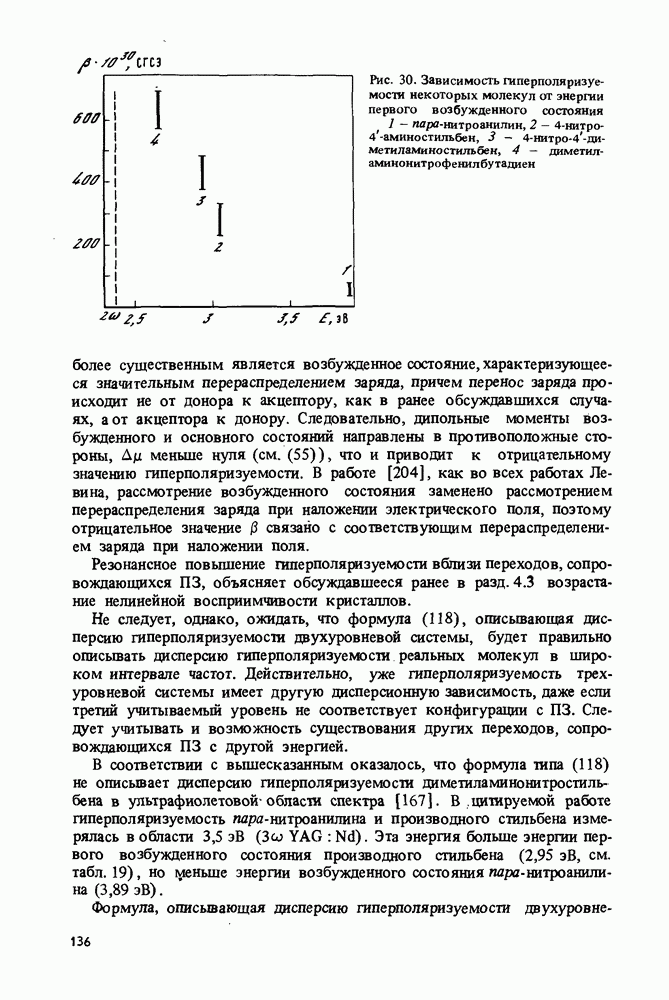
- 4.3. Особенности нелинейных восприимчивостей второго порядка молекулярных кристаллов. Роль переноса заряда
- 4.4. Расчет гиперполярнзуемостей молекул и нелинейных восприимчивостей кристаллов по аддитивной схеме. Учет распределения зарядов в основном состоянии
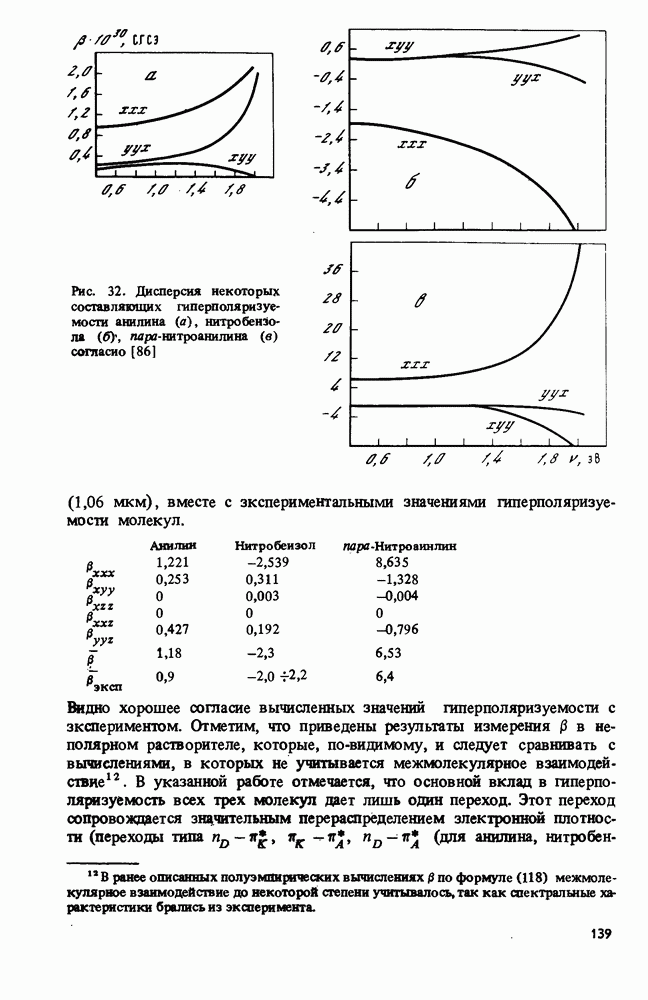
- 4.5. Расчет гиперполяризуемостей молекул при отсутствии аддитивности. Учет возбужденных состояний. Дисперсия гиперполяризуемости
- 4.6. Электрохромизм. Линейный электрооптический эффект
- 4.7. Нелинейная оптика жидких кристаллов
- ГЛАВА 5. ФАЗОВЫЙ СИНХРОНИЗМ В МОЛЕКУЛЯРНЫХ КРИСТАЛЛАХ
- 5.1. Линейный (коллинеарный) синхронизм в двуосных кристаллах
- 5.2. Векторный синхронизм в молекулярных кристаллах
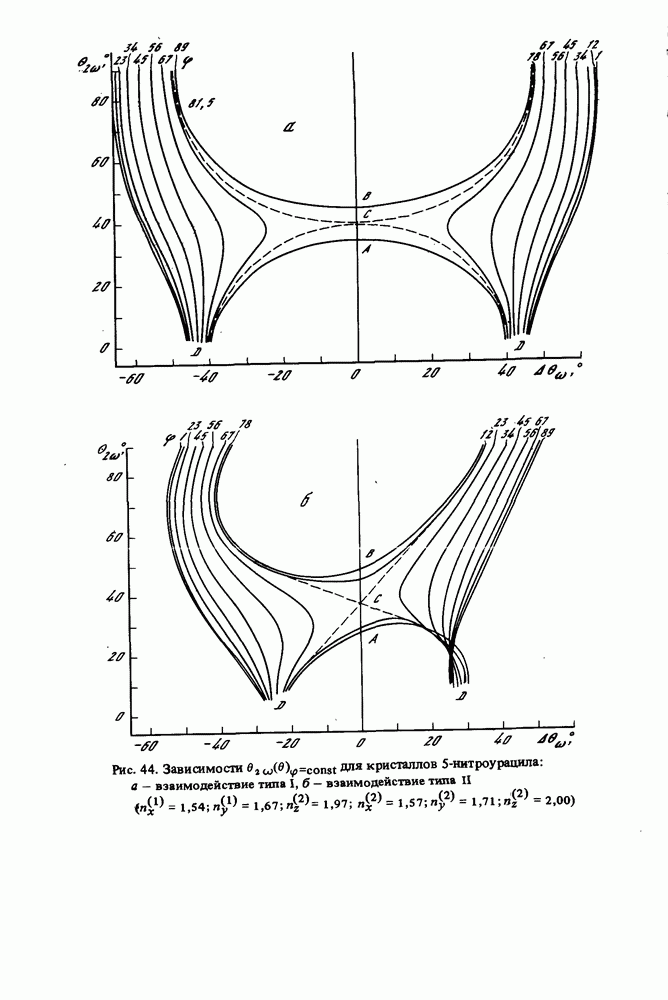
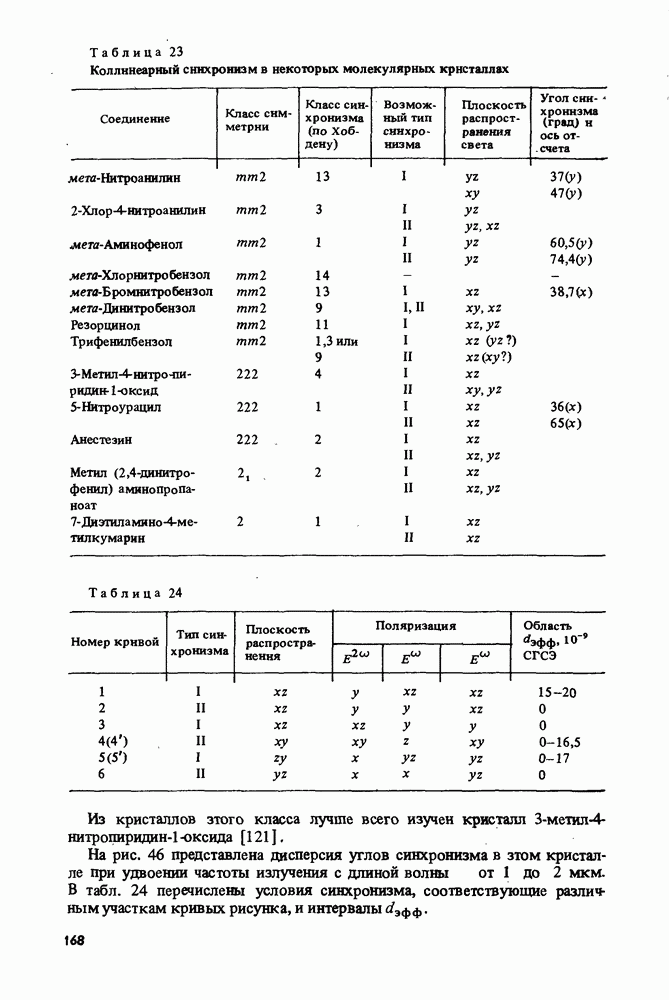
- 5.3. Коллинеарный синхронизм в некоторых молекулярных кристаллах
- 5.4. Прочие случаи синхронизма (синхронизм в растворах и жидких кристаллах)
- ГЛАВА 6. ВОЗМОЖНОСТИ ТЕХНИЧЕСКОГО ПРИМЕНЕНИЯ МОЛЕКУЛЯРНЫХ КРИСТАЛЛОВ
- 6.1. Ионные и молекулярные кристаллы с нелинейной восприимчивостью
- 6.2. Модуляторы, дефлекторы, гетеродины
- 6.3. Генерация и усиление электромагнитного излучения в результате нелинейного преобразования спектра оптической накачки
- 6.4. Преобразование ИК-излучения в оптический диапазон
- 6.5. Использдвание векторного синхронизма в молекулярных кристаллах для создания логических и других нелинейных элементов
- 6.6. Наиболее перспективные молекулярные кристаллы
- ЗАКЛЮЧЕНИЕ