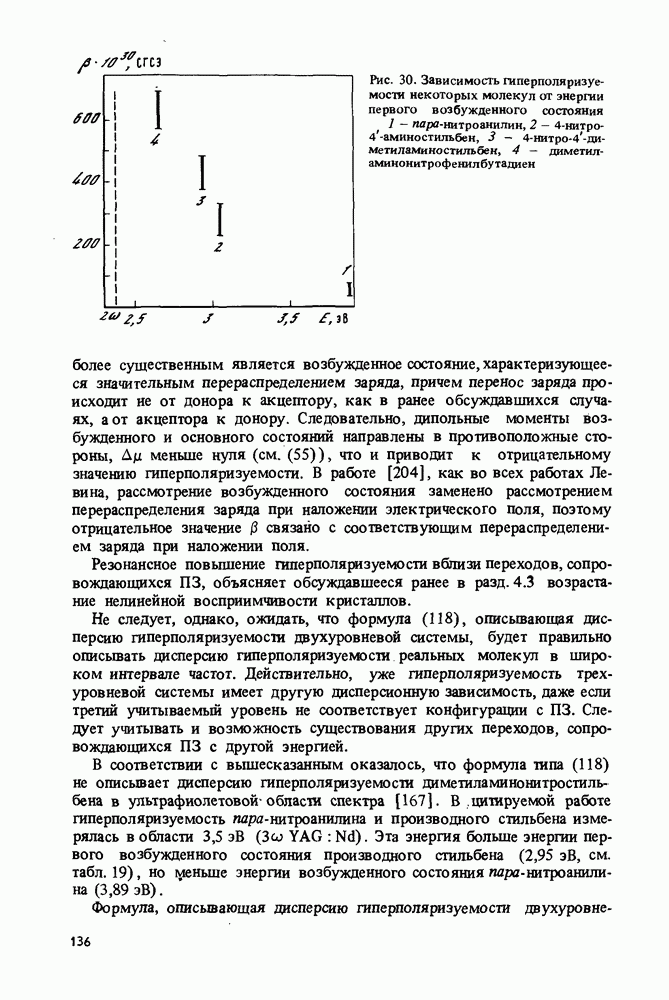
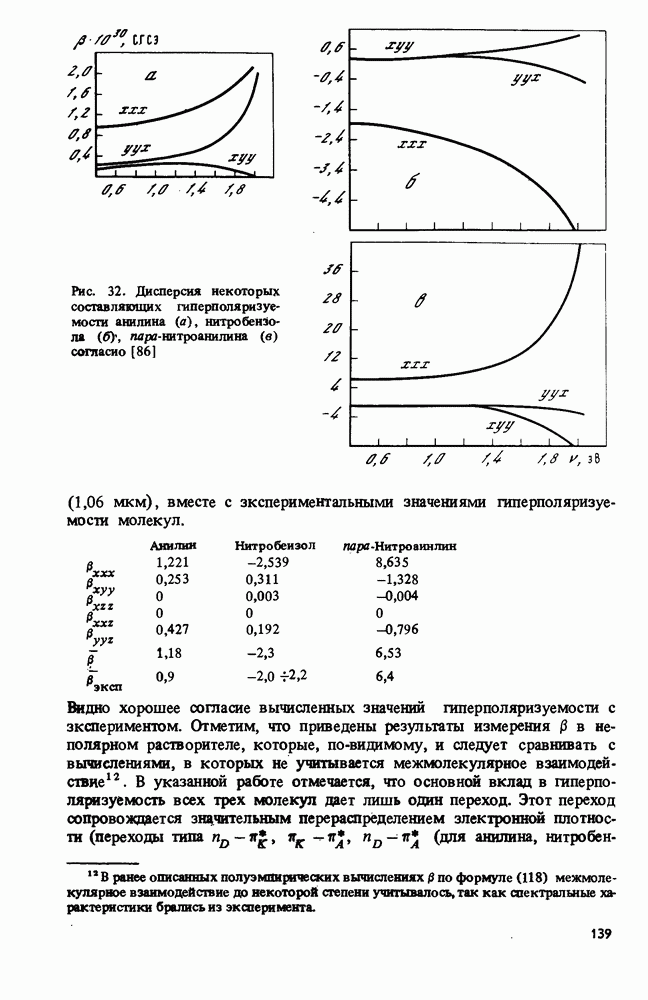
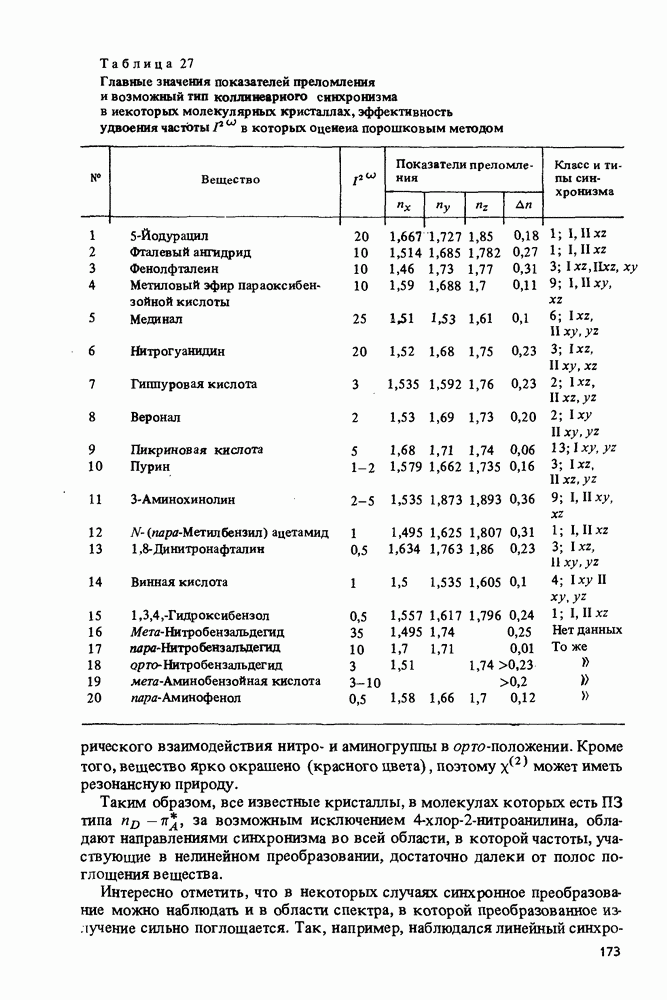
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.2. Феноменологическое описание нелинейных эффектов. Нелинейная поляризация (одномерный случай)
Для описания взаимодействия оптического излучения с веществом обычно приходится методами квантовой механики определять динамическую поляризацию среды под действием электромагнитного поля, а затем, подставляя значения поляризации в уравнения Максвелла, рассчитывать поля. Такое описание справедливо лишь при слабом и ограниченном во времени и пространстве взаимодействии внешнего электромагнитного поля со средой. В противном случае необходимо решать самосогласованную задачу, рассматривал одновременно квантовомеханическую задачу и уравнения Максвелла [1].
При исследованиях причин возникновения нелинейных оптических эффектов часто можно ограничиться материальными уравнениями, описывающими динамическую поляризацию среды, использовав лишь связанные с уравнениями Максвелла законы сохранения энергии и импульса элементарных возбуждений (фотонов, фононов и т.д.), участвующих в преобразовании.
Пусть  спектральные составляющие разложения напряженности поля
спектральные составляющие разложения напряженности поля  в ряд Фурье. Закон сохранения энергии выражается в виде
в ряд Фурье. Закон сохранения энергии выражается в виде

где  и
и  частоты полей или квантов возбуждения до и после взаимодействия.
частоты полей или квантов возбуждения до и после взаимодействия.
Амплитуды полей могут достаточно сильно измениться в результате взаимодействия только при выполнении условий согласования фаз, что
отражается условием сохранения импульса фотонов, участвующих в преобразовании

Материальные уравнения, описывающие нелинейные оптические эффекты, можно найти в целом ряде работ, например в [1-8]. В простейшем одномерном случае, в предположении слабой нелинейности, когда можно ограничиться несколькими членами разложения динамической поляризации в ряд по степеням напряженности поля, поляризацию среды можно записать в виде

где а  линейная поляризуемость,
линейная поляризуемость,  квадратичная поляризуемость (нелинейная поляризуемость низшего порядка) и т.д.
квадратичная поляризуемость (нелинейная поляризуемость низшего порядка) и т.д.
Рассмотрим распространение двух волн с напряженностью

в среде, обладающей отличной от нуля нелинейной поляризуемостью низшего порядка (3. В предположении линейной суперпозиции этих волн, ограничиваясь вторым членом разложения (3), получим

Так как  (3), легко заметить, что поляризация содержит несколько спектральных компонент, частоты которых отличаются от первоначальных:
(3), легко заметить, что поляризация содержит несколько спектральных компонент, частоты которых отличаются от первоначальных:

Простейшей моделью среды, обладающей нелинейной зависимостью поляризации, от приложенных полей, является совокупность  ангармонических осцилляторов [19]. Модель позволяет выявить все основные свойства нелинейной поляризуемости второго порядка. Она полезна как для выяснения физического смысла более общих свойств нелинейных поляризуемостей, так и для установления особенностей молекулярных кристаллов.
ангармонических осцилляторов [19]. Модель позволяет выявить все основные свойства нелинейной поляризуемости второго порядка. Она полезна как для выяснения физического смысла более общих свойств нелинейных поляризуемостей, так и для установления особенностей молекулярных кристаллов.
Движение заряда, являющегося классическим ангармоническим осциллятором, записывается в виде

где  затухание возбуждения электрона,
затухание возбуждения электрона,  энгармонизм,
энгармонизм,  приложенное электрическое поле.
приложенное электрическое поле.

где  Решение ищется в виде степенного ряда
Решение ищется в виде степенного ряда

(предполагается, что энгармонизм мал, поэтому влияние его на решение мало).
Подставляя это выражение в (5) и собирая члены одного порядка по полю, получим уравнения для нахождения 

Уравнение (7) решается сразу:

Подставляя это значение в (8), получаем для 

Зная  можно определить поляризацию:
можно определить поляризацию:

Для линейной поляризации имеем

Для поляризации, квадратичной по полю:

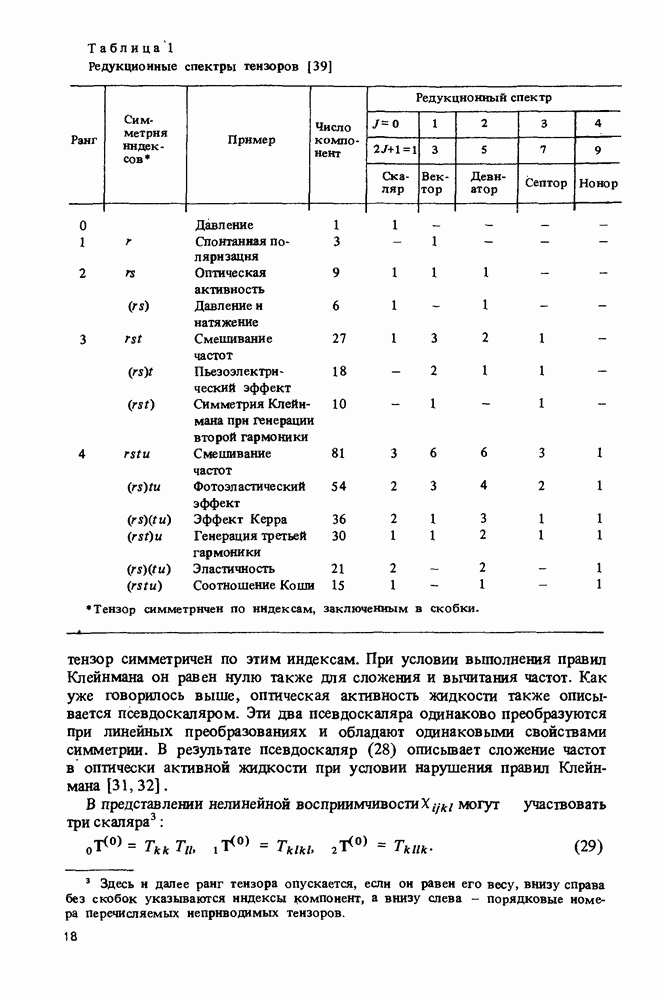
Из (12) следует, что нелинейная поляризуемость второго порядка зависит от произведения линейных восприимчивостей на частотах, участвующих в преобразовании.
Можно ввести приведенную нелинейную восприимчивость:

Эту величину иногда называют "постоянной Миллера" [20]. Основанием для такого наименования является факт, Что приведенные нелинейные восприимчивости большого количества неорганических полупроводниковых кристаллов различаются не более чем в два раза, в то время как неприведенные нелинейные восприимчивости различаются на несколько порядков. Так, нелинейная восприимчивость арсенида галлия превосходит нелинейную восприимчивость дигидрофосфата калия  на три порядка, а приведенные нелинейные восприимчивости этих веществ различаются вдвое.
на три порядка, а приведенные нелинейные восприимчивости этих веществ различаются вдвое.
Поскольку  [10], правило Миллера утверждает, что большие нелинейные восприимчивости неорганических материалов обычно связаны с большими показателями преломления
[10], правило Миллера утверждает, что большие нелинейные восприимчивости неорганических материалов обычно связаны с большими показателями преломления  Действительно, для неорганических кристаллов с большими нелинейными восприимчивостями обычно
Действительно, для неорганических кристаллов с большими нелинейными восприимчивостями обычно 
Ниже будет показано, что для молекулярных кристаллов правило Миллера не выполняется. Из (13) следует, что приведенная нелинейная восприимчивость (постоянная Миллера) пропорциональна энгармонизму осциллятора и.
Предполагая, что взаимодействующие частоты лежат в области прозрачности кристалла  из (10), (12) можно заключить, что восприимчивость второго порядка будет чисто действительной величиной,
из (10), (12) можно заключить, что восприимчивость второго порядка будет чисто действительной величиной,

Согласно (4) и (11) поляризация среды содержит компоненты с любыми возможными комбинационными частотами. Чтобы установить, какие из них будут иметь наибольшие амплитуды, необходимо рассмотреть фазы распространяющихся волн.
Согласно (4) импульс фотонов с частотой  равен
равен

 показатель преломления среды на частоте
показатель преломления среды на частоте  Фотоны с таким волновым числом образуются за счет нелинейного взаимодействия в каждой точке среды. В той же среде распространяется ранее возникшая в ней волна частоты
Фотоны с таким волновым числом образуются за счет нелинейного взаимодействия в каждой точке среды. В той же среде распространяется ранее возникшая в ней волна частоты  , волновое число которой
, волновое число которой  Обе волны частоты
Обе волны частоты  окажутся в фазе, если
окажутся в фазе, если  При этом волна частоты
При этом волна частоты  усиливается.
усиливается.
В общем случае условие согласования фаз сводится к (2). Подробнее об условии согласования фаз см. гл. 5.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. НЕЛИНЕЙНАЯ ВОСПРИИМЧИВОСТЬ
- 1.1. Электроны и нелинейная восприимчивость
- 1.2. Феноменологическое описание нелинейных эффектов. Нелинейная поляризация (одномерный случай)
- 1.3. Феноменологическое описание нелинейных эффектов (трехмерный случай). Симметрия
- 1.4. Описание нелинейных восприимчивостей с помощью неприводимых тензоров
- 1.5. Гиперполяризуемости. Связь с нелинейной восприимчивостью среды
- 1.6. Квантовомеханическое описание нелинейной восприимчивости. Двухуровневая и трехуровневая системы, двухзонная модель
- 1.7. Вклад фононов в нелинейную восприимчивость. Электрооптический эффект, электрохромизм
- ГЛАВА 2. МОЛЕКУЛЫ И МОЛЕКУЛЯРНЫЕ КРИСТАЛЛЫ
- 2.2. Электронные переходы в молекулах
- 2.3. Некоторые методы квантовой химии
- 2.4. Донорно-акцепторная сила заместителей, степень ПЗ
- 2.5. Комплексы переноса заряда
- 2.6. Молекулярные кристаллы
- 2.7. Структура конкретных молекулярных кристаллов
- 2.8. Механические и оптические свойства молекулярных кристаллов
- ГЛАВА 3. СИНТЕЗ И МЕТОДЫ ИССЛЕДОВАНИЯ МОЛЕКУЛЯРНЫХ КРИСТАЛЛОВ
- 3.1. Приготовление образцов для исследования оптических характеристик
- 3.2. Измерение коэффициентов преломления
- 3.3. Электрооптический эффект, электрохромизм, измерение дипольных моментов возбужденных состояний
- 3.4. Измерение нелинейной восприимчивости
- 3.5. Методы изучения синхронизма в монокристаллах
- 3.6. Оценка нелинейных восприимчивостей и наличия синхронизма порошковым методом
- 3.7. Измерение гиперполяризуемости
- ГЛАВА 4. ПРИРОДА НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СВОЙСТВ МОЛЕКУЛЯРНЫХ КРИСТАЛЛОВ
- 4.1 Происхождение нелинейной восприимчивости третьего порядка
- 4.2. Оценка различных методов экспериментального определения нелинейной восприимчивости второго порядка
- 4.3. Особенности нелинейных восприимчивостей второго порядка молекулярных кристаллов. Роль переноса заряда
- 4.4. Расчет гиперполярнзуемостей молекул и нелинейных восприимчивостей кристаллов по аддитивной схеме. Учет распределения зарядов в основном состоянии
- 4.5. Расчет гиперполяризуемостей молекул при отсутствии аддитивности. Учет возбужденных состояний. Дисперсия гиперполяризуемости
- 4.6. Электрохромизм. Линейный электрооптический эффект
- 4.7. Нелинейная оптика жидких кристаллов
- ГЛАВА 5. ФАЗОВЫЙ СИНХРОНИЗМ В МОЛЕКУЛЯРНЫХ КРИСТАЛЛАХ
- 5.1. Линейный (коллинеарный) синхронизм в двуосных кристаллах
- 5.2. Векторный синхронизм в молекулярных кристаллах
- 5.3. Коллинеарный синхронизм в некоторых молекулярных кристаллах
- 5.4. Прочие случаи синхронизма (синхронизм в растворах и жидких кристаллах)
- ГЛАВА 6. ВОЗМОЖНОСТИ ТЕХНИЧЕСКОГО ПРИМЕНЕНИЯ МОЛЕКУЛЯРНЫХ КРИСТАЛЛОВ
- 6.1. Ионные и молекулярные кристаллы с нелинейной восприимчивостью
- 6.2. Модуляторы, дефлекторы, гетеродины
- 6.3. Генерация и усиление электромагнитного излучения в результате нелинейного преобразования спектра оптической накачки
- 6.4. Преобразование ИК-излучения в оптический диапазон
- 6.5. Использдвание векторного синхронизма в молекулярных кристаллах для создания логических и других нелинейных элементов
- 6.6. Наиболее перспективные молекулярные кристаллы
- ЗАКЛЮЧЕНИЕ