1.6. Квантовомеханическое описание нелинейной восприимчивости. Двухуровневая и трехуровневая системы, двухзонная модель

Квантовомеханический расчет нелинейных поляризуемостей системы в принципе не отличается от расчета ее линейной поляризуемости. Взаимодействие среды с внешним электрическим полем рассматривается в дипольном приближении, т.е. энергия взаимодействия представляется в виде

где поляризуемость среды. Тогда полный гамильтониан системы есть

где гамильтониан невозмущенной системы. При использовании обычной теории возмущений [49] поляризуемость представляют в виде (15).

Тогда энергия системы имеет вид [50]

где члены разложения по полю. Представление полной энергии в виде разложения по степеням электрического поля (48) позволяет найти восприимчивость порядка по формуле

Значения и т.д. получаются с помощью стандартной теории возмущений как поправки соответствующих порядков.

Обычно энергию взаимодействия системы (47) с внешним полем можно рассматривать как малый параметр, т.е. применима стандартная теория возмущений. Эта возможность следует из сравнения этой энергии с собственной энергией системы. Действительно, для потока излучения мощностью порядка энергия взаимодействия диполей величиной в с электромагнитным полем в частотных единицах равна в то время как энергия взаимодействия ядер с электронами в атомах

Более общим способом описания измейения состояния системы под влиянием периодического возмущения является метод матрицы плотности позволяющий рассматривать смешанные состояния, которым не может быть поставлена в соответствие волновая функция [49]. Матрица плотности системы при наличии возмущений находится методом последовательных итераций:

Здесь — матрица плотности -приближения. Нелинейные восприимчивости и получаются соответственно во втором и третьем приближении. Введение матрицы плотности позволяет также учесть наличие в системе затухания.

С помощью метода матрицы плотности для линейной поляризуемости и нелинейных восприимчивостей получено

В формуле для нелинейной восприимчивости первое суммирование производится по членам, получающимся путем перестановок пар второе суммирование — по состояниям системы; - матричные элементы проекции оператора дипольного момента системы

на ось диагональные элементы матрицы плотности, имеющие смысл населенности уровня, Формула для нелинейной восприимчивости третьего порядка получается довольно длинной и здесь не приводится.

Вышеприведенные формулы получены в предположении, что возможно разложение энергии возмущения по степеням внешних полей.

Иногда для оценки исследуемого эффекта приходится удерживать несколько или даже все степени компонент поля, частоты которых близки к резонансу. Такое положение возникает, например, при исследовании насыщения магнитного резонанса на радиочастотах и в СВЧ-диапазоне. Наиболее известным примером является эффект насыщения двухуровневой системы при резонансе [1]:

Здесь фурье-компонента с нулевой частотой диагонального матричного элемента выражена через все степени квадрата модуля недиагонального матричного элемента взаимодействия системы с полем При когерентном возмущении всегда можно удержать все степени одной фурье-компоненты с помощью перехода к вращающей системе координат.

В тех случаях, когда можно пренебречь затуханием возможна перегруппировка членов в выражении для нелинейной восприимчивости -Значительно компактнее становится и выражение для нелинейной восприимчивости третьего порядка. В этом случае

Если каждое из состояний системы можно описать определенной волновой функцией, то можно перейти от описания системы с помощью

матрицы плотности и матриц Гейзенберга к описанию с помощью волновых функций. Если, кроме того, выделить чисто электронные части нелинейных восприимчивостей, то в приближении Франка-Кондона получим для линейной поляризуемости и нелинейных восприимчивостей

Здесь волновая функция и энергия возбужденного состояния, волноваяфункция и энергия основного состояния, оператор дипольного момента где оператор дипольного момента основного состояния. Оператор в выражениях (52), (53) вместо оператора в выражениях (52), (53) появляется при учете франк-кондоновского сдвига. Формулы (52), (53), как и формулы (52), (53), описывают поляризуемости и гиперполяризуемости среды или молекулы в зависимости от того, являются ли волновыми функциями среды или молекулы. В соответствии с этим выбираются декартовы оси, связанные со средой или отдельной молекулой.

Если соотношение (52) имеет смысл записать в более развернутой форме, более ясно учитывающей разнбсть диагональных матричных элементов дипольного момента:

Здесь матричные элементы оператора дипольного момента между состояниями

Выражения легко получаются с помощью стандартной теории возмущений при использовании разложения (48) и формулы (49) (см., например, [50]).

Таким образом, для полного расчета нелинейных восприимчивостей, так же как и для линейных поляризуемостей, необходимо определять матричные элементы операторов дипольных моментов переходов между всеми состояниями системы. Для этого, в свою очередь, необходимо знать волновые функции системы во всех возбужденных состояниях.

Очевидно, что учет волновых функций различных возбужденных состояний дает разные вклады в нелинейные восприимчивости. Для того чтобы выявить особенности состояний, учет которых дает максимальные вклады в восприимчивости, рассмотрим двухуровневую систему, т.е. систему, имеющую лишь один возбужденный уровень. В зтом случае первые члены суммы (54) равны нулю, и для компоненты нелинейной восприимчивости (гиперполяризуемости) получим

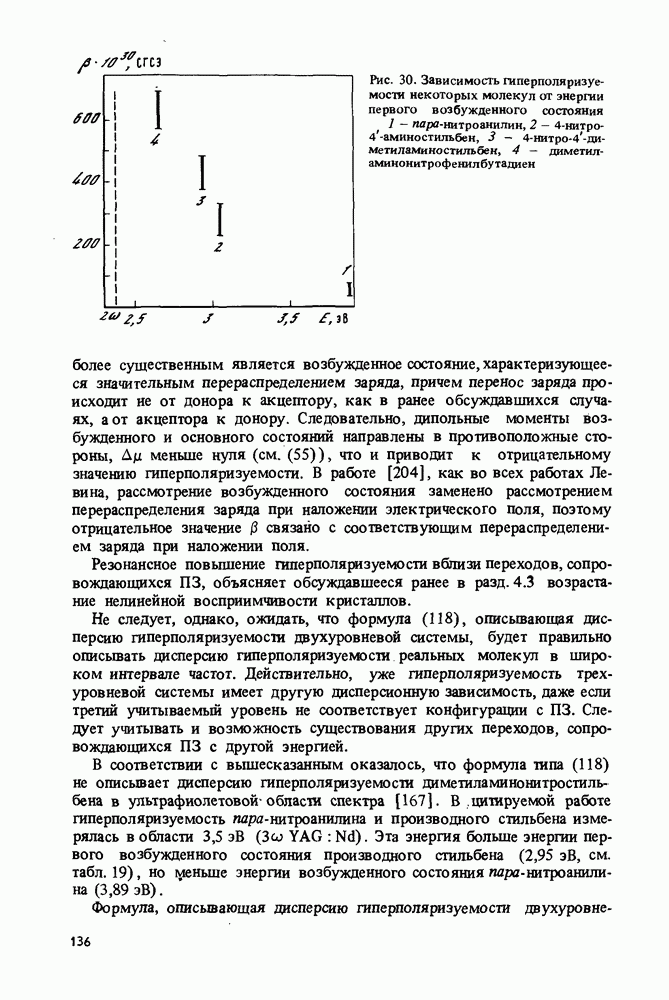
Очевидно, что двухуровневой системы (молекулы) будет велика лишь в случае, когда велик дипольный момент перехода из основного в возбужденное состояние и разность диагональных матричных элементов (дипольных моментов) основного и возбужденного состояний. Первое требование сводится к слабой связи электронов с остовом и разрешенности соответствующего перехода. Второе требование — к значительному перераспределению электронной плотности при возбуждении. Известно, что оба требования лучше всего выполняются для переходов с переносом заряда [52, 53]. Поэтому вклад в нелинейную восприимчивость переходов с переносом заряда, оцениваемый по формуле для двухуровневой системы (55), оказывается значительным (см. гл. 4). К повышению этого вклада приводит также то обстоятельство, что переходы с переносом заряда часто обладают сравнительно низкой энергией, причем частота переходов иногда близка к частоте преобразованного излучения. Это приводит к резонансному повышению

Таким образом, вывод о большом вкладе переходов с переносом заряда в гиперполяризуемость следует непосредственно из рассмотрения двухуровневой модели молекулы.

Очевидно, что те же условия возрастания нелинейной восприимчивости Должны быть справедливы и при рассмотрении нелинейных восприимчивостей полупроводников с помощью двухзонной модели [54, 55]. Однако двухзонная модель полупроводников имеет некоторые особенности. Для того чтобы их выявить, рассмотрим двухуровневую модель полупроводников. Отметим, что эта модель была исторически первой, позволившей оценить нелинейные восприимчивости ряда полупроводниковых кристаллов и объяснить возрастание в некоторых из них.

Основной идеей двухзонной модели является предположение, что во многих кристаллах, как диэлектрических, так и полупроводниковых, достаточно знать ширину запрещенной энергетической зоны чтобы с хорошей точностью описать возбуждения системы из связывающего (основного) состояния на разрыхляющую орбиталь (возбужденное состояние Линейная восприимчивость такой системы записывается как

где а — длина ребра кубической элементарной ячейки, электронная плотность, эффективная ширина запрещенной зоны для переходов в зону проводимости. Кроме того,

где эффективная ширина запрещенной зоны в гипотетическом гомеополярном (чисто ковалентном) кристалле с такой же постоянной решетки, С — величина, определяемая антисимметричной частью потенциала (ионность связи). Значения для кристаллов со структурами алмаза, цинковой обманки, вюрцита и каменной соли, для которых имеются данные сведены в таблицы (см., например [55]).

Из (55, 56) непосредственно следует, что для двухзонной модели вклад каждого электрона в нелинейную восприимчивость есть

Если принять, что начало координат находится на середине связи между рассматриваемыми атомами и потенциал С антисимметричен относительно рассматриваемой координаты х, то можно показать, что

собственные состояния гетерополярного кристалла), и выражение для принимает вид

В тех же предположениях можно получить следующие выражения для нелинейной восприимчивости третьего порядка [55]:

Из формулы (59) следует, что нелинейная восприимчивость двухзонной модели пропорциональна гетеро полярному вкладу в ширину зоны, что до некоторой степени эквивалентно требованию сильной полярности связи. Однако пропорциональность нелинейной восприимчивости разности диагональных матричных элементов при рассмотрении двухзонной модели теряется из-за предположения, что Поэтому значение перераспределения зарядов при возбуждении довольно долго не учитывалось.

В рамках двухзонйой модели ближе всего к учету этого перераспределения подходит модель Левина [56, 57]. В этой модели величина, определяющая вклад ионности связи в ширину зоны, записывается в виде

где постоянная, зависящая от параметров решетки, экранирующий фактор Томаса-Ферми, Z - число валентных электронов атома ковалентный радиус этого атома. Приложенное электрическое поле смещает связанный заряд на расстояние следовательно, вызывает поляризацию на единицу объема

Это вызывает изменение С на

коэффициент пропорциональности,

В свою очередь, согласно [57], изменение С вызывает изменение ширины запрещенной зоны и приводит к изменению линейной восприимчивости от

Вычисляя коэффициенты при первой и второй степени поля в выражении

можно получить

Из соотношения (60) следует, что приведенная нелинейная восприимчивость пропорциональна ионности связи С.

Та же особенность — связь с переносом (перераспределением) заряда при наложении внешнего поля — получается при переходе от точечных зарядов к распределенным, проведенном Тангом и Флицанисом [58, 59].

Поскольку наложение внешнего поля, как и любое возмущение, смешивает волновые функции основного и возбужденного состояний [49], перенос заряда при наложении внешнего поля до некоторой степени аналогичен переносу заряда при возбуждении. Однако, как уже говорилось ранее, эта аналогия теряется при рассмотрении двухзонной модели. Поэтому мысль о необходимости учета перераспределения зарядов при возбуждении не была высказана ни в одной работе, посвященной двухзонной модели.

Таким образом, рассмотрение двухуровневой системы и двухзонной модели приводит к выводу о важности перераспределения заряда при

возбуждений и приложении внешнего поля. Это перераспределение особенно велико при наличии переноса заряда (ПЗ).

Менее очевидна преобладающая роль ПЗ при рассмотрении трехуровневой системы. В этом случае из

Ясно, что члены формулы (61), содержащие разности диагональных матричных элементов, особенно велики при наличии ПЗ. Однако для вывода о роли ПЗ надо оценить также члены, содержащие произведения трех недиагональных дипольных моментов переходов.

Если переходы в состояния 1 и 2 интенсивны и сопровождаются лишь незначительным перераспределением электронной плотности, т.е. малы то эти состояния имеют одинаковую четность и переход между ними запрещен, т.е. мал дипольный момент Тем самым малы все три слагаемых (61). Наоборот, если один из переходов, например сопровождается ПЗ, то велико значение матричный элемент может оказаться значительным, и при наличии такого перехода велики первый и третий члены (61). Таким образом, и из рассмотрения трехуровневой системы следует вывод о значительном вкладе в х переходов, сопровождающихся ПЗ. Те же рассуждения применимы к многоуровневой системе (см. (54)).

Оценим теперь возможные величины исходя из формулы (55). Если ограничиться случаем, когда сопп, то нелинейные восприимчивости не будут зависеть от частоты. Учитывая, что где заряд электрона, а — атомный радиус, и обозначая характерную частоту движения электрона через получим

С помощью (41), (43) получим оценку

Считая, что а характерная частота движения электрона получим так называемое атомное поле — характерная величина электрического поля на расстоянии а от ядра. Отсюда следует, что атомное поле определяет радиус сходимости ряда (3), описывающего поляризацию вещества. Таким образом, условие применимости разложения (3) имеет вид