1.4. Описание нелинейных восприимчивостей с помощью неприводимых тензоров

В последнее время получило широкое распространение описание физических свойств среды с помощью неприводимых тензорных величин. Такой подход может быть применен и к описанию нелинейных восприимчивортей [38, 39]. Выражение тензора нелинейной восприимчивости в виде суммы тензоров более низких рангов или тензоров, имеющих меньшее число независимых компонент, позволяет лучше понять связь между свойствами среды и свойствами молекул, из которых она состоит.

Тензор ранга имеет компонент. При линейном преобразовании координат компоненты тензора преобразуются, согласно определению тензора [22], как

где матрица линейного преобразования. Здесь, как и в (15), предполагается суммирование по индексам, повторяющимся дважды.

Согласно (26) каждая компонента тензора в одной системе координат зависит от всех компонент этого тензора в другой системе координат. Это затрудняет переход от микроскопических свойств отдельных молекул или элементарных ячеек к макроскопическим свойствам кристаллов.

Каждый тензор ранга в декартовой системе координат может быть записан как прямая сумма неприводимых тензоров Неприводимый тензор имеет вес (целое число, меньшее n или равное ему) и содержит лишь независимых компонент. Каждая из независимых компонент при повороте осей координат преобразуется подобно базисным функциям неприводимого представления группы вращений, например сферическим гармоникам Кроме ранга и веса тензоров, им, как и физическим величинам, которые они описывают, приписывается четность равная для истинного тензора и для псевдотензора. Неприводимый

тензор, для которого называется истинным неприводимым тензором, тензор с четностью - неприводимым превдотензором. Все компоненты разложения истинного тензора на неприводимые тензоры, для. которых четное число, являются истинными тензорами, для которых нечетное — псевдотензорами (обратное имеет место для псевдотензоров).

Неприводимый тензор преобразуется как полином порядка т.е. компоненты каждого неприводимого тензора при преобразовании координат выражаются только через самих себя, а не через компоненты других тензоров. Это является одним из преимуществ представления тензора в виде суммы неприводимых тензоров. Кроме того, такое представление позволяет непосредственным образом выявить влияние среды на физические величины, представляемые тензорами, а также сравнивать между собой свойства разных кристаллов, часто имеющих разную симметрию.

Неприводимые тензоры могут быть записаны в декартовых и полярных координатах. Представление тензоров в полярных координатах широко используется в спектроскопии [40]. Разложение тензоров на неприводимые тензоры в полярных координатах, с использованием 3 символов, описано, например, в [41 и 38]. Мы ограничимся в основном декартовыми тензорами. Каждый декартов тензор представляется в виде суммы декартовых неприводимых тензоров

ранг и вес тензора, четность, индекс введен для обозначения разных тензоров одинакового веса, участвующих в разложении.

В принципе разложение (27) не вполне однозначно. Это связано с тем, что одну и ту же физическую величину можно описать тензорами разных рангов. Так, величина, описываемая антисимметричным тензором ранга всегда может быть описана псевдотензором меньшего ранга. Например, антисимметричный тензор второго ранга

где А — векторный потенциал, эквивалентный магнитной индукции которая является аксиальным вектором (псевдовектором), причем

тензор Леви-Чивита, компоненты которого равны если четная (нечетная) перестановка чисел 1, 2, 3, и равны нулю в остальных случаях. Точно так же оптическая активность жидкости может быть описана псевдоскаляром а также антисимметричным тензором третьего ранга. Компонента скаляра связана с компонентами тензора с помощью

Наиболее удобной формой, позволяющей избежать неоднозначности, является запись неприводимого тензора ранга и веса в его "естественной" форме в которой Тензор в этой форме полностью симметричен, т.е. инвариантен при любой перестановке индексов, и имеет равный нулю след (результат свертки по любой паре индексов, т. е.

где — унитарный тензор второго ранга, или символ Кронекера). Действительно, такой тензор имеет независимых компонент, Для преобразования-тензора к его естественной форме применяют свертки с тензорами или симметризацию и вычитание следов.

Для сред, обладающих разной симметрией, тензорыи их неприводимые представления имеют разное число компонент. Для сравнения между собой физических величин, описываемых этими тензорами, используют нормы тензоров. Нормой тензора называется сумма квадратов всех его элементов, т.е. свернутое по всем индексам произведение тензора самого на себя. По определению норма тензора должна быть равна сумме норм его неприводимых представлений:

Отметим, что норма тензора третьего ранга, определяющего генерацию второй гармоники излучения в среде, обладающей пренебрежимо малой дисперсией, имеет вид

Для того чтобы соотношение выполнялось, после разложения тензора на неприводимые представления в последние вводят нормировочные множители.

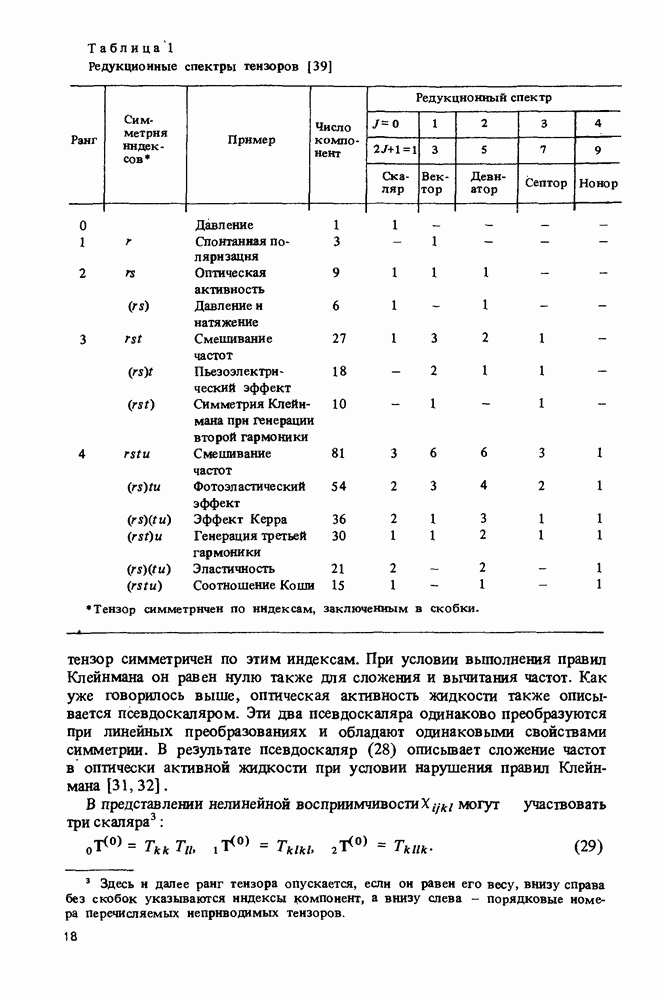
Рассмотрим смысл некоторых неприводимых тензоров, встречающихся в представлениях линейных и нелинейных поляризуемостей. Число различных членов разложения приведено в табл. 1.

Из таблицы видно, например, что в общем случае тензор третьего ранга имеет независимых компонент. Он является суммой одного псевдоскаляра трех векторов тензоров второго ранга — псевдодевиаторов и одного тензора третьего ранга - септора

Неприводимый тензор ранга имеет одну компоненту. Он участвует в разложении (27) как скаляр или псевдоскаляр в зависимости от того, имеет ли тензор четный нечетный ранг. Скаляр, участвующий в представлении линейной поляризуемости, имеет вид

(нормировочные коэффициенты опущены). Он, естественно, симметричен и описывает среднюю поляризуемость среды.

В представлении нелинейной восприимчивости минимального порядка, описываемой тензором третьего ранга, может принимать участие псевдоскаляр

Здесь и далее

Он антисимметричен по второму и третьему индексам. Рассматриваемый псевдоскаляр равен нулю для удвоения частот, так как соответствующий

Таблица 1 (см. скан) Редукционные спектры тензоров [39]

тензор симметричен по этим индексам. При условии выполнения правил Клейнмана он равен нулю также для сложения и вычитания частот. Как уже говорилось выше, оптическая активность жидкости также описывается псевдоскаляром. Эти два псевдоскаляра одинаково преобразуются при линейных преобразованиях и обладают одинаковыми свойствами симметрии. В результате псевдоскаляр (28) описывает сложение частот в оптически активной жидкости при условии нарушения правил Клейнмана [31,32].

В представлении нелинейной восприимчивости могут участвовать три скаляра:

При генерации третьей гармоники они совпадают, так как тензор симметричен при перестановке трех индексов. Этот скаляр описывает генерацию третьей гармоники в жидкости или газе.

Неприводимый тензор ранга 1 имеет три независимые компоненты. Это вектор (псевдовектор) в зависимости от нечетности (четности) исходного тензора.

В описании нелинейной восприимчивости могут участвовать три вектора. Они легко получаются в виде следов тензора:

(нормировочные коэффициенты, как и раньше, опущены). Два из указанных векторов равны друг другу, если равны две частоты из участвующих в преобразовании. При выполнении условий Клейнмана, т.е. в отсутствие дисперсии, равны между собой все три вектора.

Компоненты этого вектора могут быть представлены в виде

(в выражении (30) введены нормирующие множители).

Из выражений (30), (30) следует, что векторная часть нелинейной восприимчивости равна нулю, если отсутствует полярная ось симметрии (или плоскость симметрии). Так, она равна нулю для кристаллов, относящихся к классу . В тех же случаях пропадает пироэлектрический эффект, а также пьезоэлектрический эффект, зависящий от гидростатического давления.

Для кристаллов, относящихся к классам и т. д., вектор одну компоненту, направленную по полярной оси:

Для класса этот вектор содержит две компоненты:

В разложении нелинейной восприимчивости могут принимать участие шесть псевдовекторов (см. табл. 1):

Неприводимые тензоры ранга 2 (девиаторы и псевдодевиаторы) содержат пять независимых компонент. Девиаторы всегда описывают анизотропию рассматриваемых тензоров. Например, девиатор, описывающий анизотропию тензора линейной восприимчивости, непосредственно связан с двулучепреломлением. Его компоненты пропорциональны

Для получения компонент девиатора, описывающего тензор производится свертка с тензором симметризация и вычитание следа. Для тензора третьего ранга соответствующие псевдодевиаторы получаются следующим образом:

В разложении принимают участие два псев до девиатора. Они описывают дисперсию восприимчивости кристаллов (аналогично этому девиаторы, участвующие в разложении тензора оптической активности, описывают изменения оптической активности, вносимые кристаллической структурой). Псевдодевиаторы равны друг другу в случае, если в нелинейном преобразовании участвуют две волны с равными частотами. При отсутствии дисперсии, т.е. при выполнении условий Клейнмана, псевдодевиаторы равны нулю и для сложения частот.

Шесть независимых девиаторов, участвующих в разложении могут быть записаны следующим образом:

Девиаторы описывают анизотропию нелинейной восприимчивости. Например, в случае среды, имеющей ось симметрии, девиатор описывает различие эффекта вдоль оптической оси и в плоскости, перпендикулярной оси.

В разложении участвует тензор третьего ранга — септор. Общий способ получения септора, участвующего в представлении тензора третьего ранга:

где

Компоненты равны 3, если равны 1, если равны два из трех индексов в (31), и равны нулю в остальных случаях.

Для таких кристаллографических классов, как нелинейная восприимчивость низшего порядка содержит только септорную часть.

Общий вид компонент септорной части нелинейной восприимчивости с учетом нормировки:

Для класса септор имеет две составляющие:

Для класса 222 септор имеет одну компоненту, пропорциональную

Тензоры ранга 3, входящие в разложение (псевдосепторы), получают аналогично (31):

Кроме перечисленных, в разложении тензора участвует тензор ранга 4 — нонор. Он получается следующим образом:

где (сумма по это сумма по всем компонентам, получающимся при перестановке индексов).

При наличии двух осей симметрии нонор описывает различие восприимчивостей вдоль одной из осей и "перекрестной" восприимчивости

В дальнейшем чаще всего мы будем оценивать векторные и скалярные часта нелинейных восприимчивостей, так как связь этих величин на микро- и макроуровнях очевидна. Все остальные составляющие возникают в основном за счет анизотропии среды, и проследить их вклад на молекулярном уровне значительно труднее.