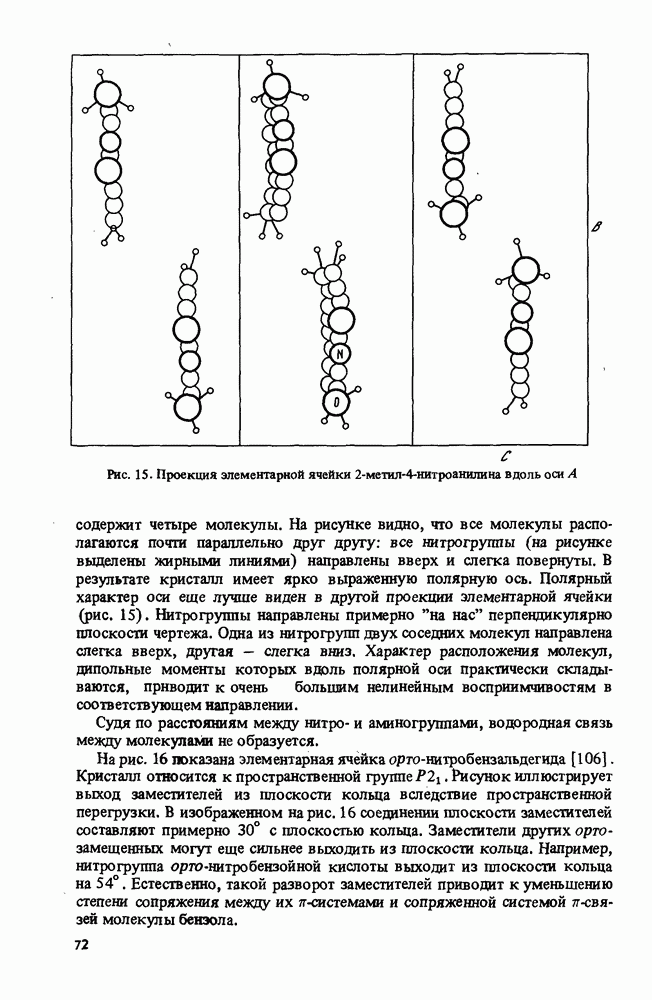
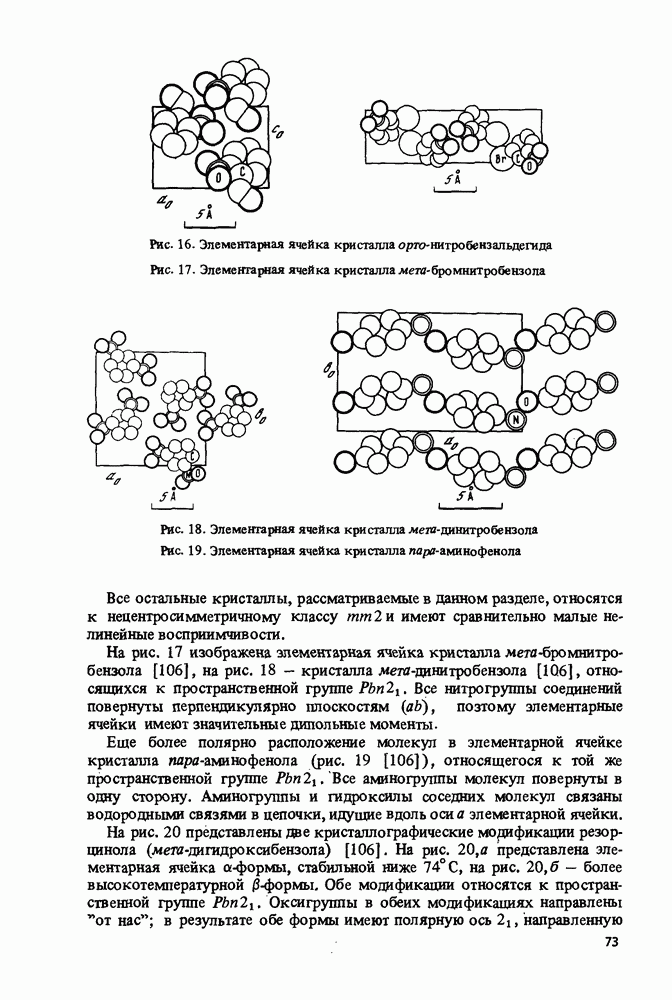
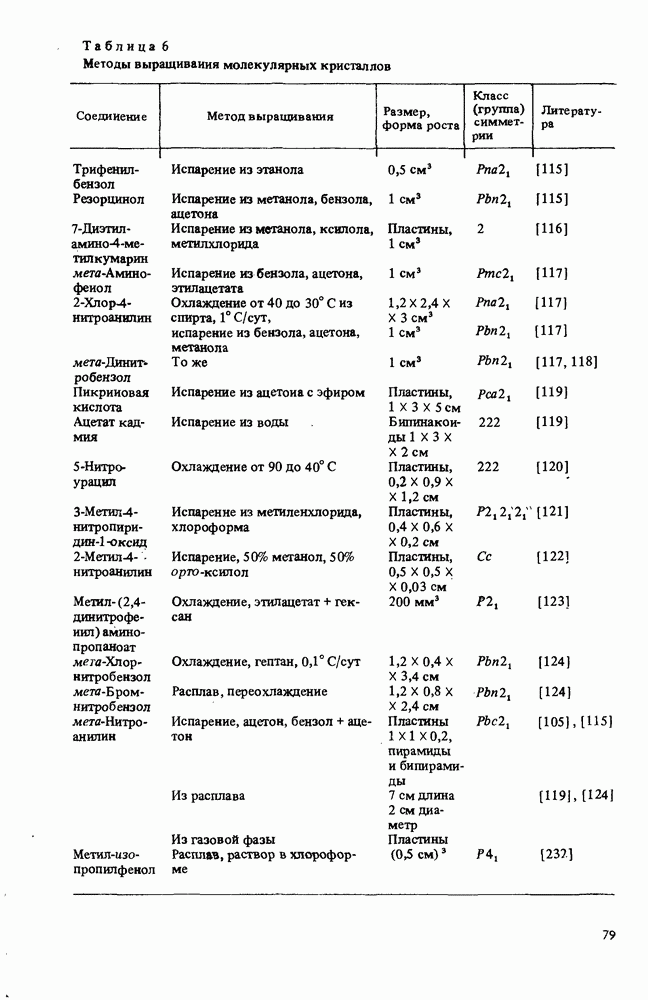
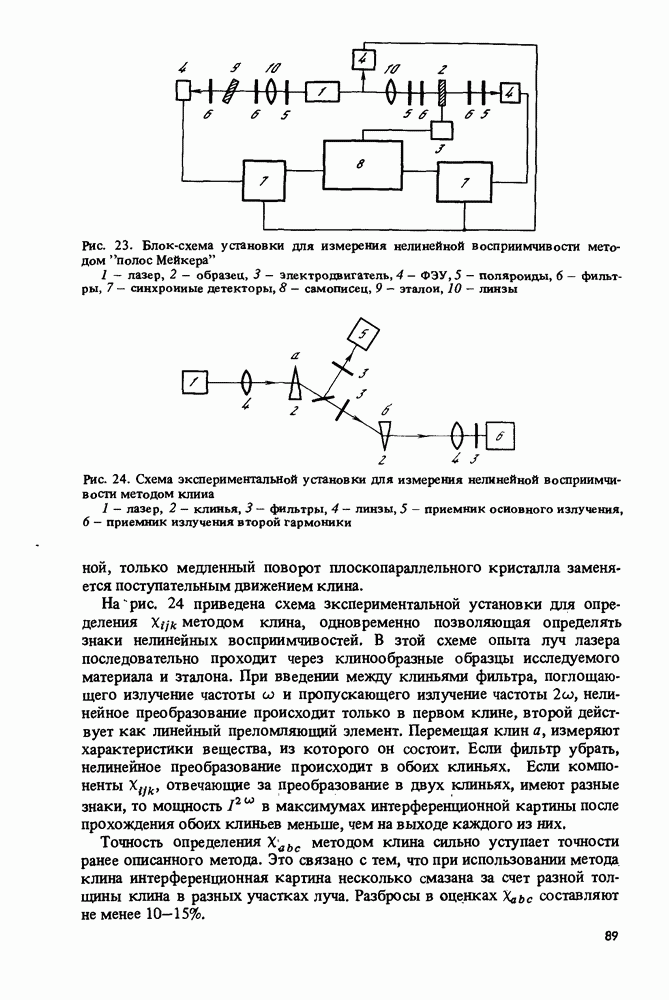
5.1. Линейный (коллинеарный) синхронизм в двуосных кристаллах

Подавляющее большинство молекулярных кристаллов оптически двуосно. Рассмотрим условия синхронизма в таких кристаллах.

При выполнении условий линейного синхронизма все три волновых вектора в (2) коллинеарны и указанная формула может быть заменена условием, налагаемым на показатели преломления:

Условие кчллинеарного синхронизма (122) для удвоения частоты имеет вид

Здесь значения некоторых показателей преломления (не обязательно главных) для основного излучения и его второй гармоники.

Рассматривают два типа коллинеарного синхронизма. При синхронизме первого типа взаимодействуют волны частоты одной поляризации; волна частоты поляризована в перпендикулярном направлении:

При синхронизме второго типа взаимодействующие волны имеют различную поляризацию:

Для нахождения возможных направлений синхронизма необходимо строить поверхности волновых нормалей или поверхности индексов кристаллов [10]. Для построения поверхности волновых нормалей из некоторой точки внутри кристалла как из начала координат в направлении единичного вектора нормали к волновому фронту и откладываются два вектора, длины которых пропорциональны двум возможным значениям фазовой скорости. Например, для направления, соответствующего оси кристалла, будут отложены величины, пропорциональные

Аналитическое выражение, описывающее поверхность волновых нормалей Френеля, имеет вид [10]

Здесь показатель преломления для света, направление волновой нормали которого задано углами в и ( — угол между направлением и осью z показателей преломления, угол между проекцией этого направления на плоскость и осью главные значения показателей преломления. Можно показать, что для каждого значения в и можно найти два значения являющиеся решениями биквадратного уравнения (126), соответствующие двум взаимно перпендикулярным поляризациям распространяющегося в этом направлении света. Исключение составляют два направления, в которых эти два значения совпадают. Эти направления соответствуют двум осям кристалла.

На рис. 34 показана часть поверхности волновых нормалей двуосного кристалла. Направление соответствует оптической оси. Другая оптическая ось находится в октанте, не показанном на рисунке.

Для графического нахождения направлений синхронизма необходимо построить поверхности нормали для частот, участвующих в преобразовании, и искать пересечения этих поверхностей. Для этой цели, однако, можно строить не поверхности волновых нормалей, а поверхности

индексов, или поверхности волновых векторов, отличающиеся от поверхностей нормалей тем, что в направлении вектора и, заданного углами в и у, откладывается не фазовая скорость, а длина вектора к, т.е. величина, пропорциональная показателям преломления Очевидно, что величины показателей преломления также можно найти по формуле (126). Поверхности индексов имеют несколько другую форму, чем поверхности волновых нормалей, однако, очевидно, имеют те же точки "самопересечения" (см. рис. 35).

При поисках направлений синхронизма первого типа надо найти пересечения поверхностей индексов, построенных для света частоты и

Рис. 34. Схема поверхности волновых нормалей двуосного кристалла

Для определения направлений синхронизма второго типа следует искать пересечение поверхности индексов, построенной для света частоты с поверхностью, соответствующей "смешанному" показателю преломления, т.е. для Последняя строится следующим образом.

Для каждого значения в и вычисляют среднее арифметическое двух показателей преломления на частоте Это значение откладывают на радиусе-векторе, направление которого задается углами

Для точного определения направлений синхронизма необходимо знать показатели преломления кристалла с точностью до третьего-четвертого десятичного знака. Однако наличие в кристалле направлений синхронизма и их расположение в главных координатных плоскостях можно определить, зная показатели преломления с гораздо меньшей точностью. Некоторые

(см. скан)

Рис. 35. Схема поверхности волновых векторов двуосиого кристалла а — двухслойная поверхность векторов к, б - пересечения этой поверхности стремя главными плоскостями, в — контурные линии поляризаций поля на двух слоях поверхности

заключения можно сделать, зная показатели преломления лишь на одной длине волны. После этих оценок можно определить направления синхронизма методами, описанными в разд. 3.5.

В работе [174] подробно рассмотрены возможные случаи коллинеарного синхронизма в оптически двуосных кристаллах.

Приняв, что и дисперсия нормальна и мала, т.е. по соотношениям показателей преломления на частотах каждый из кристаллов можно отнести к одному из четырнадцати классов [174] (табл. 20). Только для одного класса кристаллов) в случае, если

в кристалле нет направлений синхронизма для рассматриваемого удвоения частоты. В этом случае двулучепреломление меньше, чем дисперсия и двулучепреломление не может компенсировать дисперсию. Во всех остальных случаях возможно выполнение условий синхронизма. Неравенства, разбивающие кристаллы по возможным соотношениям показателей преломления на типы определяют, в каких главных плоскостях находятся направления синхронизма первого типа, а более "мелкая" классификация относится к синхронизмам второго типа. Во всех кристаллах, в которых возможен синхронизм второго типа, возможен и синхронизм первого типа. В кристаллах, относящихся к классам 5,8, 11,13, возможен только синхронизм первого типа.

Очевидно, что кристалл может быть отнесен к определенному классу, если со сравнительно небольшой точностью известны показатели

Рис. 36. Поверхности индексов для кристалла класса 2 по Хобдену

преломления на двух длинах волн. Как правило, для этого достаточно, чтобы указанные показатели были измерены с точностью до второго, иногда до первого десятичного знака. Для отнесения кристаллов к типам иногда достаточно знать показатели преломления лишь на одной длине волны. Примеры подобных оценок будут приведены в дальнейшем.

Отнесение кристалла к тому или иному классу позволяет установить, в каких плоскостях показателей преломления возможно выполнение условий синхронизма. Чаще всего кристаллы используются в режимах, когда условия синхронизма выполняются для света, распространяющегося в главных плоскостях поэтому это определение весьма полезно.

Рассмотрим в качестве примера возможные направления синхронизма в кристалле, относящемся ко второму классу (табл. 20). Поверхности индексов для для такого кристалла показаны на рис. 36. Поверхности их пересечения заштрихованы.

Ось конической поверхности, определяющей направления синхронизма первого типа, совпадает с оптической осью кристалла. Поверхность пересекает плоскостью, так как и выполнится для всех кристаллов типа а

Коническая поверхность, определяющая направления синхронизма второго типа, пересекает плоскости вследствие соотношений

Первое из этих неравенств показывает, что точка расположена внутри поверхности индексов для второе — что точка расположена между точками (указанные точки показаны на рис. 36). Выходы

Рис. 37. Схемы выходов на координатные плоскости Поверхностей, определяющих направления синхронизма в кристаллах с разными соотношениями показателей преломления

Рис. 38. Схемы выходов на координатные плоскости поверхностей, определяющих направления синхронизма при наличии некритического синхронизма

поверхностей синхронизма на координатные плоскости схематически показаны на рис. 37,2.

Поверхности индексов кристаллов класса 1 отличаются от рассмотренных тем, что точка вследствие неравенства расположена не внутри поверхности а между в результате поверхность, определяющая направления синхронизма второго типа, не пересекает плоскость (см. рис. 37,1).

На рис. 37 даны также схемы сечений координатными плоскостями поверхностей, определяющих направления синхронизма в кристаллах остальных классов.

Иногда встречаются кристаллы, в которых равны два главных показателя преломления, т.е. или В таких кристаллах может наблюдаться некритический к угловым расстройкам, или -градусный, синхронизм. В случае одноосного кристалла равенство двух главных показателей преломления означает, что соответствующие поверхности индексов для касаются друг друга. В результате синхронизм некритичен к любым угловым расстройкам вследствие близости фазовых скоростей волн разных частот вблизи точки касания. Поверхности индексов двуосных кристаллов имеют более сложную форму. При выполнении указанных выше условий синхронизм оказывается нечувствительным к изменению направления распространения света в одной плоскости и чувствительным в другой.

В табл. 21 представлены соотношения показателей преломления, соответствующие разным вариантам некритического синхронизма в двуосных кристаллах. На рис. 38 показаны схемы сечений координатными

Таблица 21 (см. скан) Условия выполнения разных типов некритического синхронизма в двуосиых кристаллах

плоскостями поверхностей, определяющих направления синхронизма при наличии некритического синхронизма рисунка соответствуют вариантам табл. 21).

Соотношение показателей преломления, обеспечивающее наличие синхронизма, не всегда обеспечивает эффективное преобразование в соответствующем направлении. Может оказаться, что преобразование запрещено симметрией кристалла. Особенно легко заметить такие случаи при выполнении условий некритического синхронизма, так как при распространении света вдоль главной оси показателей преломления в преобразовании может принимать участие лишь одна компонента тензора

В качестве примера рассмотрим кристалл класса . Свет, распространяющийся по оси кристалла, имеет составляющие Нелинейная поляризация на частоте должна иметь вид Такая поляризация была бы параллельна оси Следовательно, излучение частоты распространяющееся вдоль оси такого кристалла, должно отсутствовать, так как свет — поперечная волна. Очевидно, что то же справедливо и для случая, когда излучение распространяется вдоль двух других кристаллографических осей.

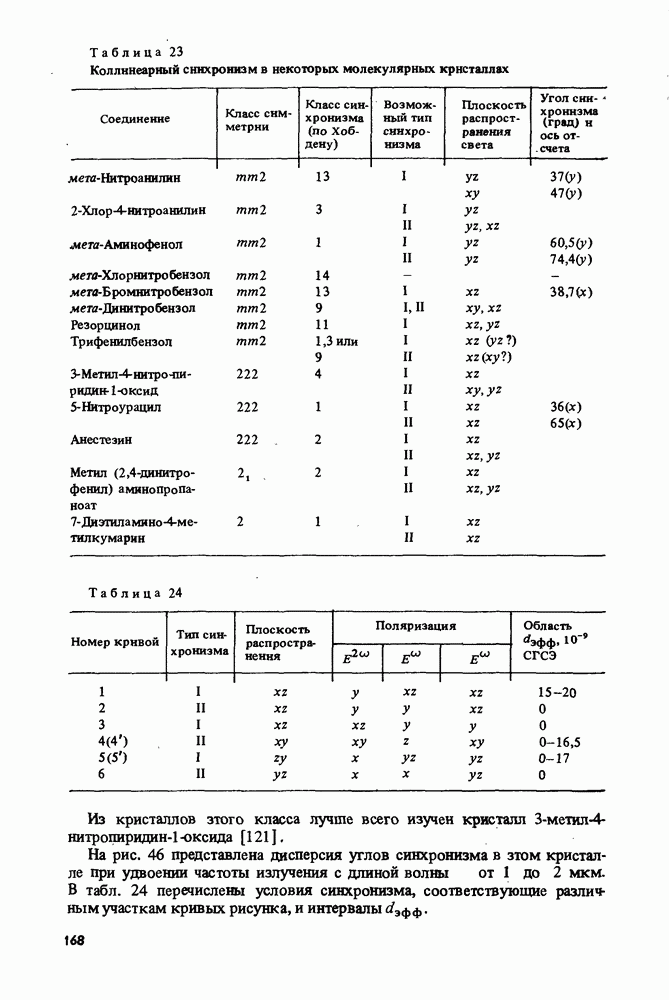
В табл. 22 перечислены возможные варианты некритического синхронизма, а также направления распространения света, в которых они могут

Таблица 22 (см. скан) Возможные направления и типы некритического синхронизма

наблюдаться, для всех классов моноклинной и орторомбической сингонии. Для удобства в таблице приведены данные для всех возможных ориентации оптических осей относительно осей, используемых для характеристики кристаллографических классов. Напомним, что при выборе главных оптических осей пользуются правилом Ориентация осей, принятая в кристаллографии для описания разных классов симметрии, приведена в примечании к табл. 22.