4.2. Оценка различных методов экспериментального определения нелинейной восприимчивости второго порядка

Как было показано ранее, нелинейные восприимчивости второго порядка, как и восприимчивости третьего порядка, можно оценивать двумя способами: измеряя кристаллов и растворов. В отличие от нелинейной восприимчивости третьего порядка, исследованной по гиперполяризуемости растворов, нелинейную восприимчивость второго порядка изучали сначала в кристаллах [113-120, 151, 155-157, 171-188]. Особенности молекулярных кристаллов подробно обсуждены в [199]. Лишь впоследствии для оценки нелинейной восприимчивости второго порядка стали привлекать гиперполяризуемость молекул в растворе [28, 43, 163— 170]. В настоящее время количество молекулярных кристаллов с известной нелинейной восприимчивостью значительно превышает число молекул с известной гиперполяризуемостью. Часто исследуется

гиперполяризуемость и нелинейная восприимчивость разных соединений. Для обоснования происхождения нелинейной восприимчивости второго порядка необходимы сведения, полученные при исследованиях как кристаллов, так и растворов. Необходимо поэтому сравнить информативность разных методов оценки нелинейной восприимчивости.

Гиперполяризуемость (3 определяют по интенсивности генерации второй гармоники излучения в растворе в присутствии постоянного электрического поля (см. разд. 1.5 и 3.7). При этом определяют проекцию векторной части гиперполяризуемости на направление постоянного дипольного момента молекулы. Значения отдельных компонент тензора остаются неизвестными. 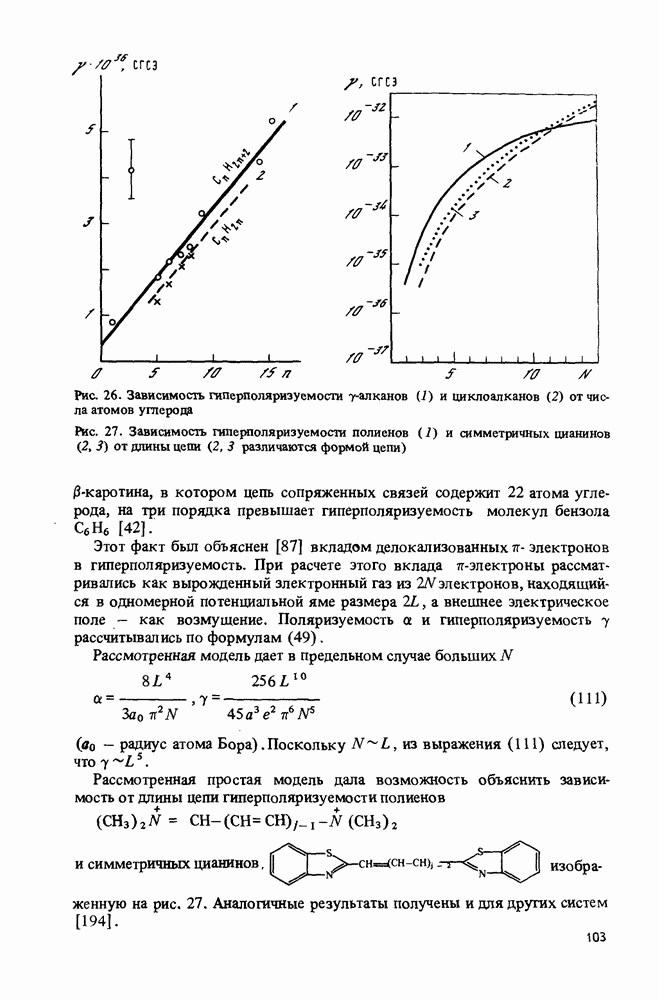Исключение составляют случаи, когда все компоненты тензора кроме (Зххх, близки к нулю ("одномерная" гиперполяризуемость [200]). Такие молекулы и исследуют чаще всего. Интерполируя соотношения (111), следует ожидать, что между гиперполяризуемостью и длиной цепи существует соотношение . В действительности наблюдается, по-видимому, более слабая зависимость [190]. И в том и в другом случае гиперполяризуемость возрастает при увеличении длины системы сопряженных связей.

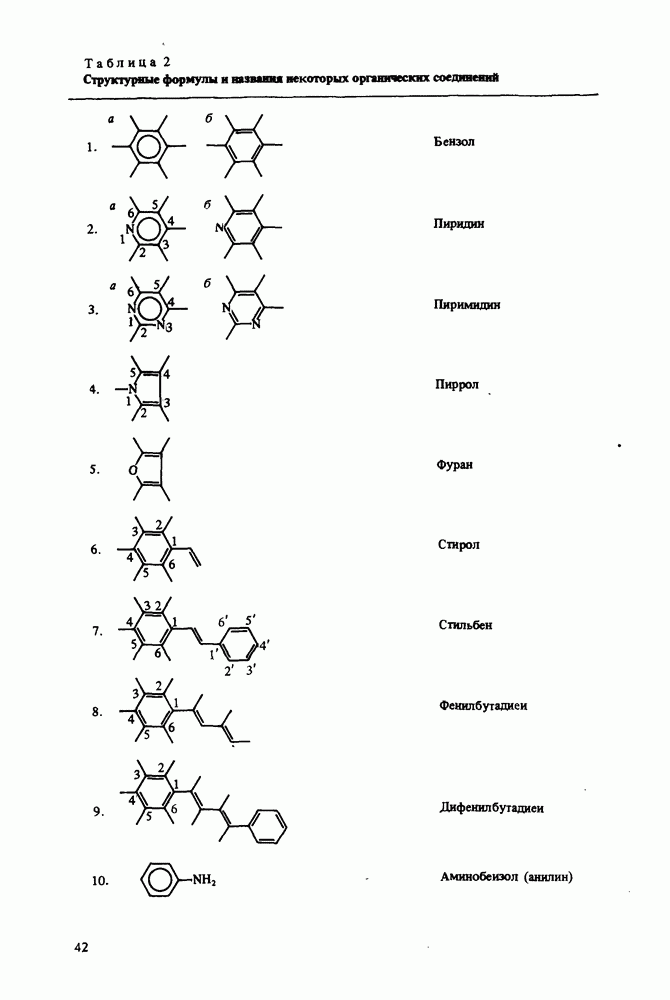
В связи с вышесказанным чаще всего исследуют гиперполяризуемость дипольных молекул, форма которых близка к линейной: монозамещенных и пара-дизамещенных бензола, стирола, стильбена и т.д. Гиперполяризуемость таких молекул имеет в основном одну составляющую и легко может быть связана с их параметрами. Это позволяет количественно связать экспериментально измеряемую гиперполяризуемость с особенностями строения молекул

Для того чтобы перенести обнаруженные закономерности на кристаллы, которые в основном и используются на практике, нужно измерить нелинейные восприимчивости кристаллов. Между тем, как было указано в разд. 2.6, дипольные линейные молекулы вследствие их высокой симметрии имеют тенденцию кристаллизоваться с центром инверсии. Поэтому нелинейные восприимчивости кристаллов таких соединений чаще всего равны нулю. Кроме того, если то средняя нелинейная восприимчивость кристаллов должна падать при увеличении длины цепи сопряжения, так как Поэтому исследуются нелинейные восприимчивости кристаллов, состоящих из сравнительно малых молекул, например производных бензола [113—124]. При этом предпочтение отдается мета-производным, которые чаще кристаллизуются без центра инверсии. Компоненты тензора гиперполяризуемости таких молекул труднее связать с их параметрами, а экспериментальное исследование генерации второй гармоники в растворе молекул при наложении постоянного поля позволяет оценить лишь норму векторной части тензора (см. [39] и разд. 3.7).

Измерение генерации второй гармоники излучения в порошках органических соединений (порошковая методика - [151—153], разд. 3.6) позволяет оценить норму нелинейной восприимчивости кристаллов, т. е. сумму норм векторной и септорной частей нелинейной восприимчивости. Таким образом, измерение генерации второй гармоники в порошках соединений, состоящих из несимметричных молекул, дает несколько больше сведений о нелинейной восприимчивости, чем измерение генерации второй гармоники в растворе этих молекул в присутствии постоянного поля.

Поскольку, как правило, векторная и септорная часть гиперполяризуемости растут одновременно, следует ожидать наличия корреляции между интенсивностью генерации второй гармоники в растворе и порошке соединений (при отсутствии в кристаллах центра инверсии).

Значительно больше сведений, чем обе вышеупомянутые методики, дает измерение всех компонент тензора в монокристаллах органических соединений. Если расположение молекул в кристалле известно, то с помощью соотношений (43) — (46) можно определить все составляющие тензора Если гиперполяризуемость молекул имеет лишь одну или две отличные от нуля компоненты ("одномерная" или "двумерная" гиперполяризуемость) то это накладывает некоторые ограничения на нелинейные восприимчивости кристаллов, что поддается экспериментальной проверке (см. [200] и разд. 4.5).

Больше всего сведений о возможности перенесения закономерностей, выявленных для гиперполяризуемости, на кристаллы получено при сравнении двух экспериментально измеренных величин: векторной части нелинейной восприимчивости и векторной части гиперполяризуемости связанных между собой соотношением Здесь V - объем элементарной ячейки; фактор локального поля; суммируются гиперполяризуемости молекул, входящих в элементарную ячейку; угол между вектором гиперполяризуемости молекулы и полярной осью кристалла. Результаты таких сравнений будут приведены ниже.

Таким образом, качественные исследования закономерностей возрастания нелинейных восприимчивостей второго порядка с помощью измерения гиперполяризуемости растворов и нелинейных восприимчивостей порошков равнозначны. Поскольку измерения нелинейных восприимчивостей порошков проще, этот метод в основном и использовался для установления критериев возрастания Для количественного вычисления нелинейных восприимчивостей необходимо исследование гиперполяризуемостей, которые позволяют вычислить компоненты тензора нелинейной восприимчивости кристаллов по параметрам отдельных молекул.