4.5. Расчет гиперполяризуемостей молекул при отсутствии аддитивности. Учет возбужденных состояний. Дисперсия гиперполяризуемости

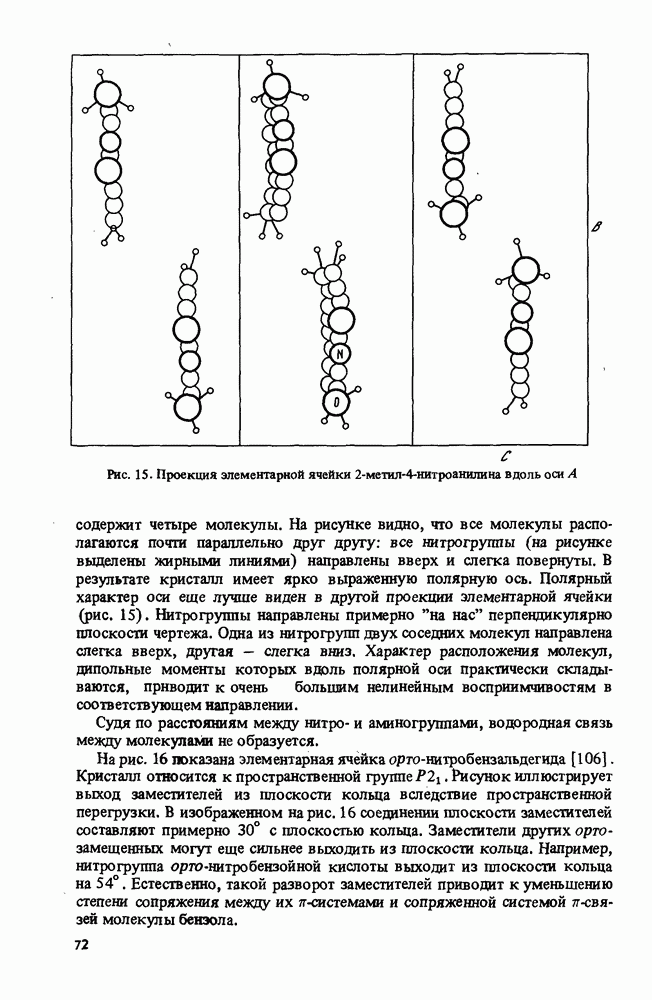
Как было показано в предыдущем разделе, аддитивная схема не позволяет рассчитать гиперполяризуемость молекул, в которых возможен ПЗ типа Попытки рассчитать гиперполяризуемость таких молекул с помощью параметров, описывающих дополнительное перераспределение зарядов в молекуле в присутствии донора и акцептора, являются искусственными. В лучшем случае они могут объяснить возрастание гипер-поляриэуемости в отдельных молекулах, содержащих донорные и акцепторные группы.

Причиной невозможности расчета гиперполяризуемости таких молекул, в том числе с помощью введения произвольно выбранных параметров, является "смешивание" орбиталей доноров и акцепторов уже в основном состоянии и увеличение этого смешивания при возбуждении.

В настоящее время, как указывалось в разд. 2.4, существуют два подхода к вычислению гиперполяризуемости таких молекул. Один из них, впервые использованный еще в 1967 г. Швейгом, заключается в вычислении дипольного момента молекулы в присутствии внешнего электрического поля, рассматриваемого как возмущение. Гиперполяризуемости находятся по формуле (87), как производные от дипольного момента по приложенному полю. Второй подход заключается в использовании для вычисления гиперполяризуемости формулы (52), выражающей ее через матричные элементы дипольных моментов переходов, т.е. учитывающей волновые функции возбужденных состояний системы.

Как уже неоднократно говорилось, оба подхода в какой-то мере идейно эквивалентны, так как возмущение смешивает основное состояние с возбужденными, и перераспределение зарядов в присутствии поля практически эквивалентно его перераспределению при возбуждении. Различие подходов, однако, сильно сказывается на методах расчетов.

Очевидно, что наилучшим образом гиперполяризуемость должна описываться с помощью второго подхода. Однако мы начнем обсуждения вычислений гиперполяризуемости при отсутствии аддитивности с первого подхода, так как он позволяет лучше понять пределы применимости аддитивной схемы вычислений.

В первых расчетах гиперполяризуемости по формулам, аналогичным (87), электроны рассматривались как электронный газ, заключенный в одномерную потенциальную яму. Для вычисления гиперполяризуемости второго порядка необходимо рассмотреть асимметричную яму (для симметричной

Были рассчитаны гиперполяризуемости набора молекул [51]. В настоящее время измерена шперполяризуемость только одной молекулы из этого набора — пара-нитро-пара-диметиламиностильбена. Вычисления Швейга дали значение Эксперимент дает если вещество растворено в спирте, и для раствора в неполярном растворителе. Таким образом, оценка Швейга в первом приближении справедлива.

Следующей работой, в которой гиперполяризуемости оценивались по формуле (87), является уже неоднократно цитированная работа [46], в которой дипольный момент молекул рассчитан методом . В качестве возмущения рассматривалось влияние постоянного электрического поля. Все вычисления проведены в произвольных единицах, поэтому невозможно сравнение с экспериментом. Основные результаты цитируемой работы — достаточно надежное установление пределов применимости аддитивной схемы.

Рассчитывались дипольные моменты, поляризуемости и гиперполяризуемости производных бензола, стирола и фенилбутадиева. Наряду с

реальной двузамещенной молекулой рассматривались "аддитивные" молекулы, параметры которых рассчитывались путем векторного суммирования параметров монозамещенных молекул.

Расчет показал, что дипольные моменты молекул хорошо описываются аддитивной схемой: дипольные моменты реальной и "аддитивной" молекул практически совпадают. Аддитивными оказываются как полные дипольные моменты, так и дипольные моменты -системы ("мезомерные моменты"). Отклонение дипольного момента -системы изомеров нитроанилина от момента, полученного векторным суммированием дипольных моментов нитробензола и анилина, не превышает Нарушение "схемы аддитивности" для производных стирола и фенилбутадиена еще меньше. Этот результат ясно показывает, что дипольный момент, отражая свойства основного состояния молекулы, мало изменяется за счет переноса заряда под влиянием поля. Таким образом, введение "дипольного момента переноса заряда" или (см. разд. 4.4) не Имеет смысла.

Наоборот, расчет показывает, что гиперполяризуемости второго порядка существенно неаддитивны. Уже гиперполяризуемости на кулевой частоте, без учета дисперсии, значительно больше, чем гиперполяризуемости, рассчитанные по аддитивной схеме. Так, "аддитивная" гиперполяризуемость пара-нитроанилина составляет лишь 35% общей гиперполяризуемости [46]. Гиперполяризуемость производных стирола и фенилбутадиена, рассчитанная по аддитивной схеме, составляет примерно 60% полной гиперполяризуемости.

В той же работе [46] была сделана попытка учесть дисперсию гиперполяризуемости. Для этого "неаддитивная" часть гиперполяризуемости, умножалась на

где энергия наиболее длинноволновой полосы поглощения соединения. Введение указанной поправки приводит к повышению "неаддитивной" гиперполяризуемости всех изучаемых молекул до 70% всей гиперполяризуемости.

Легко видеть, что введение поправки основано на предположении, что "неаддитивная" гиперполяризуемость связана с учетом лишь одного возбужденного состояния, которое считается состоянием с переносом заряда.

Справедливость такого подхода, т.е. учета лишь одного возбужденного состояния, проверялась в работе [170], с которой мы и начнем рассмотрение другого подхода к вычислению гиперполяризуемости - прямого учета возбужденных состояний молекул.

Простейший способ учета вклада ПЗ в гиперполяризуемость - рассмотрение двухуровневой системы. Этот способ предлагался еще в работах [177,179,182,199].

Гиперполяризуемость двухуровневой системы описывается формулой (55), которую удобно переписать в виде [170]

Здесь энергия перехода, сопровождающегося сила осциллятора соответствующего перехода. Простейший путь использовать формулу (119) для вычисления гиперполяризуемости, связанной с ПЗ, это определить из спектров молекул. Как указывалось в разд. 2.2, переходы типа проявляются как индивидуальные, наиболее длинноволновые полосы поглощения в спектрах молекул, если акцептором является нитро группа, а донором - любой донор сильнее, чем ОН-группа [76]. В соответствии с этим формула (119) была использована для вычисления гиперполяризуемости ряда молекул (см. табл. 19).

В цитируемых работах [170, 192] для оценки изменения дипольного момента при возбуждении использовалось соотношение где заряд, переносимый при возбуждении на расстояние Величина считалась равной расстоянию между донором и акцептором. Предполагалось, что в молекулах, содержащих одни и те же доноры и акцепторы, не зависит от длины цепи. Для вычисления использовалось значение полученное в работах [78] при исследовании пара-нитроанилина. В табл. 19 приведены значения полученные вышеописанным способом, а также экспериментально полученные величины гиперполяризуемости. Приведенные данные демонстрируют согласие экспериментальных и вычисленных значений гиперполяризуемости, откуда следует, что ПЗ, учитываемый в приближении двухуровневой системы, дает основной вклад в гиперполяризуемость.

Однако такое хорошее согласие эксперимента и теории, по-видимому, является случайным. Дело в том, что использованные в работах [170, 192] значения не соответствуют экспериментальным данным (см. например [52, 64]). Экспериментальные значения включены в таблицу вместе со значениями гиперполяризуемости, вычисленными по формуле (119) с учётом этих значений Видно, что вычисленные таким способом значения гиперполяризуемостей примерно вдвое меньше значений, приведенных в работе [170].

Отметим, что даже учет уменьшенных значений дает значительный вклад в в экспериментально наблюдаемую гиперполяризуемость. Кроме того, на самом деле вклад ПЗ в гиперполяризуемость не ограничивается вкладом двухуровневой системы, описываемой формулой (55) или (119). Для полного учета этого вклада необходимо рассмотреть по крайней мере трехуровневую схему (см. (61)). Если один из переходов сопровождается ПЗ, то повышается величина третьего члена формулы (61), содержащего произведение трех недиагональных матричных элементов дипольного момента. Поскольку для переходов с [52], то вклад этого члена, имеющего несколько другую дисперсионную зависимость, имеет тот же порядок. Оценки с учетом этого вклада также приведены в таблице.

Остается сделать несколько замечаний об экспериментальных данных, выбранных для сравнения с оценочными значениями гиперполяризуемостей. В работах [170, 192] для этого взяты значения гиперполяризуемостей, измеренные в полярных растворителях. Используемые при оценках значения также получены в полярных растворителях, поэтому такой выбор гиперполяризуемостей в какой-то мере оправдан.

Таблица 19 (см. скан) Теоретические оценки гиперполяризуемости, связанной с ПЗ, и их сравнение с экспериментом [170]

Однако, во-первых, значения и не всегда измерялись для одних и тех же растворителей. Во-вторых, есть некоторые основания считать [43, 202], что межмолекулярное взаимодействие значительно сильнее влияет на чем на Это может быть связано с тем, что взаимодействие с растворителем облегчает ВПЗ. В работе [203] было экспериментально показано, что взаимодействие молекул пара- диметиламинобензонитрила с молекулами полярного растворителя носит именно такой характер. В процессе переноса заряда от диметиламиногруппы последняя должна быть повернута относительно бензольного кольца. Такая конфигурация молекулы стабилизируется в полярных растворителях [203]. По-видимому, аналогичным образом можно объяснить многие случаи повышения гиперполяриэуемости при растворении в полярных растворителях веществ, в молекулах которых возможен ПЗ. Если это объяснение правильно, то указанное повышение гиперполяризуемости является еще одним доводом в пользу определяющей роли ПЗ.

Имея в виду значительные изменения гиперполяризуемости при изменении растворителя, следует отметить, что оценки гиперполяризуемости по полуэмпирическим формулам следовало бы проводить на основе значений измеренных в неполярных растворителях, и результаты оценок сравнивать со значениями гиперполяризуемостей, измеренных в тех же растворителях. Это, по-видимому, не делалось.

Учитывая все вышесказанное, не следует ожидать точного согласия вычисленных и экспериментальных значений для молекул с ПЗ. Однако уже простейшие оценки по формулам для двухуровневой или трехуровневой систем показывают, что вклад переходов с ПЗ в общее значение гиперполяризуемости велик (не менее 50%) и что его можно оценить, учитывая перераспределение зарядов при возбуждении. Такая оценка вместо оценки с помощью произвольных параметров типа или дтпозволяет естественным образом и одинаково рассматривать разные молекулы.

(см. скан)

Так, понижение вклада ПЗ в гиперполяризуемость мета-нитроанилина по сравнению с орто- и ядра-изомерами объясняется уменьшением степени ПЗ и учитывается понижением силы осциллятора перехода, сопровождающего ПЗ.

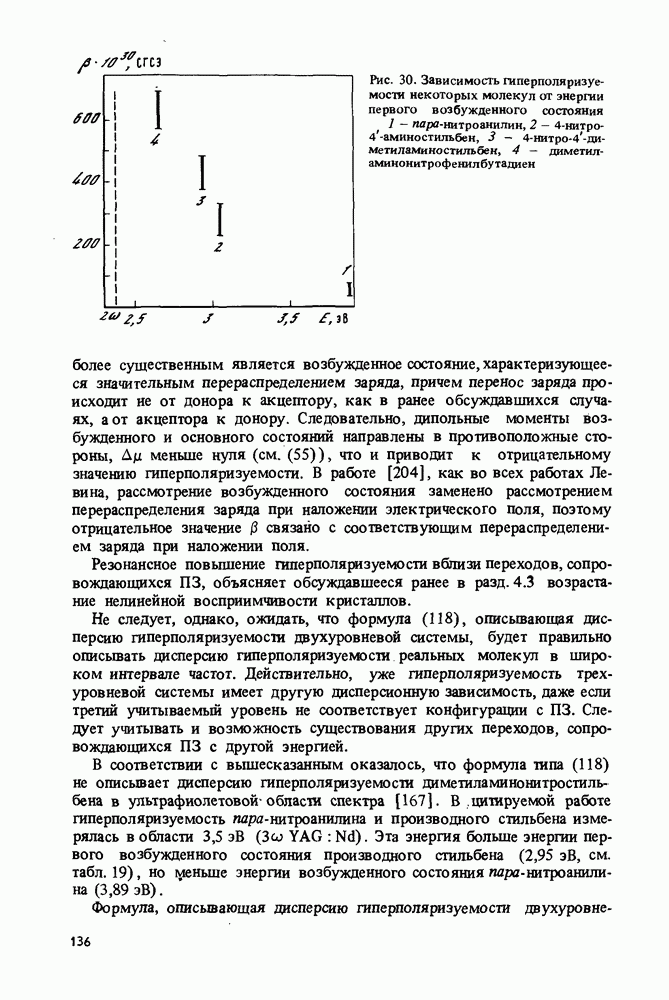
Описываемый упрощенный учет вклада ПЗ в гиперполяризуемость предсказывает резонансное увеличение гиперполяризуемости при подходе частоты преобразованного излучения к частоте перехода, сопровождающего ПЗ. Действительно, данные, представленные на рис. 30, демонстрируют указанное возрастание гиперполяризуемости.

Учет дисперсионной зависимости гиперполяризуемости, описываемой формулой (118), позволил объяснить изменение гиперполяризуемости некоторых красителей (мероцианинов) при замене растворителя [204]. Цвет растворов указанных красителей зависит от растворителя: они ярко-красные в полярном растворителе (вода, метанол: ) и ярко-синие в менее полярных растворителях (пиридин; ). Гиперполяризуемость меняется от в метаноле до в пиридине. В то же время низкочастотные значения гиперполяризуемосги равны для раствора в метаноле для раствора в пиридине, т.е. увеличение гиперполяризуемости связано практически целиком с ее дисперсией.

Интересна природа "необычного" знака гиперполяризуемости указанных красителей (минус вместо обычного плюса). Отрицательное значение гиперполяризуемости в данном случае означает, что произведение отрицательно (см., разд. 4.4). Для объяснения этого были рассмотрены [193] возбужденные состояния хиноидных структур. Оказалось, что

Рис. 30. Зависимость гиперполяризуемости некоторых молекул от энергии первого возбужденного состояния 1 — пара-нитроанилин, 2 - 4-нитро-4-аминостильбен, 3 - 4-нитро-4-ди-метиламиностильбен, 4 - диметил-аминонитрофенилбутадиен

наиболее существенным является возбужденное состояние, характеризующееся значительным перераспределением заряда, причем перенос заряда происходит не от донора к акцептору, как в ранее обсуждавшихся случаях, а от акцептора к донору. Следовательно, дипольные моменты возбужденного и основного состояний направлены в противоположные стороны, меньше нуля (см. (55)), что и приводит к отрицательному значению гиперполяризуемости. В работе [204], как во всех работах Левина, рассмотрение возбужденного состояния заменено рассмотрением перераспределения заряда при наложении электрического поля, поэтому отрицательное значение связано с соответствующим перераспределением заряда при наложении поля.

Резонансное повышение гиперполяризуемости вблизи переходов, сопровождающихся ПЗ, объясняет обсуждавшееся ранее в разд. 4.3 возрастание нелинейной восприимчивости кристаллов.

Не следует, однако, ожидать, что формула (118), описывающая дисперсию гиперполяризуемости двухуровневой системы, будет правильно описывать дисперсию гиперполяризуемости реальных молекул в широком интервале частот. Действительно, уже гиперполяризуемость трехуровневой системы имеет другую дисперсионную зависимость, даже если третий учитываемый уровень не соответствует конфигурации с ПЗ. Следует учитывать и возможность существования других переходов, сопровождающихся ПЗ с другой энергией.

В соответствии с вышесказанным оказалось, что формула типа (118) не описывает дисперсию гиперполяризуемости диметиламинонитростильбена в ультрафиолетовой области спектра [167]. В цитируемой работе гиперполяризуемость пара-нитроанилина и производного стильбена измерялась в области Эта энергия больше энергии первого возбужденного состояния производного стильбена (2,95 эВ, см. табл. 19), но меньше энергии возбужденного состояния пара-нитроанилина (3,89 эВ).

Формула, описывающая дисперсию гиперполяризуемости

двухуровневой системы, для случая сложения частот может быть переписана в виде [167]

Здесь комплексная величина энергии возбуженного уровня (введена для учета поглощения), нерезонансный, резонансный члены при Формула (120) не описывает гиперполяризуемость производного стильбена в области Она, однако, предсказывает изменение знака гиперполяризуемости при переходе через полосу поглощения. Это изменение было обнаружено экспериментально [167]. Указанное изменение знака само по себе подтверждает преимущественный вклад первого возбужденного состояния в гиперполяризуемость производного стильбена.

Таким образом, уже такая грубая оценка вклада ПЗ, как расчет гиперполяризуемости по формуле для двухуровневой системы, позволяет объяснить ряд свойств гиперполяризуемости молекул: возрастание в два-три раза при наличии хотя бы одного перехода с ПЗ, дополнительное возрастание при приближении частоты преобразованного излучения к частоте перехода, сопровождающегося ПЗ, изменение знака при изменении направления ПЗ, а также в случае, когда частота преобразованного излучения больше частоты перехода, сопровождающегося ПЗ. Некоторые свойства гиперполяризуемости, однако, не могут быть объяснены с помощью такого рассмотрения. Так, невозможно, по-видимому, точно вычислить гиперполяризуемость молекул, частоты переходов в которых находятся близко к частотам преобразованного излучения.

В соответствии с вышесказанным расчет гиперполяризуемости по формулам для двухуровневой модели особенно удачен в случае, если энергии преобразованного излучения намного ниже энергии возбужденных уровней рассматриваемых систем. Этим свойством обладают комплексы переноса заряда (КПЗ) (см. разд. 2.5) Полоса поглощения комплексов, рассмотренных в разд. 2.5, связанная с ПЗ, находится в области в то время как энергия квантов второй гармоники излучения неодимового лазера равна 2,34 эВ. В указанном случае дисперсией гиперполяризуемости можно пренебречь, и формула, описывающая гиперполяризуемость двухуровневой системы (119), примет вид [189]

Ниже приведены значения гиперполяризуемости ряда КПЗ, вычисленные по формуле (121), вместе с экспериментальными значениями гиперполяризуемостей указанных комплексов. Значения параметров комплексов были приведены в разд. 2.5.

Рис. 31. Зависимость гиперполяризуемости некоторых комплексов с переносом заряда от дипольного момента основного состояния 1 - пиридии пиридии амииопиридиц

Видно, что формула (121) правильно описывает гиперполяризуемость КПЗ [189].

Для рассматриваемых КПЗ характерно, что максимальна гиперполяризуемость комплекса, имеющего минимальный дипольный момент в основном состоянии. В соответствии с формулой (121) — это объясняется максимальным значением разности

В общем случае зависимость Рххх от Для КПЗ немонотонна Качественно характер этой зависимости может быть объяснен следующим образом. Когда перенос заряда мал, т.е. (см. разд. 2.5), то матричный элемент дипольного момент для перехода между состояниями 1 и сравнительно мал и связан в основном с ненулевым значением интеграла перекрывания мере увеличения взаимодействия с ПЗ возрастает приводя к росту 0. Однако увеличение взаимодействия приводит также (см. (94)) к возрастанию и уменьшению Поэтому уменьшается разность Возрастание при уменьшении и приводит к немонотонной зависимости от По-видимому, немонотонный характер зависимости от должен наблюдаться и для некоторых молекул с внутримолекулярным ПЗ.

В заключение рассмотрим результаты работ, в которых гиперполяризуемость молекул вычислялась по формулам (52), (54), т.е. учитывалось несколько возбужденных состояний молекул. В работе [86а] рассчитаны гиперполяризуемости анилина, нитробензола и пара-нитро анилина, в [866] — гиперполяризуемость пара-нитро анилина и 2-метил-4-нитроанилина, в [85] - пара-нитроанилина.

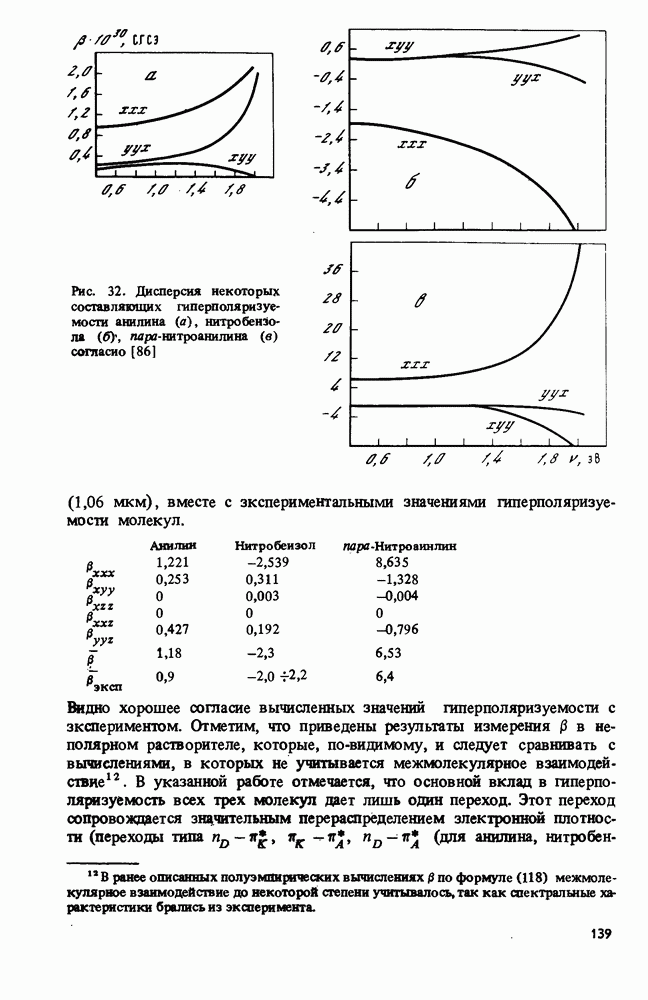
В работах [86а, 86б] волновые функции основного и возбужденных состояний были рассчитаны методом CNDO, после чего вычислялись матричные элементы дипольных моментов переходов. Для вычисления гиперполяризуемости использовалась формула (54). Анализировался вклад отдельных переходов в гиперполяризуемость. Рассчитывалась дисперсия составляющих гиперполяризуемости (см. рис. 32).

Ниже представлены значения компонент 0, а также вычисленных описанным выше способом для

Рис. 32. Дисперсия некоторых составляющих гиперполяризуемости анилина (а), нитробензола (б), пара-нитроанилина (в) согласно [86]

вместе с экспериментальными значениями гиперполяризуемости молекул.

Видно хорошее согласие вычисленных значений пшерполяризуемосш с экспериментом. Отметим, что приведены результаты измерения в неполярном растворителе, которые, по-видимому, и следует сравнивать с вычислениями, в которых не учитывается межмолекулярное взаимодействие. В указанной работе отмечается, что основной вклад в гиперполяризуемость всех трех молекул дает лишь один переход. Этот переход сопровождается значительным перераспределением электронной плотности (переходы типа (для анилина,

нитробензола и пара-нитроанилина соответственно). Согласно [86а,б] указанные переходы дают примерно 70—80% от всей, гиперполяризуемости.

В работе [85] гиперполяризуемость пара-нитроанилина вычислялась по формуле (52), в которой учитывалось разное количество возбужденных уровней. Показано, что вычисленное значение гиперполяризуемости резко возрастает при последовательном учете трех нижних уровней, доходя до (отметим, что, согласно этой работе, заметным ПЗ сопровождается переход на третий возбужденный уровень). Учет следующих трех уровней повышает значение до Учет более высоких уровней практически не меняет значение пшерполяризуемости.

Если считать, что экспериментальное значение гиперполяризуемости пара-нитроанилина — как считают авторы рассматриваемой работы, то согласие теории и эксперимента можно признать хорошим. Однако указанные значения гиперполяризуемости относятся к измерениям в полярном растворителе или расплаве (различие этих значений связано с различием значений принимаемых разными авторами). Из рассматриваемой работы не ясно, как учитывалось межмолекулярное взаимодействие и учитывалось ли оно вообще.

Таким образом, показано, что пшерполяризуемости молекул, которые не могут быть рассчитаны по аддитивной схеме, можно оценивать, учитывая возбужденные состояния. Хорошие результаты дает учет уже одного возбужденного состояния, являющегося состоянием с переносом заряда. Оценка вклада ПЗ по формулам, описывающим гиперполяризуемость двухуровневой системы, ухудшается при приближении частоты преобразования излучения к полосе поглощения, сопровождающейся ПЗ.

Пользуясь оценками вклада ПЗ в гиперполяризуемость, можно попытаться оценить этот вклад в нелинейную восприимчивость кристаллов. Для этого надо вернуться к данным, представленным, в табл. 18. Как указывалось в предыдущем разделе, нелинейная восприимчивость кристаллов № 8—10 не может быть рассчитана по аддитивной схеме. Гиперполяризуемость молекул не была измерена. Однако все эти вещества являются производными пара-нитроанилина. Поэтому естественно предположить, что вклад ПЗ в пшерполяризуемость этих молекул имеет тот же порядок, что и в пшерполяризуемость пара-нитроанилина. Следовательно, для учета вклада ПЗ пшерполяризуемость (нелинейную восприимчивость) этих соединений нужно примерно утроить. Соответствующие значения указаны в табл. 18 в скобках. Видно, что согласие с экспериментом улучшается. Учитывая малую точность экспериментальных данных, особенно для -диметил-пара-нитроанилина (оценка сделана по порошковой методике), согласие оценок с экспериментом надо признать хорошим.

При описываемых оценках не учитывалась дисперсия нелинейной восприимчивости, которая может отличаться от дисперсии пшерполяризуемости вследствие сдвига полосы поглощения при кристаллизации. Оценки дисперсии нелинейной восприимчивости будут сделаны после обсуждения линейного злектрооптического эффекта в молекулярных кристаллах.

Наличие ПЗ в молекулах отражается на свойствах тензора молекулярных кристаллов [200]. В этом случае тензор является одномерным,

если происходит между донором и акцептором в пара-положении, и двумерным, если донор и акцептор находятся в мета- или орто-положениях. Одномерность тензора приводит к тому, что х , измеренная в определенном направлении, перпендикулярном полярной оси кристалла, равна нулю, а независимо от расположения молекул в кристалле [200]. Если тензор является двумерным, то соотношения между компонентами тензора несколько сложнее. Они получены в работе [200] для кристаллов всех нецентросимметрических классов, относящихся к 17 точечным группам. Указанные соотношения позволяют проверять предположения об одномерности или двумерности а также рассчитывать составляющие тензора если известны составляющие тензора Формулы, приведенные в [200], значительно проще общих соотношений

Использование указанных соотношений привело к выводу, что тензор молекул 2-метил-4-нитроанилина является одномерным, а молекул -динитрофениламинопропаноата — двумерным, т.е. в последнем случае ПЗ происходит не только между нитро- и гидрок согруппами в пара-положении.

Использование этих соотношений позволяет выяснить, какое расположение молекул в кристалле дает максимальные значения при заданных Показано, что максимальные значения могут быть реализованы для кристаллов, относящихся к группам и не могут быть реализованы для остальных рассмотренных групп. Кристаллы 2-метил-4-нитроанилина близки к оптимальным для данной группы.

Отметим, что все описанные соотношения являются следствием наличия ПЗ в молекулах.