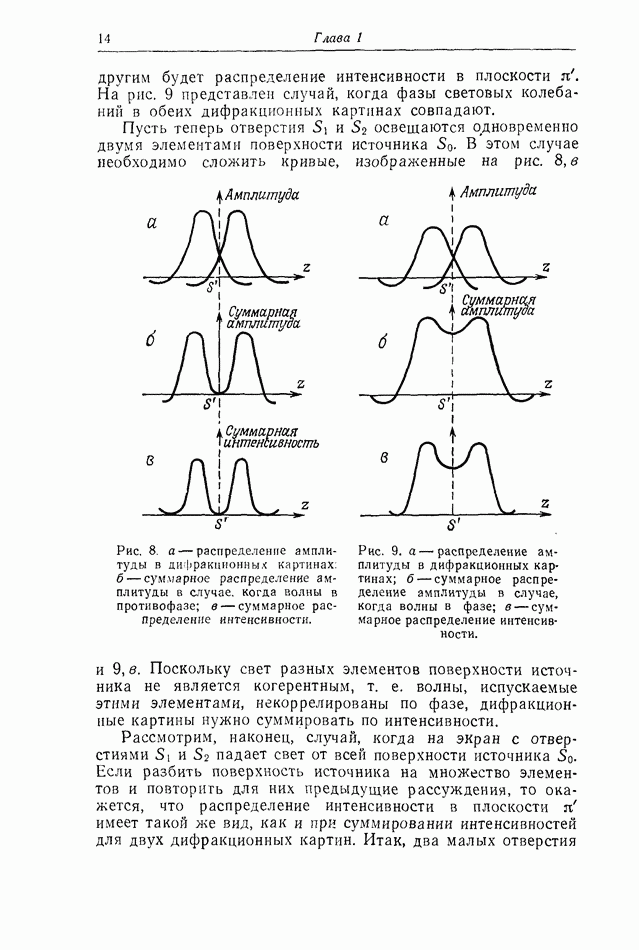
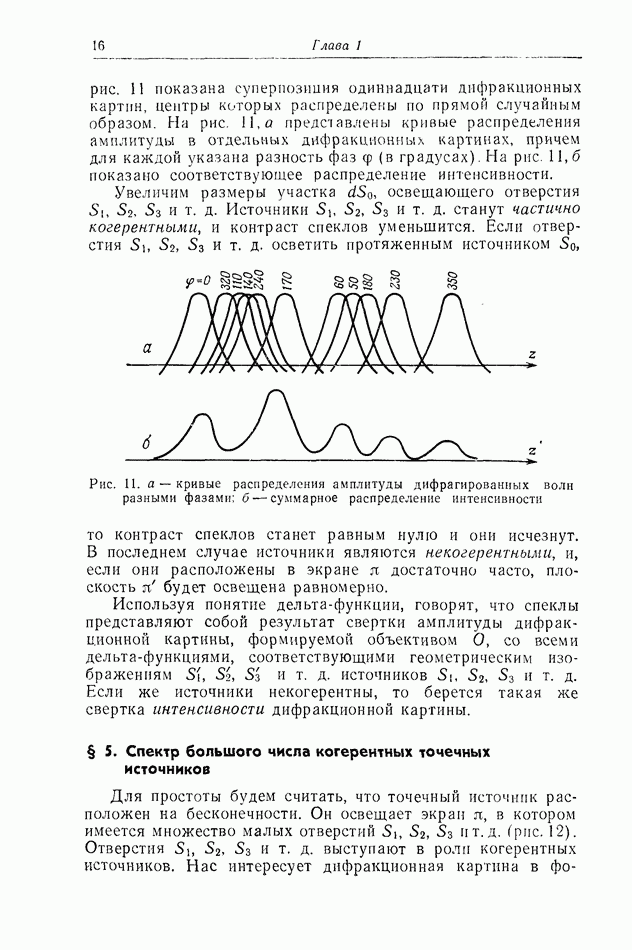
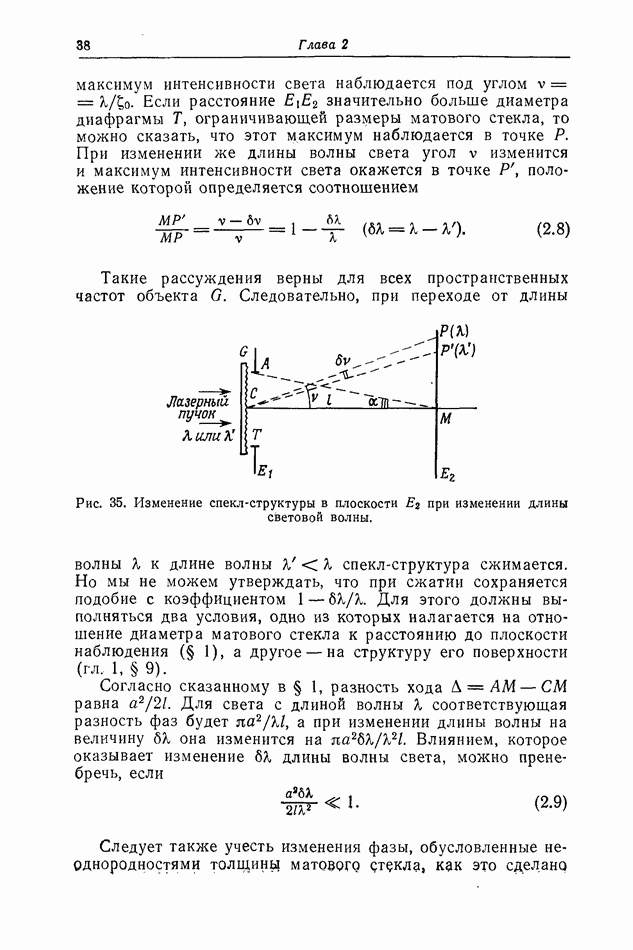
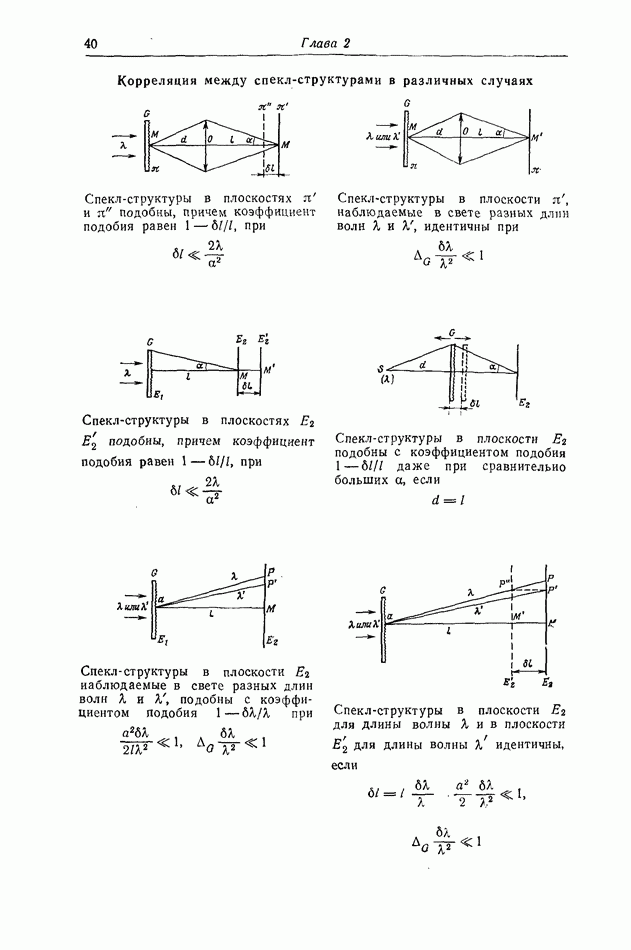
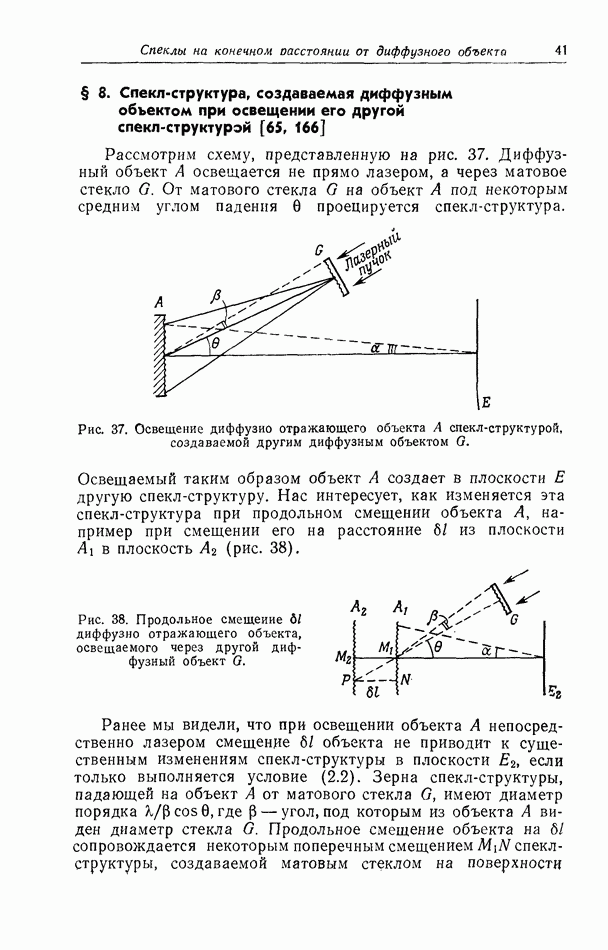
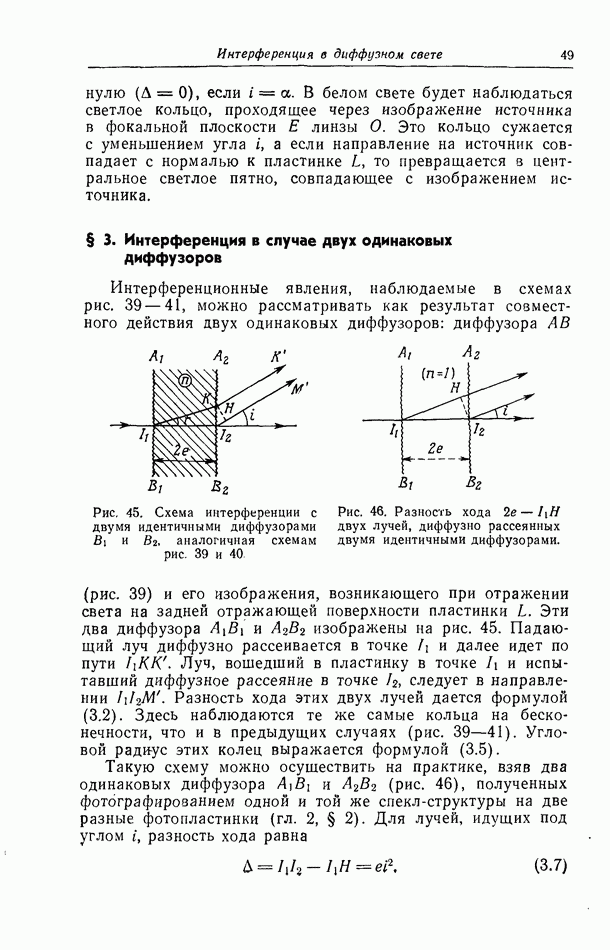
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава 1. СПЕКЛЫ В ИЗОБРАЖЕНИИ ДИФФУЗНОГО ОБЪЕКТА, ОСВЕЩАЕМОГО ЛАЗЕРОМ
§ 1. Изображение точечного источника света, преобразование Фурье
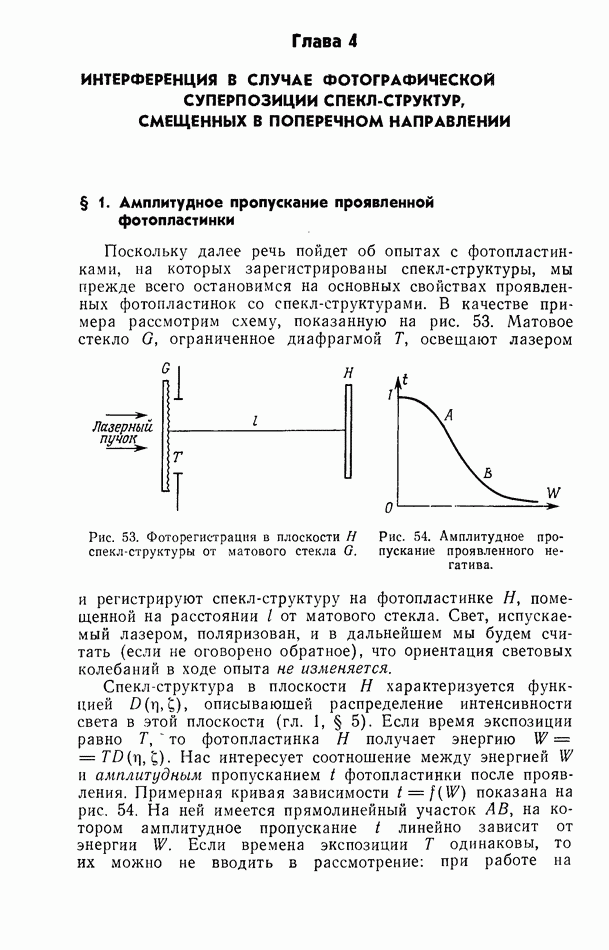
Пусть идеальный объектив О освещается точечным источником  испускающим монохроматическое излучение с длиной волны К (рис. 1). Сферическая волна 2, исходящая из точки
испускающим монохроматическое излучение с длиной волны К (рис. 1). Сферическая волна 2, исходящая из точки  преобразуется в сходящуюся сферическую волну 27 с центром в точке
преобразуется в сходящуюся сферическую волну 27 с центром в точке  геометрическом изображении точечного источника 5. Известно, что действительное изображение в точке
геометрическом изображении точечного источника 5. Известно, что действительное изображение в точке  представляет собой небольшое по размеру световое пятно, структура которого определяется явлением дифракции. Структура пятна, или вид дифракционной картины, зависит от формы отверстия, образуемого оправой объектива. Чтобы определить эту структуру, необходимо рассмотреть явление дифракции на бесконечности — явление Фраунгофера. Выражение «дифракция на бесконечности» легко понять, если представить себе, что объектив О заменен двумя другими объективами с фокусными расстояниями в 2 раза большими, чем у объектива О. Тогда источник
представляет собой небольшое по размеру световое пятно, структура которого определяется явлением дифракции. Структура пятна, или вид дифракционной картины, зависит от формы отверстия, образуемого оправой объектива. Чтобы определить эту структуру, необходимо рассмотреть явление дифракции на бесконечности — явление Фраунгофера. Выражение «дифракция на бесконечности» легко понять, если представить себе, что объектив О заменен двумя другими объективами с фокусными расстояниями в 2 раза большими, чем у объектива О. Тогда источник  будет находиться в фокальной точке первого из этих объективов, а изображение
будет находиться в фокальной точке первого из этих объективов, а изображение  в задней фокальной точке второго. Таким образом, второй объектив освещается источником, расположенным на бесконечности.
в задней фокальной точке второго. Таким образом, второй объектив освещается источником, расположенным на бесконечности.
Если известна форма волновой поверхности 2, то можно рассчитать структуру дифракционного изображения точечного источника  исходя из принципа Гюйгенса — Френеля. Предположим, что угловая апертура 2а объектива в пространстве изображений невелика и мы можем считать величину
исходя из принципа Гюйгенса — Френеля. Предположим, что угловая апертура 2а объектива в пространстве изображений невелика и мы можем считать величину  а равной единице. Принцип Гюйгенса — Френеля позволяет математически описать явление дифракции, пользуясь преобразованием Фурье. Амплитуда в какой-либо точке
а равной единице. Принцип Гюйгенса — Френеля позволяет математически описать явление дифракции, пользуясь преобразованием Фурье. Амплитуда в какой-либо точке  плоскости
плоскости  находится как фурье-образ (или спектр) распределения амплитуд и фаз на волновой поверхности 2. И наоборот, можно вычислить распределение амплитуд и фаз на волновой поверхности 2, если известно распределение амплитуд и фаз в дифракционной картине в точке
находится как фурье-образ (или спектр) распределения амплитуд и фаз на волновой поверхности 2. И наоборот, можно вычислить распределение амплитуд и фаз на волновой поверхности 2, если известно распределение амплитуд и фаз в дифракционной картине в точке  Распределение амплитуд и фаз на волновой поверхности 2 есть обратный фурье-образ распределения амплитуд и фаз в дифракционной
Распределение амплитуд и фаз на волновой поверхности 2 есть обратный фурье-образ распределения амплитуд и фаз в дифракционной
картине. На основе преобразования Фурье и его свойств явление дифракции рассчитывается просто и изящно.

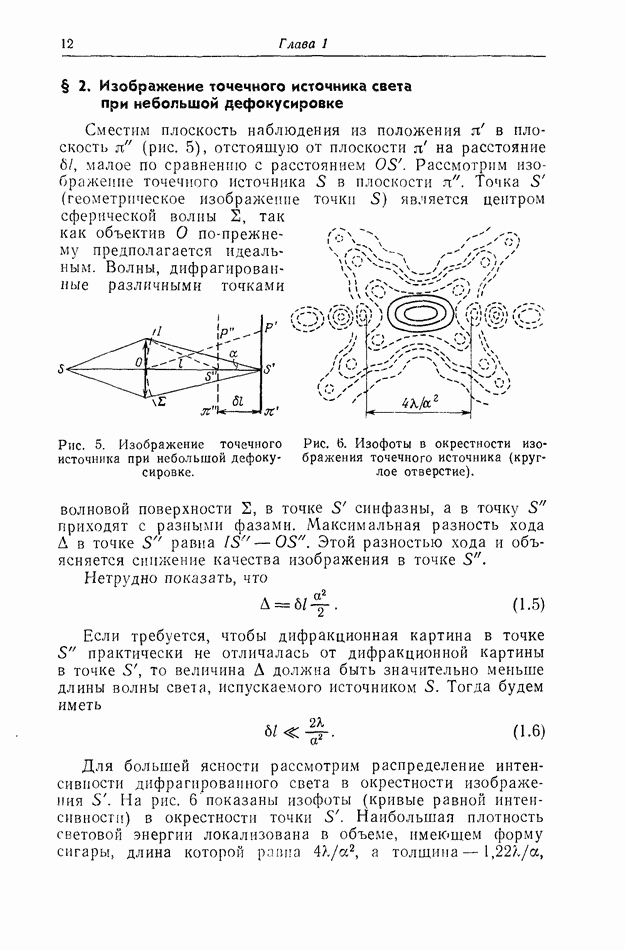
Рис. 1. Точечный источник  и его изображение
и его изображение  Рассмотрим для примера объектив О с круглой оправой. Амплитуда в плоскости изображения
Рассмотрим для примера объектив О с круглой оправой. Амплитуда в плоскости изображения  дается фурье-образом круговой функции. Пусть диаметр объектива О равен 2а, а положение произвольной точки
дается фурье-образом круговой функции. Пусть диаметр объектива О равен 2а, а положение произвольной точки  в которой вычисляется амплитуда, определяется углом
в которой вычисляется амплитуда, определяется углом  Введем обозначения
Введем обозначения

Амплитуда в точке  будет равна действительной величине
будет равна действительной величине

где  функция Бесселя первого порядка переменной
функция Бесселя первого порядка переменной 

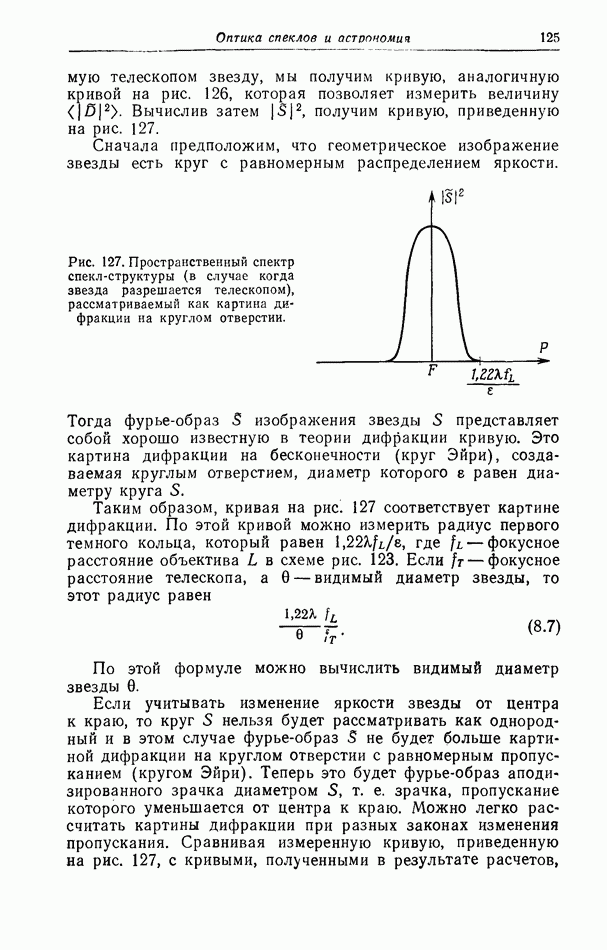
Рис. 2. Распределение амплитуды в картине дифракции на круглом отверстии.

Рис. 3. Распределение интенсивности в картине дифракции на круглом отверстии.
Кривые на рис. 2 и 3 показывают, как изменяются амплитуда  и интенсивность
и интенсивность  в зависимости от
в зависимости от  Очевидно, что рассматриваемая дифракционная картина имеет круговую симметрию (ее называют кругом Эйри). В ней имеется очень яркое центральное пятно, окруженное последовательностью светлых и темных колец. Нетрудно видеть, что амплитуда нечетных светлых колец отрицательна.
Очевидно, что рассматриваемая дифракционная картина имеет круговую симметрию (ее называют кругом Эйри). В ней имеется очень яркое центральное пятно, окруженное последовательностью светлых и темных колец. Нетрудно видеть, что амплитуда нечетных светлых колец отрицательна.
Интенсивность светлых колец значительно меньше интенсивности центрального пятна и быстро убывает от центра к периферии. Для первого темного кольца таблица функций Бесселя дает значение  По формуле (1.1) можно вычислить угловой радиус
По формуле (1.1) можно вычислить угловой радиус  этого кольца:
этого кольца:

Угловой диаметр  центрального дифракционного пятна называют также угловым диаметром дифракционной картины.
центрального дифракционного пятна называют также угловым диаметром дифракционной картины.

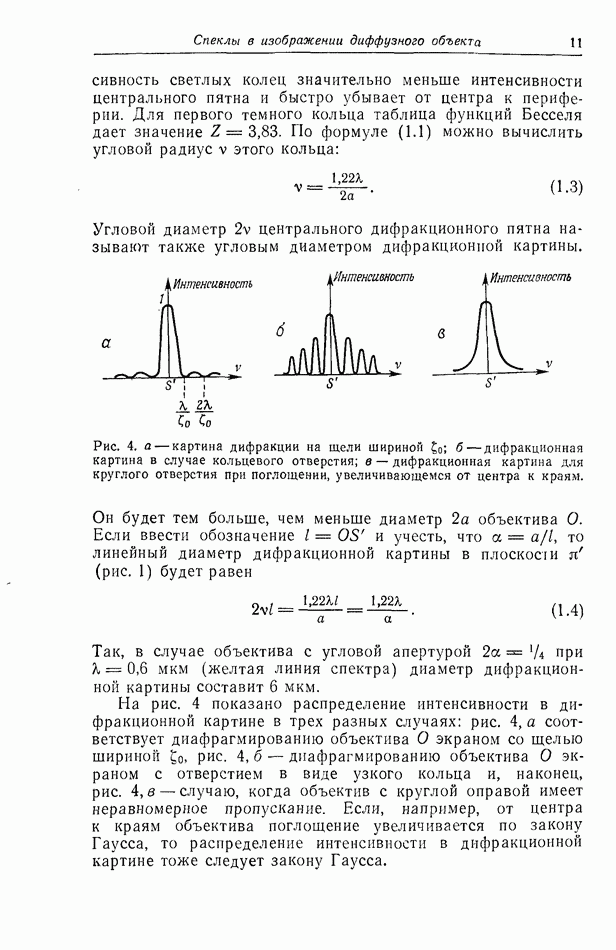
Рис. 4. а — картина дифракции на щели шириной  дифракционная картина в случае кольцевого отверстия; в — дифракционная картина для круглого отверстия при поглощении, увеличивающемся от центра к краям.
дифракционная картина в случае кольцевого отверстия; в — дифракционная картина для круглого отверстия при поглощении, увеличивающемся от центра к краям.
Он будет тем больше, чем меньше диаметр 2а объектива О. Если ввести обозначение  и учесть, что
и учесть, что  то линейный диаметр дифракционной картины в плоскости
то линейный диаметр дифракционной картины в плоскости  (рис. 1) будет равен
(рис. 1) будет равен

Так, в случае объектива с угловой апертурой  при
при  (желтая линия спектра) диаметр дифракционной картины составит 6 мкм.
(желтая линия спектра) диаметр дифракционной картины составит 6 мкм.
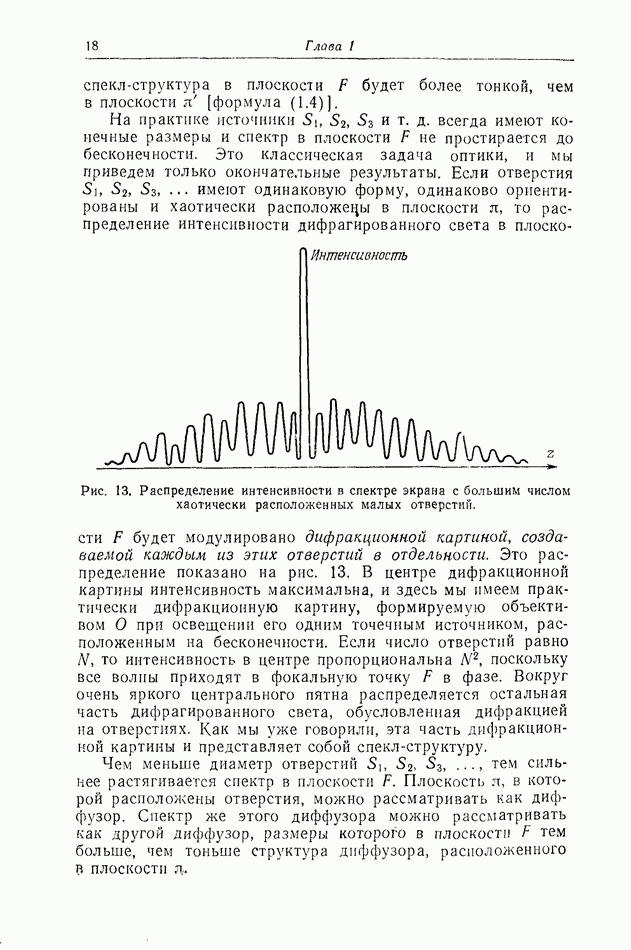
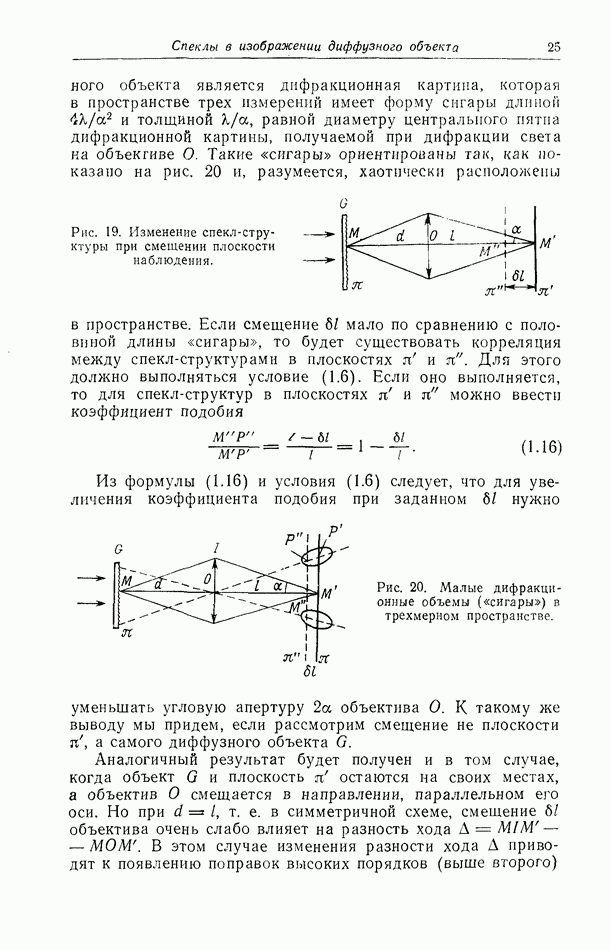
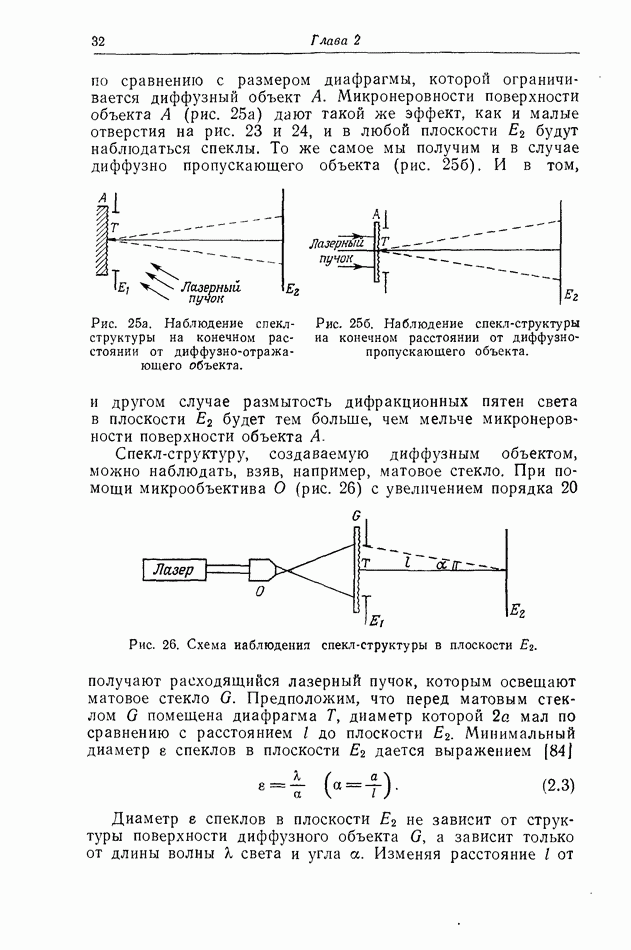
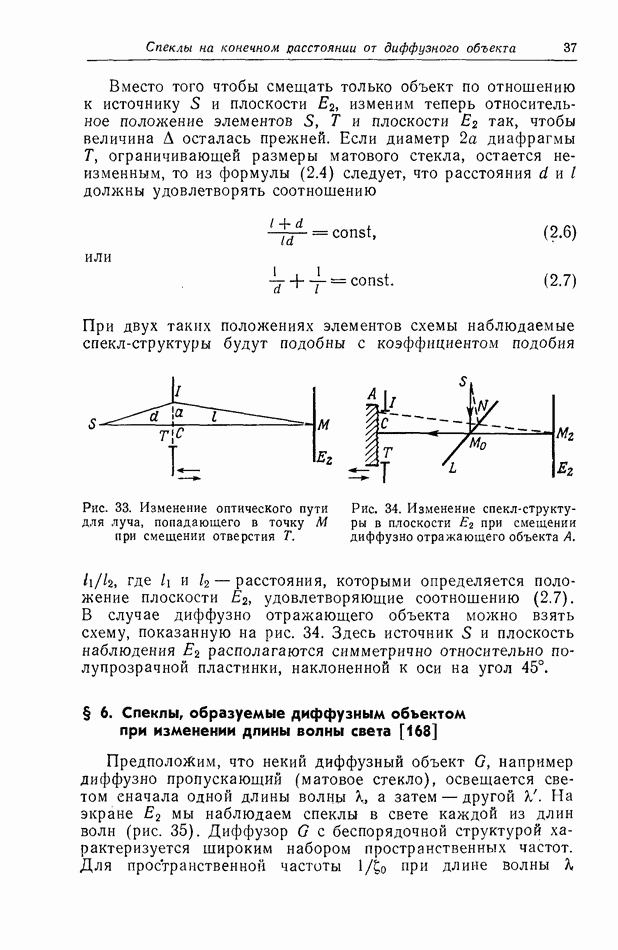
На рис. 4 показано распределение интенсивности в дифракционной картине в трех разных случаях: рис. 4, а соответствует диафрагмированию объектива О экраном со щелью шириной  рис. 4,б — диафрагмированию объектива О экраном с отверстием в виде узкого кольца и, наконец, рис. 4,8 — случаю, когда объектив с круглой оправой имеет неравномерное пропускание. Если, например, от центра к краям объектива поглощение увеличивается по закону Гаусса, то распределение интенсивности в дифракционной картине тоже следует закону Гаусса.
рис. 4,б — диафрагмированию объектива О экраном с отверстием в виде узкого кольца и, наконец, рис. 4,8 — случаю, когда объектив с круглой оправой имеет неравномерное пропускание. Если, например, от центра к краям объектива поглощение увеличивается по закону Гаусса, то распределение интенсивности в дифракционной картине тоже следует закону Гаусса.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Введение
- Глава 1. СПЕКЛЫ В ИЗОБРАЖЕНИИ ДИФФУЗНОГО ОБЪЕКТА, ОСВЕЩАЕМОГО ЛАЗЕРОМ
- § 1. Изображение точечного источника света, преобразование Фурье
- § 2. Изображение точечного источника света при небольшой дефокусировке
- § 3. Изображение двух монохроматических точечных источников света
- § 4. Изображение большого числа монохроматических точечных источников, расположенных хаотически
- § 5. Спектр большого числа когерентных точечных источников
- § 6. Спектр большого числа когерентных точечных источников, образующих идентичные, одинаково ориентированные и хаотически расположенные пары
- § 7. Спеклы в изображении объекта, освещаемого лазером
- § 8. Изменение спекл-структуры при смещении плоскости наблюдения [6, 169]
- § 9. Спекл-структура, наблюдаемая в изображении диффузного объекта при изменении длины волны света [168, 217]
- § 10. Спекл-структура, наблюдаемая в белом свете [72]
- Глава 2. СПЕКЛЫ, ВОЗНИКАЮЩИЕ НА КОНЕЧНОМ РАССТОЯНИИ ОТ ДИФФУЗНОГО ОБЪЕКТА, ОСВЕЩАЕМОГО ЛАЗЕРОМ
- § 1. Дифракция Френеля и дифракция Фраунгофера в трех измерениях
- § 2. Спеклы, наблюдаемые на конечном расстоянии от диффузного объекта
- § 3. Спеклы, наблюдаемые при смещении диффузного объекта в поперечном направлении
- § 4. Спеклы, наблюдаемые при изменении направления светового пучка, освещающего диффузный объект [56, 147]
- § 5. Спеклы, наблюдаемые при продольном смещении плоскости наблюдения или диффузного объекта [62]
- § 6. Спеклы, образуемые диффузным объектом при изменении длины волны света [168]
- § 7. Спеклы, создаваемые диффузным объектом при изменении длины вопны света и положения плоскости наблюдения [168]
- § 8. Спекл-структура, создаваемая диффузным объектом при освещении его другой спекл-структурой [65, 166]
- Глава 3. ИНТЕРФЕРЕНЦИЯ В ДИФФУЗНОМ СВЕТЕ
- § 2. Основные принципы интерференции в диффузном свете
- § 3. Интерференция в случае двух одинаковых диффузоров
- § 4. Интерферометр Берча
- § 5. Интерференция в случае двух неодинаковых диффузоров в одной плоскости [166]
- § 6. Интерференция в случае неодинаковых диффузоров в разных плоскостях [62]
- Глава 4. ИНТЕРФЕРЕНЦИЯ В СЛУЧАЕ ФОТОГРАФИЧЕСКОЙ СУПЕРПОЗИЦИИ СПЕКЛ-СТРУКТУР, СМЕЩЕННЫХ В ПОПЕРЕЧНОМ НАПРАВЛЕНИИ
- § 2. Фундаментальный опыт Берча и Токарского [101]
- § 3. Несколько экспозиций на одной фотопластинке
- § 4. Одновременная регистрация нескольких спекл-структур при помощи двулучепреломляющей пластинки [73]
- § 5. Регистрация при непрерывном перемещении фотопластинки во время экспозиции [215]
- § 6. Регистрация спекл-структуры с изменением угла падения
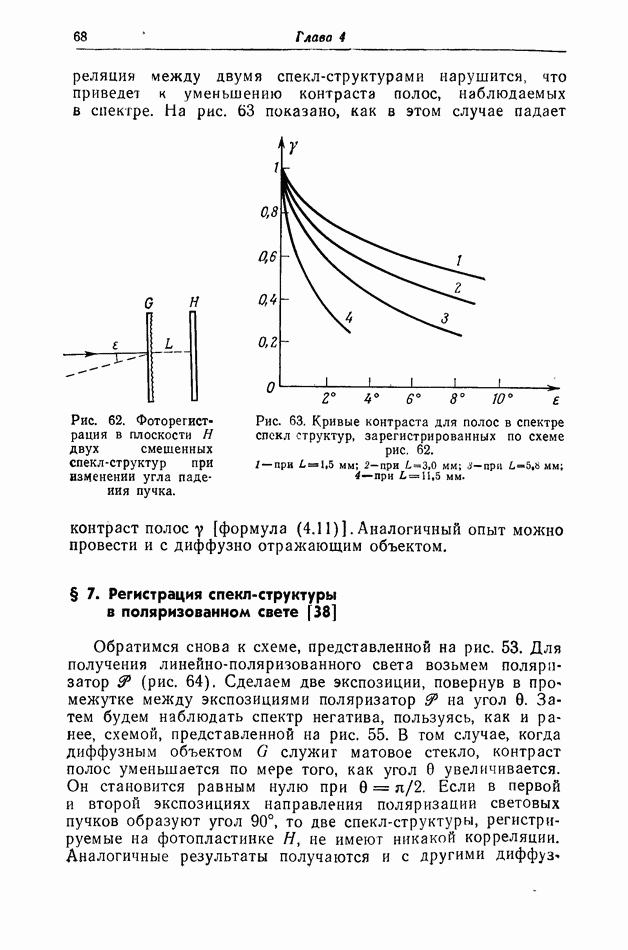
- § 7. Регистрация спекл-структуры в поляризованном свете [38]
- § 8. Регистрация с изменением угла наклона диффузора [167]
- § 9. Регистрация с изменением длины волны света
- Глава 5. ИНТЕРФЕРЕНЦИЯ В СЛУЧАЕ ФОТОГРАФИЧЕСКОЙ СУПЕРПОЗИЦИИ СПЕКЛ-СТРУКТУР, СМЕЩЕННЫХ В ПРОДОЛЬНОМ НАПРАВЛЕНИИ
- § 2. Регистрация с изменением длины световой волны между экспозициями
- § 3. Регистрация с изменением длины световой волны и смещением фотопластинки между экспозициями
- § 4. Интерференционные кольца, образуемые фотопластинкой с двумя спекл-структурами, зарегистрированными в плоскости изображения диффузного объекта [6]
- § 5. Интерференционные кольца, образуемые фотопластинкой, однократно экспонированной с применением амплитудного диффузора
- § 6. Интерференционные кольца, образуемые фотопластинкой, на которой зарегистрировано несколько спекл-структур при ее продольном смещении между экспозициями [149]
- § 7. Гиперболические или эллиптические интерференционные полосы
- Глава 6. ОПТИЧЕСКАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ, МОДУЛИРОВАННЫХ СПЕКЛАМИ
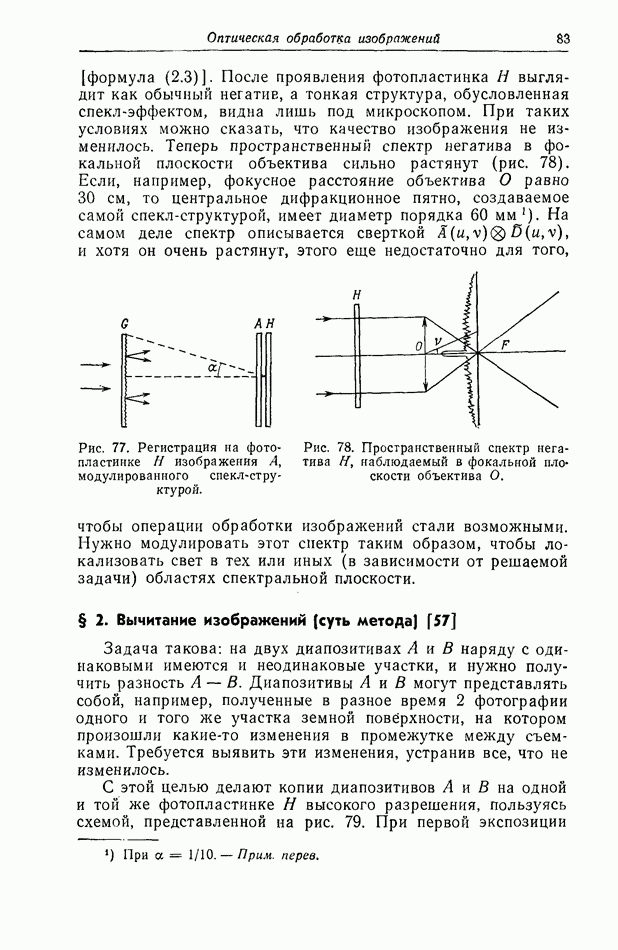
- § 2. Вычитание изображений (суть метода] [57]
- § 3. Распределение света в плоскости изображения
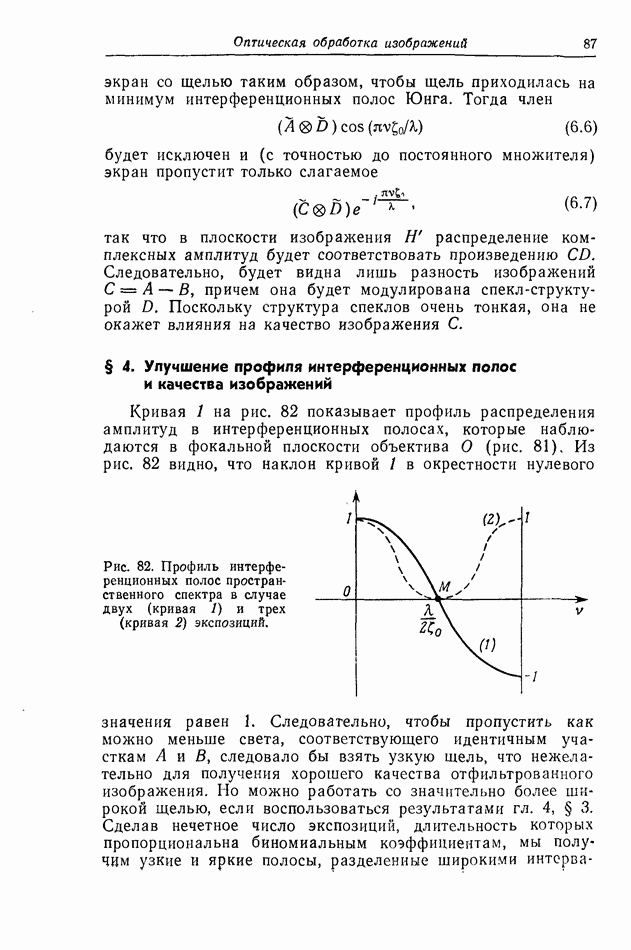
- § 4. Улучшение профиля интерференционных полос и качества изображений
- § 5. Кодирование и декодирование изображений
- § 6. Мультиплексная запись изображений методом наложения спекл-структур, сдвигаемых в поперечном направлении [106]
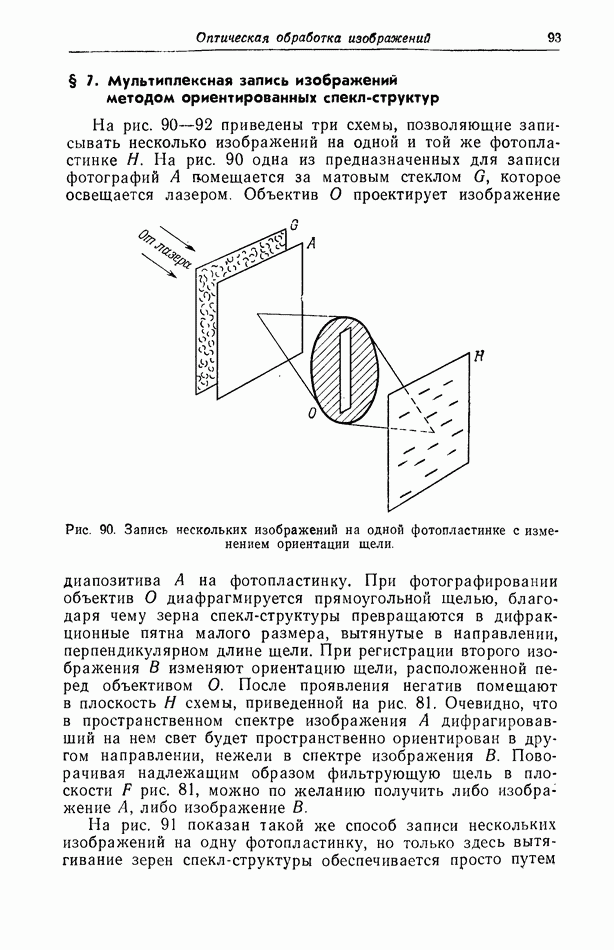
- § 7. Мультиплексная запись изображений методом ориентированных спекл-структур
- Глава 7. ИССЛЕДОВАНИЕ СМЕЩЕНИЙ И ДЕФОРМАЦИЙ ДИФФУЗНЫХ ОБЪЕКТОВ МЕТОДОМ ФОТОРЕГИСТРАЦИИ СПЕКЛ-СТРУКТУРЫ
- § 1. Поперечное смещение диффузного объекта. Случай, когда смещение больше диаметра пятна спекл-структуры [143]
- § 2. Поперечное смещение диффузного объекта. Случай, когда смещение меньше диаметра пятна спекл-структуры [59]
- § 3. Исследование поперечного смещения диффузного объекта, освещаемого двумя пучками. Случай, когда смещение меньше диаметра пятна спекл-структуры [142]
- § 4. Определение поперечного смещения диффузного объекта относительно опорной диффузной поверхности [166]
- § 5. Определение продольных смещений диффузного объекта относительно опорной диффузной поверхности [142]
- § 6. Наблюдение спекл-структуры в фокальной плоскости объектива [166]
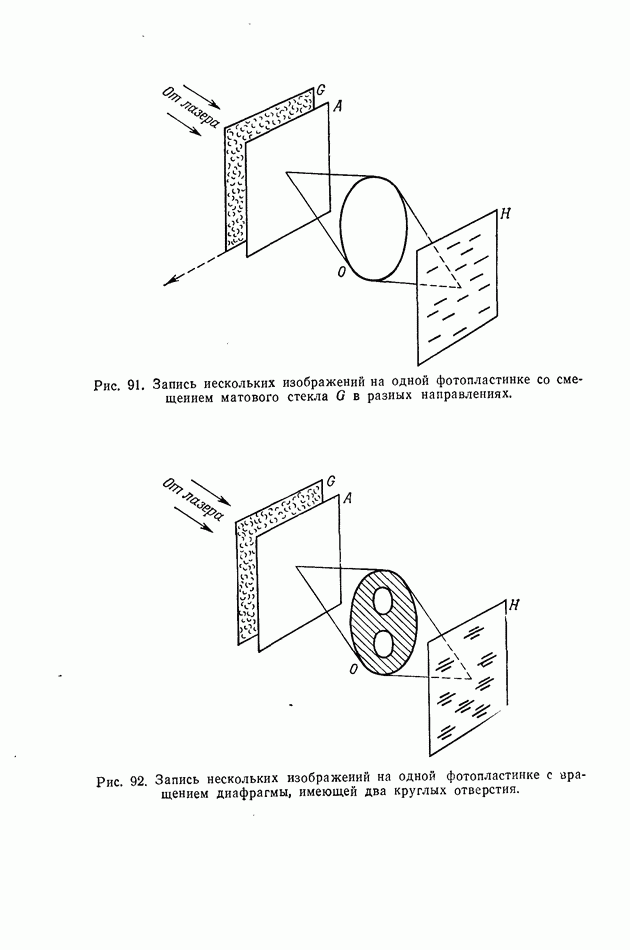
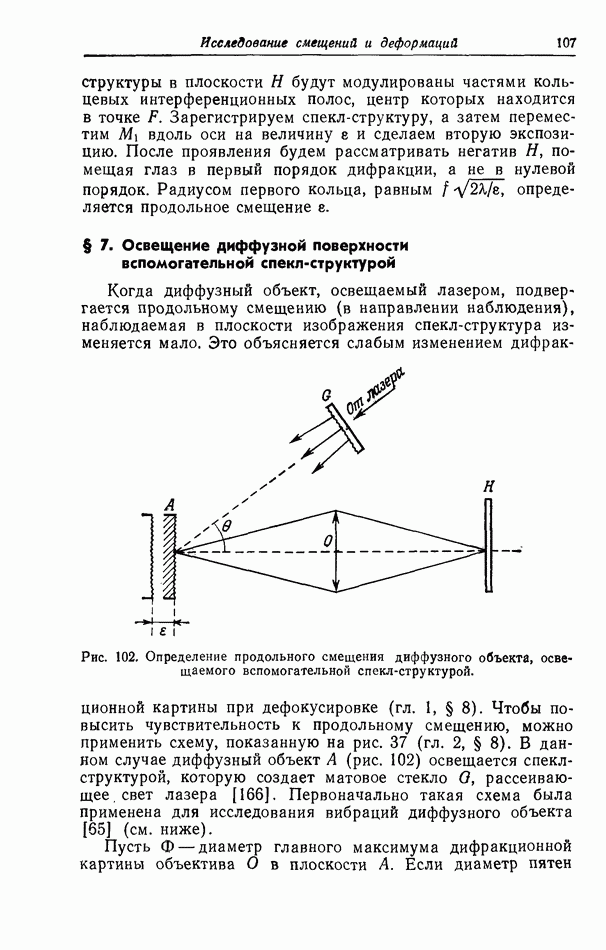
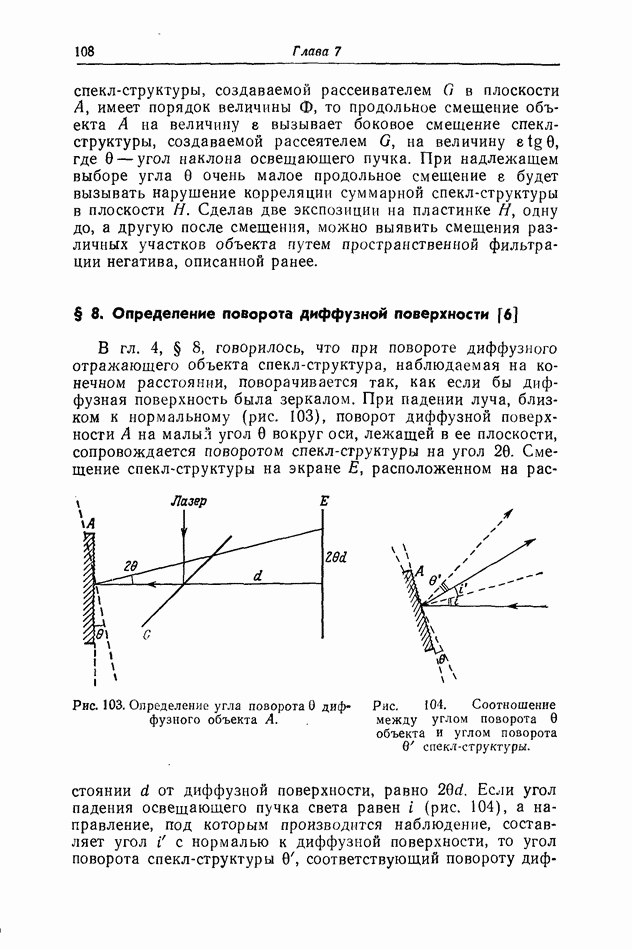
- § 7. Освещение диффузной поверхности вспомогательной спекл-структурой
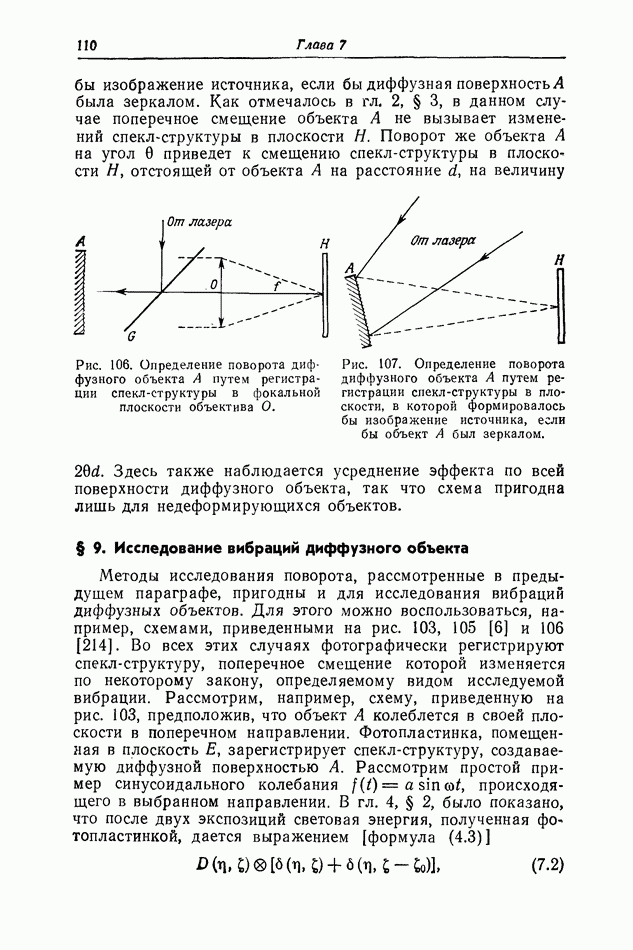
- § 8. Определение поворота диффузной поверхности [6]
- § 9. Исследование вибраций диффузного объекта
- § 10. Исследование изменений рельефа поверхности диффузного объекта
- Глава 8. ОПТИКА СПЕКЛОВ И АСТРОНОМИЯ
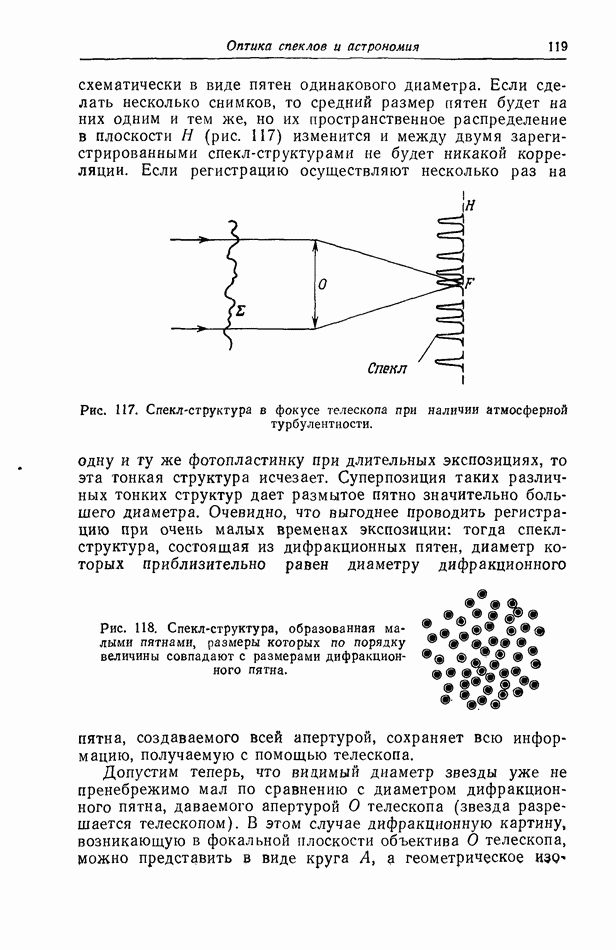
- § 1. Изображение одиночной звезды в фокусе телескопа при наличии атмосферной турбулентности
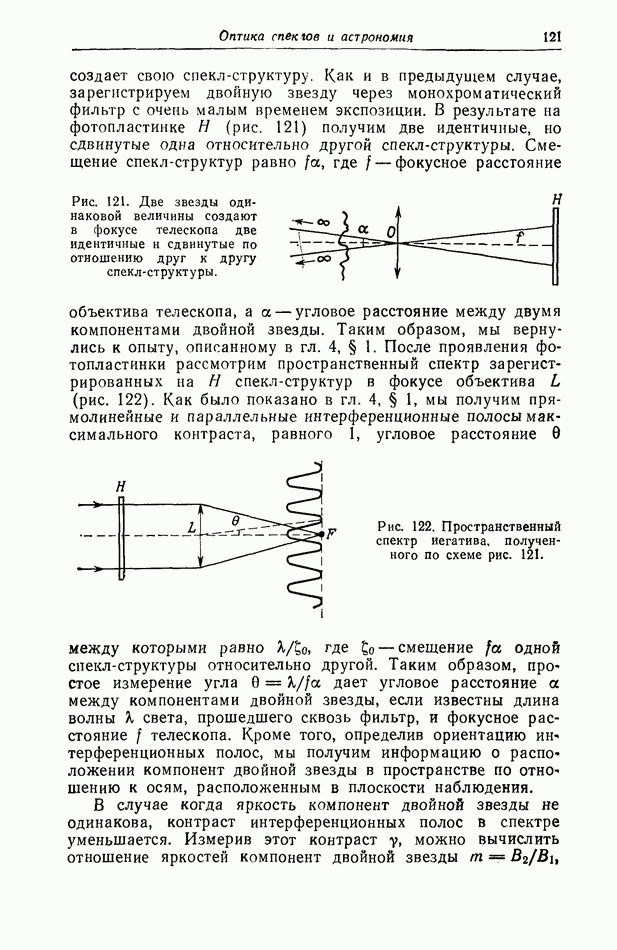
- § 2. Наблюдение двойных звезд в фокусе телескопа в присутствии втмосферной турбулентности [138]
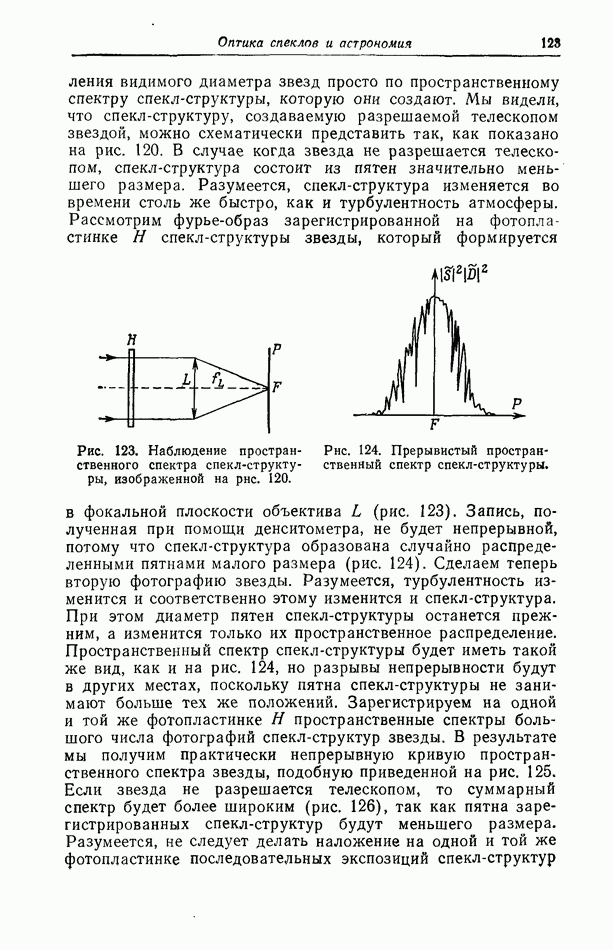
- § 3. Измерение видимого диаметра звезд методом Лабейри [137]
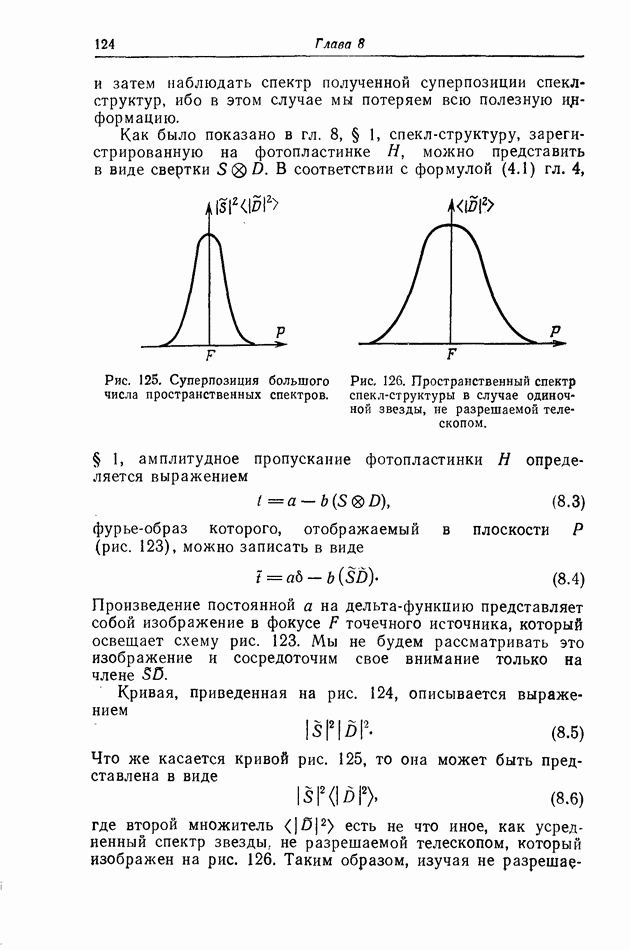
- § 4. Измерение видимого диаметра звезд с использованием нескольких телескопов
- Глава 9. ИССЛЕДОВАНИЕ ШЕРОХОВАТОСТИ ПОВЕРХНОСТЕЙ
- § 2. Применение оптики спеклов для оценки шероховатости поверхностей
- § 3. Определение шероховатости поверхности по корреляции между двумя спекл-структурами полученными при разных углах падения лазерного пучка [145]
- § 4. Определение шероховатости в реапьном времени по корреляции между амплитудами спекп-структур, соответствующих двум ориентациям лазерного пучка [147]
- § 5. Определение шероховатости по корреляции между спекл-структурами, полученными с двумя длинами волн [217]
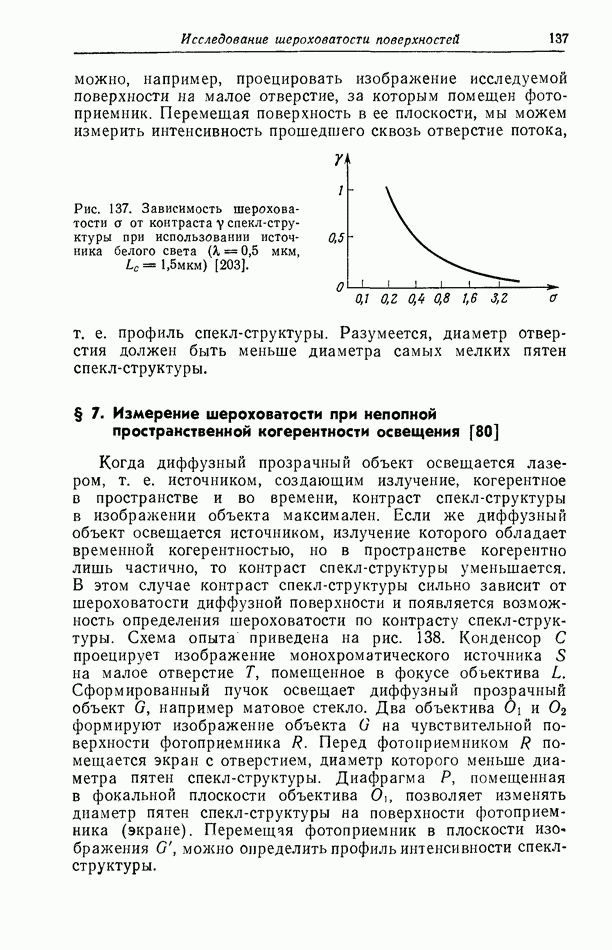
- § 6. Измерение шероховатости с помощью источника, излучающего широкую полосу спектра [203]
- § 7. Измерение шероховатости при неполной пространственной когерентности освещения [80]
- Глава 10. ДРУГИЕ ПРИМЕНЕНИЯ
- § 1. Дифференциальный интерферометр для прозрачных к объектов, основанный на фоторегистрации спекп-структуры за две экспозиции
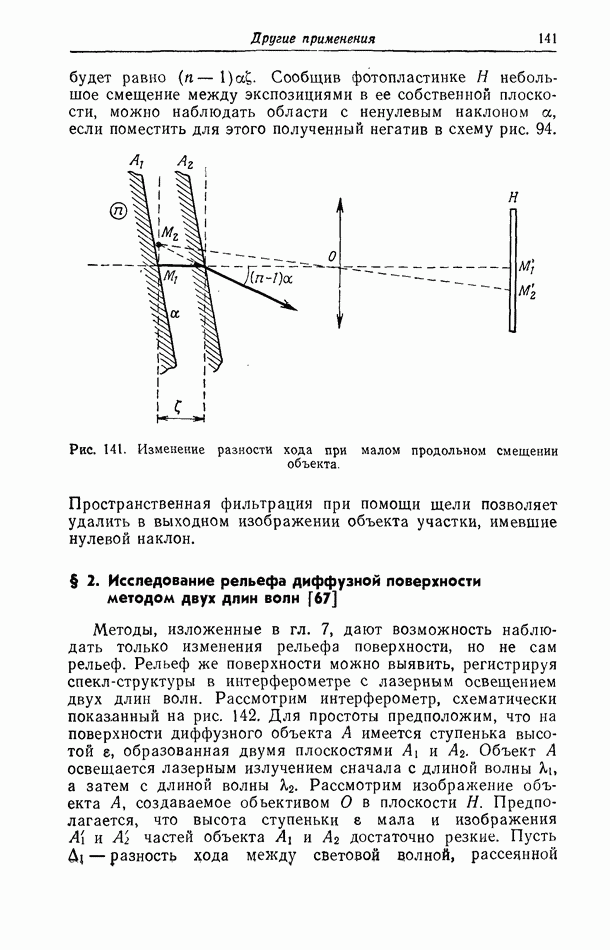
- § 2. Исследование рельефа диффузной поверхности методом двух длин волн [67]
- § 3. Определение передаточной функции оптической системы, освещаемой спекл-структурой [45]
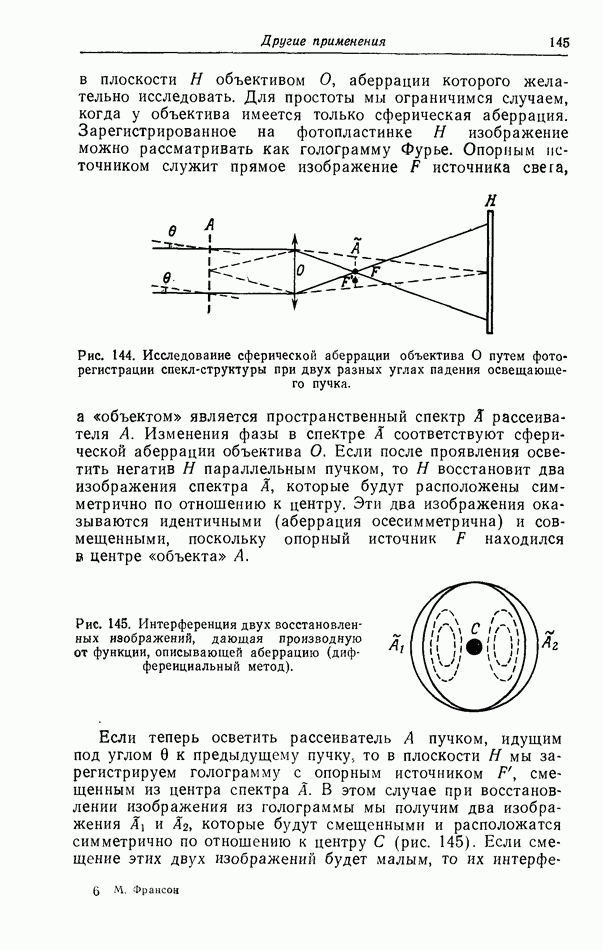
- § 4. Исследование аберраций оптической системы путем фотографирования спекл-структур [196а, 211]
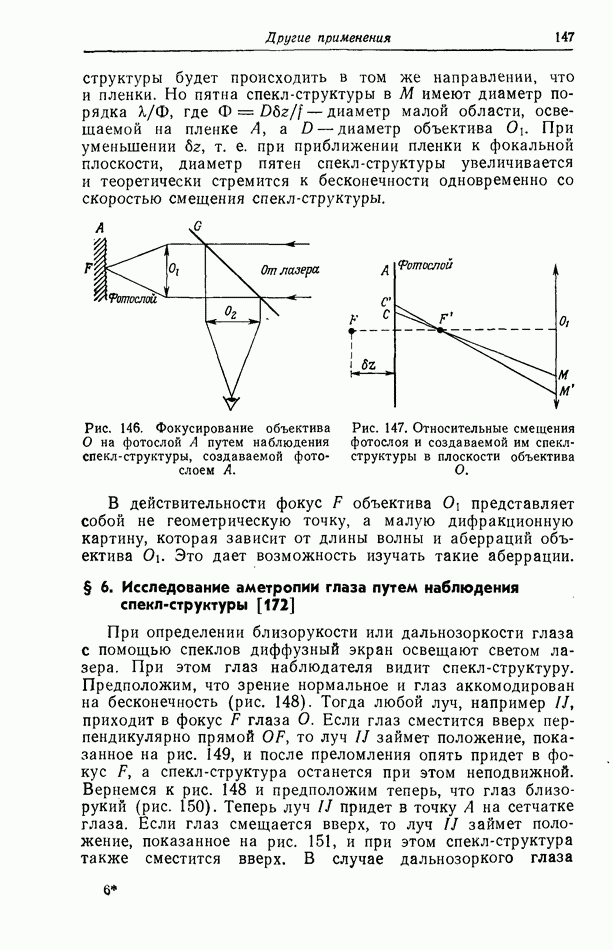
- § 5. Фокусирование объектива с помощью спекл-структуры [198]
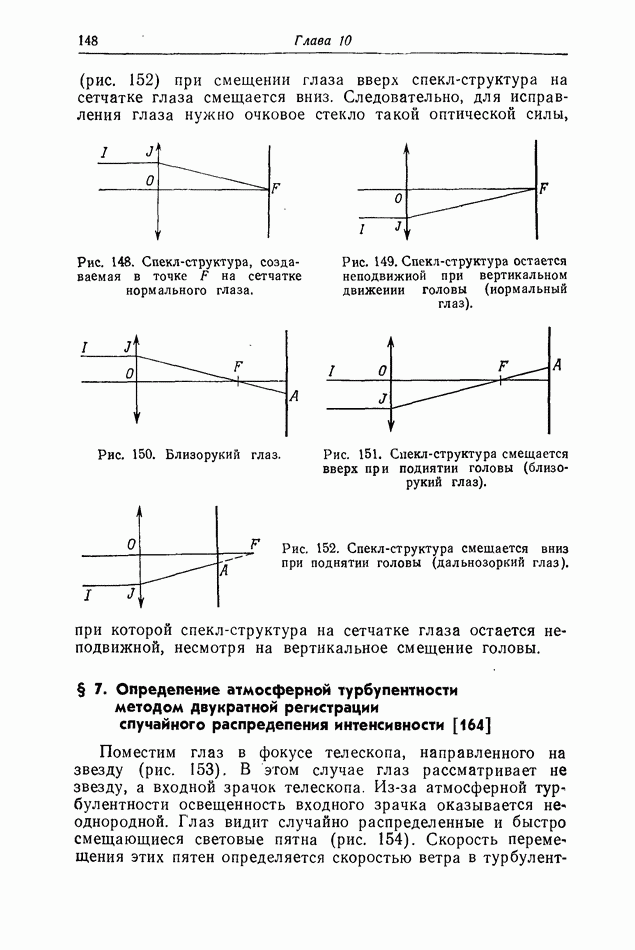
- § 6. Исследование аметропии глаза путем наблюдения спекл-структуры [172]
- § 7. Определение атмосферной турбулентности методом двукратной регистрации случайного распределения интенсивности [164]
- § 8. Восстановление траектории диффузного объекта путем регистрации спекл-структуры [151, 153]
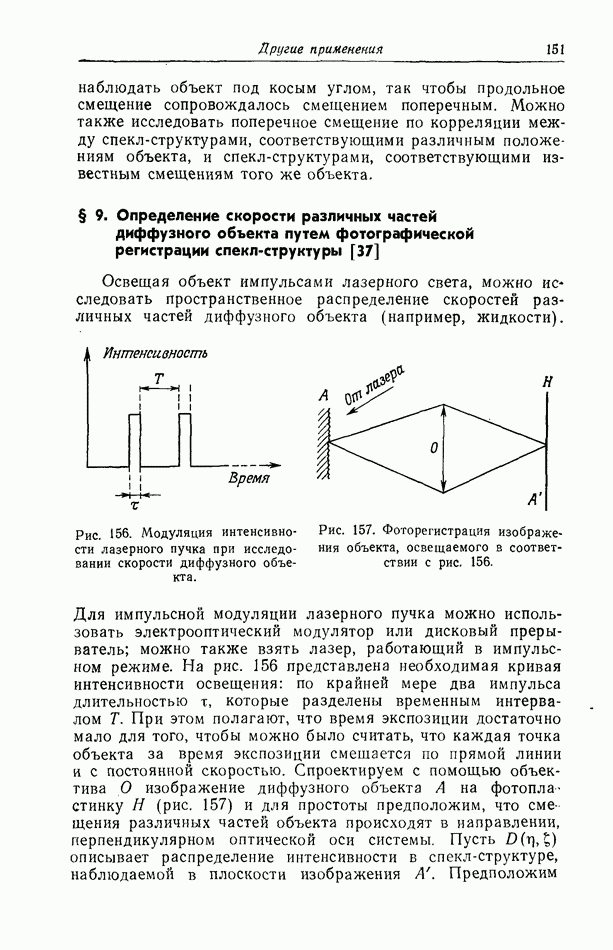
- § 9. Определение скорости различных частей диффузного объекта путем фотографической регистрации спекл-структуры [37]