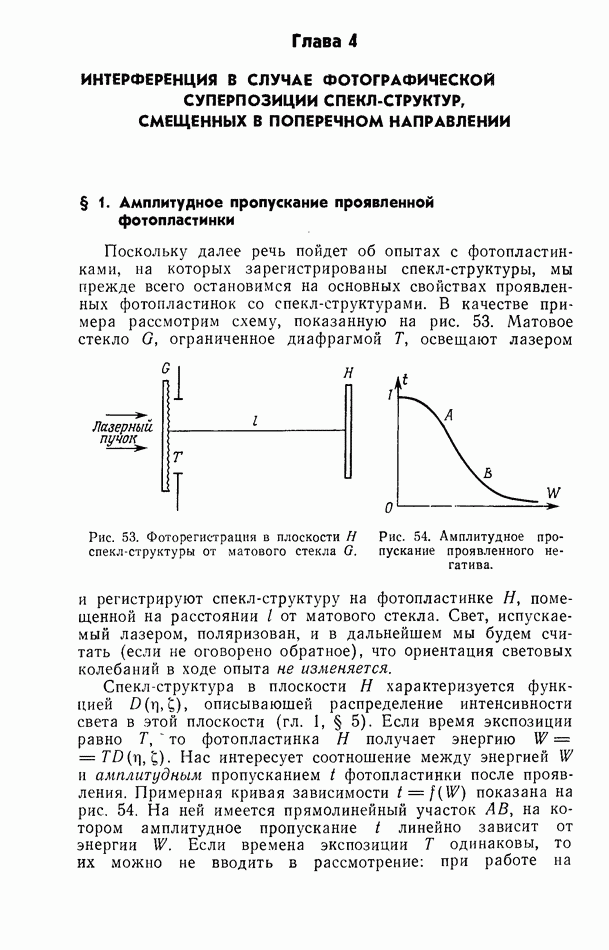
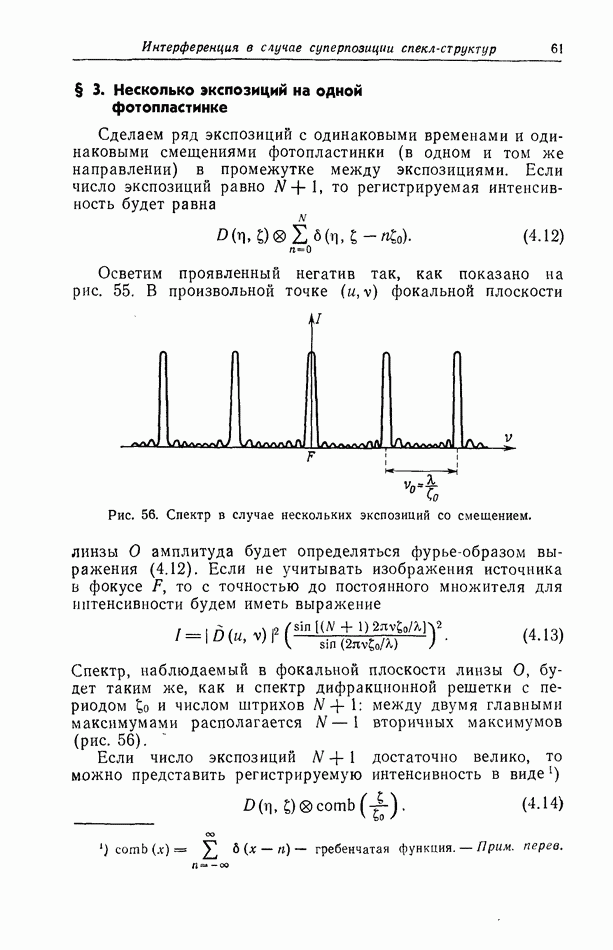
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
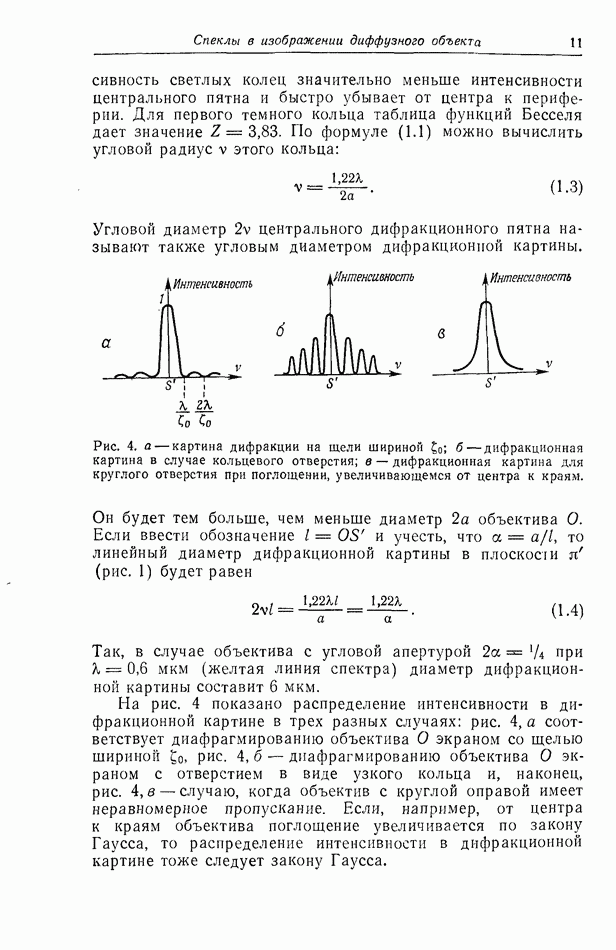
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
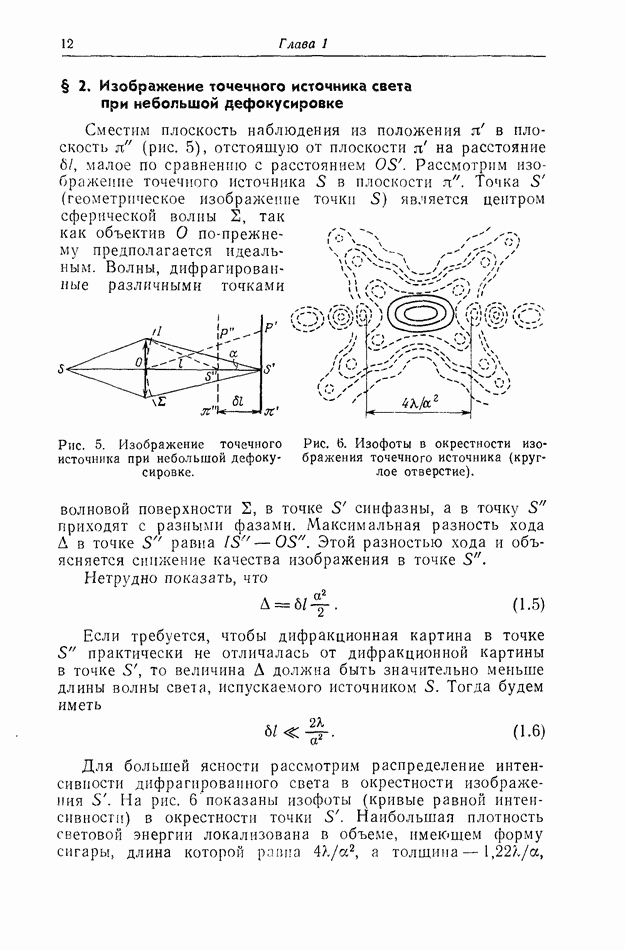
Глава 2. СПЕКЛЫ, ВОЗНИКАЮЩИЕ НА КОНЕЧНОМ РАССТОЯНИИ ОТ ДИФФУЗНОГО ОБЪЕКТА, ОСВЕЩАЕМОГО ЛАЗЕРОМ
§ 1. Дифракция Френеля и дифракция Фраунгофера в трех измерениях
Представим себе экран  с отверстием
с отверстием  освещаемый параллельным пучком света монохроматического точечного источника (рис. 22). Пусть отверстие
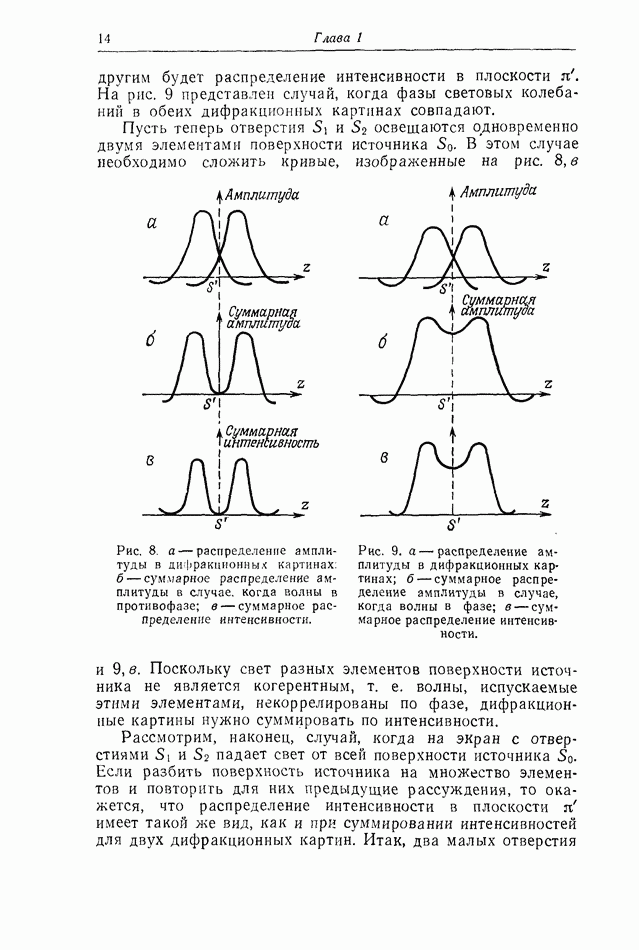
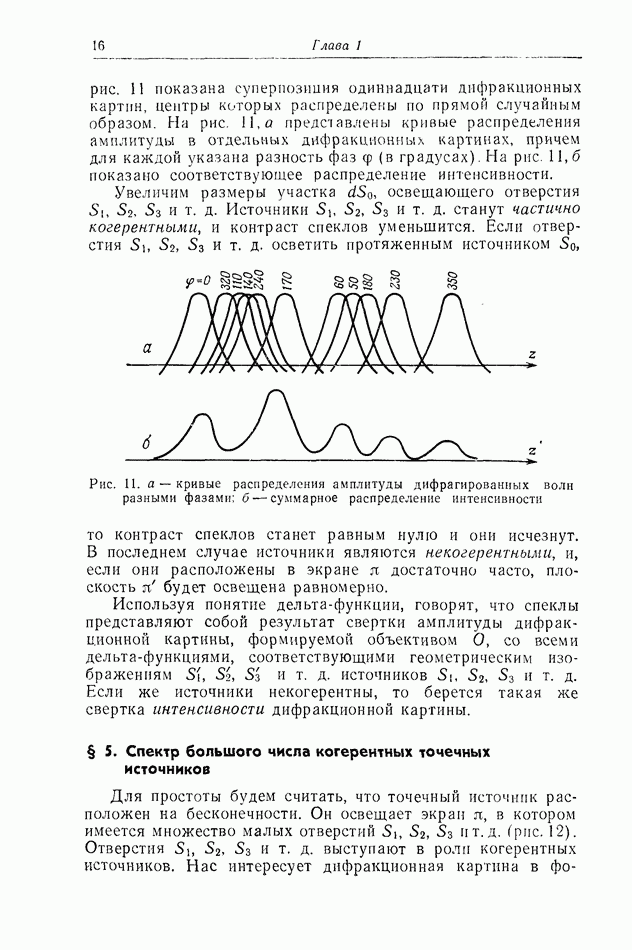
освещаемый параллельным пучком света монохроматического точечного источника (рис. 22). Пусть отверстие  круглое. В плоскости
круглое. В плоскости  находящейся на конечном расстоянии от плоскости
находящейся на конечном расстоянии от плоскости  будет наблюдаться дифракционная картина Френеля от отверстия
будет наблюдаться дифракционная картина Френеля от отверстия  Мы будем считать, что диаметр отверстия
Мы будем считать, что диаметр отверстия  мал по сравнению с расстоянием
мал по сравнению с расстоянием 
Сначала рассмотрим дифракционные явления на оси отверстия. Интенсивность в точке  представляет собой результат интерференции волн, испускаемых всеми точками круглого отверстия
представляет собой результат интерференции волн, испускаемых всеми точками круглого отверстия  Разность хода в точке
Разность хода в точке  для волн, исходящих из центра С и из крайней точки А отверстия
для волн, исходящих из центра С и из крайней точки А отверстия  дается выражением
дается выражением

где а — радиус отверстия,  расстояние
расстояние  Разность хода в точке
Разность хода в точке  для волн, испускаемых двумя произвольными точками круглого отверстия
для волн, испускаемых двумя произвольными точками круглого отверстия  меняется в интервале от О до А, так как
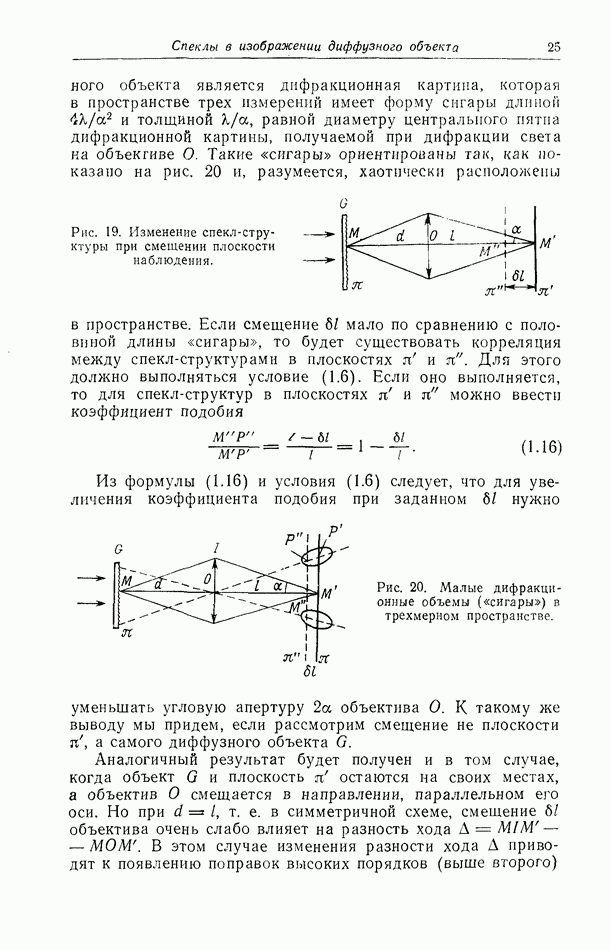
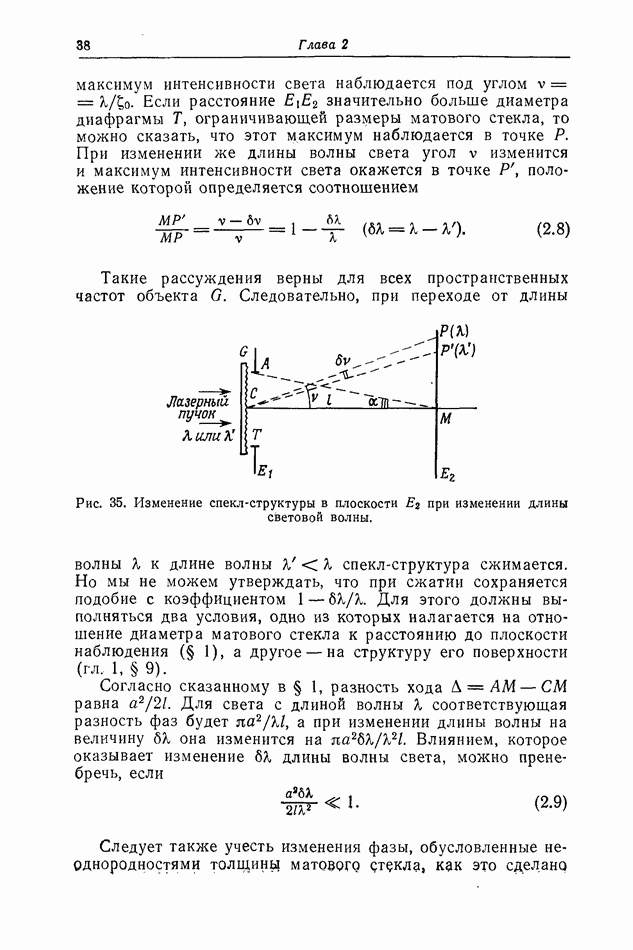
меняется в интервале от О до А, так как  -максимальная разность хода волн для рассматриваемого отверстия. Сместим плоскость наблюдения на расстояние Ы. Если величина
-максимальная разность хода волн для рассматриваемого отверстия. Сместим плоскость наблюдения на расстояние Ы. Если величина  достаточно мала, то вид интерференционной картины в точке
достаточно мала, то вид интерференционной картины в точке  будет практически таким же, как и в точке
будет практически таким же, как и в точке  Какой бы ни была интенсивность света в точке
Какой бы ни была интенсивность света в точке  ее изменения вдоль отрезка
ее изменения вдоль отрезка  пренебрежимо малы. Из выражения (2.1) видно, что смещению на
пренебрежимо малы. Из выражения (2.1) видно, что смещению на  соответствует изменение разности хода на
соответствует изменение разности хода на  Чтобы вид интерференционной картины оставался неизменным вдоль отрезка
Чтобы вид интерференционной картины оставался неизменным вдоль отрезка  изменение разности хода должно быть значительно меньше длины волны света
изменение разности хода должно быть значительно меньше длины волны света  Поскольку
Поскольку  получаем условие
получаем условие

которое мы уже встречали в гл. 1, § 2.
Рассматривая явления не на оси отверстия, например в точке  находящейся на расстоянии
находящейся на расстоянии  от оси, малом по
от оси, малом по
сравнению с расстоянием I, мы получим практически те же результаты. Вдоль отрезка  условия интерференции останутся неизменными. Можно утверждать, что дифракционные картины Френеля в плоскостях
условия интерференции останутся неизменными. Можно утверждать, что дифракционные картины Френеля в плоскостях  подобны, причем коэффициент подобия для распределения интенсивностей в этих двух плоскостях равен
подобны, причем коэффициент подобия для распределения интенсивностей в этих двух плоскостях равен 

Рис. 22. Изменение разности хода при смещении плоскости наблюдения, находящейся на конечном расстоянии от объекта.
Если экран  сместить на расстояние, превышающее
сместить на расстояние, превышающее  то дифракционная картина Френеля изменится. Из формулы (2.2) видно, что чем больше расстояние
то дифракционная картина Френеля изменится. Из формулы (2.2) видно, что чем больше расстояние  тем медленнее меняется дифракционная картина.
тем медленнее меняется дифракционная картина.
Начиная с некоторого достаточно большого расстояния между экранами  и экран
и экран  можно отодвигать сколь угодно далеко. Пока допустимое смещение
можно отодвигать сколь угодно далеко. Пока допустимое смещение  конечно, мы имеем дело с дифракцией Френеля. Если и дальше удалять экран
конечно, мы имеем дело с дифракцией Френеля. Если и дальше удалять экран  то мы постепенно перейдем в область дифракции Фраунгофера (дифракции на бесконечности), где
то мы постепенно перейдем в область дифракции Фраунгофера (дифракции на бесконечности), где  может принимать практически любые значения.
может принимать практически любые значения.
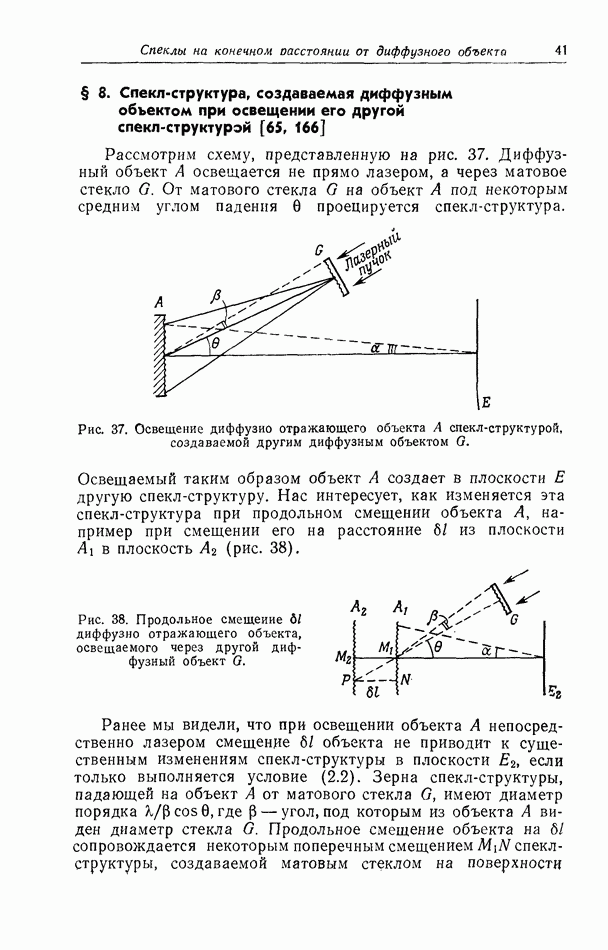
Теперь поместим в плоскости отверстия  непрозрачный экран с множеством хаотически расположенных малых отверстий (на рис. 23 они изображены в виде темных точек).
непрозрачный экран с множеством хаотически расположенных малых отверстий (на рис. 23 они изображены в виде темных точек).

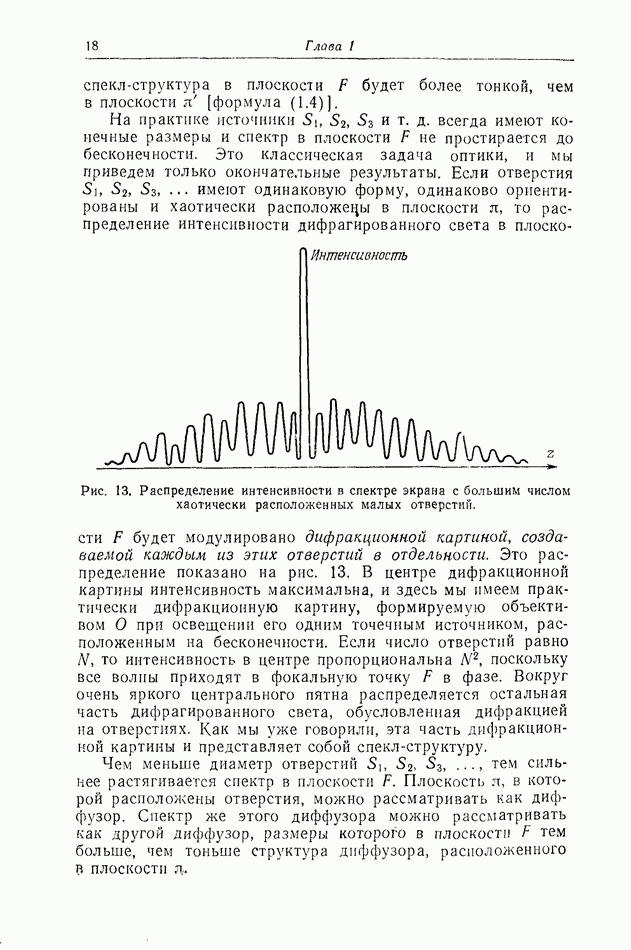
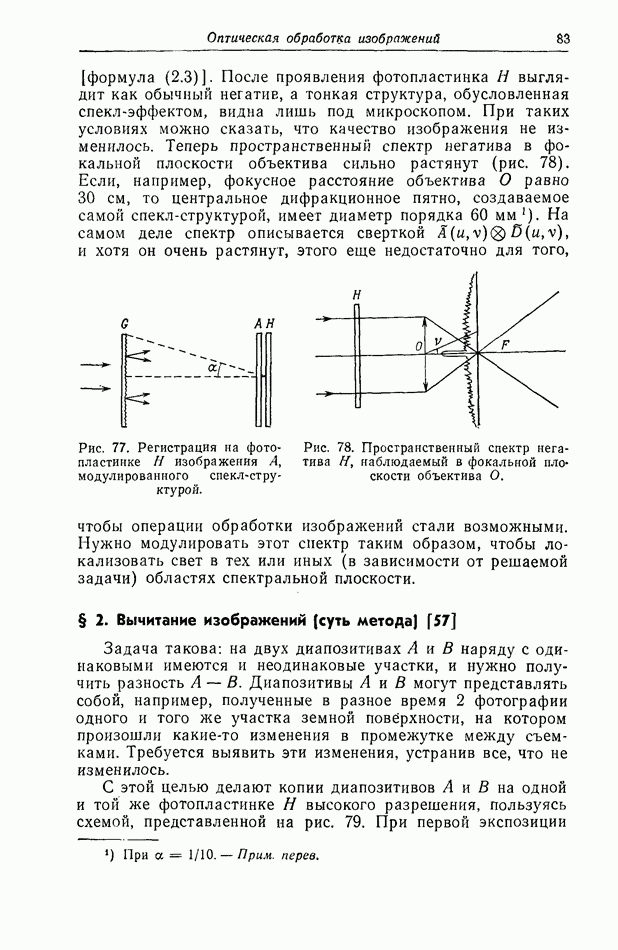
Рис. 23. Наблюдаемая на конечном расстоянии дифракция света от большого числа хаотически расположенных малых отверстий в экране, закрывающем отверстие 
Все эти отверстия испускают когерентные световые волны. Поскольку отверстия очень малы, пятна дифрагировавшего на них света в плоскости наблюдения  велики. Вследствие интерференции световых волн в плоскости
велики. Вследствие интерференции световых волн в плоскости  будет наблюдаться спекл-структура, состоящая из ярких мелких пятнышек.
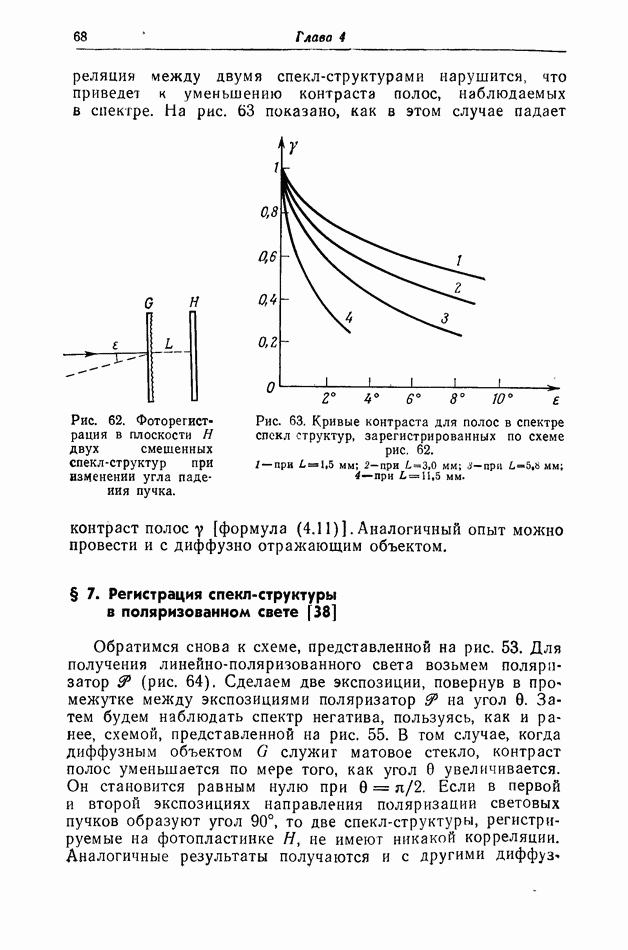
будет наблюдаться спекл-структура, состоящая из ярких мелких пятнышек.
В произвольно выбранную точку экрана  приходит множество волн, фазы которых распределены случайным образом. Если слегка сместить экран
приходит множество волн, фазы которых распределены случайным образом. Если слегка сместить экран  то относительные фазы этих волн изменятся незначительно. Для этого нужно только, чтобы смещение экрана
то относительные фазы этих волн изменятся незначительно. Для этого нужно только, чтобы смещение экрана  удовлетворяло неравенству (2.2). Тогда при переходе из точки
удовлетворяло неравенству (2.2). Тогда при переходе из точки  в точку
в точку  картина интерференции практически не изменится. Можно представить себе целый ряд пар параллельных плоскостей, разделенных тем расстоянием, на которое можно смещать плоскость наблюдения без существенных изменений в структуре спеклов (т. е. с сохранением подобия).
картина интерференции практически не изменится. Можно представить себе целый ряд пар параллельных плоскостей, разделенных тем расстоянием, на которое можно смещать плоскость наблюдения без существенных изменений в структуре спеклов (т. е. с сохранением подобия).

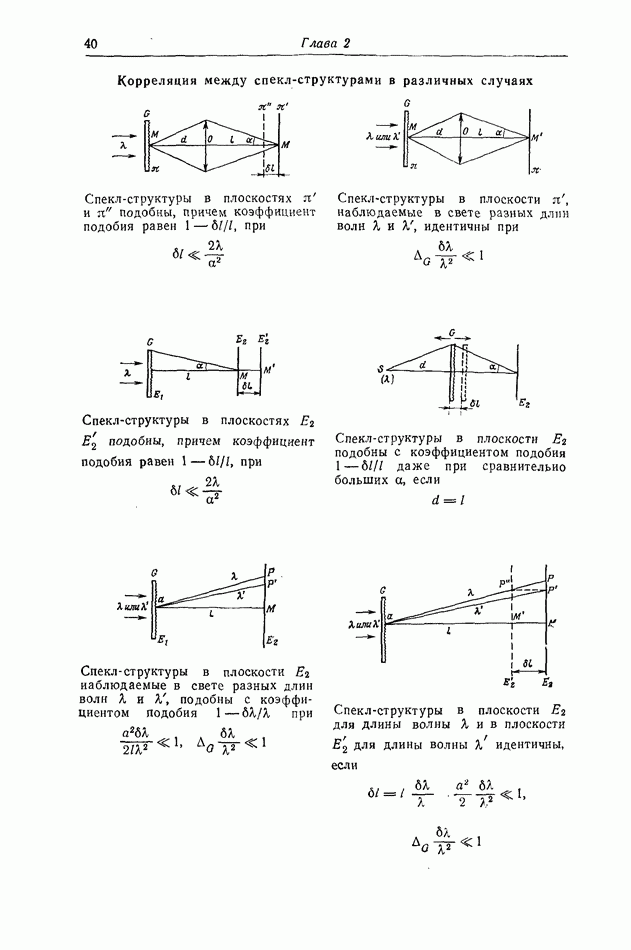
Рис. 24. Подобные спекл-структуры, наблюдаемые в двух соседних плоскостях  ).
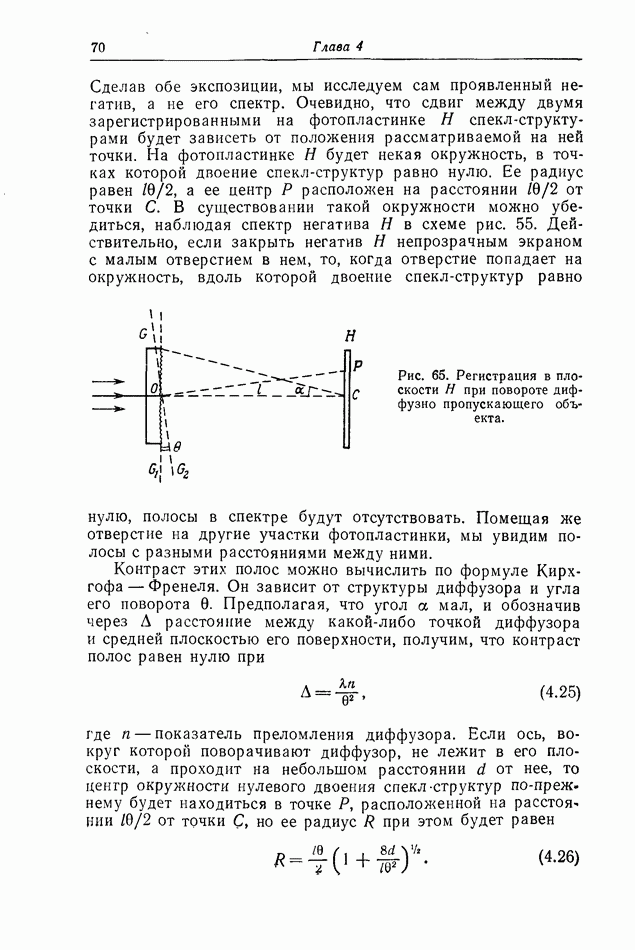
).
Так, спекл-структура в плоскости  будет подобна (с коэффициентом подобия
будет подобна (с коэффициентом подобия  где
где  спекл-структуре в плоскости
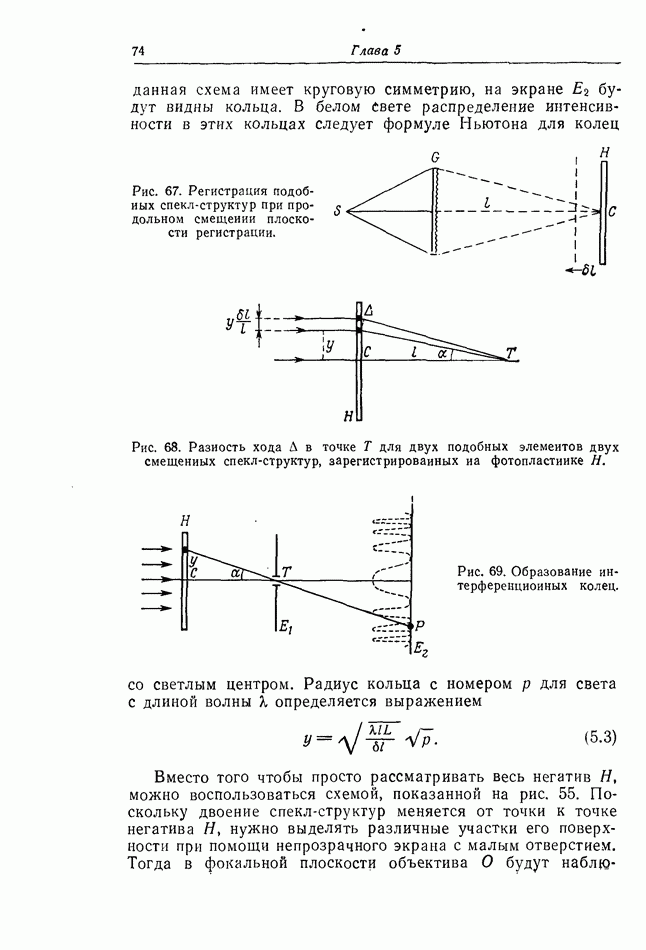
спекл-структуре в плоскости  (или в другой, более близкой к
(или в другой, более близкой к  плоскости) и такое же подобие (с аналогичным коэффициентом подобия) сохранится для плоскостей
плоскости) и такое же подобие (с аналогичным коэффициентом подобия) сохранится для плоскостей  (или другой, более близкой к
(или другой, более близкой к  плоскости)
плоскости) 
В той области пространства, где расстояния  конечны, наблюдаются спеклы Френеля. Если же все больше и больше удалять плоскость наблюдения, то мы постепенно перейдем в область спеклов Фраунгофера, где расстояние между плоскостями
конечны, наблюдаются спеклы Френеля. Если же все больше и больше удалять плоскость наблюдения, то мы постепенно перейдем в область спеклов Фраунгофера, где расстояние между плоскостями  бесконечно велико.
бесконечно велико.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Введение
- Глава 1. СПЕКЛЫ В ИЗОБРАЖЕНИИ ДИФФУЗНОГО ОБЪЕКТА, ОСВЕЩАЕМОГО ЛАЗЕРОМ
- § 1. Изображение точечного источника света, преобразование Фурье
- § 2. Изображение точечного источника света при небольшой дефокусировке
- § 3. Изображение двух монохроматических точечных источников света
- § 4. Изображение большого числа монохроматических точечных источников, расположенных хаотически
- § 5. Спектр большого числа когерентных точечных источников
- § 6. Спектр большого числа когерентных точечных источников, образующих идентичные, одинаково ориентированные и хаотически расположенные пары
- § 7. Спеклы в изображении объекта, освещаемого лазером
- § 8. Изменение спекл-структуры при смещении плоскости наблюдения [6, 169]
- § 9. Спекл-структура, наблюдаемая в изображении диффузного объекта при изменении длины волны света [168, 217]
- § 10. Спекл-структура, наблюдаемая в белом свете [72]
- Глава 2. СПЕКЛЫ, ВОЗНИКАЮЩИЕ НА КОНЕЧНОМ РАССТОЯНИИ ОТ ДИФФУЗНОГО ОБЪЕКТА, ОСВЕЩАЕМОГО ЛАЗЕРОМ
- § 1. Дифракция Френеля и дифракция Фраунгофера в трех измерениях
- § 2. Спеклы, наблюдаемые на конечном расстоянии от диффузного объекта
- § 3. Спеклы, наблюдаемые при смещении диффузного объекта в поперечном направлении
- § 4. Спеклы, наблюдаемые при изменении направления светового пучка, освещающего диффузный объект [56, 147]
- § 5. Спеклы, наблюдаемые при продольном смещении плоскости наблюдения или диффузного объекта [62]
- § 6. Спеклы, образуемые диффузным объектом при изменении длины волны света [168]
- § 7. Спеклы, создаваемые диффузным объектом при изменении длины вопны света и положения плоскости наблюдения [168]
- § 8. Спекл-структура, создаваемая диффузным объектом при освещении его другой спекл-структурой [65, 166]
- Глава 3. ИНТЕРФЕРЕНЦИЯ В ДИФФУЗНОМ СВЕТЕ
- § 2. Основные принципы интерференции в диффузном свете
- § 3. Интерференция в случае двух одинаковых диффузоров
- § 4. Интерферометр Берча
- § 5. Интерференция в случае двух неодинаковых диффузоров в одной плоскости [166]
- § 6. Интерференция в случае неодинаковых диффузоров в разных плоскостях [62]
- Глава 4. ИНТЕРФЕРЕНЦИЯ В СЛУЧАЕ ФОТОГРАФИЧЕСКОЙ СУПЕРПОЗИЦИИ СПЕКЛ-СТРУКТУР, СМЕЩЕННЫХ В ПОПЕРЕЧНОМ НАПРАВЛЕНИИ
- § 2. Фундаментальный опыт Берча и Токарского [101]
- § 3. Несколько экспозиций на одной фотопластинке
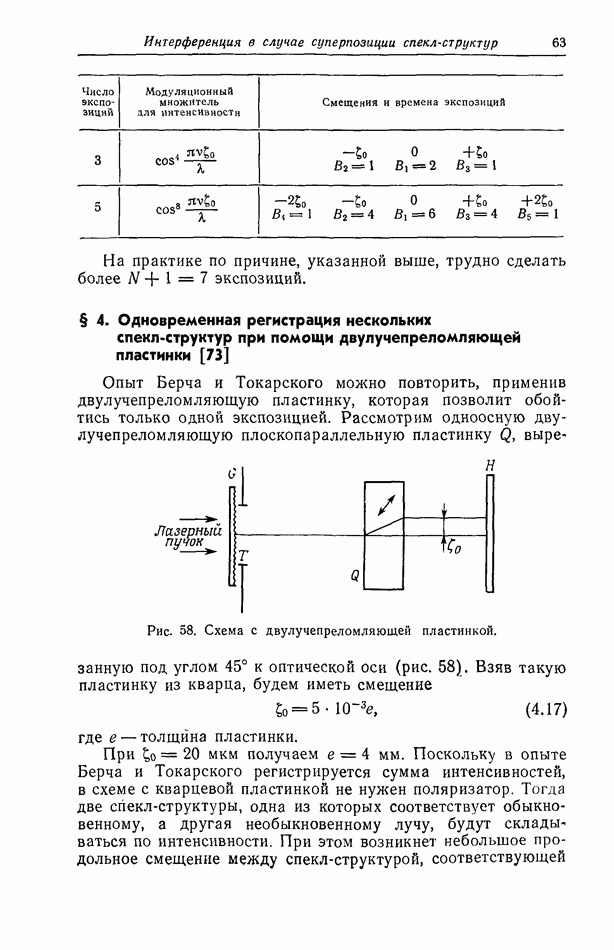
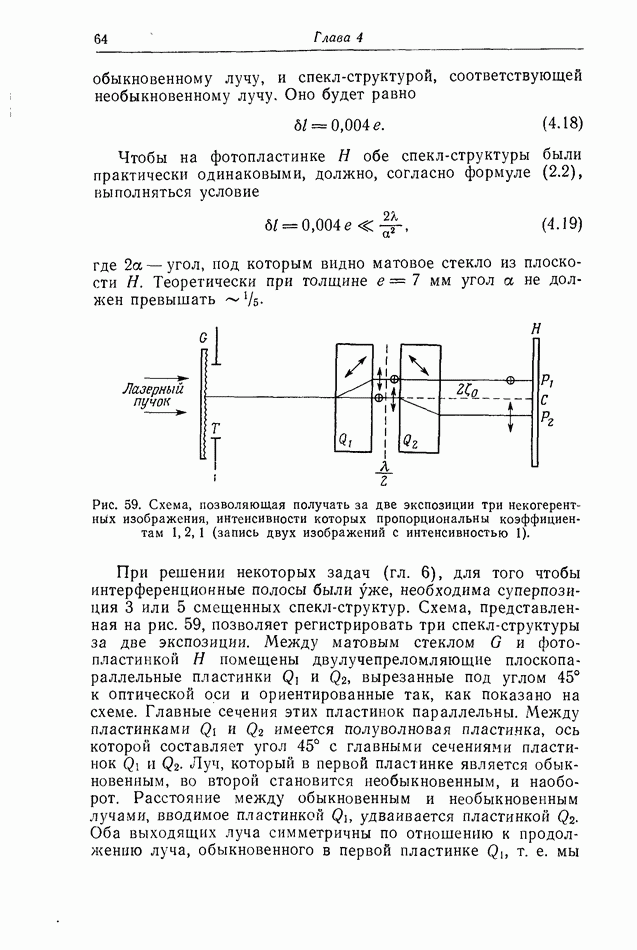
- § 4. Одновременная регистрация нескольких спекл-структур при помощи двулучепреломляющей пластинки [73]
- § 5. Регистрация при непрерывном перемещении фотопластинки во время экспозиции [215]
- § 6. Регистрация спекл-структуры с изменением угла падения
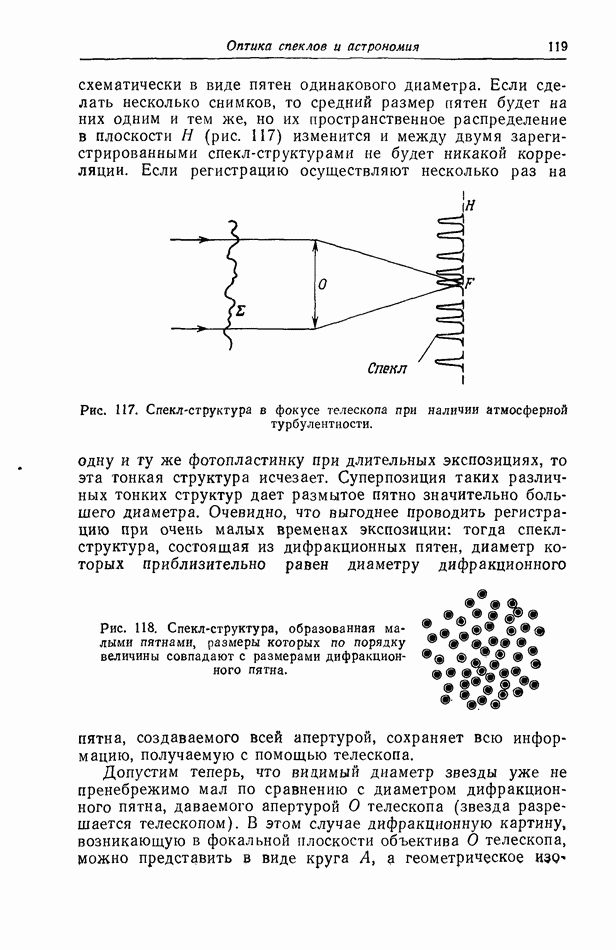
- § 7. Регистрация спекл-структуры в поляризованном свете [38]
- § 8. Регистрация с изменением угла наклона диффузора [167]
- § 9. Регистрация с изменением длины волны света
- Глава 5. ИНТЕРФЕРЕНЦИЯ В СЛУЧАЕ ФОТОГРАФИЧЕСКОЙ СУПЕРПОЗИЦИИ СПЕКЛ-СТРУКТУР, СМЕЩЕННЫХ В ПРОДОЛЬНОМ НАПРАВЛЕНИИ
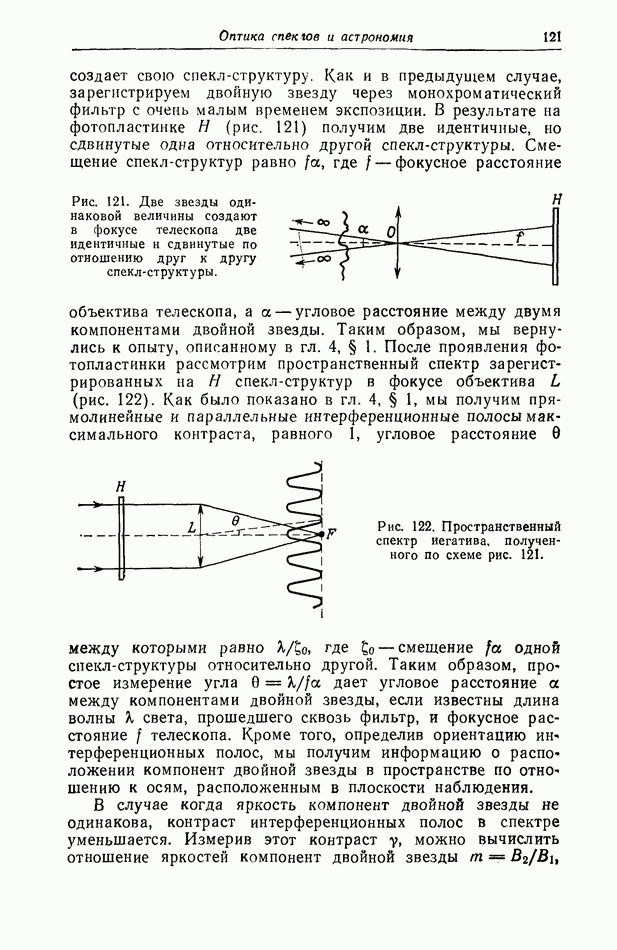
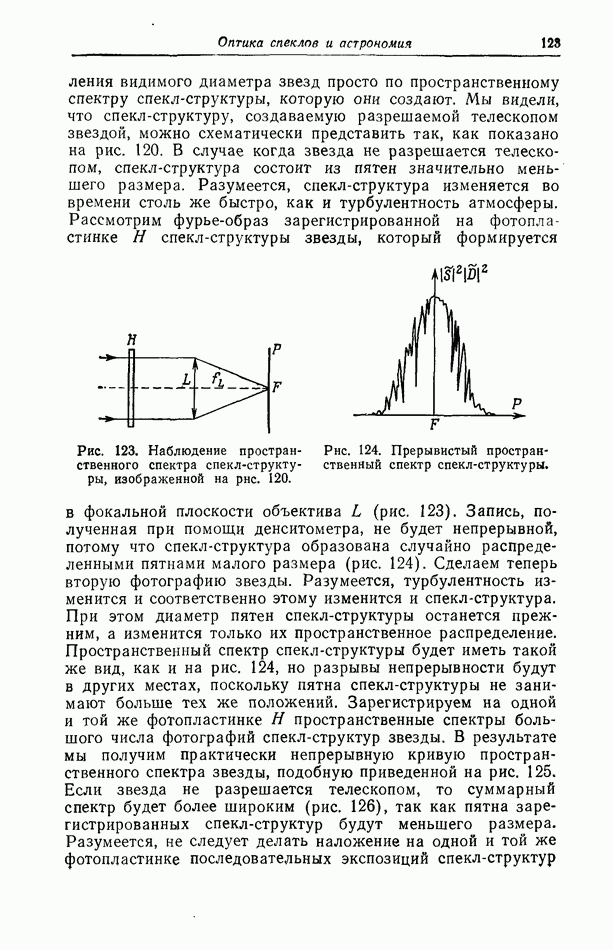
- § 2. Регистрация с изменением длины световой волны между экспозициями
- § 3. Регистрация с изменением длины световой волны и смещением фотопластинки между экспозициями
- § 4. Интерференционные кольца, образуемые фотопластинкой с двумя спекл-структурами, зарегистрированными в плоскости изображения диффузного объекта [6]
- § 5. Интерференционные кольца, образуемые фотопластинкой, однократно экспонированной с применением амплитудного диффузора
- § 6. Интерференционные кольца, образуемые фотопластинкой, на которой зарегистрировано несколько спекл-структур при ее продольном смещении между экспозициями [149]
- § 7. Гиперболические или эллиптические интерференционные полосы
- Глава 6. ОПТИЧЕСКАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ, МОДУЛИРОВАННЫХ СПЕКЛАМИ
- § 2. Вычитание изображений (суть метода] [57]
- § 3. Распределение света в плоскости изображения
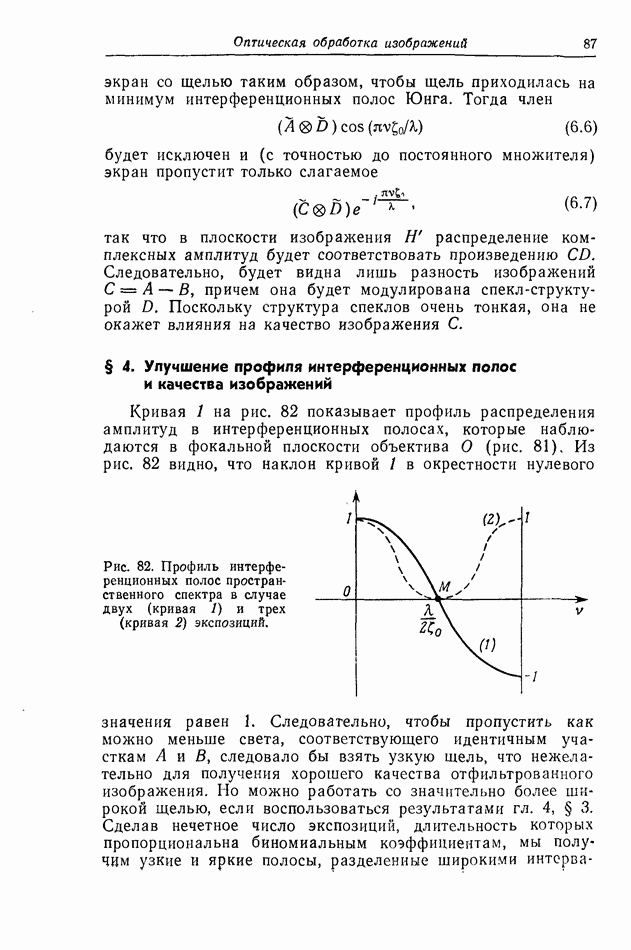
- § 4. Улучшение профиля интерференционных полос и качества изображений
- § 5. Кодирование и декодирование изображений
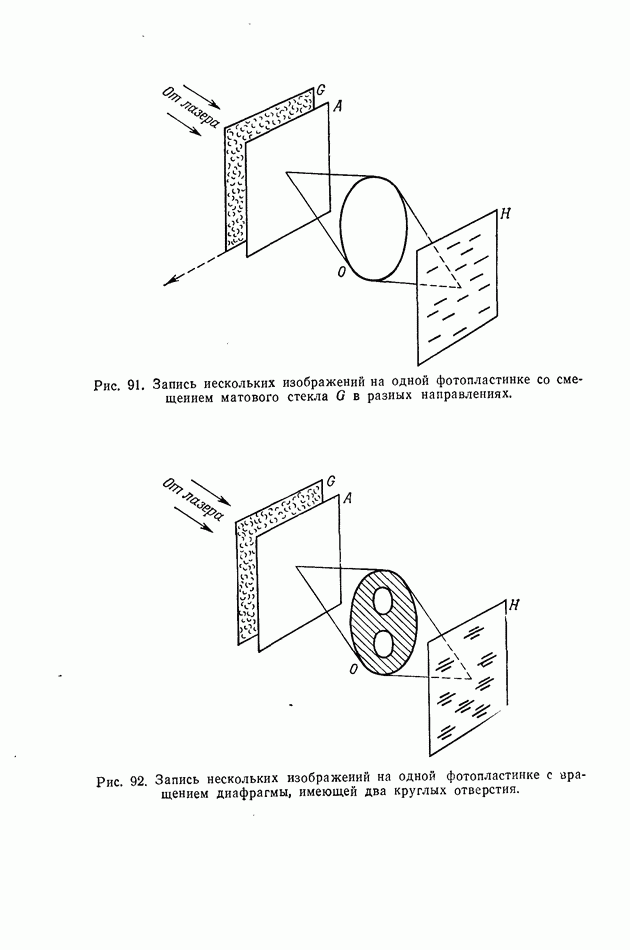
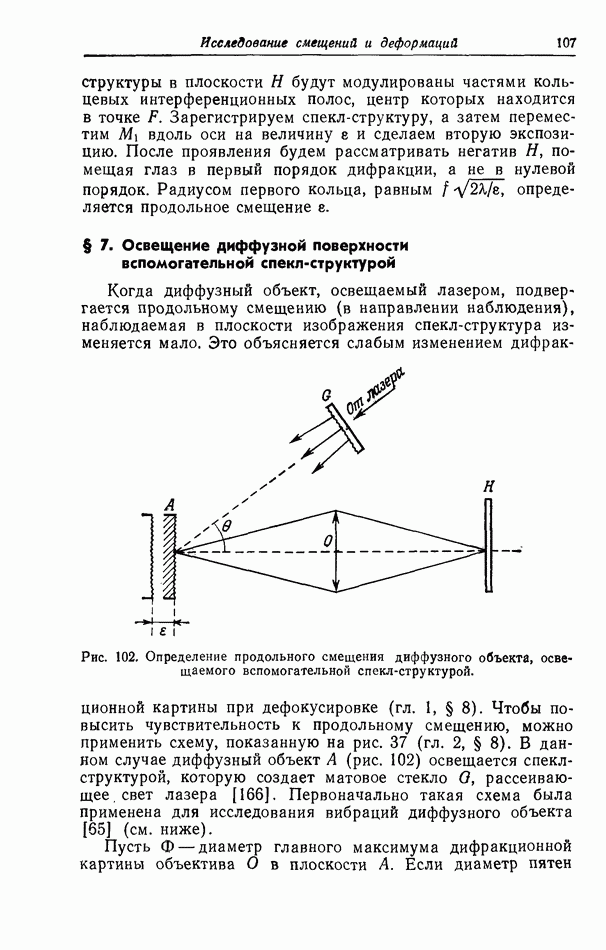
- § 6. Мультиплексная запись изображений методом наложения спекл-структур, сдвигаемых в поперечном направлении [106]
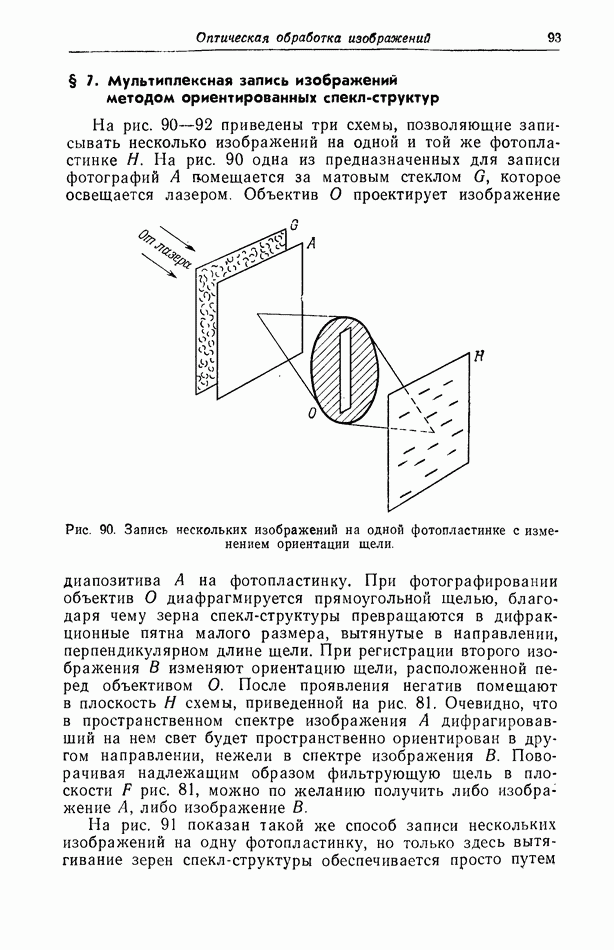
- § 7. Мультиплексная запись изображений методом ориентированных спекл-структур
- Глава 7. ИССЛЕДОВАНИЕ СМЕЩЕНИЙ И ДЕФОРМАЦИЙ ДИФФУЗНЫХ ОБЪЕКТОВ МЕТОДОМ ФОТОРЕГИСТРАЦИИ СПЕКЛ-СТРУКТУРЫ
- § 1. Поперечное смещение диффузного объекта. Случай, когда смещение больше диаметра пятна спекл-структуры [143]
- § 2. Поперечное смещение диффузного объекта. Случай, когда смещение меньше диаметра пятна спекл-структуры [59]
- § 3. Исследование поперечного смещения диффузного объекта, освещаемого двумя пучками. Случай, когда смещение меньше диаметра пятна спекл-структуры [142]
- § 4. Определение поперечного смещения диффузного объекта относительно опорной диффузной поверхности [166]
- § 5. Определение продольных смещений диффузного объекта относительно опорной диффузной поверхности [142]
- § 6. Наблюдение спекл-структуры в фокальной плоскости объектива [166]
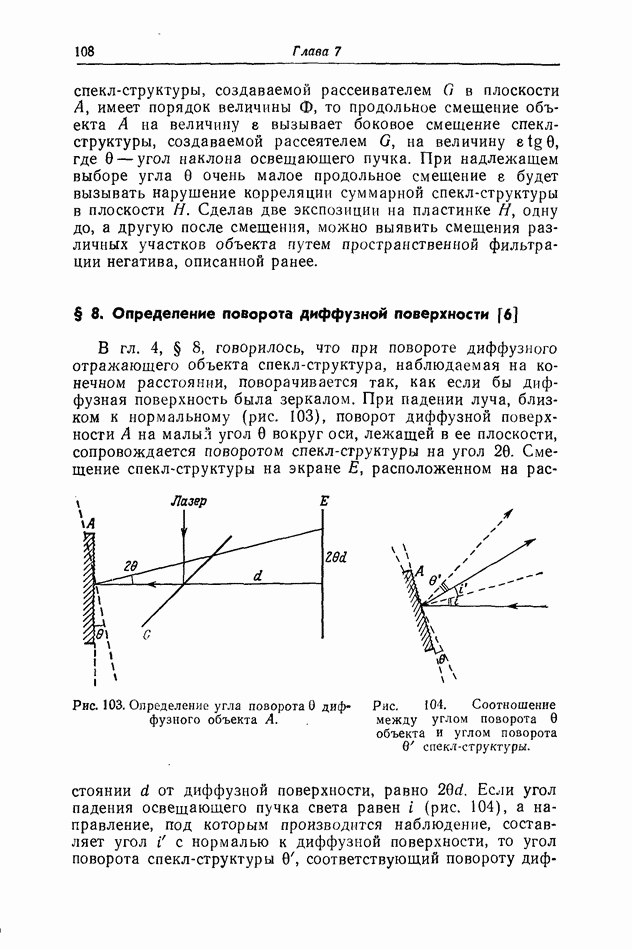
- § 7. Освещение диффузной поверхности вспомогательной спекл-структурой
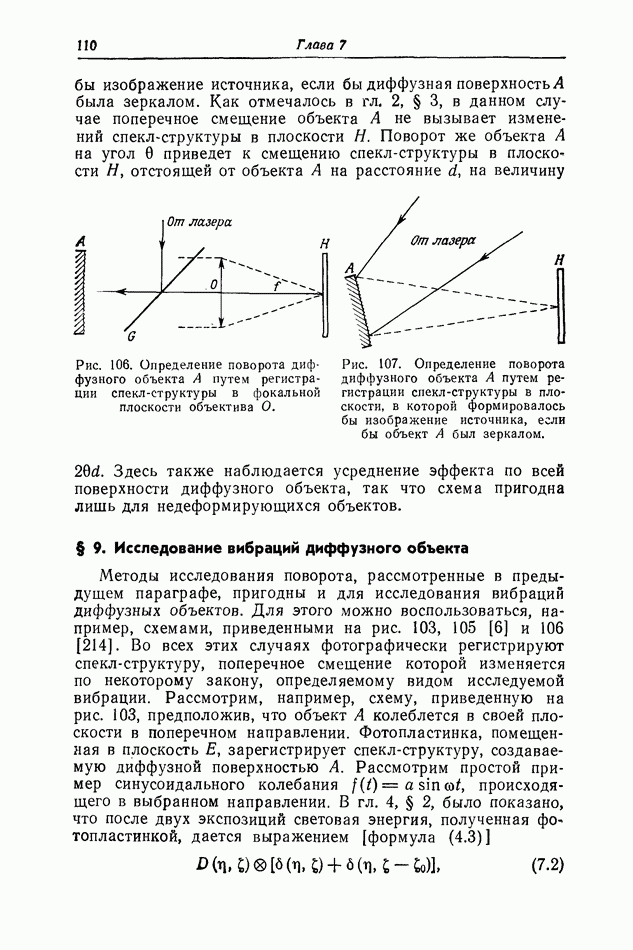
- § 8. Определение поворота диффузной поверхности [6]
- § 9. Исследование вибраций диффузного объекта
- § 10. Исследование изменений рельефа поверхности диффузного объекта
- Глава 8. ОПТИКА СПЕКЛОВ И АСТРОНОМИЯ
- § 1. Изображение одиночной звезды в фокусе телескопа при наличии атмосферной турбулентности
- § 2. Наблюдение двойных звезд в фокусе телескопа в присутствии втмосферной турбулентности [138]
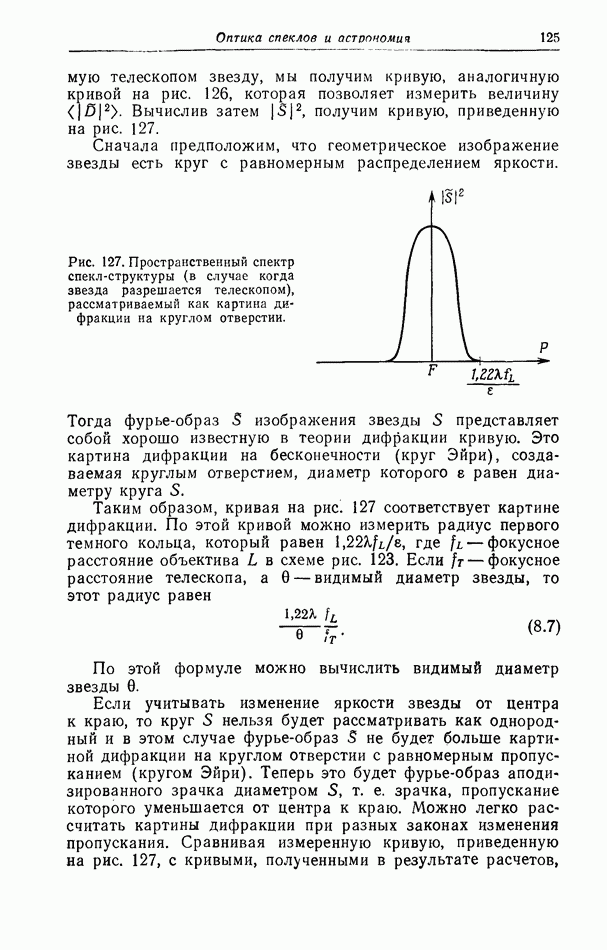
- § 3. Измерение видимого диаметра звезд методом Лабейри [137]
- § 4. Измерение видимого диаметра звезд с использованием нескольких телескопов
- Глава 9. ИССЛЕДОВАНИЕ ШЕРОХОВАТОСТИ ПОВЕРХНОСТЕЙ
- § 2. Применение оптики спеклов для оценки шероховатости поверхностей
- § 3. Определение шероховатости поверхности по корреляции между двумя спекл-структурами полученными при разных углах падения лазерного пучка [145]
- § 4. Определение шероховатости в реапьном времени по корреляции между амплитудами спекп-структур, соответствующих двум ориентациям лазерного пучка [147]
- § 5. Определение шероховатости по корреляции между спекл-структурами, полученными с двумя длинами волн [217]
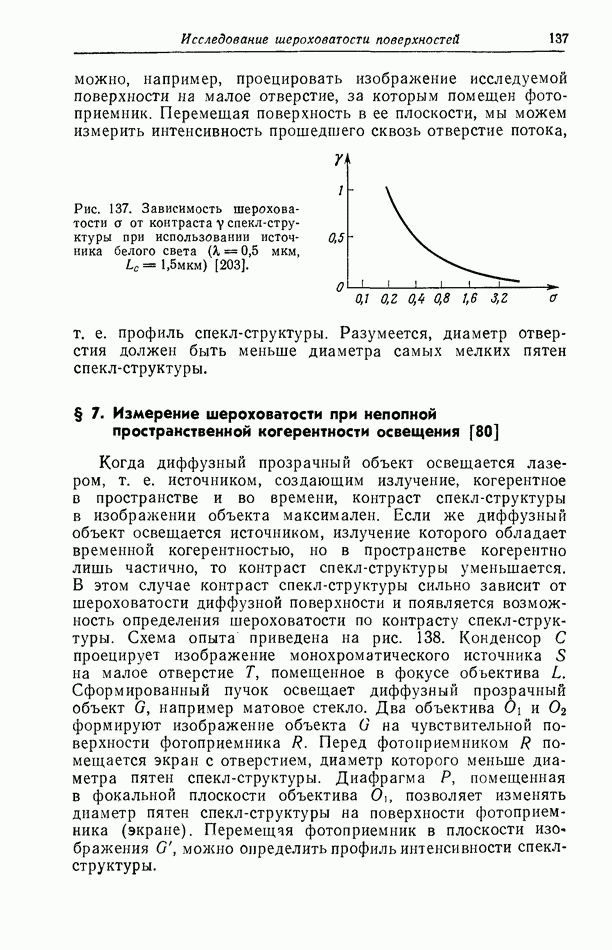
- § 6. Измерение шероховатости с помощью источника, излучающего широкую полосу спектра [203]
- § 7. Измерение шероховатости при неполной пространственной когерентности освещения [80]
- Глава 10. ДРУГИЕ ПРИМЕНЕНИЯ
- § 1. Дифференциальный интерферометр для прозрачных к объектов, основанный на фоторегистрации спекп-структуры за две экспозиции
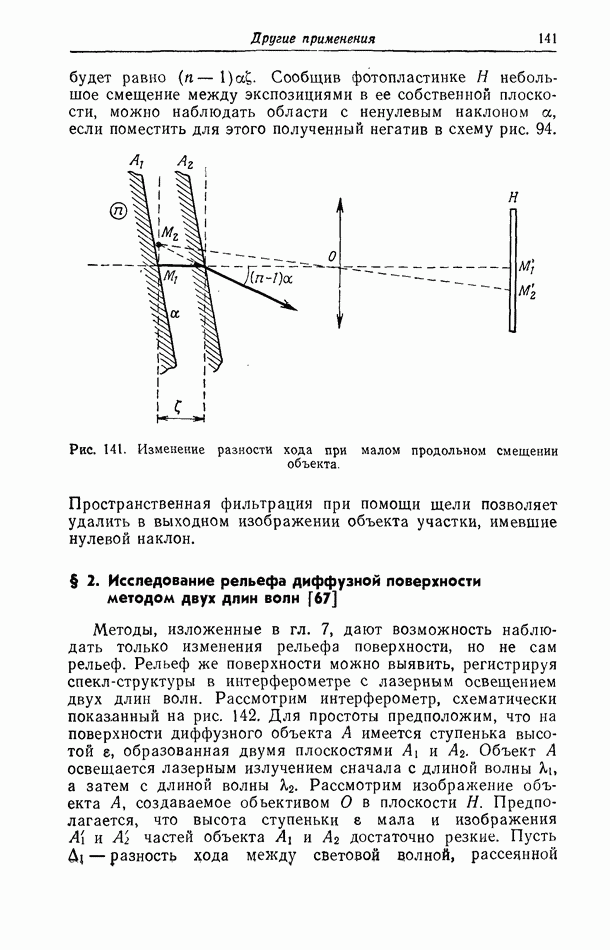
- § 2. Исследование рельефа диффузной поверхности методом двух длин волн [67]
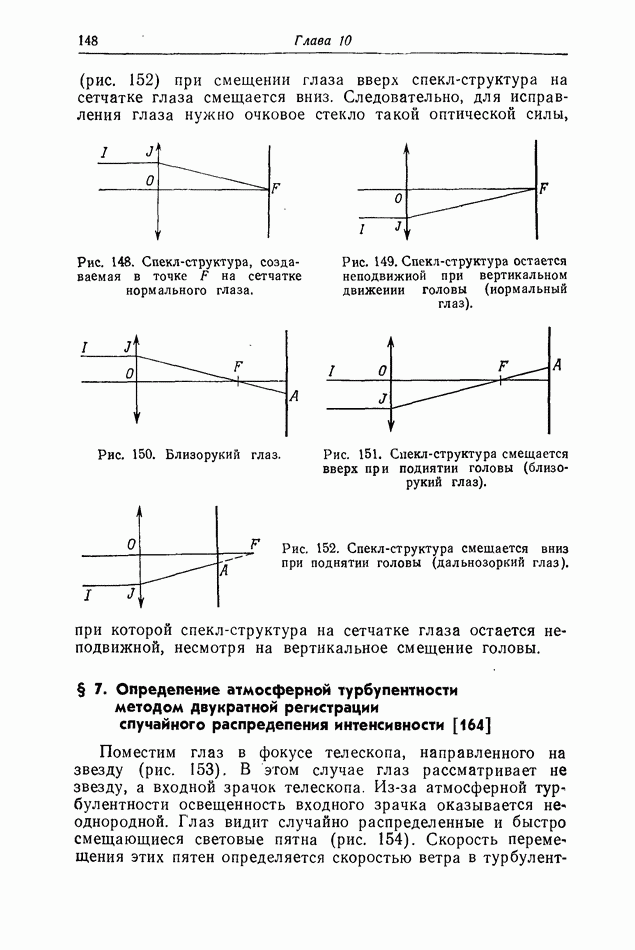
- § 3. Определение передаточной функции оптической системы, освещаемой спекл-структурой [45]
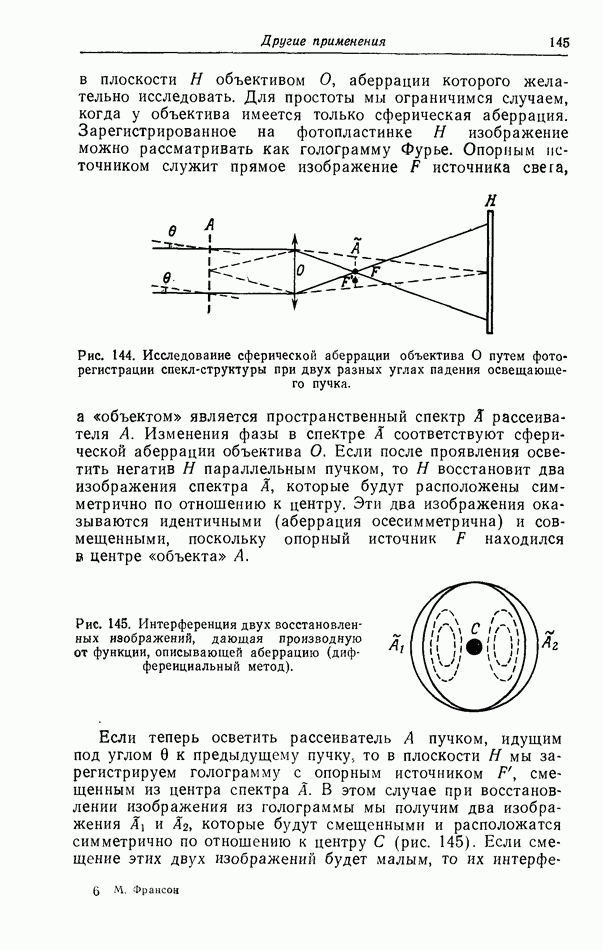
- § 4. Исследование аберраций оптической системы путем фотографирования спекл-структур [196а, 211]
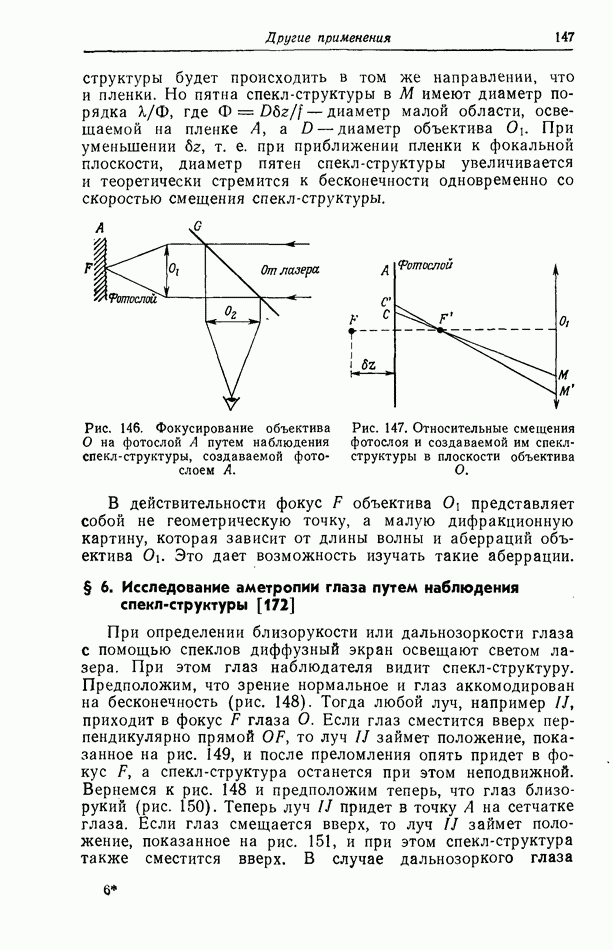
- § 5. Фокусирование объектива с помощью спекл-структуры [198]
- § 6. Исследование аметропии глаза путем наблюдения спекл-структуры [172]
- § 7. Определение атмосферной турбулентности методом двукратной регистрации случайного распределения интенсивности [164]
- § 8. Восстановление траектории диффузного объекта путем регистрации спекл-структуры [151, 153]
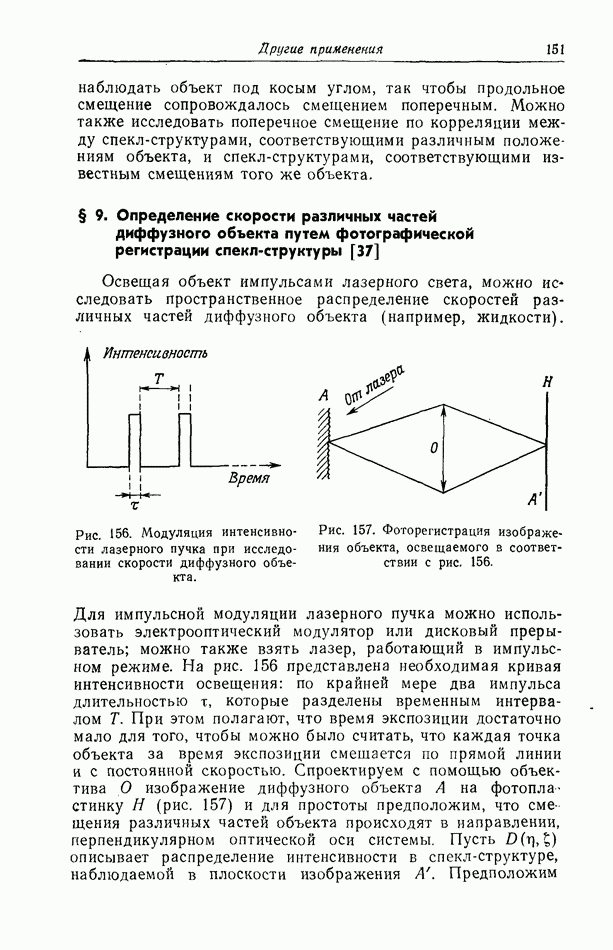
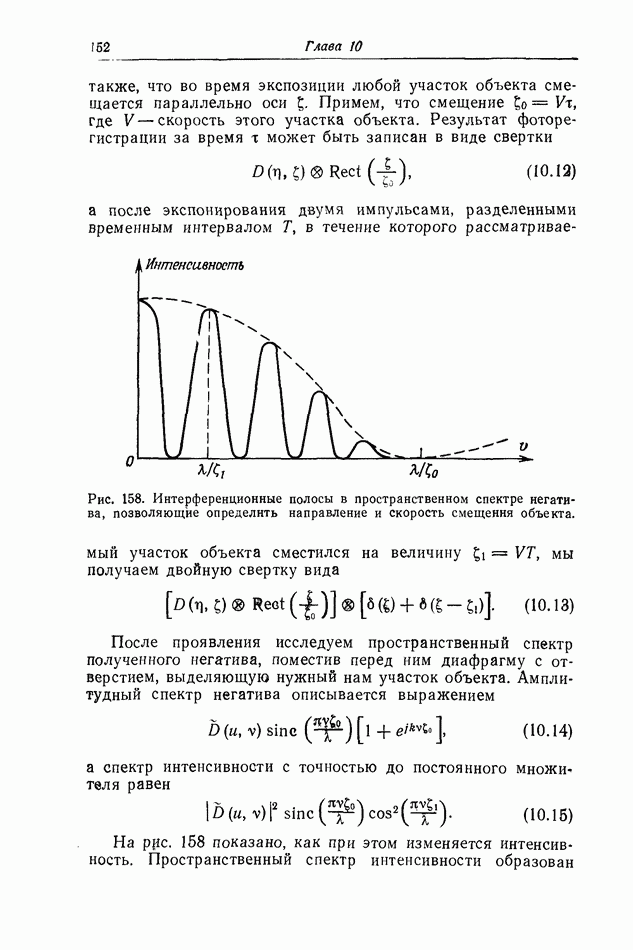
- § 9. Определение скорости различных частей диффузного объекта путем фотографической регистрации спекл-структуры [37]