| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
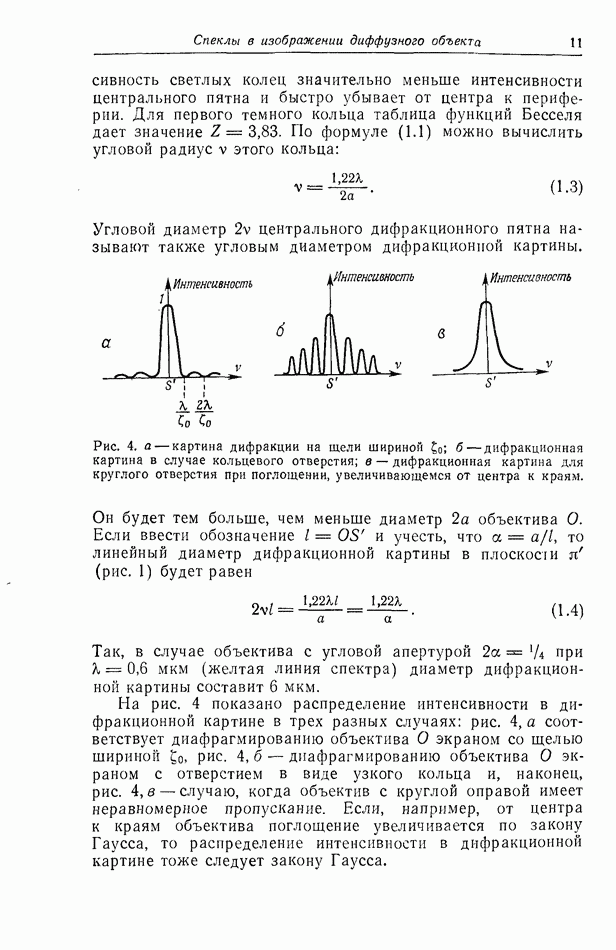
§ 3. Распределение света в плоскости изображения
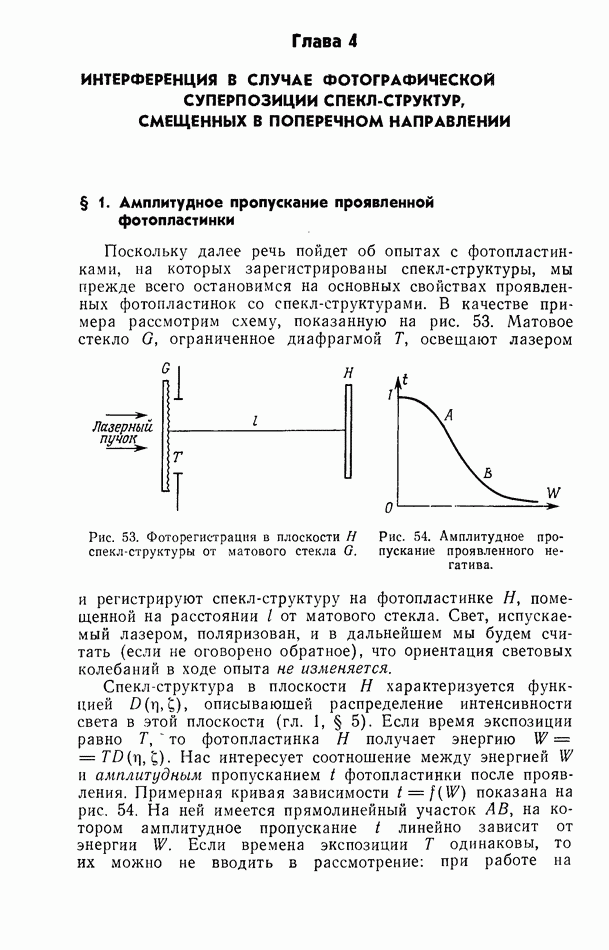
Рассмотрим изложенный метод, пользуясь не очень сложной математикой. При первой экспозиции перед неэкспонированной пластинкой высокого разрешения  помещают диапозитив А и регистрируют произведение
помещают диапозитив А и регистрируют произведение  где
где  -пропускание диапозитива А, а
-пропускание диапозитива А, а  -интенсивность спекл-структуры. Затем диапозитив А заменяют диапозитивом В так, чтобы те участки последнего, которые идентичны определенным участкам диапозитива А, оказались точно в тех же местах. После этого фотопластинку И сдвигают на очень малое расстояние в некотором направлении, например вдоль оси Обозначим это смещение через При таких условиях делают вторую экспозицию. Таким образом, регистрируют интенсивность
-интенсивность спекл-структуры. Затем диапозитив А заменяют диапозитивом В так, чтобы те участки последнего, которые идентичны определенным участкам диапозитива А, оказались точно в тех же местах. После этого фотопластинку И сдвигают на очень малое расстояние в некотором направлении, например вдоль оси Обозначим это смещение через При таких условиях делают вторую экспозицию. Таким образом, регистрируют интенсивность  Поскольку смещение эквивалентно свертке с дельта-функцией (гл. 1, § 6; гл. 4, § 2), зарегистрированную интенсивность
Поскольку смещение эквивалентно свертке с дельта-функцией (гл. 1, § 6; гл. 4, § 2), зарегистрированную интенсивность
можно записать в виде

Полная интенсивность, регистрируемая пластинкой  упрощенно записывается как
упрощенно записывается как

что после подстановки  принимает вид
принимает вид

или, в симметричной форме,

После проявления амплитудное пропускание  негатива будет равно (гл. 4, § 2)
негатива будет равно (гл. 4, § 2)

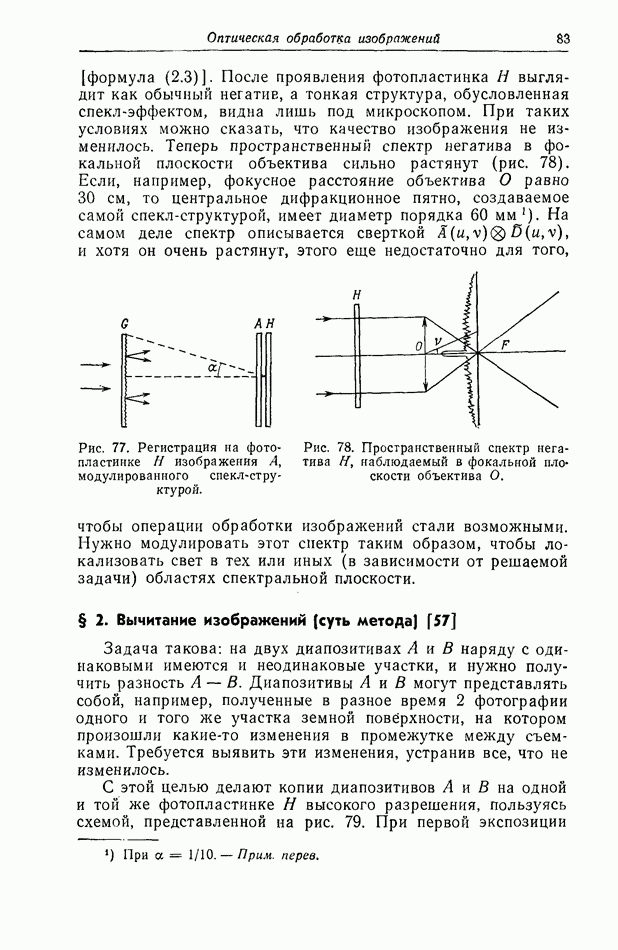
Мы рассматриваем негатив  в схеме рис. 81: негатив
в схеме рис. 81: негатив  освещается параллельным пучком, и объектив О создает его изображение в плоскости
освещается параллельным пучком, и объектив О создает его изображение в плоскости  Пространственный спектр зарегистрированного на негативе изображения представляет собой фурье-образ амплитудного пропускания
Пространственный спектр зарегистрированного на негативе изображения представляет собой фурье-образ амплитудного пропускания  и отображается в фокальной плоскости объектива О. Результаты гл. 4, § 2, показывают, что
и отображается в фокальной плоскости объектива О. Результаты гл. 4, § 2, показывают, что

Первый член  этого выражения описывает изображение точечного источника, который освещает систему, причем это изображение локализовано в фокусе
этого выражения описывает изображение точечного источника, который освещает систему, причем это изображение локализовано в фокусе  Его можно не рассматривать вследствие малых размеров. Во втором члене мы имеем (умноженный на постоянную величину
Его можно не рассматривать вследствие малых размеров. Во втором члене мы имеем (умноженный на постоянную величину  спектр
спектр  модулированный множителем
модулированный множителем

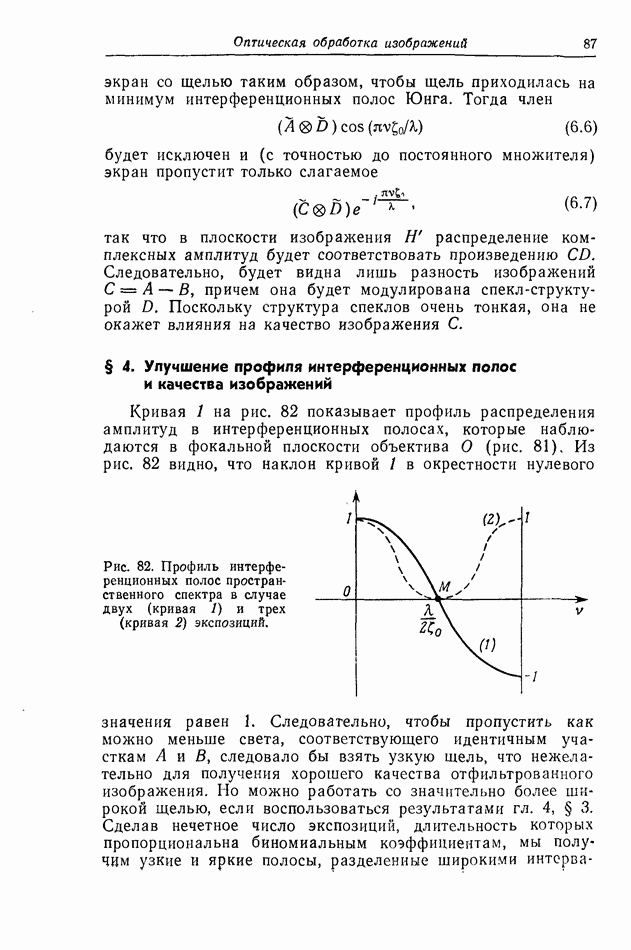
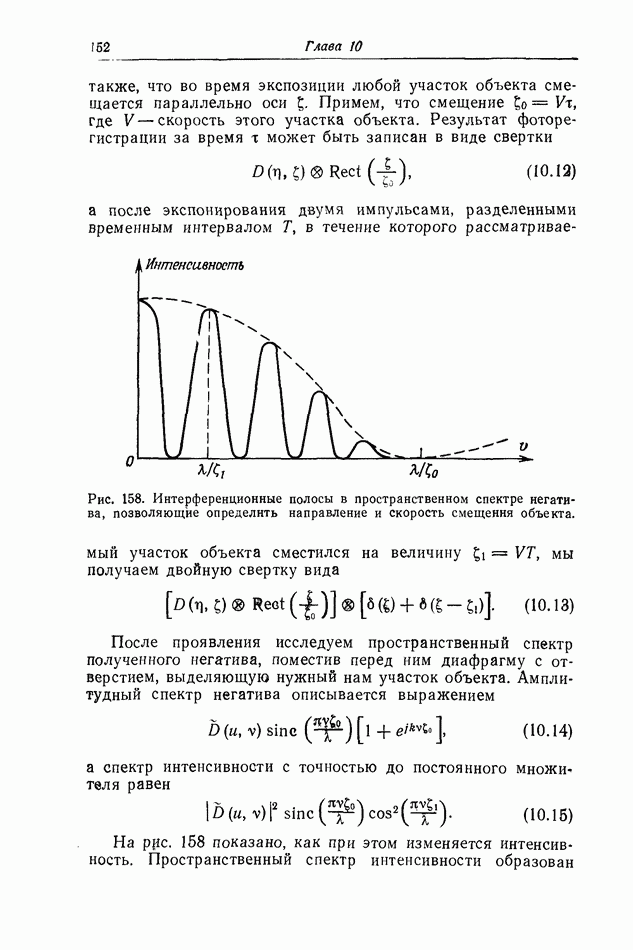
описывающим полосы Юнга. Угловое расстояние между двумя соседними (или темными) полосами равно  Поместим в фокальную плоскость объектива О непрозрачный
Поместим в фокальную плоскость объектива О непрозрачный
экран со щелью таким образом, чтобы щель приходилась на минимум интерференционных полос Юнга. Тогда член

будет исключен и (с точностью до постоянного множителя) экран пропустит только слагаемое

так что в плоскости изображения  распределение комплексных амплитуд будет соответствовать произведению
распределение комплексных амплитуд будет соответствовать произведению  Следовательно, будет видна лишь разность изображений
Следовательно, будет видна лишь разность изображений  причем она будет модулирована спекл-структурой
причем она будет модулирована спекл-структурой  Поскольку структура спеклов очень тонкая, она не окажет влияния на качество изображения С.
Поскольку структура спеклов очень тонкая, она не окажет влияния на качество изображения С.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Введение
- Глава 1. СПЕКЛЫ В ИЗОБРАЖЕНИИ ДИФФУЗНОГО ОБЪЕКТА, ОСВЕЩАЕМОГО ЛАЗЕРОМ
- § 1. Изображение точечного источника света, преобразование Фурье
- § 2. Изображение точечного источника света при небольшой дефокусировке
- § 3. Изображение двух монохроматических точечных источников света
- § 4. Изображение большого числа монохроматических точечных источников, расположенных хаотически
- § 5. Спектр большого числа когерентных точечных источников
- § 6. Спектр большого числа когерентных точечных источников, образующих идентичные, одинаково ориентированные и хаотически расположенные пары
- § 7. Спеклы в изображении объекта, освещаемого лазером
- § 8. Изменение спекл-структуры при смещении плоскости наблюдения [6, 169]
- § 9. Спекл-структура, наблюдаемая в изображении диффузного объекта при изменении длины волны света [168, 217]
- § 10. Спекл-структура, наблюдаемая в белом свете [72]
- Глава 2. СПЕКЛЫ, ВОЗНИКАЮЩИЕ НА КОНЕЧНОМ РАССТОЯНИИ ОТ ДИФФУЗНОГО ОБЪЕКТА, ОСВЕЩАЕМОГО ЛАЗЕРОМ
- § 1. Дифракция Френеля и дифракция Фраунгофера в трех измерениях
- § 2. Спеклы, наблюдаемые на конечном расстоянии от диффузного объекта
- § 3. Спеклы, наблюдаемые при смещении диффузного объекта в поперечном направлении
- § 4. Спеклы, наблюдаемые при изменении направления светового пучка, освещающего диффузный объект [56, 147]
- § 5. Спеклы, наблюдаемые при продольном смещении плоскости наблюдения или диффузного объекта [62]
- § 6. Спеклы, образуемые диффузным объектом при изменении длины волны света [168]
- § 7. Спеклы, создаваемые диффузным объектом при изменении длины вопны света и положения плоскости наблюдения [168]
- § 8. Спекл-структура, создаваемая диффузным объектом при освещении его другой спекл-структурой [65, 166]
- Глава 3. ИНТЕРФЕРЕНЦИЯ В ДИФФУЗНОМ СВЕТЕ
- § 2. Основные принципы интерференции в диффузном свете
- § 3. Интерференция в случае двух одинаковых диффузоров
- § 4. Интерферометр Берча
- § 5. Интерференция в случае двух неодинаковых диффузоров в одной плоскости [166]
- § 6. Интерференция в случае неодинаковых диффузоров в разных плоскостях [62]
- Глава 4. ИНТЕРФЕРЕНЦИЯ В СЛУЧАЕ ФОТОГРАФИЧЕСКОЙ СУПЕРПОЗИЦИИ СПЕКЛ-СТРУКТУР, СМЕЩЕННЫХ В ПОПЕРЕЧНОМ НАПРАВЛЕНИИ
- § 2. Фундаментальный опыт Берча и Токарского [101]
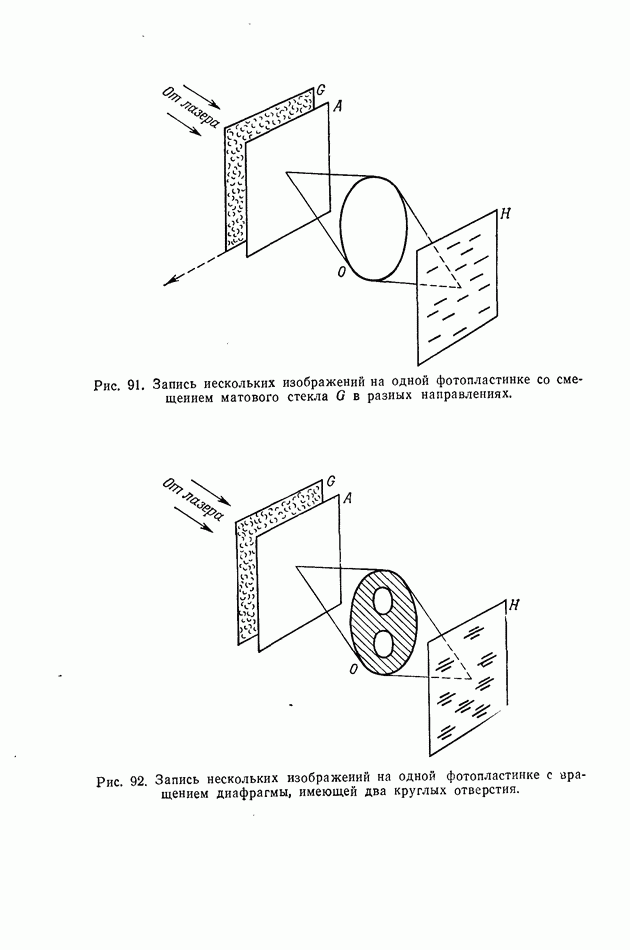
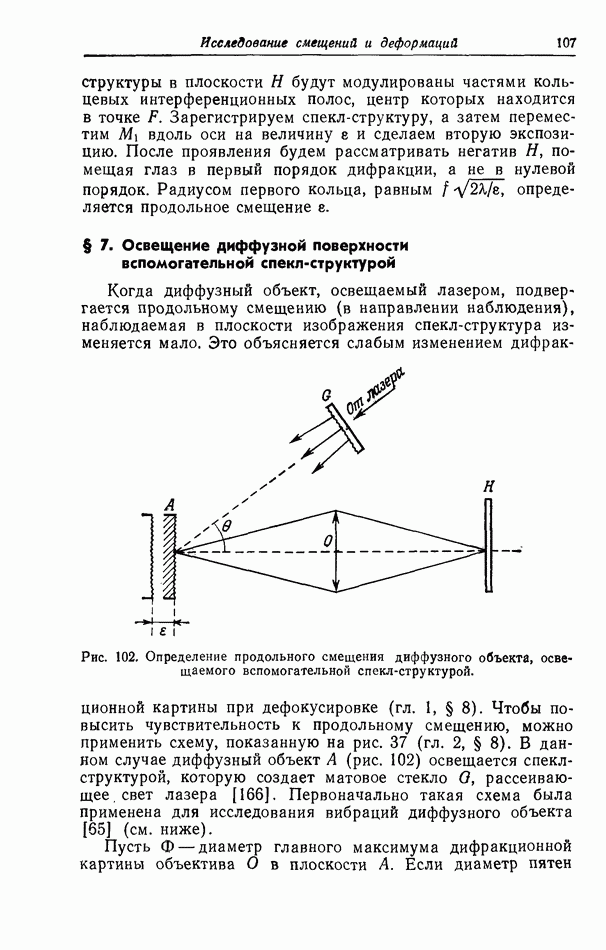
- § 3. Несколько экспозиций на одной фотопластинке
- § 4. Одновременная регистрация нескольких спекл-структур при помощи двулучепреломляющей пластинки [73]
- § 5. Регистрация при непрерывном перемещении фотопластинки во время экспозиции [215]
- § 6. Регистрация спекл-структуры с изменением угла падения
- § 7. Регистрация спекл-структуры в поляризованном свете [38]
- § 8. Регистрация с изменением угла наклона диффузора [167]
- § 9. Регистрация с изменением длины волны света
- Глава 5. ИНТЕРФЕРЕНЦИЯ В СЛУЧАЕ ФОТОГРАФИЧЕСКОЙ СУПЕРПОЗИЦИИ СПЕКЛ-СТРУКТУР, СМЕЩЕННЫХ В ПРОДОЛЬНОМ НАПРАВЛЕНИИ
- § 2. Регистрация с изменением длины световой волны между экспозициями
- § 3. Регистрация с изменением длины световой волны и смещением фотопластинки между экспозициями
- § 4. Интерференционные кольца, образуемые фотопластинкой с двумя спекл-структурами, зарегистрированными в плоскости изображения диффузного объекта [6]
- § 5. Интерференционные кольца, образуемые фотопластинкой, однократно экспонированной с применением амплитудного диффузора
- § 6. Интерференционные кольца, образуемые фотопластинкой, на которой зарегистрировано несколько спекл-структур при ее продольном смещении между экспозициями [149]
- § 7. Гиперболические или эллиптические интерференционные полосы
- Глава 6. ОПТИЧЕСКАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ, МОДУЛИРОВАННЫХ СПЕКЛАМИ
- § 2. Вычитание изображений (суть метода] [57]
- § 3. Распределение света в плоскости изображения
- § 4. Улучшение профиля интерференционных полос и качества изображений
- § 5. Кодирование и декодирование изображений
- § 6. Мультиплексная запись изображений методом наложения спекл-структур, сдвигаемых в поперечном направлении [106]
- § 7. Мультиплексная запись изображений методом ориентированных спекл-структур
- Глава 7. ИССЛЕДОВАНИЕ СМЕЩЕНИЙ И ДЕФОРМАЦИЙ ДИФФУЗНЫХ ОБЪЕКТОВ МЕТОДОМ ФОТОРЕГИСТРАЦИИ СПЕКЛ-СТРУКТУРЫ
- § 1. Поперечное смещение диффузного объекта. Случай, когда смещение больше диаметра пятна спекл-структуры [143]
- § 2. Поперечное смещение диффузного объекта. Случай, когда смещение меньше диаметра пятна спекл-структуры [59]
- § 3. Исследование поперечного смещения диффузного объекта, освещаемого двумя пучками. Случай, когда смещение меньше диаметра пятна спекл-структуры [142]
- § 4. Определение поперечного смещения диффузного объекта относительно опорной диффузной поверхности [166]
- § 5. Определение продольных смещений диффузного объекта относительно опорной диффузной поверхности [142]
- § 6. Наблюдение спекл-структуры в фокальной плоскости объектива [166]
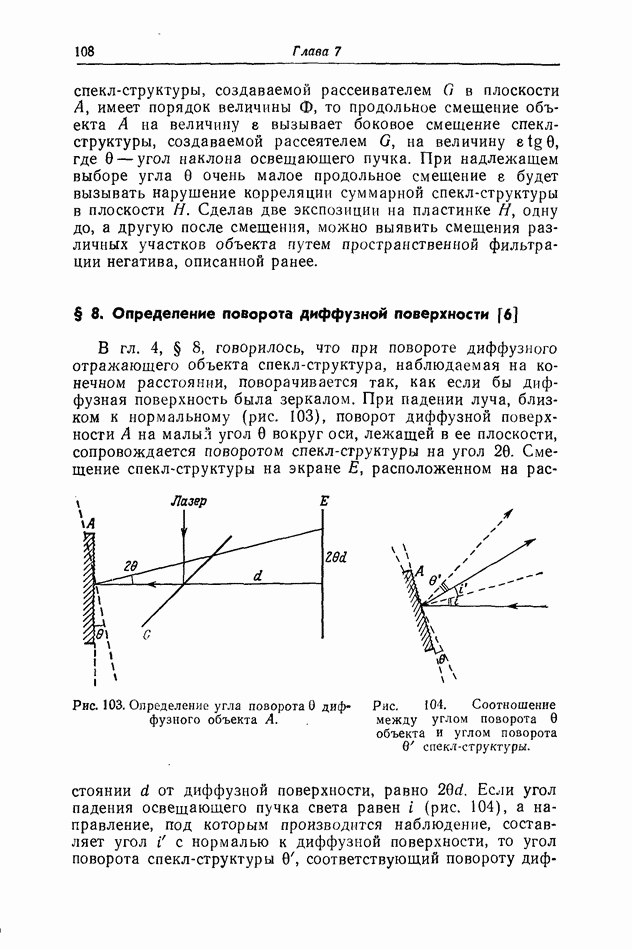
- § 7. Освещение диффузной поверхности вспомогательной спекл-структурой
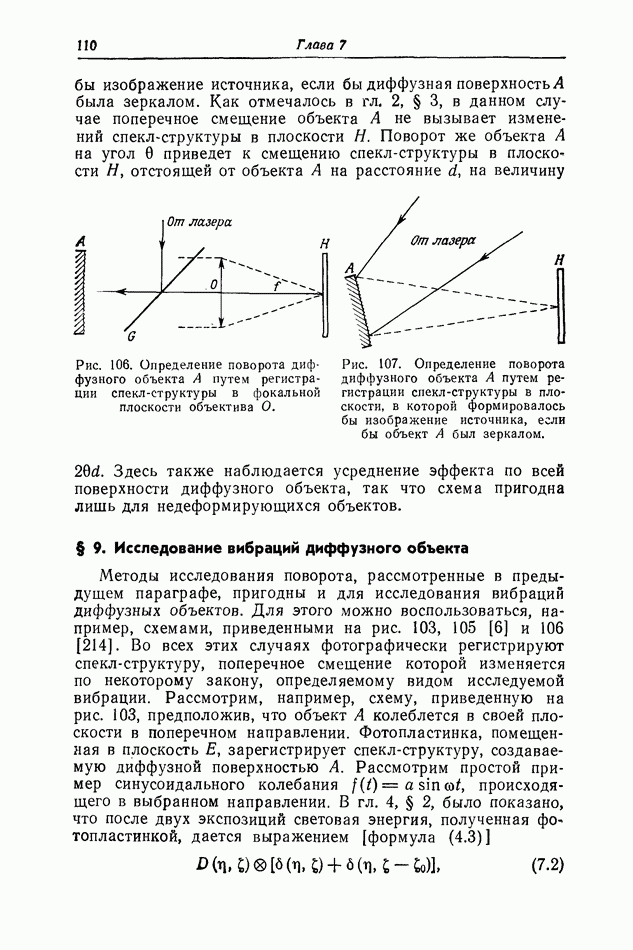
- § 8. Определение поворота диффузной поверхности [6]
- § 9. Исследование вибраций диффузного объекта
- § 10. Исследование изменений рельефа поверхности диффузного объекта
- Глава 8. ОПТИКА СПЕКЛОВ И АСТРОНОМИЯ
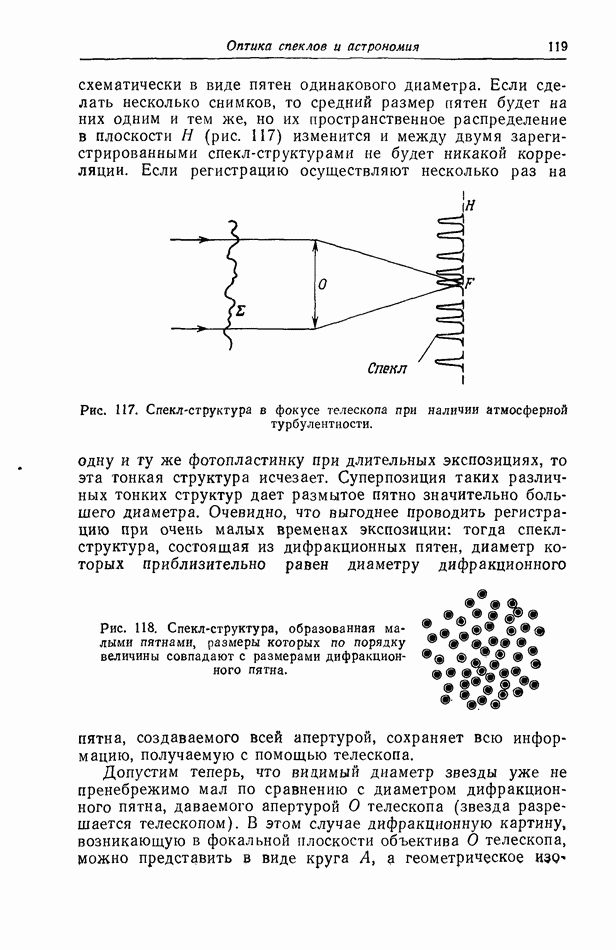
- § 1. Изображение одиночной звезды в фокусе телескопа при наличии атмосферной турбулентности
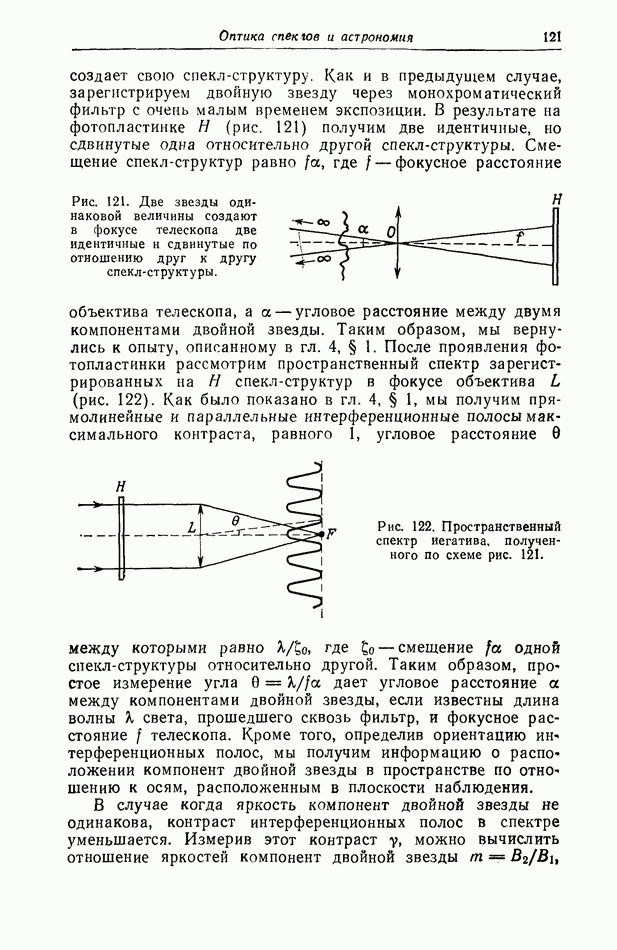
- § 2. Наблюдение двойных звезд в фокусе телескопа в присутствии втмосферной турбулентности [138]
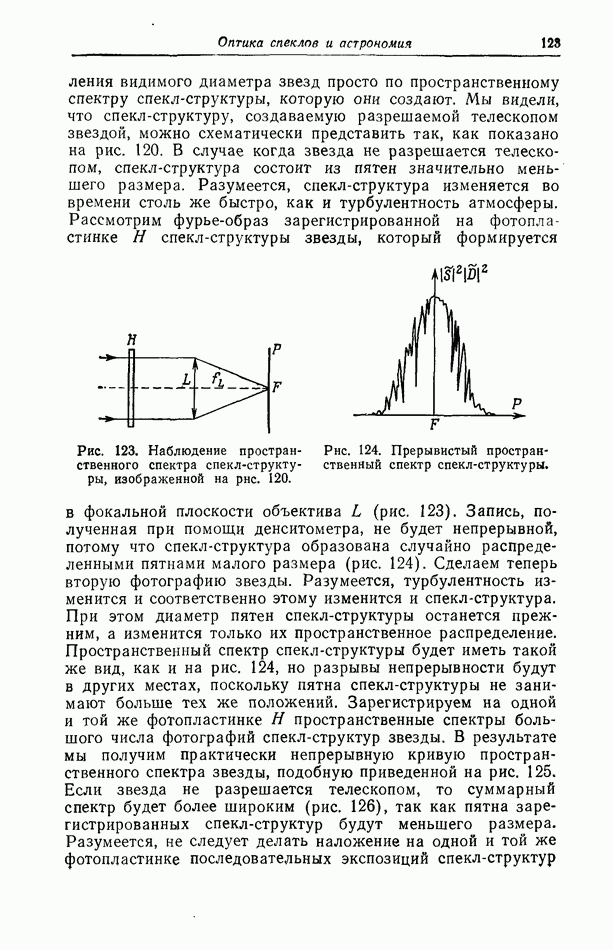
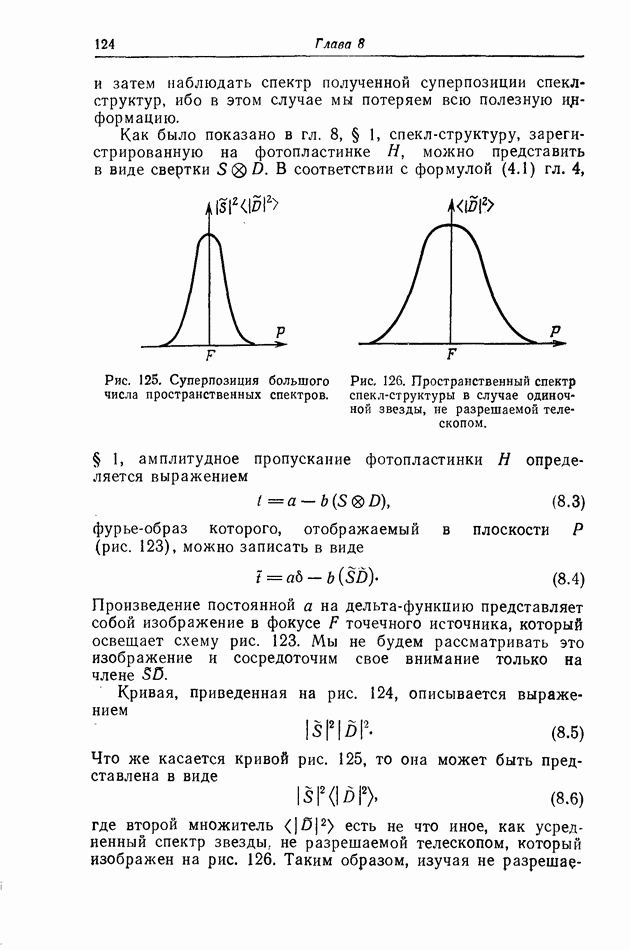
- § 3. Измерение видимого диаметра звезд методом Лабейри [137]
- § 4. Измерение видимого диаметра звезд с использованием нескольких телескопов
- Глава 9. ИССЛЕДОВАНИЕ ШЕРОХОВАТОСТИ ПОВЕРХНОСТЕЙ
- § 2. Применение оптики спеклов для оценки шероховатости поверхностей
- § 3. Определение шероховатости поверхности по корреляции между двумя спекл-структурами полученными при разных углах падения лазерного пучка [145]
- § 4. Определение шероховатости в реапьном времени по корреляции между амплитудами спекп-структур, соответствующих двум ориентациям лазерного пучка [147]
- § 5. Определение шероховатости по корреляции между спекл-структурами, полученными с двумя длинами волн [217]
- § 6. Измерение шероховатости с помощью источника, излучающего широкую полосу спектра [203]
- § 7. Измерение шероховатости при неполной пространственной когерентности освещения [80]
- Глава 10. ДРУГИЕ ПРИМЕНЕНИЯ
- § 1. Дифференциальный интерферометр для прозрачных к объектов, основанный на фоторегистрации спекп-структуры за две экспозиции
- § 2. Исследование рельефа диффузной поверхности методом двух длин волн [67]
- § 3. Определение передаточной функции оптической системы, освещаемой спекл-структурой [45]
- § 4. Исследование аберраций оптической системы путем фотографирования спекл-структур [196а, 211]
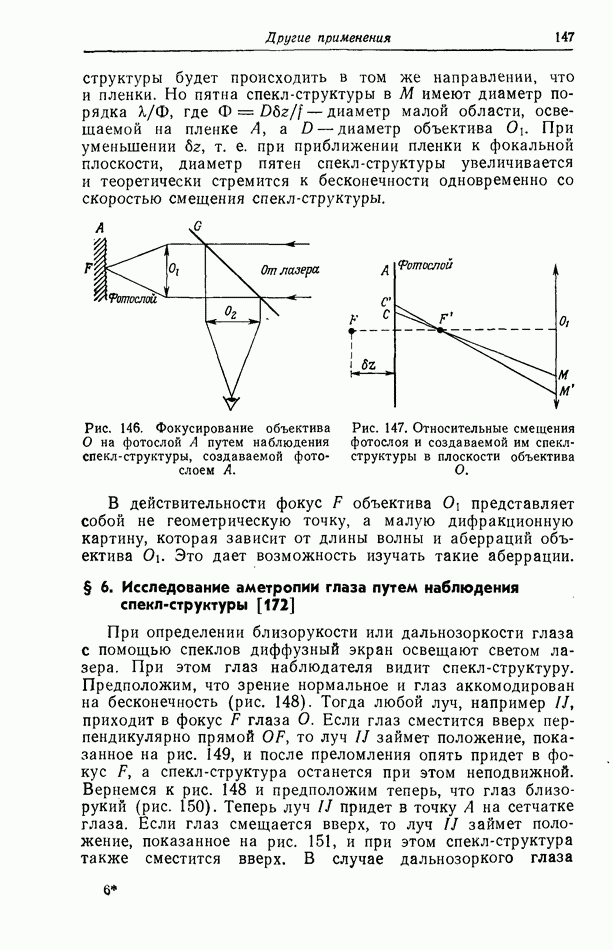
- § 5. Фокусирование объектива с помощью спекл-структуры [198]
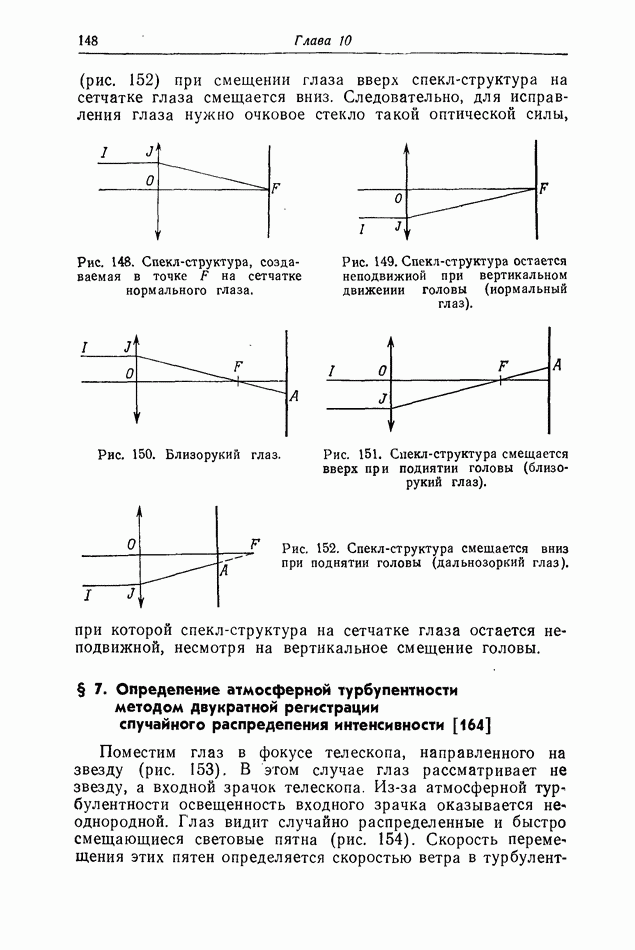
- § 6. Исследование аметропии глаза путем наблюдения спекл-структуры [172]
- § 7. Определение атмосферной турбулентности методом двукратной регистрации случайного распределения интенсивности [164]
- § 8. Восстановление траектории диффузного объекта путем регистрации спекл-структуры [151, 153]
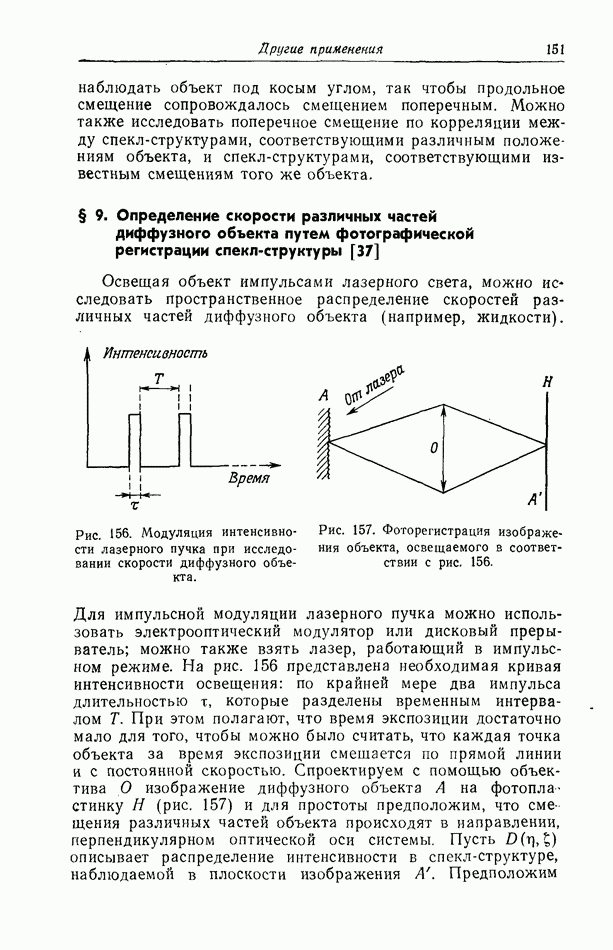
- § 9. Определение скорости различных частей диффузного объекта путем фотографической регистрации спекл-структуры [37]