| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
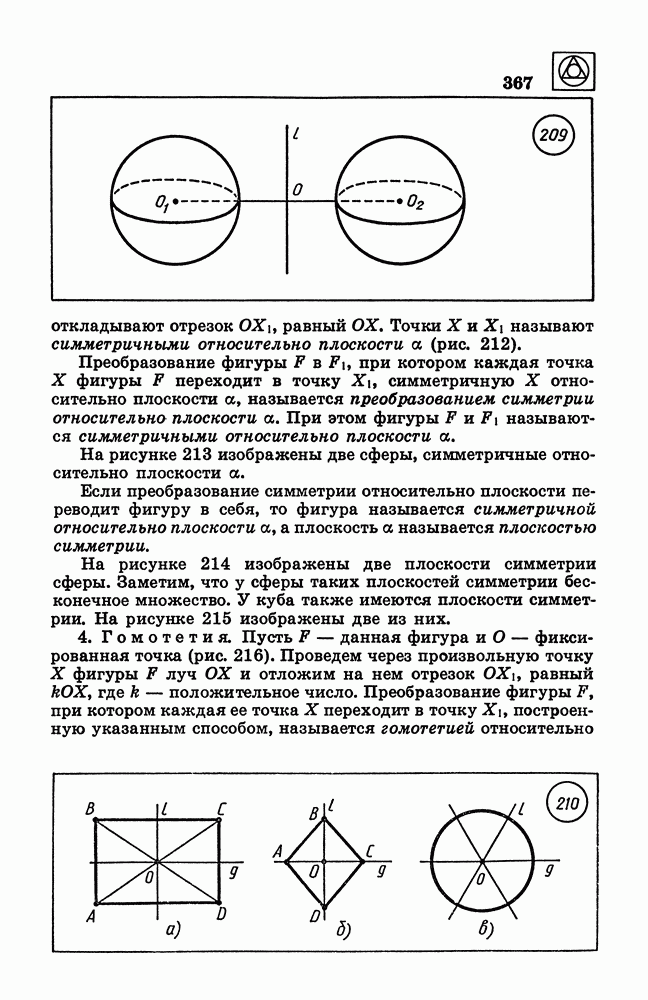
209
210
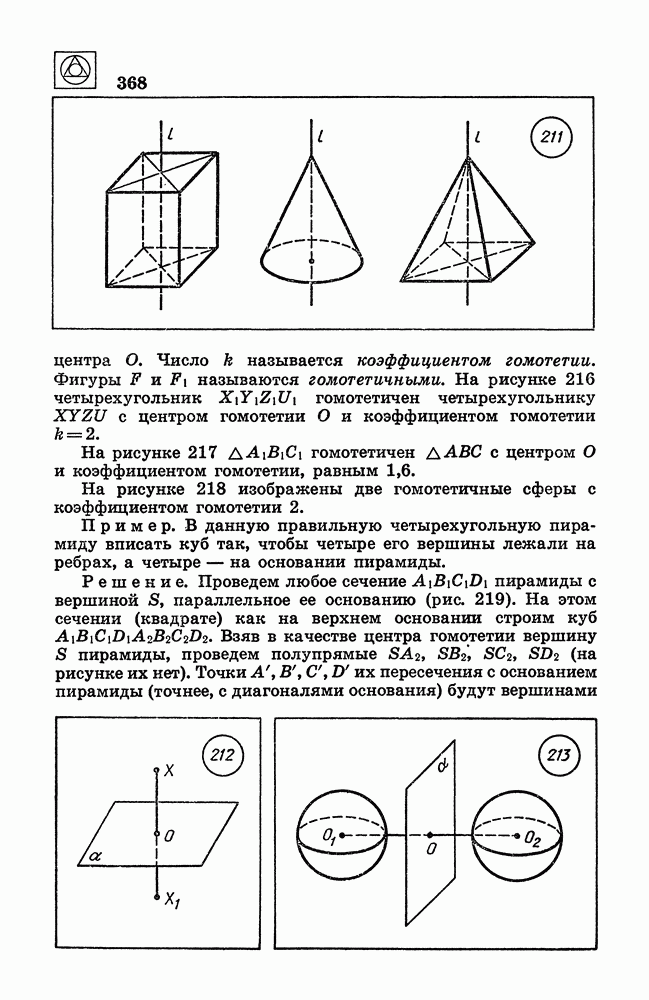
211
212
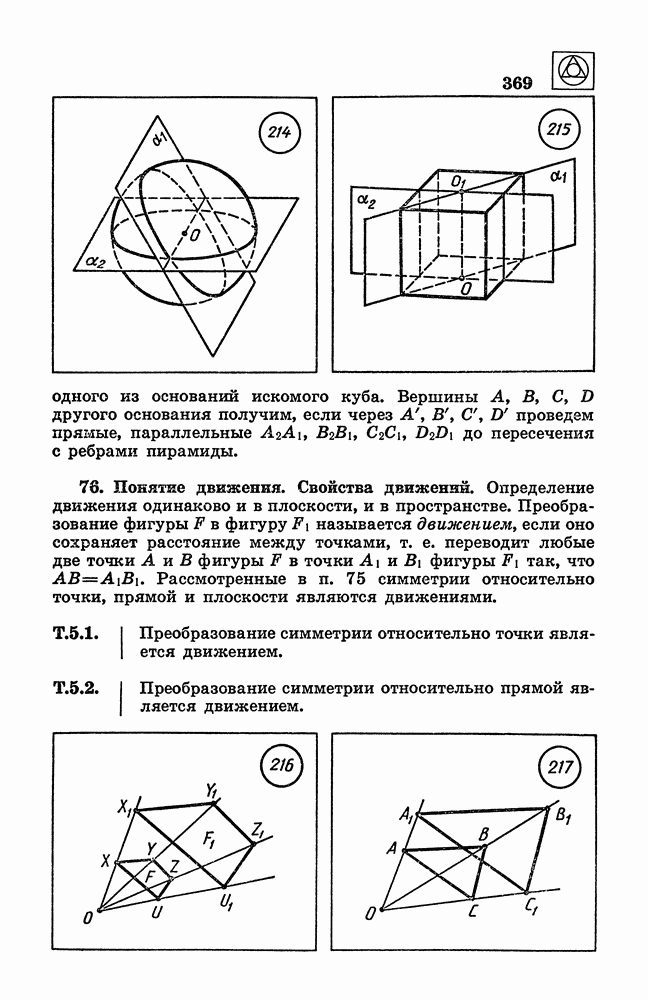
213
214
215
216
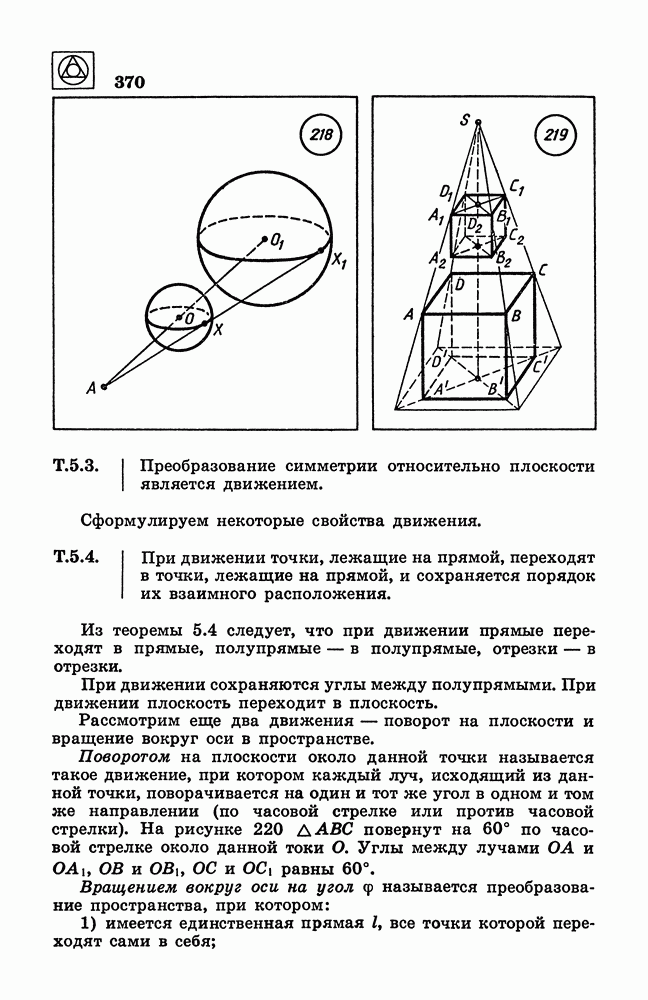
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
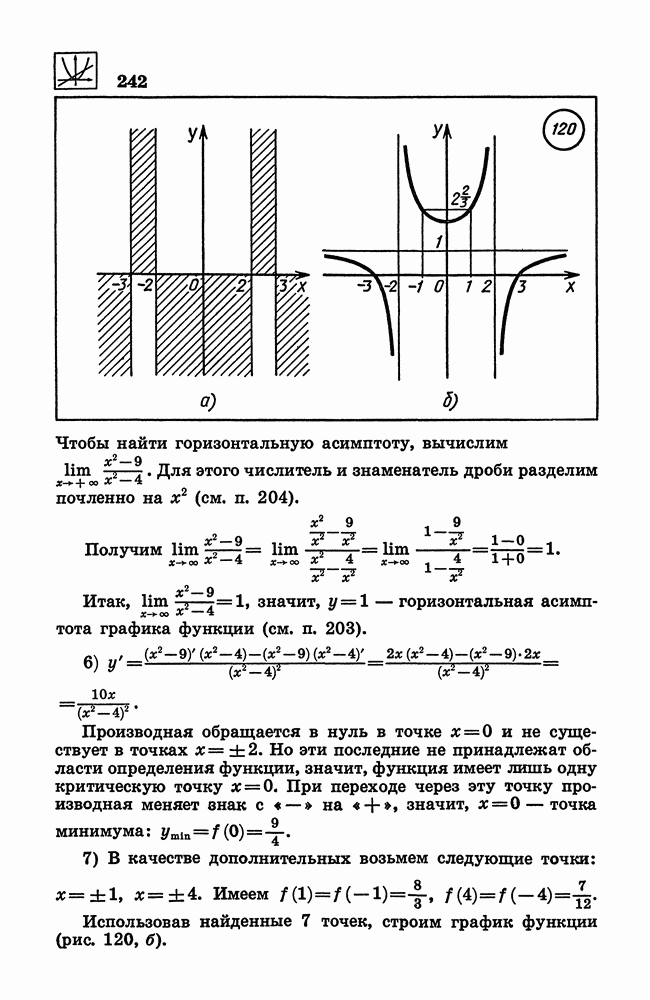
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
15. Треугольники.
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. Треугольник обозначается его вершинами. Вместо слова «треугольник» употребляется символ 
На рисунке 42 изображен треугольник ABC; А, В, С — вершины этого треугольника;  и
и  — его стороны.
— его стороны.
Углом треугольника  при вершине А называется угол, образованный полупрямыми
при вершине А называется угол, образованный полупрямыми  Так же определяются углы треугольника при вершинах В и С.
Так же определяются углы треугольника при вершинах В и С.
Т. 1.12. Если прямая, не проходящая ни через одну из вершин треугольника, пересекает одну из его сторон, то она пересекает только одну из двух других сторон.
Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведенный из этой вершины к прямой, содержащей противолежащую сторону треугольника. На рисунке 43, а отрезок  — высота остроугольного
— высота остроугольного  на рисунке 43, б основание высоты тупоугольного
на рисунке 43, б основание высоты тупоугольного  — точка D — лежит на продолжении стороны
— точка D — лежит на продолжении стороны 
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне. На рисунке 44 отрезок  — биссектриса треугольника
— биссектриса треугольника 
Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой


противолежащей стороны треугольника. На рисунке 45 отрезок  — медиана треугольника
— медиана треугольника 
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Т. 1.13. Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.
Пусть  — средняя линия треугольника
— средняя линия треугольника  (рис. 46).
(рис. 46).
Теорема утверждает, что 
Неравенством треугольника называется свойство расстояний между тремя точками, которое выражается следующей теоремой:
Т. 1.14. Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки.
Пусть А, В, С — три данные точки. Взаимное расположение этих точек может быть различным: а) две точки из трех или все три совпадают, в этом случае утверждение теоремы очевидно; б) точки различны и лежат на одной прямой (рис. 47, а), одна из них, например В, лежит между двумя другими, в этом случае  откуда следует, что каждое из трех расстояний не больше суммы двух других; в) точки не лежат
откуда следует, что каждое из трех расстояний не больше суммы двух других; в) точки не лежат





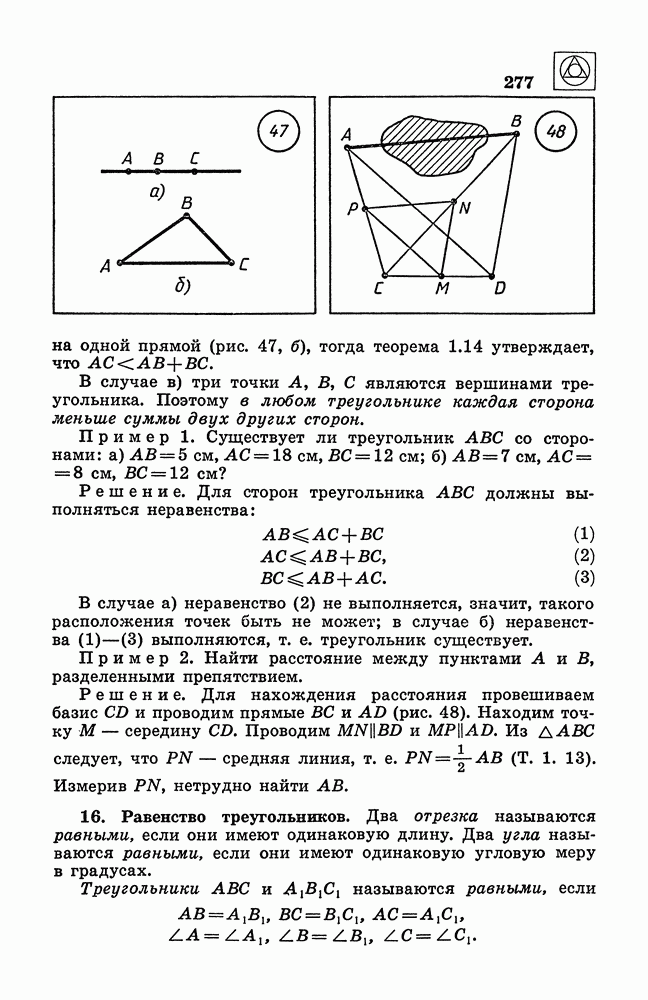
на одной прямой (рис. 47, б), тогда теорема 1.14 утверждает, что 
В случае в) три точки А, В, С являются вершинами треугольника. Поэтому в любом треугольнике каждая сторона меньше суммы двух других сторон.
Пример 1. Существует ли треугольник  со сторонами: а)
со сторонами: а)  б)
б)  ?
?
Решение. Для сторон треугольника  должны выполняться неравенства:
должны выполняться неравенства:

В случае а) неравенство (2) не выполняется, значит, такого расположения точек быть не может; в случае б) неравенства  выполняются, т. е. треугольник существует.
выполняются, т. е. треугольник существует.
Пример 2. Найти расстояние между пунктами А и В, разделенными препятствием.
Решение. Для нахождения расстояния провешиваем базис  и проводим прямые
и проводим прямые  и
и  (рис. 48). Находим точку М — середину
(рис. 48). Находим точку М — середину  Проводим
Проводим  . Из
. Из  следует, что
следует, что  — средняя линия, т. е.
— средняя линия, т. е.  (Т. 1. 13).
(Т. 1. 13).
Измерив  нетрудно найти
нетрудно найти 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- СЛОВО К УЧАЩИМСЯ
- ГЛАВА I. ЧИСЛА
- § 1. Натуральные числа
- 2. Арифметические действия над натуральными числами.
- 3. Деление с остатком.
- 4. Признаки делимости.
- 5. Разложение натурального числа на простые множители.
- 6. Наибольший общий делитель нескольких натуральных чисел.
- 7. Наименьшее общее кратное нескольких натуральных чисел.
- 8. Употребление букв в алгебре. Переменные.
- § 2. Рациональные числа
- 10. Равенство дробей. Основное свойство дроби. Сокращение дробей.
- 11. Приведение дробей к общему знаменателю.
- 12. Арифметические действия над обыкновенными дробями.
- 13. Десятичные дроби.
- 14. Арифметические действия над десятичными дробями.
- 15. Проценты.
- 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь.
- 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь.
- 18. Координатная прямая.
- 19. Множество рациональных чисел.
- § 3. Действительные числа
- 21. Действительные числа. Числовая прямая.
- 22 Обозначения некоторых числовых множеств.
- 23. Сравнение действительных чисел.
- 25. Числовые промежутки.
- 26. Модуль действительного числа.
- 27. Формула расстояния между двумя точками координатной прямой.
- 28. Правила действий над действительными числами.
- 29. Свойства арифметических действий над действительными числами.
- 30. Пропорции.
- 31. Целая часть числа. Дробная часть числа.
- 32. Степень с натуральным показателем.
- 33. Степень с нулевым показателем. Степень с отрицательным целым показателем.
- 34. Стандартный вид положительного действительного числа.
- 35. Определение арифметического корня.
- 36. Корень нечетной степени из отрицательного числа.
- 37. Степень с дробным показателем.
- 38. Свойства степеней с рациональными показателями.
- 39. Приближенные значения чисел. Абсолютная и относительная погрешности.
- 40. Десятичные приближения действительного числа по недостатку и по избытку.
- 41. Правило извлечения квадратного корня из натурального числа.
- 42. Понятие о степени с иррациональным показателем.
- 43. Свойства степеней с действительными показателями.
- § 4. Комплексные числа
- 45. Арифметические операции над комплексными числами.
- 46. Алгебраическая форма комплексного числа.
- 47. Отыскание комплексных корней уравнений.
- ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
- 49. Допустимые значения переменных.
- 50. Понятие тождественного преобразования выражения. Тождество.
- § 6. Целые рациональные выражения
- 52. Многочлены. Приведение многочленов к стандартному виду.
- 53. Формулы сокращенного умножения.
- 54. Разложение многочленов на множители.
- 55. Многочлены от одной переменной.
- 56. Разложение квадратного трехчлена на линейные множители.
- 57. Разложение на множители двучлена x^n-a^n.
- 58. Возведение двучлена в натуральную степень (бином Ньютона).
- § 7. Дробные рациональные выражения
- 60. Сокращение рациональных дробей.
- 61. Приведение рациональных дробей к общему знамена телю.
- 62. Сложение и вычитание рациональных дробей.
- 63. Умножение и деление рациональных дробей.
- 64. Возведение рациональной дроби в целую степень.
- 65. Преобразование рациональных выражений.
- § 8. Иррациональные выражения
- 67. Тождество sqrt(a^2)=|a|
- 68. Преобразование иррациональных выражений.
- Глава III. ФУНКЦИИ И ГРАФИКИ
- 70. Аналитическое задание функции.
- 71. Табличное задание функции.
- 72. Числовая плоскость. Координатная плоскость, оси координат.
- 73. График функции, заданной аналитически.
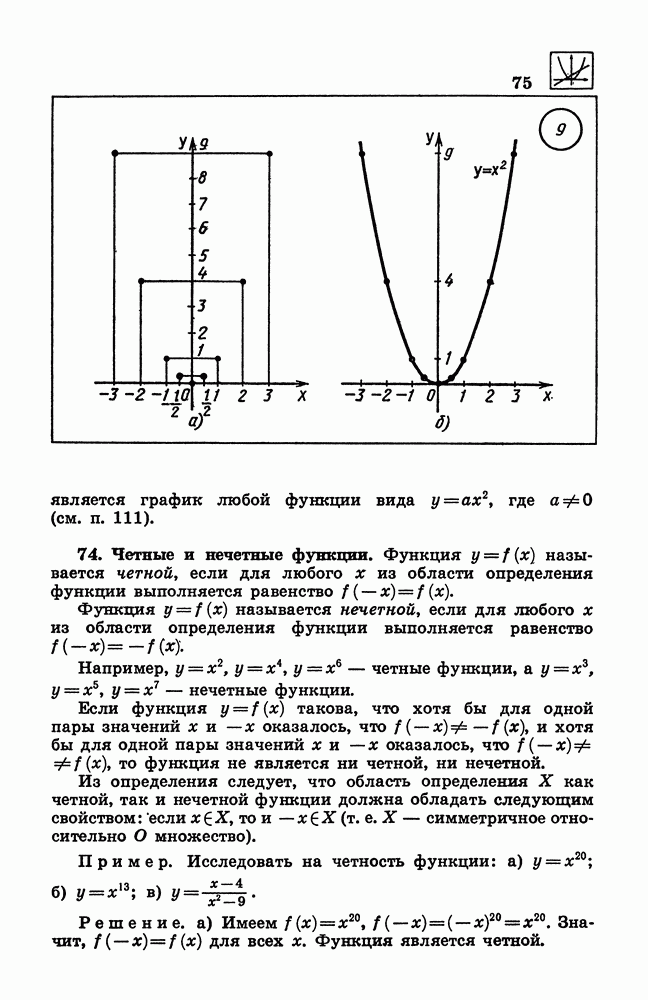
- 74. Четные и нечетные функции.
- 75. График четной функции. График нечетной функции.
- 76. Периодические функции.
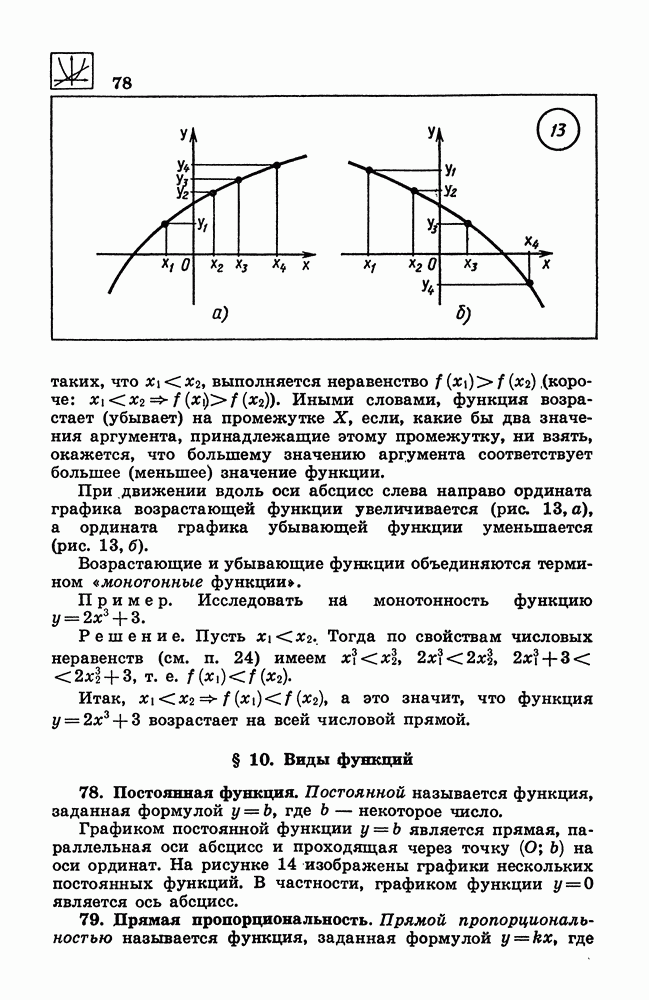
- 77. Монотонные функции.
- § 10. Виды функций
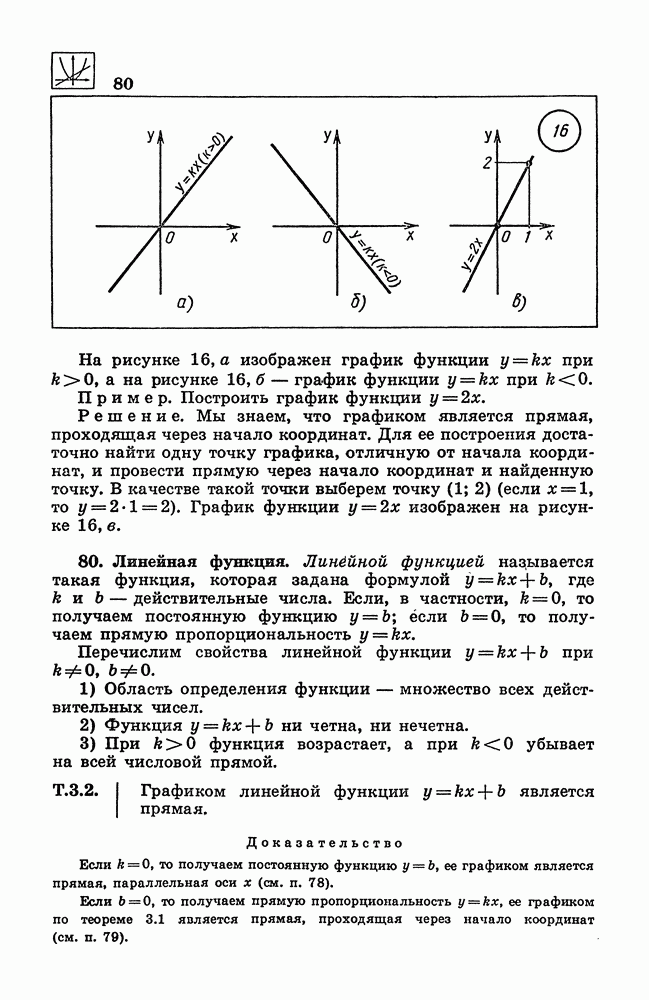
- 79. Прямая пропорциональность.
- 80. Линейная функция.
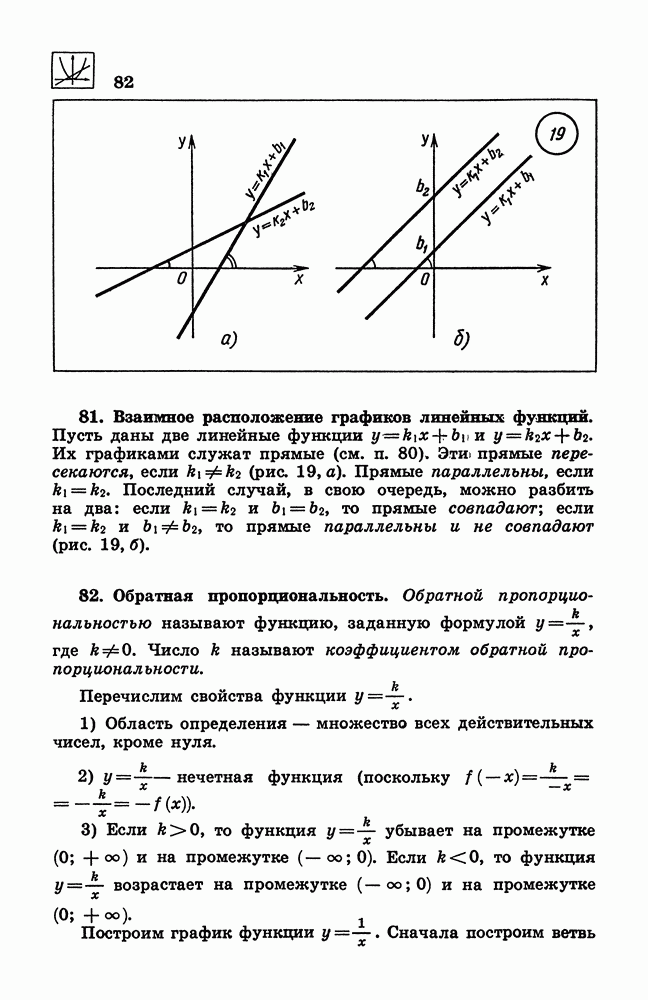
- 81. Взаимное расположение графиков линейных функций.
- 82. Обратная пропорциональность.
- 83. Функция у = x^2.
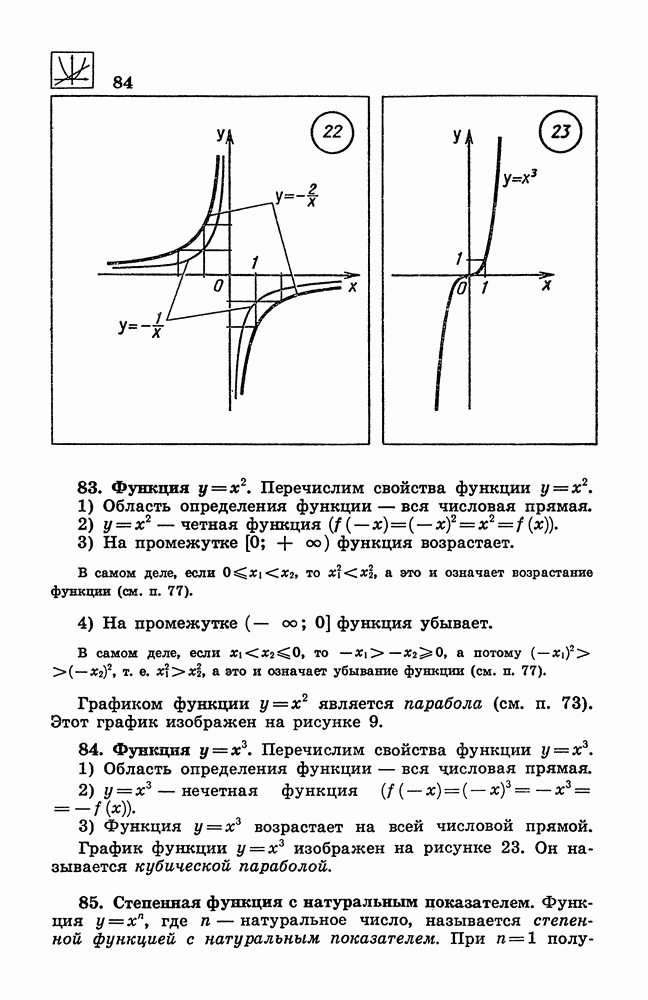
- 84. Функция y = x^3.
- 85. Степенная функция с натуральным показателем.
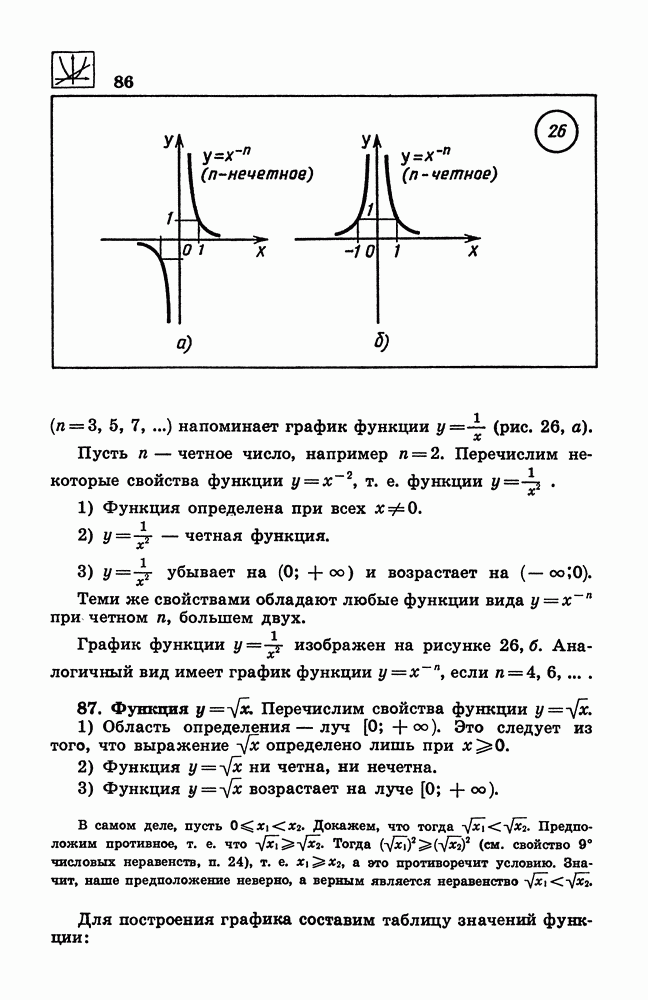
- 86. Степенная функция с целым отрицательным показателем.
- 87. Функция y = sqrt(x)
- 88. Функция y = x^(1/3)
- 89. Функция y = x^(1/n)
- 90. Степенная функция с положительным дробным показателем.
- 91. Степенная функция с отрицательным дробным показателем.
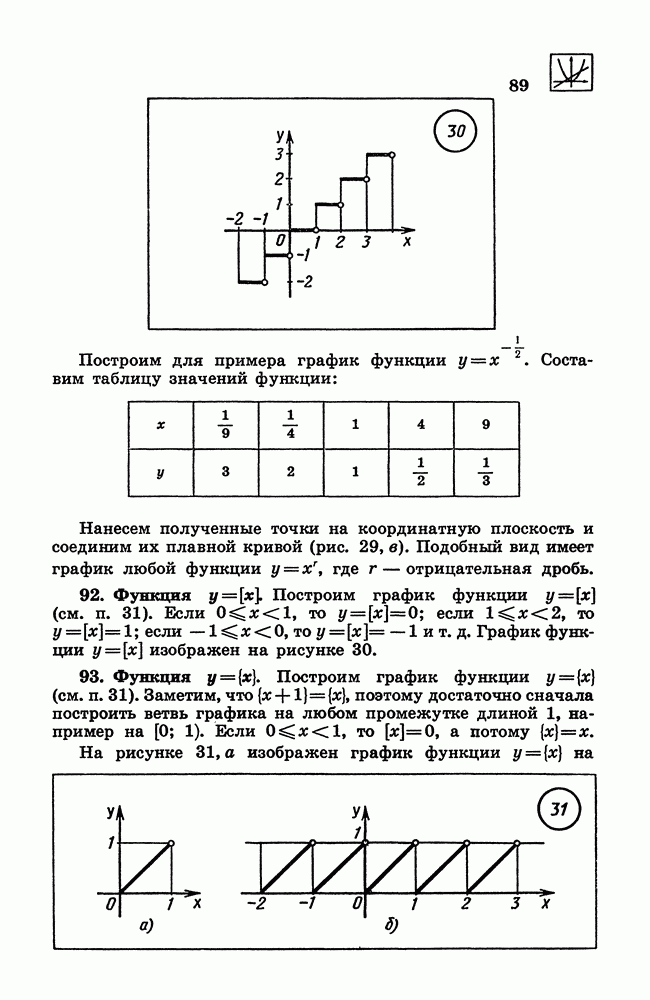
- 92. Функция у = [x].
- 93. Функция у = {х}.
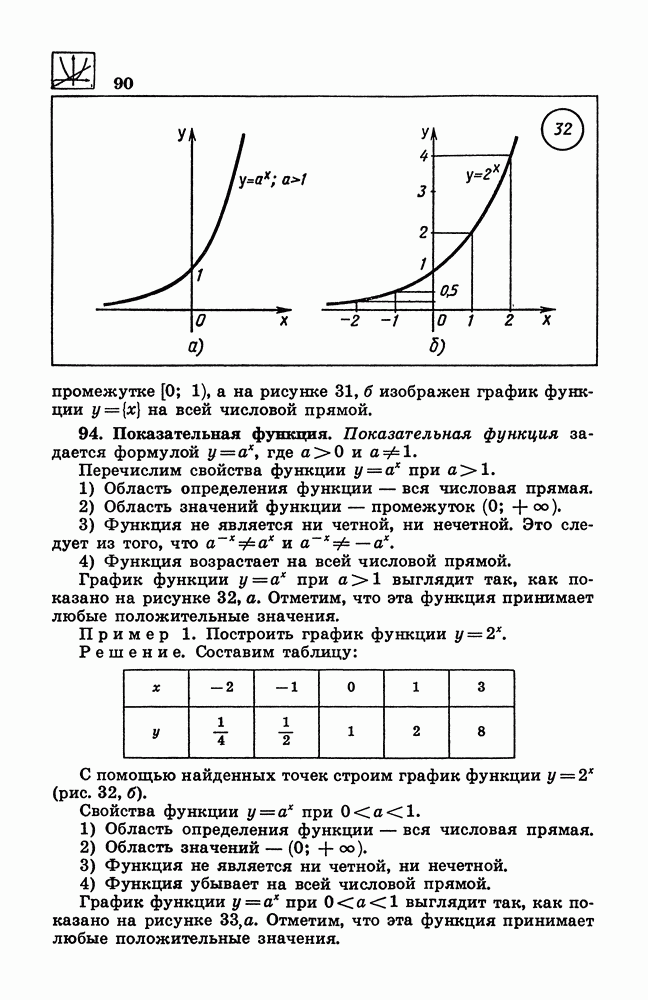
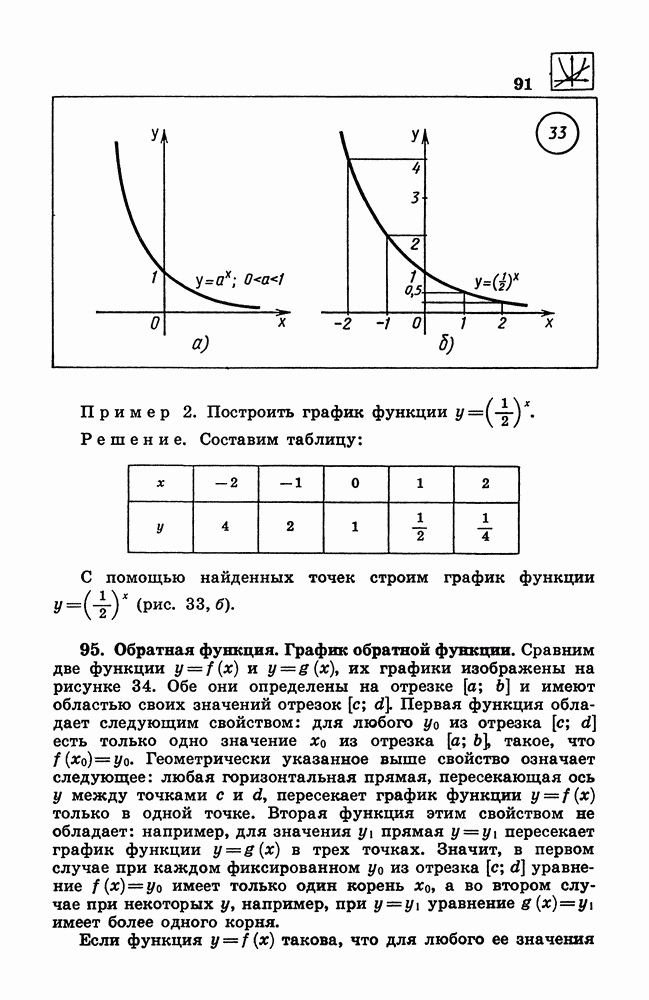
- 94. Показательная функция.
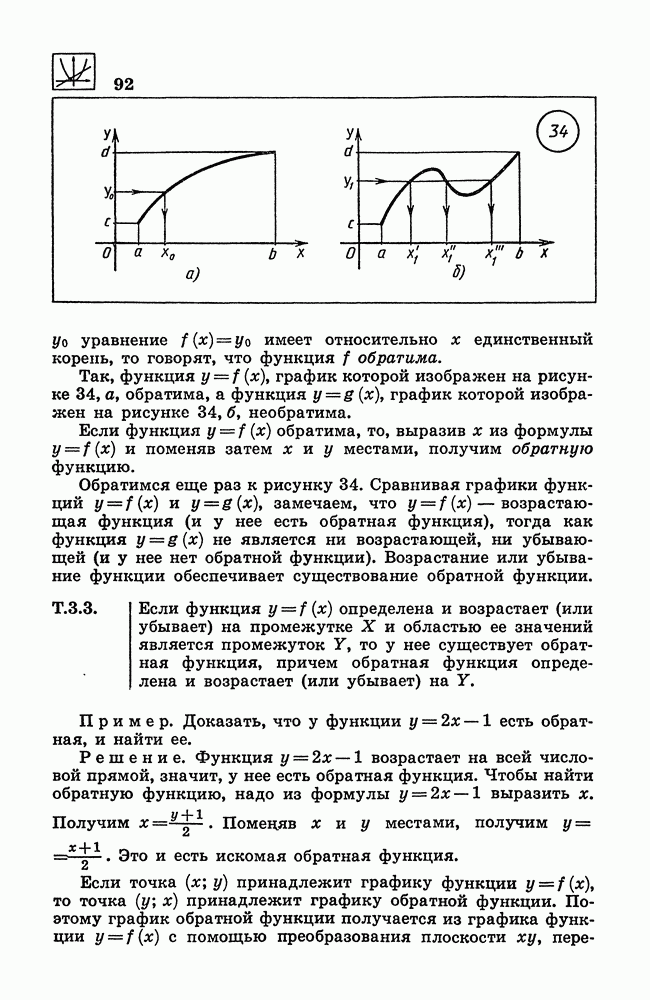
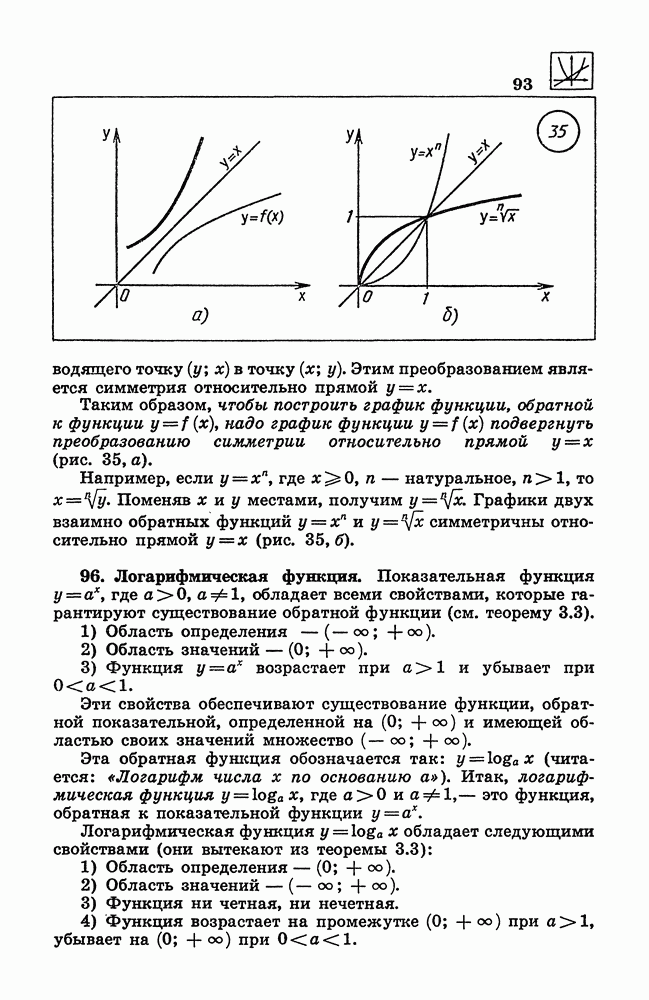
- 95. Обратная функция. График обратной функции.
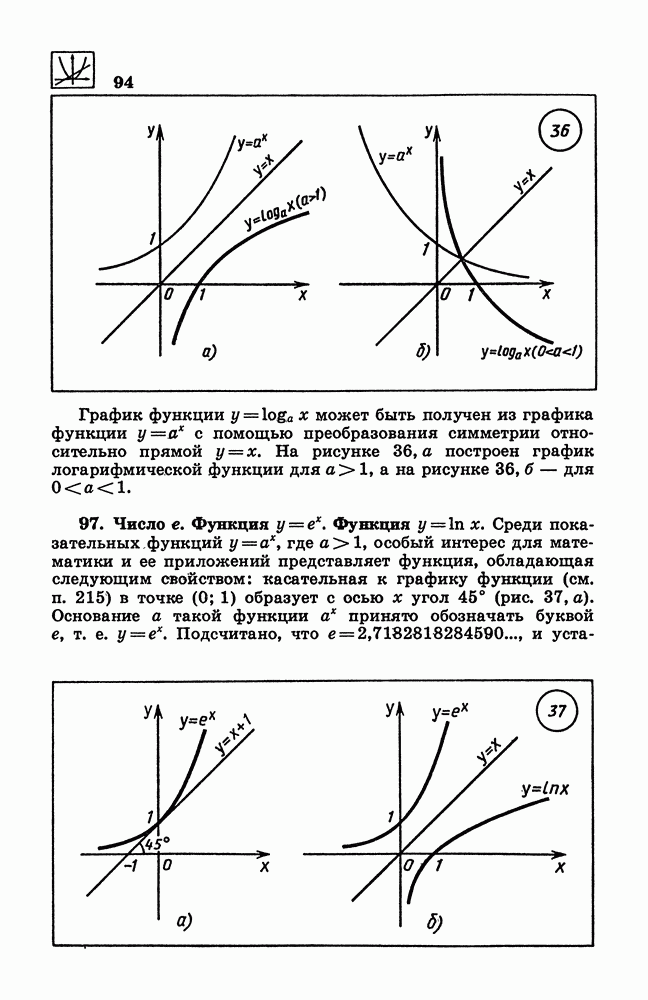
- 96. Логарифмическая функция.
- 97. Число е. Функция у = е^x. Функция у = ln х.
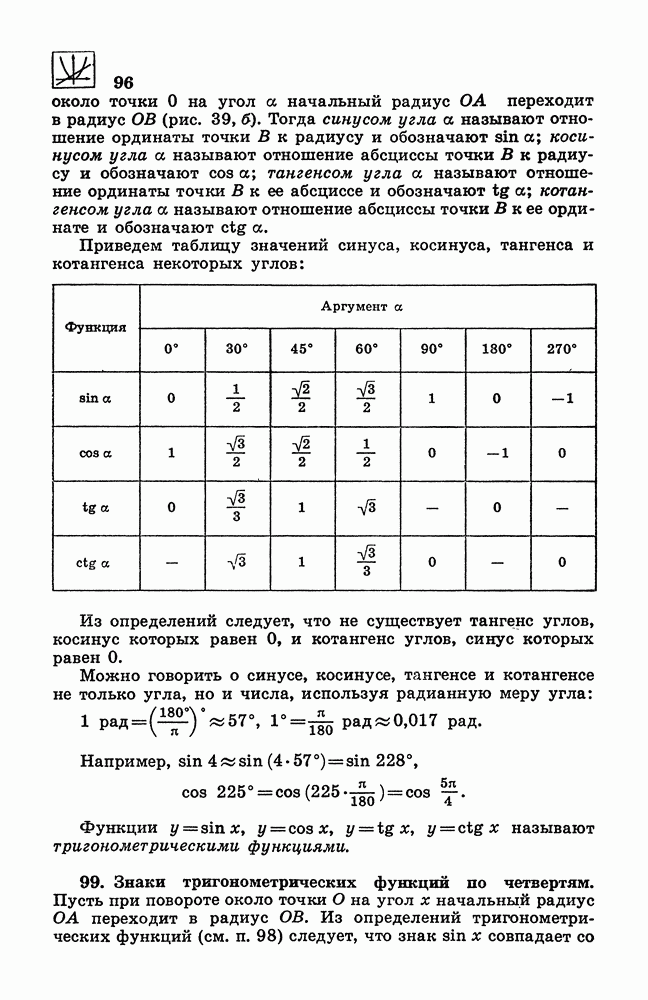
- 98. Определение тригонометрических функций.
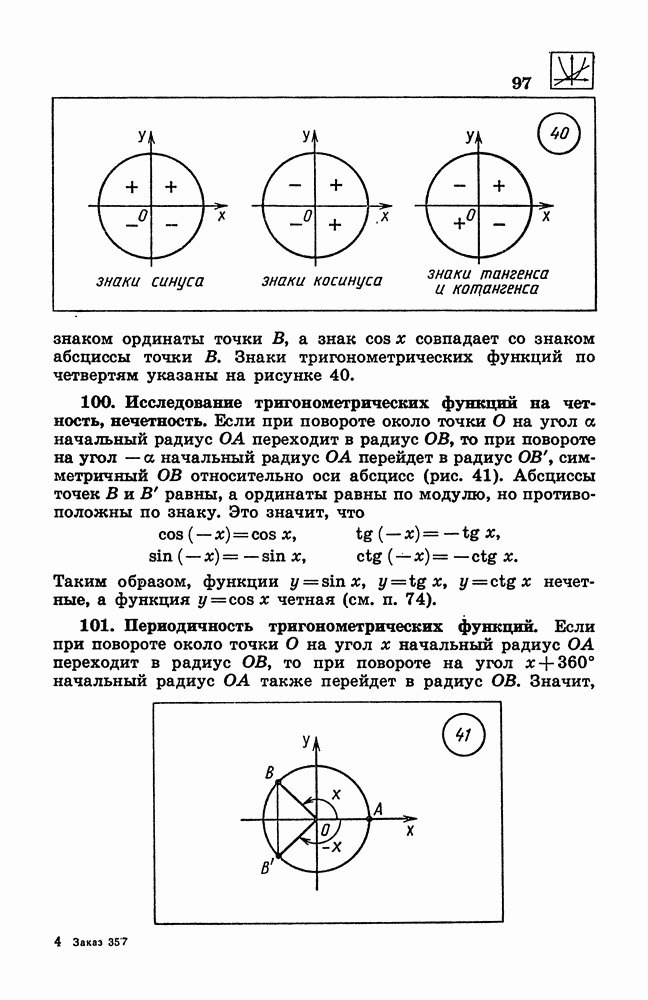
- 99. Знаки тригонометрических функций по четвертям.
- 100. Исследование тригонометрических функций на четность, нечетность.
- 101. Периодичность тригонометрических функций.
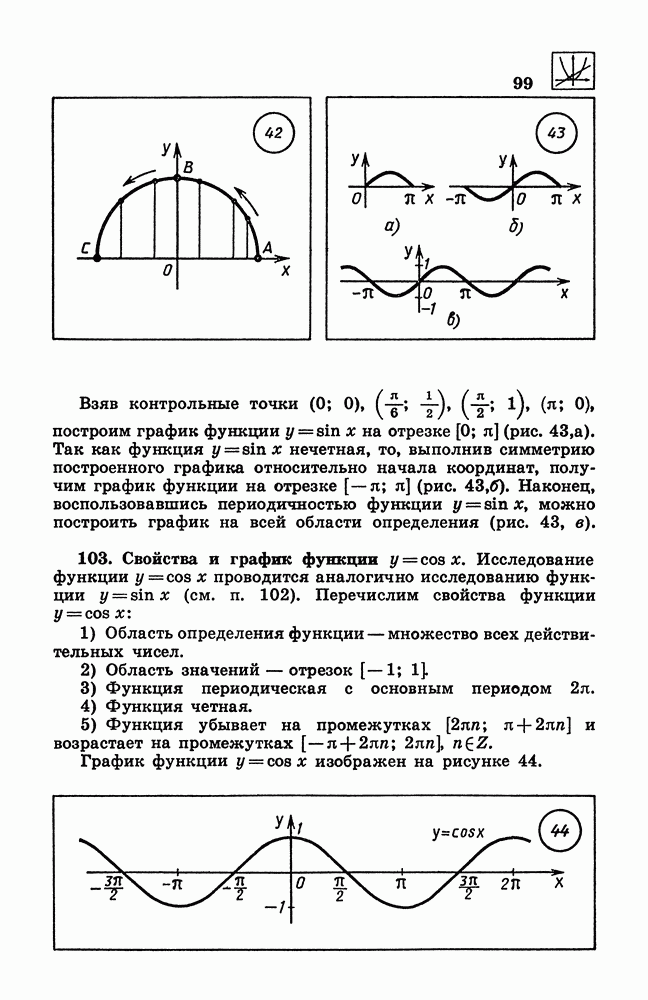
- 102. Свойства и график функции y = sin x.
- 103. Свойства и график функции у = cos x.
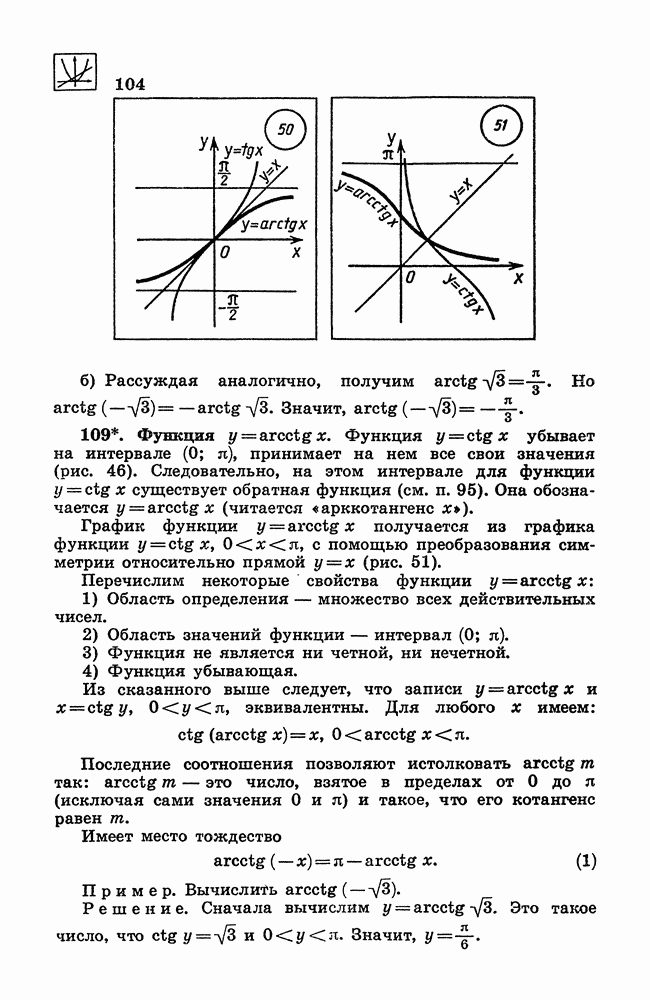
- 104. Свойства и график функции у = tg х.
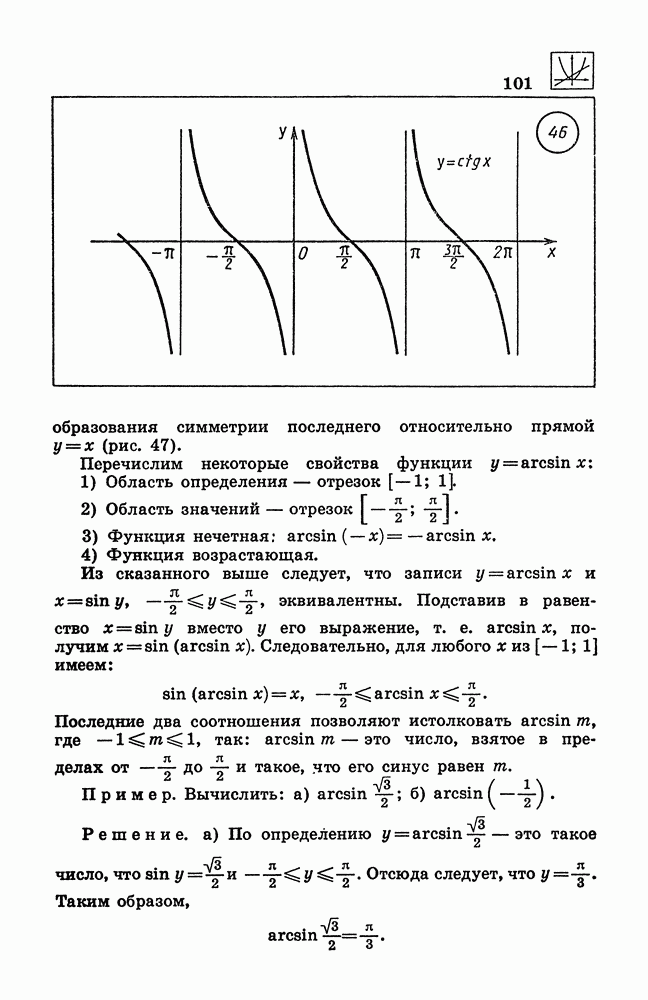
- 105. Свойства и график функции y = ctg x.
- 106. Функция у = arcsin х.
- 107. Функция y = arccos x.
- 108. Функция у = arctg x.
- 109. Функция y = arcctg х.
- § 11. Преобразования графиков
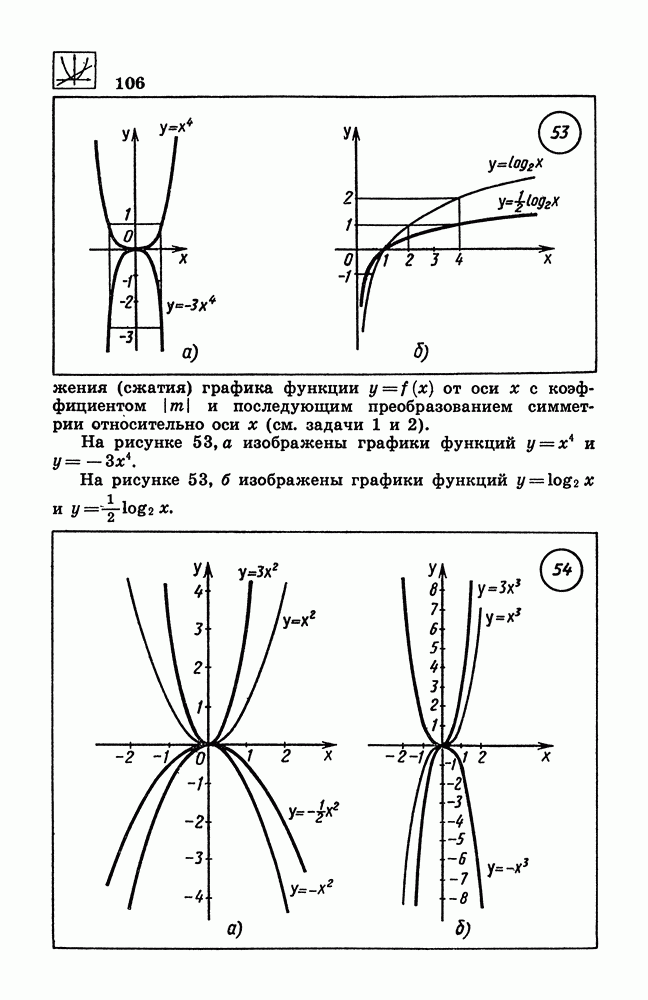
- 111. Графики функций y = ax^2, y = ax^3.
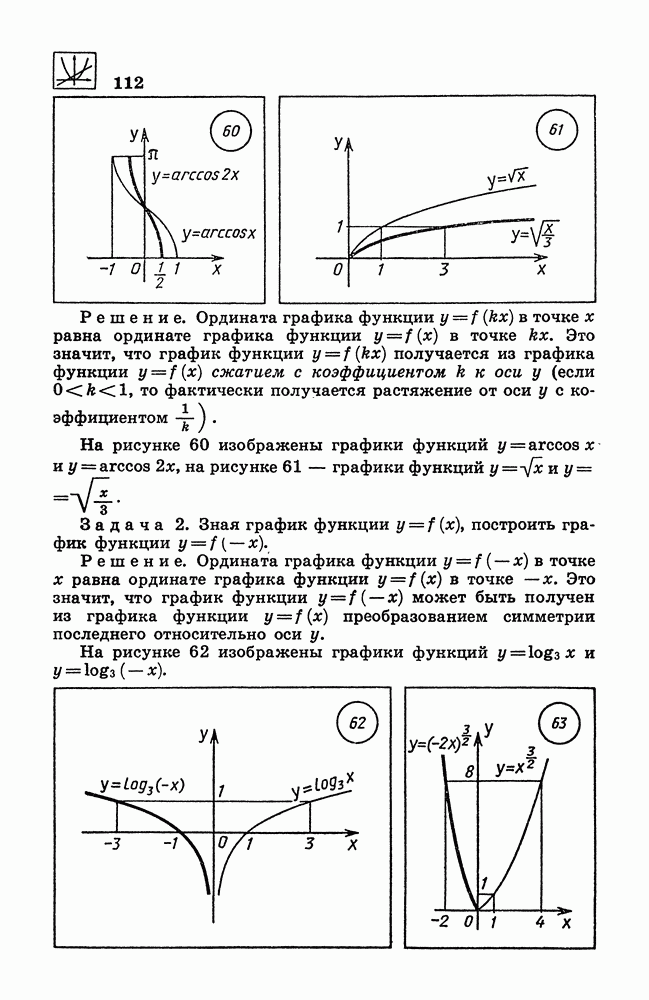
- 112. Построение графика функции y = f(x-m)+n
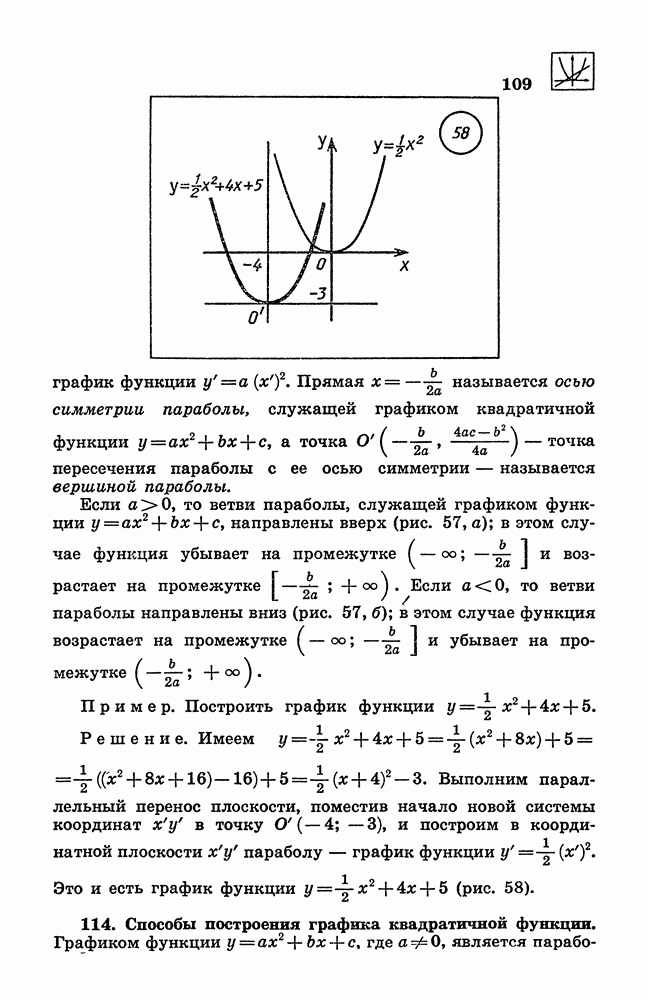
- 113. График квадратичной функции.
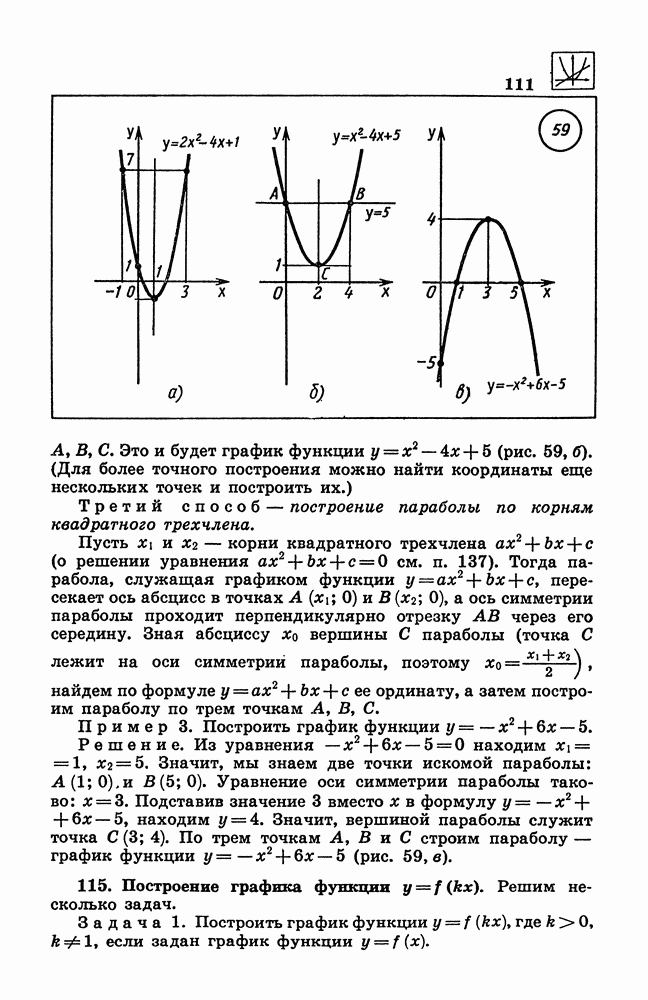
- 114. Способы построения графика квадратичной функции
- 115. Построение графика функции y = f(kx).
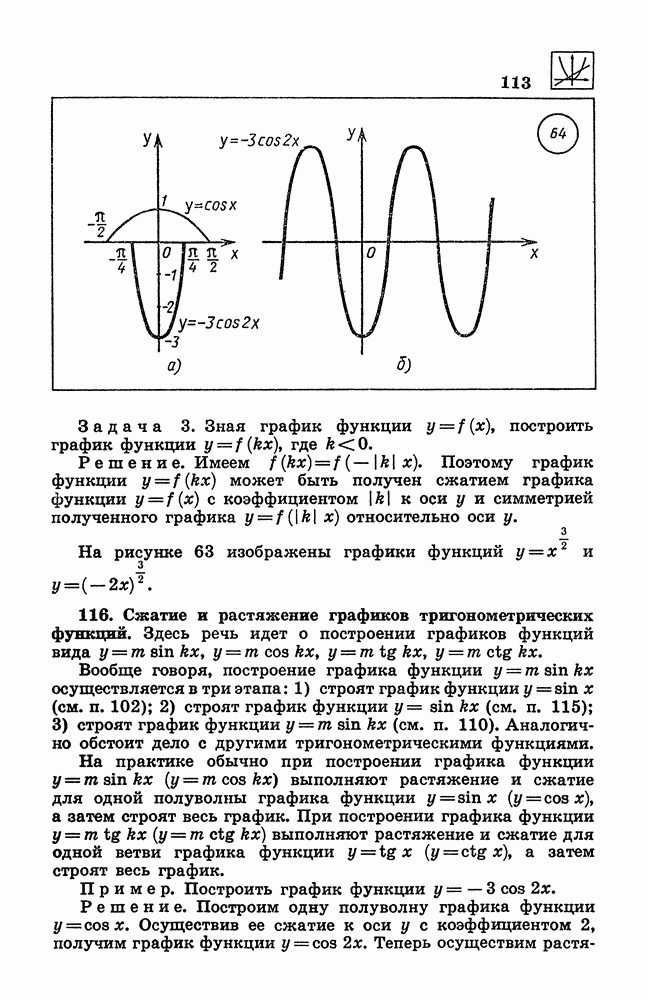
- 116. Сжатие и растяжение графиков тригонометрических функций.
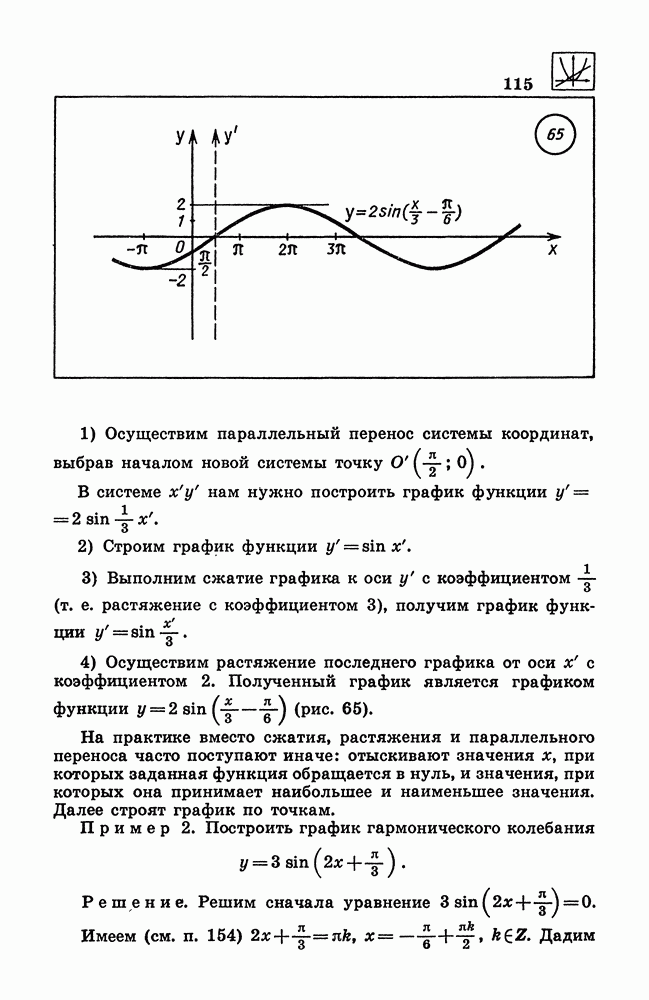
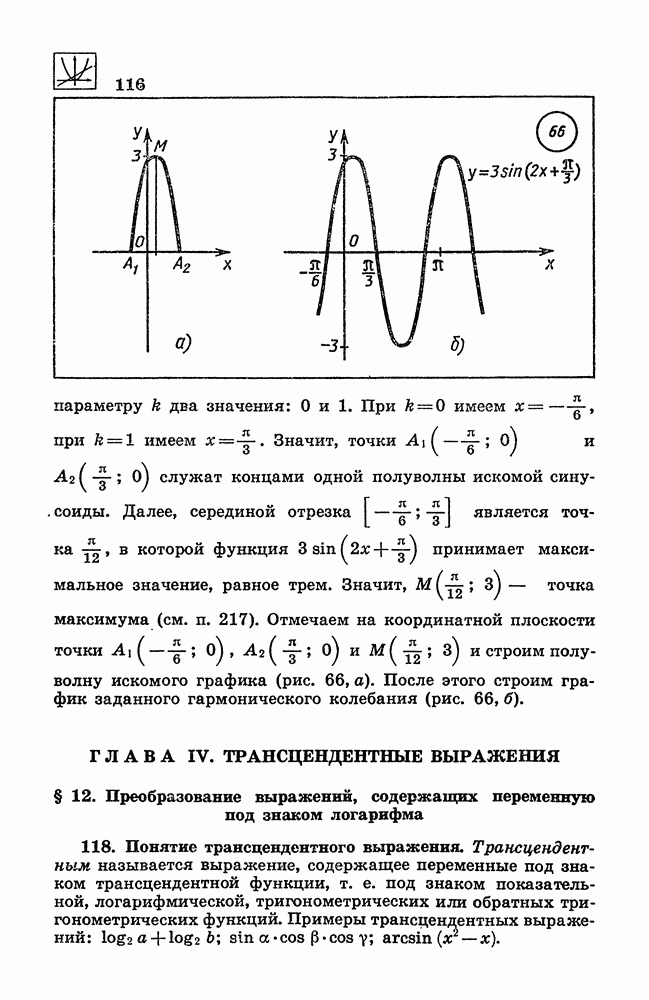
- 117. График гармонического колебания
- ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ
- § 12. Преобразование выражений, содержащих переменную под знаком логарифма
- 119. Определение логарифма положительного числа по данному основанию.
- 120. Свойства логарифмов.
- 121. Переход к новому основанию логарифма.
- 122. Логарифмирование и потенцирование.
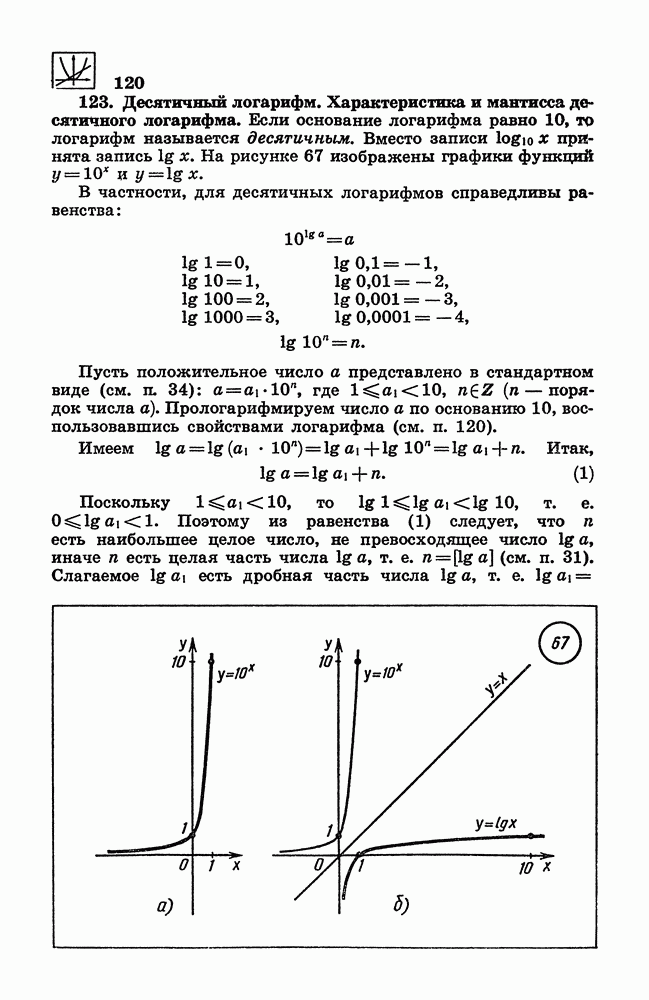
- 123. Десятичный логарифм. Характеристика и мантисса десятичного логарифма.
- § 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений
- 125. Формулы сложения и вычитания аргументов.
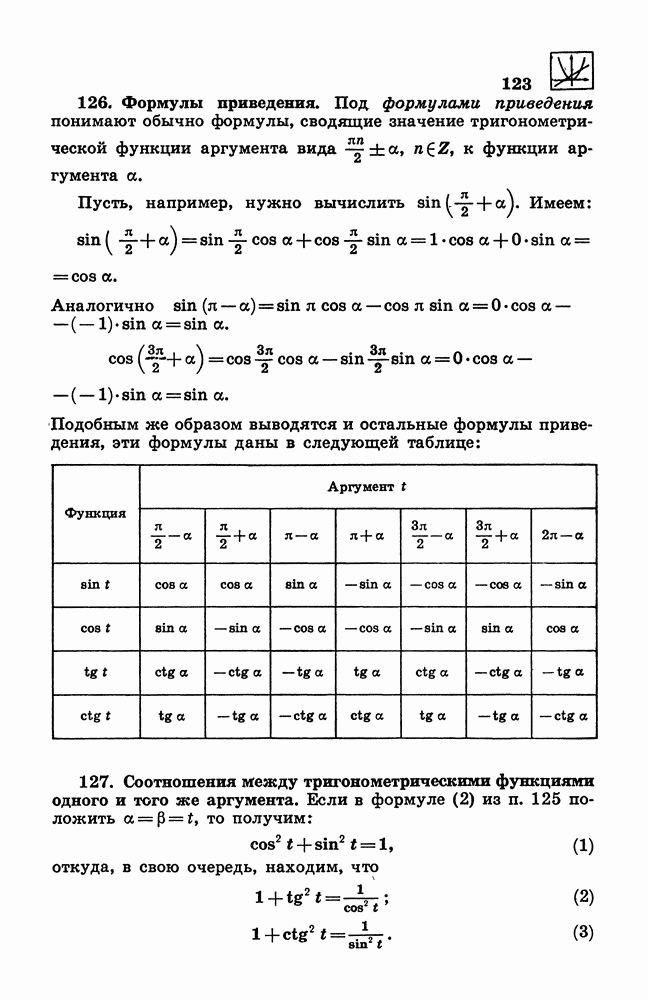
- 126. Формулы приведения.
- 127. Соотношения между тригонометрическими функциями одного и того же аргумента.
- 128. Формулы двойного угла.
- 129. Формулы понижения степени.
- 130. Преобразование суммы тригонометрических функций в произведение.
- 131. Преобразование произведения тригонометрических функций в сумму.
- 132. Преобразование выражения a cos t + b sin t к виду A sin (t + a).
- 133. Примеры преобразований выражений, содержащих обратные тригонометрические функции.
- ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ
- § 14. Уравнения с одной переменной
- 135. Равносильность уравнений.
- 136. Линейные уравнения.
- 137. Квадратные уравнения.
- 138. Неполные квадратные уравнения.
- 139. Теорема Виета.
- 140. Системы и совокупности уравнений.
- 141. Уравнения, содержащие переменную под знаком модуля.
- 142. Понятие следствия уравнения. Посторонние корни.
- 143. Уравнения с переменной в знаменателе.
- 144. Область определения уравнения.
- 145. Рациональные уравнения.
- 146. Решение уравнения p(x) = 0 методом разложения его левой части на множители.
- 147. Решение уравнений методом введения новой переменной.
- 148. Биквадратные уравнения.
- 149. Решение задач с помощью составления уравнений.
- 150. Иррациональные уравнения.
- 151. Показательные уравнения.
- 152. Логарифмические уравнения.
- 153. Примеры решения показательно-логарифмических уравнений.
- 154. Простейшие тригонометрические уравнения.
- 155. Методы решения тригонометрических уравнений.
- 156. Универсальная подстановка (для тригонометрических уравнений).
- 157. Метод введения вспомогательного аргумента (для тригонометрических уравнений).
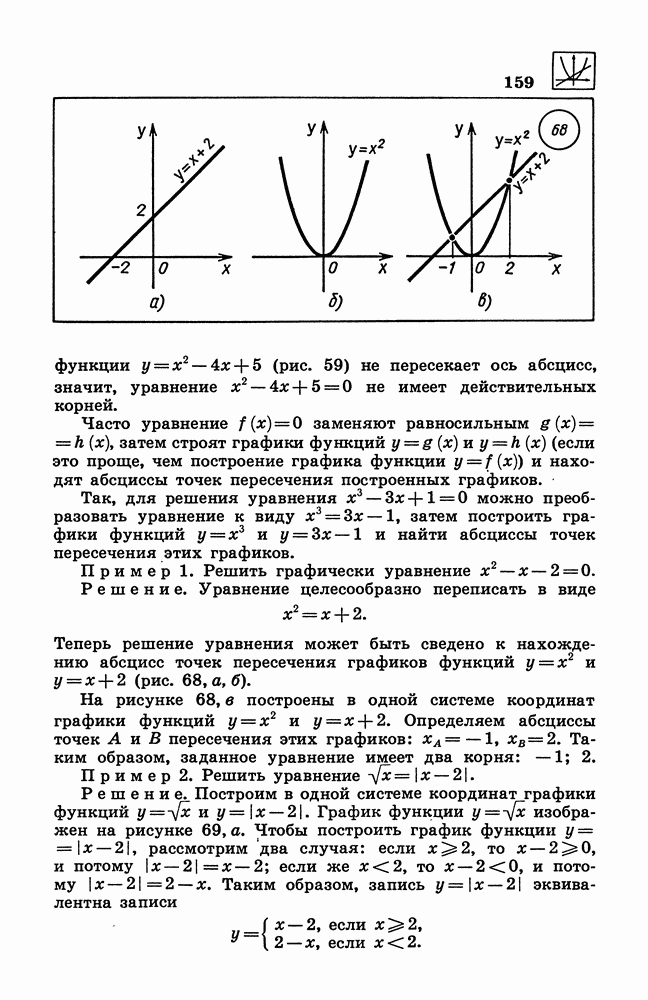
- 158. Графическое решение уравнений.
- 159. Уравнения с параметром.
- § 15. Уравнения с двумя переменными
- 161. График уравнения с двумя переменными.
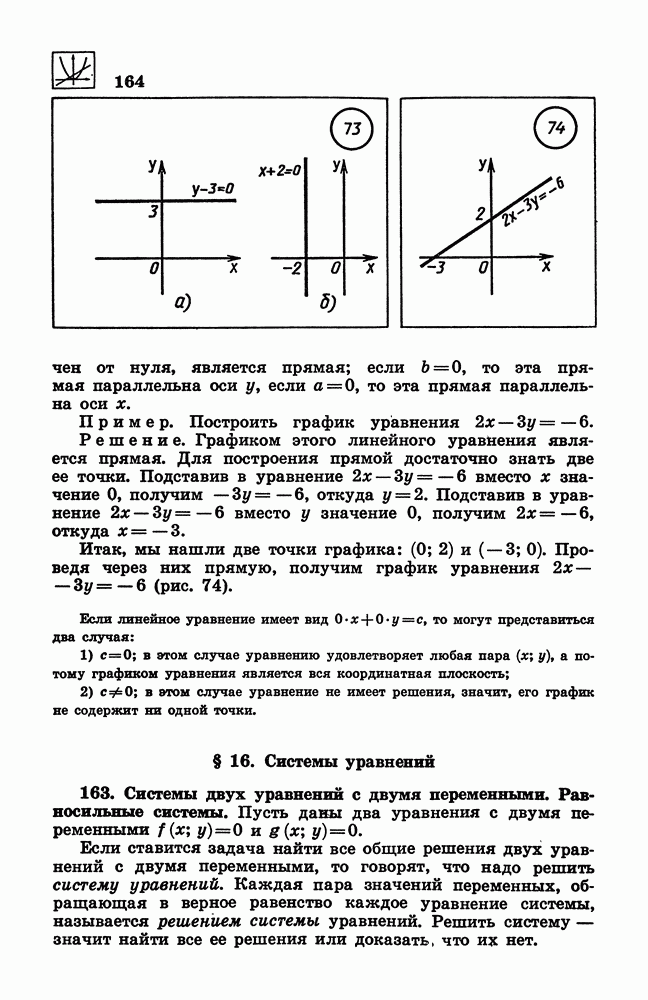
- 162. Линейное уравнение с двумя переменными и его график.
- § 16. Системы уравнений
- 164. Решение систем двух уравнений с двумя переменными методом подстановки.
- 165. Решение систем двух уравнений с двумя переменными методом сложения.
- 167. Графическое решение систем двух уравнений с двумя переменными.
- 168. Исследование системы двух линейных уравнений с двумя переменными.
- 169. Решение систем двух уравнений с двумя переменными методами умножения и деления.
- 170. Системы показательных и логарифмических уравнений.
- 171. Системы тригонометрических уравнений с двумя переменными.
- 172. Системы трех уравнений с тремя переменными.
- 173. Решение задач с помощью составления систем уравнений.
- Глава VI. НЕРАВЕНСТВА
- § 17. Решение неравенств с переменной
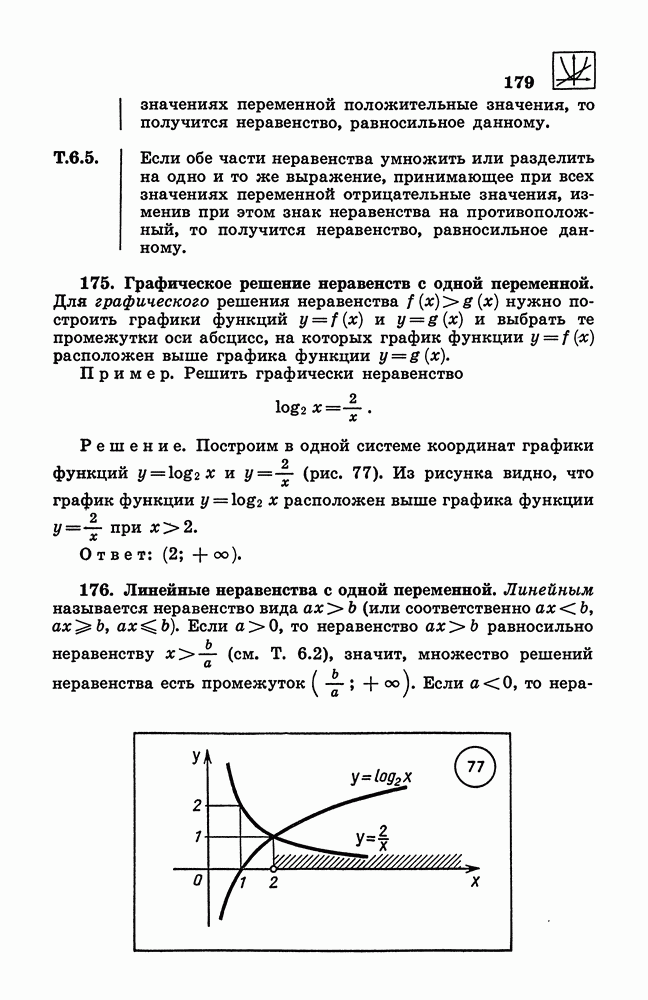
- 175. Графическое решение неравенств с одной переменной.
- 176. Линейные неравенства с одной переменной.
- 177. Системы неравенств с одной переменной.
- 178. Совокупность неравенств с одной переменной.
- 179. Дробно-линейные неравенства.
- 180. Неравенства второй степени.
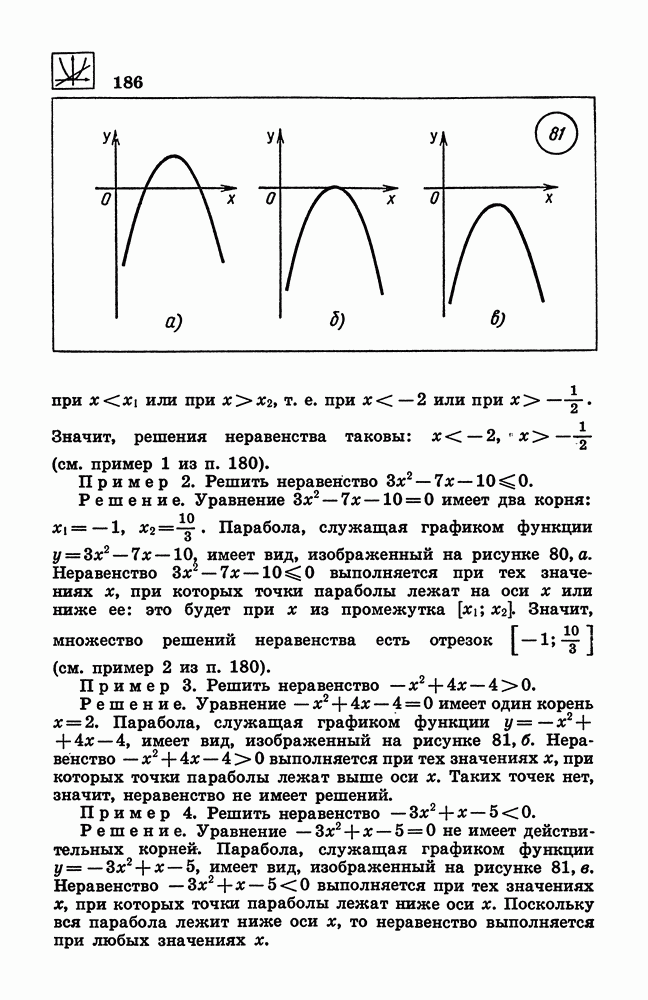
- 181. Графическое решение неравенств второй степени.
- 182. Неравенства с модулями.
- 183. Решение рациональных неравенств методом промежутков.
- 184. Показательные неравенства.
- 185. Логарифмические неравенства.
- 186. Иррациональные неравенства.
- 187. Решение тригонометрических неравенств.
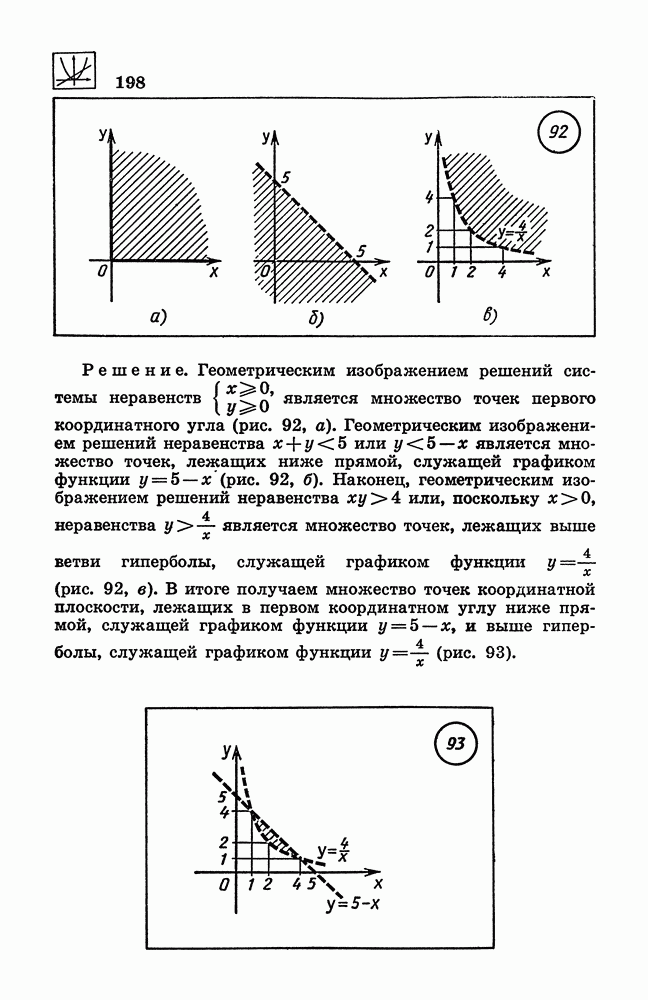
- 188. Неравенства и системы неравенств с двумя переменными.
- § 18. Доказательство неравенств
- 190. Синтетический метод доказательства неравенств.
- 191. Доказательство неравенств методом от противного.
- 192. Использование неравенств при решении уравнений.
- ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
- § 19. Числовые последовательности
- 194. Способы задания последовательности.
- 195. Возрастание и убывание последовательности.
- 196. Определение арифметической прогрессии.
- 197. Свойства арифметической прогрессии
- 198. Определение геометрической прогрессии.
- 199. Свойства геометрической прогрессии.
- 200. Понятие о пределе последовательности.
- 201. Вычисление пределов последовательностей.
- 202. Сумма бесконечной геометрической прогрессии при |q| < 1.
- § 20. Предел функции
- 204. Вычисление пределов функции при х->оо.
- 205. Предел функции в точке. Непрерывные функции.
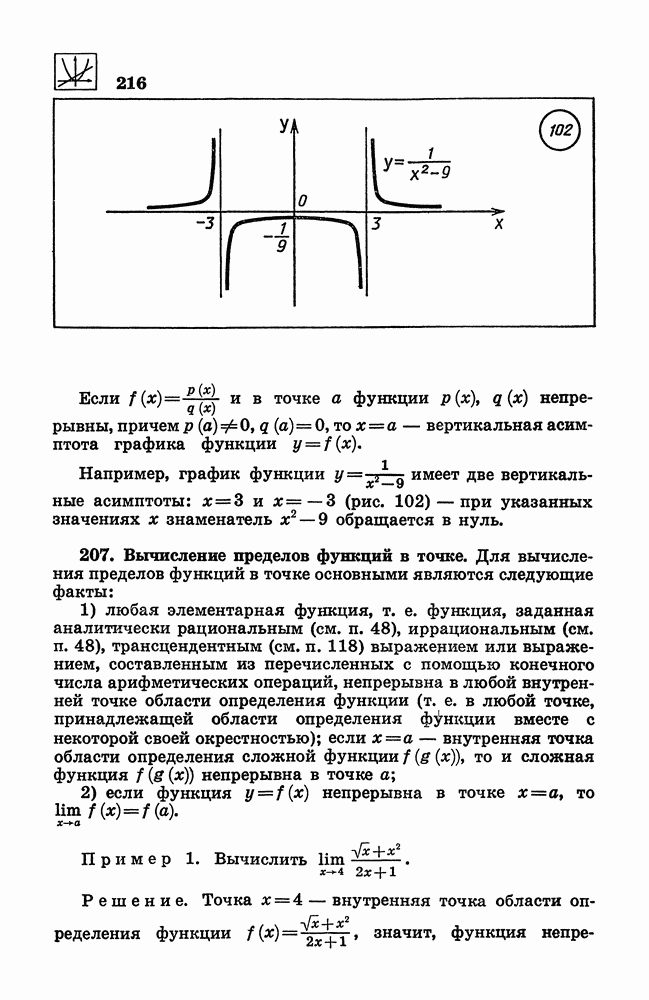
- 206. Вертикальная асимптота.
- 207. Вычисление пределов функций в точке.
- § 21. Производная и ее применения
- 209. Определение производной.
- 210. Формулы дифференцирования. Таблица производных.
- 211. Дифференцирование суммы, произведения, частного.
- 212. Сложная функция и ее дифференцирование.
- 213. Физический смысл производной.
- 214. Вторая производная и ее физический смысл.
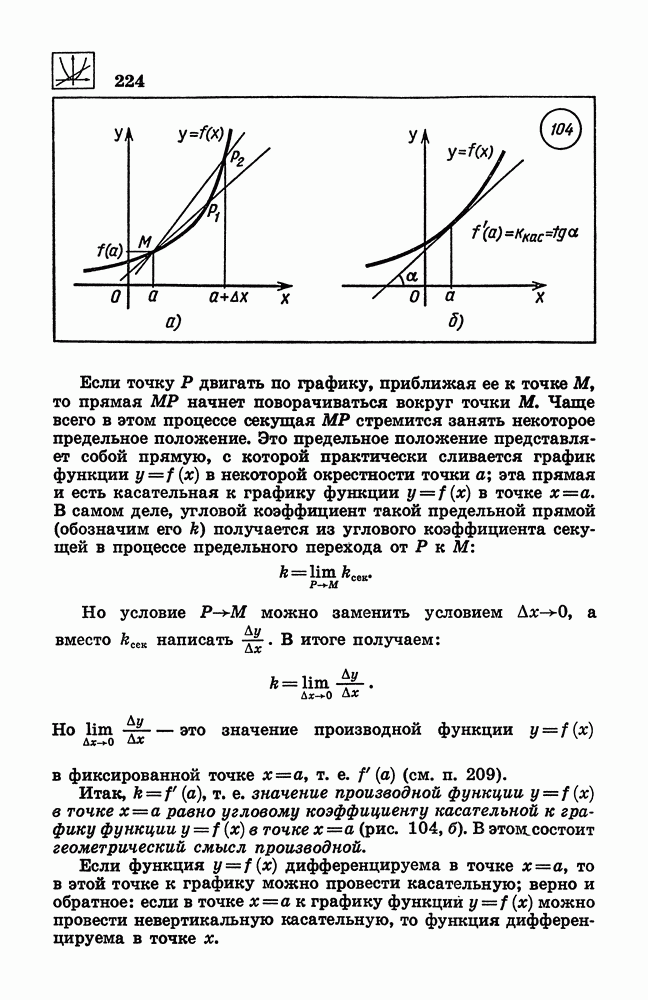
- 215. Касательная к графику функции.
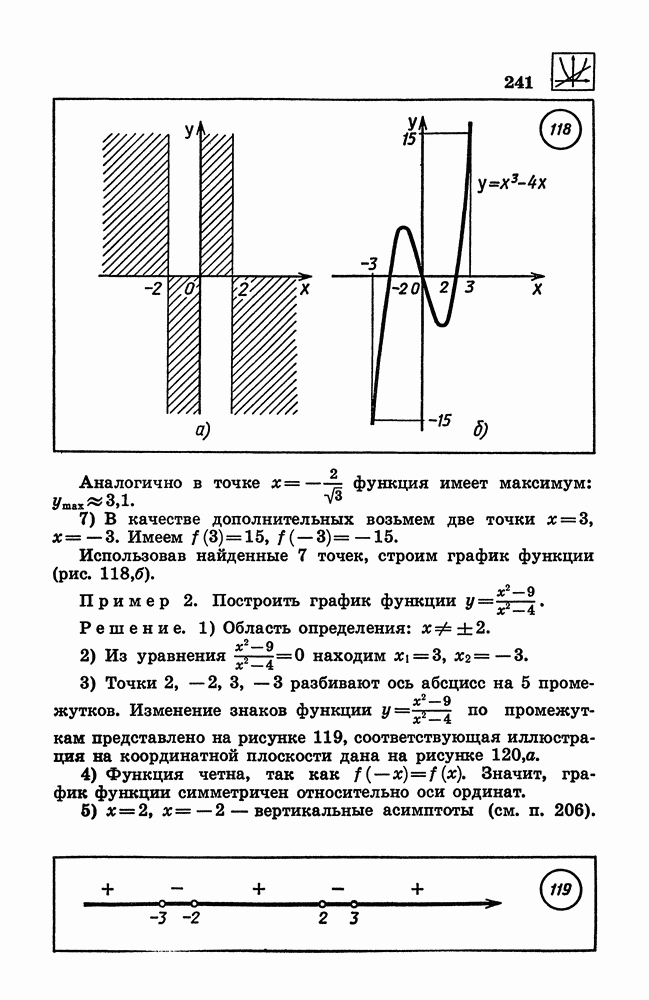
- 216. Применение производной к исследованию функций на монотонность.
- 217. Применение производной к исследованию функций на экстремум.
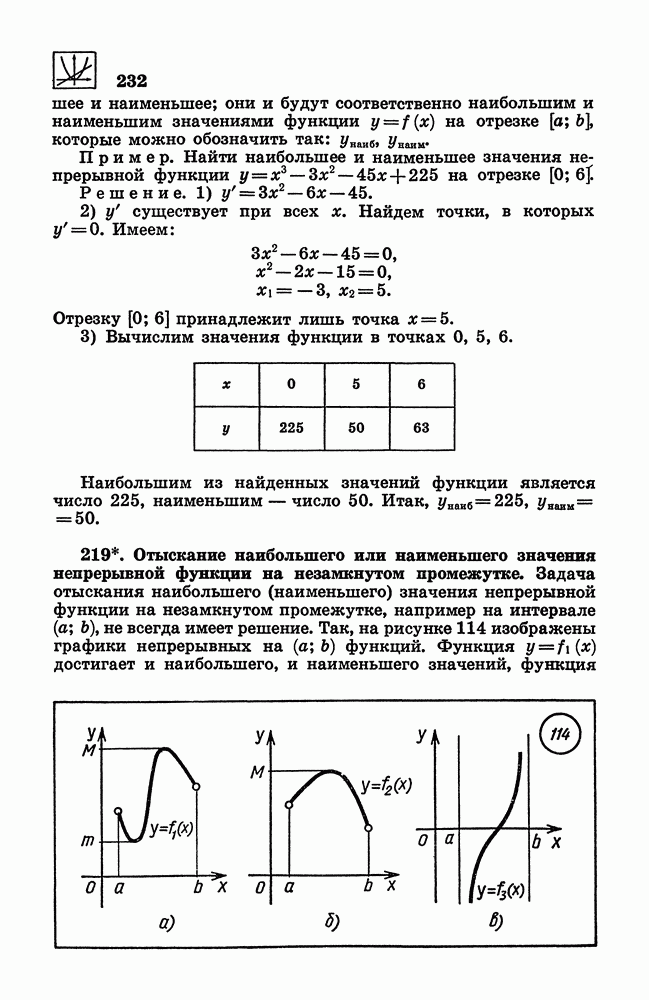
- 218. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке.
- 219. Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке.
- 220. Задачи на отыскание наибольших или наименьших значений величин.
- 221. Применение производной для доказательства тождеств.
- 222. Применение производной для доказательства неравенств.
- 223. Общая схема построения графика функции.
- § 22. Первообразная и интеграл
- 225. Таблица первообразных.
- 226. Правила вычисления первообразных.
- 227. Интеграл.
- 228. Связь между интегралов и первообразной (формула Ньютона—Лейбница).
- 229. Правила вычисления интегралов.
- 230. Использование интеграла для вычисления площадей плоских фигур.
- ГЕОМЕТРИЯ. ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ
- 2. Точка. Прямая.
- 3. Определения. Аксиомы. Теоремы.
- § 2. Основные свойства простейших геометрических фигур
- 5. Луч.
- 6. Окружность. Круг.
- 7. Полуплоскость.
- 8. Угол. Градусная мера угла.
- 9. Смежные и вертикальные углы.
- 10. Центральные и вписанные углы.
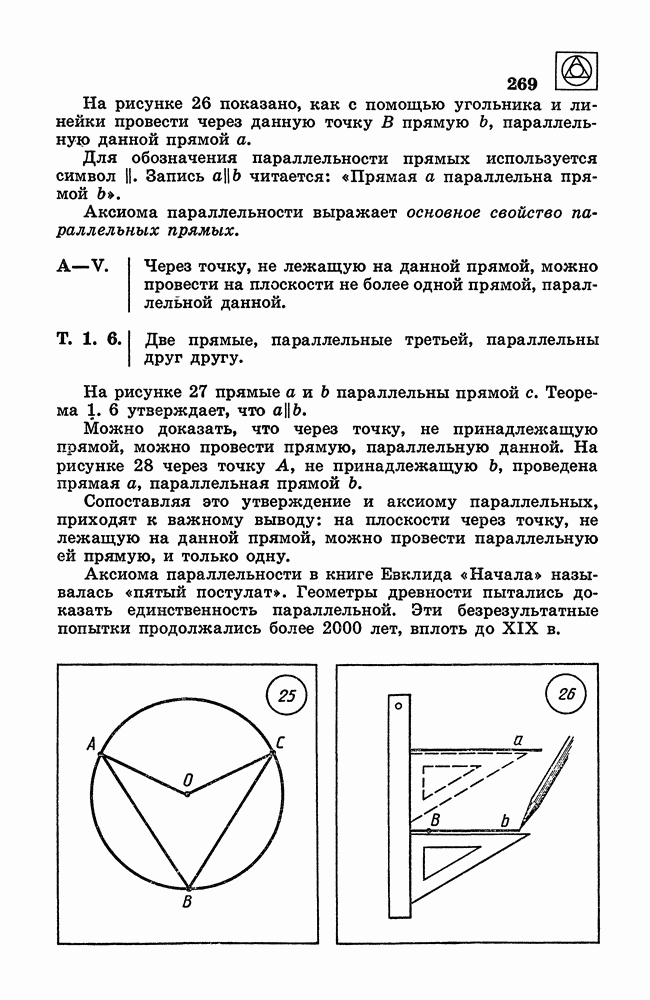
- 11. Параллельные прямые.
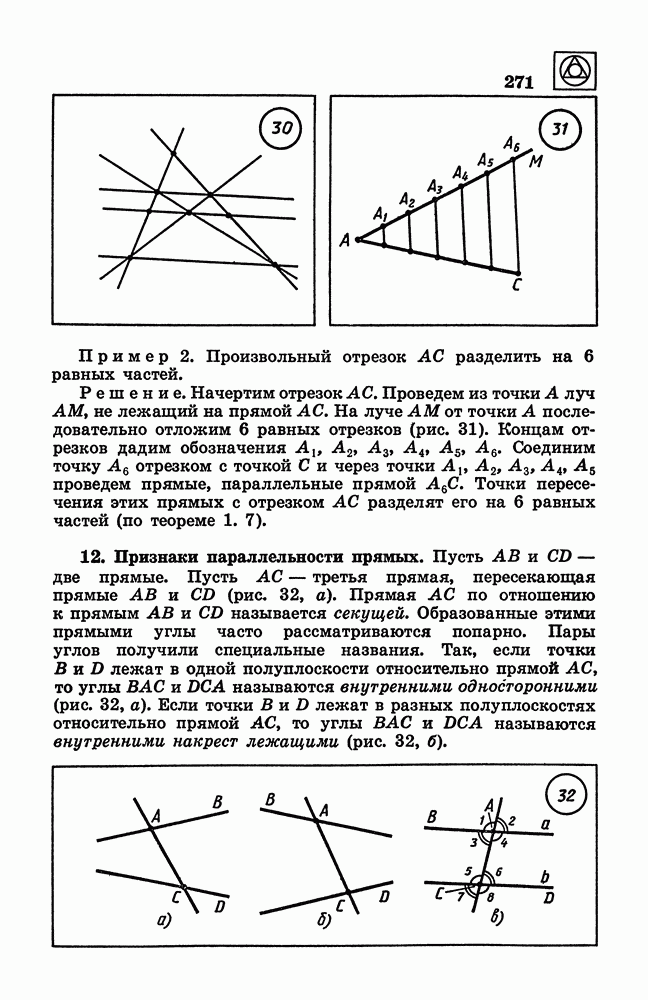
- 12. Признаки параллельности прямых.
- 13. Перпендикулярные прямые.
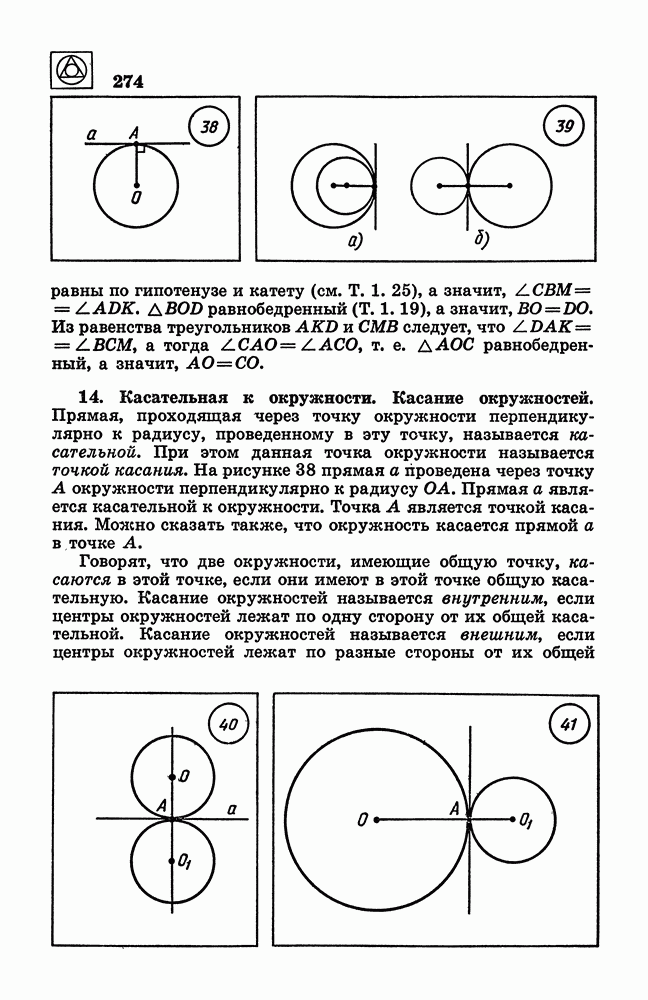
- 14. Касательная к окружности.
- 15. Треугольники.
- 16. Равенство треугольников.
- 17. Равнобедренный треугольник.
- 18. Сумма углов треугольника.
- 19. Прямоугольный треугольник. Теорема Пифагора.
- 20. Окружности, вписанные в треугольник и описанные около треугольника.
- § 3. Геометрические построения на плоскости
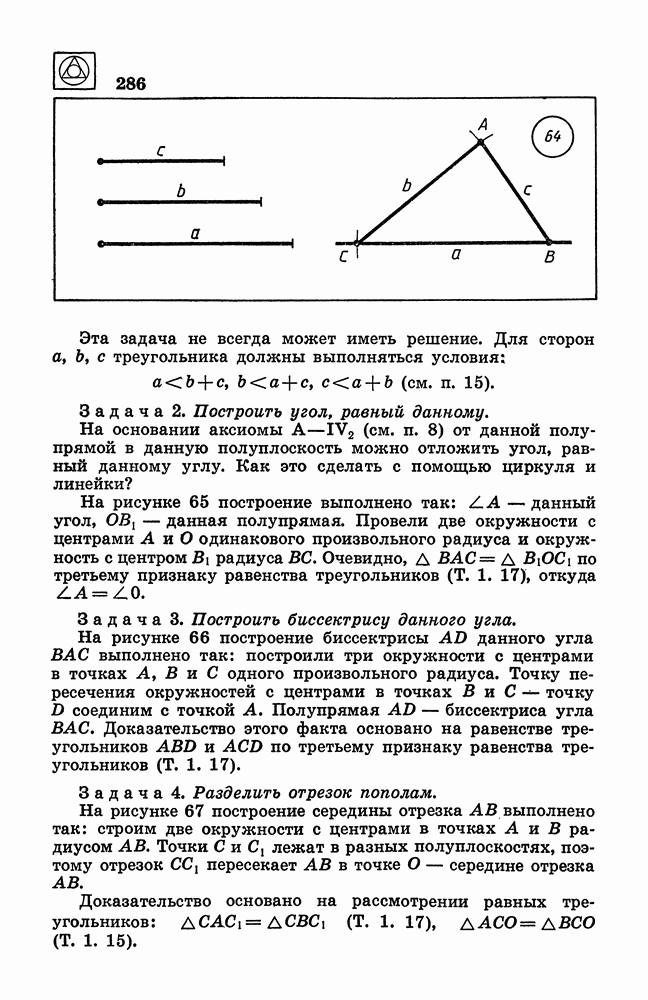
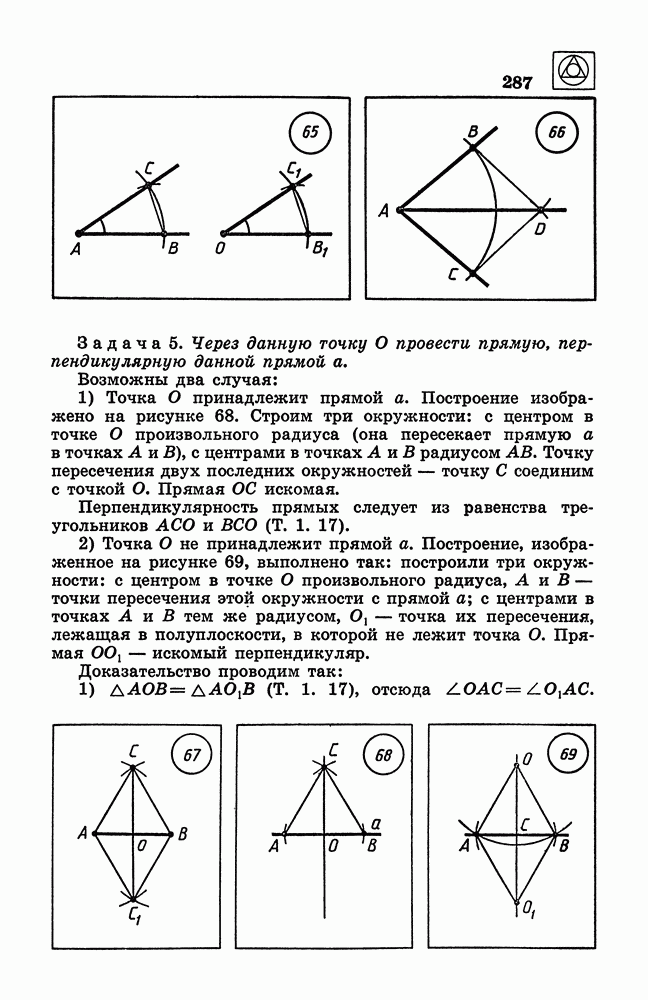
- 22. Простейшие задачи на построение.
- 23. Геометрическое место точек на плоскости.
- § 4. Четырехугольники
- 25. Параллелограмм.
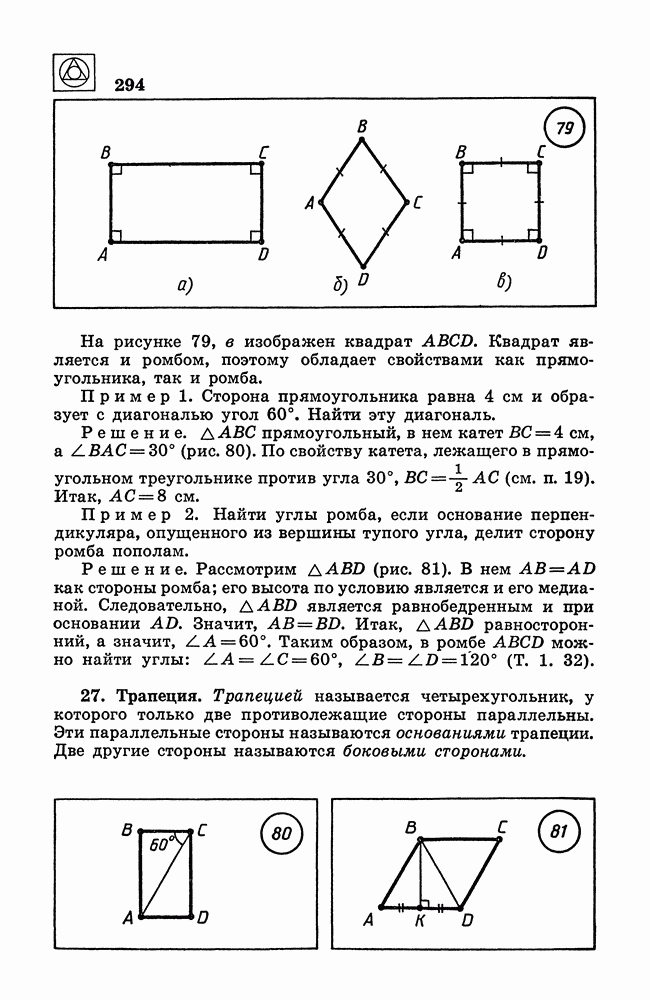
- 26. Прямоугольник. Ромб. Квадрат.
- 27. Трапеция.
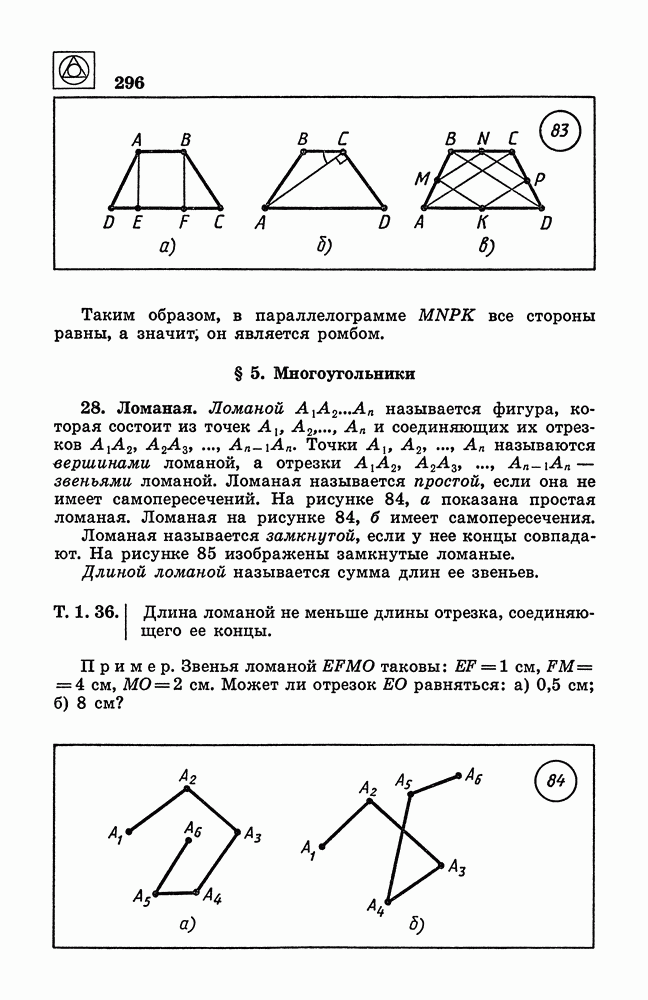
- § 5. Многоугольники
- 29. Выпуклые многоугольники.
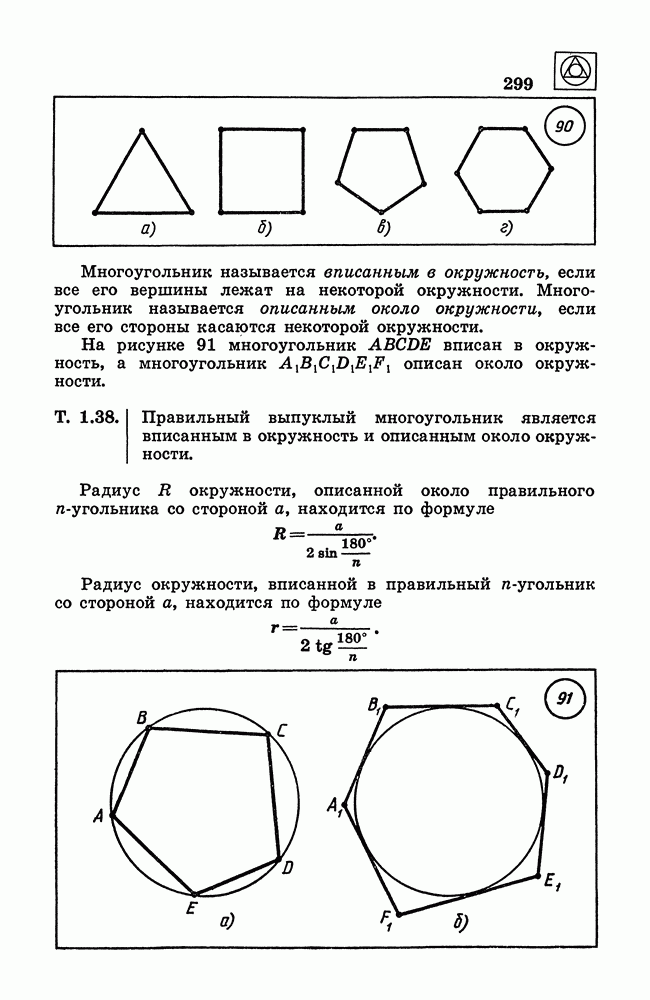
- 30. Правильные многоугольники.
- 31. Длина окружности.
- § 6. Решение треугольников
- 33. Соотношения между сторонами и углами в прямоугольном треугольнике.
- 34. Теорема косинусов. Теорема синусов.
- 35. Решение треугольников.
- § 7. Площади плоских фигур
- 37. Площади многоугольников.
- 38. Площади подобных фигур.
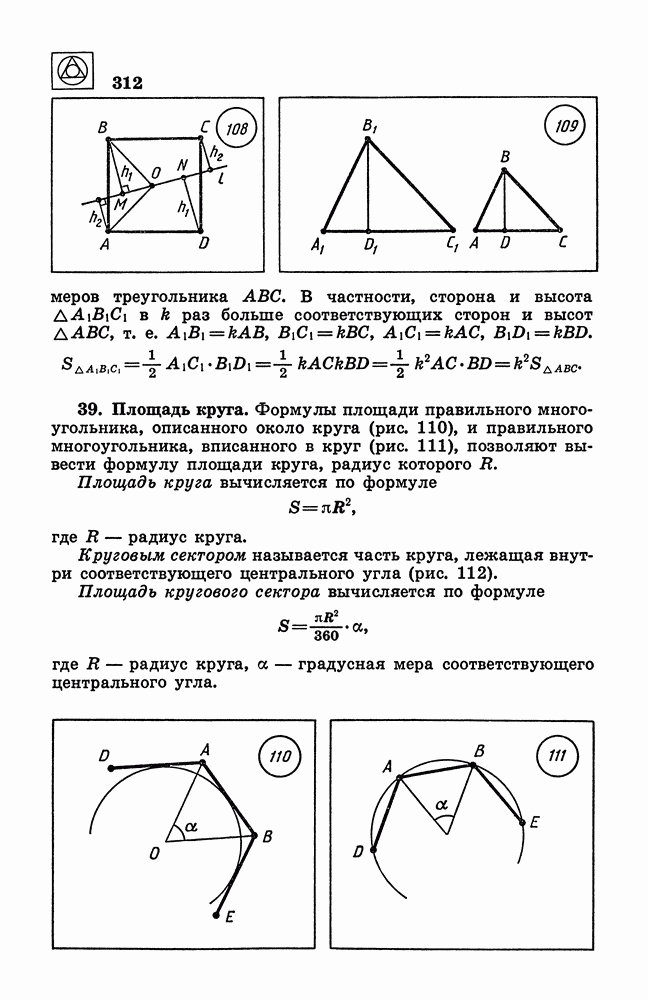
- 39. Площадь круга.
- ГЛАВА II. Прямые и плоскости в пространстве
- § 9. Параллельность прямых и плоскостей
- 42. Параллельность прямой и плоскости.
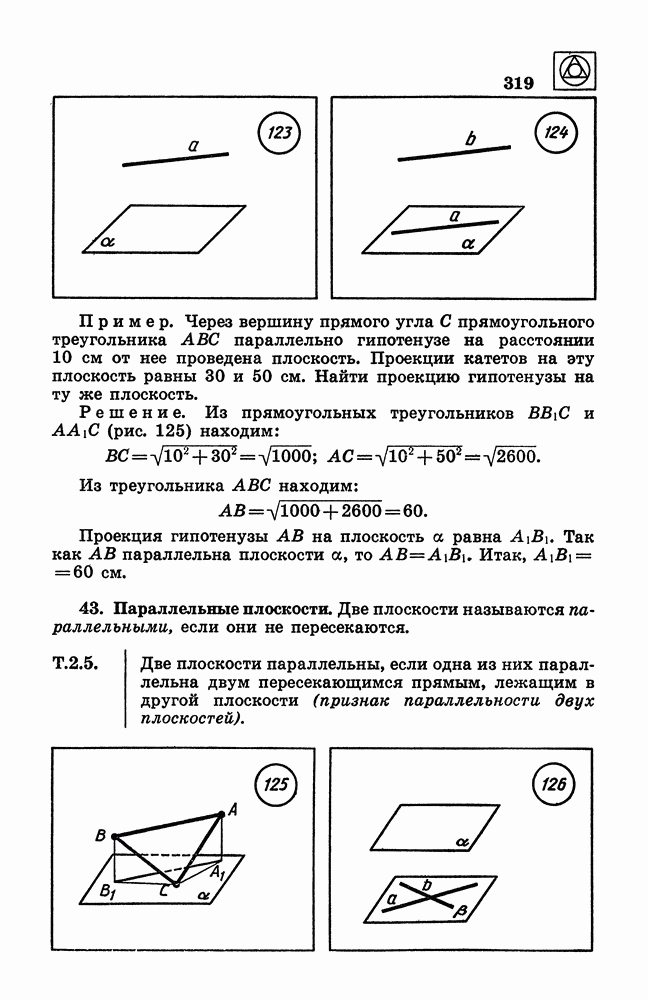
- 43. Параллельные плоскости.
- § 10. Перпендикулярность прямых и плоскостей
- 45. Перпендикуляр и наклонная к плоскости.
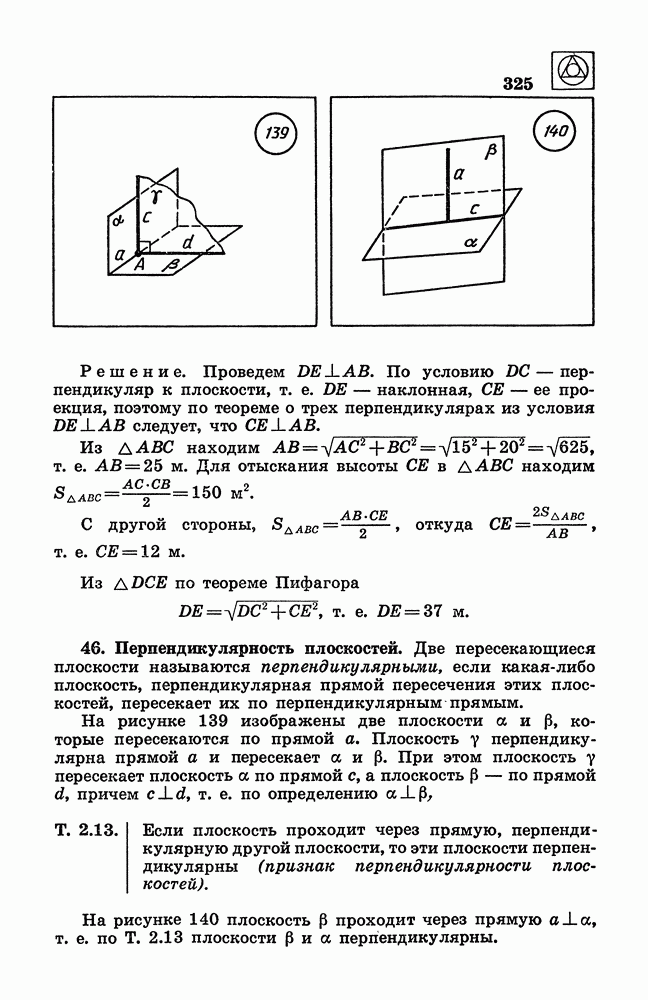
- 46. Перпендикулярность плоскостей.
- ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ
- § 11. Многогранники
- 48. Многогранные углы. Многогранники.
- 49. Призма. Параллелепипед. Куб.
- 50. Пираприда.
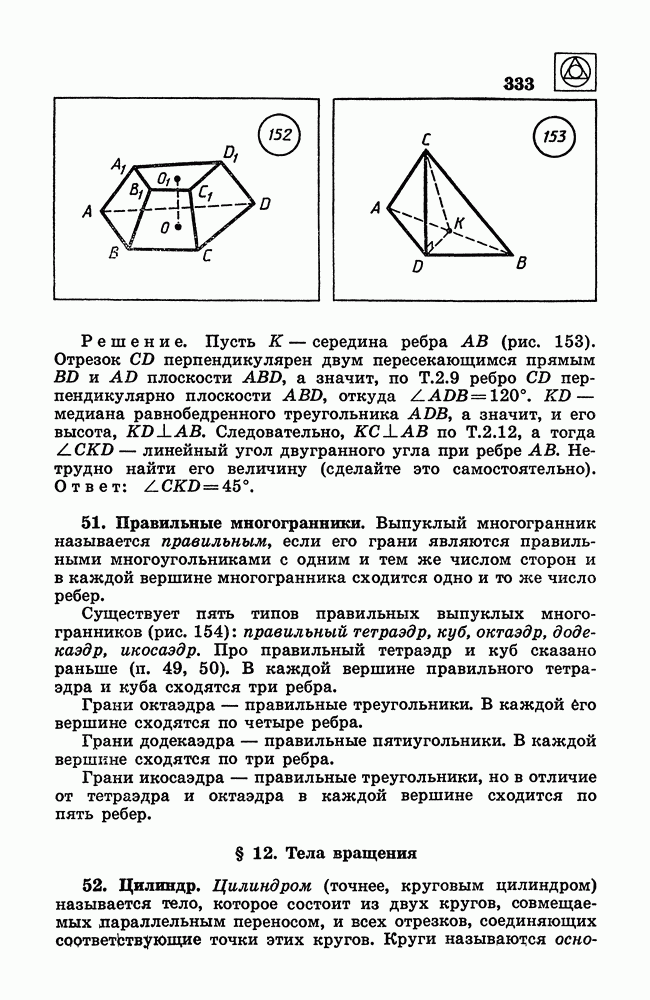
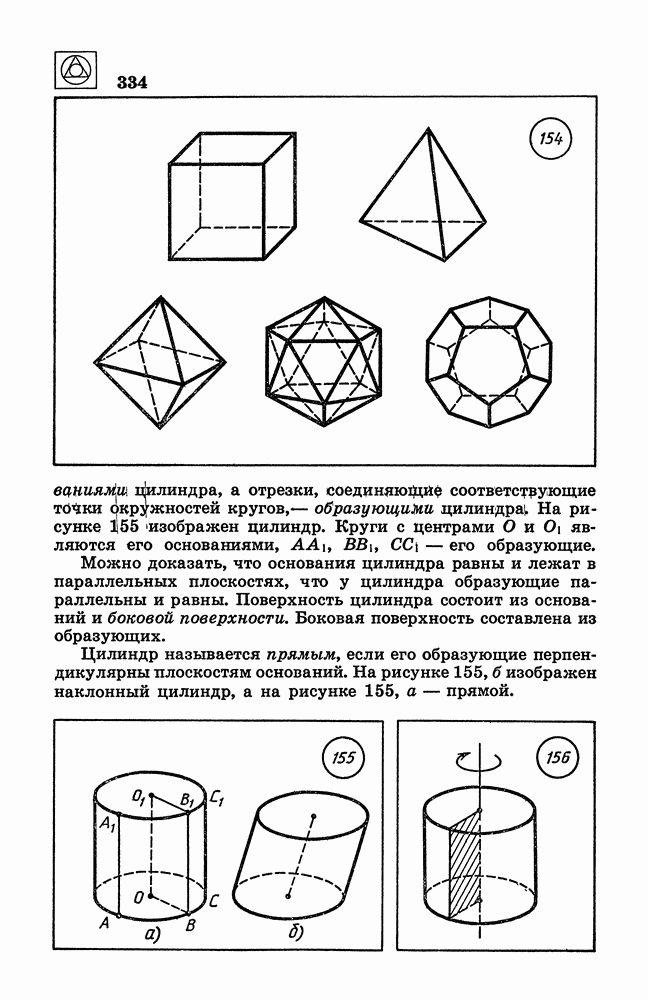
- 51. Правильные многогранники.
- § 12. Тела вращения
- 53. Конус.
- 54. Шар.
- § 13. Изображение пространственных фигур на плоскости
- 56. Ортогональное проектирование.
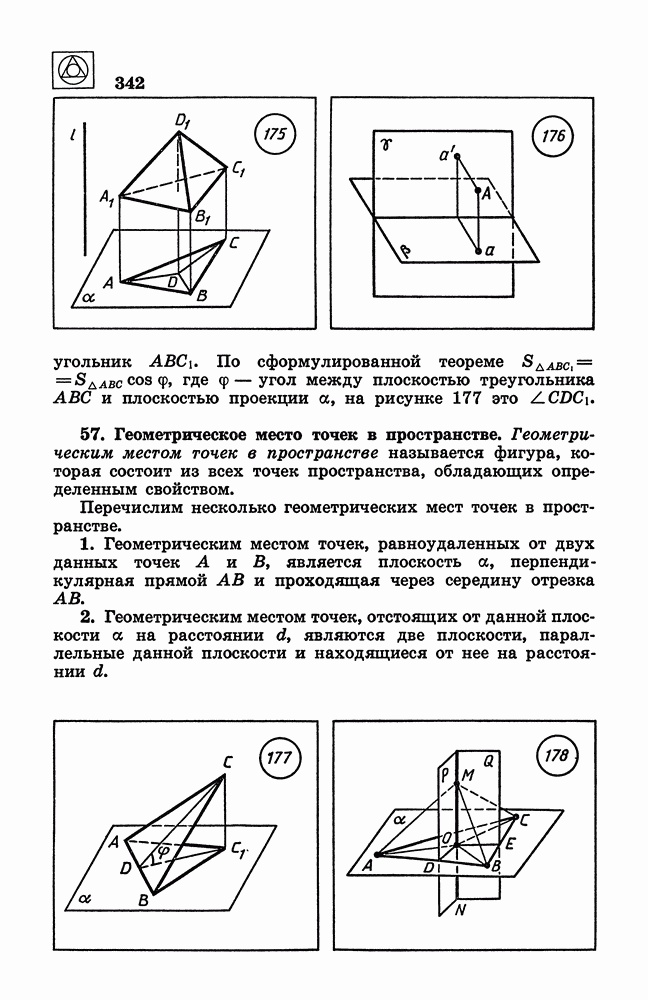
- 57. Геометрическое место точек в пространстве.
- § 14. Объемы тел
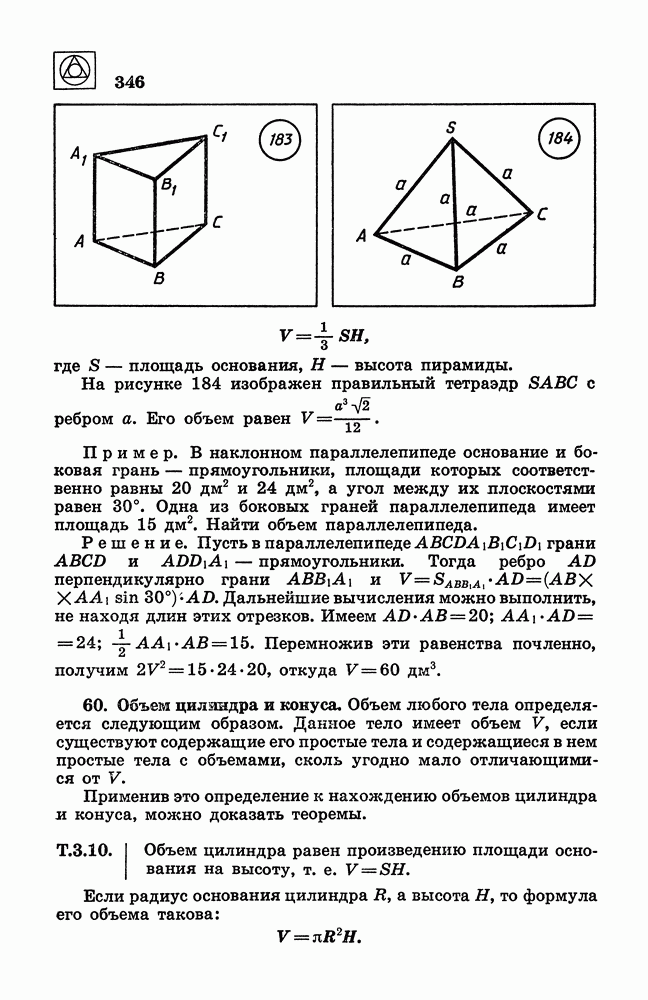
- 59. Объем параллелепипеда, призмы и пирамиды.
- 60. Объем цилиндра и конуса.
- 61. Общая формула объемов тел вращения.
- § 15. Площади поверхностей тел
- 63. Понятие площади поверхности.
- 64. Площади поверхностей тел вращения.
- ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ
- § 16. Координаты на плоскости и в пространстве
- 66. Координаты середины отрезка.
- § 17. Уравнения фигур на плоскости
- 68. Пересечение двух окружностей.
- 69. Уравнение прямой.
- 70. Пересечение прямой и окружности.
- § 18. Уравнения фигур в пространстве
- 72. Уравнение сферы.
- 73. Взаимное расположение сферы и плоскости.
- 74. Пересечение двух сфер.
- ГЛАВА V. РЕОБРАЗОВАНИЯ ФИГУР
- 76. Понятие движения.
- § 20. Подобие фигур
- 78. Подобные фигуры.
- ГЛАВА VI. ВЕКТОРЫ
- 80. Понятие вектора.
- 81. Координаты вектора.
- § 22. Операции над векторами
- 83. Умножение вектора на число. Коллинеарные векторы.
- 84. Скалярное произведение векторов.
- ПРИЛОЖЕНИЯ
- ГЕОМЕТРИЯ