| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Рекордеры
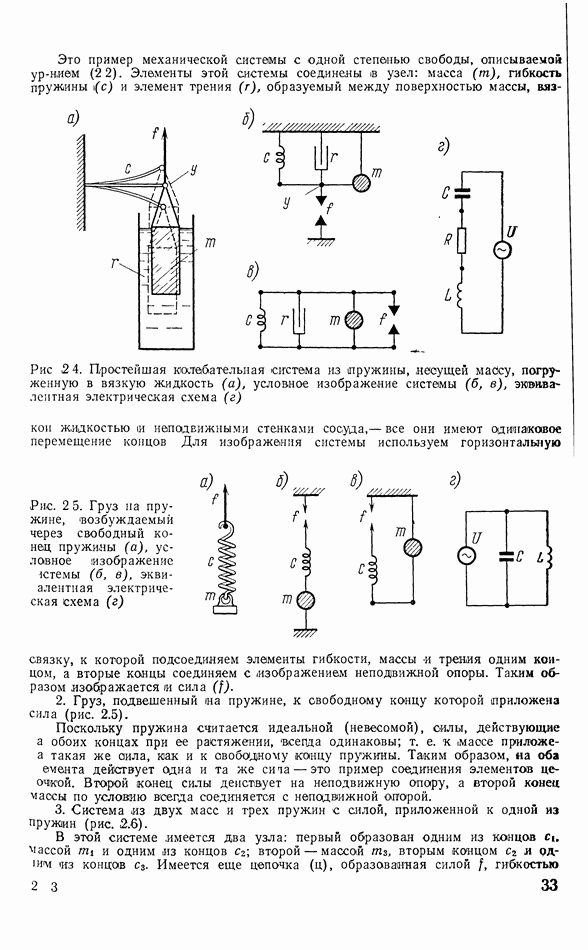
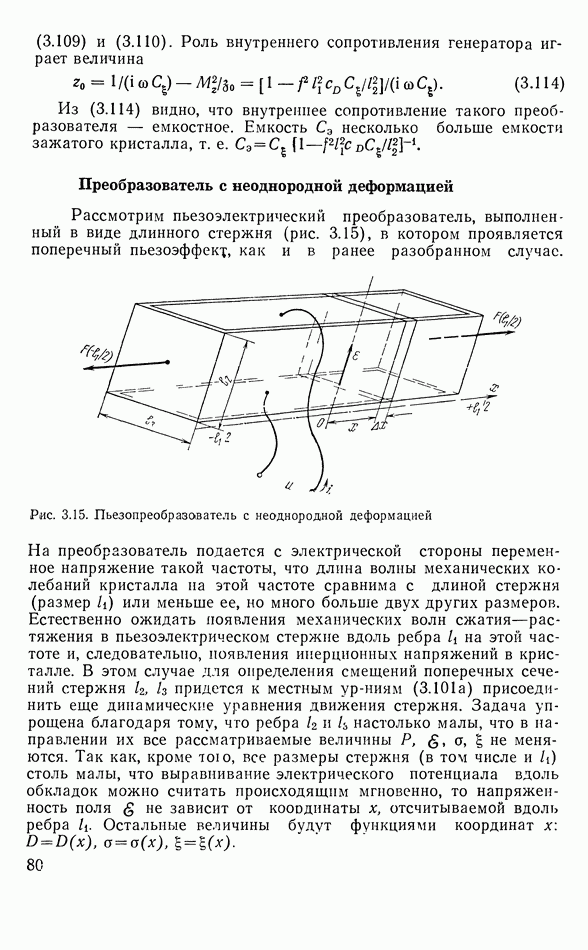
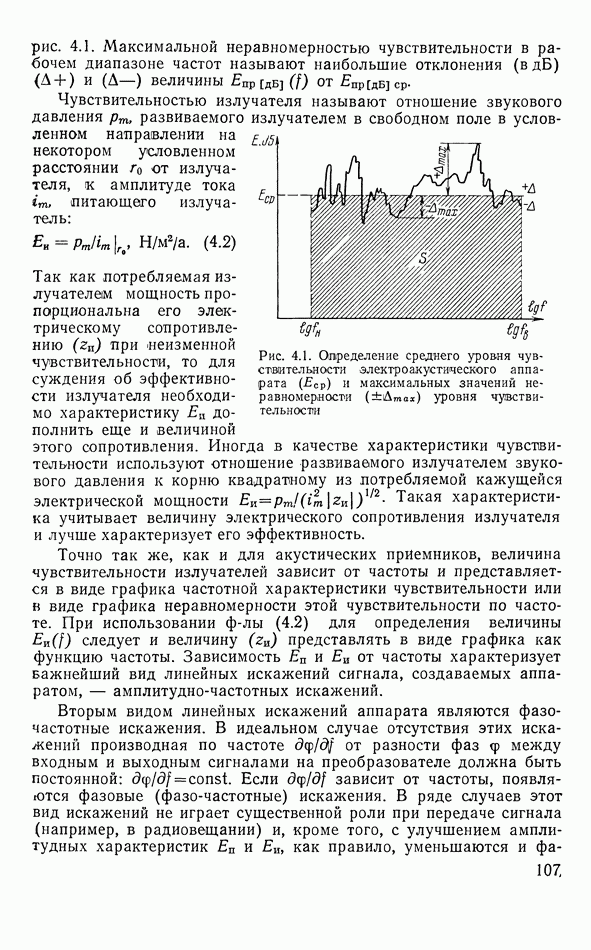
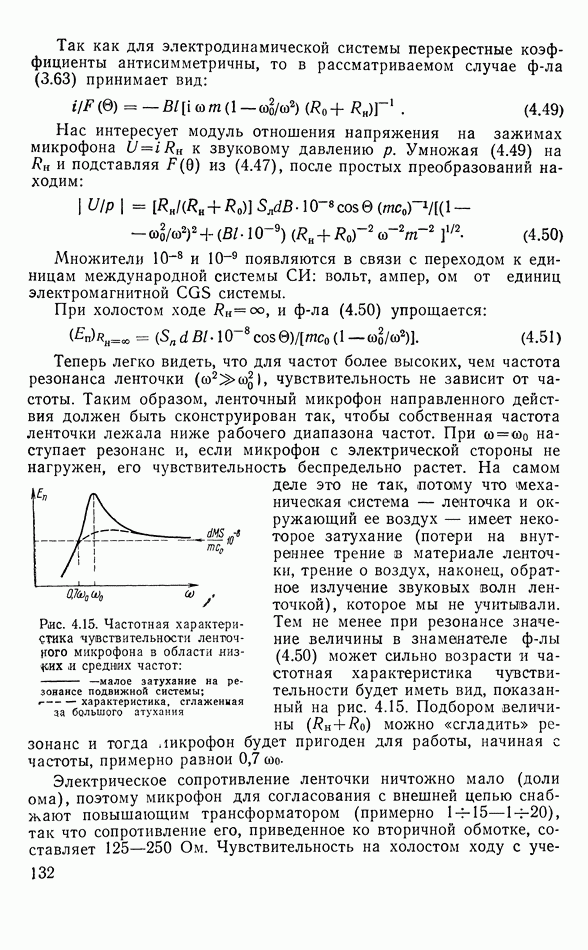
Рекордеры механической записи могут быть электромагнитные, электродинамические, пьезоэлектрические. Наиболее надежной конструкцией обладает электромагнитный рекордер (рис. 6.6). Ферромагнитный якорь из магнитомялкого материала может поворачиваться вокруг торсионной оси вместе с жестко скрепленным с ним резцом. Якорь помещен между парой  -образных наконечников сильного постоянного магнита и охвачен обмоткой, через которую пропускается ток записываемого сигнала.
-образных наконечников сильного постоянного магнита и охвачен обмоткой, через которую пропускается ток записываемого сигнала.
Характеристики рекордера могут быть получены на основании формул параграфа 3.7. В первую очередь интерес представляет амплитудно-частотная характеристика записи рекордера, т. е. отношение амплитуды скорости резца к амплитуде напряжения на
его зажимах. Используем выражение (3.63) для чувствительности преобразователя-двигателя, полагая, что  соответствует напряжению
соответствует напряжению  подводимому к рекордеру,
подводимому к рекордеру,  скорости и колебаний якоря с резцом! Тогда в выражении
скорости и колебаний якоря с резцом! Тогда в выражении  электрическое сопротивление обмотки заторможенного рекордера, которое состоит из ее индуктивного и активного сопротивлений:
электрическое сопротивление обмотки заторможенного рекордера, которое состоит из ее индуктивного и активного сопротивлений:  механическое сопротивление подвижной части рекордера при отсутствии тока в обмотке; оно складывается из инерционного сопротивления массы якоря, упругого сопротивления торсионного подвеса на оси и активного механического сопротивления потерь:
механическое сопротивление подвижной части рекордера при отсутствии тока в обмотке; оно складывается из инерционного сопротивления массы якоря, упругого сопротивления торсионного подвеса на оси и активного механического сопротивления потерь:  Активное сопротивление
Активное сопротивление  как показано ниже, должно быть большим, и с этой целью между наконечниками и якорем помещают специальную резину с большим коэффициентом потерь или пропитанные вязким маслом слои тонкой бумаги.
как показано ниже, должно быть большим, и с этой целью между наконечниками и якорем помещают специальную резину с большим коэффициентом потерь или пропитанные вязким маслом слои тонкой бумаги.
 механическое сопротивление нагрузки сопротивление звуконосителя (лакового слоя) резанию, которое можно принять чисто активным
механическое сопротивление нагрузки сопротивление звуконосителя (лакового слоя) резанию, которое можно принять чисто активным 

Рис. 6.6. Электромагнитный рекордер: 1 - П-образные наконечники магнита; 2 — якорь с резцом, 3 — упругие торсионные полуоси; 4 — обмотка; 5 — демпфирующие прокладки
М - коэффициент электромеханической связи, который определяется в соответствии с ф-лой (3.76). Следует отметить, что переменный поток  рассматриваемом рекордере разделен на две части, а постоянный
рассматриваемом рекордере разделен на две части, а постоянный  протекает только через концы якоря, находящиеся между противоположными торцами двух
протекает только через концы якоря, находящиеся между противоположными торцами двух  -образных наконечников. В этом случае под сечением 5 в
-образных наконечников. В этом случае под сечением 5 в  следует понимать сечение двух торцов
следует понимать сечение двух торцов  -образного наконечника. Коэффициент электромеханической связи
-образного наконечника. Коэффициент электромеханической связи  можно выразить через индукцию В в зазоре, создаваемую постоянным магнитом,
можно выразить через индукцию В в зазоре, создаваемую постоянным магнитом,  тогда для модуля искомой чувствительности можно написать:
тогда для модуля искомой чувствительности можно написать:

Затухание механической системы, как говорилась выше, должно быть большим, так как иначе - слагаемое  в квадратных скобках в знаменателе (6.3) будет вызывать резко выражений минимум при
в квадратных скобках в знаменателе (6.3) будет вызывать резко выражений минимум при  и характеристику чувствительности не удастся сделать гладкой функцией частоты. Таким образом, величина
и характеристику чувствительности не удастся сделать гладкой функцией частоты. Таким образом, величина  должна быть не менее нескольких единиц. Индуктивность обмотки может быть найдена по числу ее витков
должна быть не менее нескольких единиц. Индуктивность обмотки может быть найдена по числу ее витков  и магнитному сопротивлению цепи
и магнитному сопротивлению цепи  где V — приведенная длина железного магнитопровода полюсных наконечников и магнита, I — длина воздушного зазора, в см.
где V — приведенная длина железного магнитопровода полюсных наконечников и магнита, I — длина воздушного зазора, в см.
На средних частотах индуктивное сопротивление  превалирует над омическим
превалирует над омическим  сопротивлением катушки. Это значит, что на резонансе, при
сопротивлением катушки. Это значит, что на резонансе, при  произведение
произведение  по модулю не меньше, чем
по модулю не меньше, чем  Ом. Последнее слагаемое в знаменателе
Ом. Последнее слагаемое в знаменателе  выраженное также через число витков катушки, длину зазора и магнитопровода, имеет вид:
выраженное также через число витков катушки, длину зазора и магнитопровода, имеет вид:  Ом. Отношение этого сопротивления к подсчитанному выше модулю реактивного сопротивления составит
Ом. Отношение этого сопротивления к подсчитанному выше модулю реактивного сопротивления составит 
Если рабочий диапазон частот рекордера лежит в пределах 50—10000 Гц, то резонансную частоту механической системы  дует выбирать около среднегеометрической частоты этого диапазона:
дует выбирать около среднегеометрической частоты этого диапазона:  При индукции в зазоре около
При индукции в зазоре около  Гаусс эквивалентной массе подвижной системы
Гаусс эквивалентной массе подвижной системы  сечении зазора
сечении зазора  длине зазора
длине зазора  и пренебержимо малой величине V интересующее нас отношение составит
и пренебержимо малой величине V интересующее нас отношение составит  Это означает, что при достаточно большом затухании даже на резонансе подвижной системы рекордера величиной
Это означает, что при достаточно большом затухании даже на резонансе подвижной системы рекордера величиной  в знаменателе (6.3) можно пренебречь при приближенном рассмотрении частотной характеристики чувствительности рекордера. Тогда (6.3) упрощается и переходя к модулю
в знаменателе (6.3) можно пренебречь при приближенном рассмотрении частотной характеристики чувствительности рекордера. Тогда (6.3) упрощается и переходя к модулю  получим:
получим:

Представим характеристику (6.4) рекордера в следующем виде:

Первое слагаемое правой части  -постоянная величина, определяющая абсолютную величину чувствительности, и пока его рассматривать не будем. Второе слагаемое в области
-постоянная величина, определяющая абсолютную величину чувствительности, и пока его рассматривать не будем. Второе слагаемое в области  также постоянно и близко к нулю. В области
также постоянно и близко к нулю. В области  оно ассимптотичеоки приближается к
оно ассимптотичеоки приближается к 
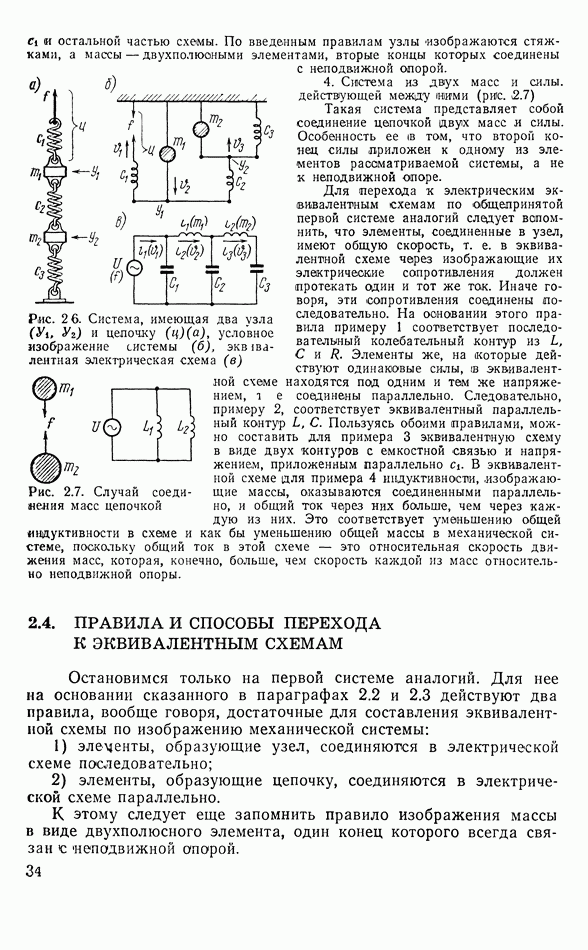
На графике рис. 6.7а пунктиром нанесены в двойном логарифмическом масштабе зависимости —  в области
в области  для
для
различных значений  Эти зависимости представляют собой прямые, имеющие наклон
Эти зависимости представляют собой прямые, имеющие наклон  на октаву. В точке
на октаву. В точке  ординаты этих прямых равны
ординаты этих прямых равны  Для некоторого данного значения
Для некоторого данного значения  (например, прямая IV рис. 6.7а), кривая -
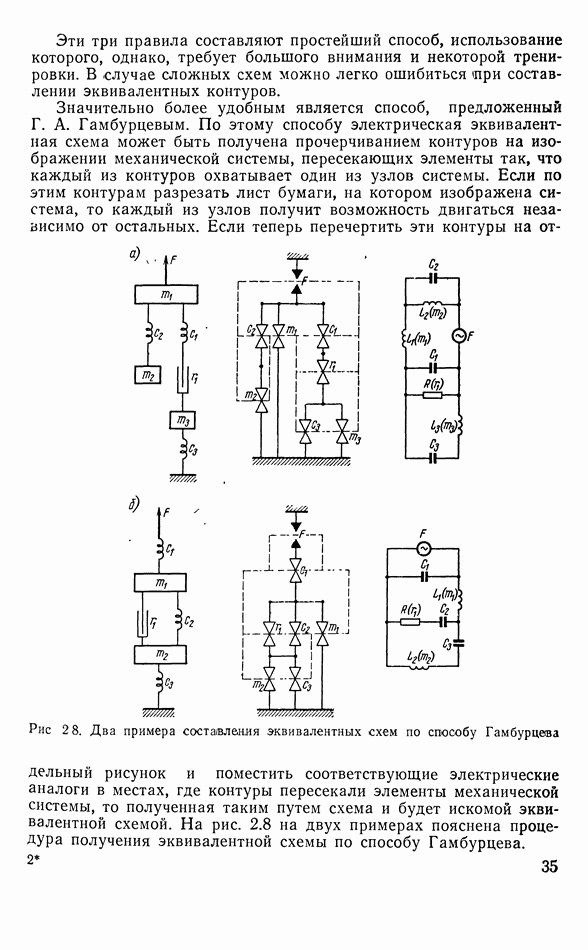
(например, прямая IV рис. 6.7а), кривая -  пройдет как показано сплошной линией II. На графике рис. 6.76 нанесены пунктиром прямые
пройдет как показано сплошной линией II. На графике рис. 6.76 нанесены пунктиром прямые  представляющие собой асимптоты третьего слагаемого правой части (6.5), т. е. величины
представляющие собой асимптоты третьего слагаемого правой части (6.5), т. е. величины  В точке
В точке  третье слагаемое становится равным —
третье слагаемое становится равным —  Сплошными линиями нанесены кривые —
Сплошными линиями нанесены кривые —  для двух разных значений
для двух разных значений  кривая I рис. 676 — для
кривая I рис. 676 — для  и кривая III рис. 6.76 для
и кривая III рис. 6.76 для 
Для получения частотной характеристики  достаточно сложить ординаты одной из кривых рис.
достаточно сложить ординаты одной из кривых рис.
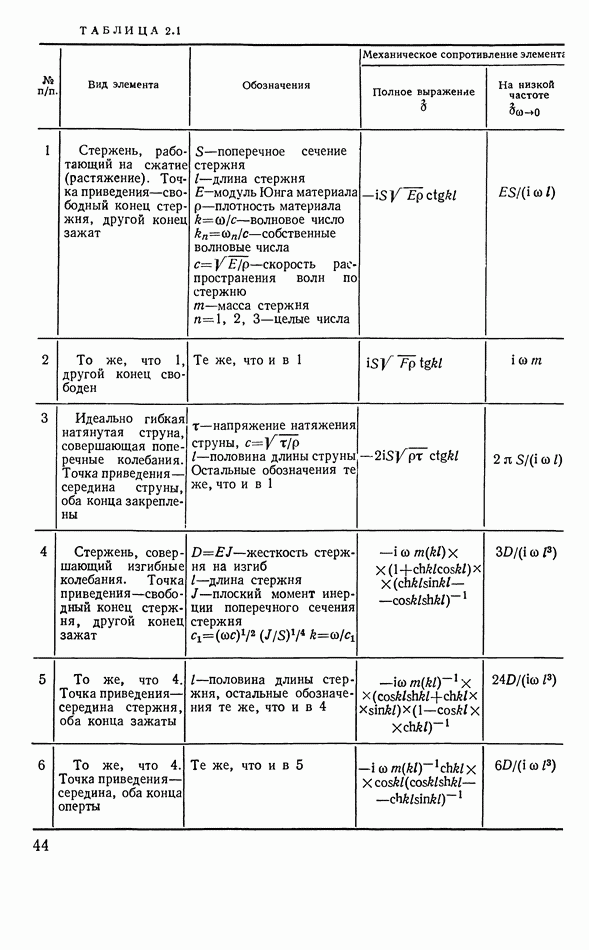
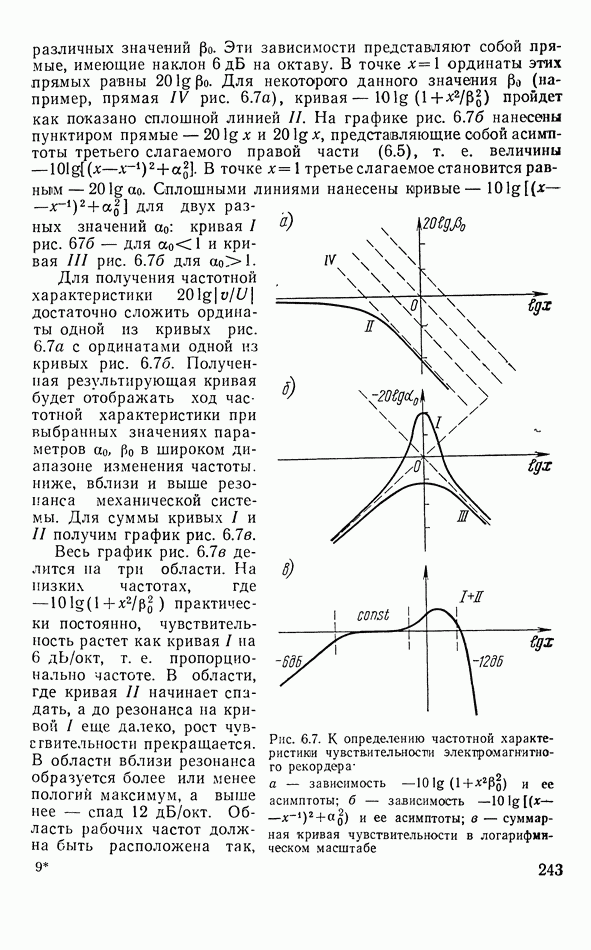
6.7а с ординатами одной из кривых рис. 6.76. Полученная результирующая кривая будет отображать ход частотной характеристики при выбранных значениях параметров  в широком диапазоне изменения частоты, ниже, вблизи и выше резонанса механической системы. Для суммы кривых I и II получим график рис. 6.7в.
в широком диапазоне изменения частоты, ниже, вблизи и выше резонанса механической системы. Для суммы кривых I и II получим график рис. 6.7в.
Весь график рис. 6.7в делится на три области. На низких частотах, где —  практически постоянно, чувствительность растет как кривая I на
практически постоянно, чувствительность растет как кривая I на  т. е. пропорционально частоте. В области, где кривая II начинает спадать, а до резонанса на кривой
т. е. пропорционально частоте. В области, где кривая II начинает спадать, а до резонанса на кривой  еще далеко, рост чувствительности прекращается.
еще далеко, рост чувствительности прекращается.
В области вблизи резонанса образуется более или менее пологий максимум, а выше нее — спад  Область рабочих частот должна быть расположена так,
Область рабочих частот должна быть расположена так,

Рис. 6.7. К определению частотной характеристики чувствительности электромагнитного рекордера а — зависимость  и ее асимптоты; б - зависимость
и ее асимптоты; б - зависимость  и ее асимптоты; в — суммарная кривая чувствительности в логарифмическом масштабе
и ее асимптоты; в — суммарная кривая чувствительности в логарифмическом масштабе
чтобы ход полученной характеристики был близок к принятой стандартной характеристике записи, т. е. чтобы спад  и подъем
и подъем  кривой III наблюдались соответственно на нижней (сон) и высшей
кривой III наблюдались соответственно на нижней (сон) и высшей  частотах диапазона. Это означает, что точка
частотах диапазона. Это означает, что точка  должна располагаться около
должна располагаться около  Затухание
Затухание  и постоянная времени электрической цепи
и постоянная времени электрической цепи  найдутся подбором соответствующих кривых из семейств рис. 6.7а и 6.7б
найдутся подбором соответствующих кривых из семейств рис. 6.7а и 6.7б
Рассмотрим теперь первое слагаемое выражения (6.5). Оно показывает, что чем выше  т. е. чем более высокие частоты нужно записывать, тем меньше чувствительность рекордера. Чем более низкие частоты хотим записывать, тем больше должна быть постоянная времени
т. е. чем более высокие частоты нужно записывать, тем меньше чувствительность рекордера. Чем более низкие частоты хотим записывать, тем больше должна быть постоянная времени  и тем больше будет чувствительность. Путь к увеличению чувствительности состоит, прежде всего, в уменьшении массы подвижной части. Кроме этого возможно, конечно, применение электрической коррекции частотной характеристики записи в предварительном усилит еле записи.
и тем больше будет чувствительность. Путь к увеличению чувствительности состоит, прежде всего, в уменьшении массы подвижной части. Кроме этого возможно, конечно, применение электрической коррекции частотной характеристики записи в предварительном усилит еле записи.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. Краткие сведения по физиологической акустике
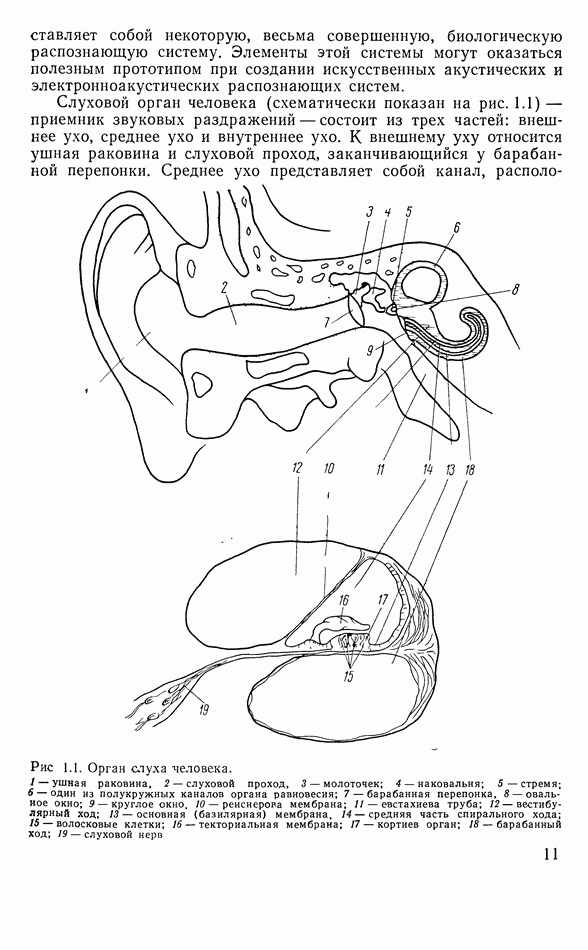
- 1.1. УСТРОЙСТВО СЛУХОВОГО ОРГАНА ЧЕЛОВЕКА
- 1.2. МЕХАНИЗМ ВОЗБУЖДЕНИЯ СЛУХОВОГО НЕРВА
- 1.3. ТЕОРИЯ СЛУХА
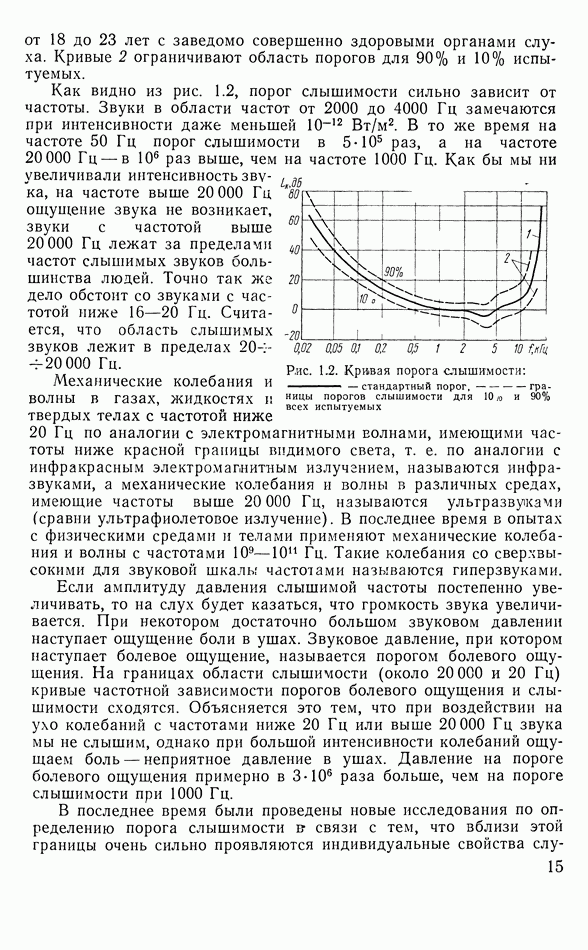
- 1.4. ПОРОГ СЛЫШИМОСТИ
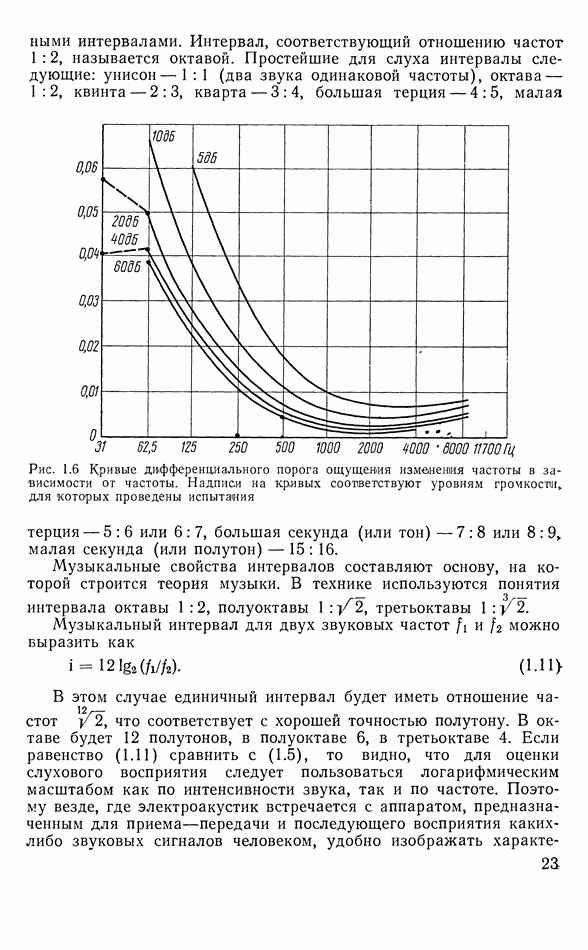
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЙ ПОРОГ ВОСПРИЯТИЯ ИНТЕНСИВНОСТИ ЗВУКА
- 1.6. ЛОГАРИФМИЧЕСКИЕ УРОВНИ. ШКАЛА ДЕЦИБЕЛ
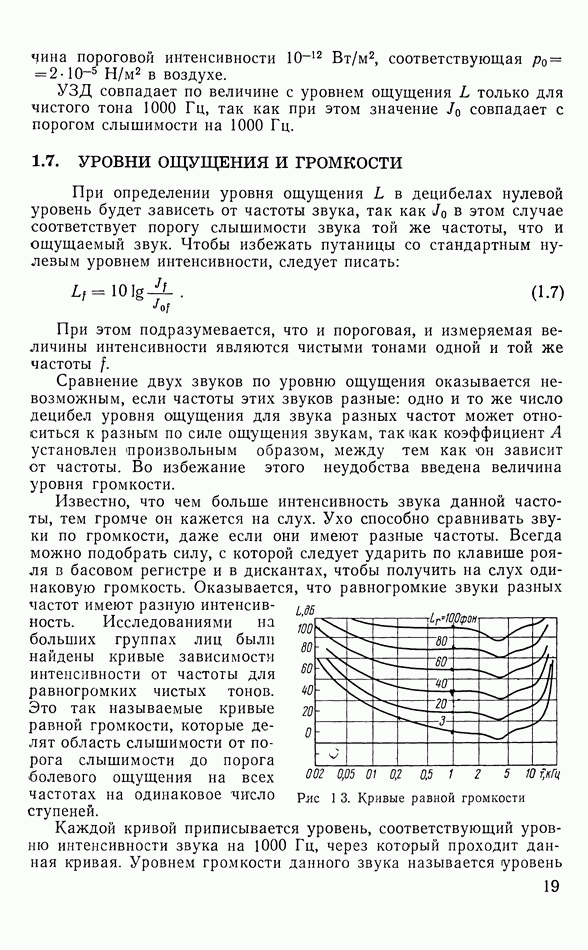
- 1.7. УРОВНИ ОЩУЩЕНИЯ И ГРОМКОСТИ
- 1.8. ГРОМКОСТЬ ЧИСТЫХ ТОНОВ
- 1.9. КРИТИЧЕСКИЕ ПОЛОСЫ СЛУХА
- 1.10. УРОВЕНЬ ГРОМКОСТИ СЛОЖНЫХ ЗВУКОВ
- 1.11. ВОСПРИЯТИЕ ВЫСОТЫ ТОНА. ШКАЛА ЧАСТОТ
- 1.12. МАСКИРОВКА ЗВУКА
- 1.13. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- 1.14. ВОСПРИЯТИЕ ОКРАСКИ (ТЕМБРА) ЗВУКА
- Глава 2. Электромеханические и электроакустические аналогии
- 2.1. ПРИНЦИП ЭЛЕКТРОМЕХАНИЧЕСКИХ АНАЛОГИЙ
- 2.2. МЕХАНИЧЕСКИЕ ЭЛЕМЕНТЫ И МЕХАНИЧЕСКИЕ СИСТЕМЫ
- 2.3. ПРИМЕРЫ ИЗОБРАЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ И ИХ ЭКВИВАЛЕНТНЫХ СХЕМ
- 2.4. ПРАВИЛА И СПОСОБЫ ПЕРЕХОДА К ЭКВИВАЛЕНТНЫМ СХЕМАМ
- 2.5. ТРАНСФОРМАЦИЯ СИЛ И СКОРОСТЕЙ. ЭЛЕКТРИЧЕСКИЙ АНАЛОГ-ТРАНСФОРМАТОР
- 2.6. ЭЛЕКТРОАКУСТИЧЕСКИЕ АНАЛОГИИ
- 2.7. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИИ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
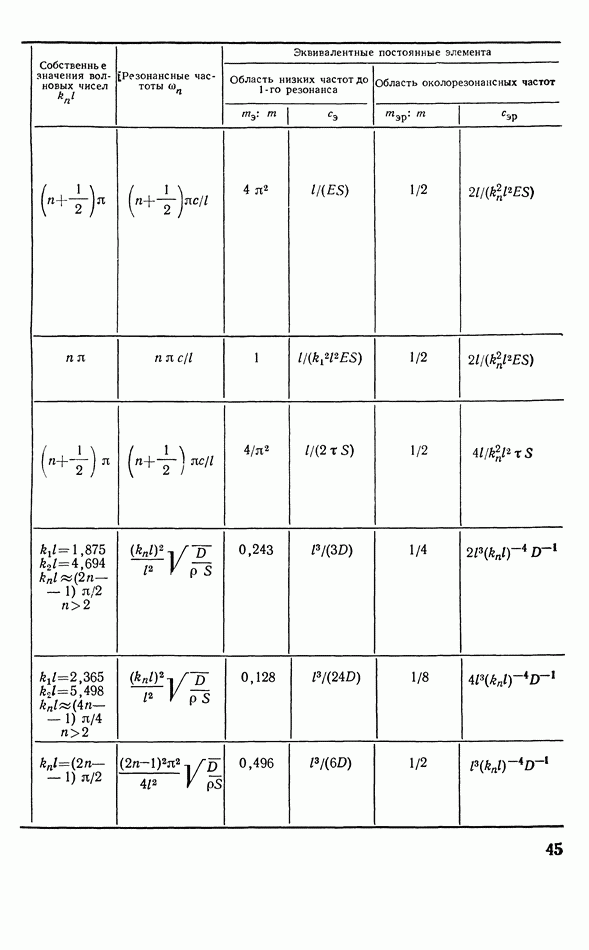
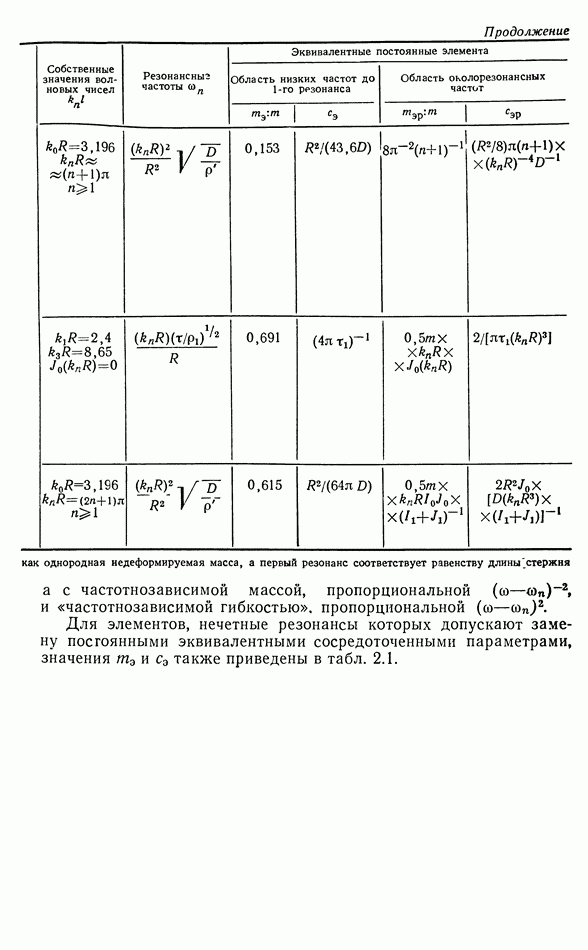
- 2.8. ЭКВИВАЛЕНТНЫЕ СОСРЕДОТОЧЕННЫЕ ПАРАМЕТРЫ МЕХАНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ
- Глава 3. Электромеханические преобразователи
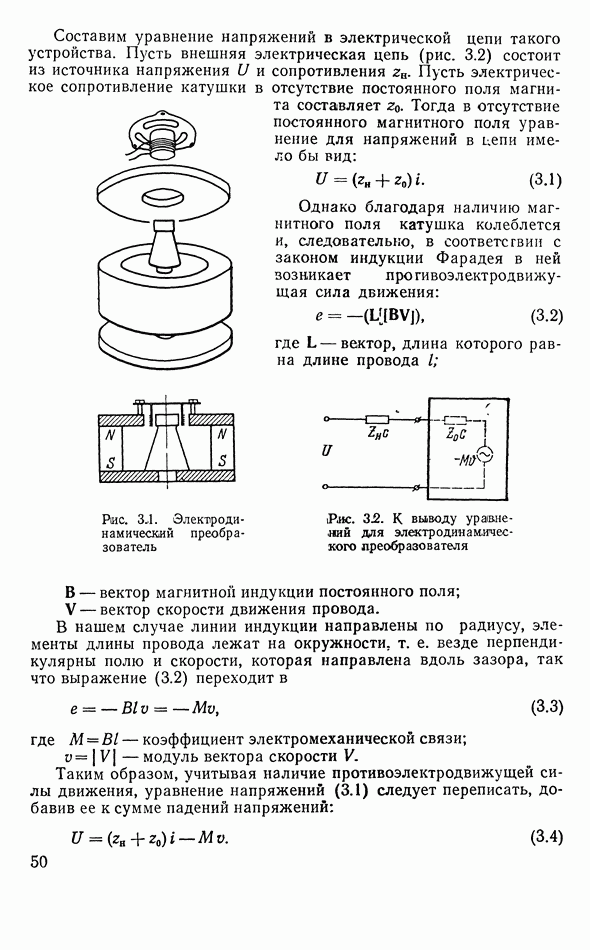
- 3.2. ДВА ОСНОВНЫХ ТИПА ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
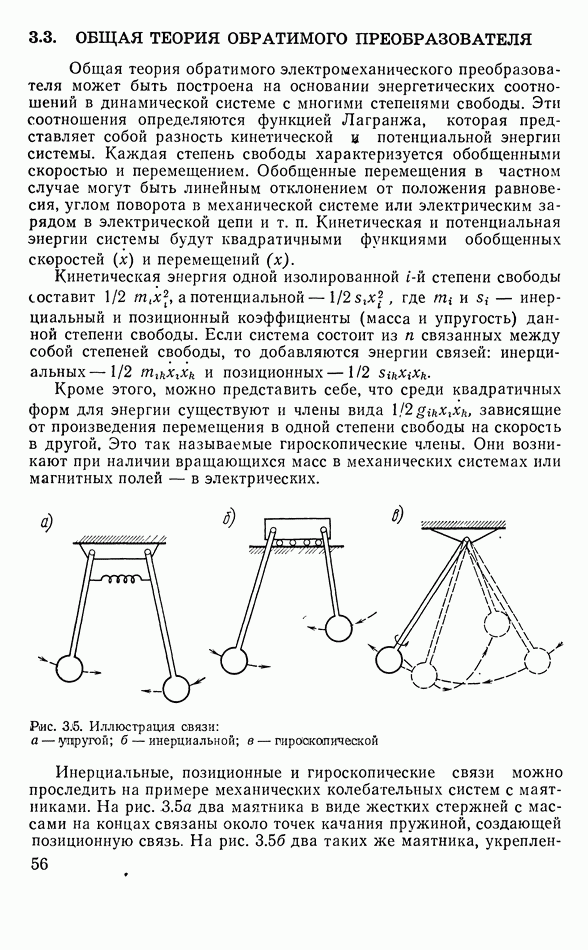
- 3.3. ОБЩАЯ ТЕОРИЯ ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.4. ВТОРИЧНЫЕ ПАРАМЕТРЫ ПРЕОБРАЗОВАТЕЛЯ
- 3.5. ПРАВИЛО ЗНАКОВ
- 3.6. ВХОДНОЕ СОПРОТИВЛЕНИЕ СИСТЕМЫ В ОБЩЕМ СЛУЧАЕ
- 3.7. ЧУВСТВИТЕЛЬНОСТЬ ПРЕОБРАЗОВАТЕЛЯ
- 3.8. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ПРЕОБРАЗОВАТЕЛЯ
- 3.9. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗОВАТЕЛИ
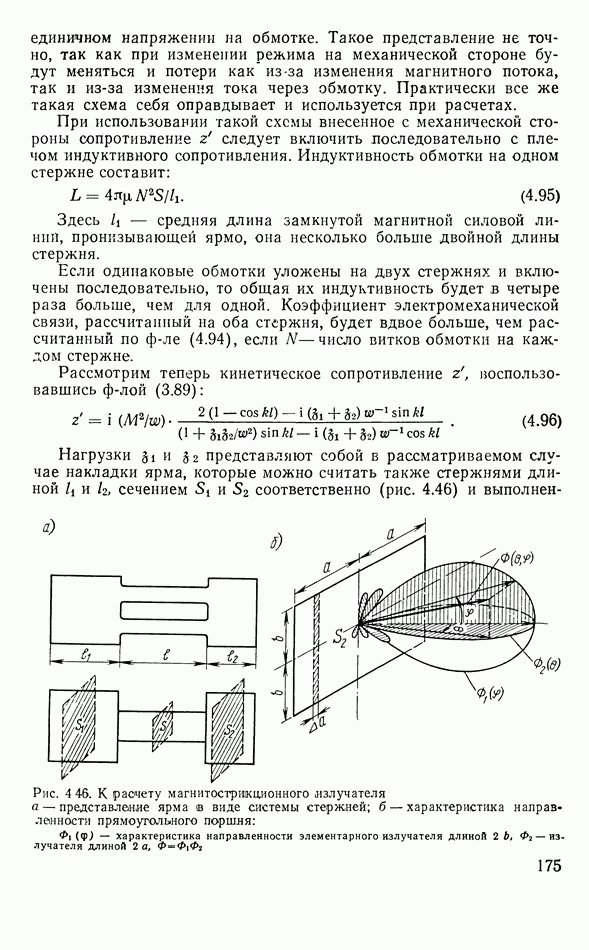
- 3.10. МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.11. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Преобразователь с однородной деформацией
- Преобразователь с неоднородной деформацией
- Местные уравнения пьезопреобразователя в тензорной форме
- Свойства основных пьезоэлектрических кристаллов
- Выбор среза кристалла при изготовлении пьезоэлементов
- Искусственные пьезокерамические материалы
- 3.12. ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 4. Электроакустическая аппаратура
- 4.1. КЛАССИФИКАЦИЯ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- 4.2. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 4.3. АНТЕННЫ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- Связь между чувствительностью приемной и излучающей антенн
- Сопротивление излучения антенны
- Сложные антенны
- Распределенные антенны
- Антенна бегущей волны
- Антенна из направленных элементов
- Оптимизация характеристики направленности антенны
- Рупорная антенна
- 4.4. ТРЕБОВАНИЯ К ЭЛЕКТРОАКУСТИЧЕСКОЙ АППАРАТУРЕ РАДИОВЕЩАНИЯ И ТЕЛЕВИДЕНИЯ
- 4.5. ЛЕНТОЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Ненаправленный микрофон-приемник давления
- Микрофон с кардиоидной характеристикой направленности
- Микрофон с регулируемой характеристикой направленности
- 4.6. КАТУШЕЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Однонаправленный микрофон
- Биградиентный микрофон
- Сверхнаправленный микрофон
- 4.7. СОГЛАСОВАНИЕ ЭЛЕКТРИЧЕСКОЙ СТОРОНЫ ЭЛЕКТРОДИНАМИЧЕСКОГО МИКРОФОНА СО ВХОДОМ МИКРОФОННОГО УСИЛИТЕЛЯ
- 4.8. КОНДЕНСАТОРНЫЕ МИКРОФОНЫ
- Об отрицательной упругости электрического поля поляризации в микрофоне
- Предельная чувствительность микрофона
- Влияние емкости входа предварительного каскада
- Микрофон направленного действия
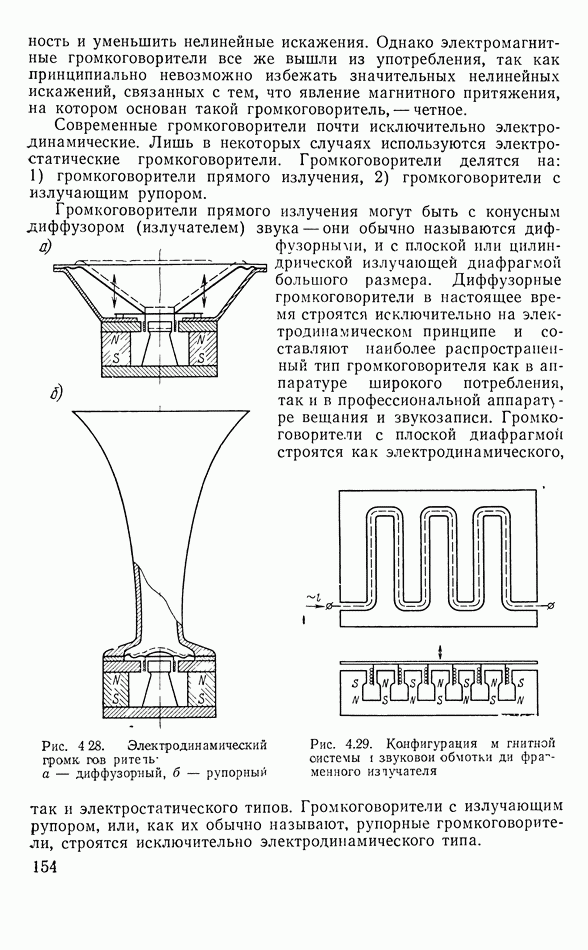
- 4.9. ОБЩИЕ СВЕДЕНИЯ О ГРОМКОГОВОРИТЕЛЯХ
- 4.10. ДИФФУЗОРНЫЕ ГРОМКОГОВОРИТЕЛИ
- Частотная характеристика чувствительности
- Влияние способа установки громкоговорителя на излучение в области низких частот
- Работа громкоговорителя в области высоких частот
- Комбинированные громкоговорители
- Нелинейные искажения в громкоговорителе
- 4.11. РУПОРНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- Влияние конечной длины рупора
- Широкогорлый громкоговоритель
- Громкоговорящие агрегаты
- 4.12. ЭЛЕКТРОСТАТИЧЕСКИЙ ГРОМКОГОВОРИТЕЛЬ
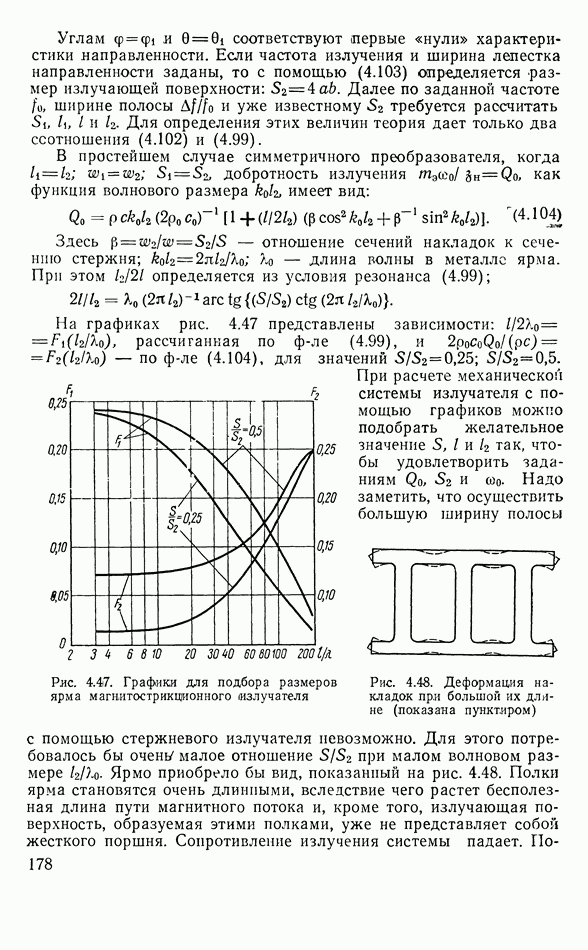
- 4.13. МАГНИТОСТРИКЦИОННЫЕ ИЗЛУЧАТЕЛИ
- Стержневой излучатель
- Кольцевой излучатель
- Круговая диаграмма преобразователя
- Коэффициент полезного действия излучателя
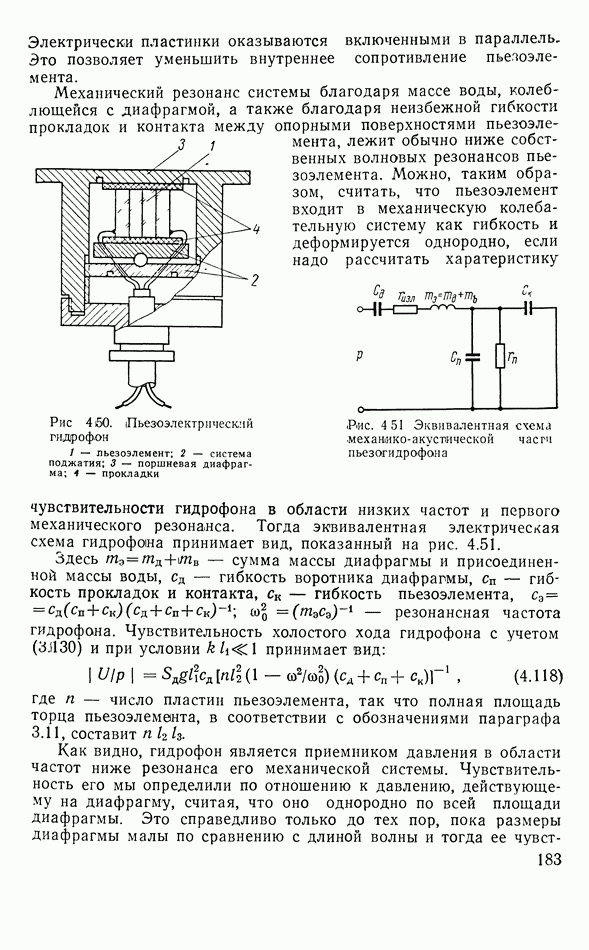
- 4.14. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- Линия задержки
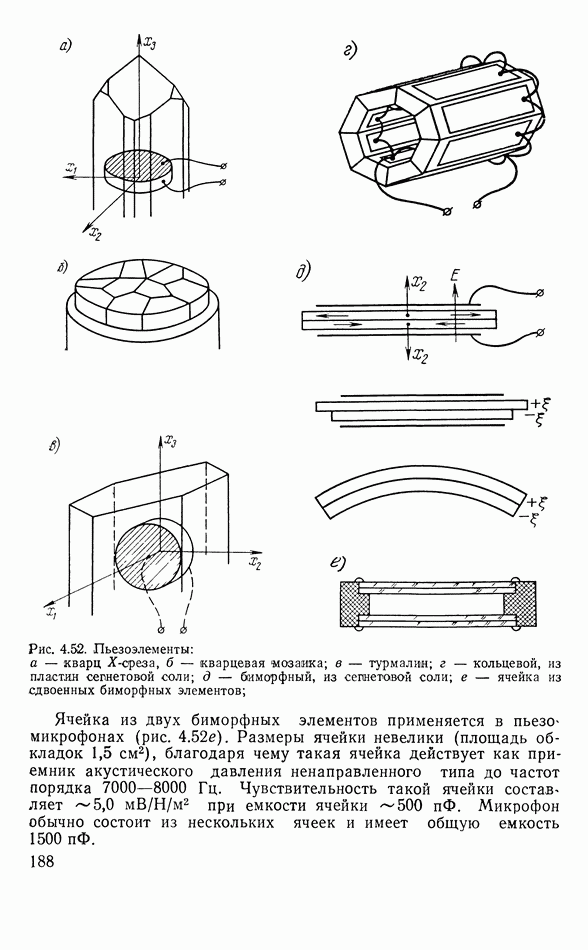
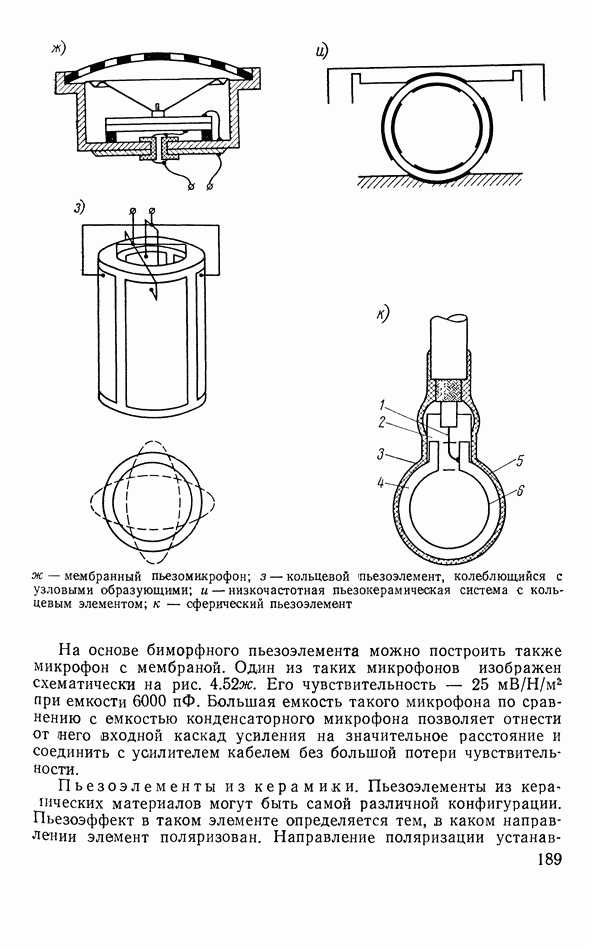
- Другие типы пьезоэлектрических элементов электроакустических аппаратов
- Согласование пьезоэлемента с электрической частью системы
- 4.15. ЭЛЕКТРОДИНАМИЧЕСКИЙ ГЕОФОН
- Частотная характеристика чувствительности
- Максимальная чувствительность
- 4.16. СЕЙСМОМЕТРИЧЕСКИЙ ПРИЕМНИК СМЕЩЕНИЯ
- 4.17. ОПТИМИЗАЦИЯ КОНСТРУКТИВНЫХ РАЗМЕРОВ ЭЛЕКТРОАКУСТИЧЕСКОГО АППАРАТА
- Глава 5. Необратимые преобразователи
- 5.2. ПНЕВМОАКУСТИЧЕСКИЕ ИЗЛУЧАТЕЛИ
- Модуляция потока воздуха
- Пневматическая сирена
- Модулятор с возвратно-поступательным движением
- 5.3. ГИДРАВЛИЧЕСКАЯ СИРЕНА
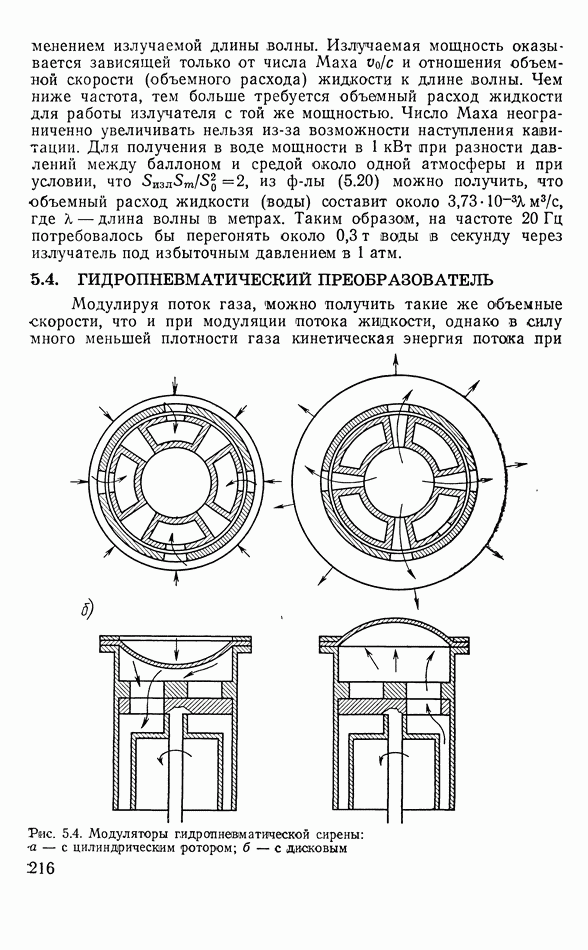
- 5.4. ГИДРОПНЕВМАТИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ
- 5.5. ПАРАМЕТРИЧЕСКИЕ ПРИЕМНИКИ
- 5.6. ПЬЕЗОРЕЗИСТИВНЫЕ ПОЛУПРОВОДНИКОВЫЕ ПРИЕМНИКИ ЗВУКА И ВИБРАЦИЙ
- Глава 6. Запись звука
- 6.2. МЕХАНИЧЕСКАЯ ЗАПИСЬ
- Рекордеры
- Электромеханическая обратная связь в рекордере
- Электродинамический рекордер
- Краткие сведения о звукоснимателях
- Стереограммофонная запись
- 6.3. ОПТИЧЕСКАЯ ЗАПИСЬ ЗВУКА
- Оптическая запись с использованием модуляции
- Уменьшение шумового фона при записи по методу переменной ширины
- Щелевые искажения записи
- 6.4. МАГНИТНАЯ ЗАПИСЬ ЗВУКА
- Головки записи и воспроизведения
- Процесс намагничения магнитной ленты полем головки
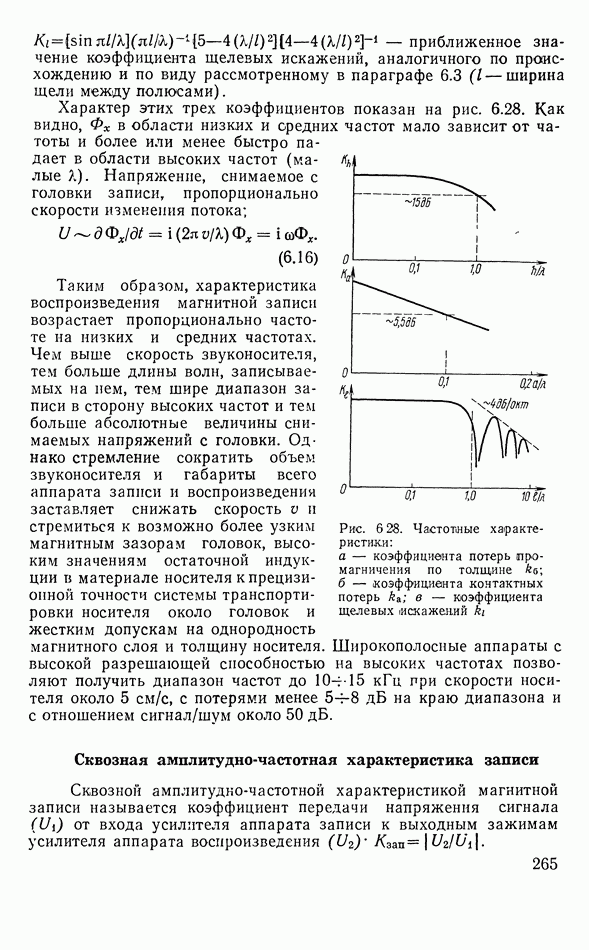
- Воспроизведение записи
- Сквозная амплитудно-частотная характеристика записи
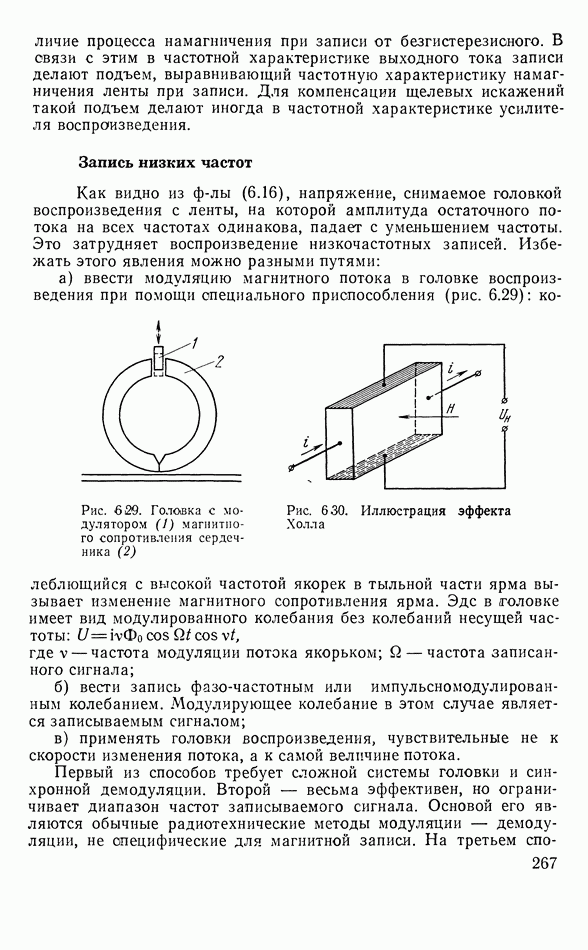
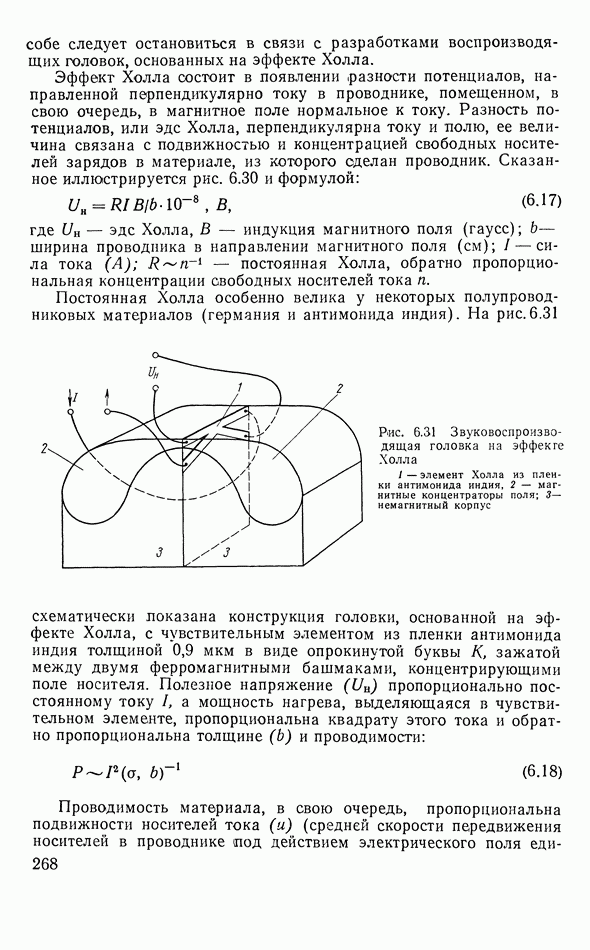
- Запись низких частот
- Плавающие головки
- Точность механизма транспортировки звуконосителя
- Список литературы