| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Местные уравнения пьезопреобразователя в тензорной форме
Рассмотренные в начале параграфа 3.11 соотношения относятся к такому случаю, при котором вид деформации пьезокристалла и вид механического напряжения заранее выбраны и считается, что они скалярио связаны между собой модулем упругости. Точно так же заранее выбран вид пьезоэффекта и вид электрической поляризации этого пьезокристалла. Между тем известно, что даже в изотропном упругом теле приложение усилий в одном направлении вызывает деформации не только в этом же направлении, но и в перпендикулярных ему. В анизотропном теле — в кристалле — упругие свойства еще более сложны: связь между напряжениями и возникающими деформациями зависит еще от ориентации приложенных напряжений или деформаций относительно кристаллической решетки кристалла. Так как структура кристаллической решетки внешне проявляется в виде определенного вида симметрии кристалла — наличия осей симметрии, — то формально можно считать, что величина и направление деформации кристалла зависят от направления приложения усилий по отношению к осям симметрии кристалла. Пьезоэлектрические и диэлектрические свойства кристаллов также оказываются зависящими от ориентации по отношению к осям симметрии.
В общем случае в упругом теле статическое смещение какой-либо точки представляет собой вектор, который может быть разложен на три взаимно перпендикулярные составляющие, направленные вдоль осей выбранной системы декартовых координат. При однородной деформации каждая из этих составляющих линейно зависит от каждой из трех координат рассматриваемой точки или, иначе говоря, от вектора, определяющего положение данной точки в координатной системе. Коэффициенты пропорциональности, связывающие координаты с проекциями смещения, суть составляющие деформации. Каждая из трех проекций смещения связана тремя составляющими деформациями с координатами. Это соотношение в развернутом виде записывается так:

где  проекции смещения у точки тела на оси 1, 2, 3;
проекции смещения у точки тела на оси 1, 2, 3;  координаты точки тела в системе осей 1, 2, 3;
координаты точки тела в системе осей 1, 2, 3;  составляющие деформации.
составляющие деформации.
Девять компонентов  образуют тензор деформации. Такой девятикомпонентный тензор носит название тензора второго ранга. Точно таким же образом можно составит зависимость составляющих механического напряжения, действующих на мысленно вырезанную единичную площадку, положение которой в теле определяется направляющими косинусами нормали к этой площадке:
образуют тензор деформации. Такой девятикомпонентный тензор носит название тензора второго ранга. Точно таким же образом можно составит зависимость составляющих механического напряжения, действующих на мысленно вырезанную единичную площадку, положение которой в теле определяется направляющими косинусами нормали к этой площадке:

где  составляющие вектора полного напряжения
составляющие вектора полного напряжения  направляющие косинусы площадки, на которую действует напряжение
направляющие косинусы площадки, на которую действует напряжение  — составляющие тензора напряжения.
— составляющие тензора напряжения.
В сокращенной форме по правилам тензорных обозначений системы равенств (3.135) и  записываются соответственно так:
записываются соответственно так:

Наличие повторяющегося значка в правой части равенства (3.137) означает, что должно быть произведено суммирование членов вида  или
или  для всех (трех) возможных значений повторяющегося значка
для всех (трех) возможных значений повторяющегося значка  и соответственно,
и соответственно,  .
.
По закону Гука деформации  в упругом теле прямо пропорциональны напряжениям
в упругом теле прямо пропорциональны напряжениям  и каждая из составляющих деформаций зависит от всех составляющих напряжения. Таким образом, элементарная скалярная зависимость, вытекающая из закона Гука
и каждая из составляющих деформаций зависит от всех составляющих напряжения. Таким образом, элементарная скалярная зависимость, вытекающая из закона Гука
 которая учитывает только связь какой-то одной составляющей деформации
которая учитывает только связь какой-то одной составляющей деформации  с одним видом напряжения о через модуль гибкости
с одним видом напряжения о через модуль гибкости  в общем случае превращается в систему из девяти уравнений для девяти составляющих
в общем случае превращается в систему из девяти уравнений для девяти составляющих 

Эта система равенств по правилам, принятым в тензорном исчислении, кратко записывается так:

Запись (3.139) предполагает, что в каждом из равенств, относящемся к данной комбинации значков  производится суммирование по всем комбинациям значков
производится суммирование по всем комбинациям значков  пробегающим значения 1, 2,
пробегающим значения 1, 2,
3. Система состоит из ряда таких равенств (в нашем случае из девяти), в каждом из которых значки  имеют определенную комбинацию двух из трех возможных значений 1, 2, 3. Величины
имеют определенную комбинацию двух из трех возможных значений 1, 2, 3. Величины  составляют квадратную таблицу из
составляют квадратную таблицу из  значения и представляют собой компоненты так называемого тензора четвертого ранга, преобразующего компоненты тензора напряжений в компоненты тензора деформации. Вследствие симметрии число независимых компонент
значения и представляют собой компоненты так называемого тензора четвертого ранга, преобразующего компоненты тензора напряжений в компоненты тензора деформации. Вследствие симметрии число независимых компонент  сокращается с 81 до 21, так как
сокращается с 81 до 21, так как

Решая систему равенств (3.138) относительно напряжений, получим новое тензорное выражение:  где
где  модули упругости, составляющие тензора
модули упругости, составляющие тензора  ранга, преобразующего деформации
ранга, преобразующего деформации  в напряжения
в напряжения 
Составляющие  с повторяющимися значками, т. е.
с повторяющимися значками, т. е.  это деформации сжатия — растяжения вдоль осей, деформации
это деформации сжатия — растяжения вдоль осей, деформации  при
при  это деформации сдвига. Соответственно напряжения
это деформации сдвига. Соответственно напряжения  при
при  нормальные напряжения, а
нормальные напряжения, а  при
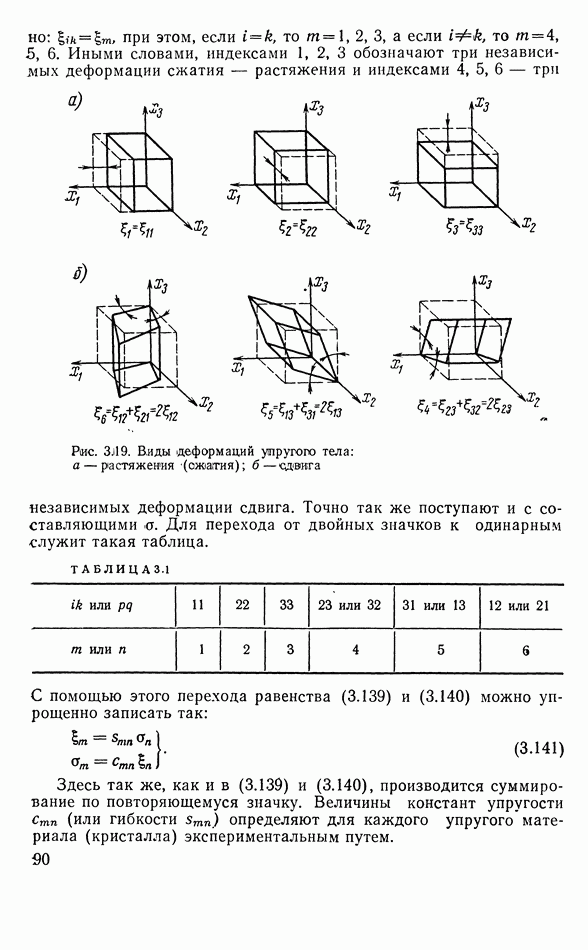
при  касательные напряжения. Вид составляющих деформаций и направления составляющих напряжений иллюстрируются рис. 3.19.
касательные напряжения. Вид составляющих деформаций и направления составляющих напряжений иллюстрируются рис. 3.19.
Если деформированное тело остается статически уравновешенным,  Необходимо
Необходимо  В этом случае тензоры деформаций и напряжений становятся симметричными и число независимых компонентов напряжения и деформации сокращается с девяти до шести. Поэтому часто пользуются более простыми обозначениями для составляющих
В этом случае тензоры деформаций и напряжений становятся симметричными и число независимых компонентов напряжения и деформации сокращается с девяти до шести. Поэтому часто пользуются более простыми обозначениями для составляющих  , а
, а
именно:  при этом, если
при этом, если  то
то  а если
а если  то
то  . Иными словами, индексами 1, 2, 3 обозначают три независимых деформации сжатия — растяжения и индексами 4, 5, 6 — три независимых деформации сдвига.
. Иными словами, индексами 1, 2, 3 обозначают три независимых деформации сжатия — растяжения и индексами 4, 5, 6 — три независимых деформации сдвига.

Рис. 3.19. Виды деформаций упругого тела: а — растяжения (сжатия); б — сдвига
Точно так же поступают и с составляющими а. Для перехода от двойных значков к одинарным служит такая таблица.
ТАБЛИЦА 3.1 (см. скан)
С помощью этого перехода равенства (3.139) и (3.140) можно упрощенно записать так:

Здесь так же, как и в (3.139) и (3.140), производится суммирование по повторяющемуся значку. Величины констант упругости  (или гибкости
(или гибкости  определяют для каждого упругого материала (кристалла) экспериментальным путем.
определяют для каждого упругого материала (кристалла) экспериментальным путем.
Рассмотрим теперь электрические свойства кристалла. Электрическая индукция  и напряженность поля
и напряженность поля  являются векторами. Их составляющие по трем взаимно перпендикулярным координатным осям связаны между собой в кристалле аналогично тому, как связаны составляющие вектора смещения точки упругого тела при однородной деформации с составляющими радиуса вектора этой точки тела в системе равенств (3.135):
являются векторами. Их составляющие по трем взаимно перпендикулярным координатным осям связаны между собой в кристалле аналогично тому, как связаны составляющие вектора смещения точки упругого тела при однородной деформации с составляющими радиуса вектора этой точки тела в системе равенств (3.135):

где  составляющие тензора диэлектрической проницаемости.
составляющие тензора диэлектрической проницаемости.
Тензор  имеет очень простой вид:
имеет очень простой вид:  при
при  при
при  т. е. имеются всего три компонента диэлектрической проницаемости
т. е. имеются всего три компонента диэлектрической проницаемости  которые показывают, что только соответственные компоненты векторов электрической индукции и напряженности поля связаны между собой.
которые показывают, что только соответственные компоненты векторов электрической индукции и напряженности поля связаны между собой.
Прямой пьезоэффект в кристалле описывался соотношением (3.92) для электрической индукции  в некотором заранее заданном направлении и механическим напряжением о также в некотором заданном направлении. Если же представить механические напряжения в общем виде как тензор с составляющими
в некотором заранее заданном направлении и механическим напряжением о также в некотором заданном направлении. Если же представить механические напряжения в общем виде как тензор с составляющими  а электрическую индукцию как вектор, то тогда следует обобщить выражение (3.92), записав его так:
а электрическую индукцию как вектор, то тогда следует обобщить выражение (3.92), записав его так:

Это равенство означает, что  общем случае любая из составляющих тензора напряжения
общем случае любая из составляющих тензора напряжения  может вызвать поляризацию вдоль любой из координатных осей и что пьезомодуль
может вызвать поляризацию вдоль любой из координатных осей и что пьезомодуль  представляет собой тензор третьего ранга с составляющими
представляет собой тензор третьего ранга с составляющими  Аналогично этому обратный пьезоэффект запишется так:
Аналогично этому обратный пьезоэффект запишется так:

Равенства (3.143) дают значения составляющих вектора электрической индукции в отсутствие электрического поля. Для получения полного значения компонента вектора  к правым частям (3.143) следует, очевидно, добавить правые части равенства (3.142):
к правым частям (3.143) следует, очевидно, добавить правые части равенства (3.142):

Здесь символ  означает, что компоненты тензора диэлектрической проницаемости берутся для случая отсутствия механических напряжений. Система трех равенств (3.145) составляет обобщенное выражение по отношению к первому из местных уравнений в скалярной форме (3.101). Вместо второго ур-ния (3.101) обобщенное выражение будет содержать в общем случае девять уравнений для девяти компонент
означает, что компоненты тензора диэлектрической проницаемости берутся для случая отсутствия механических напряжений. Система трех равенств (3.145) составляет обобщенное выражение по отношению к первому из местных уравнений в скалярной форме (3.101). Вместо второго ур-ния (3.101) обобщенное выражение будет содержать в общем случае девять уравнений для девяти компонент 

Две группы равенств (3.145) и (3.146) представляют собой общую запись местных уравнений пьезопреобразователя в тензорной форме. Пользуясь упрощенной записью в соответствии с табл. 3.1 и равенствами (3.141), можно написать:

Эта тензорная запись системы местных уравнений пьезопреобразователя в форме у в развернутом виде представится так:

В этих равенствах опущены индексы а у составляющих  также учтено общее соотношение симметрии, вследствие которого
также учтено общее соотношение симметрии, вследствие которого  Итак, уравнения пьезоэлектрического преобразователя в самом общем виде представляют собой систему из 12 ур-ний (3.144), (3.145) или, в упрошенной записи, из девяти ур-ний (3.147). Система (3.147) показывает, что в зависимости от конкретного вида пьезоэлектрика та или иная компонента
Итак, уравнения пьезоэлектрического преобразователя в самом общем виде представляют собой систему из 12 ур-ний (3.144), (3.145) или, в упрошенной записи, из девяти ур-ний (3.147). Система (3.147) показывает, что в зависимости от конкретного вида пьезоэлектрика та или иная компонента  может сказаться более подходящей для использования в конкретном электроакустическом приборе.
может сказаться более подходящей для использования в конкретном электроакустическом приборе.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. Краткие сведения по физиологической акустике
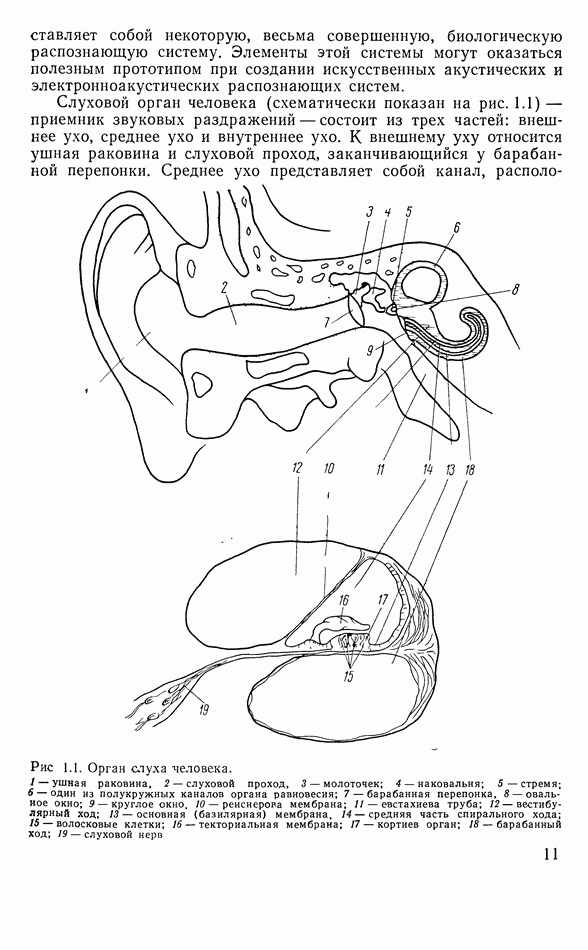
- 1.1. УСТРОЙСТВО СЛУХОВОГО ОРГАНА ЧЕЛОВЕКА
- 1.2. МЕХАНИЗМ ВОЗБУЖДЕНИЯ СЛУХОВОГО НЕРВА
- 1.3. ТЕОРИЯ СЛУХА
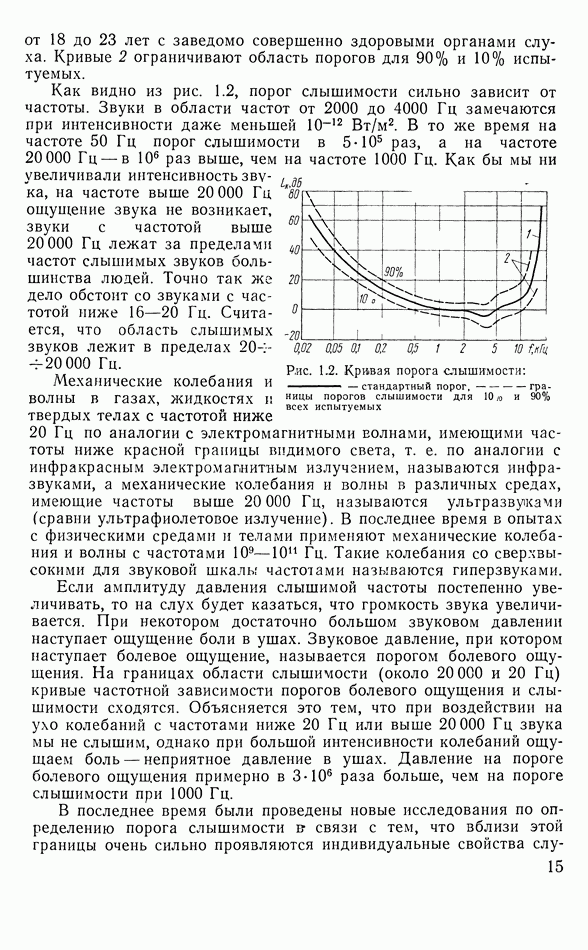
- 1.4. ПОРОГ СЛЫШИМОСТИ
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЙ ПОРОГ ВОСПРИЯТИЯ ИНТЕНСИВНОСТИ ЗВУКА
- 1.6. ЛОГАРИФМИЧЕСКИЕ УРОВНИ. ШКАЛА ДЕЦИБЕЛ
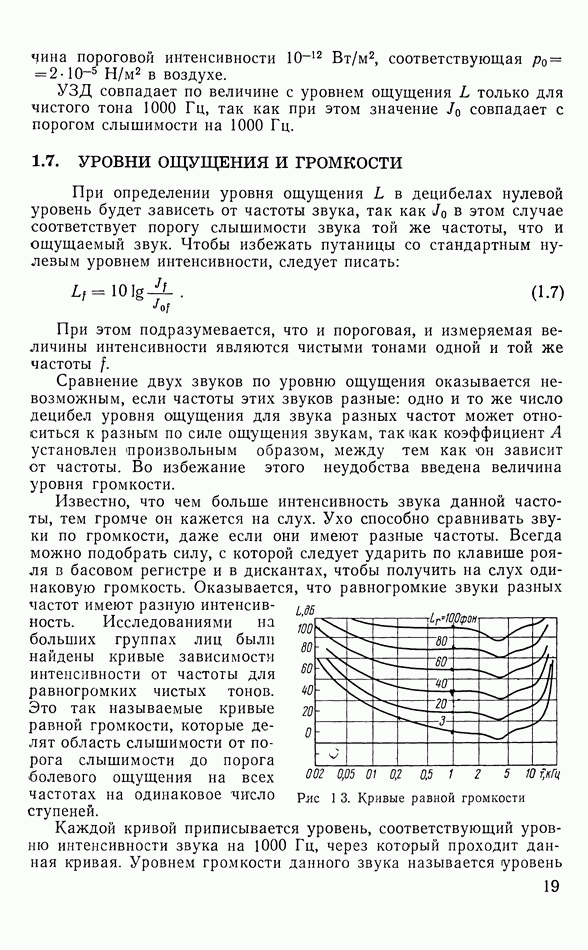
- 1.7. УРОВНИ ОЩУЩЕНИЯ И ГРОМКОСТИ
- 1.8. ГРОМКОСТЬ ЧИСТЫХ ТОНОВ
- 1.9. КРИТИЧЕСКИЕ ПОЛОСЫ СЛУХА
- 1.10. УРОВЕНЬ ГРОМКОСТИ СЛОЖНЫХ ЗВУКОВ
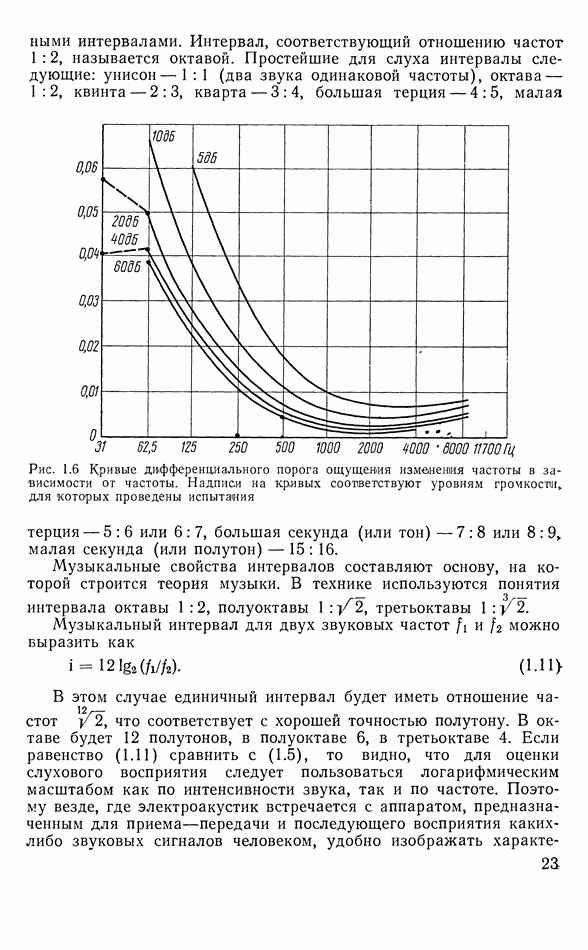
- 1.11. ВОСПРИЯТИЕ ВЫСОТЫ ТОНА. ШКАЛА ЧАСТОТ
- 1.12. МАСКИРОВКА ЗВУКА
- 1.13. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- 1.14. ВОСПРИЯТИЕ ОКРАСКИ (ТЕМБРА) ЗВУКА
- Глава 2. Электромеханические и электроакустические аналогии
- 2.1. ПРИНЦИП ЭЛЕКТРОМЕХАНИЧЕСКИХ АНАЛОГИЙ
- 2.2. МЕХАНИЧЕСКИЕ ЭЛЕМЕНТЫ И МЕХАНИЧЕСКИЕ СИСТЕМЫ
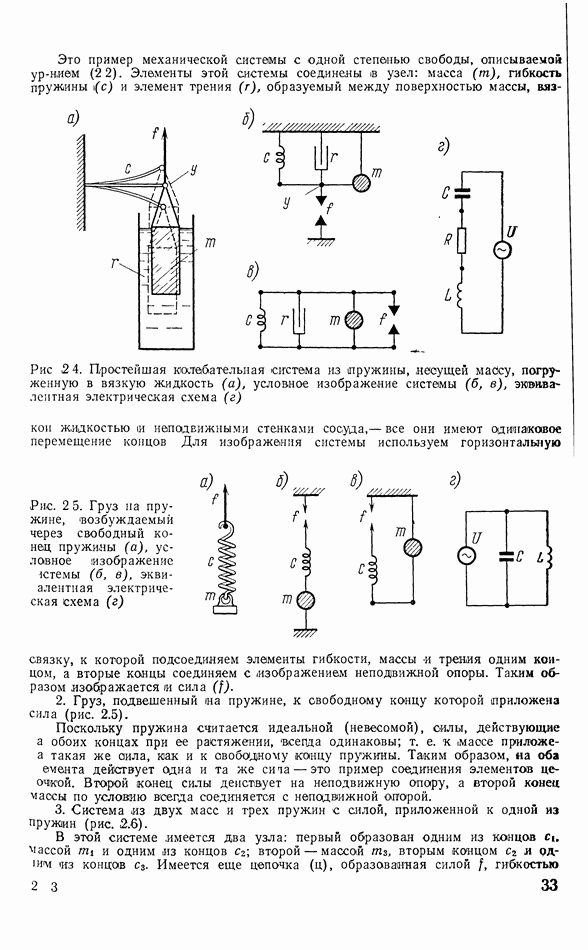
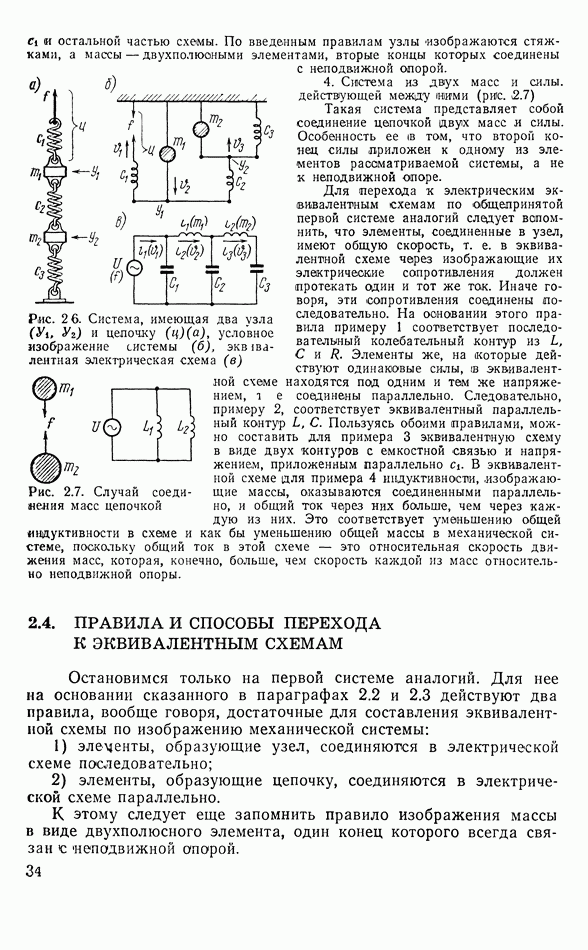
- 2.3. ПРИМЕРЫ ИЗОБРАЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ И ИХ ЭКВИВАЛЕНТНЫХ СХЕМ
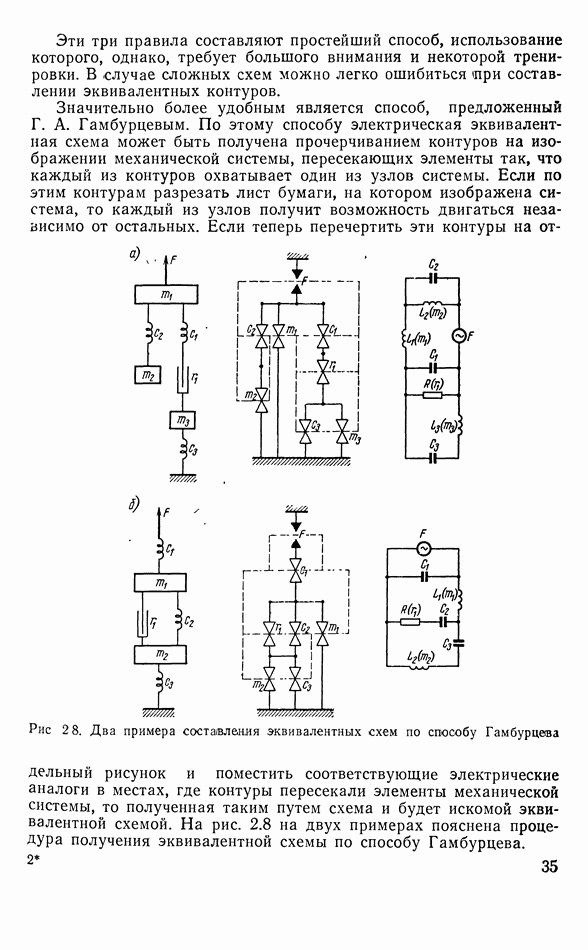
- 2.4. ПРАВИЛА И СПОСОБЫ ПЕРЕХОДА К ЭКВИВАЛЕНТНЫМ СХЕМАМ
- 2.5. ТРАНСФОРМАЦИЯ СИЛ И СКОРОСТЕЙ. ЭЛЕКТРИЧЕСКИЙ АНАЛОГ-ТРАНСФОРМАТОР
- 2.6. ЭЛЕКТРОАКУСТИЧЕСКИЕ АНАЛОГИИ
- 2.7. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИИ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
- 2.8. ЭКВИВАЛЕНТНЫЕ СОСРЕДОТОЧЕННЫЕ ПАРАМЕТРЫ МЕХАНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ
- Глава 3. Электромеханические преобразователи
- 3.2. ДВА ОСНОВНЫХ ТИПА ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.3. ОБЩАЯ ТЕОРИЯ ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.4. ВТОРИЧНЫЕ ПАРАМЕТРЫ ПРЕОБРАЗОВАТЕЛЯ
- 3.5. ПРАВИЛО ЗНАКОВ
- 3.6. ВХОДНОЕ СОПРОТИВЛЕНИЕ СИСТЕМЫ В ОБЩЕМ СЛУЧАЕ
- 3.7. ЧУВСТВИТЕЛЬНОСТЬ ПРЕОБРАЗОВАТЕЛЯ
- 3.8. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ПРЕОБРАЗОВАТЕЛЯ
- 3.9. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.10. МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.11. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Преобразователь с однородной деформацией
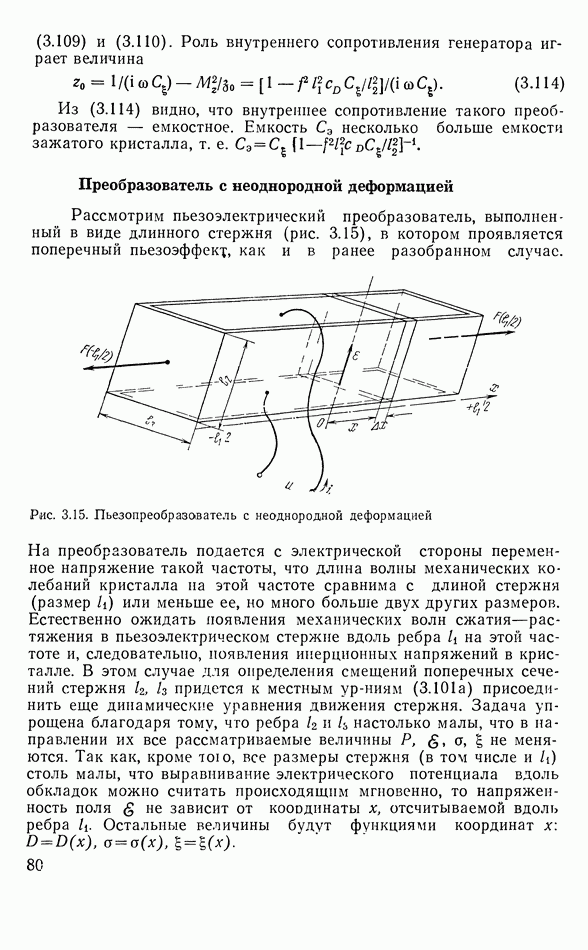
- Преобразователь с неоднородной деформацией
- Местные уравнения пьезопреобразователя в тензорной форме
- Свойства основных пьезоэлектрических кристаллов
- Выбор среза кристалла при изготовлении пьезоэлементов
- Искусственные пьезокерамические материалы
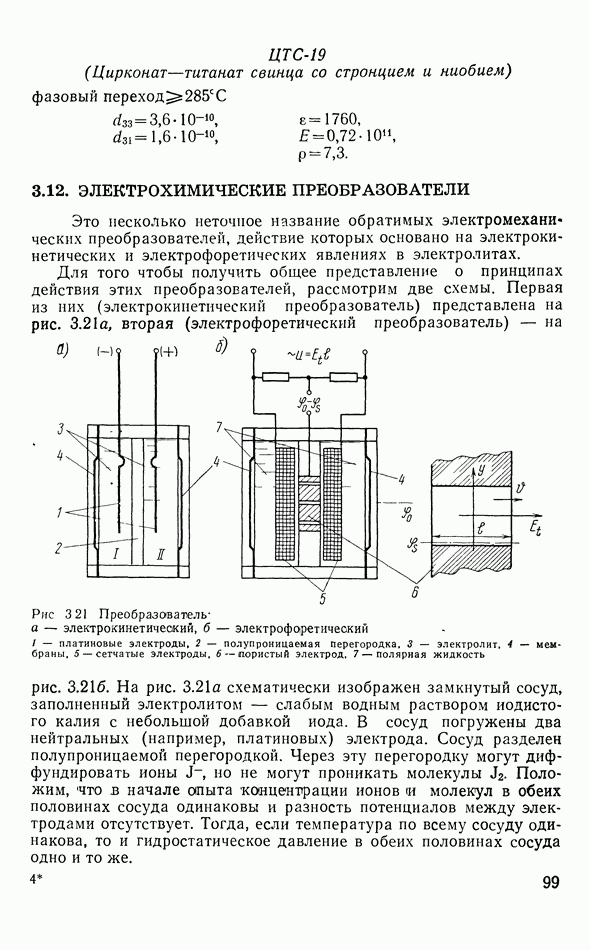
- 3.12. ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 4. Электроакустическая аппаратура
- 4.1. КЛАССИФИКАЦИЯ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- 4.2. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 4.3. АНТЕННЫ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- Связь между чувствительностью приемной и излучающей антенн
- Сопротивление излучения антенны
- Сложные антенны
- Распределенные антенны
- Антенна бегущей волны
- Антенна из направленных элементов
- Оптимизация характеристики направленности антенны
- Рупорная антенна
- 4.4. ТРЕБОВАНИЯ К ЭЛЕКТРОАКУСТИЧЕСКОЙ АППАРАТУРЕ РАДИОВЕЩАНИЯ И ТЕЛЕВИДЕНИЯ
- 4.5. ЛЕНТОЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Ненаправленный микрофон-приемник давления
- Микрофон с кардиоидной характеристикой направленности
- Микрофон с регулируемой характеристикой направленности
- 4.6. КАТУШЕЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
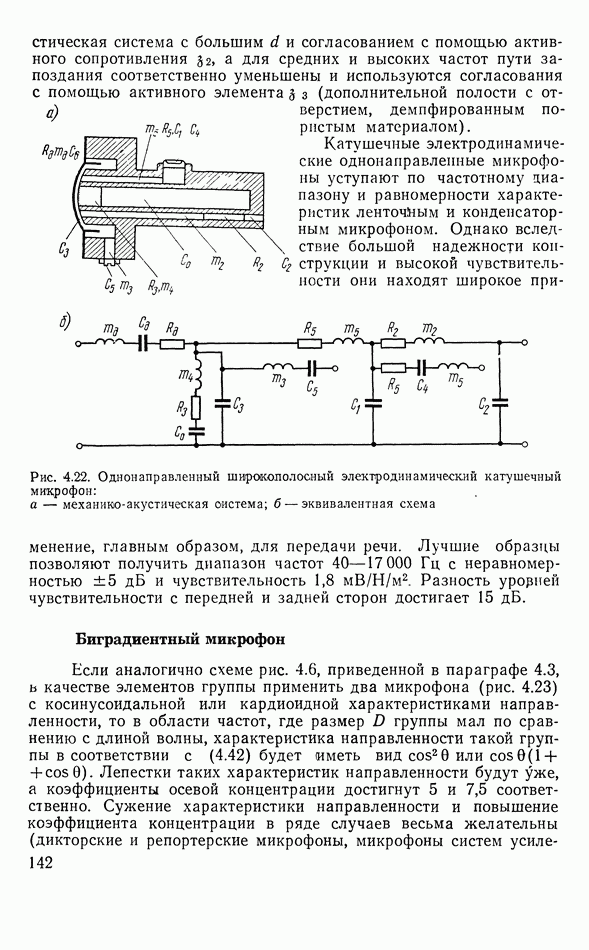
- Однонаправленный микрофон
- Биградиентный микрофон
- Сверхнаправленный микрофон
- 4.7. СОГЛАСОВАНИЕ ЭЛЕКТРИЧЕСКОЙ СТОРОНЫ ЭЛЕКТРОДИНАМИЧЕСКОГО МИКРОФОНА СО ВХОДОМ МИКРОФОННОГО УСИЛИТЕЛЯ
- 4.8. КОНДЕНСАТОРНЫЕ МИКРОФОНЫ
- Об отрицательной упругости электрического поля поляризации в микрофоне
- Предельная чувствительность микрофона
- Влияние емкости входа предварительного каскада
- Микрофон направленного действия
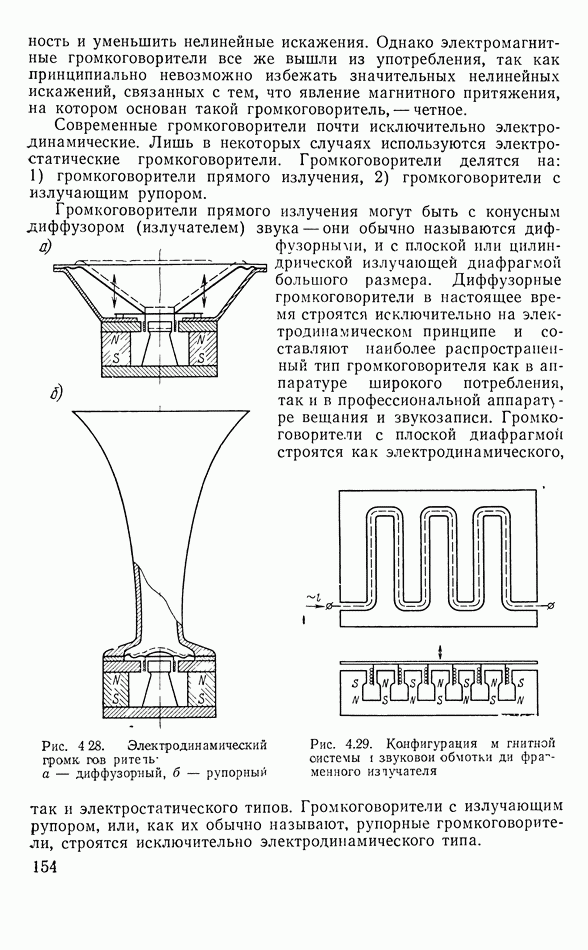
- 4.9. ОБЩИЕ СВЕДЕНИЯ О ГРОМКОГОВОРИТЕЛЯХ
- 4.10. ДИФФУЗОРНЫЕ ГРОМКОГОВОРИТЕЛИ
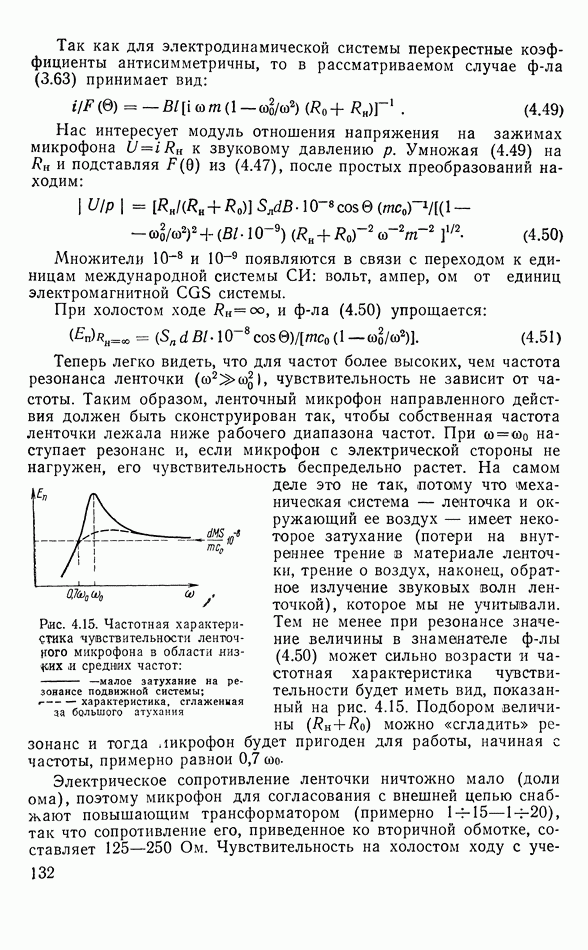
- Частотная характеристика чувствительности
- Влияние способа установки громкоговорителя на излучение в области низких частот
- Работа громкоговорителя в области высоких частот
- Комбинированные громкоговорители
- Нелинейные искажения в громкоговорителе
- 4.11. РУПОРНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- Влияние конечной длины рупора
- Широкогорлый громкоговоритель
- Громкоговорящие агрегаты
- 4.12. ЭЛЕКТРОСТАТИЧЕСКИЙ ГРОМКОГОВОРИТЕЛЬ
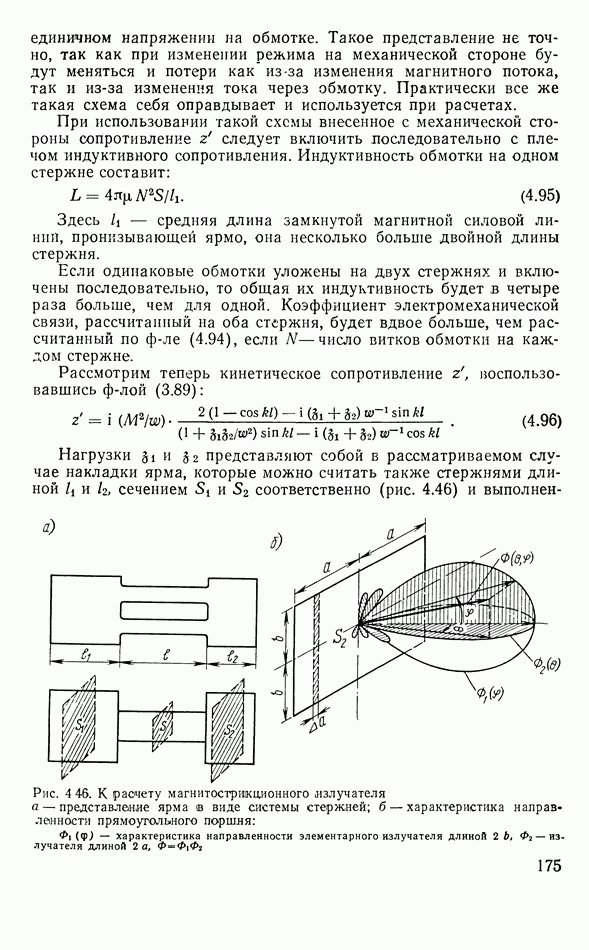
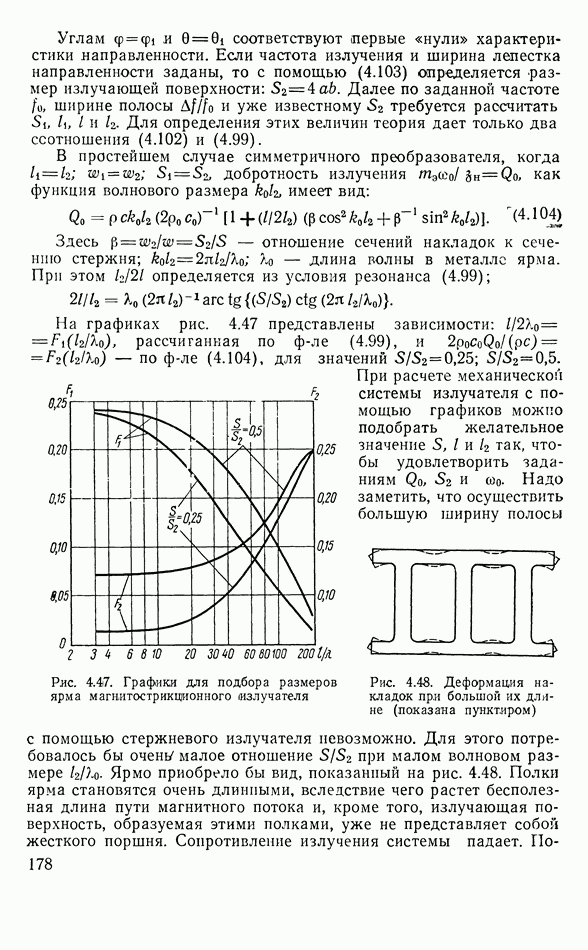
- 4.13. МАГНИТОСТРИКЦИОННЫЕ ИЗЛУЧАТЕЛИ
- Стержневой излучатель
- Кольцевой излучатель
- Круговая диаграмма преобразователя
- Коэффициент полезного действия излучателя
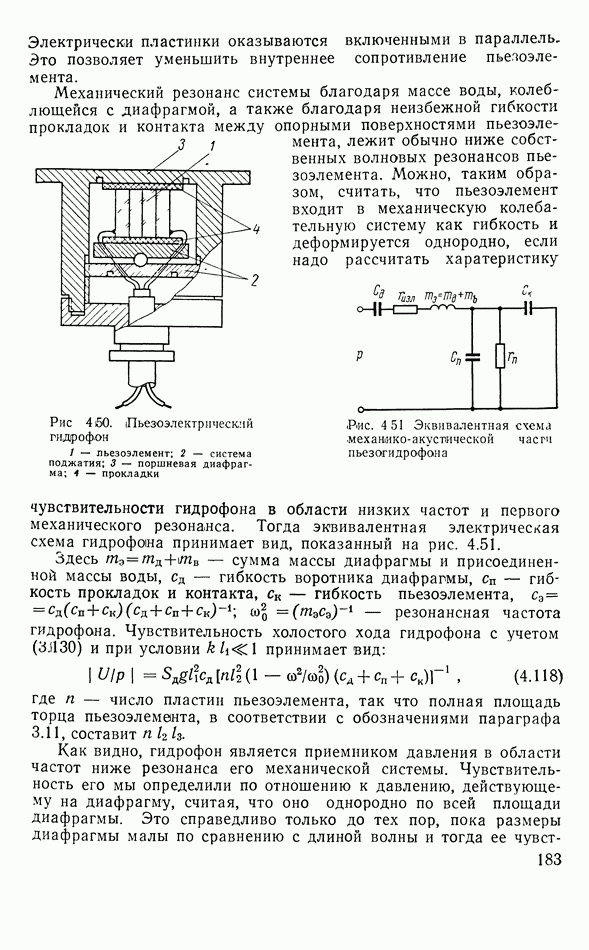
- 4.14. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- Линия задержки
- Другие типы пьезоэлектрических элементов электроакустических аппаратов
- Согласование пьезоэлемента с электрической частью системы
- 4.15. ЭЛЕКТРОДИНАМИЧЕСКИЙ ГЕОФОН
- Частотная характеристика чувствительности
- Максимальная чувствительность
- 4.16. СЕЙСМОМЕТРИЧЕСКИЙ ПРИЕМНИК СМЕЩЕНИЯ
- 4.17. ОПТИМИЗАЦИЯ КОНСТРУКТИВНЫХ РАЗМЕРОВ ЭЛЕКТРОАКУСТИЧЕСКОГО АППАРАТА
- Глава 5. Необратимые преобразователи
- 5.2. ПНЕВМОАКУСТИЧЕСКИЕ ИЗЛУЧАТЕЛИ
- Модуляция потока воздуха
- Пневматическая сирена
- Модулятор с возвратно-поступательным движением
- 5.3. ГИДРАВЛИЧЕСКАЯ СИРЕНА
- 5.4. ГИДРОПНЕВМАТИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ
- 5.5. ПАРАМЕТРИЧЕСКИЕ ПРИЕМНИКИ
- 5.6. ПЬЕЗОРЕЗИСТИВНЫЕ ПОЛУПРОВОДНИКОВЫЕ ПРИЕМНИКИ ЗВУКА И ВИБРАЦИЙ
- Глава 6. Запись звука
- 6.2. МЕХАНИЧЕСКАЯ ЗАПИСЬ
- Рекордеры
- Электромеханическая обратная связь в рекордере
- Электродинамический рекордер
- Краткие сведения о звукоснимателях
- Стереограммофонная запись
- 6.3. ОПТИЧЕСКАЯ ЗАПИСЬ ЗВУКА
- Оптическая запись с использованием модуляции
- Уменьшение шумового фона при записи по методу переменной ширины
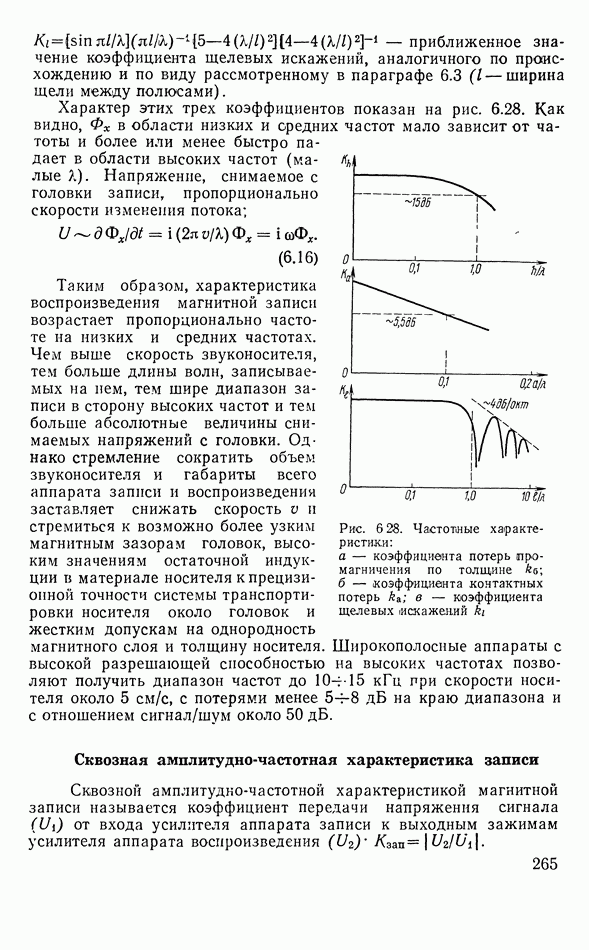
- Щелевые искажения записи
- 6.4. МАГНИТНАЯ ЗАПИСЬ ЗВУКА
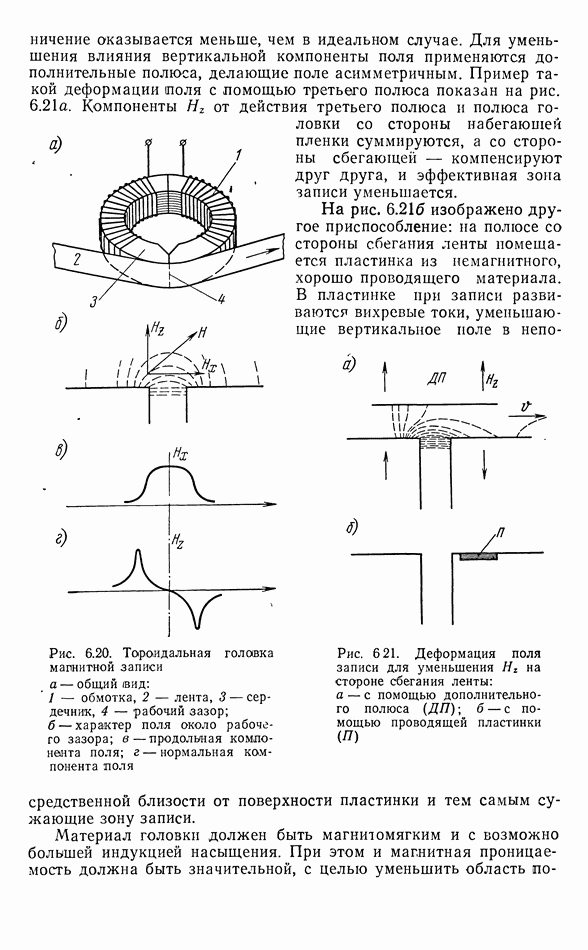
- Головки записи и воспроизведения
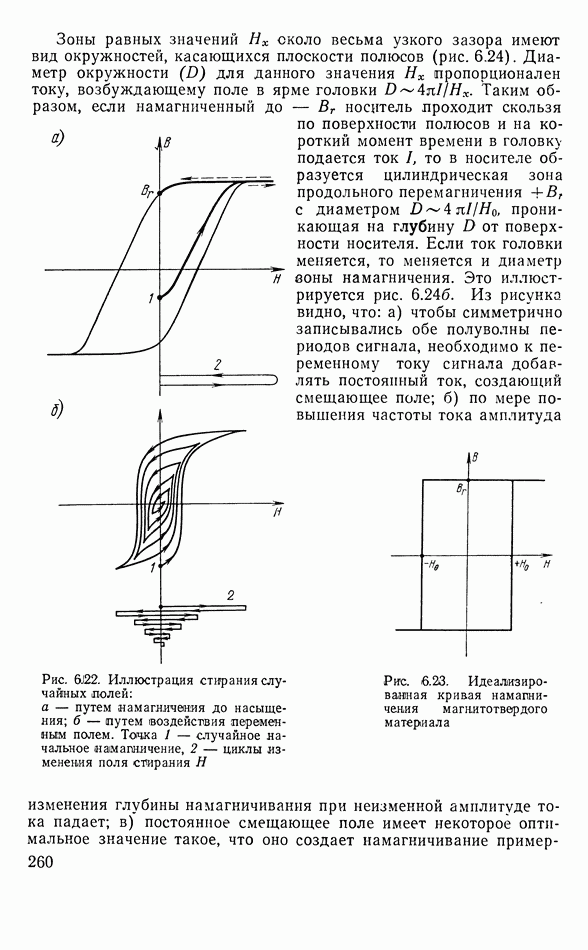
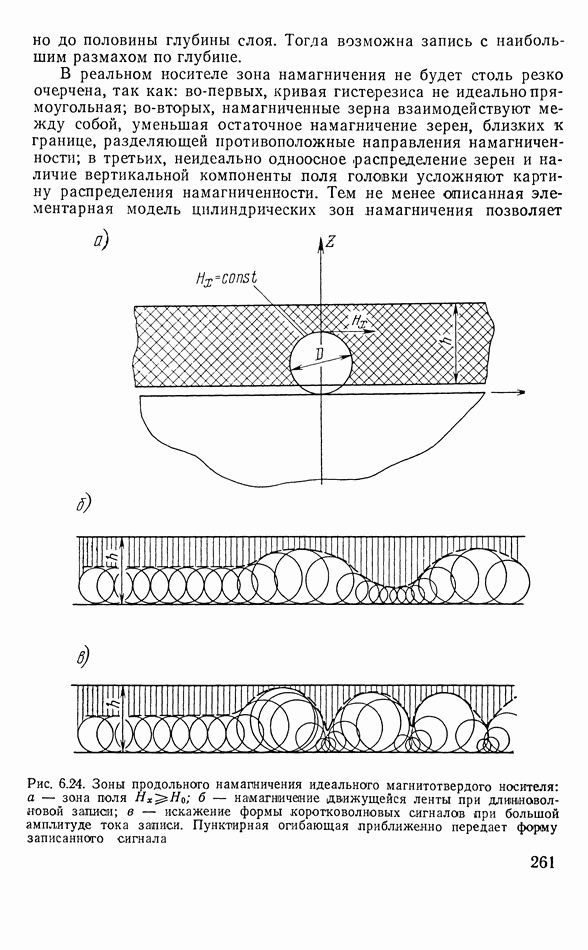
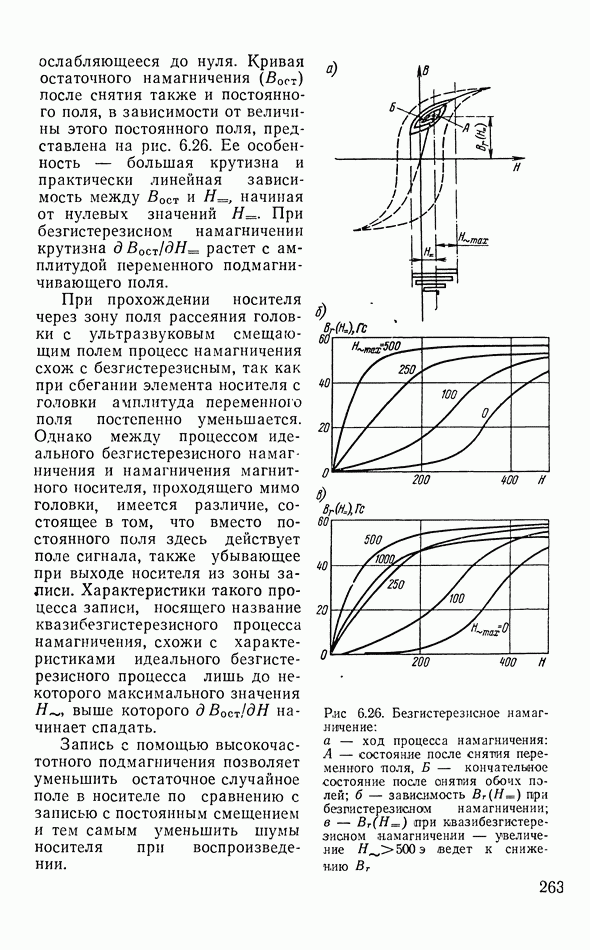
- Процесс намагничения магнитной ленты полем головки
- Воспроизведение записи
- Сквозная амплитудно-частотная характеристика записи
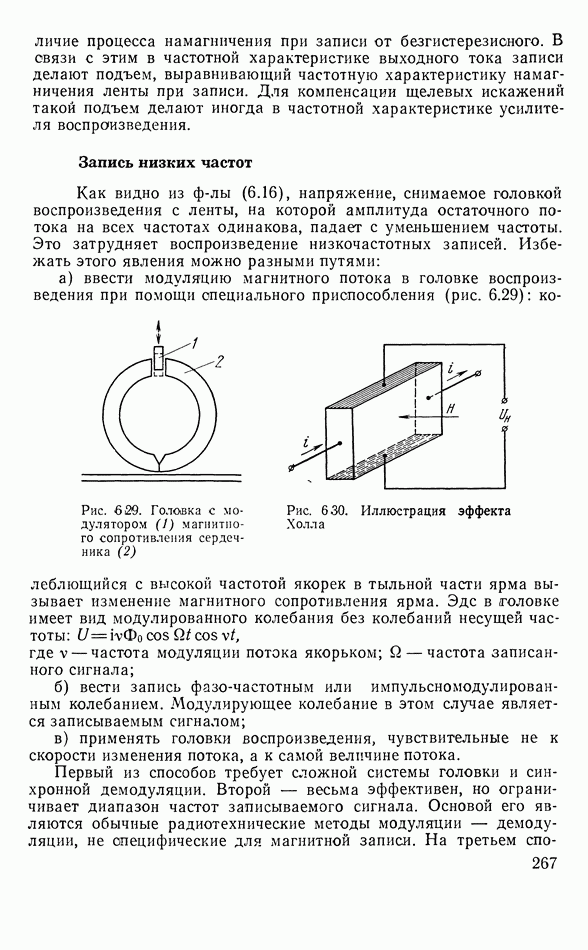
- Запись низких частот
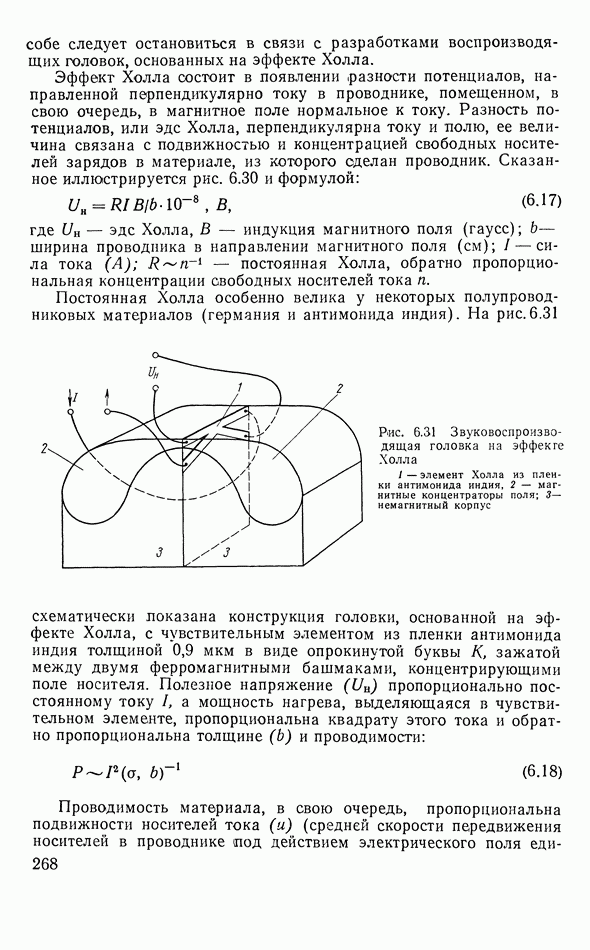
- Плавающие головки
- Точность механизма транспортировки звуконосителя
- Список литературы