| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
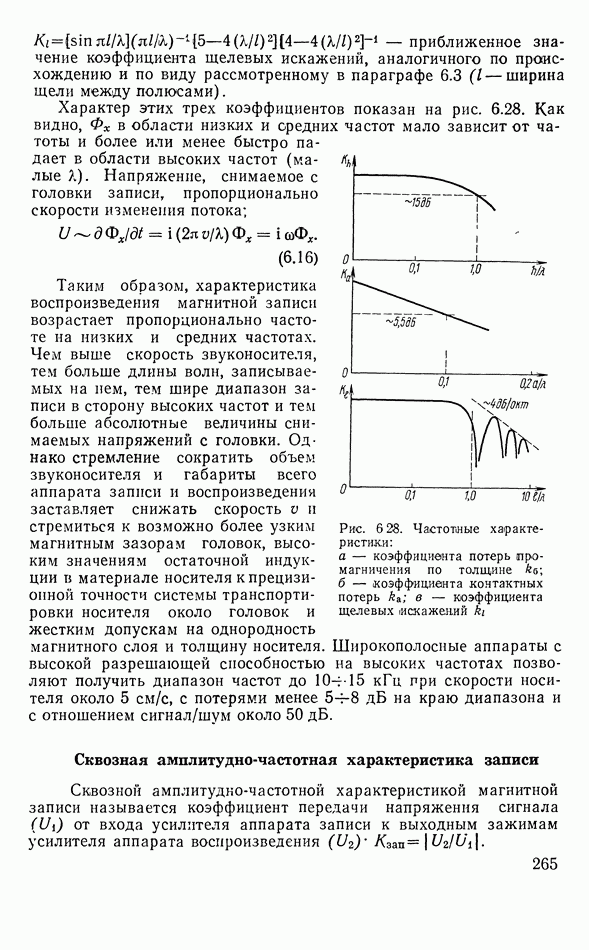
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Сложные антенны
Для получения острой направленности излучения часто используют многоэлементные антенны, называемые обычно групповыми. Для этой цели колебательные скорости составляющих элементов — антенн соответственным образом фазируются и эти антенны располагают в определенном порядке на некоторой базе — на отрезке прямой, окружности, на сфере или части ее, на плоской поверхности.

Рис. 4.6. Характеристика направленности дипольнон антенны
Приведем некоторые примеры групповых антенн:
1. Дипольная групповая антенна (рис. 4.6). Ее элементы — точечные антенны, работающие в противофазе. Характеристика направленности определяется путем сложения давлений, развиваемых обоими элементами, с учетом их фаз и фазовых запозданий на пути распространения волн от этих элементов в точку приема. Считая точку приема весьма удаленной  как
как
следует из рисунка, получим:

Если 

2. Однонаправленная антенна. Антенна из двух элементов, фазы которых сдвинуты относительно друг друга на величину  создает звуковое давление:
создает звуковое давление:

Тогда

Если волновой размер базы мал, то

3. Многоэлементная антенна с прямолинейной базой и синфазными, эквидистантными приемниками. Слйдывая, как и в случае 1, давления от ряда источников и используя свойство суммы членов геометрической прогрессии, для такой антенны получим:

где  число расстояний,
число расстояний,  расстояние между соседними элементами (рис. 4.76).
расстояние между соседними элементами (рис. 4.76).
4. Антенна с прямолинейной базой и дополнительным сдвигом фаз элементов. Если для
элементов антенны в случае 3 ввести в электрических цепях дополнительные сдвиги фаз пропорциональные номеру элемента  отсчитываемому от одного из концов базы, так что
отсчитываемому от одного из концов базы, так что  то получим
то получим


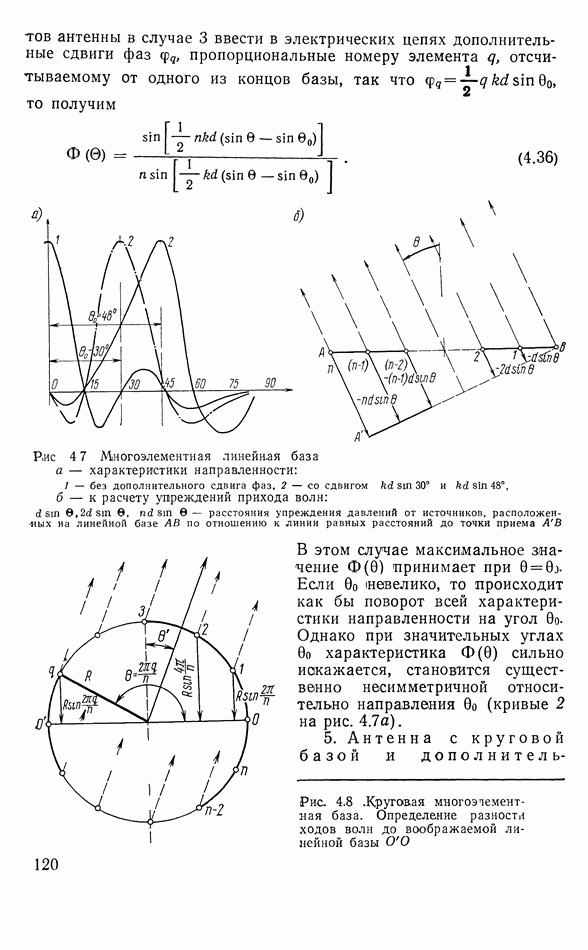
Рис. 4 7 Многоэлементная линейная база а — характеристики направленности: 1 — без дополнительного сдвига фаз, 2 — со сдвигом  к расчету упреждений прихода волн:
к расчету упреждений прихода волн:  расстояния упреждения давлений от источников, расположенных на линейной базе
расстояния упреждения давлений от источников, расположенных на линейной базе  по отношению к линии равных расстояний до точки приема
по отношению к линии равных расстояний до точки приема 
В этом случае максимальное значение  принимает при
принимает при  Если
Если  (невелико, то происходит как бы поворот всей характеристики направленности на угол
(невелико, то происходит как бы поворот всей характеристики направленности на угол  Однако при значительных углах
Однако при значительных углах  характеристика
характеристика  сильно искажается, становится существенно несимметричной относительно направления
сильно искажается, становится существенно несимметричной относительно направления  (кривые 2 на рис. 4.7а).
(кривые 2 на рис. 4.7а).
5. Антенна с круговой базой и

Рис. 4.8 Круговая многоэпементная база. Определение разности ходов волн до воображаемой линейной базы 
дополнительным сдвигом фаз элементов. Располагая  элементов на окружности, в вершинах правильного
элементов на окружности, в вершинах правильного  -угольника, и вводя в электрических цепях элементов фазовые сдвиги (рис. 4.8):
-угольника, и вводя в электрических цепях элементов фазовые сдвиги (рис. 4.8):  , мы как бы переносим все элементы на диаметр окружности, соответствующий
, мы как бы переносим все элементы на диаметр окружности, соответствующий  Если такая антенна принимает плоскую волну, направление распространения которой лежит в плоскости антенны, а ее фронт параллелен диаметру
Если такая антенна принимает плоскую волну, направление распространения которой лежит в плоскости антенны, а ее фронт параллелен диаметру  то все напряжения, снимаемые с элементов, окажутся синфазными после прохождения цепей, создающих фазовые сдвиги
то все напряжения, снимаемые с элементов, окажутся синфазными после прохождения цепей, создающих фазовые сдвиги  Таким образом, в направлении, перпендикулярном диаметру
Таким образом, в направлении, перпендикулярном диаметру  в плоскости антенны будет максимум характеристики направленности. Для характеристики направленности в этой плоскости получим:
в плоскости антенны будет максимум характеристики направленности. Для характеристики направленности в этой плоскости получим:

Здесь угол  отсчитывается от перпендикуляра к диаметру
отсчитывается от перпендикуляра к диаметру 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. Краткие сведения по физиологической акустике
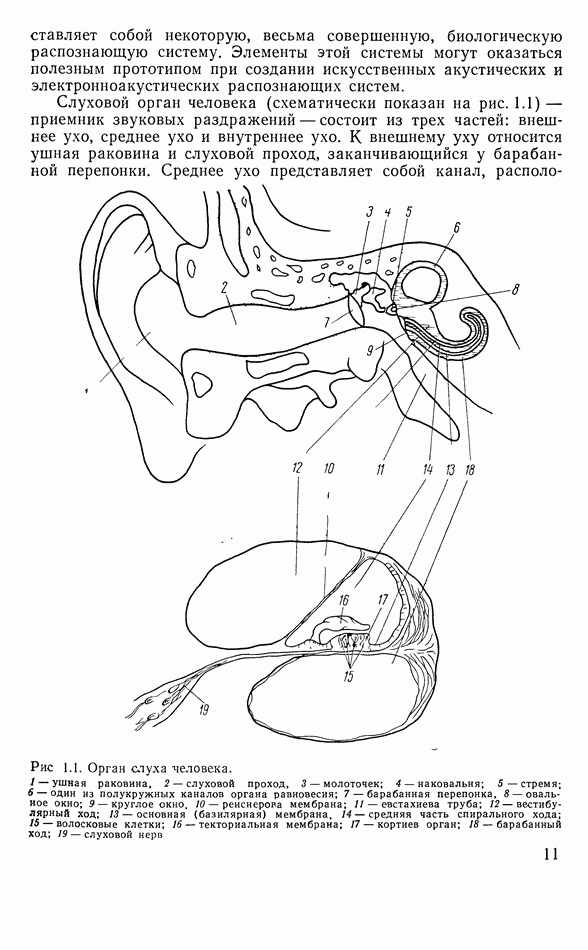
- 1.1. УСТРОЙСТВО СЛУХОВОГО ОРГАНА ЧЕЛОВЕКА
- 1.2. МЕХАНИЗМ ВОЗБУЖДЕНИЯ СЛУХОВОГО НЕРВА
- 1.3. ТЕОРИЯ СЛУХА
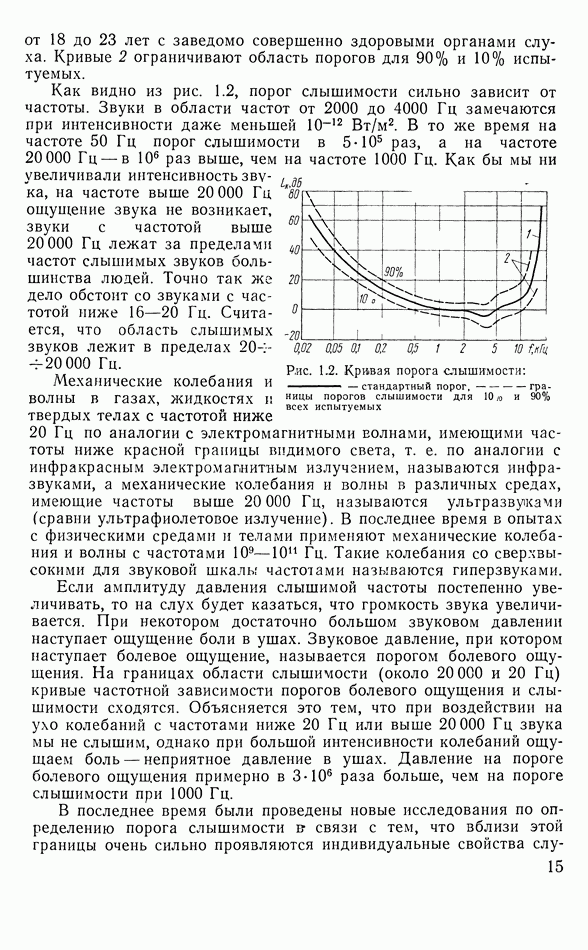
- 1.4. ПОРОГ СЛЫШИМОСТИ
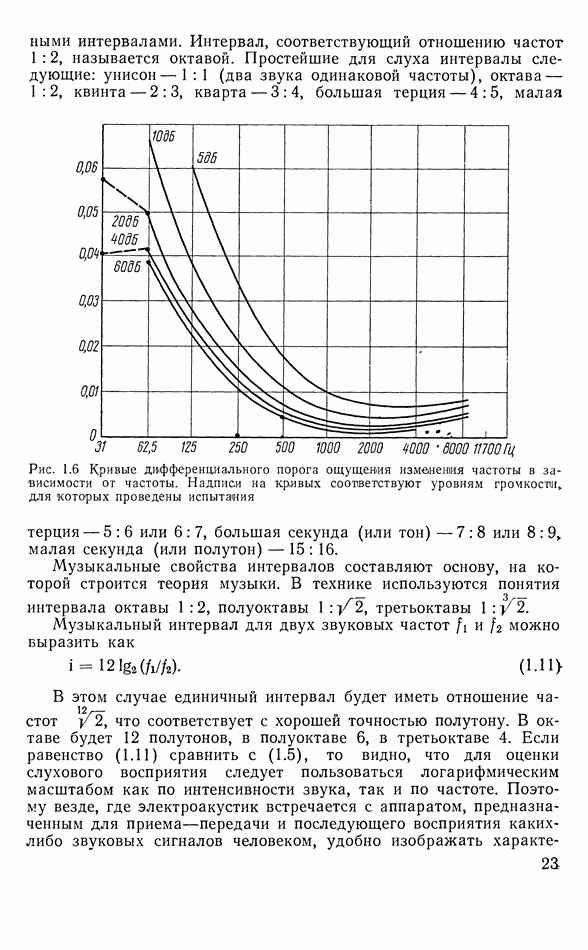
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЙ ПОРОГ ВОСПРИЯТИЯ ИНТЕНСИВНОСТИ ЗВУКА
- 1.6. ЛОГАРИФМИЧЕСКИЕ УРОВНИ. ШКАЛА ДЕЦИБЕЛ
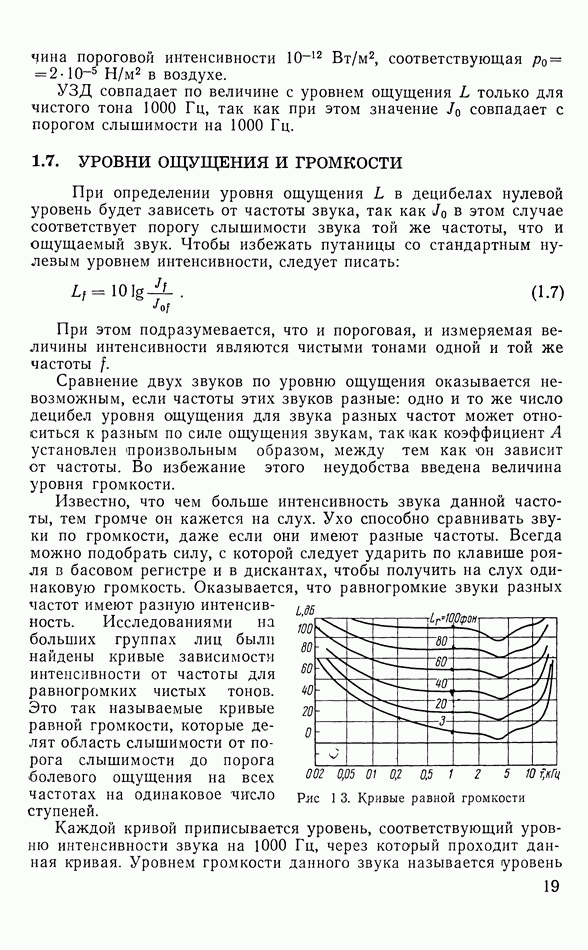
- 1.7. УРОВНИ ОЩУЩЕНИЯ И ГРОМКОСТИ
- 1.8. ГРОМКОСТЬ ЧИСТЫХ ТОНОВ
- 1.9. КРИТИЧЕСКИЕ ПОЛОСЫ СЛУХА
- 1.10. УРОВЕНЬ ГРОМКОСТИ СЛОЖНЫХ ЗВУКОВ
- 1.11. ВОСПРИЯТИЕ ВЫСОТЫ ТОНА. ШКАЛА ЧАСТОТ
- 1.12. МАСКИРОВКА ЗВУКА
- 1.13. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- 1.14. ВОСПРИЯТИЕ ОКРАСКИ (ТЕМБРА) ЗВУКА
- Глава 2. Электромеханические и электроакустические аналогии
- 2.1. ПРИНЦИП ЭЛЕКТРОМЕХАНИЧЕСКИХ АНАЛОГИЙ
- 2.2. МЕХАНИЧЕСКИЕ ЭЛЕМЕНТЫ И МЕХАНИЧЕСКИЕ СИСТЕМЫ
- 2.3. ПРИМЕРЫ ИЗОБРАЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ И ИХ ЭКВИВАЛЕНТНЫХ СХЕМ
- 2.4. ПРАВИЛА И СПОСОБЫ ПЕРЕХОДА К ЭКВИВАЛЕНТНЫМ СХЕМАМ
- 2.5. ТРАНСФОРМАЦИЯ СИЛ И СКОРОСТЕЙ. ЭЛЕКТРИЧЕСКИЙ АНАЛОГ-ТРАНСФОРМАТОР
- 2.6. ЭЛЕКТРОАКУСТИЧЕСКИЕ АНАЛОГИИ
- 2.7. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИИ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
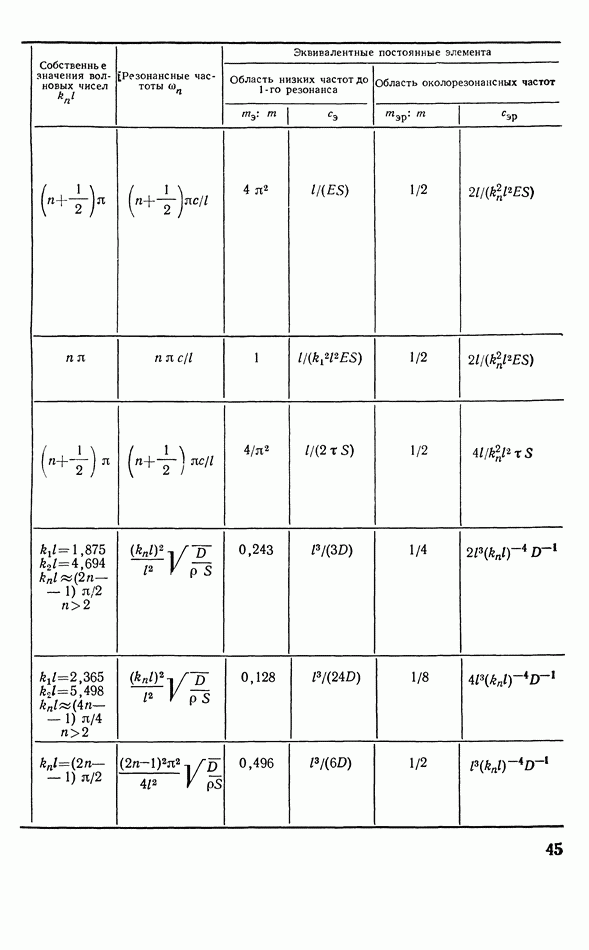
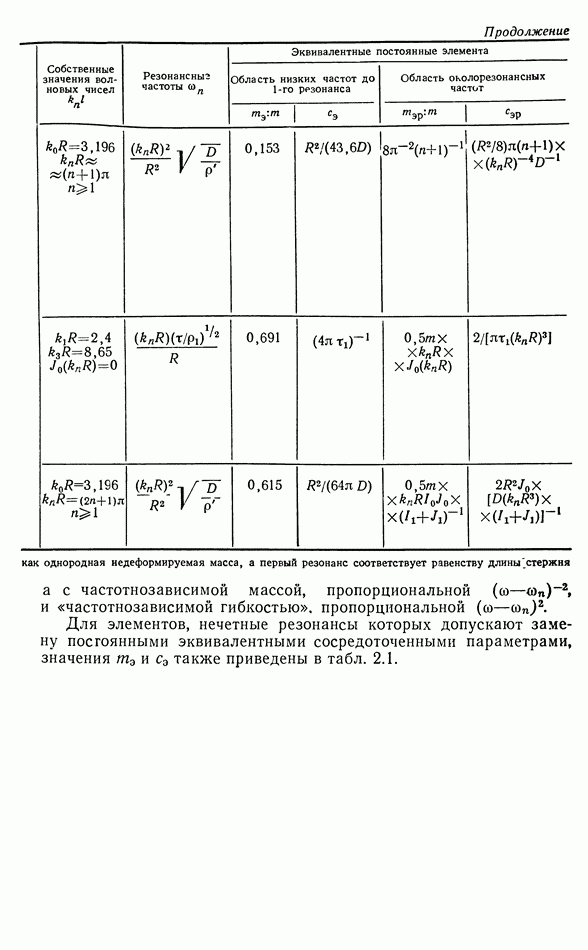
- 2.8. ЭКВИВАЛЕНТНЫЕ СОСРЕДОТОЧЕННЫЕ ПАРАМЕТРЫ МЕХАНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ
- Глава 3. Электромеханические преобразователи
- 3.2. ДВА ОСНОВНЫХ ТИПА ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.3. ОБЩАЯ ТЕОРИЯ ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.4. ВТОРИЧНЫЕ ПАРАМЕТРЫ ПРЕОБРАЗОВАТЕЛЯ
- 3.5. ПРАВИЛО ЗНАКОВ
- 3.6. ВХОДНОЕ СОПРОТИВЛЕНИЕ СИСТЕМЫ В ОБЩЕМ СЛУЧАЕ
- 3.7. ЧУВСТВИТЕЛЬНОСТЬ ПРЕОБРАЗОВАТЕЛЯ
- 3.8. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ПРЕОБРАЗОВАТЕЛЯ
- 3.9. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.10. МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.11. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Преобразователь с однородной деформацией
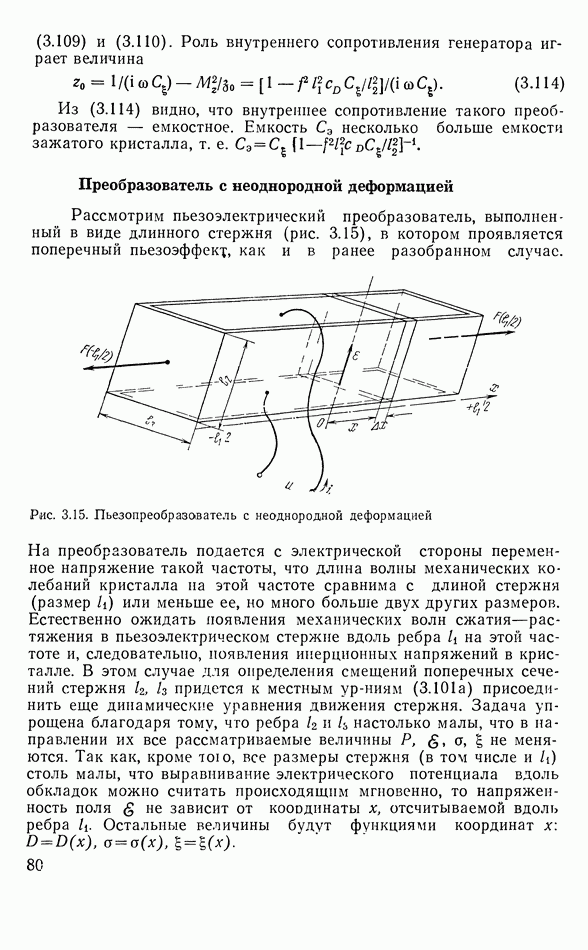
- Преобразователь с неоднородной деформацией
- Местные уравнения пьезопреобразователя в тензорной форме
- Свойства основных пьезоэлектрических кристаллов
- Выбор среза кристалла при изготовлении пьезоэлементов
- Искусственные пьезокерамические материалы
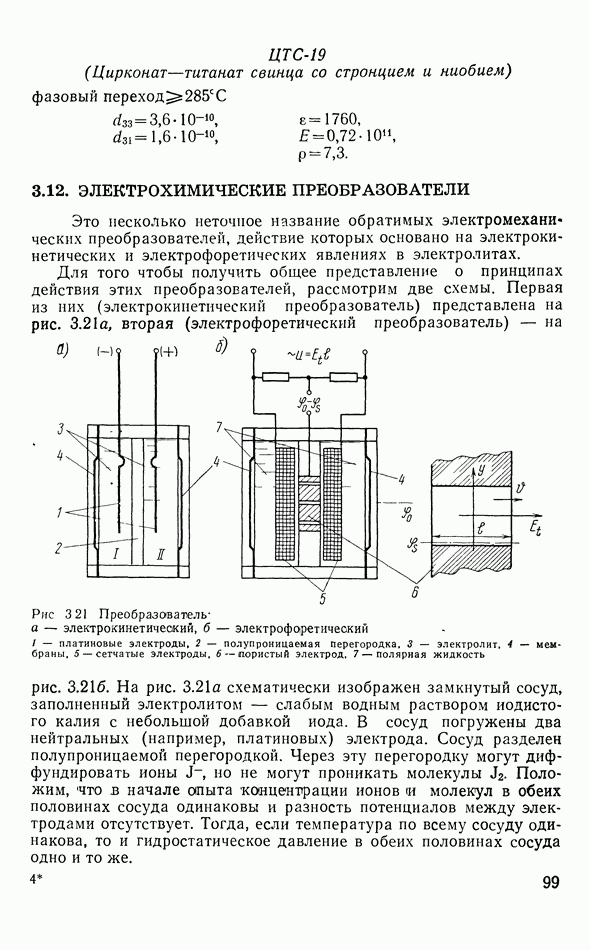
- 3.12. ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 4. Электроакустическая аппаратура
- 4.1. КЛАССИФИКАЦИЯ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
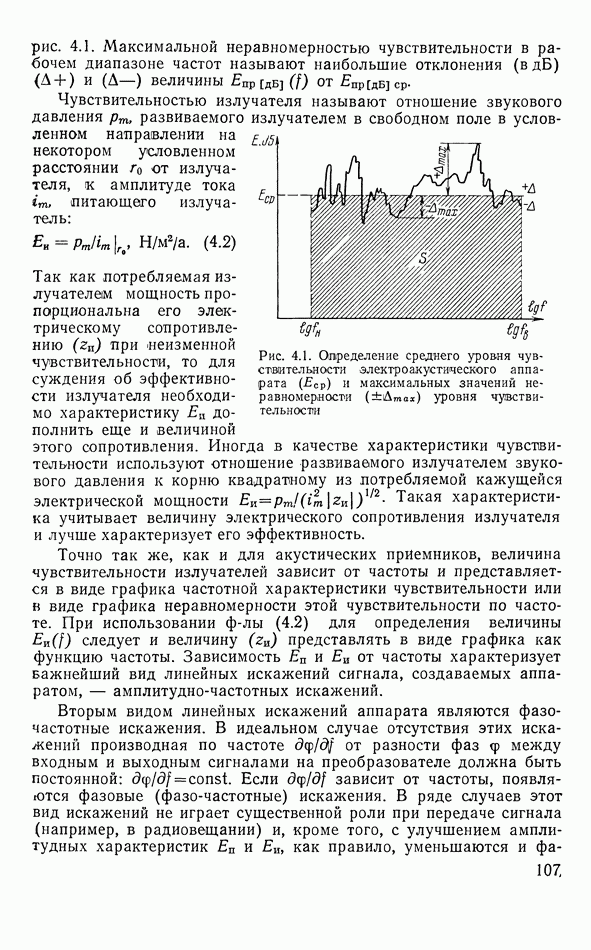
- 4.2. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 4.3. АНТЕННЫ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- Связь между чувствительностью приемной и излучающей антенн
- Сопротивление излучения антенны
- Сложные антенны
- Распределенные антенны
- Антенна бегущей волны
- Антенна из направленных элементов
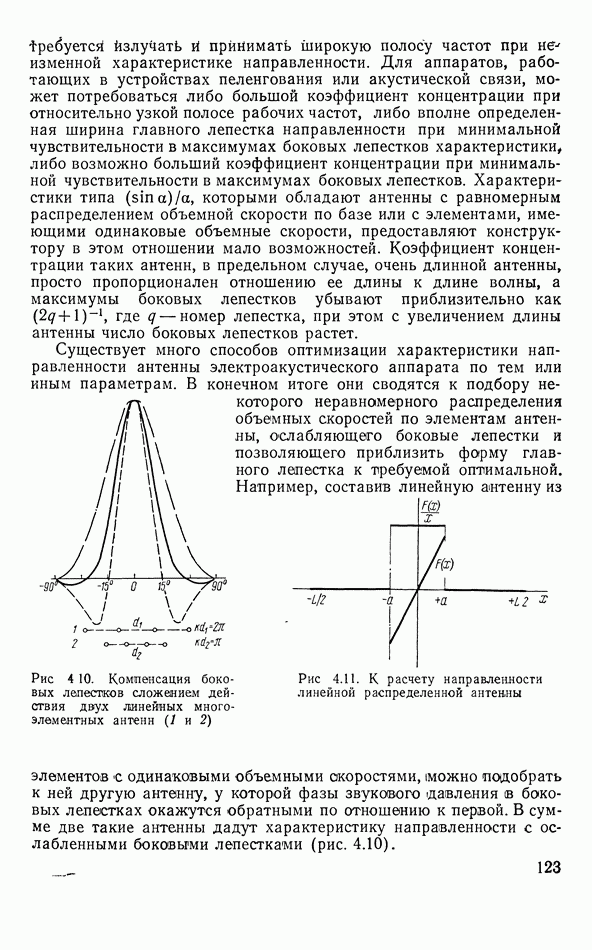
- Оптимизация характеристики направленности антенны
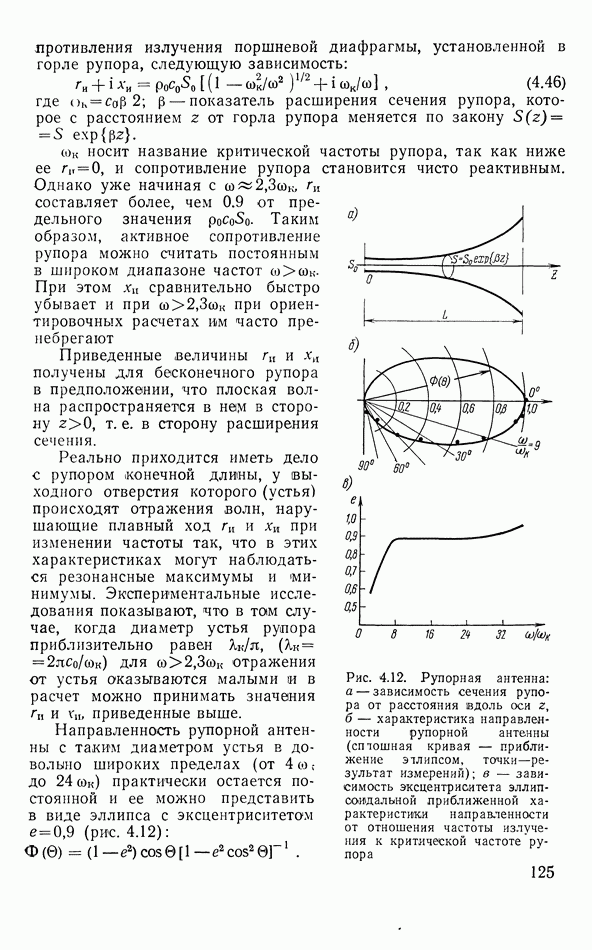
- Рупорная антенна
- 4.4. ТРЕБОВАНИЯ К ЭЛЕКТРОАКУСТИЧЕСКОЙ АППАРАТУРЕ РАДИОВЕЩАНИЯ И ТЕЛЕВИДЕНИЯ
- 4.5. ЛЕНТОЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Ненаправленный микрофон-приемник давления
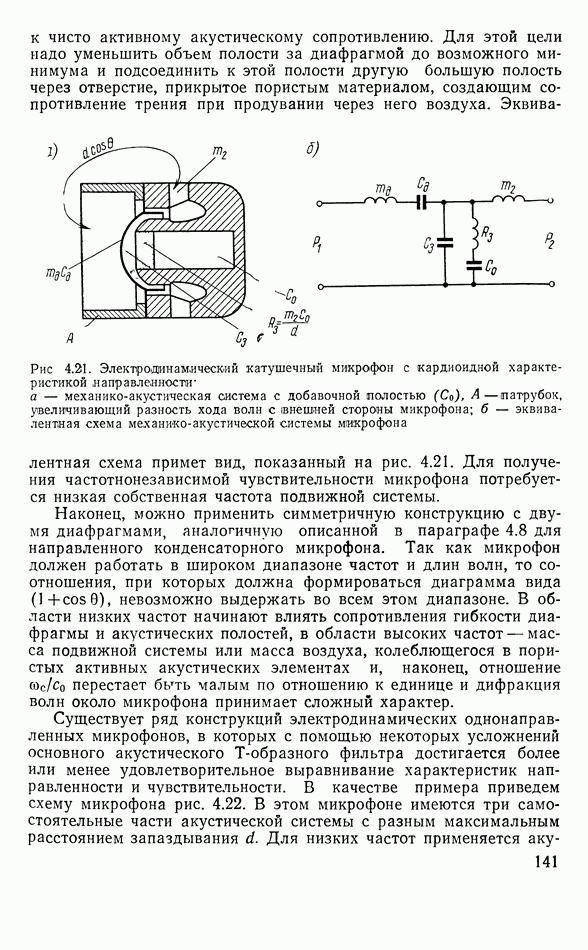
- Микрофон с кардиоидной характеристикой направленности
- Микрофон с регулируемой характеристикой направленности
- 4.6. КАТУШЕЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
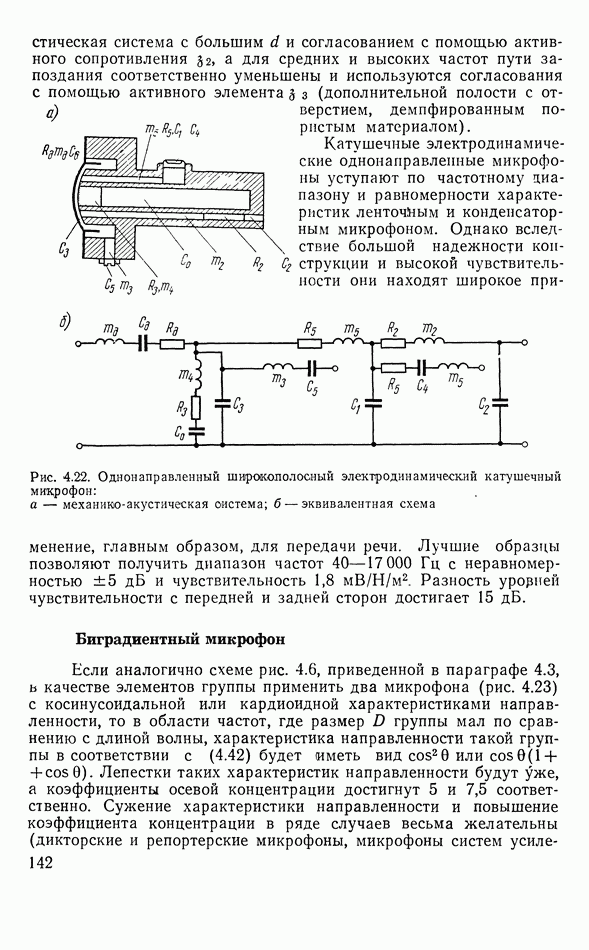
- Однонаправленный микрофон
- Биградиентный микрофон
- Сверхнаправленный микрофон
- 4.7. СОГЛАСОВАНИЕ ЭЛЕКТРИЧЕСКОЙ СТОРОНЫ ЭЛЕКТРОДИНАМИЧЕСКОГО МИКРОФОНА СО ВХОДОМ МИКРОФОННОГО УСИЛИТЕЛЯ
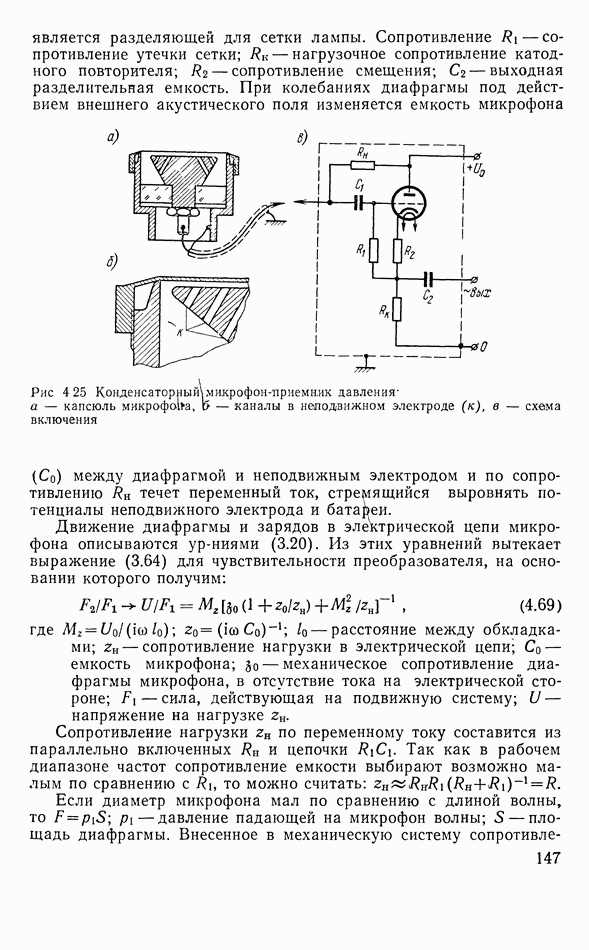
- 4.8. КОНДЕНСАТОРНЫЕ МИКРОФОНЫ
- Об отрицательной упругости электрического поля поляризации в микрофоне
- Предельная чувствительность микрофона
- Влияние емкости входа предварительного каскада
- Микрофон направленного действия
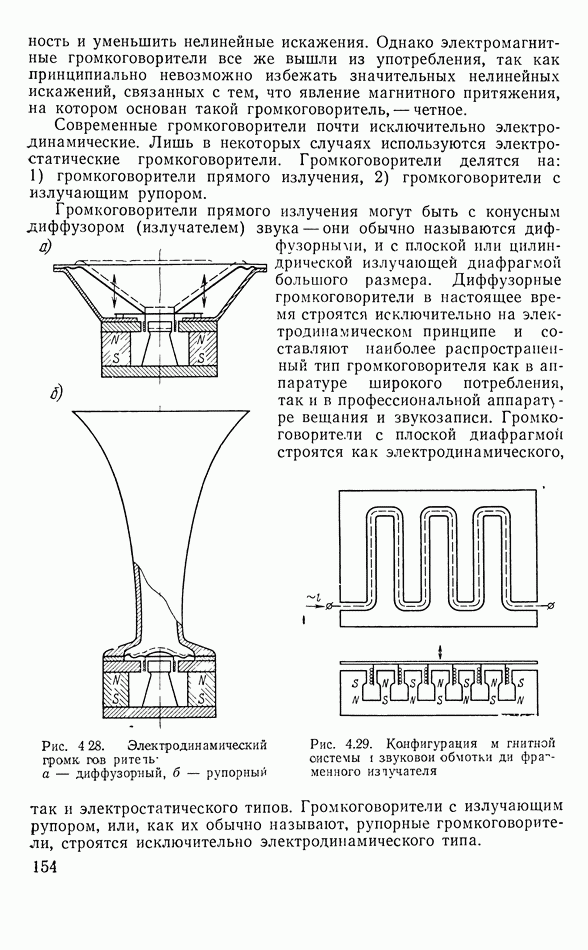
- 4.9. ОБЩИЕ СВЕДЕНИЯ О ГРОМКОГОВОРИТЕЛЯХ
- 4.10. ДИФФУЗОРНЫЕ ГРОМКОГОВОРИТЕЛИ
- Частотная характеристика чувствительности
- Влияние способа установки громкоговорителя на излучение в области низких частот
- Работа громкоговорителя в области высоких частот
- Комбинированные громкоговорители
- Нелинейные искажения в громкоговорителе
- 4.11. РУПОРНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- Влияние конечной длины рупора
- Широкогорлый громкоговоритель
- Громкоговорящие агрегаты
- 4.12. ЭЛЕКТРОСТАТИЧЕСКИЙ ГРОМКОГОВОРИТЕЛЬ
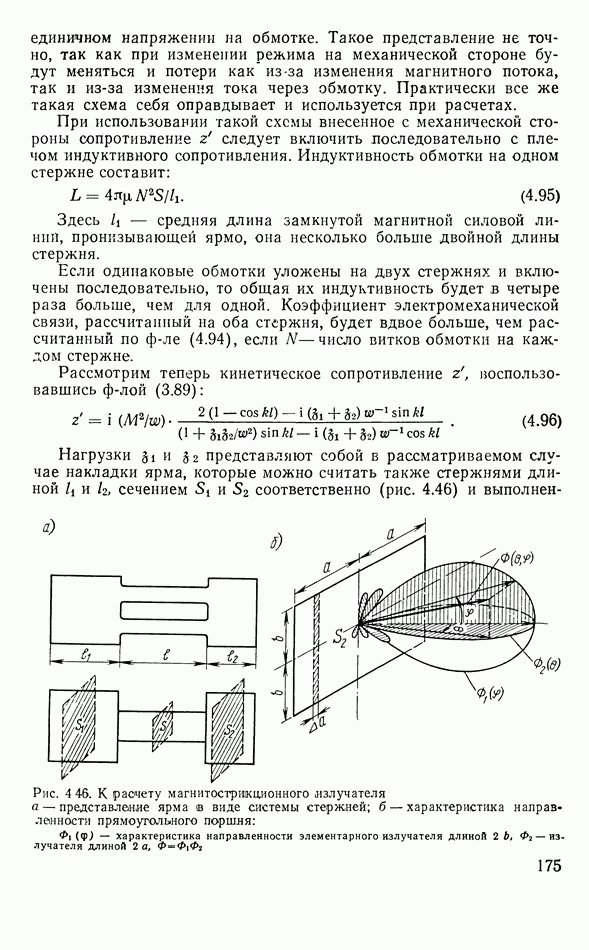
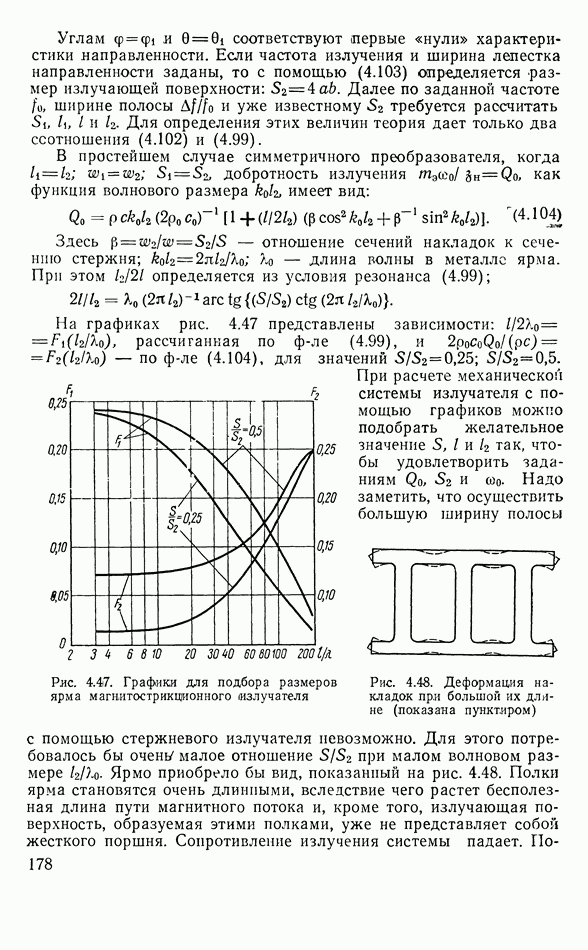
- 4.13. МАГНИТОСТРИКЦИОННЫЕ ИЗЛУЧАТЕЛИ
- Стержневой излучатель
- Кольцевой излучатель
- Круговая диаграмма преобразователя
- Коэффициент полезного действия излучателя
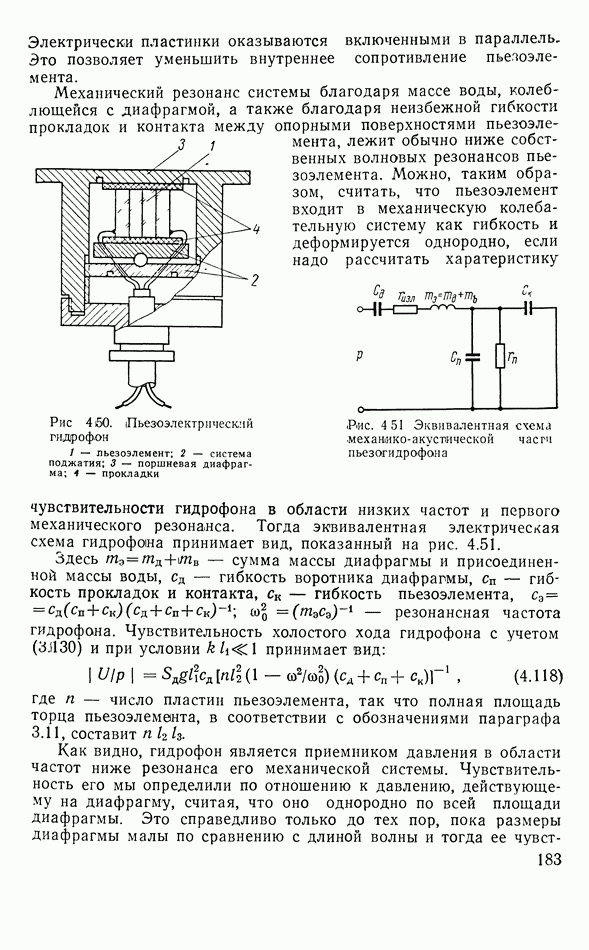
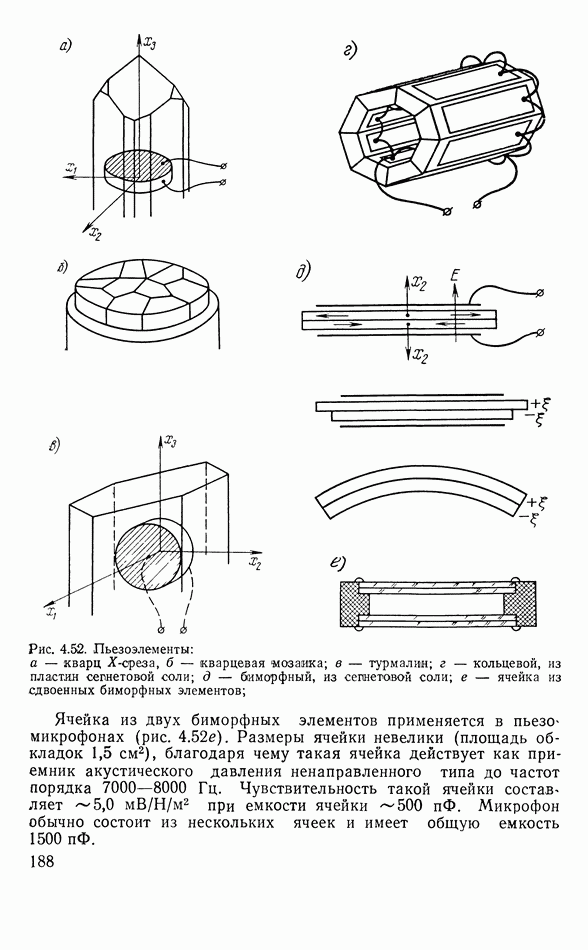
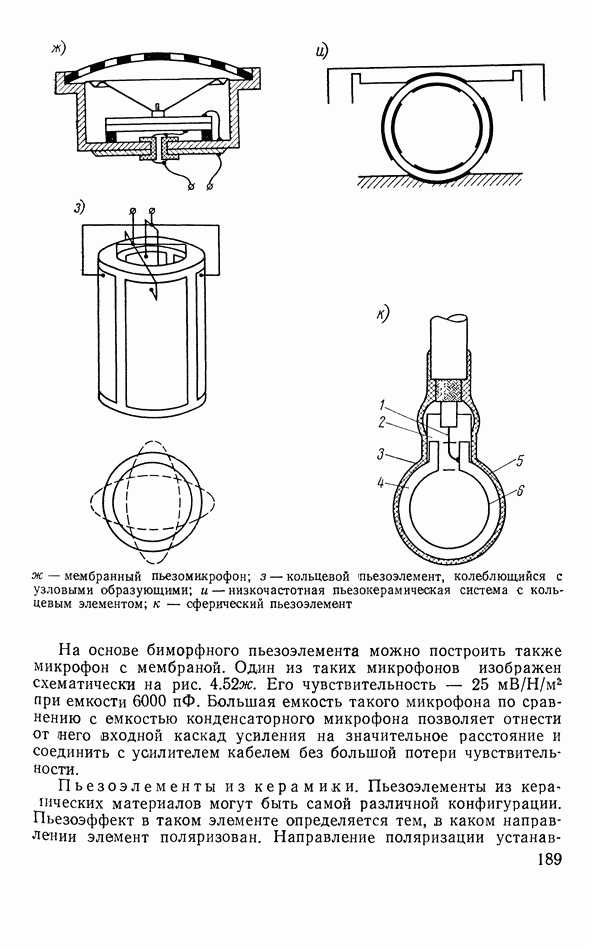
- 4.14. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- Линия задержки
- Другие типы пьезоэлектрических элементов электроакустических аппаратов
- Согласование пьезоэлемента с электрической частью системы
- 4.15. ЭЛЕКТРОДИНАМИЧЕСКИЙ ГЕОФОН
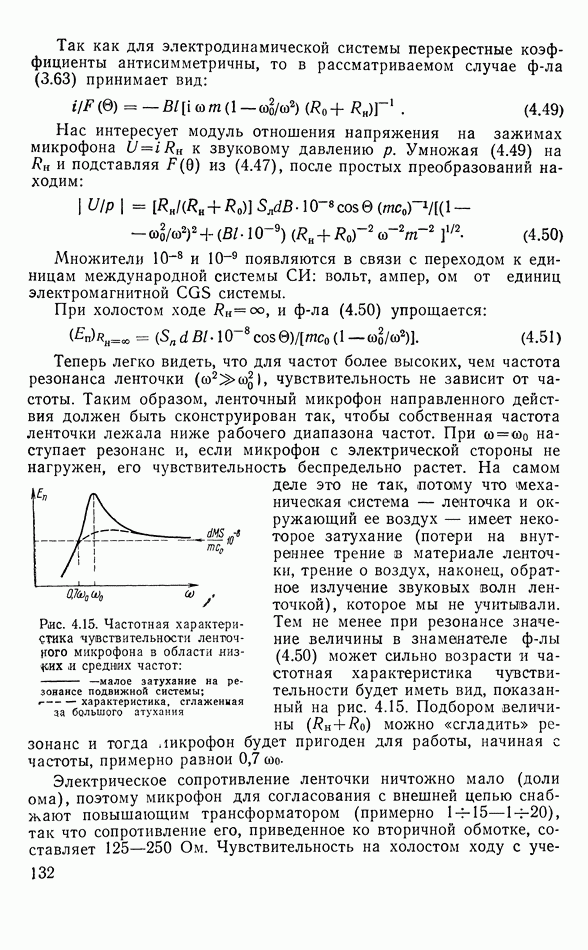
- Частотная характеристика чувствительности
- Максимальная чувствительность
- 4.16. СЕЙСМОМЕТРИЧЕСКИЙ ПРИЕМНИК СМЕЩЕНИЯ
- 4.17. ОПТИМИЗАЦИЯ КОНСТРУКТИВНЫХ РАЗМЕРОВ ЭЛЕКТРОАКУСТИЧЕСКОГО АППАРАТА
- Глава 5. Необратимые преобразователи
- 5.2. ПНЕВМОАКУСТИЧЕСКИЕ ИЗЛУЧАТЕЛИ
- Модуляция потока воздуха
- Пневматическая сирена
- Модулятор с возвратно-поступательным движением
- 5.3. ГИДРАВЛИЧЕСКАЯ СИРЕНА
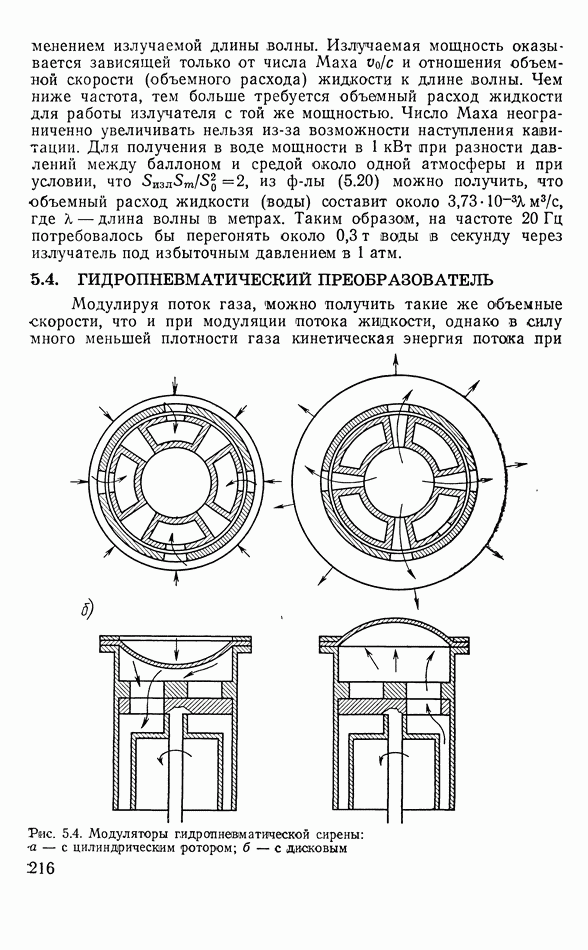
- 5.4. ГИДРОПНЕВМАТИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ
- 5.5. ПАРАМЕТРИЧЕСКИЕ ПРИЕМНИКИ
- 5.6. ПЬЕЗОРЕЗИСТИВНЫЕ ПОЛУПРОВОДНИКОВЫЕ ПРИЕМНИКИ ЗВУКА И ВИБРАЦИЙ
- Глава 6. Запись звука
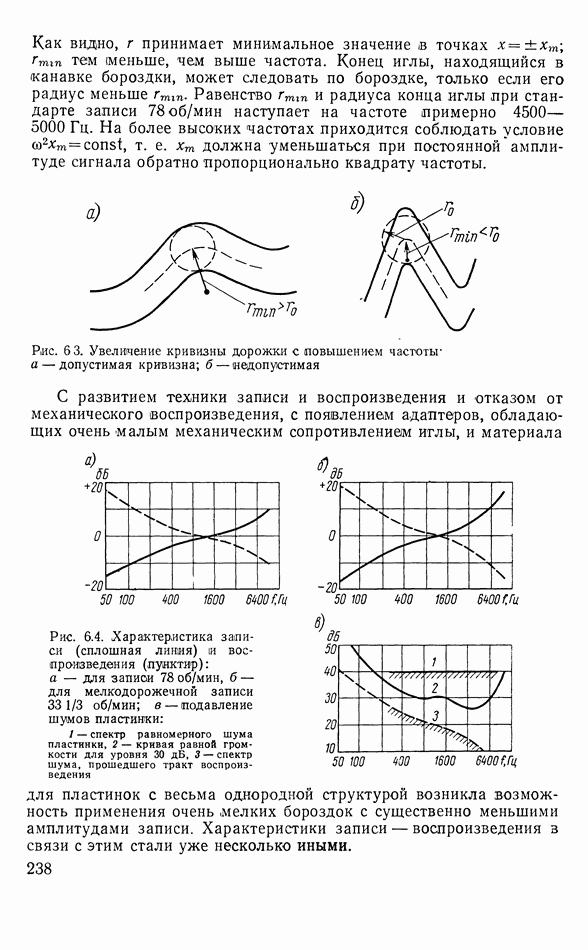
- 6.2. МЕХАНИЧЕСКАЯ ЗАПИСЬ
- Рекордеры
- Электромеханическая обратная связь в рекордере
- Электродинамический рекордер
- Краткие сведения о звукоснимателях
- Стереограммофонная запись
- 6.3. ОПТИЧЕСКАЯ ЗАПИСЬ ЗВУКА
- Оптическая запись с использованием модуляции
- Уменьшение шумового фона при записи по методу переменной ширины
- Щелевые искажения записи
- 6.4. МАГНИТНАЯ ЗАПИСЬ ЗВУКА
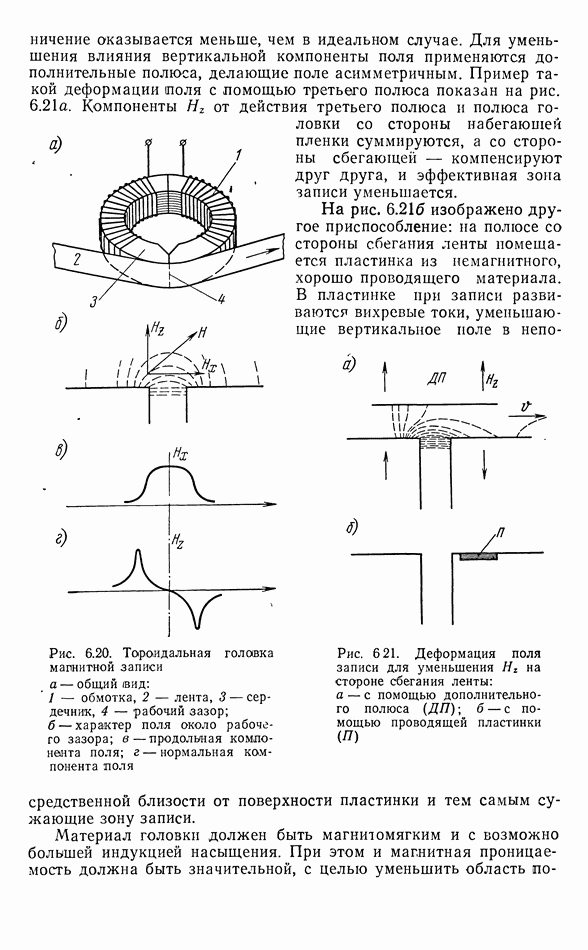
- Головки записи и воспроизведения
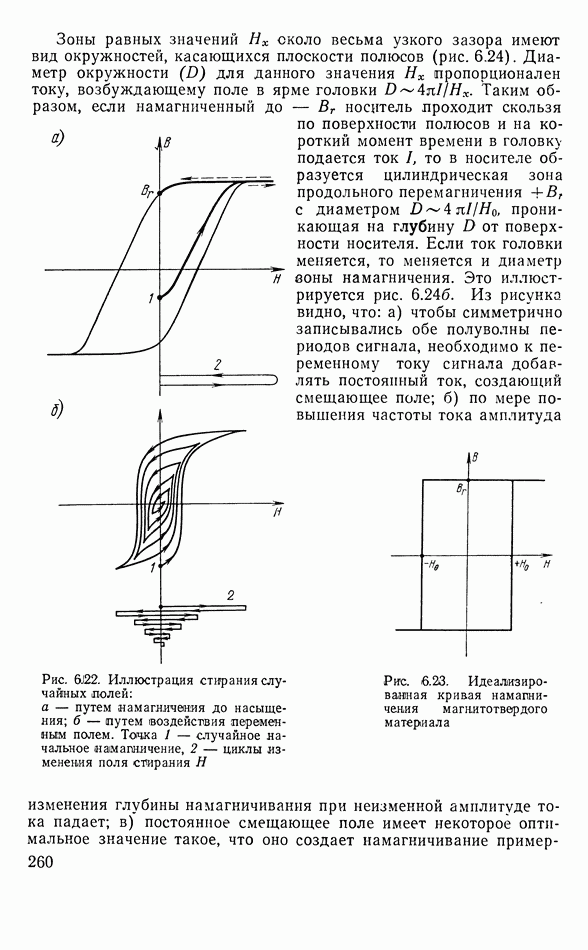
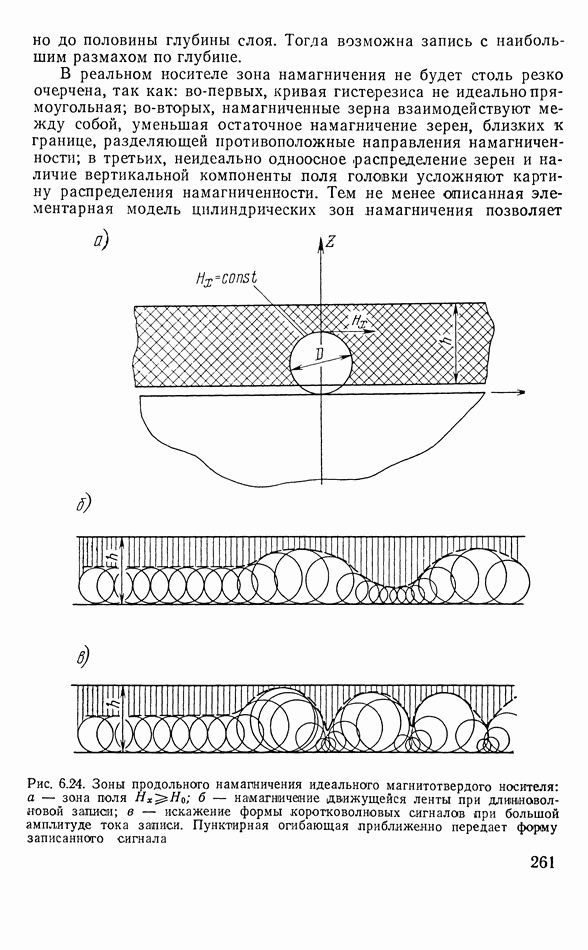
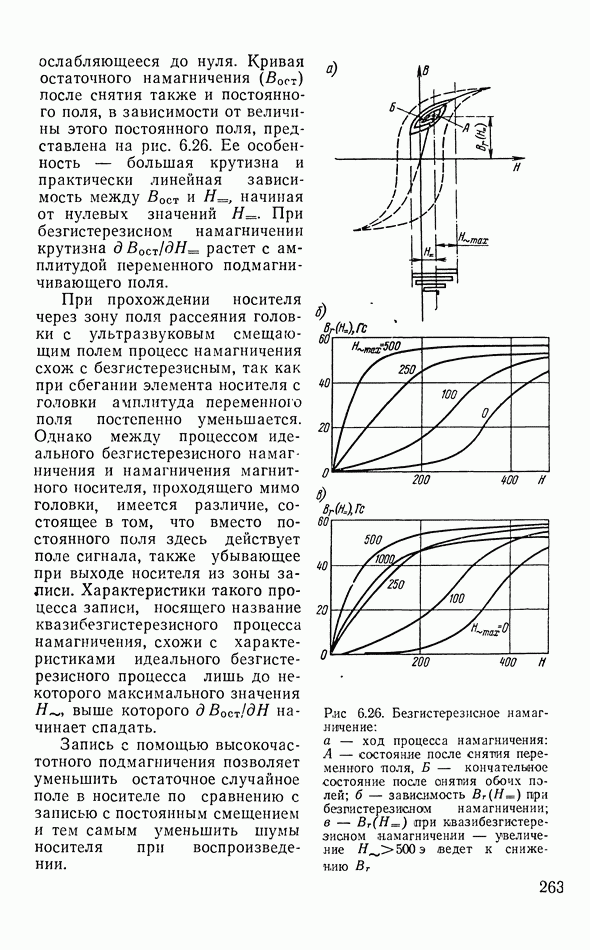
- Процесс намагничения магнитной ленты полем головки
- Воспроизведение записи
- Сквозная амплитудно-частотная характеристика записи
- Запись низких частот
- Плавающие головки
- Точность механизма транспортировки звуконосителя
- Список литературы