| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
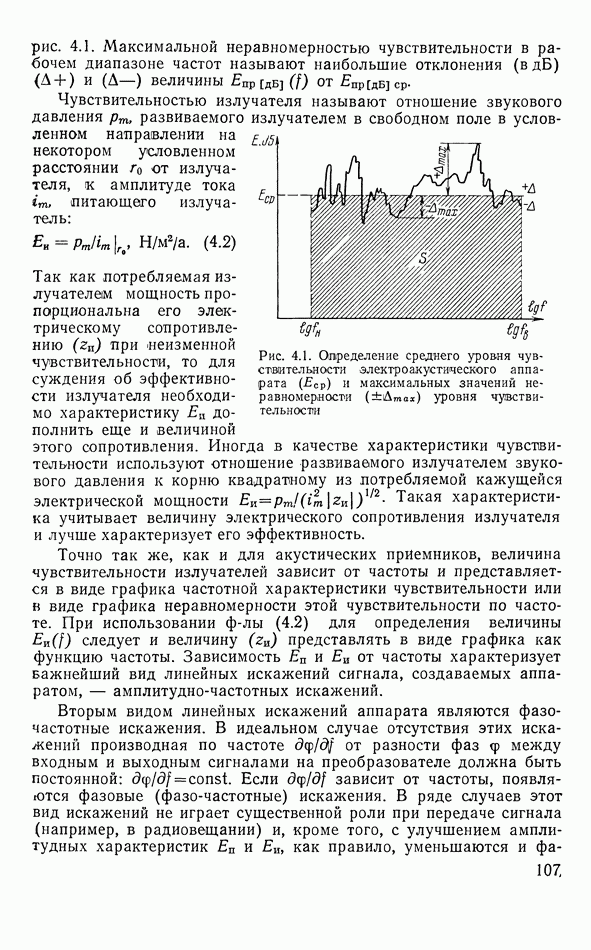
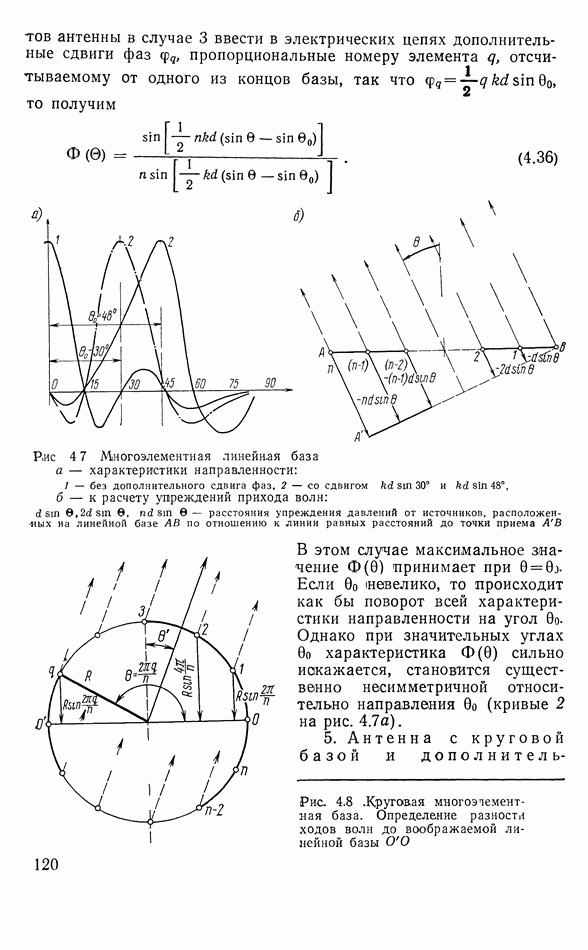
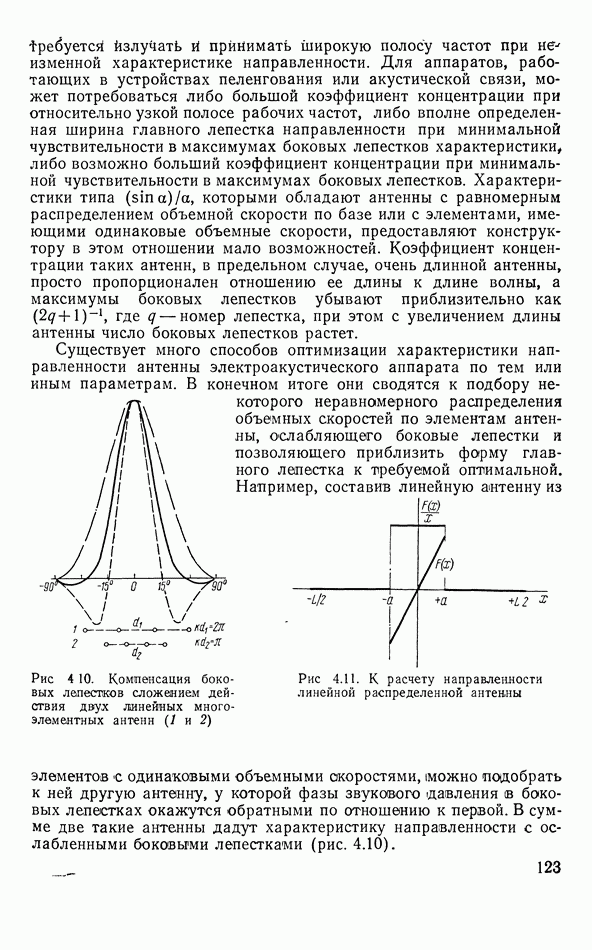
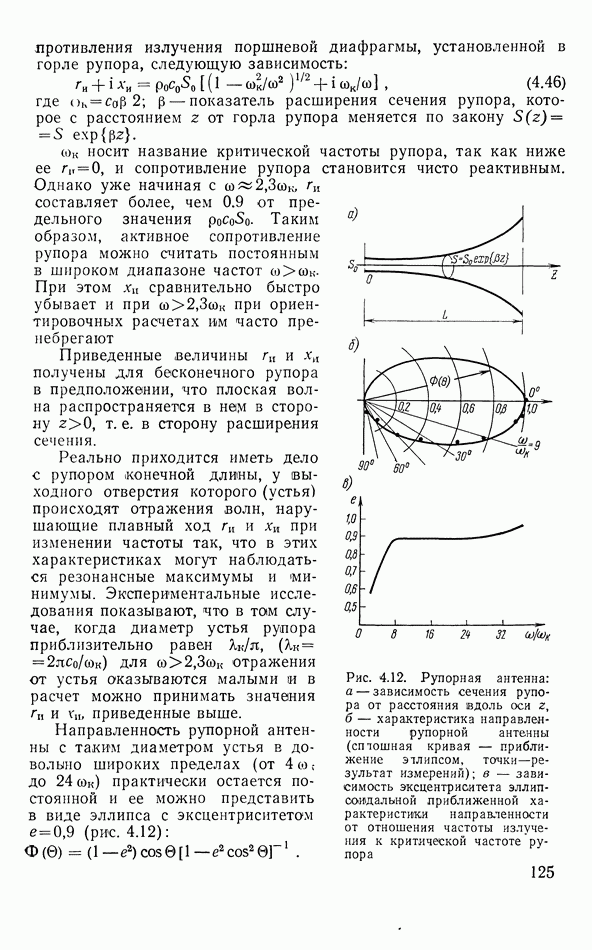
3.11. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
Местные уравнения преобразователя
Пьезоэффект, открытый братьями Кюри, состоит в том, что некоторые кристаллы поляризуются при сжатии и растяжении. При приложении механической нагрузки к граням кристалла изменяются расстояния между атомами кристаллической решетки и может
также изменяться и расположение зарядов — происходит сдвиг электронной решетки относительно положительно заряженных атомов. Такой сдвиг возможен не во всех кристаллах, а только при определенных видах симметрии кристалла, и только в том случае, когда он ведет к уменьшению общей энергии, запасаемой кристаллом под действием внешних сил. Теоретический анализ этого явления проводится на основании исследования структуры и энергетических состояний атомной кристаллической решетки.
Результатом сдвига зарядов в решетке является электрическая поляризация  кристалла. Сумма всех электрических моментов поляризованных ячеек решетки кристалла в единице объема оказывается в широких пределах пропорциональной механическому напряжению а, действующему в кристалле. Направления поляризации и механического напряжения могут совпадать, а могут и не совпадать. Механические напряжения, вызывающие пьезоэффект, могут иметь как характер растяжения (сжатия), так и сдвига. Соотношение между абсолютными величинами
кристалла. Сумма всех электрических моментов поляризованных ячеек решетки кристалла в единице объема оказывается в широких пределах пропорциональной механическому напряжению а, действующему в кристалле. Направления поляризации и механического напряжения могут совпадать, а могут и не совпадать. Механические напряжения, вызывающие пьезоэффект, могут иметь как характер растяжения (сжатия), так и сдвига. Соотношение между абсолютными величинами  можно записать так:
можно записать так:

Электрическая индукция, или поверхностная плотность зарядов в поляризованном диэлектрике, как известно, записывается так:

где  — напряженность электрического поля в диэлектрике,
— напряженность электрического поля в диэлектрике,  диэлектрическая постоянная.
диэлектрическая постоянная.
Если электрическое поле отсутствует  то
то  Поэтому соотношение (3.91) можно переписать так:
Поэтому соотношение (3.91) можно переписать так:

Знак  означает, что отношение в левой части (3.92) берется для случая отсутствия напряженности электрического поля в кристалле.
означает, что отношение в левой части (3.92) берется для случая отсутствия напряженности электрического поля в кристалле.
Величина  носит название пьезомодуля кристалла. Обратный пьезоэффект, предсказанный Липпманом, состоит в том, что приложение электрического ноля к кристаллу вызывает его деформацию. Количественно это соотношение выглядит так:
носит название пьезомодуля кристалла. Обратный пьезоэффект, предсказанный Липпманом, состоит в том, что приложение электрического ноля к кристаллу вызывает его деформацию. Количественно это соотношение выглядит так:

Коэффициентом пропорциональности между напряженностью электрического поля и деформацией  при отсутствии механических напряжений в кристалле
при отсутствии механических напряжений в кристалле  является тот же пьезомодуль. Равенства (3.92) и (3.93) дают соотношение взаимности для пьезоэлектрического преобразователя в элементарной форме:
является тот же пьезомодуль. Равенства (3.92) и (3.93) дают соотношение взаимности для пьезоэлектрического преобразователя в элементарной форме:

Соотношение (3.94) может быть записано с помощью плотности тока поляризации  или
или  Перемещение
Перемещение  может
может
быть выражено через скорость  а деформация
а деформация  через скорость деформации
через скорость деформации  после чего (3.94) приобретает вид аналогичный виду соотношения (3.51):
после чего (3.94) приобретает вид аналогичный виду соотношения (3.51):

Таким образом, соотношения взаимности, вытекающие из свойств пьезоэффекта, приводят к уравнениям в форме у. При этом следует сопоставлять  и так что уравнения примут вид:
и так что уравнения примут вид:

Теперь можно найти коэффициенты  Полагая в первом из ур-ний
Полагая в первом из ур-ний  получим
получим

Следовательно,  выражает обычное соотношение между поляризацией и напряженностью поля в диэлектрике, определяемое диэлектрической постоянной. При этом, поскольку имеем дело с пьезоэлектриком, приходится указывать, что диэлектрическая постоянная относится к кристаллу, в котором нет механических напряжений
выражает обычное соотношение между поляризацией и напряженностью поля в диэлектрике, определяемое диэлектрической постоянной. При этом, поскольку имеем дело с пьезоэлектриком, приходится указывать, что диэлектрическая постоянная относится к кристаллу, в котором нет механических напряжений  . С этой целью
. С этой целью  пишем с нижним индексом о.
пишем с нижним индексом о.
Полагая во втором ур-нии (3.96)  найдем
найдем

Как видно,  определяется отношением деформации к механическому напряжению в отсутствие электрического поля. Для элемента объема упругого тела
определяется отношением деформации к механическому напряжению в отсутствие электрического поля. Для элемента объема упругого тела  это его модуль упругости, так что можно написать:
это его модуль упругости, так что можно написать:

Индекс  у величины
у величины  означает, что модуль упругости определен для случая, когда электрическое поле в кристалле отсутствует.
означает, что модуль упругости определен для случая, когда электрическое поле в кристалле отсутствует.
Теперь уравнения для пьезопреобразователя могут быть записаны так:

Очень часто при рассмотрении свойств пьезопреобразователей используют не скорости деформаций  и плотности токов
и плотности токов  а сами деформации и плотности зарядов. Тогда вместо ур-ний (3.100) получатся следующие:
а сами деформации и плотности зарядов. Тогда вместо ур-ний (3.100) получатся следующие:

Такая запись несколько экономнее. Можно также записать уравнение в форме 

При этом модуль упругости  следует определить в отсутствие поляризации
следует определить в отсутствие поляризации  а не поля, и диэлектрическую постоянную — в отсутствие деформации
а не поля, и диэлектрическую постоянную — в отсутствие деформации  а не механических напряжений. Параметр взаимности
а не механических напряжений. Параметр взаимности  также будет другой.
также будет другой.
Уравнения (3.101) и (3.101а) называют местными уравнениями пьезопреобразователя, так как они описывают связи между величинами электрического поля и механического напряженного состояния тела в данном месте — данной бесконечно малой области этого тела.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. Краткие сведения по физиологической акустике
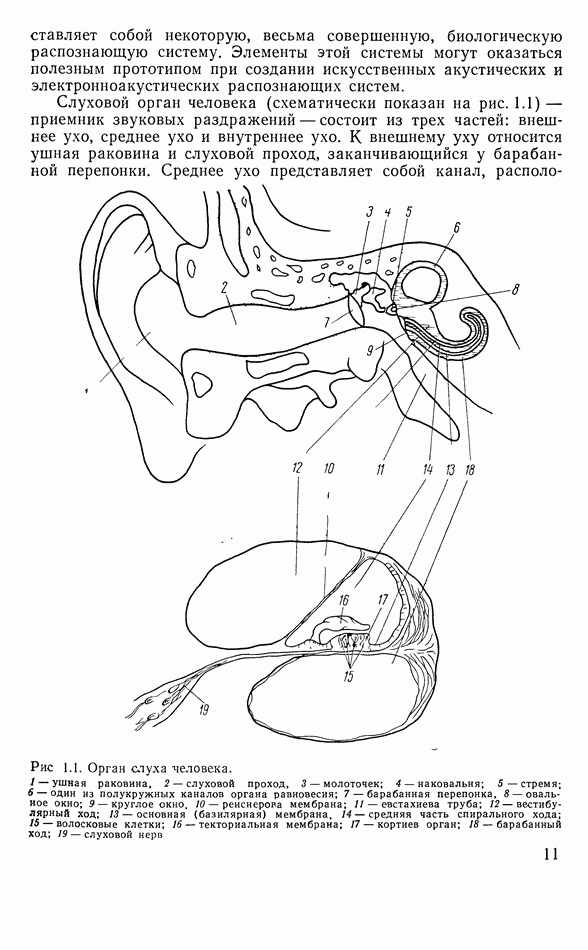
- 1.1. УСТРОЙСТВО СЛУХОВОГО ОРГАНА ЧЕЛОВЕКА
- 1.2. МЕХАНИЗМ ВОЗБУЖДЕНИЯ СЛУХОВОГО НЕРВА
- 1.3. ТЕОРИЯ СЛУХА
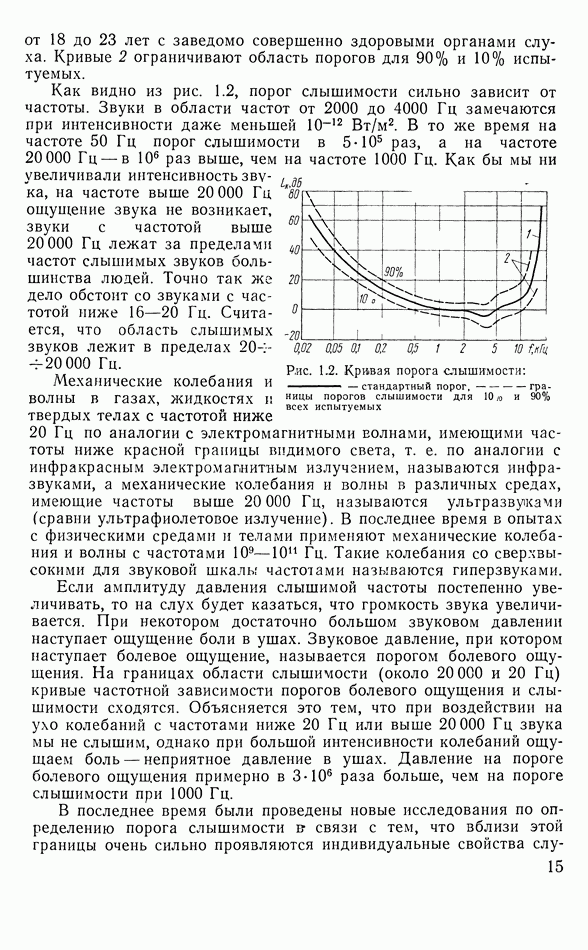
- 1.4. ПОРОГ СЛЫШИМОСТИ
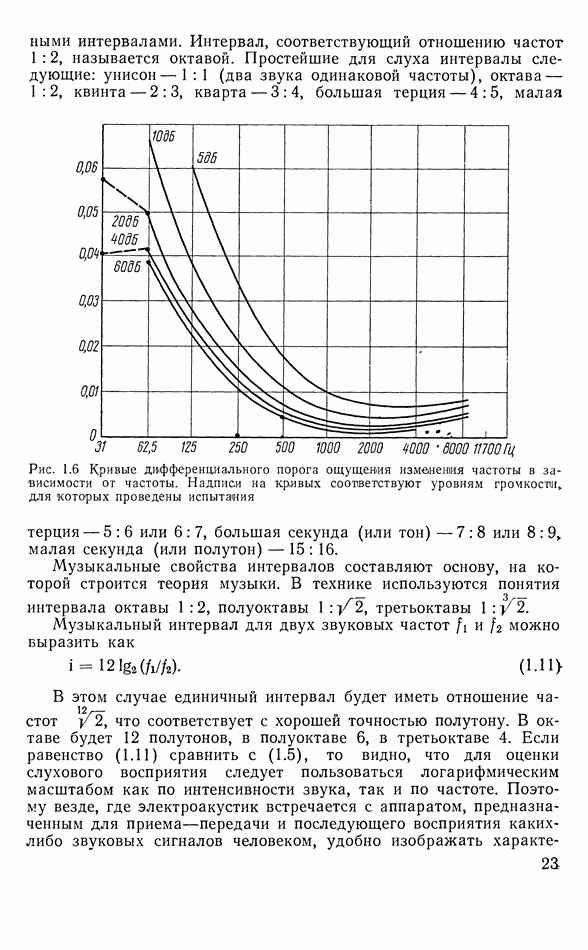
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЙ ПОРОГ ВОСПРИЯТИЯ ИНТЕНСИВНОСТИ ЗВУКА
- 1.6. ЛОГАРИФМИЧЕСКИЕ УРОВНИ. ШКАЛА ДЕЦИБЕЛ
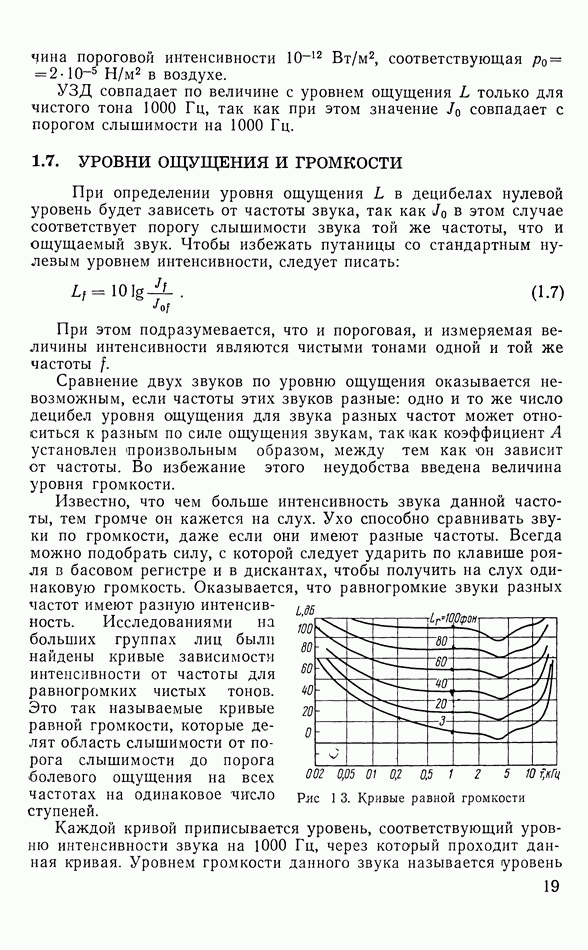
- 1.7. УРОВНИ ОЩУЩЕНИЯ И ГРОМКОСТИ
- 1.8. ГРОМКОСТЬ ЧИСТЫХ ТОНОВ
- 1.9. КРИТИЧЕСКИЕ ПОЛОСЫ СЛУХА
- 1.10. УРОВЕНЬ ГРОМКОСТИ СЛОЖНЫХ ЗВУКОВ
- 1.11. ВОСПРИЯТИЕ ВЫСОТЫ ТОНА. ШКАЛА ЧАСТОТ
- 1.12. МАСКИРОВКА ЗВУКА
- 1.13. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- 1.14. ВОСПРИЯТИЕ ОКРАСКИ (ТЕМБРА) ЗВУКА
- Глава 2. Электромеханические и электроакустические аналогии
- 2.1. ПРИНЦИП ЭЛЕКТРОМЕХАНИЧЕСКИХ АНАЛОГИЙ
- 2.2. МЕХАНИЧЕСКИЕ ЭЛЕМЕНТЫ И МЕХАНИЧЕСКИЕ СИСТЕМЫ
- 2.3. ПРИМЕРЫ ИЗОБРАЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ И ИХ ЭКВИВАЛЕНТНЫХ СХЕМ
- 2.4. ПРАВИЛА И СПОСОБЫ ПЕРЕХОДА К ЭКВИВАЛЕНТНЫМ СХЕМАМ
- 2.5. ТРАНСФОРМАЦИЯ СИЛ И СКОРОСТЕЙ. ЭЛЕКТРИЧЕСКИЙ АНАЛОГ-ТРАНСФОРМАТОР
- 2.6. ЭЛЕКТРОАКУСТИЧЕСКИЕ АНАЛОГИИ
- 2.7. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИИ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
- 2.8. ЭКВИВАЛЕНТНЫЕ СОСРЕДОТОЧЕННЫЕ ПАРАМЕТРЫ МЕХАНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ
- Глава 3. Электромеханические преобразователи
- 3.2. ДВА ОСНОВНЫХ ТИПА ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.3. ОБЩАЯ ТЕОРИЯ ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.4. ВТОРИЧНЫЕ ПАРАМЕТРЫ ПРЕОБРАЗОВАТЕЛЯ
- 3.5. ПРАВИЛО ЗНАКОВ
- 3.6. ВХОДНОЕ СОПРОТИВЛЕНИЕ СИСТЕМЫ В ОБЩЕМ СЛУЧАЕ
- 3.7. ЧУВСТВИТЕЛЬНОСТЬ ПРЕОБРАЗОВАТЕЛЯ
- 3.8. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ПРЕОБРАЗОВАТЕЛЯ
- 3.9. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.10. МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.11. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Преобразователь с однородной деформацией
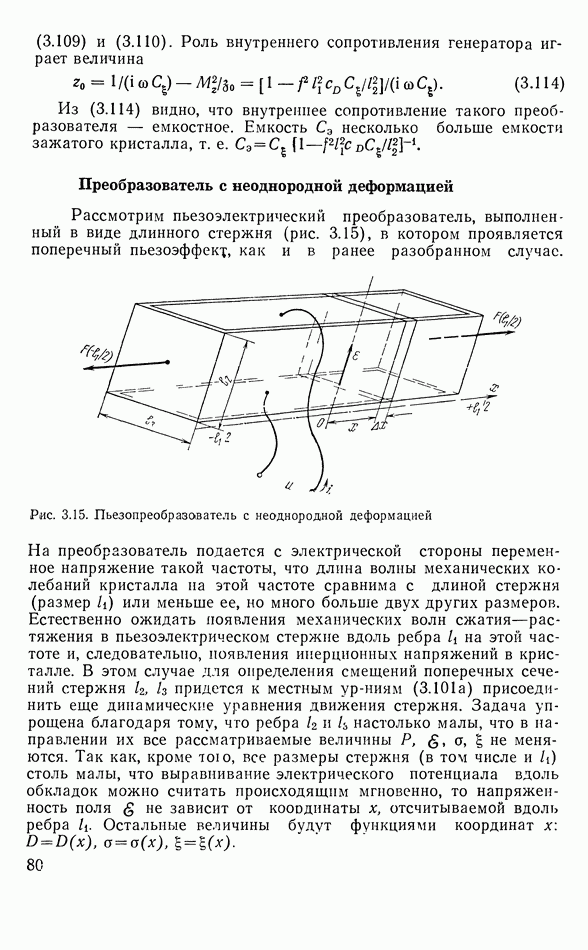
- Преобразователь с неоднородной деформацией
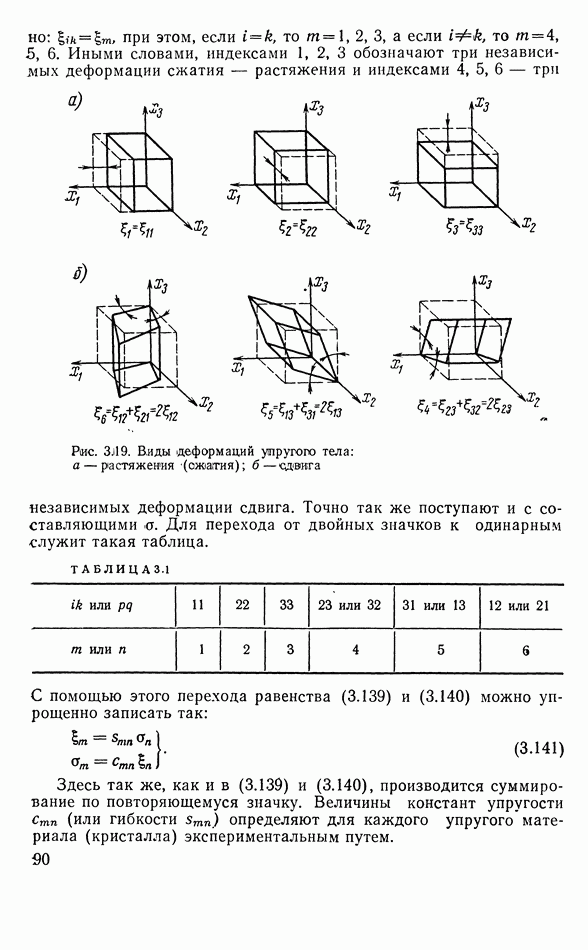
- Местные уравнения пьезопреобразователя в тензорной форме
- Свойства основных пьезоэлектрических кристаллов
- Выбор среза кристалла при изготовлении пьезоэлементов
- Искусственные пьезокерамические материалы
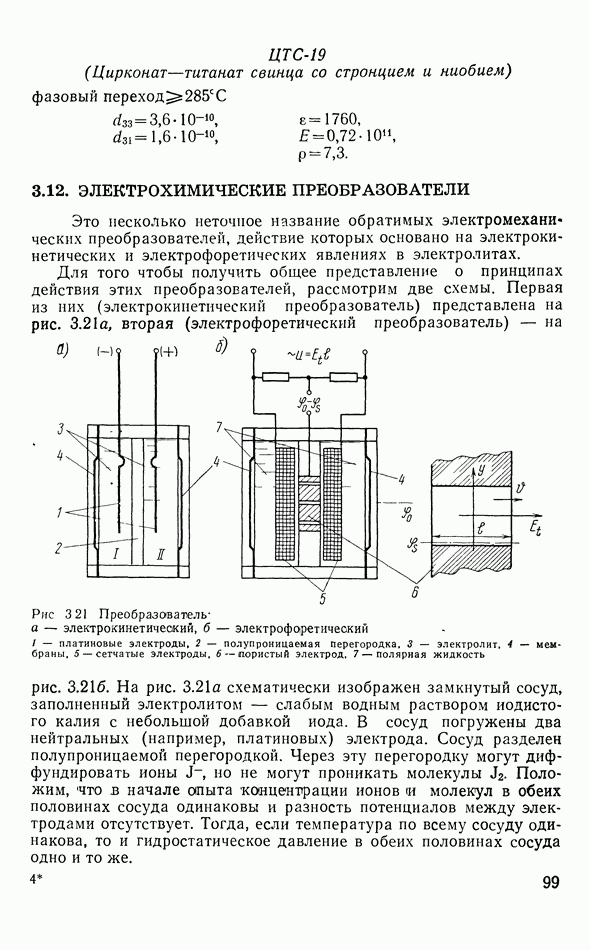
- 3.12. ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 4. Электроакустическая аппаратура
- 4.1. КЛАССИФИКАЦИЯ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- 4.2. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 4.3. АНТЕННЫ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- Связь между чувствительностью приемной и излучающей антенн
- Сопротивление излучения антенны
- Сложные антенны
- Распределенные антенны
- Антенна бегущей волны
- Антенна из направленных элементов
- Оптимизация характеристики направленности антенны
- Рупорная антенна
- 4.4. ТРЕБОВАНИЯ К ЭЛЕКТРОАКУСТИЧЕСКОЙ АППАРАТУРЕ РАДИОВЕЩАНИЯ И ТЕЛЕВИДЕНИЯ
- 4.5. ЛЕНТОЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Ненаправленный микрофон-приемник давления
- Микрофон с кардиоидной характеристикой направленности
- Микрофон с регулируемой характеристикой направленности
- 4.6. КАТУШЕЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Однонаправленный микрофон
- Биградиентный микрофон
- Сверхнаправленный микрофон
- 4.7. СОГЛАСОВАНИЕ ЭЛЕКТРИЧЕСКОЙ СТОРОНЫ ЭЛЕКТРОДИНАМИЧЕСКОГО МИКРОФОНА СО ВХОДОМ МИКРОФОННОГО УСИЛИТЕЛЯ
- 4.8. КОНДЕНСАТОРНЫЕ МИКРОФОНЫ
- Об отрицательной упругости электрического поля поляризации в микрофоне
- Предельная чувствительность микрофона
- Влияние емкости входа предварительного каскада
- Микрофон направленного действия
- 4.9. ОБЩИЕ СВЕДЕНИЯ О ГРОМКОГОВОРИТЕЛЯХ
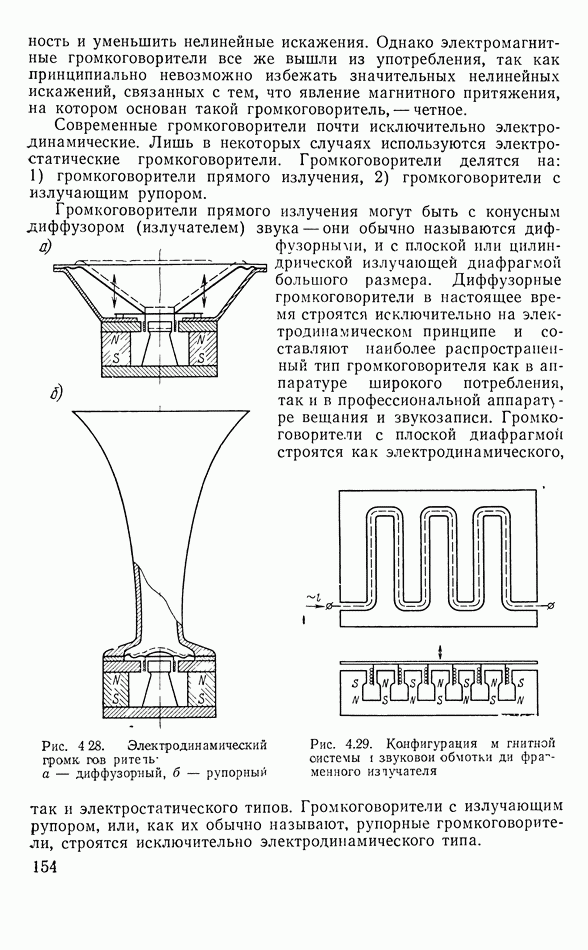
- 4.10. ДИФФУЗОРНЫЕ ГРОМКОГОВОРИТЕЛИ
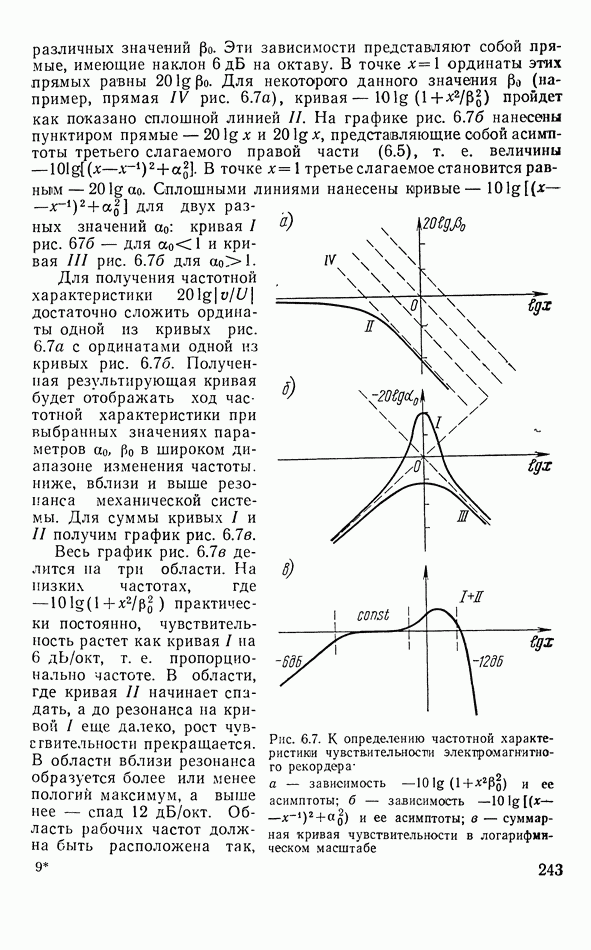
- Частотная характеристика чувствительности
- Влияние способа установки громкоговорителя на излучение в области низких частот
- Работа громкоговорителя в области высоких частот
- Комбинированные громкоговорители
- Нелинейные искажения в громкоговорителе
- 4.11. РУПОРНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- Влияние конечной длины рупора
- Широкогорлый громкоговоритель
- Громкоговорящие агрегаты
- 4.12. ЭЛЕКТРОСТАТИЧЕСКИЙ ГРОМКОГОВОРИТЕЛЬ
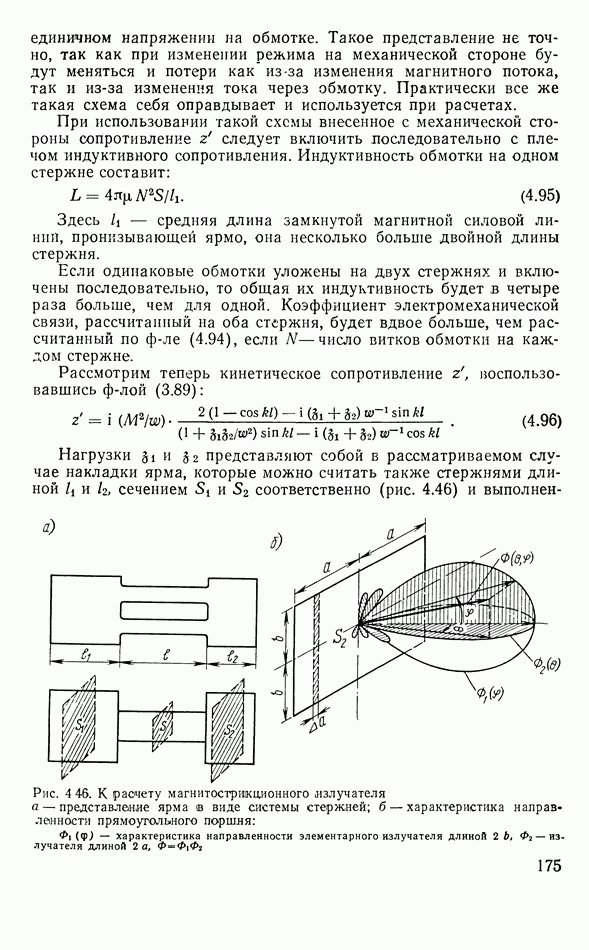
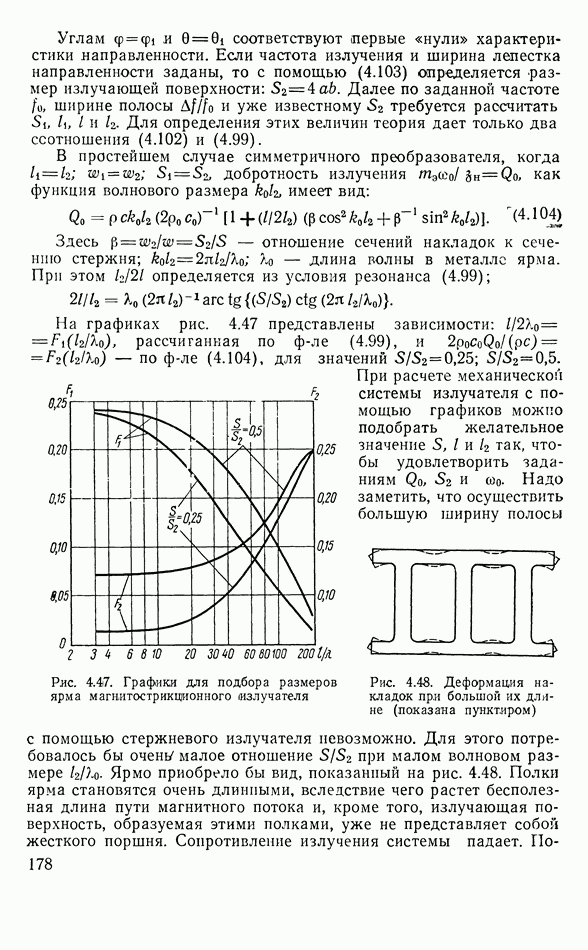
- 4.13. МАГНИТОСТРИКЦИОННЫЕ ИЗЛУЧАТЕЛИ
- Стержневой излучатель
- Кольцевой излучатель
- Круговая диаграмма преобразователя
- Коэффициент полезного действия излучателя
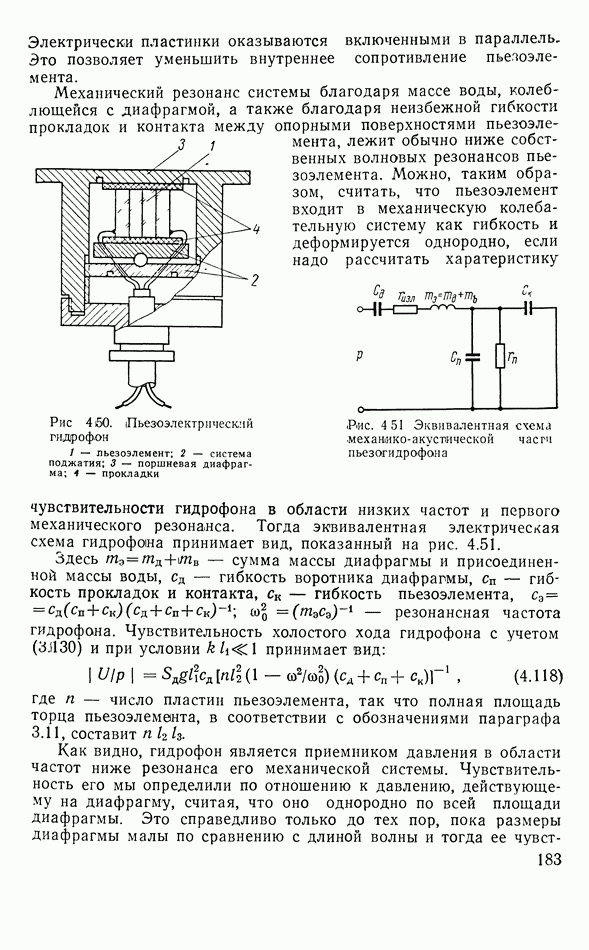
- 4.14. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- Линия задержки
- Другие типы пьезоэлектрических элементов электроакустических аппаратов
- Согласование пьезоэлемента с электрической частью системы
- 4.15. ЭЛЕКТРОДИНАМИЧЕСКИЙ ГЕОФОН
- Частотная характеристика чувствительности
- Максимальная чувствительность
- 4.16. СЕЙСМОМЕТРИЧЕСКИЙ ПРИЕМНИК СМЕЩЕНИЯ
- 4.17. ОПТИМИЗАЦИЯ КОНСТРУКТИВНЫХ РАЗМЕРОВ ЭЛЕКТРОАКУСТИЧЕСКОГО АППАРАТА
- Глава 5. Необратимые преобразователи
- 5.2. ПНЕВМОАКУСТИЧЕСКИЕ ИЗЛУЧАТЕЛИ
- Модуляция потока воздуха
- Пневматическая сирена
- Модулятор с возвратно-поступательным движением
- 5.3. ГИДРАВЛИЧЕСКАЯ СИРЕНА
- 5.4. ГИДРОПНЕВМАТИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ
- 5.5. ПАРАМЕТРИЧЕСКИЕ ПРИЕМНИКИ
- 5.6. ПЬЕЗОРЕЗИСТИВНЫЕ ПОЛУПРОВОДНИКОВЫЕ ПРИЕМНИКИ ЗВУКА И ВИБРАЦИЙ
- Глава 6. Запись звука
- 6.2. МЕХАНИЧЕСКАЯ ЗАПИСЬ
- Рекордеры
- Электромеханическая обратная связь в рекордере
- Электродинамический рекордер
- Краткие сведения о звукоснимателях
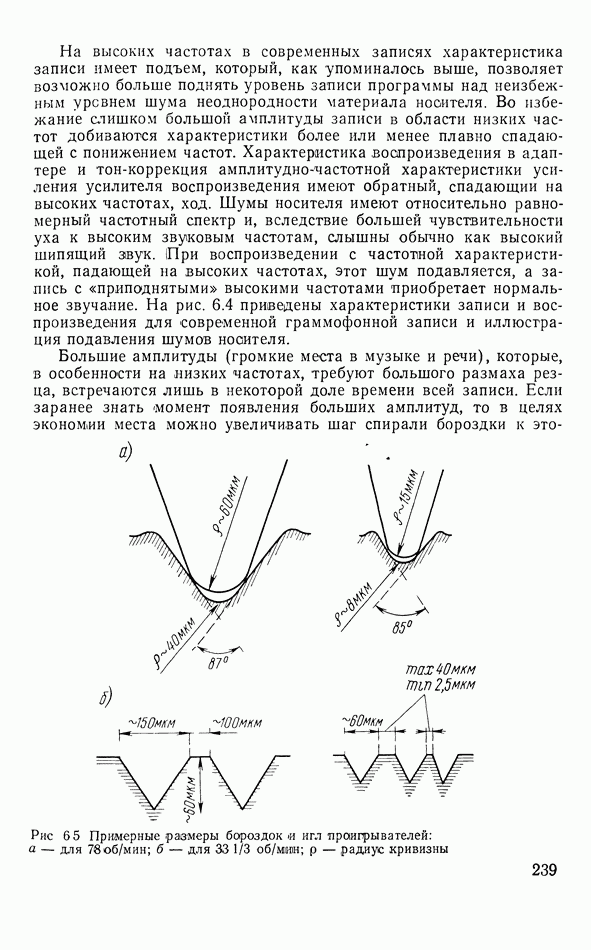
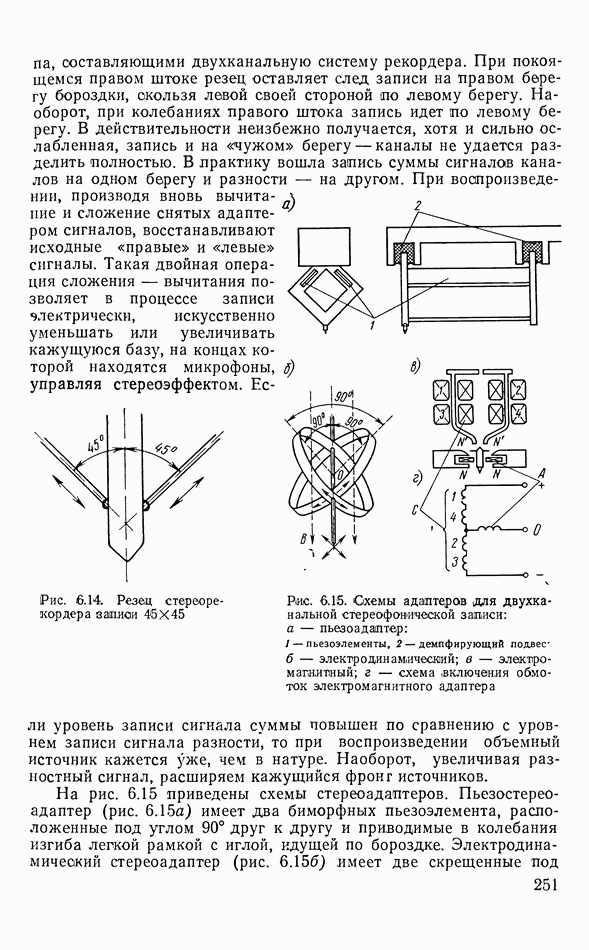
- Стереограммофонная запись
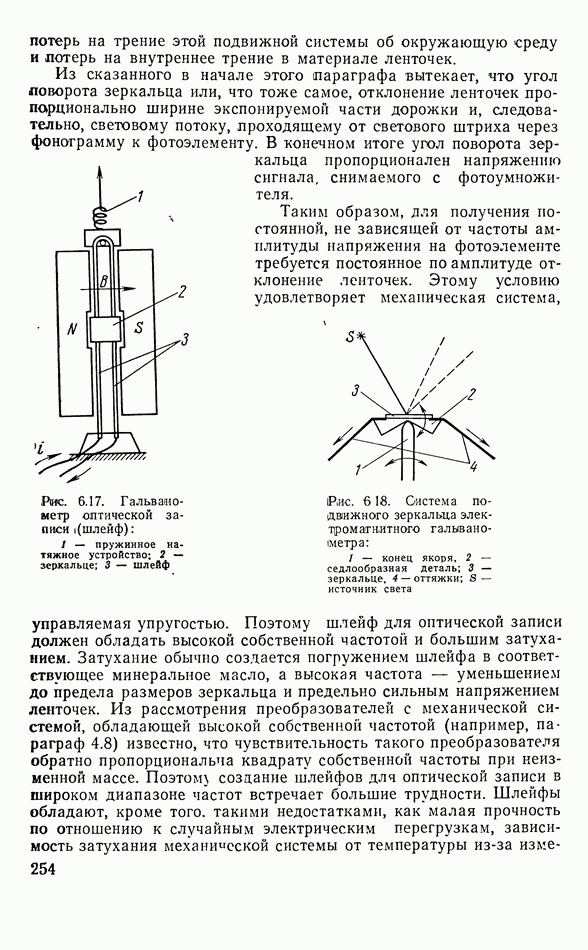
- 6.3. ОПТИЧЕСКАЯ ЗАПИСЬ ЗВУКА
- Оптическая запись с использованием модуляции
- Уменьшение шумового фона при записи по методу переменной ширины
- Щелевые искажения записи
- 6.4. МАГНИТНАЯ ЗАПИСЬ ЗВУКА
- Головки записи и воспроизведения
- Процесс намагничения магнитной ленты полем головки
- Воспроизведение записи
- Сквозная амплитудно-частотная характеристика записи
- Запись низких частот
- Плавающие головки
- Точность механизма транспортировки звуконосителя
- Список литературы