| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.2. ДВА ОСНОВНЫХ ТИПА ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
Электродинамический преобразователь
Прежде чем начать изложение общей теории, рассмотрим преобразователи двух наиболее распространенных типов — электродинамический и электростатический, — чтобы на этих примерах познакомиться с основными свойствами обратимого преобразователя.
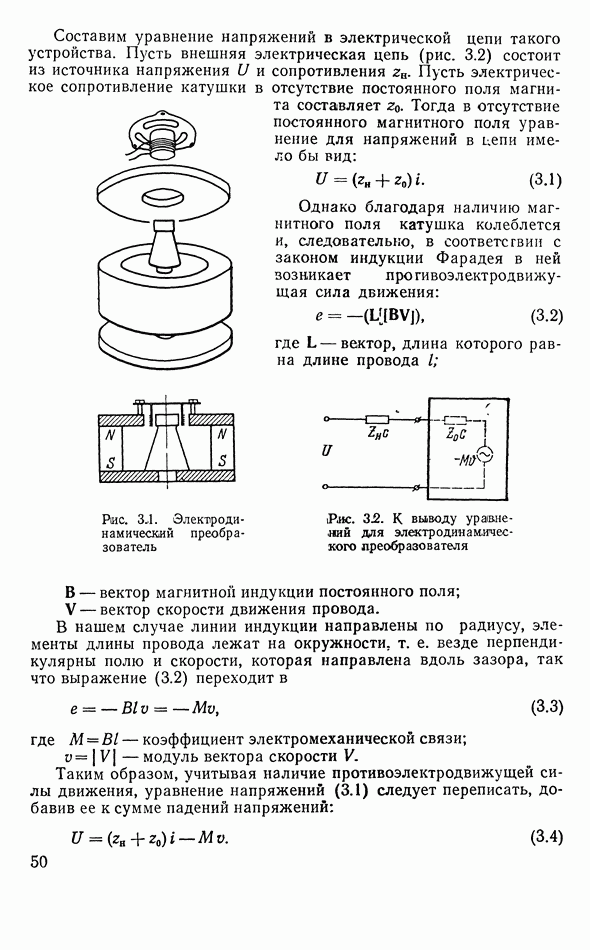
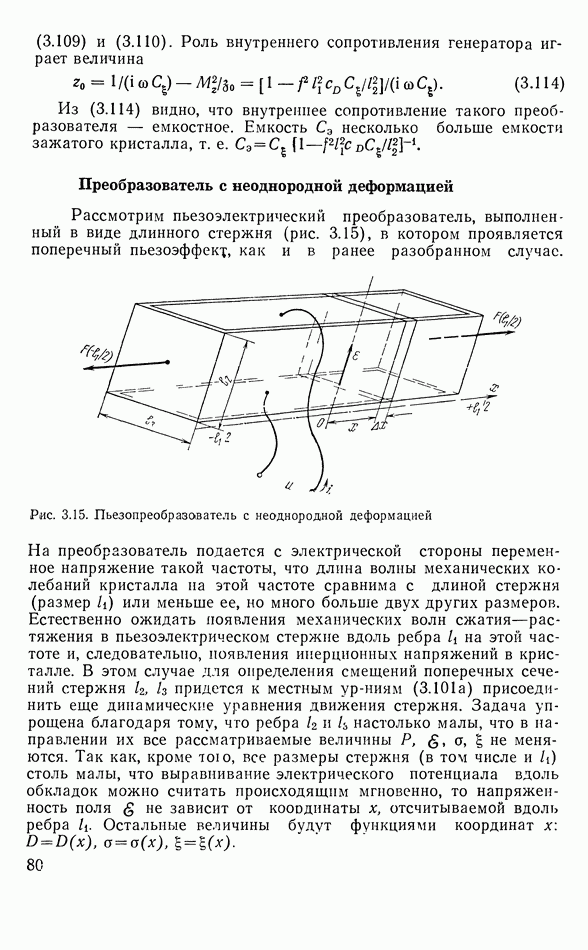
В большинстве электроакустических аппаратов используется электродинамический преобразователь, изображенный на. рис. 3.1.
Сильный кольцевой постоянный магнит создает в узком кольцевом зазоре равномерное магнитное поле. В зазоре помещена обмотка на легком кольцевом каркасе — так называемая подвижная катушка преобразователя. Она подвешена на гибком воротнике или растяжках так, что, колеблясь вдоль своей образующей (вдоль зазора), она не касается магнитной системы. Если к подвижной катушке подвести переменный ток, то, взаимодействуя с магнитным полем постоянного магнита, он вызовет механическую силу, которая будет колебать подвижную катушку. Если к подвижной катушке подсоединена какая-либо нагрузка (например, легкий поршень или диафрагма, излучающая звук в окружающий воздух), то такой преобразователь будет совершать механическую работу, преодолевая активное механическое сопротивление подвеса катушки и сопротивление излучения звука в воздух. Электрическая энергия, подводимая к катушке, частично перейдет в механическую, а частно рассеется в виде джоулева тепла. Полезный эффект в данном случае — это излученный звук. Мы не будем сейчас рассматривать, как именно излучается звук, будем просто считать, что кадушка, двигаясь, преодолевает некоторое механическое сопротивление.
Составим уравнение напряжений в электрической цепи такого устройства. Пусть внешняя электрическая цепь (рис. 3.2) состоит из источника напряжения  и сопротивления
и сопротивления  Пусть электрическое сопротивление катушки в отсутствие постоянного поля магнита составляет
Пусть электрическое сопротивление катушки в отсутствие постоянного поля магнита составляет  Тогда в отсутствие постоянного магнитного поля уравнение для напряжений в цепи имело бы вид:
Тогда в отсутствие постоянного магнитного поля уравнение для напряжений в цепи имело бы вид:

Однако благодаря наличию магнитного поля катушка колеблется и, следовательно, в соответствии с законом индукции Фарадея в ней возникает противоэлектродвижущая сила движения:

где  вектор, длина которого равна длине провода
вектор, длина которого равна длине провода  ; В — вектор магнитной индукции постоянного поля; V — вектор скорости движения провода.
; В — вектор магнитной индукции постоянного поля; V — вектор скорости движения провода.

Рис. 3.1. Электродинамический преобразователь

Рис. 3.2. К выводу уравнений для электродинамического преобразователя
В нашем случае линии индукции направлены по радиусу, элементы длины провода лежат на окружности, т. е. везде перпендикулярны полю и скорости, которая направлена вдоль зазора, так что выражение (3.2) переходит в

где  коэффициент электромеханической связи;
коэффициент электромеханической связи;  модуль вектора скорости
модуль вектора скорости 
Таким образом, учитывая наличие противоэлектродвижущей силы движения, уравнение напряжений (3.1) следует переписать, добавив ее к сумме падений напряжений:

Обозначив для сокращения  получим:
получим:

Напишем теперь уравнение равновесия сил на механической стороне нашего устройства. Для общности предположим, что к катушке приложена извне сторонняя сила  Если бы магнитное поле отсутствовало, то сторонняя сила
Если бы магнитное поле отсутствовало, то сторонняя сила  уравновешивалась бы силами, возникающими благодаря сопротивлению катушки
уравновешивалась бы силами, возникающими благодаря сопротивлению катушки  и механической нагрузке
и механической нагрузке  тогда условие равновесия сил записалось бы так:
тогда условие равновесия сил записалось бы так:

Однако благодаря наличию магнитного поля, которое взаимодействует с токами, протекающими по катушке, на нее, по закону Био-Савара, действует еще сила

В силу нормальности силовых линий к виткам катушки можно написать:

Сила  добавляется к правой части выражения (3.6), так как направление ее совпадает с направлением сил механического сопротивления катушки и нагрузки, так что:
добавляется к правой части выражения (3.6), так как направление ее совпадает с направлением сил механического сопротивления катушки и нагрузки, так что:

Здесь для краткости 
Формулы (3.5) и (3.9) — это два уравнения, связывающие механические величины  действующие на механической стороне преобразователя, с электрическими
действующие на механической стороне преобразователя, с электрическими  действующими на его электрической стороне:
действующими на его электрической стороне:

Зная любые две из величин  можно определить другие две, если известны параметры
можно определить другие две, если известны параметры  Заметим, что по абсолютной величине коэффициент при
Заметим, что по абсолютной величине коэффициент при  в первом уравнении равен коэффициенту при
в первом уравнении равен коэффициенту при  во втором уравнении, так что система (3.10) имеет только три независимых коэффициента. В ур-ниях (3.10) содержатся все свойства линейных электродинамических преобразователей, необходимые для расчетов.
во втором уравнении, так что система (3.10) имеет только три независимых коэффициента. В ур-ниях (3.10) содержатся все свойства линейных электродинамических преобразователей, необходимые для расчетов.
Для примера рассчитаем полное электрическое сопротивление преобразователя, работающего в качестве двигателя, т. е. преобразующего электрическую энергию в механическую. В этом случае на механической стороне источника энергии нет, следовательно, внешняя сила  Тогда:
Тогда:

Исключая из этих уравнений  находим:
находим:

Здесь  полное электрическое сопротивление преобразователя-двигателя — состоит из двух частей:
полное электрическое сопротивление преобразователя-двигателя — состоит из двух частей:  электрического сопротивления внешней цепи в сумме с собственным электрическим сопротивлением обмотки и
электрического сопротивления внешней цепи в сумме с собственным электрическим сопротивлением обмотки и  некоторого дополнительного сопротивления, называемого кинетическим, появляющегося в результате реакции механической стороны преобразователя на его электрическую сторону. Эквивалентная электрическая схема преобразователя становится элементарно простой (рис. 3.3). В этой схеме
некоторого дополнительного сопротивления, называемого кинетическим, появляющегося в результате реакции механической стороны преобразователя на его электрическую сторону. Эквивалентная электрическая схема преобразователя становится элементарно простой (рис. 3.3). В этой схеме  играет роль
играет роль  внутреннего сопротивления источника,
внутреннего сопротивления источника,  нагрузки.
нагрузки.

Рис. 3.3. Эквивалентная схема электродинамического преобразователя — двигателя
Легко видеть, что, затормозив (преобразователь, т. е. создав бесконечно большое сопротивление механической нагрузки ( ), получим
), получим  Ток заторможенного преобразователя определяется только чисто электрическими параметрами цепи.
Ток заторможенного преобразователя определяется только чисто электрическими параметрами цепи.
Предположив, что катушка преобразователя сделана из идеального, не имеющего инертной массы материала, ее подвесы также не оказывают никакого сопротивления и преобразователь свободен от внешней механической нагрузки, получим режим идеального холостого хода:

В режиме холостого хода в таком идеальном преобразователе ток отсутствует и напряжение, подаваемое от источника питания, в точности компенсируется противоэлектродвижущей силой движения  В реальном преобразователе собственное сопротивление
В реальном преобразователе собственное сопротивление  но так как его, естественно, стараются сделать малым, то
но так как его, естественно, стараются сделать малым, то  велико, и ненагруженный преобразователь потребляет небольшой ток.
велико, и ненагруженный преобразователь потребляет небольшой ток.
Аналогичным образом можно рассмотреть свойства преобразователя-генератора. Так, если на механической стороне преобразователя приложена сила  а на электрической стороне замкнуты зажимы источника напряжения, что соответствует
а на электрической стороне замкнуты зажимы источника напряжения, что соответствует  то легко найти
то легко найти

Если зажимы замкнуты в преобразователе накоротко, это эквивалентно тому, что  равно
равно  собственному электрическому сопротивлению преобразователя. Это выражение аналогично полученному ранее (3.11). Здесь величина
собственному электрическому сопротивлению преобразователя. Это выражение аналогично полученному ранее (3.11). Здесь величина  представляет собой добавочное механическое сопротивление электродинамического торможения, возникающее в результате воздействия электрической стороны на механическую.
представляет собой добавочное механическое сопротивление электродинамического торможения, возникающее в результате воздействия электрической стороны на механическую.
Отметим еще одно важное следствие  и (3.12). Положим, что механическое сопротивление 3 в преобразователе-двигателе чисто реактивное. Естественно, что в этом случае и кинетическое сопротивление
и (3.12). Положим, что механическое сопротивление 3 в преобразователе-двигателе чисто реактивное. Естественно, что в этом случае и кинетическое сопротивление  будет также чисто реактивным. При этом, однако, если 3 имеет инерционный характер (сопротивление массы), то
будет также чисто реактивным. При этом, однако, если 3 имеет инерционный характер (сопротивление массы), то

Таким образом, кинетическое сопротивление будет иметь емкостный характер, как если бы на электрической стороне, добавилась включенная последовательно с  емкость
емкость  Очевидно, что в случае сопротивления 3 чисто упругого вида
Очевидно, что в случае сопротивления 3 чисто упругого вида  окажется индуктивным.
окажется индуктивным.
Электростатический преобразователь
Действие электростатического преобразователя основано на появлении сил электростатического притяжения между заряженными обкладками конденсатора и на изменении напряжения на заряженном конденсаторе при изменении его емкости (сближении или удалении друг от дрга его обкладок).
Представим себе плоский конденсатор (рис. 3.4), одна обкладка которого может приближаться к другой и удаляться от нее, колеблясь вдоль силовых линий электрического поля в конденсаторе.

Рис. 3.4. К выводу уравнений для электростатического преобразователя
Рассмотрим, какие механические силы действуют на эту обкладку. Если конденсатор не заряжен, то на обкладку при движении действует механическая сила реакции  состоящая из сил инерции массы обкладки, упругости подвеса обкладки и, если к обкладке прикреплено какое-либо механическое колебательное устройство, силы механического сопротивления нагрузки этого устройства. Полное сопротивление обкладки составит:
состоящая из сил инерции массы обкладки, упругости подвеса обкладки и, если к обкладке прикреплено какое-либо механическое колебательное устройство, силы механического сопротивления нагрузки этого устройства. Полное сопротивление обкладки составит:

где  собственное механическое сопротивление обкладки (преобразователя);
собственное механическое сопротивление обкладки (преобразователя);  механическое сопротивление нагрузки.
механическое сопротивление нагрузки.
Если конденсатор зарядить, то возникнет сила взаимного притяжения пластин  где С — емкость конденсатора;
где С — емкость конденсатора;  расстояние между пластинами,
расстояние между пластинами,  заряд.
заряд.
Отсюда вытекает, что сила  изменяется не по закону изменения электрической величины
изменяется не по закону изменения электрической величины  а пропорционально ее квадрату. Поэтому, если не принять специальных мер, такой подвижный конденсатор не может быть использован для неискажающего преобразования электрических колебаний в механические. Специальные меры состоят в том, что конденсатор предварительно заряжают до некоторого постоянного напряжения
а пропорционально ее квадрату. Поэтому, если не принять специальных мер, такой подвижный конденсатор не может быть использован для неискажающего преобразования электрических колебаний в механические. Специальные меры состоят в том, что конденсатор предварительно заряжают до некоторого постоянного напряжения  т. е. сообщают ему заряд
т. е. сообщают ему заряд  При работе преобразователя напряжение только немного меняется около этого постоянного значения
При работе преобразователя напряжение только немного меняется около этого постоянного значения  и соответственно заряд на нем
и соответственно заряд на нем  Тогда
Тогда

Если  переменный заряд, меняющийся синусоидально, то его удобно выразить через ток, так что переменная составляющая силы
переменный заряд, меняющийся синусоидально, то его удобно выразить через ток, так что переменная составляющая силы  будет иметь вид:
будет иметь вид:

В формулах (3.14) и (3.15) учтено, что  для плоского конденсатора с площадью обкладок
для плоского конденсатора с площадью обкладок  Кроме того, полагаем, что
Кроме того, полагаем, что  Это допустимо, так как преобразователь может работать без искажений формы колебаний только, если отклонения пластины от среднего положения малы. Силу постоянного притяжения
Это допустимо, так как преобразователь может работать без искажений формы колебаний только, если отклонения пластины от среднего положения малы. Силу постоянного притяжения  можно уравновесить, если подвижную обкладку укрепить на упругом подвесе, позволяющем ей колебаться около положения равновесия. Поэтому в дальнейшем будем интересоваться только переменными силами. Для них можно составить уравнения равновесия, учитывая внешнюю силу
можно уравновесить, если подвижную обкладку укрепить на упругом подвесе, позволяющем ей колебаться около положения равновесия. Поэтому в дальнейшем будем интересоваться только переменными силами. Для них можно составить уравнения равновесия, учитывая внешнюю силу 

или

Рассмотрим теперь электрическую сторону устройства. Пусть на конденсаторе имеется заряд  и одна его обкладка, колеблясь, отклоняется от среднего положения на величину
и одна его обкладка, колеблясь, отклоняется от среднего положения на величину  В положении равновесия
В положении равновесия  напряжение на конденсаторе
напряжение на конденсаторе  Если расстояние между обкладками изменится с
Если расстояние между обкладками изменится с  на
на  то напряжение, как известно, возрастет пропорционально отношению расстояний:
то напряжение, как известно, возрастет пропорционально отношению расстояний: 
Учитывая постоянный заряд  можем написать:
можем написать:

или

Здесь пренебрежено величинами второго порядка малости по сравнению с  а переменные величины выражены через скорость
а переменные величины выражены через скорость  и ток
и ток  вместо
вместо  Для переменных напряжений получим
Для переменных напряжений получим

Если переменное напряжение и подается к конденсатору через внешнее сопротивление  то в правой части (3.18) следует учесть падение напряжения на нем
то в правой части (3.18) следует учесть падение напряжения на нем  Обозначив
Обозначив  получим:
получим:

Итак, для электростатического преобразователя система уравнений, аналогичная (3.10), имеет вид:

Здесь 
В уравнениях (3.20) все знаки перед членами в правых частях одинаковы. Очевидно, что при этом для полного электрического сопротивления получим выражение:

В отличие от (3.11) знак перед кинетическим сопротивлением здесь отрицателен. Однако, если принять во внимание, что  число мнимое, то, введя
число мнимое, то, введя  мы снова получим формулу, полностью совпадающую с (3.11).
мы снова получим формулу, полностью совпадающую с (3.11).
Таким образом, если определить коэффициент электромеханической связи как абсолютную величину;

то формулы для  для обоих типов преобразователей (электродинамического и электростатического) совпадают. Такое формальное заключение не вносит полной ясности в вопрос о том, какую систему уравнений преобразователя — (3.10) или (3.20) — надо принять в том или ином случае. Более того, остается неизвестным, насколько общим может считаться соотношение (3.22) и как поступить в случае преобразователей других типов.
для обоих типов преобразователей (электродинамического и электростатического) совпадают. Такое формальное заключение не вносит полной ясности в вопрос о том, какую систему уравнений преобразователя — (3.10) или (3.20) — надо принять в том или ином случае. Более того, остается неизвестным, насколько общим может считаться соотношение (3.22) и как поступить в случае преобразователей других типов.
Желательно, конечно, найти какие-то общие правила, которые юзволили бы в любом случае составить систему уравнений преобразователя, не обращаясь к длинным выводам и проверяя себя с юмощью «физических» соображений. Это можно сделать, используя общую теорию электромеханического преобразователя.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. Краткие сведения по физиологической акустике
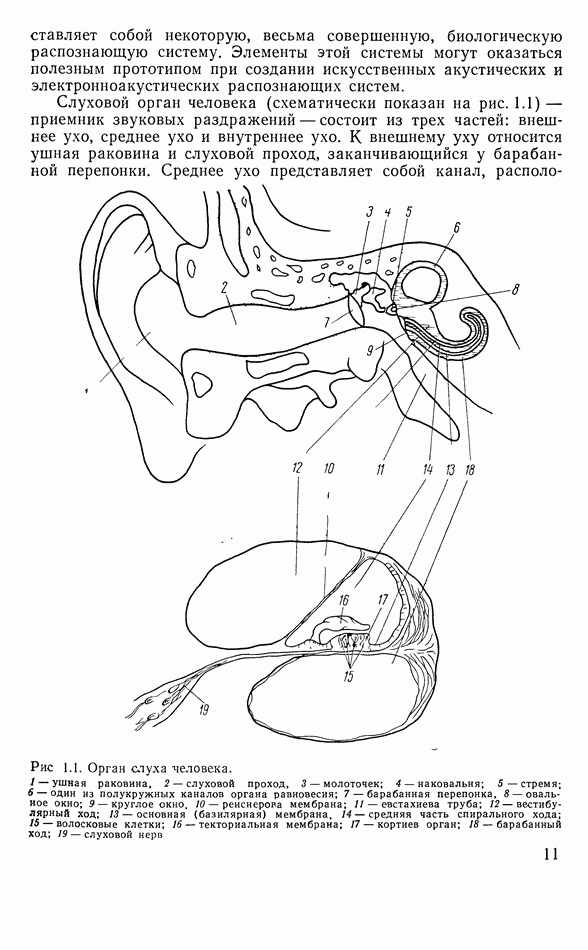
- 1.1. УСТРОЙСТВО СЛУХОВОГО ОРГАНА ЧЕЛОВЕКА
- 1.2. МЕХАНИЗМ ВОЗБУЖДЕНИЯ СЛУХОВОГО НЕРВА
- 1.3. ТЕОРИЯ СЛУХА
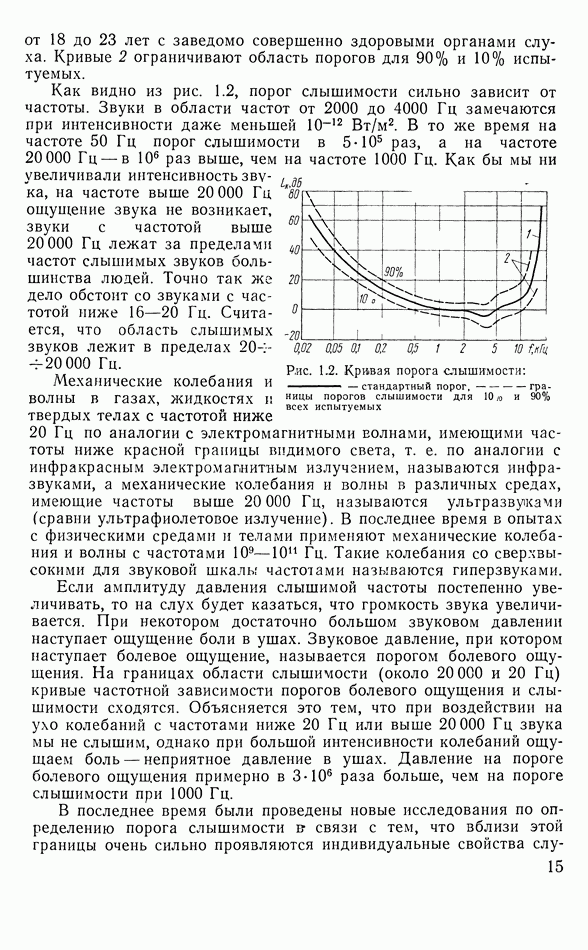
- 1.4. ПОРОГ СЛЫШИМОСТИ
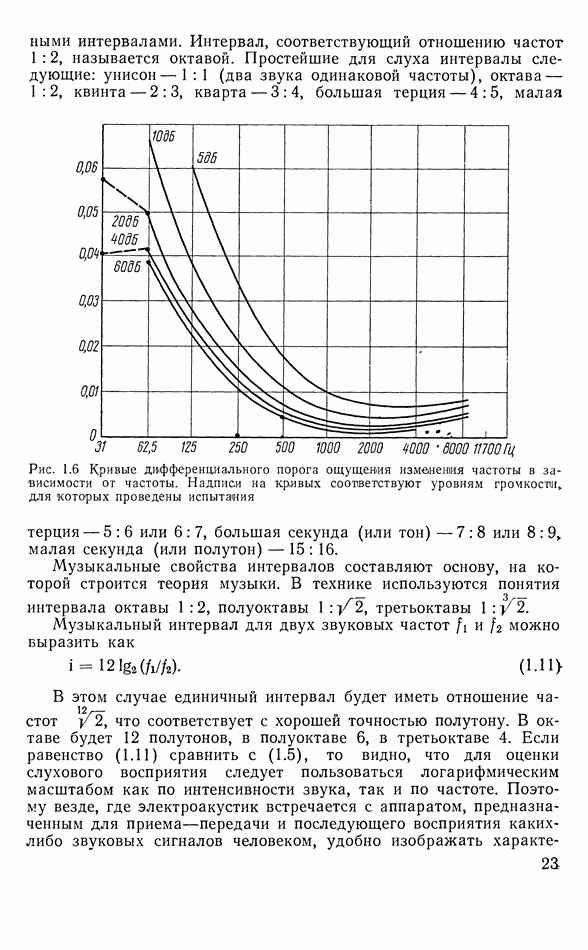
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЙ ПОРОГ ВОСПРИЯТИЯ ИНТЕНСИВНОСТИ ЗВУКА
- 1.6. ЛОГАРИФМИЧЕСКИЕ УРОВНИ. ШКАЛА ДЕЦИБЕЛ
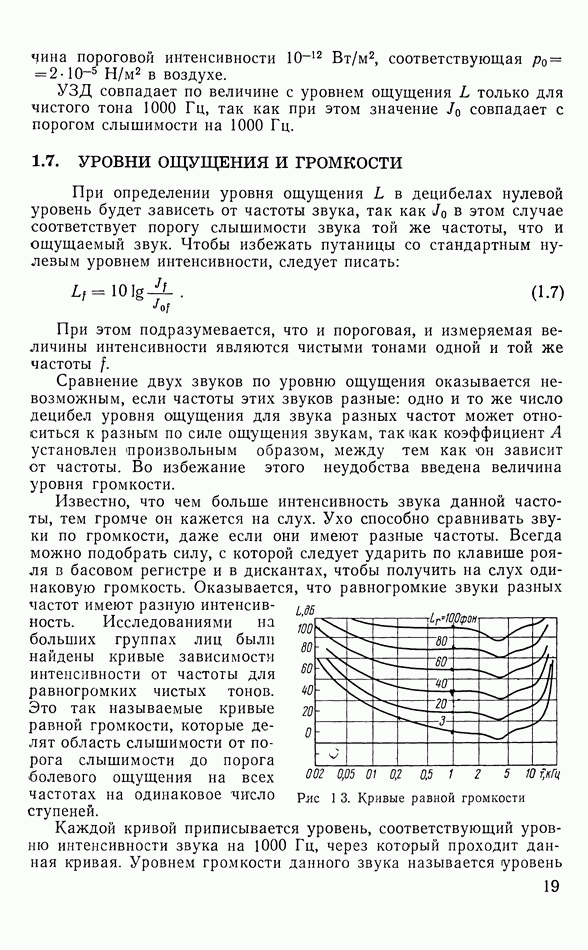
- 1.7. УРОВНИ ОЩУЩЕНИЯ И ГРОМКОСТИ
- 1.8. ГРОМКОСТЬ ЧИСТЫХ ТОНОВ
- 1.9. КРИТИЧЕСКИЕ ПОЛОСЫ СЛУХА
- 1.10. УРОВЕНЬ ГРОМКОСТИ СЛОЖНЫХ ЗВУКОВ
- 1.11. ВОСПРИЯТИЕ ВЫСОТЫ ТОНА. ШКАЛА ЧАСТОТ
- 1.12. МАСКИРОВКА ЗВУКА
- 1.13. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- 1.14. ВОСПРИЯТИЕ ОКРАСКИ (ТЕМБРА) ЗВУКА
- Глава 2. Электромеханические и электроакустические аналогии
- 2.1. ПРИНЦИП ЭЛЕКТРОМЕХАНИЧЕСКИХ АНАЛОГИЙ
- 2.2. МЕХАНИЧЕСКИЕ ЭЛЕМЕНТЫ И МЕХАНИЧЕСКИЕ СИСТЕМЫ
- 2.3. ПРИМЕРЫ ИЗОБРАЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ И ИХ ЭКВИВАЛЕНТНЫХ СХЕМ
- 2.4. ПРАВИЛА И СПОСОБЫ ПЕРЕХОДА К ЭКВИВАЛЕНТНЫМ СХЕМАМ
- 2.5. ТРАНСФОРМАЦИЯ СИЛ И СКОРОСТЕЙ. ЭЛЕКТРИЧЕСКИЙ АНАЛОГ-ТРАНСФОРМАТОР
- 2.6. ЭЛЕКТРОАКУСТИЧЕСКИЕ АНАЛОГИИ
- 2.7. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИИ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
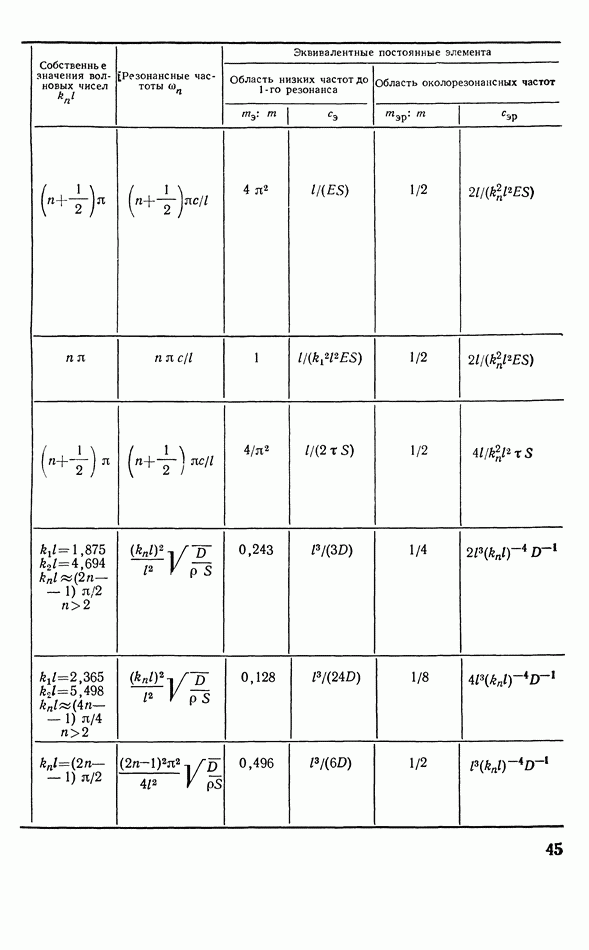
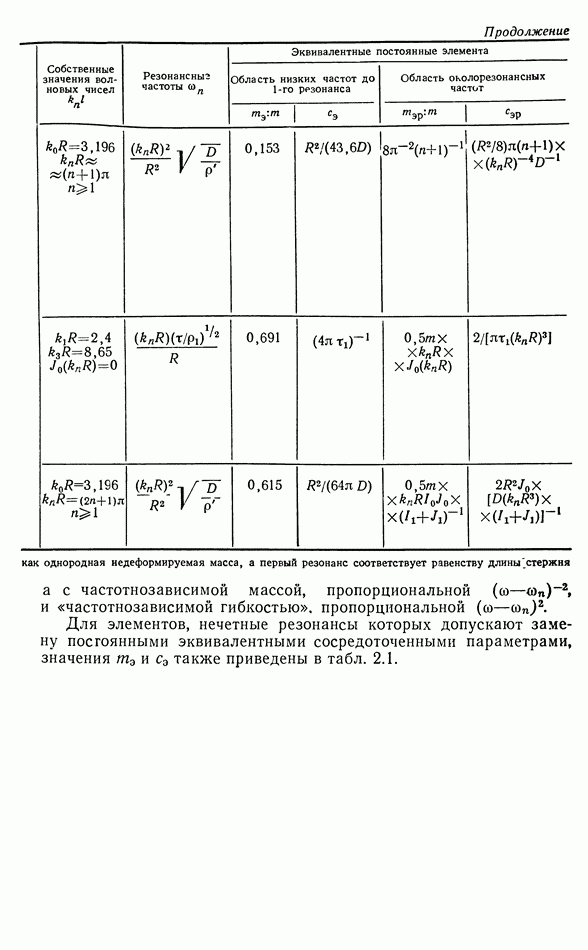
- 2.8. ЭКВИВАЛЕНТНЫЕ СОСРЕДОТОЧЕННЫЕ ПАРАМЕТРЫ МЕХАНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ
- Глава 3. Электромеханические преобразователи
- 3.2. ДВА ОСНОВНЫХ ТИПА ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.3. ОБЩАЯ ТЕОРИЯ ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.4. ВТОРИЧНЫЕ ПАРАМЕТРЫ ПРЕОБРАЗОВАТЕЛЯ
- 3.5. ПРАВИЛО ЗНАКОВ
- 3.6. ВХОДНОЕ СОПРОТИВЛЕНИЕ СИСТЕМЫ В ОБЩЕМ СЛУЧАЕ
- 3.7. ЧУВСТВИТЕЛЬНОСТЬ ПРЕОБРАЗОВАТЕЛЯ
- 3.8. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ПРЕОБРАЗОВАТЕЛЯ
- 3.9. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.10. МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.11. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Преобразователь с однородной деформацией
- Преобразователь с неоднородной деформацией
- Местные уравнения пьезопреобразователя в тензорной форме
- Свойства основных пьезоэлектрических кристаллов
- Выбор среза кристалла при изготовлении пьезоэлементов
- Искусственные пьезокерамические материалы
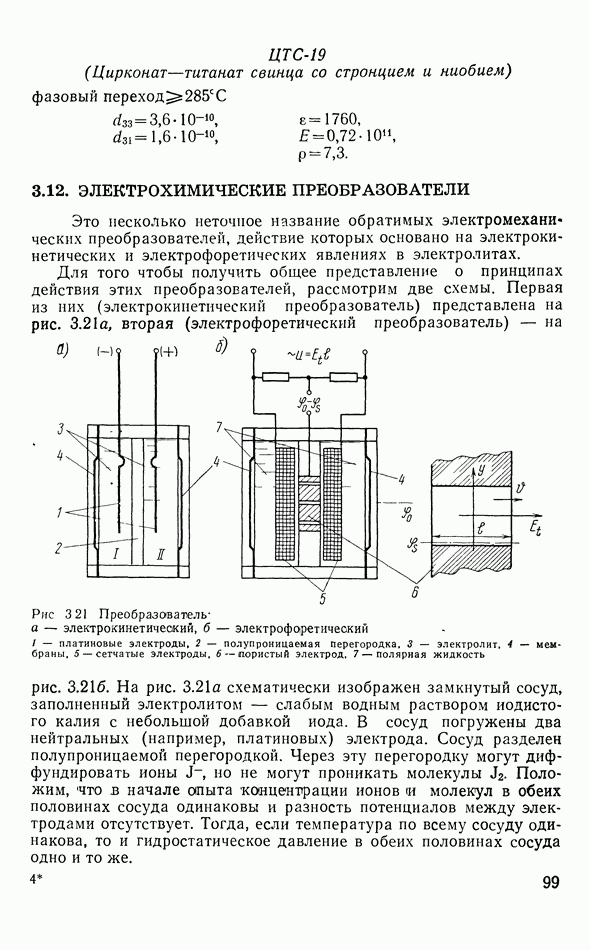
- 3.12. ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 4. Электроакустическая аппаратура
- 4.1. КЛАССИФИКАЦИЯ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- 4.2. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 4.3. АНТЕННЫ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- Связь между чувствительностью приемной и излучающей антенн
- Сопротивление излучения антенны
- Сложные антенны
- Распределенные антенны
- Антенна бегущей волны
- Антенна из направленных элементов
- Оптимизация характеристики направленности антенны
- Рупорная антенна
- 4.4. ТРЕБОВАНИЯ К ЭЛЕКТРОАКУСТИЧЕСКОЙ АППАРАТУРЕ РАДИОВЕЩАНИЯ И ТЕЛЕВИДЕНИЯ
- 4.5. ЛЕНТОЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Ненаправленный микрофон-приемник давления
- Микрофон с кардиоидной характеристикой направленности
- Микрофон с регулируемой характеристикой направленности
- 4.6. КАТУШЕЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Однонаправленный микрофон
- Биградиентный микрофон
- Сверхнаправленный микрофон
- 4.7. СОГЛАСОВАНИЕ ЭЛЕКТРИЧЕСКОЙ СТОРОНЫ ЭЛЕКТРОДИНАМИЧЕСКОГО МИКРОФОНА СО ВХОДОМ МИКРОФОННОГО УСИЛИТЕЛЯ
- 4.8. КОНДЕНСАТОРНЫЕ МИКРОФОНЫ
- Об отрицательной упругости электрического поля поляризации в микрофоне
- Предельная чувствительность микрофона
- Влияние емкости входа предварительного каскада
- Микрофон направленного действия
- 4.9. ОБЩИЕ СВЕДЕНИЯ О ГРОМКОГОВОРИТЕЛЯХ
- 4.10. ДИФФУЗОРНЫЕ ГРОМКОГОВОРИТЕЛИ
- Частотная характеристика чувствительности
- Влияние способа установки громкоговорителя на излучение в области низких частот
- Работа громкоговорителя в области высоких частот
- Комбинированные громкоговорители
- Нелинейные искажения в громкоговорителе
- 4.11. РУПОРНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- Влияние конечной длины рупора
- Широкогорлый громкоговоритель
- Громкоговорящие агрегаты
- 4.12. ЭЛЕКТРОСТАТИЧЕСКИЙ ГРОМКОГОВОРИТЕЛЬ
- 4.13. МАГНИТОСТРИКЦИОННЫЕ ИЗЛУЧАТЕЛИ
- Стержневой излучатель
- Кольцевой излучатель
- Круговая диаграмма преобразователя
- Коэффициент полезного действия излучателя
- 4.14. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- Линия задержки
- Другие типы пьезоэлектрических элементов электроакустических аппаратов
- Согласование пьезоэлемента с электрической частью системы
- 4.15. ЭЛЕКТРОДИНАМИЧЕСКИЙ ГЕОФОН
- Частотная характеристика чувствительности
- Максимальная чувствительность
- 4.16. СЕЙСМОМЕТРИЧЕСКИЙ ПРИЕМНИК СМЕЩЕНИЯ
- 4.17. ОПТИМИЗАЦИЯ КОНСТРУКТИВНЫХ РАЗМЕРОВ ЭЛЕКТРОАКУСТИЧЕСКОГО АППАРАТА
- Глава 5. Необратимые преобразователи
- 5.2. ПНЕВМОАКУСТИЧЕСКИЕ ИЗЛУЧАТЕЛИ
- Модуляция потока воздуха
- Пневматическая сирена
- Модулятор с возвратно-поступательным движением
- 5.3. ГИДРАВЛИЧЕСКАЯ СИРЕНА
- 5.4. ГИДРОПНЕВМАТИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ
- 5.5. ПАРАМЕТРИЧЕСКИЕ ПРИЕМНИКИ
- 5.6. ПЬЕЗОРЕЗИСТИВНЫЕ ПОЛУПРОВОДНИКОВЫЕ ПРИЕМНИКИ ЗВУКА И ВИБРАЦИЙ
- Глава 6. Запись звука
- 6.2. МЕХАНИЧЕСКАЯ ЗАПИСЬ
- Рекордеры
- Электромеханическая обратная связь в рекордере
- Электродинамический рекордер
- Краткие сведения о звукоснимателях
- Стереограммофонная запись
- 6.3. ОПТИЧЕСКАЯ ЗАПИСЬ ЗВУКА
- Оптическая запись с использованием модуляции
- Уменьшение шумового фона при записи по методу переменной ширины
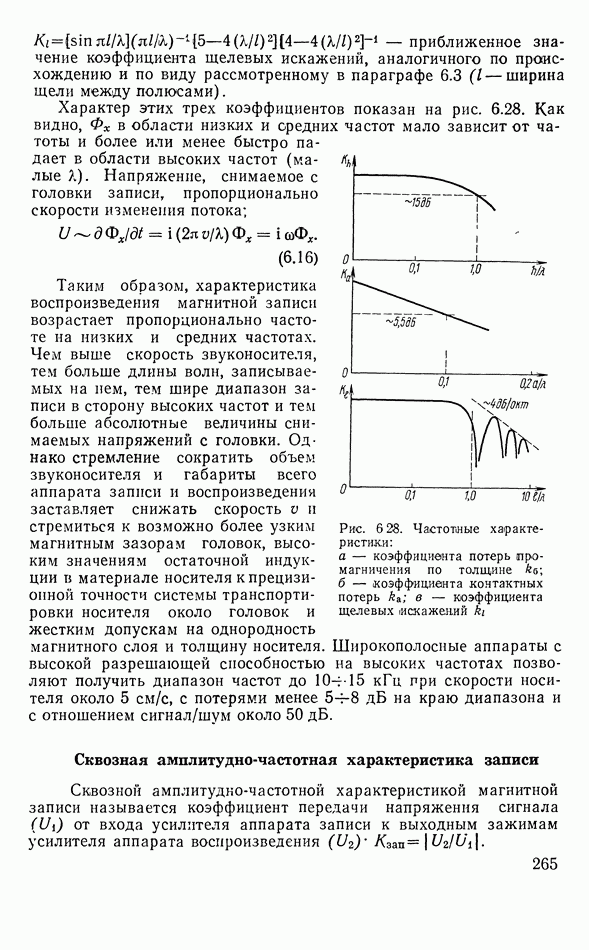
- Щелевые искажения записи
- 6.4. МАГНИТНАЯ ЗАПИСЬ ЗВУКА
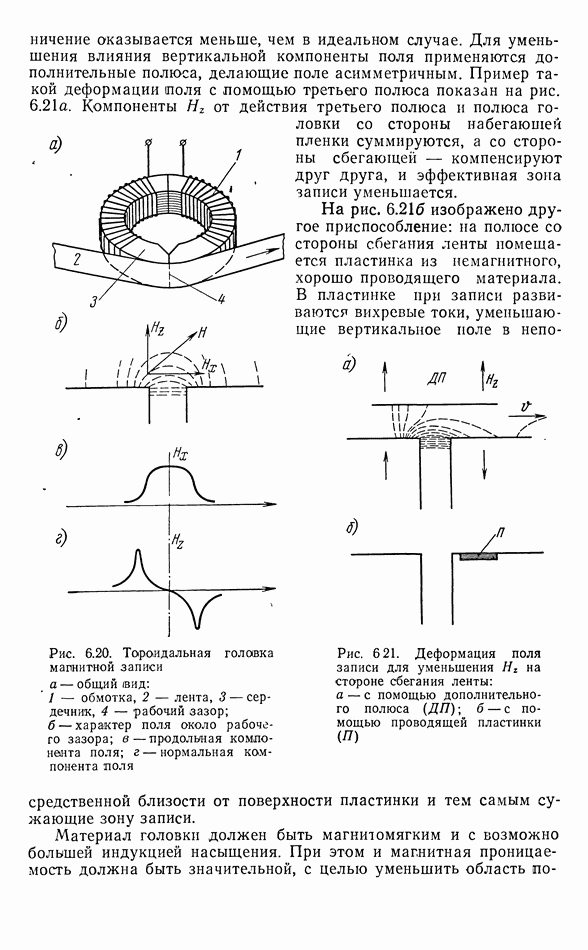
- Головки записи и воспроизведения
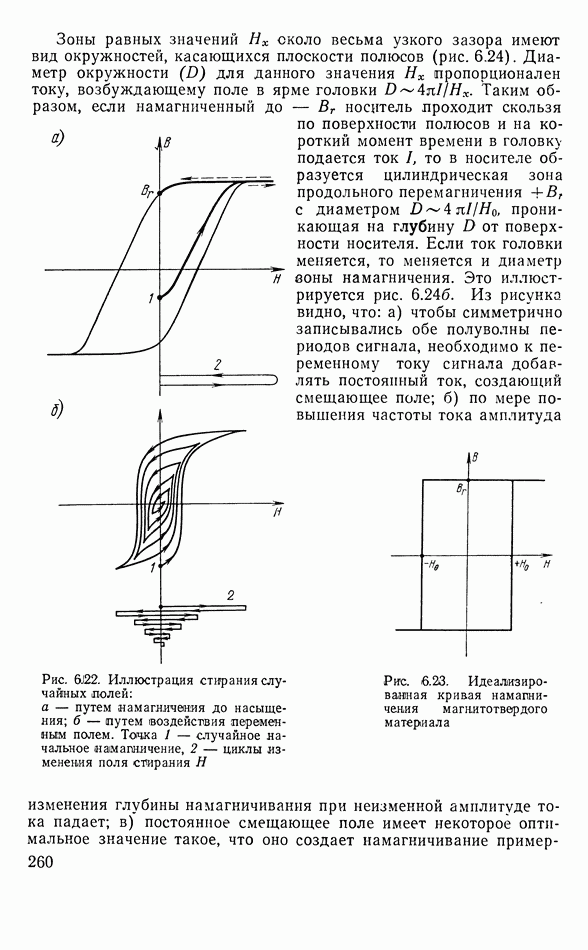
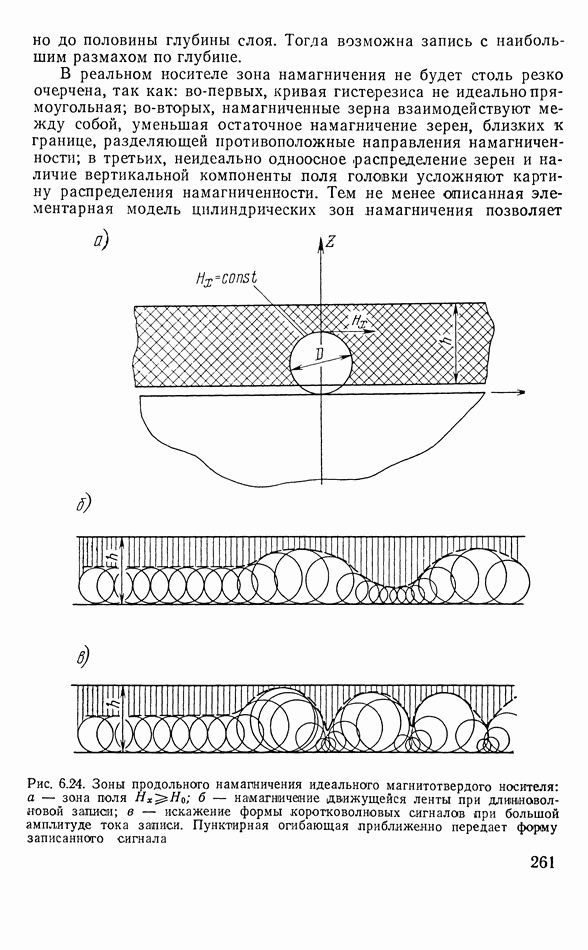
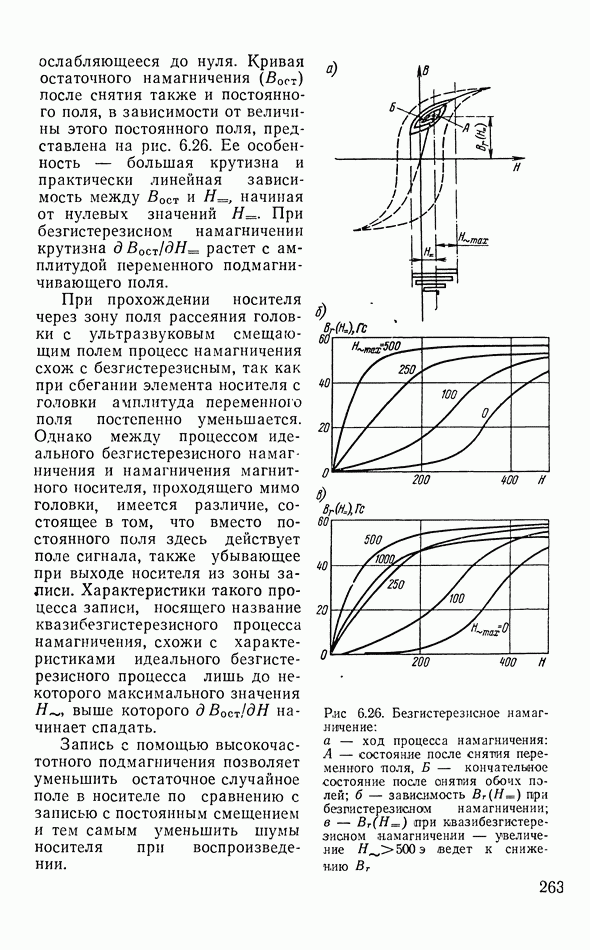
- Процесс намагничения магнитной ленты полем головки
- Воспроизведение записи
- Сквозная амплитудно-частотная характеристика записи
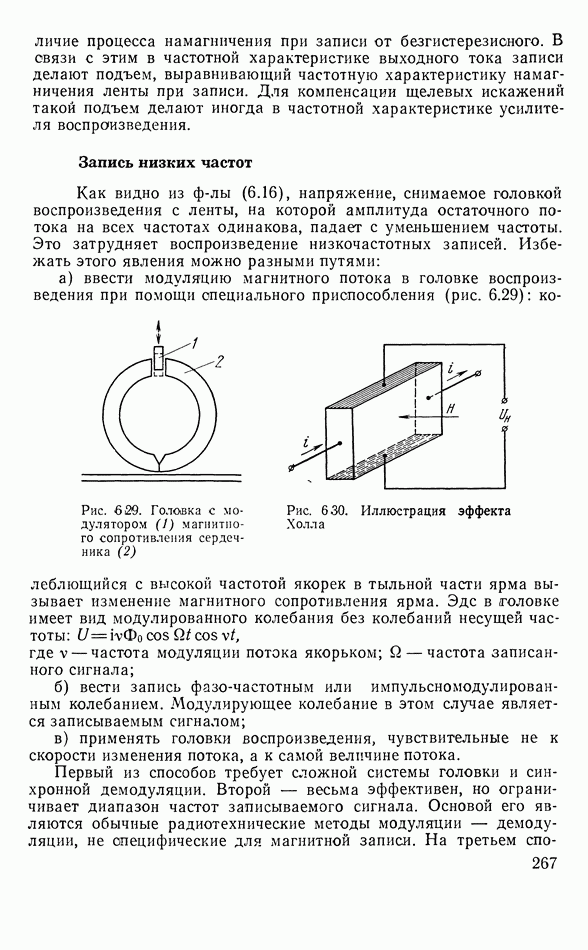
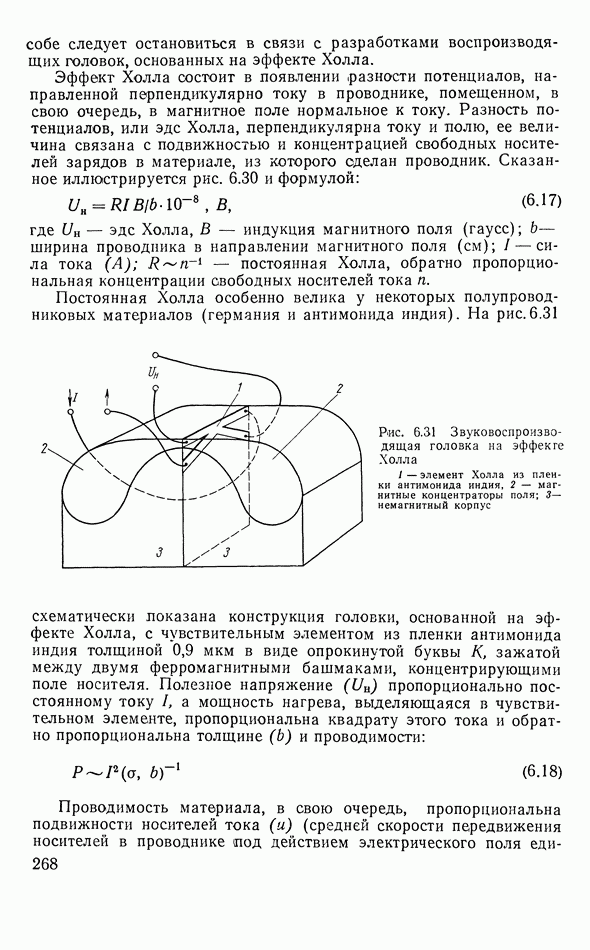
- Запись низких частот
- Плавающие головки
- Точность механизма транспортировки звуконосителя
- Список литературы