| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2.3. ПРИМЕРЫ ИЗОБРАЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ И ИХ ЭКВИВАЛЕНТНЫХ СХЕМ
Приведем несколько примеров для иллюстрации того, как изображаются механические системы с помощью указанных выше обозначений.
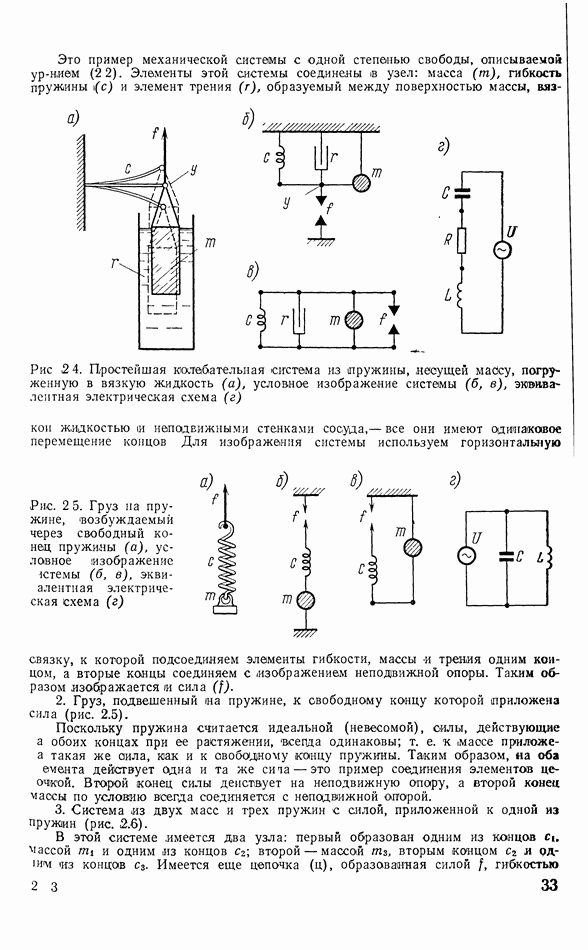
1. Груз, подвешенный на пружине и погруженный в сосуд с вязкой жидкостью, находится под действием силы, приложенной к нему (рис. 2.4).
Это пример механической системы с одной степенью свободы, описываемой ур-нием (2 2). Элементы этой системы соединены в узел: масса  гибкость пружины
гибкость пружины  и элемент трения
и элемент трения  образуемый между поверхностью массы, вязкой жидкостью
образуемый между поверхностью массы, вязкой жидкостью  неподвижными стенками сосуда, — все они имеют одинаковое перемещение концов.
неподвижными стенками сосуда, — все они имеют одинаковое перемещение концов.

Рис. 2.4. Простейшая кюлебательная система из пружины, несущей массу, погруженную в вязкую жидкость  условное изображение системы
условное изображение системы  эквивалентная электрическая схема
эквивалентная электрическая схема 
Для изображения системы используем горизонтальную связку, к которой подсоединяем элементы гибкости, массы и трения одним концом, а вторые концы соединяем с изображением неподвижной опоры.

Рис. 2.5. Груз на пружине, возбуждаемый через свободный конец пружины (а), условное изображение системы  эквивалентная электрическая схема (г)
эквивалентная электрическая схема (г)
Таким образом изображается  сила
сила 
2. Груз, подвешенный на пружине, к свободному концу которой приложена сила (рис. 2.5).
Поскольку пружина считается идеальной (невесомой), силы, действующие а обоих концах при ее растяжении, всегда одинаковы; т. е. к массе приложена такая же аила, как и к свободному концу пружины. Таким образом, на оба емента действует одна и та же сича — это пример соединения элементов цепочкой. Второй конец силы действует на неподвижную опору, а второй конец массы по условию всегда соединяется с неподвижной опорой.
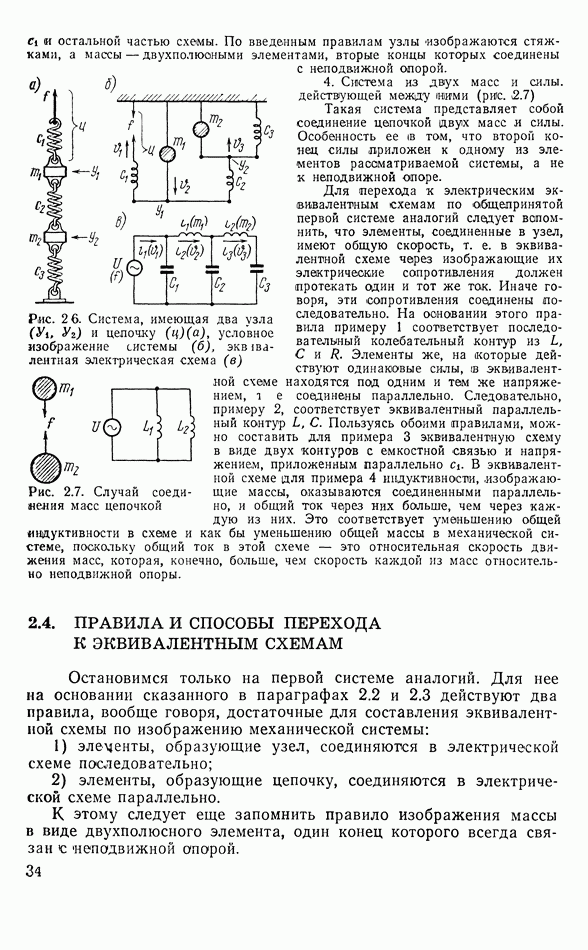
3. Система из двух масс и трех пружин с силой, приложенной к одной из пружин (рис. 2.6).
В этой системе имеется два узла: первый образован одним из концов с и массой  и одним из концов
и одним из концов  второй — массой
второй — массой  вторым концом
вторым концом  из концов
из концов  Имеется еще цепочка
Имеется еще цепочка  образованная силой
образованная силой  гибкостью
гибкостью
 и остальной частью схемы. По введенным правилам узлы - изображаются стяжками, а массы — двухполюсными элементами, вторые концы которых соединены
и остальной частью схемы. По введенным правилам узлы - изображаются стяжками, а массы — двухполюсными элементами, вторые концы которых соединены

Рис. 2 6. Система, имеющая два узла  и цепочку
и цепочку  условное изображение системы
условное изображение системы  эквивалентная электрическая схема
эквивалентная электрическая схема 
4. Система из двух масс и силы, действующей между иими (рис. 2.7)
Такая система представляет собой соединение цепочкой двух масс и силы. Особенность ее в том, что второй конец силы приложен к одному из элементов рассматриваемой системы, а не к неподвижной опоре.
Для перехода к электрическим эквивалентным схемам по общепринятой первой системе аналогий следует вспомнить, что элементы, соединенные в узел, имеют общую скорость, т. е. в эквивалентной схеме через изображающие их электрические сопротивления должен протекать один и тот же так. Иначе говоря, эти сопротивления соединены последовательно. На основании этого правила примеру 1 соответствует последовательный колебательный контур из  Элементы же, на которые действуют одинаковые силы, в эквивалентной схеме находятся под одним и тем же напряжением, т. е. соединены параллельно. Следовательно, примеру 2, соответствует эквивалентный параллельный контур
Элементы же, на которые действуют одинаковые силы, в эквивалентной схеме находятся под одним и тем же напряжением, т. е. соединены параллельно. Следовательно, примеру 2, соответствует эквивалентный параллельный контур  Пользуясь обоими правилами, можно составить для примера 3 эквивалентную схему в виде двух контуров с емкостной связью и напряжением, приложенным параллельно
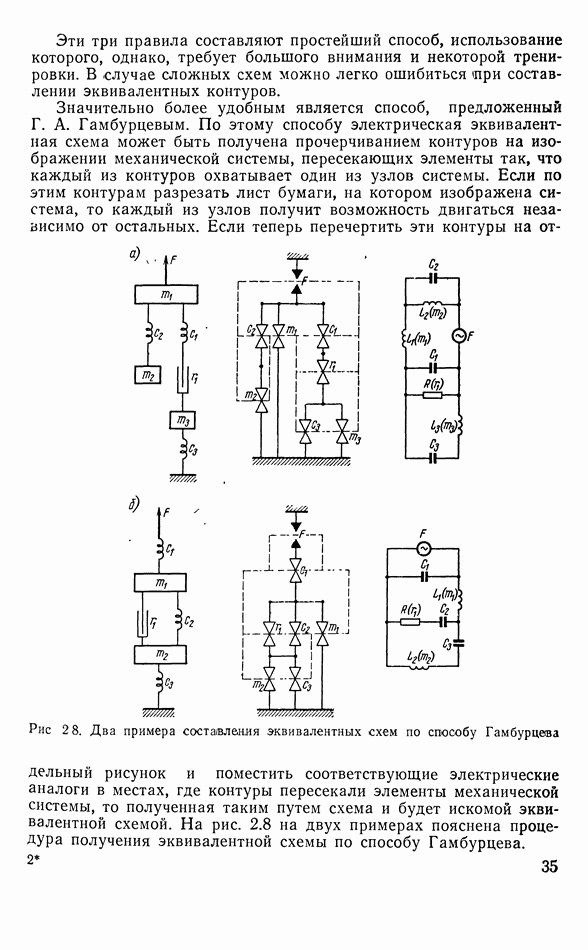
Пользуясь обоими правилами, можно составить для примера 3 эквивалентную схему в виде двух контуров с емкостной связью и напряжением, приложенным параллельно  . В эквивалентной схеме для примера 4 индуктивности, изображающие массы, оказываются соединенными параллельно, и общий ток через них больше, чем через каждую из них. Это соответствует уменьшению общей индуктивности в схеме и как бы уменьшению общей массы в механической системе, поскольку общий ток в этой схеме — это относительная скорость движения масс, которая, конечно, больше, чем скорость каждой из масс относительно неподвижной опоры.
. В эквивалентной схеме для примера 4 индуктивности, изображающие массы, оказываются соединенными параллельно, и общий ток через них больше, чем через каждую из них. Это соответствует уменьшению общей индуктивности в схеме и как бы уменьшению общей массы в механической системе, поскольку общий ток в этой схеме — это относительная скорость движения масс, которая, конечно, больше, чем скорость каждой из масс относительно неподвижной опоры.

Рис. 2.7. Случай соединения масс цепочкой
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. Краткие сведения по физиологической акустике
- 1.1. УСТРОЙСТВО СЛУХОВОГО ОРГАНА ЧЕЛОВЕКА
- 1.2. МЕХАНИЗМ ВОЗБУЖДЕНИЯ СЛУХОВОГО НЕРВА
- 1.3. ТЕОРИЯ СЛУХА
- 1.4. ПОРОГ СЛЫШИМОСТИ
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЙ ПОРОГ ВОСПРИЯТИЯ ИНТЕНСИВНОСТИ ЗВУКА
- 1.6. ЛОГАРИФМИЧЕСКИЕ УРОВНИ. ШКАЛА ДЕЦИБЕЛ
- 1.7. УРОВНИ ОЩУЩЕНИЯ И ГРОМКОСТИ
- 1.8. ГРОМКОСТЬ ЧИСТЫХ ТОНОВ
- 1.9. КРИТИЧЕСКИЕ ПОЛОСЫ СЛУХА
- 1.10. УРОВЕНЬ ГРОМКОСТИ СЛОЖНЫХ ЗВУКОВ
- 1.11. ВОСПРИЯТИЕ ВЫСОТЫ ТОНА. ШКАЛА ЧАСТОТ
- 1.12. МАСКИРОВКА ЗВУКА
- 1.13. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- 1.14. ВОСПРИЯТИЕ ОКРАСКИ (ТЕМБРА) ЗВУКА
- Глава 2. Электромеханические и электроакустические аналогии
- 2.1. ПРИНЦИП ЭЛЕКТРОМЕХАНИЧЕСКИХ АНАЛОГИЙ
- 2.2. МЕХАНИЧЕСКИЕ ЭЛЕМЕНТЫ И МЕХАНИЧЕСКИЕ СИСТЕМЫ
- 2.3. ПРИМЕРЫ ИЗОБРАЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ И ИХ ЭКВИВАЛЕНТНЫХ СХЕМ
- 2.4. ПРАВИЛА И СПОСОБЫ ПЕРЕХОДА К ЭКВИВАЛЕНТНЫМ СХЕМАМ
- 2.5. ТРАНСФОРМАЦИЯ СИЛ И СКОРОСТЕЙ. ЭЛЕКТРИЧЕСКИЙ АНАЛОГ-ТРАНСФОРМАТОР
- 2.6. ЭЛЕКТРОАКУСТИЧЕСКИЕ АНАЛОГИИ
- 2.7. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИИ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
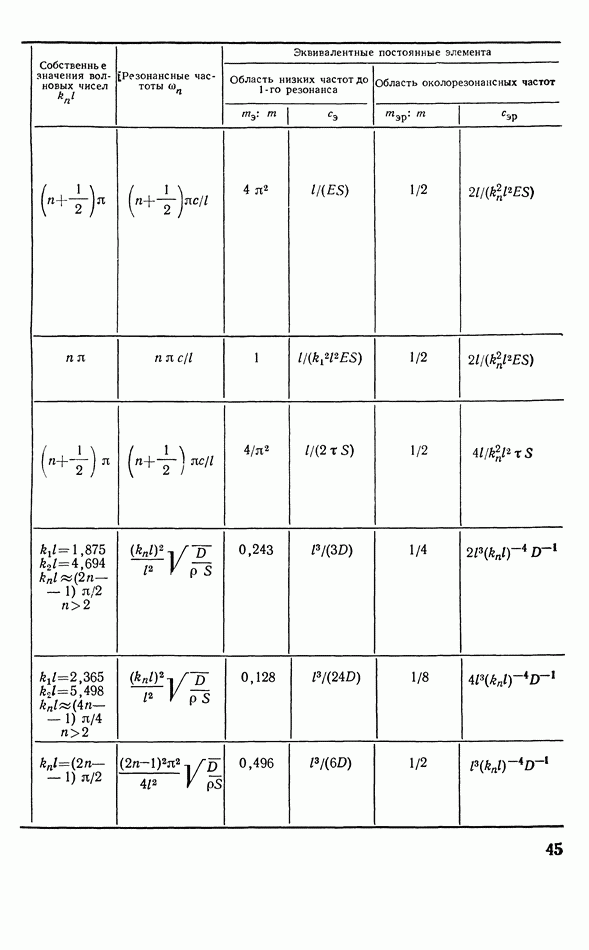
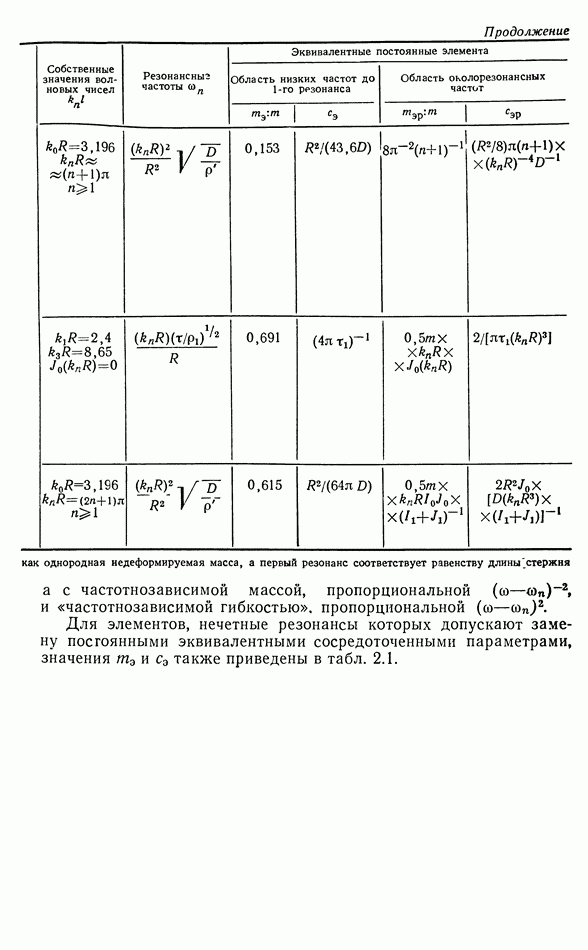
- 2.8. ЭКВИВАЛЕНТНЫЕ СОСРЕДОТОЧЕННЫЕ ПАРАМЕТРЫ МЕХАНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ
- Глава 3. Электромеханические преобразователи
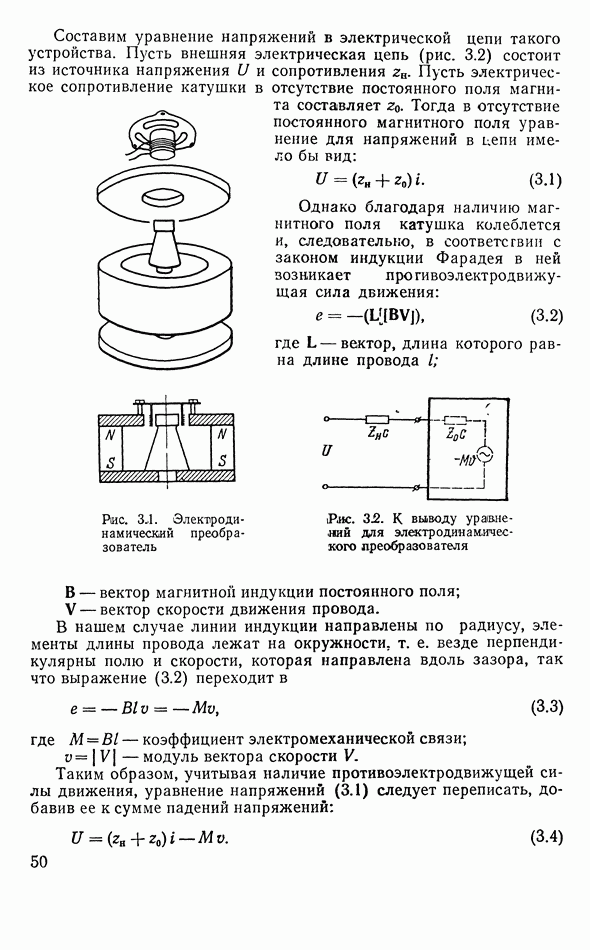
- 3.2. ДВА ОСНОВНЫХ ТИПА ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
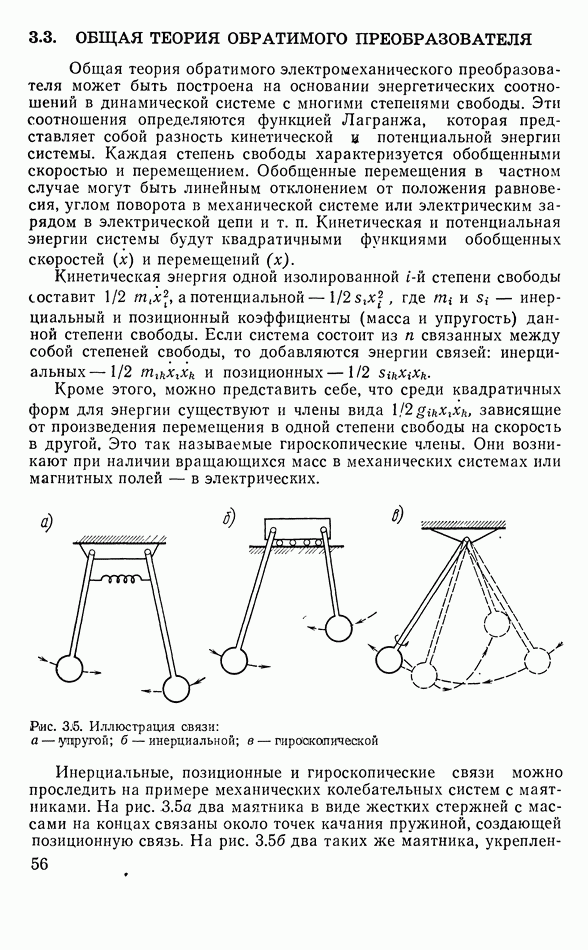
- 3.3. ОБЩАЯ ТЕОРИЯ ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.4. ВТОРИЧНЫЕ ПАРАМЕТРЫ ПРЕОБРАЗОВАТЕЛЯ
- 3.5. ПРАВИЛО ЗНАКОВ
- 3.6. ВХОДНОЕ СОПРОТИВЛЕНИЕ СИСТЕМЫ В ОБЩЕМ СЛУЧАЕ
- 3.7. ЧУВСТВИТЕЛЬНОСТЬ ПРЕОБРАЗОВАТЕЛЯ
- 3.8. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ПРЕОБРАЗОВАТЕЛЯ
- 3.9. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.10. МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.11. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Преобразователь с однородной деформацией
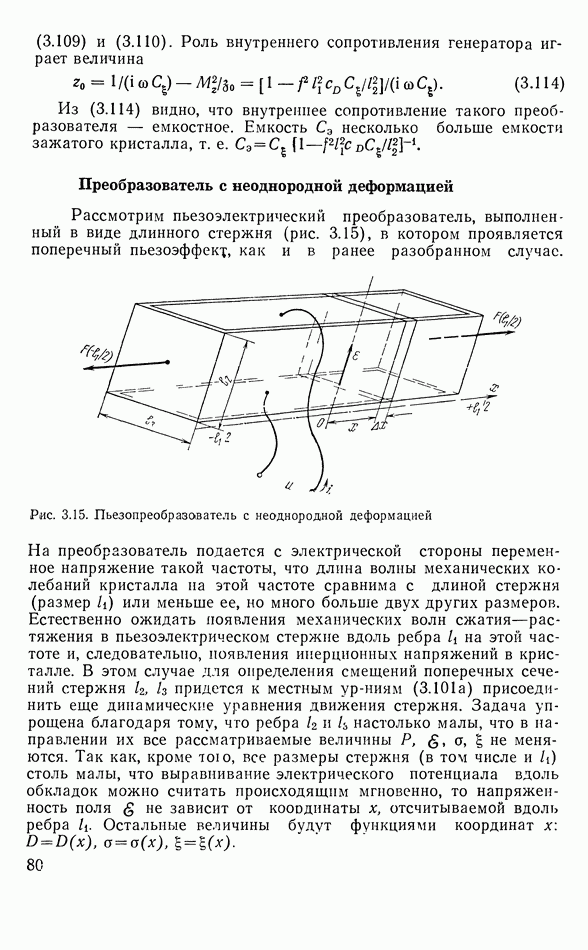
- Преобразователь с неоднородной деформацией
- Местные уравнения пьезопреобразователя в тензорной форме
- Свойства основных пьезоэлектрических кристаллов
- Выбор среза кристалла при изготовлении пьезоэлементов
- Искусственные пьезокерамические материалы
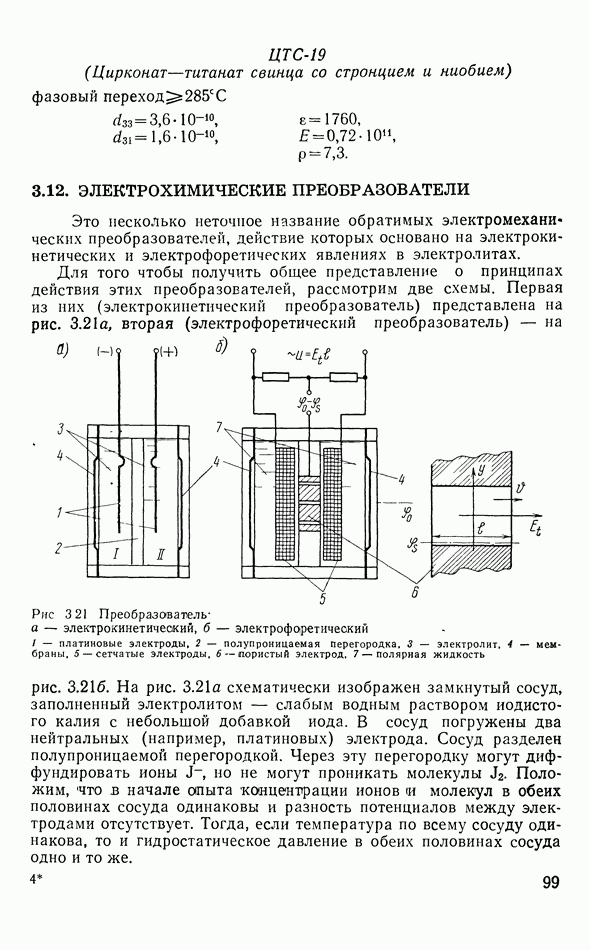
- 3.12. ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 4. Электроакустическая аппаратура
- 4.1. КЛАССИФИКАЦИЯ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- 4.2. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 4.3. АНТЕННЫ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- Связь между чувствительностью приемной и излучающей антенн
- Сопротивление излучения антенны
- Сложные антенны
- Распределенные антенны
- Антенна бегущей волны
- Антенна из направленных элементов
- Оптимизация характеристики направленности антенны
- Рупорная антенна
- 4.4. ТРЕБОВАНИЯ К ЭЛЕКТРОАКУСТИЧЕСКОЙ АППАРАТУРЕ РАДИОВЕЩАНИЯ И ТЕЛЕВИДЕНИЯ
- 4.5. ЛЕНТОЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Ненаправленный микрофон-приемник давления
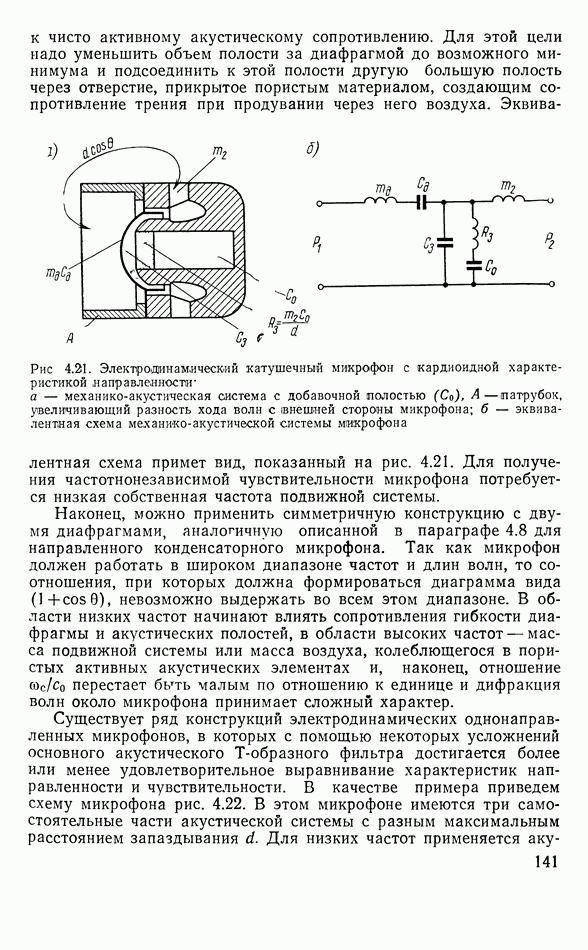
- Микрофон с кардиоидной характеристикой направленности
- Микрофон с регулируемой характеристикой направленности
- 4.6. КАТУШЕЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
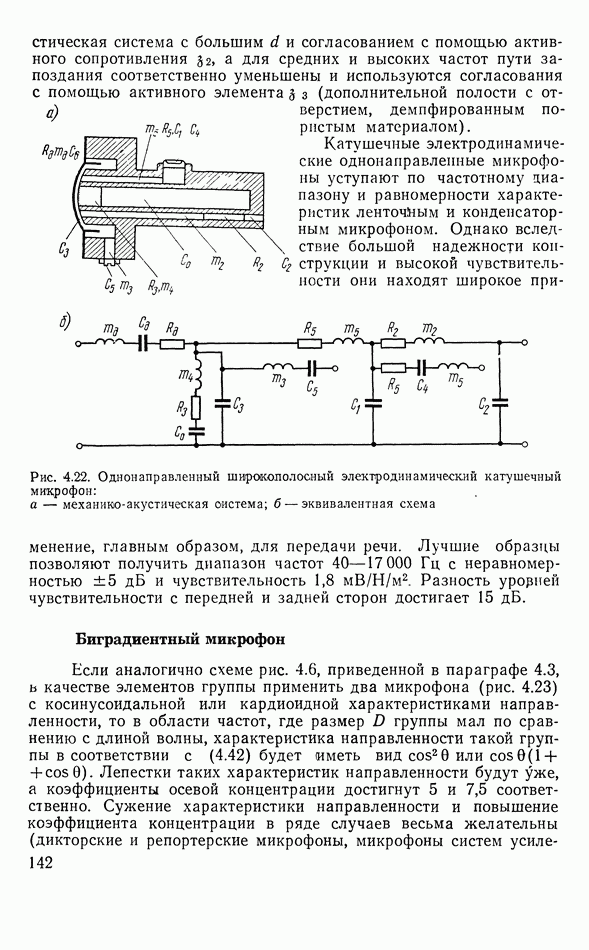
- Однонаправленный микрофон
- Биградиентный микрофон
- Сверхнаправленный микрофон
- 4.7. СОГЛАСОВАНИЕ ЭЛЕКТРИЧЕСКОЙ СТОРОНЫ ЭЛЕКТРОДИНАМИЧЕСКОГО МИКРОФОНА СО ВХОДОМ МИКРОФОННОГО УСИЛИТЕЛЯ
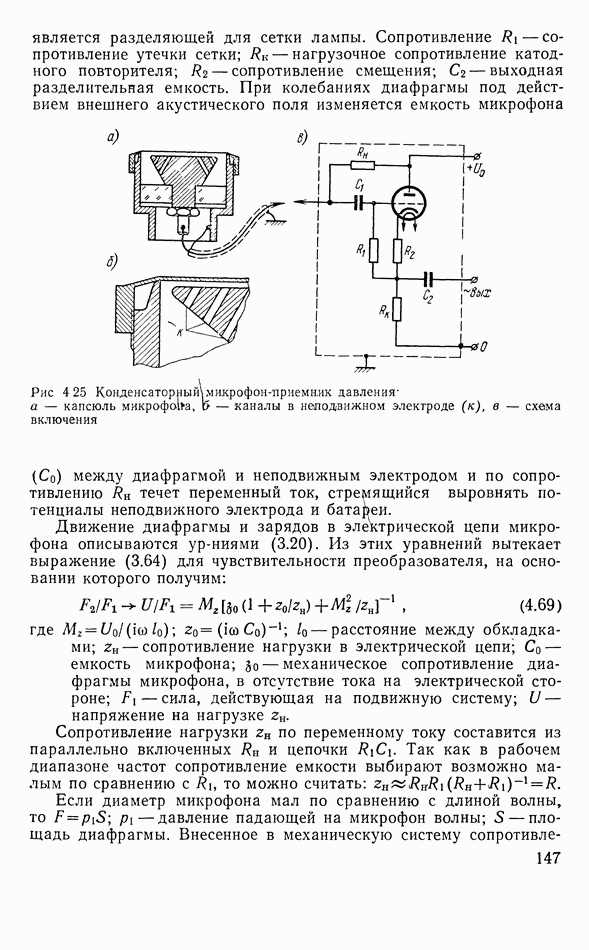
- 4.8. КОНДЕНСАТОРНЫЕ МИКРОФОНЫ
- Об отрицательной упругости электрического поля поляризации в микрофоне
- Предельная чувствительность микрофона
- Влияние емкости входа предварительного каскада
- Микрофон направленного действия
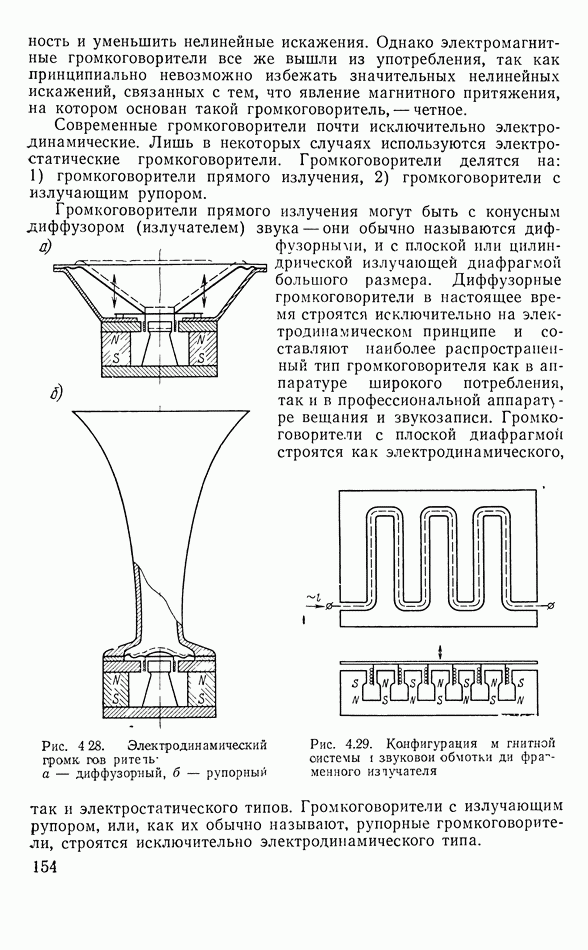
- 4.9. ОБЩИЕ СВЕДЕНИЯ О ГРОМКОГОВОРИТЕЛЯХ
- 4.10. ДИФФУЗОРНЫЕ ГРОМКОГОВОРИТЕЛИ
- Частотная характеристика чувствительности
- Влияние способа установки громкоговорителя на излучение в области низких частот
- Работа громкоговорителя в области высоких частот
- Комбинированные громкоговорители
- Нелинейные искажения в громкоговорителе
- 4.11. РУПОРНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- Влияние конечной длины рупора
- Широкогорлый громкоговоритель
- Громкоговорящие агрегаты
- 4.12. ЭЛЕКТРОСТАТИЧЕСКИЙ ГРОМКОГОВОРИТЕЛЬ
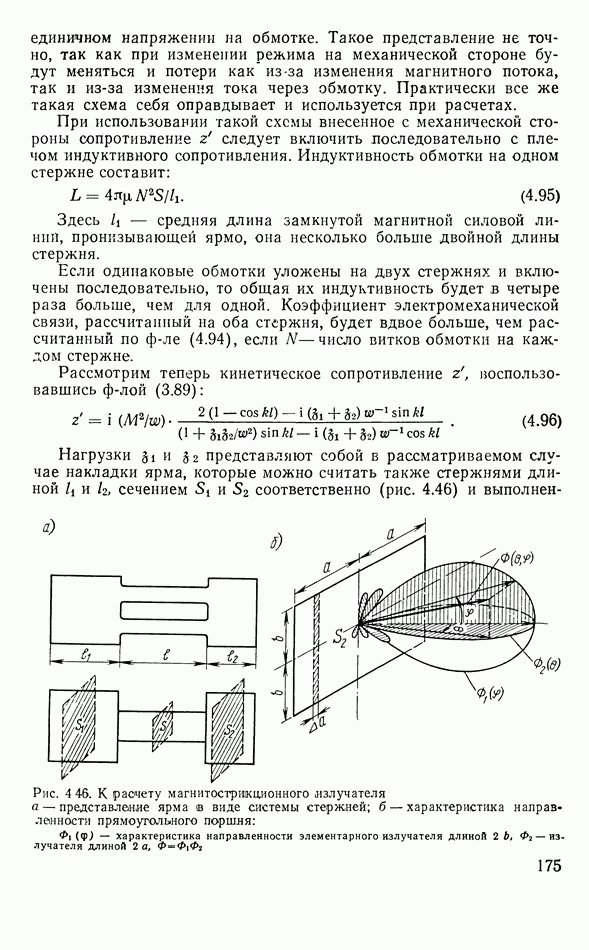
- 4.13. МАГНИТОСТРИКЦИОННЫЕ ИЗЛУЧАТЕЛИ
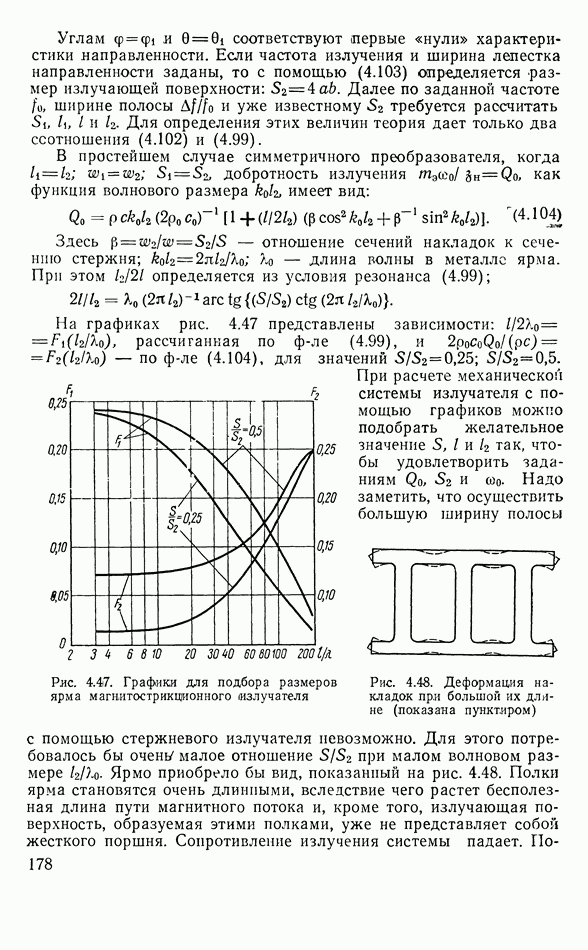
- Стержневой излучатель
- Кольцевой излучатель
- Круговая диаграмма преобразователя
- Коэффициент полезного действия излучателя
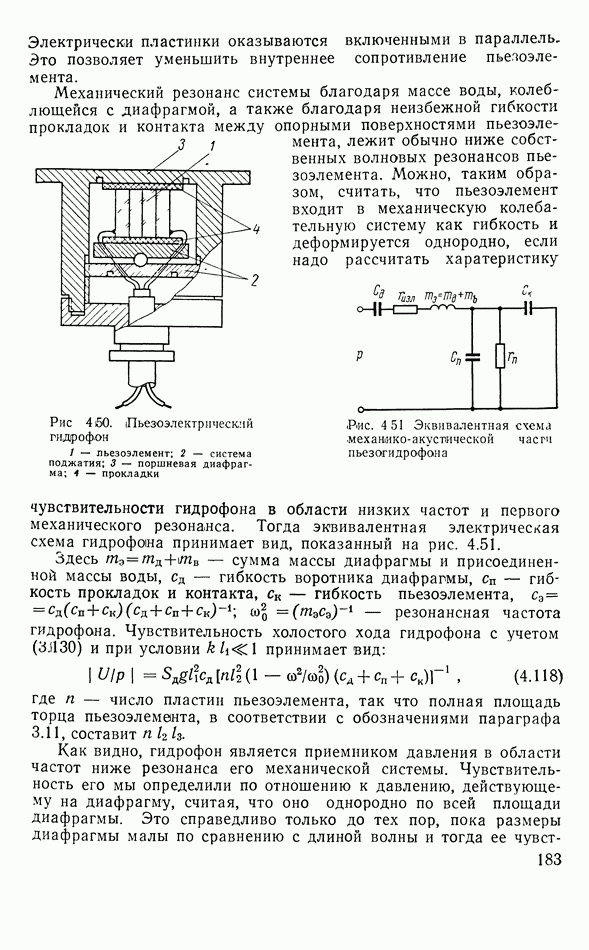
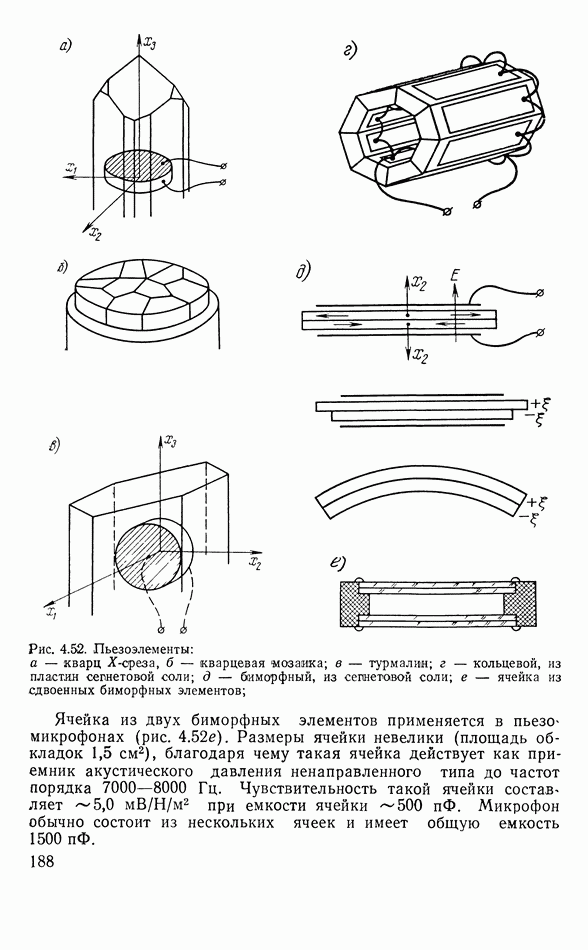
- 4.14. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- Линия задержки
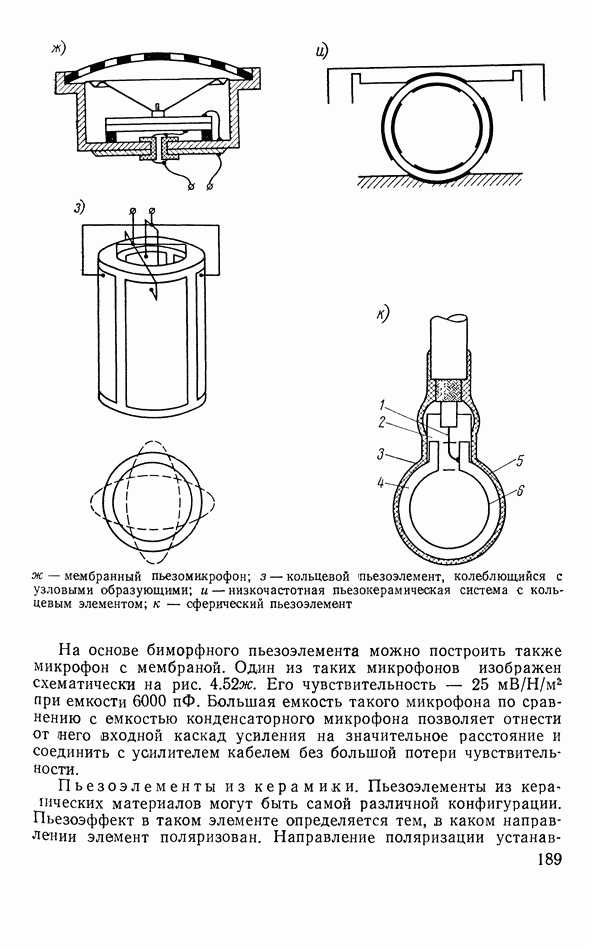
- Другие типы пьезоэлектрических элементов электроакустических аппаратов
- Согласование пьезоэлемента с электрической частью системы
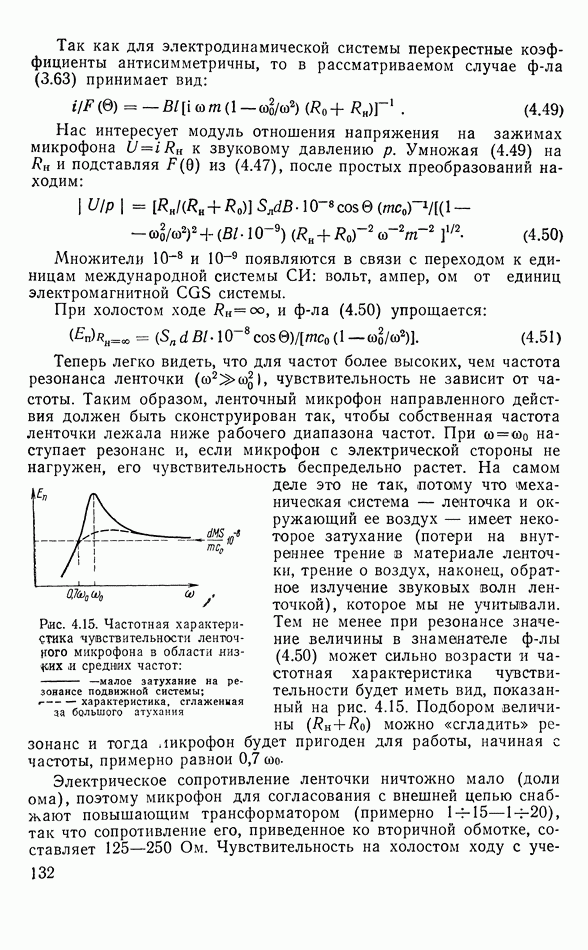
- 4.15. ЭЛЕКТРОДИНАМИЧЕСКИЙ ГЕОФОН
- Частотная характеристика чувствительности
- Максимальная чувствительность
- 4.16. СЕЙСМОМЕТРИЧЕСКИЙ ПРИЕМНИК СМЕЩЕНИЯ
- 4.17. ОПТИМИЗАЦИЯ КОНСТРУКТИВНЫХ РАЗМЕРОВ ЭЛЕКТРОАКУСТИЧЕСКОГО АППАРАТА
- Глава 5. Необратимые преобразователи
- 5.2. ПНЕВМОАКУСТИЧЕСКИЕ ИЗЛУЧАТЕЛИ
- Модуляция потока воздуха
- Пневматическая сирена
- Модулятор с возвратно-поступательным движением
- 5.3. ГИДРАВЛИЧЕСКАЯ СИРЕНА
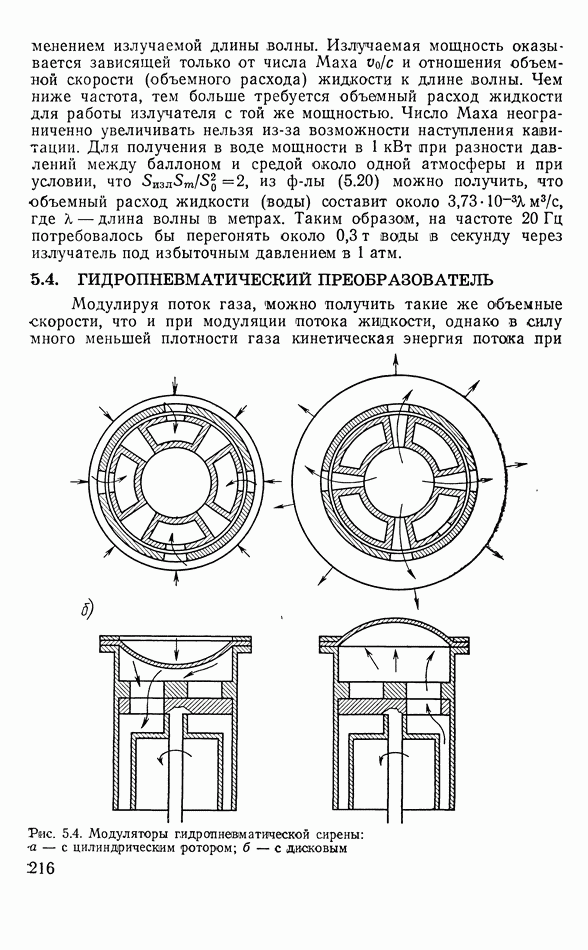
- 5.4. ГИДРОПНЕВМАТИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ
- 5.5. ПАРАМЕТРИЧЕСКИЕ ПРИЕМНИКИ
- 5.6. ПЬЕЗОРЕЗИСТИВНЫЕ ПОЛУПРОВОДНИКОВЫЕ ПРИЕМНИКИ ЗВУКА И ВИБРАЦИЙ
- Глава 6. Запись звука
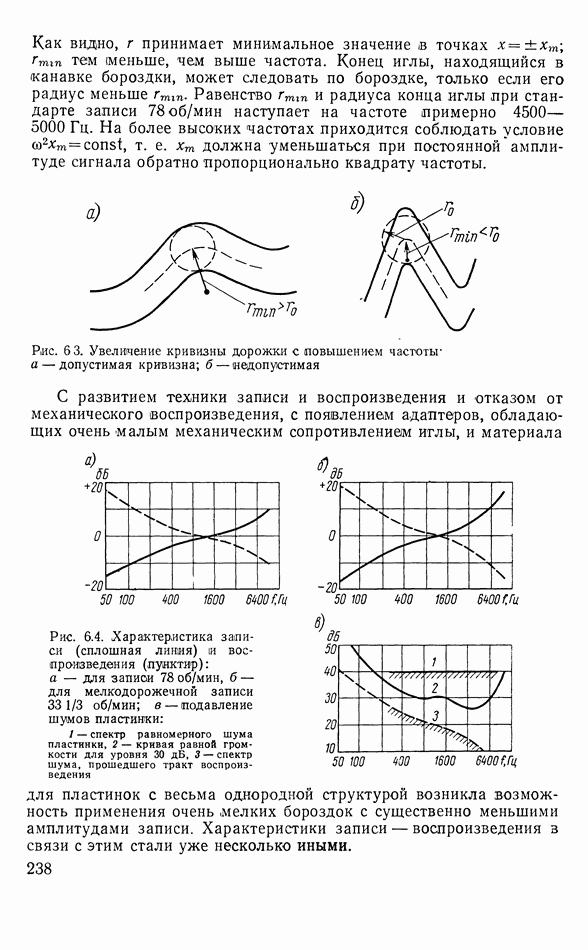
- 6.2. МЕХАНИЧЕСКАЯ ЗАПИСЬ
- Рекордеры
- Электромеханическая обратная связь в рекордере
- Электродинамический рекордер
- Краткие сведения о звукоснимателях
- Стереограммофонная запись
- 6.3. ОПТИЧЕСКАЯ ЗАПИСЬ ЗВУКА
- Оптическая запись с использованием модуляции
- Уменьшение шумового фона при записи по методу переменной ширины
- Щелевые искажения записи
- 6.4. МАГНИТНАЯ ЗАПИСЬ ЗВУКА
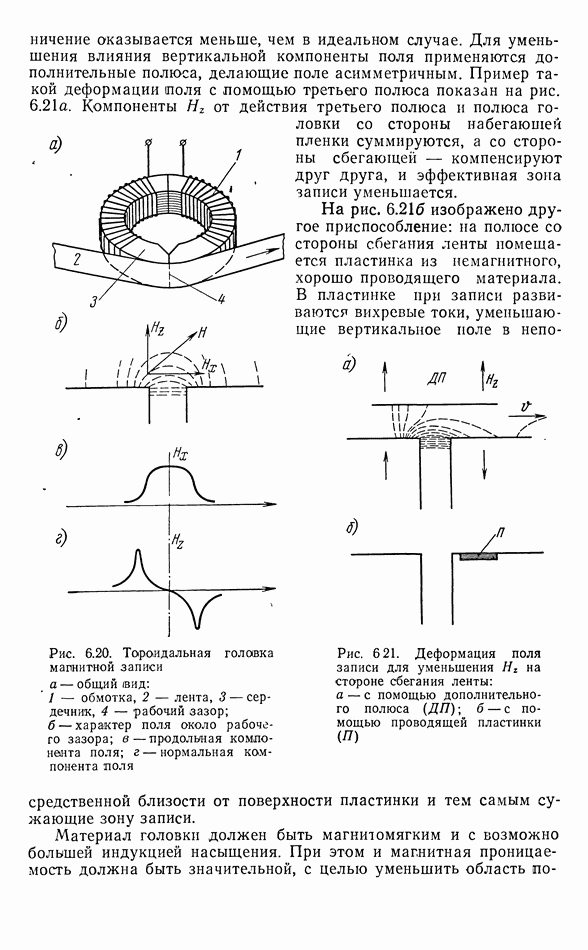
- Головки записи и воспроизведения
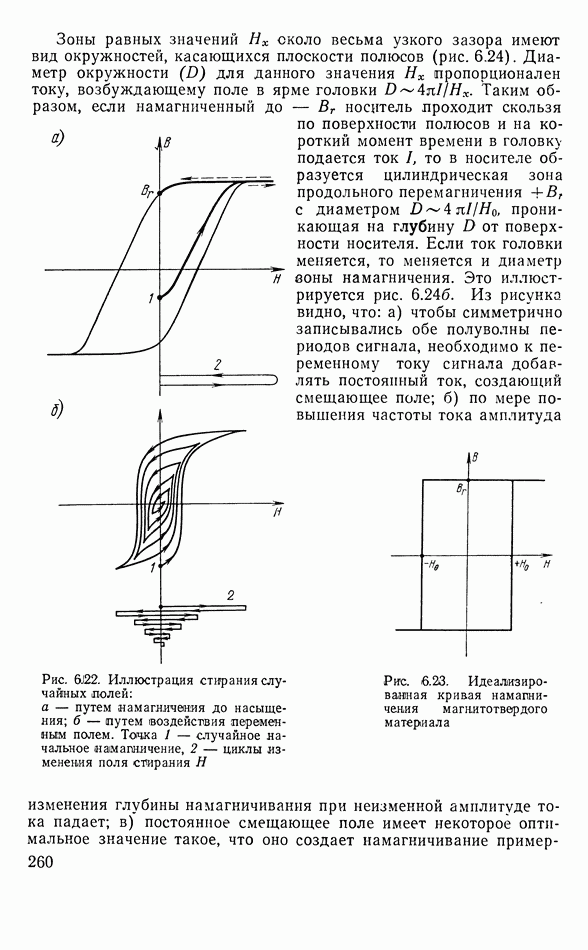
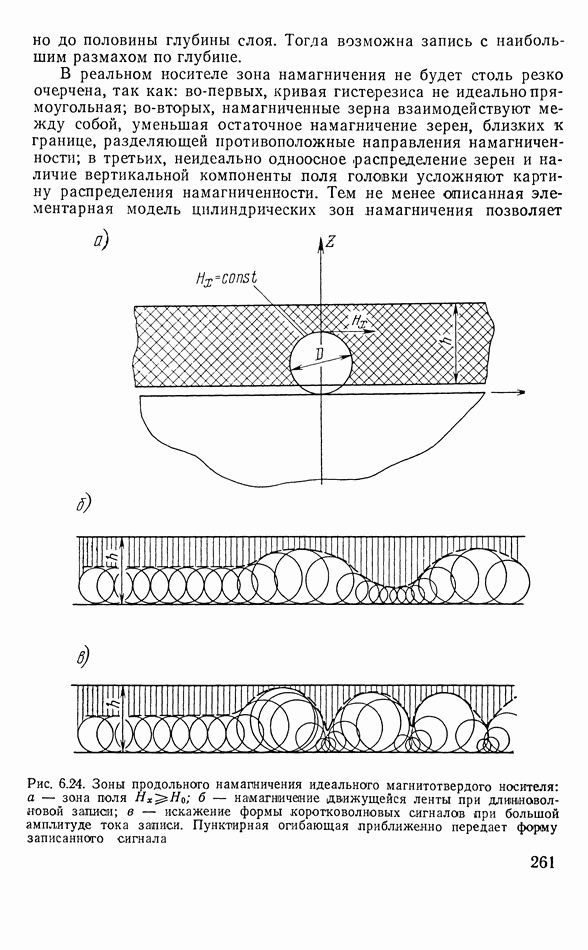
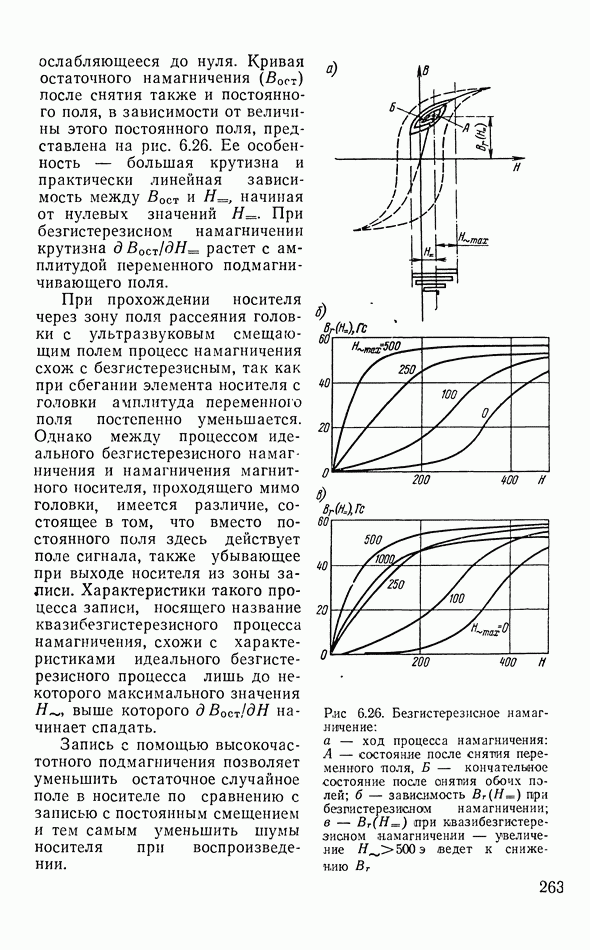
- Процесс намагничения магнитной ленты полем головки
- Воспроизведение записи
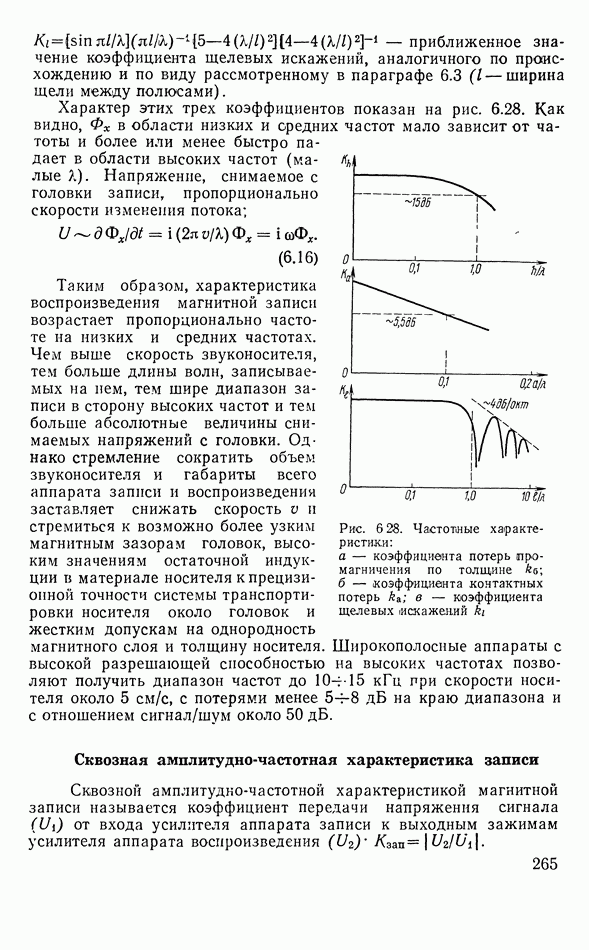
- Сквозная амплитудно-частотная характеристика записи
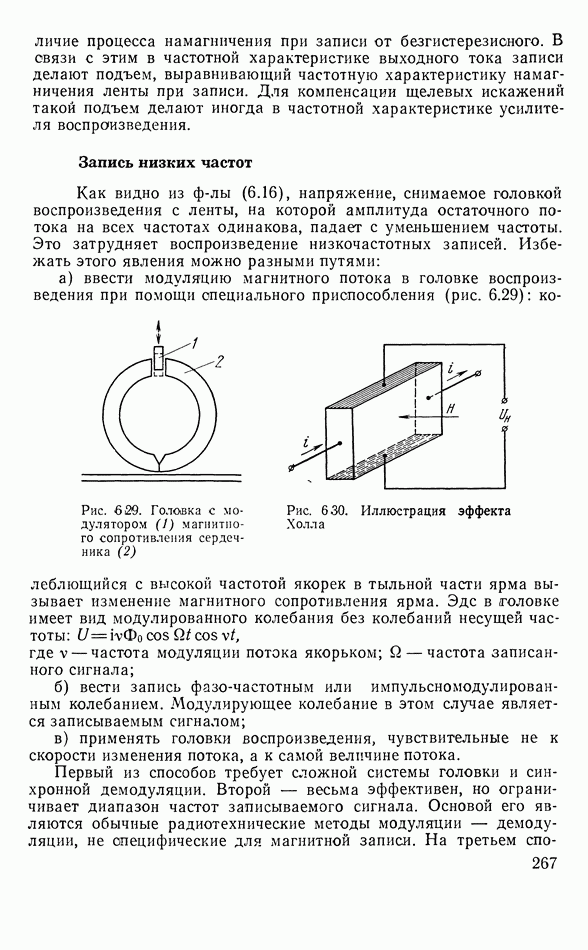
- Запись низких частот
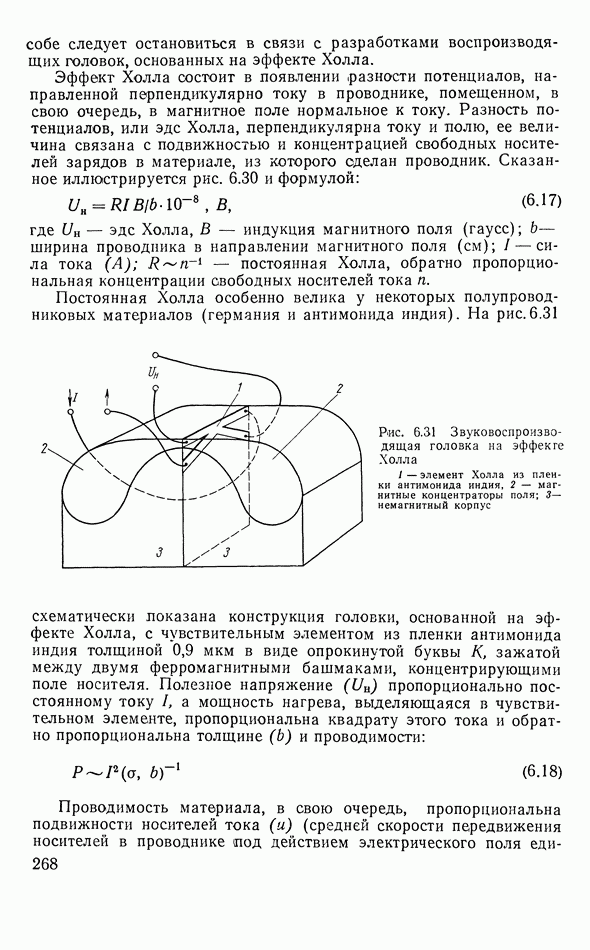
- Плавающие головки
- Точность механизма транспортировки звуконосителя
- Список литературы