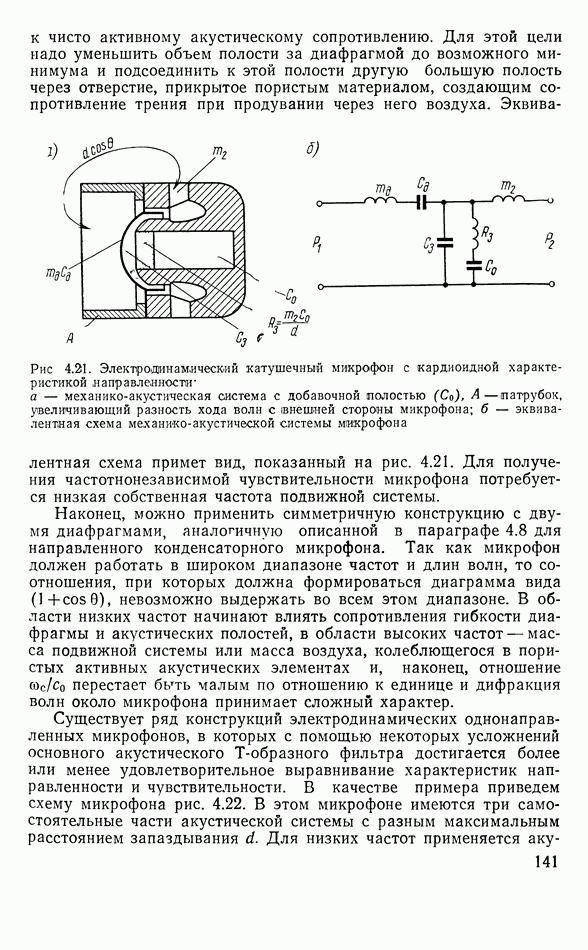
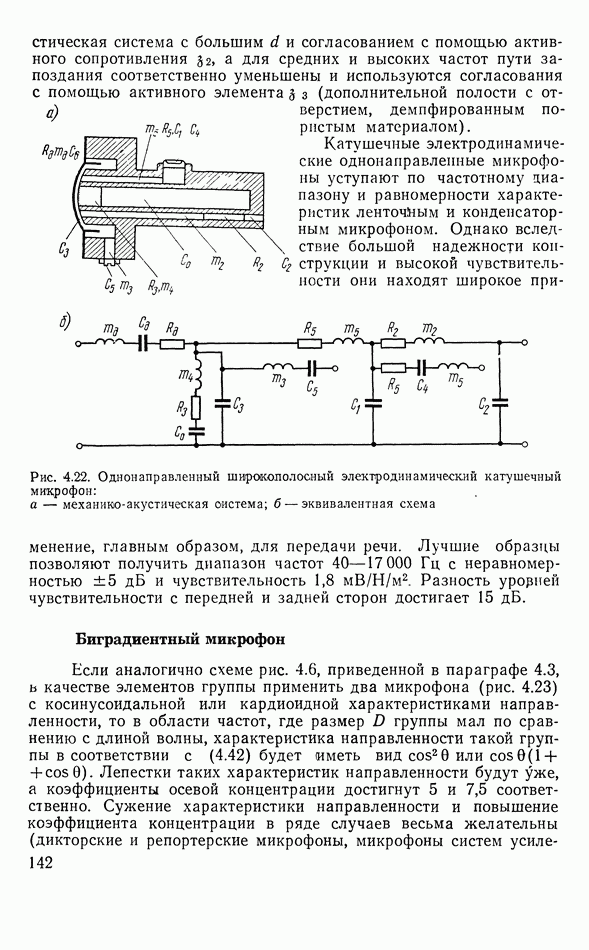
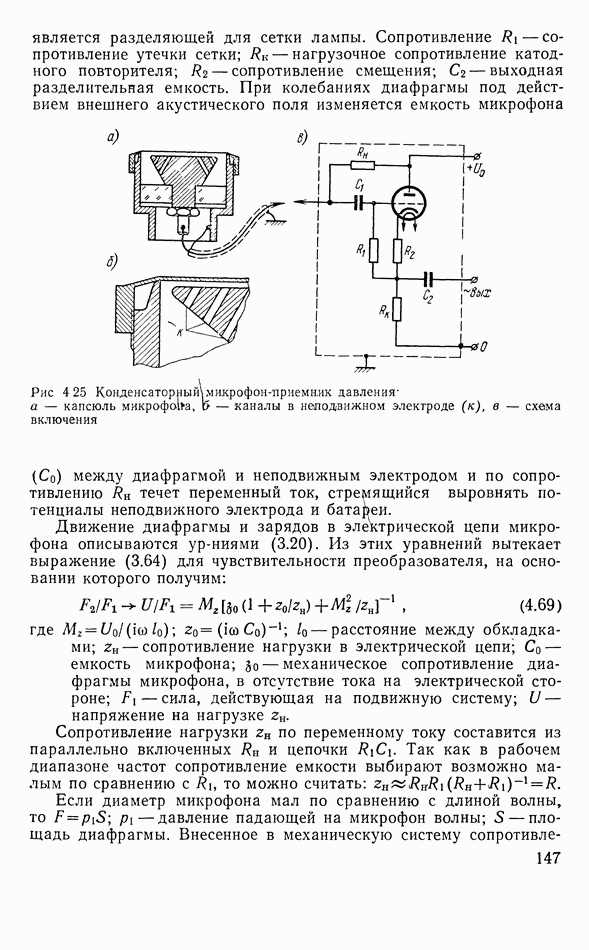
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.10. МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
Явление магнитострикции
Эффект магнитострикции состоит в том, что под действием магнитного поля ферромагнитные материалы деформируются по направлению силовых линий этого поля. Физически это объясняется перестройкой доменной структуры ферромагнетика под действием внешнего магнитного поля. Домены — микроскопические частицы поликристаллической структуры материала — представляют собой группы атомов с отличным от нуля общим для группы магнитным полем. Благодаря обменным силам магнитные поля групп выравниваются и внешнее поле у образца из такого материала отсутствует. Домены достаточно малы (линейный размер доменов  см) и расположены беспорядочно.
см) и расположены беспорядочно.
При действии внешнего поля домены, у которых направление поля совпадает с направлением внешнего поля, начинают расти. В к I чном итоге при достаточно сильном внешнем поле все домены в кристаллах устанавчиваются так, что направление легкого намагничивания совпадает с направлением внешнего поля. Этот процесс вызывает внутренние механические напряжения, для компенсации которых тело вынуждено деформироваться. Основной вид деформации — продольная (вдоль направления поля) деформация в магнитном поле, носящая название продольного эффекта
Джоуля. Кроме этого, наблюдается также и некоторая деформация в поперечных к направлению поля направлениях — поперечный эффект Джоуля. Оба эти эффекта обратимы. Обратный продольный эффект носит название эффекта Виллари: при сжатии (растяжении) магнитострикционного материала в нем наблюдается продольное намагничивание. Эффект Джоуля — четный, т. е. при повороте образца материала в поле на 180° деформация не меняет знака.

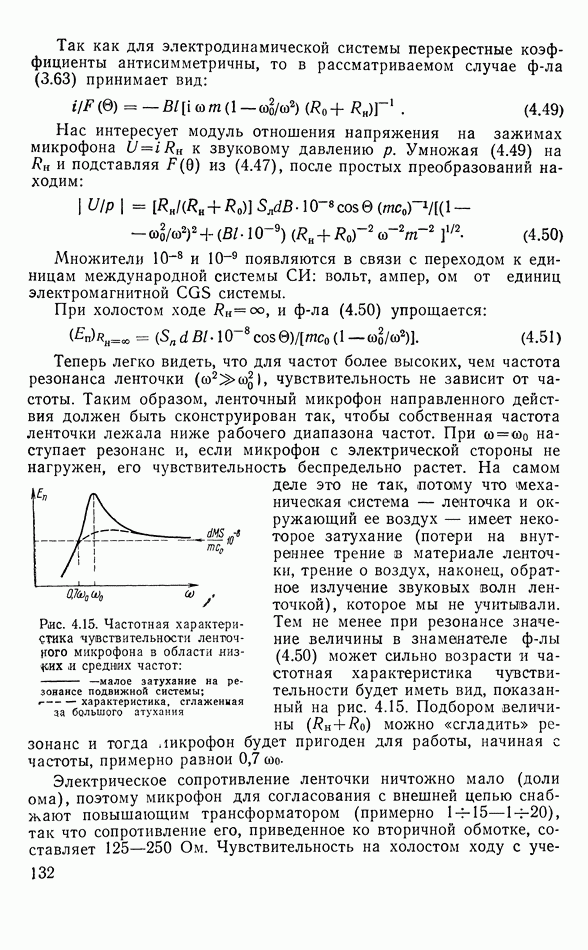
Рис. 3.11. Зависимость магнитострикционной дефармации от напряженности поля: (1 - литой кобальт; 2 — железо, 3 — отожженный кобальт; 4 — никель
Характерные опытные данные зависимости деформации  от напряженности поля приводятся на рис. 3.11. Как видно,
от напряженности поля приводятся на рис. 3.11. Как видно,  нелинейна, и для линейного преобразования можно пользоваться только небольшими участками этих зависимостей. Если поле
нелинейна, и для линейного преобразования можно пользоваться только небольшими участками этих зависимостей. Если поле  наложено на постоянное подмагничизающее поле
наложено на постоянное подмагничизающее поле  то при
то при  можно считать:
можно считать:

Коэффициент  линейно связывает переменную составляющую деформации с переменным намагничиванием. Величина этого коэффициента характеризует магнитострикционный эффект и зависит от величины подмагничивающего поля
линейно связывает переменную составляющую деформации с переменным намагничиванием. Величина этого коэффициента характеризует магнитострикционный эффект и зависит от величины подмагничивающего поля 
На практике магнитострикционный эффект оценивается не величиной  а магнитострикционной постоянной Я (которая также зависит от подмагничивающего поля), определяемой как:
а магнитострикционной постоянной Я (которая также зависит от подмагничивающего поля), определяемой как:

где а — продольное добавочное механическое напряжение, возникающее в зажатом образце магнитострикционного материала, т. е. в отсутствие деформации, при наложении добавочного поля с магнитной индукцией В. Обратный эффект выражается тогда в виде;

Здесь Н — добавочная напряженность поля, действующая в направлении деформации
Экспериментальное исследование различных ферромагнитных материалов позволило выявить те из них, в которых магнитострикция наиболее сильно выражена, найти для них зависимость  и рекомендовать выгодные режимы работы материала в преобразователе. Наиболее распространенными магнитострикционными материалами являются никель, пермендюр (сплав железа, кобальта
и рекомендовать выгодные режимы работы материала в преобразователе. Наиболее распространенными магнитострикционными материалами являются никель, пермендюр (сплав железа, кобальта
и ванадия), алфер (железо-алюминий) и некоторые ферриты — феррокерамические материалы, получаемые на основе окисей никеля, железа и цинка, спекаемых в различных пропорциях в весьма прочную керамикоподобную массу.
Механомагнитные свойства ферритов привлекают внимание техников потому, что наряду с ферритомагнитными свойствами эти материалы имеют свойства, близкие к свойствам изоляторов и при действии переменных магнитных полей в них не образуются вихревые токи. Тем самым их сравнительно высокая магнитная проницаемость и магнитострикционный эффект сохраняются даже на весьма высоких частотах. Металлические магнитострикционные материалы из-за образования вихревых токов (даже при использовании слоеных сердечников с весьма тонкими ламелями) применяют до частот порядка 100 кГц. Ферриты же могут работать в области мегагерц.
В заключение упомянем еще один относящийся к магнитострикции эффект, позволяющий осуществить крутильные колебания материала, так называемый эффект Видемана. Этот эффект возникает при пропускании через магнитострикционный материал тока, параллельного подмагничивающему полю. Поле, создаваемое этим током в материале, взаимодействуя с постоянным подмагничивающим полем, создает спиральное поле, вызывающее соответствующую ориентацию доменов и скручивание образца в плоскости, перпендикулярной подмагничивающему полю. Практическое применение из всех перечисленных эффектов иашел продольный эффект Джоуля.
Уравнения преобразователя
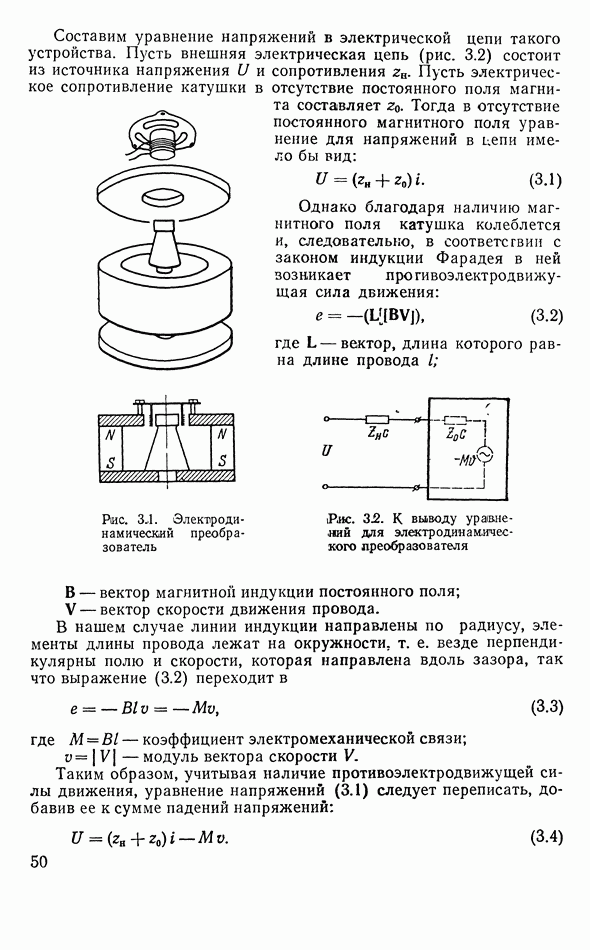
Составим теперь уравнения магнитострикционного преобразователя. Магнитострикционный преобразователь простейшего типа (рис. 3.12) представляет собой замкнутое ярмо из листов магнитострикционного материала. На длинных стержнях ярма уложена обмотка.

Рис. 3.12. Магнитострикционный преобразователь
В обмотку подается постоянный ток, создающий начальную намагничивающую силу  и переменный ток
и переменный ток  . К торцам ярма приложена внешняя сила. Перемещение торцов и сила, действующая на них, составляют механическую сторону преобразователя.
. К торцам ярма приложена внешняя сила. Перемещение торцов и сила, действующая на них, составляют механическую сторону преобразователя.
Поскольку магнитострикционный эффект связывает электрическую сторону преобразователя с механической через явления электромагнитной индукции, естественно предположить, что линеаризованные уравнения для такого преобразователя будут иметь такой же вид, как и для электродинамического. Действительно, на основании (3.78) для случая замкнутого магнитострикционного ярма можно найти отношение силы  действующей на стержень преобразователя, к переменному току
действующей на стержень преобразователя, к переменному току  текущему в его обмотке, когда преобразователь заторможен (деформации магнитострикционного материала нет). Если
текущему в его обмотке, когда преобразователь заторможен (деформации магнитострикционного материала нет). Если  число витков обмотки на единицу длины магнитострикционного стержня, то в отсутствие деформации стержня сила поля в нем
число витков обмотки на единицу длины магнитострикционного стержня, то в отсутствие деформации стержня сила поля в нем  где
где  первоначально наложенное смещающее поле. При наложении, кроме того, деформации растяжения сила поля благодаря обратному магнитострикционному эффекту возрастет:
первоначально наложенное смещающее поле. При наложении, кроме того, деформации растяжения сила поля благодаря обратному магнитострикционному эффекту возрастет:

С другой стороны, механическое напряжение растяжения при неизменной первоначальной индукции составит:  где
где  модуль упругости, а
модуль упругости, а  первоначальное механическое напряжение, возникающее благодаря постоянной индукции
первоначальное механическое напряжение, возникающее благодаря постоянной индукции  Если в стержне возникнет добавочная магнитная индукция В, то вследствие прямого магнитострикционного эффекта возникает сжимающее напряжение, равное —
Если в стержне возникнет добавочная магнитная индукция В, то вследствие прямого магнитострикционного эффекта возникает сжимающее напряжение, равное —  и тогда
и тогда

Отрицательный знак при  в этом равенстве означает, что если растяжение образца приводит к увеличению напряженности поля, увеличение индукции в зажатом образце — к появлению сжимающего напряжения. Если магнитострикционная постоянная отрицательна (это может быть в некоторых материалах при выборе соответствующего начального поля), то оба эффекта (прямой и обратный) меняют знак и ур-ния (3.80) и (3.81) остаются справедливыми.
в этом равенстве означает, что если растяжение образца приводит к увеличению напряженности поля, увеличение индукции в зажатом образце — к появлению сжимающего напряжения. Если магнитострикционная постоянная отрицательна (это может быть в некоторых материалах при выборе соответствующего начального поля), то оба эффекта (прямой и обратный) меняют знак и ур-ния (3.80) и (3.81) остаются справедливыми.
Нас интересуют только переменные составляющие:  В дальнейшем опустим значок
В дальнейшем опустим значок  при
при  будем понимать под а и
будем понимать под а и  переменные составляющие. Если магнитное сопротивление магнитопровода, через который замыкается магнитный поток, пренебрежимо мало по сравнению с сопротивлением стержня, то добавочная индукция
переменные составляющие. Если магнитное сопротивление магнитопровода, через который замыкается магнитный поток, пренебрежимо мало по сравнению с сопротивлением стержня, то добавочная индукция  где
где  динамическая магнитная проницаемость стержня вблизи его состояния начального намагничения
динамическая магнитная проницаемость стержня вблизи его состояния начального намагничения  . Тогда на основании (3.80) и (3.81):
. Тогда на основании (3.80) и (3.81):

Таким образом, сила, действующая на поперечное сечение 5 стержня,  Найдем теперь
Найдем теперь
противоэлектродвижущую силу индукции, развивающуюся в обмотке на единицу длины стержня:  В сумме с приложенным внешнем напряжением
В сумме с приложенным внешнем напряжением  эта эдс должна дать пуль, так что
эта эдс должна дать пуль, так что  Переходя к установившемуся режиму синусоидальных колебаний, получим окончательно:
Переходя к установившемуся режиму синусоидальных колебаний, получим окончательно:

Здесь  модуль упругости магнитострикционного материала при неизменном поле
модуль упругости магнитострикционного материала при неизменном поле  который оказывается меньше модуля упругости
который оказывается меньше модуля упругости  при неизменной индукции
при неизменной индукции  коэффициент электромеханической связи на единицу длины стержня;
коэффициент электромеханической связи на единицу длины стержня;  индуктивность обмотки единичной длины;
индуктивность обмотки единичной длины;  скорость деформации;
скорость деформации;  электрическое напряжение, прилагаемое к обмотке, на единицу длины стержня.
электрическое напряжение, прилагаемое к обмотке, на единицу длины стержня.
Преобразователь с однородной деформацией
Если частота тока такова, что длина стержня I мала по сравнению с длиной упругой волны сжатия на этой частоте, то деформация стержня по его длине однородна. Тогда, если один из концов стержня неподвижно закреплен, то скорость смещения у второго конца найдем, умножая скорость деформации стержня на его длину, и получим:

где  продольная гибкость стержня длиной и сечением
продольная гибкость стержня длиной и сечением  полное число витков обмотки);
полное число витков обмотки);  полное напряжена, приложенное к преобразователю;
полное напряжена, приложенное к преобразователю;  индуктивность всей обмотки;
индуктивность всей обмотки;  скорость конца стержня.
скорость конца стержня.
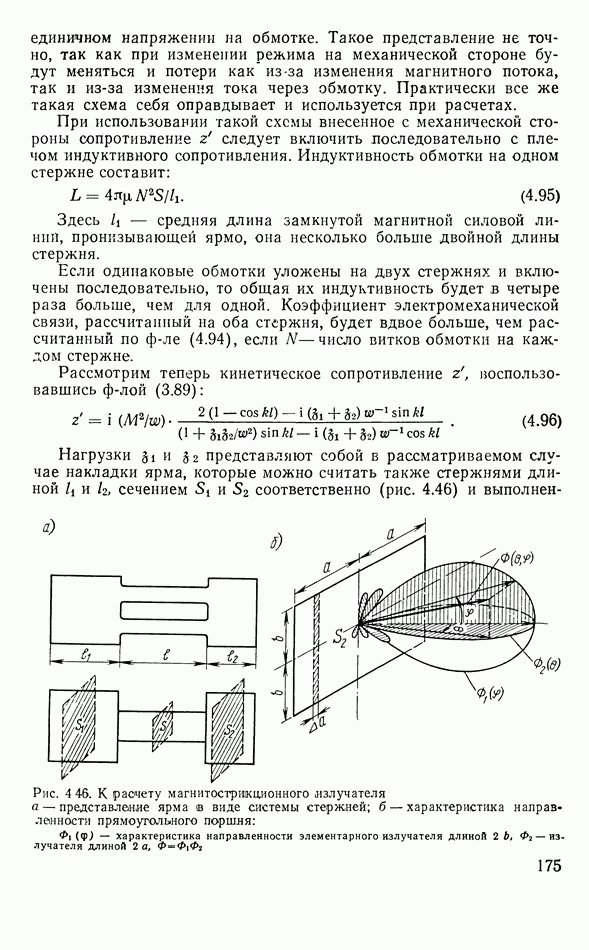
Здесь видно, что  сопротивление магнитной цепи ярма, которое в данном случае свелось к магнитному сопротивлению самого стержня, так как сопротивление остальных частей магнитопровода не учитывалось. Кроме того, очевидно, что не учтено активное сопротивление обмотки, так как противоэдс индукции приравнена прямо к внешнему напряжению. Поэтому в более общем случае следует писать:
сопротивление магнитной цепи ярма, которое в данном случае свелось к магнитному сопротивлению самого стержня, так как сопротивление остальных частей магнитопровода не учитывалось. Кроме того, очевидно, что не учтено активное сопротивление обмотки, так как противоэдс индукции приравнена прямо к внешнему напряжению. Поэтому в более общем случае следует писать:

где  полное магнитное сопротивление магнитопровода;
полное магнитное сопротивление магнитопровода;  коэффициент механических потерь при деформации стержня;
коэффициент механических потерь при деформации стержня;  активное сопротивление обмотки, учитывающее омические потери и потери на вихревые токи; численно оно равно мощности потерь при единичном токе.
активное сопротивление обмотки, учитывающее омические потери и потери на вихревые токи; численно оно равно мощности потерь при единичном токе.
При переменном намагничивании возникают потери из-за магнитного гистерезиса, которые можно учесть, считая магнитную проницаемость цепи комплексной:  Тогда к активному сопротивлению добавится еще величина сопротивления потерь на гистерезис:
Тогда к активному сопротивлению добавится еще величина сопротивления потерь на гистерезис:  так как всегда можно считать
так как всегда можно считать 
Коэффициент электромеханической связи так же будет комплексным:  что поведет к дополнительному увеличению
что поведет к дополнительному увеличению 
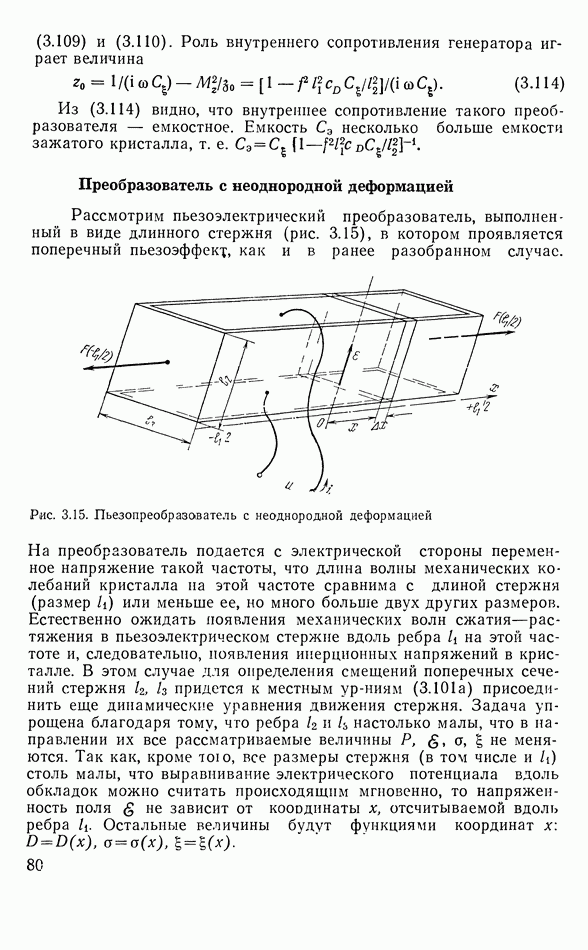
Преобразователь с неоднородной деформацией
Если длина магнитострикционного стержня, несущего возбуждающую обмотку, равна или более четверти длины волны, то деформация и механические напряжения в нем становятся существенно неоднородными по длине. Смещения сечений стержня  в этом случае сложным образом зависят от координаты
в этом случае сложным образом зависят от координаты  вдоль стержня. Деформация
вдоль стержня. Деформация  выражается как
выражается как  так что
так что  Число витков на единицу длины
Число витков на единицу длины  и сечение стержня 5 будем считать независимыми от
и сечение стержня 5 будем считать независимыми от  При неоднородной деформации силы инерции элементов стержня уравновешиваются градиентом механического напряжения. В режиме синусоидальных колебаний это динамическое равновесие запишется так:
При неоднородной деформации силы инерции элементов стержня уравновешиваются градиентом механического напряжения. В режиме синусоидальных колебаний это динамическое равновесие запишется так:  где
где  материала стержня. Обозначая через
материала стержня. Обозначая через  скорость распространения волн сжатия в стержне, получим
скорость распространения волн сжатия в стержне, получим

Решение проще всего искать в виде  где
где  постоянные интегрирования и
постоянные интегрирования и  Интегрируя второе ур-ние (3.82), получим
Интегрируя второе ур-ние (3.82), получим 

Пусть на границе  (начало стержня) к стержню подсоединена механическая нагрузка
(начало стержня) к стержню подсоединена механическая нагрузка  а на конце его,
а на конце его,  заданы сила
заданы сила  и скорость
и скорость  Тогда, учитывая очевидные соотношения:
Тогда, учитывая очевидные соотношения:

пилучим

где  волновое сопротивление стержня.
волновое сопротивление стержня.
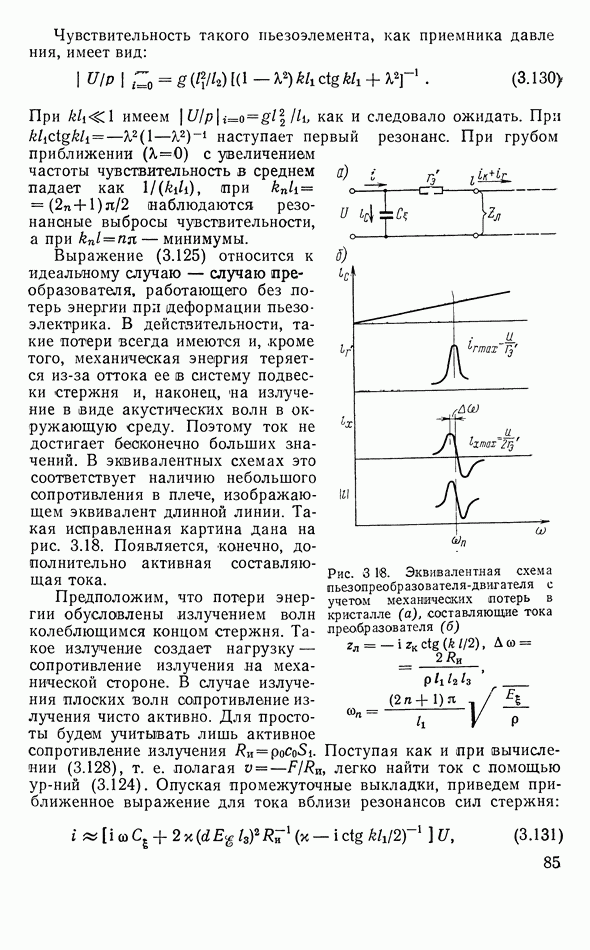
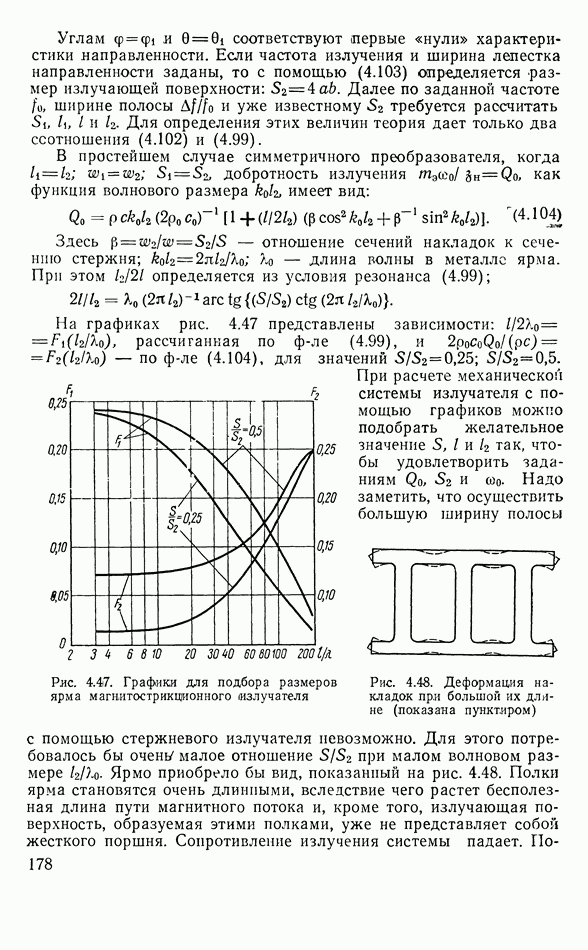
Если такой преобразователь нагрузить на стороне II нагрузкой  то можно получить выражение для полного электрического сопротивления преобразователя, состоящего из магнитострикционного стержня, нагруженного с обоих концов механическими нагрузками
то можно получить выражение для полного электрического сопротивления преобразователя, состоящего из магнитострикционного стержня, нагруженного с обоих концов механическими нагрузками 

Если сопротивления  чисто реактивные, то знаменатель второго слагаемого (которое является кинетическим сопротивлением) может обратиться в нуль и
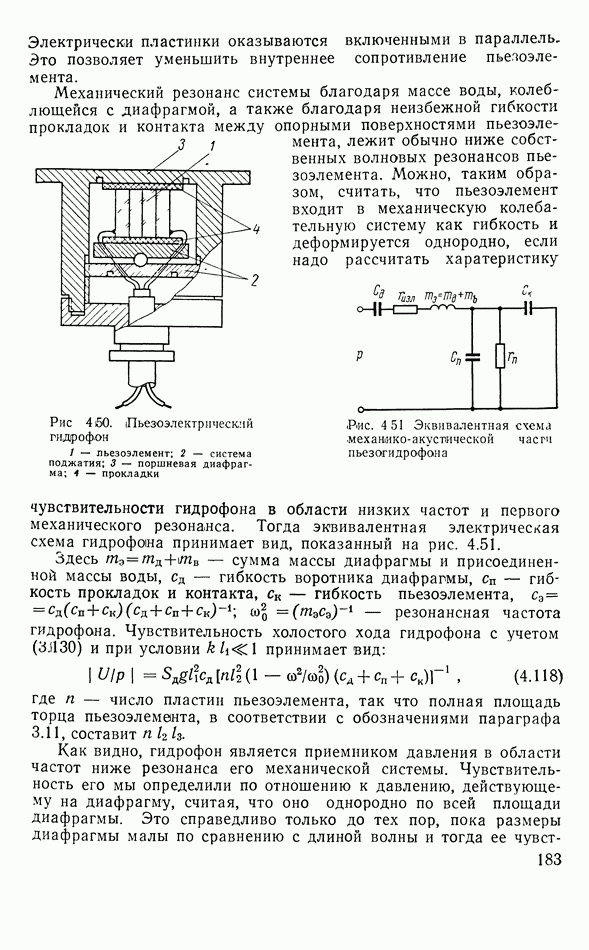
чисто реактивные, то знаменатель второго слагаемого (которое является кинетическим сопротивлением) может обратиться в нуль и  будет бесконечно большим. Например, если стержень нагружен симметричными накладками, замыкающими ярмо, и накладки коротки по сравнению с длиной волны в системе преобразователя, то, не учитывая излучения, можно положить
будет бесконечно большим. Например, если стержень нагружен симметричными накладками, замыкающими ярмо, и накладки коротки по сравнению с длиной волны в системе преобразователя, то, не учитывая излучения, можно положить  Тогда на механическом резонансе ярма
Тогда на механическом резонансе ярма 

Это условие можно записать так:

Здесь 21 — как бы добавочная длина, которую получает стержень преобразователя, так что на суммарной длине  как раз укладывается половина длины волны резонансной частоты:
как раз укладывается половина длины волны резонансной частоты:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. Краткие сведения по физиологической акустике
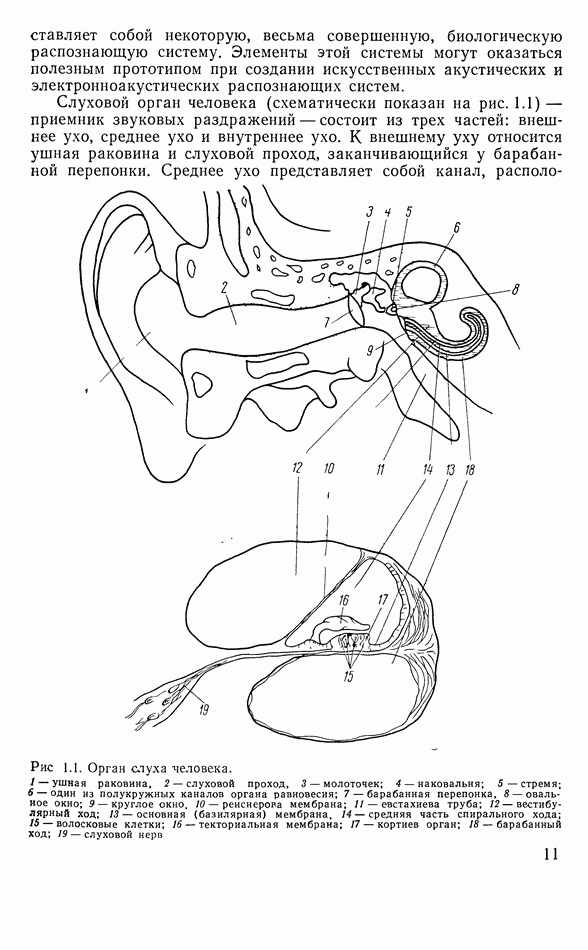
- 1.1. УСТРОЙСТВО СЛУХОВОГО ОРГАНА ЧЕЛОВЕКА
- 1.2. МЕХАНИЗМ ВОЗБУЖДЕНИЯ СЛУХОВОГО НЕРВА
- 1.3. ТЕОРИЯ СЛУХА
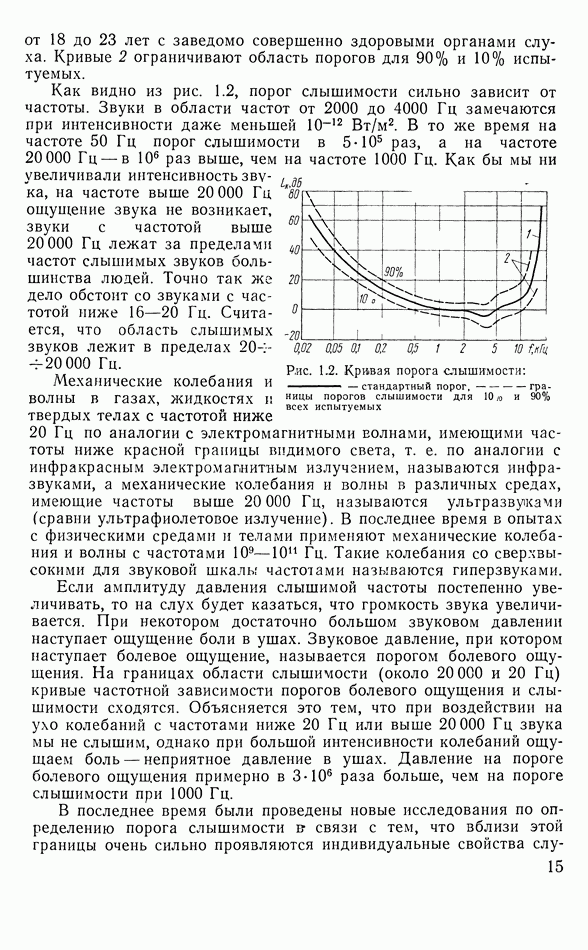
- 1.4. ПОРОГ СЛЫШИМОСТИ
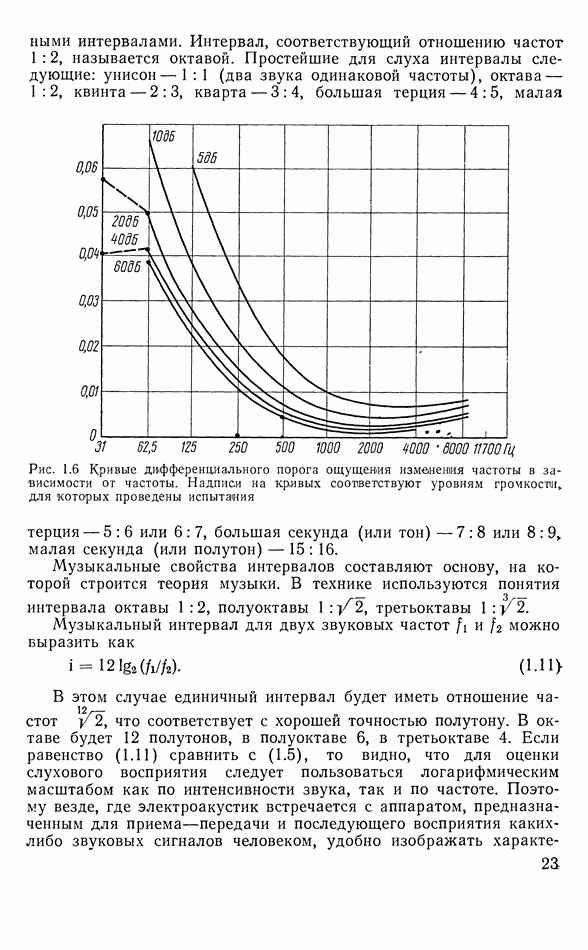
- 1.5. ДИФФЕРЕНЦИАЛЬНЫЙ ПОРОГ ВОСПРИЯТИЯ ИНТЕНСИВНОСТИ ЗВУКА
- 1.6. ЛОГАРИФМИЧЕСКИЕ УРОВНИ. ШКАЛА ДЕЦИБЕЛ
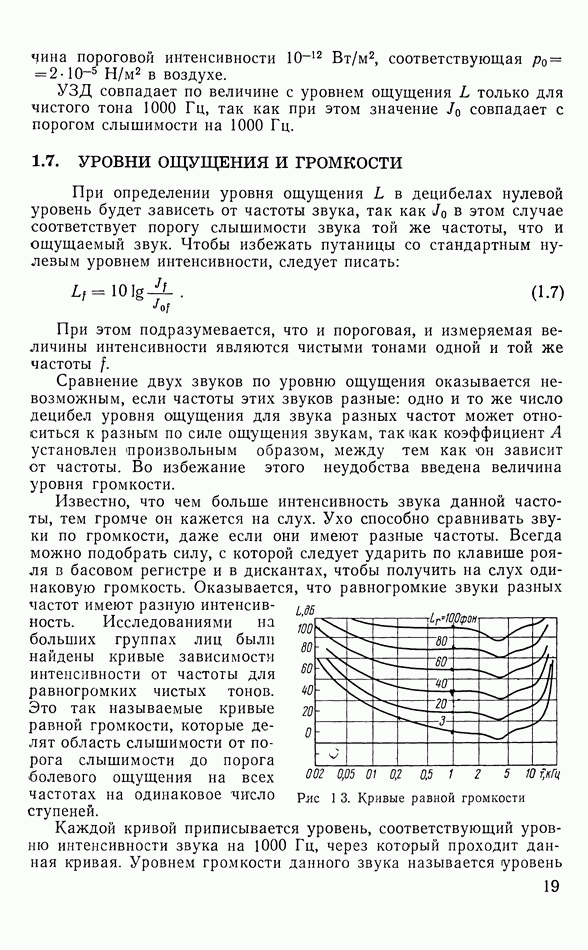
- 1.7. УРОВНИ ОЩУЩЕНИЯ И ГРОМКОСТИ
- 1.8. ГРОМКОСТЬ ЧИСТЫХ ТОНОВ
- 1.9. КРИТИЧЕСКИЕ ПОЛОСЫ СЛУХА
- 1.10. УРОВЕНЬ ГРОМКОСТИ СЛОЖНЫХ ЗВУКОВ
- 1.11. ВОСПРИЯТИЕ ВЫСОТЫ ТОНА. ШКАЛА ЧАСТОТ
- 1.12. МАСКИРОВКА ЗВУКА
- 1.13. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- 1.14. ВОСПРИЯТИЕ ОКРАСКИ (ТЕМБРА) ЗВУКА
- Глава 2. Электромеханические и электроакустические аналогии
- 2.1. ПРИНЦИП ЭЛЕКТРОМЕХАНИЧЕСКИХ АНАЛОГИЙ
- 2.2. МЕХАНИЧЕСКИЕ ЭЛЕМЕНТЫ И МЕХАНИЧЕСКИЕ СИСТЕМЫ
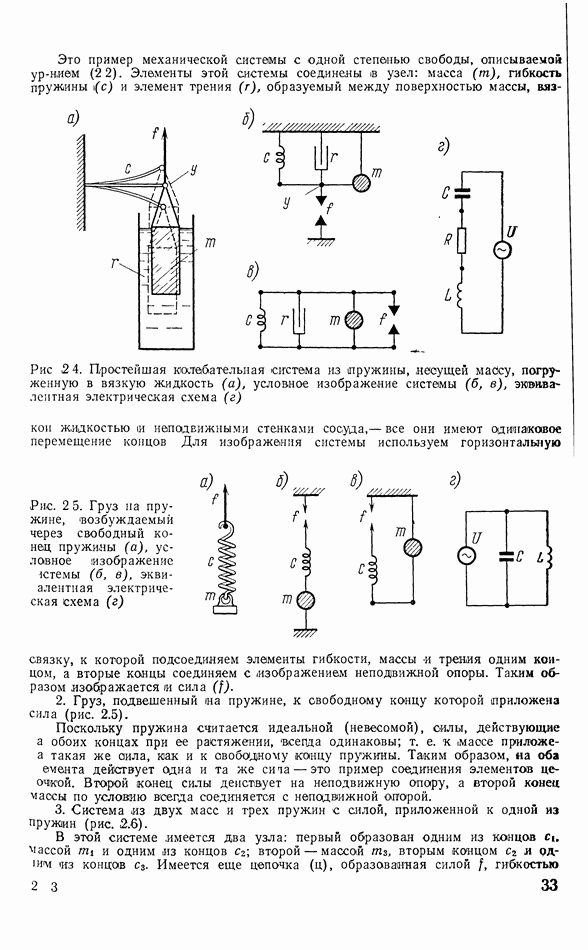
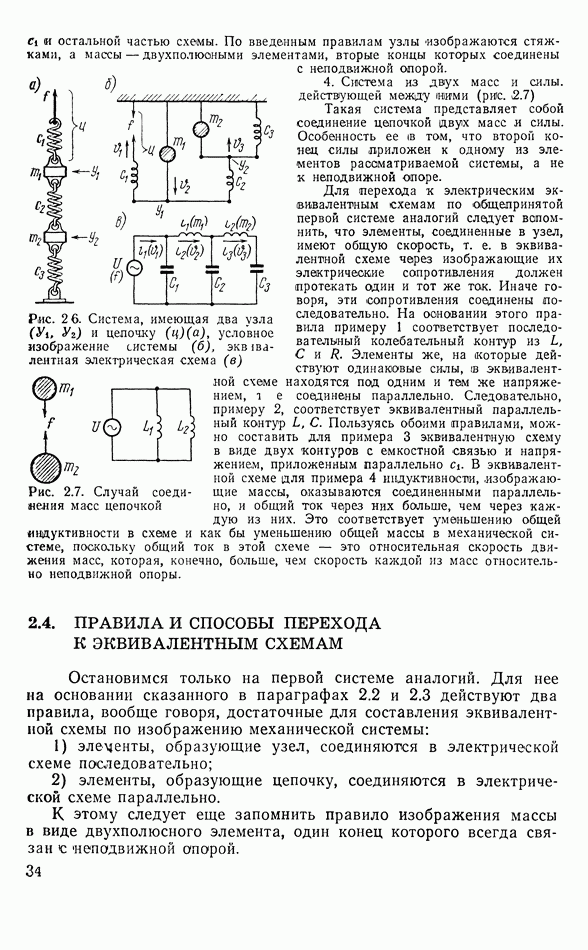
- 2.3. ПРИМЕРЫ ИЗОБРАЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ И ИХ ЭКВИВАЛЕНТНЫХ СХЕМ
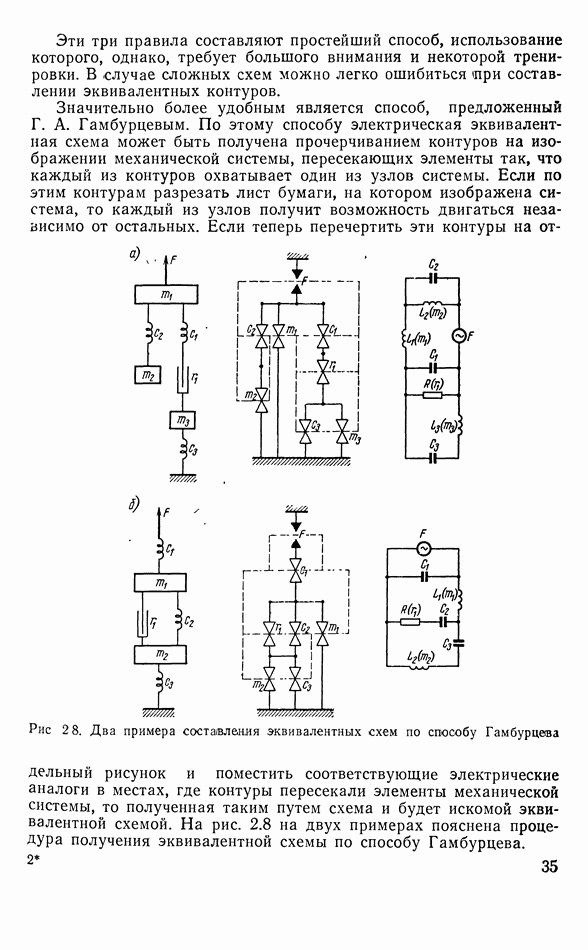
- 2.4. ПРАВИЛА И СПОСОБЫ ПЕРЕХОДА К ЭКВИВАЛЕНТНЫМ СХЕМАМ
- 2.5. ТРАНСФОРМАЦИЯ СИЛ И СКОРОСТЕЙ. ЭЛЕКТРИЧЕСКИЙ АНАЛОГ-ТРАНСФОРМАТОР
- 2.6. ЭЛЕКТРОАКУСТИЧЕСКИЕ АНАЛОГИИ
- 2.7. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИИ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
- 2.8. ЭКВИВАЛЕНТНЫЕ СОСРЕДОТОЧЕННЫЕ ПАРАМЕТРЫ МЕХАНИЧЕСКИХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ
- Глава 3. Электромеханические преобразователи
- 3.2. ДВА ОСНОВНЫХ ТИПА ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
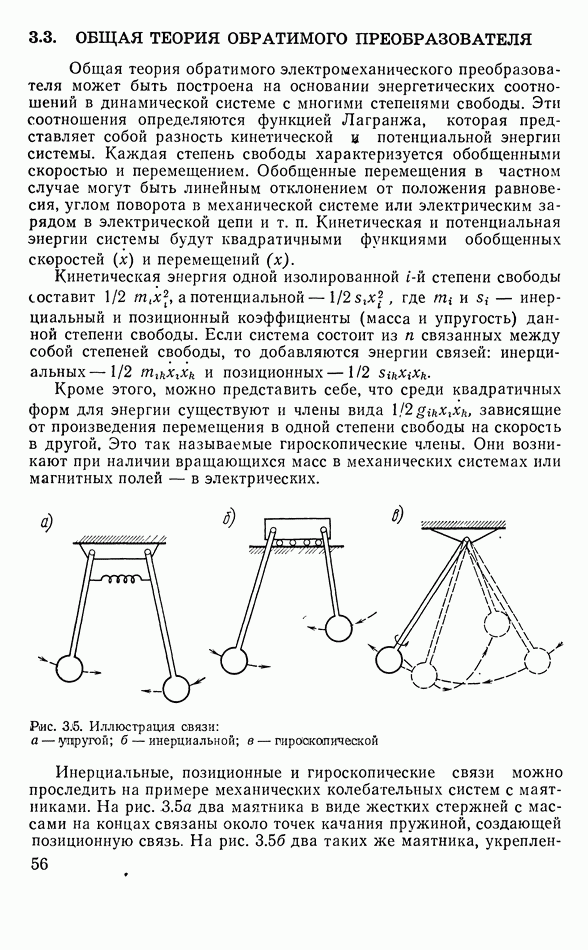
- 3.3. ОБЩАЯ ТЕОРИЯ ОБРАТИМОГО ПРЕОБРАЗОВАТЕЛЯ
- 3.4. ВТОРИЧНЫЕ ПАРАМЕТРЫ ПРЕОБРАЗОВАТЕЛЯ
- 3.5. ПРАВИЛО ЗНАКОВ
- 3.6. ВХОДНОЕ СОПРОТИВЛЕНИЕ СИСТЕМЫ В ОБЩЕМ СЛУЧАЕ
- 3.7. ЧУВСТВИТЕЛЬНОСТЬ ПРЕОБРАЗОВАТЕЛЯ
- 3.8. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ПРЕОБРАЗОВАТЕЛЯ
- 3.9. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗОВАТЕЛИ
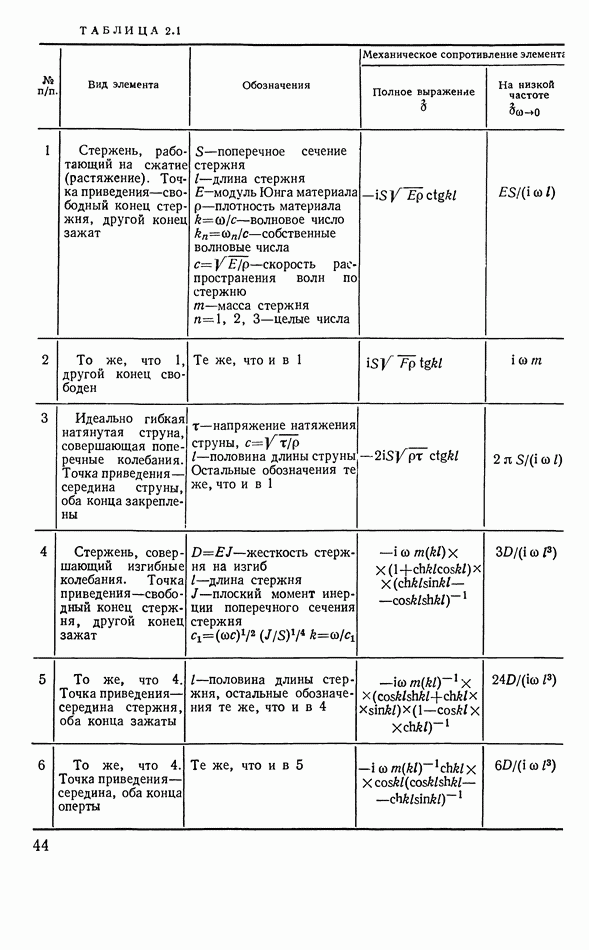
- 3.10. МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 3.11. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Преобразователь с однородной деформацией
- Преобразователь с неоднородной деформацией
- Местные уравнения пьезопреобразователя в тензорной форме
- Свойства основных пьезоэлектрических кристаллов
- Выбор среза кристалла при изготовлении пьезоэлементов
- Искусственные пьезокерамические материалы
- 3.12. ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 4. Электроакустическая аппаратура
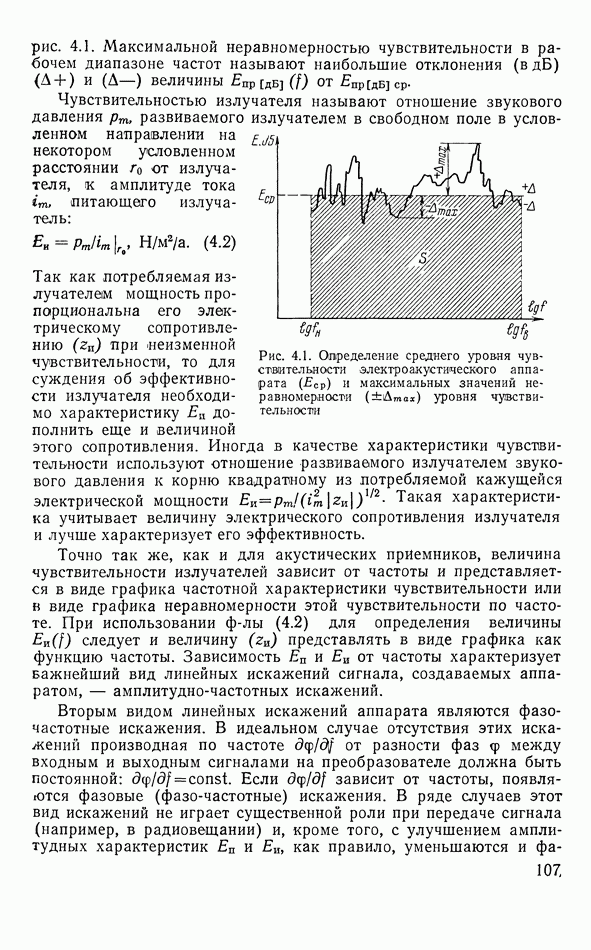
- 4.1. КЛАССИФИКАЦИЯ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- 4.2. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 4.3. АНТЕННЫ ЭЛЕКТРОАКУСТИЧЕСКИХ АППАРАТОВ
- Связь между чувствительностью приемной и излучающей антенн
- Сопротивление излучения антенны
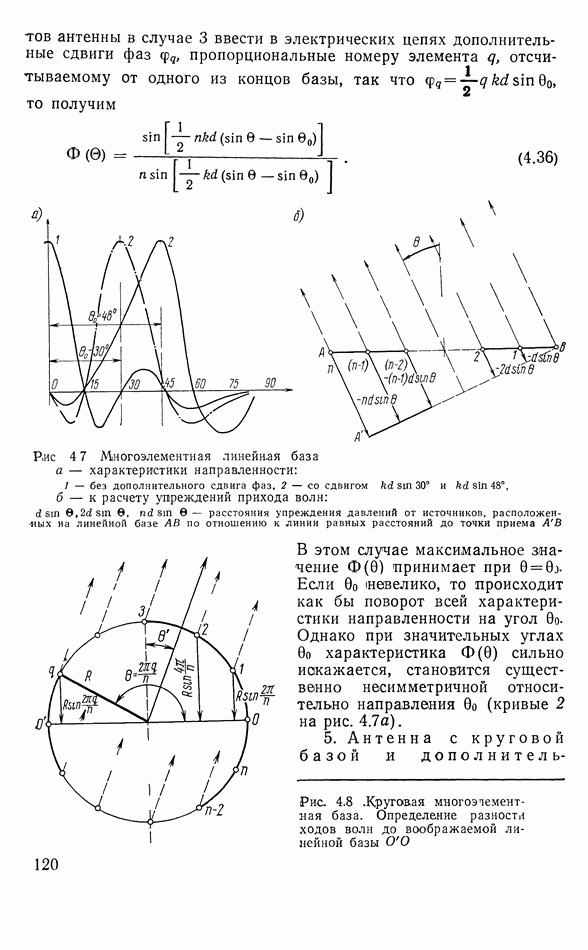
- Сложные антенны
- Распределенные антенны
- Антенна бегущей волны
- Антенна из направленных элементов
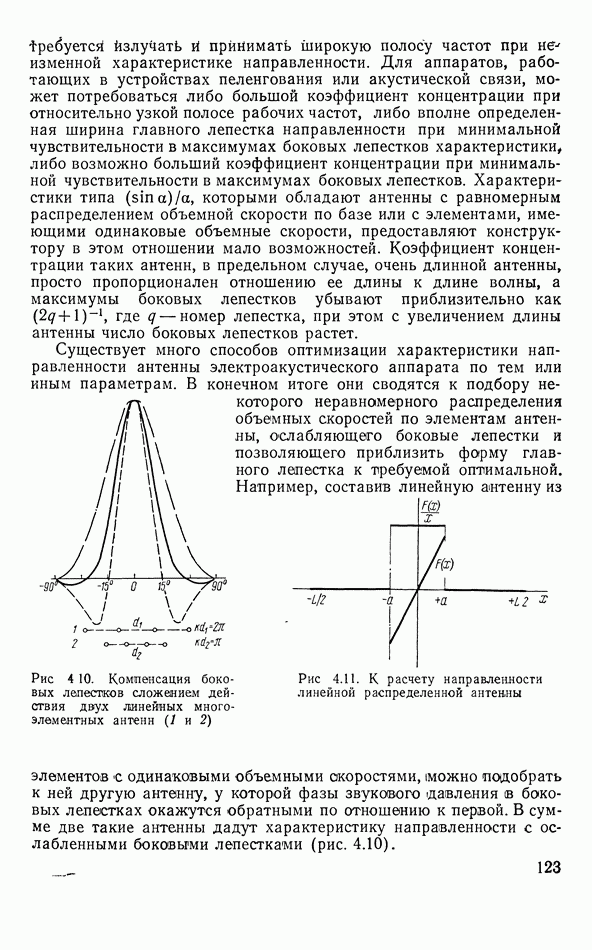
- Оптимизация характеристики направленности антенны
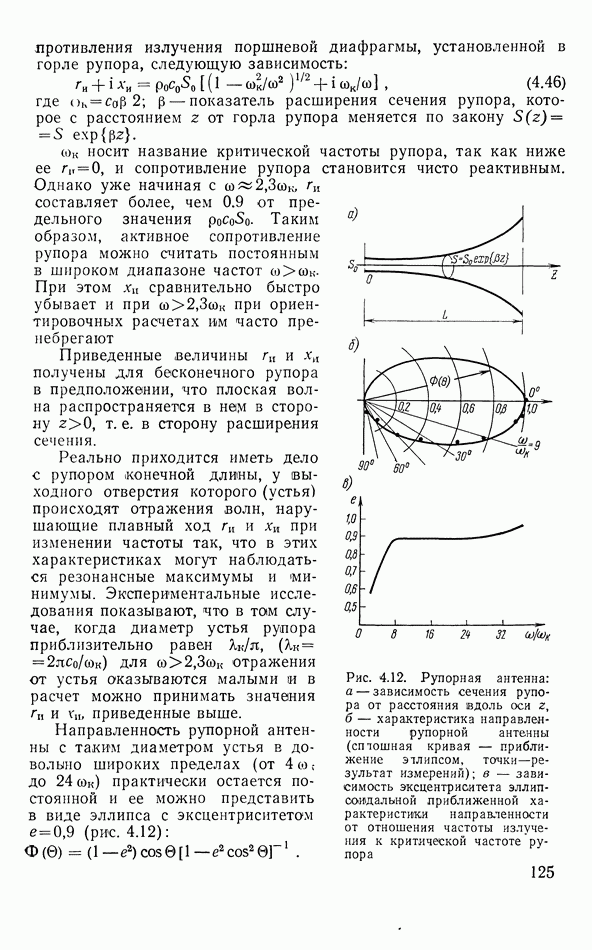
- Рупорная антенна
- 4.4. ТРЕБОВАНИЯ К ЭЛЕКТРОАКУСТИЧЕСКОЙ АППАРАТУРЕ РАДИОВЕЩАНИЯ И ТЕЛЕВИДЕНИЯ
- 4.5. ЛЕНТОЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Ненаправленный микрофон-приемник давления
- Микрофон с кардиоидной характеристикой направленности
- Микрофон с регулируемой характеристикой направленности
- 4.6. КАТУШЕЧНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- Однонаправленный микрофон
- Биградиентный микрофон
- Сверхнаправленный микрофон
- 4.7. СОГЛАСОВАНИЕ ЭЛЕКТРИЧЕСКОЙ СТОРОНЫ ЭЛЕКТРОДИНАМИЧЕСКОГО МИКРОФОНА СО ВХОДОМ МИКРОФОННОГО УСИЛИТЕЛЯ
- 4.8. КОНДЕНСАТОРНЫЕ МИКРОФОНЫ
- Об отрицательной упругости электрического поля поляризации в микрофоне
- Предельная чувствительность микрофона
- Влияние емкости входа предварительного каскада
- Микрофон направленного действия
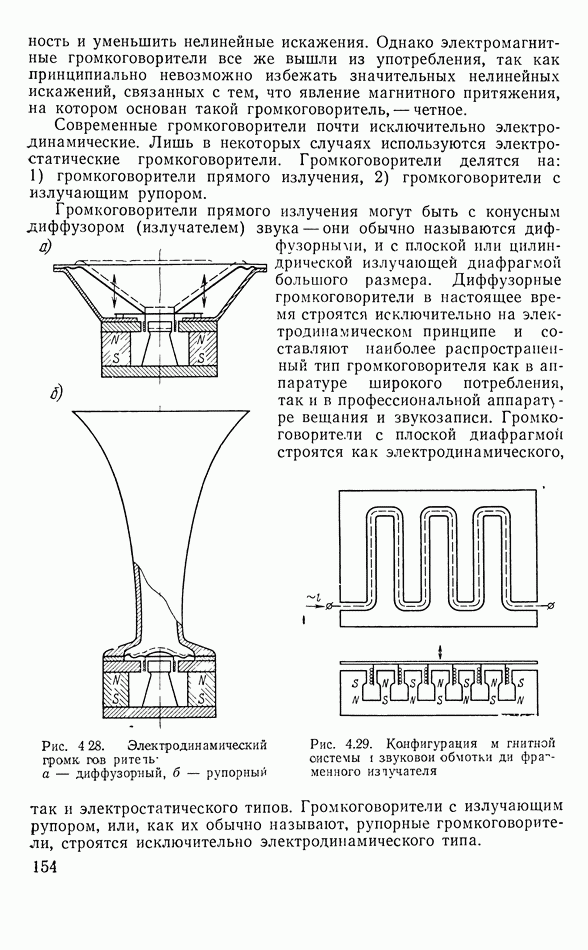
- 4.9. ОБЩИЕ СВЕДЕНИЯ О ГРОМКОГОВОРИТЕЛЯХ
- 4.10. ДИФФУЗОРНЫЕ ГРОМКОГОВОРИТЕЛИ
- Частотная характеристика чувствительности
- Влияние способа установки громкоговорителя на излучение в области низких частот
- Работа громкоговорителя в области высоких частот
- Комбинированные громкоговорители
- Нелинейные искажения в громкоговорителе
- 4.11. РУПОРНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ГРОМКОГОВОРИТЕЛИ
- Влияние конечной длины рупора
- Широкогорлый громкоговоритель
- Громкоговорящие агрегаты
- 4.12. ЭЛЕКТРОСТАТИЧЕСКИЙ ГРОМКОГОВОРИТЕЛЬ
- 4.13. МАГНИТОСТРИКЦИОННЫЕ ИЗЛУЧАТЕЛИ
- Стержневой излучатель
- Кольцевой излучатель
- Круговая диаграмма преобразователя
- Коэффициент полезного действия излучателя
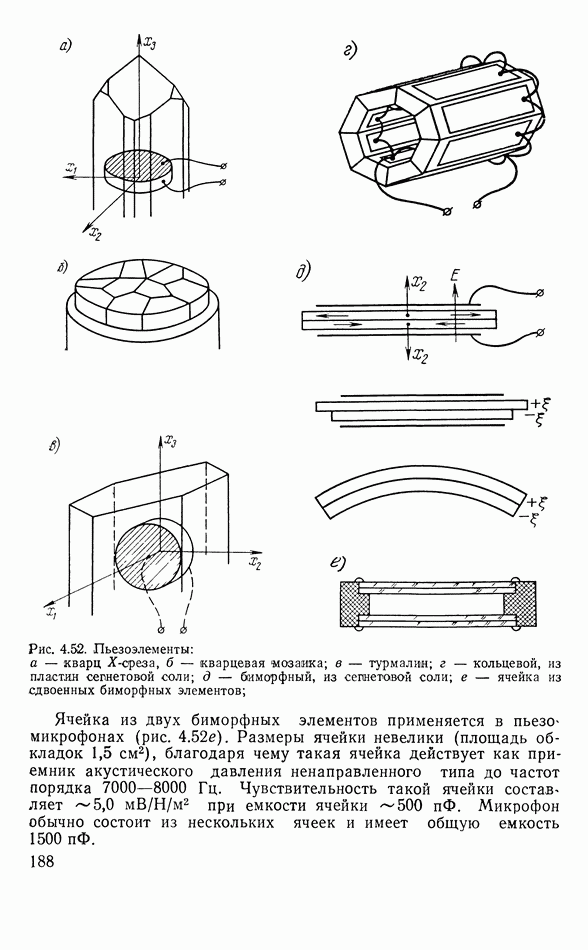
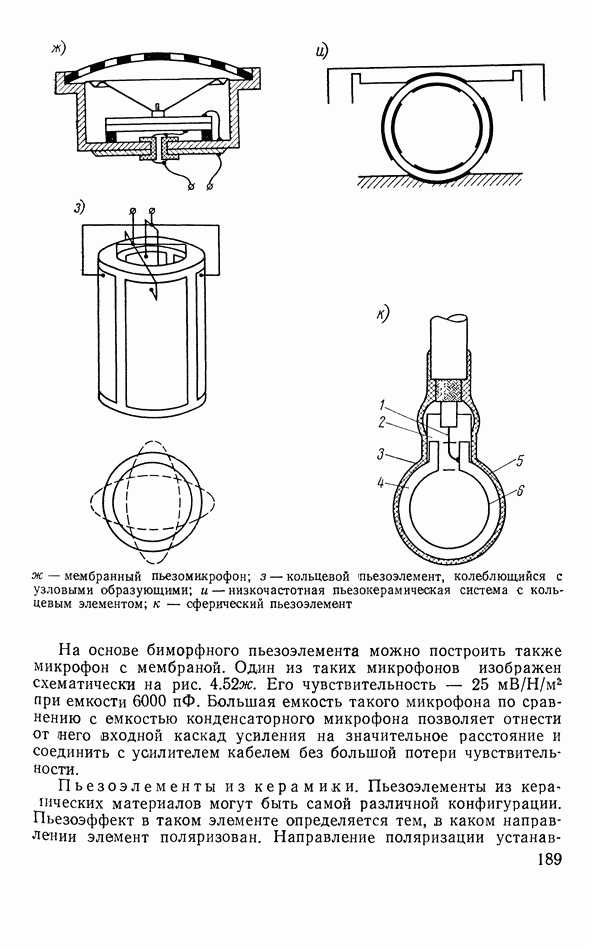
- 4.14. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ АППАРАТЫ
- Линия задержки
- Другие типы пьезоэлектрических элементов электроакустических аппаратов
- Согласование пьезоэлемента с электрической частью системы
- 4.15. ЭЛЕКТРОДИНАМИЧЕСКИЙ ГЕОФОН
- Частотная характеристика чувствительности
- Максимальная чувствительность
- 4.16. СЕЙСМОМЕТРИЧЕСКИЙ ПРИЕМНИК СМЕЩЕНИЯ
- 4.17. ОПТИМИЗАЦИЯ КОНСТРУКТИВНЫХ РАЗМЕРОВ ЭЛЕКТРОАКУСТИЧЕСКОГО АППАРАТА
- Глава 5. Необратимые преобразователи
- 5.2. ПНЕВМОАКУСТИЧЕСКИЕ ИЗЛУЧАТЕЛИ
- Модуляция потока воздуха
- Пневматическая сирена
- Модулятор с возвратно-поступательным движением
- 5.3. ГИДРАВЛИЧЕСКАЯ СИРЕНА
- 5.4. ГИДРОПНЕВМАТИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ
- 5.5. ПАРАМЕТРИЧЕСКИЕ ПРИЕМНИКИ
- 5.6. ПЬЕЗОРЕЗИСТИВНЫЕ ПОЛУПРОВОДНИКОВЫЕ ПРИЕМНИКИ ЗВУКА И ВИБРАЦИЙ
- Глава 6. Запись звука
- 6.2. МЕХАНИЧЕСКАЯ ЗАПИСЬ
- Рекордеры
- Электромеханическая обратная связь в рекордере
- Электродинамический рекордер
- Краткие сведения о звукоснимателях
- Стереограммофонная запись
- 6.3. ОПТИЧЕСКАЯ ЗАПИСЬ ЗВУКА
- Оптическая запись с использованием модуляции
- Уменьшение шумового фона при записи по методу переменной ширины
- Щелевые искажения записи
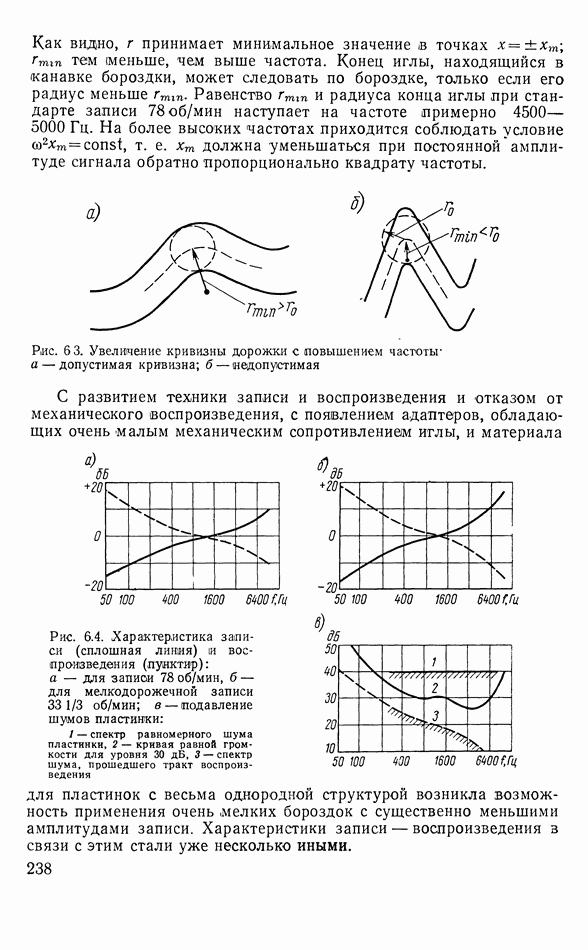
- 6.4. МАГНИТНАЯ ЗАПИСЬ ЗВУКА
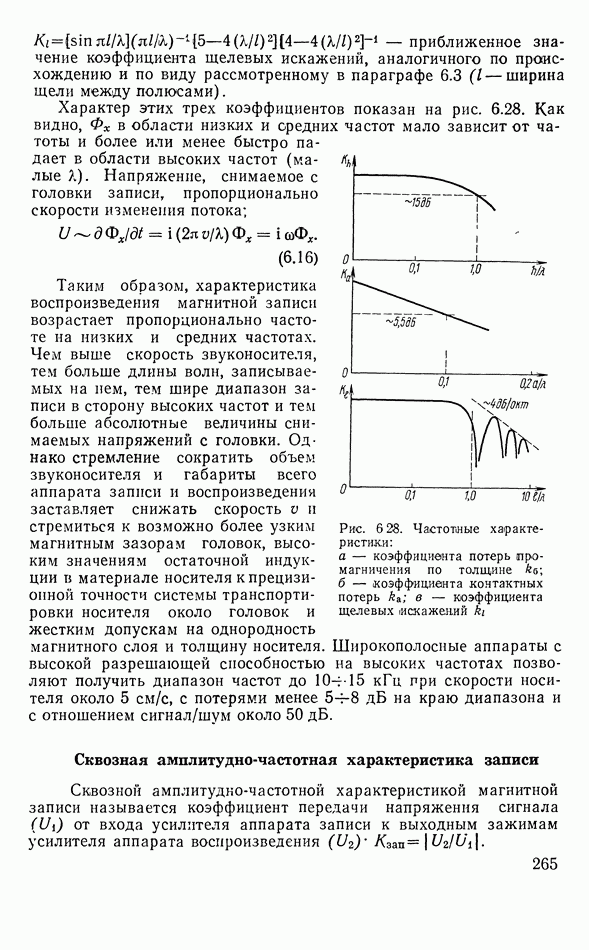
- Головки записи и воспроизведения
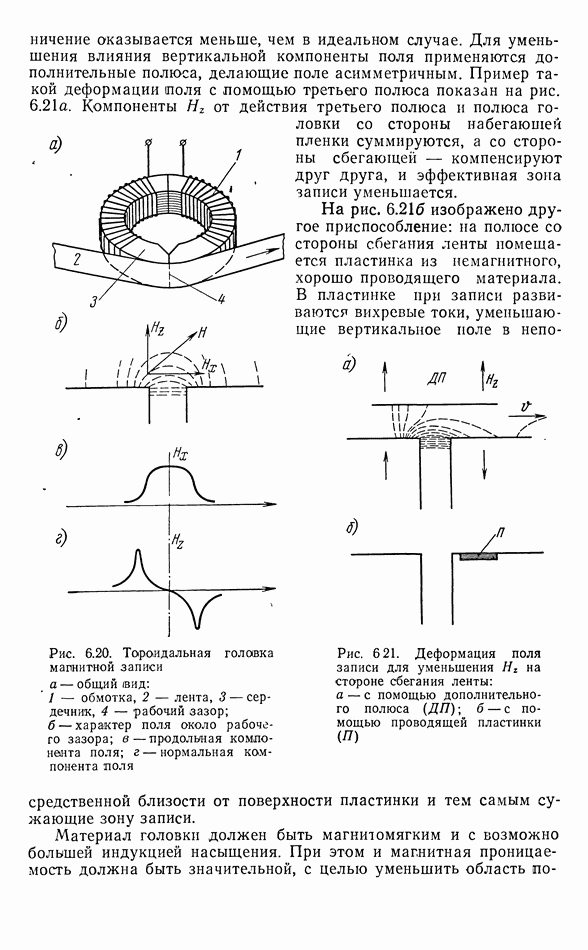
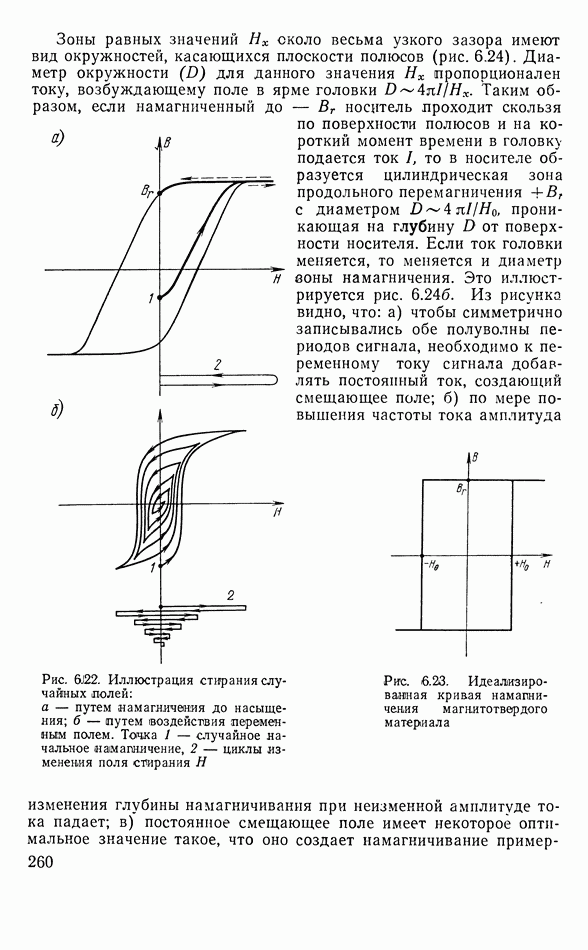
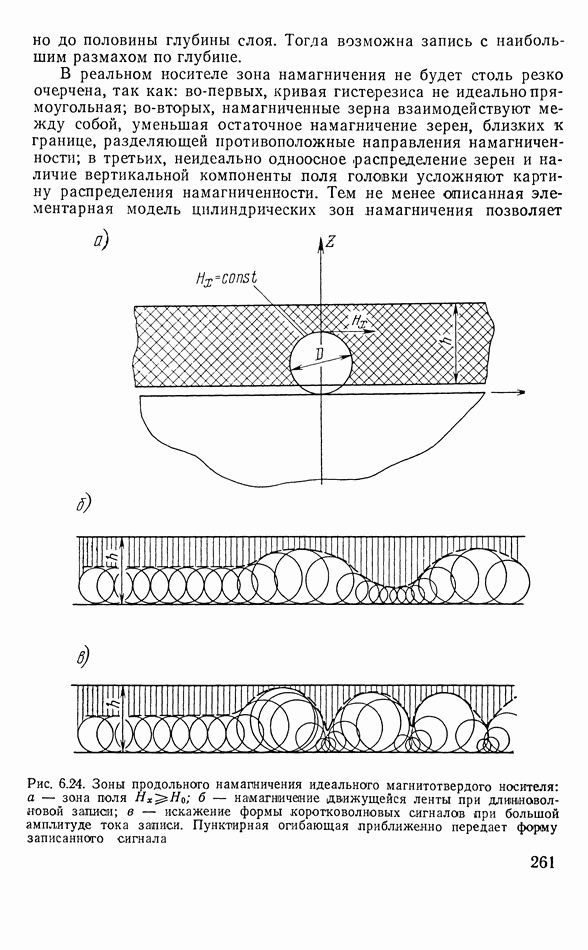
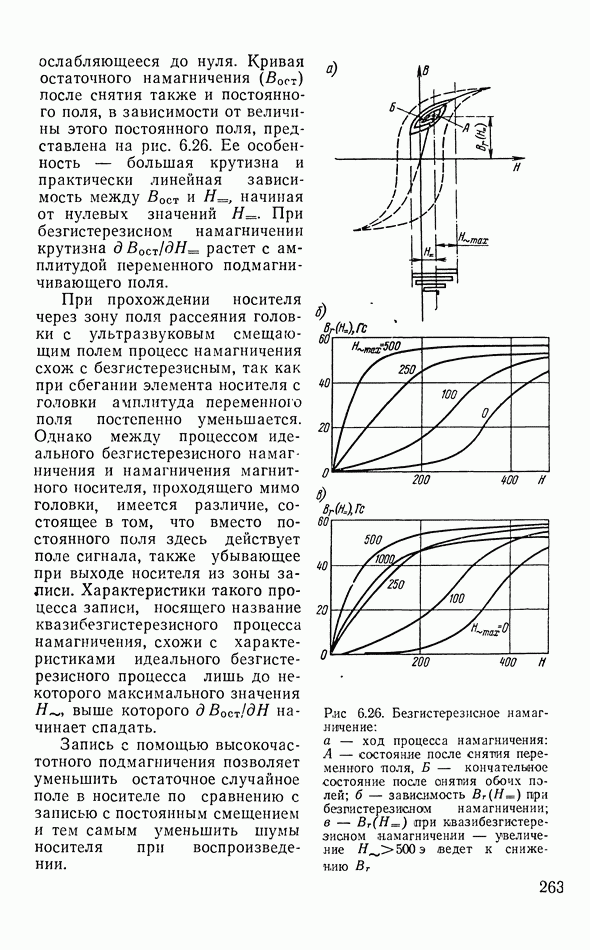
- Процесс намагничения магнитной ленты полем головки
- Воспроизведение записи
- Сквозная амплитудно-частотная характеристика записи
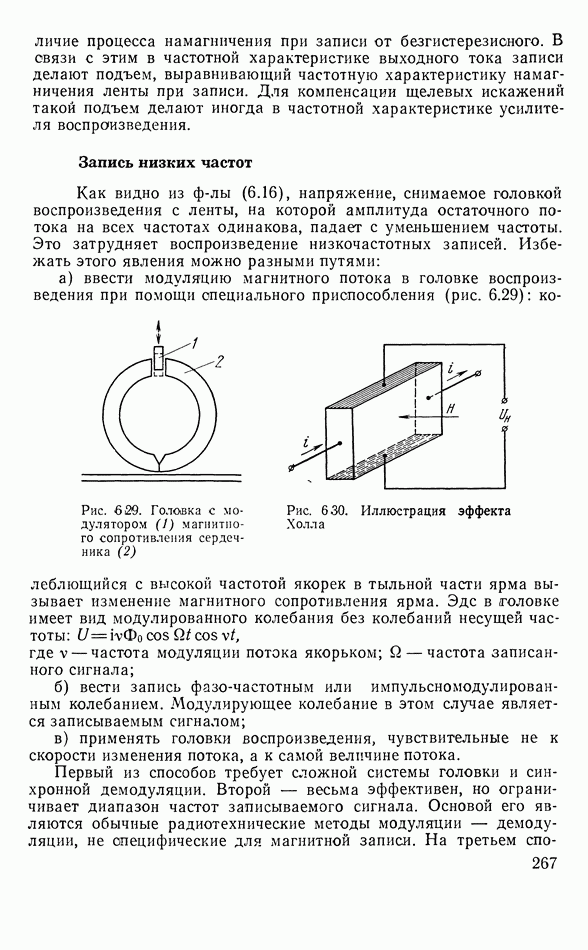
- Запись низких частот
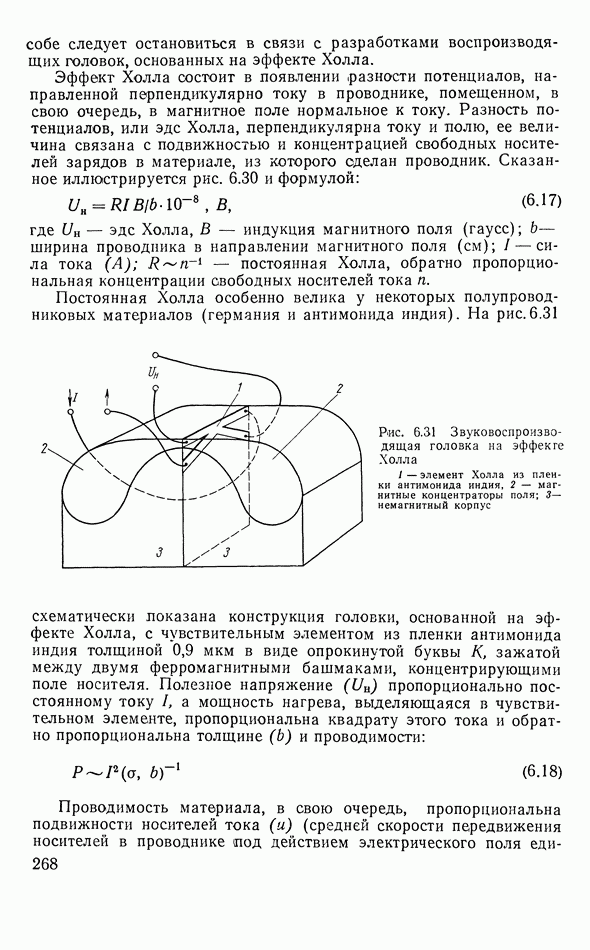
- Плавающие головки
- Точность механизма транспортировки звуконосителя
- Список литературы